Function of metabolic and organelle networks in crowded and organized media

(Macro)molecular crowding and the ability of the ubiquitous cytoskeleton to dynamically polymerize–depolymerize are prevalent cytoplasmic conditions in prokaryotic and eukaryotic cells. Protein interactions, enzymatic or signaling reactions - single, sequential or in complexes - whole metabolic pathways and organelles can be affected by crowding, the type and polymeric status of cytoskeletal proteins (e.g., tubulin, actin), and their imparted organization. The self-organizing capability of the cytoskeleton can orchestrate metabolic fluxes through entire pathways while its fractal organization can frame the scaling of activities in several levels of organization. The intracellular environment dynamics (e.g., biochemical reactions) is dominated by the orderly cytoskeleton and the intrinsic randomness of molecular crowding. Existing evidence underscores the inherent capacity of intracellular organization to generate emergent global behavior. Yet unknown is the relative impact on cell function provided by organelle or functional compartmentation based on transient proteins association driven by weak interactions (quinary structures) under specific environmental challenges or functional conditions (e.g., hypoxia, division, differentiation). We propose a qualitative, integrated structural–functional model of cytoplasmic organization based on a modified version of the Sierspinsky–Menger–Mandelbrot sponge, a 3D representation of a percolation cluster, and examine its capacity to accommodate established experimental facts.

It seems to me that cells leave very little to random processes and that they have evolved the capacity to escape much of the chaos of solutions, (…). It appears unlikely that a messy alphabet soup would be used to spell out the elaborate prose of intermediary metabolism.

James S. Clegg, 1984

Introduction

Cells are very far from random mixtures of molecules. The classical experiments of Kempner and Miller (1968) showed that cells are not bags of freely floating enzymes. Using cells from the unicellular eukaryote Euglena as “centrifuge tubes” (Clegg, 1984a), these authors (Kempner and Miller, 1968) could distinguish several layers within cells (that remained viable) after centrifugation. No macromolecules could be detected in the “soluble phase” and many of the main enzymes considered to exist free in solution were instead associated with layers containing organelles (mitochondria, lysosomes, nucleus) and subcellular structures (ribosomes).

Ideas about cytoplasmic organization have a long history that can be traced back to the notion of protoplasm as the substratum of cellular activity (Welch and Clegg, 2010). Early microscopic techniques (reviewed in Aon and Cortassa, 1997, Chapter 6) and the more recent cryoelectron tomography (Medalia et al., 2002) unveiled the overall crowded nature of the cellular cytoplasm populated by complex macromolecular assemblies besides subcellular organelles (Luby-Phelps, 2000; Minton, 2001; Grunewald et al., 2003; Ovádi and Norris, 2013) (see Figure 2A). Studies starting in the twentieth and well into the twenty-first centuries used advanced molecular–cellular biology methods including fluorescence recovery after photobleaching, in conjunction with confocal microscopy and time-resolved anisotropy methods, to establish a decrease in the diffusion coefficients of proteins in the cytoplasm and in the endoplasmic reticulum lumen compared with water (Luby-Phelps, 2000; Verkman, 2002; Rivas et al., 2004). The consequences of these results are very significant for cell function because diffusion of solutes and macromolecules in cellular compartments mediates many physiological processes, including metabolism and signaling events. On the other hand, active transport via motor proteins leads to a significantly higher mobility compared to diffusion processes (Fakhri et al., 2014).

Obtaining information about the molecular properties of proteins in the living cell is becoming an active field of research (Wirth and Gruebele, 2013). Existent and new molecular techniques and methodologies enable monitoring of native protein activity and folding in cells, offering information on concentration, dynamics, location, interactions and protein proximity (Diekmann and Hoischen, 2014; Fakhri et al., 2014).

Enzymatic Reactions in Organized Crowded Media

Supramolecular organization and crowding are two main traits of the intracellular milieu (Aon and Cortassa, 1997; Aon et al., 2001). The cellular cytoplasm contains (macro)molecules: a mixture of molecules of low (e.g., ATP, glutathione, NADH) and higher molecular weight (e.g., proteins, lipids, polysaccharides) and macromolecular arrays (e.g., tubulin and F-actin polymers, glycogen granules), at concentrations such that they occupy a large fraction of its total volume. Such media are “crowded” but no individual (macro)molecular species is present at a high concentration per se (Minton, 1997).

“Background” species concern (macro)molecules that do not interact specifically with either the reactants or products of a particular reaction. Proteins in the crowded cellular environment can stick to each other through non-specific interactions (e.g., electrostatic, hydrophobic). “Background” species can also contribute large steric repulsive forces in crowded environments (Minton, 2000) that may not be observed directly because they do not lead to the formation of complexes (Zhou et al., 2008). The excluded volume effect depends on the size and concentration of molecular crowders and refers to the volume between, e.g., a pair of interacting proteins, that cannot be occupied by a third protein (Wirth and Gruebele, 2013). If the size of a (macro)molecule is comparable to the size of background species, the available volume is considerably smaller (i.e., excluded volume higher) than in the case that the (macro)molecule is relatively tinier. Lower available volume increases the contribution of steric repulsion to reduce entropy and increase free energy (Rivas et al., 2004). If we consider that to maximize the available volume is a way to reduce free energy then (macro)molecular crowding facilitates a decrease in excluded (occupied) volume via, e.g., molecular compaction and association (Minton, 2000, 2001; Ellis, 2001). Another consequence of crowding is that, via decrease of excluded volume, the folded over the unfolded state of a protein or protein complex is favored (Wirth and Gruebele, 2013).

The reaction rate of an enzymatic reaction may be controlled at diffusional (substrate(s), S, access to the enzyme's, E, active site) and/or kinetic (an intrinsic step in the reaction scheme limits the rate) levels. Broadly speaking, diffusional and kinetic control may be assessed through diffusion, percolation or transport of the species S and E involved, and k₂, the rate constant of the enzyme–substrate, ES, complex transformation into product according to the Henri–Michaelis–Menten (HMM) formalism (Segel, 1975).

For conceptual purpose, let us consider a simple reaction converting S into P, that involves one ligand, S, one catalytic site, E, and one enzyme–substrate complex, ES (Aon et al., 2004b):

Diffusion, percolation, transport of S and/or E

$\begin{array}{cc}\to \to \to S+E\underset{k_{-1}}{\overset{k_1}{\leftarrow \to }}ES\stackrel{k_2}{\to }E+P& (1)\end{array}$

k₂, also known as the catalytic rate constant, k_cat, and k₋₁ are monomolecular rate constants whereas k₁ is a bimolecular rate constant. In the derivation of the HMM equation from a quasi–steady-state assumption, the dynamics of the ES complex association–dissociation is considered to be so fast that its concentration can be treated as if it were in steady state. Accordingly, the k₁ step is considered not to be limiting the S → P conversion. Importantly, from experiments performed over the past two decades, single-molecule enzymology has provided insights into how specific enzymes—particularly molecular motors and nucleic acid enzymes—work at the molecular level. These studies confirmed that the HMM mechanism expressed in Equation (1) holds at the single molecule level (Xie, 2013).

In heterogeneous, organized, media the rate of encounter between E and S may be subjected to transport restrictions generated by anomalous diffusion. Protein stickiness will increase the apparent viscosity of the cytoplasm thus decreasing the diffusion coefficient, D, since both (viscosity vs. D) are inversely related (Dix and Verkman, 2008). Anomalous diffusion introduces a time dependence in D, essentially due to the medium heterogeneity (Wirth and Gruebele, 2013) (see below Section Fractal Kinetics in Organized Crowded Media). Both translational and rotational diffusion can be influenced by the excluded volume and the shape of the crowding protein more than other factors such as hydrodynamic or direct interactions (Balbo et al., 2013). Thus, molecular crowding can affect k₁ decreasing enzymatic rates, essentially because as higher the excluded volume by (macro)molecules the higher the rate limitation of the E–S encounter (Homchaudhuri et al., 2006; Pastor et al., 2014). In support of this interpretation, enzymatic reactions occurring in the presence of increasing dextran concentrations exhibited lower V_max and higher K_M, the Michaelis–Menten constant (Pastor et al., 2014). The volume occupied by dextran, independent of its size, had an important role on the initial velocity of the hydrolysis of N-succinyl-L-phenyl-Ala-p-nitroanilide catalyzed by alpha-chymotrypsin (Pastor et al., 2011). The K_M increase could be attributed to a slower diffusion of the protein due to the presence of crowding, whereas the decrease in V_max could be explained by the effect of mixed inhibition by product, which is enhanced in crowded media (Pastor et al., 2014). These results also underscore the relevant role of enzyme size in the initial velocity of reactions occurring in dextran crowded media. When enzymes are small the reaction's initial velocity mainly depends on the excluded volume. However, for large enzymes, the initial velocity of the reaction is also affected by the size of obstacles present in the environment.

Modeling and experimental work (Kim and Yethiraj, 2009; Pastor et al., 2014) also supports the idea that macromolecular crowding can contribute significantly to changes in enzymatic reactions (Vasilescu et al., 2013). To simulate rapid metabolite transfer between the enzymatic components of the phosphotransferase system (PTS), macromolecular crowding had to be assumed both to increase the association rate constants and to decrease the dissociation rate constants of the PTS complexes (Rohwer et al., 1998). However, crowding was not necessary to simulate yeast glycolysis suggesting that in this eukaryote it does not affect the glycolytic pathway (referred in Rivas et al., 2004). Cortassa and colleagues have also shown that, at least for two glycolytic enzyme couples, the effects of tubulin cytoskeleton proteins was specific and independent from crowding (Cortassa et al., 1994).

Very recent studies using carbon nanotubes for intracellular tracking of kinesin-1 motility highlight stirring dynamics as another important mode of active intracellular transport. Recorded kinesin-1 motility in COS-7 cells over five orders of magnitude in time (Fakhri et al., 2014) enabled the detection of different dynamic regimes ranging between the extremes of random thermal diffusion and kinesin-driven directed transport propelled by stirring dynamics as a non-equilibrium regime between those extremes.

Weak interactions can mediate transient protein–protein interactions collectively known as “quinary structures,” a term introduced by McConkey (1982) to define a fifth level (beyond the quaternary) of inherently transient protein structural organization. Thermodynamically, the transience of a quinary structure is based on the low stability of the molecular interaction as well as the low energetic barrier between molecular states (Wirth and Gruebele, 2013). Quinary structure has been implicated in a number of cellular processes from metabolism [e.g., the metabolon (Srere, 1987), the protein synthesis pathway (Dang et al., 1985)] to cell signaling (Li et al., 2012). Its inherent transience facilitates dynamic spatial organization of macromolecules in the cytoplasm via loose groupings of, e.g., proteins, when they are working together, but not otherwise (Wirth and Gruebele, 2013).

Overall, (macro)molecular crowding can drive molecular associations in the cytoplasm, and via modulation of the available volume or transient quinary structures influence the kinetics of biochemical reactions.

Cytoskeleton Organization and Metabolic Fluxes

The intracellular environment is not only highly crowded but exhibits a high degree of dynamic organization governed by the principles of self-organization, as they apply to thermodynamically open non-equilibrium systems such as cells (Nicolis and Prigogine, 1977; Aon and Cortassa, 1997; de la Fuente, 2013). By exchanging energy, matter or information with their environment cells or tissues can exhibit emergence that is they self-organize their internal structure and dynamics with novel and sometimes surprising macroscopic properties. For example, the ubiquitous cytoskeletal protein network (actin or tubulin) behaves as a non-linear dissipative system, i.e., it consumes adenine nucleotides to polymerize, with the ability to self-organize, e.g., oscillate (Mandelkow et al., 1989; Mandelkow and Mandelkow, 1992; Tabony and Job, 1992) or alternate in a bistable manner (Aon et al., 1996b; Aon and Cortassa, 1997) between polymerized and depolymerized states. Structurally, the cytoskeletal network exhibits fractal properties (Mandelbrot, 1982; Feder, 1988), i.e., spatially organized in a self-similar manner thus exhibiting an alike form when observed at different degrees of magnification (Rabouille et al., 1992; Aon and Cortassa, 1994; Losa and Nonnenmacher, 1996).

The highly dynamic polymer composite of the cellular cytoplasm is dominated by protein polymers, e.g., microtubules, F-actin and intermediate filaments. In axons in the spinal cord the interaction between neurofilaments and F-actin results in a gel with particular viscoelastic properties (Leterrier et al., 1996). The nucleotide triphosphate hydrolysis-driven polymerization–depolymerization dynamics of cytoskeletal proteins is reciprocally influencing and being influenced by the myriad of reactions involved in intracellular transport (e.g., motors), metabolism, cell locomotion, and muscle contraction among other functions. For example, microtubule tracks are embedded in the viscoelastic actin cytoskeleton, which in turn fluctuates as a result of stresses generated by cytoplasmic myosins; myosin locally contracts the actin network with an attachment time of several seconds, followed by sudden release (Fakhri et al., 2014).

Cytoskeleton organization is also influenced by cytoplasmic molecular crowding because it favors protein interactions that may form modular complexes (Spirin and Mirny, 2003); some of these molecular complexes constitute stable or transient multienzyme associations (metabolon) (Srere, 1987) capable of metabolic channeling (Welch, 1977; Ovádi and Srere, 2000). In metabolic channels, reactions are facilitated by product–substrate transfer between closely associated enzymes (Ovádi and Srere, 2000).

Microtubules, actin microfilaments and intermediate filaments represent an enormous protein surface in the cell with an estimated area of 3000 μm² for a typical mammalian cell in culture (Luby-Phelps, 2000). Thus, the cytoskeleton provides an interface for binding a variety of proteins and enzymes. The binding affinity depends on several factors, including phosphorylation status (Luther and Lee, 1986; Roberts and Somero, 1987; Pedrotti et al., 1996), the presence of other proteins, e.g., Microtubule Associated Proteins (MAPs) (Cortassa et al., 1994; Aon and Cortassa, 1997), or enzymatic activity (Cortassa and Aon, 1994; Vertessy et al., 1997; Cassimeris et al., 2012). Protein binding also affects microtubule and enzyme dynamics (Aon et al., 2001; Ovádi and Norris, 2013; Olah et al., 2015). The enhancement of metabolic flux depends upon several factors: (i) the presence for some enzymatic reactions of MAPs apart from tubulin; (ii) the concentration of microtubular protein (MTP); and (iii) the polymeric status (Cortassa et al., 1994). For example, an increase in flux through pyruvate kinase coupled to lactate dehydrogenase was elicited by MTP in a particular concentration range (Cortassa et al., 1994; Aon et al., 1996a) (Figures 1A–C; see figure legend for details). Paclitaxel and nocodazole, two drugs affecting microtubule organization and dynamics in opposite ways, were able to alter the secretion of proteolytic enzymes associated with invasion and metastasis of tumor cells (Alonso et al., 1999). While paclitaxel promotes microtubules polymerization, nocodazole elicits de-polymerization and as such they enhanced or reduced, respectively, the secretion of the urokinase-type plasminogen activator and the matrix metalloproteinase 9 to the culture medium in F3II mammary-carcinoma cells (Alonso et al., 1999).

FIGURE 1

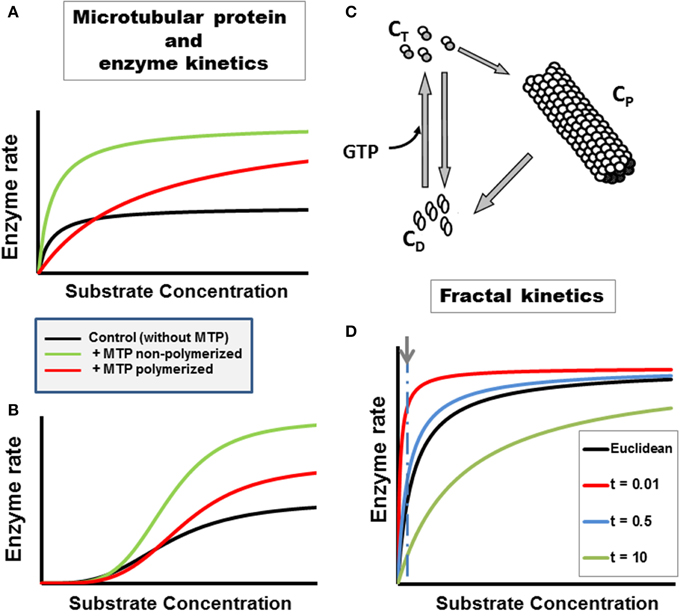
Figure 1. Enzyme kinetics in heterogeneous, organized fractal medium. The concentration and polymeric status of the cytoskeleton components tubulin and microtubule associated proteins, i.e., microtubular protein (MTP), can modulate metabolic fluxes and the kinetics of enzymatic reactions through various mechanisms (Aon and Cortassa, 1997). Examples with two enzymatic couples, glucose 6 phosphate dehydrogenase coupled to hexokinase (G6PDH/HK, A):

$\begin{array}{l}\text{ Glucose}+\text{ATP}\stackrel{\text{HK}}{\to }\text{Glucose}6\text{P}+\text{ADP}\hfill \\ \text{Glucose}6\text{P}+\text{NADP}\stackrel{\text{G6PDH}}{\to }6\text{phospho-gluconate}+\text{NADPH}\hfill \end{array}$

or pyruvate kinase coupled to lactate dehydrogenase (PK/LDH, B):

$\begin{array}{l}\text{Phosphoenolpyruvate}+\text{ADP}\stackrel{\text{PK}}{\to }\text{Pyruvate}+\text{ATP}\hfill \\ \text{Pyruvate}+\text{NADH}\stackrel{\text{LDH}}{\to }\text{Lactate}+{\text{NAD}}^{+}\hfill \end{array}$

Microtubular protein (MTP) in the flux-stimulatory range (1 mg/ml) (Cortassa et al., 1994) was added to the assay medium containing either G6PDH/HK (A) or PK/LDH (B). The substrate concentration of the limiting enzyme, NADP or phosphoenolpyruvate (PEP) for HK/GGPDH or PK/LDH couples, respectively, was varied. The presence of polymerized or non-polymerized brain MTP elicited changes in kinetic parameters: (A) In the presence of polymerized MTP, G6PDH exhibited an eight-fold increase in the K_M for NADP and a two-fold increase in V_max with respect to the control without MTP; non-polymerized MTP only induced a two-fold increase in V_max without changing the K_M. (B) In the presence of polymerized brain MTP, PK exhibited an increase in cooperativity and in V_max with respect to controls as a function of PEP whereas non-polymerized MTP induced an even higher increase in cooperativity and V_max. (C) The cycle of assembly–disassembly of MTP. In this cartoon, the cycle of polymerization–depolymerization of MTP assumes that tubulin may exist in one of three forms: polymerized (C_P), non-polymerized bound to GTP (C_T) or bound to GDP (C_D). A model of the MTP cycle and its effects on PK kinetics is presented in Aon and Cortassa (1997). (D) Michaelis–Menten kinetics in fractal medium. The dependence of the initial rate of a canonical enzymatically-catalyzed reaction as a function of its substrate is displayed. The h parameter, reflecting the characteristics of the medium, e.g., obstacle density, and the time-dependence of kinetic constants was calculated as described in Aon et al. (2004b) (see also Section Fractal Kinetics in Organized Crowded Media). The time points, t, at which the simulations were performed are those indicated in the symbol legend (in min). For simulating reactions occurring in Euclidean space, the parameter values were identical to those of fractal medium except that the rate constants were time-independent (see Aon et al., 2004b for calculation details). At short times the reaction rate becomes much larger, at low S levels, in fractal than in Euclidean medium (indicated by arrow and dashed line). As time passes the reaction rate becomes, transiently, slower in fractal than in Euclidean space; the maximal rate being identical in both cases though achieved at larger S in fractal medium.

Ultrasensitivity is a more sensitive response than the one expected from the classical hyperbola of Michaelis–Menten kinetics (Goldbeter and Koshland, 1982; Koshland et al., 1982). The “normal” hyperbolic response requires an 81-fold change in ligand (e.g., substrate, effector) to increase the reaction rate from 10 to 90% of the maximal velocity. Thus, ultrasensitive systems are those that need less than 81-fold change whereas sub-sensitive ones demand more. Depending on their polymeric status, cytoskeletal protein dynamics (actin, MTP) can modulate the ultrasensitive response of enzymatic systems (Aon et al., 2001). This modulation can be mediated by the cytoskeleton in the cell stress response involving changes in volume due to osmotic regulation (Busch et al., 1994; Haussinger et al., 1994a,b; Aon et al., 2000b).

More recent studies show that the heterodimer tubulin composed of α and β subunits can selectively modulate the mitochondrial outer membrane (MOM) permeability via the voltage-dependent anion channel (VDAC) (Rohwer et al., 1998; Rostovtseva and Bezrukov, 2012) thus having an impact on cellular and mitochondrial energetics (Guzun et al., 2011; Gonzalez-Granillo et al., 2012; Rostovtseva and Bezrukov, 2012). Tubulin in the nM range can influence the voltage sensitivity of VDAC reconstituted into planar phospholipid membranes, and ADP availability to the adenine nucleotide translocator in isolated mitochondria (Rostovtseva et al., 2008). Indeed, VDAC (or porin) is the most abundant protein in the MOM and is primarily involved in the ATP/ADP exchange between the cytoplasm and mitochondria (Rostovtseva and Colombini, 1997; Colombini, 2004).

Fractal Kinetics in Organized Crowded Media

The impact of self-organized cytoskeletal proteins in fractal forms upon the dynamics of cellular biochemistry started to be explored more than 20 years ago. Studying chemical reactions in heterogeneous media, Kopelman (1988) made two crucial observations: (i) reactions proceed faster in disconnected (shredded) topologies than in connected ones, and (ii) the rate constants become time-dependent, scaling with time as t^−h; the h parameter reflects the characteristics of the medium, e.g., obstacle density, through the fractal dimension, and provides a link with the kinetic rate constant (Kang and Redner, 1984; Dewey, 1995; Aon et al., 2004b). In a medium like the cellular cytoplasm, molecular diffusion becomes anomalous and diffusion coefficients time-dependent due to heterogeneity given not only by (macro)molecular crowding but also by rheological changes impinging on viscosity (Forgacs and Newman, 1994; Aon and Cortassa, 1997).

Aon and Cortassa (1994) and Forgacs (1995) proposed that the cellular cytoplasm is organized as a percolation cluster. It was further conjectured that as a highly shredded object, a percolation cluster may, in principle, bestow more catalytic power to cytoplasmic enzymes. Indeed, medium organization in percolation clusters may enhance reaction rates at short times (Aon et al., 2004b; Hiroi et al., 2011) (Figure 1D). The kinetics of biochemical reactions in the cytoplasm depend on (macro)molecular crowding given by the cytoskeleton organization. Hiroi et al. (2011) showed that changing the reaction rate may be possible when the degree of intracellular macromolecular crowding is modified by experimentally manipulating the structure of the cytoskeleton. Cytoskeleton disruption with cytochalasin B and colchicine changed the anomalous diffusion parameter exhibited by enzymes and substrates/products in the cellular cytoplasm. Since the total protein concentration was maintained this suggested that not merely the concentration of intracellular proteins, but also their physiological organization profoundly affects diffusion of free molecules in a cell (Hiroi et al., 2011).

In cellular biochemistry, the fractal approach has been directed to understanding the organization and behavior of (macro)molecules in cells (Rabouille et al., 1992; Savageau, 1995; Liebovitch and Todorov, 1996; Aon et al., 2004b; Schnell and Turner, 2004; Aon and Cortassa, 2009). The approach to fractal kinetics in cells differs between authors. The dependence of the rate constant upon h has been modeled according to a fractal (Zipf–Mandelbrot) distribution (Schnell and Turner, 2004); assuming HMM kinetics in 2D lattices using Monte Carlo simulations with time-dependent rate constant (Berry, 2002), or in terms of the dependence of the parameter h on the spectral dimension, Ds, for HMM or sigmoidal kinetics (Aon et al., 2004b; Hiroi et al., 2011). Main findings show that: (i) spatial segregation of substrate and products increase with the degree of obstruction in the medium making stronger the deviation of the rate constants at longer times and, consequently, the fractal kinetic description as compared with the classical approach (Berry, 2002; Schnell and Turner, 2004); (ii) at short times the reaction rate becomes much larger, at low substrate levels, in fractal than in Euclidean space (Figure 1D); this behavior depends on the time-dependence of the K_M, or an increase in cooperativity and reaction amplification in allosteric kinetics (Aon et al., 2004b). The quickly relaxing molecular mechanisms, when cells are challenged by sudden changes in environmental conditions, would provide fast and precise adaptation. Indeed, fast responses can lead to slow exhaustion processes preventing lack of substrates, effectors for reactions locally, as found in fractal media organized like percolation clusters (Hiroi et al., 2011).

Computational Modeling of Cytoplasmic Structure–Function

Interactivity in complex spatiotemporally organized systems like the cellular cytoplasm is fundamental to their counterintuitive behavior and one of the main reasons justifying the need of mathematical modeling for their study. What we seek to understand is how function is coordinated in a cell that exhibits spatially distributed heterogeneous and compartmentalized subsystems with simultaneously unfolding dynamics (Aon, 2013). Factually, (macro)molecular crowding and cytoskeleton organization (i.e., structural) are able to influence the dynamics of biochemical reactions (i.e., functional), yet how does the structural–functional coupling unfolds in physiologically meaningful spatiotemporal patterns is far from clear. One reason is that computational modeling has been mainly concerned with structural or biochemical networks but not with their integrated function. However, forced by computational burden, modeling of cytoplasmic structure–function faces some daunting challenges, beyond the complexity of the task, that demand choices between atomistic molecular-dynamic simulations (McGuffee and Elcock, 2010; Mereghetti and Wade, 2012) and lower resolution coarse-grained models (Moore et al., 2014). Mesoscale models represent a reasonable trade-off between higher simplicity (e.g., treating macromolecules as single interacting centers) while amenable to include finer biopolymer representations to address mustiscale problems of diffusion and interaction, as recently reported for the Escherichia coli cytoplasm (Trovato and Tozzini, 2014). Modeling can help decide quantitative issues such as whether moderate attraction between proteins and crowding molecules, on the order of 1 kJ/mol, can counteract the excluded volume effect (Rosen et al., 2011) or which macromolecule sizes will experience the strongest attraction and anomalous diffusion (Trovato and Tozzini, 2014).

Some insight into how structural dynamics can affect biochemical function comes from computational modeling of MTP dynamics coupled to the glycolytic pathway and its branches to the Krebs cycle, ethanolic fermentation, and the pentose phosphate (PP) pathways. This study showed that MTP dynamics can coordinately increase or decrease the flux through glycolysis, and that depending on the degree of MTP polymerization a negative control may be exerted by the PP pathway on glycolysis (Aon and Cortassa, 2002). These results may be relevant for cancer therapy because the PP pathway is critical for tumor cells to generate intermediates for nucleic acid synthesis and provide NADPH required both for the synthesis of fatty acids and cell survival under oxidative stress (Patra and Hay, 2014).

A key for progress in this complicated research field will be to adopt an experimental–modeling synergy involving iteration of the loop: simulation–validation and prediction–experimentation (Cortassa and Aon, 2013).

Emergence in Subcellular Organelle Networks

Cytoplasmic organization comprises not only biochemical reactions but also organelles representing membrane-bound subcellular compartments. Depending on their specific function and situation, subcellular compartments such as mitochondria can play substantial roles in physiology as well as pathophysiology. In heart muscle, for example, mitochondria appear as a network in the form of a regular lattice, spanning the whole myocardial tissue like a power grid (Slodzinski et al., 2008; Aon et al., 2009). Certainly, other cytoplasmic organelles can be subject to the principles of self-organization such as the nucleus and the Golgi complex (Misteli, 2001) as well as the genome itself (Misteli, 2009), but this possibility needs experimental support.

Self-organized collective dynamics in cardiac myocytes arise from synergistically coupled subcellular networks of, e.g., mitochondria (Aon et al., 2006b) or Ca²⁺ release units, the latter constituted by four compartments (sarcoplasmic and junctional reticulum, myoplasmic and dyadic space) (Nivala et al., 2012). Emergence in these networks occurs through signaling via second messengers such as reactive oxygen species (ROS) or Ca²⁺. In addition to the normal excitation–contraction–metabolism coupling, a rich dynamic spectrum results, including oscillations, electrical or chemical waves, action potential duration alternans, early or delayed after depolarizations among others (Aon et al., 2004a; Zhou et al., 2010; Nivala et al., 2012; Qu, 2013; Zorov et al., 2014).

In heart mitochondria it was found that the transition from physiological to pathophysiological behavior happens as an emergent phenomenon of the cardiac mitochondrial network, with all the characteristics of systems at critical state (Aon et al., 2006b). This transition occurs at the percolation threshold as determined by applying percolation theory (Aon et al., 2004a). Percolation describes how local neighbor–neighbor interactions among elements in a lattice can scale to produce a macroscopic response spanning from one to the other end of a mitochondrial array (Stauffer and Aharony, 1994). Such a “spanning cluster” forms when there is a critical density of elements close to the threshold for a transition (the percolation threshold). A mitochondrial percolation cluster attains criticality at a certain threshold level of ROS (Aon et al., 2004a). The transition is self-organized, occurs with all the traits of universality—that is, with similar critical exponents as predicted by percolation theory (Schroeder, 1991; Stauffer and Aharony, 1994; Sornette, 2000), and the mitochondrial cluster exhibits fractal organization (Aon et al., 2004b). The ensuing collective oscillations—which involve at least 60% of the mitochondrial network—are synchronized by ROS via ROS-induced ROS release (Zorov et al., 2000, 2014; Aon et al., 2003; Brady et al., 2006) through a diffusion-based mechanism (Zhou et al., 2010).

In yeast, spontaneous oscillations of Saccharomyces cerevisiae mitochondrial redox states and membrane potential occur within individual yeasts (Aon et al., 2007b), and synchrony of yeast population indicates the operation of an efficient system of cell–cell interaction to produce concerted metabolic multicellular behavior (Murray et al., 2003, 2013; Lloyd and Murray, 2006, 2007; Roussel and Lloyd, 2007).

Toward an Integrated Structural–Functional Model of Cytoplasmic Organization

A model compatible with the 3D visualization of the cellular cytoplasmic organization as a percolation cluster (Aon and Cortassa, 1994; Forgacs, 1995) as suggested by its crowded-organized nature (Medalia et al., 2002) (Figure 2A) is the Sierpinsky–Menger–Mandelbrot sponge (Mandelbrot, 1982; Raicu and Popescu, 2008) (Figure 2B) or a modified version introduced by (Welch and Clegg, 2010) to account also for functional aspects given by “confined regions, ranging from organelles to protein complexes…, responsible for the execution of localized metabolic processes…” (Figure 2C).

FIGURE 2

Figure 2. A fractal sponge-like model of cytoplasmic organization. (A) Visualization of actin network, membranes, and cytoplasmic macromolecular complexes from electron cryotomography. The pseudo color representation corresponds to actin filaments (red); other macromolecular complexes, mostly ribosomes (green), and membranes (blue) (modified from Medalia et al., 2002). (B) The Sierpinsky carpet (or gasket) arises from the recursive invariant procedure consisting in repeatedly removing an inverted equilateral triangle from the middle of an initial equilateral triangle (Mandelbrot, 1982). The Sierpinski–Menger–Mandelbrot sponge is an extension of the Sierpinski's carpet to the three-dimensional Euclidian space (Mandelbrot, 1982) (see also Raicu and Popescu, 2008). This fractal starts from a single cube with an iterative invariant pattern consisting in the removal of a middle cube. The fractal dimension of this structure is 2.727 and if the magnification and removal of the middle cubes continues for n → ∞, it is found that the structure becomes a surface packed into a three dimensional Euclidian space (Raicu and Popescu, 2008), or as graphically put by Welch and Clegg (2010): “a fractal geometric form whose progressive ‘fractalization’ results in the surface area increasing to (the theoretical limit of) infinity as the volume shrinks to zero” (Image created by Moses Boone; see http://www.mathworks.com/matlabcentral/fileexchange/3524-sierpinski-sponge). This is what we call the Sierpinsky–Menger–Mandelbrot sponge, or (C) the version including idealized spheres designated to account for localized metabolic microenvironments (indicated by a double white arrow on the top left), as first proposed by Welch and Clegg (2010) based on a copyrighted image created by Roman Maeder (see http://www.mathconsult.ch/showroom/pubs/MathProg/htmls/p2-16.htm) (modified from Welch and Clegg, 2010).

The modified Sierpinsky–Menger–Mandelbrot sponge captures several structural–functional features discussed in this review: (1) the cytoplasmic structure represents a surface with the appearance of a 3D object, because the surface area increases as the volume shrinks. It is straightforward to imagine that the surface area will be modulated by the degree of polymerization of the cytoskeleton in turn influenced by (macro)molecular crowding. (2) It embodies the orderly cytoskeletal organization and the intrinsic randomness of (macro)molecular crowding. These two conditions can create zones of heterogeneity via exclusion (occupied) volume based on attracting (e.g., electrostatic, hydrophobic) or repulsing (e.g., steric) forces. Locally, these regions possess levels of free energy that modulate molecular association, compaction and folding/unfolding of proteins (Zhou et al., 2008; Wirth and Gruebele, 2013). (3) Is a good model for the percolation of fluids through the cytoplasm, including “confined regions” or locally separate clusters of biochemical activity that may extend to other cytoplasmic regions depending on the concentration and status of e.g., enzymatic or organelles' physiology. These localized clusters determine a certain distance with respect to the percolation threshold where local activities become global thus providing a principle of coordinated functional organization (Aon et al., 2004a; Nivala et al., 2012). (4) Enzymes or enzymatic complexes through their binding to the cytoskeleton, and substrates/effectors/messengers percolating through the “sponge” would determine reaction rates (Figure 1) defining local clusters of activity that result in different product concentrations and gradients. (5) It accommodates the existence of “quinary” structures (McConkey, 1982) that drive transiently and loosely grouped ensemble of proteins working together in a dynamic and spatially organized way, e.g., a metabolon or supramolecularly organized enzymatic complex (Srere, 1987), thus explaining compartmentalization in cytoplasmic regions that are not bounded by membranes (Wirth and Gruebele, 2013) (Figure 2C). (6) The sponge-like model of the cytoplasm is sound from the status of intracellular water (Clegg, 1984a,b) and rheological standpoints. The ground plan of living cells has been pictured as a reversible, non-covalent gel network (Luby-Phelps et al., 1986; Rabouille et al., 1990) that can be subjected to sol–gel transitions. A colloidal sol state has liquid properties with well-defined viscosity whereas in a gel viscosity becomes practically infinite with the percolation threshold, given by the concentration of polymers in solution, as the critical parameter at which the sol–gel transitions happen (Forgacs and Newman, 1994).

With a model at hand, we can now put it to test and ask questions and/or verify certain predictions. For example, can confined cytoplasmic clusters of biochemical activity be experimentally demonstrated? Could the same enzyme(s), enzymatic complex or organelle behave differently according to local cytoplasmic conditions, e.g., higher presence of F-actin (G-actin) with respect to microtubules (tubulin)? Can clusters of biochemical activity based on quinary structures be demonstrated, and are these clusters sensitive to the dynamic intracellular environment? Which intracellular conditions define percolation thresholds, and can we show local activity become globally spread? Do these conditions change with cellular stages of growth, division (e.g., G1, S phases) or differentiation? Is the status of cellular cytoplasmic organization different in differentiated with respect to pluripotent stem cells? How, and to what extent, does the intracellular dynamic field of interrelating polymeric forces play out for the dynamics of metabolic and signaling pathways interacting or being influenced by those polymers, or forming supramolecular complexes themselves? All of these are fascinating and relevant questions that now can be addressed experimentally with emerging new methodologies and a unified structural–functional theoretical framework for cytoplasmic organization.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alonso, D. F., Farina, H. G., Arregui, C., Aon, M. A., and Gomez, D. E. (1999). Modulation of urokinase-type plasminogen activator and metalloproteinase activities in cultured mouse mammary-carcinoma cells: enhancement by paclitaxel and inhibition by nocodazole. Int. J. Cancer 83, 242–246.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Aon, M. A. (2013). “Complex systems biology of networks: the riddle and the challenge,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 19–35.

Google Scholar

Aon, M. A., Caceres, A., and Cortassa, S. (1996a). Heterogeneous distribution and organization of cytoskeletal proteins drive differential modulation of metabolic fluxes. J. Cell. Biochem. 60, 271–278.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Aon, M. A., and Cortassa, S. (1994). On the fractal nature of cytoplasm. FEBS Lett. 344, 1–4. doi: 10.1016/0014-5793(94)00321-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., and Cortassa, S. (1997). Dynamic Biological Organization. Fundamentals as Applied to Cellular Systems. London: Chapman and Hall. doi: 10.1007/978-94-011-5828-2

CrossRef Full Text | Google Scholar

Aon, M. A., and Cortassa, S. (2002). Coherent and robust modulation of a metabolic network by cytoskeletal organization and dynamics. Biophys. Chem. 97, 213–231. doi: 10.1016/S0301-4622(02)00056-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., and Cortassa, S. (2009). “Chaotic dynamics, noise and fractal space in biochemistry,” in Encyclopedia of Complexity and Systems Science, ed R. Meyers (New York, NY: Springer), 476–489.

Aon, M. A., Cortassa, S., Akar, F. G., Brown, D. A., Zhou, L., and O'Rourke, B. (2009). From mitochondrial dynamics to arrhythmias. Int. J. Biochem. Cell Biol. 41, 1940–1948. doi: 10.1016/j.biocel.2009.02.016

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Cortassa, S., and Caceres, A. (1996b). “Models of cytoplasmic structure and function,” in Computation in Cellular and Molecular Biological Systems, eds R. Cuthbertson, R. Holcombe, and R. Paton (London: World Scientific), 195–207.

Aon, M. A., Cortassa, S., Gomez Casati, D. F., and Iglesias, A. A. (2000b). Effects of stress on cellular infrastructure and metabolic organization in plant cells. Int. Rev. Cytol. 194, 239–273. doi: 10.1016/S0074-7696(08)62398-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Cortassa, S., Lemar, K. M., Hayes, A. J., and Lloyd, D. (2007b). Single and cell population respiratory oscillations in yeast: a 2-photon scanning laser microscopy study. FEBS Lett. 581, 8–14. doi: 10.1016/j.febslet.2006.11.068

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Cortassa, S., Marban, E., and O'Rourke, B. (2003). Synchronized whole cell oscillations in mitochondrial metabolism triggered by a local release of reactive oxygen species in cardiac myocytes. J. Biol. Chem. 278, 44735–44744. doi: 10.1074/jbc.M302673200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Cortassa, S., and O'Rourke, B. (2004a). Percolation and criticality in a mitochondrial network. Proc. Natl. Acad. Sci. U.S.A. 101, 4447–4452. doi: 10.1073/pnas.0307156101

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Cortassa, S., and O'Rourke, B. (2006b). The fundamental organization of cardiac mitochondria as a network of coupled oscillators. Biophys. J. 91, 4317–4327. doi: 10.1529/biophysj.106.087817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., Gomez-Casati, D. F., Iglesias, A. A., and Cortassa, S. (2001). Ultrasensitivity in (supra)molecularly organized and crowded environments. Cell Biol. Int. 25, 1091–1099. doi: 10.1006/cbir.2001.0804

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Aon, M. A., O'Rourke, B., and Cortassa, S. (2004b). The fractal architecture of cytoplasmic organization: scaling, kinetics and emergence in metabolic networks. Mol. Cell. Biochem. 256–257, 169–184. doi: 10.1023/B:MCBI.0000009867.54552.09

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Balbo, J., Mereghetti, P., Herten, D. P., and Wade, R. C. (2013). The shape of protein crowders is a major determinant of protein diffusion. Biophys. J. 104, 1576–1584. doi: 10.1016/j.bpj.2013.02.041

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Berry, H. (2002). Monte carlo simulations of enzyme reactions in two dimensions: fractal kinetics and spatial segregation. Biophys. J. 83, 1891–1901. doi: 10.1016/S0006-3495(02)73953-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Brady, N. R., Hamacher-Brady, A., Westerhoff, H. V., and Gottlieb, R. A. (2006). A wave of reactive oxygen species (ROS)-induced ROS release in a sea of excitable mitochondria. Antioxid. Redox Signal. 8, 1651–1665. doi: 10.1089/ars.2006.8.1651

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Busch, G. L., Schreiber, R., Dartsch, P. C., Volkl, H., Vom Dahl, S., Haussinger, D., et al. (1994). Involvement of microtubules in the link between cell volume and pH of acidic cellular compartments in rat and human hepatocytes. Proc. Natl. Acad. Sci. U.S.A. 91, 9165–9169. doi: 10.1073/pnas.91.19.9165

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cassimeris, L., Silva, V. C., Miller, E., Ton, Q., Molnar, C., and Fong, J. (2012). Fueled by microtubules: does tubulin dimer/polymer partitioning regulate intracellular metabolism? Cytoskeleton (Hoboken). 69, 133–143. doi: 10.1002/cm.21008

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Clegg, J. S. (1984a). Properties and metabolism of the aqueous cytoplasm and its boundaries. Am. J. Physiol. 246, R133–R151.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Clegg, J. S. (1984b). Intracellular water and the cytomatrix: some methods of study and current views. J. Cell Biol. 99, 167s–171s. doi: 10.1083/jcb.99.1.167s

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Colombini, M. (2004). VDAC: the channel at the interface between mitochondria and the cytosol. Mol. Cell. Biochem. 256–257, 107–115. doi: 10.1023/B:MCBI.0000009862.17396.8d

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cortassa, S., and Aon, M. A. (1994). Spatio-temporal regulation of glycolysis and oxidative phosphorylation in vivo in tumor and yeast cells. Cell Biol. Int. 18, 687–713. doi: 10.1006/cbir.1994.1099

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Cortassa, S., and Aon, M. A. (2013). “Dynamics of mitochondrial redox and energy networks: insights from an experimental-computational synergy,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 115–144.

Google Scholar

Cortassa, S., Caceres, A., and Aon, M. A. (1994). Microtubular protein in its polymerized or nonpolymerized states differentially modulates in vitro and intracellular fluxes catalyzed by enzymes of carbon metabolism. J. Cell. Biochem. 55, 120–132. doi: 10.1002/jcb.240550114

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dang, C. V., Ferguson, B., Burke, D. J., Garcia, V., and Yang, D. C. (1985). Interactions of aminoacyl-tRNA synthetases in high-molecular-weight multienzyme complexes from rat liver. Biochim. Biophys. Acta 829, 319–326. doi: 10.1016/0167-4838(85)90239-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

de la Fuente, I. M. (2013). “Metabolic dissipative structures,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 179–211.

Google Scholar

Dewey, T. G. (1995). Chemically-controlled reaction kinetics on fractals: application to hydrogen exchange in lysozyme. Fractals 3, 251–267. doi: 10.1142/S0218348X95000217

CrossRef Full Text | Google Scholar

Diekmann, S., and Hoischen, C. (2014). Biomolecular dynamics and binding studies in the living cell. Phys. Life Rev. 11, 1–30. doi: 10.1016/j.plrev.2013.11.011

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dix, J. A., and Verkman, A. S. (2008). Crowding effects on diffusion in solutions and cells. Annu. Rev. Biophys. 37, 247–263. doi: 10.1146/annurev.biophys.37.032807.125824

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ellis, R. J. (2001). Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 11, 114–119. doi: 10.1016/S0959-440X(00)00172-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Fakhri, N., Wessel, A. D., Willms, C., Pasquali, M., Klopfenstein, D. R., MacKintosh, F. C., et al. (2014). High-resolution mapping of intracellular fluctuations using carbon nanotubes. Science 344, 1031–1035. doi: 10.1126/science.1250170

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Feder, J. (1988). Fractals. New York, NY: Plenum Press. doi: 10.1007/978-1-4899-2124-6

CrossRef Full Text

Forgacs, G. (1995). On the possible role of cytoskeletal filamentous networks in intracellular signaling: an approach based on percolation. J. Cell Sci. 108(Pt 6), 2131–2143.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Forgacs, G., and Newman, S. A. (1994). Phase transitions, interfaces, and morphogenesis in a network of protein fibers. Int. Rev. Cytol. 150, 139–148. doi: 10.1016/S0074-7696(08)61540-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Goldbeter, A., and Koshland, D. E. Jr. (1982). Sensitivity amplification in biochemical systems. Q. Rev. Biophys. 15, 555–591. doi: 10.1017/S0033583500003449

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gonzalez-Granillo, M., Grichine, A., Guzun, R., Usson, Y., Tepp, K., Chekulayev, V., et al. (2012). Studies of the role of tubulin beta II isotype in regulation of mitochondrial respiration in intracellular energetic units in cardiac cells. J. Mol. Cell. Cardiol. 52, 437–447. doi: 10.1016/j.yjmcc.2011.07.027

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Grunewald, K., Medalia, O., Gross, A., Steven, A. C., and Baumeister, W. (2003). Prospects of electron cryotomography to visualize macromolecular complexes inside cellular compartments: implications of crowding. Biophys. Chem. 100, 577–591. doi: 10.1016/S0301-4622(02)00307-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Guzun, R., Karu-Varikmaa, M., Gonzalez-Granillo, M., Kuznetsov, A. V., Michel, L., Cottet-Rousselle, C., et al. (2011). Mitochondria-cytoskeleton interaction: distribution of beta-tubulins in cardiomyocytes and HL-1 cells. Biochim. Biophys. Acta 1807, 458–469. doi: 10.1016/j.bbabio.2011.01.010

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Haussinger, D., Lang, F., and Gerok, W. (1994a). Regulation of cell function by the cellular hydration state. Am. J. Physiol. 267, E343–E355.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Haussinger, D., Stoll, B., vom Dahl, S., Theodoropoulos, P. A., Markogiannakis, E., Gravanis, A., et al. (1994b). Effect of hepatocyte swelling on microtubule stability and tubulin mRNA levels. Biochem. Cell Biol. 72, 12–19. doi: 10.1139/o94-003

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Hiroi, N., Lu, J., Iba, K., Tabira, A., Yamashita, S., Okada, Y., et al. (2011). Physiological environment induces quick response – slow exhaustion reactions. Front. Physiol. 2:50. doi: 10.3389/fphys.2011.00050

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Homchaudhuri, L., Sarma, N., and Swaminathan, R. (2006). Effect of crowding by dextrans and Ficolls on the rate of alkaline phosphatase-catalyzed hydrolysis: a size-dependent investigation. Biopolymers 83, 477–486. doi: 10.1002/bip.20578

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kang, K., and Redner, S. (1984). Scaling approach for the kinetics of recombination processes. Phys. Rev. Lett. 52, 955–958. doi: 10.1103/PhysRevLett.52.955

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kempner, E. S., and Miller, J. H. (1968). The molecular biology of Euglena gracilis. IV. Cellular stratification by centrifuging. Exp. Cell Res. 51, 141–149. doi: 10.1016/0014-4827(68)90164-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kim, J. S., and Yethiraj, A. (2009). Effect of macromolecular crowding on reaction rates: a computational and theoretical study. Biophys. J. 96, 1333–1340. doi: 10.1016/j.bpj.2008.11.030

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kopelman, R. (1988). Fractal reaction kinetics. Science 241, 1620–1626. doi: 10.1126/science.241.4873.1620

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Koshland, D. E. Jr., Goldbeter, A., and Stock, J. B. (1982). Amplification and adaptation in regulatory and sensory systems. Science 217, 220–225. doi: 10.1126/science.7089556

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Leterrier, J. F., Kas, J., Hartwig, J., Vegners, R., and Janmey, P. A. (1996). Mechanical effects of neurofilament cross-bridges. Modulation by phosphorylation, lipids, and interactions with F-actin. J. Biol. Chem. 271, 15687–15694. doi: 10.1074/jbc.271.26.15687

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Li, P., Banjade, S., Cheng, H. C., Kim, S., Chen, B., Guo, L., et al. (2012). Phase transitions in the assembly of multivalent signalling proteins. Nature 483, 336–340. doi: 10.1038/nature10879

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Liebovitch, L. S., and Todorov, A. T. (1996). Using fractals and nonlinear dynamics to determine the physical properties of ion channel proteins. Crit. Rev. Neurobiol. 10, 169–187. doi: 10.1615/CritRevNeurobiol.v10.i2.20

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lloyd, D., and Murray, D. B. (2006). The temporal architecture of eukaryotic growth. FEBS Lett. 580, 2830–2835. doi: 10.1016/j.febslet.2006.02.066

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lloyd, D., and Murray, D. B. (2007). Redox rhythmicity: clocks at the core of temporal coherence. Bioessays 29, 465–473. doi: 10.1002/bies.20575

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Losa, G. A., and Nonnenmacher, T. F. (1996). Self-similarity and fractal irregularity in pathologic tissues. Mod. Pathol. 9, 174–182.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Luby-Phelps, K. (2000). Cytoarchitecture and physical properties of cytoplasm: volume, viscosity, diffusion, intracellular surface area. Int. Rev. Cytol. 192, 189–221. doi: 10.1016/S0074-7696(08)60527-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Luby-Phelps, K., Taylor, D. L., and Lanni, F. (1986). Probing the structure of cytoplasm. J. Cell Biol. 102, 2015–2022. doi: 10.1083/jcb.102.6.2015

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Luther, M. A., and Lee, J. C. (1986). The role of phosphorylation in the interaction of rabbit muscle phosphofructokinase with F-actin. J. Biol. Chem. 261, 1753–1759.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. New York, NY: W.H. Freeman.

Mandelkow, E., Mandelkow, E. M., Hotani, H., Hess, B., and Muller, S. C. (1989). Spatial patterns from oscillating microtubules. Science 246, 1291–1293. doi: 10.1126/science.2588005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mandelkow, E. M., and Mandelkow, E. (1992). Microtubule oscillations. Cell Motil. Cytoskeleton 22, 235–244. doi: 10.1002/cm.970220403

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

McConkey, E. H. (1982). Molecular evolution, intracellular organization, and the quinary structure of proteins. Proc. Natl. Acad. Sci. U.S.A. 79, 3236–3240. doi: 10.1073/pnas.79.10.3236

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

McGuffee, S. R., and Elcock, A. H. (2010). Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLoS Comput. Biol. 6:e1000694. doi: 10.1371/journal.pcbi.1000694

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Medalia, O., Weber, I., Frangakis, A. S., Nicastro, D., Gerisch, G., and Baumeister, W. (2002). Macromolecular architecture in eukaryotic cells visualized by cryoelectron tomography. Science 298, 1209–1213. doi: 10.1126/science.1076184

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Mereghetti, P., and Wade, R. C. (2012). Atomic detail brownian dynamics simulations of concentrated protein solutions with a mean field treatment of hydrodynamic interactions. J. Phys. Chem. B 116, 8523–8533. doi: 10.1021/jp212532h

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Minton, A. P. (1997). Influence of excluded volume upon macromolecular structure and associations in “crowded” media. Curr. Opin. Biotechnol. 8, 65–69. doi: 10.1016/S0958-1669(97)80159-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Minton, A. P. (2000). Implications of macromolecular crowding for protein assembly. Curr. Opin. Struct. Biol. 10, 34–39. doi: 10.1016/S0959-440X(99)00045-7

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Minton, A. P. (2001). The influence of macromolecular crowding and macromolecular confinement on biochemical reactions in physiological media. J. Biol. Chem. 276, 10577–10580. doi: 10.1074/jbc.R100005200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Misteli, T. (2001). The concept of self-organization in cellular architecture. J. Cell Biol. 155, 181–185. doi: 10.1083/jcb.200108110

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Misteli, T. (2009). Self-organization in the genome. Proc. Natl. Acad. Sci. U.S.A. 106, 6885–6886. doi: 10.1073/pnas.0902010106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Moore, T., Wu, S. K., Michael, M., Yap, A. S., Gomez, G. A., and Neufeld, Z. (2014). Self-organizing actomyosin patterns on the cell cortex at epithelial cell-cell junctions. Biophys. J. 107, 2652–2661. doi: 10.1016/j.bpj.2014.10.045

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Murray, D. B., Amariel, C., Sasidharan, K., Machne, R., Aon, M. A., and Lloyd, D. (2013). “Temporal partitioning of the yeast cellular network,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 323–349.

Google Scholar

Murray, D. B., Klevecz, R. R., and Lloyd, D. (2003). Generation and maintenance of synchrony in Saccharomyces cerevisiae continuous culture. Exp. Cell Res. 287, 10–15. doi: 10.1016/S0014-4827(03)00068-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Nicolis, G., and Prigogine, I. (1977). Self-organization in Nonequilibrium Systems: From Dissipative Structures to Order Through Fluctuations. New York, NY: Wiley.

Google Scholar

Nivala, M., Ko, C. Y., Weiss, J. N., and Qu, Z. (2012). Criticality in intracellular calcium signaling in cardiac myocytes. Biophys. J. 102, 2433–2442. doi: 10.1016/j.bpj.2012.05.001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Olah, J., Norris, V., and Ovádi, J. (2015). Modeling of sensing potency of cytoskeletal systems decorated with metabolic enzymes. J. Theor. Biol. 365, 190–196. doi: 10.1016/j.jtbi.2014.10.018

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Ovádi, J., and Norris, V. (2013). “Moonlighting function of the tubulin cytoskeleton: macromolecular architectures in the cytoplasm,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 165–178.

Google Scholar

Ovádi, J., and Srere, P. A. (2000). Macromolecular compartmentation and channeling. Int. Rev. Cytol. 192, 255–280. doi: 10.1016/S0074-7696(08)60529-X

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pastor, I., Pitulice, L., Balcells, C., Vilaseca, E., Madurga, S., Isvoran, A., et al. (2014). Effect of crowding by Dextrans in enzymatic reactions. Biophys. Chem. 185, 8–13. doi: 10.1016/j.bpc.2013.10.006

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pastor, I., Vilaseca, E., Madurga, S., Garces, J. L., Cascante, M., and Mas, F. (2011). Effect of crowding by dextrans on the hydrolysis of N-Succinyl-L-phenyl-Ala-p-nitroanilide catalyzed by alpha-chymotrypsin. J. Phys. Chem. B 115, 1115–1121. doi: 10.1021/jp105296c

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Patra, K. C., and Hay, N. (2014). The pentose phosphate pathway and cancer. Trends Biochem. Sci. 39, 347–354. doi: 10.1016/j.tibs.2014.06.005

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pedrotti, B., Ulloa, L., Avila, J., and Islam, K. (1996). Characterization of microtubule-associated protein MAP1B: phosphorylation state, light chains, and binding to microtubules. Biochemistry 35, 3016–3023. doi: 10.1021/bi951314f

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Qu, Z. (2013). “Network dynamics in cardiac electrophysiology,” in Systems Biology of Metabolic and Signaling Networks. Energy, Mass and Information Transfer, eds M.A. Aon, V. Saks, and U. Schlattner (Heidelberg; New York; Dordrecht; London: Springer-Verlag Berlin Heidelberg), 243–260.

Google Scholar

Rabouille, C., Aon, M. A., Muller, G., Cartaud, J., and Thomas, D. (1990). The supramolecular organization of ovomucin. Biophysical and morphological studies. Biochem. J. 266, 697–706.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Rabouille, C., Cortassa, S., and Aon, M. A. (1992). Fractal organisation in biological macromolecular lattices. J. Biomol. Struct. Dyn. 9, 1013–1024. doi: 10.1080/07391102.1992.10507973

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Raicu, V., and Popescu, A. (2008). Integrated Molecular and Cellular Biophysics. New York, NY: Springer. doi: 10.1007/978-1-4020-8268-9

CrossRef Full Text | Google Scholar

Rivas, G., Ferrone, F., and Herzfeld, J. (2004). Life in a crowded world. EMBO Rep. 5, 23–27. doi: 10.1038/sj.embor.7400056

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Roberts, S. J., and Somero, G. N. (1987). Binding of phosphofructokinase to filamentous actin. Biochemistry 26, 3437–3442. doi: 10.1021/bi00386a028

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rohwer, J. M., Postma, P. W., Kholodenko, B. N., and Westerhoff, H. V. (1998). Implications of macromolecular crowding for signal transduction and metabolite channeling. Proc. Natl. Acad. Sci. U.S.A. 95, 10547–10552. doi: 10.1073/pnas.95.18.10547

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rosen, J., Kim, Y. C., and Mittal, J. (2011). Modest protein-crowder attractive interactions can counteract enhancement of protein association by intermolecular excluded volume interactions. J. Phys. Chem. B 115, 2683–2689. doi: 10.1021/jp200625k

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rostovtseva, T., and Colombini, M. (1997). VDAC channels mediate and gate the flow of ATP: implications for the regulation of mitochondrial function. Biophys. J. 72, 1954–1962. doi: 10.1016/S0006-3495(97)78841-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rostovtseva, T. K., and Bezrukov, S. M. (2012). VDAC inhibition by tubulin and its physiological implications. Biochim. Biophys. Acta 1818, 1526–1535. doi: 10.1016/j.bbamem.2011.11.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Rostovtseva, T. K., Sheldon, K. L., Hassanzadeh, E., Monge, C., Saks, V., Bezrukov, S. M., et al. (2008). Tubulin binding blocks mitochondrial voltage-dependent anion channel and regulates respiration. Proc. Natl. Acad. Sci. U.S.A. 105, 18746–18751. doi: 10.1073/pnas.0806303105

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Roussel, M. R., and Lloyd, D. (2007). Observation of a chaotic multioscillatory metabolic attractor by real-time monitoring of a yeast continuous culture. FEBS J. 274, 1011–1018. doi: 10.1111/j.1742-4658.2007.05651.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Savageau, M. A. (1995). Michaelis-Menten mechanism reconsidered: implications of fractal kinetics. J. Theor. Biol. 176, 115–124. doi: 10.1006/jtbi.1995.0181

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schnell, S., and Turner, T. E. (2004). Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws. Prog. Biophys. Mol. Biol. 85, 235–260. doi: 10.1016/j.pbiomolbio.2004.01.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schroeder, M. (1991). Fractals, Chaos, Power Laws. Minutes from an Infinite Paradise. New York, NY: W.H. Freeman and Company.

Google Scholar

Segel, I. H. (1975). Enzyme Kinetics. Behavior and Analysis of Rapid Equilibrium and Steady State Enzyme Systems. New York, NY: Wiley-Interscience Publications.

Slodzinski, M. K., Aon, M. A., and O'Rourke, B. (2008). Glutathione oxidation as a trigger of mitochondrial depolarization and oscillation in intact hearts. J. Mol. Cell. Cardiol. 45, 650–660. doi: 10.1016/j.yjmcc.2008.07.017

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sornette, D. (2000). Critical Phenomena in Natural Sciences. Chaos, Fractals, Selforganization and Disorder: Concepts and Tools. Berlin; Heidelberg: Springer-Verlag. doi: 10.1007/978-3-662-04174-1

CrossRef Full Text | Google Scholar

Spirin, V., and Mirny, L. A. (2003). Protein complexes and functional modules in molecular networks. Proc. Natl. Acad. Sci. U.S.A. 100, 12123–12128. doi: 10.1073/pnas.2032324100

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Srere, P. A. (1987). Complexes of sequential metabolic enzymes. Annu. Rev. Biochem. 56, 89–124. doi: 10.1146/annurev.bi.56.070187.000513

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Stauffer, D., and Aharony, A. (1994). Introduction To Percolation Theory. London: Taylor and Francis.

Google Scholar

Tabony, J., and Job, D. (1992). Gravitational symmetry breaking in microtubular dissipative structures. Proc. Natl. Acad. Sci. U.S.A. 89, 6948–6952. doi: 10.1073/pnas.89.15.6948

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Trovato, F., and Tozzini, V. (2014). Diffusion within the cytoplasm: a mesoscale model of interacting macromolecules. Biophys. J. 107, 2579–2591. doi: 10.1016/j.bpj.2014.09.043

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Vasilescu, C., Olteanu, M., Flondor, P., and Calin, G. A. (2013). Fractal-like kinetics of intracellular enzymatic reactions: a chemical framework of endotoxin tolerance and a possible non-specific contribution of macromolecular crowding to cross-tolerance. Theor. Biol. Med. Model. 10, 55. doi: 10.1186/1742-4682-10-55

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Verkman, A. S. (2002). Solute and macromolecule diffusion in cellular aqueous compartments. Trends Biochem. Sci. 27, 27–33. doi: 10.1016/S0968-0004(01)02003-5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Vertessy, B. G., Orosz, F., Kovacs, J., and Ovádi, J. (1997). Alternative binding of two sequential glycolytic enzymes to microtubules. Molecular studies in the phosphofructokinase/aldolase/microtubule system. J. Biol. Chem. 272, 25542–25546. doi: 10.1074/jbc.272.41.25542

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Welch, G. R. (1977). On the role of organized multienzyme systems in cellular metabolism: a general synthesis. Prog. Biophys. Mol. Biol. 32, 103–191. doi: 10.1016/0079-6107(78)90019-6

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Welch, G. R., and Clegg, J. S. (2010). From protoplasmic theory to cellular systems biology: a 150-year reflection. Am. J. Physiol. Cell Physiol. 298, C1280–C1290. doi: 10.1152/ajpcell.00016.2010

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wirth, A. J., and Gruebele, M. (2013). Quinary protein structure and the consequences of crowding in living cells: leaving the test-tube behind. Bioessays 35, 984–993. doi: 10.1002/bies.201300080

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Xie, X. S. (2013). Biochemistry. Enzyme kinetics, past and present. Science 342, 1457–1459. doi: 10.1126/science.1248859

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhou, H. X., Rivas, G., and Minton, A. P. (2008). Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 37, 375–397. doi: 10.1146/annurev.biophys.37.032807.125817

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zhou, L., Aon, M. A., Almas, T., Cortassa, S., Winslow, R. L., and O'Rourke, B. (2010). A reaction-diffusion model of ROS-induced ROS release in a mitochondrial network. PLoS Comput. Biol. 6:e1000657. doi: 10.1371/journal.pcbi.1000657

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zorov, D. B., Filburn, C. R., Klotz, L. O., Zweier, J. L., and Sollott, S. J. (2000). Reactive oxygen species (ROS)-induced ROS release: a new phenomenon accompanying induction of the mitochondrial permeability transition in cardiac myocytes. J. Exp. Med. 192, 1001–1014. doi: 10.1084/jem.192.7.1001

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Zorov, D. B., Juhaszova, M., and Sollott, S. J. (2014). Mitochondrial reactive oxygen species (ROS) and ROS-induced ROS release. Physiol. Rev. 94, 909–950. doi: 10.1152/physrev.00026.2013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar