Power law relationship between cell cycle duration and cell volume in the early embryonic development of Caenorhabditis elegans

Cell size is a critical factor for cell cycle regulation. In Xenopus embryos after midblastula transition (MBT), the cell cycle duration elongates in a power law relationship with the cell radius squared. This correlation has been explained by the model that cell surface area is a candidate to determine cell cycle duration. However, it remains unknown whether this second power law is conserved in other animal embryos. Here, we found that the relationship between cell cycle duration and cell size in Caenorhabditis elegans embryos exhibited a power law distribution. Interestingly, the powers of the time-size relationship could be grouped into at least three classes: highly size-correlated, moderately size-correlated, and potentially a size-non-correlated class according to C. elegans founder cell lineages (1.2, 0.81, and <0.39 in radius, respectively). Thus, the power law relationship is conserved in Xenopus and C. elegans, while the absolute powers in C. elegans were different from that in Xenopus. Furthermore, we found that the volume ratio between the nucleus and cell exhibited a power law relationship in the size-correlated classes. The power of the volume relationship was closest to that of the time-size relationship in the highly size-correlated class. This correlation raised the possibility that the time-size relationship, at least in the highly size-correlated class, is explained by the volume ratio of nuclear size and cell size. Thus, our quantitative measurements shed a light on the possibility that early embryonic C. elegans cell cycle duration is coordinated with cell size as a result of geometric constraints between intracellular structures.

Introduction

Cell cycle is regulated in coordination with cell size in unicellular organisms and cells in animal embryos. In many invertebrate and vertebrate animals, the early embryonic stage after fertilization is characterized by rapid synchronous cleavage in all cells within the embryo. Later, this pattern of cell division abruptly changes to cycles of slow and asynchronous cleavage. This transition event was referred as the midblastula transition (MBT) originally in amphibian embryos (Gerhart, 1980; Newport and Kirschner, 1982). Experimental studies showed that the onset of events at or after MBT, such as asynchronous division, differentiation, and gastrulation, are affected by cell size as well as ploidy in Drosophila (Edgar et al., 1986) and Xenopus (Newport and Kirschner, 1982; Clute and Masui, 1995). These findings suggest that cell size and genome size are critical factors for determining the timing of MBT, which is the classic concept to explain the coordination between cellular events and cell size in early development of animal embryos.

Some variations of the classic concept have been reported based on quantitative measurements of cellular variables. Yoshio Masui and Wang reported that the cell cycle duration after MBT is inversely proportional to the cell radius squared in Xenopus embryos (Masui and Wang, 1998; Wang et al., 2000). Their rationale for this second power law relationship was that mitosis-promoting factor (MPF) is produced in a quantity proportional to the cell surface area. This hypothesis implies that the cell cycle durations coordinate with cell size through cell surface area, rather than volume.

On the other hand, other researchers proposed that the volume ratio between the cell and nucleus, but not the ploidy, directs the timing of blastomere adhesiveness in starfish and sea urchin embryos (Masui and Kominami, 2001; Masui et al., 2001). In starfish embryos, cell adhesiveness begins to increase after the eighth cleavage to form a monolayered hollow blastula. In accordance with the classic concept, the timing of adhesiveness was accelerated in embryos with doubled ploidy, whereas the timing was delayed in large-sized embryos by the fusion of a non-nucleate egg fragment. In contrast to the classic concept, the timing of adhesiveness was not altered in half-sized embryos, and the timing was only delayed by one cell cycle in quarter-sized embryos. They noticed that experimental manipulations changing cytoplasmic volume or changing ploidy altered the nuclear size, and they found that the cell adhesiveness appeared at a certain volume ratio of the nucleus to the cell (Masui et al., 2001). The same conclusion was derived from experimental observations of sea urchin embryos (Masui and Kominami, 2001). They concluded that the critical variable for determining the onset of blastomere adhesiveness in starfish and sea urchin embryos is the volume ratio between the nucleus and cell.

Thus, cellular events could be coordinated with cell size by the various ratios of cellular variables. However, quantitative measurements to reveal how cell cycle duration is coordinated with cell size have not been performed in embryos other than in the vertebrate, Xenopus. In the present work, we studied the time-size relationship in embryos of an invertebrate, C. elegans. In C. elegans embryo, the cell lineages and order of cell divisions are nearly invariant (Sulston et al., 1983; Schnabel et al., 1997). After fertilization, the P0 zygote divides into the large AB and smaller P1 daughters. Through several rounds of asymmetric cell division, the zygote eventually produces six founder cells: AB, MS, E, C, D, and P4.

Here, we report the time-size relationship—specifically, the cell cycle duration–cell volume (T–V) relationship—follows a power law relationship in C. elegans. Interestingly, the absolute powers differed among cell lineages in C. elegans and were less than the power in Xenopus. We discuss the possibility that cell cycle duration is coordinated with cell size through the volume ratio between nucleus and cell in C. elegans embryos. In addition, we discuss the difference and possible similarity of time-size relationships between C. elegans and Xenopus embryos.

Materials and Methods

C. elegans Culture Conditions and Recording of Embryonic Cell Divisions

Wild-type C. elegans (N2) embryos were maintained at 22.5°C (Brenner, 1974). Embryos were isolated from gravid hermaphrodites. Cell divisions were recorded in a temperature-controlled room on an upright differential interference contrast (DIC) microscope with the Plan-Apochromat 63×/1.40 oil DIC objective lens (Carl Zeiss, Germany). Cell divisions were recorded at one-minute time intervals and 0.5-μm Z-axis intervals after the one-cell stage with Metamorph software (Molecular Devices, USA). Embryos were attached to a cover glass coated with polylysine (Sigma-Aldrich, USA). Cover glass was footed with petroleum jelly (Vaseline, Nacalai Tesque, Japan) on the slide glass. In this set-up, embryos that attached to the cover glass were separated from the slide glass, such that cell divisions proceed without the physical stress of compression between the cover glass and slide glass (Lee and Goldstein, 2003; Arata et al., 2010; Edgar and Goldstein, 2012). Polylysine attachment did not change the embryo shape (Figure S1). C. elegans embryos exhibited normal developmental progression and hatched in this setting.

Measurements of Cell Volume

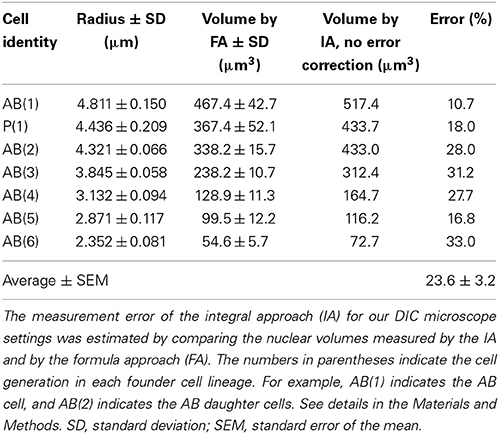
Cell volumes were measured by integrating 10 or more cylinder volumes (integral approach; IA). The volume of each cylinder was calculated from the cell area at each Z-plane and a constant height, which was set as the Z-axis interval in the stage control system of the Metamorph software (Molecular Devices, USA). The cell area in a cylinder was determined as shown in Figure S1A. The length of one pixel in the DIC image was calibrated by an objective micrometer (Carl Zeiss, Germany). Measurement error was estimated by comparing the nuclear volume measured by the IA to the volume measured by the formula approach (FA). In the FA, the nucleus in each cell was assumed to be a perfect sphere and its volume was determined by 4πr³ /3, by using the mean of four times measurements of the nuclear radius. The assumption is approximately correct, because the shape of the nucleus was close to a perfect circle in the X-Y and X-Z axes (Figure S1B). The measurement error in the IA was estimated to be 23.6% larger than the precise cell volume (Table 1). The error might be caused by integration error or slight elongation of the nucleus in the Z-axis (Figure S1B), probably due to the difference of refractive indices in the light path (Born and Wolf, 1999). Final cell volumes were determined by correcting measurement errors and averaging the volumes measured at three different time points during the cell cycle due to an absence of detectable cell growth in the embryonic cell cycle.

TABLE 1

Table 1. Volume correction measured by differential interference contrast (DIC) microscopy.

Statistical Analyses

To examine the power of the T–V relationship in cell lineages, the cell cycle duration and cell volume variables in the logarithmic or linear scale were fitted by the linear least-squares method or the Levenberg-Marquardt algorithm, respectively. To estimate the confidence interval (CI) of the estimated powers, a method combining regression analysis and a bootstrap method was used (Efron and Tibshirani, 1993). The values of power were resampled 10,000 times using residuals between experimental data and values derived from a model function. The 95% CIs were determined at the 2.5th and 97.5th percentiles in the appearance frequency of the values of power in linear scale data fitted by the Levenberg-Marquardt algorithm. The 95% CIs in the logarithmic scale fitted by the linear least-squares method were determined practically by the same method. The percentile method to estimate CIs can be applied to any symmetric statistical distribution.

Results

Quantitative Determination of the T–V Relationship in C. elegans Embryos

We observed the timing of cell division in wild-type C. elegans embryos cultured at 25°C. The intervals of cell divisions between the generations in the same lineage appeared to increase gradually in all the founder cell lineages in an embryo (Figure 1A). The average and standard deviation of coefficient of variation (CV) of cell division timings in AB and MS lineages among different embryos were around several percent (1 to 4 ± 0.5 to 2.1) (Figure 1B), indicating that the cell divisions occurred synchronously in a highly reproducible manner among embryos. Thus, the C. elegans embryo is a good model system to study a deterministic mechanism to regulate cell division timings in animal embryos.

FIGURE 1

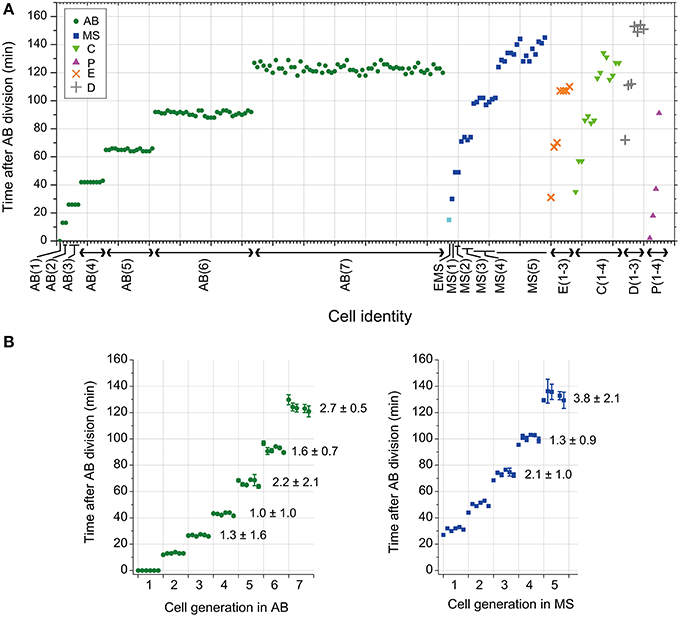
Figure 1. Cell division timing of C. elegans embryos. (A) The cell division timings in an embryo cultured at 25°C. Cell identity is indicated on the horizontal axis. Cell division timing was determined by nuclear envelope breakdown (NEBD). The numbers in parentheses indicate the cell generation in each founder cell lineage. For example, AB(1) indicates the AB cell, and AB(2) indicates the AB daughter cells. (B) The average and standard deviation (SD) of cell division timings in the same generation in AB and MS lineages in an embryo were obtained; data obtained from six embryos were aligned on the horizontal axis in order (the leftmost of AB and in the leftmost of MS were obtained from an embryo). The CV of cell division timings in the same generation in AB and MS lineages in an embryo were averaged among the six embryos and were shown with SD [the average CV ± SD (%)] in the right side of data in the graphs after the third generation. The NEBD of the AB cells was set as time 0. AB, MS, C, P, E, and D are indicated with a green dot, blue square, light green triangle, magenta triangle, orange x-mark, and gray cross, respectively. The EMS cell was indicated by a light blue square.

Next, we examined the T–V relationship. Cell cycle duration was defined as the time from nuclear formation in a cell to nuclear formation in one of the daughter cells, in which the nucleus was formed earlier. Cell cycle duration correlated negatively with cell volume (Figures 2A,B). When we classified the T–V relationship data by cell lineage, cell cycle duration vs. cell volume appeared linear in double logarithmic plots (Figures 2C–H), suggesting a power law relationship. We fitted three different models (Gaussian, exponential, and power law) to the plots of cell cycle duration vs. cell volume in linear scale. The χ²-value in the model fitting was smallest (except for the E lineage) when the data were fitted by the power law model (Figure S2). Therefore, we concluded that the C. elegans T–V relationship in the AB, MS, C, and P lineages follows a power law relationship.

FIGURE 2

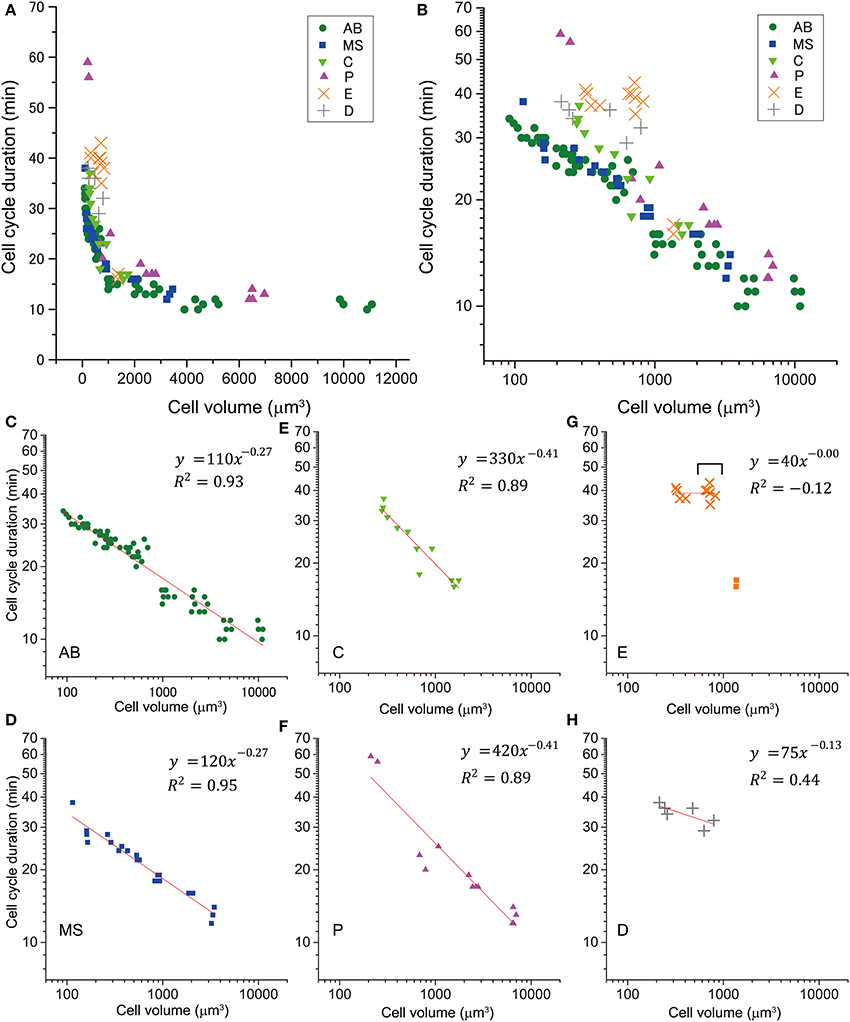
Figure 2. Relationship between cell cycle duration and cell volume. This relationship of cells in embryos is shown in a double logarithmic plot (A) and a linear plot (B). The relationship of cells in AB [green dot, (C)], MS [blue square, (D)], C [light green triangle, (E)], P [magenta triangle, (F)], E [orange x-mark, (G)], and D [gray cross, (H)] lineages are shown in the double logarithmic plot. Cell volume and cell cycle duration data were obtained from four wild-type embryos. Data in the logarithmic scale were fitted to the formula, y = a + bx, by the linear least-squares method. (G) E cells are indicated by squares, and their descendants are indicated by orange x-marks. Downward bracket indicates the daughter cells of E cells. Regression analysis of cells in E lineage was performed without the E cells. Degrees of freedom in fitting in (C–H) were 68, 19, 10, 11, 8, and 4, respectively.

Absolute values of power in the T–V relationship (Figure 2) were similar between AB and MS lineages (0.27) and between C and P lineages (0.41). Bootstrapping statistical analyses showed that the 95% CIs of the powers overlapped between AB and MS, C and P, and E and D lineages (Figures 3A,B). The larger absolute values of power in the C and P lineages indicated that the cell cycle duration elongates rapidly as the cell volume decreases (the highly size-correlated class). In contrast, the smaller absolute values of power in the AB and MS lineages indicated that the cell cycle duration elongates slowly (the moderately size-correlated class). When the power is zero, the cell cycle duration is constant or does not correlate with changes in cell size, indicating a size-non-correlated class. Cells in the E and D lineages exhibited lower values of power. Although it remains unclear due to small sample number, cells in the E and D lineages may be classified in another class with lower values of power, possibly the size-non-correlated class. These results suggest that the powers of the T–V relationship could be grouped into at least three classes.

FIGURE 3

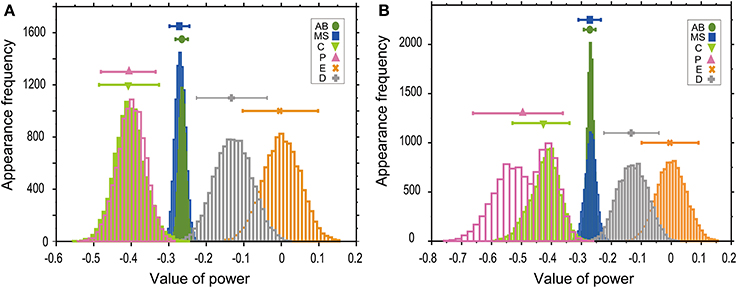
Figure 3. Powers of the T–V relationship could be classified into three classes. T–V relationships in each lineage in the logarithmic (A) or linear (B) scale were fitted by a power law model. Statistical analysis combining regression analysis and a bootstrap method were performed 10,000 times, using the same data used in Figure 2. The estimated power is indicated in the horizontal axis, while the appearance frequencies of the values of power is indicated in the vertical axis. The 95% CIs of the power of the T–V relationship were determined by the appearance frequency and are shown by long horizontal bars. Data for AB, MS, C, P, E, and D lineages are shown in green, blue, light green, magenta, orange, and gray, respectively.

In the bootstrap analysis performed to evaluate the T–V relationship in the logarithmic scale, the appearance frequencies of the values of power were symmetrically distributed (Figure 3A), which supports the validity of our estimation of the CIs. In the bootstrap analysis of the T–V relationship in the linear scale, the appearance frequencies of the AB, MS, E, and D lineages were symmetrically distributed, whereas the appearance frequencies of the C and P lineages showed monomodal and bimodal distributions with the shorter tail in the side of the larger values of power, respectively (Figure 3B). In these asymmetric distributions, the estimation of the CIs could be biased to the shorter tail side of the distributions. Because the similar skewness of the distributions was observed both in the C and P lineages, the asymmetry of the distributions does not affect our conclusion that the 95% CIs of the values of powers overlapped between the C and P lineages.

Intermitotic Phase Duration Elongates Exponentially as Cell Volume Decreases in the Size-Correlated Classes

To determine which cell cycle phase was responsible for elongation of the cell cycle duration, we measured the duration of the intermitotic and mitotic phases in cells in the size-correlated AB, MS, C, and P lineages. The duration of the intermitotic phase was elongated exponentially as the rounds of cell division increased, and became dominant in cell cycle duration in later generations (Figure 4A), whereas the duration of the mitotic phase was relatively constant among these lineages (Figure 4B). These observations indicated that cell cycle elongation was due to lengthening of the intermitotic phase but not the mitotic phase.

FIGURE 4

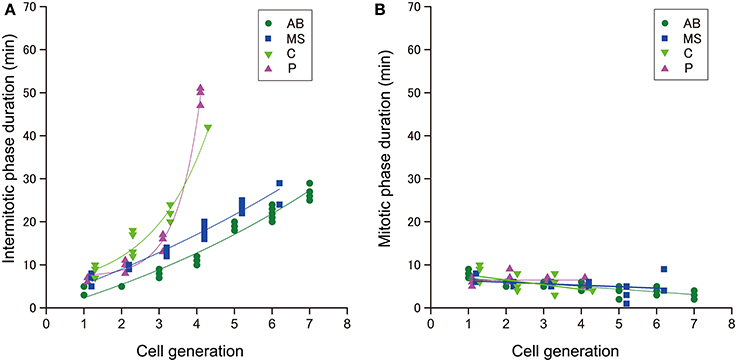
Figure 4. The duration of cell cycle phases in C. elegans embryos. The duration of the (A) intermitotic phase or (B) mitotic phase in the size-correlated class; AB (green dot), MS (blue square), C (light green triangle), and P (magenta triangle) lineages are shown in linear plots in the vertical axis. The cell generations in each founder cell lineage are shown in the horizontal axis. Data points are displaced along the horizontal axis to avoid overlap (A,B). This data displacement does not affect exponentiation of data. Duration data were obtained from three wild-type embryos.

The Relationship Between the Nuclear and Cell Volumes in the Size-Correlated Classes

To explain the C. elegans power law T–V relationship, we focused on the relationship between the cell and nuclear volumes. We plotted the nuclear vs. cell volumes for cells in size-correlated AB, MS, C, and P lineages (Figure 5A). The relationship between the nuclear and cell volumes was non-linear in a linear plot, and showed a linear relationship in a double logarithmic plot (Figure 5B). The relationship was well-fitted by a power law model (R² = 0.94; Figure 5B). Nuclear volume varied with cell volume, in a power law relationship with a slope of 0.63 (Figure 5B). If the volumes of the two spheres varied in a corresponding manner, then the power was unity; thus, the C. elegans relationship between the nuclear and cell volumes was allometric. Supposing that a factor critical for cell cycle regulation is transported between the nucleus and cytoplasm, we considered the ratio of the nuclear volume (V_n) to the cell volume (V_c). The power of the volume ratio was −0.37 (V_n /V_c ∝ V^0.63_c /V_c = V^−0.37_c). We found that the absolute value of the power of the volume ratio (0.37) was closest to that of the T–V relationship in the highly size-correlated class (C and P lineages) (0.41), indicating a strong correlation with the volume ratio between the nucleus and cell.

FIGURE 5

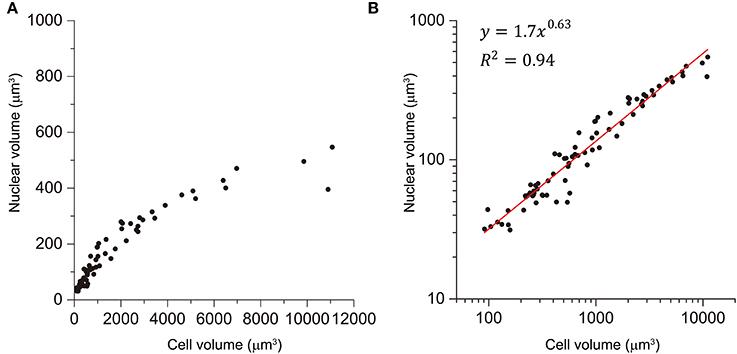
Figure 5. Power law relationship between the nuclear and cell volume. Relationship between nuclear and cell volume in size-correlated classes (AB, MS, C, and P) is shown in linear (A) and double logarithmic (B) plots. Cell volumes were determined by the integral approach with error correction, whereas nuclear volumes were determined by the formula approach in three wild-type embryos. Data in logarithmic scale were fitted to the formula, y = a + bx, by the linear least-squares method. Degree of freedom in fitting was 75.

Genetic Analysis of the T–V Relationship in C. elegans Embryos

We employed a genetic approach to assess the impact of altered cell volume and to examine the molecular mechanism of the T–V relationship. In C. elegans, genome-wide screening and classic genetics have identified genes related to egg size determination. Homozygous mutant embryos of ptp-2/SH2 domain-containing protein tyrosine phosphatase are larger than wild-type embryos, whereas ima-3/importin α RNAi embryos are smaller than wild-type embryos (Figure 6A) (Gutch et al., 1998; Sonnichsen et al., 2005). We measured cell cycle duration and cell volume in the AB lineage of these two loss-of-function embryos. Volumes of AB cells in the ptp-2 mutant embryos and ima-3 RNAi embryos were approximately twice and half the sizes, respectively, of AB cells from wild-type embryos (compare gray and black brackets in Figures 6B,C). The T–V relationship of the ptp-2 AB lineage was well-fitted with a power law model with the absolute power, 0.25 (R² = 0.87; Figure 6B), which was close to that of the wild-type AB lineage (0.27; Figure 2). Larger AB cells in ptp-2 mutant embryos (black brackets) did not further shorten cell cycle durations compared to AB cells in wild-type embryos (gray brackets; Figure 6B). Thus, the cell cycle duration may have a minimum limit, and eventually appeared to have the minimum limit in the T–V relationship.

FIGURE 6

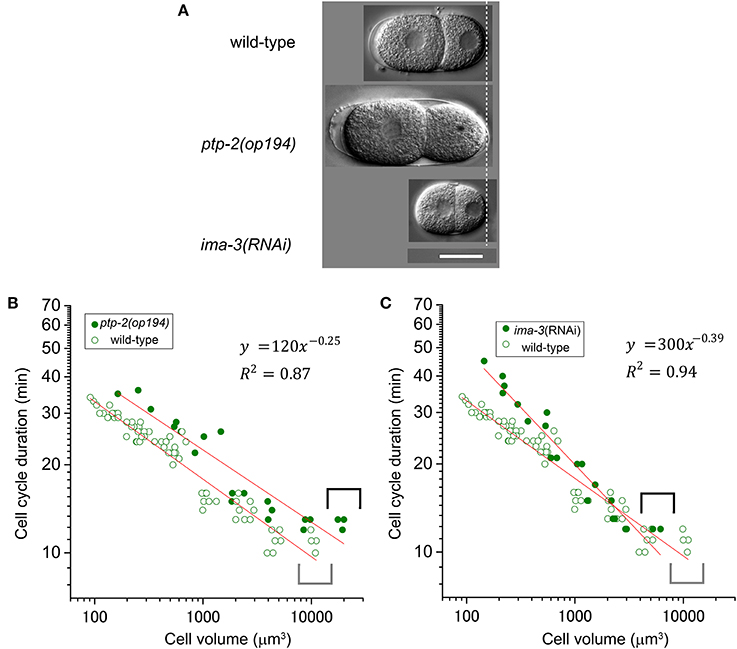
Figure 6. Relationship between cell cycle duration and cell volume in loss-of-function embryos. (A) Images of embryos at the two-cell stage for wild-type, ptp-2(op194), and ima-3 RNAi embryos were obtained by differential interference contrast (DIC) microscopy. Scale bar = 20 μm. Relationship between cell cycle duration and cell volume in AB lineage in ptp-2(op194) [filled circles in (B)] and ima-3(RNAi) [filled circles in (C)] embryos are shown with that in wild-type embryos [open circles in (B,C)] in double logarithmic plots. Cell volume and cell cycle duration data in loss-of-function embryos were obtained from each of three embryos. Data in the logarithmic scale were fitted to the formula, y = a + bx, by the linear least-squares method. Degrees of freedom in fitting (B,C) were 19 and 19, respectively.

The power law relationship was maintained in the ima-3 AB lineage, but the absolute value of the power of the ima-3 RNAi embryos was increased (0.39, R² = 0.94; Figure 6C) close to the absolute value of the power of the highly size-correlated class (C and P lineages) in wild-type embryos (0.41; Figure 2). Thus, ima-3 is required to determine the proper cell cycle elongation, and eventually appeared to determine the proper power of the T–V relationship. The order of cell divisions in the ima-3 RNAi embryos was the same as in the wild-type embryos, at least until the 16-cell stage (data not shown). Thus, it is unlikely that the rapid elongation of cell cycle in ima-3 RNAi embryos was caused by defects in cell fate determination of the founder cells.

Discussion

Cell cycle duration is coordinated with cell size in cultured mammalian cells and unicellular organisms. For example, Amoeba proteus cells did not enter the mitotic phase when the cell volume was reduced by cytoplasmic amputation (Prescott, 1955). By changing cell size with genetic or culture manipulations, cell cycle progression has been shown to be affected in budding yeast (Johnston et al., 1977), fission yeast (Nurse, 1975; Sveiczer et al., 1996), ciliates (Berger, 1984), and mammalian cultured cells (Dolznig et al., 2004). A quantitative relationship between cell cycle duration and cell size was reported in embryos of the vertebrate, Xenopus (Masui and Wang, 1998; Wang et al., 2000). In this work, we studied the quantitative relationship in embryos of an invertebrate, C. elegans.

Powers of the T–V Relationship Among Cell Lineages in C. elegans

We found that the relationship between cell volume and cell cycle duration followed a power law relationship. In C. elegans, AB and P1 cells divide asynchronously, with the larger AB cells dividing before the smaller P1 cells (Sulston et al., 1983; Brauchle et al., 2003). The zygotes that are depleted of subunits of the heterotrimeric G-proteins, GOA-1/GPA-16, or GoLoco-containing proteins, GPR-1/GPR-2, exhibit normal anterior-posterior polarity, but divide into equally sized AB and P1 cells (Gotta and Ahringer, 2001; Colombo et al., 2003; Gotta et al., 2003; Srinivasan et al., 2003). The equally sized AB and P1 cells divide in a more synchronized manner compared to the differently sized AB and P1 cells in wild-type embryos. Thus, the cell cycle duration in AB and P1 cells is strongly correlated with cell size. Brauchle et al. proposed that unequal cell size of AB and P1 cells contributes to asynchrony of cell division, although it is still possible that G protein signaling is specifically required for differential checkpoint activation at the two-cell stage or for another cellular process modulating cell cycle progression (Brauchle et al., 2003). The power law relationship between cell cycle duration and cell size in later embryonic development may be regulated by a mechanism similar to the asynchrony of AB and P1 divisions.

Our statistical analyses suggest that there are at least three different classes of the T–V relationship according to the founder cell lineages in C. elegans: highly size-correlated, moderately size-correlated, and probably size-non-correlated classes (absolute powers of 0.41, 0.27, and <0.13 for volume, respectively). C. elegans founder cells give rise to different types of differentiated cells: cells in AB and MS lineages primarily produce ectodermal and mesodermal cells, C and P lineages produce mesodermal and germline cells, and E and D lineages produce endodermal and mesodermal cells, respectively (Sulston et al., 1983). Thus, the cell fates do not correlate with the classes according to the power of the T–V relationship. Instead, the classification might correlate with a mode of cell divisions. Cells in AB and MS lineages of the moderately size-correlated class share prominently synchronous and symmetric cell divisions (Figure 1) (Sulston et al., 1983), while cells in the P lineage undergo asymmetric cell divisions, in which the two daughter cells clearly differ in size from each other (Sulston et al., 1983). Similarly, many cells in the C lineage undergo asymmetric cell division, which has a clear size asymmetry (Figure S3). Thus, cells in P and C lineages in the highly size-correlated class share size-asymmetric cell division. It remains unclear what cell feature the E and D lineages share. Daughter cells of each E cell exhibited an abrupt deviation from the T–V relationship that the mother E cell followed, and subsequently, the descendants appeared to exhibit a lower power in the T–V relationship (Figures 2B,G). The E daughters are the first cells that have the Gap phase (G2 phase) in C. elegans embryos (Edgar and McGhee, 1988). Therefore, the deviation may be caused by the introduction of the Gap phase. This cell cycle dynamics in E lineage may be shared with D lineage.

Overall, our quantitative measurements revealed the diversity of powers in the T–V relationship among C. elegans cell lineages. Cells may sense their own size through distinct mechanisms among cell lineages in C. elegans embryos.

Powers of the T–V Relationship in C. elegans and Xenopus

We found that any of the absolute powers of the C. elegans lineages (<0.39, 0.81, and 1.2 in radius; <0.13, 0.27, and 0.41 in volume, respectively) were smaller than that in Xenopus embryos (2.0 in radius; 0.67 in volume). The cell cycle duration of C. elegans embryos elongates more slowly than that in Xenopus after MBT. Thus, the T–V relationship in C. elegans may be determined by mechanisms different from those used by Xenopus embryos. Alternatively, there remains a possibility that a same mechanism functions for the time-size relationship in C. elegans and Xenopus embryos. In Xenopus embryos, the time-size relationship has only been examined in cells near the animal cap. It is possible that the diversity according to cell lineages is also observed in the Xenopus embryo. Recently, it has been reported that nuclear size correlates non-linearly with cell size in Xenopus embryos (Jevtic and Levy, 2015), similarly to C. elegans (Figure 5A). In budding and fission yeasts, the relationship between the nuclear and cell volumes was reported to be linear (Jorgensen et al., 2007; Neumann and Nurse, 2007). In addition, nuclear size has been strongly correlated with cell size (Jorgensen et al., 2007; Neumann and Nurse, 2007), even when cell size was changed 35-fold or nuclear DNA content was changed 16-fold in fission yeast (Neumann and Nurse, 2007). The volume ratio of the nucleus to the cell was rapidly corrected by the growth of the cell or nucleus, when the nuclear or cell size was changed by manipulating the genetic or culture conditions (Neumann and Nurse, 2007). Thus, there is a mechanism that links the sizes of the nucleus and cell in yeasts. Although the mechanism to link the sizes of the nucleus and cell in yeasts is different from animal embryos, the interesting correlation of volume ratio between the nucleus and cell in yeasts and animal embryos raise a possibility that the volume ratio can be a general mean by which cells “sense” their size. The power of the time-size relationship was different between C. elegans and Xenopus embryos, while the time-size relationship may strongly correlate with the volume ratio between the nucleus and cell in Xenopus embryos, like C. elegans embryos (See Section The Relationship Between the Nuclear and Cell Volumes in the Size-Correlated Classes). As a future issue, it is interesting to test this possibility to seek a general mechanism that coordinates cell size and cell cycle duration in animal embryos.

In C. elegans, cell cycle elongation was due to lengthening of the intermitotic, but not the mitotic, phase in size-correlated AB, MS, C, and P lineages. The C. elegans embryonic cell cycle is occupied with S phase at least until the 16-cell stage (Edgar and McGhee, 1988). The gradual elongation of cell cycle duration in the size-correlated AB, MS, C, and P lineages was not due to introduction of the Gap phase, rather due to the elongation of the S phase at least before the 16-cell stage. On the other hand, the Gap phase introduction, which first occurs in the daughters of the E cell (Edgar and McGhee, 1988) was accompanied with abrupt deviation from the T–V relationship that followed by cells in the AB and MS lineages (Figures 2B,G). In Xenopus, the transition to size-correlated elongation of cell cycle duration is accompanied, in order, by elongation of the S phase just after MBT, introduction of G1 and G2 phases, and elongation of S and G1 phases (Iwao et al., 2005). Durations of the G2 phase are not correlated with cell cycle elongation. Therefore, size-correlated elongation of the cell cycle duration in C. elegans embryos is caused by a cell cycle control mechanism different from Xenopus.

Possible Model to Explain the Power Law Relationship Between Cell Cycle Duration and Cell Volume in the Highly Size-Correlated Class

The C. elegans cell cycle duration is likely elongated by S phase elongation at least before the 16-cell stage (Edgar and McGhee, 1988). DNA replication is initiated from specific sites in the chromosomes in eukaryotic cells, called replication origins (Costa et al., 2013). The initiation step of DNA replication, or origin firing, is tightly controlled by the interaction of the replication origin with the initiation factors for DNA replication (IFs) to ensure that the entire genome is replicated precisely once in each cell cycle (Pospiech et al., 2010; Costa et al., 2013). It has been reported that IFs were involved in the asynchrony of division timing of AB and P1 cells (Benkemoun et al., 2014). The asynchrony was explained by the different frequency of the origin firing, such that the length of DNA replication responsible for a single origin may be different between AB and P1 cells (Benkemoun et al., 2014). In this explanation, more origin firing in AB, with DNA replication proceeding from more origins, a shorter time is needed to completely replicate the whole genome DNA than less origin firing in P1.

In C. elegans embryos depleted of the ataxia telangiectasia mutated (ATM)-like kinase, atl-1, and the checkpoint kinase, chk-1, the AB and P1 cell divisions are more synchronous than in wild-type embryos (Brauchle et al., 2003). In Xenopus egg extract, ATM-related (ATR)/Chk1 signaling regulates the initiation and progression of DNA synthesis in S phase, even in the absence of DNA damage (Marheineke and Hyrien, 2004; Shechter et al., 2004), probably through modulating the activity of S phase-promoting kinases (Cdk2 and Cdc7) (Marheineke and Hyrien, 2004; Shechter et al., 2004). Therefore, through the regulation of S phase-promoting kinases, ATR/Chk1 signaling may eventually regulate the rate of replication origin firing. Although it remains unknown whether IFs and ATR/Chk1 signaling affect cell cycle duration in C. elegans embryos after the two-cell stage, the elongation of cell cycle duration observed in this work may be regulated by the differential regulation of origin firing rate.

We found that the cell cycle was rapidly elongated in ima-3 RNAi embryos. It has been reported that loss-of-function embryos of ima-3 exhibit an embryonic lethal phenotype (Geles and Adam, 2001). The rapid elongation of cell cycle in ima-3 RNAi embryos may be caused by pleiotropic effects of the embryonic lethal phenotype in the late embryonic stage. However, the cell cycle elongation in ima-3 RNAi embryos was gradual, but not stepwise, such that the slope can be fitted by a power law function. One interesting possibility is that ima-3 is directly involved in a mechanism regulating the cell cycle progression in C. elegans embryos, especially under the control of cell size. The importin family encodes proteins that mediate nuclear import and various molecular processes, including transcription by RNA polymerase III, spindle formation, chromosome segregation, and nuclear envelope assembly (Adam, 2009). Further analyses are necessary to study which of IMA-3 functions causes the rapid elongation of cell cycle in ima-3 RNAi embryos. Importin α was found to be involved in nuclear size determination (Levy and Heald, 2010; Edens et al., 2013). Recently, it has been shown that by manipulating expression or function of factors to regulate nuclear size, including Importin α, it has been shown nuclear size contributes to the regulation of MBT timing in Xenopus embryos (Jevtic and Levy, 2015). The same mechanism could function in the T–V relationship in C. elegans embryos. Although it remains an open question whether loss of function of ima-3 leads to altering of nuclear volume in C. elegans, there are two intriguing possibilities that IMA-3 mediates the T–V relationship; (1) by regulating nuclear import rate of IFs and/or (2) by regulating nuclear size. Both of the mechanisms affect the T–V relationship through determining their nucleoplasmic concentration of IFs. It will be necessary to test whether one or both of these possibilities were true for evaluating our hypothesis. A theoretical formularization was discussed based on the results of quantitative measurements in this work (Appendix).

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Masashi Tachikawa, Hirofumi Wada, Yoshimi Tanaka, and Noriko Hiroi for valuable discussions, Tomomi Takano for technical assistance, and the Caenorhabditis Genetics Center for strains. This work was supported by Special Postdoctoral Researchers Program, RIKEN (Yukinobu Arata) and by a grant from the Japanese Ministry of Education, Culture, Sports, Science and Technology (Yukinobu Arata and Hitoshi Sawa).

Supplementary Material

The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fphys.2014.00529/abstract

Figure S1. Integral approach for measuring cell volume. (A) Serial images of an embryo at the four-cell stage along the Z-axis at 3-μm intervals. The image at 0 μm was at the closest side of the embryo to the objective lens. The focus position moved to the farther side of the embryo in an upright microscope. Cell contours were shown as blue circles, which were traced by following the cell periphery and granules in focus located around the cell boundary. (B) Three-dimensional reconstruction of an embryo in the two-cell stage from serial images obtained along the Z-axis at 0.5-μm intervals using Image J. In the reconstructed image in the X-Z axis, nuclear peripheries are indicated by black dots.

Figure S2. Statistical analyses to select a model to explain the T–V relationships in C. elegans. Relationship between cell cycle duration and cell volume in AB (A), MS (B), C (C), P (D), E (E), and D (F) lineages in the linear scale was fitted by three different models: Gaussian, exponential, or power law function by the Levenberg-Marquardt algorithm, using the same data used in Figure 2. Fitted functions and χ²-values are shown in the boxes.

Figure S3. Size asymmetry between daughter cells in C. elegans C lineage. Diagram shows the cell division pattern in C lineage. Anterior and posterior daughters are indicated as “a” and “p,” respectively. The cell sizes were observed in serial images along the Z-axis, and are shown at the Z axis plane, where the nuclei are located in focus with blue circles. Cell division of Ca, Caa, Cp, and Cpa was asymmetric in the daughter cell sizes, in which the anterior daughter was larger than the posterior daughter. Cpa and Cpp were located in different Z-planes in an embryo. Scale bar = 10 μm.

References

Adam, S. A. (2009). The nuclear transport machinery in Caenorhabditis elegans: a central role in morphogenesis. Semin. Cell Dev. Biol. 20, 576–581. doi: 10.1016/j.semcdb.2009.03.013

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Arata, Y., Lee, J. Y., Goldstein, B., and Sawa, H. (2010). Extracellular control of PAR protein localization during asymmetric cell division in the C. elegans embryo. Development 137, 3337–3345. doi: 10.1242/dev.054742

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Benkemoun, L., Descoteaux, C., Chartier, N. T., Pintard, L., and Labbe, J. C. (2014). PAR-4/LKB1 regulates DNA replication during asynchronous division of the early C. elegans embryo. J. Cell Biol. 205, 447–455. doi: 10.1083/jcb.201312029

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Berger, J. D. (1984). “The ciliate cell cycle,” in The Microbial Cell Cycle, eds P. Nurse and E. Streiblová (Boca Raton, FL: CRC Press), 191.

Born, M., and Wolf, E. (1999). Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light. Cambridge; New York: Cambridge University Press.

Google Scholar

Brauchle, M., Baumer, K., and Gonczy, P. (2003). Differential activation of the DNA replication checkpoint contributes to asynchrony of cell division in C. elegans embryos. Curr. Biol. 13, 819–827. doi: 10.1016/S0960-9822(03)00295-1

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Brenner, S. (1974). The genetics of Caenorhabditis elegans. Genetics 77, 71–94.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Clute, P., and Masui, Y. (1995). Regulation of the appearance of division asynchrony and microtubule-dependent chromosome cycles in Xenopus laevis embryos. Dev. Biol. 171, 273–285. doi: 10.1006/dbio.1995.1280

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Colombo, K., Grill, S. W., Kimple, R. J., Willard, F. S., Siderovski, D. P., and Gonczy, P. (2003). Translation of polarity cues into asymmetric spindle positioning in Caenorhabditis elegans embryos. Science 300, 1957–1961. doi: 10.1126/science.1084146

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Costa, A., Hood, I. V., and Berger, J. M. (2013). Mechanisms for initiating cellular DNA replication. Annu. Rev. Biochem. 82, 25–54. doi: 10.1146/annurev-biochem-052610-094414

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dolznig, H., Grebien, F., Sauer, T., Beug, H., and Mullner, E. W. (2004). Evidence for a size-sensing mechanism in animal cells. Nat. Cell Biol. 6, 899–905. doi: 10.1038/ncb1166

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Edens, L. J., White, K. H., Jevtic, P., Li, X., and Levy, D. L. (2013). Nuclear size regulation: from single cells to development and disease. Trends Cell Biol. 23, 151–159. doi: 10.1016/j.tcb.2012.11.004

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Edgar, B. A., Kiehle, C. P., and Schubiger, G. (1986). Cell cycle control by the nucleo-cytoplasmic ratio in early Drosophila development. Cell 44, 365–372. doi: 10.1016/0092-8674(86)90771-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Edgar, L. G., and Goldstein, B. (2012). Culture and manipulation of embryonic cells. Methods Cell Biol. 107, 151–175. doi: 10.1016/B978-0-12-394620-1.00005-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Edgar, L. G., and McGhee, J. D. (1988). DNA synthesis and the control of embryonic gene expression in C. elegans. Cell 53, 589–599. doi: 10.1016/0092-8674(88)90575-2

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Efron, B., and Tibshirani, R. (1993). An Introduction to the Bootstrap. New York, NY: Chapman and Hall. doi: 10.1007/978-1-4899-4541-9

CrossRef Full Text | Google Scholar

Geles, K. G., and Adam, S. A. (2001). Germline and developmental roles of the nuclear transport factor importin alpha3 in C. elegans. Development 128, 1817–1830.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Gerhart, J. C. (1980). “Mechanisms regulating pattern formation in the amphibian egg and early embryo,” in Biological Regulation and Development, ed R. F. Goldberger (New York, NY: Springer), 133–316.

Pubmed Abstract | Pubmed Full Text

Gotta, M., and Ahringer, J. (2001). Distinct roles for Galpha and Gbetagamma in regulating spindle position and orientation in Caenorhabditis elegans embryos. Nat. Cell Biol. 3, 297–300. doi: 10.1038/35060092

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gotta, M., Dong, Y., Peterson, Y. K., Lanier, S. M., and Ahringer, J. (2003). Asymmetrically distributed C. elegans homologs of AGS3/PINS control spindle position in the early embryo. Curr. Biol. 13, 1029–1037. doi: 10.1016/S0960-9822(03)00371-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gutch, M. J., Flint, A. J., Keller, J., Tonks, N. K., and Hengartner, M. O. (1998). The Caenorhabditis elegans SH2 domain-containing protein tyrosine phosphatase PTP-2 participates in signal transduction during oogenesis and vulval development. Genes Dev. 12, 571–585. doi: 10.1101/gad.12.4.571

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Iwao, Y., Uchida, Y., Ueno, S., Yoshizaki, N., and Masui, Y. (2005). Midblastula transition (MBT) of the cell cycles in the yolk and pigment granule-free translucent blastomeres obtained from centrifuged Xenopus embryos. Dev. Growth Differ. 47, 283–294. doi: 10.1111/j.1440-169X.2005.00802.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jevtic, P., and Levy, D. L. (2015). Nuclear Size Scaling during Xenopus early development contributes to midblastula transition timing. Curr. Biol. 25, 45–52. doi: 10.1016/j.cub.2014.10.051

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Johnston, G. C., Pringle, J. R., and Hartwell, L. H. (1977). Coordination of growth with cell division in the yeast Saccharomyces cerevisiae. Exp. Cell Res. 105, 79–98. doi: 10.1016/0014-4827(77)90154-9

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Jorgensen, P., Edgington, N. P., Schneider, B. L., Rupes, I., Tyers, M., and Futcher, B. (2007). The size of the nucleus increases as yeast cells grow. Mol. Biol. Cell 18, 3523–3532. doi: 10.1091/mbc.E06-10-0973

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Lee, J. Y., and Goldstein, B. (2003). Mechanisms of cell positioning during C. elegans gastrulation. Development 130, 307–320. doi: 10.1242/dev.00211

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Levy, D. L., and Heald, R. (2010). Nuclear size is regulated by importin alpha and Ntf2 in Xenopus. Cell 143, 288–298. doi: 10.1016/j.cell.2010.09.012

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Marheineke, K., and Hyrien, O. (2004). Control of replication origin density and firing time in Xenopus egg extracts: role of a caffeine-sensitive, ATR-dependent checkpoint. J. Biol. Chem. 279, 28071–28081. doi: 10.1074/jbc.M401574200

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Masui, M., and Kominami, T. (2001). Change in the adhesive properties of blastomeres during early cleavage stages in sea urchin embryo. Dev. Growth Differ. 43, 43–53. doi: 10.1046/j.1440-169x.2001.00555.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Masui, M., Yoneda, M., and Kominami, T. (2001). Nucleus: cell volume ratio directs the timing of the increase in blastomere adhesiveness in starfish embryos. Dev. Growth Differ. 43, 295–304. doi: 10.1046/j.1440-169x.2001.00573.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Masui, Y., and Wang, P. (1998). Cell cycle transition in early embryonic development of Xenopus laevis. Biol. Cell 90, 537–548. doi: 10.1111/j.1768-322X.1998.tb01062.x

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Neumann, F. R., and Nurse, P. (2007). Nuclear size control in fission yeast. J. Cell Biol. 179, 593–600. doi: 10.1083/jcb.200708054

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Newport, J., and Kirschner, M. (1982). A major developmental transition in early Xenopus embryos: I. characterization and timing of cellular changes at the midblastula stage. Cell 30, 675–686. doi: 10.1016/0092-8674(82)90272-0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Nurse, P. (1975). Genetic control of cell size at cell division in yeast. Nature 256, 547–551. doi: 10.1038/256547a0

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Pospiech, H., Grosse, F., and Pisani, F. M. (2010). The initiation step of eukaryotic DNA replication. Subcell Biochem. 50, 79–104. doi: 10.1007/978-90-481-3471-7_5

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Prescott, D. M. (1955). Relations between cell growth and cell division. I. Reduced weight, cell volume, protein content, and nuclear volume of Amoeba proteus from division to division. Exp. Cell Res. 9, 328–337. doi: 10.1016/0014-4827(55)90106-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Schnabel, R., Hutter, H., Moerman, D., and Schnabel, H. (1997). Assessing normal embryogenesis in Caenorhabditis elegans using a 4D microscope: variability of development and regional specification. Dev. Biol. 184, 234–265. doi: 10.1006/dbio.1997.8509

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Shechter, D., Costanzo, V., and Gautier, J. (2004). ATR and ATM regulate the timing of DNA replication origin firing. Nat. Cell Biol. 6, 648–655. doi: 10.1038/ncb1145

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sonnichsen, B., Koski, L. B., Walsh, A., Marschall, P., Neumann, B., Brehm, M., et al. (2005). Full-genome RNAi profiling of early embryogenesis in Caenorhabditis elegans. Nature 434, 462–469. doi: 10.1038/nature03353

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text

Srinivasan, D. G., Fisk, R. M., Xu, H., and van den Heuvel, S. (2003). A complex of LIN-5 and GPR proteins regulates G protein signaling and spindle function in C elegans. Genes Dev. 17, 1225–1239. doi: 10.1101/gad.1081203

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sulston, J. E., Schierenberg, E., White, J. G., and Thomson, J. N. (1983). The embryonic cell lineage of the nematode Caenorhabditis elegans. Dev. Biol. 100, 64–119. doi: 10.1016/0012-1606(83)90201-4

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Sveiczer, A., Novak, B., and Mitchison, J. M. (1996). The size control of fission yeast revisited. J. Cell Sci. 109(pt 12), 2947–2957.

Pubmed Abstract | Pubmed Full Text | Google Scholar

Wang, P., Hayden, S., and Masui, Y. (2000). Transition of the blastomere cell cycle from cell size-independent to size-dependent control at the midblastula stage in Xenopus laevis. J. Exp. Zool. 287, 128–144. doi: 10.1002/1097-010X(20000701)287:2<128::AID-JEZ3>3.0.CO;2-G

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Appendix

Numerical Formularization of Our Model

We showed that the C. elegans T–V relationship in the highly size-correlated class correlated with the volume ratio between the nucleus and cell (Section The Relationship Between the Nuclear and Cell Volumes in the Size-Correlated Classes). Here, we discuss a possible molecular mechanism to regulate the T–V relationship (Section Possible Model to Explain the Power Law Relationship Between Cell Cycle Duration and Cell Volume in the Highly Size-Correlated Class), based on a theoretical numerical formularization of our model. The causal relationship between the cell cycle duration and cell volume has not previously been shown in C. elegans embryos, and knowledge of molecular mechanisms regulating cell cycle duration are insufficient. Thus, this model does not exclude alternative numerical models.

We presume that the cell cycle duration in the highly size-correlated class (T), which is occupied with S phase, is determined by the whole genome size (L; [n.a.]), the replication velocity (k, [n.a./s]) which is assumed to be constant in embryonic cells, and the number of replication origins that are fired during S phase (N [−]), where. n.a. indicates the number of nucleic acids:

$\begin{array}{cc}T=\frac{L}{N·k}& \left(\text{A}1\right)\end{array}$

In addition, we presumed that the number of fired origins during S phase is in proportion to the concentration of the IFs in the nucleoplasm ([nucIF]):

$\begin{array}{cc}N\propto \left[nucIF\right]& \left(\text{A}2\right)\end{array}$

We also presumed that the total amount of IFs is constant in embryos. The amount of IFs in each cell (cytoIF) is determined following the segregation of daughter cells from the mother cell according to the daughter cell volume. The nucleoplasmic IF concentration is presumed to be determined by active transport via the Importin system (Section Possible Model to Explain the Power Law Relationship Between Cell Cycle Duration and Cell Volume in the Highly Size-Correlated Class), so that the nucleoplasmic concentration of the IFs is reduced according to embryonic cell cleavage events that follow the power law of the volume ratio between the nucleus and cell (Figure 5B). Consequently, the T–V relationship in the highly size-correlated class elongated according to the volume ratio between the nucleus and cell.

$\begin{array}{cc}\left[nucIF\right]\propto \frac{cytoIF}{V_n}\propto \frac{V_c}{V_n}& \left(\text{A}3\right)\end{array}$

From Equations (A2, A3):

$\begin{array}{cc}N\propto V_c/V_n& \left(\text{A}4\right)\end{array}$

From Equations (A1, A4):

$\begin{array}{cc}T\propto \frac{L}{V_c/V_n·k}\propto \frac{V_n}{V_c}& \left(\text{A}5\right)\end{array}$

From our experimental measurements of nuclear and cell volume (Section The Relationship Between the Nuclear and Cell Volumes in the Size-Correlated Classes),

$\begin{array}{cc}\frac{V_n}{V_c}\propto V_c^{-0.37}& \left(\text{A}6\right)\end{array}$

Therefore, from Equations (A5, A6):

$T\propto V_c^{-0.37}.$

Thus, the cell cycle duration in the highly size-correlated class can be determined by the amount of IFs that are inherited in proportion to cell size and function in proportion to nuclear size. Eventually, cell cycle duration is elongated in proportion to cell volume with the power −0.37.