- 1Department of Physics and Institute of Biophysics, Huazhong Normal University, Wuhan, China
- 2Department of Physics, College of Science, Huazhong Agricultural University, Wuhan, China
- 3Institute of Applied Physics, College of Science, Huazhong Agricultural University, Wuhan, China
Coherent feed-forward loops exist extensively in realistic biological regulatory systems, and are common signaling motifs. Here, we study the characteristics and the propagation mechanism of the output noise in a coherent feed-forward transcriptional regulatory loop that can be divided into a main road and branch. Using the linear noise approximation, we derive analytical formulae for the total noise of the full loop, the noise of the branch, and the noise of the main road, which are verified by the Gillespie algorithm. Importantly, we find that (i) compared with the branch motif or the main road motif, the full motif can effectively attenuate the output noise level; (ii) there is a transition point of system state such that the noise of the main road is dominated when the underlying system is below this point, whereas the noise of the branch is dominated when the system is beyond the point. The entire analysis reveals the mechanism of how the noise is generated and propagated in a simple yet representative signaling module.
Introduction
The biological world is filled with interaction of deterministic laws and randomness (Monod, 1972). Fluctuation and noise have penetrated into every level of biology, from the most essential molecular, sub-cellular processes to the kinetics of tissues, organs, organisms, and populations (Tsimring, 2014). In a biochemical reaction system, it is known that the external noise and the internal noise are both unavoidable (Harada et al., 1999; Hasty et al., 2000; Swain et al., 2002). The internal noise (referred to expression noise here) originates from random fluctuations of stochastic chemical reaction events (McAdams and Arkin, 1997; Arkin et al., 1998; Barkai and Leibler, 2000; Rao et al., 2002) in finite-size biochemical systems, which can lead to cell-to-cell variability. Increasing evidence suggests that this expression noise has significant impacts on many cellular processes.
A prominent feature of gene transcription regulatory networks is the presence of a large number of motifs, i.e., patterns of interconnection. These motifs include the auto-regulation loop, feedback loop, feed-forward loop and so on. An important task in the post-genome era is to understand how these different regulation mechanisms of expression noise affect the functioning of cells and how they contribute to cell-to-cell variability. Our ultimate purpose is to understand how the characteristics of noise in the complex networks can be derived from the properties of modules that are used to compose these networks.
It has been recognized that feedback loops play significant roles in a variety of biological processes, such as calcium signaling (Berridge, 2001; Lewis, 2001), p53 regulation (Harris and Levine, 2005), galactose regulation (Acar et al., 2005), cell cycle (Morgan, 2006; Yang et al., 2013; Liu et al., 2015), and cell fate decision in budding yeast (Li et al., 2014, 2015). Some studies suggested that negative feedbacks typically attenuated noise and positive feedbacks tended to amplify noise (Becskei and Serrano, 2000; Austin et al., 2006; Alon, 2007); however, there were other studies revealing that positive feedbacks could attenuate noises and there were no strong correlations between the sign of feedbacks (negative or positive) and the noise attenuation properties (Hooshangi and Weiss, 2006; Hornung and Barkai, 2008).
It is well-known that the feed-forward loop is also a typical of biological motif. The feed-forward loop, a pattern of three genes, consists of two input transcription factors, one of which regulates the other, conjointly regulating a target gene. Each of the interactions of three genes in the feed-forward loop can be activation or inhibition so that the feed-forward loop has eight possible structural types. Among them, the coherent feed-forward loop appears with the highest frequency in the organism (Mangan and Alon, 2003). The structures, functions, as well as noise characteristics of feed-forward loop have received increasing attention over the last decade (Mangan and Alon, 2003; Mangan et al., 2003, 2006; Ghosh et al., 2005; Dekel et al., 2005; Kalir et al., 2005; Prill et al., 2005; Wall et al., 2005; Alon, 2006, 2007; Kaplan et al., 2008; Kim et al., 2008; Goentoro et al., 2009; Guo and Li, 2009; Macía et al., 2009; Kittisopikul and Suel, 2010; Sontag, 2010).
Few studies, however, focused attentions on the effect of feed-forward on expression noise in biochemical systems. The current study has ever studied the mechanisms of feed-forward regulation in cell fate decisions in budding yeast (Li et al., 2015). As is shown in (Mangan and Alon, 2003), the authors have found that the coherent feed-forward loop rejects transient input pulses and responds only to persistent stimuli. The feed-forward loop attains their steady states if the stimuli act over a sufficiently long time interval. In the paper (Ghosh et al., 2005), the noise characteristics of coherent and incoherent feed-forward loop in the steady state have been studied using the Langevin formalism as well as a numerical simulation. However, it is still unclear how expression noise is associated with the feed-forward structure. Furthermore, a challenging task is to trace the sources of expression noise and elucidate their roles in the feed-forward-mediated pathway. In addition, how noise is propagated in the feed-forward loop has not been fully solved.
To address the above questions, fluctuation and noise propagation in the coherent feed-forward transcriptional regulatory loop are investigated in this paper. Our motivation is to clarify the potential relationships between network structure, noise characteristics, and biological function. The main contribution of our study is that we decompose the expression noise of each element in the coherent feed-forward loop into different noise sources (denoted as fine structure here). We believe that our study presents a possible understanding for why has the biological system evolved into a coherent feed-forward regulatory mechanism. This paper is organized as follows. In Section Mathematical modeling and analytical noise, the mathematical models of coherent feed-forward loop, including its main road and branch subsystems, are presented first. Then the related theoretical methods are introduced to calculate variances and normalized variations of each expression production in these motifs. Further, in Section Results, we analyse the fluctuation and noise propagation in the coherent feed-forward loop and its subsystems. Finally, the conclusions and discussions are given in Section Conclusion.
Mathematical Modeling and Analytical Noise
A coherent feed-forward loop is composed of three components: Two transcription factors X and Y, where the former regulates the latter, and a target gene Z, where X and Y both bind the regulatory region of Z and jointly modulate the transcription rate (Figure 1A). In order to fully investigate noise characteristics in the coherent feed-forward loop, two subsystems, the main road (Figure 1B) and branch (Figure 1C), are chosen for comparison. The main road is a two-step cascade, through which transcription factor X regulates the expression of transcription factor Y and Y regulates Z. The branch is a one-step cascade, namely transcription factor X regulate target gene Z directly, which acts as a regulatory pathway. Therefore, we will explore how the intrinsic noise is propagated in the coherent feed-forward loop, also including the one-step cascade (i.e., branch) and the two-step cascade (i.e., main road). Below, X means the upstream factor, Y represents the intermediate component, and Z is the downstream element. In our research, the analytical formulas of noise are derived by using the linear noise approximation (Kampen, 2007). The numerical results with Gillespie method (Gillespie, 1977) are used to compare with the analytic results.
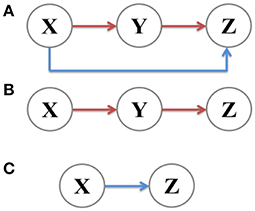
Figure 1. Signal transmission in different gene motifs, including (A) coherent feed-forward loop, (B) main road, i.e., two-step cascade, and (C) branch, i.e., one-step cascade.
Deterministic Model and Steady State
Based on the biochemical reaction rules, the mathematical models of these corresponding gene regulation motifs are built by virtue of ordinary differential equations. Two conditions are considered, respectively.
(A) Treating the level of X as an adjustable parameter.
First, the expression process of X is neglected and the concentration of X is regarded as the control parameter. Hence, the model of coherent feed-forward loop has only two variables. The deterministic dynamics can be described by the following equations:
where x, y, and z are the concentration variables for X,Y, and Z, αy and αz are the maximum level of activated protein production for Y and Z, which are set to ten, respectively. K is the corresponding Hill constant, which is set to unity. The dilution and degradation rate of Y and Z are δy and δz, which are set to unity, respectively. The model of the branch is defined by ω1 = 0, ω2 = 1, the main road by ω1 = 1 and ω2 = 0, and the coherent feed-forward loop by ω1 = 1 and ω2 = 1.
For equations (1) and (2), there exists an attracting fixed point The corresponding phase portrait of this coherent feed-forward loop is illustrated in Figure 2A when the concentration of X is five. It shows that the system converges to a final steady state when the system starts from different initial states, i.e., the attractor of the system. Furthermore, from the phase plane, it is observed that each trajectory from different initial states is nearly close to a straight line, only a small number of trajectories are a little curved. In the case of other parameters, the phase diagram is qualitatively invariant.
(B) Treating the level of X as a variable.
Then, we consider the birth and death processes of X. Therefore, the model of coherent feed-forward loop has three variables whose dynamics can be described by the following equations:
Similarly, the branch is defined by ω1 = 0, ω2 = 1, the main road by ω1 = 1 and ω2 = 0, and the coherent feed-forward loop by ω1 = 1and ω2 = 1. We will consider αx as a control parameter under this condition. αy = αz = 10, δx = δy = δz = 1.
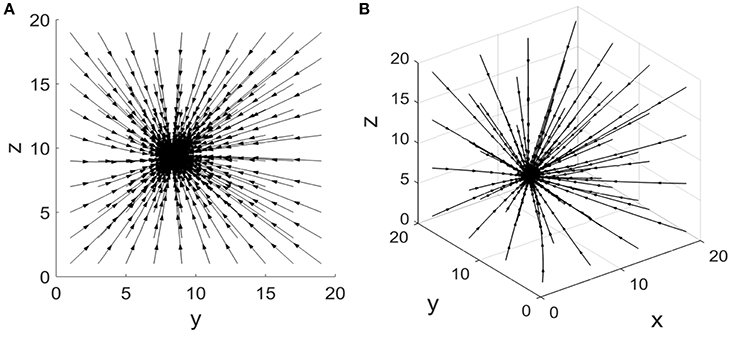
Figure 2. Phase portrait of the coherent feed-forward loop. (A) Treating the concentration of X as an adjustable parameter.(B) Treating the concentration of X as a variable.
Equations (3–5) have an attracting fixed point . Phase portrait of this coherent feed-forward loop is also presented in Figure 2B when the production rate αx is five. The three-dimensional phase diagram (Figure 2B) is similar to the previous two dimensional phase diagram (Figure 2A). Starting some different initial states, after almost straight trajectories, then the system finally reaches a stable state. For other parameters values, the phase diagram remains unchanged from the qualitative perspective.
Stochastic Model and Derivation for the Analytical Formula of Noise
(A) Treating the level of X as an adjustable parameter.
Under small molecular numbers, the stochastic noise can be described exactly with the master equations. A theoretical derivation about the noise expression is given below, starting from the master equations. The numbers of the expression productions can be expressed as Ni, i ∈ {x, y, z}. Relatively, The numbers of the expression productions of Y and Z can be expressed as Ny = Ωy, Nz = Ωz, where Ω is defined as the size of system. Throughout the paper, Ω is set to 100.To characterize the noise, the linear noise approximation is adopted as below.
The joint probability distribution P(Ny, Nz, t) of coupled ordinary differential equations Eqs. (1) and (2) obey the following master equation (Jia and Li, 1997; Kampen, 2007; Brett and Galla, 2013):
where the symbol E represents a step operator, which is defined as . The master equation cannot be solved exactly, so a systematic approximation method has been developed here. By using van Kampen's Ω -expansion method, the numbers of Y and Z is approximated by setting , . The joint probability distribution is written by . Collecting the terms of Ω1/2 in the expansion of Equation (6) reproduces the concentration form of the macroscopic rate equation and the terms of Ω0 get a linear Fokker-Planck equation,
A is the stationary Jacobian matrix of the deterministic equations. B is the stationary diffusion matrix.
Thus,
The linear noise approximation is summarized by (Elf and Ehrenberg, 2003; Thomas et al., 2012)
where matrix C contains both the variances Cyy, Czz,which characterizes the fluctuation in Y and Z. Substituting Equations (8) and (9) into Equation (10), we obtain
To quantify the noise propagation around the steady state, Equation (10) is normalized as
To measure how the balance between production and elimination of Ni is affected by Nk (Paulsson, 2004, 2005; Pedraza and van Oudenaarden, 2005; Hornung and Barkai, 2008; Jia et al., 2009; Pei et al., 2015), Ni and Nk represent the numbers of the expression productions, respectively. i, k ∈ {x, y, z}. The logarithmic gain is defined by , where is the pure production rate and is the pure elimination rate of the expression production. Hik represents a common method of the sensitivity of a response to changes in parameter Nk, also known as logarithmic gain (Savageau, 1977), sensitivity amplification (Goldbeter and Koshland, 1982; Heinrich and Schuster, 1996), or susceptibility (Scott et al., 2006). Considering the constant death rates and the constant transition rates, we can get the logarithmic gains as follows
Under the steady state (i.e., ), the average lifetime τi is determined by the total rate of elimination, Thus, the drift matrix A is represented by .
Then its normalized formation M is rewritten as
In order to study noise propagation, we substitute Equation (15) into Equation (16), and then solve Equation (14) for the normalized variations Vyy, and Vzz. Hence we have
It is seen that the upstream X has no contribution to the total noise in downstream Z, while the intermediate Y transmits a part of expression noise to Z, as shown in Figure 3A. Noise from neighbor is called the one-step propagation noise.
Equations (1) and (2) can be translated into the following set of birth-death processes:
where Equations (19) and (20) describe the production of Y and Z,respectively. In Equations (19), , and in Equations (20), . The degradations of Y and Z are described by Equations (21) and (22), respectively. Stochastic simulation of chemical reactions is performed using the Gillespie algorithm (Gillespie, 1977).
B. Treating the level of X as a variable.
The joint probability distribution P(Nx, Ny, Nz, t) of coupled ordinary differential equations (Equations 3–5) obey the following master equation:
Thus,
The linear noise approximation is summarized by AC + CAT + ΩB = 0. We get
Taking into account the constants of both the self-proliferation rates and the death rates, the logarithmic gain Hik can be obtained
Under the steady state, the average lifetime τi is determined by the total rate of elimination, respectively. In order to study noise propagation, we substitute Equation (32) into Equation (16), and then solve Equation (14) for the normalized variations Vxx, Vyy, and Vzz here, and then we have
We can see that, accompanied by signal transduction in the network, the noise is also transmitted along these pathways. The upstream X has contributions to the total noise in Y and Z via one-step (branch road) and two-step (main road) propagation, respectively (see Figure 3B). Y also delivers a part of noise to Z by one-step propagation. It is noted that the analytic expression of total noise in Z seems to be complex. However, the third term Vtwo−steps propagation noise from X on the right describes the two-step propagation noise from X to Z.
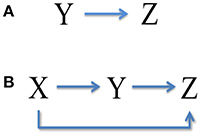
Figure 3. Noise transmission in coherent feed-forward loop. (A) Treating the concentration of X as an adjustable parameter. (B) Treating the concentration of X as a variable.
Results
Based on the theoretical formulas of variances and normalized variations obtained above, we can make a further analysis about how noise is transmitted in the coherent feed-forward loop. Some interesting results are observed.
The Total Noise Level of Downstream Component is Always the Smallest
In order to illustrate noise characteristic of different nodes in these small gene networks, as observed in Equations (18)and(35), we investigate the normalized variations of each element in a variety of situations, which can present a global feature.
When the concentration of X is constant and regarded as a control parameter, the normalized variations Vyy and Vzz under different conditions are given in Figures 4A–C. It shows that with the increasing of x, the normalized noise levels in Y and Z both decrease. For the two-step cascade in the main road (Figure 4B), there is a critical value, below which the normalized variation of the Y is larger than that of Z. Beyond the critical point, the situation is slightly reversed, the noise of downstream component becomes larger than that of the upstream. However, for the coherent feed-forward loop, it can be found that the critical value almost disappears (Figure 4C). That is to say, no matter how much the value of x is, the normalized variation of Z is always smaller than that of Y. The result shows that, due to the addition of regulation branch, the noise of the downstream element becomes the smallest.
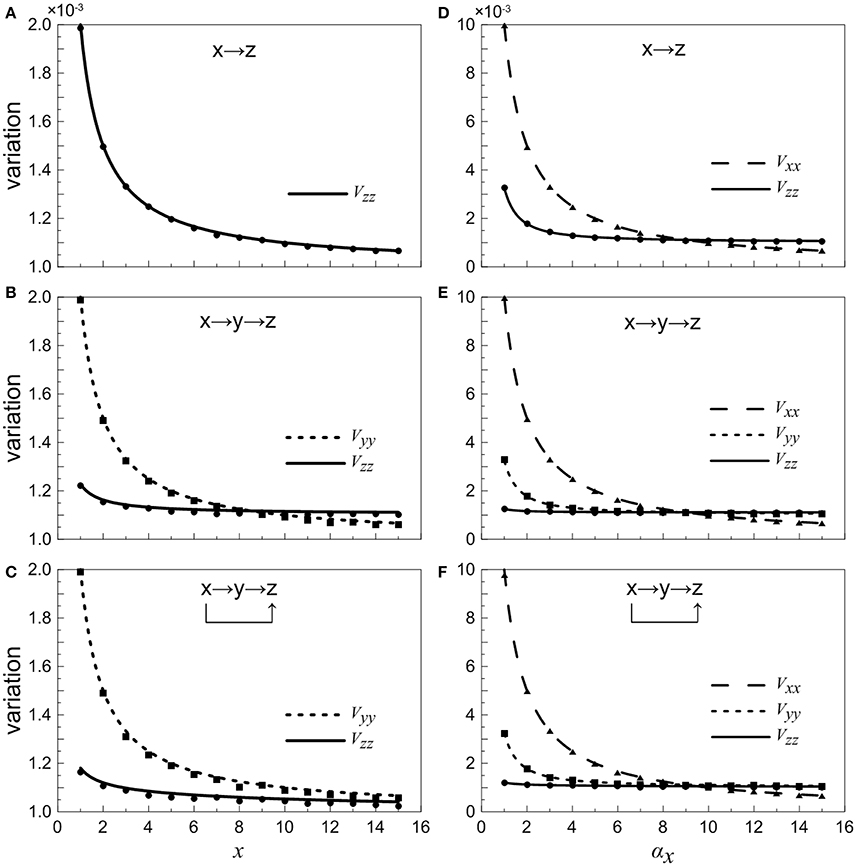
Figure 4. Dependences of normalized variations of different genes on control parameters for different motifs. (A–C) Treating the concentration of X as an adjustable parameter. (D–F) Treating the concentration of X as a variable. From top to bottom, the results for one-step cascade (branch), two-step cascade(main road) and coherent feed-forward loop are shown, respectively. Lines are theoretical predictions with Equations (17, 18) and (33–36), and solid markers are from simulations using the Gillespie method.
When we treat the production rate αx as a control parameter, both X and Y have contributions to the total noise of Z. The noise curves of X are calculated and supplied in Figures 4D–F. The noise of X is the largest when αx is less than certain threshold for all cases. When αx increases to a certain value, the concentration of X increases, hence the intrinsic noise of X is reduced. It is illustrated that, in the region below a certain critical point, the total noise level of downstream component is the smallest compared with other upstream components. Basically, if the stochastic birth-death process of X is involved, the noise levels are enhanced, but the critical points are only modified slightly.
Noise Characteristics of Gene Z
Because the target gene Z is a downstream gene and can be considered as the system's output, we focus on the noise characteristics of gene Z. A comparison between the normalized variations Vzz for different motifs is plotted in Figure 5. It is observed that the noise curve of coherent feed-forward loop is the lowest especially when the control parameter αx is small. Our theoretical findings reveal that the multi-step process is beneficial for signal transmission from X to Z, i.e., the coherent feed-forward loop can attenuate effectively the noise level of downstream gene. Therefore, living organisms could utilize feed forward for better survival in fluctuating environments.
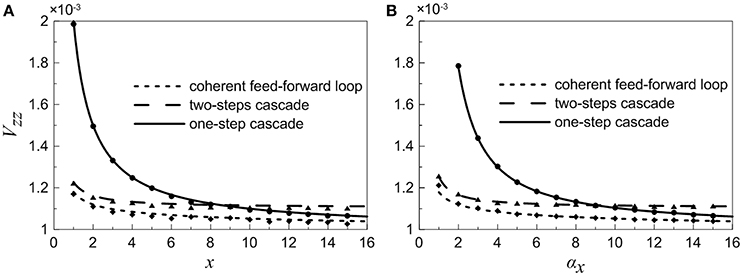
Figure 5. Normalized variations of gene Z for different motifs. (A) Treating the concentration of X as an adjustable parameter. (B) Treating the concentration of X as a variable. Lines are theoretical predictions with Equations (18), (35), and (36), and solid markers are from simulations using the Gillespie method.
For the one-step cascade, signal X can be propagated directly to Z, however, the noise level is always larger than that of the other motifs. In addition, the two noise curves of one-step cascade and two-step cascade intersect at a certain point.
Noise Decomposition
As is mentioned above, the total noise can be decomposed into a series of noise terms, and each noise term represents different sources. As observed in Equation (18), when X is considered as an adjustable constant, the total noise in Z consists of two noise components, in which the first one is pure intrinsic noise in Z, the second one is the fluctuation propagated from the neighbor Y (i.e., one-step noise propagation). However, as seen in Equation (35), if we treat X as a variable, then the total noise in Z contains more noise sources, including pure intrinsic noise of Z, one-step propagation noise from X (X regulates Z directly via feed forward loop), one-step propagation noise from neighboring Y, and two-step propagation noise from X (X modulates Z indirectly through Y). In order to study noise propagation in the coherent feed-forward loop, the total noise and different-step noise sources are theoretically discussed in Equations (18) and (35).
Case (i): The concentration of X is an adjustable constant. The inset in Figure 6A shows that the total noise and pure intrinsic noise in Z both vary monotonously with increasing x. The noise levels are slightly large at the beginning and then decreases rapidly, which is agreed qualitatively with the fact that molecular noise is negatively correlated with molecular number. Furthermore, it is obvious that the total noise is mainly caused by pure intrinsic noise of Z, and only a small proportion of noise is originated from the one-step propagation. In Figure 6A, the noise term from one-step propagation is plotted. It can be found that with the increase of the concentration of X, the transmitted noise is reduced and finally disappears.
Case (ii): The concentration of X is a variable. The inset in Figure 6B shows that the total noise in Z is also mainly determined by its intrinsic noise. However, the fine structure of noise components can be further observed by our theoretical results. The three curves exhibit clearly the different-steps noise propagation.
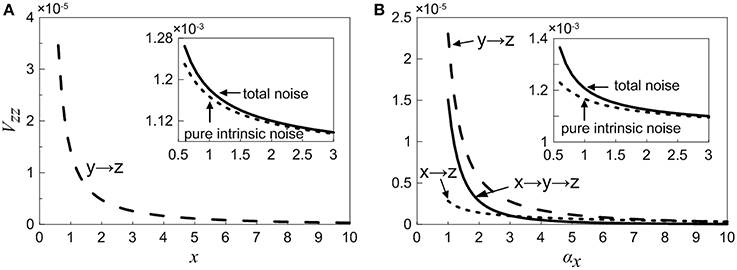
Figure 6. Noise propagation in coherent feed-forward loop. (A) Treating the concentration of X as an adjustable parameter. (B) Treating the concentration of X as a variable. Long point line represents the one-step propagation noise of Y, short dot line represents the one-step propagation noise of X. Solid line shows two-step propagation noise of X. In the inset, solid line shows the total noise and short dot line represents pure intrinsic noise of Z.
Contributions of Upstream And Intermediate Components to Downstream Element's Total Noise
In order to study the propagation feature of the intrinsic expression noise along the direction of signaling transduction, we add the one-step and two-step noise terms of X together. Then, the contribution of noise propagation from X to Z is compared with the contribution from Y to Z, as shown in Figure 7A. It is observed that the noise contribution of the upstream factor X is relatively smaller. With the increasing of the control parameter, the noise contribution to Z from Y becomes close to that from X. Roughly speaking, the noise transmitted from upstream is weaker than the noise propagated from intermediate neighbor.
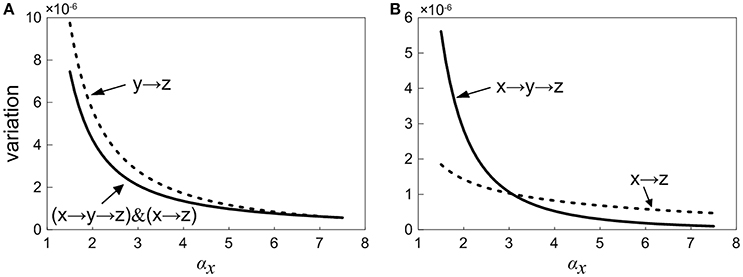
Figure 7. Normalized variation in Z with increasing the control parameter for different propagation pathway. (A) Solid line shows the noise level including the first-step and two-step noise propagation pathways from X to Z. Short dot line represents the first-step noise propagation pathway from Y to Z. (B) Short dot line represents the one-step noise propagation pathway from X to Z. The solid line shows two-step noise propagation pathway from X to Z.
Characteristics of Noise Propagation via Main Road and Branch in the Loop
We further consider how the expression noise of upstream component X is transferred to downstream Z via the main road and branch. The curves of noises propagated through main road and branch are plotted in Figure 7B, respectively. It shows that there is an intersection point for two noise curves, i.e., there exists a critical point. When the control parameter is below the critical value, the noise transmitted through the branch is relatively smaller. On the other hand, when the system is beyond the critical value, the noise transmitted via main road is comparatively smaller. It might be caused by the fact that for signaling systems, the regulation of branch occupies the strategic position in the early stage, however, the main road plays a major role in the late stage. Coherent feed-forward loop meets the requirements of different periods. Therefore, our result provides a potential club to explain the reason a large number of coherent feed-forward transcriptional regulatory motifs exists in the cell.
Conclusion
A population of genetically identical cells exposing to the same extracellular environment may exhibit considerable noise in the mRNA or protein level. This cell-to-cell noise is generated largely due to the limited number of reacting molecules such as gene copies, mRNA, or proteins. Understanding the dynamics of noise propagation in gene regulation systems is an important question on noise analysis in biophysics and system biology.
In this paper, we studied how the expression noise is propagated through a coherent feed-forward loop. First we established a toy yet representative model of gene regulation with feed-forward. Then the theoretical formulas for noise propagation were derived by using the linear noise approximation of master equation and logarithmic gain. We have analytically shown that the total noise is a simple sum of different noise sources including the intrinsic noise and the transmitted noise from other elements in the loop. Therefore, signal transmission is accompanied by noise propagation. In principle, the sub-processes in signal transduction may also contribute to the total noise. By analyzing this decomposition of expression noise, we have further obtained some interesting results about noise characteristics and propagation.
(i) Compared with other upstream components, the noise level of downstream component is smaller in the coherent feed-forward loop due to the addition of branch. The multi-channel process in the coherent feed-forward loop is advantageous to the propagation of signals, which means that the expression noise level of downstream gene can be reduced due to feed forward loop. Our finding may present a clue to understand why the fate decision system in budding yeast would evolve into a coherent feed forward structure (Li et al., 2015).
(ii) The main noise source in the total noise for downstream component is intrinsic noise. The noise propagated from upstream factor is weaker than the noise transmitted from intermediate component when the system is below this critical point. By comparing the different noise contributions of upstream factors, a transition point in the coherent feed-forward loop is observed. When the system is below this transition point, the noise of the main road is relatively higher while the noise of branch is higher when the system is beyond this point. The two-phase mechanism could be advantageous to the signal propagation.
Phosphotransferase system (PTS) is a signaling network in bacteria, responsible for sensing and using a certain nutrient. In the PTS, enzyme I (EI) is first autophosphorylated and then transfers the phosphoryl group to enzyme IIA-Glucose (EIIAGlc) via enzyme histidine phosphorcarrier (HPr). As an alternative pathway, we found that, EIIAGlc can be phosphorylated directly by EI in the absence of HPr. Therefore, the PTS is similar to the above feed-forward system. Recently, using the paramagnetic NMR spectroscopy and mathematical model, we have investigated the mechanism of phosphoryl transfer between the EI and EIIAGlc and demonstrated the physical basis for their ultraweak interaction (Xing et al., 2014). Interestingly, by a further dynamical analysis, a critical point is also found in the PTS system with feed-forward loop. When the concentration of HPr is smaller than a critical value, the main road plays a major role on transfer phosphate, however the transfer of phosphoryl group through the branch is dominated when the system is beyond the point. We hope that the potential relationship between the two transition points in the feed-forward system and the PTS system can be clarified in our next work.
Our research has clarified the potential relationships between feed-forward structure, noise characteristics, and signal transduction. By comparing the properties of three different motifs, we easily find that the feed-forward motif is a best design for signal transduction because it excels in the noise-reduction function. So far, it is the first time to clarify noise characteristics and propagation mechanism in a coherent feed-forward loop by analytical method. The ability to dissect theoretically noise propagation through complex biological networks enables the researchers to understand the role of noise in function and evolution. Our work provides a preliminary result for noise decomposition in gene regulation circuits. However, there still exist some deficiencies in our theoretical work. (i) Because the coherent feed-forward loop has the highest abundance in nature, we have only analyzed this form of coherent feed-forward loop. It is worthy to study the noise transmission in other feed-forward loops. (ii) Due to lack of experimental data, it is difficult to build a quantitative coherent feed-forward loop model. Only a coarse model of coherent feed-forward loop is used to explore the qualitative behaviors. For example, in the reaction process, the Hill coefficient is equal to 1 without taking into account the case of N greater than 1. (iii) We only select one set of parameter values to make a simple analysis. We can see the fine structure of total noise for each component, but the noise level is very small, especially the first-step propagation noise via branch.
Author Contributions
Conceived and designed the experiments: RG, YJ, and MY. Performed the experiments: RG, QL, YY, HD, and CM. Analyzed the data: RG, QL, YY, HD, CM, YJ, and MY. Contributed reagents/materials/analysis tools: RG, QL, YY, HD, and CM. Wrote the paper: RG, YJ, and MY.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported by the Fundamental Research Funds for the Central Universities (Grant No. 2662015QC041 and 2662014BQ069), Huazhong Agricultural University Scientific & Technological Self-innovation Foundation (Program No. 2015RC021), and the National Natural Science Foundation of China (Grant No. 11675060, No.11547244, No.91330113, No.11275259, No.11175068, No.11474117).
References
Acar, M., Becskei, A., and van Oudenaarden, A. (2005). Enhancement of cellular memory by reducing stochastic transitions. Nature 435, 228–232. doi: 10.1038/nature03524
Alon, U. (2006). An Introduction to Systems Biology: Design Principles of Biological Circuits. Boca Raton, FL: Chapman & Hall/CRC.
Alon, U. (2007). Network motifs: theory and experimental approaches. Nat. Rev. Genet. 8, 450–461. doi: 10.1038/nrg2102
Arkin, A., Ross, J., and McAdams, H. H. (1998). Stochastic kinetic analysis of developmental pathway bifurcation in phage λ-infected Escherichia coli Cells. Genetics 149, 1633–1648.
Austin, D. W., Allen, M. S., McCollum, J. M., Dar, R. D., Wilgus, J. R., Sayler, G. S., et al. (2006). Gene network shaping of inherent noise spectra. Nature 439, 608–611. doi: 10.1038/nature04194
Barkai, N., and Leibler, S. (2000). Circadian clocks limited by noise. Nature 403, 267–268. doi: 10.1038/35002258
Becskei, A., and Serrano, L. (2000). Engineering stability in gene networks by autoregulation. Nature 405, 590–593. doi: 10.1038/35014651
Berridge, M. J. (2001). The versatility and complexity of calcium signalling. Novartis Found. Symp. 239, 52–64.: discussion 64–67, 150–159.
Brett, T., and Galla, T. (2013). Stochastic processes with distributed delays: chemical langevin equation and linear-noise approximation. Phys. Rev. Lett. 110:250601. doi: 10.1103/physrevlett.110.250601
Dekel, E., Mangan, S., and Alon, U. (2005). Environmental selection of the feed-forward loop circuit in gene-regulation networks. Phys. Biol. 2, 81. doi: 10.1088/1478-3975/2/2/001
Elf, J., and Ehrenberg, M. (2003). Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Res. 13, 2475–2484. doi: 10.1101/gr.1196503
Gillespie, D. T. (1977). Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 81, 2340–2361. doi: 10.1021/j100540a008
Ghosh, B., Karmakar, R., and Bose, I. (2005). Noise characteristics of feed forward loops. Phys. Biol. 2, 36. doi: 10.1088/1478-3967/2/1/005
Goentoro, L., Shoval, O., Kirschner, M. W., and Alon, U. (2009). The incoherent feedforward loop can provide fold-change detection in gene regulation. Mol. Cell 36, 894–899. doi: 10.1016/j.molcel.2009.11.018
Goldbeter, A., and Koshland, D. E. (1982). Sensitivity amplification in biochemical systems. Q. Rev. Biophys. 15, 555–591. doi: 10.1017/S0033583500003449
Guo, D., and Li, C. (2009). Stochastic and coherence resonance in feed-forward-loop neuronal network motifs. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 79(5Pt 1):051921. doi: 10.1103/PhysRevE.79.051921
Harada, Y., Funatsu, T., Murakami, K., Nonoyama, Y., Ishihama, A., and Yanagida, T. (1999). Single-molecule imaging of RNA polymerase-DNA interactions in real time. Biophys. J. 76, 709–715. doi: 10.1016/S0006-3495(99)77237-1
Harris, S. L., and Levine, A. J. (2005). The p53 pathway: positive and negative feedback loops. Oncogene 24, 2899–2908. doi: 10.1038/sj.onc.1208615
Hasty, J., Pradines, J., Dolnik, M., and Collins, J. J. (2000). Noise-based switches and amplifiers for gene expression. Proc. Natl. Acad. Sci. U.S.A. 97, 2075–2080. doi: 10.1073/pnas.040411297
Heinrich, R., and Schuster, S. (1996). The Regulation of Cellular Systems. (New York, NY: Springer).
Jia, Y., and Li, J.-R. (1997). Reentrance phenomena in a bistable kinetic model driven by correlated noise. Phys. Rev. Lett. 78, 994–997. doi: 10.1103/PhysRevLett.78.994
Hooshangi, S., and Weiss, R. (2006). The effect of negative feedback on noise propagation in transcriptional gene networks. Chaos 16:026108. doi: 10.1063/1.2208927
Hornung, G., and Barkai, N. (2008). Noise propagation and signaling sensitivity in biological networks: a role for positive feedback. PLoS Comput. Biol. 4:e8. doi: 10.1371/journal.pcbi.0040008
Jia, Y., Liu, W., Li, A., Yang, L., and Zhan, X. (2009). Intrinsic noise in post-transcriptional gene regulation by small non-coding RNA. Biophys. Chem. 143, 60–69. doi: 10.1016/j.bpc.2009.04.001
Kalir, S., Mangan, S., and Alon, U. (2005). A coherent feed-forward loop with a SUM input function prolongs flagella expression in Escherichia coli. Mol. Syst. Biol. 1, 2005 0006. doi: 10.1038/msb4100010
Kampen, N. G. V. (2007). Stochastic Processes in Physics and Chemistry, 3rd Edn. (Amsterdam: North Holland Publishing Company).
Kaplan, S., Bren, A., Dekel, E., and Alon, U. (2008). The incoherent feed-forward loop can generate non-monotonic input functions for genes. Mol. Syst. Biol. 4, 203. doi: 10.1038/msb.2008.43
Kim, D., Kwon, Y. K., and Cho, K. H. (2008). The biphasic behavior of incoherent feed-forward loops in biomolecular regulatory networks. Bioessays 30, 1204–1211. doi: 10.1002/bies.20839
Kittisopikul, M., and Süel, G. M. (2010). Biological role of noise encoded in a genetic network motif. Proc. Natl. Acad. Sci. U.S.A. 107, 13300–13305. doi: 10.1073/pnas.1003975107
Lewis, R. S. (2001). Calcium signaling mechanisms in T lymphocytes. Annu. Rev. Immunol. 19, 497–521. doi: 10.1146/annurev.immunol.19.1.497
Li, W., Yi, M., and Zou, X. (2015). Mathematical modeling reveals the mechanisms of feedforward regulation in cell fate decisions in budding yeast. Quant. Biol. 3, 55–68. doi: 10.1007/s40484-015-0043-0
Li, Y., Yi, M., and Zou, X. (2014). The linear interplay of intrinsic and extrinsic noises ensures a high accuracy of cell fate selection in budding yeast. Sci. Rep. 4:5764. doi: 10.1038/srep05764
Liu, X., Wang, X., Yang, X., Liu, S., Jiang, L., Qu, Y., et al. (2015). Reliable cell cycle commitment in budding yeast is ensured by signal integration. Elife 4. doi: 10.7554/eLife.03977
Macía, J., Widder, S., and Solé, R. (2009). Specialized or flexible feed-forward loop motifs: a question of topology. BMC Syst. Biol. 3:84. doi: 10.1186/1752-0509-3-84
Mangan, S., and Alon, U. (2003). Structure and function of the feed-forward loop network motif. Proc. Natl. Acad. Sci. U.S.A. 100, 11980–11985. doi: 10.1073/pnas.2133841100
Mangan, S., Itzkovitz, S., Zaslaver, A., and Alon, U. (2006). The incoherent feed-forward loop accelerates the response-time of the gal system of Escherichia coli. J. Mol. Biol. 356, 1073–1081. doi: 10.1016/j.jmb.2005.12.003
Mangan, S., Zaslaver, A., and Alon, U. (2003). The coherent feedforward loop serves as a sign-sensitive delay element in transcription networks. J. Mol. Biol. 334, 197–204. doi: 10.1016/j.jmb.2003.09.049
McAdams, H. H., and Arkin, A. (1997). Stochastic mechanisms in gene expression. Proc. Natl. Acad. Sci. U.S.A. 94, 814–819. doi: 10.1073/pnas.94.3.814
Monod, J. (1972). Chance and Necessity: An Essay on the Natural Philosophy of Modern Biology by Jacques Monod. (New York, NY: Vintage Books).
Paulsson, J. (2004). Summing up the noise in gene networks. Nature 427, 415–418. doi: 10.1038/nature02257
Paulsson, J. (2005). Models of stochastic gene expression. Phys. Life Rev. 2, 157–175. doi: 10.1016/j.plrev.2005.03.003
Pedraza, J. M., and van Oudenaarden, A. (2005). Noise propagation in gene networks. Science 307, 1965–1969. doi: 10.1126/science.1109090
Pei, Q. M., Zhan, X., Yang, L. J., Shen, J., Wang, L. F., Qui, K., et al. (2015). Fluctuation and noise propagation in phenotypic transition cascades of clonal populations. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 92:012721. doi: 10.1103/PhysRevE.92.012721
Prill, R. J., Iglesias, P. A., and Levchenko, A. (2005). Dynamic properties of network motifs contribute to biological network organization. PLoS Biol. 3:e343. doi: 10.1371/journal.pbio.0030343
Rao, C. V., Wolf, D. M., and Arkin, A. P. (2002). Control, exploitation and tolerance of intracellular noise. Nature 420, 231–237. doi: 10.1038/nature01258
Savageau, M. A. (1977). Biochemical Systems Analysis: Study of Function and Design in Molecular Biology. (Massachusetts: Addison-Wesley Educational Publishers Inc).
Scott, M., Ingalls, B., and Kaern, M. (2006). Estimations of intrinsic and extrinsic noise in models of nonlinear genetic networks. Chaos 16, 026107. doi: 10.1063/1.2211787
Sontag, E. D. (2010). Remarks on feedforward circuits, adaptation, and pulse memory. IET Syst. Biol. 4, 39–51. doi: 10.1049/iet-syb.2008.0171
Swain, P. S., Elowitz, M. B., and Siggia, E. D. (2002). Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. U.S.A. 99, 12795–12800. doi: 10.1073/pnas.162041399
Thomas, P., Straube, A. V., and Grima, R. (2012). The slow-scale linear noise approximation: an accurate, reduced stochastic description of biochemical networks under timescale separation conditions. BMC Syst. Biol. 6:39. doi: 10.1186/1752-0509-6-39
Tsimring, L. S. (2014). Noise in biology. Rep. Prog. Phys. 77:026601. doi: 10.1088/0034-4885/77/2/026601
Wall, M. E., Dunlop, M. J., and Hlavacek, W. S. (2005). Multiple functions of a feed-forward-loop gene circuit. J. Mol. Biol. 349, 501–514. doi: 10.1016/j.jmb.2005.04.022
Xing, Q., Huang, P., Yang, J., Sun, J. Q., Gong, Z., Dong, X., et al. (2014). Visualizing an ultra-weak protein-protein interaction in phosphorylation signaling. Angew. Chem. Int. Ed. Engl. 53, 11501–11505. doi: 10.1002/anie.201405976
Keywords: coherent feed-forward loop, noise propagation, noise decomposition, linear noise approximation, expression noise
PACS numbers: 87.18.Tt, 87.16.dj, 87.17.Aa
Citation: Gui R, Liu Q, Yao Y, Deng H, Ma C, Jia Y and Yi M (2016) Noise Decomposition Principle in a Coherent Feed-Forward Transcriptional Regulatory Loop. Front. Physiol. 7:600. doi: 10.3389/fphys.2016.00600
Received: 27 July 2016; Accepted: 17 November 2016;
Published: 30 November 2016.
Edited by:
Francisco Monroy, Complutense University of Madrid, SpainReviewed by:
Tianshou Zhou, Sun Yat-sen University, ChinaJuan Belmonte, Universidad de Castilla-La Mancha (UCLM), Spain
Copyright © 2016 Gui, Liu, Yao, Deng, Ma, Jia and Yi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ming Yi, eWltaW5nQG1haWwuaHphdS5lZHUuY24=
 Rong Gui1,2,3
Rong Gui1,2,3 Ming Yi
Ming Yi