- 1Auckland Bioengineering Institute, University of Auckland, Auckland, New Zealand
- 2Department of Surgery, University of Auckland, Auckland, New Zealand
- 3Department of Surgery, Vanderbilt University, Nashville, TN, United States
Gastrointestinal (GI) motility is regulated in part by electrophysiological events called slow waves, which are generated by the interstitial cells of Cajal (ICC). Slow waves propagate by a process of “entrainment,” which occurs over a decreasing gradient of intrinsic frequencies in the antegrade direction across much of the GI tract. Abnormal initiation and conduction of slow waves have been demonstrated in, and linked to, a number of GI motility disorders. A range of mathematical models have been developed to study abnormal slow waves and applied to propose novel methods for non-invasive detection and therapy. This review provides a general outline of GI slow wave abnormalities and their recent classification using multi-electrode (high-resolution) mapping methods, with a particular emphasis on the spatial patterns of these abnormal activities. The recently-developed mathematical models are introduced in order of their biophysical scale from cellular to whole-organ levels. The modeling techniques, main findings from the simulations, and potential future directions arising from notable studies are discussed.
Gastrointestinal Electrophysiological Definitions and Disorders
Cyclical contractions of the gastrointestinal (GI) tract are initiated and coordinated by rhythmic, propagating bioelectrical events, termed slow waves (Szurszewski, 1998). Abnormal slow wave activity has long been observed to occur in the gut, and their putative causation of gastrointestinal symptoms and disorders remains an area of significant interest (Lammers, 2013; O'Grady et al., 2014). In the healthy stomach, slow waves normally originate from a single pacemaker located in the proximal stomach along the greater-curvature, rapidly establishing ring wavefronts that propagate antegrade toward the distal stomach, terminating at the pylorus (O'Grady et al., 2010a). A number of mathematical models have been developed to study both normal slow wave activity, and a wide range of slow wave abnormalities observed in functional disorders and animal models (Lammers et al., 2012, 2015; O'Grady et al., 2012a; Angeli et al., 2015). This review presents the current state of mathematical modeling of these slow wave abnormalities, and also discusses the methods for validating these models.
Terminology
Several terminologies have been applied to describe abnormal GI slow wave activities. While some of these terms have been adopted from cardiac electrophysiology, where they have been well-defined, it is worthwhile to also review these terms in the context of their usage in the GI field. Earlier cardiac electrophysiologists pointed out the granular difference between arrhythmias, i.e., absence of rhythm, and dysrhythmias, i.e., abnormalities of rhythm (Trommer, 1982), but usages in practice over the years have converged the two terms to become synonyms (Marriott, 1984). Conventionally in the GI field, dysrhythmias, and arrhythmias have also been used inter-changeably to represent any abnormal slow waves (Lammers, 2013; O'Grady et al., 2014). Nelsen et al., used both arrhythmias and dysrhythmias to describe abnormal slow waves as early as 1968 (Nelsen and Kohatsu, 1968), while other investigators have maintained both usages to describe abnormal slow wave events (Code and Marlett, 1974).
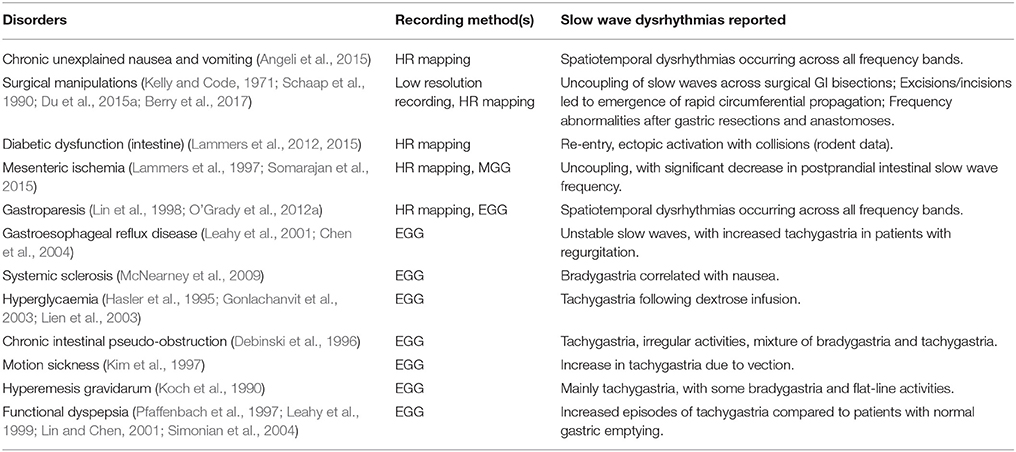
Dysrhythmias can either be defined in terms of frequency, or in terms of spatial pattern. In the stomach, frequency abnormalities have typically been defined as either quiescence, bradygastria, or tachygastria (Code and Marlett, 1974; Stern et al., 1987); while spatial abnormalities have been subjected to a growing list of classifications by various researchers and in various animal models (Table 1). Furthermore, following cardiac conventions, spatial dysrhythmias could also be defined as either abnormal initiation, e.g., ectopic pacemaker, or abnormal conduction, e.g., retrograde propagation. It is worth noting that each of these terms typically describes a single aspect of a dysrhythmia, but in practice dysrhythmic episodes may not occur in isolation. For example, an ectopic initiation event could occur simultaneously with conduction block and collision (Figure 1C), and a conduction block could lead to an aberrant focus of initiation, or a re-entrant conduction abnormality could give rise to secondary conduction abnormalities (O'Grady et al., 2014).

Table 1. Definitions of gastric dysrhythmias. Spatial information was obtained from HR mapping taken directly from the gastric serosal surface.
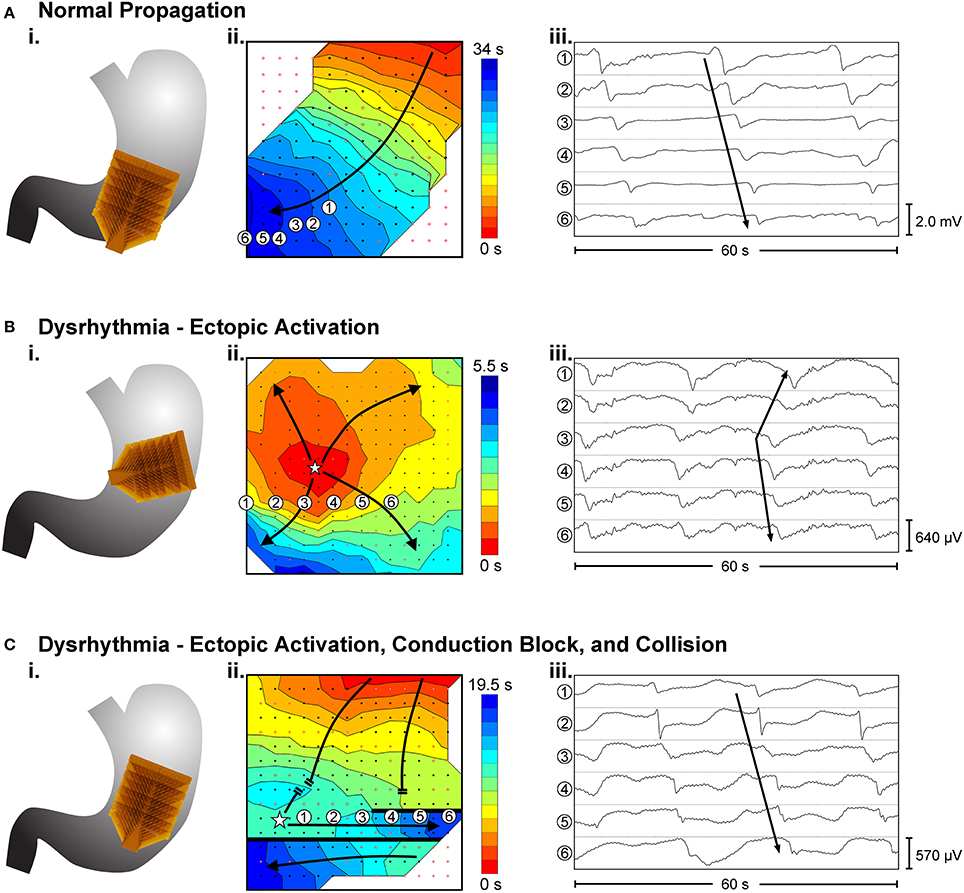
Figure 1. Examples of high-resolution mapping of in-vivo gastric slow waves. (i) An array of 16 × 16 electrodes (brown patch) were placed on the serosal surface of the stomach. (ii) Activation times of slow waves were identified and reconstructed into activation maps with red representing early activation and blue presenting late activation. (iii) Example slow wave recordings from six electrodes are shown in each case. (A) Normal antegrade propagation pattern of gastric slow wave activation (Angeli et al., 2015). (B) An ectopic activation (star) in the proximal stomach. (C) Simultaneous ectopic activation, conduction block and collision of slow waves in the gastric corpus. Adapted from (Angeli et al., 2015).
Dysrhythmias and GI Functional Disorders
Several GI functional disorders have been associated with slow wave dysrhythmias (O'Grady et al., 2014), as detailed in Table 2, with examples of the types of dysrhythmias that have been reported with each disorder. The majority of previous studies of slow wave activity have utilized low-resolution recording methods, where a sparse number of electrodes were placed on the body-surface (electrogastrography/EGG) or directly on the serosal or mucosal surfaces of the GI organs (Familoni et al., 1987; Lin et al., 1998; Lin and Chen, 2001; Coleski and Hasler, 2009). These studies established foundational discoveries of normal and dysrhythmic slow wave activation, but analysis was largely restricted to the frequency domain, although propagation analysis was also attempted (Simonian et al., 2004; Coleski and Hasler, 2009). The results of these EGG and low-resolution electrode studies thereby focused primarily on ectopic activation as a mechanism of slow wave dysrhythmias (Lin et al., 1998; Lin and Chen, 2001; Simonian et al., 2004).
More recently, high-resolution GI mapping has emerged as a key methodological advance, where spatially-dense arrays of hundreds of electrodes are placed directly on the GI organ, enabling analysis of slow wave propagation in spatiotemporal detail (Lammers et al., 2008a; Du et al., 2009a). Recent high-resolution mapping studies in patients with diabetic and idiopathic gastroparesis, and chronic unexplained nausea and vomiting, have now demonstrated that spatially-complex dysrhythmias are prevalent in these functional GI disorders (O'Grady et al., 2012a; Angeli et al., 2015). Importantly, many of these spatial dysrhythmias (Table 1) are now known to occur within the normal slow wave frequency range, such that they may likely have gone undiagnosed with previous frequency-reliant methods. Furthermore, it has also been reported that the slow wave dysrhythmias were correlated with loss of the interstitials cells of Cajal (ICC) (O'Grady et al., 2012a; Angeli et al., 2015), which could result in ICC network remodeling (Ordog et al., 2000).
Current State of GI Electrophysiological Modeling
Mathematical modeling uses equations to formulate relationships between parameters of a biophysical process. Additional analyses can then be performed on the equations to infer the causal relationship between the parameters over a large parameter space in silico, complementary to experimental data, which are needed to validate the model in some capacity. It is worth noting that although a goal is to develop models capable of predictive simulations of physiological functions, no model in its current state can realistically accomplish this ambitious aim in a way that mimics real biological events. Instead, mathematical models are developed to represent electrophysiological mechanisms at discrete biophysical scales as simply and accurately as possible, with input from experimental data at each scale, and attempts are then made to link mechanisms together across these scales.
One particularly significant approach of mathematical modeling is thus to develop a system of equations by following the hierarchy of biological systems across multiple spatiotemporal scales. Such an approach is also called multi-scale modeling, which has been increasingly applied with great effect to study normal and dysrhythmic GI slow waves and dysmotility (Cheng et al., 2013; Du et al., 2013, 2016b). Generally, in a multi-scale model of dysrhythmias the lowest scale relates to the kinetics of the ion channels, which are usually collected into individual ion conductances, with Hill-type activation and inactivation parameters fitted to experimental data (Lees-Green et al., 2011). The dependence of an ion conductance on membrane potential can be modeled using a Hodgkin & Huxley approach, and applied over multiple types of conductance to model the change in slow waves. It is worth noting that the conductance modeled presents an averaged activity of all the same type of conductance in the cell, rather than individual ion channels. As our knowledge of the subcellular processes becomes increasingly clear, more sophisticated techniques such as stochastic modeling and subcellular domain diffusion have also been incorporated to cell models (Lees-Green et al., 2011).
Tissue models require connecting multiple cell models together in a continuum, i.e., spatially averaged, sense has typically been achieved using a reaction-diffusion technique, either in the form of monodomain, bidomain, or tridomain (extended bidomain) equations (Equations 1–6) (Buist and Poh, 2010; Corrias et al., 2012; Du et al., 2013, 2016b; Sathar et al., 2015). The number of domains typically represents the predominant avenues through which the cells are coupled to each other. In the monodomain representation, ICC are assumed to be predominantly coupled via the intracellular domain, whereas in the bidomain representation, the current flow through the extracellular space is also modeled. In contrast to cardiac applications of the tridomain model, which is used to model an additional phase due to non-excitable elements such as fibroblasts (Sachse et al., 2009), the more recently proposed tridomain model represents the coupling between the intracellular spaces of ICC and smooth muscle cells (SMC) and a shared extracellular space (Corrias et al., 2012; Sathar et al., 2015). In each of these cases, under certain assumptions, the higher-order domain models could be reduced to the monodomain model, and extracellular potentials could then be estimated based on the membrane potentials.
Monodomain:
Bidomain:
Tridomain:
where σ represents the tissue conductivity, which could be further characterized as intracellular conductivity (σi; [S m−1]) or extracellular conductivity (σe; [S m−1]). Membrane potential (Vm; [V]) can also be expressed as the difference between intracellular potential and extracellular potential, i.e., ϕi − ϕe. The total current is denoted by Iion [A]. Am [m−1] denotes the surface-to-volume ratio and Cm [F m−2] denotes the membrane capacitance. In the case of the tridomain equations, conductivities, surface-to-volume ratio, membrane capacitance and intracellular potentials are further distinguished between two cell types, with an added coupling current (Icouple) between the two cell types. One of the intracellular domains (Equation 4) represents the cytoplasm of ICC, while the other intracellular domain (Equation 5) represents the cytoplasm of SMC. The two intracellular domains share a common extracellular domain (Equation 6).
The choice of the governing equations in the continuum model typically depends on the specific applications. For example, in the absence of detailed measurements of conductivity parameters, applications involving entrainment modeling would typically only require the monodomain model (Du et al., 2015b, 2017), whereas simulations involving an extracellular stimulus would typically require a bidomain/tridomain approach (Sathar et al., 2015). On the other hand, the higher-domain approach would require more computational power due to the increased complexity of formulation. Though direct comparisons between computational times of GI models are difficult to ascertain with varying parameters and numerical solvers involved in the process, on average the computational time of cardiac bidomain models can be an order of magnitude longer than monodmain models (Plank et al., 2009).
Relating the slow wave activity at the whole-organ level to specific individual cells is a challenging, if not impossible, aspect to resolve. Conceptually, the multi-scale models represent slow waves in a spatially-averaged sense, meaning the “continuum” represents an averaged activity of a group of the same cell types within the immediate vicinity in the underlying tissue (Angeli et al., 2013a). A similar loss of spatial information occurs when whole-organ activity is inferred electromagnetically from the body-surface (Kim et al., 2013; Bradshaw et al., 2016b). In this case, the electrophysiological activation of the organ is approximated using dipole(s), which represent the net activation state of the organ at an instance in time. Despite the loss of specificity in the electrical information when upscaling, the higher-level spatial scales also remain a particularly useful approximation of slow waves in the in vivo state. The appropriate scale of models should be considered according to the level of mechanisms and specific research questions of interest.
Cell Models
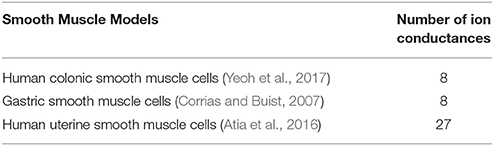
The two main types of biophysically-based cell models being developed over recent years are SMC and ICC, which have been covered extensively in previous reviews (Lees-Green et al., 2011). In general, ICC models incorporate self-excitatory intracellular calcium-based mechanisms to generate slow waves at a specific intrinsic frequency, whereas SMC models require an input stimulus to drive the membrane potentials. Key conductance and/or intracellular calcium dynamics in these cell models are generally fitted to experimental data and validated by reproducing membrane potentials and response to perturbations such as electrical stimuli and drugs. The number of SMC models is limited, including a gastric SMC model derived from animal experimental data (Corrias and Buist, 2007), and uterine SMC derived from uterine human smooth muscle cells (Atia et al., 2016). A list of biophysically-based SMC models is presented in Table 3.
A recent example of ICC model development is the finite-state machine based biophysical model by Sathar et al. (2014). In this model, the cellular activity of the model was represented by an active state and passive state, whereby the active state corresponded to the ionic dynamics of the ICC model developed by Corrias and Buist (2008). The transition between the states was modeled using a finite-state machine approach that was dependent on membrane potential, calcium dynamics, and the refractory/non-refractory period parameters defining the intrinsic frequency of the slow wave pacemaker activity (Figure 2A; Sathar et al., 2014). The finite-state machine approach enabled modeling the effects of external current on the cellular activity and has successfully reproduced experimentally observations of gastric pacing. The finite-state machine model is governed by two important rules: (i) if the cellular activity is “active,” it remains active until the calcium dynamics returns to a quiescent state—after which, it changes to a “passive” state; (ii) on the other hand, if the current cellular activity is “passive,” it remains “passive” until the membrane potential exceeds an excitation potential or until the cellular activity has passed the non-refractory period (Figure 2B).
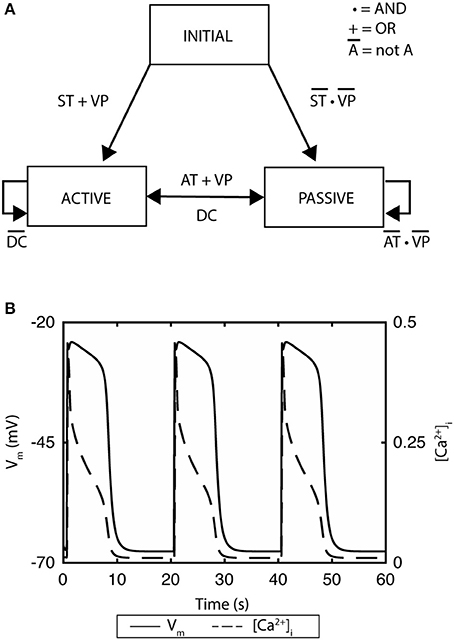
Figure 2. A finite state machine cell model of gastric interstitial cells of Cajal. (A) The model consists of an active state and a passive state. ST indicates if time has passed the startTime, which is set as a parameter and which determines initial excitation when there is no threshold voltage. AT indicates if the non-refractory period has been passed and signals transition from passive state to active state. DC identifies if the change in concentration of intracellular Ca2+ has returned to quiescent state. VP variable is set to true if there is a voltage which is greater than the threshold of the cell. (B) Simulated gastric slow waves and the associated intracellular calcium. Adapted from (Sathar et al., 2014).
In addition to ICC and SMC, other types of cells have also been proposed to play a role in the electrophysiology and neurotransmission of the GI tract. One such cell is the fibroblast-like cell (FLC), which form discrete networks in the myenteric plexus and are widely distributed within the muscular layer of the colon (Kurahashi et al., 2012). One specific FLC positive for platelet-derived growth factor receptor (PDGFRα+) is of particular interest because they are involved in purinergic inhibitory neurotransmissions (Yeoh et al., 2016). Purines released by enteric motor neurons bind to the G-protein coupled receptors in the membrane of the PDGFRα+ cells. The binding initiates a series of intracellular processes resulting in the release of Ca2+ due to inositol 1,4,5-triphosphate (IP3) entering the cytoplasm. The elevation of intracellular Ca2+ in turns activates small Ca2+-activated K+ (SK3) conductance, leading to hyperpolarization of the membrane potential, and potentially also neighboring SMC. Yeoh et al. developed a PDGFRα+ cell model by modifying a spatially-independent version of the model proposed by Bennett et al. (2005) and Yeoh et al. (2016), and with their specific description of the SK3 conductance. The authors were able to demonstrate ATP-induced hyperpolarisation and inhibitory effects of MRS2500 and apamin (SK3 channel blocker) (Bennett et al., 2005). The potential applications of this model may be significant in future, as it may be coupled with existing ICC and SMC models to simulate the effects of neural innervation and feedback on slow wave generations and smooth muscle membrane potentials.
Biophysically-based mathematical models of GI cells have been developed at a steady pace, mainly governed by the availability of experimental data and convergence of evidence regarding key electrophysiological mechanisms. However, nearly all GI cell models have been developed as an “after thought” based on published data that were not originally designed with the potential for modeling in mind. The models were generally only able to reproduce the cellular responses over a set of specific interventions that had already been demonstrated experimentally, although some interesting and clinically-relevant applications have already been demonstrated through the predictive modeling of GI channelopathies (Poh et al., 2012). While this is not a unique problem to the GI field, the true predictive power of cell models could be better realized if investigators would consider modeling when developing their experimental design, as has been done in the cardiac field (Maltsev et al., 2017).
Tissue Models
Propagation of slow waves has typically been modeled as a series of coupled phenomenologically-based oscillators, or by employing biophysically-based ICC models. While there are many ways to formulate the specific coupling between ICC models, the ability of an ICC with a higher intrinsic frequency to “entrain” another coupled ICC with lower intrinsic frequency is fundamental (van Helden et al., 2010). The process of entrainment is a key point of distinction between GI and cardiac electrophysiological models. Whereas the cardiac models represent myocytes as single-event active potentials in response to a pacemaker (often modeled as a stimulus), GI models require an interconnected network of pacemakers, where every point in the network is potentially capable of intrinsically generating slow wave activation (Cheng et al., 2013; Du et al., 2013, 2016b). Previous reviews have covered models that have successfully simulated propagation of gastric and intestinal slow waves at the tissue levels (Du et al., 2013, 2016b). This review covers recent work on the simulation of GI slow wave dysrhythmias.
Most recent tissue-level investigations have focused predominantly on the effects of perturbations on the organization of slow waves. Weakly-coupled oscillators have been used to model both intestinal and colonic slow waves (Linkens, 1978; Linkens and Mhone, 1979). This concept was explored further in a recent study to explore the effects of spatial noise in the intrinsic frequency gradient on intestinal slow wave propagation (Parsons and Huizinga, 2016). The study demonstrated that as the coupling (modeled as a gap junction) between the oscillators decreased over a segment of intestine, more slow wave frequency plateaus appeared (Parsons and Huizinga, 2016). One of the conclusions of this study points to the role of a spatial noise on the organization of slow wave propagation and motor patterns in the intestine. As a limitation of the model, the authors pointed out that the intestinal “waxing and waning” phenomenon was not reproduced by the model, but could be explained by a phase-amplitude modulation mechanism (Huizinga et al., 2014). The dynamic interactions between intestinal slow waves in response to a field-stimulus were later quantified using a phase response curve (Parsons and Huizinga, 2017). The weakly-coupled oscillator was extended to a 2D model to reproduce intestinal slow waves in a number of species, as well as the effects of circumferential ICC loss on partitioning of slow waves (Wei et al., 2017).
Recent high-resolution mapping studies have reported re-entry activities in the stomach and intestine (Table 1). Two specific re-entry activities were discovered: functional re-entry (Du et al., 2015b), where slow waves propagate in a sustained manner around a core either as in a rotor (Figure 3), or figure-of-eight pattern; and anatomical re-entry, where slow wave propagation occurs in continuity around the lumen of the intestine (Angeli et al., 2013b). These re-entry activities were recently modeled in two-dimensional models using a simplified ICC model and the monodomain equation, using a stimulus-driven protocol to invoke the re-entry (Du et al., 2015b, 2017). In order to invoke a rotor in a short segment intestinal tissue, single-pulse stimulus (100 μA mm−2; 100 ms) was used to initiate the re-entry next to a temporary conduction block prescribed by the refractory period in the middle of the model (Plank et al., 2009). In particular, it was demonstrated that there was a relatively narrow parameter space in terms of the timing relative to the refractory tail of the previous wavefronts, during which a sustained functional re-entry could be invoked; otherwise, the prescribed intrinsic frequency gradient in the models was essentially able to correct the wavefront over time (Du et al., 2015b, 2017). Anatomical re-entry around the circumference of a 3D lumen was also demonstrated to occur under a similar set of constraints to the functional re-entry, with the added consideration of the geometry of the lumen (Du et al., 2017). One of the features of a sustained re-entry is the elevated frequency associated with the entrainment of slow waves in the core, as demonstrated experimentally (Lammers et al., 2008b). This elevated frequency serves to sustain the re-entry and can lead to entrainment of a substantial section of adjacent intestine. A secondary observation was a frequency-conduction restitution type of relationship where the elevated frequency induces a local reduction in conduction velocity of slow waves (Du et al., 2015b, 2017). Other investigators have modeled the effects of temperature on intestinal slow waves and the formation of re-entry activities (Gizzi et al., 2010).
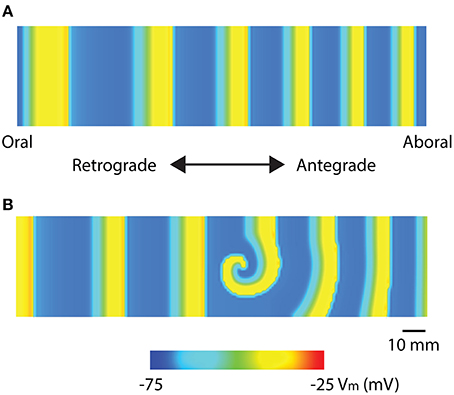
Figure 3. Mathematical models of intestinal slow wave propagation. (A) Entrained slow waves over an intrinsic frequency gradient of 17–14.6 cpm (entrained to 17 cpm) were simulated over a 2D model. (B) A functional rotor was invoked in the middle of the 2D model using a 30 s long prolonged temporary conduction block. The rotor could be sustained with entrained waves propagating in both antegrade and retrograde directions, with an elevated frequency of 21 cpm. Adapted from (Du et al., 2017).
A bi-directionally coupled model of ICC networks, achieved through coupling of myenteric and intramuscular ICC populations, has been proposed as a homeostatic mechanism in the gut (O'Grady et al., 2012b). Gastric slow waves demonstrate a high degree of anisotropy, whereby slow waves propagate 2.5 times faster in the circumferential axis than the longitudinal axis (O'Grady et al., 2012b; Du et al., 2016a). Similar anisotropy also exists in the small intestine of some species, albeit to a much lesser extent (Angeli et al., 2013b). During normal gastric slow wave propagation, this anisotropy is only observed in the region of the normal pacemaker; thereafter, ring wavefronts are rapidly formed that propagate solely in the longitudinal axis without the need for circumferential spread (O'Grady et al., 2010a). However, during dysrhythmias, the rapid circumferential propagation is routinely observed to emerge in regions adjacent to dysrhythmic sources, due to either aberrant foci of initiation or conduction abnormalities interrupting the normal longitudinal pattern (O'Grady et al., 2012b; Cheng et al., 2013).
The impact of conduction anisotropy was further explored in a simulation where a small full-thickness segment of gastric tissue was excised as part of a biopsy (Du et al., 2015a). Gastric slow wave propagation around this type of excisional biopsy was also mapped experimentally from human subjects. The results demonstrated that area of rapid circumferential conduction was dependent on the orientation of the excision. At all orientations, the slow waves began to normalize in the longitudinal direction at a distance distal to the stapled wound within the field of mapping (60 × 60 mm2). It is notable that there is no standard guideline on the dimensions and orientations of gastric excisional procedures in practice (Du et al., 2015a), and these findings could theoretically provide novel insights to minimize post-operative motility changes associated with gastric incisions in future.
In contrast to cell modeling work, recent GI tissue models were generally designed with specific experimental protocols to explore key physiological questions, and/or to provide predictions of potential protocols to invoke sustained dysrhythmia behaviors. Particular efforts have been invested by multiple groups to investigate the organization of intestinal slow waves over extended tissue scales and the formation of re-entry in the stomach and intestine (Gizzi et al., 2010; Du et al., 2015b, 2017; Parsons and Huizinga, 2016). Experimentally, one of the next steps is to attempt to invoke sustained periods of re-entry to thoroughly explore the conditions under which these dysrhythmias occur and possible ways to eliminate them. The proposed relationship between the timing of stimulus and the refractory tail of the preceding wave in invoking re-entry already suggests the potential requirement for monitoring slow wave propagation in real-time experimentally (Bull et al., 2011). Another important avenue of tissue modeling studies has been to explore the structure-function relationship between the ICC network, slow wave propagation and other GI cells, such as the FLC. One potential approach is to reconstruct the structural distributions of these cells from immunofluorescence images and develop a continuum framework in which the interactions between multiple cell types could be taken into account. The structural networks and cellular functions could then be perturbed to explore the effects of ion chancel inhibition and/or cell loss on GI slow waves. Effects of non-electrically active tissues could be modeled by detailed description of the extracellular tissue conductivities in the higher domain models.
Organ Models
The techniques of simulating slow waves over the whole-organ are similar to the tissue models, with a few added considerations (Du et al., 2013, 2016b). First, gastric slow wave propagation has been shown to exhibit significant inter-regional variations within the stomach (Kelly and Code, 1971; Lammers and Stephen, 2008; Egbuji et al., 2010; O'Grady et al., 2010a). In vivo high-resolution mapping data have demonstrated that the fundus is generally quiescent in large monogastric species, and a pacemaker region exists in the proximal corpus along the greater curvature, from which gastric slow waves rapidly form ring wavefronts that propagate distally toward the antrum (Lammers and Stephen, 2008; Egbuji et al., 2010; O'Grady et al., 2010a). In humans, a marked acceleration of slow wave activation is then seen in the region of the terminal antrum, just proximal to the pylorus, which constitutes the basis of the terminal antral contraction (Berry et al., 2016). Second, a resting membrane potential gradient due to the action of ICC-derived carbon monoxide as a hyperpolarizing agent exists from the proximal to the distal stomach, as well as across the gastric and small intestinal wall (Farrugia et al., 2003). In the colon, the direction of the resting membrane potential gradient across the colonic wall is reversed compared to the stomach and intestine (Szurszewski and Farrugia, 2004). Finally, gastric slow waves entrain to a singular frequency in the healthy stomach, whereas in the intestine slow waves occur at multiple frequencies organized into plateaus along the length of the organ, each governed by an independent pacemaker, effectively forming a step-wise gradient of decreasing frequency along the intestine (Diamant and Bortoff, 1969; Lammers and Stephen, 2008; Angeli et al., 2013c). Previous reviews have covered studies that have attempted to unify all three aspects in a single model by prescribing parameters in the cell model to reproduce the intrinsic frequency, resting membrane potential gradients, and the conduction velocities in each region of the stomach (Du et al., 2010a, 2013). Recent modeling studies have now expanded on the whole-organ model to investigate the mechanisms of slow wave recovery and gastric dysrhythmias (Calder et al., 2016; Paskaranandavadivel et al., 2017).
In a notable recent study, the basis of the slow wave refractory/recovery was explored by sampling simulated slow waves from 96 solution points sampled over a whole-organ model (Paskaranandavadivel et al., 2017). The unipolar potential recorded in standard extracellular mapping techniques was simulated as a combination of a local component, i.e., membrane potential, and a spatially-independent component based on a scaled average of the residuals between the local component and the extracellular potentials from the whole-organ (Figure 4; Paskaranandavadivel et al., 2017). The simulations demonstrated that the resting membrane potential gradient may be a significant contributor to the recovery phase of the gastric slow wave extracellular potential. Specifically focusing on the spatially-independent component (Figure 4B), the gradient of resting membrane potentials had the effect of “averaging out” the defined profile of the spatially-independent component, as also seen in the cardiac simulations (Potse et al., 2009). The result was a pronounced recovery phase in the extracellular potential (Figure 4B).
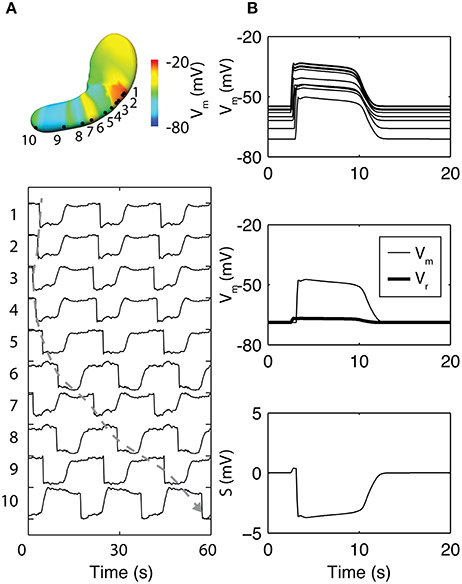
Figure 4. Simulation of whole-organ gastric slow waves. (A) Gastric slow waves originate from a pacemaker region along the greater curvature in the proximal stomach. Simultaneous and multiple wavefronts occur in the stomach, with each propagating wavefront taking up to 60 s to reach to the terminal antrum. (B) The existence of resting membrane potential gradient in the stomach plays a key role to the recovery component in the extracellular signals, when calculated as a difference between membrane potential (Vm) and a spatially invariant term (Vr). Adapted from (Paskaranandavadivel et al., 2017).
Whole-organ gastric dysrhythmias were simulated by adding a stimulus driven protocol and/or conduction block based on the tissue models (Calder et al., 2016). Three dysrhythmias have been reproduced to date: re-entry, conduction block and ectopic pacemaker (Figure 5; see Table 1 for definitions). Gastric re-entry was successfully invoked in the corpus where the distance between the refractory-depolarization of two subsequent waves is the longest, allowing more time for re-entry to develop. Both conduction blocks and ectopic pacemakers (of equal frequency to the entrainment frequency) were prescribed to the antrum, where the two dysrhythmias have been most commonly identified. The potential applications of these whole-organ gastric dysrhythmia models include investigations of forward and inverse modeling techniques, relating the effects of dysrhythmias with motility through computational fluid dynamic studies, and in identifying enhanced methods of gastric pacing (Berry et al., 2016).
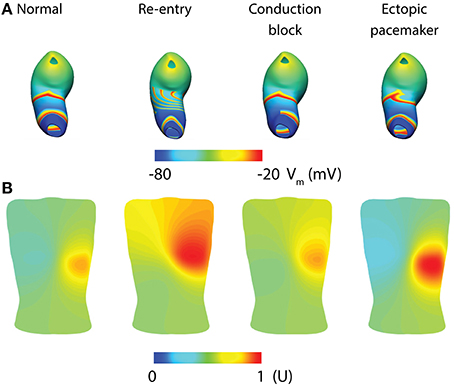
Figure 5. Whole-organ gastric slow wave dysrhythmias and electrogastrography (EGG) simulations (Calder et al., 2016). (A) Four instance of gastric slow wave activation (normal, re-entry, conduction block in the antrum and ectopic pacemaker in the proximal stomach). (B) Corresponding EGG simulations are calculated using a forward approach over an anatomically realistic torso, with the EGG potentials normalized (U).
Whole-organ modeling studies of slow waves have mainly focused on the stomach, where both in vivo and in vitro data are most abundant. With the development of a foundational gastric model, recent investigations have utilized this model to investigate detailed mechanisms for physiological recordings, as well as simulations of dynamic dysrhythmias over the entire organ. Similar intestinal models will likely be developed in idealized geometry segments, as the overall intestinal length of multiple meters poses a significant computational challenge to the current models that rely on a high spatial resolution of solution points (<0.3 mm). Furthermore, there is also uncertainty in whether some of the “abnormal” intestinal slow waves are truly dysrhythmic, or rather occur as stochastic behaviors as part of the natural pacemaking and/or dynamic interactions between intestinal slow wave plateaus (Parsons and Huizinga, 2016, 2017).
Non-Invasive Recordings
One of the ultimate aims of GI slow wave recordings is the ability to more reliably interpret slow wave activities non-invasively from the body surface. For gastric slow waves, the interpretation has principally been done through cutaneous recordings known as electrogastrography (EGG) (Bortolotti, 1998). It is also possible to detect the magnetic fields associated with the generation of slow waves with a superconducting quantum interference device (SQUID) using a technique called magnetogastrography (MGG) (Somarajan et al., 2015; Bradshaw et al., 2016b). Modeling investigations on both techniques have been ongoing as our understanding of the detailed activation sequence of gastric slow waves has improved. In particular, investigators are increasingly focusing on multi-channel/high-resolution EGG for detecting the underlying gastric slow wave propagation (Gharibans et al., 2016).
Given the relatively low signal-to-noise ratio of EGG, and the complexity of the underlying sources, investigators have long struggled with reliably separating the EGG signal component from other sources, e.g., respiration interference and cardiac electrical activity, though signal processing techniques have recently been developed to minimize these contaminants (Komorowski and Tkacz, 2015; Komorowski and Pietraszek, 2016). As a result, the sensitivity and specificity of the EGG has remained suboptimal, limiting clinical uptake. Mathematical modeling offers an attractive platform to assist in further development, because it can provide a “noise free” environment in which simulated EGG can be directly matched with gastric slow waves, provided that the correct slow wave behaviors are reproduced. A recent modeling investigation studied the EGG associated with normal and dysrhythmias gastric slow waves as demonstrated by high-resolution mapping (Calder et al., 2016). The whole-organ simulations were conducted as outlined in the whole-organ section of this review above (Figure 5A). The network activation of the whole-organ slow waves was represented using a dipole, which was placed inside an anatomically-realistic model of the adult torso with 192 cutaneous EGG electrodes (Figure 5B; Calder et al., 2016). EGG was modeled using the boundary-element method with the assumption of homogeneity inside the torso. The main finding was that, in addition to detecting the frequency of slow waves, it is also theoretically possible to detect and reliably distinguish spatial dysrhythmias (re-entry, conduction block, and ectopic pacemaker) using multi-channel (HR) EGG. Alternatively, slow wave activation has also been modeled as a 1D propagation source, and EGG calculated as a weighted summation of slow waves at every instance in time (Gharibans et al., 2016). Crucially, this study also used surface Laplacian and wave estimation techniques to determine the direction and propagation of slow waves from EGG recorded from eight human subjects (Gharibans et al., 2016). The clinical significance of these interesting recent developments will be more clear once the ability to interpret clinical EGG recordings improves.
The relationship between slow wave dysrhythmias and MGG has been validated experimentally with gastric disease models and intestinal ischemia (Bradshaw et al., 2007, 2016a; Somarajan et al., 2015). Investigators have resolved the theoretical relationship of MGG to normal gastric slow wave activation. One recent study compared the surface current density method and a second-order blind source separation method to the theoretical prediction of the source location based on a dipole, and found close agreement with the measurements and the predicted data (Bradshaw et al., 2016b). This study also raised the question of whether gastric slow waves can be well captured using a single dipole, or better represented by multiple dipoles to track the simultaneous propagating wavefronts.
The current progress in non-invasive recording techniques is mirrored with the improved understanding of the underlying gastric slow wave activation. The technical capabilities of inferring data from multiple channels are allowing more quantifiable techniques to be applied to EGG and MGG. Most simulation studies in this field have updated their source to represent a more realistic activation pattern based on experimental data. However, questions will always remain regarding the sensitivity of the EGG and MGG until experimental studies can definitively prove that the EGG and MGG can be related to specific spatial activation states of gastric slow waves, beyond just a frequency correlation, which will require simultaneous HR recordings from the stomach and body-surface. In addition, reliable protocols for invoking specific types of dysrhythmias in a consistent manner are also still needed to determine the relationship between EGG/MGG and dysrhythmias. One potential such method, for example, is through high-energy gastric pacing to create a stable ectopic activation (Du et al., 2009b; O'Grady et al., 2010b; Sathar et al., 2015).
Simulation Environments and Standards
As models increase in scale there is an associated increase in the computational cost in order to solve these models. This is especially important in GI modeling because the time-scale is typically orders of magnitudes higher than neural and cardiac simulations (milliseconds to minutes vs. milliseconds). Furthermore, as models gain sophistication it is ever more important to develop a standard by which these models can be encoded and reproduced in a consistent manner, as well as for encapsulation of meta-data. To this end, a number of standards and simulation tools have been developed (Table 4). The list of tools in Table 4 is by no means exhaustive, but is listed to highlight some examples of the available modeling standards and tools. One important reason for adopting similar standards is to allow rapid exchange of information and reproducibility of simulation results.
Final Remarks and Future Direction
Mathematical modeling of GI electrophysiology has seen remarkable progress in recent years. While still lacking the depth of detailed understanding in physiological and pathological mechanisms that exists in the cardiac and neural fields, the recent advance in cellular slow wave mechanisms and the detailed spatiotemporal descriptions of gastric spatial dysrhythmias have enabled a new focus and level of impact for many GI modeling studies. As new knowledge of cellular ion channelopathies and tissue degradation in diseases becomes available (Beyder and Farrugia, 2016), existing models can be updated with improved specificity to understand a particular pathology, infer its influence on the organ through multi-scale modeling, and determine detectability through non-invasive recording methodologies.
As biological modeling is often informed by experimental data, the focus on technical setup in experiments is becoming increasingly important. For example, EGG and MGG at the body surface have different signal characteristics compared to the signals recorded by direct contact on the serosal surface. Therefore, more consideration needs to be given to the choice of amplifiers and signal processing techniques. Inappropriate applications of recording and/or processing techniques could lead to incorrect interpretation of signals (Paskaranandavadivel et al., 2013). Furthermore, there is a danger of relying on recordings at one scale to interpret recordings obtained at a different scale. For example, some investigators have incorrectly discussed how the slow wave signals recorded using extracellular mapping do not appear to have the same rate of change as the intracellular recordings obtained from individual cells (Sanders et al., 2016). This interpretation relies on the false presumption that the extracellular serosal recordings directly accord with the activation of an individual cell, which is not the case in practice (Angeli et al., 2013a; O'Grady et al., 2017).
The role of the structure-function relationship of ICC and smooth muscles in GI dysrhythmias is a critical current question in clinical GI motility. Structural imaging and calcium functional recordings have both pointed to a strong relationship between the spatial distribution of ICC/cellular manipulations and loss of synchronicity of calcium activities and motility (Singh et al., 2014; Malysz et al., 2017), which are associated with slow wave dysrhythmias. At present, imaging and functional recording techniques are applied in isolation. It would be of great value to develop a foundational modeling framework that can integrate the experimental data from different modalities using biophysically-based models. Previous modeling investigations have attempted simulating slow wave propagation over a small-scale ICC network, either obtained from imaging data or using network generation algorithms (Du et al., 2010b; Gao et al., 2015). Validation for these studies was difficult because functional recording of the tissue-specific networks was not available at the time. With the advent of ratiometric Ca2+ imaging in live GI tissues (Singh et al., 2014; Malysz et al., 2017), it is now possible to compare the simulated intracellular Ca2+ activities that accompany slow wave generation to experimental data under varied physiological conditions.
The capability of recording Ca2+ transients at the tissue level could also lead to the development of new electromechanical models (Du et al., 2011; Singh et al., 2014; Malysz et al., 2017). This is critical because motility is a functional consequence of slow wave activation, and ICC have been shown to exhibit significant mechano-sensitivity (Beyder et al., 2010), which has been studied using a mathematical cell model (Poh et al., 2012). Both a passive constitutive model and an active tension model should be developed in order to translate the electromechanical coupling to the tissue level. Experiments based on biaxial stretch of the GI tissues are needed to quantify the parameters for the constitutive models, while a steady-state tension–length–calcium relationship could be adapted to define the active tension model. Perturbations to ion channel and tissue conductances could then be prescribed to the electrometrical models to simulate dysmotility. When translated to the whole-organ level, the simulated deformation of the GI wall could be used as a boundary condition input to computational fluid dynamic simulations of the mixing and breakdown of luminal contents due to different motility patterns (Fullard et al., 2014).
In summary, recent GI mathematical models have increased in sophistication and their ability to simulate key physiological mechanisms. These models have been applied in a predictive manner, across multiple biophysical scales, to begin to address some of the long-standing questions in the GI field, including the mechanisms, significance, and non-invasive diagnostics of gastric dysrhythmias. The progress of models relating to slow wave dysrhythmias is encouraging to date. However, as both experimental and technical capabilities within the field continue to improve, models will be better informed and validated by additional types of data. In turn, mathematical models of GI slow wave activity will continue to provide an ever-expanding platform for an integrative understanding of experimental data across multiple modalities.
Author Contributions
PD: manuscript preparation, study design. SC, TA, GO, NP, SS and LC: manuscript preparation. SS and NP contributed to drafting and preparation of the manuscript.
Conflict of Interest Statement
PD, TA, NP, GO, and LC hold intellectual property/patent applications in the field of mapping gastrointestinal electrophysiology. PD, TA, NP, SS, GO, LC are shareholders in FlexiMap. No commercial or industry funding was provided for this work.
Acknowledgments
This work was funded in part by grants from the National Institutes of Health (R01 DK64775), Health Research Council of New Zealand, New Zealand Medical Technologies Center of Research Excellence (MedTech CoRE), and the Riddet Institute. PD is supported by a Rutherford Discovery Fellowship administered by the Royal Society of New Zealand. SC is supported by the Andrew Pullan Doctoral Scholarship. TA is supported by an Edith C. Coan Postdoctoral Fellowship from the Auckland Medical Research Foundation.
References
Angeli, T. R., Cheng, L. K., Du, P., Wang, T. H., Bernard, C. E., Vannucchi, M. G., et al. (2015). Loss of interstitial cells of cajal and patterns of gastric dysrhythmia in patients with chronic unexplained nausea and vomiting. Gastroenterology 149, 56-66 e5. doi: 10.1053/j.gastro.2015.04.003
Angeli, T. R., Du, P., Paskaranandavadivel, N., Janssen, P. W., Beyder, A., Lentle, R. G., et al. (2013a). The bioelectrical basis and validity of gastrointestinal extracellular slow wave recordings. J. Physiol. 591, 4567–479. doi: 10.1113/jphysiol.2013.254292
Angeli, T. R., O'Grady, G., Du, P., Paskaranandavadivel, N., Pullan, A. J., Bissett, I. P., et al. (2013c). Circumferential and functional re-entry of in vivo slow-wave activity in the porcine small intestine. Neurogastroenterol. Motil. 25, e304–e314. doi: 10.1111/nmo.12085
Angeli, T. R., O'Grady, G., Paskaranandavadivel, N., Erickson, J. C., Du, P., Pullan, A. J., et al. (2013b). Experimental and automated analysis techniques for high resolution electrical mapping of small intestine slow wave activity. J. Neurogastroenterol. Motil. 19, 179–191. doi: 10.5056/jnm.2013.19.2.179
Atia, J., McCloskey, C., Shmygol, A. S., Rand, D. A. H. A., and van den Berg Blanks, A. M. (2016). Reconstruction of cell surface densities of ion pumps, exchangers, and channels from mRNA expression, conductance kinetics, whole-cell calcium, and current-clamp voltage recordings, with an application to human uterine smooth muscle cells. PLoS Comput. Biol. 12:e1004828. doi: 10.1371/journal.pcbi.1004828
Bennett, M. R., Farnell, L., and Gibson, W. G. (2005). A quantitative model of purinergic junctional transmission of calcium waves in astrocyte networks. Biophys. J. 89, 2235–2250. doi: 10.1529/biophysj.105.062968
Berry, R., Cheng, L. K., Du, P., Paskaranandavadivel, N., Angeli, T. R., Mayne, T., et al. (2017). Patterns of abnormal gastric pacemaking after sleeve gastrectomy defined by laparoscopic high-resolution electrical mapping. Obes. Surg. 27, 1929–1937. doi: 10.1007/s11695-017-2597-6
Berry, R., Miyagawa, T., Paskaranandavadivel, N., Du, P., Angeli, T. R., Trew, M. L., et al. (2016). Functional physiology of the human terminal antrum defined by high-resolution electrical mapping and computational modeling. Am. J. Physiol. Gastrointest. Liver Physiol. 311, G895–G902. doi: 10.1152/ajpgi.00255.2016
Beyder, A., and Farrugia, G. (2016). Ion channelopathies in functional GI disorders. Am. J. Physiol. Gastrointest. Liver Physiol. 311, G581–G586. doi: 10.1152/ajpgi.00237.2016
Beyder, A., Rae, J. L., Bernard, C., Strege, P. R., Sachs, F., and Farrugia, G. (2010). Mechanosensitivity of Nav1.5, a voltage-sensitive sodium channel. J. Physiol. 588, 4969–4985. doi: 10.1113/jphysiol.2010.199034
Bortolotti, M. (1998). Electrogastrography: a seductive promise, only partially kept. Am. J. Gastroenterol. 93, 1791–1794. doi: 10.1111/j.1572-0241.1998.01791.x
Bradley, C., Bowery, A., Britten, R., Budelmann, V., Camara, O., Christie, R., et al. (2011). OpenCMISS: a multi-physics & multi-scale computational infrastructure for the VPH/Physiome project. Prog. Biophys. Mol. Biol. 107, 32–47. doi: 10.1016/j.pbiomolbio.2011.06.015
Bradshaw, L. A., Cheng, L. K., Chung, E., Obioha, C. B., Erickson, J. C., Gorman, B. L., et al. (2016a). Diabetic gastroparesis alters the biomagnetic signature of the gastric slow wave. Neurogastroenterol. Motil. 28, 837–848. doi: 10.1111/nmo.12780
Bradshaw, L. A., Kim, J. H., Somarajan, S., Richards, W. O., and Cheng, L. K. (2016b). Characterization of electrophysiological propagation by multichannel sensors. IEEE Trans. Biomed. Eng. 63, 1751–1759. doi: 10.1109/TBME.2015.2502065
Bradshaw, L. A., Sims, J. A., and Richards, W. O. (2007). Noninvasive assessment of the effects of glucagon on the gastric slow wave. Am. J. Physiol. Gastrointest. Liver Physiol. 293, G1029–G1038. doi: 10.1152/ajpgi.00054.2007
Buist, M. L., and Poh, Y. C. (2010). An extended bidomain framework incorporating multiple cell types. Biophys. J. 99, 13–18. doi: 10.1016/j.bpj.2010.03.054
Bull, S. H., O'Grady, G., Cheng, L. K., and Pullan, A. J. (2011). A framework for the online analysis of multi-electrode gastric slow wave recordings. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2011, 1741–1744. doi: 10.1109/IEMBS.2011.6090498
Calder, S., O'Grady, G., Cheng, L., and Du, P. (2016). A theoretical analysis of electrogastrography (EGG) signatures associated with gastric dysrhythmias. IEEE Trans. Biomed. Eng. 64, 1592–1601. doi: 10.1109/TBME.2016.2614277
Chaouiya, C., Berenguier, D., Keating, S. M., Naldi, A., van Iersel, M. P., Rodriguez, N., et al. (2013). SBML qualitative models: a model representation format and infrastructure to foster interactions between qualitative modelling formalisms and tools. BMC Syst. Biol. 7:135. doi: 10.1186/1752-0509-7-135
Chen, C. L., Lin, H. H., Huang, L. C., Huang, S. C., and Liu, T. T. (2004). Electrogastrography differentiates reflux disease with or without dyspeptic symptoms. Dig. Dis. Sci. 49, 715–719. doi: 10.1023/B:DDAS.0000030079.20501.62
Cheng, L. K., Du, P., and O'Grady, G. (2013). Mapping and modeling gastrointestinal bioelectricity: from engineering bench to bedside. Physiology 28, 310–317. doi: 10.1152/physiol.00022.2013
Christie, G. R., Nielsen, P. M., Blackett, S. A., Bradley, C. P., and Hunter, P. J. (2009). FieldML: concepts and implementation. Philos. Trans. A Math. Phys. Eng. Sci. 367, 1869–1884. doi: 10.1098/rsta.2009.0025
Coleski, R., and Hasler, W. L. (2009). Coupling and propagation of normal and dysrhythmic gastric slow waves during acute hyperglycaemia in healthy humans. Neurogastroenterol Motil 21, 492-9, e1–2. doi: 10.1111/j.1365-2982.2008.01235.x
Corrias, A., and Buist, M. L. (2007). A quantitative model of gastric smooth muscle cellular activation. Ann. Biomed. Eng. 35, 1595–1607. doi: 10.1007/s10439-007-9324-8
Corrias, A., and Buist, M. L. (2008). Quantitative cellular description of gastric slow wave activity. Am. J. Physiol. Gastrointest. Liver Physiol. 294, G989–G995. doi: 10.1152/ajpgi.00528.2007
Corrias, A., Pathmanathan, P., Gavaghan, D. J., and Buist, M. L. (2012). Modelling tissue electrophysiology with multiple cell types: applications of the extended bidomain framework. Integr. Biol. 4, 192–201. doi: 10.1039/c2ib00100d
Debinski, H. S., Ahmed, S., Milla, P. J., and Kamm, M. A. (1996). Electrogastrography in chronic intestinal pseudoobstruction. Dig. Dis. Sci. 41, 1292–1297. doi: 10.1007/BF02088549
Diamant, N. E., and Bortoff, A. (1969). Nature of the intestinal slow-wave frequency gradient. Am. J. Physiol. 216, 301–307.
Du, P., Hameed, A., Angeli, T. R., Lahr, C., Abell, T. L., Cheng, L. K., et al. (2015a). The impact of surgical excisions on human gastric slow wave conduction, defined by high-resolution electrical mapping and in silico modeling. Neurogastroenterol. Motil. 27, 1409–1422. doi: 10.1111/nmo.12637
Du, P., O'Grady, G., and Cheng, L. K. (2017). A theoretical analysis of anatomical and functional intestinal slow wave re-entry. J. Theor. Biol. 425, 72–79. doi: 10.1016/j.jtbi.2017.04.021
Du, P., O'Grady, G., Cheng, L. K., and Pullan, A. J. (2010a). A multiscale model of the electrophysiological basis of the human electrogastrogram. Biophys. J. 99, 2784–2792. doi: 10.1016/j.bpj.2010.08.067
Du, P., O'Grady, G., Egbuji, J. U., Lammers, W. J., Budgett, D., Nielsen, P., et al. (2009a). High-resolution mapping of in vivo gastrointestinal slow wave activity using flexible printed circuit board electrodes: methodology and validation. Ann. Biomed. Eng. 37, 839–846. doi: 10.1007/s10439-009-9654-9
Du, P., O'Grady, G., Gao, J., Sathar, S., and Cheng, L. K. (2013). Toward the virtual stomach: progress in multiscale modeling of gastric electrophysiology and motility. Wiley Interdiscip. Rev. Syst. Biol. Med. 5, 481–493. doi: 10.1002/wsbm.1218
Du, P., O'Grady, G., Gibbons, S. J., Yassi, R., Lees-Green, R., Farrugia, G., et al. (2010b). Tissue-specific mathematical models of slow wave entrainment in wild-type and 5-HT(2B) knockout mice with altered interstitial cells of Cajal networks. Biophys. J. 98, 1772–1781. doi: 10.1016/j.bpj.2010.01.009
Du, P., O'Grady, G., Paskaranandavadivel, N., Tang, S. J., Abell, T., and Cheng, L. K. (2016a). Simultaneous anterior and posterior serosal mapping of gastric slow-wave dysrhythmias induced by vasopressin. Exp. Physiol. 101, 1206–1217. doi: 10.1113/EP085697
Du, P., O'Grady, G., Windsor, J. A., Cheng, L. K., and Pullan, A. J. (2009b). A tissue framework for simulating the effects of gastric electrical stimulation and in vivo validation. IEEE Trans. Biomed. Eng. 56, 2755–2761. doi: 10.1109/TBME.2009.2027690
Du, P., Paskaranandavadivel, N., Angeli, T. R., Cheng, L. K., and O'Grady, G. (2016b). The virtual intestine: in silico modeling of small intestinal electrophysiology and motility and the applications. Wiley Interdiscip. Rev. Syst. Biol. Med. 8, 69–85. doi: 10.1002/wsbm.1324
Du, P., Paskaranandavadivel, N., O'Grady, G., Tang, S. J., and Cheng, L. K. (2015b). A theoretical study of the initiation, maintenance and termination of gastric slow wave re-entry. Math. Med. Biol. 32, 405–423. doi: 10.1093/imammb/dqu023
Du, P., Poh, Y. C., Lim, J. L., Gajendiran, V., O'Grady, G., Buist, M. L., et al. (2011). A preliminary model of gastrointestinal electromechanical coupling. IEEE Trans. Biomed. Eng. 58, 3491–3495. doi: 10.1109/TBME.2011.2166155
Egbuji, J. U. G., O'grady Du, P., Cheng, L. K., Lammers, W. J., Windsor, J. A., et al. (2010). Origin, propagation and regional characteristics of porcine gastric slow wave activity determined by high-resolution mapping. Neurogastroenterol. Motil. 22, e292–300. doi: 10.1111/j.1365-2982.2010.01538.x
Familoni, B. O., Kingma, Y. J., and Bowes, K. L. (1987). Study of transcutaneous and intraluminal measurement of gastric electrical activity in humans. Med. Biol. Eng. Comput. 25, 397–402. doi: 10.1007/BF02443360
Farrugia, G., Lei, S., Lin, X., Miller, S. M., Nath, K. A., Ferris, C. D., et al. (2003). A major role for carbon monoxide as an endogenous hyperpolarizing factor in the gastrointestinal tract. Proc. Natl. Acad. Sci. U.S.A. 100, 8567–8570. doi: 10.1073/pnas.1431233100
Fullard, L., Lammers, W., Wake, G. C., and Ferrua, M. J. (2014). Propagating longitudinal contractions in the ileum of the rabbit–efficiency of advective mixing. Food Funct. 5, 2731–2742. doi: 10.1039/C4FO00487F
Gao, J., Sathar, S., O'Grady, G., Archer, R., and Cheng, L. K. (2015). A Stochastic algorithm for generating realistic virtual interstitial cell of Cajal networks. IEEE Trans. Biomed. Eng. 62, 2070–2078. doi: 10.1109/TBME.2015.2412533
Gharibans, A. A., Kim, S., Kunkel, D., and Coleman, T. P. (2016). High-resolution electrogastrogram: a novel, noninvasive method for determining gastric slow-wave direction and speed. IEEE Trans. Biomed. Eng. 64, 807–815. doi: 10.1109/TBME.2016.2579310
Gizzi, A., Cherubini, C., Migliori, S., Alloni, R., Portuesi, R., and Filippi, S. (2010). On the electrical intestine turbulence induced by temperature changes. Phys. Biol. 7:16011. doi: 10.1088/1478-3975/7/1/016011
Gonlachanvit, S., Chen, Y. H., Hasler, W. L., Sun, W. M., and Owyang, C. (2003). Ginger reduces hyperglycemia-evoked gastric dysrhythmias in healthy humans: possible role of endogenous prostaglandins. J. Pharmacol. Exp. Ther. 307, 1098–1103. doi: 10.1124/jpet.103.053421
Hasler, W. L., Soudah, H. C., Dulai, G., and Owyang, C. (1995). Mediation of hyperglycemia-evoked gastric slow-wave dysrhythmias by endogenous prostaglandins. Gastroenterology 108, 727–736. doi: 10.1016/0016-5085(95)90445-X
Huizinga, J. D., Chen, J. H., Zhu, Y. F., Pawelka, A., McGinn, R. J., Bardakjian, B. L., et al. (2014). The origin of segmentation motor activity in the intestine. Nat. Commun. 5, 3326. doi: 10.1038/ncomms4326
Kelly, K. A., and Code, C. F. (1971). Canine gastric pacemaker. Am. J. Physiol. 220, 112–118. doi: 10.1152/ajplegacy.1971.220.1.112
Kim, J. H., Du, P., and Cheng, L. K. (2013). Reconstruction of normal and abnormal gastric electrical sources using a potential based inverse method. Physiol. Meas. 34, 1193–1206. doi: 10.1088/0967-3334/34/9/1193
Kim, M. S., Chey, W. D., Owyang, C., and Hasler, W. L. (1997). Role of plasma vasopressin as a mediator of nausea and gastric slow wave dysrhythmias in motion sickness. Am. J. Physiol. 272, G853–G862. doi: 10.1152/ajpgi.1997.272.4.G853
Koch, K. L., Stern, R. M., Vasey, M., Botti, J. J., Creasy, G. W., and Dwyer, A. (1990). Gastric dysrhythmias and nausea of pregnancy. Dig. Dis. Sci. 35, 961–968. doi: 10.1007/BF01537244
Komorowski, D., and Pietraszek, S. (2016). The Use of Continuous wavelet transform based on the fast fourier transform in the analysis of multi-channel electrogastrography recordings. J. Med. Syst. 40, 10. doi: 10.1007/s10916-015-0358-4
Komorowski, D., and Tkacz, E. (2015). A new method for attenuation of respiration artifacts in electrogastrographic (EGG) signals. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2015, 6006–6009. doi: 10.1109/EMBC.2015.7319760
Kurahashi, M., Nakano, Y., Hennig, G. W., Ward, S. M., and Sanders, K. M. (2012). Platelet-derived growth factor receptor alpha-positive cells in the tunica muscularis of human colon. J. Cell. Mol. Med. 16, 1397–1404. doi: 10.1111/j.1582-4934.2011.01510.x
Lammers, W. J. (2013). Arrhythmias in the gut. Neurogastroenterol. Motil. 25, 353–357. doi: 10.1111/nmo.12116
Lammers, W. J., el-Kays, A., Manefield, G. W., Arafat, K., and el-Sharkawy, T. Y. (1997). Disturbances in the propagation of the slow wave during acute local ischaemia in the feline small intestine. Eur. J. Gastroenterol. Hepatol. 9, 381–388. doi: 10.1097/00042737-199704000-00012
Lammers, W. J., Michiels, B., Voeten, J., Ver Donck, L., and Schuurkes, J. A. (2008a). Mapping slow waves and spikes in chronically instrumented conscious dogs: automated on-line electrogram analysis. Med. Biol. Eng. Comput. 46, 121–129. doi: 10.1007/s11517-007-0294-7
Lammers, W. J., and Stephen, B. (2008). Origin and propagation of individual slow waves along the intact feline small intestine. Exp. Physiol. 93, 334–346. doi: 10.1113/expphysiol.2007.039180
Lammers, W. J., Stephen, B., and Karam, S. M. (2012). Functional reentry and circus movement arrhythmias in the small intestine of normal and diabetic rats. Am. J. Physiol. Gastrointest. Liver Physiol. 302, G684–G689. doi: 10.1152/ajpgi.00332.2011
Lammers, W. J., Stephen, B. S., and Karam, S. M. (2015). Slow wave dysrhythmias in the diabetic small intestine. Neurogastroenterol. Motil. 27, 1344. doi: 10.1111/nmo.12608
Lammers, W. J., Ver Donck, L., Stephen, B., Smets, D., and Schuurkes, J. A. (2008b). Focal activities and re-entrant propagations as mechanisms of gastric tachyarrhythmias. Gastroenterology 135, 1601–1611. doi: 10.1053/j.gastro.2008.07.020
Leahy, A., Besherdas, K., Clayman, C., Mason, I., and Epstein, O. (1999). Abnormalities of the electrogastrogram in functional gastrointestinal disorders. Am. J. Gastroenterol. 94, 1023–1028. doi: 10.1111/j.1572-0241.1999.01007.x
Leahy, A., Besherdas, K., Clayman, C., Mason, I., and Epstein, O. (2001). Gastric dysrhythmias occur in gastro-oesophageal reflux disease complicated by food regurgitation but not in uncomplicated reflux. Gut 48, 212–215. doi: 10.1136/gut.48.2.212
Lees-Green, R., Du, P., O'Grady, G., Beyder, A., Farrugia, G., and Pullan, A. J. (2011). Biophysically based modeling of the interstitial cells of cajal: current status and future perspectives. Front. Physiol. 2:29. doi: 10.3389/fphys.2011.00029
Lien, H. C., Sun, W. M., Chen, Y. H., Kim, H., Hasler, W., and Owyang, C. (2003). Effects of ginger on motion sickness and gastric slow-wave dysrhythmias induced by circular vection. Am. J. Physiol. Gastrointest. Liver Physiol. 284, G481–G489. doi: 10.1152/ajpgi.00164.2002
Lim, H. C., Lee, S. I., Chen, J. D., and Park, H. (2012). Electrogastrography associated with symptomatic changes after prokinetic drug treatment for functional dyspepsia. World J. Gastroenterol. 18, 5948–5956. doi: 10.3748/wjg.v18.i41.5948
Lin, X., and Chen, J. Z. (2001). Abnormal gastric slow waves in patients with functional dyspepsia assessed by multichannel electrogastrography. Am. J. Physiol. Gastrointest. Liver Physiol. 280, G1370–G1375. doi: 10.1152/ajpgi.2001.280.6.G1370
Lin, Z. Y., McCallum, R. W., Schirmer, B. D., and Chen, J. D. (1998). Effects of pacing parameters on entrainment of gastric slow waves in patients with gastroparesis. Am. J. Physiol. 274, G186–G191. doi: 10.1152/ajpgi.1998.274.1.G186
Linkens, D. A. (1978). Canine colonic pacing and coupled oscillator synchronization [proceedings]. J. Physiol. 278, 26P-27P.
Linkens, D. A., and Mhone, P. G. (1979). Frequency transients in a coupled oscillator model of intestinal myoelectrical activity. Comput. Biol. Med. 9, 131–144. doi: 10.1016/0010-4825(79)90029-5
Lloyd, C. M., Halstead, M. D., and Nielsen, P. F. (2004). CellML: its future, present and past. Prog. Biophys. Mol. Biol. 85, 433–450. doi: 10.1016/j.pbiomolbio.2004.01.004
Maltsev, A. V., Maltsev, V. A., and Stern, M. D. (2017). Clusters of calcium release channels harness the Ising phase transition to confine their elementary intracellular signals. Proc. Natl. Acad. Sci. U.S.A. 114, 7525–7530. doi: 10.1073/pnas.1701409114
Malysz, J., Gibbons, S. J., Saravanaperumal, S. A., Du, P., Eisenman, S. T., Cao, C., et al. (2017). Conditional genetic deletion of Ano1 in interstitial cells of Cajal impairs Ca2+ transients and slow waves in adult mouse small intestine. Am. J. Physiol. Gastrointest. Liver Physiol. 312, G228–G245. doi: 10.1152/ajpgi.00363.2016
Marriott, H. J. (1984). Arrhythmia versus dysrhythmia. Am. J. Cardiol. 53, 628. doi: 10.1016/0002-9149(84)90043-2
McNearney, T. A., Sallam, H. S., Hunnicutt, S. E., Doshi, D., Wollaston, D. E., Mayes, M. D., et al. (2009). Gastric slow waves, gastrointestinal symptoms and peptides in systemic sclerosis patients. Neurogastroenterol. Motil. 21, 1269–e120. doi: 10.1111/j.1365-2982.2009.01350.x
Nelsen, T. S., and Kohatsu, S. (1968). Clinical electrogastrography and its relationship to gastric surgery. Am. J. Surg. 116, 215–222. doi: 10.1016/0002-9610(68)90496-0
O'Grady, G., Angeli, T. R., Du, P., Lahr, C., Lammers, W. J., Windsor, J. A., et al. (2012a). Abnormal initiation and conduction of slow-wave activity in gastroparesis, defined by high-resolution electrical mapping. Gastroenterology 143, 589-98 e1–e3. doi: 10.1053/j.gastro.2012.05.036
O'Grady, G., Du, P., Cheng, L. K., Egbuji, J. U., Lammers, W. J., Windsor, J. A., et al. (2010a). Origin and propagation of human gastric slow-wave activity defined by high-resolution mapping. Am. J. Physiol. Gastrointest. Liver Physiol. 299, G585–G592. doi: 10.1152/ajpgi.00125.2010
O'Grady, G., Du, P., Lammers, W. J., Egbuji, J. U., Mithraratne, P., Chen, J. D., et al. (2010b). High-resolution entrainment mapping of gastric pacing: a new analytical tool. Am. J. Physiol. Gastrointest. Liver Physiol. 298, G314–G321. doi: 10.1152/ajpgi.00389.2009
O'Grady, G., Du, P., Paskaranandavadivel, N., Angeli, T. R., Lammers, W. J., Asirvatham, S. J., et al. (2012b). Rapid high-amplitude circumferential slow wave propagation during normal gastric pacemaking and dysrhythmias. Neurogastroenterol. Motil. 24, e299–e312. doi: 10.1111/j.1365-2982.2012.01932.x
O'Grady, G., Paskaranandavadivel, N., Du, P., Angeli, T., Erickson, J. C., and Cheng, L. K. (2017). Correct techniques for extracellular recordings of electrical activity in gastrointestinal muscle. Nat. Rev. Gastroenterol. Hepatol. 14, 372. doi: 10.1038/nrgastro.2017.15
O'Grady, G., Wang, T. H., Du, P., Angeli, T., Lammers, W. J., and Cheng, L. K. (2014). Recent progress in gastric arrhythmia: pathophysiology, clinical significance and future horizons. Clin. Exp. Pharmacol. Physiol. 41, 854–862. doi: 10.1111/1440-1681.12288
Ordog, T., Takayama, I., Cheung, W. K., Ward, S. M., and Sanders, K. M. (2000). Remodeling of networks of interstitial cells of Cajal in a murine model of diabetic gastroparesis. Diabetes 49, 1731–1739. doi: 10.2337/diabetes.49.10.1731
Owyang, C., and Hasler, W. L. (2002). Physiology and pathophysiology of the interstitial cells of Cajal: from bench to bedside. VPathogenesis, I and therapeutic approaches to human gastric dysrhythmias. Am. J. Physiol. Gastrointest. Liver Physiol. 283, G8–G15. doi: 10.1152/ajpgi.00095.2002
Parkman, H. P., Hasler, W. L., Barnett, J. L., and Eaker, E. Y. (2003). Electrogastrography: a document prepared by the gastric section of the American motility society clinical GI motility testing task force. Neurogastroenterol. Motil. 15, 89–102. doi: 10.1046/j.1365-2982.2003.00396.x
Parsons, S. P., and Huizinga, J. D. (2016). Spatial noise in coupling strength and natural frequency within a pacemaker network; consequences for development of intestinal motor patterns according to a weakly coupled phase oscillator model. Front. Neurosci. 10:19. doi: 10.3389/fnins.2016.00019
Parsons, S. P., and Huizinga, J. D. (2017). The phase response and state space of slow wave contractions in the small intestine. Exp. Physiol. 102, 1118–1132. doi: 10.1113/EP086373
Paskaranandavadivel, N., Cheng, L. K., Du, P., Rogers, J. M., and O'Grady, G. (2017). High-resolution mapping of gastric slow wave recovery profiles: biophysical model, methodology and demonstration of applications. Am. J. Physiol. Gastrointest. Liver Physiol. 313, G265–G276. doi: 10.1152/ajpgi.00127.2017
Paskaranandavadivel, N., O'Grady, G., and Du, P. (2013). Comparison of filtering methods for extracellular gastric slow wave recordings. Neurogastroenterol. Motil. 25, 79–83. doi: 10.1111/nmo.12012
Pfaffenbach, B., Adamek, R. J., Bartholomaus, C., and Wegener, M. (1997). Gastric dysrhythmias and delayed gastric emptying in patients with functional dyspepsia. Dig. Dis. Sci. 42, 2094–2099. doi: 10.1023/A:1018826719628
Pitt-Francis, J., Bernabeu, M. O., Cooper, J., Garny, A., Momtahan, L., Osborne, J., et al. (2008). Chaste: using agile programming techniques to develop computational biology software. Philos. Trans. A Math. Phys. Eng. Sci. 366, 3111–3136. doi: 10.1098/rsta.2008.0096
Plank, G., Burton, R. A., Hales, P., Bishop, M., Mansoori, T., Bernabeu, M. O., et al. (2009). Generation of histo-anatomically representative models of the individual heart: tools and application. Philos. Trans. A Math. Phys. Eng. Sci. 367, 2257–2292. doi: 10.1098/rsta.2009.0056
Poh, Y. C., Beyder, A., Strege, P. R., Farrugia, G., and Buist, M. L. (2012). Quantification of gastrointestinal sodium channelopathy. J. Theor. Biol. 293, 41–48. doi: 10.1016/j.jtbi.2011.09.014
Potse, M., Vinet, A., Opthof, T., and Coronel, R. (2009). Validation of a simple model for the morphology of the T wave in unipolar electrograms. Am. J. Physiol. Heart Circ. Physiol. 297, H792–801. doi: 10.1152/ajpheart.00064.2009
Sachse, F. B., Moreno, A. P., Seemann, G., and Abildskov, J. A. (2009). A model of electrical conduction in cardiac tissue including fibroblasts. Ann. Biomed. Eng. 37, 874–889. doi: 10.1007/s10439-009-9667-4
Sanders, K. M., Ward, S. M., and Hennig, G. W. (2016). Problems with extracellular recording of electrical activity in gastrointestinal muscle. Nat. Rev. Gastroenterol. Hepatol. 13, 731–774. doi: 10.1038/nrgastro.2016.161
Sathar, S., Trew, M. L., Du, P., O'Grady, G., and Cheng, L. K. (2014). A biophysically based finite-state machine model for analyzing gastric experimental entrainment and pacing recordings. Ann. Biomed. Eng. 42, 858–870. doi: 10.1007/s10439-013-0949-5
Sathar, S., Trew, M. L. O. G. G., and Cheng, L. K. (2015). A Multiscale tridomain model for simulating bioelectric gastric pacing. IEEE Trans. Biomed. Eng. 62, 2685–2692. doi: 10.1109/TBME.2015.2444384
Schaap, H. M., Smout, A. J., and Akkermans, L. M. (1990). Myoelectrical activity of the Billroth II gastric remnant. Gut 31, 984–988. doi: 10.1136/gut.31.9.984
Simonian, H. P., Panganamamula, K., Chen, J. Z., Fisher, R. S., and Parkman, H. P. (2004). Multichannel electrogastrography (EGG) in symptomatic patients: a single center study. Am. J. Gastroenterol. 99, 478–485. doi: 10.1111/j.1572-0241.2004.04103.x
Singh, R. D., Gibbons, S. J., Saravanaperumal, S. A., Du, P., Hennig, G. W., Eisenman, S. T., et al. (2014). Ano1, a Ca2+-activated Cl- channel, coordinates contractility in mouse intestine by Ca2+ transient coordination between interstitial cells of Cajal. J. Physiol. 592, 4051–4068. doi: 10.1113/jphysiol.2014.277152
Somarajan, S., Muszynski, N. D., Cheng, L. K., Bradshaw, L. A., Naslund, T. C., and Richards, W. O. (2015). Noninvasive biomagnetic detection of intestinal slow wave dysrhythmias in chronic mesenteric ischemia. Am. J. Physiol. Gastrointest. Liver Physiol. 309, G52–G58. doi: 10.1152/ajpgi.00466.2014
Stern, R. M., Koch, K. L., Stewart, W. R., and Lindblad, I. M. (1987). Spectral analysis of tachygastria recorded during motion sickness. Gastroenterology 92, 92–97. doi: 10.1016/0016-5085(87)90843-2
Szurszewski, J. H. (1998). A 100-year perspective on gastrointestinal motility. Am. J. Physiol. 274, G447–G453. doi: 10.1152/ajpgi.1998.274.3.G447
Szurszewski, J. H., and Farrugia, G. (2004). Carbon monoxide is an endogenous hyperpolarizing factor in the gastrointestinal tract. Neurogastroenterol. Motil. 16(Suppl. 1), 81–85. doi: 10.1111/j.1743-3150.2004.00480.x
Trommer, P. R. (1982). Cardiolocution and dysrhythmia. Am. J. Cardiol. 50, 1198. doi: 10.1016/0002-9149(82)90445-3
van Helden, D. F., Laver, D. R., Holdsworth, J., and Imtiaz, M. S. (2010). Generation and propagation of gastric slow waves. Clin. Exp. Pharmacol. Physiol. 37, 516–524. doi: 10.1111/j.1440-1681.2009.05331.x
Wei, R., Parsons, S. P., and Huizinga, J. D. (2017). Network properties of interstitial cells of Cajal affect intestinal pacemaker activity and motor patterns, according to a mathematical model of weakly coupled oscillators. Exp. Physiol. 102, 329–346. doi: 10.1113/EP086077
Yeoh, J. W., Corrias, A., and Buist, M. L. (2016). A mechanistic model of a PDGFRalpha(+) cell. J. Theor. Biol. 408, 127–136. doi: 10.1016/j.jtbi.2016.08.004
Keywords: slow wave, GI, multi-scale modeling, arrhythmias, Electrophysiology
Citation: Du P, Calder S, Angeli TR, Sathar S, Paskaranandavadivel N, O'Grady G and Cheng LK (2018) Progress in Mathematical Modeling of Gastrointestinal Slow Wave Abnormalities. Front. Physiol. 8:1136. doi: 10.3389/fphys.2017.01136
Received: 03 October 2017; Accepted: 22 December 2017;
Published: 15 January 2018.
Edited by:
S. Sridhar, Robert Bosch Centre for Cyber- Physical Systems, Indian Institute of Science, IndiaReviewed by:
Arun V. Holden, University of Leeds, United KingdomAlok Ranjan Nayak, International Institute of Information Technology, India
Martin Buist, National University of Singapore, Singapore
Copyright © 2018 Du, Calder, Angeli, Sathar, Paskaranandavadivel, O'Grady and Cheng. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peng Du, cGVuZy5kdUBhdWNrbGFuZC5hYy5ueg==
 Peng Du
Peng Du Stefan Calder
Stefan Calder Timothy R. Angeli
Timothy R. Angeli Shameer Sathar
Shameer Sathar Niranchan Paskaranandavadivel
Niranchan Paskaranandavadivel Gregory O'Grady
Gregory O'Grady Leo K. Cheng
Leo K. Cheng