- Department of Mechanical Engineering, University College London, London, United Kingdom
It is widely accepted that salt intake reduction and regular exercise is a healthy lifestyle, which can prevent cardiovascular diseases (CVD). Meanwhile, there is evidence that the endothelial glycocalyx layer (EGL) is related to CVD. However, how such a healthy lifestyle helps to prevent CVD via the function of the EGL has not been scientifically established. In this research, a series of large-scale molecular dynamics simulations have been conducted to study ion transport inside the EGL under varying flow velocities. Results show that a fast blood flow velocity favors the Na+ transport out of the EGL, which can explain the increase in the thickness of an exclusion layer between red blood cells and the EGL under fast blood flow situations, as witnessed in some previous experiments. Based on findings from this fundamental research, a theory is proposed, which can answer the open-ended question “Why do we need to reduce salt intake and exercise regularly”. The findings may also have implications for other therapies to combat cardiovascular diseases.
Introduction
The endothelial glycocalyx layer (EGL), the first and foremost barrier in direct contact with blood (Curry and Adamson, 2012), is closely related to cardiovascular diseases (CVD) (Rabelink and de Zeeuw, 2015). EGL also acts as a crucial buffer barrier for sodium (Oberleithner, 2012). In the meantime, empirical studies suggest that reducing salt intake (He and MacGregor, 2011, 2018; Aburto et al., 2013) and exercising regularly (Agarwal, 2012; Schuler et al., 2013) can lower the risk of CVD or reduce the chance of CVD getting worse.
When sodium intake exceeds the excretory capacity of the kidney, sodium is retained. Previous studies have experimentally demonstrated that salt overload stiffens vascular endothelial cells and increases vascular sodium permeability, thereby damaging the glycocalyx sodium barrier of vascular endothelium (Oberleithner et al., 2011). Thus, intake of sodium chloride would have implications for the function of the endothelial glycocalyx as a foremost sodium barrier. These findings elucidate the significance of the EGL as a barrier from the perspective of cell mechanics. Also, the EGL features highly negatively charged sugar chains (Weinbaum et al., 2007). How the crucial function of EGL is affected by electrostatics requires further investigation.
In the meanwhile, an interesting phenomenon occurring between the EGL and red blood cells (RBCs) may explain the benefit of doing regular exercise (Lott et al., 2001): when RBCs flow through our vessels, an exclusion layer between the RBCs and EGL forms, facilitating the motion of the RBCs; the layer thickness increases as RBCs accelerate (Vink and Duling, 1996). The behavior of the RBCs on the EGL can be compared to human skiing, and a lubrication theory for the principle of skiing has been extended to understand the formation of the exclusive layer (Feng and Weinbaum, 2000). However, the theory is unable to explain the layer thickness variation with the varying blood velocity. Meanwhile, the charge properties of the EGL have not been considered either.
To scientifically explain the different experimental results and empirical observations, we conduct an in silico numerical experiment focusing on Na+ ion transport in the presence of the EGL under varying blood flow velocities. The Na+ distributions in various scenarios are determined by molecular dynamics (MD) simulations. Based on the results, the function of the EGL as a sodium barrier is discussed from the perspective of electrostatics. Also, explanations will be provided to elucidate the response of the exclusion layer thickness to the varying blood velocities.
Materials and Methods
System Construction
A flow/glycocalyx system was constructed, using the currently most detailed structural information of the glycocalyx to mimic flow on a patch of an endothelial cell lipid member (Figure 1A). In this system, three glycocalyx elements are involved. One glycocalyx element is composed of a core protein and six sugar chains. Syndecan-4 (Syn-4) proteoglycan and heparin sulfate (HS) sugar residues were selected to model the glycocalyx core protein and sugar chains, respectively. As shown in Figure 1A, the whole space is divided into two compartments by the lipid bilayer. Above the lipid bilayer is the ectodomain, representing the space outside the endothelial cells, where flow passes by. This region contains negatively charged HS sugar chains, Syn-4 ectodomain in connection with HS sugar chains, water molecules and ions. Below the lipid bilayer is the cytoplasm, representing the inner space of the cell, which is filled with the Syn-4 cytoplasmic protein, water molecules and ions. All the biomolecules are solvated and ionized to 0.1 M NaCl solution. The simulation box is a hexagonal prism with an area of 820 nm2 and height of 72 nm. The glycocalyx-flow system comprises about 5,800,000 atoms in total.
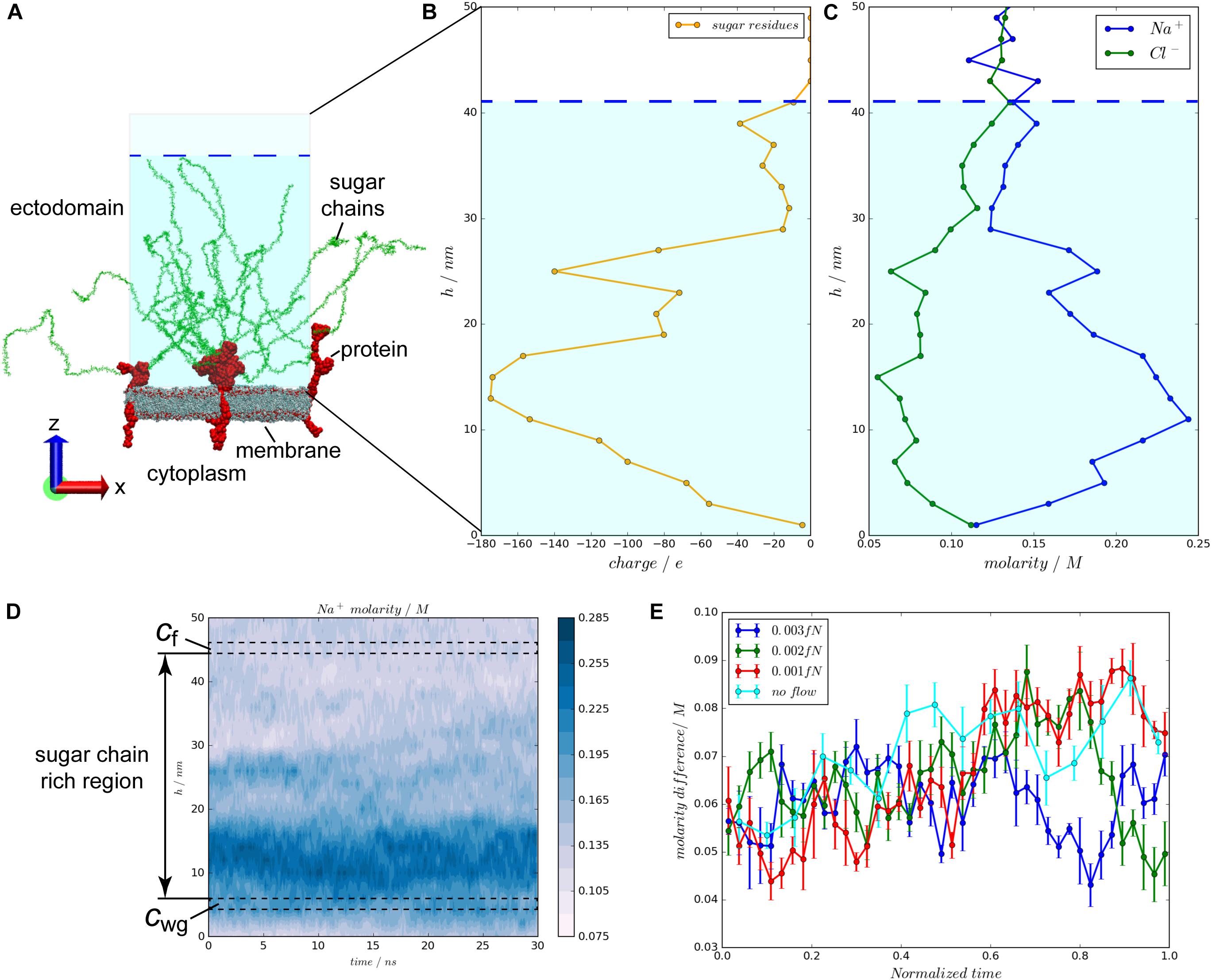
FIGURE 1. The configuration of the flow/glycocalyx system and charge distributions over the glycocalyx layer under varying flow velocities. (A) The configuration of the flow/glycocalyx system. The system is solvated in a NaCl solution with a molarity of 0.1 M. Water and ions are not shown. (B) Charge distributions of the negatively charged sugar chains along the height in the ectodomain. (C) Molarity distributions of the Na+ and Cl- ions along the height in the ectodomain. (D) Molarity difference continues throughout the entire simulation. cwg is continuously greater than cf in the simulation. (E) The molarity difference between two regions beneath and above the sugar chain region, cwg–cf, changes with the varying blood flow velocities. The largest average molarity difference appears in the no flow case, followed by the 0.001, 0.002, and 0.003 fN cases in sequence.
Protocol Details
The TIP3P water model (Jorgensen et al., 1983) was adopted for water molecules. The CHARMM biomolecular force field (MacKerell et al., 1998) was applied on proteins and the lipid bilayer. Force field parameters for sugar residues have been validated in previous studies (Cruz-Chu et al., 2014).
The system was equilibrated under isothermal-isobaric (NPT) and canonical (NVT) ensembles. The velocity Verlet integration method (Allen and Tildesley, 1987) was used to advance the positions and velocities of atoms in time steps of 2 fs. Particle mesh Ewald (Darden et al., 1993) electrostatics with a grid density of 1/Å3 was used. The SETTLE algorithm (Miyamoto and Kollman, 1992) was used to enable the rigid bonds connected to all hydrogen atoms. The van der Waals interactions were calculated using a cut-off of 12 Å with a switching function starting at 10 Å. In flow simulations, the Lowe-Andersen thermostat, a specific thermostat exclusively for flow problems, was selected to maintain the temperature at 310 K.
All MD simulations were performed using the software suite NAMD 2.9 (Phillips et al., 2005). The visualization of the molecular structures was performed via the VMD (Humphrey et al., 1996) package. All parallel simulations and non-visualized post-processing were conducted on ARCHER, UK’s national supercomputing service. To obtain a simulation result with physical time of 1 ns, 9,000 compute cores have been simultaneously employed for about 2 h.
Details about the construction of the flow/glycocalyx system and the protocol information can be found in our previous publications (Jiang et al., 2017).
Flow Simulation and Case Set-Up
To mimic flow, external forces were imposed on oxygen atoms of the water molecules in the ectodomain, which has been successfully demonstrated in previous studies (Jiang et al., 2017, 2018a,b; Pikoula et al., 2018). As reported in a previous study (Jiang et al., 2017), an external force with an order of magnitude of 0.001 fN would generate a laminar flow with a physiological bulk flow velocity; the complex and moving structures of the glycocalyx structures disturb the flow profiles, resulting in an oscillating velocity distribution in space. According to the Newton’s Law of Motion, the resulting bulk flow velocity is assumed to be in proportion to the external force. By imposing various external forces (0.003, 0.002, and 0.001 fN, respectively) on water oxygens in the ectodomain, the changing blood flow velocity conditions were mimicked. A diffusion (no flow) case was included for comparison, in which all the external forces imposed on water oxygens were set to 0.
Geometric Stratification
To investigate the ion distribution in space, the height origin of the ectodomain was first determined by the average positions of heavy atoms (i.e., carbon, nitrogen, and phosphor atoms) of the upper lipid heads. An ectodomain space with 50 nm in height starting from the origin was divided into 25 equal bins where the charges of sugar chains and the concentrations of ions were individually calculated. Detailed description about the geometric stratification can be found in a previous study (Jiang et al., 2017).
Statistical Information
The error bars on all bar charts show the standard errors. Statistical significance was determined with t-tests.
Results
The EGL features highly negatively charged sugar chains (Rabelink and de Zeeuw, 2015). As a result, in the initial configuration of the system, Na+ ions (Figure 1C) follow a nearly symmetric distribution with the charge distribution of the sugar chains (Figure 1B). Meanwhile, the Na+ molarity near the membrane (a space from 2 nm to 12 nm in height) is greater than its counterpart in the flow region (a space from 42 to 50 nm in height). The molarity difference is also ubiquitously found throughout a 30-ns simulation of the flow case with the external of 0.003 fN as shown in Figure 1D. The molarity gradient suggests Na+ ion transport through the sugar-chain-rich region. To measure the Na+ movement through the sugar-chain-rich region, molarity difference between two 2-nm layers beneath and above (i.e., cwg and cf in Figure 1D) the sugar-chain-rich region is scrutinized. The time evolutions of the molarity differences, cwg–cf, under varying blood flow velocities are compared in Figure 1E. The mean molarity differences over time in the four situations are then calculated. Statistics have shown that the largest mean molarity difference occurs in the no-flow case with the mean difference of (0.0705 ± 0.0012) M, followed by the 0.001 fN case of (0.0670 ± 0.0010) M and the 0.002 fN case of (0.0653 ± 0.0008) M. The smallest average molarity difference occurs in the fastest flow case (0.003 fN) with a mean difference of (0.0620 ± 0.0005) M [p(no flow > 0.001 fN) = 0.014, p(no flow > 0.002 fN) = 0.0003, p(no flow > 0.003 fN) = 2 × 10-9, p(0.001 fN > 0.002 fN) = 0.09, p(0.001 fN > 0.003 fN) = 6 × 10-6, and p(0.002 fN > 0.003 fN) = 0.0002 by one-side t-tests]. Such a sequence suggests that the flow promotes the Na+ ion transport across the glycocalyx layer to the main flow region.
Discussion
It is important to put the reported findings in the context of the existing literature. Previous studies have demonstrated the significance of the EGL as a sodium barrier (Oberleithner, 2012) from the perspective of cell mechanics as mentioned in the Introduction. By introducing the RBCs, the present research further demonstrates the importance of such a barrier in regulating the motion of RBCs, from the perspective of electrostatics. The formation of the repulsive layer between the RBCs and the EGL can be attributed to their repulsive interactions, as the surfaces of the RBCs are coated with negative charges. Even in healthy conditions, if extra salt is taken in, Na+ may gather around the EGL and neutralize some of negative charges of the EGL, resulting in a decrease in repulsive interactions between RBCs and EGL and a pertinent decline in the exclusion layer thickness. In other words, sodium renders the endothelial cells “sticky” for RBCs, as observed in a recent experiment (Oberleithner et al., 2015). In this regard, to keep a low level of salt intake can benefit the smooth movement of the RBCs, which has also been validated by experiments (Oberleithner, 2015).
According to the present results, a slightly faster blood velocity assists the transport of Na+ ions to the outside of the EGL. Particularly, the number of Na+ ions remaining in the EGL decreases, and the net negative charges in the EGL increase. Consequently, the repulsive interaction between RBCs and EGL is strengthened, leading to the thickness growth of the exclusion layer. The thickness increase then facilitates the smooth flowing of the RBCs which are intimately bound with metabolism. It is therefore expected that regular exercise is beneficial for maintaining the normal operation of the body, as the blood velocity will slightly increase during exercise (Lott et al., 2001).
The present research provides an alternative answer to the open-ended question “Why do we need to reduce salt intake and exercise regularly” based on the atomistic behavior of Na+ ions under varying blood flow velocities. Indeed, the atomic behavior revealed in this study may also provide scientific evidence for seeking breakthrough in therapies to EGL-related diseases. In future research, dynamics of the EGL in abnormal conditions (e.g., with the shedding of sugar chains) under varying blood flow velocities will be investigated.
Author Contributions
XJ conducted the simulation and post-processing. KL and YV are co-leaders of the project. All authors contributed to technical discussions, data analysis, and editing of the manuscript.
Funding
This work was supported by the UK Engineering and Physical Sciences Research Council under the project “UK Consortium on Mesoscale Engineering Sciences (UKCOMES)” (Grant Nos. EP/L00030X/1 and EP/R029598/1). XJ gratefully acknowledges full support from a Dean’s Prize Scholarship from the Faculty of Engineering Sciences, University College London.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Aburto, N. J., Ziolkovska, A., Hooper, L., Elliott, P., Cappuccio, F. P., and Meerpohl, J. J. (2013). Effect of lower sodium intake on health: systematic review and meta-analyses. Br. Med. J. 346:f1326. doi: 10.1136/bmj.f1326
Agarwal, S. K. (2012). Cardiovascular benefits of exercise. Int. J. Gen. Med. 5, 541–545. doi: 10.2147/IJGM.S30113
Allen, M. P. A., and Tildesley, D. J. (1987). Computer Simulation of Liquids. New York, NY: Oxford University Press.
Cruz-Chu, E. R., Malafeev, A., Pajarskas, T., Pivkin, I. V., and Koumoutsakos, P. (2014). Structure and response to flow of the glycocalyx layer. Biophys. J. 106, 232–243. doi: 10.1016/j.bpj.2013.09.060
Curry, F. E., and Adamson, R. H. (2012). Endothelial glycocalyx: permeability barrier and mechanosensor. Ann. Biomed. Eng. 40, 828–839. doi: 10.1007/s10439-011-0429-8
Darden, T., York, D., and Pedersen, L. (1993). Particle mesh Ewald: an N⋅log(N) method for Ewald sums in large systems. J. Chem. Phys. 98, 10089–10092. doi: 10.1063/1.464397
Feng, J., and Weinbaum, S. (2000). Lubrication theory in highly compressible porous media: the mechanics of skiing, from red cells to humans. J. Fluid Mech. 422, 281–317. doi: 10.1017/S0022112000001725
He, F. J., and MacGregor, G. A. (2011). Salt reduction lowers cardiovascular risk: meta-analysis of outcome trials. Lancet 378, 380–382. doi: 10.1016/S0140-6736(11)61174-4
He, F. J., and MacGregor, G. A. (2018). Role of salt intake in prevention of cardiovascular disease: controversies and challenges. Nat. Rev. Cardiol. 15, 371–377. doi: 10.1038/s41569-018-0004-1
Humphrey, W., Dalke, A., and Schulten, K. (1996). VMD: visual molecular dynamics. J. Mol. Graph. 14, 33–38. doi: 10.1016/0263-7855(96)00018-5
Jiang, X. Z., Feng, M., Luo, K. H., and Ventikos, Y. (2018a). Large-scale molecular dynamics simulation of flow under complex structure of endothelial glycocalyx. Comput. Fluids 173, 140–146. doi: 10.1016/j.compfluid.2018.03.014
Jiang, X. Z., Feng, M., Ventikos, Y., and Luo, K. H. (2018b). Regimes of flow over complex structures of endothelial glycocalyx: a molecular dynamics simulation study. Sci. Rep. 8:5732. doi: 10.1038/s41598-018-24041-7
Jiang, X. Z., Gong, H., Luo, K. H., and Ventikos, Y. (2017). Large-scale molecular dynamics simulation of coupled dynamics of flow and glycocalyx: towards understanding atomic events on an endothelial cell surface. J. R. Soc. Interface 14, 20170780. doi: 10.1098/rsif.2017.0780
Jorgensen, W. L., Chandrasekhar, J., Madura, J. D., Impey, R. W., and Klein, M. L. (1983). Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935. doi: 10.1063/1.445869
Lott, M. E., Hogeman, C. S., Vickery, L., Kunselman, A. R., Sinoway, L. I., and Maclean, D. A. (2001). Effects of dynamic exercise on mean blood velocity and muscle interstitial metabolite responses in humans. Am. J. Physiol. Heart Circ. Physiol. 281, H1734–H1741. doi: 10.1152/ajpheart.2001.281.4.H1734
MacKerell, A. D., Bashford, D., Bellott, M., Dunbrack, R. L., Evanseck, J. D., Field, M. J., et al. (1998). All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 102, 3586–3616. doi: 10.1021/jp973084f
Miyamoto, S., and Kollman, P. A. (1992). Settle - an analytical version of the shake and rattle algorithm for rigid water models. J. Comput. Chem. 13, 952–962. doi: 10.1002/jcc.540130805
Oberleithner, H. (2012). Two barriers for sodium in vascular endothelium? Ann. Med. 44, S143–S148. doi: 10.3109/07853890.2011.653397
Oberleithner, H. (2015). Sodium selective erythrocyte glycocalyx and salt sensitivity in man. Pflugers. Arch. 467, 1319–1325. doi: 10.1007/s00424-014-1577-0
Oberleithner, H., Peters, W., Kusche-Vihrog, K., Korte, S., Schillers, H., Kliche, K., et al. (2011). Salt overload damages the glycocalyx sodium barrier of vascular endothelium. Pflugers. Arch. 462, 519–528. doi: 10.1007/s00424-011-0999-1
Oberleithner, H., Walte, M., and Kusche-Vihrog, K. (2015). Sodium renders endothelial cells sticky for red blood cells. Front. Physiol. 6:188. doi: 10.3389/fphys.2015.00188
Phillips, J. C., Braun, R., Wang, W., Gumbart, J., Tajkhorshid, E., Villa, E., et al. (2005). Scalable molecular dynamics with NAMD. J. Comput. Chem. 26, 1781–1802. doi: 10.1002/jcc.20289
Pikoula, M., Tessier, M. B., Woods, R. J., and Ventikos, Y. (2018). Oligosaccharide model of the vascular endothelial glycocalyx in physiological flow. Microfluid Nanofluidics 22:21. doi: 10.1007/s10404-018-2037-5
Rabelink, T. J., and de Zeeuw, D. (2015). The glycocalyx–linking albuminuria with renal and cardiovascular disease. Nat. Rev. Nephrol. 11, 667–676. doi: 10.1038/nrneph.2015.162
Schuler, G., Adams, V., and Goto, Y. (2013). Role of exercise in the prevention of cardiovascular disease: results, mechanisms, and new perspectives. Eur. Heart J. 34, 1790–1799. doi: 10.1093/eurheartj/eht111
Vink, H., and Duling, B. R. (1996). Identification of distinct luminal domains for macromolecules, erythrocytes, and leukocytes within mammalian capillaries. Circ. Res. 79, 581–589. doi: 10.1161/01.RES.79.3.581
Keywords: endothelial glycocalyx layer, lifestyle, molecular dynamics, ion transport, sodium intake
Citation: Jiang XZ, Luo KH and Ventikos Y (2018) Reducing Salt Intake and Exercising Regularly: Implications From Molecular Dynamics Simulations of Endothelial Glycocalyx. Front. Physiol. 9:1667. doi: 10.3389/fphys.2018.01667
Received: 22 July 2018; Accepted: 06 November 2018;
Published: 21 November 2018.
Edited by:
John D. Imig, Medical College of Wisconsin, United StatesReviewed by:
Pingnian He, Pennsylvania State University, United StatesOzlem Yalcin, Koç University, Turkey
Copyright © 2018 Jiang, Luo and Ventikos. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kai H. Luo, ay5sdW9AdWNsLmFjLnVr Yiannis Ventikos, eS52ZW50aWtvc0B1Y2wuYWMudWs=
 Xi Zhuo Jiang
Xi Zhuo Jiang Kai H. Luo
Kai H. Luo Yiannis Ventikos
Yiannis Ventikos