- 1Department of Physics, Institute for Advanced Studies in Basic Sciences (IASBS), Zanjan, Iran
- 2School of Cognitive Sciences, Institute for Research in Fundamental Sciences (IPM), Tehran, Iran
- 3Department of Neurosurgery, Stanford University School of Medicine, Stanford, CA, United States
Biological neuronal networks are highly adaptive and plastic. For instance, spike-timing-dependent plasticity (STDP) is a core mechanism which adapts the synaptic strengths based on the relative timing of pre- and postsynaptic spikes. In various fields of physiology, time delays cause a plethora of biologically relevant dynamical phenomena. However, time delays increase the complexity of model systems together with the computational and theoretical analysis burden. Accordingly, in computational neuronal network studies propagation delays were often neglected. As a downside, a classic STDP rule in oscillatory neurons without propagation delays is unable to give rise to bidirectional synaptic couplings, i.e., loops or uncoupled states. This is at variance with basic experimental results. In this mini review, we focus on recent theoretical studies focusing on how things change in the presence of propagation delays. Realistic propagation delays may lead to the emergence of neuronal activity and synaptic connectivity patterns, which cannot be captured by classic STDP models. In fact, propagation delays determine the inventory of attractor states and shape their basins of attractions. The results reviewed here enable to overcome fundamental discrepancies between theory and experiments. Furthermore, these findings are relevant for the development of therapeutic brain stimulation techniques aiming at shifting the diseased brain to more favorable attractor states.
1. Introduction
Time delays play an important role in various fields of physiology (Glass et al., 1988; Batzel and Kappel, 2011). Neurophysiological time delays crucially affect generation, transmission, and processing of information among different components of a living system, and more specifically, between interconnected neurons in the nervous system. The time required for neuronal communication can be significantly prolonged due to the physical distance between sending and receiving units (Knoblauch and Sommer, 2003, 2004), finite velocity of signal transmission (Desmedt and Cheron, 1980), morphology of dendrites and axons (Manor et al., 1991; Boudkkazi et al., 2007) and information processing time of the cell (Wang et al., 2009). The physiological range of such time delays may vary from a few milliseconds in dendritic trees (Agmon-Snir and Segev, 1993; Schierwagen and Claus, 2001) to tens of milliseconds in axonal components of cortico-thalamic circuits (Swadlow and Weyand, 1987).
The presence of such experimentally observed propagation delays can have significant impacts on the performance, structure, and function of the nervous system (Sirota et al., 2005; Joris and Yin, 2007; Chomiak et al., 2008; Spencer et al., 2012, 2018; Squire et al., 2012; Walters et al., 2013; Esfahani et al., 2016; Stoelzel et al., 2017). In fact, the diversity of dendritic and axonal propagation delays in the nervous system can underlie different response properties of the relevant neuronal populations (Sirota et al., 2005; Stoelzel et al., 2017). For instance, axonal propagation delays in visual and motor cortico-thalamic circuits correspond to different response functions associated with sensory, movement-related, or spontaneous activity of neurons (Sirota et al., 2005; Stoelzel et al., 2017). The auditory system employs compensatory delay mechanisms to modulate the asynchrony in inputs, in this way reducing the sensitivity of brainstem neurons to interaural time delays (Spencer et al., 2012, 2018). Propagation delays also can affect the communication between connected neurons by modulating the spatio-temporal properties of pre- and postsynaptic activity patterns (Chomiak et al., 2008). One major role of axonal propagation delays might be their involvement in the generation of nearly synchronous responses in postsynaptic neurons by regulating the outgoing impulses in axons with several postsynaptic target neurons (Chomiak et al., 2008).
Despite their inevitable physiological significance in living systems, propagation delays are usually overlooked in mathematical models, presumably to avoid further complexity. Although this assumption simplifies the theoretical calculations and reduces the computational cost of multiscale computer simulations, it renders mathematical models unable to provide insight into relevant physiological mechanisms. However, a number of theoretical and computational studies have shown that propagation delays modify weight and neuronal dynamics by affecting the co-evolution of synaptic strengths and neuronal activity, and therefore, shaping the emergent functional and structural properties of plastic neuronal networks (Lubenov and Siapas, 2008; Aoki and Aoyagi, 2009; Kozloski and Cecchi, 2010; Rubinov et al., 2011; Knoblauch et al., 2012; Babadi and Abbott, 2013; Kerr et al., 2013; Madadi Asl et al., 2017, 2018a), where the synaptic strengths are regulated by spike-timing-dependent plasticity (STDP) (Gerstner et al., 1996; Markram et al., 1997; Bi and Poo, 1998; Song et al., 2000). Hence, incorporation of time delays in mathematical models can significantly modify the dynamical properties of neuronal systems, such as the emergence of different connectivity patterns (Madadi Asl et al., 2017, 2018a), affecting the dynamics of fixed points and synchronization properties between interconnected neurons (D'Huys et al., 2008; Popovych et al., 2011), and the emergence of different multistable dynamical attractors (Song et al., 2009; Madadi Asl et al., 2018a).
Neglecting realistic time delays in mathematical models has led to discrepancies between theoretical and experimental findings over the past few years. In this manuscript, we review recent physiological and computational studies that have shown that a simple classic STDP rule enhanced by realistic dendritic and axonal propagation delays is able to explain some of the corresponding experimental results. We highlight the pivotal role of dendritic and axonal propagation delays in regulating the emergent activity and connectivity patterns in plastic neuronal networks under the influence of classic pair-based STDP which significantly affects the information transmission in neuronal populations. Ultimately, we point out the importance of propagation delays in the computation-based development of therapeutic brain stimulation techniques that are used for modulating plastic neuronal networks in diseased brains.
2. Propagation Delays: Physiological Aspects
From a physiological standpoint, the measurement of propagation delays in dendrites or axons of neuronal populations requires complex experimental setups, stimulation protocols, or modern clinical instruments. Several experimental studies investigated dendritic and axonal propagation delays in neuronal populations of various species (Swadlow and Weyand, 1987; Swadlow, 1990; Agmon-Snir and Segev, 1993; Schierwagen and Claus, 2001; Ferraina et al., 2002; Briggs and Usrey, 2009; Stoelzel et al., 2017). The physiological range of dendritic and axonal propagation delays may attain a range of different values, based on different experimental model systems in which they were measured. For instance, the value of dendritic propagation delays may vary from sub-milliseconds to a few milliseconds (Agmon-Snir and Segev, 1993; Schierwagen and Claus, 2001). Axonal propagation delays, however, may take a wider range from a few milliseconds in cortico-tectal connections (Swadlow and Weyand, 1987) to tens of milliseconds in cortico-cortical (Swadlow, 1990) and cortico-thalamic circuits (Swadlow and Weyand, 1987). Axonal delays are typically greater than dendritic delays in a neuron, however, values of dendritic delays greater than the axonal delays were experimentally measured in distal dendrites of neocortical pyramidal neurons (Stuart and Spruston, 1998; Sjöström and Häusser, 2006).
In the auditory system, dendritic and axonal propagation delays modify the mechanisms of interaural time sensitivity by regulating coincident or lagged inputs from the two sides, and therefore, play a constructive/destructive role in binaural sound localization depending on the location of the sound source and the leading ear (Joris and Yin, 2007; Squire et al., 2012). Dendritic propagation delays are hypothesized to play a compensatory role for the input asynchrony in the auditory brainstem of mammals using plastic synaptic weights (Spencer et al., 2012, 2018). In the motor system, propagation delays can impose functional limitations on the efficiency of feedback control in situations where time-critical performance of the sensory feedback is vital for the biological system (Squire et al., 2012). The functional significance of diverse range of axonal propagation delays in cortico-thalamic circuits are shown to be strongly related to multiple visual response properties (Stoelzel et al., 2017). Axonal delays act as a timing mechanism in the neuronal networks responsible for path integration of head direction and were computationally shown to promote the accuracy of path integration in the absence of visual input (Walters et al., 2013). Experimentally delayed visual feedback was used as a tool to manipulate and disentangle different motor control regulatory brain mechanisms (Tass et al., 1996; Rougier, 2003; van den Heuvel et al., 2009).
The role of dendritic or axonal propagation delays has been implicated in a number of nervous system disorders such as Parkinson's disease (PD) (Hauptmann and Tass, 2007; Ebert et al., 2014; Shouno et al., 2017), epilepsy (Wendling et al., 2010), and multiple sclerosis (MS) (Waxman, 2006). Subthalamic nucleus (STN) parkinsonian oscillations are shown to be sensitive to feedback oscillatory inputs of cortical circuits in a delay-dependent manner (Shouno et al., 2017). Neurophysiological latencies are hypothetically involved in the complex propagation mechanisms of epileptic activity in the brain (Wendling et al., 2010). In MS patients a demyelination of axonal components may lead to significant transmission delays along the axon of the cell (Waxman, 2006). This process reduces the conduction velocity of signals along the axon and can ultimately result in a blockage of information transmission and conduction failure of the axon (Waxman, 2006). Furthermore, propagation delays can have significant impact on methods used to record or modulate brain activity. For instance, time delays can affect procedures that estimate the degree of association and phase relationships between electroencephalogram (EEG) signals (Lopes da Silva F et al., 1989), or adjust the performance of therapeutic brain stimulation techniques (see below).
3. Propagation Delays: Computational Aspects
From a computational standpoint, one of the most important roles of propagation delays might be their potential to address the challenging inconsistencies between theoretical and computational studies regarding the functional, structural, and dynamical properties of plastic neuronal networks driven by the pair-based STDP (Abbott and Nelson, 2000; Song and Abbott, 2001; Pfister and Gerstner, 2006; Masuda and Kori, 2007; Lubenov and Siapas, 2008; Clopath et al., 2010; Kozloski and Cecchi, 2010; Knoblauch et al., 2012) on the one hand and relevant experimental observations (Bi and Poo, 1998; Van Rossum et al., 2000; Sjöström et al., 2001; Song et al., 2005; Wang et al., 2005; Lea-Carnall et al., 2017) on the other hand, e.g., the prevalence of strong bidirectional loops between pairs of neurons in cortical circuits (Song et al., 2005; Morishima and Kawaguchi, 2006) and the dependence of emergent synaptic structures on the firing rate of neurons (Sjöström et al., 2001; Wang et al., 2005; Lea-Carnall et al., 2017).
In fact, the classic pair-based STDP model (Gerstner et al., 1996; Markram et al., 1997; Bi and Poo, 1998; Song et al., 2000), through which the change of the synaptic strengths is induced by pairwise temporal interactions between pre- and postsynaptic spikes, has shown to be unable to account for the emergence of strong bidirectional connections and neuronal loops (Abbott and Nelson, 2000; Song and Abbott, 2001; Lubenov and Siapas, 2008; Kozloski and Cecchi, 2010; Knoblauch et al., 2012; Babadi and Abbott, 2013). Furthermore, it fails to address the experimentally measured dependency of weight dynamics on the frequency of oscillations (Sjöström et al., 2001; Wang et al., 2005; Lea-Carnall et al., 2017). Several attempts were made in order to overcome the limitations of the pair-based STDP model over the past few years via the introduction of variations or improvements of the STDP model, such as the triplet-based STDP (Pfister and Gerstner, 2006), STDP with shifted learning window (Babadi and Abbott, 2013), or application of independent noise (Popovych et al., 2013; Lücken et al., 2016). Furthermore, there are several biophysical models that attempt to identify variables with specific biophysical quantities and include them in biophysics-based models of STDP (Castellani et al., 2001; Shouval et al., 2002a,b, 2010; Abarbanel et al., 2003; Rachmuth et al., 2011). For instance, Shouval et al. developed a model of long-term potentiation/depression that includes the back propagating potential in the STDP model (Castellani et al., 2001; Shouval et al., 2002a,b). For a review of the shortcomings of pair-based STDP and its variations see (Morrison et al., 2008; Madadi Asl et al., 2018b).
A number of studies, however, have focused on the role of propagation delays to resolve the aforementioned discrepancies. Short axonal propagation delays were shown to decouple synchronous neurons in the presence of STDP (Knoblauch and Sommer, 2003, 2004), whereas long axonal propagation delays promote inter-areal synchronized activity and result in a potentiation of the synaptic strengths (Knoblauch and Sommer, 2004). Taking into account only dendritic propagation delays in the modeling can result in the emergence of strong two-neuron loops (Morrison et al., 2007). Also, it was shown that a combination of dendritic and axonal propagation delays along with an unbalanced STDP profile can lead to the emergence of self-organized states in recurrent neuronal networks (Lubenov and Siapas, 2008). The role of dendritic and axonal propagation delays on the dynamics of recurrent neuronal networks has also been pointed out by considering the effect of time delays in terms of a shift in the STDP temporal window (Babadi and Abbott, 2013). Pairwise interactions of STDP-driven recurrent neuronal populations with such shifts can explain mechanisms underlying loop formation and elimination in bidirectional synapses (Kozloski and Cecchi, 2010; Babadi and Abbott, 2013).
Recently, by presenting a theoretical framework comprising regular spiking neurons we showed that by taking into account dendritic and axonal propagation delays in the modeling of a STDP-driven two-neuron motif different patterns of synaptic connectivity may emerge (Madadi Asl et al., 2017). The synaptic strengths are modified according to the following pair-based STDP rule (Bi and Poo, 1998):
where A+(A−) and τ+(τ−) are the learning rate and the effective time window of synaptic potentiation (depression), respectively, and sgn(Δt′) is the sign function. Δt′ = Δt + ξ is the effective delayed time lag between pre- and postsynaptic spikes at the synaptic site (Madadi Asl et al., 2017, 2018a). Δt = tpost − tpre is the original time lag between pre- and postsynaptic spike pairs, and ξ = τd − τa is the difference between dendritic and axonal propagation delays. The synaptic strengths are updated by an additive rule at each step gij→gij+Δgij, and they are confined in the range (gmin, gmax) ∈ [0, 1] by using a hard bound saturation constraint.
When propagation delays are ignored or, equivalently, when dendritic and axonal delays are identical for both directions of the reciprocal synapses, ξ = τd − τa = 0, the original and the effective delayed time lags are equal, Δt′ = Δt. Therefore, the type of synaptic modification is simply determined by the sign of the original time lag, i.e., Δt ≥ 0 leads to a potentiation of the synapse whereas Δt < 0 results in a depression. Hence, in the absence of propagation delays, the potentiation of one synapse is accompanied by the depression of the other synapse, leading to a unidirectional connection when the potentiation and depression amplitude of the STDP profile is balanced. However, in the presence of dendritic and axonal propagation delays and assuming that the spiking neurons are relatively phase-locked with a small time lag with respect to the propagation delays, |ξ| > |Δt|, the effective delayed time lag Δt′ perceived at the synaptic site may be different from the time lag of the spikes at the cell bodies. Hence, as shown in Figure 1A, when the dendritic delay is greater than the axonal τd > τ a, reciprocal synapses are both potentiated, which lead to the emergence of a strong bidirectional loop. On the contrary, greater axonal delays τd < τa result in a depression of both reciprocal synapses, in this way generating a loosely connected motif (see Figure 1B).
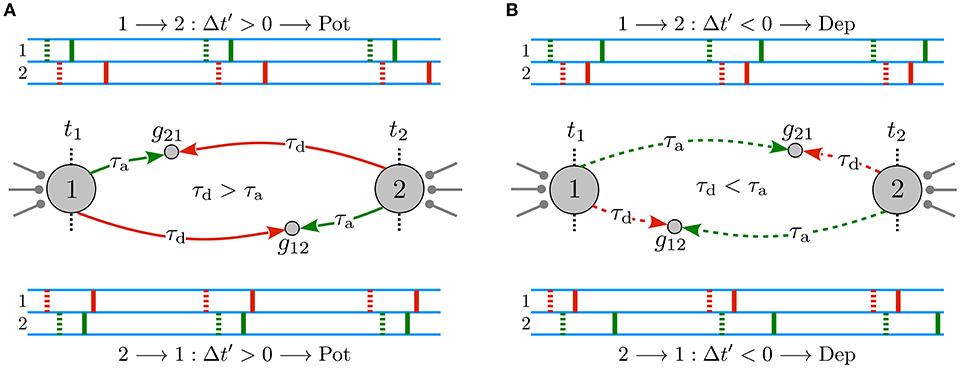
Figure 1. Delay-induced connectivity patterns in a two-neuron motif. Spiking neurons are connected to each other via initially symmetric synapses with strengths g21 (g12) of the synapse 1 → 2 (2 → 1) with a small time lag Δt = tpost − tpre. Δt′ = Δt + ξ is the effective delayed time lag perceived at the synapse which STDP employs to modify the synapse, where ξ = τd − τ a and |ξ| > |Δt|. Green and red dotted (solid) markers indicate the original, t1 and t2 (delayed) forward and backpropagated spike time of pre- and postsynaptic neurons at the synapse, respectively. (A) Emergence of a strong bidirectional loop: both synapses are reciprocally potentiated when τd > τ a. (B) A loosely connected motif: both reciprocal synapses are depressed when τd < τa. Figure partly adopted from Madadi Asl et al. (2018b) with authors' permission.
By assuming that the neurons remain phase-locked, it was illustrated that the two-neuron results can be extended to recurrent networks of spiking neurons (Madadi Asl et al., 2017, 2018a). Different combinations of dendritic and axonal propagation delays can lead to the emergence of symmetric connections, i.e., either two-neuron bidirectional loops, in the case that dendritic propagation delays are greater than the axonal delays (Figure 2A), or loosely connected motifs when axonal propagation delays are greater than the dendritic delays (Figure 2C) (Madadi Asl et al., 2017). As shown in Figure 2C, the disconnected network is highly unstable and ultimately leads to the emergence of unidirectional connections. However, we showed that the loosely connected motif can be stabilized by assigning a finite value to the lower bound of the synaptic strengths gmin (Madadi Asl et al., 2018a). In this framework, unidirectional connections can also arise when dendritic and axonal propagation delays are identical in both directions of the reciprocal synapses (Figure 2B).
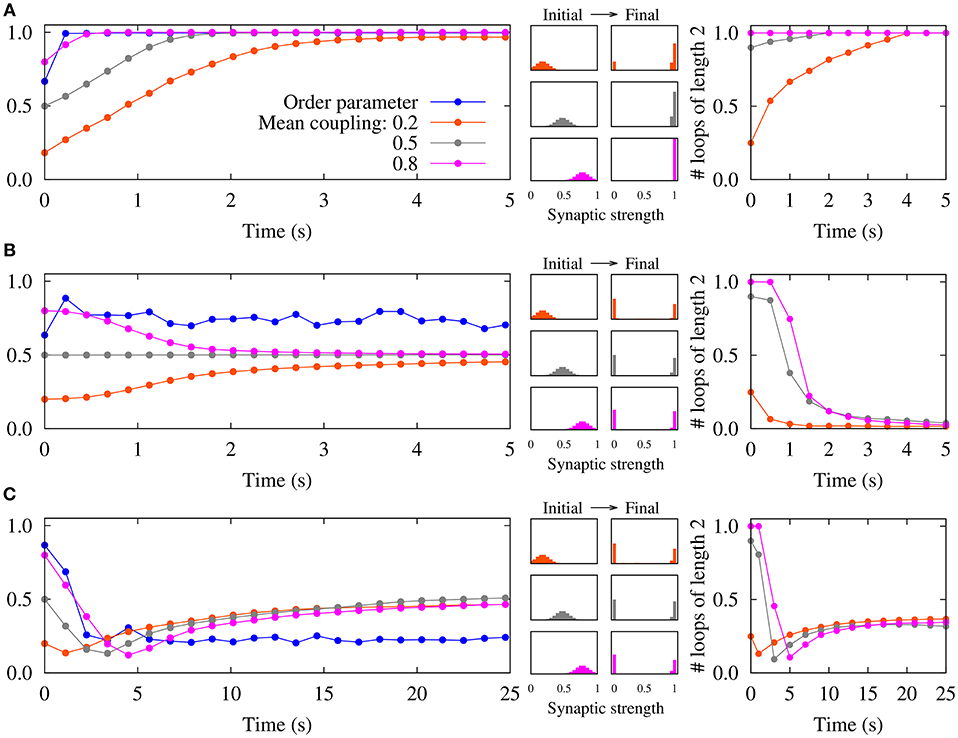
Figure 2. Emergence of different connectivity patterns in a recurrent network of spiking neurons mediated by STDP. (Left panels) Simulated order parameter and time course of three different mean couplings of weight distributions. (Middle panels) Initial Gaussian distribution around different mean values and final distribution of the synaptic strengths. (Right panels) Time course of the normalized number of closed loops of length 2 measuring the number of two-neuron loops in the network (Madadi Asl et al., 2017). (A) The synaptic strengths are potentiated and bidirectional connections are significantly enhanced in the inphase firing when τd = 0.5ms>τa = 0.3ms. (B) STDP breaks strong two-neuron loops and results in unidirectional connections in nearly inphase firing when τd = τa = 0.5ms. (C) A loosely connected network is achieved where bidirectional loops are eliminated in the nearly antiphase firing when τd = 0.5ms < τa = 1.0ms. STDP parameters are A+ = A− = 0.005, and τ+ = τ− = 10ms. Figure partly adopted from Madadi Asl et al. (2017) with authors' permission.
Furthermore, we studied the emergence of delay-induced multistable dynamics in recurrent networks of spiking neurons attributed to the distribution of the initial synaptic strengths modified by STDP (Madadi Asl et al., 2018a). Such a multistability of the network evolution can be theoretically addressed by the emergence of different attractor states representing the two-dimensional space of the initial synaptic strengths in a two-neuron motif (Madadi Asl et al., 2018a). Moreover, it was shown that the basin of attraction of each dynamical state depends on the firing rate of the neurons in a way that higher firing frequencies favor the emergence of symmetric connections in expense of eliminating the unidirectional connections (Madadi Asl et al., 2018a). Intriguingly, the aforementioned nontrivial dynamics are only present when the dendritic and axonal propagation delays are considered in the neuronal networks models. In the simplest setting, characterized by ignoring dendritic and axonal propagation delays as well as the absence of independent noise, any initial preparation leads to the emergence of unidirectional connections regardless of the neuronal firing pattern and the initial synaptic strengths.
4. Concluding Remarks
Propagation delays are inevitable in living systems, and in particular, in the nervous system. The presence of propagation delays has significant impact on the performance, structure, and function of the nervous system. However, from a physiological as well as theoretical standpoint, systems with time delays are considerably more complex, and therefore, delays have typically not been taken into account in relevant studies to simplify the experimental setups in physiological measurements or the mathematical approach in theoretical studies. Incorporating time delays can impose significant levels of complexity and computational cost to the problem. Time delay differential equations are more complicated to deal with from an analytical standpoint. For this reason, in a first approximation, theoretical and computational studies typically ignored the effects of time delays in the modeling. This has led to some discrepancies between theoretical and computational studies with physiological measurements over the past few years (Bi and Poo, 1998; Abbott and Nelson, 2000; Van Rossum et al., 2000; Sjöström et al., 2001; Song and Abbott, 2001; Song et al., 2005; Wang et al., 2005; Pfister and Gerstner, 2006; Masuda and Kori, 2007; Lubenov and Siapas, 2008; Clopath et al., 2010; Kozloski and Cecchi, 2010; Lea-Carnall et al., 2017). However, in an attempt to overcome unphysiological simplifications, we recently demonstrated that incorporating dendritic and axonal propagation delays in STDP-driven networks of spiking model neurons can lead to the emergence of different synaptic connectivity patterns characterized by different dynamical attractors (Madadi Asl et al., 2017, 2018a).
The shortcomings of the pair-based STDP model can be resolved by several improvements proposed during the past decade: The experimentally demonstrated dependency of the weight dynamics on the frequency of the neuronal oscillations can be addressed by considering triplets of spikes (Pfister and Gerstner, 2006) or postsynaptic voltage (Clopath et al., 2010) in the plasticity model. In fact, the triplet-based STDP model is proposed to comply with the experimentally observed dependence of the weight changes on the firing frequency of the oscillations (Sjöström et al., 2001; Wang et al., 2005; Lea-Carnall et al., 2017), showing that bidirectional connections can be promoted at high firing rates (Pfister and Gerstner, 2006). Strong bidirectional loops can be retained by employing an unbalanced STDP model with a shifted learning window (Babadi and Abbott, 2013) or the application of independent noise (Popovych et al., 2013; Lücken et al., 2016). A pair-based STDP model with a rightward shifted learning window was shown to preserve bidirectional connections, provided that potentiation dominates over depression (Babadi and Abbott, 2013). Furthermore, STDP-driven neuronal populations subjected to independent noise counteract the desynchronizing effect of noise by reorganizing their synaptic connectivity (Popovych et al., 2013; Lücken et al., 2016). This ultimately leads to a self-organized noise resistance and promotes bidirectional connections between neurons.
The findings reviewed in this paper highlight the key role of the presence and the range of dendritic and axonal propagation delays in modifying the arising dynamics of synaptic connectivity patterns in recurrent networks of spiking neurons. In fact, short-range propagation delays may favor strong two-neuron loops, whereas connections with long propagation delays may result in the stabilization of a loosely connected network. Hence, the difference of dendritic and axonal propagation delays play a crucial role in determining the final stable coupling regime selected by the network dynamics (Madadi Asl et al., 2017, 2018a). In this way, delay-induced dynamics can overcome the shortcomings of the pair-based STDP model: Strong two-neuron loops can be preserved even with a balanced STDP profile in the absence of independent noise, provided dendritic and axonal propagation delays are considered in the model, and furthermore, the experimentally observed dependency of the weight dynamics on the frequency of the oscillations can be addressed in this setting (Madadi Asl et al., 2017, 2018a).
Abnormal neuronal synchronization is a hallmark of several brain disorders (Lenz et al., 1994; Nini et al., 1995; Hammond et al., 2007). Coordinated reset (CR) stimulation is a computationally developed patterned multichannel stimulation (Tass, 2003) which aims at specifically counteracting abnormal synchrony by desynchronization (Tass, 2003), thereby causing a decrease of neuronal coincidences and, hence, a down-regulation of synaptic weights, ultimately shifting the affected neuronal networks from pathological attractor states (with strong synchrony and strong synaptic connectivity) to more physiological attractor states (with loose coupling and desynchronized activity) (Tass and Majtanik, 2006). The very goal of this approach is to induce long-lasting desynchronization which persists after cessation of stimulation (Tass and Majtanik, 2006). Computationally predicted desynchronizing effects (Tass, 2003), cumulative effects (Hauptmann and Tass, 2009) and long-lasting effects (Tass and Majtanik, 2006) were experimentally validated in the field of deep brain stimulation for the treatment of Parkinson's disease in pre-clinical studies in Parkinsonian monkeys (Tass et al., 2012b; Wang et al., 2016) as well as in a proof of concept study in patients with Parkinson's disease (Adamchic et al., 2014a). As computationally predicted (Popovych and Tass, 2012; Tass and Popovych, 2012), CR stimulation can also be realized by sensory stimulation modalities. Acoustic CR stimulation caused a significant relief of symptoms in patients with chronic subjective tinnitus (Tass et al., 2012a), combined with a significant reduction of abnormal neuronal synchrony (Tass et al., 2012a; Adamchic et al., 2014b) and abnormal effective connectivity (Silchenko et al., 2013), as shown in a proof of concept study employing clinical scores and EEG recordings. By the same token, vibrotactile CR stimulation (Tass, 2017) caused long-lasting treatment effects, as observed in a first in man study in Parkinson's patients (Syrkin-Nikolau et al., 2018).
The findings reviewed above are relevant for the development of desynchronizing brain stimulation techniques. From a model perspective, long-lasting treatment effects are caused by shifting networks from pathological, strongly synchronized model attractor states to physiological, desynchronized attractor states (Tass and Majtanik, 2006). One the one hand, propagation delays determine which attractors actually emerge. On the other hand, propagation delays additionally shape the basins of attraction and, hence, determine to which extent attractors get accessible by appropriate stimulus protocols. Finally, propagation delays may favorably or unfavorably impact on multichannel stimulation protocols with dedicated stimulus sequences, since delays may counteract proper stimulus timing.
Data Availability Statement
All datasets generated or analyzed for this study are included in the manuscript.
Author Contributions
AV and PT conceived the study. MM conducted the numerical simulations and theoretical approximations. MM, AV, and PT analyzed the results. MM, AV, and PT wrote and reviewed the paper.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
PT gratefully acknowledges the generous research funding support from the John A. Blume Foundation.
References
Abarbanel, H. D., Gibb, L., Huerta, R., and Rabinovich, M. I. (2003). Biophysical model of synaptic plasticity dynamics. Biol. Cybern. 89, 214–226. doi: 10.1007/s00422-003-0422-x
Abbott, L. F., and Nelson, S. B. (2000). Synaptic plasticity: taming the beast. Nat. Neurosci. 3, 1178–1183. doi: 10.1038/81453
Adamchic, I., Hauptmann, C., Barnikol, U., Pawelcyk, N., Popovych, O. V., Barnikol, T., et al. (2014a). Coordinated reset has lasting aftereffects in patients with parkinson's disease. Mov. Disord. 29, 1679–1684. doi: 10.1002/mds.25923
Adamchic, I., Toth, T., Hauptmann, C., and Tass, P. A. (2014b). Reversing pathologically increased eeg power by acoustic coordinated reset neuromodulation. Hum. Brain Mapp. 35, 2099–2118. doi: 10.1002/hbm.22314
Agmon-Snir, H., and Segev, I. (1993). Signal delay and input synchronization in passive dendritic structures. J. Neurophysiol. 70, 2066–2085.
Aoki, T., and Aoyagi, T. (2009). Co-evolution of phases and connection strengths in a network of phase oscillators. Phys. Rev. Lett. 102:034101. doi: 10.1103/PhysRevLett.102.034101
Babadi, B., and Abbott, L. F. (2013). Pairwise analysis can account for network structures arising from spike-timing dependent plasticity. PLoS Comput. Biol. 9:e1002906. doi: 10.1371/journal.pcbi.1002906
Batzel, J. J., and Kappel, F. (2011). Time delay in physiological systems: Analyzing and modeling its impact. Math. Biosci. 234, 61–74. doi: 10.1016/j.mbs.2011.08.006
Bi, G. Q., and Poo, M. M. (1998). Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J. Neurosci. 18, 10464–10472.
Boudkkazi, S., Carlier, E., Ankri, N., Caillard, O., Giraud, P., Fronzaroli-Molinieres, L., et al. (2007). Release-dependent variations in synaptic latency: a putative code for short-and long-term synaptic dynamics. Neuron 56, 1048–1060. doi: 10.1016/j.neuron.2007.10.037
Briggs, F., and Usrey, W. M. (2009). Parallel processing in the corticogeniculate pathway of the macaque monkey. Neuron 62, 135–146. doi: 10.1016/j.neuron.2009.02.024
Castellani, G. C., Quinlan, E. M., Cooper, L. N., and Shouval, H. Z. (2001). A biophysical model of bidirectional synaptic plasticity: dependence on ampa and nmda receptors. Proc. Natl. Acad. Sci. U.S.A. 98, 12772–12777. doi: 10.1073/pnas.201404598
Chomiak, T., Peters, S., and Hu, B. (2008). Functional architecture and spike timing properties of corticofugal projections from rat ventral temporal cortex. J. Neurophysiol. 100, 327–335. doi: 10.1152/jn.90392.2008
Clopath, C., Büsing, L., Vasilaki, E., and Gerstner, W. (2010). Connectivity reflects coding: a model of voltage-based stdp with homeostasis. Nat. Neurosci. 13, 344–352. doi: 10.1038/nn.2479
Desmedt, J. E. and Cheron, G. (1980). Central somatosensory conduction in man: neural generators and interpeak latencies of the far-field components recorded from neck and right or left scalp and earlobes. Electroencephal. Clin. Neurophysiol. 50, 382–403.
D'Huys, O., Vicente, R., Erneux, T., Danckaert, J., and Fischer, I. (2008). Synchronization properties of network motifs: influence of coupling delay and symmetry. Chaos 18:037116. doi: 10.1063/1.2953582
Ebert, M., Hauptmann, C., and Tass, P. A. (2014). Coordinated reset stimulation in a large-scale model of the stn-gpe circuit. Front. Comput. Neurosci. 8:154. doi: 10.3389/fncom.2014.00154
Esfahani, Z. G., Gollo, L. L., and Valizadeh, A. (2016). Stimulus-dependent synchronization in delayed-coupled neuronal networks. Sci. Rep. 6:23471. doi: 10.1038/srep23471
Ferraina, S., Paré, M., and Wurtz, R. H. (2002). Comparison of cortico-cortical and cortico-collicular signals for the generation of saccadic eye movements. J. Neurophysiol. 87, 845–858. doi: 10.1152/jn.00317.2001
Gerstner, W., Kempter, R., van Hemmen, J. L., and Wagner, H. (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383:76. doi: 10.1038/383076a0
Glass, L., Beuter, A., and Larocque, D. (1988). Time delays, oscillations, and chaos in physiological control systems. Math. Biosci. 90, 111–125.
Hammond, C., Bergman, H., and Brown, P. (2007). Pathological synchronization in parkinson's disease: networks, models and treatments. Trends Neurosci. 30, 357–364. doi: 10.1016/j.tins.2007.05.004
Hauptmann, C., and Tass, P. A. (2007). Therapeutic rewiring by means of desynchronizing brain stimulation. Biosystems 89, 173–181. doi: 10.1016/j.biosystems.2006.04.015
Hauptmann, C., and Tass, P. A. (2009). Cumulative and after-effects of short and weak coordinated reset stimulation: a modeling study. J. Neural Engineer. 6:016004. doi: 10.1088/1741-2560/6/1/016004
Joris, P., and Yin, T. C. (2007). A matter of time: internal delays in binaural processing. Trends Neurosci. 30, 70–78. doi: 10.1016/j.tins.2006.12.004
Kerr, R. R., Burkitt, A. N., Thomas, D. A., Gilson, M., and Grayden, D. B. (2013). Delay selection by spike-timing-dependent plasticity in recurrent networks of spiking neurons receiving oscillatory inputs. PLoS Comput. Biol. 9:e1002897. doi: 10.1371/journal.pcbi.1002897
Knoblauch, A., Hauser, F., Gewaltig, M.-O., Körner, E., and Palm, G. (2012). Does spike-timing-dependent synaptic plasticity couple or decouple neurons firing in synchrony? Front. Comput. Neurosci. 6:55. doi: 10.3389/fncom.2012.00055
Knoblauch, A., and Sommer, F. T. (2003). Synaptic plasticity, conduction delays, and inter-areal phase relations of spike activity in a model of reciprocally connected areas. Neurocomputing 52, 301–306. doi: 10.1016/S0925-2312(02)00792-0
Knoblauch, A., and Sommer, F. T. (2004). Spike-timing-dependent synaptic plasticity can form “zero lag links” for cortical oscillations. Neurocomputing 58, 185–190. doi: 10.3389/fncom.2010.00019
Kozloski, J., and Cecchi, G. A. (2010). A theory of loop formation and elimination by spike timing-dependent plasticity. Front. Neural Circuits 4:7. doi: 10.3389/fncir.2010.00007
Lea-Carnall, C. A., Trujillo-Barreto, N. J., Montemurro, M. A., El-Deredy, W., and Parkes, L. M. (2017). Evidence for frequency-dependent cortical plasticity in the human brain. Proc. Natl. Acad. Sci. U.S.A. 114, 8871–8876. doi: 10.1073/pnas.1620988114
Lenz, F., Kwan, H., Martin, R., Tasker, R., Dostrovsky, J., and Lenz, Y. (1994). Single unit analysis of the human ventral thalamic nuclear group: tremor-related activity in functionally identified cells. Brain 117, 531–543.
Lopes da Silva, F, Pijn, J. P., and Boeijinga, P. (1989). Interdependence of eeg signals: linear vs. nonlinear associations and the significance of time delays and phase shifts. Brain Topogr. 2, 9–18.
Lubenov, E. V., and Siapas, A. G. (2008). Decoupling through synchrony in neuronal circuits with propagation delays. Neuron 58, 118–131. doi: 10.1016/j.neuron.2008.01.036
Lücken, L., Popovych, O. V., Tass, P. A., and Yanchuk, S. (2016). Noise-enhanced coupling between two oscillators with long-term plasticity. Phys. Rev. E 93:032210. doi: 10.1103/PhysRevE.93.032210
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2017). Dendritic and axonal propagation delays determine emergent structures of neuronal networks with plastic synapses. Sci. Rep. 7:39682. doi: 10.1038/srep39682
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2018a). Delay-induced multistability and loop formation in neuronal networks with spike-timing-dependent plasticity. Sci. Rep. 8:12068. doi: 10.1038/s41598-018-30565-9
Madadi Asl, M., Valizadeh, A., and Tass, P. A. (2018b). Propagation delays determine neuronal activity and synaptic connectivity patterns emerging in plastic neuronal networks. Chaos 28:106308. doi: 10.1063/1.5037309
Manor, Y., Koch, C., and Segev, I. (1991). Effect of geometrical irregularities on propagation delay in axonal trees. Biophys. J. 60, 1424–1437.
Markram, H., Lübke, J., Frotscher, M., and Sakmann, B. (1997). Regulation of synaptic efficacy by coincidence of postsynaptic aps and epsps. Science 275, 213–215.
Masuda, N., and Kori, H. (2007). Formation of feedforward networks and frequency synchrony by spike-timing-dependent plasticity. J. Comput. Neurosci. 22, 327–345. doi: 10.1007/s10827-007-0022-1
Morishima, M., and Kawaguchi, Y. (2006). Recurrent connection patterns of corticostriatal pyramidal cells in frontal cortex. J. Neurosci. 26, 4394–4405. doi: 10.1523/JNEUROSCI.0252-06.2006
Morrison, A., Aertsen, A., and Diesmann, M. (2007). Spike-timing-dependent plasticity in balanced random networks. Neural Comput. 19, 1437–1467. doi: 10.1162/neco.2007.19.6.1437
Morrison, A., Diesmann, M., and Gerstner, W. (2008). Phenomenological models of synaptic plasticity based on spike timing. Biol. Cybern. 98, 459–478. doi: 10.1007/s00422-008-0233-1
Nini, A., Feingold, A., Slovin, H., and Bergman, H. (1995). Neurons in the globus pallidus do not show correlated activity in the normal monkey, but phase-locked oscillations appear in the mptp model of parkinsonism. J. Neurophysiol. 74, 1800–1805.
Pfister, J. P., and Gerstner, W. (2006). Triplets of spikes in a model of spike timing-dependent plasticity. J. Neurosci. 26, 9673–9682. doi: 10.1523/JNEUROSCI.1425-06.2006
Popovych, O. V., and Tass, P. A. (2012). Desynchronizing electrical and sensory coordinated reset neuromodulation. Front. Hum. Neurosci. 6:58. doi: 10.3389/fnhum.2012.00058
Popovych, O. V., Yanchuk, S., and Tass, P. A. (2011). Delay- and coupling-induced firing patterns in oscillatory neural loops. Phys. Rev. Lett. 107:228102. doi: 10.1103/PhysRevLett.107.228102
Popovych, O. V., Yanchuk, S., and Tass, P. A. (2013). Self-organized noise resistance of oscillatory neural networks with spike timing-dependent plasticity. Sci. Rep. 3:2926. doi: 10.1038/srep02926
Rachmuth, G., Shouval, H. Z., Bear, M. F., and Poon, C.-S. (2011). A biophysically-based neuromorphic model of spike rate-and timing-dependent plasticity. Proc. Natl. Acad. Sci. U.S.A. 108, E1266–E1274. doi: 10.1073/pnas.1106161108
Rougier, P. (2003). Visual feedback induces opposite effects on elementary centre of gravity and centre of pressure minus centre of gravity motions in undisturbed upright stance. Clin. Biomech. 18, 341–349. doi: 10.1016/s0268-0033(03)00003-2
Rubinov, M., Sporns, O., Thivierge, J.-P., and Breakspear, M. (2011). Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput. Biol. 7:e1002038. doi: 10.1371/journal.pcbi.1002038
Schierwagen, A., and Claus, C. (2001). Dendritic morphology and signal delay in superior colliculus neurons. Neurocomputing 38, 343–350. doi: 10.1016/S0925-2312(01)00417-9
Shouno, O., Tachibana, Y., Nambu, A., and Doya, K. (2017). Computational model of recurrent subthalamo-pallidal circuit for generation of parkinsonian oscillations. Front. Neuroanat. 11:21. doi: 10.3389/fnana.2017.00021
Shouval, H. Z., Bear, M. F., and Cooper, L. N. (2002a). A unified model of nmda receptor-dependent bidirectional synaptic plasticity. Proc. Natl. Acad. Sci. U.S.A. 99, 10831–10836. doi: 10.1073/pnas.152343099
Shouval, H. Z., Castellani, G. C., Blais, B. S., Yeung, L. C., and Cooper, L. N. (2002b). Cq Biol. Cybern. 87, 383–391. doi: 10.1007/s00422-002-0362-x
Shouval, H. Z., Wang, S. S.-H., and Wittenberg, G. M. (2010). Spike timing dependent plasticity: a consequence of more fundamental learning rules. Front. Comput. Neurosci. 4:19. doi: 10.1016/j.neucom.2004.01.041
Silchenko, A. N., Adamchic, I., Hauptmann, C., and Tass, P. A. (2013). Impact of acoustic coordinated reset neuromodulation on effective connectivity in a neural network of phantom sound. Neuroimage 77, 133–147. doi: 10.1016/j.neuroimage.2013.03.013
Sirota, M. G., Swadlow, H. A., and Beloozerova, I. N. (2005). Three channels of corticothalamic communication during locomotion. J. Neurosci. 25, 5915–5925. doi: 10.1523/JNEUROSCI.0489-05.2005
Sjöström, P. J., and Häusser, M. (2006). A cooperative switch determines the sign of synaptic plasticity in distal dendrites of neocortical pyramidal neurons. Neuron 51, 227–238. doi: 10.1016/j.neuron.2006.06.017
Sjöström, P. J., Turrigiano, G. G., and Nelson, S. B. (2001). Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron 32, 1149–1164. doi: 10.1016/s0896-6273(01)00542-6
Song, S., and Abbott, L. F. (2001). Cortical development and remapping through spike timing-dependent plasticity. Neuron 32, 339–350. doi: 10.1016/s0896-6273(01)00451-2
Song, S., Miller, K. D., and Abbott, L. F. (2000). Competitive hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci. 3, 919–926. doi: 10.1038/78829
Song, S., Sjöström, P. J., Reigl, M., Nelson, S., and Chklovskii, D. B. (2005). Highly nonrandom features of synaptic connectivity in local cortical circuits. PLoS Biol. 3:e68. doi: 10.1371/journal.pbio.0030068
Song, Y., Makarov, V. A., and Velarde, M. G. (2009). Stability switches, oscillatory multistability, and spatio-temporal patterns of nonlinear oscillations in recurrently delay coupled neural networks. Biol. Cybern. 101, 147–167. doi: 10.1007/s00422-009-0326-5
Spencer, M. J., Grayden, D. B., Bruce, I. C., Meffin, H., and Burkitt, A. N. (2012). An investigation of dendritic delay in octopus cells of the mammalian cochlear nucleus. Front. Comput. Neurosci. 6:83. doi: 10.3389/fncom.2012.00083
Spencer, M. J., Meffin, H., Burkitt, A. N., and Grayden, D. B. (2018). Compensation for traveling wave delay through selection of dendritic delays using spike-timing-dependent plasticity in a model of the auditory brainstem. Front. Comput. Neurosci. 12:36. doi: 10.3389/fncom.2018.00036
Squire, L., Berg, D., Bloom, F. E., Du Lac, S., Ghosh, A., and Spitzer, N. C. (2012). Fundamental Neuroscience. San Diego, CA: Academic Press.
Stoelzel, C. R., Bereshpolova, Y., Alonso, J.-M., and Swadlow, H. A. (2017). Axonal conduction delays, brain state, and corticogeniculate communication. J. Neurosci. 37, 6342–6358. doi: 10.1523/JNEUROSCI.0444-17.2017
Stuart, G., and Spruston, N. (1998). Determinants of voltage attenuation in neocortical pyramidal neuron dendrites. J. Neurosci. 18, 3501–3510.
Swadlow, H. A. (1990). Efferent neurons and suspected interneurons in s-1 forelimb representation of the awake rabbit: receptive fields and axonal properties. J. Neurophysiol. 63, 1477–1498.
Swadlow, H. A., and Weyand, T. G. (1987). Corticogeniculate neurons, corticotectal neurons, and suspected interneurons in visual cortex of awake rabbits: receptive-field properties, axonal properties, and effects of eeg arousal. J. Neurophysiol. 57, 977–1001.
Syrkin-Nikolau, J., Neuville, R., O'day, J., Anidi, C., Miller Koop, M., Martin, T., et al. (2018). Coordinated reset vibrotactile stimulation shows prolonged improvement in parkinson's disease. Mov. Disord. 33, 179–180. doi: 10.1002/mds.27223
Tass, P., Kurths, J., Rosenblum, M., Guasti, G., and Hefter, H. (1996). Delay-induced transitions in visually guided movements. Phys. Rev. E 54:R2224.
Tass, P. A. (2003). A model of desynchronizing deep brain stimulation with a demand-controlled coordinated reset of neural subpopulations. Biol. Cybern. 89, 81–88. doi: 10.1007/s00422-003-0425-7
Tass, P. A. (2017). Vibrotactile coordinated reset stimulation for the treatment of neurological diseases: concepts and device specifications. Cureus 9:8. doi: 10.7759/cureus.1535
Tass, P. A., Adamchic, I., Freund, H. J., von Stackelberg, T., and Hauptmann, C. (2012a). Counteracting tinnitus by acoustic coordinated reset neuromodulation. Restorat. Neurol. Neurosci. 30, 137–159. doi: 10.3233/RNN-2012-110218
Tass, P. A., and Majtanik, M. (2006). Long-term anti-kindling effects of desynchronizing brain stimulation: a theoretical study. Biol. Cybern. 94, 58–66. doi: 10.1007/s00422-005-0028-6
Tass, P. A., and Popovych, O. V. (2012). Unlearning tinnitus-related cerebral synchrony with acoustic coordinated reset stimulation: theoretical concept and modelling. Biol. Cybern. 106, 27–36. doi: 10.1007/s00422-012-0479-5
Tass, P. A., Qin, L., Hauptmann, C., Dovero, S., Bezard, E., Boraud, T., et al. (2012b). Coordinated reset has sustained aftereffects in parkinsonian monkeys. Ann. Neurol. 72, 816–820. doi: 10.1002/ana.23663
van den Heuvel, M. R., Balasubramaniam, R., Daffertshofer, A., Longtin, A., and Beek, P. J. (2009). Delayed visual feedback reveals distinct time scales in balance control. Neurosci. Lett. 452, 37–41.
Van Rossum, M. C., Bi, G. Q., and Turrigiano, G. G. (2000). Stable hebbian learning from spike timing-dependent plasticity. J. Neurosci. 20, 8812–8821. doi: 10.1523/jneurosci.20-23-08812.2000
Walters, D., Stringer, S., and Rolls, E. (2013). Path integration of head direction: updating a packet of neural activity at the correct speed using axonal conduction delays. PLoS ONE 8:e58330. doi: 10.1371/journal.pone.0058330
Wang, H. X., Gerkin, R. C., Nauen, D. W., and Bi, G. Q. (2005). Coactivation and timing-dependent integration of synaptic potentiation and depression. Nat. Neurosci. 8, 187–193. doi: 10.1038/nn1387
Wang, J., Nebeck, S., Muralidharan, A., Johnson, M. D., Vitek, J. L., and Baker, K. B. (2016). Coordinated reset deep brain stimulation of subthalamic nucleus produces long-lasting, dose-dependent motor improvements in the 1-methyl-4-phenyl-1, 2, 3, 6-tetrahydropyridine non-human primate model of parkinsonism. Brain Stimul. 9, 609–617. doi: 10.1016/j.brs.2016.03.014
Wang, Q., Perc, M., Duan, Z., and Chen, G. (2009). Synchronization transitions on scale-free neuronal networks due to finite information transmission delays. Phys. Rev. E 80:026206. doi: 10.1103/PhysRevE.80.026206
Waxman, S. G. (2006). Axonal conduction and injury in multiple sclerosis: the role of sodium channels. Nat. Rev. Neurosci. 7:932. doi: 10.1038/nrn2023
Keywords: propagation delays, spike-timing-dependent plasticity, synchronization, mathematical modeling, living systems
Citation: Madadi Asl M, Valizadeh A and Tass PA (2018) Dendritic and Axonal Propagation Delays May Shape Neuronal Networks With Plastic Synapses. Front. Physiol. 9:1849. doi: 10.3389/fphys.2018.01849
Received: 25 August 2018; Accepted: 07 December 2018;
Published: 20 December 2018.
Edited by:
Alexey Zaikin, University College London, United KingdomReviewed by:
Jihwan Myung, Taipei Medical University, TaiwanSilvina Ponce Dawson, Universidad de Buenos Aires, Argentina
Copyright © 2018 Madadi Asl, Valizadeh and Tass. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Mojtaba Madadi Asl, bS5tYWRhZGlAaWFzYnMuYWMuaXI=
 Mojtaba Madadi Asl
Mojtaba Madadi Asl Alireza Valizadeh
Alireza Valizadeh Peter A. Tass
Peter A. Tass