- 1Institute of Allied Health Sciences, College of Medicine, National Cheng Kung University, Tainan, Taiwan
- 2Department of Physical Therapy, College of Medicine, National Cheng Kung University, Tainan, Taiwan
- 3Physical Education Office, Asian University, Taichung, Taiwan
- 4Department of Physical Therapy, College of Medical Science and Technology, Chung Shan Medical University, Taichung, Taiwan
- 5Physical Therapy Room, Chung Shan Medical University Hospital, Taichung, Taiwan
Although error amplification (EA) feedback has been shown to improve performance on visuomotor tasks, the challenge of EA is that it concurrently magnifies task-irrelevant information that may impair visuomotor control. The purpose of this study was to improve the force control in a static task by preclusion of high-oscillatory components in EA feedback that cannot be timely used for error correction by the visuomotor system. Along with motor unit behaviors and corticomuscular coherence, force fluctuations (Fc) were modeled with non-linear SDA to contrast the reliance of the feedback process and underlying neurophysiological mechanisms by using real feedback, EA, and low-frequency error amplification (LF-EA). During the static force task in the experiment, the EA feedback virtually potentiated the size of visual error, whereas the LF-EA did not channel high-frequency errors above 0.8 Hz into the amplification process. The results showed that task accuracy was greater with the LF-EA than with the real and EA feedback modes, and that LF-EA led to smaller and more complex Fc. LF-EA generally led to smaller SDA variables of Fc (critical time points, critical point of Fc, the short-term effective diffusion coefficient, and short-term exponent scaling) than did real feedback and EA. The use of LF-EA feedback increased the irregularity of the ISIs of MUs but decreased the RMS of the mean discharge rate, estimated with pooled MU spike trains. Beta-range EEG–EMG coherence spectra (13–35 Hz) in the LF-EA condition were the greatest among the three feedback conditions. In summary, amplification of low-frequency errors improves force control by shifting the relative significances of the feedforward and feedback processes. The functional benefit arises from the increase in the common descending drive to promote a stable state of MU discharges.
Introduction
A general outcome of motor control is variability (Frank et al., 2006; Bays and Wolpert, 2007). The structures of movement variability [such as force fluctuations (Fc)] are not necessarily a direct consequence of neural noises. Contrary to the whiteness assumption, Fc are colored time series contingent upon environmental contexts and task demands (Miall et al., 1986, 1993). Fc are composed of numerous centrally scaled pulse-like elements that remedy tracking deviations during a visuomotor task (Navas and Stark, 1968; Miall et al., 1986; Slifkin et al., 2000; King and Newell, 2015). The spatial and temporal information in visual feedback determines the transitions of the motor state with respect to target constraints (Hwang et al., 2013; Chen et al., 2017b). Hence, Fc with visual feedback are smaller and have greater complexity as compared to those in a no-vision condition (Baweja et al., 2009). Force tracking results in higher complexity of Fc when the visual display has high spatial resolution than when it has low spatial resolution (Sosnoff et al., 2006). The reason is that high-sensitivity feedback with precise visual information can facilitate richer error correction strategies. A major determinant of Fc is variations in the discharge properties of MUs. In addition, corticomuscular coherence (EEG–EMG coherence) in the beta range (13–35 Hz) plays a critical role in stabilizing corticospinal communication during static contraction (Kristeva et al., 2007; Omlor et al., 2011). Greater beta EEG–EMG coherence represents more effective sensorimotor integration and greater attentional focus being directed toward stabilizing the force output (Witte et al., 2007).
Accurate visual feedback is important to develop a reliable perception–action link. Interestingly, visual display of performance outcomes that are worse than the actual performance can better expedite motor adaptations to novel task constraints than can accurate visual feedback (Patton et al., 2006; Domingo and Ferris, 2010; Reisman et al., 2013). The virtual amplification of task errors, or EA, is frequently used in combination with robotic technology to facilitate motor recovery in patients with neurological disorders (Abdollahi et al., 2014; Kao et al., 2015; Israely and Carmeli, 2016; Bouchard et al., 2017). EA is thought to inflate response conflicts in the error-monitoring network such that participants are more attentive to execution of the motor task (Boussaoud and Kermadi, 1997; Jueptner and Weiller, 1998; Shirzad and Van der Loos, 2012). Alternatively, a model-based study predicted that EA could minimize the effect of overt task fluctuations by reducing the neuromotor noise variance (Hasson et al., 2016). In addition to task improvement, a force-tracking task with EA leads to smaller Fc with higher spectral components and complexity (Williams et al., 2016; Chen et al., 2017b; Hwang et al., 2017). These scenarios support the potential functional benefits of visual EA, including deliberate and richer tuning behaviors with more frequent corrective attempts than with real visual feedback. Physiologically, visually exaggerated mismatches with visual EA favors the use of a feedback process to regulate the MU discharge and the variability of the ISI among those MUs (Chen et al., 2017b). However, the use of visual EA does not always result in behavior success (Wei et al., 2005; Sung and O’Malley, 2011; Bouchard et al., 2015). For instance, EA may add to perceptual conflicts among the visual, proprioceptive, and haptic inputs due to the distortion of real visual consequences (Ogawa and Imamizu, 2013). Moreover, EA may augment the visual information load by proportionately amplifying the full spectrum of execution errors, including functionally irrelevant visual stimuli that could impair the efficacy of corrective behaviors (Lipowski, 1975; Chen et al., 2017a). Hence, to optimize visual EA, it is necessary to focus on the usability of task-related information.
Given the potential positive effects with EA, this study aimed to contrast EA with and without high-frequency error components during low-level static contraction. We argue that not all of the error information, especially the fast-oscillatory components, is helpful to improve visuomotor performance. As a visuomotor task with EA favors the use of a feedback mechanism (Chen et al., 2017b), the amplified fast-oscillatory error components (>0.8 Hz) within visual feedback cannot be effectively used due to a significant delay of 150 ms in the visuomotor loop (Miall et al., 1985, 1986, 1993). The amplification of these high-frequency error components could offset the positive effect of EA on a visuomotor task. Only LF-EA, wherein the error information of rapid fluctuations is excluded, could increase the effectiveness of visual feedback (or a feedback-prone process) for corrections of force-tracking deviations. Employing non-linear Fc dynamics and mathematical decomposition of surface electromyography, this study contrasted the behavior and neural mechanisms of static force-tracking in the real, EA, and LF-EA feedback conditions. Due to potential changes in force gradation strategies, it was hypothesized that (1) the size, complexity, and SDA variables of Fc would be different in the three visual feedback modes (traditional visual feedback, EA, and LF-EA), and (2) the variations in MU discharge and central drive to stabilize corticomuscular communication would vary among the visual feedback modes.
Materials and Methods
Subjects
The participants were 15 healthy adults (8 males and 7 females; mean age: 24.8 ± 0.9 years, range: 21–31 years old) from a university campus or the local community. All were self-reported as being right-handed, and none had symptoms or signs of neuromuscular diseases. The experiments were conducted in accordance with the Declaration of Helsinki and approved by an authorized institutional human research review board (IRB) at the University Hospital of the Chung Shan Medical University, Taiwan. All participants signed a written informed consent form prior to inclusion.
Experimental Procedures
The participants completed a unilateral static force task of isometric index abduction at a low force level (20% MVC) under three error feedback conditions: control, error-amplification (EA), and low-frequency error-amplification (LF-EA). The participants were seated with the palm and forearm of the right hand firmly fixed within a thermoplastic splint on the table. The index finger was held slightly abducted (5 degrees of abduction), and its abduction force was measured using a force transducer (Model: MB-100, Interface Inc., United States) followed by an analog amplifier (gain = 10). The cut-off frequency of the amplifier was 20 Hz so that fast-oscillatory force components such as 8–12 Hz physiological tremor would not be attenuated by the experiment setting. For each individual, the MVC of the FDI was pre-determined from three maximal contraction trials of 3 s separated by 3 min pauses, by averaging the largest force produced in each trial. Interleaved with 3-min pauses, separate experimental trials in the control, EA, and LF-EA conditions commenced in a randomized order, after three practice trials in all conditions. There were four experimental trials for the control, EA, or LF-EA conditions. During the force-tracking in the control condition, the participants were given 2 s to reach the target force (slope: 10% MVC/second) after a latent period of 3 s (Figure 1A). Then they coupled isometric force to the target signal (20% MVC) as precisely as possible by pushing their index finger against the force transducer for another 34 s under visual guidance. The force output returned to the resting level in 2 s, followed by a 3-s latency period. The time window of interest was denoted as the 8th to 37th seconds in a total of 44 s for an experimental trial. The resolution of the display of visual feedback on the monitor was 1,920 pixels × 1,080 pixels.
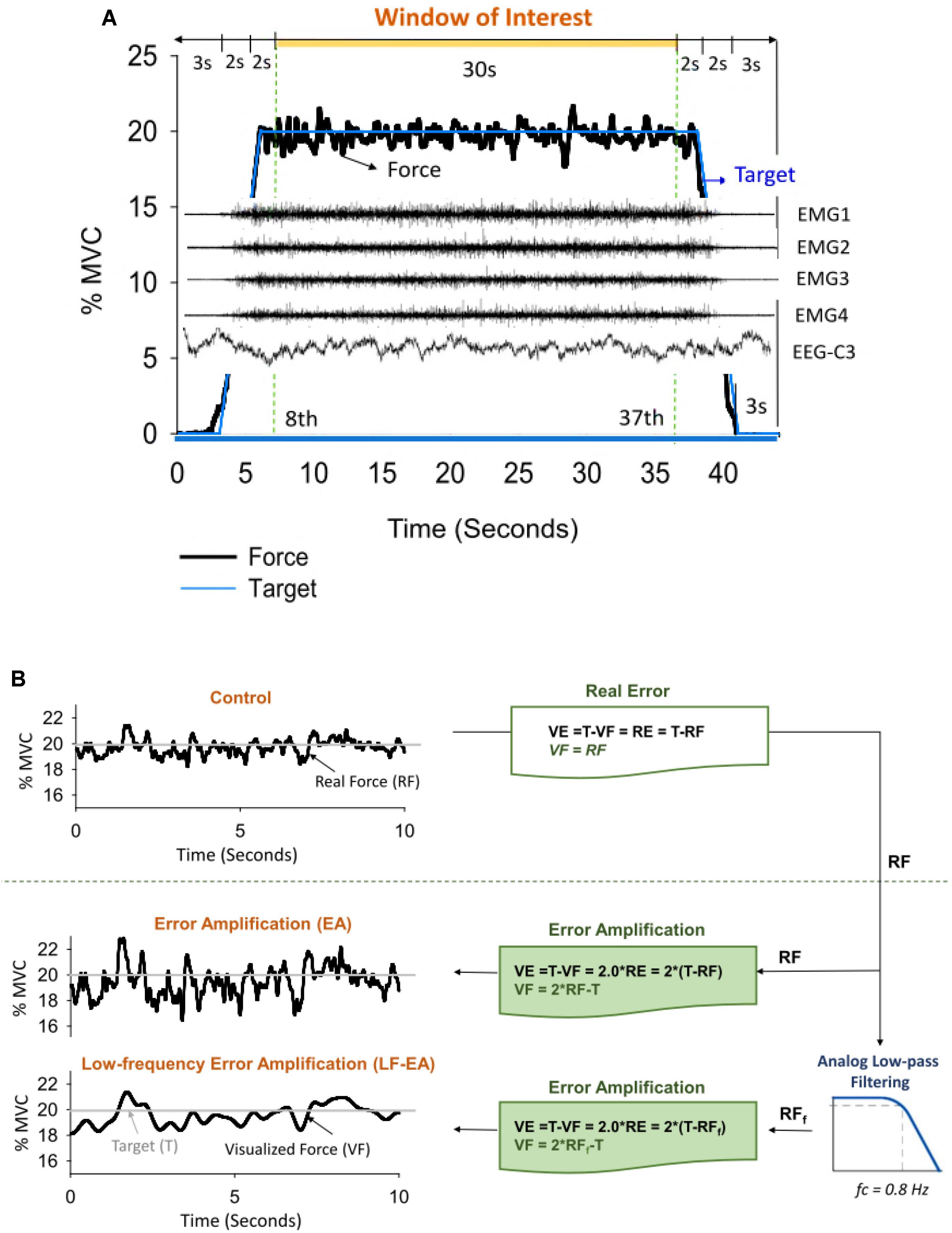
Figure 1. (A) Target signal and representative data. Only force data, EMG, and EEG in the time window of interest were presumably stable for subsequent feature extraction. (B) Illustration of manipulation of error augmentation for visual feedback. In the control condition, real force (RF) was shown on the monitor to guide the force task, so that real error (RE) is equivalent to visualized error (VE) during tracking. In the error amplification (EA) and low-frequency error amplification (LF-EA) conditions, the VE of the tracking task were magnified with mathematical transformation. The visualized force outputs (VF) in the EA condition represent on-line force feedback information that doubles the size of the execution error during force-tracking. The LF-EA feedback consists of a low-pass filtering process and an error amplification process during force-tracking. The low-pass filtering process suppresses high-frequency components (>0.8 Hz) of real force. Error amplification process based on the filtered real force (RFf) magnifies VE that contains only low-frequency components (<0.8 Hz).
In the EA condition, the VF displayed on the monitor was mathematically transformed to potentiate execution error [mismatches between the real force output (RF) and the target signal (T)] (Figure 1B). The VF was equal to the sum of twice the RF minus the target signal (T) (VF = 2RF-T), so the participant would perceive twice the amount of the RE of the static force-tracking task (VE = 2RE). RF in the EA condition was low-pass filtered at 20 Hz, and the VF was relatively noisy, containing enhanced fast-oscillatory force components and tremulous movements. In the LF-EA condition, the RF came from a parallel force channel that pre-conditioned the force output with an analog low-pass filter (cut-off frequency: 0.8 Hz) prior to amplification (Figure 1B). The VF was much smoother in the LF-EA condition than in the EA condition. The participants could hardly correct high-frequency errors above 0.8 Hz via visual feedback (Pew, 1974; Miall et al., 1985), because the time period between the pick-up of visual information and its use in producing a required adjustment was at least 150 ms (Miall et al., 1986). For all the feedback conditions, the spatial gain to display the target signal and the force output was roughly 25 pixels per 1% MVC. The inter-trial interval of rest was 2 min. In the LabVIEW platform (LabVIEW v.8.5, National Instruments Inc., United States), the RF conditioned with a low-pass filter at 20 Hz and the target signal were digitalized at 1 kHz by a 16-bit analog-to-digital converter (DAQCard-6024E; National Instruments Inc., United States) in the EA and LF-EA conditions. For the LF-EA condition, the smoother force channel, conditioned with an analog low-pass filter (cut-off frequency: 0.8 Hz), was also recorded.
Electromyographic and Electroencephalographic Recordings
In addition to the force signal, we synchronized multi-electrode surface EMG with 5 surface pin-sensors (0.5 mm diameter at the center and corners of a 5 mm × 5 mm square) (Bagnoli sEMG system, Delsys Inc., United States) to record activities of the FDI muscle. By careful skin preparation and proper sensor application, the peak-to-peak value of baseline noise was controlled under 20 μV to secure the accuracy of EMG decomposition using EMG works v.4.1 (Delsys Inc., United States). The analog EMG signals from each pin-sensor were amplified (gain = 1,000) and filtered with a bandwidth of 20–450 Hz (De Luca et al., 2014). After that, four single differential EMG channels were obtained with pair-wise subtractions of the five pin-detections (voltages of the pin-sensor at the corner minus voltage of the pin-sensor at the center) (De Luca et al., 2006; Nawab et al., 2010; Hu et al., 2013). A high sampling rate of 20 KHz was used to avoid introducing phase skew across channels (De Luca et al., 2006, 2014; Nawab et al., 2010). Two active Ag-AgCl electrodes (3 mm diameter; Model F-E9M-40-5, Grass, United States) were placed 1 cm apart on the C3 area, which was over the hand area of the primary motor cortex. The reference electrodes for the EEG were placed on the bilateral earlobes. After amplification of the recorded signal (gain = 5,000), the EEG signal was hardware-filtered in the frequency range of 0.01–100 Hz and 60 Hz (Model P511, Grass, United States). Synchronized with the EMG system and force data, the EEG signal was sampled at 1,000 Hz.
Stochastic Modeling of Force Fluctuation Dynamics
The force data used for behavior analysis were the RF data low-pass filtered at 20 Hz. To exclude force data irrelevant to visuo-motor processes and error correction (such as 8–12 Hz physiological tremor) (Slifkin et al., 2000; Vaillancourt et al., 2002), the RF was further conditioned with a digital low-pass filter (cut-off frequency: 6 Hz) (Chen et al., 2013; Lin et al., 2014). Then the conditioned force data in the time window of interest (8th to 37th second) were down-sampled to 100 Hz. The quality of the force-tracking performance was visualized with a return map for the time series of task errors, a graph of the task error Ei+1 versus the previous task error Ei (Shenker, 1982; Mendez-Balbuena et al., 2012). A poor performance led to a dispersive distribution of error points in the map. In contrast, error points for a good performance concentrated near to the center of the map. The size of the task error was quantified with RMS of mismatch between target and force signal. In the temporal domain, RMS and SampEn were applied to calculate the size and complexity of Fc, defined as force data after removal of a linear trend (Hong and Newell, 2008). Fc characteristics reflect the degree of force steadiness and gradation strategy for force stabilization. SampEn is a popular and reliable entropy measure of the temporal aspects of biological variability (Richman and Moorman, 2000). The mathematical formula of sample entropy was SampEn , where r = 15% of the standard deviation of the force channel, m is the length of the template (m = 3), and N is the number of data points in the time series. Ai is the number of matches of the ith template of length m + 1 data points, and Bi is the number of matches of the ith template of length m data points (Pethick et al., 2015). A larger value represents a more complex structure of the low-frequency Fc. In the spectral domain, the MF of Fc was determined based on the spectral profile estimated with a fast Fourier transform and the Welch method (Hanning window; window length: 2.048 s, overlapping time segment: 1/4 × window length) with a spectral resolution of 0.1 Hz. In addition, we quantified the spectral DOF, a statistic to reveal the power dispersion of Fc. Spectral DOF is calculated as DOF = . The quantity is unity for a perfect single spectral peak, and a greater value of DOF represents a broader band of Fc (maximal value of N for white noise).
Force fluctuation dynamics were characterized with SDA, a probabilistic tool first proposed by Collins and De Luca (1993). The mathematical concept of the SDA approach was originally designated to resolve the statistical mechanics of a one-dimensional generalized family of Gaussian stochastic processes, such as postural sway (Collins and De Luca, 1993, 1995) and Fc (Chen et al., 2017a). The SDA describes the power-law relationship between the <dF2> and the dt in which these values occur; i.e., < dF2 >∼ dt2H. H is the scaling factor, a real number ranging from 0 to 1. For classic Brownian motion, H = 0.5. For the purpose of the present study, SDA was calculated by using the following equation: , where <•> indicates the mean of the time series. The computation of dF2 was empirically repeated with increasing dt values ranging from 0 to 3 s. The diffusion plot (linear–linear plots or log–log plots) was the mean square of Fc <dF2> against the time intervals dt (Figures 2A,B). Specifically, for biological systems regulated jointly by open-loop and closed-loop processes, the diffusion plots could be best-fitted with piecewise linear regression models, the cross-over phenomenon (Delignières et al., 2011). The dtc was the intersection of the two regression lines of the linear-linear diffusion plot (Figure 2A), and variations in the <dFc2> reflected a paradigm shift in force control (Collins and De Luca, 1993; Toosizadeh et al., 2015). In the linear–linear diffusion plot, the regression slopes (Ds and Dl) of the short-term and long-term regions were two effective diffusion coefficients, which parameterized the control of the force stochastic activities in those regions, respectively. The Hs and Hl were linear fits of the log–log plot of the SDA (Figure 2B). A scaling exponent greater than 0.5 indicates that the system is governed by the open-loop process (persistence) and that the data series of the past and future are positively correlated (Collins and De Luca, 1993, 1995). Conversely, a scaling exponent smaller than 0.5 indicates that the data series of the past and future are negatively correlated, as regulated by the closed-loop process (anti-persistence). The selection of this model was a matter of physiological concern, due to the underlying shift in feedback and feedforward control for force stabilization with better use of the error information within the visual feedback.
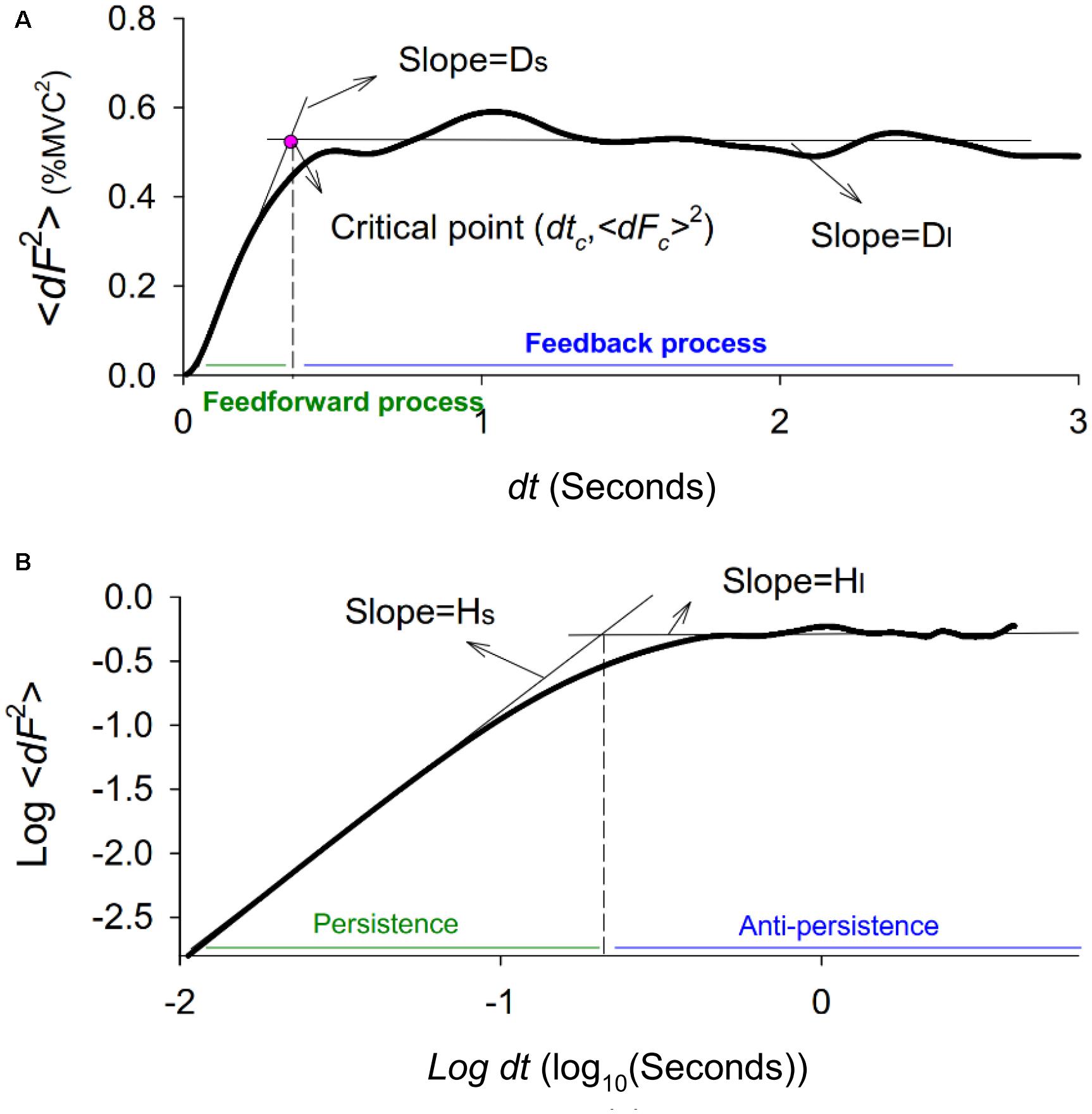
Figure 2. Stabilogram-diffusion plot. (A) A typical linear-linear stabilogram-diffusion plot. The short-term effective diffusion coefficient (Ds), and long-term effective diffusion coefficients (Dl) are regression slopes for the short time scale (0–0.5 s) and long time (0.5–3 s) scales. The critical point (dtc, <dFc2>) is the intersection point of the two regression lines, indexing a shift in open-loop and closed-loop control for the stochastic dynamics of force fluctuations. (B) A typical log-log stabilogram-diffusion plot. The computed short-term scaling exponent (Hs) and long-term scaling exponent (Hl) are regression slopes of the short time and long time scales of the log–log stabilogram-diffusion plot.
Probability of Motor Unit Discharge
The action potential “templates” of MUs were decomposed from differential EMG channels using a previous proof-of-principle (De Luca et al., 2006; Nawab et al., 2010). Recent studies have shown that the artificial-intelligence-based computation algorithm can produce convincing decomposition results (Nawab et al., 2004; De Luca et al., 2015) via independent verification methods (Hu et al., 2013). The entire data collection period (44 s) was decomposed, resulting in binary spike trains that coded the activations of all MUs with values of 0 or 1 (Figure 3). Only discharge patterns of the window of interest were further analyzed. The validity of the EMG decomposition of each MU action potential train (MUAPT) was evaluated with the Decomposition-Synthesis-Decomposition-Compare (DSDC) test (De Luca et al., 1982, 2006). In brief, the DSDC test was used to decompose a synthetic sEMG signal, which was reconstructed by the summation of the predefined MUAPTs (or decomposed results) and Gaussian noise. The decomposed results were compared with the firing instances of predefined MUAPTs, and the percentage of the accuracy and location error of decomposition for each MUAPT was defined as decomposition accuracy. Previous studies have reported that the decomposition accuracy of MUAPTs ranges from 92.5 to 97.6% (De Luca et al., 1982, 2006). In this study, MUs of low decomposition accuracy (<90%) were excluded from the analysis. The discharge variables of MUs were determined in the time window of interest based on the decomposed EMG data of the overall 44 s. Three MU discharge variables were calculated, including global averaged inter-spike interval (ISIGAV), CV-ISImean, and global averaged irregularity index (IR) of all MUs (IRGAV). In an experimental trial, ISImean was the mean value of all ISIs for an individual MUAPT, and the ISIGAV was the averaged value of the ISImean for a group of MUs. Experimentally observed ISI variability among MUs was represented with the CV of the ISImean of a group of MUs (CV-ISImean). Given a series of inter-spike intervals (ISIi) for a single MU, the irregularity index (IR) (Davies et al., 2006; Witham and Baker, 2007) is mathematically formulated as: . The IRGAV was the averaged value of the IR for a group of MUs. An increase in force steadiness with LF-EA was likely associated with changes in inter-spike variability. The pooled behaviors of MU discharges were characterized with the mean discharge rate (Figure 3). To estimate the mean discharge trace, the global discharge rate was first determined by convolution of the cumulative spike trains of all the MUs with a Hanning window (window duration: 400 ms) (Hwang et al., 2017). The mean discharge rate was the global discharge rate divided by the number of detectable MUs in the experimental trial. The averaging process was used to standardize the amplitude of the global discharge rate across trials. Low-frequency oscillations of the mean discharge rate likely correspond to the common input to the motoneurons, providing a reasonable estimate of the force exerted by the muscle (Farina and Negro, 2015; Farina et al., 2016).
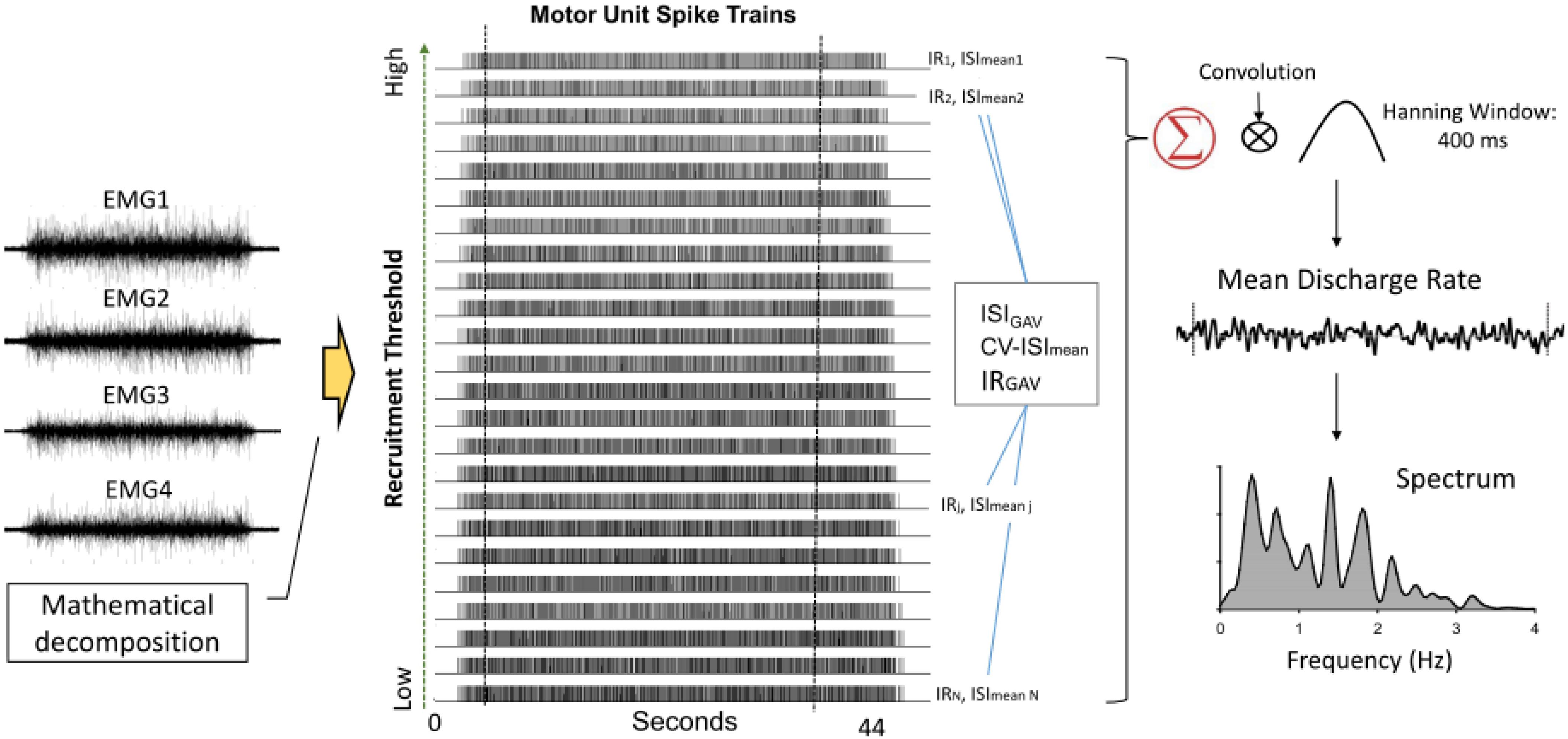
Figure 3. Acquisition of variables of inter-spike interval and mean discharge rate following mathematical decomposition of surface EMG into motor unit spike trains. Mean discharge interval (ISImean) and irregularity index (IR) of each spike train are determined. The global averages of ISImean and IR, as well as coefficient of variance of ISImean (CV-ISImean) among motor units (MUs). Mean discharge rate is obtained by smoothing the cumulative MU spike trains following convolution with a Hanning window (window length: 400 ms). Spectral distributions of mean discharge rate are estimated.
Corticomuscular Coherence Estimation
Corticomuscular coherence, especially in the spectral range of 13–35 Hz, is known to reflect efferent neural transmission to maintain force steadiness (Kristeva-Feige et al., 2002; Omlor et al., 2011). Four undecomposed EMG signals directly from differential channels were used to calculate CMC. The analog EMG signals were first resampled at 1 KHz, followed by signal conditioning with a band-pass filter (cut-off frequencies: 10 and 400 Hz). The conditioned EMG signal was rectified and high-pass filtered at 5 Hz (Chen et al., 2013). Ocular artifacts in the EEG recordings were removed. The EEG–EMG coherence was determined with EEG C3 and each conditioned EMG signal. The resulting EEG–EMG coherence spectra were averaged to represent the CMC of the experimental trial. The coherence between signals x and y at frequency f, Cohxy(f), was determined according to the following equation: Cohxy(f) = . The cross-spectrum between signals x and y at frequency f averaged across N data segments, Sxy(f), was calculated as follows: , where Xi (f) denotes the Fourier transform of the data segment i of the channel x at frequency f, and Yi (f)∗ denotes the complex conjugate of the Fourier transform of the data segment i of the channel y at frequency f. To estimate Cohxy(f), EEG, and EMG signals were segmented into artifact-free epochs of 1.024 s without overlapping. Each segmented EEG and four EMG data from the differential channels were Hanning-windowed to minimize spectral leakage, and the Cohxy(f) of a given experimental trial was estimated with a total of 116 epochs (29 epochs/trial × 4 experimental trials). Spectral resolution was 1 Hz. The significance level of EEG–EMG coherence was the 95% CL. The CL was defined as: . Both the peak coherence and spectral area of the pooled EEG–EMG coherence spectrum in the beta band frequencies (13–35 Hz) were determined for each experimental trial, and those spectral variables of the three experimental trials were averaged for all the feedback conditions. All the behavior/physiological variables and their functional implications in this study are briefly summarized in Figure 4.
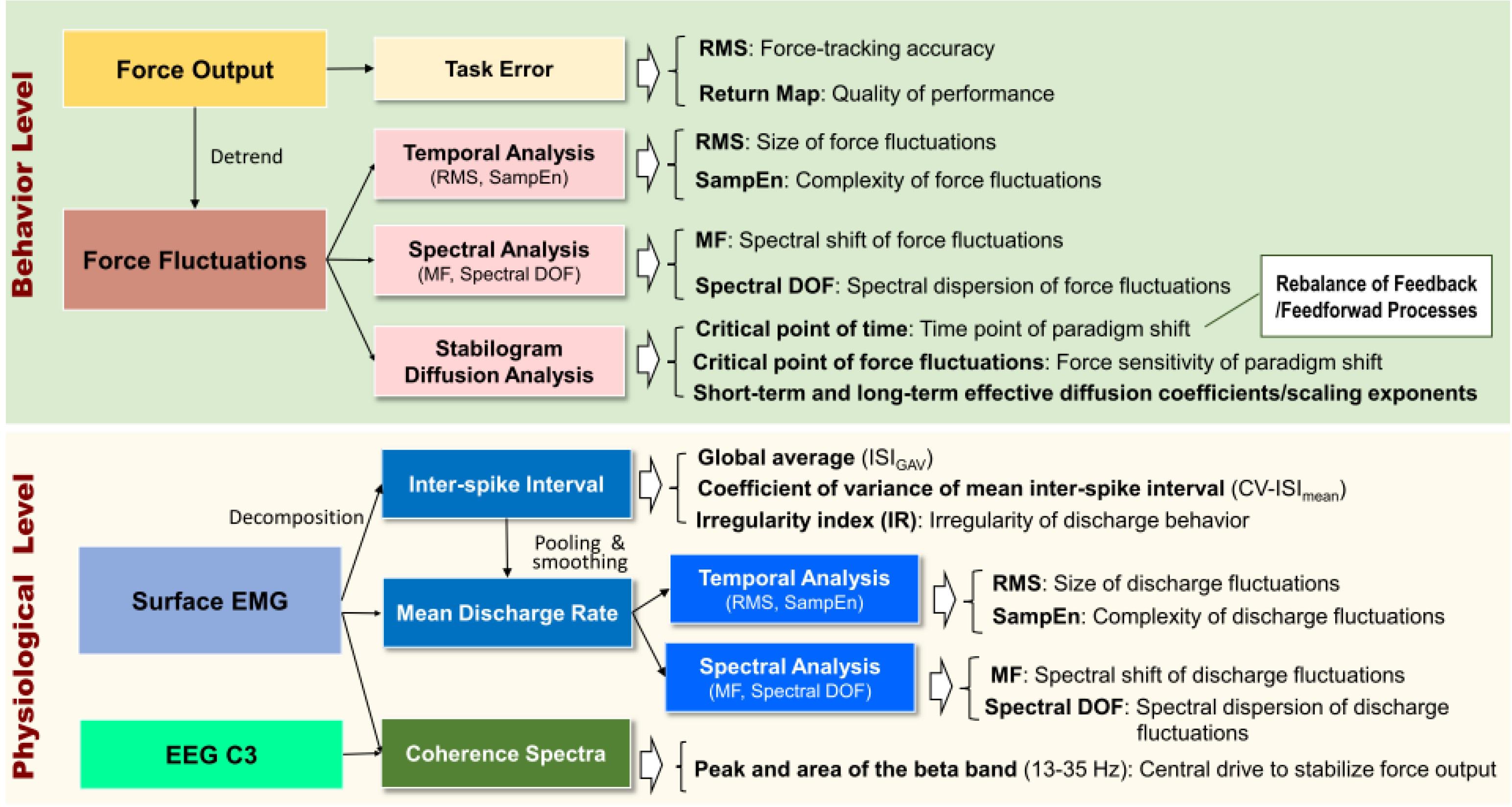
Figure 4. A summary diagram of behavior and physiological variables and their functional implications.
Statistical Analysis
With reference to typical visual feedback to guide force-tracking, the primary research interest of this study was to contrast variations in the stochastic force behaviors and probability structure of MU discharges with the use of EA feedback and LF-EA feedback. On account of the relatively small sample size, the Wilcoxon signed-rank test was used to examine the task error, Fc variables (including SDA variables), inter-spike variables, variables of the mean discharge rate, and EEG–EMG coherence in the beta band in the three feedback conditions. The level of significance was 0.05. In the presence of significant main effects, post hoc testing was conducted using the Mann–Whitney U test with Bonferroni correction to determine the alpha level of significance (p = 0.0167). Spearman rank correlation was used to assess functional linkages between differences in task error between the EA/LF-EA and control conditions with the corresponding changes in those neurophysiological metrics that were sensitive to manipulation of EA. Signal processing and statistical analyses were completed in Matlab R2015b (Mathworks Inc., United States) and the statistical package for IBM SPSS software for Windows v.19.0 (IBM Inc., United States), respectively. Data reported in the text and figures without specific notations indicating otherwise are presented as mean ± standard error.
Results
Figure 5A displays the return maps of the task errors from a typical subject in the three conditions: control, EA, and LF-EA. The dispersion of the error points in the maps for the LF-EA condition was smaller than those for the EA and control conditions. This was a qualitative way to characterize stable and accurate force-tracking with LF-EA. Figure 5B shows the population means, standard errors, and individual values of force-tracking errors for all three visual conditions. The results of the Wilcoxon signed-rank test revealed that force-tracking errors varied with feedback mode (χr2 = 10.13, p = 0.006), with the smallest error for the LF-EA condition (p ≤ 0.006). Figure 5C shows the distribution of differences in tracking error between the EA/LF-EA and control conditions. The majority of the participants exhibited a more positive performance benefit with LF-EA than with EA, as indicated by the smaller mean tracking error relative to that of the control condition. Table 1 contrasts the differences in the Fc variables among the three visual conditions. The results revealed that all Fc variables were dependent on the feedback mode (p < 0.05). Post hoc analysis further revealed that the LF-EA condition exhibited the smallest RMS and the largest SampEn of Fc among the three feedback conditions (p < 0.01). Both the EA and the LF-EA conditions exhibited mean frequencies and spectral DOF larger than those of the control condition (p < 0.01). Functionally, LF-EA led to fine-grained and richer force gradation to rapidly remedy tracking deviations. In addition, the Fc dynamics were characterized with SDA, and all the SDA variables varied with manipulation of the feedback mode (p ≤ 0.006) (Table 2). Post hoc test indicated that dtc was smallest in the LF-EA condition and largest in the control condition (p < 0.01). In addition, <dFc2> was smaller in the LF-EA condition than in the control and EA conditions (p < 0.01). Ds and Hs were smallest in the LF-EA condition (p < 0.01), whereas Dl and Hl were largest in the LF-EA condition (p < 0.01). The observations indicated that the preclusion of high-frequency feedback components from the EA process led to task improvement during static force-tracking. The functional benefits were associated with the sensible detection of Fc (smallest dtc and <dFc2> in the LF-EA condition) and a shift in Fc control toward the feedback-prone process.
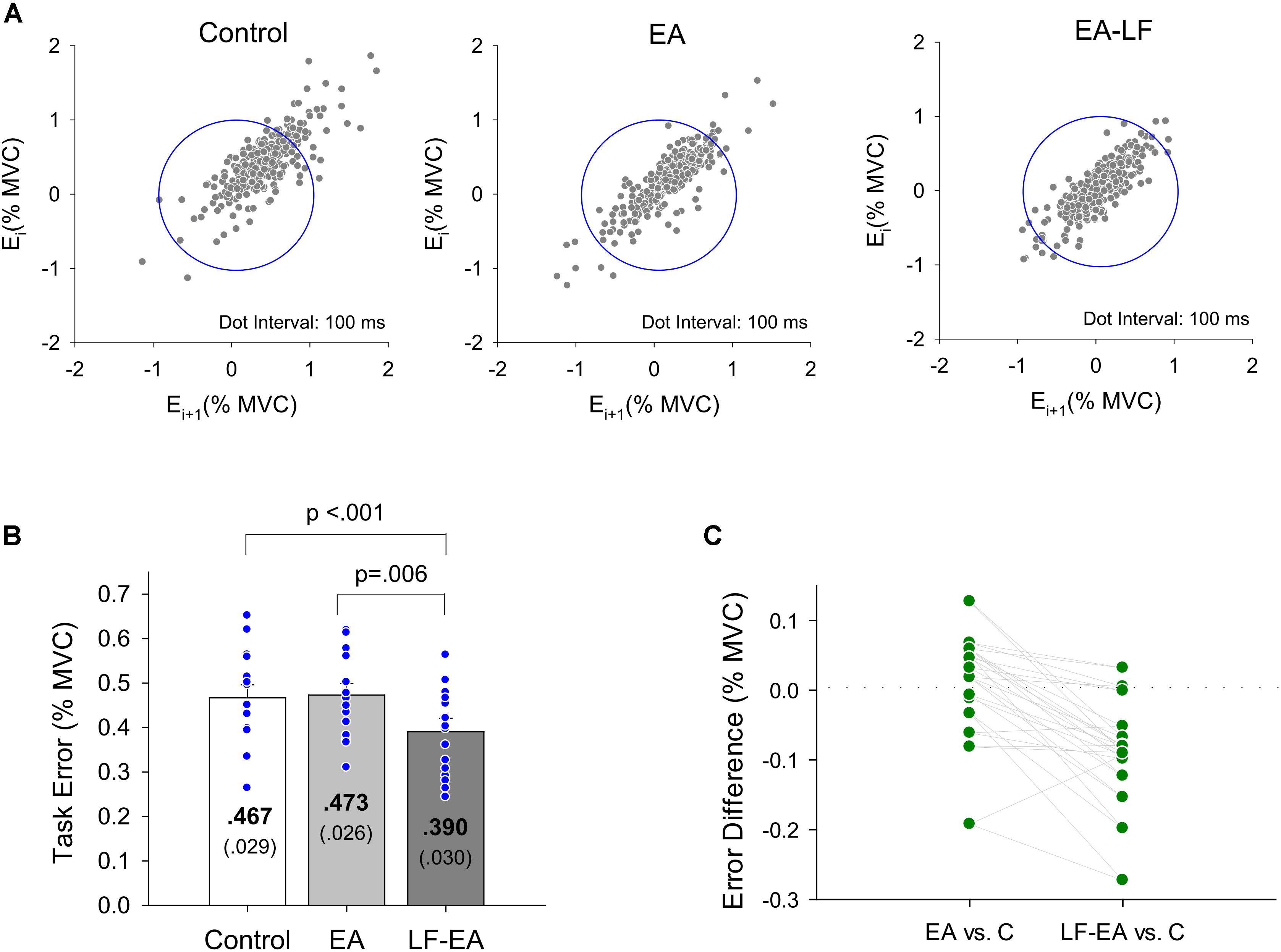
Figure 5. Task error properties. (A) Return maps of the force-tracking for a typical subject in the control, EA, and LF-EA condition. Graph of the error Ei+1 versus previous error Ei where i is the sampling point. For brevity, the interval between two error data is set at 100 ms. Good performance of force-tracking exhibits error points that are concentrated near the center of the blue circle. (B) The contrasts of force-tracking error among the three visual feedback conditions. The blue dots represent force-tracking error of all individuals in this study. (C) A schematic plot to display scattering of differences in tracking error between the error amplification (EA)/low-frequency error amplification (LF-EA) and control (C) conditions. A more negative value of the error difference indicates a more positive performance benefit, underlying a relatively smaller tracking error in the EA or LF-EA condition. Each green dot represents EA-related differences in tracking error for an individual.

Table 1. Mean and standard errors of task error and force fluctuation variables for the control, error amplification (EA), and low-frequency error amplification (LF-EA).
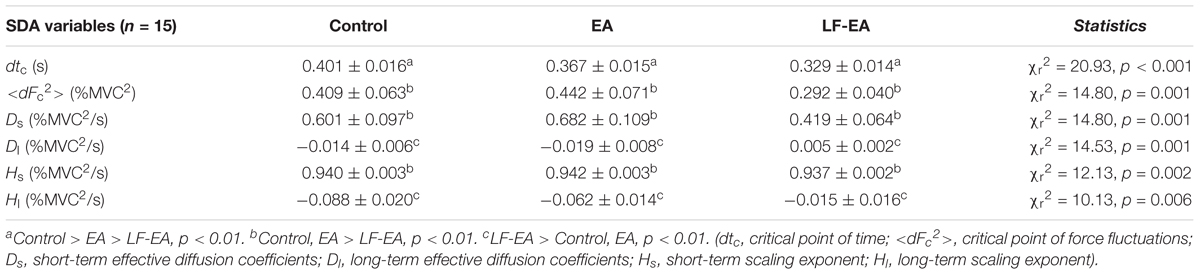
Table 2. Parameters of stabilogram diffusion analysis (SDA) of static force tracking in the control and error amplification (EA), low-frequency error amplification (LF-EA) conditions.
Under the condition of acceptable decomposition accuracy using the DSDC test (Control: 93.10 ± 0.42%; EA: 93.45 ± 0.42%; LF-EA: 93.76 ± 0.46%), the average numbers of analyzed MUs of an experimental trial did not vary with the feedback conditions (Control: 30.8 ± 1.8; EA: 32.1 ± 2.0; LF-EA: 31.5 ± 1.9; χr2 = 1.97, p = 0.374), (χr2 = 1.20, p = 0.549). Table 3A contrasts the inter-spike (ISI) variables of all MUs among the three feedback conditions. The global averages of the mean inter-spike interval (ISIGAV) and CV-ISImean were not affected by the feedback mode (p > 0.05). Only the discharge irregularity in terms of IRGAV (or global average of IR for all MUs) varied significantly with feedback mode (p < 0.05). IRGAV was generally highest in the LF-EA condition (p < 0.01). Table 3B contrasts the characteristics of the mean discharge rate of the all MUs among the three feedback conditions. Only the RMS of the mean discharge rate was subject to feedback mode (p = 0.005). Post hoc test revealed that the RMS of the mean discharge rate was significantly smaller in the LF-EA condition than in the control condition (p = 0.012). However, the SampEn, MF, and DOF of the mean discharge rate did not significantly vary with feedback mode (p > 0.05). Figure 6A presents an example of the pooled coherence spectra of the EEG and rectified EMG from a typical participant in the control, EA, and LF-EA conditions. The typical coherence spectra manifested with large power in the beta frequencies (13–35 Hz), exceeding the 95% CL. Figure 6B contrasts the population means of the peak coherence and spectral area in the beta frequencies among the three feedback conditions. Both the peak coherence (χr2 = 7.60, p = 0.022) and the spectral area in the beta frequencies (χr2 = 9.73, p = 0.008) varied significantly with feedback mode. Beta peak coherence was larger in the LF-EA condition than in the control condition (p = 0.005), and the spectral area in the beta frequencies was largest in the LF-EA condition (p ≤ 0.009). The use of LF-EA appeared to enhance CMC at 13–35 Hz, which might serve to stabilize the motor output and decrease the discharge variability.
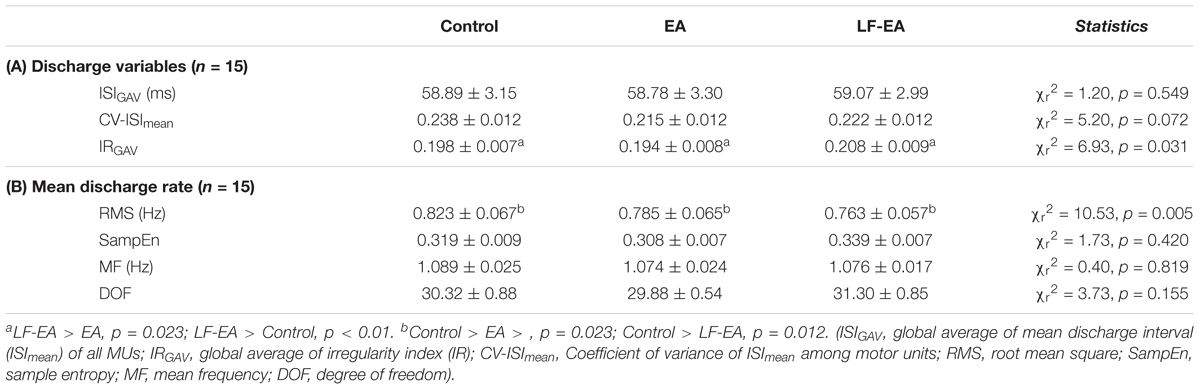
Table 3. Means and standard errors of variables of inter-spike interval (A) mean discharge rate (B) from all motor units in the control, error amplification (EA), and low-frequency error amplification (LF-EA) conditions.
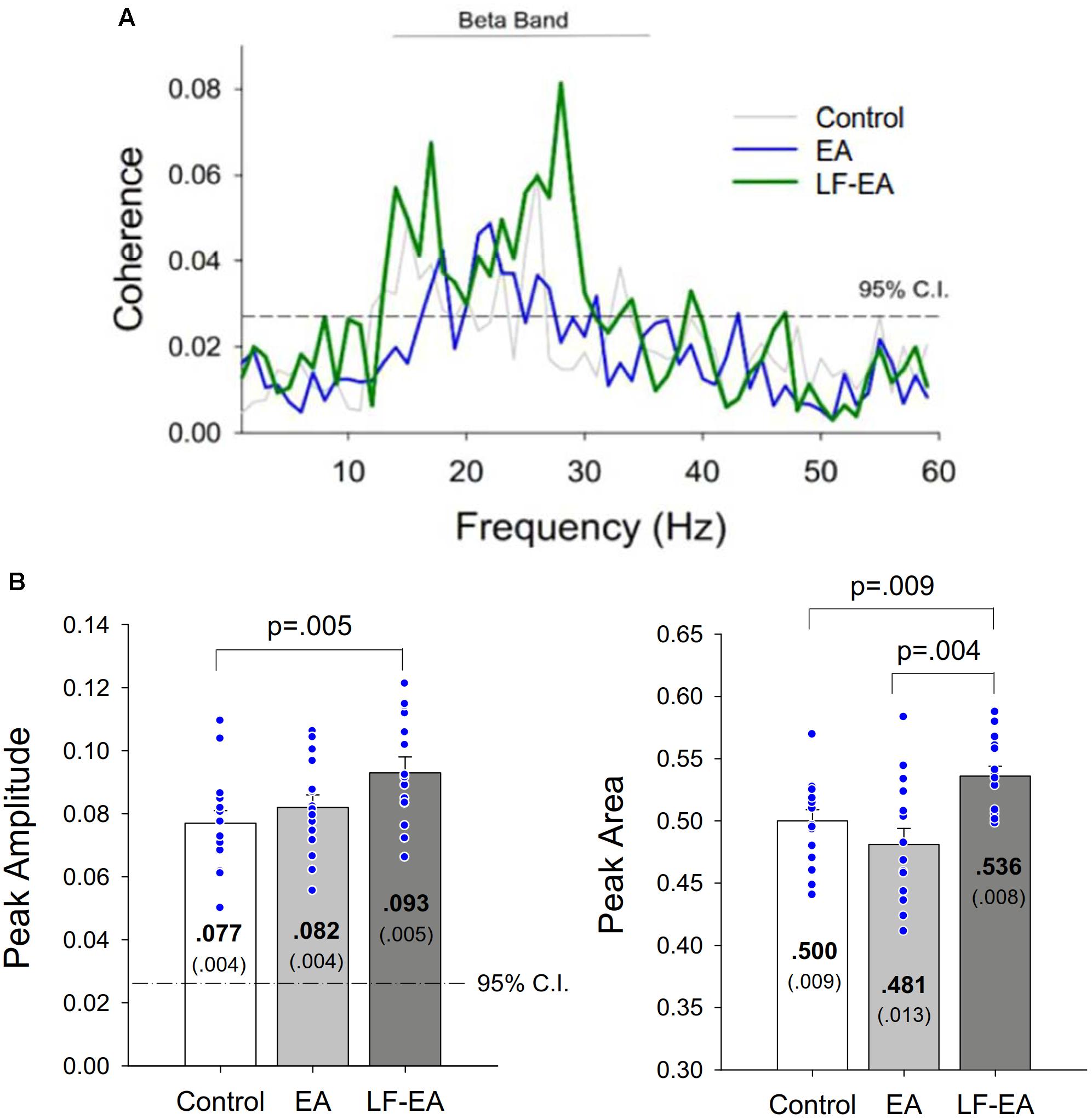
Figure 6. (A) Pooled coherence spectra between the EEG and rectified EMG of a typical participant in the control, error amplification (EA), and low-frequency error amplification (LF-EA) conditions. (B) the contrasts of peak coherence and spectral area in the beta band (13–35 Hz) among the three feedback conditions. The blue dots represent coherence values of all individuals in this study.
Figure 7 presents three scatterplots showing the associations between differences in task error and the neurophysiological metrics (ΔIRGAV, ΔMDRRMS, and Δβ-CohEMG-EEG) sensitive to manipulation of EA. In terms of Spearman rank correlation (rs), the change in task error between the LF-EA and control conditions was significantly correlated to ΔMDRRMS and Δβ-CohEMG-EEG (p < 0.05). In contrast, the change in task error between the EA and control conditions was not significantly correlated to ΔIRGAV, ΔMDRRMS, or Δβ-CohEMG-EEG (p > 0.05). These facts implied that task improvement in the LF-EA condition relative to that of the control condition could be linked to centrally mediated change in the amplitude of pooled discharges of the MUs.
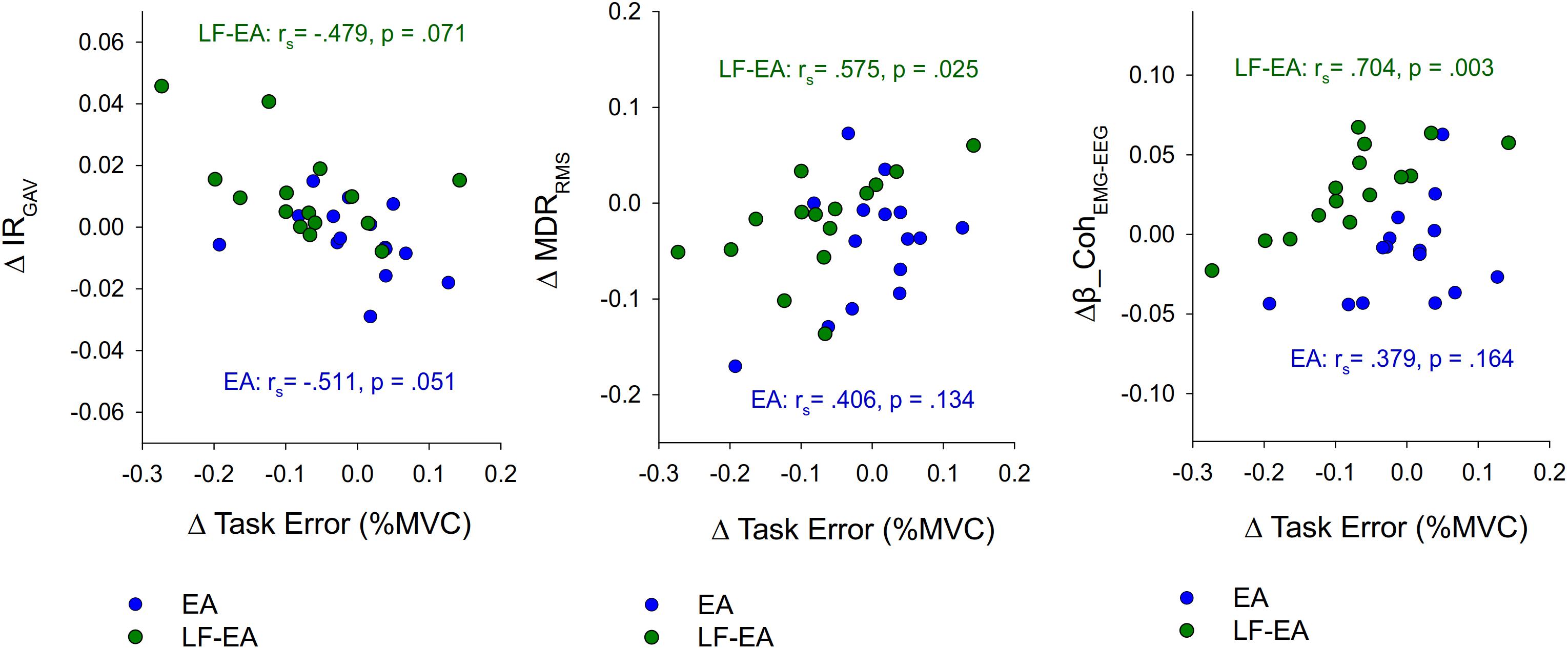
Figure 7. Scatter plots to show the relationships between EA-related changes in task error and neurophysiological metrics. Negative value of ΔTask Error represents task improve with EA or EA-LF feedback. (ΔTask Error, difference in task errors between the EA/LF-EA and control conditions; ΔIRGAV, differences in discharge irregularity between the EA/LF-EA and control conditions; ΔMDRRMS, differences in root mean square of mean discharge rate between the EA/LF-EA and control conditions; Δβ_CohEMG-EEG, differences in beta-range EMG-EEG coherence area between the EA/LF-EA and control conditions; rs, Spearman rank correlation).
Discussion
The novel finding of this study was that gating of the high-frequency execution errors prior to virtual amplification (the LF-EA feedback) provided a functional benefit to the stabilization of static force, due to the smaller Fc with higher complexity, MF, and spectral DOF. The LF-EA feedback reduced the perceptual sensitivity to Fc (smaller <dFc2>) with a greater reliance on the visual feedback process for error corrections (smaller dtc). Physiologically, the shift in force control was associated with greater global discharge irregularity (IRGAV), smaller fluctuation in the mean discharge rate, and enhanced EMG-EEG coherence in the beta band.
Structural Changes in Force Fluctuations and Implications for Force Control
The time series of Fc modeled with SDA was different from ordinary Brownian motion (un-correlated random-walk), as the diffusion curve of Brownian motion is linear and unbounded with the scaling exponent equal to 0.5 (Mandelbrot and van Ness, 1968; Collins and De Luca, 1993). The diffusion curve of the Fc changed slope after the critical point, and the scaling exponents for Fc were, respectively, greater than and less than 0.5 for short-term and long-term intervals (Figure 2B and Table 2). Hence, like postural sway (Collins and De Luca, 1993, 1995; Delignières et al., 2011), Fc are correlated and bounded random-walk signals, regulated distinctively by two subsystems. An open-loop process predominates Fc control in the short-term region with a scaling exponent greater than 0.5, for the stochastic activity was persistent and Fc data of the past and future were positively correlated. In contrast, a closed-loop process predominates Fc control in the long-term region. The stochastic activity with a scaling exponent smaller than 0.5 was anti-persistent, for Fc data of the past and future were negatively correlated (Collins and De Luca, 1993, 1995). This stochastic model of Fc is reminiscent of a continuum of the control regime of a visuomotor act ranging from feedback (closed-loop) to feedforward (open-loop) (Slifkin et al., 2000). Central to this interpretation is that the SDA variables of Fc in the LF-EA condition indicated a scheme switch of open- and closed-loop controls for static force control, as compared with those of the EA and control feedback modes. The smaller dtc and <dFc2> in the LF-EA condition (Table 2) reflected a drift in the equilibrium point of Fc control toward a closed-loop process (Kurz et al., 2013; Coubard et al., 2014; Toosizadeh et al., 2015). The interval of short-term stochastic activity governed by the open-loop regime (dtc) was significantly shortened, and feedback control was called into play when a smaller degree of Fc (<dFc2>) took place. The experimental observation was congruent with reductions in the Ds and scaling exponent (Hs). After deconditioning of the feedforward mechanism, force-tracking in the LF-EA condition was more dependent on the feedback mechanism, with a functional benefit of superior task accuracy (Table 1). Hence, the prevailing use of the feedback process was conceptually in agreement with the perceptual narrowing (Easterbrook, 1959) and enhanced attentive control (Boussaoud and Kermadi, 1997; Jueptner and Weiller, 1998; Shirzad and Van der Loos, 2012) reported in behavioral studies.
Due to the smaller Fc with greater complexity (Table 1), the participants could develop fine-grained force-scaling with a richer correction strategy in the LF-EA condition with the feedback-prone process (Vaillancourt et al., 2002; Chen et al., 2013). Several lines of indirect evidence have shown that modulation of Fc dynamics in the LF-EA condition resembles characteristic changes in Fc after motor practice (Deutsch and Newell, 2004; Hwang et al., 2013). Moreover, the increase in the MF of Fc and flattening of the spectral DOF support of LF-EA indicated that the participants could increase the number of corrective attempts with abundant exploratory efforts to remedy tracking deviations. Gating the high-frequency components brought about these performance benefits because VEs above 0.8 Hz are too fast to be corrected. The interval to accomplish visuomotor correction in humans is at least 1 s (Navas and Stark, 1968; Miall et al., 1985), and primates cannot follow the full excursion of a target higher than 0.9 Hz with the feedback process (Miall et al., 1986). If visual EA contains information that cannot be rapidly responded with the feedback process, lag-induced feedback instability taxes attentional resources with processing visuomotor information that is irrelevant to task success. That is why the task accuracy, Fc properties, and SDA variables between EA and LF-EA were distinct.
Variations in Motor Unit Discharge for Low-Frequency Error Amplification
The adaptation of the Fc dynamic originated from variations in the probability structures of the MU discharges. Physiologically, the decrease in the size of Fc with LF-EA was correspondent with the decrease in RMS of the mean discharge rate (Table 3B) rather than CV-ISImean (Table 3A). It is known that modeling of the mean discharge rate with a pooling process could accentuate synaptic inputs common to a population of active motoneurons but also attenuate the role of independent synaptic inputs to motoneurons (Farina and Negro, 2015; Farina et al., 2016). Therefore, the amplitude modulation of the mean discharge rate implies that LF-EA could effectively reduce the variations in the common input to a muscle. The observed influence of the common input confirms the model-based conjectures, implying a reduction in the intrinsic neuromotor noises at the motoneuronal level with EA (Wei et al., 2005; Hasson et al., 2016; Williams et al., 2016). The modulation of the size of the mean discharge rate was critical to the increase in task precision in the LF-EA condition (Figure 7). However, the reduction in the size of Fc with LF-EA is unlikely to have resulted from modulation of independent synaptic inputs to motoneurons because CV-ISImean, which highlights the influence of synaptic inputs to motoneurons that differ from those that are common, was insensitive to feedback mode. On the other hand, the enhancement of the complexity of Fc in the LF-EA condition (Table 1) was nicely compatible with the irregularity of the increases in MU discharge (IRGAV) (Table 3A). However, the structures of the mean discharge rate, such as SampEn and DOF (Table 3B), did not well index the change in the complexity of Fc in the LF-EA condition. In addition to some unidentified organizational discharge activities, the viscous resistances of the musculotendon system attenuate the transmission of high-frequency neural drive to a muscle (Günther et al., 2007). This non-linearity often complicates the discharge–force relationship.
Variation in Corticospinal Coupling for Low-Frequency Error Amplification
Instead, superior task accuracy and force steadiness in the LF-EA condition were associated with increased EEG–EMG coherence in the beta range (Figure 4). An increase in the beta-range EEG–EMG coherence represents greater synchronization of cortical activity to regulate common spinal inputs, a neural marker of steady-state motor output during static contraction (Perez et al., 2006; Kristeva et al., 2007). The beta-range CMC is greatly reduced when a force task is not steady (Salenius et al., 1997; Boonstra et al., 2009). Previous studies have reported that repetitive training can increase the precision of control in a static force task, in association with enhancement of beta-range CMC (Perez et al., 2006; Witte et al., 2007; Larsen et al., 2016). From all the neural sequelae, the enhanced beta-range CMC should contribute to a smaller size of discharge variability with enhanced complexity (Table 3 and Figure 7) and fine-grained force scaling with the feedback-prone process (Tables 1, 2) in the LF-EA condition. Since the beta-range corticomuscular rhythm is modifiable to peripheral sensory afferents (Riddle and Baker, 2005; Lalo et al., 2007), the precise force control in the LF-EA condition might be attributable to the reduction of the cognitive load of processing task-irrelevant error information, which would facilitate rapid integration of the visual and somatosensory information.
Methodological Issues
A contrasting approach to enhance static force control is stochastic resonance (Mendez-Balbuena et al., 2012; Trenado et al., 2014). In addition to an increase in corticomuscular synchronization at 13–35 Hz, a better force precision with a return map of concentrated error points was noted following application of an optimal mechanical Gaussian noise. The task improvement was hypothesized to detect subthreshold sensory signals in the peripheral receptors, pertaining to noise-enhanced sensorimotor integration. However, stochastic resonance differs with the use of LF-EA, which minimizes cognitive load to process functionally irreverent noises. The return map with concentrated error points speaks for additional functional benefits for removal of high-frequency error components (noises) prior to EA (Figure 5A). Besides, one matter of concern is the decomposition of multi-electrode surface EMG. Although we cannot deny the likelihood of a small decomposition error (Piotrkiewicz and Türker, 2017), the state-of-the-art decomposition algorithm is a trade-off to capture the discharge variability among MUs and the force–discharge relation, based on a relatively large number of active MUs. To be rigorous, we applied a “reconstruct-and-test” procedure (Nawab et al., 2010; De Luca et al., 2015) to support the accuracy of the obtained identifications (91.2–97.1%) (De Luca et al., 2006; Nawab et al., 2010; Chen et al., 2017a,b; Hwang et al., 2017). The use of multi-channel surface EMG to explore MU behaviors has gained popularity in recent studies (Hu et al., 2014; Laine et al., 2015; Contessa et al., 2016; Chen et al., 2017a,b). In particular, the inconsistent changes in the complexity measures between IRGAV and the SampEn of the mean discharge rate with LF-EA (Tables 3A,B) reinforce the role of decomposition in revealing diverse fractal myoelectric manifestations. A simulated EMG study showed that the fractal characteristic of surface EMG, which accounts for pooled MU behaviors, is jointly subject to variations in the CV of the discharge rate and the degree of MU synchronization (Mesin et al., 2016). Hence, fractal changes in the surface EMG are evident during fatiguing (Ravier et al., 2005) or higher-force (>25% MVC) contractions (Beretta-Piccoli et al., 2018). When the CV of the ISI is not expected to change, the discharge irregularity of a single MU such as IRGAV could be masked by the interference pattern of surface EMG (or the mean discharge rate). Next, a low-pass filtering effect was likely to be effective only in the visual EA condition, though this study did not examine tracking performance in the non-EA condition. According to our preliminary study in healthy adults (n = 14), the task error of the control condition (0.467 ± 0.029% MVC) did not differ significantly from the task error in the condition of low-frequency feedback without EA (0.446 ± 0.039% MVC) (t13 = 0.648, p = 0.528) (unpublished data). Therefore, low-frequency error signals without amplification could not facilitate feedback control, and the performance benefit and paradigm shift were evident only in the LF-EA condition. Also, the selection of a low pass threshold of 0.8 Hz for EA was empirically determined. The time period necessary for the detection of visual information and motor adjustments was at least 150 ms (Miall et al., 1985, 1986), which prevented the participants from timely correcting fast-oscillatory error components. However, on account of the slow tracking response and perceptual motor conflict, the excessive removal of high-frequency error components is disadvantageous to task precision due to the lack of ample information for remedying tracking deviations. The effects of various low-pass thresholds on EA feedback will require further investigation.
Conclusion
Virtual potentiation of low-frequency errors below 0.8 Hz for visual feedback more effectively improves task performance than does traditional EA or real visual feedback in a static isometric task. The selective gating of high-frequency error components reduces the task-irrelevant information in the visual feedback that cannot be rapidly processed with a feedback process. This study reveals that the amplification of low-frequency error information could increase the sensitivity to detect Fc and facilitate the state shift to the negative feedback process for force stabilization. The behavior adaptations arise from the promotion of effective corticospinal interactions to enhance discharge irregularity and minimize fluctuations of the common drive to a muscle.
Author Contributions
I-SH and Y-CC: conception or design of the work. C-LH and Z-RY: acquisition. I-SH and C-LH: analysis. Y-CC, I-SH, and Y-TL: interpretation of data. I-SH and Y-CC: drafted the work or revised it critically for important intellectual content. Y-CC: final approval of the version to be published. Y-CC and I-SH: agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
Funding
This research was supported by grants from the Ministry of Science and Technology, Taiwan, R.O.C., under grant nos. MOST 105-2410-H-040-009 and MOST 104-2314-B-006 -016 -MY3.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Abbreviations
Δ MDRRMS, differences in root mean square of mean discharge rate between the EA/LF-EA and control conditions; Δβ_CohEMG-EEG, differences in beta-range EMG-EEG coherence area between the EA/LF-EA and control conditions; ΔIRGAV, differences in discharge irregularity between the EA/LF-EA and control conditions; ΔTask Error, difference in task errors between the EA/LF-EA and control conditions; CL, confidence level; CMC, corticomuscular coherence; CV-ISImean, coefficient of variance of mean ISI among motor units; <dF2>, mean-squared value of the force fluctuations; <dFc2>, critical point of force fluctuations; Dl, long-term effective diffusion coefficient; DOF, degree of freedom; Ds, short-term effective diffusion coefficient; DSDC, Decomposition-Synthesis-Decomposition-Compare test; dt, time interval; dtc, critical point of time; EA, error amplification; EEG, electroencephalography; EMG, electromyography; Fc, force fluctuations; FDI, first dorsal interosseus; Hl, long-term scaling exponent; Hs, short-term scaling exponent; IR, irregularity index of inter-spike interval; IRGAV, global average of irregularity index of inter-spike interval for all motor units; ISI, inter-spike interval; ISIGAV, global average of mean inter-spike interval for all motor units; ISImean, mean value of inter-spike intervals in an individual MUAPT; LF-EA, low-frequency error amplification; MF, mean frequency; MU, motor unit; MUAPT, motor unit action potential train; MVC, maximal voluntary contraction; RE, real error; RF, real force; RMS, root mean square; SampEn, sample entropy; SDA, stabilogram diffusion analysis; T, target signal; VE, visualized error; VF, visualized force.
References
Abdollahi, F., Case Lazarro, E. D., Listenberger, M., Kenyon, R. V., Kovic, M., Bogey, R. A., et al. (2014). Error augmentation enhancing arm recovery in individuals with chronic stroke: a randomized crossover design. Neurorehabil. Neural Repair 28, 120–128. doi: 10.1177/1545968313498649
Baweja, H. S., Patel, B. K., Martinkewiz, J. D., Vu, J., and Christou, E. A. (2009). Removal of visual feedback alters muscle activity and reduces force variability during constant isometric contractions. Exp. Brain Res. 197, 35–47. doi: 10.1007/s00221-009-1883-5
Bays, P. M., and Wolpert, D. M. (2007). Computational principles of sensorimotor control that minimize uncertainty and variability. J. Physiol. 578, 387–396. doi: 10.1113/jphysiol.2006.120121
Beretta-Piccoli, M., Boccia, G., Ponti, T., Clijsen, R., Barbero, M., and Cescon, C. (2018). Relationship between isometric muscle force and fractal dimension of surface electromyogram. Biomed. Res. Int. 2018, 5373846. doi: 10.1155/2018/5373846
Boonstra, T. W., van Wijk, B. C., Praamstra, P., and Daffertshofer, A. (2009). Corticomuscular and bilateral EMG coherence reflect distinct aspects of neural synchronization. Neurosci. Lett. 463, 17–21. doi: 10.1016/j.neulet.2009.07.043
Bouchard, A. E., Corriveau, H., and Milot, M. H. (2015). Comparison of haptic guidance and error amplification robotic trainings for the learning of a timing-based motor task by healthy seniors. Front. Syst. Neurosci. 9:52. doi: 10.3389/fnsys.2015.00052
Bouchard, A. E., Corriveau, H., and Milot, M. H. (2017). A single robotic session that guides or increases movement error in survivors post-chronic stroke: which intervention is best to boost the learning of a timing task? Disabil. Rehabil. 39, 1607–1614. doi: 10.1080/09638288.2016.1205151
Boussaoud, D., and Kermadi, I. (1997). The primate striatum: neuronal activity in relation to spatial attention versus motor preparation. Eur. J. Neurosci. 9, 2152–2168.
Chen, Y. C., Lin, L. L., Lin, Y. T., Hu, C. L., and Hwang, I. S. (2017a). Variations in static force control and motor unit behavior with error amplification feedback in the elderly. Front. Hum. Neurosci. 11:538. doi: 10.3389/fnhum.2017.00538
Chen, Y. C., Lin, Y. T., Chang, G. C., and Hwang, I. S. (2017b). Paradigm shifts in voluntary force control and motor unit behaviors with the manipulated size of visual error perception. Front. Physiol. 8:140. doi: 10.3389/fphys.2017.00140
Chen, Y. C., Lin, Y. T., Huang, C. T., Shih, C. L., Yang, Z. R., and Hwang, I. S. (2013). Trajectory adjustments underlying task-specific intermittent force behaviors and muscular rhythms. PLoS One 8:e74273. doi: 10.1371/journal.pone.0074273
Collins, J. J., and De Luca, C. J. (1993). Open-loop and closed-loop control of posture: a random-walk analysis of center-of-pressure trajectories. Exp. Brain Res. 95, 308–318. doi: 10.1007/bf00229788
Collins, J. J., and De Luca, C. J. (1995). The effects of visual input on open-loop and closed-loop postural control mechanisms. Exp. Brain Res. 103, 151–163. doi: 10.1007/bf00241972
Contessa, P., De Luca, C. J., and Kline, J. C. (2016). The compensatory interaction between motor unit firing behavior and muscle force during fatigue. J. Neurophysiol. 116, 1579–1585. doi: 10.1152/jn.00347.2016
Coubard, O. A., Ferrufino, L., Nonaka, T., Zelada, O., Bril, B., and Dietrich, G. (2014). One month of contemporary dance modulates fractal posture in aging. Front. Aging Neurosci. 6:17. doi: 10.3389/fnagi.2014.00017
Davies, R. M., Gerstein, G. L., and Baker, S. N. (2006). Measurement of time-dependent changes in the irregularity of neural spiking. J. Neurophysiol. 96, 906–918. doi: 10.1152/jn.01030.2005
De Luca, C. J., Adam, A., Wotiz, R., Gilmore, L. D., and Nawab, S. H. (2006). Decomposition of surface EMG signals. J. Neurophysiol. 96, 1646–1657. doi: 10.1152/jn.00009.2006
De Luca, C. J., Kline, J. C., and Contessa, P. (2014). Transposed firing activation of motor units. J. Neurophysiol. 112, 962–970. doi: 10.1152/jn.00619.2013
De Luca, C. J., LeFever, R. S., McCue, M. P., and Xenakis, A. P. (1982). Control scheme governing concurrently active human motor units during voluntary contractions. J. Physiol. 329, 129–142. doi: 10.1113/jphysiol.1982.sp014294
De Luca, C. J., Nawab, S. H., and Kline, J. C. (2015). Clarification of methods used to validate surface EMG decomposition algorithms as described by Farina et al. (2014). J. Appl. Physiol. 118:1084. doi: 10.1152/japplphysiol.00061.2015
Delignières, D., Torre, K., and Bernard, P. L. (2011). Transition from persistent to anti-persistent correlations in postural sway indicates velocity-based control. PLoS Comput. Biol. 7:e1001089. doi: 10.1371/journal.pcbi.1001089
Deutsch, K. M., and Newell, K. M. (2004). Changes in the structure of children’s isometric force variability with practice. J. Exp. Child Psychol. 88, 319–333. doi: 10.1016/j.jecp.2004.04.003
Domingo, A., and Ferris, D. P. (2010). The effects of error augmentation on learning to walk on a narrow balance beam. Exp. Brain Res. 206, 359–370. doi: 10.1007/s00221-010-2409-x
Easterbrook, J. A. (1959). The effect of emotion on cue utilization and the organization of behavior. Psychol. Rev. 66, 183–193. doi: 10.1037/h0047707
Farina, D., and Negro, F. (2015). Common synaptic input to motor neurons, motor unit synchronization, and force control. Exerc. Sport Sci. Rev. 43, 23–33. doi: 10.1249/JES.0000000000000032
Farina, D., Negro, F., Muceli, S., and Enoka, R. M. (2016). Principles of motor unit physiology evolve with advances in technology. Physiology 31, 83–94. doi: 10.1152/physiol.00040.2015
Frank, T. D., Friedrich, R., and Beek, P. J. (2006). Stochastic order parameter equation of isometric force production revealed by drift-diffusion estimates. Phys. Rev. E Stat. Nonlin. Soft. Matter Phys. 74:051905. doi: 10.1103/PhysRevE.74.051905
Günther, M., Schmitt, S., and Wank, V. (2007). High-frequency oscillations as a consequence of neglected serial damping in Hill-type muscle models. Biol. Cybern. 97, 63–79. doi: 10.1007/s00422-007-0160-6
Hasson, C. J., Zhang, Z., Abe, M. O., and Sternad, D. (2016). Neuromotor noise is malleable by amplifying perceived errors. PLoS Comput. Biol. 12:e1005044. doi: 10.1371/journal.pcbi.1005044
Hong, S. L., and Newell, K. M. (2008). Visual information gain and the regulation of constant force levels. Exp. Brain Res. 189, 61–69. doi: 10.1007/s00221-008-1403-z
Hu, X., Rymer, W. Z., and Suresh, N. L. (2013). Assessment of validity of a high-yield surface electromyogram decomposition. J. Neuroeng. Rehabil. 10:99. doi: 10.1186/1743-0003-10-99
Hu, X., Rymer, W. Z., and Suresh, N. L. (2014). Accuracy assessment of a surface electromyogram decomposition system in human first dorsal interosseus muscle. J. Neural Eng. 11:026007. doi: 10.1088/1741-2560/11/2/026007
Hwang, I. S., Huang, C. T., Yang, J. F., and Guo, M. C. (2013). Characterization of information-based learning benefits with submovement dynamics and muscular rhythmicity. PLoS One 8:e82920. doi: 10.1371/journal.pone.0082920
Hwang, I. S., Lin, Y. T., Huang, W. M., Yang, Z. R., Hu, C. L., and Chen, Y. C. (2017). Alterations in neural control of constant isometric contraction with the size of error feedback. PLoS One 12:e0170824. doi: 10.1371/journal.pone.0170824
Israely, S., and Carmeli, E. (2016). Error augmentation as a possible technique for improving upper extremity motor performance after a stroke - a systematic review. Top. Stroke Rehabil. 23, 116–125. doi: 10.1179/1945511915Y.0000000007
Jueptner, M., and Weiller, C. (1998). A review of differences between basal ganglia and cerebellar control of movements as revealed by functional imaging studies. Brain 121, 1437–1449. doi: 10.1093/brain/121.8.1437
Kao, P. C., Srivastava, S., Higginson, J. S., Agrawal, S. K., and Scholz, J. P. (2015). Short-term performance-based error-augmentation versus error-reduction robotic gait training for individuals with chronic stroke: a Pilot Study. Phys. Med. Rehabil. Int. 2:1066.
King, A. C., and Newell, K. M. (2015). Selective visual scaling of time-scale processes facilitates broadband learning of isometric force frequency tracking. Atten. Percept. Psychophys. 77, 2507–2518. doi: 10.3758/s13414-015-0936-z
Kristeva, R., Patino, L., and Omlor, W. (2007). Beta-range cortical motor spectral power and corticomuscular coherence as a mechanism for effective corticospinal interaction during steady-state motor output. Neuroimage 36, 785–792. doi: 10.1016/j.neuroimage.2007.03.025
Kristeva-Feige, R., Fritsch, C., Timmer, J., and Lücking, C. H. (2002). Effects of attention and precision of exerted force on beta range EEG–EMG synchronization during a maintained motor contraction task. Clin. Neurophysiol. 113, 124–131. doi: 10.1016/S1388-2457(01)00722-2
Kurz, I., Oddsson, L., and Melzer, I. (2013). Characteristics of balance control in older persons who fall with injury–a prospective study. J. Electromyogr. Kinesiol. 23, 814–819. doi: 10.1016/j.jelekin.2013.04.001
Laine, C. M., Martinez-Valdes, E., Falla, D., Mayer, F., and Farina, D. (2015). Motor neuron pools of synergistic thigh muscles share most of their synaptic input. J. Neurosci. 35, 12207–12216. doi: 10.1523/JNEUROSCI.0240-15.2015
Lalo, E., Gilbertson, T., Doyle, L., Di Lazzaro, V., Cioni, B., and Brown, P. (2007). Phasic increases in cortical beta activity are associated with alterations in sensory processing in the human. Exp. Brain Res. 177, 137–145. doi: 10.1007/s00221-006-0655-8
Larsen, L. H., Jensen, T., Christensen, M. S., Lundbye-Jensen, J., Langberg, H., and Nielsen, J. B. (2016). Changes in corticospinal drive to spinal motoneurones following tablet-based practice of manual dexterity. Physiol. Rep. 4:e12684. doi: 10.14814/phy2.12684
Lin, Y. T., Kuo, C. H., and Hwang, I. S. (2014). Fatigue effect on low-frequency force fluctuations and muscular oscillations during rhythmic isometric contraction. PLoS One 9:e85578. doi: 10.1371/journal.pone.0085578
Lipowski, Z. J. (1975). Sensory and information inputs overload: behavioral effects. Compr. Psychiatry 16, 199–221. doi: 10.1016/0010-440X(75)90047-4
Mandelbrot, B. B., and van Ness, J. W. (1968). Fractional Brownian motions, fractional noises and applications. SIAM Rev. 10, 422–437. doi: 10.1137/1010093
Mendez-Balbuena, I., Manjarrez, E., Schulte-Mönting, J., Huethe, F., Tapia, J. A., Hepp-Reymond, M. C., et al. (2012). Improved sensorimotor performance via stochastic resonance. J. Neurosci. 32, 12612–12618. doi: 10.1523/JNEUROSCI.0680-12.2012
Mesin, L., Dardanello, D., Rainoldi, A., and Boccia, G. (2016). Motor unit firing rates and synchronisation affect the fractal dimension of simulated surface electromyogram during isometric/isotonic contraction of vastus lateralis muscle. Med. Eng. Phys. 38, 1530–1533. doi: 10.1016/j.medengphy.2016.09.022
Miall, R. C., Weir, D. J., and Stein, J. F. (1985). Visuomotor tracking with delayed visual feedback. Neuroscience 16, 511–520. doi: 10.1016/0306-4522(85)90189-7
Miall, R. C., Weir, D. J., and Stein, J. F. (1986). Manual tracking of visual targets by trained monkeys. Behav. Brain Res. 20, 185–201. doi: 10.1016/0166-4328(86)90003-3
Miall, R. C., Weir, D. J., and Stein, J. F. (1993). Intermittency in human manual tracking tasks. J. Mot. Behav. 25, 53–63. doi: 10.1080/00222895.1993.9941639
Navas, F., and Stark, L. (1968). Sampling or intermittency in hand control system dynamics. Biophys. J. 8, 252–302. doi: 10.1016/S0006-3495(68)86488-4
Nawab, S. H., Chang, S. S., and De Luca, C. J. (2010). High-yield decomposition of surface EMG signals. Clin. Neurophysiol. 121, 1602–1615. doi: 10.1016/j.clinph.2009.11.092
Nawab, S. H., Wotiz, R., and De Luca, C. J. (2004). “Resolving EMG pulse superpositions via utility maximization,” in Proceedings of the 8th World Multiconf. Systemics, Cybernetics, Informatics, (Orlando, FL), 233–236.
Ogawa, K., and Imamizu, H. (2013). Human sensorimotor cortex represents conflicting visuomotor mappings. J. Neurosci. 33, 6412–6422. doi: 10.1523/JNEUROSCI.4661-12.2013
Omlor, W., Patino, L., Mendez-Balbuena, I., Schulte-Mönting, J., and Kristeva, R. (2011). Corticospinal beta-range coherence is highly dependent on the pre-stationary motor state. J. Neurosci. 31, 8037–8045. doi: 10.1523/JNEUROSCI.4153-10.2011
Patton, J. L., Stoykov, M. E., Kovic, M., and Mussa-Ivaldi, F. A. (2006). Evaluation of robotic training forces that either enhance or reduce error in chronic hemiparetic stroke survivors. Exp. Brain Res. 168, 368–383. doi: 10.1007/s00221-005-0097-8
Perez, M. A., Lundbye-Jensen, J., and Nielsen, J. B. (2006). Changes in corticospinal drive to spinal motoneurones following visuo-motor skill learning in humans. J. Physiol. 573, 843–855. doi: 10.1113/jphysiol.2006.105361
Pethick, J., Winter, S. L., and Burnley, M. (2015). Fatigue reduces the complexity of knee extensor torque fluctuations during maximal and submaximal intermittent isometric contractions in man. J. Physiol. 593, 2085–2096. doi: 10.1113/jphysiol.2015.284380
Pew, R. W. (1974). “Human perceptual-motor performance,” in Human Information Processing: Tutorials in Performance and Cognition, ed. B. H. Kantowitz (Hills-dale: Erlbaum), 1–39.
Piotrkiewicz, M., and Türker, K. S. (2017). Onion skin or common drive? Front. Cell Neurosci. 11:2. doi: 10.3389/fncel.2017.00002
Ravier, P., Buttelli, O., Jennane, R., and Couratier, P. (2005). An EMG fractal indicator having different sensitivities to changes in force and muscle fatigue during voluntary static muscle contractions. J. Electromyogr. Kinesiol. 15, 210–221. doi: 10.1016/j.jelekin.2004.08.008
Reisman, D. S., McLean, H., Keller, J., Danks, K. A., and Bastian, A. J. (2013). Repeated split-belt treadmill training improves poststroke step length asymmetry. Neurorehabil. Neural Repair 27, 460–468. doi: 10.1177/1545968312474118
Richman, J. S., and Moorman, J. R. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278, H2039–H2049. doi: 10.1152/ajpheart.2000.278.6.H2039
Riddle, C. N., and Baker, S. N. (2005). Manipulation of peripheral neural feedback loops alters human corticomuscular coherence. J. Physiol. 566, 625–639. doi: 10.1113/jphysiol.2005.089607
Salenius, S., Portin, K., Kajola, M., Salmelin, R., and Hari, R. (1997). Cortical control of human motoneuron firing during isometric contraction. J. Neurophysiol. 77, 3401–3405. doi: 10.1152/jn.1997.77.6.3401
Shenker, S. J. (1982). Scaling behavior in a map of a circle onto itself: empirical results. Physica D 5, 405–411. doi: 10.1016/0167-2789(82)90033-1
Shirzad, N., and Van der Loos, H. F. (2012). Error amplification to promote motor learning and motivation in therapy robotics. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2012, 3907–3910. doi: 10.1109/EMBC.2012.6346821
Slifkin, A. B., Vaillancourt, D. E., and Newell, K. M. (2000). Intermittency in the control of continuous force production. J. Neurophysiol. 84, 1708–1718. doi: 10.1152/jn.2000.84.4.1708
Sosnoff, J. J., Valantine, A. D., and Newell, K. M. (2006). Independence between the amount and structure of variability at low force levels. Neurosci. Lett. 392, 165–169. doi: 10.1016/j.neulet.2005.09.010
Sung, C., and O’Malley, M. K. (2011). Effect of progressive visual error amplification on human motor adaptation. IEEE. Int. Conf. Rehabil. Robot. 2011:5975399. doi: 10.1109/ICORR.2011.5975399
Toosizadeh, N., Mohler, J., Wendel, C., and Najafi, B. (2015). Influences of frailty syndrome on open-loop and closed-loop postural control strategy. Gerontology 61, 51–60. doi: 10.1159/000362549
Trenado, C., Mendez-Balbuena, I., Manjarrez, E., Huethe, F., Schulte-Mönting, J., Feige, B., et al. (2014). Enhanced corticomuscular coherence by external stochastic noise. Front. Hum. Neurosci. 8:325. doi: 10.3389/fnhum.2014.00325
Vaillancourt, D. E., Larsson, L., and Newell, K. M. (2002). Time-dependent structure in the discharge rate of human motor units. Clin. Neurophysiol. 113, 1325–1338. doi: 10.1016/S1388-2457(02)00167-0
Wei, Y., Bajaj, P., Scheidt, R., and Patton, J. L. (2005). “Visual error augmentation for enhancing motor learning and rehabilitative relearning,” in Proceedings of the IEEE International Conf. on Rehabil Robotics, (Chicago: IEEE), 505–510.
Williams, C. K., Tremblay, L., and Carnahan, H. (2016). It pays to go off-track: practicing with error-augmenting haptic feedback facilitates learning of a curve-tracing task. Front. Psychol. 7:2010. doi: 10.3389/fpsyg.2016.02010
Witham, C. L., and Baker, S. N. (2007). Network oscillations and intrinsic spiking rhythmicity do not covary in monkey sensorimotor areas. J. Physiol. 580, 801–814. doi: 10.1113/jphysiol.2006.124503
Keywords: force fluctuations, stochastic processes, visuomotor, EMG, EEG
Citation: Hwang I-S, Hu C-L, Yang Z-R, Lin Y-T and Chen Y-C (2019) Improving Precision Force Control With Low-Frequency Error Amplification Feedback: Behavioral and Neurophysiological Mechanisms. Front. Physiol. 10:131. doi: 10.3389/fphys.2019.00131
Received: 20 April 2018; Accepted: 01 February 2019;
Published: 20 February 2019.
Edited by:
Srdjan Kesić, University of Belgrade, SerbiaReviewed by:
Tara Thiagarajan, Sapien Labs, United StatesElias Manjarrez, Benemérita Universidad Autónoma de Puebla, Mexico
Copyright © 2019 Hwang, Hu, Yang, Lin and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yi-Ching Chen, eWljaGluZ0Bjc211LmVkdS50dw==
 Ing-Shiou Hwang
Ing-Shiou Hwang Chia-Ling Hu
Chia-Ling Hu Zong-Ru Yang1
Zong-Ru Yang1 Yen-Ting Lin
Yen-Ting Lin Yi-Ching Chen
Yi-Ching Chen