- 1Department of Mechanical Engineering, University of Maryland, College Park, College Park, MD, United States
- 2Office of Science and Engineering Laboratories, Center for Devices and Radiological Health, U.S. Food and Drug Administration, Silver Spring, MD, United States
Individualizing physiological models to a patient can enable patient-specific monitoring and treatment in critical care environments. However, this task often presents a unique “practical identifiability” challenge due to the conflict between model complexity and data scarcity. Regularization provides an established framework to cope with this conflict by compensating for data scarcity with prior knowledge. However, regularization has not been widely pursued in individualizing physiological models to facilitate patient-specific critical care. Thus, the goal of this work is to garner potentially generalizable insight into the practical use of regularization in individualizing a complex physiological model using scarce data by investigating its effect in a clinically significant critical care case study of blood volume kinetics and cardiovascular hemodynamics in hemorrhage and circulatory resuscitation. We construct a population-average model as prior knowledge and individualize the physiological model via regularization to illustrate that regularization can be effective in individualizing a physiological model to learn salient individual-specific characteristics (resulting in the goodness of fit to individual-specific data) while restricting unnecessary deviations from the population-average model (achieving practical identifiability). We also illustrate that regularization yields parsimonious individualization of only sensitive parameters as well as adequate physiological plausibility and relevance in predicting internal physiological states.
Introduction
Clinical care automation has been a domain of interest for a few decades by virtue of its potential for error-free and vigilant performance of routine and low-level patient monitoring and treatment tasks (Hemmerling et al., 2010; Salinas et al., 2011; Dussaussoy et al., 2014; Rinehart et al., 2015; Brogi et al., 2017; Hundeshagen et al., 2017; Pasin et al., 2017), yet realizing this potential is contingent upon establishing the safety and the performance characteristics of clinical care automation. Patient physiology models built upon physical principles (hereafter called physiological models) can facilitate the development (Jin-Oh et al., 2012; Bighamian et al., 2014; Jin et al., 2018) and the testing (Kovatchev et al., 2009; Ortiz et al., 2010; Brown et al., 2015) of clinical care automation capabilities. However, individualizing physiological models (which can enable the systematic development and the testing of patient-specific clinical care automation) presents formidable challenge due to the conflict between model complexity and data scarcity. That is, physiological models are complex and involve a large number of unknown patient-specific parameters that frequently exhibit interaction properties, whereas clinical data pertaining to an individual patient are scarce in both quantity and quality. For example, blood pressure (BP) can increase in response to an increase in cardiac output (CO) and an increase in total peripheral resistance (TPR), but routine clinical measurements often provide only BP which does not offer sufficient information to uniquely determine CO- and TPR-related model parameters. In fact, such a conflict appears to be a main obstacle in characterizing a wide range of mechanistic models in physiology as well as in broader fields of biology and physics, which has been called the sloppiness property (Transtrum et al., 2010, 2015; Machta et al., 2013; White et al., 2016) or lack of practical identifiability (Raue et al., 2009; Maiwald et al., 2011) in different contexts. If not properly addressed, such conflict may yield a physiological model suffering from non-unique and physically irrelevant parameter values as well as poor individual-specific internal (i.e., unmeasured) state predictions.
The existing body of work has addressed the practical identifiability challenge mainly in two ways: (i) by modifying the model structure or parameterization toward more simplified or lumped models and (ii) by utilizing some form of regularization (or more generally, prior knowledge) to additionally inform the modeling procedure and effectively reduce the complexity of the model search space. Analyzing and modifying the model structure has particularly strong precedents in physiological modeling, where effective tools such as variation-based sensitivity analysis (Sobol, 2001; Saltelli et al., 2008, 2010) and profile-likelihood (Raue et al., 2009, 2014; Maiwald et al., 2016) methods are used to assess the appropriateness of a model structure and the importance of model parameters with respect to given data. While useful in informing potential modifications to the model structure and parameterization (Machta et al., 2013; Mattingly et al., 2018), many of these tools are formalized on a pre-determined level of data availability, making them less powerful if data availability varies (which is quite common in clinical scenarios). Regularization is an established framework to cope with conflicts between model complexity and data scarcity, by which one can potentially compensate for the scarce data available to individualize a physiological model based on prior knowledge. To date, the notion of prior distribution (Toni et al., 2009; Gelman et al., 2013) and its closely related counterpart in regularization (Benning and Burger, 2018) have been pursued in a wide range of deterministic and stochastic modeling problems to incorporate additional information into the modeling problem and control the complexity of the model search space (Davidian and Giltinan, 2003; Tivay et al., 2019; Zhang et al., 2019).
The goal of this work is to garner potentially generalizable insight into the role of regularization in individualizing a complex physiological model using scarce data by studying its effect in a clinically significant critical care case study of blood volume (BV) kinetics and cardiovascular hemodynamics in hemorrhage and circulatory resuscitation. We construct a population-average physiological model as prior knowledge and individualize the physiological model via regularization to elucidate how regularization enables the physiological model to capture salient individual-specific characteristics (leading to the goodness of fit to individual-specific data) while restricting unnecessary deviations from prior knowledge (achieving practical identifiability). We also analyze how regularization affects the plausibility and the relevance of the physiological model under varying levels of scarcity in individual-specific data in terms of its parameter values and internal state predictions.
This paper is organized as follows: section “Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation” outlines the physiological model and the experimental data used in the case study. Section “Materials and Methods” describes a step-by-step procedure for applying regularization to individualize the physiological model. Section “Results” presents the results, which are discussed in section “Discussion”. Section “Conclusions” concludes the paper with suggested future work.
Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation
Credible physiological models of BV kinetics and cardiovascular hemodynamics have the potential to facilitate the development and the testing of circulatory resuscitation devices and algorithms (Parvinian et al., 2018). Prior work has reported a wide spectrum of physiological models (in terms of scale and detail) to represent volume kinetics (Hahn, 2010; Bighamian et al., 2016) and cardiovascular hemodynamics (Moss et al., 2012; Bighamian et al., 2018) in response to stimuli. In some cases, these physiological models were also analyzed for practical identifiability (Moss et al., 2012; Marquis et al., 2018; Pathmanathan et al., 2019; Pironet et al., 2019). In this work, we employ an extended and enhanced version of a physiological model reported in our prior work (Bighamian et al., 2018), which concerns the effect of hemorrhage and circulatory resuscitation on the changes in BV kinetics and cardiovascular hemodynamics.
Model Description
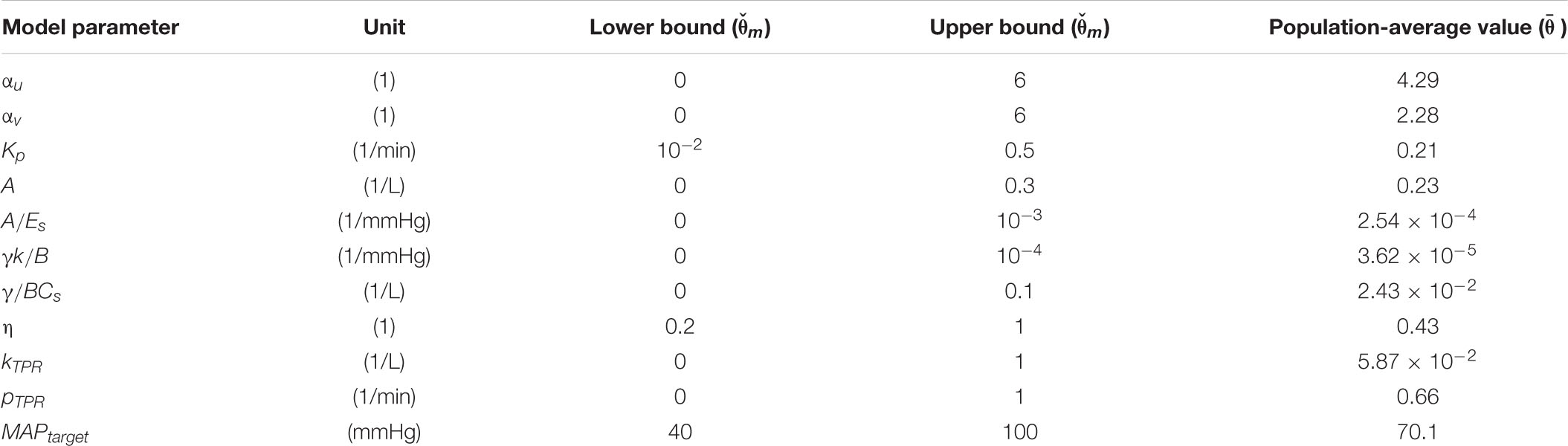
The physiological model is composed of component mathematical models that represent BV kinetics, cardiovascular function, and BP regulation, all at the systems level (Figure 1).
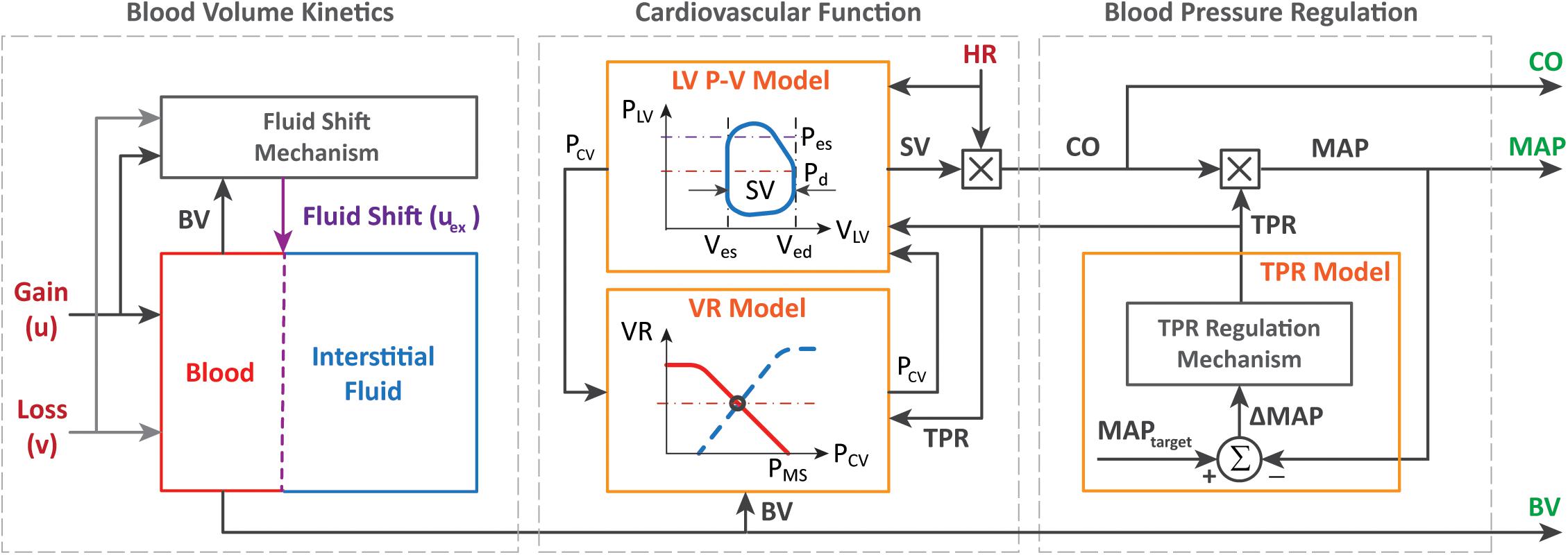
Figure 1. Physiological model of blood volume kinetics and cardiovascular hemodynamics in response to hemorrhage and circulatory resuscitation.
The BV kinetics model is a lumped-parameter model that simulates the effect of fluid gain, blood loss, and inter-compartmental fluid exchange on changes in BV. In this model, the time rate of change in BV (ΔVB) can be described by the following differential equation:
where u, v, and uex, respectively, denote the rate of external fluid gain (e.g., fluid resuscitation), external fluid loss (e.g., hemorrhage and urinary output), and internal fluid exchange between BV and interstitial tissue compartments. The rate of fluid exchange is macroscopically modeled as a control input signal that regulates BV to a target value rBV as follows:
where Kp is the controller gain and rBV represents the target change in BV, which is computed according to the history of external fluid gain and loss as follows:
where the ratio determines the fraction of the total external fluid gain that eventually remains within the BV compartment (with the rest shifted to the interstitial tissue compartment), and the ratio determines the fraction of the total fluid loss that is not compensated for by a refill from the interstitial tissue compartment. In our prior work, we demonstrated that the macroscopic expressions above can reproduce BV kinetic responses to volume perturbations with crystalloid, colloid, and blood (Bighamian et al., 2016, 2018).
The cardiovascular function model is built to compute CO from BV based on the CO–venous return equilibrium principle (Guyton et al., 1975) and the left ventricular (LV) pressure–volume relationship (Lankhaar et al., 2009). The details of such a derivation can be found in our previous work (Bighamian et al., 2018), which yields the following model relating BV to CO:
where HR(t) is the heart rate, TPR(t) is the TPR associated with the arterial circulation, Cs is the systemic capacitance, Es is the left ventricular elastance, A and B define the shape of the LV pressure–volume loop, γ represents the approximate proportionality constant between central venous (PCV) and LV end diastolic (PLVED) pressures (γ≈PLVED/PCV), k denotes the ratio between the resistance to venous return and TPR (k = RVR/TPR), VB0 is the initial BV, and η represents a proportional relationship between VB0 and the unstressed BV VBU: VBU = ηVB0.
The BP regulation component of the model approximates the regulatory mechanism in the body that monitors the discrepancy between a pre-specified, intrinsic mean arterial BP (MAP) set point (MAPtarget) versus the subject’s actual MAP (MAP(t)) and adjusts TPR (and accordingly, the resistance to venous return) to maintain MAP near the set point level. This component is modeled with the following equations:
where TPR0 is the initial value of TPR, which can be found from the initial value of CO and MAP (TPR0 = MAP0/CO0), kTPR is the gain of MAP regulation, and pTPR represents the speed of MAP regulation. Due to the relatively short time period (180 min) associated with the dataset as well as the presumably maximal level of short-term BP regulation responses due to large initial hemorrhage, the full mechanistic details of BP regulation mechanisms (e.g., the long-term aspects associated with the responses of the renin–angiotensin–aldosterone and anti-diuretic hormone systems) are not considered, and the collective short-term effects of BP regulation mechanisms are macroscopically expressed by Eq. 5.
Experimental Dataset
The experimental measurements acquired from animals in an array of prior work (Rafie et al., 2004; Vaid et al., 2006; Marques et al., 2017) were used as data in this case study. A total of N = 23 sheep constituted the population considered in this study. The data included the time series sequences of BV, CO, and MAP acquired from these sheep subjects. In each sheep, initial BV was measured using a dye concentration method. Then, subsequent changes in BV were measured with hemoglobin dilution after correction for the loss of red blood cells. CO was measured with a flow probe placed on the pulmonary artery. MAP was measured with arterial catheterization. These signals were measured at 5-min intervals during a measurement period of 180 min. Each sheep was subjected to a large initial hemorrhage (25 ml/kg; see “H” at 0–15 min in Figure 4) followed by resuscitation (see “I” at 30–180 min in Figure 4) and subsequent minor hemorrhages (5 ml/kg; see “H” at 50–55 and 70–75 min in Figure 4). Fluid resuscitation was performed by previously developed closed-loop control algorithms (Rafie et al., 2004; Vaid et al., 2006; Marques et al., 2017) designed to maintain MAP. Hemorrhage and fluid resuscitation yielded diverse BV, CO, and MAP responses in the datasets, which is appropriate to analyze the role of regularization in individualizing the physiological model (Table 1).

Table 1. Range of blood volume (BV), cardiac output (CO), and mean arterial BP (MAP) responses at important time instants during the experimental protocol [mean (SD), N = 23].
Materials and Methods
In this section, we present a procedure for applying regularization to the physiological model outlined in section “Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation”. Special emphasis is given to the construction of prior knowledge, which involves the choice of a regularization function employed in individualizing the physiological model. Then, data analysis details are presented.
Individualizing the Physiological Model
Given the data associated with an individual subject i, the inputs given to the subject (i.e., hemorrhage and fluid resuscitation) are denoted by , while the outputs of the subject are denoted by a vector . For instance, in case BV, CO, and MAP data are available in the individual i, then is defined as:
where is a row vector containing the measurements of X at times (t1,…,tnX). The nominal noise covariance matrix associated with is .
To obtain model predictions corresponding to the elements of the data vector , the model equations in section “Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation” are numerically solved given the inputs and the vector of lumped model parameters θ, which is defined as follows (see Appendix Table A1 for details and ranges):
The problem of individualizing the physiological model can be formulated as solving the following maximum a posterioi estimation problem (Gelman et al., 2013):
where is the vector of model parameters associated with the individual i, corresponds to the likelihood of the individual-specific data with respect to the model output, and J2(θ) = −logP(θ) is a regularization term that corresponds to prior knowledge P(θ) about the parameter values. Assuming that is a Gaussian distribution due to noise on the output measurements, we can set J1(θ) as the covariance-weighted mean-squared output errors:
In case there is no informative prior knowledge about the probability distribution of the model parameters, J2(θ) in Eq. 8 does not depend on θ and is effectively removed. However, in that case, the optimization problem in Eq. 8 is likely to become ill-posed and suffer from practical identifiability challenges when the physiological model is too complex relative to the available individual-specific data (which is frequently the case).
The main idea to address the practical identifiability problem in the absence of sufficient individual-specific data is to construct an appropriate prior distribution P(θ) to additionally inform the modeling problem. This prior distribution can be constructed based on the prior knowledge about plausible parameter ranges as well as heterogeneous data from a population of individuals. In this work, we formulate a prior in the shape of a Laplace distribution of the following form:
where θm is the m-th element in θ, is the m-th element of the mode of the distribution , λ is the regularization weight, and bm is a normalization factor for θm, which reflects prior knowledge about reasonable and/or physiological ranges for the model parameter [i.e., given physiological upper and lower bounds on θm, we set ; see Appendix Table A1 for and associated with the physiological model in section “Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation”]. Equation 10 is a form of L1-regularization (Bach et al., 2011; Jenatton et al., 2011), which represents the inter-individual variability observed in the population data by compressed parametric deviations from a mode denoted by . This representation may be possible if the studied physiological modeling problem has the sloppiness property (Machta et al., 2013; Transtrum et al., 2015), i.e., a wide range of parameter sensitivities, implying compressibility (see section “Role of Regularization in Individualizing Physiological Models” for more details as far as our case study is concerned).
Having Eq. 10, the problem of constructing the prior reduces to determining the parameters λ and from heterogeneous population data. Techniques exist in the field of non-linear mixed-effects modeling (Davidian and Giltinan, 2003) and system identification (Pan et al., 2018) that can deal with such problems, often with comparable results (Kataria et al., 1994; Hahn et al., 2011). In this work, we define as the solution to the following maximum-likelihood optimization problem based on the population data from L = N−1 individuals:
Note that the population-based modeling problem in Eq. 11 is supposedly less susceptible to practical identifiability challenges than the individualization problem in Eq. 8 by virtue of the larger amount of heterogeneous data available from the population. The resulting model with will hereafter be called the population-average model, which is intended to represent an aggregated and sensible model of typical physiological behavior.
The regularization weight λ serves as the relative scaling factor between the spread of the prior in Eq. 10 and the spread of the likelihood in Eq. 9. To find an appropriate individual-specific weight , we adopt an approach related to the L-curve method (Hansen, 1992; Hansen and O’Leary, 1993). The weight may be estimated by solving the optimization problem in Eq. 8 for a range of λ ∈ [0λmax] and plotting the resulting values for the goodness of fit cost J1(θ) and the deviation distance D(θ) = J2(θ)/λ (Figure 2). An initial increase of λ from zero tends to decrease D by compressing parametric deviations from in low-sensitivity directions. This increases J1, but the extent is not large relative to the decrease in D since the effect of restricting low-sensitivity (i.e., sloppy) deviations on J1 is, by definition, small. This trend continues until λ reaches a critical value. However, beyond this critical value, sensitive deviations also become restricted, leading to a substantial increase in J1 relative to the decrease in D. The appropriate can be chosen as the value of λ in between these regime changes (Figure 2).
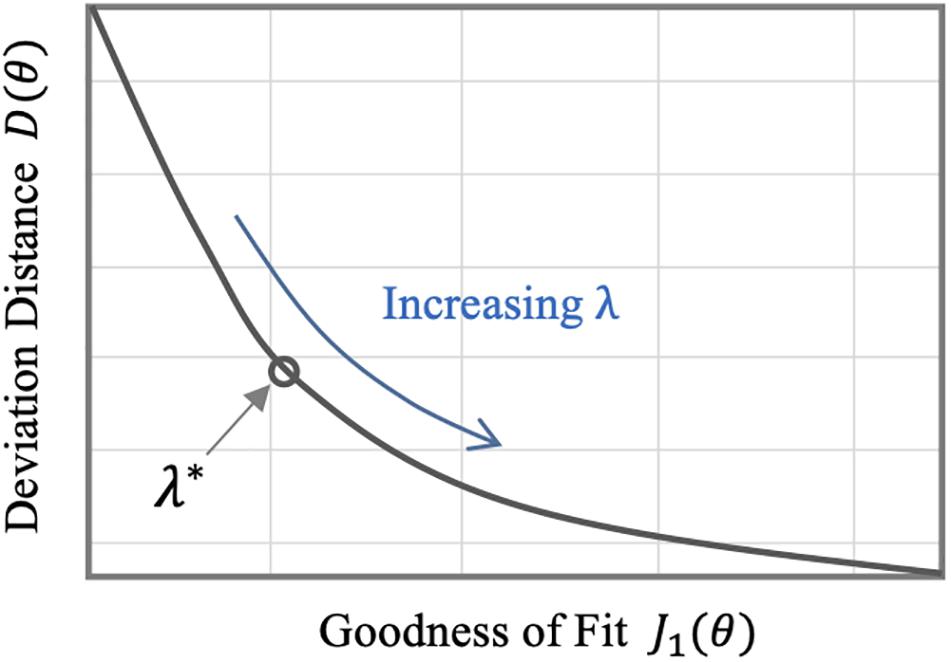
Figure 2. Typical trend of the goodness of fit metric J1 and the deviation distance D with respect to λ in individualizing physiological models.
In sum, individualizing a physiological model via regularization can be performed in two steps: (i) constructing a prior (regularization function) from heterogeneous data measured in a population by solving Eq. 11 and (ii) individualizing the physiological model with regularization using scarce individual-specific data by solving Eq. 8 (Figure 3).
Figure 3. Individualizing physiological models with scarce data via regularization. In the first step, a prior (regularization) is constructed from heterogeneous data measured in a population by solving Eq. 11. In the second step, the physiological model is individualized with regularization using scarce data by solving Eq. 8.
Data Analysis
We applied the individualization procedure outlined in section “Individualizing the Physiological Model” to the physiological model outlined in section “Cardiovascular Hemodynamics in Hemorrhage and Circulatory Resuscitation”. In particular, we constructed an appropriate regularization function and individualized the physiological model under varying levels of scarcity in the individual-specific data. To enable the data analysis with relatively small sample size, we performed a leave-one-out type of data analysis (details follow).
We individualized the physiological model under three levels of increasing data scarcity: (i) case 1, in which the physiological model was individualized given BV, CO, and MAP data, (ii) case 2, in which the physiological model was individualized given CO and MAP data, and (iii) case 3, in which the model was individualized given only MAP data. We considered these data scarcity scenarios for two investigational reasons: (i) comparison of the physiological models individualized with and without the use of regularization in the three cases may offer insight into how regularization affects the parameter values in response to varying data scarcity and (ii) analysis of the prediction errors for unmeasured internal states (i.e., BV in case 2 and BV and CO in case 3) with and without the use of regularization may offer insight into how regularization affects the physiological plausibility and the relevance of the physiological model under data scarcity.
For each animal subject, we analyzed the data pertaining to the rest of the L = 22 animal subjects with the maximum-likelihood method in Eq. 11 to derive a population-average physiological model, characterized by , that predicts BV, CO, and MAP responses to hemorrhage and fluid resuscitation inputs. Then, we individualized the physiological model to the (excluded) animal via regularization by solving Eq. 8 with Eq. 10 as the regularization function. We selected the appropriate value of λ for each individual subject as described in section “Individualizing the Physiological Model” (Figure 2). We repeated individualizing the physiological model in this way for the three dataset scarcity cases. For comparative analysis, we also individualized the physiological model to each animal without using regularization for all the three data scarcity scenarios.
With the goal of assessing the plausibility and the relevance of the physiological models, we compared the models individualized with and without regularization as well as the population-average model. We devised two quantitative error metrics for this purpose: (i) output prediction error e1, defined as the normalized root-mean-square error (RMSE) between model-predicted and measured output signals (among BV, CO, and MAP) explicitly used for individualizing the physiological model and (ii) state prediction error e2, defined as the normalized RMSE between model-predicted and measured internal state signals not used in individualizing the physiological model. For example, in case 3, e1 is the normalized RMSE associated with MAP:
while e2 is the normalized RMSE associated with BV and CO:
We employed the Wilcoxon signed-rank test in conjunction with the Bonferroni correction to assess the statistical significance of the difference in these metrics between the models.
A numerical simulation of the physiological model was performed using MATLAB®’s ODE solvers in the Simulink® environment. The numerical optimization was performed using MATLAB®’s Optimization Toolbox. Data analysis and visualization was performed using the seaborn and the matplotlib libraries in Python.
Results
Table 2 shows the output (e1) and the internal state (e2) prediction errors associated with the population-average model and the individualized models (both with and without the use of regularization), while Figure 4 presents the measured versus the model-predicted output and internal state signals associated with the population-average and the individualized physiological models. Figure 5 presents the representative behaviors of the output prediction error (e1), the internal state prediction error (e2), and the parametric deviation distance (D) with respect to the regularization weight λ in an individual subject. Figure 6 presents the regularized parametric deviations from the population-average model with respect to varying degrees of data scarcity.
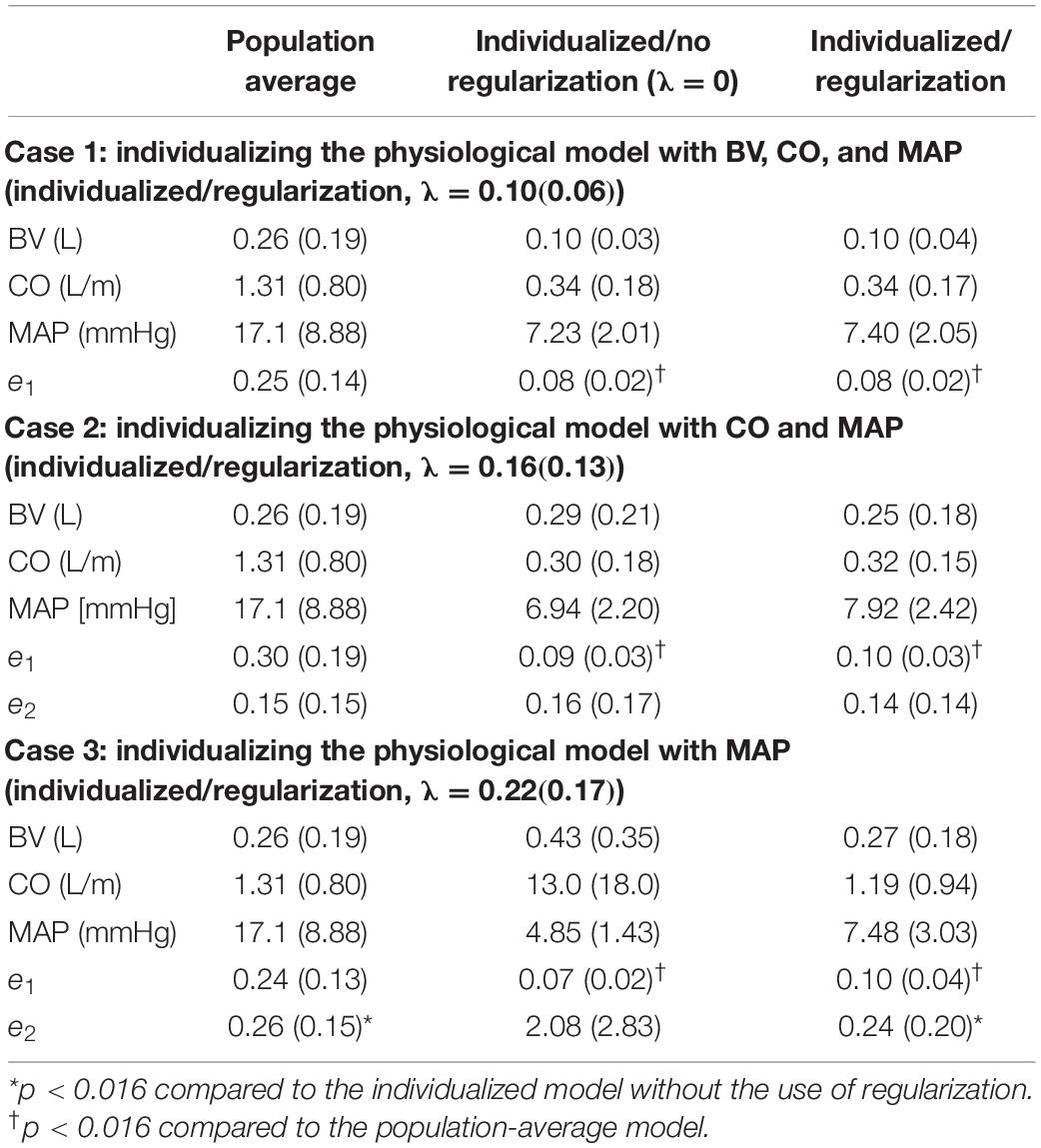
Table 2. Output and state prediction errors associated with population-average model as well as individualized models with and without the use of regularization [mean (SD), N = 23].
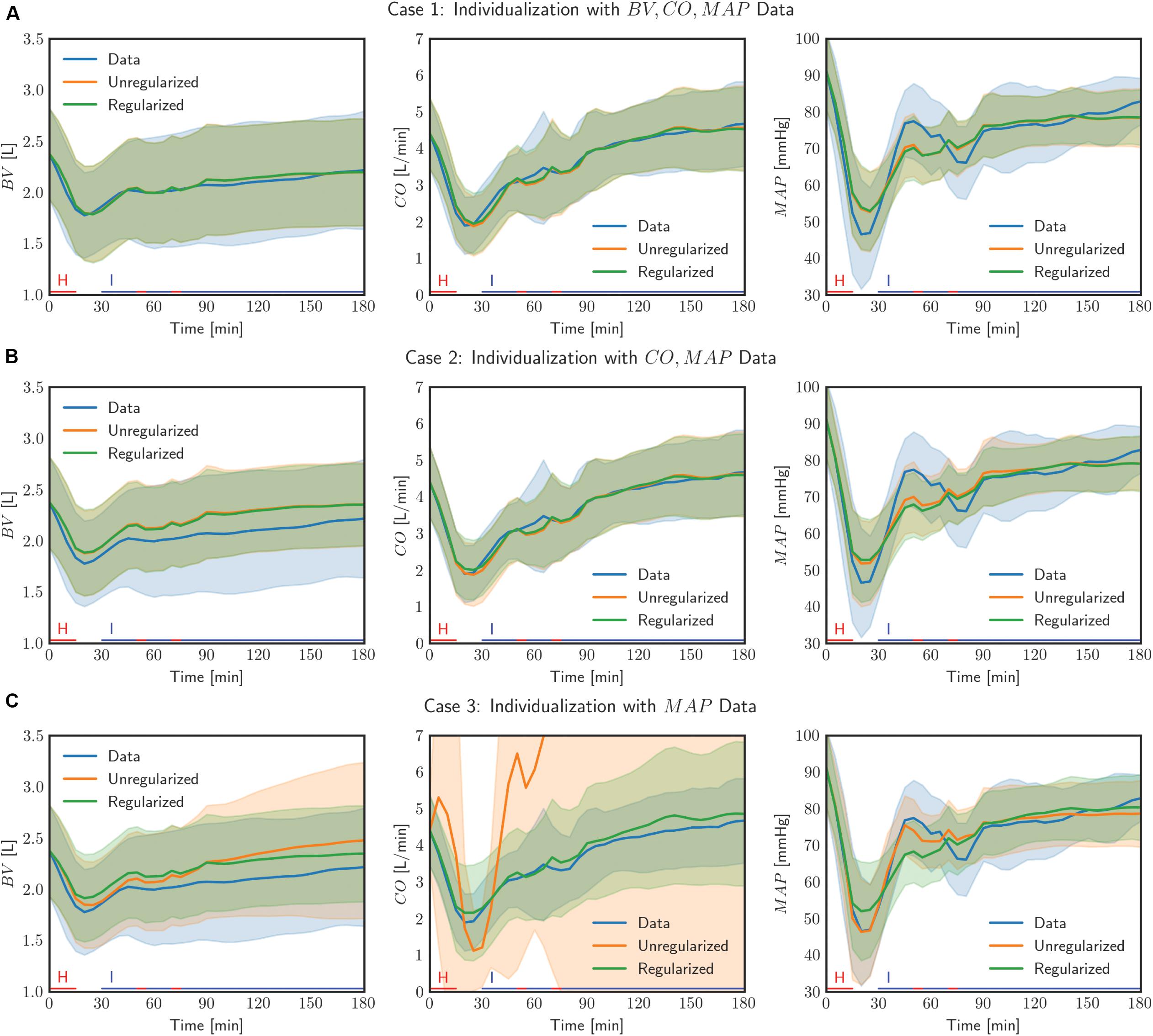
Figure 4. Comparison of measured data with model outputs in all (N = 23) individualized models, with and without the use of regularization, in three cases of data scarcity. Solid lines correspond to the mean response across all individuals and the shaded bands show the standard deviation of the response across all individuals. The lines on the horizontal axis indicate the timings of hemorrhage and infusion in the experimental protocol.
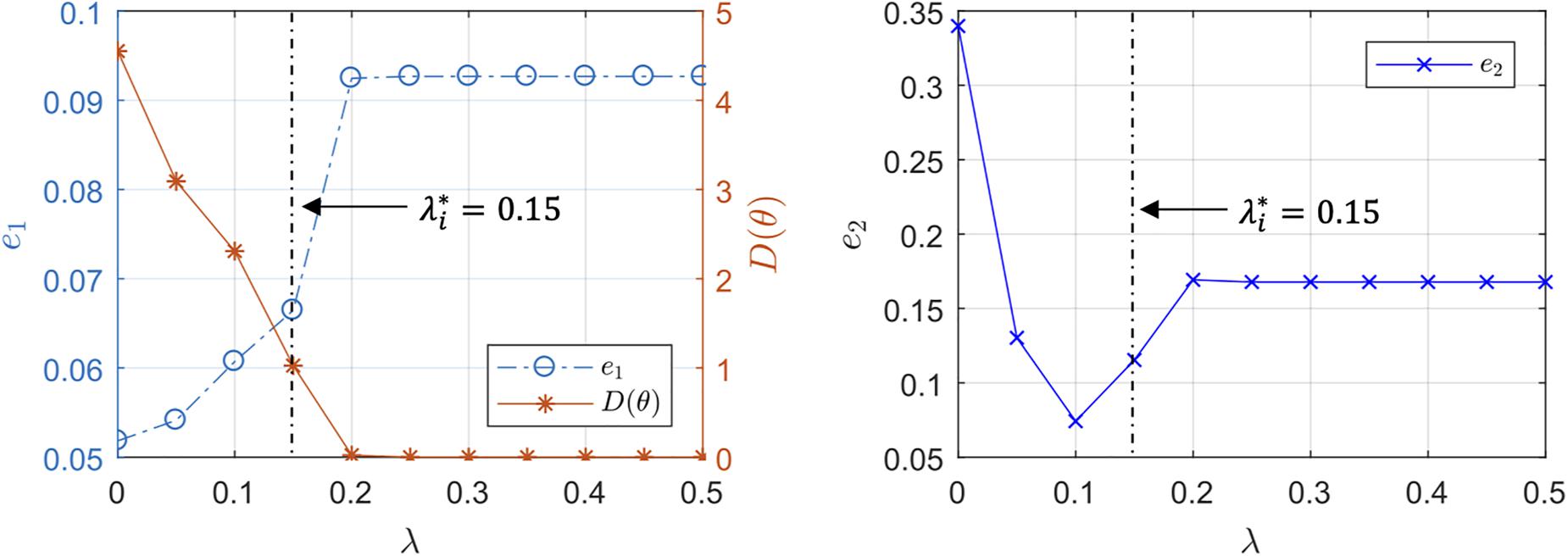
Figure 5. Representative trends of the output prediction error e1, the internal state prediction error e2, and the parametric deviation distance in a subject with respect to the regularization weight λ.
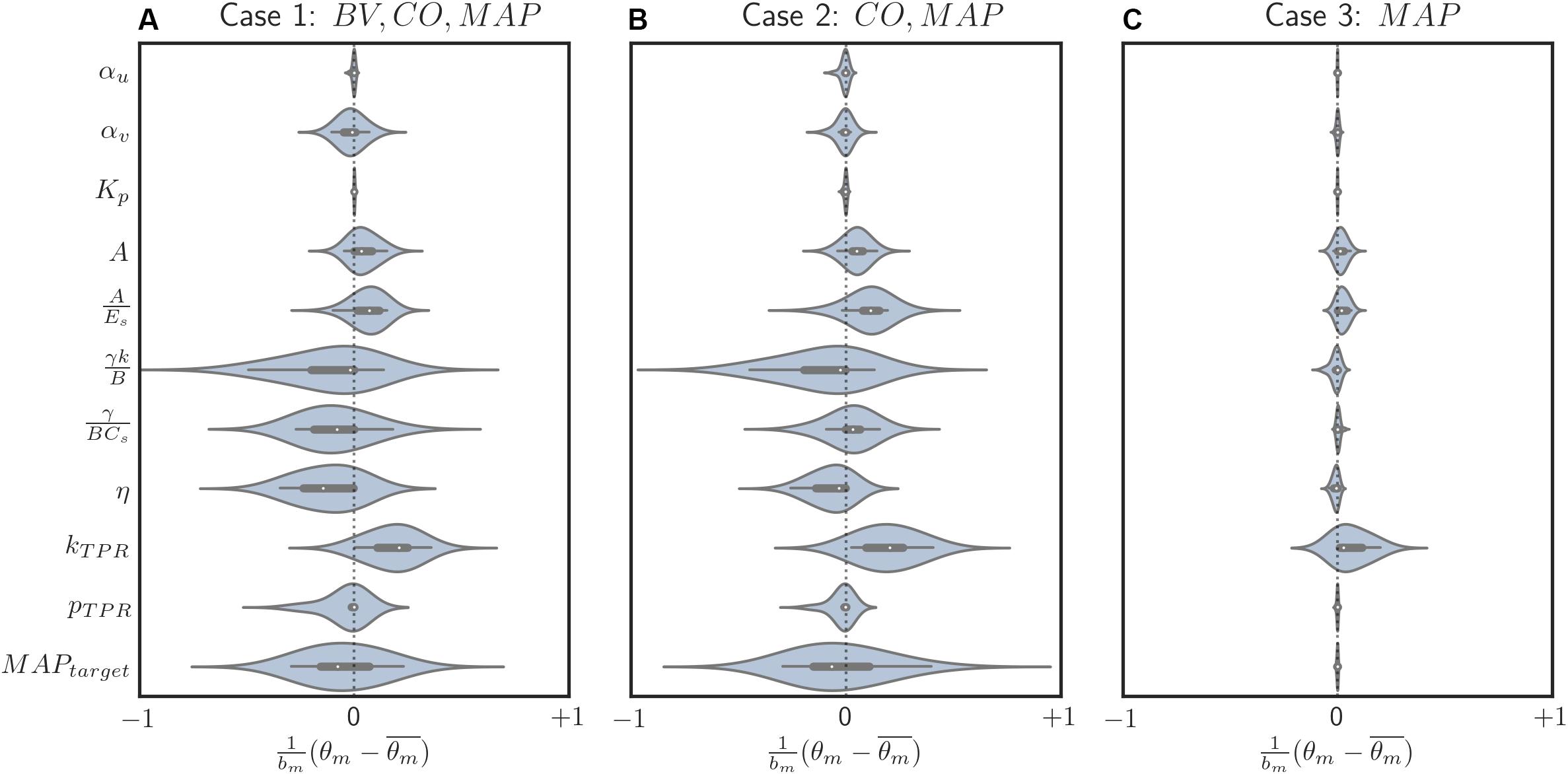
Figure 6. Box and violin (density estimate) plots of regularized parametric deviations from the population-average values across all individualized models, with respect to varying levels of data scarcity. (A) Case 1 (individualization with BV, CO, and MAP data). (B) Case 2 (individualization with CO and MAP data). (C) Case 3 (individualization with MAP data). Horizontal axis: normalized parametric deviations from the population-average values, where model parameters were normalized according to their nominal range (bm’s in Eq. 10; see Appendix Table A1). Vertical axis: model parameters.
Discussion
With the long-term goal of advancing the future development and the testing of clinical care automation based on physiological models, we sought to investigate the role of regularization in individualizing a physiological model using scarce data. Our findings from the case study of blood volume kinetics and cardiovascular hemodynamics in hemorrhage and circulatory resuscitation suggest that regularization can be effective in individualizing the physiological model to capture salient individual-specific characteristics and restrict unnecessary deviations from the population-average model. Furthermore, regularization results in appropriately varying parametric deviations to cope with the varying levels of data scarcity, thereby securing the physiological plausibility and the relevance of the individualized physiological model (details follow).
Role of Regularization in Individualizing Physiological Models
First, the use of regularization effectively maintained the goodness of fit to individual-specific data while reducing parametric deviations in insensitive directions. In all scenarios associated with the three levels of data scarcity (see section “Data Analysis”), the difference in e1 was small between the physiological models individualized with and without the use of regularization (Table 2 and Figure 4). In contrast, the parametric deviations [in terms of the distance D(θ) = J2(θ)/λ averaged across all the animals] were smaller when regularization was employed (1.19 in case 1, 1.14 in case 2, and 0.30 in case 3) than when it was not (1.87 in case 1, 1.89 in case 2, and 2.82 in case 3). This suggests that regularization assists in individualizing a physiological model to achieve an adequate level of goodness of fit while restricting parametric deviations that may only result in overfitting.
Second, the physiological model individualized with the use of regularization exhibited improved physiological plausibility and relevance in comparison with the one individualized without the use of regularization in terms of the accuracy in predicting internal state signals. In general, the goodness of fit associated with BV and CO responses was deteriorated when the corresponding measurement was removed in individualizing the physiological model. Figure 4 shows that indeed (i) BV prediction is deteriorated when BV data become unavailable (case 1 → case 2 and case 3) and (ii) CO prediction is likewise deteriorated when CO data become unavailable (case 2 → case 3). In case 2, e2 (i.e., BV prediction error) was smaller when regularization was employed than when it was not employed (p = 0.03) (Table 2). In case 3, e2 (i.e., BV and CO prediction errors) was likewise smaller when regularization was employed than when it was not employed (p < 0.01) (Table 2). Interestingly, MAP prediction was notably improved as data became more scarce when regularization was not employed [case 1 (7.23 mmHg) to case 2 (6.94 mmHg) to case 3 (4.85 mmHg), all in terms of mean errors; see Table 2]. Thus, the large deterioration in e2 may be attributed to overfitting to MAP data. In conjunction with the finding above on the role of regularization in restricting unnecessary parametric deviations, this suggests that regularization improves the ability of the individualized physiological model to predict the internal states accurately by preventing the undesired over-tuning of model parameters away from their population-average values. One additional minor note is that BV prediction achieved with regularization was comparable between case 2 and case 3. This can be interpreted as follows: (i) both case 2 and case 3 did not use BV data in individualizing the physiological model, and regularization tended to reduce the BV component in the physiological model to the population-average model (as can be seen by the comparable BV prediction errors associated with these models; see Table 2) and (ii) presumably CO data did not provide much implications on the behavior of BV on top of the prior knowledge [as can be seen by the BV prediction errors in case 2 with and without the use of regularization (0.25 L and 0.29 L, both in terms of mean errors; see Table 2].
Third, the individualized physiological model exhibited goodness of fit parametric deviation behavior with respect to the regularization weight λ as anticipated in Figure 2, especially in the case of very scarce data (case 3; see Figure 5). A sharp initial decrease in D(θ) = J2(θ)/λ relative to a modest increase in e1 was observed when λ was initially increased from zero. Further increase in λ after a critical point caused e1 to largely increase relative to a steady decrease in the parametric deviation distance and eventually approach that of the population-average model. In sum, an appropriate could be selected as outlined in section “Individualizing the Physiological Model” (λ∗ = 0.15). Interestingly, there appeared to be a notable link between the behaviors of D(θ) and e2: e2 initially showed a notably decreasing trend similar to that of D(θ), which suggests that regularization improves the ability of the individualized model to predict internal states (Figure 5). For larger values of λ, e2 increased, which can be attributed to the restriction of sensitive parametric deviations, degenerating the individualized model to the population-average model.
Fourth, the physiological model individualized with the use of regularization was associated with a significantly superior output prediction error and a comparable internal state prediction error in comparison with the population-average model (Table 2). This suggests that regularization is effective in judiciously individualizing sensitive model parameters to achieve desirable goodness of fit to individual-specific data while at the same time capitalizing on prior knowledge (in the form of regularization) to preserve the ability to adequately predict unmeasured internal states.
Parametric Deviations in Relation to Varying Data Scarcity
In our case study, regularization-induced deviations from the population-average model showed two noteworthy trends. First, with regularization, deviations tended to decrease as the data became more scarce (Figure 6). In other words, (i) regularization allowed meaningful deviations if ample data were available so that the physiological model could be better individualized by absorbing the individual-specific characteristics represented by the data, whereas (ii) it restricted unwarranted deviations if scarce data were available so that the physiological model could fall back to the population-average model. This can be viewed as a desirable behavior in that increasingly leveraging the prior knowledge (i.e., the population-average model) as the data scarcity increases is the intended effect of regularization. In contrast, such a parametric deviation trend was not observed when regularization was not used. The opposite occurred instead: scarce data resulted in more aggressive deviations from the population-average model (see the deviation distance results reported in section “Role of Regularization in Individualizing Physiological Models”), which consequently compromised the fidelity of the individualized physiological models (e.g., its internal state prediction was deteriorated; see Table 2). Second, regularization appeared to effectively individualize those parameters relevant to the presented data. For example, the most visibly deviated parameter in case 3 was the one associated with BP regulation (kTPR), which is reasonable in that only MAP measurements were presented to individualize the physiological model in case 3 (Figure 6C). The parameters associated with both CV function (γ/BCs and η) and BP regulation (kTPR and MAPtarget) were likewise visibly deviated in case 2, in which CO and MAP measurements were presented (Figure 6B). Finally, the parameters associated with BV were likewise largely deviated (αv, in particular) when BV measurements were presented in addition to CO and MAP data (Figure 6A). One caveat is that, despite the presence of these trends, the studied parameters belong to a complex physiological system and it may not be possible to attribute each parametric deviation completely to the availability of a specific type of measurement.
Study Limitations
This work has limitations. First, this work investigated the role of regularization in a specific case study. Hence, the insights obtained from the case study may not be universally true in all physiological modeling problems. In particular, the legitimacy of the key assumption used to address the adverse effect of scarce data on the quality of individualized models (that the inter-individual variability observed in the population data can be represented by compressed deviations from a population-average model according to the Laplace distribution in Eq. 10) may depend on the specificity of the physiological modeling problem at hand. On the one hand, such a compressed representation may indeed be valid in many real-world physiological modeling problems with the sloppiness property (Machta et al., 2013; Transtrum et al., 2015) (which implies parameter-space compressibility). On the other hand, regularization may not prove effective if the quality of the data and the model structure are such that the majority of the model parameters are associated with sensitive deviations (where individualizing the physiological model requires deviations in all the model parameters; in this case, regularization is not needed) or insensitive deviations (where a population-average model may suffice because of negligible inter-individual variability). In any case, the validity of the “parameter-space compressibility” assumption in a specific physiological modeling application can be assessed based on model prediction errors and parameter values in the individualized physiological models: the bias introduced by the inadequacy of the assumption will manifest itself as poor goodness of fit of the individualized physiological model to the data, while a lack of compressibility will manifest itself as estimated elements of in Eq. 8 that all deviate from in Eq. 11. Second, regularization does not guarantee, and may even prevent, the convergence of the physiological model to the “true” individual-specific physiological model. Indeed its main purpose is to minimize the deviations from the prior knowledge (i.e., population-average model). Thus, the quality of a physiological model individualized with regularization, especially using highly scarce data, hinges upon the quality of prior knowledge. Hence, the physiological model individualized with regularization is a candidate approximation to the ideal individual-specific physiological model (which would be obtained with sufficiently diverse and high-quality data obtained from an individual). Taking these aspects into account, regularization may be viewed as an effective tool to individualize a physiological model in cases with a relatively complex model and scarce individual-specific data.
Conclusion
We sought to garner potentially generalizable insight into the role of regularization as prior knowledge in individualizing physiological models using scarce data. The findings obtained from a clinically significant case study illustrated that regularized individualization creates physiological models equipped with several desirable properties: (i) an adequate trade-off between goodness of fit to scarce individual-specific data and deviation from a population-average model, (ii) improved physiological plausibility and relevance, and (iii) parametric deviations relevant to the scarcity level of the data. Noting that regularization is not prevalently used in the physiological modeling domain, future work must be devoted to exploring the use of regularization in individualizing a range of physiological models and developing appropriate theory and novel structures for the regularization functions based on appropriate physiological assumptions.
Data Availability Statement
The datasets analyzed in this study can be obtained from Dr. George C. Kramer at the University of Texas Medical Branch (Z2tyYW1lckB1dG1iLmVkdQ==).
Author Contributions
AT, CS, and J-OH formulated the procedure to individualize the physiological model via regularization and wrote and revised the manuscript. XJ, AL, CS, and J-OH developed the physiological model. AT and J-OH analyzed the data. XJ and AL reviewed the manuscript.
Funding
This work was supported by the United States National Science Foundation (NSF) CAREER Award (Grant No. CNS-1748762) and the United States Office of Naval Research (ONR) (Grant No. N00014-19-1-2402).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We thank Dr. George C. Kramer at the University of Texas Medical Branch for provision of the experimental dataset for analysis as well as his physiological consultation and guidance in data analysis.
References
Bach, F., Jenatton, R., Mairal, J., and Obozinski, G. (2011). Optimization with sparsity-inducing penalties. Found. Trends§Mach. Learn. 4, 1–106. doi: 10.1561/2200000015
Benning, M., and Burger, M. (2018). Modern regularization methods for inverse problems. Acta Numer. 27, 1–111. doi: 10.1017/S0962492918000016
Bighamian, R., Parvinian, B., Scully, C. G., Kramer, G., and Hahn, J.-O. (2018). Control-oriented physiological modeling of hemodynamic responses to blood volume perturbation. Control Eng. Pract. 73, 149–160. doi: 10.1016/j.conengprac.2018.01.008
Bighamian, R., Reisner, A. T., and Hahn, J. (2016). A lumped-parameter subject-specific model of blood volume response to fluid infusion. Front. Physiol. 7:390. doi: 10.3389/fphys.2016.00390
Bighamian, R., Reisner, A. T., and Hahn, J. O. (2014). An analytic tool for prediction of hemodynamic responses to vasopressors. IEEE Trans. Biomed. Eng. 61, 109–118. doi: 10.1109/TBME.2013.2277867
Brogi, E., Cyr, S., Kazan, R., Giunta, F., and Hemmerling, T. M. (2017). Clinical performance and safety of closed-loop systems. Anesth. Analg. 124, 446–455. doi: 10.1213/ANE.0000000000001372
Brown, D., Namas, R. A., Almahmoud, K., Zaaqoq, A., Sarkar, J., Barclay, D. A., et al. (2015). Trauma in silico: individual-specific mathematical models and virtual clinical populations. Sci. Transl. Med. 7:285ra61. doi: 10.1126/scitranslmed.aaa3636
Davidian, M., and Giltinan, D. M. (2003). Nonlinear models for repeated measurement data: an overview and update. J. Agric. Biol. Environ. Stat. 8, 387–419. doi: 10.1198/1085711032697
Dussaussoy, C., Peres, M., Jaoul, V., Liu, N., Chazot, T., Picquet, J., et al. (2014). Automated titration of propofol and remifentanil decreases the anesthesiologist’s workload during vascular or thoracic surgery: a randomized prospective study. J. Clin. Monit. Comput. 28, 35–40. doi: 10.1007/s10877-013-9453-6
Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (2013). Bayesian Data Analysis. Boca Raton, FL: CRC press.
Guyton, A. C., Taylor, A. E., and Granger, H. J. (1975). Dynamics and Control of Body Fluid. Philadelphia: W.B. Saunders Company.
Hahn, J. O., Khosravi, S., Dumont, G. A., and Ansermino, J. M. (2011). Two-stage vs mixed-effect approach to pharmacodynamic modeling of propofol in children using state entropy. Paediatr. Anaesth. 21, 691–698. doi: 10.1111/j.1460-9592.2011.03584.x
Hahn, R. G. (2010). Volume kinetics for infusion fluids. Anesthesiology 113, 470–481. doi: 10.1097/ALN.0b013e3181dcd88f
Hansen, P. C. (1992). Analysis of discrete Ill-posed problems by means of the L-curve. SIAM Rev. 34, 561–580. doi: 10.1137/1034115
Hansen, P. C., and O’Leary, D. P. (1993). The use of the L-curve in the regularization of discrete Ill-posed problems. SIAM J. Sci. Comput. 14, 1487–1503. doi: 10.1137/0914086
Hemmerling, T. M., Charabati, S., Zaouter, C., Minardi, C., and Mathieu, P. A. (2010). A randomized controlled trial demonstrates that a novel closed-loop propofol system performs better hypnosis control than manual administration. Can. J. Anesth. Can. d’anesthésie 57, 725–735. doi: 10.1007/s12630-010-9335-z
Hundeshagen, G., Kramer, G. C., Ribeiro Marques, N., Salter, M. G., Koutrouvelis, A. K., Li, H., et al. (2017). Closed-loop– and decision-assist–guided fluid therapy of human hemorrhage. Crit. Care Med. 45, e1068–e1074. doi: 10.1097/CCM.0000000000002593
Jenatton, R., Audibert, J.-Y., and Bach, F. (2011). Structured variable selection with sparsity-inducing norms. J. Mach. Learn. Res. 12, 2777–2824.
Jin, X., Bighamian, R., and Hahn, J.-O. (2018). Development and in silico evaluation of a model-based closed-loop fluid resuscitation control algorithm. IEEE Trans. Biomed. Eng. [Epub ahead of print]. doi: 10.1109/TBME.2018.2880927
Jin-Oh, H., Dumont, G. A., and Ansermino, J. M. (2012). System identification and closed-loop control of end-tidal CO2 in mechanically ventilated patients. Inf. Technol. Biomed. IEEE Trans. 16, 1176–1184. doi: 10.1109/titb.2012.2204067
Kataria, B. K., Ved, S. A., Nicodemus, H. F., Hoy, G. R., Lea, D., Dubois, M. Y., et al. (1994). The pharmacokinetics of propofol in children using three different data analysis approaches. Anesthesiology 80, 104–122. doi: 10.1097/00000542-199401000-00018
Kovatchev, B. P., Breton, M., Dalla Man, C., and Cobelli, C. (2009). In silico preclinical trials: a proof of concept in closed-loop control of type 1 diabetes. J. Diabetes Sci. Technol. 3, 44–55. doi: 10.1177/193229680900300106
Lankhaar, J. W., Rövekamp, F. A., Steendijk, P., Faes, T. J. C., Westerhof, B. E., Kind, T., et al. (2009). Modeling the instantaneous pressure-volume relation of the left ventricle: a comparison of six models. Ann. Biomed. Eng. 37, 1710–1726. doi: 10.1007/s10439-009-9742-x
Machta, B. B., Chachra, R., Transtrum, M. K., and Sethna, J. P. (2013). Parameter space compression underlies emergent theories and predictive models. Science 342, 604–607. doi: 10.1126/SCIENCE.1238723
Maiwald, T., Hass, H., Steiert, B., Vanlier, J., Engesser, R., Raue, A., et al. (2016). Driving the model to its limit: profile likelihood based model reduction. PLoS One 11:e0162366. doi: 10.1371/journal.pone.0162366
Maiwald, T., Timmer, J., Kreutz, C., Klingmüller, U., and Raue, A. (2011). Addressing parameter identifiability by model-based experimentation. IET Syst. Biol. 5, 120–130. doi: 10.1049/iet-syb.2010.0061
Marques, N. R., Ford, B. J., Khan, M. N., Kinsky, M., Deyo, D. J., Mileski, W. J., et al. (2017). Automated closed-loop resuscitation of multiple hemorrhages: a comparison between fuzzy logic and decision table controllers in a sheep model. Disaster Mil. Med. 3, 1–10. doi: 10.1186/s40696-016-0029-0
Marquis, A. D., Arnold, A., Dean-Bernhoft, C., Carlson, B. E., and Olufsen, M. S. (2018). Practical identifiability and uncertainty quantification of a pulsatile cardiovascular model. Math. Biosci. 304, 9–24. doi: 10.1016/j.mbs.2018.07.001
Mattingly, H. H., Transtrum, M. K., Abbott, M. C., and Machta, B. B. (2018). Maximizing the information learned from finite data selects a simple model. Proc. Natl. Acad. Sci. U.S.A. 115, 1760–1765. doi: 10.1073/PNAS.1715306115
Moss, R., Grosse, T., Marchant, I., Lassau, N., Gueyffier, F., and Thomas, S. R. (2012). Virtual patients and sensitivity analysis of the Guyton model of blood pressure regulation: towards individualized models of whole-body physiology. PLoS Comput. Biol. 8:e1002571. doi: 10.1371/journal.pcbi.1002571
Ortiz, J. L., Guarini, M. W., Borzone, G. R., and Olmos, P. R. (2010). In silico evaluation of a control system and algorithm for automated insulin infusion in the ICU setting. Biomed. Eng. Online 9, 1–19. doi: 10.1186/1475-925X-9-35
Pan, W., Yuan, Y., Ljung, L., Goncalves, J., and Stan, G. B. (2018). Identification of nonlinear state-space systems from heterogeneous datasets. IEEE Trans. Control Netw. Syst. 5, 737–747. doi: 10.1109/TCNS.2017.2758966
Parvinian, B., Scully, C., Wiyor, H., Kumar, A., and Weininger, S. (2018). Regulatory considerations for physiological closed-loop controlled medical devices used for automated critical care: food and drug administration workshop discussion topics. Anesth. Analg. 126, 1916–1925. doi: 10.1213/ANE.0000000000002329
Pasin, L., Nardelli, P., Pintaudi, M., Greco, M., Zambon, M., Cabrini, L., et al. (2017). Closed-loop delivery systems versus manually controlled administration of total IV anesthesia. Anesth. Analg. 124, 456–464. doi: 10.1213/ANE.0000000000001394
Pathmanathan, P., Cordeiro, J. M., and Gray, R. A. (2019). Comprehensive uncertainty quantification and sensitivity analysis for cardiac action potential models. Front. Physiol. 10:721. doi: 10.3389/fphys.2019.00721
Pironet, A., Docherty, P. D., Dauby, P. C., Chase, J. G., and Desaive, T. (2019). Practical identifiability analysis of a minimal cardiovascular system model. Comput. Methods Programs Biomed. 171, 53–65. doi: 10.1016/j.cmpb.2017.01.005
Rafie, A. D., Rath, P. A., Michell, M. W., Kirschner, R. A., Deyo, D. J., Prough, D. S., et al. (2004). Hypotensive resuscitation of multiple hemorrhages using crystalloid and colloids. Shock 22, 262–269. doi: 10.1097/01.shk.0000135255.59817.8c
Raue, A., Karlsson, J., Saccomani, M. P., Jirstrand, M., and Timmer, J. (2014). Comparison of approaches for parameter identifiability analysis of biological systems. Bioinformatics 30, 1440–1448. doi: 10.1093/bioinformatics/btu006
Raue, A., Kreutz, C., Maiwald, T., Bachmann, J., Schilling, M., Klingmüller, U., et al. (2009). Structural and practical identifiability analysis of partially observed dynamical models by exploiting the profile likelihood. Bioinformatics 25, 1923–1929. doi: 10.1093/bioinformatics/btp358
Rinehart, J., Lilot, M., Lee, C., Joosten, A., Huynh, T., Canales, C., et al. (2015). Closed-loop assisted versus manual goal-directed fluid therapy during high-risk abdominal surgery: a case–control study with propensity matching. Crit. Care 19:94. doi: 10.1186/s13054-015-0827-7
Salinas, J., Chung, K. K., Mann, E. A., Cancio, L. C., Kramer, G. C., Serio-Melvin, M. L., et al. (2011). Computerized decision support system improves fluid resuscitation following severe burns: an original study. Crit. Care Med. 39, 2031–2038. doi: 10.1097/CCM.0b013e31821cb790
Saltelli, A., Annoni, P., Azzini, I., Campolongo, F., Ratto, M., and Tarantola, S. (2010). Variance based sensitivity analysis of model output. Design and estimator for the total sensitivity index. Comput. Phys. Commun. 181, 259–270. doi: 10.1016/J.CPC.2009.09.018
Saltelli, A., Ratto, M., Andres, T., Campolongo, F., and Cariboni, J. (2008). Global Sensitivity Analysis: The Primer. Hoboken, NJ: John Wiley & Sons.
Sobol, I. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Math. Comput. Simul. 55, 271–280. doi: 10.1016/S0378-4754(00)00270-6
Tivay, A., Arabi, G., Dor, D., Bighamian, R., Kramer, G. C., and Hahn, J.-O. (2019). “A regularized system identification approach to subject-specific physiological modeling with limited data,” in Proceedings of 2019 American Control Conference, (Philadelphia, PA: American Automatic Control Council), 3468–3473.
Toni, T., Welch, D., Strelkowa, N., Ipsen, A., and Stumpf, M. P. H. (2009). Approximate Bayesian computation scheme for parameter inference and model selection in dynamical systems. J. R. Soc. Interface 6, 187–202. doi: 10.1098/rsif.2008.0172
Transtrum, M. K., Machta, B. B., Brown, K. S., Daniels, B. C., Myers, C. R., and Sethna, J. P. (2015). Perspective: sloppiness and emergent theories in physics, biology, and beyond. J. Chem. Phys. 143:010901. doi: 10.1063/1.4923066
Transtrum, M. K., Machta, B. B., and Sethna, J. P. (2010). Why are nonlinear fits to data so challenging? Phys. Rev. Lett. 104:060201. doi: 10.1103/PhysRevLett.104.060201
Vaid, S. U., Shah, A., Michell, M. W., Rafie, A. D., Deyo, D. J., Prough, D. S., et al. (2006). Normotensive and hypotensive closed-loop resuscitation using 3.0% NaCl to treat multiple hemorrhages in sheep. Crit. Care Med. 34, 1185–1192. doi: 10.1097/01.CCM.0000207341.78696.3A
White, A., Tolman, M., Thames, H. D., Withers, H. R., Mason, K. A., and Transtrum, M. K. (2016). The limitations of model-based experimental design and parameter estimation in sloppy systems. PLoS Comput. Biol. 12:e1005227. doi: 10.1371/journal.pcbi.1005227
Zhang, L., Jiang, Z., Choi, J., Lim, C. Y., Maiti, T., and Baek, S. (2019). Patient-specific prediction of abdominal aortic aneurysm expansion using bayesian calibration. IEEE J. Biomed. Heal. Informatics 23, 2537–2550. doi: 10.1109/JBHI.2019.2896034
Appendix
Keywords: individualization, physiological model, regularization, practical identifiability, volume kinetics, cardiovascular hemodynamics, hemorrhage, resuscitation
Citation: Tivay A, Jin X, Lo AK-Y, Scully CG and Hahn J-O (2020) Practical Use of Regularization in Individualizing a Mathematical Model of Cardiovascular Hemodynamics Using Scarce Data. Front. Physiol. 11:452. doi: 10.3389/fphys.2020.00452
Received: 03 February 2020; Accepted: 09 April 2020;
Published: 26 May 2020.
Edited by:
Joseph L. Greenstein, Johns Hopkins University, United StatesReviewed by:
Thomas Desaive, University of Liège, BelgiumJohn S. Clemmer, University of Mississippi Medical Center, United States
Copyright © 2020 Tivay, Jin, Lo, Scully and Hahn. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jin-Oh Hahn, amhhaG4xMkB1bWQuZWR1
 Ali Tivay1
Ali Tivay1 Xin Jin
Xin Jin Alex Kai-Yuan Lo
Alex Kai-Yuan Lo Christopher G. Scully
Christopher G. Scully Jin-Oh Hahn
Jin-Oh Hahn