- School of Physics and Electronic Science, East China Normal University, Shanghai, China
Understanding the human brain and its functions has always been an interesting and challenging problem. Recently, a significant progress on this problem has been achieved on the aspect of chimera state where a coexistence of synchronized and unsynchronized states can be sustained in identical oscillators. This counterintuitive phenomenon is closely related to the unihemispheric sleep in some marine mammals and birds and has recently gotten a hot attention in neural systems, except the previous studies in non-neural systems such as phase oscillators. This review will briefly summarize the main results of chimera state in neuronal systems and pay special attention to the network of cerebral cortex, aiming to accelerate the study of chimera state in brain networks. Some outlooks are also discussed.
1. Introduction
Network physiology is a new field initiated by Ivanov et al. in 2012, aiming to reveal the relationship between network topology and physiologic function (Bashan et al., 2012; Ivanov and Bartsch, 2014; Bartsch et al., 2015; Ivanov et al., 2016). Generally, a physiological network is consist of different physiologic organ systems, such as the dynamical network of six physiologic systems with nodes being brain activity (EEG waves: δ, θ, α, σ, β), cardiac (HR), respiratory (Resp), chin muscle tone, leg, and eye movements. In contrast to a static complex network, the topology (i.e., number and strength of network links) of physiological network usually vary with time, resulting in different physiologic states such as different sleep stages [deep, light, rapid eye movement (REM) sleep, and quite wake]. That is, each physiological state of physiological network corresponds to a specific network structure. The transition from one physiologic state to another is associated with fast reorganization of physiological interactions. Network physiology can be successfully applied to explain phase synchronization between organ systems (Chen et al., 2006; Xu et al., 2006; Ivanov et al., 2009; Bartsch et al., 2012; Bartsch and Ivanov, 2014). A typical system of network physiology is the brain network, which is the focus of this review.
One of the most challenging and long standing problems is the understanding of the powerful brain functions such as data processing, function approximation, and pattern recognition etc., which has been considered as a black box for a long time. To solve this problem, it is necessary to figure out the brain network first. So far, it is well known that the human cerebral cortex is a huge network, consisting of 1011 neurons and 1014 links. Thus, it is almost impossible to figure out the structure of this huge network. Fortunately, owing to the modern physical detections such as electroencephalogram (EEG), magnetic resonance imaging (MRI), magnetoencephalogram (MEG), and diffusion tensor imaging (DTI) etc., we can now conveniently obtain a coarse-grained brain network with a finite size of hundreds to thousands nodes. It has been found that the obtained brain network is of a modular structure with a complex connectivity (Hilgetag and Kaiser, 2004), which provides a base for the inherent parallel nature of brain computations (Meunier et al., 2010; Zamora-Lopez et al., 2010). The quantification of complexity in brain networks can be also measured by the multifractality and other factors (Liu et al., 2015; Lin et al., 2016; Xue and Bogdan, 2017; Racz et al., 2018; Gupta et al., 2019; Yang et al., 2019). A larger or more precise brain network can be obtained by reconstructing the connectivity under partial observability assumptions, which is common to many real world settings or experiments (Gupta et al., 2018; Xue and Bogdan, 2019).
By the physical detections, it is revealed that synchronization of neuronal ensembles in the network of cerebral cortex is the base of various neurobiological processes. For example, the alpha synchronization is task-related and is also associated to top-down processing (Benedek et al., 2011). Further, it is pointed out that synchronization and desynchronization of neural activity are closely related to both the normal functions of brain and its disorders, such as epileptic seizures and Parkinson's disease etc. (Rothkegel and Lehnertz, 2014). For instance, during an epileptic seizure, some regions of brain are strongly synchronized but the others are desynchronized (Ayala et al., 1973). While in Parkinson's disease, synchronized activity is absent in the brain regimes of damaged neurons (Levy et al., 2000).
Moreover, it was found that the synchronized and desynchronized behaviors are usually co-existed in the time series of brains. For example, the EEG data showed that during sleep of dolphin, its two brain hemispheres have independently synchronized and desynchronized behaviors at the same time (Mukhametov et al., 1977), i.e., one hemisphere is in sleep and another remains awake. This phenomenon is called as unihemispheric slow-wave sleep and has been also found in other aquatic animals and migrated birds (Rattenborg et al., 2000). On the other hand, the similar phenomenon was reported in the context of neuroscience, called bump state, where the firing rate is higher at some spatial locations but a constant at other spatial positions (Laing and Chow, 2001). This bump state takes an important role for feature selectivity in models of the visual system (Somers et al., 1995), the head direction system (Zhang, 1996), and working memory (Camperi and Wang, 1998).
To understand the mechanisms of these coexisted behaviors in brains, numerous efforts have been paid to the synchronization of coupled oscillators. One of its recent progresses is chimera state, which is closely related to the phenomenon of unihemispheric sleep. Chimera state represents the coexistence of coherent and incoherent dynamics. It is surprising that this behavior occurs in symmetrically coupled identical oscillators. This counterintuitive phenomenon was first discovered in 2002 (Kuramoto and Battogtokh, 2002) and then named in 2004 (Abrams and Strogatz, 2004). Since then, chimera state has become a hot topic and different kinds of chimera states have been revealed in different systems such as the chaotic dynamical systems (Omelchenko et al., 2012), time-delayed system Sethia et al. (2008), and systems with regular topology (Ko and Ermentrout, 2008; Yao et al., 2013; Tian et al., 2017) etc. Initially, chimera states were shown to emerge in systems of nonlocal coupling. Recently, it has been extended to the system of globally coupled oscillators (Chandrasekar et al., 2014), and even in complex networks (Zhu et al., 2014). Further, to explain the alternating activity patterns between the hemispheres over time (Mukhametov et al., 1977), Ma et al. considered the effect of time-delay in two coupled populations and found that the synchronous and desynchronous behavior do alternate between the two groups over time (Ma et al., 2010). At the same time, chimera states have also been implemented in several experiments such as on chemical oscillators (Tinsley et al., 2012), mechanical oscillators (Martens et al., 2013), electronic oscillators (Larger et al., 2013), electrochemical oscillators (Wickramasinghe and Kiss, 2013; Schmidt et al., 2014), and optoelectronic oscillators (Larger et al., 2015). See reviews Panaggio and Abrams (2015) and Majhi et al. (2019) for details.
In sum, chimera states are mainly studied on phase oscillators. As chimera state may represent the mechanism of unihemispheric sleep where the neurons in the sleepy hemisphere are synchronized and the neurons in the awake hemisphere are desynchronized, it is necessary to pay more attention on the chimera state in neural systems. Fortunately, some interesting results have already been obtained in this line, which involve most typical neural models. For examples, chimera states have been studied in leaky integrate-and-fire neurons (Olmi et al., 2010), Morris-Lecar neurons (Calim et al., 2018), FitzHugh-Nagumo neurons (Omelchenko et al., 2013, 2015), Hindmarsh-Rose neurons (Hizanidis et al., 2014, 2016), and Hodgkin-Huxley neurons (Sakaguchi, 2006; Glaze et al., 2016). To accelerate the study of chimera state in brain networks, it is necessary to systematically summarize the measures of chimera state and its recent progress in empirical brain systems, which has not been paid enough attention in the previous reviews (Panaggio and Abrams, 2015; Majhi et al., 2019). Thus, we here briefly summarize the main results of chimera state in neuronal systems and pay a special attention to the network of cerebral cortex.
2. Three Measures of Chimera State
To characterize the chimera state, three statistical measures have been proposed so far, by using the time series of network. The first measure is the order parameter by
where ρ represents the phase coherence of oscillators, Φ(t) is the average phase of all oscillators, θj(t) is the phase variable of the j-th oscillator. The system is a complete synchronization when ρ = 1 and a complete desynchronization when ρ = 0. This measure can be conveniently used to the system consisting of two groups. It is a chimera state when one group has an order parameter ρ ≈ 1 and the other ρ ≈ 0.
A key element of this measure is to calculate the phase variable θi(t). However, there is not such an explicit variable in all the neuronal models, in contrast to the Kuramoto phase oscillator. Generally, there are two ways to solve this problem. The first one can be used to a general nonlinear oscillator not necessarily having a well-defined rotational center. Let ui and vi represent two variables of the i-th neuron, respectively. The phase θi(t) can be calculated as (Osipov et al., 2003; Liu et al., 2009)
where and denote the derivatives of ui and vi, respectively. The second one is to calculate the phase θi(t) by
provided that ui and vi move around the origin. An alternative way of Equation (3) is to calculate its instantaneous angular frequency (Pereira et al., 2007) by
Then, the phase θi can be integrated from Equation (4).
The second measure is based on the first one but only for the networks having more than two communities (Shanahan, 2010). Consider a network with m communities. We let ρi(t)(i = 1, …, m) represent the order parameter for each community i at time t. A chimera state means that the values of ρi(t) for different communities are not the same. Based on this feature, two indices are introduced to measure the chimera state, i.e., the index of the metastability λ and the chimera-like index χ. For the former, we first calculate ρi(t) for T points, i.e., t ∈ {1 … T}. Then, their variance can be obtained as
σmet(i) gives the fluctuation of synchronization in the community-i, i.e., the metastability. The index of the metastability for the entire network is
Similarly, an instantaneous variance over all the m communities can be introduced as (Shanahan, 2010)
Then, the chimera-like index χ is
Thus, the chimera-like χ and metastability λ indices quantify the degree of synchronization along time and among communities, respectively.
The third measure is for a general network with or without clear communities (Kemeth et al., 2016). Its idea is based on the local curvature for the spatial coherence, represented by the second derivative in the case of one spatial dimension. In this case of one dimension, the local curvature D can be calculated as
where f represents the spatial data on a snapshot at time t. Figure 1 shows its schematic figure where (Figure 1A) is a typical snapshot of chimera state and (Figure 1B) is the mapped D, with Dm being the maximal value of |Df|. Dm represents the curvature of the oscillator with its two neighbors being shifted 180o in phase (Kemeth et al., 2016). From Equation (9) we see that |Df| equals to zero in the synchronous regime and finite values with pronounced fluctuations in the desynchronized regime.
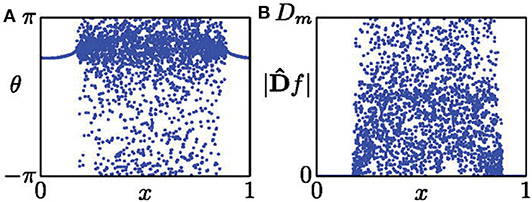
Figure 1. (A) Snapshot of a chimera state. (B) Distribution of |Df| from the data set of (A). Reprinted with permission from Kemeth et al. (2016).
From Figure 1B, we see that |Df| is distributed between 0 and Dm. Letting g be the normalized probability density of |Df|, g(|Df| = 0) is the fraction of spatially synchronous regimes. Thus, g(|Df| = 0) is unity for a complete synchronized state, zero for a complete desynchronized state, and a value between zero and unity for a chimera state. As numerical simulations have fluctuation, it was suggested that those points with |Df| < 0.01Dm should be considered as synchronized, and otherwise desynchronized (Kemeth et al., 2016). That is, the fraction of coherent regions can be calculated by
with δ = 0.01Dm. Therefore, we have g0 = 1 for a complete coherent, g0 ≈ 0 for desynchronized, and 0 < g0 < 1 for chimera states.
Except these three main measures, Gopal et al. introduced another approach to characterize the chimera and multichimera states (Gopal et al., 2014). Their approach is based on a transformation from the framework of xi to a new framework zi, i = 1, 2, …, N, where zi = xi − xi+1. In their approach, chimera states can be measured by two indices, i.e., the strength of incoherence and discontinuity measure. Although these measures are different each other, they are all robust in numerical simulations and can be applied in different systems.
3. Chimera State in Neuronal Systems
Although chimera state is mainly studied in phase oscillators, it has also been observed in other oscillators with amplitudes, including the neuronal systems. We here make a brief review on the results of chimera state in neuronal systems, mainly focusing on the FitzHugh-Nagumo (FHN) neurons and Hindmarsh-Rose (HR) neurons.
We first introduce the studies of chimera state in FHN neurons. In this aspect, Omelchenko et al. considered the case of FHN neurons by a stronger coupling and found a multi-chimera state (Omelchenko et al., 2013). For the sake of simplicity, they introduced a rotational coupling matrix and found that it is possible for the system to show both chimera and multichimera states. Their discussion is as follows. Consider N FHN neurons coupled nonlocally on a ring
where uk and vk are the activator and inhibitor variables, respectively. ϵ is taken as ϵ = 0.05. A neuron is excitable for |a| > 1 and oscillatory otherwise (Omelchenko et al., 2013). For simplicity, Omelchenko et al. (2013) considered the case of identical neurons with ak ≡ a ∈ (−1, 1). In the framework of Equation (11), the coupling strength σ is a constant within the R nearest neighbors from both sides but zero otherwise, marking the feature of nonlocal coupling. To observe chimera states in neuronal systems, Omelchenko et al. introduced the rotational coupling matrix (Omelchenko et al., 2013)
where ϕ is a parameter of coupling phase, representing the relative phase difference of interacting oscillators. This is a kind of cross-coupling. The value of chosen ϕ determines the property of coupling, i.e., attractive or repulsive.
For convenience, the parameter r = R/N is used to represent the coupling radius. The system of Equation (11) has different behaviors for different r and σ. For example, for fixed a = 0.5 and ϕ = π/2−0.1, a chimera state can be observed for small coupling strength σ and multichimeras state for larger σ. Figure 2 shows the case of small σ where Figure 2A represents a snapshot of uk at the moment of t = 5, 000. It is a typical chimera state consisting of coherent and incoherent parts. Figure 2B shows a further confirmation where the desynchronized part is distributed along the limit cycle.
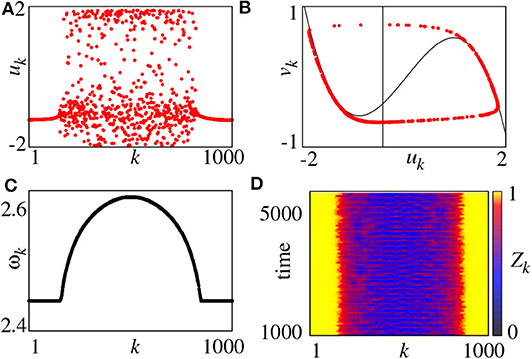
Figure 2. (A) Snapshot of the variables uk for t = 5, 000, (B) snapshot in the (uk, vk) plane for t = 5, 000 (black lines denote the nullclines of the FHN system), (C) mean phase velocities ωk, (D) local order parameter Zk. Parameters: N = 1000, r = 0.35, σ = 0.1, a = 0.5, ϕ = π/2 − 0.1. Reprinted with permission from Omelchenko et al. (2013).
On the other hand, we may also use the mean phase velocity of oscillators to characterize the chimera state, which is defined as
where ΔT is the considered time interval and Mk is the total firing number of node-k in ΔT. Figure 2C represents the results. ωk is a constant for coherent part but lie on a continuous curve for incoherent part. Moreover, we can also use the local order parameter to represent chimera state, defined as
where θj is defined by Equation (3). The k-th unit is in the coherent part of the chimera state when Zk = 1 and incoherent parts otherwise. Figure 2D shows the evolution of Zk by choosing the window size δ = 25, where the yellow parts denote the coherent regions.
For a larger coupling σ, we may observe a multichimera state where the incoherent part is divided into several independent domains, in contrast to the single incoherent domain in chimera state. Figure 3 shows the phase diagram of chimera states on the r − σ plane, where the red region represents the chimera state with one incoherent domain, while the green and blue regions represent the multichimera states with two or three incoherent domains, respectively.
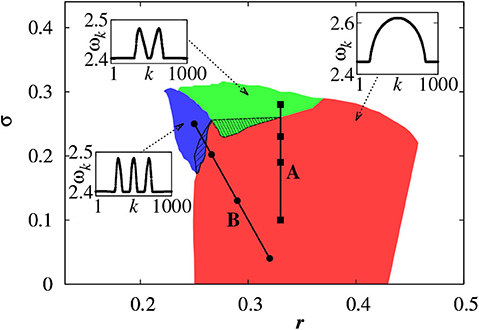
Figure 3. Phase diagram of chimera states on the r − σ plane where the red, green, and blue regions represent the chimera states with one, two and three incoherent domains, respectively. Other parameters as in Figure 2. Insets show typical profiles of the mean phase velocities. Reprinted with permission from Omelchenko et al. (2013).
Further, Omelchenko et al. extended chimera state to the case of nonidentical FHN units (Omelchenko et al., 2015). They randomly choose the parameters ak from a normal (Gaussian) distribution with mean value amean and variance δa, so that the neurons have different frequencies. For fixed amean = 0.5, chimera state changes with δa. Figure 4 represents a few typical snapshots and corresponding ωk for chimera states with one, two, and three incoherent regions, as δa increases. It is clear that these chimera states have some robustness to the nonidentity of oscillators (Omelchenko et al., 2015).
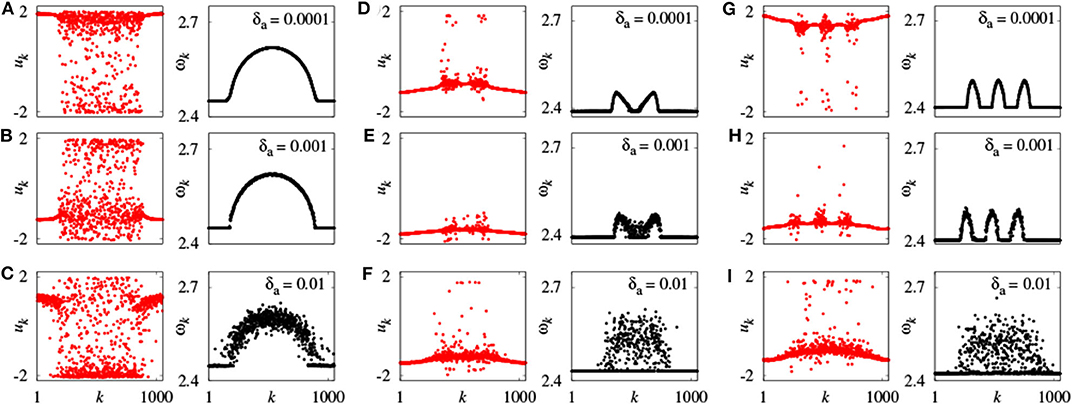
Figure 4. Snapshots of the variables uk and mean phase velocities ωk for inhomogeneous oscillators. (A–C) r = 0.35, σ = 0.1; (D–F) r = 0.33, σ = 0.28; (G–I) r = 0.25, σ = 0.25; values of δa shown for each panel above the mean phase velocities plots. Other parameters as in Figure 2. Reprinted with permission from Omelchenko et al. (2015).
Semenova et al. considered the case with noise (Semenova et al., 2016), as it is unavoidable in real systems. They focus on the question whether noise is beneficial for chimera states. In fact, this consideration is related to the phenomenon of coherence resonance (Hu et al., 1993; Pikovsky and Kurths, 1997; Liu and Lai, 2001), where an optimal noise intensity can result in the counterintuitive increase of temporal coherence. Semenova et al. found that noise is essential for chimera behavior and call it coherence-resonance chimera (Semenova et al., 2016). That is, an optimal noise can even induce a spatial chimera state, rather than purely temporal coherence. Their model is a slight modification of Equation (11) and can be written as
where ξi(t) represents the Gaussian white noise with 〈ξi(t)〉 = 0 and , and D denotes the noise intensity. The rotational coupling matrix and phase parameter are fixed as the same as in Equation (11) except ai ≡ a = 1.001, indicating that all neurons are excitable but close to the threshold.
The presence of noise may induce a spike for a single FHN neuron in the excitable regime of |a| > 1. When the noise intensity is too small, it is not enough to induce a spike in the system of Equation (15). While a strong enough noise may induce too many spikes and results in irregular behaviors. Thus, there may exist an optimum intermediate noise to induce a chimera state. To confirm this analysis, Figure 5 shows four distinct regimes by ui and Zi from Equation (14). Figure 5A shows the case of D = 0, with no spikes. Figure 5B shows the case of intermediate noise with D = 0.0002. The values of Zi show the characteristic feature of chimera state, i.e., the coexistence of coherent and incoherent spiking. Thus, Semenova et al. called it as coherence-resonance chimera (Semenova et al., 2016). Figure 5C shows the case of strong noise with D = 0.0004, where the coherence-resonance chimera is destroyed. Figure 5D shows the case of much stronger noise with D = 0.1, where the spiking is incoherent in both time and space.
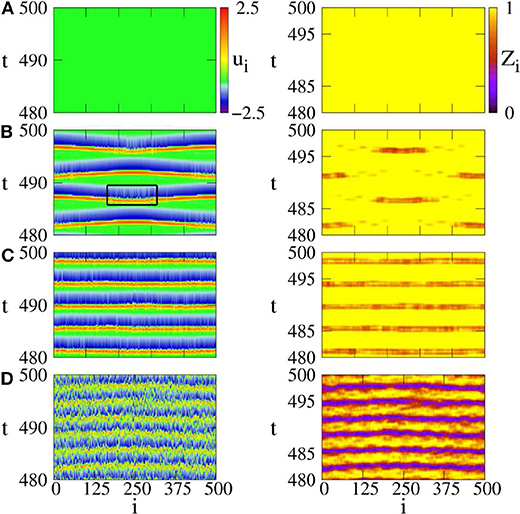
Figure 5. Space-time plots of activator ui (left column) and local order parameter Zi (right column) for different noise intensities. (A) D = 0: steady state, (B) D = 0.0002: coherence resonance chimera, (C) D = 0.0004: incoherent in space but periodic in time, (D) D = 0.1: incoherent in space and time. Parameters: ϵ = 0.05, a = 1.001, σ = 0.4, r = 0.12. Reprinted with permission from Semenova et al. (2016).
To see how the coupling parameters r and σ influence the coherence resonance chimera, Figure 6 shows the phase diagram by fixing the parameters ϵ, a, D, N. Region (a) represents a homogeneous steady state, region (b) shows the state of spiking patterns with temporal periodicity and spatial incoherence, regions (c–e) represent the coherence-resonance chimeras with one, two, and three incoherent domains, respectively. Therefore, except the noise intensity D, the coherence-resonance chimeras are also influenced by the two parameters r and σ.
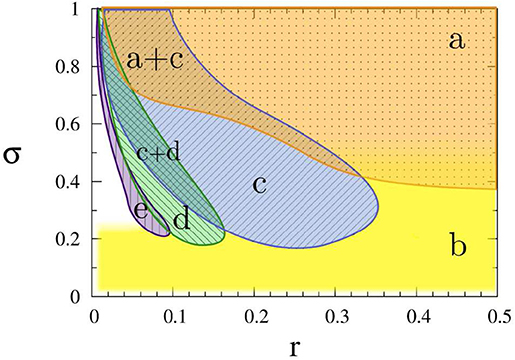
Figure 6. Dynamic regimes in the (r, σ) parameter plane: (a) steady state (orange dotted), (b) incoherent in space and periodic in time (yellow plain), (c) coherence-resonance (CR) chimera with one incoherent domain (blue crosshatched), (d) CR chimera with two incoherent domains (green crosshatched), (e) CR chimera with three incoherent domains (purple vertically hatched). Other parameters: ϵ = 0.05, a = 1.001, D = 0.0002, N = 500. Reprinted with permission from Semenova et al. (2016).
Further, the values of Zi in Figure 5B show a periodic switching between the coherent and incoherent regimes of chimera state. This feature may be helpful for the understanding of unihemispheric sleep, where the coherent and incoherent behaviors are known to switch between the two hemispheres of brain (Mukhametov et al., 1977). In fact, this kind of alternating chimera behavior has been previously addressed in a phase model by a sinusoidal signal (Ma et al., 2010), which can be also considered as an external perturbation.
Tian et al. considered the case of time-delay and electromagnetic induction in FHN neurons and found that either the time delay or electromagnetic induction can induce chimera states (Tian et al., 2018). By considering both the effect of time-delay and electromagnetic induction, Equation (11) becomes
where φ represents the magnetic flux and τ denotes the time-delay. The term kρ(φi)ui is the induction current (Tian et al., 2018). The nonlinear function ρ(φ) is taken as ρ(φ) = α + 3βφ2 (Ma et al., 2017), where α and β are two parameters.
In numerical simulations, the parameters are fixed as N = 256, k1 = 0.1, k2 = 1.0, α = 0.1, β = 0.1, τ = 1.0, σ = 0.02 and r = 0.35. Figure 7 shows the results where Figures 7A–D denote the cases of k = 0.8, 1.2, 5.2, and 7.4, respectively. It is clear from Figures 7A–D that with the increase of k, the multi-chimera state gradually becomes a chimera state.
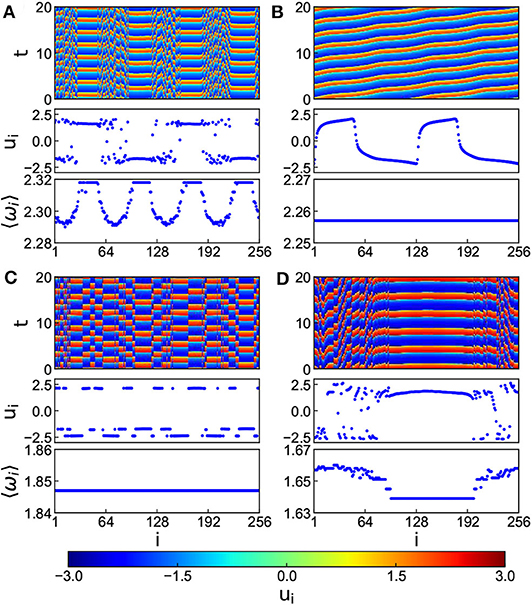
Figure 7. Chimera states for the situation of both time-delay and electromagnetic induction with positive k and r = 0.35, τ = 1.0, and c = 0.02. (A–D) Represent the cases of k = 0.8, 1.2, 5.2, and 7.4, respectively. Reprinted with permission from Tian et al. (2018).
Now, we turn to the studies of chimera state in HR neurons. Different from the FHN model of spiking neurons, HR model may represent the bursting behavior of neurons. We here concern about how this bursting behavior influences the chimera state.
Bera et al. studied a network of bursting HR neurons with global coupling as follows (Bera et al., 2016)
where k is the coupling strength, x is the membrane potential, and y and z are the transport of ions across the membrane through the fast and slow channels, respectively. The HR neuron is excitatory for xi(t) < vs, where vs = 2 is the reversal potential. (cij) is the adjacent matrix with cij = 1 if i ≠ j and cii = 0. The coupling function Γ(x) is assumed to be the sigmoidal nonlinear function
where λ′ determines the slope of the function and Θs is the synaptic threshold. These two parameters are taken as Θs = −0.25 and λ′ = 10.
To characterize the chimera state, a new transformed variable w1,i = xi − xi+1 is introduced (Bera et al., 2016). Figure 8 shows the results for snapshots of the state variables xi and w1,i by black and red color dotted points, respectively. Figure 8A shows the case of a weak coupling k = 1.0. It is a disordered state. Figure 8B shows the case of a middle coupling k = 1.2. It is a multichimera state with two domains of disordered oscillators. The inset shows a typical time series of xi (blue color line). Its behavior changes between the square-wave and plateau bursting. Figure 8C shows the case of a strong coupling k = 1.28. Its chimera state has only one incoherent domain, in contrast to the two incoherent domains in Figure 8B. Figure 8D shows the case of a stronger coupling k = 1.3, where all the neurons become coherent.
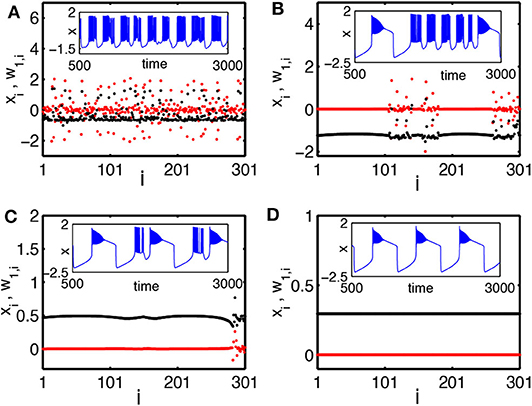
Figure 8. Snapshots of a system of globally coupled HR neurons for different values of the synaptic coupling strength k in terms of the variables xi (black color) and the transformed variables w1,i = xi − xi+1 (red color): (A) incoherent state, k = 1.0; (B) chimera state (with two desynchronized groups), k = 1.2; (C) chimera state (with single desynchronized group), k = 1.28; and (D) coherent state, k = 1.3. The inset figures are the corresponding time series (blue color). The number of oscillators is N = 301. Reprinted with permission from Bera et al. (2016).
Hizanidis et al. considered a modular network of HR neurons (Hizanidis et al., 2016), which is from the C. elegans network and consists of six communities. They let the neurons be connected by two types of synapses: electrical and chemical. The former is for the connections within each community and the latter for the connections across the communities. Their model can be described as follows
where pi represents the membrane potential, qi and ni are associated with the fast and slow currents, respectively. The parameters are chosen as r = 0.005, a = 1, Vsyn = 2, b = 3, d = 5, c = 1, s = 4, p0 = −1.6 and Iext = 3.25 so that each neuron has the spiking-bursting behavior (Hizanidis et al., 2016). L is the Laplacian matrix with Lij = Eij − δijki, where δij = 1 if i = j, and δij = 0 otherwise. E is the adjacency matrix with Eij = 1 if there is an electrical synapse connecting the neurons i and j, and Eij = 0 otherwise. gel is the strength of the electrical coupling and its functionality is governed by the linear function H(p) = p. The adjacency matrix T is Tij = 1 if there is a chemical synapse between neurons i and j, and Tij = 0 otherwise. gch is the strength of the chemical coupling and its functionality is defined by the sigmoidal function Γ(p) from Equation (18).
To study the chimera state of Equation (19), Hizanidis et al. (2016) used ρ to represent the order parameter of Equation (1) where θ is calculated through Equation (4) by p and q. Figures 9A–G show the phase diagrams of ρ on the (gch, gel) parameter space for each of the six communities and for the entire network, respectively. It is clear that ρ is not homogeneously distributed in the (gch, gel) plane but with higher ρ in some region and lower ρ in other regions. For example, the red regions have ρ ≈ 1 and the yellow regions have 0 < ρ < 1.
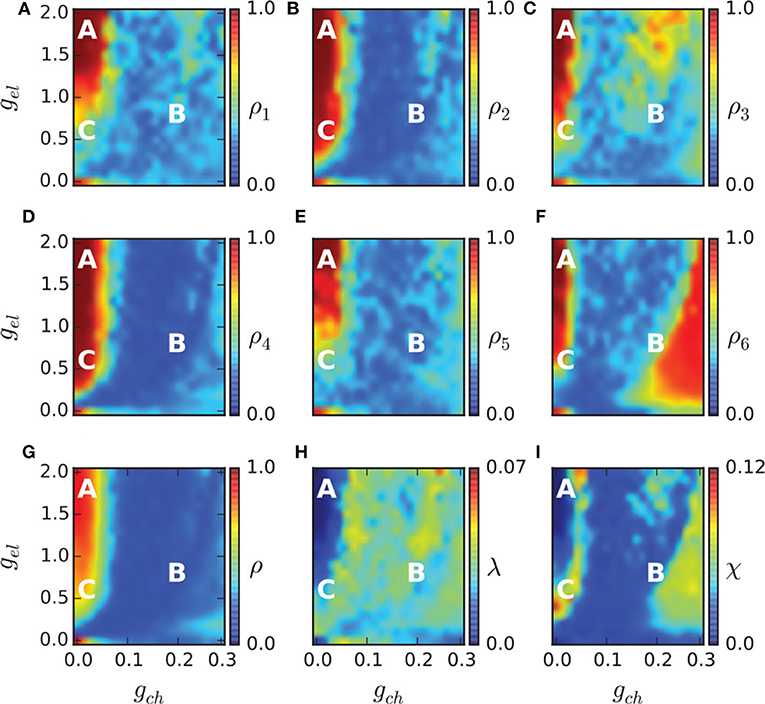
Figure 9. Phase diagram in the (gch, gel) parameter spaces. The order parameter of each community ρ1, …, 6 is shown in (A–F), and of the entire network in (G). The metastability index λ is shown in (H) and the chimera-like index χ in (I). The marked points A (gch = 0.015, gel = 1.7), B (gch = 0.18, gel = 0.7), and C (gch = 0.015, gel = 0.5) denote three different dynamical regimes and their dynamical behaviors are illustrated in Figure 10. Reprinted with permission from Hizanidis et al. (2016).
The regions with 0 < ρ < 1 in Figures 9A–G may represent the chimera states. To confirm it, the two measures of metastability index λ of Equation (6) and chimera-like index χ of Equation (8) are used. Figures 9H,I show the results on the (gch, gel) parameter space. From Figure 9H we see that λ reaches higher values in some regions, implying that the system often changes between coherent and incoherent states. From Figure 9I we see that χ reaches its highest values in the two synchronization “islands” of communities 3 and 6. For more detailed information on chimera state, Hizanidis et al. chose 3 interest points on the (gch, gel) phase diagram, marked by letters A, B, and C (Hizanidis et al., 2016), where A has both low-valued λ and χ, B has λ ≫ χ, and C has χ ≫ λ, i.e., “chimera-like” state. Figure 10 shows the dynamical behaviors of p for the three points. The snapshots of the system state in the bottom confirm the corresponding behaviors, where only the point C shows the feature of chimera state, i.e., the coexistence of coherent and incoherent domains.
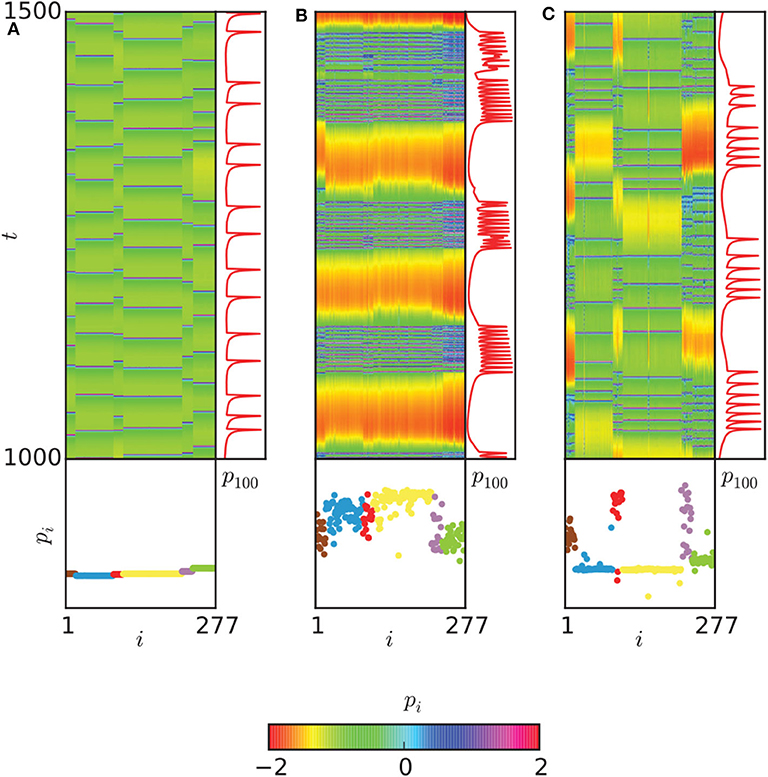
Figure 10. Dynamical behaviors of the three points A, B, and C in Figure 9. (A) The spatiotemporal evolution of pi (upper left), with a time series of the neuron with index 100 of community 3 (upper right) and a snapshot of the system state (bottom) are shown for the point A of Figure 9. (B) The same plot for point B. (C) The same plot for point C. A chimera-like state is illustrated here. Neurons are ordered according to their community. Reprinted with permission from Hizanidis et al. (2016).
Moreover, Majhi et al. studied the chimera state in uncoupled HR neurons induced by a multilayer network (Majhi et al., 2016), where the neurons in the upper layer is unconnected but can share information through the neurons in the lower layer. This topology is related to the remote synchronization (Bergner et al., 2012) and thus may help us to understand brain functions. Bera et al. reported a new type of non-stationary chimera pattern in coupled HR neurons (Bera et al., 2019), called spike chimera.
In summary, these studies show different ways to induce chimera states, including both cross-coupling and single-variable coupling. At the same time, these studies also show that chimera states are available in different neuronal models, indicating the robustness to neuronal models. The drawbacks or limitations are that all the considered network structures are artificial but not empirical brain networks. And the models are for individual neurons but not the average behaviors of an ensemble of neurons, which are the only available time series in experiments such as EEG data.
4. Chimera States in Empirical Brain Networks
Except the above extensive studies of chimera states in artificial neural systems, recently, some attention has been paid to the networks of human cerebral cortex measured by DTI. The former helps us to understand the mechanism of chimera state such as how chimera state is induced and what is the condition for chimera state to show up. While the latter highlights a way to cure or control brain diseases such as schizophrenia, Alzheimer's disease and brain tumors. It is well-known that in the fields of nonlinear science and complex network, brain functions can be represented by their corresponding dynamical patterns, i.e., a variety of patterns of partial synchronization. These patterns have a close relationship with chimera states and can be considered as a natural link between coherent and incoherent dynamics. Thus, the studies of chimera states on empirical brain networks is very helpful for exploring the mechanism of brain functions such as cognition and memory. We here make a brief summary for those results on the empirical brain networks, i.e., from the brain networks with smaller size to the middle and then to the larger ones.
Firstly, we introduce the study on an empirical brain network with smaller size. In this case, Bansal et al. considered an empirical brain network consisting of 76 brain regions (or nodes) and paid attention to how brain structure influences the dynamical patterns produced by stimulation (Bansal et al., 2019). They divided this network into nine cognitive systems by using personalized brain network models, named attention, visual, cingulo-opercular, subcortical, medial default mode, somatosensory and motor, frontoparietal, ventral temporal association, and auditory systems. Each of the nine cognitive systems is consist of the coactivated regions for supporting a generalized class of cognitive functions. Then, they presented a chimera-based, cognitively informed framework to study how large-scale brain structure influences brain dynamics and functions, called cognitive chimera states. In their study, the dynamics of each node was modeled by the Wilson-Cowan oscillators (Wilson and Cowan, 1972), a biologically motivated neural mass model, represented as follows
where
and Aij is the weighted coupling matrix. c5 and c6 represent the excitatory and inhibitory coupling strength, respectively, with c6 = c5/4. Pi(t) is the external stimulation. is the time-delay, where dij is the spatial distance between nodes i and j and td = 10m/s is the signal transmission speed. Other parameters are biologically taken as c1 = 16, c2 = 12, c3 = 15, c4 = 3, τ = 8, θI = 3.7, θE = 4, aI = 2, and aE = 1.3.
In numerical simulations, the dynamical behaviors of the nine cognitive systems were investigated by stimulating a brain region with Pi = 1.15 (Bansal et al., 2019). The stimulation gradually spreads to other parts of the brain network by the links of the stimulated node and form a dynamical state. By this way, different dynamical states are observed when different brain regions are stimulated. Then, Bansal et al. calculated a cognitive system-based order parameter ρsi,sj from Equation (1). This parameter ρsi,sj measures the degree of synchrony among all oscillators within the two cognitive systems si and sj. By this way, a cognitive system-based 9 × 9 matrix can be obtained. Further, two cognitive systems si and sj are considered as synchronized if ρsi,sj exceeds a threshold value ρTh = 0.8. The whole brain network is a coherent state when all nine cognitive systems are synchronized, a cognitive chimera state when some cognitive systems are synchronized while the other systems are desynchronized, and a metastable state when no stable synchrony between cognitive systems is formed (Bansal et al., 2019).
Figure 11 shows the relative contribution of the nine cognitive systems for the three states after nodes stimulation. We see that the contributions to the three states are different from one cognitive system to another, implying a close relationship between cognitive systems and brain functions. Figure 11A shows that coherent states are mainly from the nodes stimulation within subcortical and medial default mode systems. Figure 11C shows that the frontoparietal and cingulo-opercular systems are the main contributions for metastable states, while the ventral temporal association and auditory systems also contribute substantially to metastable states. Figure 11B shows that all nine systems produce chimera states, implying that chimera states have higher possibility to be observed than either coherent or metastable states (Bansal et al., 2019). Bansal et al. also pointed that the regions of coherent states are distributed more closely to the midline of the brain, and the regions of metastable states are distributed farther from the midline, i.e., along the edges of the hemispheres, while the regions of chimera states are relatively uniformly distributed within the brain space. The metastable states enable segregated neural processing, while coherent states enable integrated neural processing. As the brain system must integrate information across spatially distributed, segregated regions to implement cognitive tasks, a balance between integration and segregation is required for adaptive cognition. This balance is automatically satisfied in chimera states and thus enables segregation and integration in brain dynamics, which guarantees the diverse processing requirements.
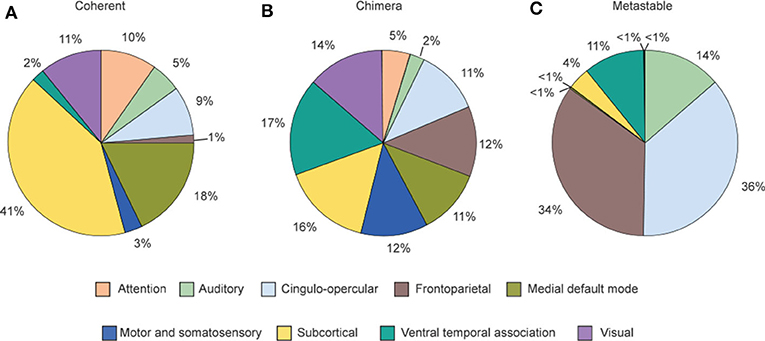
Figure 11. Distribution of the contribution fractions from the nine cognitive systems after nodes stimulation where (A–C) represent the cases of final dynamical states as coherent, chimera and metastable states, respectively. This distribution tells a relationship between the dynamical states and individual cognitive systems. Reprinted with permission from Bansal et al. (2019).
Secondly, Chouzouris et al. considered a slightly larger empirical brain network consisting of 90 nodes (Chouzouris et al., 2018), motivated by studies of epileptic seizures. They let the neurons be the FitzHugh-Nagumo oscillators. As this empirical brain network has a topology of complex network, Equation (11) has to be modified into
where ϵ = 0.05 and G is the adjacency matrix. The rotational coupling matrix B = (buu) is taken as the same as in Equation (12).
Chouzouris et al. found that when a is in the range a ∈ (0, 0.8), the network exhibits chimera states for small coupling strength σ (Chouzouris et al., 2018). When the parameters are taken as a = 0.5, σ = 0.2, and N = 90, the network shows a stationary moving chimera. That is, the order parameter r from Equation (1) has a strong fluctuation or changes in time. Figure 12A shows such an example, where the parameters are a = 0.5 and σ = 0.6. The average of order parameter is 〈r〉 ≈ 0.5. Except the strong fluctuation, another feature is that the highest value of r appears right before its drop. Both effects were discovered in the synchronization of epileptic seizures (Jiruska et al., 2013). Chouzouris et al. further pointed out that the high coherence events can be controlled (Chouzouris et al., 2018). Larger σ increases the probability for chimera states to occur. Figure 12B shows the result that the variation of coupling results in a switching between the chimera state and synchronization, which controls the epileptic seizures.
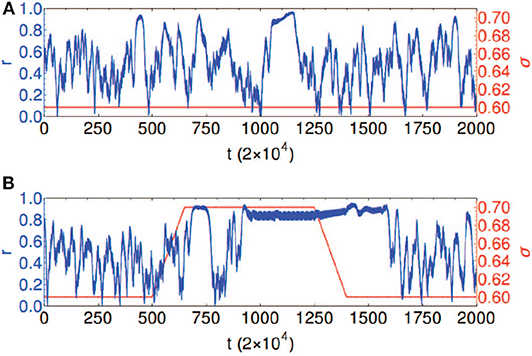
Figure 12. Temporal evolution of the global order parameter r shown in blue for the network with empirical structural connectivity with a = 0.5 and N = 90. The coupling strength σ is shown in red. (A) Chimera state: constant coupling strength σ = 0.6. (B) Controlled dynamics: coupling strength σ = 0.6 is increased to the value σ = 0.7 and kept fixed for the time interval 650 < t/2 × 104 < 1, 350, followed by a decrease back to σ = 0.6; this causes the transitions between the chimera state and frequency synchronized states. Reprinted with permission from Chouzouris et al. (2018).
This empirical brain network of 90 nodes was further studied by Ramlow et al. (2019), where a dynamical asymmetry between the hemispheres was addressed by considering natural structural asymmetry.
Finally, we discuss the situation of empirical brain network with larger size. This network is much larger than the above two and is constructed by the data of Hagmann et al. (2008) where the cerebral cortex was divided into 989 nodes and 17, 865 connections. For this network, Huo et al. first considered the case of adaptive coupling (Huo et al., 2019), based on the fact that in empirical brain network, both the coupling strength and neural activities influence each other and thus change with time. In Huo's model, the coupling matrix is adaptively evolved with the dynamics of neurons. They found that the adaptive coupling finally reaches a self-organized state and induces chimera states. This kind of self-organization may support the high flexibility of brain functions. In details, they let the nodes be the FitzHugh-Nagumo oscillators and the dynamics be represented as follows
where ϵ = 0.05, a = 0.5, and the rotational coupling matrix B is defined as in Equation (12). The adaptive coupling λij is set as
where γ is a small constant. Equation (24) does not influence the topology of network but only change the value of λij.
Huo et al. chose γ = 0.01 and found that it is possible for chimera states to appear in this realistic network (Huo et al., 2019). Figure 13 represents the resulted chimera state for β = −0.5π + 1.2 and ϕ = −π + 4.45, where (Figure 13A) is the initial matrix of λij, (Figure 13B) the stabilized matrix of λij, (Figure 13C) the evolutionary pattern of ui(t), and (Figure 13D) a snapshot of the fast variable ui(t). Comparing Figure 13A with (Figure 13B), we see that the stabilized matrix λij in (Figure 13B) is significantly different from the initial matrix λij in (Figure 13A). This may help us to understand how the brain network is self-organized into chimera states.
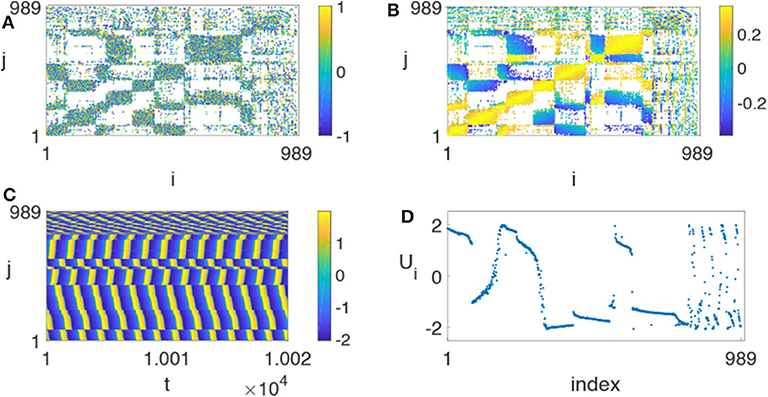
Figure 13. Chimera state on the realistic network of cerebral cortex with N = 989, ϕ = −π + 4.45 and β = −0.5π + 1.2. (A) Represents the initial matrix λij chosen randomly from [−1, 1], (B) the stabilized matrix λij, (C) the evolutionary pattern of ui(t), and (D) the snapshot of the fast variable ui(t) at a specific time t. Reprinted with permission from Huo et al. (2019).
To reflect the dependence of chimera states on the parameters ϕ and β, Huo et al. calculated the measure g0 of chimera state by Equation (10). Figure 14 shows its phase diagram on the parameter plane of ϕ and β. The stabilized behaviors consist of disorder, coherent, and chimera states but the fraction of chimera states is the largest one on the phase diagram.
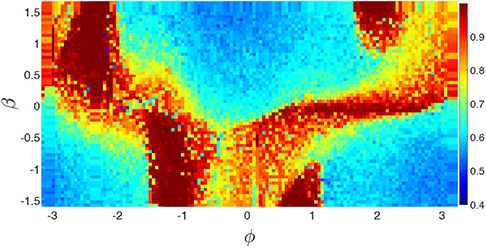
Figure 14. Phase diagram of g0 of chimera state in the parameter plane of ϕ and β for the realistic network of cerebral cortex. Reprinted with permission from Huo et al. (2019).
Kang et al. further considered the empirical brain network of 989 nodes as a two-layered network where the left and right hemispheres of cerebral cortex are considered as different layers, respectively (Kang et al., 2019). In their model, the intra- and inter-coupling strengths are considered to be different. Very interesting, they found that the model can reproduce the phenomenon of unihemispheric sleep where one hemisphere is completely synchronized while the other is completely desynchronized. This finding provides an explanation for the first-night effect in human sleep (Tamaki et al., 2016). Their model for the first layer-A is represented as follows
where ϵ = 0.05 and a = 0.5. and are the inter- and intra-degrees of node i, respectively. (AB)ij and Aij denote the inter- and intra-coupling matrices, respectively. The other quantities are the same as in Equations (11) and (12).
The similar dynamics equations can be written for the network B.
Figure 15 shows the results for four typical cases where ωi is calculated by Equation (13), the up and down panels are for the network-A and network-B, respectively, and the insets are their corresponding dynamics of ui. The panels of Figure 15 represent four typical cases where (Figures 15A,E) are for the case of disorder with λin = 0.1 and λout = 0.3; (Figures 15B,F) for the case of chimera state with λin = 0.1 and λout = 1.8; (Figures 15C,G) for the case of disordered network-A and synchronized network-B, with λin = 0.4 and λout = 3.5; and (Figures 15D,H) for the case of synchronization with λin = 4.0 and λout = 3.5. These four cases represent different states. The first case of Figures 15A,E and the last case of Figures 15D,H denote the two extreme states of desynchronized and synchronized states, respectively. The second case of Figures 15B,F represents a chimera state where there is a plateau of ωi in both the up and down panels and their insets show a coexistence of synchronized and unsynchronized ui(t). The most interesting is the third case of Figures 15C,G where the network-A is disordered but the network-B is synchronized, marking the unihemispheric sleep. Kang et al. further showed that the parameter region for the state of unihemispheric sleep is much smaller than that of chimera state, implying that it is usually difficult to observe the phenomenon of unihemispheric sleep. This is consistent with the first-night effect (Tamaki et al., 2016), which can be observed only in the first-night sleep when a person is located in an unfamiliar place.
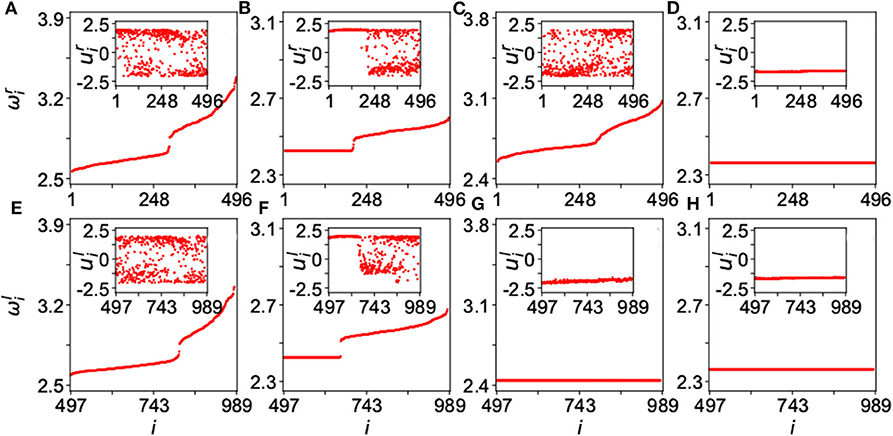
Figure 15. Four typical dynamical states in the two-layered network model of Equation (25) where the up panels represent the layer-A and down panels the layer-B. The inset in each panel is a snapshot of ui at time t. (A,E) Represent the case of disorder with λin = 0.1 and λout = 0.3; (B,F) the case of chimera state with λin = 0.1 and λout = 1.8; (C,G) the case of unihemispheric sleep with λin = 0.4 and λout = 3.5; and (D,H) the case of synchronization with λin = 4.0 and λout = 3.5. Reprinted with permission from Kang et al. (2019).
In sum, these studies showed the recent progress of chimera states in empirical brain networks, but did not pay much attention to the aspects of characteristic features of brain networks, such as the heterogeneous communities and hub nodes of rich-club, and deeper connection to concrete brain functions, such as cognitive and memory etc.
5. Discussions
Chimera state is in fact one of the three kinds of partial synchronization. The other two of them are the cluster synchronization and remote synchronization. Cluster synchronization represents the case where the oscillators of network are automatically evolved into different synchronized clusters but the oscillators in different clusters are not synchronized each other (Schaub et al., 2016; Cao et al., 2018). The relationship between the synchronized cluster and network symmetry is discussed recently (Pecora et al., 2014; Sorrentino et al., 2016), including the case where the synchronized cluster is not directly from the symmetry but due to the same total amounts of inputs received from their neighboring nodes (Siddique et al., 2018). While remote synchronization represents the synchrony among the leaf nodes of a hub but not synchronized with the hub, i.e., the synchronized nodes are not directly connected (Bergner et al., 2012). However, these three partial synchronization are not completely independent of each other but may sometimes represent the same phenomenon. For example, chimera state can appear simultaneously with cluster synchronization in some systems (Hart et al., 2016; Cho et al., 2017; Bansal et al., 2019). It is also possible for remote synchronization to be related to cluster synchronization (Bergner et al., 2012; Kang et al., 2020; Wang and Liu, 2020). For example, in a star network with remote synchronization, if the leaf nodes of the hub is considered as a cluster, their synchronization is in fact the cluster synchronization. Based on these results, it is an open but promising direction to highlight the mechanisms of brain functions such as cognition, memory, and signal spreading etc, from these three aspects of partial synchronization.
One purpose of studying chimera states in neural systems is for its potential applications. On one hand, some attention has been paid to the phenomenon of unihemispheric sleep (Rattenborg et al., 2000; Ma et al., 2010). On the other hand, the study of chimera state may help us to understand neuronal diseases such as epileptic seizures, Parkinson's disease, schizophrenia, Alzheimer's disease and brain tumors (Uhlhaas and Singer, 2006). For example, a therapy for Parkinson's disease is external electric stimulation at high frequencies, called deep brain stimulation (Benabid et al., 1991). These studies are still very primary. More deeper studies are expected, such as the connections of chimera states to the mechanisms of cognitive and memory and the control of various brain diseases in clinical medicine etc.
Author Contributions
ZL and ZW conceived the research project and wrote the paper. All authors contributed to the article and approved the submitted version.
Funding
This work was partially supported by the NNSF of China under Grant Nos. 11675056 and 11835003.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abrams, D. M., and Strogatz, S. H. (2004). Chimera states for coupled oscillators. Phys. Rev. Lett. 93:174102. doi: 10.1103/PhysRevLett.93.174102
Ayala, G. F., Dichter, M., Gumnit, R. J., Matsumoto, H., and Spencer, W. A. (1973). Genesis of epileptic interictal spikes. New knowledge of cortical feedback systems suggests a neurophysiological explanation of brief paroxysms. Brain Res. 52, 1–17. doi: 10.1016/0006-8993(73)90647-1
Bansal, K., Garcia, J. O., Tompson, S. H., Verstynen, T. Vettel, J. M., and Muldoon, S. F. (2019). Cognitive chimera states in human brain networks. Sci. Adv. 5:eaau8535. doi: 10.1126/sciadv.aau8535
Bartsch, R. P., and Ivanov, P. Ch. (2014). Coexisting forms of coupling and phase-transitions in physiological networks. Commun. Comput. Inform. Sci. 438, 270–287. doi: 10.1007/978-3-319-08672-9_33
Bartsch, R. P., Liu, K. K. L., Bashan, A., and Ivanov, P. Ch. (2015). Network physiology: how organ systems dynamically interact. PLoS ONE 10:e0142143. doi: 10.1371/journal.pone.0142143
Bartsch, R. P., Schumannc, A. Y., Kantelhardtd, J. W., Penzele, T., and Ivanov, P. Ch. (2012). Phase transitions in physiologic coupling. Proc. Natl. Acad. Sci. U.S.A. 109, 10181–10186. doi: 10.1073/pnas.1204568109
Bashan, A., Bartsch, R. P., Kantelhardt, J. W., Havlin, S., and Ivanov, P. Ch. (2012). Network physiology reveals relations between network topology and physiologic function. Nat. Commun. 3:702. doi: 10.1038/ncomms1705
Benabid, A. L., Pollak, P., Gervason, C., Hoffmann, D., Gao, D. M., Hommel, M., et al. (1991). Long-term suppression of tremor by chronic stimulation of the ventral intermediate thalamic nucleus. Lancet 337, 403–406. doi: 10.1016/0140-6736(91)91175-T
Benedek, M., Bergner, S., Konen, T., Fink, A., and Neubauer, A. C. (2011). EEG alpha synchronization is related to top-down processing in convergent and divergent thinking. Neuropsychologia 49, 3505–3511. doi: 10.1016/j.neuropsychologia.2011.09.004
Bera, B. K., Ghosh, D., and Lakshmanan, M. (2016). Chimera states in bursting neurons. Phys. Rev. E 93:012205. doi: 10.1103/PhysRevE.93.012205
Bera, B. K., Rakshit, S., Ghosh, D., and Kurths, J. (2019). Spike chimera states and firing regularities in neuronal hypernetworks. Chaos 29:053115. doi: 10.1063/1.5088833
Bergner, A., Frasca, M., Sciuto, G., Buscarino, A., Ngamga, E. J., Fortuna, L., et al. (2012). Remote synchronization in star networks. Phys. Rev. E 85:026208. doi: 10.1103/PhysRevE.85.026208
Calim, A., Hovel, P., Ozer, M., and Uzuntarla, M. (2018). Chimera states in networks of type-I Morris-Lecar neurons. Phys. Rev. E 98:062217. doi: 10.1103/PhysRevE.98.062217
Camperi, M., and Wang, X.-J. (1998). A model of visuospatial working memory in prefrontal cortex: recurrent network and cellular bistability. J. Comput. Neurosci. 5, 383–405. doi: 10.1023/A:1008837311948
Cao, B., Wang, Y. F., Wang, L., Yu, Y. Z., and Wang, X. G. (2018). Cluster synchronization in complex network of coupled chaotic circuits: an experimental study. Front. Phys. 13:130505. doi: 10.1007/s11467-018-0775-1
Chandrasekar, V. K., Gopal, R., Venkatesan, A., and Lakshmanan, M. (2014). Mechanism for intensity-induced chimera states in globally coupled oscillators. Phys. Rev. E 90:062913. doi: 10.1103/PhysRevE.90.062913
Chen, Z., Hu, K., Stanley, H. E., Novak, V., and Ivanov, P. Ch. (2006). Cross-Correlation of instantaneous phase increments in pressure-flow fluctuations: applications to cerebral autoregulation. Phys. Rev. E 73:031915. doi: 10.1103/PhysRevE.73.031915
Cho, Y. S., Nishikawa, T., and Motter, A.E. (2017). Stable chimeras and independently synchronizable clusters. Phys. Rev. Lett. 119:084101. doi: 10.1103/PhysRevLett.119.084101
Chouzouris, T., Omelchenko, I., Zakharova, A., Hlinka, J., Jiruska, P., and Scholl, E. (2018). Chimera states in brain networks: empirical neural vs. modular fractal connectivity. Chaos 28:045112. doi: 10.1063/1.5009812
Glaze, T. A., Lewis, S., and Bahar, S. (2016). Chimera states in a Hodgkin-Huxley model of thermally sensitive neurons. Chaos 26:083119. doi: 10.1063/1.4961122
Gopal, R., Chandrasekar, V. K., Venkatesan, A., and Lakshmanan, M. (2014). Observation and characterization of chimera states in coupled dynamical systems with nonlocal coupling. Phys. Rev. E 89:052914. doi: 10.1103/PhysRevE.89.052914
Gupta, G., Pequito, S., and Bogdan, P. (2018). “Re-thinking EEG-based non-invasive brain interfaces: modeling and analysis,” in Proceedings of the 2018 ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS) (Porto).
Gupta, G., Pequito, S., and Bogdan, P. (2019). “Learning latent fractional dynamics with unknown unknowns,” in American Control Conference (ACC) (Philadelphia, PA), 217–222.
Hagmann, P., Cammoun, L., Gigandet, X., Meuli, R., Honey, C. J., Wedeen, J. V., et al. (2008). Mapping the structural core of human cerebral cortex. PLoS Biol. 6, 1479–1493. doi: 10.1371/journal.pbio.0060159
Hart, J. D., Bansal, K., Murphy, T. E., and Roy, R. (2016). Experimental observation of chimera and cluster states in a minimal globally coupled network. Chaos 26:094801. doi: 10.1063/1.4953662
Hilgetag, C., and Kaiser, M. (2004). Clustered organization of cortical connectivity. Neuroinformatics 2, 353–360. doi: 10.1385/NI:2:3:353
Hizanidis, J., Kanas, V. G., Bezerianos, A., and Bountis, T. (2014). Chimera states in networks of nonlocally coupled Hindmarsh–Rose neuron models. Inter. J. Bif. Chaos 24:1450030. doi: 10.1142/S0218127414500308
Hizanidis, J., Kouvaris, N. E., Zamora-Lopez, G., Diaz-Guilera, A., and Antonopoulos, C. G. (2016). Chimera-like states in modular neural networks. Sci. Rep. 6:19845. doi: 10.1038/srep22314
Hu, G., Ditzinger, T., Ning, C. Z., and Haken, H. (1993). Stochastic resonance without external periodic force. Phys. Rev. Lett. 71, 807–810. doi: 10.1103/PhysRevLett.71.807
Huo, S., Tian, C., Kang, L., and Liu, Z. (2019). Chimera states of neuron networks with adaptive coupling. Nonlinear Dyn. 96, 75–86. doi: 10.1007/s11071-019-04774-4
Ivanov, P. Ch., and Bartsch, R. P. (2014). Network physiology: mapping interactions between networks of physiologic networks,” in Networks of Networks: the Last Frontier of Complexity, eds G. D'Agostino and A. Scala. Book Series: Understanding Complex Systems Springer Complexity, (Cham: Springer), 203–222. doi: 10.1007/978-3-319-03518-5_10
Ivanov, P. Ch., Liu, K. K. L., and Bartsch, R. P. (2016). Focus on the emerging new fields of network physiology and network medicine. New J. Phys. 18:100201. doi: 10.1088/1367-2630/18/10/100201
Ivanov, P. Ch., Ma, Q. D. Y., and Bartsch, R. P. (2009). Maternal-fetal heartbeat phase-synchronization. Proc. Natl. Acad. Sci. U.S.A. 106, 13641–13642. doi: 10.1073/pnas.0906987106
Jiruska, P., de Curtis, M., Jefferys, J. G. R., Schevon, C. A., Schiff, S. J. K. Schindler. (2013). Synchronization and desynchronization in epilepsy: controversies and hypotheses. J. Physiol. 591, 787–797. doi: 10.1113/jphysiol.2012.239590
Kang, L., Tian, C., Huo, S., and Liu Z. (2019). A two-layered brain network model and its chimera state. Sci. Rep. 9:14389. doi: 10.1038/s41598-019-50969-5
Kang, L., Wang, Z., Huo, S., Tian, C., and Liu, Z. (2020). Remote synchronization in human cerebral cortex network with identical oscillators. Nonlinear Dyn. 99:1577. doi: 10.1007/s11071-019-05375-x
Kemeth, F. P., Haugland, S. W., Schmidt, L., Kevrekidis, I. G., and Krischer, K. (2016). A classification scheme for chimera states. Chaos 26:094815. doi: 10.1063/1.4959804
Ko, T. W., and Ermentrout, G. B. (2008). Partially locked states in coupled oscillators due to inhomogeneous coupling. Phys. Rev. E 78:016203. doi: 10.1103/PhysRevE.78.016203
Kuramoto, Y., and Battogtokh, D. (2002). Coexistence of coherence and incoherence in nonlocally coupled phase oscillators. Nonlin. Phenom. Complex Syst. 5, 380–385.
Laing, C. R., and Chow, C. C. (2001). Stationary bumps in networks of spiking neurons. Neural Comput. 13, 1473–1494. doi: 10.1162/089976601750264974
Larger, L., Penkovsky, B., and Maistrenko, Y. (2015). Laser chimeras as a paradigm for multistable patterns in complex systems. Nat. Commun. 6:7752. doi: 10.1038/ncomms8752
Larger, L., Penkovsky, B., and Maistrenko, Y. L. (2013). Virtual chimera states for delayed-feedback systems. Phys. Rev. Lett. 111:054103. doi: 10.1103/PhysRevLett.111.054103
Levy, R., Hutchison, W. D., Lozano, A. M., and Dostrovsky, J. O. (2000). High-frequency synchronization of neuronal activity in the subthalamic nucleus of parkinsonian patients with limb tremor. J. Neurosci. 20, 7766–7775. doi: 10.1523/JNEUROSCI.20-20-07766.2000
Lin, A., Liu, K. K. L., Bartsch, R. P., and Ivanov, P. Ch. (2016). Delay-correlation landscape reveals characteristic time delays of brain rhythms and heart interactions. Philos. Trans. R. Soc. A 374:20150182. doi: 10.1098/rsta.2015.0182
Liu, K. K. L., Bartsch, R. P., Lin, A., Mantegna, R. N., and Ivanov, P. Ch. (2015). Plasticity of brain wave network interactions and evolution across physiologic states. Front. Neural Circuits 9:62. doi: 10.3389/fncir.2015.00062
Liu, Z., and Lai, Y.-C. (2001). Coherence resonance in coupled chaotic oscillators. Phys. Rev. Lett. 86, 4737–4740. doi: 10.1103/PhysRevLett.86.4737
Liu, Z., Zhou, J., Munakata, T. (2009). Detecting generalized synchronization by the generalized angle. Europhys. Lett. 87:50002. doi: 10.1209/0295-5075/87/50002
Ma, J., Wang, Y., Wang, C.N., Xu, Y., and Ren, G.D. (2017). Mode selection in electrical activities of myocardial cell exposed to electromagnetic radiation. Chaos Solitons Fract. 99, 219–225. doi: 10.1016/j.chaos.2017.04.016
Ma, R., Wang, J., and Liu, Z. (2010). Robust features of chimera states and the implementation of alternating chimera states. Europhys. Lett. 91:40006. doi: 10.1209/0295-5075/91/40006
Majhi, S., Bera B. K., Ghosh D., and Perc, M. (2019). Chimera states in neuronal networks: a review. Phys. Life Rev. 28, 100–121. doi: 10.1016/j.plrev.2018.09.003
Majhi, S., Perc, M., and Ghosh, D. (2016). Chimera states in uncoupled neurons induced by a multilayer structure. Sci. Rep. 6:39033. doi: 10.1038/srep39033
Martens, E. A., Thutupalli, S., Fourrire, A., and Hallatschek, O. (2013). Chimera states in mechanical oscillator networks. Proc. Natl. Acad. Sci. U.S.A. 110, 10563–10567. doi: 10.1073/pnas.1302880110
Meunier, D., Lambiotte, R., and Bullmore, E. T. (2010). Modular and hierarchically modular organization of brain networks. Front. Neurosci. 4:200. doi: 10.3389/fnins.2010.00200
Mukhametov, L., Supin, A., and Polyakova, I. (1977) Interhemispheric asymmetry of the electroencephalographic sleep patterns in dolphins links open overlay panel. Brain Res. 134, 581–584. doi: 10.1016/0006-8993(77)90835-6
Olmi, S., Politi, A., and Torcini, A. (2010). Collective chaos in pulse-coupled neural networks. Europhys. Lett. 92:60007. doi: 10.1209/0295-5075/92/60007
Omelchenko, I., Omelchenko, E., Hovel, P., and Scholl, E. (2013). When nonlocal coupling between oscillators becomes stronger: patched synchrony or multichimera states. Phys. Rev. Lett. 110:224101. doi: 10.1103/PhysRevLett.110.224101
Omelchenko, I., Provata, A., Hizanidis, J., Scholl, E., and Hovel, P. (2015). Robustness of chimera states for coupled FitzHugh-Nagumo oscillators. Phys. Rev. E 91:022917. doi: 10.1103/PhysRevE.91.022917
Omelchenko, I., Riemenschneider, B., Hovel, P., Maistrenko Y., and Scholl, E. (2012). Transition from spatial coherence to incoherence in coupled chaotic systems. Phys. Rev. E 85:026212. doi: 10.1103/PhysRevE.85.026212
Osipov, G. V., Hu, B., Zhou, C., Ivanchenko, M. V., Kurths, J. (2003). Three types of transitions to phase synchronization in coupled chaotic oscillators. Phys. Rev. Lett. 91:024101. doi: 10.1103/PhysRevLett.91.024101
Panaggio, M. J., and Abrams, D. M. (2015). Chimera states: coexistence of coherence and incoherence in networks of coupled oscillators. Nonlinearity 28:R67. doi: 10.1088/0951-7715/28/3/R67
Pecora, L. M., Sorrentino, F., Hagerstrom, A. M., Murphy, T. E., and Roy, R. (2014). Cluster synchronization and isolated desynchronization in complex networks with symmetries. Nat. Commun. 5:4079. doi: 10.1038/ncomms5079
Pereira, T., Baptista, M. S., and Kurths, J. (2007). Detecting phase synchronization by localized maps: application to neural networks. Europhys. Lett. 77:40006. doi: 10.1209/0295-5075/77/40006
Pikovsky, A. S., and Kurths, J. (1997). Coherence resonance in a noise-driven excitable system. Phys. Rev. Lett. 78, 775–778. doi: 10.1103/PhysRevLett.78.775
Racz, F. S., Stylianou, O., Mukli, P., and Eke, A. (2018). Multifractal dynamic functional connectivity in the resting-state brain. Front. Physiol. 9:1704. doi: 10.3389/fphys.2018.01704
Ramlow, L., Sawicki, J., Zakharova, A., Hlinka, J., Claussen, J. C., and Scholl, E. (2019). Partial synchronization in empirical brain networks as a model for unihemispheric sleep. Europhys. Lett. 126:50007. doi: 10.1209/0295-5075/126/50007
Rattenborg, N. C., Amlaner, C. J., and Lima, S. L. (2000). Behavioral, neurophysiological and evolutionary perspectives on unihemispheric sleep. Neurosci. Biobehav. Rev. 24, 817–842. doi: 10.1016/S0149-7634(00)00039-7
Rothkegel, A., and Lehnertz, K. (2014). Irregular macroscopic dynamics due to chimera states in small-world networks of pulse-coupled oscillators. New J. Phys. 16:055006. doi: 10.1088/1367-2630/16/5/055006
Sakaguchi, H. (2006). Instability of synchronized motion in nonlocally coupled neural oscillators. Phys. Rev. E 73:031907. doi: 10.1103/PhysRevE.73.031907
Schaub, M. T., O'Clery, N., Billeh, Y. N., Delvenne, J. C., Lambiotte, R., and Barahona, M. (2016). Graph partitions and cluster synchronization in networks of oscillators. Chaos 26:094821. doi: 10.1063/1.4961065
Schmidt, L., Schonleber, K., Krischer, K., and Garcia-Morales, V. (2014). Coexistence of synchrony and incoherence in oscillatory media under nonlinear global coupling. Chaos 24:013102. doi: 10.1063/1.4858996
Semenova, N., Zakharova, A., Anishchenko, V., and Scholl, E. (2016). Coherence-resonance chimeras in a network of excitable elements. Phys. Rev. Lett. 117:014102. doi: 10.1103/PhysRevLett.117.014102
Sethia, G. C., Sen, A., and Atay, F. M. (2008). Clustered chimera states in delay-coupled oscillator systems. Phys. Rev. Lett. 100:144102. doi: 10.1103/PhysRevLett.100.144102
Shanahan, M. (2010). Metastable chimera states in community-structured oscillator networks. Chaos 20:013108. doi: 10.1063/1.3305451
Siddique, A. B., Pecora, L., Hart, J. D., and Sorrentino, F. (2018). Symmetry-and input-cluster synchronization in networks. Phys. Rev. E 97:042217. doi: 10.1103/PhysRevE.97.042217
Somers, D. C., Nelson, S. B., and Sur, M. (1995). An emergent model of orientation selectivity in cat visual cortical simple cells. J. Neurosci. 15, 5448–5465. doi: 10.1523/JNEUROSCI.15-08-05448.1995
Sorrentino, F., Pecora, L. M., Hagerstrom, A. M., Murphy, T. E., and Roy, R. (2016). Complete characterization of the stability of cluster synchronization in complex dynamical networks. Sci. Adv. 2:e1501737. doi: 10.1126/sciadv.1501737
Tamaki, M., Bang, J. W., Watanabe, T., and Sasaki, Y. (2016). Night watch in one brain hemisphere during sleep associated with the first-night effect in humans. Curr. Biol. 26:1190. doi: 10.1016/j.cub.2016.02.063
Tian, C., Bi, H., Zhang, X., Guan, S., and Liu, Z. (2017). Asymmetric couplings enhance the transition from chimera state to synchronization. Phys. Rev. E 96:052209. doi: 10.1103/PhysRevE.96.052209
Tian, C., Cao, L., Bi, H., Xu K., and Liu, Z. (2018). Chimera states in neuronal networks with time delay and electromagnetic induction. Nonlinear Dyn. 93, 1695–1704. doi: 10.1007/s11071-018-4285-z
Tinsley, M. R., Nkomo, S., and Showalter, K. (2012). Chimera and phase-cluster states in populations of coupled chemical oscillators. Nat. Phys. 8, 662–665. doi: 10.1038/nphys2371
Uhlhaas, P. J., and Singer, W. (2006). Neural synchrony in brain disorders: relevance for cognitive dysfunctions and pathophysiology. Neuron 52, 155–168. doi: 10.1016/j.neuron.2006.09.020
Wang, Z., and Liu Z. (2020). Partial synchronization in complex networks: chimera state, remote synchronization, and cluster synchronization. Acta Phys. Sin. 69:088902. doi: 10.7498/aps.69.20191973
Wickramasinghe, M., and Kiss, I. Z. (2013). Spatially organized dynamical states in chemical oscillator networks: synchronization, dynamical differentiation, and chimera patterns. PLoS ONE 8:e80586. doi: 10.1371/journal.pone.0080586
Wilson, H. R., and Cowan, J. D. (1972). Excitatory and inhibitory interactions in localized populations of model neurons. Biophys. J. 12, 1–24. doi: 10.1016/S0006-3495(72)86068-5
Xu, L., Chen, Z., Hu, K., Stanley, H. E., and Ivanov, P. Ch. (2006). Spurious detection of phase synchronization in coupled nonlinear oscillators. Phys. Rev. E 73:065201. doi: 10.1103/PhysRevE.73.065201
Xue, Y., and Bogdan, P. (2017). Reliable multi-fractal characterization of weighted complex networks: algorithms and implications. Sci. Rep. 7:7487. doi: 10.1038/s41598-017-07209-5
Xue, Y., and Bogdan, P. (2019). Reconstructing missing complex networks against adversarial interventions. Nat. Commun. 10:1738. doi: 10.1038/s41467-019-09774-x
Yang, R., Gupta, G., and Bogdan, P. (2019). “Data-driven perception of neuron point process with unknown unknowns,” in Proceedings of the 10th ACM/IEEE International Conference on Cyber-Physical Systems (ICCPS) (Montreal, QC).
Yao, N., Huang, Z.-G., Lai, Y.-C., and Zheng, Z. (2013). Robustness of chimera states in complex dynamical systems. Sci. Rep. 3:3522. doi: 10.1038/srep03522
Zamora-Lopez, G., Zhou, C. S., and Kurths, J. (2010). Cortical hubs form a module for multisensory integration on top of the hierarchy of cortical networks. Front. Neuroinform. 4:1. doi: 10.3389/neuro.11.001.2010
Zhang, K. (1996). Representation of spatial orientation by the intrinsic dynamics of the head-direction cell ensembles: a theory. J. Neurosci. 16, 2112–2126. doi: 10.1523/JNEUROSCI.16-06-02112.1996
Keywords: synchronization, chimera state, order parameter, neuronal system, cerebral cortex
PACS numbers: 89.75.Hc, 05.45.Xt, 68.18.Jk
Citation: Wang Z and Liu Z (2020) A Brief Review of Chimera State in Empirical Brain Networks. Front. Physiol. 11:724. doi: 10.3389/fphys.2020.00724
Received: 03 February 2020; Accepted: 02 June 2020;
Published: 30 June 2020.
Edited by:
Plamen Ch. Ivanov, Boston University, United StatesReviewed by:
Ulrich Parlitz, Max Planck Society (MPG), GermanyPaul Bogdan, University of Southern California, Los Angeles, United States
Copyright © 2020 Wang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Zonghua Liu, emhsaXVAcGh5LmVjbnUuZWR1LmNu
 Zhenhua Wang
Zhenhua Wang Zonghua Liu
Zonghua Liu