Peak Running Velocity or Critical Speed Under Field Conditions: Which Best Predicts 5-km Running Performance in Recreational Runners?

This study aimed to examine which variable, between the peak running velocity determined on the track field (V_{peak_TF}) and critical speed (CS), is the best predictor of the 5-km running performance in recreational runners. Twenty-five males performed three tests to determine the V_{peak_TF}, CS, and 5-km running performance on the track field, with a minimal interval of 48 h between each test. The V_{peak_TF} protocol started with a velocity of 8 km⋅h^–1, followed by an increase of 1 km⋅h^–1 every 3 min until volitional exhaustion, which was controlled by sound signals, with cones at every 25 m indicating when the participants were required to pass the cone’s position to maintain the required velocity. The participants performed three time trials (TTs) (1: 2,600 m; 2: 1,800 m; and 3: 1,000 m) on the same day, with a 30-min rest period to determine the CS through the combinations of three (CS₁,₂,₃) and two TTs (CS₁,₂, CS₁,₃, and CS₂,₃). The 5-km running performance time was recorded to determine the test duration, and the mean velocity (MV) was calculated. There was a significant difference observed between the V_{peak_TF} and the MV 5-km running performance. However, no differences were found between the CS values and the MV 5-km running performance. A correlation was observed between the V_{peak_TF} (R = −0.90), CS₁,₂,₃ (R = −0.95), CS₁,₃ (R = −0.95), and the 5-km running performance time. Linear regression indicated that the V_{peak_TF} (R² = 0.82), CS₁,₂,₃ (R² = 0.90), and CS₁,₃ (R² = 0.90) significantly predicted the 5-km running performance time. The CS results showed a higher predictive power for the 5-km running performance, slightly better than the V_{peak_TF}. Also, CS₁,₂,₃ and the CS₁,₃ presented the highest predictive power for the 5-km running performance of recreational runners.

Introduction

Millions of recreational runners participate in long-distance running competitions (i.e., 5 and 10 km) each year, being consistently considered among the most popular distances and with the greatest number of competitions, even greater than marathons (Cushman et al., 2014; Vickers and Vertosick, 2016). Therefore, it is important to apply test protocols that assess the aerobic capacity to accurately predict the running performance, to which aerobic metabolism contributes about 95% of the total energy expenditure (Busso and Chatagnon, 2006). It is possible through these test protocols to be able to identify the physiological and performance variables that might be used to improve the prediction of the runners’ performances, such as the maximal oxygen uptake (${\dot{\text{V}}\text{O}}_{\text{2max}}$), the velocity of ${\dot{\text{V}}\text{O}}_{\text{2max}}$ occurrence (v${\dot{\text{V}}\text{O}}_{\text{2max}}$), running economy (RE), the responses associated with the blood lactate concentrations during exercise [i.e., lactate threshold (LT), anaerobic threshold (AnT), and maximal lactate steady state (MLSS)], peak running velocity (V_peak), and critical speed (CS) (Machado et al., 2013; da Silva et al., 2015; Nimmerichter et al., 2016).

Among these variables, the V_peak and CS stand out, which can be determined in simple, objective, and sensitive protocols that do not require the use and handling of expensive and delicate equipment or invasive techniques, considered accessible and of great practical application (Jones and Poole, 2009).

V_peak is defined as the highest effort intensity achieved during an incremental test until the maximum volitional exhaustion (Noakes et al., 1990), which is considered a strong predictor of endurance running performance and presents high correlation with the 3–90 km events (Slattery et al., 2006; Stratton et al., 2009; Machado et al., 2013). For instance, Machado et al. (2013) reported high correlation (R = 0.95) and predictive power (R² = 0.91) between the V_peak determined on the incremental treadmill test protocol (V_{peak_T}) with a 3-min stage duration, defined according to Kuipers et al. (2003), and the 5-km running performance of recreational runners.

CS represents the intensity of effort (e.g., running speed) that can be maintained for an extended period (≈30–60 min) without a continual rise in systemic [e.g., blood lactate concentration (La) and oxygen uptake (${\dot{\text{V}}\text{O}}_{\text{2max}}$)] and intramuscular metabolism (e.g., pH and phosphocreatine concentration) homeostasis (Jones et al., 2008, 2010; Poole et al., 2016; Jones and Vanhatalo, 2017). This concept is based on the hyperbolic relation between the predetermined intensities of effort (i.e., distance or running speed) and the time it takes to reach exhaustion (i.e., time limit- t_lim) (Hughson et al., 1984; Hill, 1993). Previous studies have also investigated the use of CS for running performance prediction in distances ranging from 40 m to longer distances such as that of a marathon (Kranenburg and Smith, 1996; Florence and Weir, 1997; Nimmerichter et al., 2016). A recent study involving trained endurance athletes has observed higher correlations (R = −0.79 and 0.82) and predictive power (R² = 0.64 and 0.67) between the CS estimated on the treadmill test protocol performed on the same day with time and the mean velocity (MV) 5-km running performance, respectively, suggesting that CS is valuable for predicting performance compared to ${\dot{\text{V}}\text{O}}_{\text{2max}}$ (Nimmerichter et al., 2016).

Nevertheless, to predict the endurance of running performances, the determination of V_{peak_T} and the estimation of CS were exclusively performed under laboratory conditions (Stratton et al., 2009; Machado et al., 2013; Nimmerichter et al., 2016), which do not provide ecological validity due to the different characteristics of a treadmill and track field running regarding propulsion, overcoming air resistance, inertia, and gait pattern that might affect the utilization of treadmill-derived measures into field conditions (Van Caekenberghe et al., 2013). Tests performed on a track field are more applicable due to the higher specificity to the sports’ performance, which can be easily integrated into a daily training routine and, therefore, are less time-consuming than laboratory tests. Furthermore, the development of knowledge concerning the prediction of the 5-km running performance that underlies these variables present on the track field will enable greater specificity on the prescription of training intensities and could also provide practitioners and their coaches the optimal pacing and tactical strategies that will allow improvements on their competitive results.

At the moment, there is no consensus on the best predictor variable (V_peak or CS) contributor determined on the track field relative to the 5-km running performance. Thus, this study aimed to examine which variable, between the peak running velocity determined on the track field (V_{peak_TF}) and the critical speed (CS), is the best predictor of the 5-km running performance in recreational runners. The study’s hypothesis is that V_{peak_TF} has a higher predictive power for the 5-km running performance than does the CS, given that V_peak is the “determined” velocity associated with the ${\dot{\text{V}}\text{O}}_{\text{2max}}$ established through an incremental protocol, while CS is “estimated” through linear regression using mathematical models with a constant distance path protocol.

Materials and Methods

Participants

Twenty-five male recreational runners, regional and local level competitors (mean ± SD: age = 28.6 ± 4.7 years, height = 176.2 ± 9.7 cm, body mass = 78.5 ± 10.4 kg, relative lean mass = 89.3 ± 4.5%, relative adipose mass = 10.7 ± 4.5%), with a 5-km running performance time of 25.3 ± 3.0 min and MV of 12.0 ± 1.3 km⋅h^–1 (which represented 49.8% of the MV from the world record) were recruited as the participants in this study.

All participants were physically active with a training running experience of at least 2 years and had a training frequency of 3.0 ± 0.7 days⋅week^–1, with an average distance of 24.4 ± 7.3 km⋅week^–1. They presented medical clearance to perform exhaustive physical tests and reported no use of nutritional ergogenic supplements for the duration of the study. To include the participant’s data in the final analysis, the following requirement was adopted: Presenting a 5-km running performance time between 21.4 and 32.6 min (Machado et al., 2013; Vickers and Vertosick, 2016; Peserico et al., 2019). The participants were informed that they were free to withdraw from the study at any time. Prior to testing, a written consent form was obtained from all participants. The experimental protocol was approved by the local Human Research Ethics Committee (no. 2.698.091/2018).

Design

After the familiarization process with the track field test protocols, each participant performed three randomly ordered tests to determine the V_{peak_TF}, the CS, and the 5-km running performance on the official outdoor track field (400 m) at the same time of the day under similar climatic conditions (temperature = 25–29 °C and relative humidity = 60–75%), with an interval of 48 h between each test. They were instructed to report for testing well rested, well hydrated, and wearing lightweight comfortable clothing and also to avoid eating 2 h before the maximal exercise tests, to abstain from caffeine and alcohol, and to refrain from strenuous exercise for 24 h before testing (Machado et al., 2013). All of the participants were verbally encouraged throughout the tests, and mineral water was provided ad libitum so that the participants could hydrate themselves, as they were used to do in long-distance races.

Determination of V_peak on the Track Field

The protocol used to determine V_{peak_TF} was the same one used for the determination of V_{peak_T} (Machado et al., 2013). After a warm-up, consisting of walking at 6 km⋅h^–1 for 3 min, the protocol started with an initial velocity of 8 km⋅h^–1, followed by an increase of 1 km⋅h^–1 every 3 min (Machado et al., 2013). The velocity during the protocol on the track field was controlled by sound signals, with cones at every 25 m, indicating when the participants were required to pass the cone’s position to maintain the required velocity (Léger and Boucher, 1980). The protocol ended when the participants reached volitional exhaustion (i.e., the participant was unable to continue running) or when the evaluator identified that the participants failed to cross the cone line with one of two feet on three consecutive occasions (Léger and Boucher, 1980). If the last stage was not completed, V_{peak_TF} was calculated with the partial time remaining in the last stage according to the equation: V_{peak_TF} = V_complete + (Inc × t/T), where V_complete is the running velocity of the last complete stage, Inc is the velocity increment (i.e., 1 km⋅h^–1), t is the number of seconds sustained during the incomplete stage, and T is the number of seconds required to complete a stage (i.e., 180 s) (Kuipers et al., 2003).

Determination of Critical Speed

Each participant performed three time trials (TTs) on the track field (1: 2,600 m; 2: 1,800 m; and 3: 1,000 m). These TTs were selected according to Galbraith et al. (2011) and Hughson et al. (1984) to result in completion times between 3 and 12 min before volitional exhaustion. Consistent with Triska et al. (2017) and Galbraith et al. (2011), the sequence of TTs was conducted in the order of the longest to the shortest effort, on the same day, with a 30-min rest period to ensure a fully reconstituted D′ (maximum distance covered above the CS). The participants completed a 5-min self-paced low-intensity warm-up exercise and were encouraged to cover the set TTs as quickly as possible; time was measured using a stopwatch (Galbraith et al., 2014). The CS was estimated through a linear regression between the distance run (d) and t_lim using the d = (CS × t_lim) + D′ model, where d is the distance run (in meters), CS the critical speed (in meters per second), t_lim the time to exhaustion (in seconds), and D′ is the maximum distance covered (in meters) above the CS (Hughson et al., 1984; Galbraith et al., 2011). CS was estimated through the combinations of three (CS₁,₂,₃) and two TTs (CS₁,₂, CS₁,₃, and CS₂,₃).

5-km Running Performance

The 5-km running performance was preceded by a self-selected warm-up of 10 min. The participants freely choose their pacing strategy during this performance and were encouraged to cover the set distance as quickly as possible on the track field. The 5-km running performance time for each participant was recorded and registered by the evaluator using a stopwatch to determine the test duration, and MV was calculated by dividing the total distance by the trial duration. No information on the elapsed time was provided for the participants.

Statistical Analysis

The Statistical Package for the Social Sciences (SPSS^® v25.0 for Windows, Inc., Chicago, IL, United States) was used to conduct the analysis. The normality assumption was verified using the Shapiro–Wilk test, and the results are presented as the mean ± SD. Sphericity was tested using Mauchly’s test. Greenhouse–Geisser corrections were made when the assumptions of sphericity were violated. One-way ANOVA for repeated measures followed by Bonferroni post hoc test was used to evaluate the differences between V_{peak_TF} and CS that resulted from the different time trial (TT) combinations and the 5-km running performance. Separate linear regression models were fit to establish Pearson’s product-moment correlations (R), coefficients of determination (R²), and the standard error of the estimate (SEE) to examine the goodness of fit of the univariate relation between the V_{peak_TF} and CS that resulted from the different TT combinations (independent variables) and the 5-km running performance (dependent variable). The correlation coefficients (R) were interpreted using the following qualitative descriptors: Trivial (<0.1), small (<0.3), moderate (0.3–0.5), large (0.5–0.7), very large (0.7–0.9), nearly perfect (>0.9), and perfect (1.0) (Hopkins et al., 2009). Absolute agreement and the overall mean bias between CS₁,₂,₃ with CS₁,₂, CS₁,₃, and CS₂,₃ were determined using limits of agreement (LoA) analysis (Bland and Altman, 1986). Furthermore, SEE was also calculated to show any error between the CS results from the different TT combinations. The significance level was set at P < 0.05 for all statistical analyses.

Results

The V_{peak_TF}, the CS values estimated from the different TT combinations, and the MV for the 5-km running performance are shown in Table 1. There were significant differences between the V_{peak_TF} and CS values and the MV for the 5-km running performance. However, there were no differences between the CS values as well as between the CS values with MV for the 5-km running performance.

TABLE 1

Table 1. Mean ± SD and range obtained from the V_{peak_TF}, CS values estimated through different TT combinations, and the MV for the 5-km running performance (n = 25).

Figure 1 shows the relation between each independent variable (the V_{peak_TF} and CS values estimated from the different TT combinations) and the 5-km running performance time. The V_{peak_TF} (R = −0.90) and the CS (R = −0.80 to −0.95) values showed high and negative correlations with the 5-km running performance time. Linear regression analysis indicated that the V_{peak_TF}, CS₁,₂,₃, CS₁,₂, CS₁,₃, and CS₂,₃ significantly predicted 82, 90, 70, 90, and 64% of the variance in the 5-km running performance time, respectively.

FIGURE 1

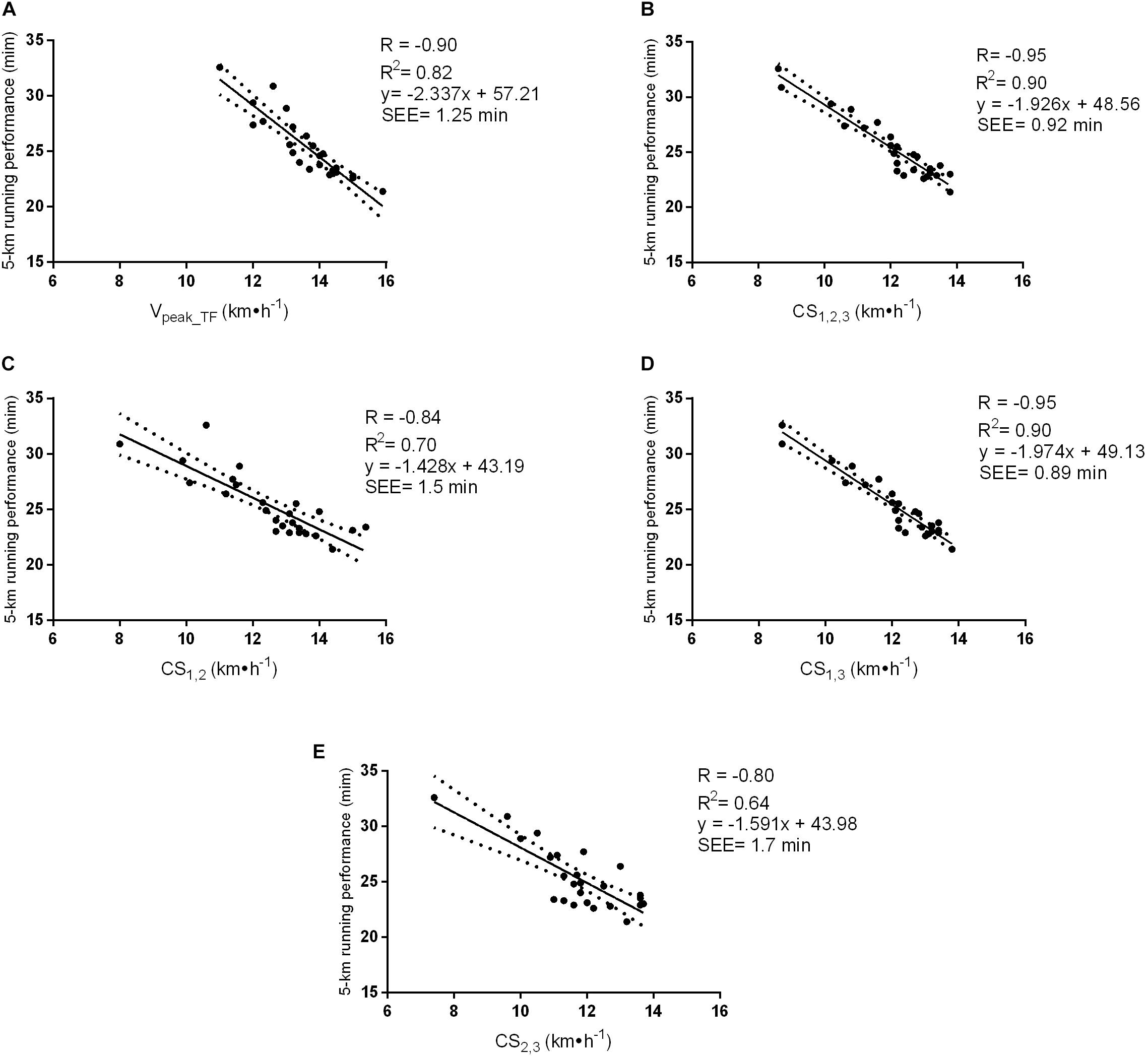
Figure 1. Correlation and linear regression between the (V_{peak_TF}) (A), CS₁,₂,₃ (B), CS₁,₂ (C), CS₁,₃ (D), and CS₂,₃ (E) with the 5-km running performance time in minutes (n = 25). SEE: standard error of the estimate; V_{peak_TF}: Peak running velocity determined on the track field; CS_1,2,3: Critical speed at 2,600, 1,800 and 1,000 m; CS_1,2: Critical speed at 2,600 and 1,800 m; CS_1,3: Critical speed at 2,600 and 1,000 m; CS_2,3: Critical speed at 1,800 and 1,000 m.

The Bland–Altman plots of the differences between CS₁,₂,₃ and CS₁,₂, CS₁,₃, and CS₂,₃ are presented in Figure 2. The results revealed the highest agreement (i.e., the overall mean bias was least and the 95% LoA narrowest) in the comparison between CS₁,₂,₃ and CS₁,₃. In comparison to CS₁,₂,₃, CS₁,₃ showed a SEE of 0.08 km⋅h^–1 and CS₁,₂ and the CS₂,₃ showed SEEs of 0.76 and 0.67 km⋅h^–1, respectively.

FIGURE 2

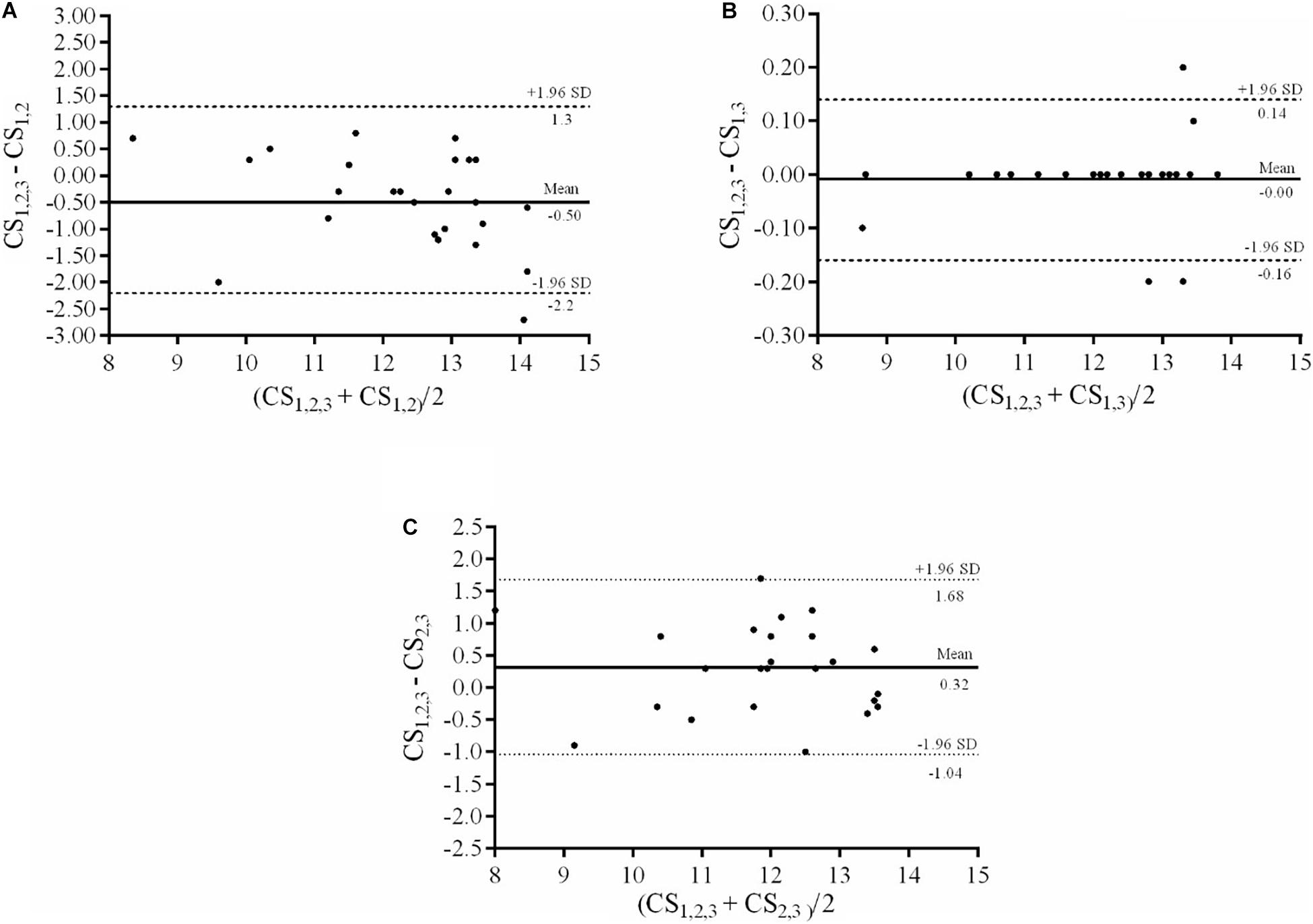
Figure 2. Bland–Altman plots of the differences between CS₁,₂,₃ and CS₁,₂ (A), CS₁,₃ (B), and CS₂,₃ (C). Solid horizontal lines represent the mean bias, while dashed lines represent the lower and upper 95% limits of agreement. CS_1,2,3: Critical speed at 2,600, 1,800 and 1,000 m; CS_1,2: Critical speed at 2,600 and 1,800 m; CS_1,3: Critical speed at 2,600 and 1,000 m; CS_2,3: Critical speed at 1,800 and 1,000 m.

Discussion

The present study aimed to examine which variable, between the peak running velocity determined on the track field (V_{peak_TF}) and the critical speed (CS), is the best predictor of the 5-km running performance in recreational runners. The main finding was that CS showed a higher correlation and predictive power for the 5-km running performance, slightly better than that of V_{peak_TF}, which is contrary to the initial hypothesis. Also, the CS values estimated through three TTs (i.e., CS₁,₂,₃) and the combination of the shortest and the longest TTs (i.e., CS₁,₃) presented the highest correlation and predictive power for this performance in recreational runners.

This is the first study that demonstrated the relation between both the V_{peak_TF} and CS determined on the track field and the 5-km running performance in recreational runners. These results are in accordance with previous studies that demonstrated a higher correlation and predictive power between the V_{peak_T} and CS determined from a treadmill test protocol performed on the same day and the 5-km running performance in untrained volunteers (Stratton et al., 2009), recreational runners (Machado et al., 2013), and endurance athletes (Nimmerichter et al., 2016). However, it must be emphasized that, unlike the method used in this study, Stratton et al. (2009) determined the V_{peak_T} using a different protocol, not only the duration of the tests but also the initial speed, and the aforementioned studies also conducted both the CS and V_peak protocols under laboratory conditions, which could explain the high predictive power for both variables determined on the track field in our study, reflecting the demands of competitive reality and endurance training, as well as the highest ecological validity.

Although the V_{peak_TF} and CS determined on the track field have been shown to be effective predictors of the 5-km running performance, CS₁,₂,₃ and CS₁,₃ demonstrated higher correlations and predictive power that were slightly better than those of V_{peak_TF}. This result may be explained by the fact that all values of CS were similar to the MV for the 5-km running performance in the present study (Table 1), thus suggesting that the participants may have performed the 5-km running performance at intensities close to 100% of the CS. Previous studies have reported that the t_lim at an intensity associated with the CS during running could be sustained for less than 30 min (Pepper et al., 1992; Bull et al., 2008). Interestingly, this is very similar to the average time performed during the 5-km running performance in this study (25.3 ± 3.0 min), confirming that the CS may be held for the length of time taken to complete this performance in recreational runners. However, unlike the CS, previous studies have shown that the t_lim at an intensity associated with 100% of the V_peak during a treadmill protocol could be sustained for less than 7 min by recreational runners (da Silva et al., 2015; Peserico et al., 2019). Thus, we suggest that the similarity between the CS and the MV for the 5-km running performance may in part explain the higher power of the CS to predict performance.

The present study also showed that the CS estimated through three TTs (i.e., CS₁,₂,₃) was not different from the combination of the shortest and the longest TTs (i.e., CS₁,₃) (Table 1). These data are in agreement with those of Smith et al. (2011) showing that the CS estimated from the shortest and the longest t_lim trials (i.e., 110 and 90% v${\dot{\text{V}}\text{O}}_{\text{2max}}$, respectively) can produce similar estimates and the lowest standard error of the mean (SEM) when compared with the CS data from the four t_lim trials (i.e., 90, 100, 105, and 110% v${\dot{\text{V}}\text{O}}_{\text{2max}}$) on a treadmill in moderately trained runners, respectively. Similarly, Kordi et al. (2019), using a similar method to that proposed in our study, reported that the CS values estimated from the shortest and the longest TTs (i.e., 3,600 and 1,200 m, respectively) were similar and also showed an overall lowest mean bias and SEE in comparison with the CS estimated through three TTs (i.e., 3,600, 2,400, and 1,200 m) in experienced, highly trained runners.

Nonetheless, Maturana et al. (2018) demonstrated that an accurate estimation of critical power (CP) in cyclists was achieved when TTs with longer durations were included when compared with five predictive TTs. However, when only short TTs (i.e., less than 10 min) are used, it might result in a higher or a lower estimation of the CP, leading to poor agreement with the CP estimated from a predetermined criterion method (i.e., five TTs) (Maturana et al., 2018). Thus, longer TTs should be included in order to model the CP that more realistically predicts the upper boundary of sustainable endurance exercise, which required a high level of ${\dot{\text{V}}\text{O}}_{\text{2max}}$ (Morton, 2006). In addition, Bishop et al. (1998) showed that the estimation of CP was higher when the TT durations became shorter, and the opposite was true when the TT durations were lengthened.

Thus, it is necessary that the duration and the number of these distances are carefully selected. Previous studies have recommended the TTs range between 2 and 15 min (Hill, 1993; Bishop et al., 1998), with a minimum of 5 min difference between the shortest and the longest TTs (Housh et al., 1990) to help participants with slower ${\dot{\text{V}}\text{O}}_{\text{2}}$ kinetics and also to ensure attainment of the ${\dot{\text{V}}\text{O}}_{\text{2max}}$ and discharging D′ at the end of each exhaustive TT (Simpson and Kordi, 2017). In addition, previous studies have shown that the total number of TTs required to estimate the CS ranges between three and five (Kranenburg and Smith, 1996; Galbraith et al., 2014; Triska et al., 2018), although it is usual for at least three TTs to be performed, especially in non-athletes (Karsten et al., 2014), which is in agreement with the number and the duration range used in the present study.

Although our results suggest that CS₁,₂,₃ and the CS₁,₃ accounted for the majority of the total variance associated with predicting the 5-km running performance time when compared to the V_{peak_TF}, this should be carefully interpreted due to the slight differences in the predictive power found between these variables and the 5-km running performance time (Figure 1), with the V_{peak_TF} being almost as good as the CS₁,₂,₃ and CS₁,₃. Nevertheless, previous studies have shown that V_{peak_T} is highly reliable (Peserico et al., 2014) and has been reported to be a valid measure to prescribe and evaluate improvements in the endurance performance of recreational runners (Peserico et al., 2019).

In contrast, the lack of reliability on the test for CS that resulted from the different TT combinations in recreational runners can be considered a potential limitation. This may arguably increase the potential use of V_{peak_TF} compared to CS in predicting the 5-km running performance of recreational runners. Thus, further studies are required to examine whether the reliability of the CS that resulted from the different TT combinations has as high reliability as the V_{peak_T} in recreational runners in order to effectively predict endurance performance as well as for the prescription and analysis of the training effects.

Therefore, we conclude that the CS results showed a higher predictive power for the 5-km running performance, slightly better than that of V_{peak_TF}. Also, CS₁,₂,₃ and the CS₁,₃ presented the highest predictive power for the 5-km running performance of recreational runners.

Practical Application

Understanding the relation between the V_{peak_TF} and CS determined on the track field with the 5-km running performance would enable coaches, practitioners, and endurance runners to increase specificity in the training methods, which will allow improvements of their competitive results. These variables could be considered a more practical way to evaluate and monitor the effects of endurance training, as well as in elucidating a more homogeneous response when used to prescribe adequate exercise intensities compared to other physiological parameters such as the ${\dot{\text{V}}\text{O}}_{\text{2max}}$, v${\dot{\text{V}}\text{O}}_{\text{2max}}$, and LT. We suggest that a well-structured and periodized training program should take these variables into consideration on the track field as a way of improving the 5-km running performance of recreational runners.

Moreover, the proposed equations can be used to predict the 5-km running performance from the results of the V_{peak_TF}, the CS₁,₂,₃, and the CS₁,₃ estimated on the track field, which has an easy accessibility for coaches, practitioners, and endurance runners. Finally, the estimation of the CS using the combination of the shortest and the longest TTs (i.e., CS₁,₃) is extremely relevant regarding time efficiency and employing applicability setting (i.e., one training session), which can minimize the time commitment of practitioners and endurance runners during assessments.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the Human Research Ethics Committee, State of University of Maringá. The patients/participants provided their written informed consent to participate in this study.

Author Contributions

DioF, DieF, FdAM, and FAM performed material preparation, data collection, and analysis. DioF wrote the first draft of the manuscript. All authors commented on previous versions of the manuscript, read and approved the final version of the manuscript, and contributed to the study conception and design.

Funding

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior—Brazil (CAPES), Finance Code 001.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to thank the participants for their time and effort in this study and Med. Cardiologist Geraldo Nogueira for clinical support.

References

Bishop, D., Jenkins, D. G., and Howard, A. (1998). The critical power function is dependent on the duration of the predictive exercise tests chosen. Int. J. Sports Med. 19, 125–129.

Google Scholar

Bland, J. M., and Altman, D. G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet 1, 307–310. doi: 10.1016/S0140-6736(86)90837-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bull, A. J., Housh, T. J., Johnson, G. O., and Rana, S. R. (2008). Physiological responses at five estimates of critical velocity. Eur. J. Appl. Physiol. 102, 711–720. doi: 10.1007/s00421-007-0649-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Busso, T., and Chatagnon, M. (2006). Modelling of aerobic and anaerobic energy production in middle-distance running. Eur. J. Appl. Physiol. 97, 745–754. doi: 10.1055/s-2007-971894

PubMed Abstract | CrossRef Full Text | Google Scholar

Cushman, D. M., Markert, M., and Rho, M. (2014). Performance trends in large 10-km road running races in the united states. J. Strength Cond. Res. 28, 892–901. doi: 10.1519/JSC.0000000000000249

PubMed Abstract | CrossRef Full Text | Google Scholar

da Silva, D. F., Simões, H. G., and Machado, F. A. (2015). v${\dot{\text{V}}\text{O}}_{\text{2max}}$ versus V_peak, what is the best predictor of running performances in middle-aged recreationally-trained runners? Sci. Sports 30, e85–e92. doi: 10.1016/j.scispo.2014.10.006

CrossRef Full Text | Google Scholar

Florence, S. L., and Weir, J. P. (1997). Relationship of critical velocity to marathon running performance. Eur. J. Appl. Physiol. 75, 274–278. doi: 10.1007/s0042210050160

CrossRef Full Text | Google Scholar

Galbraith, A., Hopker, J., Jobson, S. A., and Passfield, L. (2011). A Novel Field Test to Determine Critical Speed. J. Sports Med. Doping Stud. 1, 1–4. doi: 10.4172/2161-0673.1000101

CrossRef Full Text | Google Scholar

Galbraith, A., Hopker, J., Lelliott, S., Diddams, L., and Passfield, L. (2014). A single-visit field test of critical speed. Int. J. Sports Physiol. Perform. 9, 931–935. doi: 10.1123/ijspp.2013-0507

PubMed Abstract | CrossRef Full Text | Google Scholar

Hill, D. W. (1993). The critical power concept. A Review. Sports Med. 16, 237–254. doi: 10.2165/00007256-199316040-00003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hopkins, W. G., Marshall, S. W., Batterham, A. M., and Hanin, J. (2009). Progressive statistics for studies in sports medicine and exercise Science. Med. Sci. Sports Exerc. 41, 3–13. doi: 10.1249/MSS.0b013e31818cb278

PubMed Abstract | CrossRef Full Text | Google Scholar

Housh, D. J., Housh, T. J., and Bauge, S. M. (1990). A methodological consideration for the determination of critical power and anaerobic work capacity. Res. Q. Exerc. Sport 61, 406–409. doi: 10.1080/02701367.1990.10607506

PubMed Abstract | CrossRef Full Text | Google Scholar

Hughson, R. L., Orok, C. J., and Staudt, L. E. (1984). A high velocity treadmill running test to assess endurance running potential. Int. J. Sports Med. 5, 23–25.

Google Scholar

Jones, A. M., and Poole, D. C. (2009). “Physiological demands of endurance exercise,” in Olympic Textbook of Science in Sport, ed. R. J. Maughan (Chichester, United Kingdom: Blackwell Publishing), 43–55.

Google Scholar

Jones, A. M., and Vanhatalo, A. (2017). The ‘critical power’ concept: applications to sports performance with a focus on intermittent high intensity exercise. Sports Med. 47, 65–78. doi: 10.1007/s40279-017-0688-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Jones, A. M., Vanhatalo, A., Burnley, M., Morton, R. H., and Poole, D. C. (2010). Critical Power: implications for determination of VO_2max and exercise tolerance. Med. Sci. Sports Exerc. 42, 1876–1890.

Google Scholar

Jones, A. M., Wilkerson, D. P., DiMenna, F., Fulford, J., and Poole, D. C. (2008). Muscle metabolic responses to exercise above and below the “critical power” assessed using 31P-MRS. Am. J. Physiol. Regul. Integr. Comp. Physiol. 294, 585–593. doi: 10.1152/ajpregu.00731.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

Karsten, B., Jobson, S. A., Hopker, J., Jimenez, A., and Beedie, C. (2014). High agreement between laboratory and field estimates of critical power in cycling. Int. J. Sports Med. 35, 298–303. doi: 10.1055/s-0033-1349844

PubMed Abstract | CrossRef Full Text | Google Scholar

Kordi, M., Menzies, C., and Galbraith, A. (2019). Comparison of critical speed and D’ derived from 2 or 3 maximal tests. Int. J. Sports Physiol. Perform. 14, 685–688. doi: 10.1123/ijspp.2017-0809

PubMed Abstract | CrossRef Full Text | Google Scholar

Kranenburg, K. J., and Smith, D. J. (1996). Comparison of critical speed determined from track running and treadmill tests in elite runners. Med. Sci. Sports Exerc. 28, 614–618.

Google Scholar

Kuipers, H., Rietjens, G., Verstappen, F., Schoenmakers, H., and Hofman, G. (2003). Effects of stage duration in incremental running tests on physiological variables. Int. J. Sports Med. 24, 486–491. doi: 10.1055/s-2003-42020

PubMed Abstract | CrossRef Full Text | Google Scholar

Léger, L., and Boucher, R. (1980). An indirect continuous running multistage field test: the Université de Montreal track test. Can. J. Sport Sci. 5, 77–84.

Google Scholar

Machado, F. A., Kravchychyn, A. C. P., Peserico, C. S., Da Silva, D. F., and Mezzaroba, P. V. (2013). Incremental test design, peak ‘aerobic’ running speed and endurance performance in runners. J. Sci. Med. Sport 16, 577–582. doi: 10.1016/j.jsams.2012.12.009

PubMed Abstract | CrossRef Full Text | Google Scholar

Maturana, F. M., Fontana, F. Y., Pogliaghi, S., Passfield, L., and Murias, J. M. (2018). Critical power: how different protocols and models affect its determination. J. Sci. Med. Sport 21, 742–747. doi: 10.1016/j.jsams.2017.11.015

PubMed Abstract | CrossRef Full Text | Google Scholar

Morton, R. H. (2006). The critical power and related whole-body bioenergetic models. Eur. J. Appl. Physiol. 96, 339–354. doi: 10.1007/s00421-005-0088-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Nimmerichter, A., Novak, N., Triska, C., Prinz, B., and Breese, B. C. (2016). Validity of treadmill-derived critical speed on predicting 5000-meter track-running performance. J. Strength Cond. Res. 31, 706–714. doi: 10.1519/JSC.0000000000001529

PubMed Abstract | CrossRef Full Text | Google Scholar

Noakes, T. D., Myburgh, K. H., and Schall, R. (1990). Peak treadmill running velocity during the ${\dot{\text{V}}\text{O}}_{\text{2max}}$ test predicts running performance. J. Sports Sci. 8, 35–45. doi: 10.1080/02640419008732129

PubMed Abstract | CrossRef Full Text | Google Scholar

Pepper, M. L., Housh, T. J., and Johnson, G. O. (1992). The accuracy of the critical velocity test for predicting time to exhaustion during treadmill running. Int. J. Sports Med. 13, 121–124. doi: 10.1055/s-2007-1021242

PubMed Abstract | CrossRef Full Text | Google Scholar

Peserico, C. S., Zagatto, A. M., and Machado, F. A. (2014). Reliability of peak running speeds obtained from different incremental treadmill protocols. J. Sports Sci. 32, 993–1000. doi: 10.1080/02640414.2013.876087

PubMed Abstract | CrossRef Full Text | Google Scholar

Peserico, C. S., Zagatto, A. M., and Machado, F. A. (2019). Effects of endurance running training associated with photobiomodulation on 5-Km performance and muscle soreness: a randomized placebo-controlled trial. Front. Physiol. 10:211. doi: 10.3389/fphys.2019.00211

PubMed Abstract | CrossRef Full Text | Google Scholar

Poole, D., Burnley, M., Rossiter, H. B., and Jones, A. M. (2016). Critical power: an important fatigue threshold in exercise physiology. Med. Sci. Sports Exerc. 48, 2320–2334. doi: 10.1249/MSS.0000000000000939

PubMed Abstract | CrossRef Full Text | Google Scholar

Simpson, L. P., and Kordi, M. (2017). Comparision of critical power and W’ derived from two or three maximal test. Int. J. Sports Physiol. Perform. 12, 825–830.

Google Scholar

Slattery, K., Wallace, L., Murphy, A., and Coutts, A. (2006). Physiological determinants of three kilometer running performance in experiences triathletes. J. Strength Cond. Res. 20, 47–52. doi: 10.1519/00124278-200602000-00008

CrossRef Full Text | Google Scholar

Smith, A. E., Kendall, K., Fukuda, D., Cramer, J. T., and Stout, J. R. (2011). Determination of aerobic and anaerobic performance: a methodological consideration. Physiol. Meas. 32, 423–431. doi: 10.1088/0967-3334/32/4/004

CrossRef Full Text | Google Scholar

Stratton, E., O’Brien, B. J., Harvey, J., Blitvich, J., McNicol, A. J., Janissen, D., et al. (2009). Treadmill velocity best predicts 5000-m run performance. Int. J. Sports Med. 30, 40–45. doi: 10.1055/s-2008-1038761

PubMed Abstract | CrossRef Full Text | Google Scholar

Triska, C., Karsten, B., Beedie, C., Koller-Zeisler, B., Nimmerichter, A., and Tschan, H. (2018). Different durations within the method of best practice affect the parameters of the speed-duration relationship. Eur. J. Sport Sci. 18, 332–340. doi: 10.1080/17461391.2017.1418025

PubMed Abstract | CrossRef Full Text | Google Scholar

Triska, C., Karsten, B., Nimmerichter, A., and Tschan, H. (2017). Iso-duration determination of D’ and CS under laboratory and field conditions. Int. J. Sports Med. 38, 527–533. doi: 10.1055/s-0043-102943

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Caekenberghe, I., Segers, V., Willems, P., Gosseye, T., Aerts, P., and De Clercq, D. (2013). Mechanics of overground accelerated running vs. running on an accelerated treadmill. Gait Posture 38, 125–131.

Google Scholar

Vickers, A. J., and Vertosick, E. A. (2016). An empirical study of race times in recreational endurance runners. BMC Sports Sci. Med. Rehabil. 8:26. doi: 10.1186/s13102-016-0052-y

PubMed Abstract | CrossRef Full Text | Google Scholar