- 1Inria, Université Côte d’Azur, Sophia-Antipolis, France
- 2Airbus DS, Toulouse, France
Small object tracking in low-resolution remote sensing images presents numerous challenges. Targets are relatively small compared to the field of view, do not present distinct features, and are often lost in cluttered environments. In this paper, we propose a track-by-detection approach to detect and track small moving targets by using a convolutional neural network and a Bayesian tracker. Our object detection consists of a two-step process based on motion and a patch-based convolutional neural network (CNN). The first stage performs a lightweight motion detection operator to obtain rough target locations. The second stage uses this information combined with a CNN to refine the detection results. In addition, we adopt an online track-by-detection approach by using the Probability Hypothesis Density (PHD) filter to convert detections into tracks. The PHD filter offers a robust multi-object Bayesian data-association framework that performs well in cluttered environments, keeps track of missed detections, and presents remarkable computational advantages over different Bayesian filters. We test our method across various cases of a challenging dataset: a low-resolution satellite video comprising numerous small moving objects. We demonstrate the proposed method outperforms competing approaches across different scenarios with both object detection and object tracking metrics.
Introduction
In recent years, object detection and tracking in remote sensing videos have become a widely attractive area of research. Novel satellite and Wide Area Motion Imagery (WAMI) technologies have created an unprecedented demand for fast and automatic information retrieval. For example, Airbus’ Zephyr high altitude drones can cover up to 20, ×, 30 km2 of continuous video surveillance, or the Chinese Jilin-1 satellite captures ground images spanning several kilometers with a 1-m spatial resolution imaged at 20 Hz.
The generated images contain essential information for civilian and military domains when ground sensors are not locally available. Sample civilian applications include urban planning (Wijnands et al., 2021), automatic traffic monitoring (Kaack et al., 2019), driving behavioral research (Chen et al., 2021), or commerce management with ship monitoring (Cao et al., 2019). Similarly, object detection and tracking contribute to military applications such as border protection or abnormal activity monitoring. For example, the work proposed by Kirubarajan et al. (2000) presents an approach to detect and tracks convoys in different scenarios such as road networks or open fields.
While object tracking has dramatically improved during the last years, a significant amount of approaches solve problems that contain large training datasets and feature-rich targets, such as pedestrian tracking in surveillance cameras or city landscapes. Nevertheless, novel methods need to tackle application-related challenges such as small object tracking in remote sensing images and have to overcome challenges such as datasets with scarce and incomplete annotations.
Particularly, targets in satellite images and high altitude drones present notable challenges to common detectors and trackers. First, objects of interest are very small compared to the field of view. For instance, Figure 1 shows a ground image with a resolution of 1 m/pixel where vehicles span on average 5 × 6 pixels and resemble white moving blobs. In fact, numerous small objects appear at subpixel levels such as motorcycles and are not detectable for common appearance-based object detectors. Additionally, images show diverse noise sources such as illumination changes, clouds, shadows and environmental phenomena such as wind or rain. These noise sources generate numerous false positives when using motion as the main feature for object detection. Moreover, satellites and drones orbit introduce parallax effect noise for object detectors and motion prediction noise for object trackers.
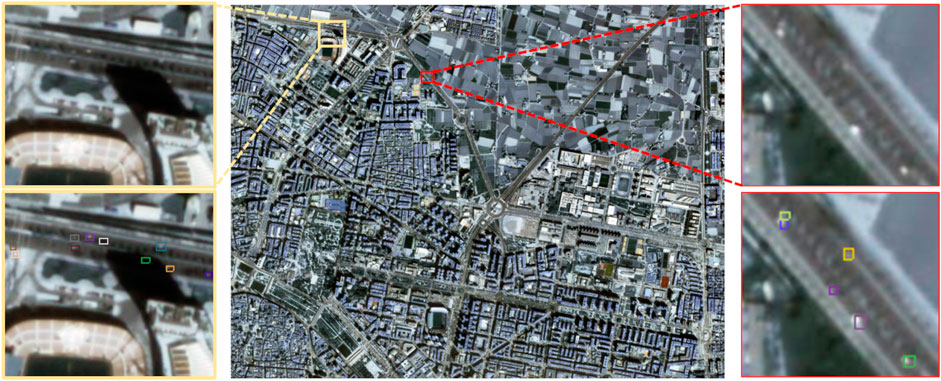
FIGURE 1. Jilin-1 satellite image with provided annotations. Each colored box represents a target instance.
In this paper, we present improvements and further results of our work presented by Aguilar et al. (2021) where we detect small objects using motion and appearance information. We use three consecutive frames to estimate moving object locations and we refine the detections using a patch-based Faster RCNN (Ren et al. (2015)). Specifically, in this paper we improve the patch-based detection by adding the motion response into the Faster RCNN input. The combination of motion and appearance information on extracted patches improves significantly Faster RCNN’s object detection.
Once we obtain object measurements, we feed the extracted data to the probability hypothesis density (PHD) filter, proposed by Mahler (2003). This filter models multi-object states under a Markovian framework, where the state of each tracked object is conditionally independent of all but the previous step. This assumption simplifies the filter and allows it to be computationally efficient in comparison to other related filters at the cost of tracking single state instances instead of full target trajectories. In this paper, we propose an enhanced version of the PHD filter to propagate labels in time without compromising the filter’s performance and also to discriminate surviving and appearing objects in each frame.
This paper is divided into five sections. We discuss popular object detection and tracking approaches used in satellite images in Section 2. We discuss the proposed method in Section 3 where we present the object detection and object tracking approaches. We show results for a challenging dataset in Section 4 and we discuss the conclusion and future work in Section 5.
Related Work
While object detection and tracking are related, for sake of simplicity, we divide our literature review into two categories composed of object detection and tracking applied to satellite images.
Object Detection
Static Image Object Detection
Static image object detection methods rely on spatial information to extract features and obtain object segmentation masks or bounding boxes. Popular approaches include Faster-RCNN, proposed by Ren et al. (2015), YOLO, proposed by Redmon et al. (2016), Retina-Net, proposed by Lin et al. (2017). Although these works obtain remarkable results across several benchmarks, their performance decreases significantly when tested with small objects or weakly labeled datasets such as in remote sensing images. In fact, Acatay et al. (2018) presented a comprehensive review and the drawbacks from using the base Faster-RCNN, YOLO, and Single Shot Detectors (SSD) on aerial images. Several researchers approached satellite object detection with modified appearance-based object detector approach for remote sensing images. For example, Ren et al. (2018) proposed a modified Faster-RCNN to detect small objects in satellite images by modifying the anchor boxes, adding skipped connections, and including contextual information. However, this method focuses on capturing relatively large objects such as planes and large ships. Similarly, Qian et al. (2020) proposed a modified version of Faster-RCNN with a new architecture, new metric, and loss to optimize the training of small objects bounding boxes that do not overlap.
Motion-Only Object Detection
Motion-based detections consist principally in background subtraction and frame differencing. A popular approach is to model backgrounds with Gaussian distributions and parameters derived from observations. This model has been extensively expanded such as with the method proposed by Stauffer and Grimson (2000) to use Gaussian mixture models (GMM) instead of a single Gaussian distribution, or the work proposed by Han and Davis (2012) which uses kernel density estimators (KDE) to estimate background distributions and support vector machines (SVM) to discriminate objects. Yang et al. (2016) proposed ViBe, an approach that updates the background estimation persistently and locally by using random selection. However, background subtraction methods generate noisy results when dealing with long sequences of images with a moving imaging system such as a satellite or drone.
Similarly, frame differencing has shown robustness across several methods. For example, Teutsch and Grinberg (2016) proposed to use frame differencing together with numerous post-processing filters to perform object detection in WAMI images. Also, Ao et al. (2020) proposed to use frame differencing together with noise estimation and shape-based filters to extract objects. These approaches obtain reasonable results but they rely on complex hand-crafted post-processing steps that can be hardly adapted to different noise sources.
Motion models are often robust and computationally lightweight; however, their performance relies heavily on frame registration. Small errors in frame registration or illumination changes often lead to large errors in motion-based object detection.
Spatio-Temporal Convolutional Neural Networks
State-of-the-art methods aim to combine approaches from both appearance and motion to improve object detection. Generally, these methods use CNNs that take into account both motion and appearance information to extract object locations. For instance, LaLonde et al. (2018) proposed ClusterNet and FoveaNet, a two-stage approach for exploiting spatial and temporal data in small object detection. They use five consecutive frames as input to an under-sampling network to create clusters of object locations (ClusterNet), and then they use a region specialized network (FoveaNet) to refine the outputs of the first network. Also, Canepa et al. (2021) proposed T-Rex Net, a network that uses frame differencing as inputs to the network to improve small object detection performance. Sommer et al. (2021) proposed an appearance-based and motion-based object detector by combining two networks, one to estimate moving objects locations, and one to extract image features. These methods showed promising results for ultra high resolution datasets such as the WPAFB 2009 (AFRL (2009)) dataset which contains a resolution of up to 0.25 cms/pixel; however, these approaches cannot be directly applied to lower resolution data such as at 1m/pixel as the target features are lost and performing undersampling could miss the small targets.
Object Tracking
Feature Tracking
Common tracking approaches for satellite images include the use of correlation filters and expansions to this approach. Correlation filters find similarities between frames to responses to learned filters and match the coordinates and responses. For example, Du et al. (2017) employed a correlation filter combined with three frame difference to track objects in satellite images, and Xuan et al. (2020) used correlation filters together with linear equations to track objects even under occlusions. While these methods are robust for object tracking, they rely on initialization and are normally adapted to track single objects.
Joint Tracking and Detection
Numerous state-of-the-art tracking methods are deep learning-based and learn to jointly detect and track objects. For instance Bergmann et al. (2019) proposed Tracktor++ to use a CNN to perform both object detection and tracking. Similarly, Feichtenhofer et al. (2017) proposed Track to Detect and Detect to Track to regress both bounding boxes for the object dimensions and for the object temporal displacement. Among robust CNN tracking approaches are attention-based methods such as Patchwork, proposed by Chai (2019), which consists in using an attention mechanism to predict the location of an object in future frames. Jiao et al. (2021) created a survey of novel generation deep learning-based techniques used for object tracking, where methods mostly depend on correlating learned features in time.
Track by Detection
Tracking by detection approaches include SORT, proposed by Bewley et al. (2016) and its extension DeepSORT, proposed by Wojke et al. (2017). SORT consists of an online multiple object tracker (MOT) that uses multiple Kalman filters for tracking and the Hungarian algorithm (Kuhn and Yaw (1955)) for data association, and DeepSORT is an extension that uses object features similarity to modify the data association step. These approaches obtain state-of-the-art results in remarkable computational times; however, due to their pragmatic approach, they do not process a unified multi-object data uncertainty model that can model ambiguous target paths.
Reid (1979) proposed a Bayesian framework named multiple hypothesis tracking (MHT) and Fortmann et al. (1980) proposed the joint probabilistic data association (JDPA). These approaches consider unified probabilistic models and propagate the data association combinatoric metrics on time. However, these filters are often slow due to the complicated data association process and the exponential increase of complexity with time.
Finally, the random finite set (RFS) framework and random finite set statistics proposed by Mahler (2007) propose an attractive track-by-detection paradigm without compromising the computational time. Among popular trackers are the PHD filter, proposed by Mahler (2003), the cardinally PHD filter, presented by Vo et al. (2006), and novel methods such as the Labelled Multi-Bernoulli Filter, developed by Vo and Vo (2013) and its computationally efficient version Vo et al. (2017). In our case, we propose an extended version of PHD filter due to its robust results and significant computational advantages.
Proposed Approach
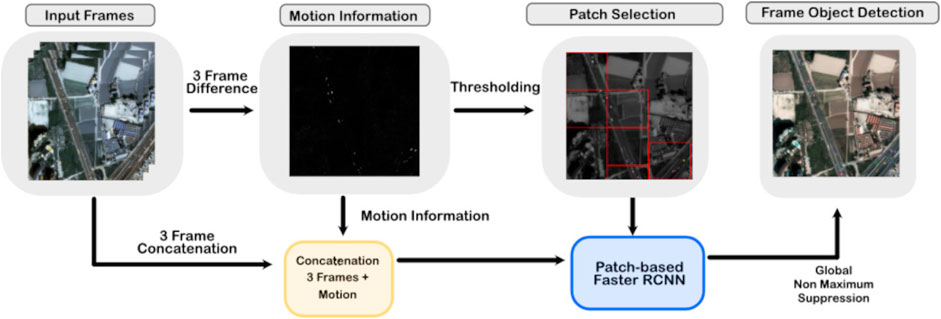
In this paper, we extend the work proposed by Aguilar et al. (2021) which employs a 3-frame difference algorithm to approximate target locations and a patch-based CNN to refine detections. We extend this work by 1) concatenating the frame difference response to the input for the neural network, 2) by performing a tile-based patch selection rather than coordinate-based patch selection. Finally, we use an extended version of the PHD filter, a Bayesian multi-object tracker, to convert frame-wise object detections into track hypothesis.
Motion Aware CNN for Object Detection
Motion Detector
We estimate object motion by finding differences between consecutive frames and adding their responses to create a likelihood 3FDk (i, j), where
Sequentially, we binarize the 3FDk (i.j) response with a frame-adaptive threshold to obtain rough object location estimates by applying the formulas:
Where c ∈ (0, 1) is a percentage-based threshold hyper-parameter and is used to remove noisy 3-frame difference responses. We chose c by performing grid search and choosing values of c that would favor higher detection rates, in particular we set c = 15% for all the experiments shown in Section 4. The 3-frame difference approach yields good object location estimates but it fails to perform shape regularization, detect low contrast objects, and detect slow-moving targets. Therefore, we complement the frame difference response with Faster RCNN (Ren et al. (2015)). This addition helped to filter false positives, discriminate nearby objects, and increase the detection rate.
We use the frame difference for two objectives: to reduce the target search space and to feed this information to the neural network. We begin by tiling the image starting at the origin and using the response G (i, j) to find patches with moving objects. The patch-based approach rather than full image-based approach presents significant advantages: it contributes to focusing on relevant areas rather than the whole image space, and it contributes to training a network with scarce data because one image can yield several training patches. We extract patches that contain object hypothesis (given by the frame difference response) and refine the detections using Faster RCNN.
We modify the inputs to the traditional Faster RCNN by including three consecutive frames (shown in Figure 2B) and by concatenating these images to the frame difference response (shown in Figure 2C). This step is different from our previous approach Aguilar et al. (2021) where we used only one patch as input for the CNN. Using three frames together with the frame-difference response provides an additional cue for the network to detect moving objects (denoted by cyan and yellow colors in the concatenated inputs in Figure 2D. Figure 2E shows that our approach detects very small moving objects such as motorcycles that would have been missed by using only one frame as input. The addition of motion information improves detection rates for small moving objects and also reduces false positives of vehicle-looking static objects. Section 4.3 shows further details in the effect of using three frames and frame difference as opposed to one frame.
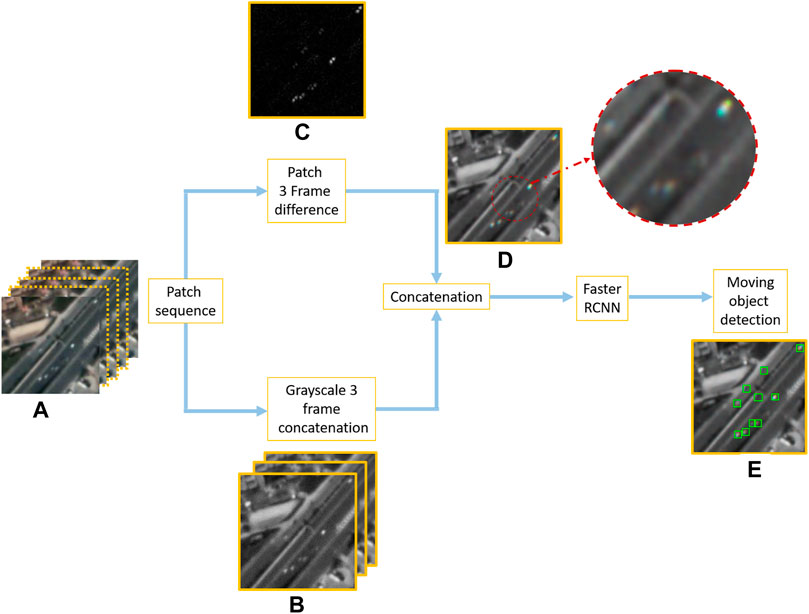
FIGURE 2. Modified input for Faster RCNN to incorporate motion information. (A) Sample input patch sequence. (B) Grayscale 3 frame concatenation. (C) Patch 3 frame difference response. (D) Concatenation of (C) and (B). (E) Sample object detector output.
Finally, we merge the patch results by performing global non-maximum suppression and applying the respective offset to the patch-based detections. The whole object detection process is summarized in Figure 3.
Object Tracking With the GM-PHD Filter
Motion and Measurement Modeling
We define the state vector for the jth target at time k as
Where τ is a hyperparameter related to the sampling frequency. Similarly, we define the ith measurement at time k as
PHD Filter
We aim to estimate the multi-target states from a sequence of possibly noisy or cluttered measurements. We approach this task by using the random finite set (RFS) statistics defined by Mahler (2007). This setup provides a Bayesian formulation for modeling objects and observations as set-valued random variables. Specifically, the collection of targets state at time k is defined by
The PHD filter provides an approximation to the optimal multi-target filter by modeling the posterior pk|1:k (Xk|Z1:k) as a Poisson random finite set and by recursively propagating its first-order statistical moment, called probability hypothesis density (PHD) function. The PHD filter achieves this task by iteratively performing a two step process: the prediction step and the update step.
The prediction step consists on estimating the PHD function Dk|1:k−1 (Xk|Z1:k−1) at time k given only previous measurements, abbreviated as Dk|k−1(x). The update step consists on estimating the posterior PHD Dk|1:k (Xk|Z1:k) using the predicted information and the new measurement obtained at time k and is abbreviated to Dk|k(x).
The GM-PHD Filter
The Gaussian Mixture PHD Filter (GM-PHD), proposed by Vo and Ma (2006), is a close form solution to the PHD recursion and its convergence properties are analyzed by Clark and Vo (2007). The GM-PHD relies on the assumptions of linear Gaussian motion and measurement models explained in Section 3.2.1. Additionally, the GM-PHD assumes the form of the posterior at the previous time frame, Dk−1|k−1(x), has the form of a Gaussian mixture given by:
Where Jk−1|k−1 is the number of Gaussian components and
The GM-PHD filter estimates the predicted Dk|k−1(x) and updated Dk|k(x) PHDs with Gaussian mixtures. The closed form solution for the GM-PHD prediction step is given by the equation:
Where Fk and Q are respectively the transition and motion covariance matrices defined in Section 3.2.1, ps is the survival probability, and λ(x) is the birth RFS intensity which will be described in Section 3.2.4. Finally, we update the GM-PHD posterior following the equation:
Where Dk|k−1(x) denotes the predicted GM components and pD is the probability of detection. The terms
The updated component weight
Where κk(z) denotes the clutter process intensity (modeled with a Poisson Random Finite Set) and
We estimate the filter’s inference cardinality by adding all the weights in the posterior PHD and we apply merging and pruning for components with very small weights in order to preserve the computational advantages of the PHD filter.
PHD Filter Enhancements
We use a measurement-driven approach to estimate the birth λ(x) intensity. Specifically, we use an adapted measurement classification similar to Fu et al. (2018) to discriminate measurements into surviving measurements,
We implement the label preserving structure proposed by Panta et al. (2009) as the original GM-PHD filter does not account for target labels or past trajectories. This extension initializes a label for every Gaussian mixture component and propagates the label in time without affecting the filter performance. Each birth step initializes new labels for each birth component and the labels are tracked during the prediction and the data association step. These advantages contribute to keeping track of possible target trajectories without compromising the filter computational load.
Results
Evaluation Metrics
We evaluate our methods by using object detection and object tracking metrics. We use ground truth annotations in the form of ok = {o1, o2, … , oN}, where k is the frame number and oi = (px, py, l) is a single annotated object at coordinates (px, py) with associated label l. We let an estimated target be
Object Detection Metrics
For object detection, we report the F1 score which is a widely accepted evaluation metric to evaluate the quality of the detector. The F1 score is defined as:
Where precision denotes the ratio of relevant hypothesis proposed by the object detector and is defined as:
Recall denotes the percent of correctly detected objects in comparison to the total number of available objects and is defined as:
We report these metrics as percentages, where the best score is of 100 and the worst score is 0. Additionally, we present a precision-recall curve to show the robustness of the proposed approach over the possible parameter ranges and to show its improved performance over possible competing approaches. We use these tests to choose the parameters for running the F1 score for each listed method.
Object Tracking Metrics
We also report tracking metric ClearMOT, proposed by Bernardin and Stiefelhagen (2008), as it has become a popular and robust metric for tracking algorithms. We report the multiple object tracking accuracy (MOTA) which evaluates the quality of the recovered tracks. It considers FPs, FNs, and identity switches (IDSs), The MOTA score is defined as:
Where N refers to the number of frames, and FNk, FPk, IDSk, GTK refers to the false negatives, false positives, identity switches and number of ground truth objects at frame k respectively. The MOTA score has a range in (−∞, 1), where negative values report poor performances, and one is the best possible score. In this work, we report the scores as a percentages to keep consistency with literature. We also report the multiple object tracking precision (MOTP), which considers the average distance error between the detected objects and the ground truth objects. The MOTP is defined as:
Where ck refers to the number of correctly detected objects at frame k and di,k denotes the distance between a ground truth object and the detected hypothesis. The MOTP score is in the range [0, ∞) where 0 denotes the perfect score and large values denote worse performances.
Finally, we report track quality measures in a similar format to Dendorfer et al. (2021). We call a trajectory mostly tracked (MT) if we can persistently track at least 80% of its path. Similarly, we call a trajectory mostly lost (ML) is we can track 20% or less of its ground truth trajectory. We report these scores as percentages where larger percentages of MT scores denote better performances but larger percentages of ML scores denote worse performances.
Experiment Set up
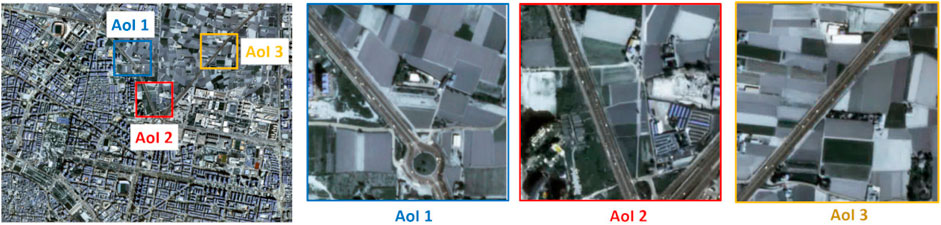
For evaluation purposes, we use the CGSTL dataset, available at https://mall.charmingglobe.com. This dataset contains a video of the city of Valencia, Spain, recorded on 7 March 2017, by the Jilin-1 satellite. Its spatial resolution is 1 m/pixel and the video spans 12 kms2, with a size of 3,071 × 4,096 pixels. The video contains 580 frames and represents 29 s of video imaged at 20 frames per second. The labels were provided by Ao et al. (2020) and contain the (x, y) object center coordinates, the width, and height of the object bounding boxes. The provided ground truth contains strong labeling for only moving targets in three areas of interest (AoI) of size 500, ×, 500 pixels (shown in Figure 4). The approximate coordinate location for each area are AoI 1 [520, 1616], AoI 2 [1074, 1895] and AoI 3 [450, 2810] with respect to the first frame. Additionally, we performed image stabilization (ORB(Rublee et al. (2011)) to compensate for the satellite motion during the recorded video. Finally, only one every ten frames is labeled (58 total labeled frames), hence, we used the stabilization procedure and linear interpolation between frames to fill the label subsampling. The stabilization procedure has a significant impact on object detection, object tracking, and score evaluation across all 580 frames as these methods depend on linear object motion and static background. It is worth mentioning we improve the stabilization procedure over our previous work (Aguilar et al. (2021)) by using the Python OpenCV implementation of ORB(Rublee et al. (2011)); hence our ‘true positive’ distance criteria is set to five pixels rather than 20 pixels as in our previous work.
All of the AoIs contain highways and moving vehicles at high speed. AoI one contains a roundabout, where objects reduce their velocity and travel in clusters. AoI two contains a highway next to farming structures that create numerous false positives for both motion and appearance-based object detectors. AoI three contains a highway with objects moving at high speeds. It is worth mentioning all AoIs contain numerous motorcycles and very small objects that are often missed in the ground truth annotations due to the difficulty of labeling such objects at such low image resolution. For each AoI, we trained the network using the other two AoIs as training data due to the ground truth data scarcity. We trained the networks using extracted patches of size 128 × 128 centered at ground truth objects and we augmented data by using patch vertical and horizontal flips, and random translations. We used the Pytorch implementation for Faster-RCNN using a pre-trained ResNet50 proposed by He et al. (2016) as backbone for feature extraction. The networks were trained using an NVIDIA QUADRO using stochastic gradient descend as optimizer with a learning rate of lr = 0.005 and a weight decay of 0.0005.
Ablation Studies
We perform ablation studies to investigate the impact of using patch-based inference and the impact of including motion information on object detection quality. We report the F1 scores for our method using path-selection only, motion-information only, and patch-selection and motion-information combined. We evaluate these scores across all AoIs and report the average precision, recall, and the F1 scores for each combination.
Patch-Based Inference
We test the effect of using a patch-based method by comparing a full-image and patch-based inference with Faster RCNN. Table 1 shows that a full-image Faster RCNN obtains a F1 metric of 61.69 but using a patch-based Faster RCNN increased the F1 score to 69.22. The patch-based approach outperforms Faster RCNN in the precision score because it reduces the search space to areas with moving objects and decreases the ratio of FPs. This result is expected as satellite images contain numerous blob-looking objects that yield false positives and Faster RCNN alone would detect the objects as vehicles. These results are developed further and shown numerically and visually in Section 4.4. Additionally, we test the effect of varying the patch size by evaluating average object detection metrics using patch sizes of 32, 64, 128, 256, and 512 (full image). The size effects for the patch selection are depicted in Table 2, were the highest F1 score is obtained for the patch size of 128 × 128 pixels. During our experiments, we concluded that the patch size of 128 × 128 focuses the CNN to smaller regions while preserving contextual information. In fact, a patch size of 64 × 64 yielded numerous false positives from static objects with white-blob appearance. On the contrary, large patch sizes such as 256 × 256 and 512 × 512 obtained large numbers of misdetections due to the small object size in comparison with the field of view.
Motion-Based Inference
We investigate the effect of including motion information by testing the full-image Faster RCNN combined with motion information. We achieve this task by feeding three consecutive frames concatenated with the three frame difference algorithm to Faster RCNN. Table 1 shows that including motion information for the full-image Faster RCNN improves the F1 score from 61.69 to 70.05. This improvement occurs due to the increase in the precision score, from 56.73 to 69.46. Our results show that including motion information also helps Faster RCNN to filter non-moving objects in a similar fashion to using a patch-based approach.
Motion and Patch-Based Inference
Finally, we test the effects of including motion information and a patch-based approach to the original Faster RCNN. Table 1 shows that adding both motion information and patch-based inference increased the F1 score of the original Faster RCNN by 6 and 7% respectively. The combined effect of using a patch inference and including motion information reduced the false-positive ratios further, thus, increasing the precision score from 69.46 to 69.06 to 78.13. It is worth noting that neither the addition of motion or a patch-based approach contributed to increasing the recall score. In fact, full-image Faster RCNN obtains higher recall values than the proposed approach at the cost of increasing the number of false detections. These results suggest further development explained in Section 5.
Object Detection Evaluation
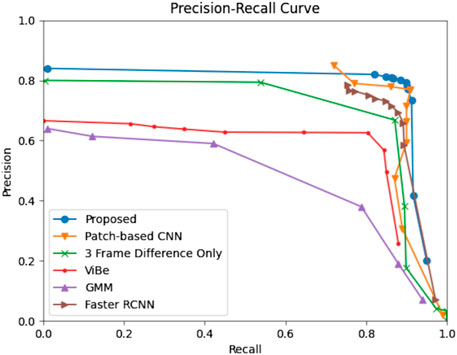
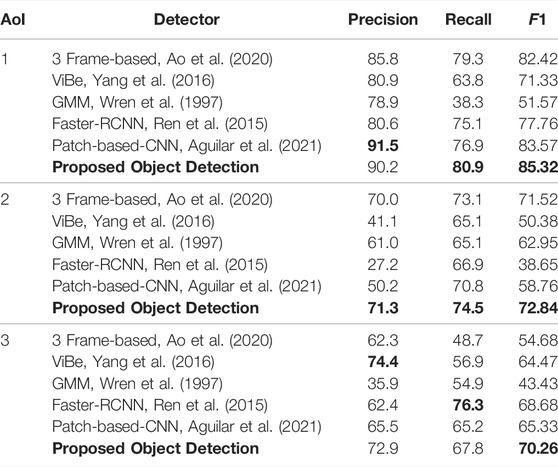
We evaluate the proposed object detector using the F1 metric mentioned in Section 4.1.1 and we compare its performance with five competing object detectors: custom 3-frame difference proposed by Ao et al. (2020), background subtraction using Gaussian mixture models proposed by Wren et al. (1997), ViBe, proposed by Yang et al. (2016), Faster RCNN, proposed by Ren et al. (2015) and the Patch-based object detector presented by Aguilar et al. (2021). We calibrate each method parameters by running a precision-recall curve on AoI 1, shown in Figure 5. We also show visual and numerical results for each AoI by reporting the precision, recall, and F1 scores for each competing method in Table 3 and by showing sample object detection results in Figure 6 and in Figure 7.

FIGURE 6. Sample object detection in sub-region of AoI 1. First row: (A) sample patch . (B) Ground truth bounding boxes. (C) 3-frame difference response. Second row: (D) Proposed method. (E) Output of patched-based Faster RCNN. (F) Output of Faster RCNN. Third row: (G) Output of ViBe. (H) Output of 3 frame based detector. (I) Output of GMM detector.

FIGURE 7. Sample object detection in sub-region of AoI 2. First row: (A) sample patch . (B) Ground truth bounding boxes. (C) 3-frame difference response. Second row: (D) Proposed method. (E) Output of patched-based Faster RCNN. (F) Output of Faster RCNN. Third row: (G) Output of ViBe. (H) Output of 3 frame based detector. (I) Output of GMM detector.
We varied the threshold and confidence parameters for 11 points in the range (0, 1) for the methods: 3-frame difference, GMM, Faster RCNN, Patch-based RCNN, and the proposed approach. For ViBe, we changed the neighbor radius parameter: R for 11 points in the range (5, 50). Figure 5 shows that our method is robust to parameter variations: it obtains better F1 scores across a diverse parameter range as the combination of appearance and time information increases true positives and decreases false negatives.
Figure 6 shows sample results for AoI 1. This area contains clusters of small moving objects at a roundabout and also presents numerous small vehicles such as motorcycles or bicycles. Figure 6 shows that ViBe and GMM struggle to detect small and low contrast targets; hence, their recall values in Table 3 are the lowest for AoI 1. Similarly, the 3-frame difference approach merges and splits nearby targets. On the other side, Figure 6 shows that the supervised approaches detect a large number of relevant objects; thus their recall score for all these methods is greater than 75%. However, both Faster RCNN and patch-based RCNN suffer from false positives such as detecting objects in farms or buildings. These artifacts reduce the overall F1 score for the detectors.
Figure 7 shows AoI two which contains two high-speed highways next to buildings with rich textures that generate false positives. For example, Figure 7 shows clusters of moving objects. Figure 7 shows that both Faster RCNN and the patch-based RCNN detect false positives in the static background while our approach can discriminate only moving objects. Table 3 shows that the proposed approach obtains better F1 scores than all the competing methods, thanks to the better combination of precision-recall. It detects more relevant objects while reducing the overall ratio of false positives.
Object Tracking Evaluation
We compare object tracking using the MOTA, MOTP, MT and ML and F1 scores shown in Tables 4, 5, 6. We compare the proposed GM-PHD tracker with the SORT tracker, developed by Bewley et al. (2016) and with the Generalized Labeled Multi-Bernoulli filter (GLMB), developed by Vo et al. (2017). We test the tracking outputs applied to each object detector shown in Table 3 combined with all 3 filters.
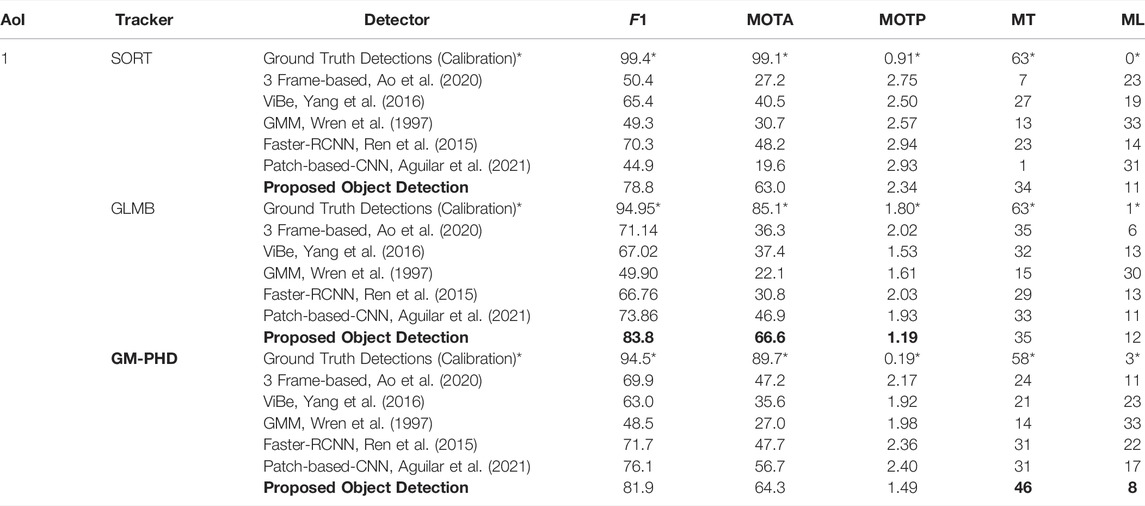
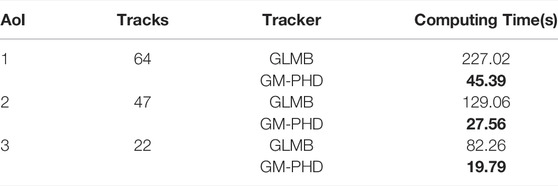
TABLE 4. Tracking Metrics for AoI 1. *Denotes ground truth measurements used for calibration and filter-only testing.
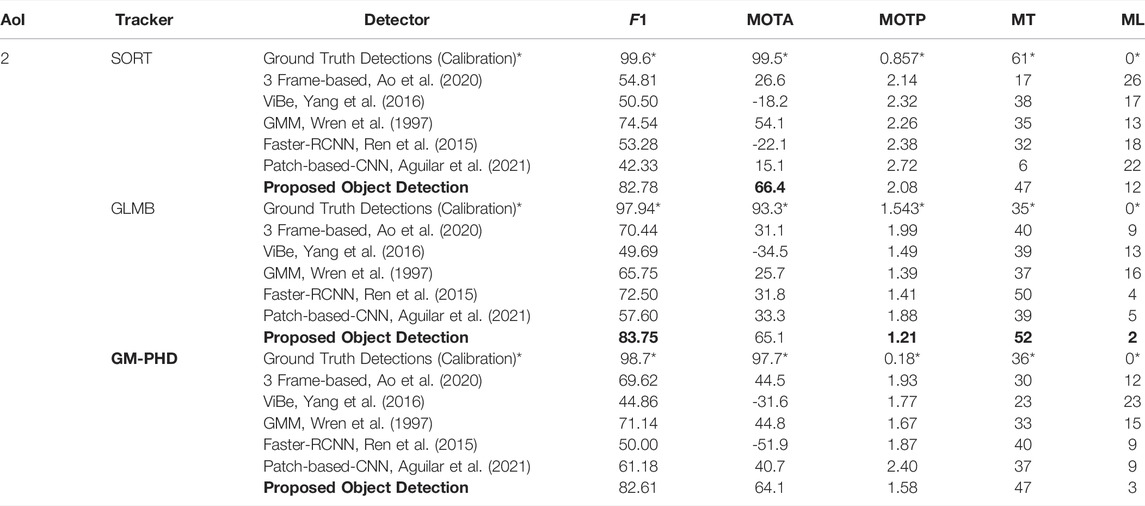
TABLE 5. Tracking Metrics for AoI 2. *Denotes ground truth measurements used for calibration and filter-only testing.
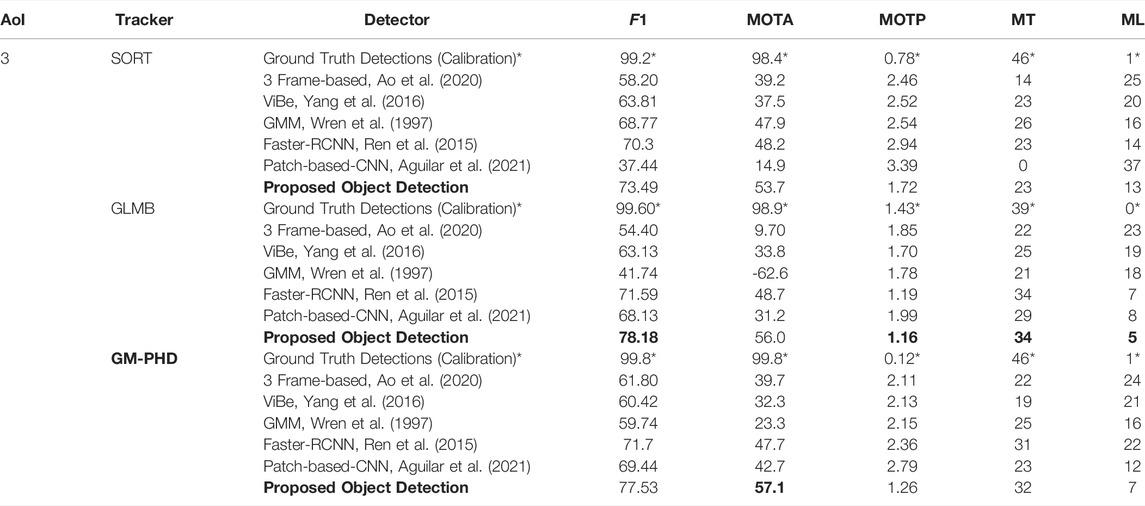
TABLE 6. Tracking Metrics for AoI 2. *Denotes ground truth measurements used for calibration and filter-only testing.
The rows marked with an asterisk* in Tables 4, 5, 6 show tracking metrics using ground truth object detections as filter inputs. These measurements simulate ideal object detectors and contribute to calibrating the filters’ parameters. Tables 5, 6 show robust performance for all three trackers across AoI two and AoI 3 (high-speed highways): all three filters obtain MOTA scores close to 99%. However, Table 4 shows a case where SORT outperforms the GM-PHD and the GLMB filter when tracking with ground truth labels. SORT obtains a MOTA score of 99.4% while the GLMB filter 85.1% and GM-PHD filter obtains 89.7%. The GM-PHD and GLMB filter decrease their performance mostly due to the increased uncertainty and label switches for nearby slow-moving targets inside the roundabout of AoI 1.
The second to seventh row of Tables 4, 5, 6 show metrics for tracking results applied to each object detector output. These detectors present considerable challenges for trackers due to clutter measurements and numerous misdetections. Tables 4, 5, 6 show that both the GLMB and GM-PHD filter outperform the SORT filter for object detectors with high detection rate. For instance, the GM-PHD filter obtains higher MOTA scores for 3-frame difference, Faster-RCNN, patch-based Faster-RCNN, and the proposed method. These results are reflected in Figure 8 where the GM-PHD recovers most of the objects moving in the roundabout. On the other hand, SORT outperforms the GM-PHD and GLMB filters for object detection with low detection rate such as ViBe and GMM, where SORT obtains higher MOTA scores than the GM-PHD filter but lower MOTA scores compared to the proposed object detection and GM-PHD filter.

FIGURE 8. Sample Object Tracking. The square denotes the object current location and the line the object past locations. First column: ground truth marks. Second Column: Faster RCNN (Ren et al., 2015) and SORT (Bewley et al., 2016). Third column: proposed tracking algorithm.
During our experiments, we determined that SORT performs better in tracking cases with linear constant motions, such as in AoI one and AoI 2. In fact, SORT obtained better results than the GM-PHD and GLMB filter for AoI two when applied in our proposed method. However, SORT presented difficulties adapting to high-speed tracks as in AoI 3. Figure 8 shows the incomplete track trajectories of applying SORT to the outputs of Faster RCNN.
Finally, our modified GM-PHD filter presents similar tracking performances to the GLMB filter. The GLMB tracker slightly outperforms the modified GM-PHD filter in most tracking scores in all three AoIs. This is an expected result as the GLMB tracker shares the RFS framework with GM-PHD but has been extended to jointly estimate object states and tracks. Nevertheless, the GLMB filter retrieves tracks at the cost of a high computational burden. In fact, the efficient implementation of the GLMB filter (Vo et al. (2017)) relies on a pre-processing PHD filter lookup step and a Gibbs sampler step to perform joint prediction and update. Vo et al. (2017) explain that the efficient GLMB filter has a complexity of
Conclusion and Future Work
In this paper, we presented an improved track-by-detection approach where we use motion information together with neural networks to detect small moving objects on satellite images. Additionally, we perform tracking by using a modified version of the GM-PHD filter. Our version of the GM-PHD uses a measurement-driven birth intensity approximation and a label propagation in time. We present results for three AoIs in a challenging dataset where our approaches do not only outperform competing detection and tracking algorithms, but also detect objects not labeled by the ground truth annotations.
While our method performs detection and tracking, the method still requires several improvements. For example, our approach still misses several objects at sub-pixel level that appear and disappear. This drawback could be improved by including the tracking information into the object detection in order to perform a unified track-and-detection approach.
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/Supplementary Material.
Author Contributions
CA contributed with the experimental design, production of results, and writing of this manuscript. MO and JZ contributed with developing the main idea, data analysis, and supervision of this study. All authors contributed to the manuscript and approved the submitted version.
Funding
This research work has been funded by BPI France under the LiChIE contract. The open access publication fees are provided by Inria.
Conflict of Interest
Author MO was employed by Airbus Defense and Space, France.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The authors are grateful to the OPAL infrastructure from Université Côte d’Azur for providing resources and support. Additionally, the authors would like to thank BPI France for the financial support under the LiChiE contract.
References
Acatay, O., Sommer, L., Schumann, A., and Beyerer, J. (2018). “Comprehensive Evaluation of Deep Learning Based Detection Methods for Vehicle Detection in Aerial Imagery,” in 2018 15th IEEE International Conference on Advanced Video and Signal Based Surveillance (AVSS), Auckland, New Zealand, 27-30 Nov. 2018 (IEEE), 1–6. doi:10.1109/AVSS.2018.8639127
[Dataset] AFRL (2009). Wright-Patterson Air Force Base (WPAFB) Dataset. Available at: https://www.sdms.afrl.af.mil/index.php?collection=public-data&page=public-data-list.
Aguilar, C., Ortner, M., and Zerubia, J. (2021). “Small Moving Target MOT Tracking with GM-PHD Filter and Attention-Based CNN,” in 2021 IEEE 31st International Workshop on Machine Learning for Signal Processing (MLSP), Gold Coast, Australia, 25-28 Oct. 2021 (IEEE), 1. –6. doi:10.1109/MLSP52302.2021.9596204
Ao, W., Fu, Y., Hou, X., and Xu, F. (2020). Needles in a Haystack: Tracking City-Scale Moving Vehicles from Continuously Moving Satellite. IEEE Trans. Image Process. 29, 1944–1957. doi:10.1109/TIP.2019.2944097
Bergmann, P., Meinhardt, T., and Leal-Taixé, L. (2019). “Tracking without bells and Whistles,” in 2019 IEEE/CVF International Conference on Computer Vision (ICCV), Seoul, Korea (South), 27 Oct.-2 Nov. 2019, 941–951. doi:10.1109/iccv.2019.00103
Bernardin, K., and Stiefelhagen, R. (2008). Evaluating Multiple Object Tracking Performance: The CLEAR MOT Metrics. EURASIP J. Image Video Process. 2008, 1–10. doi:10.1155/2008/246309
Bewley, A., Ge, Z., Ott, L., Ramos, F., and Upcroft, B. (2016). “Simple Online and Realtime Tracking,” in 2016 IEEE International Conference on Image Processing (ICIP), Phoenix, AZ, USA, 25-28 Sept. 2016 (IEEE), 3645–3649. doi:10.1109/ICIP.2016.7533003
Bohyung Han, B., and Davis, L. S. (2012). Density-based Multifeature Background Subtraction with Support Vector Machine. IEEE Trans. Pattern Anal. Mach. Intell. 34, 1017–1023. doi:10.1109/TPAMI.2011.243
Canepa, A., Ragusa, E., Zunino, R., and Gastaldo, P. (2021). T-RexNet-A Hardware-Aware Neural Network for Real-Time Detection of Small Moving Objects. Sensors 21, 1252. doi:10.3390/s21041252
Cao, C., Mao, X., Zhang, J., Meng, J., Zhang, X., and Liu, G. (20192018). “Ship Detection Using X-Bragg Scattering Model Based on Compact Polarimetric SAR,” in The Proceedings of the International Conference on Sensing and Imaging. Editors E. T. Quinto, N. Ida, M. Jiang, and A. K. Louis (Cham: Springer International Publishing), 87–96. doi:10.1007/978-3-030-30825-4_8
Chai, Y. (20192019). IEEE/CVF International Conference on Computer Vision (ICCV). Los Alamitos, CA, USA: IEEE Computer Society, 3414–3423. doi:10.1109/ICCV.2019.00351Patchwork: A Patch-wise Attention Network for Efficient Object Detection and Segmentation in Video Streams
Chen, Y., Qin, R., Zhang, G., and Albanwan, H. (2021). Spatial Temporal Analysis of Traffic Patterns during the Covid-19 Epidemic by Vehicle Detection Using Planet Remote-Sensing Satellite Images. Remote Sensing 13, 208. doi:10.3390/rs13020208
Clark, D., and Vo, B.-N. (2007). Convergence Analysis of the Gaussian Mixture PHD Filter. IEEE Trans. Signal. Process. 55, 1204–1212. doi:10.1109/TSP.2006.888886
Dendorfer, P., Os̆ep, A., Milan, A., Schindler, K., Cremers, D., Reid, I., et al. (2021). MOTChallenge: A Benchmark for Single-Camera Multiple Target Tracking. Int. J. Comput. Vis. 129, 845–881. doi:10.1007/s11263-020-01393-0
Du, B., Sun, Y., Cai, S., Wu, C., and Du, Q. (2018). Object Tracking in Satellite Videos by Fusing the Kernel Correlation Filter and the Three-Frame-Difference Algorithm. IEEE Geosci. Remote Sensing Lett. 15, 168–172. doi:10.1109/LGRS.2017.2776899
Feichtenhofer, C., Pinz, A., and Zisserman, A. (2017). “Detect to Track and Track to Detect,” in International Conference on Computer Vision (ICCV), Venice, Italy, 22-29 Oct. 2017, 1–11. doi:10.1109/iccv.2017.330
Fortmann, T., Bar-Shalom, Y., and Scheffe, M. (1980). “Multi-target Tracking Using Joint Probabilistic Data Association,” in 1980 19th IEEE Conference on Decision and Control including the Symposium on Adaptive Processes, Albuquerque, NM, USA, 10-12 Dec. 1980, 807–812. doi:10.1109/CDC.1980.271915
Fu, Z., Angelini, F., Naqvi, S. M., and Chambers, J. A. (2018). “GM-PHD Filter Based Online Multiple Human Tracking Using Deep Discriminative Correlation Matching,” in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, 15-20 April 2018, 4299–4303. doi:10.1109/ICASSP.2018.8461946
He, K., Zhang, X., Ren, S., and Sun, J. (2016). “Deep Residual Learning for Image Recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27-30 June 2016, 770–778. doi:10.1109/CVPR.2016.90
Jiao, L., Zhang, R., Liu, F., Yang, S., Hou, B., Li, L., et al. (2021). New Generation Deep Learning for Video Object Detection: A Survey. IEEE Trans. Neural Netw. Learn. Syst. 2021, 1–21. doi:10.1109/tnnls.2021.3053249
Kaack, L. H., Chen, G. H., and Morgan, M. G. (2019). Truck Traffic Monitoring with Satellite Images. COMPASS ’19, 155–164. doi:10.1145/3314344.3332480
Kirubarajan, T., Bar-Shalom, Y., Pattipati, K. R., and Kadar, I. (2000). Ground Target Tracking with Variable Structure IMM Estimator. IEEE Trans. Aerosp. Electron. Syst. 36, 26–46. doi:10.1109/7.826310
Kuhn, H. W., and Yaw, B. (1955). The Hungarian Method for the Assignment Problem. Naval Res. Logistics 2, 83–97. doi:10.1002/nav.3800020109
LaLonde, R., Zhang, D., and Shah, M. (2018). “Clusternet: Detecting Small Objects in Large Scenes by Exploiting Spatio-Temporal Information,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Salt Lake City, UT, USA, 18-23 June 2018 (IEEE), 4003–4012. doi:10.1109/CVPR.2018.00421
Lin, T.-Y., Goyal, P., Girshick, R., He, K., and Dollár, P. (2017). “Focal Loss for Dense Object Detection,” in 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22-29 Oct. 2017 (IEEE), 2999–3007. doi:10.1109/ICCV.2017.324
Mahler, R. P. S. (2003). Multitarget Bayes Filtering via First-Order Multitarget Moments. IEEE Trans. Aerosp. Electron. Syst. 39, 1152–1178. doi:10.1109/TAES.2003.1261119
Mahler, R. P. S. (2007). Statistical Multisource-Multitarget Information Fusion. USA: Artech House, Inc.
Panta, K., Clark, D. E., and Vo, B.-N. (2009). Data Association and Track Management for the Gaussian Mixture Probability Hypothesis Density Filter. IEEE Trans. Aerosp. Electron. Syst. 45, 1003–1016. doi:10.1109/TAES.2009.5259179
Qian, X., Lin, S., Cheng, G., Yao, X., Ren, H., and Wang, W. (2020). Object Detection in Remote Sensing Images Based on Improved Bounding Box Regression and Multi-Level Features Fusion. Remote Sensing 12, 143. doi:10.3390/rs12010143
Redmon, J., Divvala, S., Girshick, R., and Farhadi, A. (2016). “You Only Look once: Unified, Real-Time Object Detection,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27-30 June 2016 (IEEE), 779–788. doi:10.1109/CVPR.2016.91
Reid, D. (1979). An Algorithm for Tracking Multiple Targets. IEEE Trans. Automat. Contr. 24, 843–854. doi:10.1109/TAC.1979.1102177
Ren, S., He, K., Girshick, R. B., and Sun, J. (2015). “Faster R-CNN: Towards Real-Time Object Detection with Region Proposal Networks,” in Neural Information Processing Systems. Editors C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett (Cambridge, Massachusetts: MIT Press), 91–99.
Ren, Y., Zhu, C., and Xiao, S. (2018). Small Object Detection in Optical Remote Sensing Images via Modified Faster R-CNN. Appl. Sci. 8, 813. doi:10.3390/app8050813
Rublee, E., Rabaud, V., Konolige, K., and Bradski, G. (2011). “Orb: An Efficient Alternative to SIFT or SURF,” in 2011 International Conference on Computer Vision, Barcelona, Spain, 6-13 Nov. 2011, 2564–2571. doi:10.1109/ICCV.2011.6126544
Sommer, L., Kruger, W., and Teutsch, M. (2021). “Appearance and Motion Based Persistent Multiple Object Tracking in Wide Area Motion Imagery,” in Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV) Workshops, Montreal, BC, Canada, 11-17 Oct. 2021, 3878–3888. doi:10.1109/iccvw54120.2021.00434
Stauffer, C., and Grimson, W. E. L. (2000). Learning Patterns of Activity Using Real-Time Tracking. IEEE Trans. Pattern Anal. Machine Intell. 22, 747–757. doi:10.1109/34.868677
Teutsch, M., and Grinberg, M. (2016). “Robust Detection of Moving Vehicles in Wide Area Motion Imagery,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Las Vegas, NV, USA, 26 June-1 July 2016 (IEEE), 1434–1442. doi:10.1109/CVPRW.2016.180
Vo, B.-N., and Ma, W.-K. (2006). The Gaussian Mixture Probability Hypothesis Density Filter. IEEE Trans. Signal. Process. 54, 4091–4104. doi:10.1109/TSP.2006.881190
Vo, B.-N., Vo, B.-T., and Hoang, H. G. (2017). An Efficient Implementation of the Generalized Labeled Multi-Bernoulli Filter. IEEE Trans. Signal. Process. 65, 1975–1987. doi:10.1109/TSP.2016.2641392
Vo, B.-T., Vo, B.-N., and Cantoni, A. (2006). “The Cardinalized Probability Hypothesis Density Filter for Linear Gaussian Multi-Target Models,” in 2006 40th Annual Conference on Information Sciences and Systems, Princeton, NJ, USA, 22-24 March 2006, 681–686. doi:10.1109/CISS.2006.286554
Vo, B.-T., and Vo, B.-N. (2013). Labeled Random Finite Sets and Multi-Object Conjugate Priors. IEEE Trans. Signal. Process. 61, 3460–3475. doi:10.1109/TSP.2013.2259822
Wijnands, J. S., Zhao, H., Nice, K. A., Thompson, J., Scully, K., Guo, J., et al. (2021). Identifying Safe Intersection Design through Unsupervised Feature Extraction from Satellite Imagery. Computer‐Aided Civil Infrastructure Eng. 36, 346–361. doi:10.1111/mice.12623
Wojke, N., Bewley, A., and Paulus, D. (2017). “Simple Online and Realtime Tracking with a Deep Association Metric,” in 2017 IEEE International Conference on Image Processing (ICIP), Beijing, China, 17-20 Sept. 2017 (IEEE), 3645–3649. doi:10.1109/ICIP.2017.8296962
Wren, C. R., Azarbayejani, A., Darrell, T., and Pentland, A. P. (1997). Pfinder: Real-Time Tracking of the Human Body. IEEE Trans. Pattern Anal. Machine Intell. 19, 780–785. doi:10.1109/34.598236
Xuan, S., Li, S., Han, M., Wan, X., and Xia, G.-S. (2020). Object Tracking in Satellite Videos by Improved Correlation Filters with Motion Estimations. IEEE Trans. Geosci. Remote Sensing 58, 1074–1086. doi:10.1109/TGRS.2019.2943366
Yang, Y., Han, D., Ding, J., and Yang, Y. (2016). “An Improved ViBe for Video Moving Object Detection Based on Evidential Reasoning,” in 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden-Baden, Germany, 19-21 Sept. 2016 (IEEE), 1709–1724. doi:10.1109/MFI.2016.7849462
Keywords: object detection, object tracking, PHD filter, CNNs, remote sensing
Citation: Aguilar C, Ortner M and Zerubia J (2022) Small Object Detection and Tracking in Satellite Videos With Motion Informed-CNN and GM-PHD Filter. Front. Sig. Proc. 2:827160. doi: 10.3389/frsip.2022.827160
Received: 01 December 2021; Accepted: 04 March 2022;
Published: 29 April 2022.
Edited by:
Maria Sabrina Greco, University of Pisa, ItalyReviewed by:
Allan De Freitas, University of Pretoria, South AfricaDeepayan Bhowmik, University of Stirling, United Kingdom
Copyright © 2022 Aguilar, Ortner and Zerubia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Josiane Zerubia, am9zaWFuZS56ZXJ1YmlhQGlucmlhLmZy
 Camilo Aguilar
Camilo Aguilar Mathias Ortner2
Mathias Ortner2 Josiane Zerubia
Josiane Zerubia