1
KTH, Stockholm, Sweden
2
Stockholm University, Stockholm, Sweden
Is there any hope of achieving a thorough understanding of higher functions such as perception, memory, thought and emotion or is the stunning complexity of the brain a barrier which will limit such efforts for the foreseeable future? In this perspective we discuss methods to handle complexity, approaches to model building, and point to detailed large-scale models as a new contribution to the toolbox of the computational neuroscientist. We elucidate some aspects which distinguishes large-scale models and some of the technological challenges which they entail.
With its 20 billion neurons connected in networks made of millions of kilometers of axons the brain is a very complex system. In our quest for understanding it we need tools to handle this complexity. Using the strategy of divide-and-conquer, we can study smaller and smaller parts and attempt to understand the whole through the principle of hierarchical reductionism (Dawkins, 1986
). Employing such principles, a century of neuroscience has advanced our understanding tremendously on all levels from molecules to behavior, but there are still gaping holes in our knowledge, for example with regard to the nature of the neural code and the principle of operation of the cerebral cortex. While it remains uncertain whether a brain system can be understood as the interaction between independently describable subsystems, the brain does display a hierarchy of spatial scales with repeated structure such as molecules, synapses, neurons, microcircuits, networks, regions and systems. Churchland and Sejnowski (1992)
called these scales levels of organization. Here we discuss how the advent of large-scale modeling in computational neuroscience opens the possibility to study the dynamics of models simultaneously incorporating levels from molecules to regions. This kind of model is an important aid when working with questions such as the neural correlates of memory and the nature of cortical information processing.
When addressing questions related to dynamics, even the interaction of a few species of molecule introduces new dimensions of complexity which cannot be handled without the tools of mathematical modeling (see, e.g., Aurell et al., 2002
). Hodgkin and Huxley (1952)
described the interaction of ion channels in a patch of neuronal membrane using a set of coupled non-linear ordinary differential equations and could explain and quantitatively reproduce the basic features of the action potential. Via the equivalent cylinder model of the dendrite (Rall, 1959
), developments in computational neuroscience led to the first descriptions of the dynamics of neocortical neurons (see, e.g., Traub, 1979
).
Mathematical modeling has a long tradition outside of neuroscience. Experience shows that a model should be as simple as possible in order to be tractable (possible to analyze, easy to do computations with) and in order to make strong statements about the physical system being modeled. Einstein (1934)
stated “It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.” Most importantly, a model should have as few free parameters as possible.
With increased model complexity, uncertainty of modeling results increases. In addition, the model also loses explanatory power – it becomes difficult to understand the dynamics of the system. Note, though, Einsteins caution about “adequate representation” – the degree of simplicity that is achievable is dependent on the scientific question posed.
It may seem natural that the concept of hierarchical reductionism implies that a model targeted at a higher level of organization should be composed of component models at a lower level, and that this, in turn, implies that a model of a network necessarily must be much more complex and have more parameters than a model of a neuron. If that were true, one might ask what is the proper lowest level to build on in order to achieve a “realistic” model. The deeper the level, the more realistic? No, including more details from lower levels leads to more model parameters. In fact, this makes it harder to obtain a realistic model since the realism of a model is related to how well constrained it is by experimental data. More model parameters means that more data is required to determine them, data which can often contain uncertainties and be hard to acquire. In contrast, for a given question and domain it is often possible to find a valid simple model which is well constrained by data and, therefore, realistic. Consider, for example, how we describe the propagation of sound through air. A simple model based on the wave equation is in most cases adequately realistic in that the parameters are well constrained by data and that it gives correct predictions at the given level of description, while it is significantly harder to obtain the same degree of realism in a more detailed model involving the interactions of air molecules.
The tool which the modeler uses to keep the model simple is abstraction. By taking away aspects not important for answering the scientific questions which the model is designed to address, useful models can be formulated at different levels of organization without loss of tractability. For example, using the mean field approximation (for a review, see Renart et al., 2004
) the effect of individual synapses onto neurons can be abstracted and represented as its average. Yet, provided that the underlying assumptions hold, such models give valid answers to questions regarding the dynamics of populations of neurons. Note that abstraction is not limited to the removal of unnecessarily detailed levels; in virtually any model spanning multiple levels of organization, abstraction is used on every level to preserve only what is important for the study. For further discussion of mathematical modeling in biology, see, e.g., May (2004)
.
Numerical simulations of brain network models have typically been based on either abstract connectionist-type units (e.g., Dehaene et al., 1998
; Hopfield, 1984
) or integrate-and-fire units (e.g., Brunel, 2000
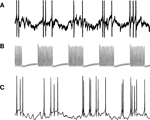
). In order to decrease model size, subsampling is often employed, that is, only a small subset of the real neurons are actually simulated. With fewer presynaptic units providing synapses, it becomes necessary to exaggerate connection density, or synaptic conductance – most of the time both. This results in a network with unnaturally few and strong signals circulating, in contrast to the real network, where many weak signals interact. Such differences tend to significantly distort the network dynamics. For example, artificial synchronization can easily arise, which is a problem especially since synchronization is one of the more important phenomena one might want to study. Cells in the model may not even be operating in the same dynamic regime as the real cells so that their behavior is ruled by different mechanisms. Figure 1
illustrates this effect in two different simulations of the Lamprey locomotor central pattern generator (CPG) network (Grillner, 2003
). Figure 1
B shows a simulation with a subsampled model and few, strong signals. In the simulation in Figure 1
C, all neurons of the real network are simulated. By modeling the full network with a one-to-one correspondence between real and model neurons we get natural dynamics, but for large networks this entails a large number of state variables, and, thus, heavy computations. (For a discussion of effects of unnatural connection density in a network with a larger number of units, see Morrison et al., 2007
).
Figure 1. Membrane potential of Lamprey locomotor CPG excitatory interneuron (EIN) plotted against time. (A) Recording from live animal. (B) Simulation with one modeled EIN per hemisegment. (C) Simulation with 30 modeled EINs per hemisegment.
Thanks to increasingly powerful massively parallel supercomputers and a parallel development of multi-core chip design, large-scale models of neural networks with hundreds of millions of state variables are now within reach. A review of the state-of-the-art within this field is available in a report from the 1st INCF
[1
workshop on large-scale modeling of the nervous system (Djurfeldt and Lansner, 2007
; see Brette et al., 2007 and Cannon et al., 2007
for discussion on related topics).
In general, we use large-scale models the same way as other models:
- to formulate hypotheses regarding the function of the nervous system
- to falsify hypotheses
- as a tool to identify what we don’t know
- to suggest new experiments
- to validate self-consistency of the description of a phenomenon or function
A model can be explicit in the sense that there is a simple relationship between its state variables and empirical data. Since a large-scale model can harbour a large number of state variables it can afford to be explicit at several levels of organization. This can be an advantage in situations where there is interest in effects spanning multiple levels. For example, in a model of memory function based on Hodgkin-Huxley formalism and conductance-based synapses, ionic currents are explicitly represented. This opens new possibilities for studying pharmacological effects on memory function. For similar reasons large-scale models can be especially valuable when used as a platform for integrating knowledge and to validate self-consistency of the description of multi-scale phenomena or functions.
The Blue Brain project (Markram, 2006
) is largely based on the bottom-up approach to modeling which means taking the physical structure of the tissue as a starting point with the hope of capturing function. The aim is to reconstruct, in the computer, a full cortical column, including all neuron types and all connectivity. The model will consist of ∼10000 multi-compartment neurons modeled with the Hodgkin-Huxley formalism.
However, when modeling the complex and intricate structure of the cortex, it turns out that we may need information from additional sources. Some model parameters are well constrained by experiment, while others, for example the structure of long-range connectivity, are still largely unknown. Hypotheses of cortical function, expressed in more abstract models, can guide model development, in selecting what elements to include in the model, in giving additional constraints, and in “filling in” where empirical data are still missing. This is the top-down approach to modeling.
In practise, the approach of the modeler is usually neither purely top-down nor purely bottom-up. For example, Djurfeldt et al. (2008)
describe a full-scale model of cortical layers II/III approaching the size of a cortical area. Simulations of this model, also based on multi-compartment Hodgkin-Huxley units, have comprised up to 22 million neurons. The model is mainly designed to target the question: Is the hypothesis of attractor memory network function in neocortex consistent with neocortical microarchitecture and dynamics at the levels of the cell and synapse? Here, most parameters of the neuron models are determined from experimental data in a bottom-up manner. However, the connectivity parameters are determined by combining a long-range connectivity structure required for attractor memory network function with currently existing empirical constraints on connectivity.
Another example of the top-down approach is given by Potjans et al. (2007)
where a theory of system level function (the actor-critic architecture of TD-learning) is mapped to a spiking neuronal network.
In the model of Djurfeldt et al. (2008)
, and in most or all other network models, the parameters of a neuron type are replicated over the population of model neurons, with or without stochastic variability, in a crystal-like manner. This means that even if a large-scale model has a large number of state variables, it can still have a comparatively small total number of parameters, and in this sense be tractable and amenable to analysis.
On the other hand, large-scale simulations also open the possibility of incorporating large quantities of empirical data into models. New experimental techniques with the ability to extract empirical data on an industrial scale are under development. For example, serial block-face scanning electron microscopy (Denk and Horstmann, 2004
) holds the promise of dissection of the cortical column at the nanoscale level. Such data could be used to set a large number of distinct morphology and connectivity parameters, yielding a complex and realistic model. Would this type of heavily data-driven model be a branching point for model development in that it would be qualitatively different from models with fewer parameters?
Importing large amounts of data into a model also means importing large amounts of unknown, or unexplained, structure. It will, thus, be more difficult to understand why the model behaves in a certain way. The model can be studied by varying parameters, but this can also be more difficult when the number of parameters is large. Heavily data-driven models may therefore require new types of knowledge-building strategies. Consider, for example, a model where connectivity has been imported from an experimental data set. If we use the top-down recurrent attractor memory hypothesis, we might want to device an algorithm to look for attractors, either in the data set itself or in model dynamics. In practise, we foresee a development with a continuum of models with regard to the number of experimentally determined parameters. It is generally useful to combine information from models targeted at different levels.
Large-scale models place new demands on simulation software, such as tools for model construction and specification, simulators, visualization tools and database systems. Djurfeldt and Lansner (2007)
summarize some of the existing and planned software. For models based on Hodgkin-Huxley formalism, the standard distribution of NEURON (Hines, 2005
) supports parallel simulation on cluster computers using MPI (Message Passing Interface) starting with version 5.9. A parallel version of GENESIS, PGENESIS (Hood, 2005
), exists and Genesis 3 (Bhalla, 2007
; Cornelis and De Schutter, 2003
), with improved support for parallelism, is under development. A parallel version of NEST (Gewaltig, 2005
), often used for the simulation of integrate-and-fire models, exists, to name a few examples.
Large-scale models produce large amounts of data. Visualization tools are needed which can compute the equivalent of brain imaging signals from electroencephalography (EEG), magnetoencephalography (MEG), fMRI (BOLD) and voltage sensitive dyes (VSD). These signals have in common that they correlate with activity of large populations of neurons. Such visualization tools have the dual role of providing a way to analyze and understand population activity in the simulation and providing a way to connect to experimental results in brain imaging.
An aspect of software for neural modeling discussed in Djurfeldt and Lansner (2007)
is the need for re-usability through modularity and software interoperability (see also Cannon et al., 2007
). For large-scale models, the suggestion was made to implement a framework for connecting software components enabling on-line communication for example between two parallel simulators or between a parallel simulator and a visualization tool. This would make it possible to connect multiple large-scale models into systems and would enable independent development of software for visualization of data from large-scale simulations. The INCF has initiated the MUSIC project which aims to develop a standard for such communication frameworks.
One challenge, with applicability to modeling in general, is to improve reproducibility of simulation results. There is a need to standardize criteria for how models are published to ensure reproducibility. There is also a need to create an infrastructure supporting the validation of models and simulators, ensuring that results from the same model, obtained using different simulators, are similar. Another challenge, less technological but rather political, is to create an awareness of the increased dependence of computational neuroscience on simulation technology. More funding needs to be available for the development of simulation software and in particular its long-term sustainability.
The field of mathematical modeling today provides powerful tools to master the complexity of the brain. Large-scale models are a recent development, enabled by the astonishing development of chip technology and parallel computing, with a computational power now being unleashed by special purpose software. Computational neuroscience will benefit from the possibility of modeling multiple cortical areas and systems with high detail. Such models have the potential to link dynamic phenomena at the cellular and synaptic levels to memory function or other cognitive functions of the brain, which enables a quantitative understanding of the underlying processes and interactions.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was supported by grants from the European Union (FACETS project, FP6-2004-IST-FETPI-015879), the Swedish Foundation for Strategic Research (through the Stockholm Brain Institute), and the International Neuroinformatics Coordinating Facility (INCF).
Footnote
- ^ International Neuroinformatics Coordinating Facility
Brette, R., Rudolph, M., Carnevale, T., Hines, M., Beeman, D., Bower, J. M., Diesmann, M., Morrison, A., Goodman, P. H., Harris, F. C. Jr, Zirpe, M., Natschläger, T., Pecevski, D., Ermentrout, B., Djurfeldt, M., Lansner, A., Rochel, O., Vieville, T., Muller, E., Davison, A. P., Boustani, S. E., and Destexhe, A. (2007). Simulation of networks of spiking neurons: a review of tools and strategies. J. Comput. Neurosci. 23, 349–398.