1
Department of Bioengineering, University of California, San Diego, La Jolla, CA, USA
2
Department of Ophthalmology, University of California, San Diego, La Jolla, CA, USA
3
Neurosciences Program, University of California, San Diego, La Jolla, CA, USA
Network signaling through astrocyte syncytiums putatively contribute to the regulation of a number of both physiological and pathophysiological processes in the mammalian central nervous system. As such, an understanding of the underlying mechanisms is critical to determining any roles played by signaling through astrocyte networks. Astrocyte signaling is primarily mediated by the propagation of intercellular calcium waves (ICW) in the sense that paracrine signaling results in measurable intracellular calcium transients. Although the molecular mechanisms are relatively well known, there is conflicting data regarding the mechanism by which the signal propagates through the network. Experimentally there is evidence for both a point source signaling model in which adenosine triphosphate (ATP) is released by an initially activated astrocyte only, and a regenerative signaling model in which downstream astrocytes release ATP. We modeled both conditions as a simple lumped parameter phenomenological diffusion model and show that the only possible mechanism that can accurately reproduce experimentally measured results is a dual signaling mechanism that incorporates elements of both proposed signaling models. Specifically, we were able to accurately simulate experimentally measured in vitro ICW dynamics by assuming a point source signaling model with a downstream regenerative component. These results suggest that seemingly conflicting data in the literature are actually complimentary, and represents a highly efficient and robustly engineered signaling mechanism.
Astrocytes in the central nervous system possess a full compliment of membrane receptors and ion channels that allow them to respond to intercellular signals from both other astrocytes and from neurons on a millisecond time scale (Barres et al., 1990
; MacVicar and Tse, 1988
; Newman and Zahs, 1997
; Salm and McCarthy, 1990
; Serrano et al., 2006
; Usowic et al., 1989
; Winshop et al., 2007
). First shown in culture (Charles et al., 1991
; Cornell-Bell et al., 1990
), the principal mechanism of long distance signaling in astrocyte networks are intercellular calcium waves (ICW) mediated by the extracellular diffusion of adenosine 5′-triphosphate (ATP) and related purines interacting with the P2Y family of membrane receptors (Coco et al., 2003
; Guthrie et al., 1999
). This causes a rise in intracellular calcium levels, which is part of a cascade that can result in the vesicular release of gliotransmitters, in particular ATP, that can signal other downstream astrocytes (i.e., thereby propagating the calcium wave) and neurons (Kang et al., 1998
; Nedergaard, 1994
; Parpura et al., 1994
; Parri et al., 2001
; Verkhratsky et al., 1998
). More recently, ICW have been shown to occur in situ in brain slices (Dani et al., 1992
; Newman and Zahs, 1997
; Schipke et al., 2002
) and in vivo in the rat neocortex using two photon microscopy (Hirase et al., 2004
). Although the physiological and pathophysiological roles of ICW in vivo are not clearly understood and are very much an area of active research, potential roles include modulating neuronal synaptic signaling, controlling brain microcirculation and related metabolic processes (Zonta et al., 2003
). A particularly intriguing and clinically important function may be augmentation of ICW following disease or injury, for instance, during ischemic insults (Harris and Symon, 1984
) or seizures (Heinemann and Louvel, 1983
), essentially acting as a pathological signaling mechanism that may augment reactive gliosis and secondary injury processes.
The functional extent of any physiological or pathophysiological contributions of ICW will necessarily depend on the dynamics of signal propagation through the network, which will in turn depend on the molecular mechanisms that underlie the dynamics. In particular, extracellular ATP diffusion and binding to P2Y receptors and, to a lesser extent, IP3 mediated gap junctional signaling mediate intercellular propagation while intracellular dynamics are governed by IP3 and Ca2+ levels (Guthrie et al., 1999
). However, there is considerable conflicting data and debate as to the dynamics of ATP secretion (Scemes and Giaume, 2006
), and whether it is secreted from a single cell activated in response to a stimulation (e.g., pharmacological, electrical, or mechanical; Arcuino et al., 2002
, 2004
; Cotrina et al., 1998
, 2000
; Iacobas et al., 2006
), or whether the signal is regenerated in the form of additional ATP release from downstream astrocytes (Anderson et al., 2004
; Hassinger et al., 1996
; Newman, 2001
; Parpura et al., 1994
). Among the data supporting a point source model are studies of membrane permeability to propidium iodide, a DNA intercalating indicator (Arcuino et al., 2002
). Only cells at the center of spontaneous and mechanically stimulated calcium waves exhibited uptake of propidium iodide, suggesting a point source release of ATP with no further downstream release. A later study by the same group found that the distance traveled by ICW was independent of whether it had to cross a cell free lane, also consistent with a non-regenerative point source release of ATP (Arcuino et al., 2004
).
On the other hand, data supporting a regenerative model of ATP signaling includes work that has demonstrated ATP-induced ATP release (Ballerini et al., 1996
; Queiroz et al., 1997
, 1999
), for example by labeling astrocyte cultures with 14C-purines and showing subsequent ATP-induced release of 14C-ATP from cells (Anderson et al., 2004
). Other work used a luciferin/luciferase ATP assay to show that blocking P2Y receptors with suramin resulted in the decreased release of ATP and a decrease in calcium wave propagation by downstream cells (Newman, 2001
). Furthermore, in contrast to work described above, the propagation of ICW across cell free gaps have been shown to cross cell-free areas at points closest to where the waves reach the gap, and not closest to the point of initial stimulation, consistent with a regenerative downstream release of ATP (Hassinger et al., 1996
).
In general, experimental papers have focused on and present data in support of one or the other of these two mechanisms, while providing very little comment on the alternative. There is no experimental work that we are aware of that has reconciled these conflicting results. Theoretically, a number of biophysical models have been proposed that replicate the molecular mechanisms associated with ATP release in astrocytes that successfully account for and model intracellular calcium transients and ATP release curves for individual cells (Bennett et al., 2005
). However, these models tend to fail when used to extrapolate beyond the effects of the cell membrane to model and simulate ICW, since the induced propagation of ICW through simulated networks of astrocytes consistently extend to include every cell in the entire network, a condition which experimentally is not the case, as we show below.
Here, we introduce an alternative to biophysical models of astrocyte ATP signaling based on a simple phenomenological lumped parameter diffusion model. It consists of a set of simple but physiologically realistic and measurable signal propagation parameters that model individual astrocytes in a network as the product of a derived state variable, similar to neuronal integrate and fire models. It can accommodate and account for spatially and temporally complex signal propagations through astrocyte networks and produces finite ICW that are qualitatively similar to experimentally observed ICW measured under controlled in vitro conditions. The model suggests that to produce experimentally realistic waves, downstream cells must release smaller amounts of ATP in response to a larger point source release from an initially stimulated astrocyte, effectively resulting in what we call a partially regenerative mechanism that incorporates both the point source release and fully regenerative release mechanisms. Thus, our model reconciles what appears to at first be contradictory experimental data and suggests follow up testable experimental hypotheses. In addition, these results suggest that intercellular astrocyte signaling has evolved to be a very efficient and robust signaling mechanism that takes advantage of the inherent physical properties of the system independent of the underlying molecular details.
Reagents and Cell Cultures
Primary dissociated spinal cord astrocytes were cultured as previously described (Silva et al., 1998
). All experiments were performed with cells seeded on P35 glass-bottom Petri dishes (Mat-Tek Corp., Ashland, MA, USA) at approximately 200,000 cells cm2 incubated in culture media [high glucose DMEM supplemented with 10% FBS, 2 mM L-glutamine, and 1% (v/v) Pen/Strep] at 37°C and 5% CO2. Media changes, in which all media was replaced, were performed every 2 days. Unless otherwise stated, all reagents were obtained from Sigma (St. Louis, MO, USA).
Calcium Imaging
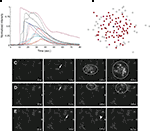
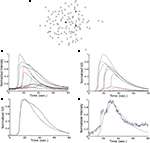
Astrocyte cultures were washed twice with Kreb-HEPES buffer (KHB) solution (10 mM HEPES, 4.2 mM NaHCO3, 10 mM glucose, 1.18 mM MgSO4, 1.18 mM KH2PO4, 4.69 mM KCL, 118 mM NaCl, 1.29 mM CaCl2, pH 7.4) and incubated with 5 μM Fluo-4AM in KHB for 1 h at room temperature. Excess indicator dye was removed by washing twice with KHB followed by an additional 30 min incubation at room temperature to allow equilibration of intracellular dye concentration and ensure full esterification. ICW were initiated by a single mechanical stimulation delivered to a localized region of one to three cells using a 0.5-μm internal diameter micropipette tip (WPI Inc., Sarasota, FL, USA) mounted on an M325 micrometer slide micromanipulator (WPI Inc., Sarasota, FL, USA). All images were acquired using an Olympus IX81 inverted fluorescent confocal microscope (Olympus Optical, Tokyo, Japan) that included epifluorescence, confocal, phase, brightfield, and Hoffman differential interference contrast modalities. It was equipped with a Hamamatsu ORCA-ER digital camera (Hamamatsu Photonics K.K., Hamamatsu City, Japan) and Image-Pro Plus data acquisition and morphometric software (version 5.1.0.20 Media Cybernetics, Inc., Silver Spring, MD, USA). Images were taken at 16 Hz. Comparable calcium wave data were obtained using pharmacological ATP stimulation by localized puffing. Image sequences were then processed by circling cells by hand and computing the average fluorescent intensity across each cell at each time point, so that for every cell in a culture a time series of the calcium fluorescence I(t) was measured (Figure 1
A). Cell activation times were extracted from calcium transients, such that when the first derivative of the calcium fluorescence exceeded a threshold value defined by 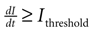 , which in all cases were two standard deviations above the mean noise baseline level, the cell was labeled as ‘active’. Using these thresholds a map of cells that participated in experimental calcium waves were constructed (Figure 1
B). In total, 26 experimentally recorded movies were compared with the model. One representative example is shown in the results.
, which in all cases were two standard deviations above the mean noise baseline level, the cell was labeled as ‘active’. Using these thresholds a map of cells that participated in experimental calcium waves were constructed (Figure 1
B). In total, 26 experimentally recorded movies were compared with the model. One representative example is shown in the results.
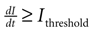 , which in all cases were two standard deviations above the mean noise baseline level, the cell was labeled as ‘active’. Using these thresholds a map of cells that participated in experimental calcium waves were constructed (Figure 1
B). In total, 26 experimentally recorded movies were compared with the model. One representative example is shown in the results.
, which in all cases were two standard deviations above the mean noise baseline level, the cell was labeled as ‘active’. Using these thresholds a map of cells that participated in experimental calcium waves were constructed (Figure 1
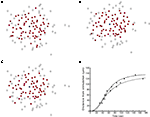
B). In total, 26 experimentally recorded movies were compared with the model. One representative example is shown in the results.Figure 1. Intracellular calcium transients and propagating intercellular calcium waves in cultured astrocyte networks. (A) Calcium transient responses from individual astrocytes from a representative intercellular calcium wave. A threshold value was defined for the rising phase of the responses in order to identify activated astrocytes (see text). (B) The pattern of astrocyte activations and spread of calcium waves (red dots) were mapped to the relative spatial locations of astrocytes in fields of view. This example was derived from the data in (A). The blue dot represents the initially activated cell. (C–E) In culture at least, macroglial intercellular calcium waves are qualitatively non-uniform in their propagation. Three examples of calcium waves are shown for the same field of view in an rMC-1 Muller glial cell line culture with four panels from each recorded movie (across). The arrow in the second panel of each movie points to the initially stimulated cell. (C) A relatively large activated network that recruited many of the cells in the field of view (encircled in panels 3 and 4). (D) In contrast, stimulating a different adjacent cell from the one in (C) resulted in a different and smaller activated network. However, there was an overlap between the two functional networks; the three cells marked by asterisks participated in both signaling events. (Note the group of three cells lined up in a row near the upper right for reference). (E) Stimulating a third cell resulted in no network propagation, with only the activation of its neighboring cell (arrowhead). Similar results were obtained with primary astrocyte cultures, although the examples shown here represent our best data illustrating this effect.
Model Description
The activation of astrocytes in a network produce intracellular calcium transients that result in propagating ICW responsible for mediating signaling through the network (Figure 1
). In order to investigate geometrically realistic network topologies, the relative spatial location of all cells in a recorded movie were represented as point sources centered at each cell (e.g., see Figure 1
B). The dynamics of a cell was modeled as an independent state variable Vi [which has units of (amol s)/μm2, derived in the Supplementary Material online], where i ranged from 1 to the number of cells in the network. The state function grows as a function of the concentration of ATP and returns to 0 in the absence of ATP, similar to a leaky integrate and fire model (see for example Tuckwell, 1988
). We only consider the role of ATP diffusion in this model, and ignore the contribution of gap junctional signaling to ICW (see the Discussion below). When the state function crosses a threshold Vth the cell becomes activated and immediately releases its own ATP that in turn diffuses outwards and signals other downstream cells. As a first approximation and for simplicity, the model assumes that each cell only releases ATP once throughout the course of a signaling event (i.e., one ICW; see Supplementary Material and Figure S1
). The equation for the state function of astrocyte i is given by

where γ is a damping rate (with units of s−1) that ensures that in the absence of any external stimuli the state of the cell will return to 0. The summation over Fi,j represents a sum of the ATP signals emitted from all cells j ≠ i (i.e., no autocrine signaling was assumed). This model represents two processes – a first order decay of the signal and an extracellular diffusion based input represented by Fi,j.
The magnitude or strength of ATP signal on an astrocyte is derived from the two dimensional diffusion equation, such that the effect F of signal release from cell j on cell i at any time τ will be
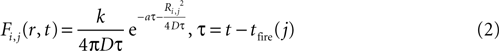
where k is a coupling constant linearly related to the amount of ATP released from cell j (roughly equivalent in physical units to attomoles), and τ is the time at which cell j becomes active. D is the diffusion coefficient (μm2 · s−1), a is the rate of ATP degradation (s−1), and Ri,j is the distance between the two cells i and j. (See the Supplementary Material for the full derivation from the diffusion equation.) Thus, the full state equation that describes the net effect of all astrocytes j on astrocyte i is given by
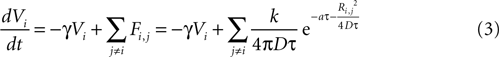
At time t = 0 in a simulation an initial cell was set to be above the threshold Vth, thereby initiating a signaling event. Having both Vth and k as free parameters results in the lack of a unique solution for the system, since doubling Vth (i.e., ATP threshold) or doubling k (i.e., the amount of ATP released) would give the same result. As such, we fixed Vth and allowed k to be a fitted parameter since the latter is the key variable of interest for exploring the point source and regenerative ATP release models. In order to decide on an experimentally realistic value for Vth we considered that ICW can be initiated by bathing astrocytes and retinal Muller glial cells in a 3-μM solution of ATP but not less (Newman, 2001
). We therefore set Vth = 0.25 amol · s/μm2 to give results consistent with previous experimental data. (A detailed derivation of Vth is also given in the Supplementary Material.) The summed state function for every cell in a network was calculated as a function of time and if Vi exceeded Vth at any time then that cell was considered activated during that particular ICW.
Finally, two classes of network geometries were used in model simulations. Uniform two dimensional arrays of cells 25 μm apart (40 × 40 and 20 × 20 cell grids) were used to test the assumptions underlying the regenerative and point source signaling models. Experimentally derived geometries were used to test the model’s ability to generate experimentally realistic ICW by comparing the model’s output to measured data for the same network geometries. In the case of the grid geometry, the first cell stimulated was the center cell in the grid. In the case of the experimentally derived geometries the first cell measured in the experimental preparations to have exhibited a calcium transient was simulated in the model as the initiating cell (indicated as the blue cell in all relevant figures).
A Fully Regenerative Diffusion Model Cannot Reproduce Experimentally Measured Data
We began by considering the dynamics of the fully regenerative ATP diffusion model whereby every astrocyte participating in an ICW event secretes the same amount of ATP upon being activated, and compared the results to measured experimental data. A diffusion constant value of D = 300 um2/s was chosen as the diffusion rate of ATP for cultured astrocyte networks (Bennett et al., 1995
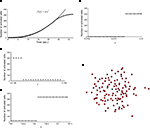
). The wave was initiated by setting the cell in the center of a 40 × 40 grid to an activated state. Simulating a fully regenerative signaling mechanism resulted in all the cells in the grid becoming activated, contrary to experimental observations where only finite waves were observed. No set of model parameters could be found in which the calcium wave died out before activating every cell in the grid. A plot of the number of cells activated versus time showed that the number of cells being activated by the spreading waves followed a power law, which by about 28 s had recruited all the cells in the grid (Figure 2
A). Interestingly, this shows some similarity to recent work (Beggs and Plenz, 2003
) in which the authors modeled neural avalanches in neocortical networks and showed that the propagation of spontaneous activity in those networks is well described by power-law based equations that govern avalanche phenomena.
Figure 2. Modeling intercellular calcium waves as a fully regenerative release model of adenosine triphosphate (ATP) from an arbitrarily stimulated astrocyte resulted in the recruitment of all cells in the network. (A) The recruitment of astrocytes as a function of time quickly resulted in the activation of all cells and followed a power law function; one representative simulation result is shown. This resulted in intercellular calcium waves that never died out or attenuated until they reached the end of the network, a condition that is not observed experimentally. (B–D) In all cases a fully regenerative model resulted in an instantaneous recruitment of all cells in the network, which is also experimentally inaccurate. Despite an extensive search at high parameter value resolutions, there were no parameter values in the diffusion model or combinations of parameter values (a, γ, and k, respectively in B,C,D) that provided a smooth transition towards the activation of the network. (E) The result of a representative simulation of the fully regenerative model for the experimentally measured network geometry shown in Figure 1
. Note the activation of all cells in the field of view. The blue dot represents the initially activated cell.
Varying each of the three parameters γ, a and k by small increments near the transition threshold from inactivation to activation revealed an essentially instantaneous transition phase, meaning that all cells activated at or above the parameter transition threshold while no cells activated below it (Figures 2
B–D). A similar result was observed for experimentally realistic network geometries, where the model could not produce an ICW that did not recruit all astrocytes in the network every time (Figure 2
E). If the outgoing signal strength, represented by k, is strong enough to activate downstream cells that in turn signal with the same strength, the result is a cascade of activations that always recruit every cell in the network. These results do not agree with experimental results that never recruit all astrocytes in a network (see Figures 1
B–E). This suggests that a fully regenerative ATP signaling model cannot account for experimentally observed results, and that astrocytes in a network cannot be sending out a signal (i.e., releasing ATP) that is the same strength as the incoming signal.
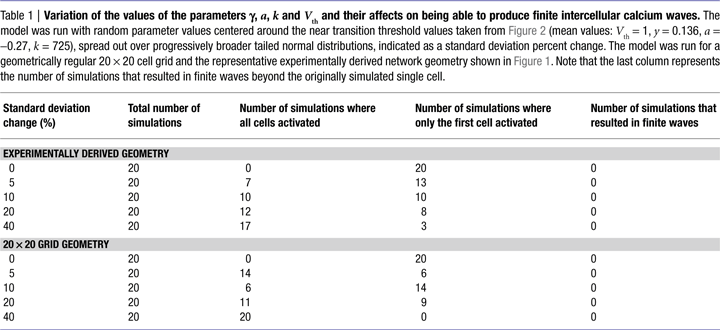
We further explored whether varying the values of γ, a, k, and Vth in the model could produce experimentally accurate ICW, since real astrocytes are not all the same and would presumably have different values of γ, a, k, and Vth. We ran the model with random parameter values centered around the near transition threshold values from Figure 2
(mean values were Vth = 1, γ = 0.136, a = −0.27, k = 725), spread out over progressively broader tailed normal distributions. Random parameter values were taken from distributions defined by progressively increasing standard deviations, and the model was run for both regular 20 × 20 cell grid and the representative experimentally derived network geometry shown in Figure 1
. Table 1
summarizes the results. There were no outcomes that resulted in finite wave propagation, with either only the initially stimulated cell or all the cells in the network being activated, similar to the results described above, even with very broad distributions from which parameter values could be chosen. Thus, for variations in the parameters to account for a finite wave size, the parameter values would have to display a non-random distribution. For example increasing Vth as a function of distance from the initially stimulated cell. Non-random distributions of γ, a, and Vth are not realistic since a network of astrocytes cannot anticipate which cell will be stimulated first; and even if that were the case recruited cells would have to have a priori knowledge about the parameter values of their neighbors in order to adjust theirs accordingly, since no matter where an ICW is initiated the result is always a non-uniform propagating finite wave. The parameter k however, which represents the amount of ATP released by an individual astrocyte, could theoretically vary in a given cell as a function of distance from the site of stimulation due to cells sensing differing ATP concentrations, which would in turn affect how much ATP that cell itself secretes. This is addressed in the next section.
A Partially Regenerative Diffusion Model Produced Spatiotemporally Realistic Propagating Waves
We then explored point source and partially regenerative models of ATP release, with the latter implying that downstream cells released less ATP than the first stimulated astrocyte. Mathematically these two diffusion models are modeled the same way (i.e., are represented by the same set of equations), since a pure point source model is the extreme case of a partially regenerative model when the downstream release of ATP is 0. Computationally, we modeled this by damping downstream signals relative to the signal amplitude of the originating cell such that the net effect on cell i from all cells j (similar to Eq. 3) is given by
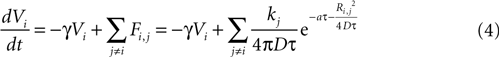
where kj = k1 when j represents the originally stimulated cell and kj = k2 for all other j. Thus k1 represents the amount of ATP released from the original cell while k2 represents the amount of ATP released from all downstream cells. k2 as defined here assumes that all downstream cells secrete the same amount of ATP and represents the simplest case. This is of course a simplification, since different astrocytes could be releasing differing amounts of downstream ATP. However, with this assumption in place the model is able to produce wave kinetics qualitatively indistinguishable from experimental measurements. Furthermore, a constant small amount of ATP release by downstream cells is sufficient to produce a significant amplification of the distance the wave can propagate while still resulting in a finite wave. An extension of the current model could let kj to vary as a function of some network parameter; such as spatial distance from k1, i.e., kj = (k1, r), where r is the radial distance from the source of the wave or ATP input to the cell. As suggested above though, to a first approximation the model as is with a fixed k2 was able to accurately model experimentally measured wave kinetics that did not necessitate varying k2.
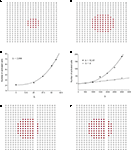
Using the updated version of the diffusion model given by Eq. 4, simulated grid ICW were finite and did not recruit all astrocytes in the network, consistent with experimental data and in contrast to the fully regenerative model. This was the case for both a pure point source model of ATP release (i.e., k2 = 0; Figure 3
A) and a partially regenerative model (k2 > 0; Figure 3
B). Interestingly, while a point source model (k2 = 0) resulted in a finite wave, a partially regenerative model (k2 > 0) extended signal propagation considerably further for a comparatively small amount of ATP release by downstream cells. In the example shown in Figure 3
a partially regenerative model where each downstream cell was simulated to have released just over 2.8% of the amount of ATP secreted by the initial activated cell (located in the center of both grids; i.e., a ratio of k2/k1 = 0.028) extended the ICW from 21 to 69 cells, or an increase of about 329%. In order to explore this further, we plotted differing ranges of changing k1 versus k2 and vice versa. For a fixed value of k1, increasing k2 non-linearly recruited more cells at a rate proportional to k2 (Figure 3
C). Increasing k1 relative to k2 also recruits more cells but the effect of a positive k2 increases non-linearly as a power law relative to a pure point source model when k2 = 0 (Figure 3
D).
Figure 3. Modeling intercellular calcium waves as a point source model and partially regenerative model produced experimentally realistic finite waves. (A) Representative example of a finite ICW in a simulated grid of cells following the point source release of ATP by the center cell. (B) Representative example of a finite wave in the same simulated grid for the partially regenerative ATP release model. A very small amount of ATP released by downstream astrocytes (i.e., k2 > 0 in Eq. 4) resulted in considerably larger but still finite waves. (C) Plot of the number of activated cells for a constant point source release component (i.e., k1) while varying the downstream release component k2. Note the increase in the number of astrocytes recruited for comparatively small changes in k2. (D) Effect of varying k1 on the number of activated astrocytes for two fixed values of k2. Each function was fit to a power law of the form 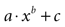 . The exponents b were found to be 2.699 (c), 1.008 (d, k2 = 0) and 2.38 (d, k2 = 52.65). The goodness of fit for each as measured by R2 values were 0.998 (C) and 0.991 (for both plots in (D)). (E,F) The partially regenerative ATP signaling model was able to replicate experimental finite ICW propagation across cell free gaps. In (E) a low degree of ATP degradation affects the wave because no downstream release of ATP occurs and the distance the wave travels decreases compared to (F), where an increase in the rate of ATP degradation along with an increase in signal strength k increases the distance the wave travels across the gap because a lack of ATP degradation in the gap balances the regeneration of signal.
. The exponents b were found to be 2.699 (c), 1.008 (d, k2 = 0) and 2.38 (d, k2 = 52.65). The goodness of fit for each as measured by R2 values were 0.998 (C) and 0.991 (for both plots in (D)). (E,F) The partially regenerative ATP signaling model was able to replicate experimental finite ICW propagation across cell free gaps. In (E) a low degree of ATP degradation affects the wave because no downstream release of ATP occurs and the distance the wave travels decreases compared to (F), where an increase in the rate of ATP degradation along with an increase in signal strength k increases the distance the wave travels across the gap because a lack of ATP degradation in the gap balances the regeneration of signal.
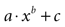 . The exponents b were found to be 2.699 (c), 1.008 (d, k2 = 0) and 2.38 (d, k2 = 52.65). The goodness of fit for each as measured by R2 values were 0.998 (C) and 0.991 (for both plots in (D)). (E,F) The partially regenerative ATP signaling model was able to replicate experimental finite ICW propagation across cell free gaps. In (E) a low degree of ATP degradation affects the wave because no downstream release of ATP occurs and the distance the wave travels decreases compared to (F), where an increase in the rate of ATP degradation along with an increase in signal strength k increases the distance the wave travels across the gap because a lack of ATP degradation in the gap balances the regeneration of signal.
. The exponents b were found to be 2.699 (c), 1.008 (d, k2 = 0) and 2.38 (d, k2 = 52.65). The goodness of fit for each as measured by R2 values were 0.998 (C) and 0.991 (for both plots in (D)). (E,F) The partially regenerative ATP signaling model was able to replicate experimental finite ICW propagation across cell free gaps. In (E) a low degree of ATP degradation affects the wave because no downstream release of ATP occurs and the distance the wave travels decreases compared to (F), where an increase in the rate of ATP degradation along with an increase in signal strength k increases the distance the wave travels across the gap because a lack of ATP degradation in the gap balances the regeneration of signal.We then explored the consequence of introducing a cell free gap into the grid, similar to experimental work that created cell free lanes in culture to test the propagation of ICW in areas devoid of cells (Takano et al., 2002
). The model was able to reproduce observed experimental results. Simulated ICW were able to cross cell free gaps and produce finite patterns of cell activations. The range of signal propagation was found to again be critically dependent on the rate of ATP degradation and uptake, represented by the parameter a in Eq. 4. With a low degree of ATP uptake and/or degradation, the distance the wave traveled across the gap was less than through a field of cells since no release of downstream ATP occurred in the gap (Figure 3
E). Upon increasing the rate of ATP uptake, the distance the wave traveled increased (Figure 3
F). This is because there was no ATP uptake in the gap, which balanced the regeneration of signal in the direction of propagation where cells were present by allowing diffusion without uptake. This suggests that the dynamics of gap crossing in the partially regenerative model are sensitive to the parameters in the model.
To compare the simulated calcium transients to experimental data, a simulation was run using the geometry in Figure 1
. One modification was made to the term Fi,j. To account for ATP release of a cell being received at that cell in a possible positive feedback mechanism, when i = j, the function was evaluated such that Ri,j = 5 μm. The transients generated by a wave are shown in Figure 4
. The experimental geometry is shown in Figure 4
A, reproduced from Figure 1
B. The calcium transients from 10 cells in the experiment are shown in Figure 4
B (reproduced from Figure 1
A) with the respective state functions (V) in the simulation shown in Figure 4
C. While not all cells matched the experiment closely, they show the same trends of decreasing maximum height with time of onset. Derived transients for two cells which matched very well are shown in the simulation and compared to the calcium transients measured from the experiment (Figures 4
D,E). The cell in Figure 4
D reached Vth, while the cell in Figure 4
E did not.
Figure 4. Comparison of the measured calcium signals from an experiment and those generated in a simulation. (A) The geometry of the cells from the experiment, used in the simulation. The blue cell marks the initial cell stimulated, the red cell marks the transient shown in (D), and the cyan cell marks the cell shown in (E). (B,C) show the calcium signals for 10 different cells in experiment (B) and in the simulation (C). The colors between (B) and (C) match up i.e., the purple trace in (B) represents the same cell as the purple trace in (C).
Despite the success of Eq. 4 in reproducing spatially finite ICW, it was not able to reproduce the experimental observation of non-uniform activation of astrocytes within the signaling range of an ICW, in the sense that experimentally not all astrocytes within the functionally activated network defined by the propagating ICW front necessarily activate (see Figures 1
B–E). As such, a purely diffusion based model cannot account for this aspect of the dynamics of real astrocyte signaling networks. This makes intuitive sense since based on diffusion arguments alone one would expect a signal to extend equally within the diffusion boundaries. We have observed this phenomenon of spatial heterogeneity in wave propagation experimentally under controlled in vitro conditions in different macroglial networks, and in situ in astrocytes in intact neural retinal preparations, by stimulating different initial cells within the same field of view (i.e., portion of the network) and measuring the propagation of the resulting ICW (Figure 1
). In some cases large portions of the observable network were activated in response to an arbitrarily chosen cell (Figure 1
C), while in other cases a smaller number of cells participated in an ICW in response to the initial stimulation of an adjacent cell (Figure 1
D). Still in other cases very little intercellular signaling occurred at all, with the activation of one or a few nearby cells (Figure 1
E). In all cases we observed some cells within the boundary of ICW that did not participate in the wave. In addition, we routinely observed cells farther away from the stimulus activating before nearby cells closer to the stimulus. While spontaneous activation has been observed both in culture (Fatatis and Russell, 1992
) and in situ (Parri and Crunelli, 2001
), the phenomenon of non-uniform signaling we describe here was a coordinated property of the propagating wave front and not an artifact of observation (by controlling for uncoordinated spontaneous activity). Further evidence for this phenomenon is provided by intracellular calcium transients in neural retinal Muller cells, the principle macroglial cell type in the retina, which have been shown to exhibit spatially complex patterns of correlated co-activation (Agulhon et al., 2007
), suggesting complex spatiotemporal coordinated signaling between cells in the network.
We attempted to model these effects as a stochastic term in the state equation. The purpose of this term is to add random fluctuations to the state function that determine its sensitivity to perturbations. If upon the addition of small amounts of Brownian noise to the state function the network changes significantly from trial to trial with regards to its pattern of activation, then small perturbations in experimental conditions could be expected to be important in trial-to-trial variability. The state equation was modified to be
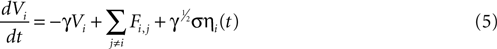
where ηi(t) is a zero-mean Gaussian white noise term with standard deviation σ. This equation is a form of a Langevin equation, which describes the effect of adding Brownian (thermal) noise to a state function (Reif, 1965
). The γ1/2 term ensures that the effect of the noise term on the system will remain constant regardless of the damping constant. Using this equation in simulated ICW experiments for fields of astrocytes with experimentally derived geometries resulted in a large degree of trial-to-trial variation as well as some cells farther away from the initial stimulus becoming active before those nearer to the stimulus, accurately reproducing experimentally observed properties. The partially regenerative stochastic diffusion model represented by Eq. 5 was able to capture and reproduce the dynamics of experimentally measured ICW as well as reproduce the non-uniform recruitment seen in experiments (Figures 5
A–C). Furthermore, the model was able to accurately reproduce the spatiotemporal propagation dynamics of measured ICW, i.e., how a wave propagates in space as a function of time in addition to what its final state is. Figure 5
D plots the distance traveled by both simulated and measured ICW for the data shown in Figure 1
as a function of time. Both modeled and experimental data sets were fit by a Naka–Rushton function with similar parameters (see figure legend for details), which ubiquitously describes the dynamics of a large number of physiological phenomena. Interestingly, gap junction signaling between contiguous cells could potentially underlie the stochastic characteristics of wave propagation (see Discussion below).
Figure 5. Simulating intercellular calcium waves in geometrically realistic astrocyte networks (taken from the data shown in Figure 1
) with the partially regenerative diffusion model and an additional stochastic noise term (Eq. 5) produced spatiotemporally realistic propagating waves that qualitatively matched measured experimental results. Three independent representative simulation runs are shown (A–C). Note the qualitatively similar dynamics but differing pattern of cell activations between all three simulated panels. Compare these results with the experimentally measured wave from Figure 1
. The blue dot represents the initially activated cell. (D) The distance traveled by the ICW wave front for one simulation example (solid circles) as a function of time compared to the experimental data from Figure 1
(open circles). Both sets of data were fit to the Naka–Rushton equation given by S(P) = rPN/(ΘN + PN), with the fitted parameters are r = 140 and 133, Θ = 55.47 and 58.97, and n = 2.79, 2.16, for the simulation and experimental data, respectively. The goodness of fit for each as measured by their R2 values was 0.990 and 0.993, respectively.
Data in the literature support both a point source model whereby an activated astrocyte releases a finite amount of ATP that diffuses to and activates nearby cells (Arcuino et al., 2002
, 2004
; Cotrina et al., 1998
, 2000
; Iacobas et al., 2006
) and a regenerative model whereby downstream astrocytes propagate the signal by releasing their own ATP in response to external stimuli (Anderson et al., 2004
; Ballerini et al., 1996
; Hassinger et al., 1996
; Newman 2001
; Parpura et al., 1994
; Queiroz et al., 1997
, 1999
). Although not mutually exclusive, most studies provide evidence for one or the other, and it is not immediately apparent from the literature how the two mechanisms function with respect to each other. Here we introduce a simple phenomenological lumped parameter diffusion model that can replicate the main aspects of the dynamics associated with experimentally measured ICW. Based on our modeling and simulations, separate point source and partially regenerative signaling mechanisms simulate results consistent with experimental measurements that necessarily imply the contribution of both signaling mechanisms to astrocyte ICW. As such, we propose that apparently conflicting data described in the literature are not in conflict but merely selecting for and measuring a part of the overall system. Furthermore, this model is reductionist by design and purposely omits a considerable amount of biophysical details, yet is able to accurately reproduce the kinetics of ICW (see Figure 4 and Figure 5
). This suggests that the functional dynamics of astrocyte signaling via ICW are dominated by the inherent properties of the relevant physics, independent of the underlying molecular details that give rise to it. This is a very efficient and robust approach for reliable intercellular signaling. This also is an energetically efficient method for communicating long-distance with cells as it requires little release of ATP from downstream cells to amplify the ICW.
While some work has modeled calcium dynamics and ATP release by astrocytes, they have been primarily realistic biophysical models at the single cell level (Bennett et al., 2005
; Hofer et al., 2002
; Iacobas et al., 2006
; Stamatakis and Mantzaris, 2006
). The extrapolation of fully regenerative biophysical models to networks of astrocytes results in every cell in a network releasing the majority of its store of ATP upon activation and a non-attenuated continuous calcium wave that recruits every cell in the simulated field of view. We obtained the same result when using the diffusion model to simulate fully regenerative ATP release, resulting in an essentially instantaneous transition from all cells being inactive to the entire network becoming activated (Figure 2
).
It has been proposed that internal dynamics such as PLC activity, calcium buffering, and the filling of internal Ca2+ stores can account for the finite signaling range in these regenerative models (Giaume and Venance, 1998
); however these require specific restricted ranges of parameters or gap junctional dominated signaling. Models of ATP diffusion in which IP3 concentration is uncoupled from or weakly coupled to calcium excitability also exhibit finite waves (Hofer et al., 2002
; Stamatakis and Mantzaris, 2006
), however they need a restricted parameter range of the coupling between Ca2+ and subsequent IP3 regeneration. It has been shown that IP3 can be generated through Ca2+ dependent activation of PLC (Berridge, 1993
; Venance et al., 1997
), however it is unclear whether this coupling is weak enough to allow the decay of the IP3 signal and therefore ATP release as the wave spreads, which these models assume. Our model is a realistic alternative that naturally results in finite ICW that match the spatiotemporal kinetics of experimental ICW without constrained parameter restrictions (Figure 5
).
As discussed in the introduction, propidium iodide is only taken up by the initial cell involved in a wave, which would be the case in both a single point source release model and a partially regenerative model as we propose. This would be consistent with the suggestion that vesicular ATP is the predominant cause of intercellular ATP signaling (Bowser and Khakh, 2007
), since a vesicular release mechanism for ATP in downstream cells would not result in propidium iodide uptake yet could be responsible for extending the wave distance. Similarly, data showing a mechanism for ATP-induced ATP release (which is at odds with the suggestion of a point source release of ATP) is also consistent with our model. Purinergic receptor antagonists such as suramin (which would stop ATP-induced ATP release) only partially inhibit the range of ATP propagation. This is consistent with an initial point source release of ATP followed by limited downstream release due to inhibition of purinergic receptors by suramin. Finally, recent work has shown that ATP can be released extracellularly through connexin 43 hemichannels (Kang et al., 2008
), which are gated both mechanically (Cherian et al., 2005
) and electrically (Contreras et al., 2003
) and are upregulated by inflammatory and pathological processes in astrocytes and microglia (Retamal et al., 2007
). As hypothesized, this therefore could be the initial mechanism of release in an ICW (Cotrina et al., 1998
).
This dual signaling mechanism also provides an explanation as to why an initial release of ATP by an astrocyte can result in a wave that travels well beyond the ability of a point source release to propagate based on diffusion alone. Even a small amount of downstream released ATP can significantly contribute to the propagation of the wave, as shown above. This provides a mechanism to increase the dynamic range of ICW. Based on diffusion arguments alone, for a point source release to travel twice the distance four times as much ATP would need to be secreted, while for the dual signaling mechanism only about twice as much needs to be released from the initial source.
Although phenomenological by design, the diffusion model makes a number of simplifying assumptions about the underlying cell biology and biophysics. First of all, the model uses an integrate-and-fire based approach in which the cell’s ATP is released instantaneously, which is an idealization of all basic integrate-and-fire models but not biologically realistic since it ignores the temporal delays associated with internal processes such as the diffusion and interaction between biochemical species. The model also does not take into account cell morphology, receptor locations, or a spatially varying diffusivity constant for ATP. However, we found that this degree of detail was not necessary to model the propagation dynamics of ICW, which suggests that the principle mechanisms associated with wave dynamics are primarily governed by diffusion considerations at the level of the whole network.
This model also purposely ignores possible effects from gap junctions that can potentially couple contiguous astrocytes. IP3 diffuses through gap junctions (Sneyd et al., 1994
), and gap junctional inhibitors such as octanol and halothane have been shown to decrease the wave size (Finkbeiner, 1992
). In addition, C6 glioma cells, which display limited gap junctional coupling, show limited calcium wave sizes; while C6 cells transfected with Cx43 display enhanced calcium waves comparable to other glial cells (Charles et al., 1992
). Although these data suggest a role for gap junctional communication in ICW, the actual mechanism may still be ATP dependent but modulated by gap junctional signaling. ATP can be released extracellularly by Cx43 hemichannels (Kang et al., 2008
), so that gap junction blockers could also be directly inhibiting ATP secretion and diffusion. In addition, an increase in connexin expression in C6 cells is accompanied by a complimentary increase in ATP release (Cotrina et al., 1998
). Finally, although astrocytes exhibit gap junctional connections, retinal Muller cells normally do not, yet can also exhibit robust ICW mediated purely by extracellular diffusion (Newman, 2001
). Finally, the diffusion of IP3 through gap junctions itself can produce an increase in intracellular ATP that can then be vesicularly secreted (Haydon, 2001
). Collectively these data suggest that gap junctional signaling might be more involved with the modulation of ICW mediated by ATP diffusion rather than participating as a mechanism of wave propagation itself. This would also be in agreement with the results of our model, which is able to accurately reproduce realistic finite ICW based on ATP diffusion mechanisms alone. The macro scale dynamics of the waves, such as signaling speed and extent, can therefore be accounted for essentially entirely by ATP diffusion. However, as discussed above, this diffusion model is sensitive to small noise perturbations, and indeed we had to introduce a non-specific noise term into the diffusion equations in order to capture the stochastic nature of propagating ICW. This could point to a role for gap junctions acting as the molecular mechanism for this stochasticity and would be an interesting question for further both experimental and modeling exploration.
Finally, the diffusion model’s predictions should be testable experimentally, which is the focus of on-going work. For example, we are investigating signal propagation in astrocyte networks under ecto-ATPase inhibition in order to determine if the model’s predictions about signaling properties across cell free gaps are valid. Another series of experiments will stimulate the same initial cell in a field of view repeatedly in order to correlate the degree of trial-to-trial variation with model predictions about the contribution of noise to the stochastic nature of signaling patterns versus other possible contributors. Furthermore, the simplicity of the model offers the opportunity to derive parameter values during an experiment in real time, which would allow its use, for example, as a classifier of astrocyte functional signaling sub-populations or measuring network responses to pharmacological perturbations.
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
This work was funded by NIH grant NINDS R01 NS054736 and a Walter Coulter Foundation for Biomedical Engineering Early Career Award to G.S.
The Diffusion Equation and its Solution
We begin by assuming each glial cell has an internal state function, V, which represents the accumulation of signal that leads to a calcium transient and release of ATP upon reaching a certain threshold, Vth. We then assume this state function increases due to the presence of ATP at the cell and decreases with time.
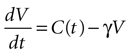
where γ is the decay rate of the state function (chosen to be .12 s−1 to match the experimental decay rates in Figure 1
) and C is the concentration of ATP at the location of the cell at time t.
Next, assume that there is a second cell present, and the concentration C of ATP at the surface of cell 1 is due to discrete release events of ATP from cell 2. This ATP then diffuses through space to the location of cell 1. The diffusion of ATP through media is modeled by the diffusion equation,
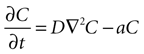
where C is a four dimensional variable given by C(x, y, z, t) that represents the concentration of ATP as a function of space and time, D is the diffusion constant of ATP through the media, and a is the rate of uptake and/or degradation of ATP.
One can model the release of ATP from a cell as an amount of ATP, k, released at a point source located at the center of the cell. This can be represented as a Dirac delta function of height k at the location of the cell. In polar coordinates centered at the cell that is releasing the ATP (i.e. cell 2 in this case) this is
C(r, T) = k · δ(r, T)
where r is distance measured in μm and T is time measured in seconds. This serves as the initial concentration for solving the diffusion equation. For the purposes of this work, we solved the equation in two dimensions with the general solution
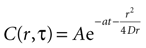
Assuming a boundary condition such that when the rate of ATP uptake and degradation is zero (a = 0), the total concentration of ATP in solution will always be k, the initial release amount. This is mathematically represented by
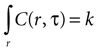
which leads to a solution of the form
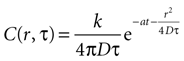
with C being the concentration in attomoles · μm2. The diffusion constant was chosen to be 300 μm2 · sec−1 (see main text). This results in the units of k, the amount of ATP released per event, being attomoles (10−18 mol). This equation will give concentration of at any distance r from a cell releasing ATP at any time T.
Expanding to a Network Level Representation
For a field of N cells, let each cell have a state function Vi where i is numbered from 1 to N. In a field of N cells releasing ATP, the concentration of ATP at cell i will be a summation of the concentration due to all other cells in the field, i.e.
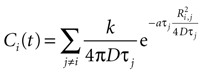
with j ≠ i meaning summation over all cells in the field except for cell i. Ri,j is the distance between cells i and j in μm and Ti the time since cell j released ATP.
Combining this with the original equation,
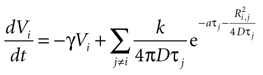
which can be written as separate equations,


Equation 1 describes the state function as a sum of the internal damping and external ATP concentration, while Eq. 2 provides the function to calculate the external ATP concentration.
Derivation of Vth
Based on experimental results we assume a constant application of ATP at a concentration of 3 μm will induce a calcium transient, but not less (see main text).
Solving the original equation for a constant C,
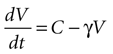
results in
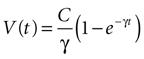
where the steady state value t → +∞ will reach
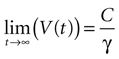
Since the threshold is to be activated when C 3 μM but not less, the threshold is set to
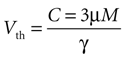
Since this model is a two dimensional diffusion model, we need to assume something about the third dimension. Assuming astrocytes and 2-D plane have a thickness of 10 μm, this produces a concentration in 2-D coordinates of
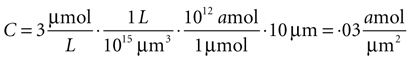
given γ 0.12 sec.−1,
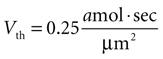
Basis for Assuming Single Astrocyte Activations During an ICW
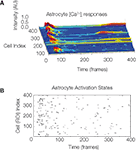
The model assumes that each astrocyte in the network can only activate once throughout the course of a wave and that it remains refractory until the end of the signaling event. This is not physiologically valid, since our own data has shown that astrocytes participating in an ICW can respond more than once during a given signaling event (Figure S1
). However, our measurements suggest that the frequency of feedback and re-signaling by astrocytes within a given ICW event is very low. As such, this assumption is a reasonable first approximation.
Figure S1. The temporal sequence astrocyte activation states and presence
of recurring activation within the same calcium wave suggests
that recurring signaling by previously recruited astrocytes occurs at
a non-zero but low frequency. One representative example is shown. (A)
Selected intracellular calcium transient intensity profi les in normalized arbitrary
units for selected astrocytes. The higher the peaks (blue being baseline
levels and red representing two standard deviations above baseline) the
greater the intracellular calcium concentrations. Note the two astrocytes that
re-activated following an initial activation. (B) Raster plot of the same data
showing all participating cells. ROI refers to the traced out region of interest
that defi ned cell volumes prior to the analysis.