Abstract
Learning from complex, multidimensional data has become central to computational mathematics, and among the most successful high-dimensional function approximators are deep neural networks (DNNs). Training DNNs is posed as an optimization problem to learn network weights or parameters that well-approximate a mapping from input to target data. Multiway data or tensors arise naturally in myriad ways in deep learning, in particular as input data and as high-dimensional weights and features extracted by the network, with the latter often being a bottleneck in terms of speed and memory. In this work, we leverage tensor representations and processing to efficiently parameterize DNNs when learning from high-dimensional data. We propose tensor neural networks (t-NNs), a natural extension of traditional fully-connected networks, that can be trained efficiently in a reduced, yet more powerful parameter space. Our t-NNs are built upon matrix-mimetic tensor-tensor products, which retain algebraic properties of matrix multiplication while capturing high-dimensional correlations. Mimeticity enables t-NNs to inherit desirable properties of modern DNN architectures. We exemplify this by extending recent work on stable neural networks, which interpret DNNs as discretizations of differential equations, to our multidimensional framework. We provide empirical evidence of the parametric advantages of t-NNs on dimensionality reduction using autoencoders and classification using fully-connected and stable variants on benchmark imaging datasets MNIST and CIFAR-10.
1 Introduction
With the explosion of computing resources, including cloud-based storage and accessible advanced hardware, learning from large-scale, multiway data has become possible. Two distinct fields have emerged as the gold standards for handling multidimensional data: tensor analysis for featurization and compression and deep learning for high-dimensional function approximation. Both deep learning and tensor methods have achieved strong performance in image and video recognition (Vasilescu and Terzopoulos, 2002; Krizhevsky et al., 2012), medical imaging analysis (Omberg et al., 2007; Ronneberger et al., 2015), spatiotemporal weather analysis (Chattopadhyay et al., 2020; Li et al., 2020), and more. This work focuses on leveraging advantages of tensor methods to enhance deep learning design.
Fundamentally, deep learning approximates mappings from (high-dimensional) inputs (e.g., images) to targets (e.g., classes) using deep neural networks (DNNs), which are simply nonlinear, composite functions parameterized by learnable weights. Despite the success and flexibility of DNNs, the storage and computational costs to design and apply these models can be a significant impediment—there can be millions of network weights and learning requires an immense amount of time and top-of-the-line computational hardware (e.g., GPU clusters).
These computational challenges become bottlenecks for the classic feed-forward neural network, which builds DNNs using dense linear operators (matrices). Such operations uses network weights in an highly inefficient manner, and composing many of these dense matrices can require millions of weights, which is both computationally demanding and can lead to algorithmic problems, such as overfitting. To reduce these inefficiencies, we propose a new type of fully-connected layer that replaces dense linear operators with dense tensor operators. The proposed tensor operators can reduce the number of network weights by an order of magnitude, that leverage the inherent multidimensionality of the input data, and offer the potential for distributed computation. Thus, we call our architecture tensor neural networks (t-NNs).
The foundation of t-NNs is the ⋆M-product (pronounced “star-M”), a family of tensor-tensor products which induces an algebraic structure on a multidimensional space (Kernfeld et al., 2015). The ⋆M-framework provably encodes information more efficiently than traditional matrix algorithms (Kilmer et al., 2021) and has had success facial recognition (Hao et al., 2013), tomographic image reconstructions (Soltani et al., 2016; Newman and Kilmer, 2020), video completion (Zhang et al., 2014), image classification (Newman et al., 2018), and solving tensor linear systems (Ma and Molitor, 2022). We call the ⋆M-product matrix-mimetic; that is, familiar notions such as the identity and transpose are well-defined for the multilinear operation. The advantages of processing data multidimensionally including better leveraging inherit multiway structure and reducing the number of learnable network weights by an order of magnitude. The matrix-mimeticity enables the proposed t-NNs to naturally extend familiar deep learning concepts, such as backward propagation and loss functions, and non-trivial architectural designs to tensor space. We propose two additional extensions: tensor-based loss functions and a stable multidimensional framework, motivated by Haber and Ruthotto (2017), that brings topological advantages of featurization.
1.1 Our contributions
Because of the popularity of this area of research, we want to clarify the objectives and contributions of this paper from the outset. Our contributions are the following:
Tensor algebra and processing for efficient parameterization: we introduce a basic framework for t-NNs, describe the associated tensor algebra, and demonstrate the inherit properties from stable network architectures. We also derive the training algorithm for t-NNs, leveraging matrix-mimeticity for elegant formulations. We show that this tensor parameterization, compared to an equivalent matrix approach, can reduce the number of weights by an order of magnitude.
Tubal loss functions: our the algebraic structure imposed by the ⋆M-product is applied end-to-end. This includes defining new loss functions based on the outputs of the t-NN, which are no longer scalars, but the high-dimensional analog called tubes. This requires a new definition of tubal functions, and opens the door to a wide range of new evaluation metrics. These metrics offer more rigorous requirements to fit the training data, and hence can yield networks that generalize better.
Stable t-NNs: we demonstrate how matrix-mimeticity preserves of desirable network architecture properties, specifically stability. This will enable the development of deeper, more expressive t-NNs.
Open-source code: for transparency and to expand the use of t-NNs, we provide open-source at https://github.com/elizabethnewman/tnn.
Scope: our goal is to explore a new algebraic structure imposed on neural networks and its the advantages over equivalent architectures. This paper serves as the introduction of t-NNs and, similar to the original neural networks, we consider fully-connected layers only. We acknowledge that to obtain state-of-the-art results, we would need tools like convolutional and subsampling layers and significant hyperparameter tuning; however, these are outside the scope of this paper. Convolutional layers apply multiple translation-invariant filters to extract local connections; our t-NNs examine the global structure of the data. Subsampling or pooling layers reduce the dimensionality of our data and hence provide multi-scale features; our t-NNs use no pooling in order to preserve the algebraic structure. We address extensions of t-NNs to convolutional and subsampling layers in the conclusions.
1.2 Organization
This paper is organized as follows. In Section 2, we give a brief outline of related work combining tensors and deep learning. In Section 3, we give the background notation on tensor-tensor products. In Section 4, we formally introduce tensor neural networks (t-NNs) and tubal loss functions. In Section 5, we extend t-NNs to stable architectures and outline a Hamiltonian-inspired architecture. In Section 6, we provide numerical support for using t-NNs over comparable traditional fully-connected neural networks. In Section 7, we discuss future work including implementations for higher-order data and new t-NN designs.
2 Related work
The high dimensional nature of neural network weights has driven the need to reduce the number of weights through structure. Early studies, such as LeCun et al. (1989), demonstrated that neural networks could learn faster from less data and generalize better by removing redundant weights. Following the observation, several works showed that structured weights, such as convolutions (Krizhevsky et al., 2012), low rank weight matrices (Denil et al., 2013), and Kronecker-structured matrices (Jagtap et al., 2022), could perform well with significantly fewer parameters.
Tensor methods for compression high dimensional data and operators grew in popularity concurrently with the development of structured operators for neural networks. Many popular tensor frameworks are designed to featurize multiway arrays (Tucker, 1966; Carroll and Chang, 1970; Harshman, 1970; de Lathauwer et al., 2000; Kolda and Bader, 2009) or to approximate a given high-dimensional operator (Oseledets, 2011; Cichocki et al., 2016). Because the weights and features of deep neural networks are notoriously high-dimensional, tensorized approaches have gained traction. In Novikov et al. (2015), the authors combine efficient tensor storage and processing schemes with DNN training, resulting up to seven times fewer network weights. This work specifically used the tensor train style of weight storage, which is notable for compression of very high dimensional data, but does not have linear algebraic motivations in this context. Further studies followed, such as Chien and Bao (2018) that used multiway operations to extract features convolutionally. This work computes a Tucker factorization of convolutional features rather than treating tensors as operators. Similar layer contraction approaches, called tensor regression layers, have appeared in works such as in Cao et al. (2017) and Kossaifi et al. (2020). These approaches utilize low-rank Tucker-based factorizations to successfully reduce the number of weights in a network without sacrificing performance. These are more similar in spirit to pooling layers of convolutional neural networks rather than operations that preserve multilinearity. Many more studies have connected tensors and neural networks, and we recommend the survey (Wang et al., 2023) for a more complete history of the intersection of the two fields.
As we eluded to in the previous paragraph, in this work, we take a notably different perspective on tensors. We consider tensors as multiway operators and process our layers under this tensor operation. This provides a linear algebraic structure that enables us to extend desirable neural network structure to high dimensions with ease. Because of our strong algebraic foundation, we are able to express forward and backward propagation simply; in comparison, other tensor frameworks require heavy indexing notation. We share and achieve the same goal as other tensor approaches of reducing the number of network weights.
3 Background and preliminaries
To motivate our multidimensional neural network design, we start by introducing our notation and the tensor algebra in which we work. We use Matlab indexing notation throughout the paper, such as selecting the j-th column of a matrix via A(:, j) or A:, j.
3.1 Tensor preliminaries
Let be a real-valued, third-order tensor. Fixing the third-dimension, frontal slices are matrices for k = 1, …, n. Fixing the second-dimension, lateral slices are matrices oriented along the third dimension for j = 1, …, m2. Fixing the first and second dimensions, tubes are vectors oriented along the third dimension for i = 1, …, m1 and j = 1, …, m2. We depict these partitions in Figure 1. While this paper focuses on real-valued, third-order tensors (three indexes), we note all of the presented concepts generalize to higher-order and complex-valued tensors.
Figure 1
We interpret tensors as t-linear operators (Kilmer and Martin, 2011; Kernfeld et al., 2015). Through our operator lens, it is possible to define analogous matrix algebraic properties for tensors, such as orthogonality and rank. Thus, this framework has been described as matrix-mimetic. We describe the fundamental tools to understand how tensors operate for this paper, and refer the reader to Kilmer et al. (2013, 2021) and Kernfeld et al. (2015) for details about the underlying algebra.
We define a product to apply matrices along the third dimension of a tensor (i.e., along the tubes).
Definition 3.1 (mode-3 product). Given and M ∈ ℝℓ × n, the mode-3 product, denoted , outputs an m1×m2×ℓ tensor with entries
for i1 = 1, …, m1, i2 = 1, …, m2, and k = 1, …, ℓ.
The mode-3 product can be generalized along any mode; see Kolda and Bader (2009) for details.
Next, we define the facewise product to multiply the frontal slices of two third-order tensors in parallel.
Definition 3.2 (facewise product). Given and , the facewise product, denoted , returns an m1×m2×n tensor where
for k = 1, …, n.
Combining Definition 3.1 and Definition 3.2, we define our tensor operation, the ⋆M-product, as follows:
Definition 3.3 (⋆M-product). Given , , and an invertible n×n matrix M, the ⋆M-product outputs an m1×m2×n tensor of the following form:
where .
We say that and live in the spatial domain and and live in the transform domain. We perform the facewise product in the transform domain, then return to the spatial domain by applying M−1 along the tubes. If M is the identity matrix, the ⋆M-product is exactly facewise product. If M were the discrete Fourier transformation matrix (DFT), we obtain the t-product (Kilmer and Martin, 2011). In this case, the frontal slices of correspond to different frequencies in the Fourier domain and are therefore decoupled.
We can interpret the ⋆M-product as a block-structured matrix product via
where ⊗ is the Kronecker product (Petersen and Pedersen, 2012). The block matrix structure, , depends on the choice of transformation, M. We consider two familiar examples: the facewise product (M = In) and the t-product (M = Fn, the DFT matrix):
While we never explicitly form Equation (2), the block structure will be helpful for subsequent analysis.
3.2 Matrix-mimetic tensor algebra
The ⋆M-product yields a well-defined algebraic structure. Specifically, suppose we have tubes a, b∈ℝ1 × 1 × n. Then,
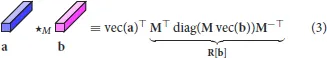
where turns a tube into a column vector. The ⋆M-product of tubes (3) is equivalent to post-multiplying by the structured matrix, R[b]. Note that R[·] implicitly depends on the choice of M, but we omit explicitly writing this dependence for notational simplicity. The tubes form a matrix subalgebra which dictates the algebraic structure imposed on the high-dimensional space (Kernfeld et al., 2015). As a result, the ⋆M-product is matrix-mimetic and yields several familiar concepts.
Definition 3.4 (⋆M-identity tube). The identity tube e ∈ ℝ1 × 1 × n under the ⋆M-product is
where 1 is the 1 × 1 × n tube containing all ones.
This gives rise to the notion of an identity tensor.
Definition 3.5 (⋆M-identity tensor). A tensor is the identity tensor if for i = 1, …, m where e is the ⋆M-identity tube.
Note that if the size of third dimension is equal to one (i.e., n = 1), then Definition 3.5 collapses into the identity matrix. This is a hallmark of our ⋆M-framework and matrix-mimeticity; the product and definitions reduce to the equivalent matrix definitions when the third dimension is removed.
Definition 3.6 (⋆M-transpose). Given , its transpose is
for k = 1, …, n.
Note that if our transformation M is complex-valued, the transpose operator in the transform domain performs the conjugate transpose. However, because we are working with real-valued tensors in the spatial domain, the transpose will be real-valued as well.
4 Tensor neural networks (t-NNs)
In general, neural networks are parameterized mappings from an input space to the target space . These mappings are composite functions of the form
Each subfunction fj(·, θj) for j = 1, …, d is called a layer. The goal is to find a good set of weights θ ≡ (θ1, …, θd) ∈ Θ such that FNN(y, θ) ≈ c for all input-target pairs . Here, Θ is the parameter space and is the data space.
The most common layer of feed forward neural networks (4) consists of an affine transformation and pointwise nonlinearity of the form
where is a weight matrix, is a bias vector, and is a one-dimensional nonlinear activation function, applied entrywise. In practice, activation functions are monotonic, such as the sigmoid function, σ(x) = 1/(1+e−x), or Rectified Linear Unit (ReLU), σ(x) = max(x, 0). We call yj the features of layer j and are the input features. Notationally, we use θj ≡ (Wj, bj) to collect all of the learnable weights for layer j.
4.1 Improved parameterization with the ⋆M-product
When designing a neural network, we seek to balance a simple parameter space with an expressive feature space. However, traditionally fully-connected layers like (5) use parameters in a highly inefficient manner. We propose new tensor fully-connected layers for a more efficient parametrization while still creating a rich feature space. Specifically, we consider the following tensor forward propagation scheme:
for j = 1, …, d. Suppose our input features is of size m0×1 × n. Here, the weight tensor is of size mj+1×mj×n and the bias is of size mj+1×1 × n. The forward propagation through Equation (6) results in a tensor neural network Ftnn(·, θ) where .
Through the illustration in Figure 2, we depict the number of weight parameters required to preserve the size of our feature space using either a dense matrix (Figure 2A) or a dense tensor under the ⋆M-product (Figure 2B). Using the ⋆M-algebra, we can reduce the number of weight parameters by a factor of n while maintaining the same number of features (i.e., maintaining a rich feature space). Beyond the parametric advantages, the multilinear ⋆M-product incorporates the structure of the data into the features. This enables our t-NNs to extract more meaningful features, and hence improve the richness of our feature space.
Figure 2
4.2 The training problem
Training a (tensor) neural network is posed as a stochastic optimization problem given by
where is the loss function that measures the misfit between the network prediction and the true target. The expectation is taken over all input-target pairs . The additional function regularizes the weights to promote desirable properties (e.g., smoothness), weighted by a regularization parameter λ > 0.
4.3 Tubal loss (t-loss) functions
The loss function is chosen based on the given task. For regression, we often use mean squared error, and for classification, which is the focus of this paper, we often use cross entropy. Cross entropy loss, related to the Kullback–Leibler (KL) divergence (Kullback and Leibler, 1951), measures the distance between two probability distributions. In practice, we first transform the network outputs into a set of probabilities using exponential normalization. Specifically, we use the softmax function , defined entrywise as
where Δp is the p-dimensional unit simplex.
To preserve the algebraic integrity of t-NNs, we introduce a tubal variant of the softmax function. Drawing inspiration from Lund (2020), a tubal function, we start by defining tubal functions generally.
Definition 4.1 (tubal function). Given b ∈ ℝ1 × 1 × n, a tubal function acts on the action of b under the ⋆M-product; that is,
In practice, a tubal function is applied pointwise in the transform domain.
We note that the pointwise function in Definition 4.1 is equivalent to applying a matrix function to the eigenvalues of the matrix R[b]. We provide a visualization of the effects of tubal functions compared to applying an entry-wise function in Example 4.2.
Example 4.2 (Visualizations of tubal functions). Consider the following RGB image of a Tufts Community Apeal elephant (TCA, 2023), where 3 is the number of color channels (Figure 3A). We rescale each entry of between 0 to 1 and consider the following transformation matrix:
To illustrate the effect of using tubal functions, we compare applying various functions as pointwise functions (i.e., independent of M) and as tubal functions using Equation (9) in Figure 3B.
Figure 3
Tubal functions are able to capture shared patterns among the tubes that entrywise operators ignore. Each choice of tubal function highlights different features of the image, such as the body with f(x) = max(x, 0) and the heart with f(x) = tanh(x). In comparison, the entrywise counterparts do not bring new insights or structure. A striking difference occurs for f(x) = sign(x). The entrywise operator turns all pixels white because the RGB entries are all nonnegative. In contrast, the tubal equivalent is applied in the transform domain, and hence reveals meaningful features of the image.
Note that the results depend on the chosen tubal function and transform M. We deliberately chose M to emphasize green and blue channels and diminish the effect of the red channel, enabling easy-to-interpret distinctions between tubal and entrywise functions.
We can now define a tubal softmax function based on the traditional softmax function in (8).
Definition 4.3 (tubal softmax). Consider a lateral slice as a p×1 vector of 1 × 1 × n tubes. Then, the tubal softmax function performs the following mapping:
for i = 1, …, p where and the exponential functions are applied as tubal functions. Here, Δp×1 × n is the tubal-equivalent of p-dimensional unit simplex.
We interpret as a vector of “tubal probabilities” in that the tubes sum to the identity tube
Through Definition 4.3, we demonstrate the parallels between tubal functions and traditional functions; the similarities are a direct consequence of a matrix-mimetic tensor framework.
The last step to define the tubal cross entropy function that converts the output of tubal function to a scalar. Recall, traditional cross entropy for one sample is given by
where x is the output of the network, c is the corresponding target class, and h is the softmax function. We generalize (11) to a tubal variant as follows:
Definition 4.4 (tubal cross entropy (t-cross entropy)). The tubal cross entropy function is given by
where h is the tubal softmax function, log is applied as a tubal function, c is the index corresponding to the target class, and ||·||q is a vector norm.
The intuition behind Definition 4.4 is the following. If we have good features , then , the identity tube, and the remaining tubes will be closer to 0. In the transform domain, and the remaining entries will be close to zero. When we apply the log pointwise in the transform domain, the tube and the remaining entries will be large negative numbers. As a result, Ltce is smallest when the , as desired.
In practice, if q-norm corresponds to a finite integer, we can instead use for t-cross entropy for easier derivative computations. For numerical benefits when training, we consider normalized versions based on the number of tubal entries, e.g., multiply by 1/n. These suggested modifications should not change performance in theory, but could change preferred training hyperparameters.
4.4 Backward propagation with t-NNs
The workhorse of neural network training is backward propagation (Rumelhart et al., 1986; Bengio et al., 1994; Shalev-Shwartz et al., 2017; Nielsen, 2018), a method to calculate the gradient of the objective function (7) with respect to the weights. With gradient information, one can apply standard stochastic gradient optimization techniques to train.
In the ⋆M-framework, for an orthogonal transformation M, the backpropagation formulas are analogous to the matrix case. For example, the derivatives of the ⋆M-product are
where indicates a direction or perturbation of the same size as . For full details on the derivation, we refer the reader to Newman (2019).
The simplicity of the back-propagation formulas (12) is one of the hallmarks of our choice of leveraging a matrix-mimetic tensor framework. Other tensor-based neural network designs (Wang et al., 2023) often require complicated indexing and non-traditional notation which, in addition to being cumbersome, can preclude extending more sophisticated neural network architectures to higher dimensions. The ⋆M-framework yields derivative formulations that are easy to interpret, implement, and analyze.
5 Stable t-NNs
As the depth (number of layers) of a network increases, gradient-based training is subject to numerical instability such as vanishing or exploding gradient problem (Bengio et al., 1994; Shalev-Shwartz et al., 2017). To avoid these instabilities, one can interpret deep neural networks as discretizations of differential equations (Ee, 2017; Haber and Ruthotto, 2017; Haber et al., 2018) and analyze the stability of forward propagation as well as the well-posedness of the learning problem; i.e., whether the classifying function depend continuously on the initialization of the parameters (Ascher, 2010). By ensuring stability and well-posedness, networks can generalize better to similar data and can classify data more robustly.
We emphasize that the notion of stability is related to the formal numerical analysis definition in the Lyapunov sense (i.e., stability of dynamical systems). This is a property of the model itself and independent of the data. From a statistical and foundational learning theory perspective, neural networks are typically over-parameterized models, which tend to overfit. In this context, stability can promote better generalization by imposing constraints of the structure of the weight matrices, effectively reducing the number of degrees of freedom. The tensorial structure imposes additional constraints and further reduces the number of parameters, which can again lead to better generalization.
5.1 Well-posed learning problem criterion
Consider the residual neural network (He et al., 2016) with tensor operations, given by
where , , and . With the addition of the step size h, we can interpret Equation (13) as a forward Euler discretization of the continuous ordinary differential equation (ODE)
for all t ∈ [0, T] where T is the final time corresponding to the depth of the discretized network.
The stability of non-autonomous ODEs like (14) depends on the eigenvalues of the Jacobian with repsect to the features. To perform analogous analysis for tensor operators, it is useful to consider the equivalent block matrix version of the ⋆M-product in Equation (1) where . It follows that we can matricize (14) via
The Jacobian of the matricized system (15) with respect to is
where and J(t) ∈ ℝmn×mn. In most cases, the activation function σ is non-decreasing, and thus the entries in diag(σ′(x(t))) are nonnegative. As a result, the stability and well-posedness of the ODE relies on the eigenvalues of . As described in Haber and Ruthotto (2017), the learning problem is well-posed if
where λi(A) is the i-th eigenvalue of A. This criterion implies that the imaginary part of the eigenvalues drive the dynamics, promoting rotational movement of features. This produces stable forward propagation that avoids features diverging and prevents inputs from distinct classes from converging to indistinguishable points; the latter would lead to ill-posed back propagation and hence an ill-posed learning problem.
We can be more concrete about the eigenvalues because in Equation (1), is block-diagonalized in the transform domain. Thus, we can equivalently write Equation (16) as follows:
for i = 1, …, m and k = 1, …, n. In short, if the eigenvalues of each frontal slice in the transform domain have a real part close to zero, the t-NN learning problem will be well-posed, save one more requirement.
A subtle, yet important requirement for stability is that the weights change gradually over time (i.e., layers). This ensures that small perturbations of the weights yield small perturbations of the features. To promote this desired behavior, we imposed a smoothing regularizer in (discrete) time via
5.2 Hamiltonian-inspired stable t-NNs
While theoretically useful, it is impractical to evaluate the eigenvalues of the weight tensors to satisfy the well-posedness condition (17) as we train a network. Instead, motivated by the presentation in Haber and Ruthotto (2017), we implement a forward propagation that inherently satisfies (17) independent of the weights. This forward propagation scheme is inspired by Hamiltonian dynamics, which we briefly describe and refer to Ascher (2010) and Brooks et al. (2011) for further details. We define a Hamiltonian as follows:
Definition 5.1 (Hamiltonian). Let , , and t ∈ [0, T]. A Hamiltonian is a system governed by the following dynamics:
Intuitively, the Hamiltonian H describes the total energy of the system with y as the position and z as the momentum or velocity. We can separate total energy into potential energy U and kinetic energy T; that is, H(y, z, t) = U(y)+T(z). This separability ensures the Hamiltonian dynamics conserve energy; i.e.,
In terms of neural networks, energy conservation (19) ensures that network features are preserved during forward propagation, thereby avoiding the issue of exploding/vanishing gradients and enabling the use of deeper networks. Additionally, Hamiltonians are symplectic or volume-preserving in the sense that the dynamics are divergence-free. For neural networks, this ensures the distance between features does not change significantly, avoiding converging and diverging behaviors. We also note that Hamiltonians are time-reversible. This ensures that if we have well-posed dynamics during forward propagation, we will have similar dynamics for backward propagation.
5.3 Discretizing Hamiltonians with leapfrog integration
To preserve the benefits of Hamiltonians in the discretized setting, we symmetrize the Hamiltonian (Definition 5.1) and use a leapfrog integration method (Skeel, 1993; Ascher, 2010; Haber and Ruthotto, 2017). For t-NNs, we write the new system in terms of the ⋆M-product (with slight abuse of notation)
where and . Here, indicates the data features and is an auxilary variable not related to the data directly. We add the bias tube, b(t), to each element. The equivalent matricized version of Equation (20) is
The (matricized) system (21) is inherently stable, independent of the weight tensors , because of the block antisymmetric structure. The eigenvalues of antisymmetric matrices are purely imaginary, which exactly satisfy the stability condition in Equation (17).
We discretize Equation (20) using the leapfrog method, a symplectic integration technique, defined as
for j = 0, …, d−1. We demonstrate the benefits of stable forward propagation (22) in Example 5.2.
Example 5.2 (Trajectories of stable t-NNs). We construct a dataset in ℝ3 randomly drawn from a multivariate normal distribution with mean of 0 and a covariance matrix of 3I3. The points are divided into three classes based on distance to the origin with yellow points inside a sphere with radius r = 3.5, green points inside a sphere with radius R = 5.5, and purple points outside both spheres. We train with 1200 data points and store the data as 1 × 1 × 3 tubes.
We forward propagate using one of two integrators with weights and biases as 1 × 1 × 3 tubes:
We create a network with d = 32 layers and use a step size of h = 2. We use the discrete cosine transform for M. We train for 50 epochs using Adam (Kingma and Ba, 2015) with a batch size of 10 and a learning rate of γ = 10−2. To create smoother dynamics, we regularize the weights using Equation (18) with regularization parameter λ = 10−4/h. We illustrate the dynamics of trained networks in Figure 4.
Figure 4
The dynamics in Figure 4 show the topological benefits of leapfrog integration. The data points exhibit smoother, rotational dynamics to reach the desired linearly-separable final configuration. In comparison, forward Euler propagation significantly changes topology during forward propagation. Such topological changes may yield ill-posed learning problems and poor network generalization.
6 Numerical results
We present two image classification problems to compare tensor linear layers and stable tensor neural networks to comparable matrix versions. Overall, the results show that t-NN trained with tubal loss functions generalize better to unseen data than equivalent matrix networks, and can do so with 20–30 times fewer network weights.
6.1 Experiment setup and hardware
We implement both tensor and matrix frameworks using PyTorch (RRID:SCR_018536) (Paszke et al., 2017). All of the code to reproduce the experiments is provided in https://github.com/elizabethnewman/tnn. All experiments were run on an Exxact server with four RTX A6000 GPUs, each with 48 GB of RAM. Only one GPU was used to generate each result. The results we report are for the networks that yielded the best accuracy on the validation data.
We train all models using the stochastic gradient method Adam (Kingma and Ba, 2015), which uses a default learning rate of 10−3. In most cases, we select hyperparameters and weight initialization based on the default settings in PyTorch. We indicate the few exceptions to this at the start of the corresponding sections. We also pair the stochastic optimizers with a learning rate scheduler that decreases the learning rate by a factor of γ every M steps. In all cases, we used the default γ = 0.9 and M = 100. This is a common practice to ensure convergence of stochastic optimizer in idealized settings (Bottou et al., 2018). We utilize a weight decay parameter in some experiments to reduce overfitting.
For the tensor networks in all experiments, we use the discrete cosine transform for M, which is a close, real-valued version of the discrete Fourier transform (DFT). The DFT matrix corresponds to the t-product, which has been shown to be effective for natural image applications (Kilmer and Martin, 2011; Hao et al., 2013; Newman et al., 2018).
6.2 MNIST dimensionality reduction
The MNIST dataset (LeCun et al., 2010) is composed of 28 × 28 grayscale images of handwritten digits. We train on 50, 000 images and reserve 10, 000 for validation. We report test accuracy on 10, 000 images not used for training nor validation. For NNs, we vectorize images and store as columns, resulting in a matrix of size 282×b where b is the number of images. For t-NNs, we store the images as lateral slices, resulting in a tensor of size 28 × b×28.
In this experiment, we train an autoencoder to efficiently represent the high-dimensional MNIST data in a low-dimensional subspace. Autoencoders can be thought of as nonlinear, parameterized extensions of the (truncated) singular value decomposition. Our goal is to solve the (unsrpervised) learning problem
where is the encoder and is the decoder. Here, is the latent space that is smaller than the data space; in terms of dimension, we say . Note that the mean squared error (MSE) tubal loss is the same as the MSE loss function when using an orthogonal transformation matrix, as we have done in our experiments. We describe the NN and t-NN autoencoder architectures used in Figure 5 and report results in Figure 6.
Figure 5
Figure 6
We observe that the t-NN outperforms the NN autoencoders with similar numbers of weights with an order of magnitude smaller training and validation loss and test error as well as qualitative improvements of the approximations. The neural network autoencoder with the same feature space dimensions, NN(560,280), performs best in terms of the loss and error metrics, but requires over 20 times more network weights than the t-NN autoencoder. The t-NN layers are able capture spatial correlations more effectively using multilinear operations, resulting in quality approximations with significantly fewer weights.
6.3 MNIST classification
We use the same MNIST dataset as for the autoencoder example. We train for 20 epochs using Adam with a batch size of 32 and a learning rate of 10−2. We add Tikhonov regularization (weight decay) with a regularization parameter of λ = 10−4. We use the PyTorch defaults for the other optimizer hyperparameters. For the t-cross entropy loss, we use a squared ℓ2-norm and normalize by the number of entries in the tube.
We compare four different two-layer neural network architectures, described in Table 1. We use either cross entropy loss or t-cross entropy loss, depending on the architecture.
Table 1
| Name | Architecture | Layer 1 | Layer 2 | |θ| |
|---|---|---|---|---|
| NN | W2σ(W1y0+b1)+b2 | W1: 39 × 282 | W2: 10 × 39 | 31, 015 |
| b1: 39 × 1 | b2: 10 × 1 | |||
| NN, square | W2σ(W1y0+b1)+b2 | W1: 282×282 | W2: 10 × 282 | 623, 290 |
| b1: 282×1 | b2: 10 × 1 | |||
| t-NN | : 28 × 28 × 28 | W2: 10 × 282 | 30, 586 | |
| : 28 × 1 × 28 | b2: 10 × 1 | |||
| t-NN, t-loss | : 28 × 28 × 28 | : 10 × 28 × 28 | 30, 856 | |
| : 28 × 1 × 28 | : 10 × 1 × 28 |
Description of MNIST two-layer network architectures with σ(x) = tanh(x).
The t-NN architectures were chosen to preserve the size of the images. The NN width of 39 is chosen to be as small as possible such that the NN architecture does not have fewer parameters than the t-NN architecture. The final column reports the total number of learnable weights.
We report the convergence and accuracy results in Figure 7 and Table 2, respectively.
Figure 7
Table 2
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | Overall | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | NN | 97.05 | 96.54 | 90.58 | 89.73 | 93.03 | 88.91 | 92.36 | 91.91 | 87.79 | 84.57 | 91.33 |
| NN, square | 96.67 | 93.85 | 92.58 | 84.82 | 94.84 | 89.11 | 97.91 | 88.76 | 77.98 | 85.56 | 90.24 | |
| t-NN | 98.98 | 99.64 | 97.12 | 97.88 | 98.29 | 96.06 | 98.68 | 97.60 | 93.30 | 95.59 | 97.36 | |
| t-NN, t-loss | 97.28 | 97.06 | 95.97 | 91.09 | 94.92 | 92.50 | 97.26 | 92.26 | 91.99 | 91.61 | 94.22 | |
| Valid | NN | 96.90 | 96.46 | 89.50 | 89.79 | 92.13 | 89.94 | 92.28 | 91.33 | 88.85 | 81.02 | 90.94 |
| NN, square | 94.50 | 93.36 | 90.60 | 84.68 | 94.99 | 89.83 | 97.36 | 89.26 | 77.81 | 82.16 | 89.52 | |
| t-NN | 97.60 | 99.29 | 95.40 | 97.01 | 97.34 | 95.66 | 96.75 | 97.08 | 92.47 | 93.26 | 96.26 | |
| t-NN, t-loss | 96.20 | 97.08 | 94.80 | 90.94 | 93.46 | 93.60 | 97.26 | 92.46 | 92.16 | 89.21 | 93.76 | |
| Test | NN | 98.16 | 97.18 | 89.44 | 92.18 | 93.08 | 88.00 | 90.50 | 89.49 | 87.58 | 85.43 | 91.20 |
| NN, square | 97.14 | 94.89 | 92.44 | 85.84 | 95.01 | 88.79 | 97.49 | 87.45 | 78.23 | 83.35 | 90.11 | |
| t-NN | 98.67 | 99.38 | 95.25 | 97.03 | 98.37 | 94.96 | 97.08 | 96.50 | 93.74 | 94.05 | 96.55 | |
| t-NN, t-loss | 98.16 | 98.33 | 95.35 | 93.66 | 95.21 | 91.59 | 97.18 | 90.66 | 93.94 | 91.08 | 94.57 | |
MNIST training, validation, and test accuracy per class and overall for the four architectures.
The t-NN architecture with cross entropy loss consistently produces the highest accuracy. The bolded values indicate the highest accuracy for the class and dataset.
The t-NN architecture with cross entropy loss outperforms all networks in terms of test accuracy and accuracy per class. The second-best performing network is the t-NN with t-loss. These results are evidence that the features learned from the tensor linear layer (layer 1) are better than those learned by a dense matrix layer. We further note that matrix network NN with square weights has the same final layer shape as the t-NN with cross entropy loss; the only difference between the networks is the first layer. We depict the learned features of each network that preserves the size of the images in Figure 8. The t-NN features from the first layer contain more structure than the NN features with square weights. This reflects the ⋆M-operation, which first acts along the tubes (rows of the images in Figure 8). We also observe that the features of NN are more extreme, close to +1 and −1, the limits of the range of the activation function σ(x) = tanh(x). In comparison, the features extracted from the t-NN with t-loss offer more variety of entries, but still hits the extreme values often. This demonstrates that t-NNs still produce rich feature spaces and are able to achieve these features with about 20 times fewer weights.
Figure 8
We note that the t-NN network with t-cross entropy loss performs well, and we gain insight into the beneifts of t-losses from the accuracy per class in Figure 9. We observe that when we use tubal losses, we require high values for many frontal slices. This creates a more rigorous classification requirement and, as we will see in subsequent experiments, can yield networks that generalize better. Additionally, the distribution of values in the tubal softmax function is reflective of the predicted class. For the second image (true = 3), the two most likely predicted classes were, in order, 3 and 8. Qualitatively, the particularly handwritten 3 has similarities to the digit 8, and the tubal softmax captures this similarity. For the cases that were incorrectly predicted the digit, the handwritten image had structure emblematic of the predicted class and second most likely predicted class matched the true label.
Figure 9
6.4 CIFAR-10
The CIFAR10 dataset (Krizhevsky and Hinton, 2009) is composed of 32 × 32 × 3 RGB natural images belonging to ten classes. We train on 40, 000 images and reserve 10, 000 for validation. We report test accuracy on 10, 000 images not used for training nor validation. For NNs, we vectorize images and store as columns, resulting in a matrix of size (3·322) × b where b is the number of images. For t-NNs, we store the images as lateral slices and stack the color channels vertically, resulting in a tensor of size (3·32) × b×32. We train for 500 epochs using Adam with a batch size of 32. We use a learning rate of 10−3 that decays after every 100 epochs by a factor of 0.9. We use the PyTorch defaults for the other optimizer hyperparameters. For the t-cross entropy loss, we use a squared ℓ2-norm and normalize by the number of entries in the tube.
We compare the performance of the Hamiltonian networks with dense matrix operators and dense tensor operators for various numbers of layers (d = 4, 8). In conjunction with the Hamiltonian network, we use the smoothing regularizer (20) with a regularization parameter of λ = 10−2. We describe the network architectures and number of parameters in Table 3. The NN architectures require more than 30 times the number of weights than the t-NN architectures. We compare the convergence and accuracy results in Figure 10 and Table 4, respectively.
Table 3
| Name | Hamiltonian layers | Final layer | |θ| |
|---|---|---|---|
| NN | Wj: (3·322) × (3·322) | Wd+1: 10 × 3072 | 4 layers: 37, 779, 470 |
| bj: 1 × 1 | bd+1: 10 × 1 | 8 layers: 75, 528, 210 | |
| t-NN | Wj: (3·32) × (3·32) × 32 | Wd+1: 10 × (3·322) | 4 layers: 1, 210, 506 |
| bj: 1 × 1 × 32 | bd+1: 10 × 1 | 8 layers: 2, 390, 282 | |
| t-NN, t-loss | : (3·32) × (3·32) × 32 | : 10 × (3·32) × 32 | 4 layers: 1, 210, 816 |
| : 1 × 1 × 32 | : 10 × 1 × 32 | 8 layers: 2, 390, 592 |
Description of CIFAR-10 Hamiltonian network architectures with σ(x) = tanh(x).
The architectures were chosen to preserve the sizes of the CIFAR-10 images. The final column |θ| reports the total number of learnable weights.
Figure 10
Table 4
| Plane | Car | Bird | Cat | Deer | Dog | Frog | Horse | Ship | Truck | Overall | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Train | NN4 | 99.95 | 100.00 | 99.95 | 100.00 | 99.98 | 99.97 | 100.00 | 99.97 | 100.00 | 100.00 | 99.98 |
| NN8 | 99.90 | 99.97 | 99.80 | 99.95 | 99.93 | 100.00 | 100.00 | 100.00 | 99.93 | 99.93 | 99.94 | |
| t-NN4 | 74.12 | 79.97 | 60.44 | 43.02 | 59.82 | 65.27 | 65.66 | 88.47 | 77.14 | 74.83 | 68.84 | |
| t-NN8 | 76.09 | 81.15 | 61.12 | 35.80 | 69.04 | 58.83 | 62.52 | 91.45 | 76.94 | 75.28 | 68.79 | |
| Valid | NN4 | 54.57 | 62.77 | 40.85 | 29.58 | 39.36 | 42.77 | 58.24 | 59.52 | 70.84 | 60.06 | 51.99 |
| NN8 | 62.08 | 65.54 | 39.76 | 33.92 | 38.53 | 43.36 | 62.34 | 56.62 | 70.74 | 59.06 | 53.30 | |
| t-NN4 | 59.51 | 68.32 | 49.11 | 32.68 | 49.53 | 52.25 | 51.41 | 73.62 | 67.64 | 62.86 | 56.83 | |
| t-NN8 | 60.43 | 66.63 | 47.12 | 23.37 | 53.79 | 44.82 | 47.90 | 73.24 | 65.33 | 59.86 | 54.37 | |
| Test | NN4 | 57.30 | 64.70 | 40.60 | 28.10 | 38.30 | 42.10 | 57.30 | 58.20 | 69.20 | 57.90 | 51.37 |
| NN8 | 62.60 | 63.10 | 40.70 | 33.20 | 39.10 | 44.80 | 61.60 | 55.30 | 69.00 | 55.80 | 52.52 | |
| t-NN4 | 61.00 | 66.90 | 48.40 | 34.40 | 48.10 | 54.70 | 54.50 | 72.50 | 67.30 | 63.30 | 57.11 | |
| t-NN8 | 62.60 | 67.30 | 48.70 | 25.20 | 52.50 | 46.70 | 50.20 | 72.90 | 63.40 | 60.10 | 54.96 |
CIFAR-10 training, validation, and test accuracy per class and overall for the four architectures.
The t-NN architectures with t-cross entropy loss produce the highest overall validation and test accuracy, the traditional metrics to indicate generalization ability. The bolded values indicate the highest accuracy for the class and dataset.
There are several key takeaways from the numerical results. First, the depth of the network did not significantly change performance in this experiment. We state this observation cautiously. We observe this behavior for a certain set of fixed hyperparameters (e.g., step size h, learning rate, regularization parameter λ,...). The interaction of the hyperparameters and performance is complex and a complete ablation study is outside of the scope of this paper. A second takeaway is that the t-NN trained with the tubal loss generalizes better the NN networks and better than t-NNs with cross entropy loss (not shown for simplicity; see Figure 10 for details). This behavior is especially apparent when looking at the test loss in Table 4. The t-NN with four Hamiltonian layers and t-loss performs well overall, obtaining almost 5% better overall test accuracy. In comparison, the matrix NN quickly overfits the training data and thus does not generalize as well. In terms of the test accuracy per class, the t-NN architectures achieve the best performance in all but two classes.
To look into the performance further, we examine the extracted features of Hamiltonian NNs and t-NNs in Figure 11. We see that the NN and t-NN features share similarities. Both features gradually remove the structure of the original image at similar rates. The t-NN architecture achieves this pattern with significantly fewer network weights (over 30 times fewer). The noisy artifacts differ between the two architectures. In particular, we see that the t-NN layers produce blockier artifacts because of the structured ⋆M-operation.
Figure 11
In the last numerical study in Figure 12, we explore how quickly we can train Hamiltonian t-NNs compared to NNs. In addition to an order of magnitude fewer weights, training t-NNs takes less time than training NNs. As we increase the depth of the networks, we see that each NN epoch takes approximately 1.75 times longer to complete. This performance could potentially be further improved if we optimized the ⋆M-product, e.g., using fast transforms instead of matrix multiplication.
Figure 12
6.5 CIFAR-100
The CIFAR100 dataset (Krizhevsky and Hinton, 2009) is composed of 32 × 32 × 3 RGB natural images belonging to 100 classes. We train on 40, 000 images and reserve 10, 000 for validation. We report test accuracy on 10, 000 images not used for training nor validation. We use the same setup and training parameters as the CIFAR10 experiment (Section 6.4). For all experiments, we use Hamiltonian networks with a depth of d = 16, a step size of h = 0.25, and a regularization parameter λ = 10−2. We report the accuracy results in Figure 13.
Figure 13
Observing the results in Figure 13, the conclusions are the same as in the CIFAR-10 experiment. Specifically, training with the t-NN and t-loss produces the best test accuracy, about a 4% improvement from the comparable NN network. This demonstrates that the benefits of dense tensor operations over dense matrix operations can be realized for more challenging classification problems and motivates further development of these tools to improve state-of-the-art convolutional neural networks and other architectures.
7 Conclusion
We presented tensor neural networks (t-NNs) as a new approach to parameterize fully-connected neural networks. We operate using the ⋆M-product which can reduce the number of network weights by an order of magnitude while maintaining the same expressiveness. We introduced tubal loss functions that are an algebraically-consistent t-NN architecture. Because the ⋆M-framework gives rise to a tensor algebra that preserves matrix properties, we extended the notion of stable neural networks to t-NNs, which enable the development of deeper, more expressive networks. Through numerical experiments on benchmark image classification tasks, we demonstrated that t-NNs offer a more efficient parameterization and, when trained with tubal loss functions, can generalize better to unseen data.
Our work opens the door to several natural extensions. First, we note that while this paper focused on imaging benchmark problems in machine learning, the ⋆M-framework can be applied to many data sets, including dynamic graphs (Malik et al., 2021), longitudinal omics data (Mor et al., 2022), and functional magnetic resonance imaging (fMRI) (Keegan et al., 2022). Second, we could use tensor parameterizations to improve convolutional neural networks (CNNs), just as we used t-NN layers to improve fully-connected networks. CNNs are state-of-the-art for image classification and rely on convolution operations. The ⋆M-product is, in some sense, a convolution based on the transformation M; in fact, when M is the discrete Fourier transform, the result is a circulant convolution. A t-CNN could offer more efficient parameterization and a greater range of convolutional features that could increase the expressibility of the network. Third, we could extend the use of tubal loss functions to any network architecture. Tubal loss functions offer more stringent requirements to fitting data which can mitigate overfitting. Additionally, tubal loss functions foster a new level of flexibility to evaluate performance, such as various norms to transform tubal probabilities into scalars and new measures of accuracy per frontal slice. Fourth, we can consider learning the operator M based on the data or allowing the operator to evolve with the layers. Lastly, we can explore methods to improve t-NN efficiency on CPUs and GPUs by exploiting the parallelize of the ⋆M-products.
Statements
Data availability statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at: https://pytorch.org/vision/main/datasets.html and https://github.com/elizabethnewman/tnn.
Author contributions
EN: Conceptualization, Data curation, Formal analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing—original draft, Writing—review & editing. LH: Conceptualization, Data curation, Funding acquisition, Writing—original draft, Writing—review & editing. HA: Conceptualization, Data curation, Writing—original draft, Writing—review & editing. MK: Funding acquisition, Writing—original draft, Writing—review & editing.
Funding
The author(s) declare financial support was received for the research, authorship, and/or publication of this article. This work was partially funded by the Exploratory Science program at IBM. EN's work was partially supported by the National Science Foundation (NSF) under grants [DMS-2309751]. HA's work was partially funded an IBM Faculty Award. Any opinions, findings, conclusions, or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
Acknowledgments
We thank Dr. Eldad Haber and Dr. Lars Ruthotto for providing additional insight on their work which helped us generalize their ideas to our high-dimensional framework.
Conflict of interest
LH is employed by IBM. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1
AscherU. M. (2010). Numerical Methods for Evolutionary Differential Equations. Philadelphia, PA: SIAM.
2
BengioY.SimardP.FrasconiP. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 5, 157–166. 10.1109/72.279181
3
BottouL.CurtisF. E.NocedalJ. (2018). Optimization methods for large-scale machine learning. SIAM Rev.60, 223–311. 10.1137/16M1080173
4
BrooksS.GelmanA.JonesG. L.MengX.-L. (2011). Handbook of Markov Chain Monte Carlo. Boca Raton, FL: Chapman and Hall/CRC. 10.1201/b10905
5
CaoX.RabusseauG.PineauJ. (2017). Tensor regression networks with various low-rank tensor approximations. arXiv [Preprint]. arxiv:1712.09520. 10.48550/arxiv.1712.09520
6
CarrollJ. D.ChangJ.-J. (1970). Analysis of individual differences in multidimensional scaling via an n-way generalization of “Eckart-Young” decomposition. Psychometrika35, 283–319. 10.1007/BF02310791
7
ChattopadhyayA.HassanzadehP.PashaS. (2020). Predicting clustered weather patterns: a test case for applications of convolutional neural networks to spatio-temporal climate data. Sci. Rep. 10:1317. 10.1038/s41598-020-57897-9
8
ChienJ.-T.BaoY.-T. (2018). Tensor-factorized neural networks. IEEE Trans. Neural Netw. 29, 1998–2011. 10.1109/TNNLS.2017.2690379
9
CichockiA.LeeN.OseledetsI.PhanA.-H.ZhaoQ.MandicD. P.et al. (2016). Tensor networks for dimensionality reduction and large-scale optimization: part 1 low-rank tensor decompositions. Found. Trends Mach. Learn. 9, 249–429. 10.1561/2200000059
10
de LathauwerL.de MoorB.VandewalleJ. (2000). A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21, 1253–1278. 10.1137/S0895479896305696
11
DenilM.ShakibiB.DinhL.RanzatoM.de FrietasN. (2013). “Predicting parameters in deep learning,” in Advances in Neural Information Processing Systems 26, eds. C. J. C. Burges, L. Bottou, M. Welling, Z. Ghahramani, and K. Q. Weinberger (Curran Associates, Inc.), 2148–2156. Available online at: http://papers.nips.cc/paper/5025-predicting-parameters-in-deep-learning.pdf (accessed December 18, 2023).
12
EeW. (2017). A proposal on machine learning via dynamical systems. Comm. Math. Stat. 5, 1–11. 10.1007/s40304-017-0103-z
13
HaberE.RuthottoL. (2017). Stable architectures for deep neural networks. Inverse Probl. 34:1. 10.1088/1361-6420/aa9a90
14
HaberE.RuthottoL.HolthamE.JunS.-H. (2018). Learning across scales–multiscale methods for convolution neural networks. Proc. AAAI Conf. Artif. Intell. 32, 3142–3148. 10.1609/aaai.v32i1.11680
15
HaoN.KilmerM. E.BramanK.HooverR. C. (2013). Facial recognition using tensor-tensor decompositions. SIAM J. Imaging Sci. 6, 437–463. 10.1137/110842570
16
HarshmanR. A. (1970). “Foundations of the parafac procedure: models and conditions for an “explanatory” multimodal factor analysis,” inUCLA Working Papers in Phonetics, 16, 1–84. (University Microfilms, Ann Arbor, Michigan, No. 10,085).
17
HeK.ZhangX.RenS.SunJ. (2016). “Deep residual learning for image recognition,” in 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR) (Las Vegas, NV: IEEE), 770–778. 10.1109/CVPR.2016.90
18
JagtapA. D.ShinY.KawaguchiK.KarniadakisG. E. (2022). Deep kronecker neural networks: a general framework for neural networks with adaptive activation functions. Neurocomputing468, 165–180. 10.1016/j.neucom.2021.10.036
19
KeeganK.VishwanathT.XuY. (2022). A tensor SVD-based classification algorithm applied to fmri data. SIAM Undergrad. Res. Online15, 270–294. 10.1137/21S1456522
20
KernfeldE.KilmerM.AeronS. (2015). Tensor-tensor products with invertible linear transforms. Linear Algebra Appl. 485, 545–570. 10.1016/j.laa.2015.07.021
21
KilmerM. E.BramanK.HaoN.HooverR. C. (2013). Third-order tensors as operators on matrices: a theoretical and computational framework with applications in imaging. SIAM J. Matrix Anal. Appl. 34, 148–172. 10.1137/110837711
22
KilmerM. E.HoreshL.AvronH.NewmanE. (2021). Tensor-tensor algebra for optimal representation and compression of multiway data. Proc. Natl. Acad. Sci. USA. 118:e2015851118. 10.1073/pnas.2015851118
23
KilmerM. E.MartinC. D. (2011). Factorization strategies for third-order tensors. Linear Algebra Appl. 435, 641–658. 10.1016/j.laa.2010.09.020
24
KingmaD. P.BaJ. (2015). “Adam: a method for stochastic optimization,” in 3rd International Conference on Learning Representations, ICLR 2015, May 7-9, 2015, Conference Track Proceedings, eds. Y. Bengio, and Y. LeCun (San Diego, CA).
25
KoldaT. G.BaderB. W. (2009). Tensor decompositions and applications. SIAM Rev. 51, 455–500. 10.1137/07070111X
26
KossaifiJ.LiptonZ. C.KolbeinssonA.KhannaA.FurlanelloT.AnandkumarA.et al. (2020). Tensor regression networks. J. Mach. Learn. Res. 21, 1–21. 10.48550/arXiv.1707.08308
27
KrizhevskyA.HintonG. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto. Available online at: https://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf
28
KrizhevskyA.SutskeverI.HintonG. E. (2012). “ImageNet classification with deep convolutional neural networks,” in Advances in Neural Information Processing Systems, Vol. 25, eds. F. Pereira, C. J. Burges, L. Bottou, and K. Q. Weinberger (Red Hook, NY: Curran Associates, Inc.) 1091–1105. Available online at: https://proceedings.neurips.cc/paper_files/paper/2012/file/c399862d3b9d6b76c8436e924a68c45b-Paper.pdf
29
KullbackS.LeiblerR. A. (1951). On information and sufficiency. Ann. Math. Stat. 22, 79–86. 10.1214/aoms/1177729694
30
LeCunY.CortesC.BurgesC. J. C. (1998). The MNIST Database of Handwritten Digits. New York, NY. Available online at: http://yann.lecun.com/exdb/mnist/
31
LeCunY.DenkerJ.SollaS. (1989). “Optimal brain damage,” in Advances in Neural Information Processing Systems, Volume 2, ed. D. Touretzky (Cambridge, MA: Morgan-Kaufmann).
32
LiD.YuZ.WuF.LuoW.HuY.YuanL.et al. (2020). The tensor-based feature analysis of spatiotemporal field data with heterogeneity. Earth Space Sci. 7:e2019EA001037. 10.1029/2019EA001037
33
LundK. (2020). The tensor t- function: a definition for functions of third-order tensors. Numer. Linear Algebra Appl. 27:e2288. 10.1002/nla.2288
34
MaA.MolitorD. (2022). Randomized Kaczmarz for tensor linear systems. BIT Numer. Math. 62, 171–194. 10.1007/s10543-021-00877-w
35
MalikO. A.UbaruS.HoreshL.KilmerM. E.AvronH. (2021). “Dynamic graph convolutional networks using the tensor M-product,” in Proceedings of the 2021 SIAM International Conference on Data Mining (SDM) (Philadelphia, PA), 729–737. 10.1137/1.9781611976700.82
36
MorU.CohenY.Valdés-MasR.KviatcovskyD.ElinavE.AvronH.et al. (2022). Dimensionality reduction of longitudinal omics data using modern tensor factorizations. PLoS Comput. Biol. 18, 1–18. 10.1371/journal.pcbi.1010212
37
NewmanE. (2019). A Step in the Right Dimension: Tensor Algebra and Applications [PhD thesis]. Medford, MA: Tufts University.
38
NewmanE.KilmerM.HoreshL. (2018). “Image classification using local tensor singular value decompositions,” in 2017 IEEE 7th International Workshop on Computational Advances in Multi-Sensor Adaptive Processing (CAMSAP) (Curacao: IEEE). 10.1109/CAMSAP.2017.8313137
39
NewmanE.KilmerM. E. (2020). Nonnegative tensor patch dictionary approaches for image compression and deblurring applications. SIAM J. Imaging Sci. 13, 1084–1112. 10.1137/19M1297026
40
NielsenM. A. (2018). Neural Networks and Deep Learning. San Francisco, CA: Determination Press.
41
NovikovA.PodoprikhinD.OsokinA.VetrovD. (2015). “Tensorizing neural networks,” in Advances in Neural Information Processing Systems 28, eds. C. Cortes, N. D. Lawrence, D. D. Lee, M. Sugiyama, and R. Garnett (Curran Associates, Inc.), 442–450. Available online at: http://papers.nips.cc/paper/5787-tensorizing-neural-networks.pdf (accessed December 20, 2023).
42
OmbergL.GolubG. H.AlterO. (2007). A tensor higher-order singular value decomposition for integrative analysis of dna microarray data from different studies. Proc. Nat. Acad. Sci. 104, 18371–18376. 10.1073/pnas.0709146104
43
OseledetsI. V. (2011). Tensor-train decomposition. SIAM J. Sci. Comput. 33, 2295–2317. 10.1137/090752286
44
PaszkeA.GrossS.ChintalaS.ChananG.YangE.DeVitoZ.et al. (2017). “Automatic differentiation in pytorch,” in NIPS-W (Long Beach, CA).
45
PetersenK. B.PedersenM. S. (2012). The Matrix Cookbook. Lyngby: Technical University of Denmark.
46
RonnebergerO.FischerP.BroxT. (2015). “U-net: convolutional networks for biomedical image segmentation,” in Medical Image Computing and Computer-Assisted Intervention-MICCAI 2015, eds. N. Navab, J. Hornegger, W. M. Wells, and A. F. Frangi (Cham: Springer International Publishing), 234–241. 10.1007/978-3-319-24574-4_28
47
RumelhartD. E.HintonG. E.WilliamsR. J. (1986). Learning representations by back-propagating errors. Nature323, 533–536. 10.1038/323533a0
48
Shalev-ShwartzS.ShamirO.ShammahS. (2017). “Failures of gradient-based deep learning,” in Proceedings of the 34th International Conference on Machine Learning-Volume 70, ICML'17, 3067–3075. Available online at: https://JMLR.org (accessed December 12, 2023).
49
SkeelR. D. (1993). Variable step size destabilizes the stromer/leapfrog/verlet method. BIT33, 172–175. 10.1007/BF01990352
50
SoltaniS.KilmerM. E.HansenP. C. (2016). A tensor-based dictionary learning approach to tomographic image reconstruction. BIT Numer. Math. 56, 1425–1454. 10.1007/s10543-016-0607-z
51
TCA (2023). Tufts community appeal. Available online at: https://communityrelations.tufts.edu/engage-us/faculty-staff-students/tufts-community-appeal-tca (accessed December 20, 2023).
52
TuckerL. R. (1966). Some mathematical notes on three-mode factor analysis. Psychometrika31, 279–311. 10.1007/BF02289464
53
VasilescuM. A. O.TerzopoulosD. (2002). “Multilinear analysis of image ensembles: tensorfaces,” in Computer Vision – ECCV 2002, eds. A. Heyden, G. Sparr, M. Nielsen, and P. Johansen (Berlin: Springer Berlin Heidelberg), 447–460. 10.1007/3-540-47969-4_30
54
WangM.PanY.XuZ.YangX.LiG.CichockiA.et al. (2023). Tensor networks meet neural networks: A survey and future perspectives. arXiv, Cornell University, Ithaca, NY.
55
ZhangZ.ElyG.AeronS.HaoN.KilmerM. (2014). “Novel methods for multilinear data completion and denoising based on tensor-SVD,” in 2014 IEEE Conference on Computer Vision and Pattern Recognition (Columbus, OH: IEEE). 10.1109/CVPR.2014.485
Summary
Keywords
tensor algebra, deep learning, machine learning, image classification, inverse problems
Citation
Newman E, Horesh L, Avron H and Kilmer ME (2024) Stable tensor neural networks for efficient deep learning. Front. Big Data 7:1363978. doi: 10.3389/fdata.2024.1363978
Received
31 December 2023
Accepted
29 April 2024
Published
30 May 2024
Volume
7 - 2024
Edited by
Yanqing Zhang, Yunnan University, China
Reviewed by
Yubai Yuan, The Pennsylvania State University (PSU), United States
Yuanyuan Ju, Kunming University of Science and Technology, China
Updates
Copyright
© 2024 Newman, Horesh, Avron and Kilmer.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Elizabeth Newman elizabeth.newman@emory.edu
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.