Soil-structure interaction: A state-of-the-art review of modeling techniques and studies on seismic response of building structures

Bapir, Baban; Abrahamczyk, Lars; Wichtmann, Torsten; Prada-Sarmiento, Luis Felipe

doi:10.3389/fbuil.2023.1120351

REVIEW article

Front. Built Environ., 03 February 2023

Sec. Earthquake Engineering

Volume 9 - 2023 | https://doi.org/10.3389/fbuil.2023.1120351

Soil-structure interaction: A state-of-the-art review of modeling techniques and studies on seismic response of building structures

Baban Bapir¹*

Lars Abrahamczyk¹

Torsten Wichtmann²

Luis Felipe Prada-Sarmiento²

¹Chair of Advanced Structures, Faculty of Civil Engineering, Bauhaus-Universität Weimar, Weimar, Germany
²Chair of Soil Mechanics, Foundation Engineering and Environmental Geotechnics, Ruhr-Universität Bochum (RUB), Bochum, Germany

The present article aims to provide an overview of the consequences of dynamic soil-structure interaction (SSI) on building structures and the available modelling techniques to resolve SSI problems. The role of SSI has been traditionally considered beneficial to the response of structures. However, contemporary studies and evidence from past earthquakes showed detrimental effects of SSI in certain conditions. An overview of the related investigations and findings is presented and discussed in this article. Additionally, the main approaches to evaluate seismic soil-structure interaction problems with the commonly used modelling techniques and computational methods are highlighted. The strength, limitations, and application cases of each model are also discussed and compared. Moreover, the role of SSI in various design codes and global guidelines is summarized. Finally, the advancements and recent findings on the SSI effects on the seismic response of buildings with different structural systems and foundation types are presented. In addition, with the aim of helping new researchers to improve previous findings, the research gaps and future research tendencies in the SSI field are pointed out.

1 Introduction

Following the 1964 Niigata earthquake (M 7.5) in Japan, it became clear that structural damage depends not only on the behaviour of the superstructure but also on the subsoil beneath it (Ohsaki, 1966). Consequently, several researchers have examined the behaviour of soil subjected to dynamic loading including experimental, analytical, and numerical investigations. These investigations revealed that the response of soil to dynamic loads has a significant impact on structural damage. The behaviour of soil becomes much more complicated, and various elements must be considered. Civil engineering structures are in direct contact with soil. When an external dynamic force such as an earthquake or vibration acts on these structures, the structural response and the ground response are affecting each other. This interaction between the soil and the structure is known as dynamic Soil-Structure Interaction (SSI). In practical designs, it is common that the seismic response of buildings is determined by assuming fixed support at the base of the structure, however, this is an oversimplified assumption, and this hypothesis can be only valid when a structure is resting on very stiff soil and solid rock layers (Stewart et al., 1999b). In other cases when a structure is subjected to an earthquake motion on relatively soft soil, the underlying soil can induce two different effects on the structure. The first effect is known as Kinematic Interaction, which is a direct result of the difference in stiffness between the foundation and the soil underneath. When an earthquake ground motion propagates in the free-field motion (FFM) the waves will be modified and scattered due to the presence of a rigid foundation. The resulting motion at the base of the foundation is denoted as foundation input motion (FIM). Kinematic interaction effects are more predominant for embedded and deep foundations. The second phenomenon is Inertial Interaction, this happens when the developed inertia in the vibrating structure leads to an increase of base shear and overturning moment at the foundation level and causes additional deformation in the soil. The deformation in the underneath soil provides more flexibility to the SSI system and further modification of base motion (Kramer, 1996).

There have been diverse research and investigations on SSI in the past 50 years, among them several review studies on modelling technique improvements and application cases were conducted. However, due to a lack of consensus, the SSI consequences on building structures remain debatable among research communities as discussed by (Mylonakis and Gazetas, 2000). The historical development of static and dynamic SSI has been very well documented by (Kausel, 2010; Roesset, 2013). While (Dutta and Roy, 2002) presented a comprehensive critical review of different simplified techniques to idealize the structure and the soil domain, where the strength and limitations of various models were discussed. Afterwards, (Lou et al., 2011) presented the historical development and the state of SSI studies on buildings with a focus on the analytical and numerical methods to resolve SSI issues. Previous efforts in developing and implementing the Finite Element Methods (FEM) and Boundary Element Methods (BEM) techniques for discretizing the soil domains were summarized. Further, (Dhadse et al., 2021) discussed the advantages and difficulties of finite element modelling in SSI problems. The study reviewed the mathematical modelling of FEM with appropriate soil constitutive models to solve non-linear problems, more specifically the interface between the foundation and the soil. A recent review study by (Far, 2017; Anand and Kumar, 2018) focused on presenting and comparing various approaches and modelling techniques to evaluate SSI effects on structures. The significance of including SSI effects in the design process is pointed out with a bunch of evidence on how SSI causes extra damage in buildings during an earthquake. Further, the advancements and the recent state of SSI research on different structures were summarized.

Based on the revisions from the literature, it is concluded that the importance of soil-structure interaction has attained several researchers’ attention to study the SSI consequences on different structures as well as developing numerous modelling techniques in different levels of rigour. Nevertheless, considering SSI effects in practical designs has not yet attained structural engineers’ attention. This is possibly due to a lack of global guidelines and the common belief that SSI effects on structures are always beneficial. However, contemporary studies and past earthquakes imply that ignoring SSI effects could lead to an unsafe design. This paper has four major objectives:

1) To discuss the significance of SSI and its consequences on the seismic response of buildings. A short review of the past and recent findings in the area is presented in Section 2.

2) To provide an overview of the main approaches to evaluate SSI problems with the most commonly used modelling techniques and computational methods. The strength, limitations, and application cases of each modelling technique are discussed and compared as shown in Sections 3 and 4. Moreover, recommendations and instructions are provided to support new researchers in defining the input parameters and reducing uncertainties, especially in the case of continuum modelling.

3) To present an overview of the current state of global guidelines and design codes on soil-structure interaction problems in Section 5.

4) To review the advancements and contemporary findings of SSI effects on seismic response of different structural and foundation systems, as presented in Section 6.

It is worth mentioning that, the wide-ranging review presented in this paper could help the researchers in the SSI area to improve the previous findings and to continue working on the existing open issues listed in Section 7. Further, it provides a clear vision to the new researchers on understanding the SSI effects on various structural and foundation systems and choosing different modelling techniques based on the nature of the SSI problem.

2 Consequences of dynamic SSI

The importance of soil-structure interaction for static and dynamic problems has been very well established and the literature covers at least 50 years of computational and analytical developments (Jennings and Bielak, 1973; Bielak, 1974; Veletsos and Meek, 1974; Wolf, 1989; Stewart et al., 1999a; Mylonakis and Gazetas, 2000). The common conclusion of these studies states that, for structures that rested on rock and stiff soil, the base could be considered fixed. While in the case of medium to soft soil, the SSI effects are significant and should not be neglected. However, the role of SSI effects on the seismic response of structures rested on soft soil is still debatable among research communities and the design code provisions. On the one hand, soil-structure interaction has been traditionally considered beneficial for the seismic response, as it is evident from some design codes (ASCE, 2016; ATC, 1978; EN 1998-5, 2004; JSCE, 2007; NZS 1170.5, 2004). Among these design codes, the (ASCE, 2016; FEMA P-2091, 2020) provides a guideline to calculate the modified natural period and base shear forces of the structure considering SSI effects, where the seismic demand of the structure including SSI is always calculated less compared to the fixed-base system. The reason for this belief is from oversimplification of the nature of seismic demand adopted in design code provisions. This simplification states that SSI makes the structure more flexible, which increases the natural period and damping ratio of the system. This leads to a reduction of the base shear demand of the structure compared to the fixed-base counterpart.

On the other hand, several investigations and contemporary studies on SSI consequences tell a different story, especially in considering soil non-linearity. Investigations on increasing seismic and ductility demand by several researchers proved that SSI effects could be detrimental in different considerations, where ignoring these effects leads to inadequate design. Kraus and Džakić (2013) outlined that the assumption of fix-base analysis for buildings is only valid in the case where the stiffness of foundation soil is relatively higher than that of the superstructure. According to the analysis results, they also concluded that the common assumption of SSI elongating natural period and thus decreasing internal forces showed to be wrong. This assumption is not valid in the case of stiff low-rise buildings resting on soft soil. Dutta et al. (2004) also pointed out that the soil–structure interaction plays a significant role in the increase of the seismic base shear of low-rise stiff building frames. The effect was strongly influenced by the frequency content of the earthquake motion (ground motions with a period of one second or less, causing a larger increase in response). However, this effect is decreased by increasing soil hardness and increasing the number of stories (high-rise buildings). Similar conclusions were also drawn by (Abdel Raheem et al., 2015). Further, (Avilés and Pérez-Rocha, 2003) highlighted that the combined effect of base flexibility and structural yielding was beneficial for slender structures with a natural period longer than the site period. While for the shorter structures where the natural period is less than the site period, these effects were found to be quite detrimental. Jarernprasert et al. (2013) discovered that for elastic structures, the response of SSI systems is usually lower than in the case of fixed-base structures. By contrast, for inelastic structures compared to fixed-base structures, SSI may lead to an increase in ductility demands and higher lateral displacement. Since most of the structures in case of severe earthquakes are experiencing inelastic deformation, the current seismic provisions could be inadequate. Similar detrimental consequences were observed by (El Ganainy and El Naggar, 2009). The state-of-the-art review and conclusions on SSI effects on the seismic response of building structures are presented in detail in Section 6.

In addition, there is evidence from previous earthquake damages, showing that SSI affected building seismic responses detrimentally. The magnitude M = 8.1 earthquake of Mexico City in 1985 occurred at a distance of approximately 380 km from the epicentre. However, the convergence in the site response factors caused severe damage in the buildings located in the Lake Zone of the city (Scholl, 1989). The seismic waves filtered to long-period motion in travelling from the epicentre to the city region. In Lake Zone due to the availability of deep soft soil deposits, the intensity of the seismic waves significantly amplified to approximately two seconds, also due to the inertial interaction effects the natural period of several (9–13 storey) buildings increased the range of two seconds. This matching between the natural period of the structures and the ground motion caused a resonance in several structures and consequently, several severe damages occurred (Scholl, 1989). The 1995 Kobe earthquake also caused severe damage in the elevated sections of the Hanshin expressway. Gazetas and Mylonakis (1998) reported that the period lengthening of the bridge due to foundation flexibility might have resulted in an increase in structural forces in the bridge piers and caused failure. There are several similar observations in the past earthquakes, Christchurch 2011 in New Zealand, Chili earthquake in 2010, and many others that clearly illustrated the serious effects of local site properties on the structural response. Therefore, a site-dependent dynamic response analysis to assess free-field earthquake motions for different foundation types has a strong engineering motivation. Nevertheless, the effects between the superstructure and the substructure cannot be neglected either way and need to be dealt with more accurately based on various circumstances, especially in the case of heavy structures resting on soft soil (Galal and Naimi, 2008). A summary of the detrimental and beneficial effects of soil-structure interaction on building structures is shown in Table 1.

TABLE 1

TABLE 1. Summary of SSI consequences on building structures.

3 Approaches and computational methods to evaluate dynamic SSI

In general, to evaluate a soil-structure interaction system, there are two main approaches: the substructure and the direct approach. The concept of these two approaches with the main differences are explained in this section, while the modelling techniques based on these approaches are presented in Section 4.

3.1 Substructure approach

It is also known as the multi-step approach. In this approach, the soil and the structure are considered separately, then solved independently and the final seismic response of the structure is calculated by combining these effects using superposition principles (Kramer, 1996). In other words, the substructure approach has the capability to solve inertial and kinematic interactions separately by means of impedance and transfer functions respectively. Since the substructure technique is based on superposition principles, linear assumption of the soil and the structural behaviour is necessary for the substructure approach. Although, this problem has been solved through equivalent-linear and non-linear numerical models developed for the soil domains, such as beam on non-linear Winkler foundation model for shallow foundations (Raychowdhury, 2008) and non-linear spring models for pile foundation (Boulanger et al., 1999). Regardless of the foundation type and the soil model, the non-linear behaviour of the superstructures could be also modelled using simplified constitutive models (Hassani et al., 2018). The solution of SSI problems with the substructure approach is broken down into three main steps as depicted in Figure 1:

1) Evaluation of the Foundation Input Motion (FIM); this includes evaluating the transfer functions to convert the Free-Field Motion (FFM) to FIM that is based on the stiffness and geometry of the foundation and the soil. To evaluate FIM, the structure and foundation are supposed to be massless. The applied seismic demand to the foundation is represented by rotational (θ_FIM) and translational (U_FIM) components. The ratio of FIM to FFM is named as a transfer function that expresses the effects of the kinematic interaction only and neglects the inertial interaction.

2) Evaluation of foundation impedance functions; impedance functions define the stiffness and damping characteristics of the soil-foundation interaction. This is usually represented by simple function models or a set of springs and dashpots which is defined by horizontal (K_u) and rotational (K_θ) stiffness of the foundation soil. The dynamic impedance functions are frequency-dependent and represent the interaction between the foundation and the soil.

3) Calculating seismic response of the structure; the structure is modelled with springs and dashpots as a support base and the FIM as an input motion. The seismic response of the structure is then calculated using either response spectrum or time history analysis. This step is representing the inertial interaction effects. Several modelling techniques based on this approach and the definition of impedance functions are discussed in detail in Section 4.

FIGURE 1

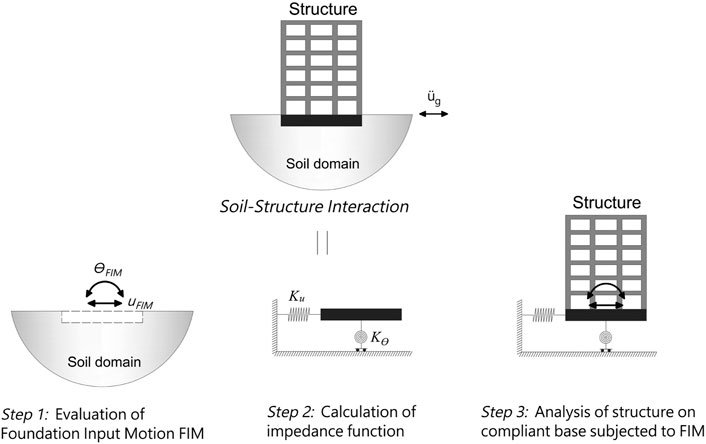
FIGURE 1. Substructure approach to the analysis of the soil-structure interaction problem. After (Stewart and Kramer, 2004).

3.2 Direct approach

The direct approach is considered the most rigorous approach to solving SSI problems, especially in the case of complicated structural geometry and non-linear soil modelling. Figure 2 depicts a schematic illustration of the direct approach. Where the soil and the structure are modelled together and analyzed in a single step by solving the governing equations of motion. The soil is represented as a continuum and connected to the foundation with interface elements. Proper boundary conditions must be assigned so that the scattering waves do not reflect when they are passing through it. In this method, the complete system is solved in the time domain with free-field motion as input. Section 4.5 goes into more detail about the modelling approach. The direct approach is a very powerful method to solve a wide range of SSI problems including the linear and non-linear soil model for various foundation types. Although, in engineering practice direct method is rarely used because of its complexity and time-consuming analysis, especially for complex geometry and non-linear problems. The governing equation of motion for a soil-structure system can be written as follows:

[M] \ddot{u} + [C] \dot{u} + [K] u = - [M] {\ddot{u}}_{g} (1)

FIGURE 2

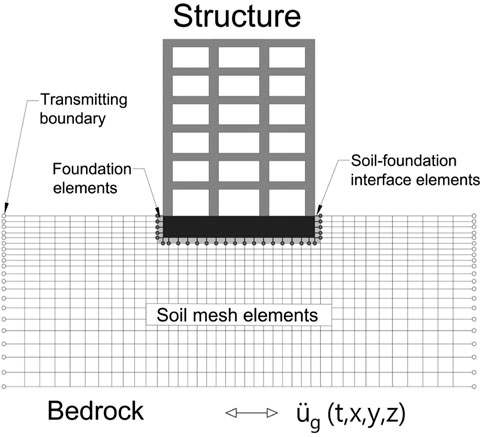
FIGURE 2. Schematic illustration of a direct analysis of soil-structure interaction using continuum modelling by finite elements. After (NIST, 2012).

Where [M], [C], and [K] are mass, damping, and stiffness matrices. üg is input ground acceleration. ü, ú, and u are acceleration, velocity, and displacement vectors of the system.

The main computational methods that have been used in SSI studies to discretize the soil domain are: Finite-Element Method (FEM), Finite-Difference Method (FDM), and Boundary-Element Method (BEM).

The FEM is the most well-known computational method in analyzing structural and geotechnical engineering problems. With the availability of powerful computers, numerical methods have been used in a broader range compared to analytical methods. FEM has a very good capability to address the real and complex problem of SSI with significant details, especially in the case of non-linear modelling. However, in the case of complete 3D models and complex structures, it is computationally costly. Nevertheless, FEM is used frequently in the study of soil-structure interaction and has produced some notable achievements in the field of SSI. Both FEM and FDM are discretizing the whole domain into finite numbers of small elements and connect these elements through the nodal points. In FEM the element matrices are combined in order to form a large global stiffness matrix. While this combination is usually not done in the FDM method, because in each time step the finite difference equations are regenerated more efficiently. This made FDM computationally more efficient than FEM. Desai et al. (1973) documented the general principles of FDM and FEM with their application cases.

Following FEM, a new numerical method called the boundary element method was developed. The basic idea of BEM is to discretize the surface of the problem instead of the whole domain and unlike the FEM, the equations of motion of the domain will be formulated in a form of integral equations instead of the differential equation. Furthermore, unlike FEM, BEM does not require the use of special sophisticated non-reflecting boundaries to satisfy the radiation criterion. As a result, the number of degrees of freedom and the computational time will be reduced. In this regard, BEM is more advantageous than FEM. The details on the formulation of BEM and fields of application are well documented (Brebbia et al., 1985). BEM presents an attractive computational framework, especially for problems in unbounded domains. However, in complex engineering problems, BEM is less efficient than FEM because of its difficulty of application in the case of a heterogeneous and anisotropic medium (Wolf and Deeks, 2004). In addition, BEM has limitations to consider non-linear problems (Lou et al., 2011).

3.3 Comparison and discussions

Based on the discussion in Sections 3.1 and 3.2, there are several differences between the two approaches, especially in terms of accuracy and efficiency. Since in substructure approaches the semi-infinite soil medium does not need to be discretized, it is computationally more efficient and less time is required to solve the problem compared to the direct approach. Therefore, the substructure approach has a wider range of practical uses than the direct approach and many researchers have adopted this approach for the SSI analysis (Mylonakis et al., 2006; Givens, 2013; Hassani et al., 2018; Mercado et al., 2020; Oz et al., 2020). Moreover, unlike the direct approach, in the substructure approach the effects of inertial and kinematic interactions could be separated and calculated individually. However, a recent study by (Rahmani et al., 2016) questioned the accuracy of the substructure approach and observed an overestimation in top displacement and design base forces. In addition (Mercado et al., 2020), concluded that the substructure approach produces a larger inter-story drift demand in the structure compared to the direct approach. Jahromi et al. (2008), Jabini Asli et al. (2019) also concluded that the substructure approach cannot accurately deal with the material and geometric non-linearity. Therefore, in case of complex and important structures, it is required to use more sophisticated soil models (direct approach) where the soil and structural non-linearity are taken into account. Nevertheless, to draw a better conclusion on the performance of substructure models in various SSI problems in buildings, a more extensive study is required, especially in considering the effects of structural non-linearity.

4 Common modelling techniques to idealize the soil domain

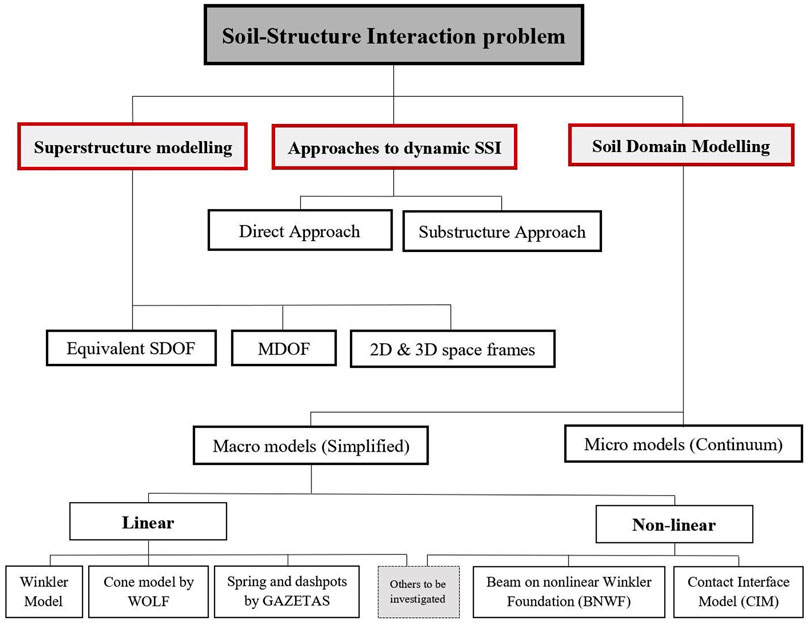
Modelling of superstructures and foundations is generally found to be more straightforward and less complicated in comparison to the soil medium underneath (Bhattacharya and Dutta, 2004). However, the most challenging part of dealing with soil-structure interaction problems is modelling the soil domain. Therefore, this section attempts to present a comprehensive review of the most common available modelling techniques and computational methods of the soil domain. The advantages and disadvantages of each model will also be discussed. An overview of the commonly used modelling techniques and approaches to evaluate the SSI problem is illustrated in Figure 3.

FIGURE 3

FIGURE 3. Overview on Soil-Structure Interaction problem.

4.1 Winkler model

In this model, the soil medium is idealized and represented by linearly elastic springs, which are distributed independently and discretely in close spaces along the foundation area, as shown in Figure 4. Since the springs are independent, the deformation of the foundation due to the applied load is localized in the loaded region only (Bowles, 1996). The relationship between load and deflection at any point in the soil is given by:

p = k w (2)

FIGURE 4

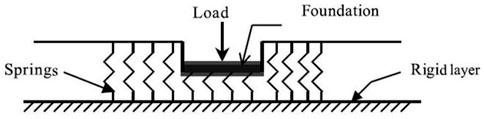
FIGURE 4. Winkler foundation model (Dutta and Roy, 2002).

Where p denotes the applied pressure, k is the coefficient of subgrade reaction and w is the deflection. Due to its simplicity, several studies in the area of soil-structure interaction have been conducted based on the Winkler hypothesis (Popov, 1951; Kramrisch and Rogers, 1961; Vesić, 1961; Daloglu and Vallabhan, 2000).

In a critical review study (Dutta and Roy, 2002), concluded that despite the simplicity and less computational time of this approach, the basic limitation is the consideration of linear stress-strain behaviour of the soil. Furthermore, the determination of the elastic springs used to replace the soil beneath is also a major issue. Because the coefficient of the subgrade is affected not only by the subgrade but also by the dimensions of the loaded area. Since the subgrade reaction is the only parameter in Winkler’s idealization, great care should be taken in the determination of this parameter. To overcome the shortcomings and limitations of this approach, several improved versions of Winkler’s model are available in the literature (Filonenko-Borodich, 1940; Hetenyi, 1946; Pasternak, 1954; Kerr and York, 1965).

Despite the limitations explained above (Dutta and Roy, 2002), recommended using Winkler’s hypothesis for practical purposes at least instead of the fixed-base considerations.

4.2 Lumped parameter models

The concept of lumped parameter model represents frequency-dependent soil-structure interaction models of massless foundations resting on or embedded in homogeneous elastic half-space. In this model type, the soil domain is replaced with a set of frequency-dependent springs, dashpots and masses in the direction of degrees of freedom. The system is then could be solved in the frequency or time domains. As per (Wolf, 1994; Ibsen and Liingard, 2006) various versions of physical models based on the lumped parameter concept have been developed. The key differences between these versions are the arrangement and mathematical formulation of foundation impedances. In this section, two commonly used physical models from the lumped parameter family are presented.

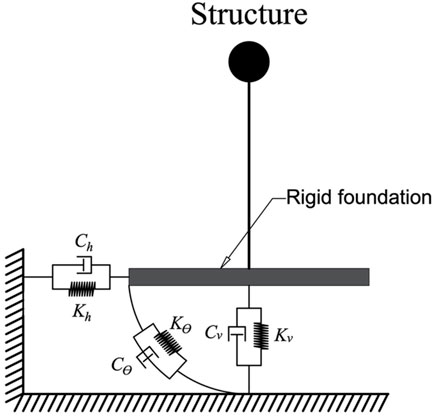
4.2.1 Spring and dashpots by Gazetas

In this approach a set of springs and dashpots are provided for each mode of vibration under the foundation. The springs are describing the stiffness of the soil under or/and around the foundation, while the dashpots are placed to consider the soil damping. In general, for a rigid foundation, there are six modes of vibration (three translational and three rotational) for each mode the soil is replaced by dynamic spring stiffness K and dashpot damping coefficients C. The schematic illustration of the spring and dashpot model for a single foundation is shown in Figure 5. In the last 50 years, there have been extensive studies conducted in this area to develop and compute the foundation impedances (Lysmer, 1978; Roesset, 1980; Luco, 1982; Novak, 1987; Pais and Kausel, 1988). Those approaches rely on analytical and numerical solutions. On the other hand, several researchers developed simplified methods as a practical alternative. Gazetas (1991) presented a complete set of dimensionless graphs and algebraic formulas to calculate the value of these springs and dashpots in each mode of vibration. Based on this approach, the static springs and dashpots are firstly calculated depending on foundation geometry, soil stiffness and soil density. Then the frequency-dependent impedances are calculated by multiplying the static impedance to a frequency-dependent factor. These formulas were valid for nearly all types of foundation shapes on the surface, partially and fully embedded foundations in homogeneous soil.

FIGURE 5

FIGURE 5. Soil-structure model (replacing soil with springs and dashpots).

(Bowles, 1996) pointed out that the frequency-dependent effects and the additional damping coefficients of this model have a higher effect on the overall structural response in comparison with the frequency-independent springs of the Winkler model. However, it is concluded that this model is not accurate enough in analyzing complex SSI problems. Dutta and Roy (2002) recommended using the spring and dashpot models to analyze the SSI effects on structural dynamic behaviour, however, in case of important structure where more rigorous analysis is required, the finite element method should be taken.

4.2.2 Discrete element cone model by Wolf

This model is developed by (Wolf, 1994) based on truncated cone theory which was previously introduced by (Meek and Wolf, 1992b; a; Veletsos and Verbič, 1973). The basic idea of this theory is to replace the soil domain with a semi-infinite truncated cone for translational and rotational components of motion. The system is composed of a rigid circular base that is connected to the soil medium with a set of springs and dashpots under each separate foundation. The sway and rocking DOFs are represented by translational and rotational springs respectively. While viscous dampers are employed to account for the soil and foundation radiation damping. Unlike the spring-dashpot model, the vertical component of the base foundation in this model is assumed to be restricted to any movements. The definition of spring stiffness and damping coefficients are similar to the static parameters proposed by (Gazetas, 1991). However, the arrangement of the SSI system and the number of input parameters are different compared to the spring-dashpot model. Further, the definition of dynamic impedances is also different. In cone model, an internal degree of freedom θ₁ having a mass moment of inertia M_θ₁ is assigned to the foundation node by rotational dashpot to consider frequency dependency of the rotational spring and dashpot coefficients. Also, for rocking motions in case of nearly incompressible soil (1/3 $\leq v < 1 / 2$ ) a trapped mass moment of inertia ΔM_θ is assigned to the foundation.

To consider the soil hysteresis damping ξ_g, (Meek and Wolf, 1994) presented the modified discrete element model as shown in Figure 6. In the modified version, each of the original springs is augmented by a dashpot and each original dashpot is augmented by a mass, all of which are connected in parallel. For practical applications of the model, the ω₀ is usually assumed to be equal to the fundamental circular frequency of the system. Unlike the spring-dashpot model, the modified version of the cone model accounts for higher damping effects in the SSI system and the numbers of input parameters are higher. This brings the concern of increasing uncertainties in the model. Based on a quality assessment study by (Nasser, 2012), the hypothesis of increasing uncertainty with decreasing complexity was investigated for several simplified SSI models. The hypothesis proved to be wrong for SSI models and the study showed that the spring-dashpot model has fewer uncertainties compared to the cone model.

FIGURE 6

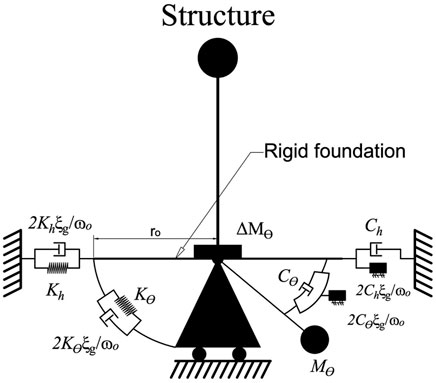
FIGURE 6. Discrete-element sway-rocking model based on the cone theory After (Wolf, 1994).

The discrete elements of the cone model have a relatively wide range of practical applications from the literature. Several researchers (Bararnia et al., 2018; Hassani et al., 2018; Lu et al., 2018; Ganjavi et al., 2019; Kechidi et al., 2021) have adopted the cone models to investigate the SSI effects on the dynamic response of structures with different types of foundations and structural models. Nevertheless, Yang (2016) pointed out that the basic limitation of discrete elements of the cone model is the inability of capturing plastic deformations in the soil under the foundation because this model is derived considering elastic half-space soil. Hence, residual displacement and settlements cannot be determined from this model. Further, the model cannot capture the separation between the foundation and the soil. Therefore the model may not be appropriate for slender or light structures resting on sandy soil. In addition, (Jahromi et al., 2008; Jabini Asli et al., 2019) highlighted that the cone model cannot accurately deal with the material and geometric non-linearity. Therefore, in the case of complex and important structures it is required to use more sophisticated soil models where the soil and structural non-linearity are taken into account.

4.3 Beam on non-linear winkler foundation (BNWF) model

Another simplified spring-type model to evaluate SSI effects and consider the non-linearity of the soil medium is the Beam on Non-linear Winkler Foundation (BNWF) model. This model is idealizing the soil domain by numbers of one-dimensional non-linear springs that are distributed along with the interface between soil and foundation (Raychowdhury, 2008). During strong earthquake events, the soil under the foundation is very likely to undergo plastic deformation due to the increase of pressure under the foundation which comes from the rocking and sliding motions of the foundation (Yang, 2016). Consequently, such reduction of contact between the foundation and the soil results in progressive loss of the system stiffness. To consider this phenomenon, the BNWF model provides a set of vertical and horizontal non-linear springs to measure the plastic deformations and energy dissipation in the soil domain. As illustrated in Figure 7 the springs that are distributed vertically along the length of the footing (q-z elements) are capturing rocking, uplift, and settlement. While the horizontal springs (t-x and p-x elements) are placed to capture the sliding and passive resistance of the soil respectively. At the end of the footing, the springs are intensified so that the rotational springs are accounted for appropriately.

FIGURE 7

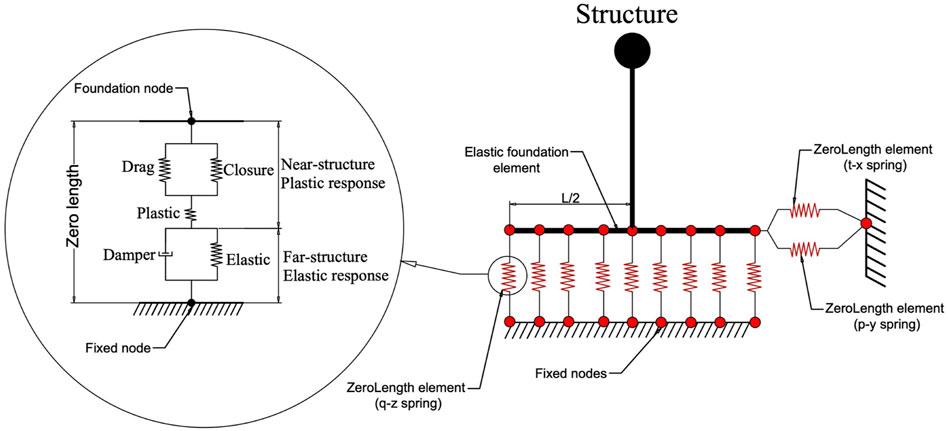
FIGURE 7. Schematic illustration of a Beam-on-Nonlinear Winkler Foundation (BNWF) model (Raychowdhury, 2008)

The implementation of BNWF into OpenSees is presented by (Raychowdhury and Hutchinson, 2009) for a 2-dimensional structural model. The foundation is modelled as elastic beam-column elements, while the interface is defined by several independent zero-length Winkler springs. The constitutive relation of the (q-z, t-x, and p-x elements) are represented by non-linear backbone curves that were originally developed by (Boulanger et al., 1999) and calibrated by (Harden et al., 2005; Raychowdhury, 2008). The BNWF model is appropriate for every type of surface and embedded foundation. It could be also applied in the case of clay and sand soil deposits regardless of the structural model. Therefore, the model is applicable to a wide range of SSI problems in structural engineering.

The basic limitation of this approach comes from its one-dimensional nature. The spring responds to the loads in the direction of the springs only, any load acting perpendicular to the spring axis does not affect the response of the springs. However, due to the simplicity and abilities of a variety of problems, the BNWF approach is very popular and widely used by many researchers in the past 15 years (Shirzadi et al., 2020; Tahghighi and Mohammadi, 2020; Patro et al., 2021).

4.4 Plasticity-based macro element (PBM) model

PBM is a relatively recent development for solving SSI problems, initiated by (Nova and Montrasio, 1991). The PBM family models aim to make a bridge gap between the BNWF and continuum models by combining elements from both formulations. These model types have the capability of capturing the non-linear response of the soil and rigid foundations. A developed version of PBM is presented by (Gajan and Kutter, 2009) and it is known as Contact Interface Model (CIM). This model uses a single interface element between the soil and rigid foundation to represent flexibility as well as energy dissipation in soil-structure interaction. From a numerical point of view, the macro element is exactly located at the soil-footing interface, which replaces the foundation and the surrounding soil. The notation for the loads and displacements is shown in Figure 8.

FIGURE 8

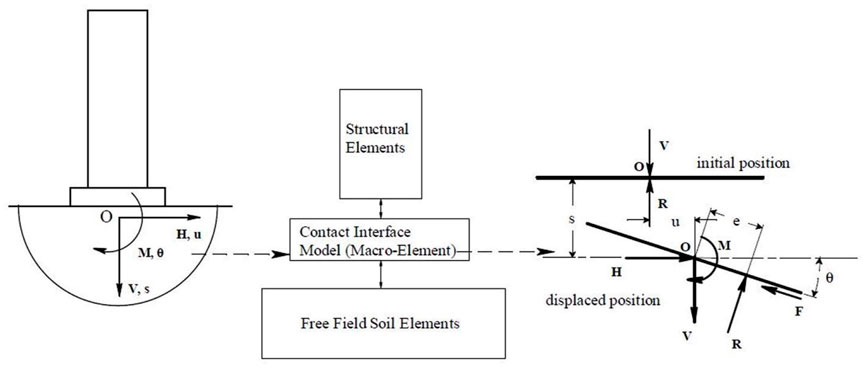
FIGURE 8. Concept of macro-element contact interface model (Gajan and Kutter, 2009)

Previous macro element models were describing the constitutive relations based on yield surface theory, while CIM is different in the sense that constitutive relations are obtained from tracking the gap geometry and contact interface between soil and foundation. Hence, CIM provides a non-linear constitutive relation between the cyclic loading and displacements of the foundation-soil system when it is subjected to bi-directional cyclic loadings. The CIM is shown to have an advantage over BNWF by having the ability to consider the coupling between the vertical load, shear, and moment capacities (Hutchinson and Stewart, 2008; Gajan et al., 2010). However, the main disadvantage of these model types is their inability to incorporate flexible foundation behavior. In addition, the experimental validation of these models is very limited. Despite the implementation of this model into OpenSees by (Gajan and Kutter, 2009) the practical application of CIM is still very rare in the literature compared to BNWF and cone models.

4.5 Micro-element model (Continuum)

Micro-element models are a direct approach for solving SSI problems in the time domain by modelling the soil and superstructure together. The soil domain is modelled as a continuum with an infinite number of degrees of freedom. To solve the problem, the whole domain is discretized into smaller sub-domain with finite degrees of freedom for each element. This discretization can be accomplished through the use of various computational techniques, including (FEM, FDM, and BEM) as described in Section 3.2. The micro-element model is capable of solving any complex type of SSI problem with a high degree of accuracy. However, the modelling process and computational time are costly especially for complex geometry and non-linear problems. Nevertheless, with the advances in computer software, the use of FEM numerical methods has been wider used compared to analytical methods. Several researchers adopted this approach to analyze non-linear dynamic SSI problems for different foundation and structural systems (Xu et al., 2016; Van Nguyen et al., 2017; Fatahi et al., 2018; Yeganeh and Fatahi, 2019). In addition, (Bowles, 1996; Dutta and Roy, 2002) highly recommends using micro-element modelling in case of analyzing important structures or when the non-linearity effects in the soil are required. Apart from computational techniques, there are three other issues that need to be considered carefully to obtain more realistic and accurate modelling.

4.5.1 Dynamic behaviour of soil

This relates to the mechanical behaviour of the soil material during earthquakes which is described by the stress-strain relationship of the soil under cyclic loading. These relations are a set of mathematical expressions that models the soil behaviour known as the constitutive model. Several constitutive models have been developed in the past such as Mohr-Coulomb, Drucker-Prager, Duncan-Chang, hyper-elastic, and cam clay model (Wani and Showkat, 2018). However, due to its simplicity and practicality in geotechnical engineering problems, the Mohr-Coulomb model has been widely adopted by many researchers in soil-structure interaction investigations. This model is an elastic-perfectly plastic model and defines the failure criteria through several basic geotechnical parameters (friction angle, shear strength, and dilation angle of the soil). Alternatively, the non-linear effects in the soil can be defined by a pair of dimensionless curves, which are known as the modulus reduction curve and damping ratio curve (Seed and Idriss, 1970; Darendeli, 2001). These curves show the relationship between shear modulus and the damping corresponding to the cyclic shear strain level in the soil. Due to the simplicity in practical application, these dimensionless curves are widely used by researchers in SSI simulations (Tabatabaiefar et al., 2015; Fatahi et al., 2018; Zhang and Far, 2021).

4.5.2 Interface element

The interface between the foundation and soil must be modelled properly to simulate frictional contact. Generally, the interface is modelled to understand the effects of slipping, bonding, and re-bonding between the foundation and the soil. Amongst very few interface elements developed in the past 40 years, zero thickness and thin layer elements are the most well-known models among the researchers in the field of soil-structure interaction studies. This is because of its compatibility with the available constitutive models (Desai et al., 1984; Day and Potts, 1994; Dalili Shoaei et al., 2015). A comprehensive review of these two types of interface elements has been conducted by (Dhadse et al., 2021) where the computational difficulties of the zero-thickness interface element and its solution are discussed in detail. Further, several versions of the thin layer interface element are presented with their applicability in soil-structure interaction problems. Nevertheless, the simplified approach presented by (Rayhani and El Naggar, 2008) to define the contact between rigid foundations and soft clays has been widely used by several researchers in the SSI investigations, where the performance of this approach has been experimentally verified by (Tabatabaiefar et al., 2014).

4.5.3 Boundary condition

In the direct modelling, a large portion of the soil must be considered in the SSI model to exclude the effects of wave reflection on the response of the structure. However, the increase in soil size causes an increasing number of finite elements which results in a higher computational time. Alternatively, a smaller portion of the soil will be modelled with proper artificial boundary conditions in a manner that the scattering waves do not reflect when they are passing through the boundary. In general, boundary conditions are classified into three main categories: Elementary, Consistent (global), and Viscous (local) boundary conditions (Kant and Samanta, 2020). Elementary boundary conditions are used in the case of static analysis only. The consistent boundary conditions are non-reflecting boundary conditions and could be applied in dynamic analysis with highly accurate results. However, due to the complexity of modelling and being computationally costly, the implementation of these boundary condition types is not easy with finite element programs compared to the local boundary conditions (Kant and Samanta, 2020). The third type is a local boundary (or viscous boundary) which was first introduced by (Lysmer and Kuhlemeyer, 1969) known as the LK boundary condition. This model proposed to attach dashpots to the boundaries in both normal and shear direction to absorb the seismic waves. Several studies on the use of different boundary conditions in dynamic SSI problems have been carried out. Among the various boundaries, (Jingbo and Yandong, 1998; Gentela, 2011) showed that viscous boundary is the most convenient one to be used in the time-domain analysis because it provides a good balance between efficiency and effectiveness.

5 Guidelines to consider SSI in structural design

Despite the research advancements in the area of soil-structure interaction consequences on building structures, there are still very few international and national codes or standard guidelines for incorporating SSI. This is possibly due to a lack of consensus among researchers in the area of SSI or due to the common belief that neglecting SSI leads to a conservative design. Nevertheless, some international design codes recommended considering SSI effects in the design process and only a handful of them makes it mandatory to include SSI effects in the design. ASCE (2016) provides a guideline for the implementation of SSI in the analysis and design of structures. Further, the new draft version of Eurocode made an attempt to improve SSI considerations in the structural design process by employing the frequency-dependent spring and dashpot models. The rest of the other standards are suggesting conditions for considering SSI analysis in the design practice.

To the author’s knowledge, the first draft provisions considering SSI were provided by the Applied Technology Council (ATC) (ATC, 1978), which is a predecessor of the National Earthquake Hazard Reduction Program (NEHRP) seismic provisions. In this design code, based on the equivalent lateral force design procedure, the base shear of the flexible base structure will be reduced from the original fixed-base shear forces. This is due to the lengthening of the natural period and increasing the damping of the system. In the 1997 edition of NEHRP with the title “Recommended Provisions for Seismic Regulations for New Buildings and Other Structures” (BSSC, 1997) the SSI effects were incorporated into the computation of earthquake design forces and lateral deflections using detailed procedures and impedance functions. Based on the provisions, the SSI effects would have a direct effect on reducing the base shear forces (up to a max of 30%) as well as lateral force and overturning moments, while these effects might reduce or increase the lateral deflections. Later, the NEHRP came up with provisions to consider SSI effects in the form of (FEMA 440, 2005). In this provision the base shear reduction was tied to the response modification factor R. It was recommended that base shear reduction is less for the structures which have larger response modification factors (i.e. structures with larger inelastic deformation capacity).

Besides the equivalent lateral force procedures in (ATC, 1978), chapter nineteen of (ASCE, 2016) presented the linear dynamic analysis by using either SSI modified response spectrum (which is specified in the code) or SSI modified site response spectrum (to be developed by design engineer). Based on the design procedure, including SSI tends to reduce the design base shear force with not less than 70% of the fixed-base counterpart. For considering the non-linear effects of the soil model, the design procedure recommends using the equivalent linear method by using the reduced shear wave velocity (Vs/Vs₃₀) and shear modulus (G/G₀) which are calculated based on the soil type and the design earthquake motion. Including the kinematic interaction, effects are not permitted in the linear dynamic analysis. To include the kinematic interaction in the design process, (ASCE, 2016) permitted a non-linear response history procedure by using acceleration histories scaled to a site-specific response spectrum, where the structure and soil shall be modelled non-linearly.

Regarding the European provisions, (EN 1998-5, 2004) is setting some conditions for including SSI effects in the design process and recommending simplified but conservative approaches to consider SSI. However, the code does not specify a design procedure for the technical computation. On the one hand, it is recommended to ignore SSI effects for low seismic classes and also when the shear wave velocity of the ground is higher than 800 m/s for embedded foundations. On the other hand, it provides some general conditions where SSI effects must be taken into account, such as: i) when the second-order (P − Δ) effects play an important role. ii) When an increase in the fundamental period due to SSI increases spectral acceleration. iii) Structures supported on very soft soils when shear wave velocity is less than 250 m/s. iv) Structures having deep foundations or having large dimensions in plan $(> 50 m)$ . v) Bridge abutments with large embankments. For the above conditions, the code provides a general procedure based on the lumped parameter model (springs and dashpot coefficients) for different soil conditions.

Similar to the (EN 1998-5, 2004), there are other design codes in different countries, such as Indian standard (IS 1893, 2016), Japanese guidelines (JSCE, 2007), and New Zealand standards (NZS 1170.5, 2004) recommends accounting for SSI effects with different condition and considerations. However, these design codes are only providing general procedures and recommendations without prescribing specific computational procedures to consider SSI in the design practice. Hence, including SSI in the practical design is typically neglected by structural engineers.

From the above-reviewed design codes, one can conclude that building codes are dealing with soil-structure interaction effects in three aspects: i) codes that do not highlight the importance of soil-structure interaction effects. ii) Codes that take into account the importance of SSI in specific conditions but do not provide a specific design procedure. iii) codes that highlight the importance of SSI and provide simplified design procedures or recommend simplified models to analyze the SSI effects.

6 SSI studies on buildings

Investigation of soil-structure interaction effects on the seismic response of building structures has been very well established and the literature covers at least 50 years of computational and analytical developments in this area. Nevertheless, due to the advancements in computational power, the last two decades is witnessing a vast improvement in SSI studies with various modelling approaches. Generally, these investigations are categorized into two main parts: firstly, researchers who tried to examine detrimental and beneficial effects of soil-structure interaction on the seismic response of buildings, and secondly, researchers who tried to find the parameters and different factors that influence the criticality of the SSI effects. In this section, a review of the advancements and most recent findings from researchers will be presented. The summary of these studies is presented in Table 2.

TABLE 2

TABLE 2. Summary SSI studies on buildings with different structural systems and soil modelling.

6.1 Moment Resisting Frame structures MRFs

(Abdel Raheem et al., 2015) pointed out that there is a strong connection between structural damage and soil conditions during earthquake events. The study investigated the SSI effects on several typical moment-resisting frame buildings resting on different types of soil with a surface mat foundation. The research showed how seismic demand and structural response of the structure will be altered when considering flexible base conditions. More specifically in the case of soft soil deposits where the lateral displacement and inter-story drift are increasing compared to the fixed-base counterpart. The study concluded that SSI effects are amplified with increasing height of the structure, the lower and higher parts of the structure will be affected more than the middle stories. Similarly, (Ghandil and Behnamfar, 2017) investigated the non-linear response of several short to tall MRFs rested on a soft soil deposit. The study showed that the natural period of the SSI system is increasing compared to the fixed-base counterpart, and these effects are more prominent for taller structures. Contrary to the common belief, this study concluded that in high-rise buildings, the story drifts due to SSI effects were observed to be even larger compared to the fixed-base model, especially in the lower stories of the structure. This happens because of the increase in (P − Δ) effects which comes from the greater relative lateral displacement in the lower stories due to the foundation rocking. However, the base shear and story shear forces are calculated to be less in SSI cases for all heights of buildings. Further, it is found that SSI raises ductility demand in the lower levels of a building while decreasing it in the top stories, with these impacts being more obvious in taller buildings. Similar conclusions were also drawn by (Awchat and Monde, 2021). Regarding SSI effects on deep foundations (Visuvasam and Chandrasekaran, 2019) highlighted that the detrimental consequences of SSI are also existing for pile-raft foundation system structures. The results of the numerical investigations showed that the piles will be subjected to lateral displacement and rocking at the raft foundation level. These effects amplify when the soil type changes from dense to loose sand. It has been shown that spacing between the piles also has significant effects on these deformations. Reduction of pile spacing will reduce soil lateral resistance between the piles. This leads to further lateral displacement and rocking in the piles. As a result, more story drift and lateral displacements are induced in the structure. In addition, (Carbonari et al., 2014) studied the seismic response of reinforced concrete structures supported by monopile foundation systems. Investigations on the building in the case of soft soil deposits showed that SSI has a considerable effect on the seismic response of the building by increasing structural deformation, especially in the early plastic ranges. The study observed that inter-story drifts are also increasing especially in the lower parts of the building, this is possibly due to foundation compliance. As for the pile foundation, it is found that SSI increases pile rotations considerably.

To investigate the influence of SSI on the seismic performance and vulnerability of reinforced concrete buildings, (Tahghighi and Mohammadi, 2020) performed an incremental dynamic analysis on several MRF buildings laying on various soil-type deposits. The study highlighted that SSI reduces base shear for low-rise MRFs while for medium-rise buildings foundation flexibility will cause an increase in the base shear. Further, it is observed that the SSI has a significant role in modifying the fixed-based fragility curves, where considering non-linear SSI might cause significant structural damages. However, the author recommended expanding the studying cases to draw more precise conclusions. In addition, (Arboleda-Monsalve et al., 2020) found that the direct economic loss for buildings is increasing up to 33% when considering SSI in the analysis in comparison to building losses with ignoring SSI. Therefore, the study encouraged researchers and engineers to include SSI in the analysis of seismic performance and losses, especially in high seismicity areas.

As a concern for the differences between equivalent linear and fully non-linear soil models, (Luo et al., 2016) highlighted that the equivalent linear approach is underestimating the ground response acceleration during the site response analysis. Further, it has been shown that seismic soil-pile-structure interaction is significantly affected by soil deformation. A separation of the pile from the surrounding soil has a great effect on the structural response. Therefore, in seismic analysis of a pile-raft foundation system, the fully-nonlinear behaviour of the soil must be considered through a proper constitutive model. Similarly, (Tabatabaiefar et al., 2015) compared the results of an experimental shaking table test result to a numerical result with an equivalent linear soil model for raft foundation. The analysis concluded that the equivalent linear method underestimates the inelastic seismic response of the structure resting on soft soil. Thus, in the inelastic design procedure, an equivalent linear model doe not guarantee the safety of the structure. However, the results from the fully-nonlinear soil model were fitting to the experimental results. Therefore, the fully non-linear soil model is highly recommended to achieve realistic results.

6.2 Wall-Frame structures

Apart from the moment-resisting frame MRF structural system and regular structures, several researchers tried to investigate the structural irregularity effects on SSI and the influences of the shear wall availability in the system. Patro et al. (2021) compared the SSI effects on the response of a typical eight-story geometric irregular building with the original regular building. Based on the probabilistic seismic demand and fragility curves for the two structures, it has been shown that vertical geometric irregular buildings are more vulnerable to SSI compared to the regular building and the probability of failure of flexible-based structures is higher than the fixed counterpart. In addition, (Shirzadi et al., 2020) investigated several steel structures with mass eccentricity ranging from (0%–30%). The results showed that regardless of eccentricity, seismic soil-structure interaction increases the first story drift ratio up to 30% more than the fix-based. The study concluded that the more eccentric the building, the more sensitive it becomes to SSI.

Regarding shear wall system buildings, (Carbonari et al., 2011) studied the effect of SSI on the response of low-rise buildings on pile foundations with a coupled-wall system. A linear finite element procedure in the frequency domain was conducted. The study showed that the rocking of the wall foundation significantly depends on the soil and it is rapidly increasing with decreasing soil stiffness. Investigation results observed that the seismic base shear of the columns increased while the base shear of the wall decreased when compared to the fix-based system. These findings imply that as the soil softens, shear forces migrate more from the wall to the frame. Carbonari et al. (2012) extended the earlier study for the non-linear behaviour of the structure using the substructure method. The non-linearity of the soil was also taken into account using an equivalent linear approach. According to the findings, SSI increases the overall structure’s lateral deformability. In addition, the rocking of the foundation significantly reduced the base shear at the walls and increased the same in the frame bases. In addition, (Arboleda-Monsalve et al., 2020) pointed out that SSI is less effective for a tall building with a wall-frame system. The availability of shear walls tends to reduce the natural period, inter-story drift, and foundation settlements in comparison to MRF systems. Hence, the earthquake-induced losses are decreased in wall-frame systems. From these studies, it is observed that the response of wall-frame structures is significantly different than MRF buildings which foundation rocking plays a key role in base shear redistribution in the column frame bases. Ignoring SSI in the analysis of wall-frame structures may lead to inadequate design. However, these studies need to be extended considering a more sophisticated model with a full non-linearity of the system.

The structural behaviour of adjacent buildings during pounding impacts has been a subject of discussion for many years and the soil-structure interaction effects were ignored in this regard. However, several studies showed that SSI can increase the lateral deflection of building structures especially when it rested on soft soil deposits. This encouraged researchers to start investigations on the SSI effects on structural pounding for adjacent buildings during earthquakes. Sobhi and Far (2021) conducted a comprehensive review of recent studies of structural pounding with and without the SSI effects. The study emphasized the significance of considering SSI in the calculation of pounding impacts, especially for adjacent structures at close distances. Further, the study recommended that structural engineers consider pounding impact and soil-structure interaction simultaneously to guarantee a safe design for adjacent buildings. Fatahi et al. (2018) assessed the adequacy of separation gaps between adjacent buildings during severe earthquakes. The study considered three adjacent buildings rested on pile foundations with different separation gaps. According to the findings of this research, the minimum gaps to avoid structural pounding between two structures must be 1.75% of the structural height. Nevertheless, this amount could be higher for structures resting on mat foundations. Therefore, the study highly recommends performing similar studies for buildings with mat foundation systems. Similar findings from (Elwardany et al., 2019; Jaradat et al., 2021; Awchat et al., 2022) emphasized the importance of including SSI effects in the calculation for the pounding impacts.

6.3 Parameters and factors affecting seismic SSI

As previously mentioned, the influences of soil-structure interaction on the seismic response of structures are not only functions of the structural system and soil types. Studies have shown that several other factors are playing a key role in determining the SSI effects on building responses. Hokmabadi and Fatahi (2016) investigated the influence of the different types of foundations on the SSI effects of mid-rise moment-resisting concrete buildings. The results demonstrated that type of foundation plays a major role in the seismic response of buildings with SSI. In general, the base shear force of SSI systems was less than for the fixed-based counterpart. However, this reduction ratio was a function of foundation type. The base shear force for the raft foundation was less than for the floated pile and raft-pile types. The structures supported on the raft foundation experienced the most severe rocking angle compared to the piles. Moreover, structures supported by raft-pile foundations experienced around 20% less rocking than floated pile foundations. This is due to the settlement, which was higher than pile-raft. Furthermore, (Bagheri et al., 2018; Ebadi-jamkhaneh, 2019) discovered that there are other factors influencing the performance level of the structures on soft soil deposits such as (area replacement ratio, size and spacing between piles, ground motion characteristics, and aspect ratio of the building). The seismic soil-pile-structure interaction (SSPSI) tends to reduce the base shear force at the foundation level. The redistribution of story forces will be also altered based on different pile sizes, distances, and distributions. Therefore, the study highly recommended changing the mentioned factors to find an optimized force distribution throughout the structure. Nevertheless, further investigation is required to find a relationship between those parameters and the structural response. Similarly, (Van Nguyen et al., 2017) highlighted that the size and type of the piles will influence the seismic response of the building due to the interaction happening between soil and the pile. Based on the findings, increasing the length of the floating pile causes extra lateral deflection and drifts in the superstructure and sometimes it might exceed the life-safety limit. It has also shown that SSPSI alters the distribution of the forces along with the height of the structure. The study recommends that structural engineers should be aware that the reduction of the maximum base shear due to interaction between the pile and the soil is not equal along with the height of the structure. Therefore, it has to be carefully analyzed, otherwise, it could result in an unsafe design. As a concern for shallow foundation systems (Nguyen et al., 2016) investigated the relations between the foundation size on soil-structure interaction effects. According to the findings of the study, a reduction in foundation size brings fewer shear forces compared to a larger foundation. This is because, in a smaller foundation, there is a higher natural period in the structure. Further, it was observed that larger shallow foundations attract more inertial force from the earthquake compared to the small foundation.

Apart from foundation type, other factors (soil profile, soil constitutive model, and ground motion characteristics) have a significant influence on the soil-structure interaction on the seismic response of the building. Yeganeh et al. (2017) highlighted that considering a uniform soil profile to calculate the average shear wave velocity for the whole soil mass is not adequate. Non-uniform soil layers significantly affects on seismic response of the structure. The actual soil profile with different layers is essential in SSI modelling to achieve realistic results. Based on the study findings, the non-uniform soil profile amplifies the ground motion more than the uniform soil profile, especially in the short period ranges. Thus, the results from the uniform soil profile is underestimating the seismic demands of the building in terms of drift and lateral deflections. The study showed the necessity of modelling the soil profile as realistically as possible. However, to improve the findings of this research, further studies are required to be conducted in this area, especially with proper non-linear soil modelling. Furthermore, (Yeganeh and Fatahi, 2019) pointed out that, not only the soil profile but also different constitutive soil models will affect the seismic response of the building and the foundation. The research findings showed a significant difference between the plastic and non-plastic pre-failure soil models in capturing the foundation settlement, rocking, and base shear of the structure. It was observed, the non-plastic soil models are underestimating the total seismic response of the building, as well as the foundation rocking and settlements. The results of this study were for a specific foundation and structural system. Therefore, the findings can be improved for other structural and foundation systems. Another parameter that has been found to be critical in studying soil-structure interaction is the ground motion characteristics. Zhang and Far (2022) studied the effects of far-field and near-field ground motions on a range of hypothetical tall buildings. It has been found that SSI has a remarkable impact on the response of the buildings, however, a significant difference between applying the near-field and far-field earthquake records was observed. For the far-field earthquakes, the increase in lateral deflection and storey drift was more obvious than in the near-field records.

Based on the revision of previous findings and as a general conclusion, SSI has major effects on the seismic response of buildings and there are different factors governing the criticality of these effects. Ignoring SSI effects is not always beneficial, several situations proved that SSI increases the seismic demand of the structure and changes the performance level of the building. Therefore, to guarantee the safety of the buildings, especially in soft soil deposits, the soil-structure interaction effects should not be ignored.

7 Conclusion and future research tendency

The literature covers at least a half-century of computational and analytical studies to investigate the consequences of soil-structure interaction on the seismic response of buildings. As a common conclusion, there is a consensus among researchers on ignoring SSI effects for structures placed on very stiff soil and rocks. However, the role of SSI for structures resting on soft soil is still debatable among research communities. On the one hand, SSI effects have been traditionally considered beneficial as it is evident in some design code provisions. On the other hand, several researchers and past earthquake events prove that for buildings resting on soft soil deposits, the SSI plays a significant role in increasing the seismic demands of the structure and causing extra damages. Ignoring SSI effects may lead to an inadequate design. In general, there are two main approaches to evaluate the SSI effects: the direct approach and the substructure approach. In the past decades, several modelling techniques have been developed based on these two approaches. The commonly used modelling techniques from the simplest to the most rigorous and accurate models are presented. The strength, limitations and application cases of these simplified models are discussed and compared.

The current state of the global guidelines and design codes on soil-structure interaction is summarized. Based on the revision, one can conclude that very few international design codes recommended considering SSI effects in the design process and, only a handful of them makes it mandatory to include SSI effects into the design. Probably the (ASCE, 2016) and the new draft version of Eurocode be the only standard to provide a guideline for the implementation of SSI in the analysis and design of structures.

According to recent findings, SSI elongates the natural period of structures in most cases. This leads to a reduction in the base shear force while the inter-story drifts and seismic demands are amplified especially in the lower stories of the structure. In several cases, these modifications in the structural response may lead to changing the performance level of the structure from life safety to near collapse limit state. However, these effects are varying for different structural heights and soil types. In addition, researchers found that besides the soil and the structural stiffness, SSI effects are functions of several other factors. It is concluded that the SSI behaviour for the moment-resisting frame and wall-frame systems are different. Whereas in wall-frame systems rocking of the shear wall base plays a significant role. In the same manner, the response of buildings supported by pile and mat foundations is also different. Buildings on mat foundation systems are more sensitive to SSI effects than on pile foundations. Moreover, other factors (size and spacing between piles, size of the shallow foundation, structural model, characteristics of the ground motion, soil constitutive model, and soil profile) are all significantly affecting the SSI consequences. Thus, researchers highly recommended for important structures resting on soft soil, the soil-structure interaction effects must be evaluated with a proper modelling technique considering the soil and structural non-linear behaviours.

Based on the review of the available literature, it is clear that many studies have been carried out in the investigation of SSI consequences in various soil and structural conditions. However, several open issues are still existing that need to be investigated further to draw a better conclusion about the SSI effects on buildings.

1) Since the SSI increases the lateral deflection of structures, the pounding impact for adjacent buildings has recently become an interesting field for researchers to investigate the SSI effects. Several studies have been conducted in the area, however, further investigation on pounding impact including SSI needs to be performed, especially for buildings on mat foundations and considering non-linear structural models.

2) Most of the SSI studies from the literature have been considered regular MRF structures. There is still very little research conducted on buildings with wall-frame systems and geometrically irregular MRFs.

3) Several studies pointed out that SSI is causing an increase in story drifts and lateral deflections. Performing a parametric study to find a mechanism to define how various parameters are affecting these deformations is essential.

4) The design codes provide inadequate guidelines to include SSI effects on buildings. A clear computational procedure is essential to encourage practical engineers to include SSI in the design process.

5) Based on the revision of the literature, there are several simplified SSI models available. Performing an assessment study on the performance and accuracy of each model is necessary for different foundation types.

6) Studying the effects of SSI on prestressed precast RC buildings is very rare. The seismic behaviour of this type of building showed to be different than regular structures. Thus, investigating the SSI effects on these types of structures is necessary.

7) Several studies were conducted on buildings with straight pile foundations of different sizes and spacings, however, there is scarcely any research considering inclined piles.

8) Conventionally the effects of foundation embedment are considered to be beneficial for SSI. Nevertheless, expanding these studies for structures with underground stories considering different soil profiles and different ground motion characteristics is important, especially taking into account the 3D non-linear FEM modelling for the soil domain.

9) The current FEM and FDM-based models are difficult for practical engineers to model and analyze the SSI effects. Providing practical simplified models is vital for practical engineers to include the SSI effects in the design process.

10) The SSI effects of non-structural elements such as infill walls have rarely been investigated. Since SSI effects are increasing lateral deformation and story drifts, the SSI influences on in-plane and out-of-plane behaviours of infill walls are highly recommended.

Author contributions

BB and LA contributed to the conception and design of this study. Material preparation, literature review and the first draft of the manuscript prepared by BB. TW and LS commented, internally reviewed, and contributed to the final design of the manuscript.

Acknowledgments

The author gratefully acknowledges the financial support from the German Academic Exchange Service (DAAD) within the (Research Grant—Doctoral Programmes in Germany) scholarship program. In addition, we acknowledge support for the publication costs by the Open Access Publication Fund of Bauhaus Universität Weimar and the Deutsche Forschungsgemeinschaft (DFG).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdel Raheem, S. E., Ahmed, M. M., and Alazrak, T. M. (2015). Evaluation of soil–foundation–structure interaction effects on seismic response demands of multi-story MRF buildings on raft foundations. Int. J. Adv. Struct. Eng. 7, 11–30. doi:10.1007/s40091-014-0078-x