Efficient numerical simulations on the forest barrier for seismic wave attenuation: engineering safe constructions

This paper aims to elucidate the clear visibility of attenuating seismic waves (SWs) with forest trees as natural metamaterials known as forest metamaterials (FMs) arranged in a periodic pattern around the protected area. In analyzing the changeability of the FM models, five distinct cases of “metawall” configurations were considered. Numerical simulations were conducted to study the characteristics of bandgaps (BGs) and vibration modes for each model. The finite element method (FEM) was used to illustrate the generation of BGs in low frequency ranges. The commercial finite element code COMSOL Multiphysics 5.4a was adopted to carry out the numerical analysis, utilizing the sound cone method and the strain energy method. Wide BGs were generated for the Bragg scattering BGs and local resonance BGs owing to the gradual variations in tree height and the addition of a vertical load in the form of mass to simulate the tree foliage. The results were promising and confirmed the applicability of FEM based on the parametric design language ANSYS 17.2 software to apply the boundary conditions of the proposed models at frequencies below 100 Hz. The effects of the mechanical properties of the six layers of soil and the geometric parameters of FMs were studied intensively. Unit cell layouts and an engineered configuration for arranging FMs based on periodic theory to achieve significant results in controlling ground vibrations, which are valuable for protecting a large number of structures or an entire city, are recommended. Prior to construction, protecting a region and exerting control over FM characteristics are advantageous. The results exhibited the effect of the ‘trees’ upper portion (e.g., leaves, crown, and lateral bulky branches) and the gradual change in tree height on the width and position of BGs, which refers to the attenuation mechanism. Low frequency ranges of less than 100 Hz were particularly well suited for attenuating SWs with FMs. However, an engineering method for a safe city construction should be proposed on the basis of the arrangement of urban trees to allow for the shielding of SWs in specific frequency ranges.

1 Introduction

Seismic waves (SWs) are one of the physical phenomena that affect people and their property, and because the occurrence of this phenomenon is difficult to prevent, it must be minimized (Thompson et al., 2008). Thus, comprehending the causes of its danger, how to deal with it, and the possibility of reducing its risk is critical. Even though elastic waves (EWs) can cause significant structural damage (Marazzani et al., 2021; Qahtan et al., 2022), there must be techniques to reduce their destructive harms to protect constructions that can resist the coercion of a disaster when it occurs. The complete understanding of EW propagation is the first step toward developing attenuation techniques (Du et al., 2017). Pu et al. (Pu and Shi, 2018) investigated the effectiveness of periodic barriers and developed a better method for reducing elastic surface wave propagation and damping in soil. New methods for dramatically reducing the propagation of EWs (Sang et al., 2018; Mandal and Somala, 2020; Huang et al., 2021; Li G. et al., 2022), mitigating SWs (Jia and Shi, 2010; Colombi et al., 2020; Daradkeh et al., 2022), controlling ground vibrations (Dijckmans et al., 2015; Gao et al., 2015; Jiang et al., 2015; Schevenels and Lombaert, 2017; Thompson et al., 2019; An, 2022), utilizing seismic clocks (Sens-Schönfelder, 2008; Aravantinos-Zafiris and Sigalas, 2015; Gahlmann and Tassin, 2022), using sound sensors (Dong, 2021; Yang et al., 2021), and guiding waves (Prati, 2006; Li et al., 2021; Thomes et al., 2022) based on periodic structure theory have emerged. For attenuation purposes, locally resonant structures have been used as periodic structures in the frequency of interest to mitigate EWs (Wang M. Y. and Wang X., 2013). Huang et al. (Huang and Shi, 2013) investigated a periodic array of piles with their dispersion relation for vibration attenuation. Wood et al. (Woods et al., 1974) came up with the idea of using a regular pattern of vertical holes to deliberate down surface waves.

In natural disasters, most damage is caused by elastic surface waves (Uhlemann et al., 2016). Protecting civil structures from EWs can be accomplished by converting surface waves into shear waves (Wei et al., 2015). Engineered metawall barriers use local resonance (LR) to transform surface waves into bulk waves that permeate far below the surface (Mir et al., 2018). Kim et al. (Kim, 2012) shed light on a number of exciting design challenges, such as the effect of urban trees on the attenuation of EWs and their applications for SW hazard. Over a specific frequency range, periodically arranged metamaterials show significant attenuation of surface waves better than those arranged in a random way (Huang et al., 2019). Metamaterials are synthetic composites with desirable properties that are more valuable than the individual components (Kaushik, 2023). In essence, the expression “metamaterial” is a novel concept in the field of material design (Seive, 2019). To realize appropriate material operations, this concept overcomes the apparent natural rule of order structure on a critical performance scale (Barbuto, 2015). The main purpose of using seismic metamaterials is to protect building structures from wave hazards (Mu et al., 2020). However, the use of inexpensive materials and the realization of ecological construction are desirable. Urban trees are becoming increasingly popular because they greatly attenuate surface waves in cities (Liu et al., 2019). Forest metamaterials (FMs) are organized in a periodic way as seismic metamaterials (Colombi et al., 2016a). In comparison with the normal state’s disorganized arrangement, FMs have distinct bandgaps (BGs) (Muhammad et al., 2020). As a result, they are an efficient, economical, and environment-friendly way to reduce the effects of EWs and control ground vibrations. Recent studies have addressed a number of construction problems, which include the role of forest trees in EW attenuation (Colombi et al., 2016a; Colombi et al., 2016b; Lott et al., 2020; Muhammad et al., 2020; Qahtan et al., 2022; He et al., 2023). Because of indirect interactions between plants and ground reflection, low-frequency EWs are attenuated (Lim, 2021).

Natural available metamaterials of forest trees can be used at the subwavelength scale of low-frequency BGs (Colombi et al., 2016a; Miniaci et al., 2016; Liu et al., 2019; Muhammad et al., 2020; Lim, 2021). Maurel et al. (Maurel et al., 2018) reported the coupling between the LR modes and impedance mismatch of converting elastic Love waves into bulk waves due to planting trees in the ground. Although BGs appear generally in the frequency range of interest (low frequencies bellow 100 Hz), many studies have been conducted on the results of experiments and simulations for the LR and Bragg scattering (BS) characters (Wang Y.-F. and Wang Y.-S., 2013; Brûlé et al., 2014; Lim, 2019; Sánchez et al., 2021; Wang et al., 2021; Zeng et al., 2022). The arrangement of trees and their resonance eigenvalues are coupled with the induced elastic surface waves (Muhammad et al., 2020). The mechanism of attenuating EWs and obtaining wide BGs in low frequency ranges is still obscure. The influence of various factors of FMs, such as the geometric properties of natural trees and the mechanical properties of soil, is not clear enough to achieve a distinctive model of BGs with the same order at least as other industrial materials, such as steel sections (Zhang et al., 2021). In the realm of planting and urbanity, trees have the potential to contribute to ecological conception, economic effects, and civilization and environmental values (Roux et al., 2018). Related works show an arrangement for protecting functionality by using rows of forest trees on the upper layer of substrate soil (Muhammad et al., 2020; Li S. et al., 2022). Trees in the forest have been used as seismic shields given their properties as natural metamaterials (Colquitt et al., 2017; Sewar et al., 2022). The numerical calculation of (2D) models, which ignores information about the propagation in the third direction, may lead to the loss of an essential calculation point (Audusse et al., 2021). Through a three dimension (3D) simulation model, which is a type of engineering, numerical analysis can be used to represent the visibility of an urban forest in a way that effectively protects against low-frequency EWs (Huang et al., 2019). The use of vegetation as an environmental solution to ground vibration problems has gained popularity (Lombi and Susini, 2009). Environmental solutions for noise and ground vibration reduction in the low frequency range are achieved through the interplay between periodic structures and ground reflections, which occurs in a roundabout way (Garg, 2022).

The increasing interest in natural metamaterials opens new paths to protect threatened areas of EW propagation. A qualitative investigation has been carried out to study the effects of various geometrical characteristics, including green belt configurations, resonator height, radius, lateral side branches, multilayers of soil, water content, and mechanical properties (i.e., elastic modulus, density, and Poisson’s ratio), on the elimination and control of BG characteristics (Azzouz, 2021). The search for sustainable and eco-friendly solutions to such problems has become a necessity. Forest trees can be manipulated and engineered to provide protection and safety against ground vibration and noise (Cook and Van Haverbeke, 1974). FM-on substrate soil provide an effective offense in EWs’ attenuation mechanism (Maurel et al., 2018). However, the mechanism and modeling of vibration reduction should be clearly emphasized. Incident elastic surface waves can be transformed into bulk shear waves or reflected, resulting in a “seismic rainbow” effect similar to the electromagnetic surface optical rainbow (Colombi et al., 2016a). Although investigations have shown essential and promising development in the use of FMs as vibratory EW attenuators, considerable knowledge gaps remain in this research field. For example, several proposed models have been implemented to confirm observed simulation results (Colombi et al., 2016a; Zhang and He, 2021). While a surface wave propagates in forested areas and then gradually increases or decreases, it is reflected back or converted into a body wave and propagated downward (Colombi et al., 2017). There is a decent understanding of the effectiveness of resonators/FMs to produce a BG at their resonant frequency (Huang et al., 2019). Although, the ability to produce a wide BG at low frequencies (<100 Hz) for practical applications is desirable, it is still unclear for vibration reduction applications.

Accordingly, in this paper, 3D simulations of FMs, including their upper parts, are numerically highlighted and modeled in an engineering way. The aim is to identify the role of urban trees in the attenuation of EWs, as well as the effect of different heights of periodic structures upward and downward on creating wide BGs in the frequencies of interest less than 100 Hz. Research methods have shifted to metamaterials, rearranging periodic structures in soil in a specific geometric way. FMs’ extensive range of applications toward urban areas includes the capacity to generate BS and LR BGs. The increasing interest in metamaterials is opening up new paths for future study toward defending major cities and buildings that are in danger from the propagation of EWs. Within the context of the significant interest shown in research activities, an opportunity has arisen to investigate the benefits offered by urban trees in the formation of environmental systems that are free from the effects of noise pollution and secure against the dangers posed by earthquakes and other forms of natural calamity.

This paper introduces a metawall composed of a forest, in which each unit has a unique configuration in terms of height, width, lattice, and distance from the source of EW energy. The proposed model investigates the role of the upper part of forest trees in attenuating SWs. It demonstrates the effectiveness of a 3D simulation of metawall with various configurations to assess the effect of foliage to create BGs on dispersion curves of wave propagation. Furthermore, this study examines how the width and position of BGs are influenced by multiple layers of soil, each with its own mechanical properties. The innovation of this work centers around the use of forest trees as natural metamaterials, termed FMs, for attenuating SWs. This paper introduces an innovative concept: using forest trees, arranged in a periodic pattern around a protected area, as a method for seismic wave suppression. It explores how different configurations of these forest metamaterials, including variations in tree height and the addition of mass to simulate foliage, can create band gaps in low-frequency ranges. This approach is novel in its integration of natural elements into engineering solutions for seismic wave attenuation, providing a sustainable and ecologically friendly method to protect urban areas from seismic activity. The main objective of this study is to determine the optimal distribution pattern of forest trees around designated conservation areas for maximum protection and effectiveness.

2 Numerical analysis and design methods

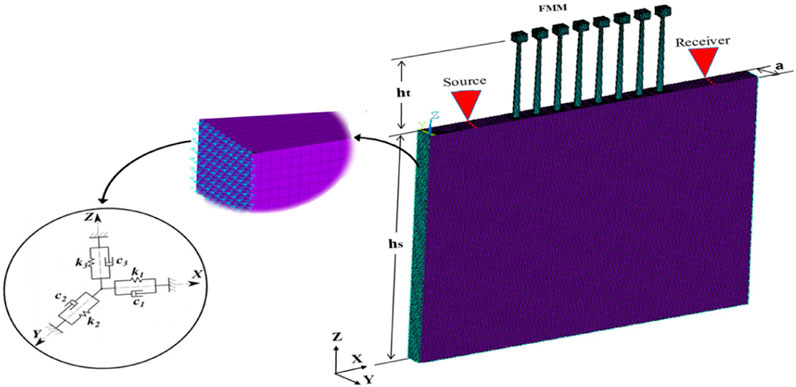
This work advances numerically in simulating SWs to address specific problems. It focuses on the effectiveness of FMs under SW excitation at low frequencies less than 100 Hz. The metawall of FMs represents that resonators interact with SWs in substrate soil; thus, behavior toward attenuating SWs in mechanism is called BG in the field of metamaterials, in which FMM is used as a natural material and the low frequency range is extended to 100 Hz. Through swapping waves via the first irreducible Brillouin zone, the features of BG are realized to attenuate SW propagation.

2.1 Metawall calculation model

This work is limited to the analysis of SWs by using a 3D model. The velocities of primary and secondary waves differ depending on how particles are distributed along the longitudinal and transverse axes. To avoid complexity, when the band structures of the FM resonator are arranged in a periodic pattern, EWs are attenuated. The lattice is considered a function of the wavelength of EW in the soil substrate. Herein, it equals to 50% of λ_ω, where λ_ω is the wavelength of EW in the first BG of BS. The commercial code of COMSOL Multiphysics 5.4a software is valuable to solving the model through the solid mechanics study module. COMSOL Multiphysics 5.4a is also adequate to calculate the corresponding eigenvalues of the unit cell frequency modes of the first irreducible Brillouin zone and swap the periodic arrangement in ΓXMΓ as shown in Figure 1B. In this study, the real growth of a tree species resembling a unit cell is shaped as a circular truncated cone, expressing the radius of the truck at the top equal to the half value of the bottom radius (r), i.e., r = a/10. A mass-effect model is used to make simulations easy and represent the branches and crowns, measured in meters. The dimensions are considered a percentage of wavelength λ_ω, as demonstrated in Figure 1.

FIGURE 1

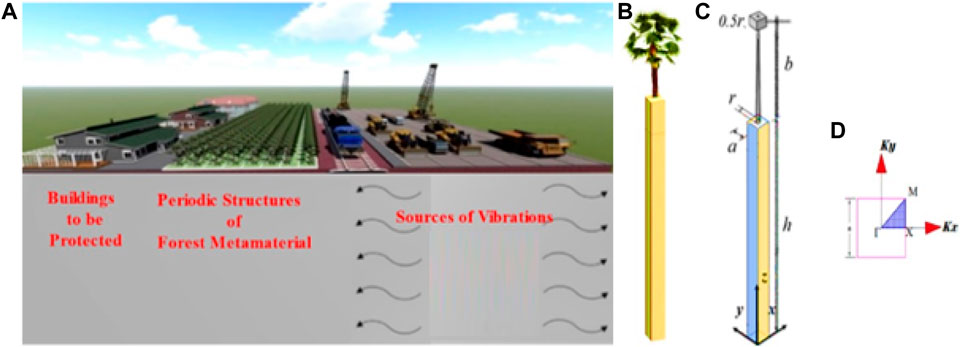
FIGURE 1. Seismic waves and periodic FM barriers, (B) Comparison of FM in Nature, (C) Tree-soil unit cell, and (D) first BZs (hatched blue areas) and first irreducible Brillouin zones (solid line).

A periodic structure has a similar effect to the atomic periodic potential field on electrons. On the basis of this similarity, this study directly refers to the lattice in physics to describe the periodicity of structures. The concept of this phenomenon extends periodic structures to nanoscale. A periodic structure is represented as “metawall,” which can be simplified into a cantilever bending wall on soil as locally vertical resonators, FMs. The effects of tree branches and crowns are considered when establishing the numerical model. The influence of roots on scattering is negligible, on the basis that the roots act as a connecting tool between the soil and the trees. Different configurations of a unit cell are demonstrated to represent the unit cell of urban trees in real images. The mechanical properties of unit cell configurations include the following: ρ is the density of the material, E is the modulus of elasticity, and υ is the Poisson’s ratio for the corresponding material, as presented in Table 1.

TABLE 1

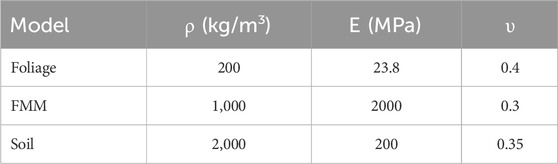
TABLE 1. Mechanical properties for the proposed FM (Maurel et al., 2018; Muhammad et al., 2020).

An inhomogeneous mechanism is used by replacing an equivalent “metawall” filled with an isotropic medium of soil (Marigo and Maurel, 2017). The conforming proposed model of different configurations allows for an analysis to study the influence of many factors, such as the mechanical properties of the unit cell, changing height of trees, lattice shape, distance from wave sources, number of resonator rows, and multilayered soil. A user-controlled adaptive mesh for the unit cell is utilized, ensuring that the maximum element size is less than 1/10 of the wavelength of an ancient wave. Mesh size convergence is performed, and a portion of this analysis is achieved. A maximum element size of 0.2 m and a corresponding triangular finer mesh size are determined as adequate. Convergence plots are provided in Section 3.3 of this study to visually represent the stability and accuracy of the results as the mesh is refined.

2.2 Governing wave equation

The mathematically governing equation for the propagation of waves in a medium is considered the same as that in a linear elastic homogeneous medium (Mei et al., 2003), ignoring the body forces, regardless of whether the damping is expressed by the displacement vector, i.e.,:

$\frac{\mathrm{E}}{2\left(1+\mathrm{v}\right)}{\nabla }^2\mathrm{u}+\frac{\mathrm{E}}{2\left(1+\mathrm{v}\right)\left(1-2\mathrm{v}\right)}\nabla \left(\nabla .\mathrm{u}\right)=-\mathrm{\rho }{\mathrm{\omega }}^2\mathrm{u}(1)$

The proposed FMs should satisfy periodic boundary conditions based on Bloch theory as:

$\mathrm{u}\left(\mathrm{r}+\mathrm{a}\right)={\mathrm{e}}^{\text{ik}.\mathrm{a}}\mathrm{u}\left(\mathrm{r}\right)(2)$

where r = (r_x, r_y, r_z) refers to the components of location vector matching on the FM boundary, u(r) is the displacement vector of the “metawall” nodes, and a is the lattice constant. Then, through substituting Eq. 1 into Eq. 2, the equation of calculation eigenvalues can be expressed as:

$\left(\mathrm{\Omega }\left(\mathrm{K}\right)-{\mathrm{\omega }}^2\mathrm{M}\left(\mathrm{K}\right)\right).\mathrm{u}=0(3)$

where ω is the angular frequency; K is the wave vector; Ω and M are the stiffness and the mass matrix of the unit cell, respectively, which are functions of the wave vector, K. The wave propagation follows the equilibrium equation in the time domain for an inhomogeneous elastic medium, and the body force term is not included because it has no significant effect (Irschik et al., 1994). Several mathematical schemes and techniques could be used to calculate the swapping vector of elastic surface waves propagating in a given frequency range. To eliminate numerical calculations, the finite element method is used to estimate the solution inside a particular elastic domain as a compilation of basic solutions created by a collection of virtual sources located outside the domain. When the amplitude factor (K) is known, the systems of Eq. 2 can be established to solve the eigenvalue problems adopted via COMSOL Multiphysics 5.4a directly in a finite medium by sweeping the K-vector along the transition (front) sides of the irreducible Brillouin zone under complex boundary conditions. A free surface must be imposed on this situation (to the resonator), whereas a fixed boundary must be imposed on the bottom (u = 0). As a result of sweeping the wave vector, dispersion curves of the total dispersion relation are produced.

2.3 Comparison cases

To verify the reliability of the calculation methods in this paper with those applied in the electromagnetic field and postprocessing methods, two previous research models are selected; both are carried out on a nanoscale and are similar to the model studied in this work. Figure 2 compares the dispersion curve and the calculation model of a similar technique that was reported. The dispersion curve and calculation model depict the band structure of resonant frequencies applied on the top of a semi-infinite substrate soil for model validation by Colombi et al. (Colombi et al., 2016a), of hollow black origin. The sound cone method (SCM) processes the dispersion curve of periodic structures, and the calculated results have good correlation, which can be used to derive the surface wave eigenmodes from the bulk wave modes with excellent agreement. The substrate is composed of sedimentary soil, and the scatterers on the surface are trees. It is also used SCM to process the dispersion curve of their proposed model. The blue solid line in the figure is the sound line, and the light solid lines are the surface wave dispersion curves screened by SCM. The red dots in the figure represent the surface wave mode screened by Muhammad et al. (Muhammad et al., 2020), and the space areas represent the BGs. The figure shows that the computed BG result is compatible with past study results, confirming the accuracy of the current method. The calculation results are compared in the figure with all those obtained from the existing calculation methods. The double line is the difference between the 3D analysis and the 2D ones presented in previous studies.

FIGURE 2

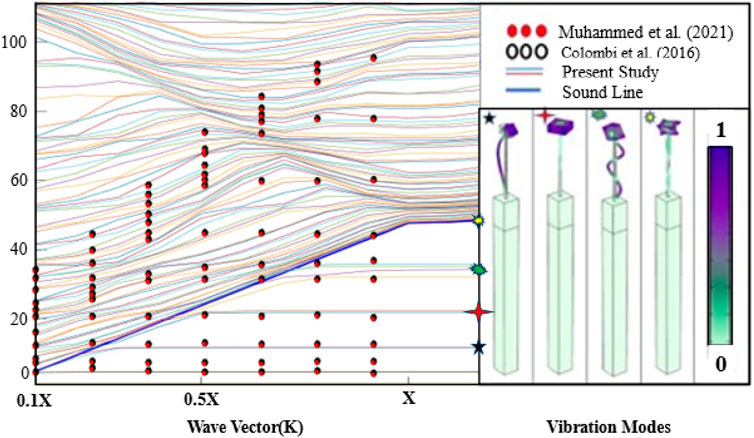
FIGURE 2. Validation of the dispersion curve through case verification with (Colombi et al., 2016a; Muhammad et al., 2020).

3 Numerical simulation

3.1 Model shapes under analysis

In this section, the focus is on analyzing wave propagation and mode shapes in the context of EWs interacting with forest metamaterials. By employing numerical simulations, the study examines the combined effects of bulk and surface waves, which are fundamental to EW formation due to subsurface complexities. This section delves into the dispersion characteristics of these waves, highlighting their interactions with the metamaterials. EWs’ BG characteristics are predicted via numerical simulations. Various bulk and surface waves combine to form EWs as a result of the subsurface formation’s complexity. Seismic surveys can produce EWs when the shear wave velocity of one layer is substantially lower than the velocity of the layer above it. The mode shape analysis is consistent with periodicity, as shown in Figure 3. The metawall unit cell of FMM in square lattice with foliage for compression ignores the foliage effect and includes multilayers of soil.

FIGURE 3

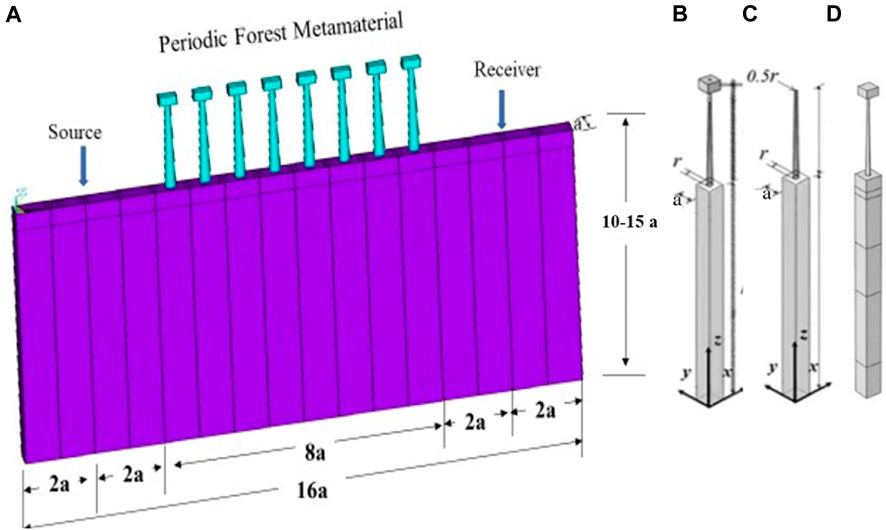
FIGURE 3. Various model shapes (A) 3D metawall, (B) with foliage, (C) without foliage, (D) with layered soil.

Bulk and surface wave modes are included in the dispersion curves of the 3D model. SCM is used to differentiate between pure wave modes because of the peculiarities of EW propagation. The surface wave’s dispersion curve is shown under the sound line, and the BGs visible in the blue hatched area are its dispersion gaps. Seismic surface wave BGs and bulk wave modes with extremely high frequencies can be found outside the sound cone. Moreover, the dispersion properties of elastic waves (EWs) and their interactions with forest metamaterials are explored. The mode shapes relevant to the analysis capture both surface and bulk wave dynamics. Emphasis is placed on modeling the upper sections of forest trees, representing tree branches and biomass as vertical loads to simulate foliage effects. This approach aligns the simulation outcomes with real-world forest configurations, ensuring a realistic representation of wave interactions within varied forest densities.

3.2 Postprocessing physics methods

Bulk waves travel down into deeper soil layers, while surface waves travel along the soil surface (Matthews et al., 1996). Surface waves concentrate their energy primarily on the ground within one or two Rayleigh wavelengths (Pu and Shi, 2017). To achieve surface waves, SCM is used, in which pure surface waves clearly appear below the acoustic line caused by the peculiarities of wave propagation on the surface (Khelif et al., 2010). The sound line constrains the sound cone when it corresponds to the smallest value of the soil phase velocity concept (Huang et al., 2017). Software such as COMSOL Multiphysics 5.4a offers predefined equations to simulate various physical phenomena (Huang and Shi, 2013). COMSOL Multiphysics 5.4a is used to calculate the dispersion curves of periodic systems because it can integrate the formula of eigenvalue and deal with boundary conditions. In this study, the dispersion curves for surface and bulk SWs are calculated using 3D periodic modes with no clear distinction; a locally resonant system is well suited for SCM. In terms of LR and BS, no surface wave mode occurs outside the sound line diagram. Pure surface SW modes are obtained inside the sound line (Khelif et al., 2010). Sound cone lines are calculated in various directions to plot the sound cone diagram, as shown as follows:

$\mathrm{w}=\mathrm{K}\times \mathrm{C}s(4)$

where C_s is the shear wave velocity of the upper soil layer, which can be calculated as:

${\mathrm{C}}_{\mathrm{s}}=\sqrt{\frac{\mathrm{\mu }}{\mathrm{\rho }}}(5)$

where µ is the shear factor of the upper soil layer, and $\mathrm{\rho }$ refers to the soil’s bulk density. The infinite periodic structure in the first irreducible Brillouin zone can be calculated using only a unit cell through the similarity of BZs. The EW vector (K) can be demarcated in the first irreducible Brillouin zone only. The unit cell must meet the periodic boundary conditions. Then, COMSOL Multiphysics 5.4a software with complex boundaries is used to solve the eigenvalues for calculating the dispersion curves of the 3D model. This work proposes the use of the energy density method (EDM) to comprehensively study high-frequency surface modes. In accordance with the propagation characteristics of surface EWs in the upper layer of the ground soil and bulk wave propagation in lower layers, the energy of surface waves should be mainly concentrated in 1 or 2 times of the wavelength for EWs on the ground (Huang and Shi, 2015). Hence, the energy dispersal in the 3D model can be observed, and the dispersion curves are verified by the EDM, as presented in the following equation:

$\text{DOE}=\frac{{\iiint }_{{\mathrm{h}}_{\mathrm{t}}}\frac{1}{2}{\mathrm{T}}_{\text{ij}}{{\mathrm{S}}_{\text{ij}}}^{*}\text{dxdydz}}{{\iiint }_{\mathrm{H}}\frac{1}{2}{\mathrm{T}}_{\text{ij}}{{\mathrm{S}}_{\text{ij}}}^{*}\text{dxdydz}}(6)$

The distribution of energy in Eq. 6 is defined as the energy of EW distribution factor, where ${\mathrm{T}}_{\text{ij}}$ represents the tensors of stresses, and ${\mathrm{S}}_{\text{ij}}^{*}$ refers to the conjugate tensors of the strain. The integral limits on the numerators range of sedimentary soil from 0 to ${\mathrm{h}}_1$ = 2a, measured from the ground surface in the z-axis, and the integral limits on the denominators range of bottom soil from ${\mathrm{h}}_1\text{\hspace{0.17em}to\hspace{0.17em}}{\mathrm{h}}_{\mathrm{s}}$, measured through the bottom layers of soil where, h₁ is the sedimentary soil, and h_s is the total height of soil layers; strain energy density is integrated to achieve elastic strain energy (Huang et al., 2017). Therefore, the value of energy distribution factor must change between 0 and 1. A high value of distribution of energy means that the energy on the soil surface (2a) is high. The strain energy generated by vibration is concentrated on the soil surface. Thus, the critical value of distribution of energy can be defined in small values, such as 0.6–0.9. The recognized surface wave mode is produced by the energy concentrated near the ground surface. In accordance with the ratio of the wavelength in BG frequencies to FM dimensions, as well as the lattice constant, BGs can be divided into BS and LR. Generally, these two types of BG formation are the result of the collective properties of periodic structures. No obvious difference exists between LR and BS systems. The BGs produced by these two actions are likely to exist in the proposed system. Although the “metawall” system mainly reflects the resonance characteristics, BGs are still produced by the apparatus of BS in the system. The periodicity of scatterer configurations plays a key role in determining BS BGs; for LR, the greatest role is played by the resonance characteristics of single FM. The SCM approach is mostly applicable to systems with BGs that are obtained by the apparatus of LR; however, it is blind to surface wave modes that are not shear waves. The dispersion curve of the surface wave can be seen below the sound cone; the blue line is the sound line, and the surface wave modes are inside the sound cone. Outside of the sound cone is a continuous area that represents entirely probable bulk wave modes and high frequencies of surface wave BGs. This region could be assumed as an extension of the sound cone. A representative unit cell is used in the calculation of dispersion curves and presented beside the dispersion curve in Figure 4, and a perfect wave-forbidding function is found in an infinite periodic FM. By contrast, practical uses of periodic trees require that they are structured with a limited number of unit cells. The BG generation mechanism is illustrated by calculating low and high BG vibration modes only at boundary of BGs.

FIGURE 4

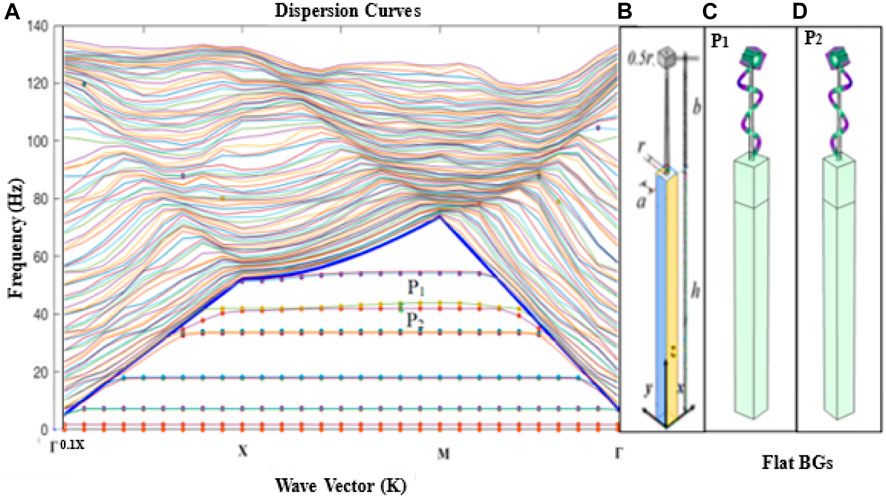
FIGURE 4. (A) dispersion curves in ΓXMΓ, (B) unit cell, and (C, D) flat bands vibration modes in the same frequency.

According to the results of this calculation, wave mode coupling occurs at the resonance attachment point between the longitudinal patterns of FMs and the vertical motion of incoming waves. This coupling causes SWs to move in phase, and the periodic arrangement of trees acts constructively to provide a large BG. The upper section of FM depicts supplementary branches and/or foliage that appear to improve the coupling strength even further. It is demonstrated a significant degree of vibration reduction within the BG frequency by establishing the boundary conditions of the 3D model. The vibration modes in Figure 4 (a) include points (P₁) and (P₂). Owing to the bending of FMs within SCM, not all FM resonances can produce LR BGs. The vibration mode only differs in the direction of vibration and has the same vibration deformation. Several straight bands can be seen in the dispersion curves of Figure 4. No BG exists between these frequency bands. In the study of metamaterials, such bands are called flat bands. These flat bands are composed of two curves of frequency bands that are located for observation, and the vibration modes of points in the upper and lower frequency bands are selected.

3.3 Transmission spectrum analysis

To absorb propagating EWs, a symmetric load of boundary condition is added to the left and right sides of the model, which is perpendicular to the y direction, to simulate the actual mode of FMs. The “metawall” has a width of one unit representing the periodically planted forest on the ANSYS 17.2 finite element software. This model assumes that the forest is planted in a periodic manner, and the model volume is reduced to simplify the calculation. Transmission pertains to the ratio of the transmitted wave energy and the incident wave energy in sound cone theory. The mathematical expression of transmission is:

$T=20\times \log \left(\frac{w_t}{w_i}\right)(7)$

where $w_t$ and $w_i$ are the transmitted wave energy and incident wave energy, respectively. The amplitude reduction factor (ARF) offers a transmission help in visualizing the attenuation mechanism. ARF is used to evaluate the transmission efficiency of barriers for SW attenuation and defined as follows:

$ARF=\frac{Amplitudeofsubstratesoilwithinbarriers}{Amplitudeofsubstratesoilthroughoutbarriers}(8)$

With regard to physical properties, such as acceleration and displacement in the z-axis, maximum values are known as amplitudes. Over a certain range, ARF exhibits some degree of freedom. FRF, also known as the transfer function, is defined as the ratio of the complex output amplitude to the complex input amplitude. The frequency response function (FRF) represents the output per unit sinusoidal input at a specific frequency for a sinusoidal input. Measuring the frequency response typically entails stimulating the system with an input signal, determining the resulting output signal, calculating the frequency spectra of the two signals, and comparing the spectra to isolate the system’s effect. In this case, the sources are turned on sequentially. It is also found that when the first source excites the FM, FRF can be calculated by dividing the FM response signal by the model without the FM signal. The average value of FRF is also used to describe the efficiency of the attenuation mechanism, and it can be calculated using the following formula:

$FRF=\frac{1}{S}{\int }_{S}20{\log }_{10}\left(ARF\right)ds(9)$

where s is the vibration-sensitive range located behind the barriers. The EW in the BG is forbidden from propagation, and the transmission factor will decay in parallel to the normal case of propagation. As a result, metawall arrangement is an excellent indicator of the location and width of the BG that has been created. Furthermore, the transmission changeability indicates the physical mechanism of the BG structure. The plot of dispersion curves and the FRF in the same plot are the best way to find the BGs. To ensure that resonance occurs at the expected frequencies, an evaluation of each configuration is carried out in each mode of the metaforest. At frequencies in which the transmission ratio is less than 1, the total amount of displacement is plotted against frequency to assess how it changes over time. After the meshing of the model divided by a small fine value, such as 0.2 m, in each direction by using ANSYS 17.2, a spring is added in the x, y, and z directions of each node. The viscoelastic spring boundary conditions are added, as shown in Figure 5. Afterward, the absorbed EW is measured smoothly, ensuring the simulation accuracy and reliability.

FIGURE 5

FIGURE 5. Mesh size and viscoelastic boundary conditions for 3D metawall with periodic FMM.

The analysis of the dynamic responses of “metawall” models is conducted using the ANSYS17.2 finite element software. In this study, the source of the excitation wave is set up at (2a) away from the closest side surface, and the observation (receiver) line is located at (2a) away from the other side. Viscoelastic boundaries are mainly interpreted as artificial boundaries. A damper for absorbing the energy of the wave propagating toward the boundary is utilized, in which the elastic modulus of the spring and the damping constant of the damper are determined by chosen material parameters of the periodic FMs. A comprehensive mesh convergence study was conducted, employing a user-controlled adaptive mesh for the unit cell. This study ensured that the maximum element size was maintained at less than one-tenth of the wavelength of an incident wave, adhering to rigorous accuracy standards. To scientifically quantify mesh convergence, it is incorporated specific metrics, including the percentage of allowable error. The results showed convergence with a maximum element size of 0.2 m and a finer mesh, which was determined to be adequate for our simulations. Through the ANSYS 17.2 parametric design language, when the viscoelastic boundary conditions are applied, the periodic FMs are set perpendicular to the x-axis and the bottom with the z-axis. A frequency-domain analysis is used instead of a time-domain analysis in COMSOL Multiphysics 5.4a because of the enormous computing time required. The x-direction end face of the wall receives a predetermined displacement. The other end face is subjected to a traction-free boundary condition, and the wall’s lateral faces are subjected to periodic boundary conditions.

4 Results and discussions

Numerical computation of the incident SW values is performed using extensions of the eigenmode method via COMSOL Multiphysics 5.4a. The 3D model, with the mechanical properties presented in Section 2.1, is adopted. In this case, the effective surface wave velocity of the model is 190.4 m/s. The first BS BG center frequency (ƒ_m) is 41.5 Hz. The corresponding wavelength ${\lambda }_w$ is:

${\lambda }_w=\frac{C_s}{f_m}=\frac{190.4}{41.5}=4.57m(10)$

This wavelength is almost twice the lattice constant, or ${\lambda }_w$ = 2a. Accordingly, a = 2.3 m. The geometric parameters used in this case are expressed as a ratio of wavelength, as mentioned in Sec. 2.1. The tree space is a = 2.3 m; thus, the height of trunk h_t = 11.5 m, and the radius of the bottom of the trunk is r = 0.23 m. The soil depth should be sufficiently large compared to the tree spacing (Oudich and Badreddine Assouar, 2012; Xu and Peng, 2015). The accuracy of these calculations has been corroborated by the findings of Liu et al. (Liu et al., 2019). Hence, a unit cell with a height of 30 m (i.e., 10–15 times ‘a') was considered reasonable for band gap calculation (Miniaci et al., 2016; Du et al., 2017; Du et al., 2018; Lim and Reddy, 2019). This method allows for an accurate determination of the stress-strain relationship when subjected to seismic wave excitations, offering a deeper understanding of the wave attenuation properties of the metamaterials. The soil, h_S2 = 25.4 m, for ground height and, h _S1 = 4.6 m, for the guiding layer. For the starting frequency represented by P₁, the tree and soil exhibit some degree of deformation. The bands are not fully opened, and only BGs in the “ГX” region are determined. The best approach to explain the wave reflections induced by FMs is creating a model and calculating the finite size of “metawall”.

In this study, the FEM is employed to simulate the interaction between seismic waves and forest metamaterials. The FEM allows for detailed analysis of the complex geometries and material properties inherent in the proposed model. It is utilized a discretized model of the physical system, subdividing the forest metamaterials into smaller, manageable finite elements. The results from FEM simulations are instrumental in understanding and optimizing the design and arrangement of forest metamaterials for effective seismic wave attenuation. The simulation modeling is realized via ANSYS 17.2. The viscoelastic boundary elements are accurately modeled to a sufficient level. Boundary finite elements are added to the surfaces parallel to the x direction and the bottom face. To simplify the computation model, periodic boundary conditions are also added to the surface that is orthogonal to the y direction. Furthermore, the vibration modes of FMs/resonators are computed at the edges of the BGs, as highlighted in the gray area in Figure 6. The patterns through the points in the scattering curve of the upper and lower edges of the paired BGs show the patterns of the edge bands in all BGs. If the wave primarily propagates along the ground surface and is outside the BG, the EW would pass through the entire model without causing any disruption. Frequencies of 16 and 48 Hz are used as an example of permitting surface waves to pass outside BGs. However, the BG suppresses the EW’s ability to propagate, such as at frequencies of 47, 50, and 73 Hz, inside BG frequencies, and both points inside and outside of the BGs. Figure 6A depicts the FRF curves. The FRF’s attenuation region closely matches the BGs that could be solved within the sound cone, as observed in the dispersion curves in Figure 6B. The vibration patterns of maximum and minimum low-order longitudinal resonances of the resonator FMs are indicated by dark and light points, respectively, which are highlighted in the vibration modes presented in Figure 6C. Figure 6D displays the displacement distribution for simulating the surface wave feature in the metawall model. The outcomes demonstrate the BG’s wave-forbidding property in FMs; at the same time, the earth surface’s soil movement is nearly constant. Because the FMs are positioned as a cantilever column in the soil, when the soil shakes on the earth’s surface, it indicates the movement of the stand; the FMs vibrate in accordance with this movement, as depicted in Figure 6D. The vibration of trees is a clear curvature movement during the arrival of the wave to the soil’s surface and its vibration. The LR BGs below the sound line in the dispersion curves are observed. In consideration of the geometric parameters, the band structure shows the presence of wide LR in the frequency ranges of 30.61–36.12 Hz and 38.47–46.81 Hz separated at a passband around 37.25 Hz as gray highlighted regions. This solution is considered to elucidate the mechanism of BG generation in the BS eigenmodes beyond the sound line (black solid line), indicating highlighted BS (shaded gray regions) from 48.17 Hz to 53.61 Hz and from 68.11 Hz to 74.45 Hz. These gaps dampen the shear wave by about 40%. In general, the symmetric and antisymmetric eigenmodes’ characteristics, as well as those of the substrate where the resonators are integrated, cause the longitudinal and curvature modes, which depend on these characteristics to produce BGs.

FIGURE 6

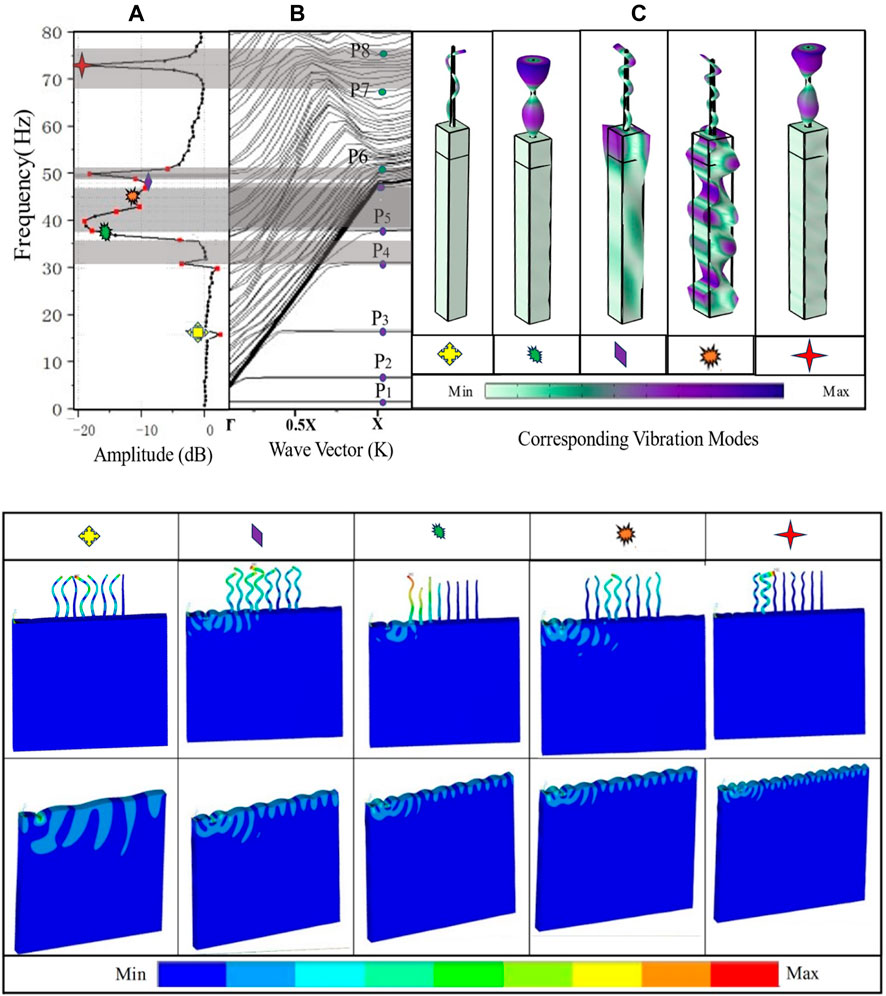
FIGURE 6. 3D band structure of FMMs: (A) FRF curve, (B) dispersion curves in “ΓX,” (C) vibration modes, (D) displacement distribution diagram in the corresponding frequencies.

In the past few years, numerical simulations have been extensively used to determine the effectiveness of periodic structures for the attenuation of EWs and earthquakes in general and to study the factors affecting the attenuation mechanism in particular. Designing periodic structures based on the results of modular analysis is usually a fast, economical, and high-precision method. Therefore, numerical simulations are conducted to examine a group of models of natural metamaterials, arrange them as periodic structures in soil, know the effectiveness of 3D models of these resonators for mitigating the propagation of SWs, and prove the most effective models for attenuating SWs and protecting cities from the dangers of ground vibrations. The mechanism of the attenuation for SW hazard by periodic FMs is applied in this section in consideration of the effects of several factors, including multilayered soil with different properties, “tree–soil” unit cell with various configurations and lattice shapes, FMs’ upper part, bulky side branches, and foliage with crown, and metawall with gradually changing trunk height. The numerical simulation of these factors is performed on the basis of the finite element analysis of the 3D model in five cases.

4.1 Layered soil medium

The simulations in the model of this case are repeated as a transitional step, using soil parameters, via COMSOL Multiphysics 5.4a. Medium dense, dry, uniform sand is chosen as the type of soil because it exhibits the most linear behavior in reality. The assigned soil is still considered as a linear elastic material. On the basis of the assumption that studying and modeling soil layers with inhomogeneity and different consolidated soil characteristics, as well as the universal properties of many layers, are difficult, there may be considerable attenuation in ground vibrations. This condition validates the study’s findings and concludes that resonant trees reduce vibrations better than single homogeneous layers of sedimentary soil, confirming the effectiveness of FMs in attenuating SWs in other stratified ground conditions. To make this study universal, layered soils are considered in the model of Figure 7A. The heterogeneity in the properties obtained from in situ experiments is accounted for to suit the properties of the soil layers (Pu and Shi, 2018). The dispersion available in multilayer soils comprises different modulus of elasticity, density, and Poisson’s ratio compared with that in single-layer soils. The dispersion curves of SWs propagating in various layers of soil return unlike the dispersion curves with different rigidity and density in one-layer soil (Lim and Reddy, 2019). Gao et al. (Gao et al., 2015) conducted cone penetration experiments in the coastal plain of Shanghai City, China and discovered that soils may be classified into six strata on the basis of their mechanical properties (i.e., Young’s modulus, Poisson’s ratio, and density). The properties of the layers for simulation in this case are indicated in Table 2. The properties of the material effects for single- and multilayer profiles are explored in relation to many geotechnical tests performed in situ. Previous studies (Atala et al., 2013; Davis and Hussein, 2014; Dai et al., 2017) have applied perfectly matched layers (PML) at the bottom and both ends of the finite domain model to ensure an infinite boundary and to avoid the back reflection of incident waves. It brief, it is proposed another effective approach by applying the concept of a viscous-spring boundary condition. The fixed boundary is applied at the bottom of the model in COMSOL Multiphysics 5.4a.

FIGURE 7

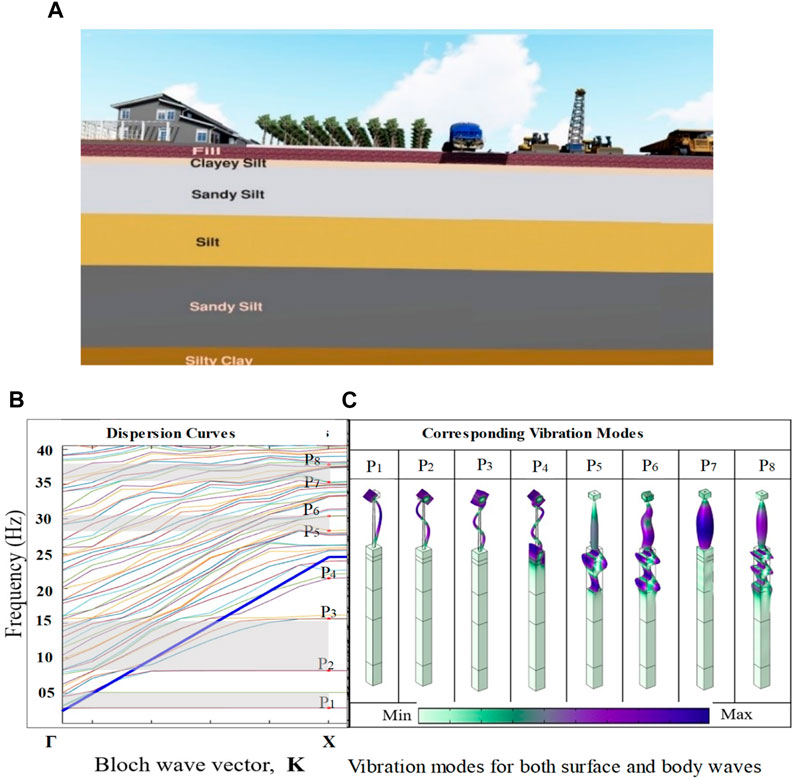
FIGURE 7. FMs on multilayers of soil strata: (A) proposed model, (B) dispersion curves, and (C) vibration modes.

TABLE 2

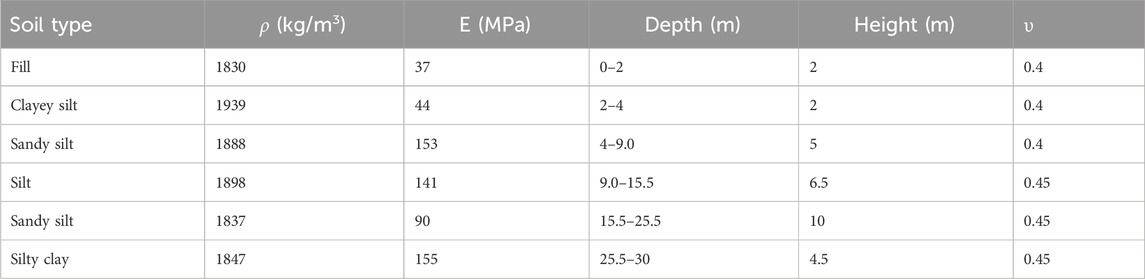
TABLE 2. Properties of layers for simulating a multilayer model (Gao et al., 2015; Lim and Reddy, 2019).

The dispersion curves in the direction of ΓX are presented in Figure 7B. The BGs are governed by the coupling of FMs with SWs that travel on the layered soils, as shown in Figure 7B; the vibration modes for surface waves move in this hypothetical periodic system, as illustrated in Figure 7C. The geometric parameters used in this case are expressed as follows: The tree space is a = 2 m, the height of the trunk is h_t = 11.5 m, the radius of the bottom of the trunk is r = 0.3 m, and the dimension of the foliage volume is 1.5 m × 1.5 m × 1 m. The properties of the foliage and the forest metamaterials (FMs) are consistent with those outlined in Table 1, Section 2.1. Table 2 primarily focuses on detailing the characteristics of the soil layers.

The resonant modes of the infinitely periodic resonator act in a way that helps produce low-frequency BGs when periodicity conditions are applied. When the soil medium is replaced with layered soil and the geometric characteristics of this instance are maintained, the resonance of LR depends on the resistance misalliance and coupling of SW modes between the FMs and soil. The increase in the width of BG is attributed to the interaction with the resonant FMs. Because the velocity patterns of SWs change in each layer of a homogeneous medium, surface impulses travel at amplitudes and phase velocities. The ground effect results in deductive and eradicative intervention, causing a rise and minimizing the BG width and having an effective influence on the attenuation mechanism. For acoustically rigid and stiff surfaces, the changes in the magnitude of elastic modulus and in relative bulk density led to a decay in the attenuation ratio, thus improving the effectiveness of periodic barriers. For spongy soil surfaces, such as clay, sandy, forestay sand, and gray sandy clay, ground actions can result in relevant low frequencies. At high frequencies, soft ground can absorb SWs, so the resonance’s amplitude is changed. The attenuation mechanism is determined clearly in the vibration modes of these models, as shown in Figure 7C. The medium’s dispersion relation classifies waves depending on their component speeds. The sound cone technique can differentiate between surface and body waves because the surface wave speed is lower than the body wave speed. SCM is used to depict the BG for plane waves, and BG positions are marked as gray regions. According to Figure 7, the model’s dispersion spectra exhibit three locally resonant BGs at frequencies of 2.55–5.04 Hz, 7.194–15.07 Hz, and 16.68–22.61 Hz. Wide low-frequency BGs are achieved as a result of LR BGs developing because of the increased impedance mismatch between soil strata and built-up FMs. Meanwhile, the layered soil model shows other BGs on the outside of the sound line; those bands are BS BGs in the range of frequencies of 28.04–30.92 Hz and 36.08–37.54 Hz. BGs using SCM when applying the boundary condition refer to the radiation of the slowest bulk wave.

4.2 Characteristic of the upper part of trees

Owing to the unstable, irregular movement of trees’ leaves caused by wind and the disparity in the shapes and sizes of foliage and secondary branches, they differ from one species of tree to another (Hong et al., 2018). Thus, realizing a geometric simulation model with actual shapes and sizes in the engineering software used for analysis is a very complex matter. In this study, the consideration of a cube block shape with mass added at the top of the resonator FMs is valuable to investigating the real configuration of tree foliage to study their contribution to the attenuation mechanism and verify the changes in BG width and position (Maurel et al., 2018). FMs interact with EWs, resulting in a wide BG in the low frequencies of interest (Liu et al., 2019). The movement of the lateral branches of trees during the occurrence of vibrations is in different directions, which in turn positively affects the ability to damp the vibrations (Lim, 2021). Hence, the effect of side branches connected to the trunk of trees should be considered to fully understand this mechanism. This case is evaluated using a simulation approach with the model including vertical load instead of the upper part of foliage on the top of the trunk (i.e., equal to 5 times the lattice constant in this study). The FMs are arranged at a distance (2a) from the source of vibration and the receiver at the same distance (2a) from the latest periodic FM. The lattice transformation constant in this case is 2.3 m center to center of FMs, as shown in Figure 8A. Dispersion relations of moving EWs in the X direction, as well as FRF curves, clearly demonstrate the FM BGs in the LR and BS BGs, as depicted in Figure 8B, C, respectively.

FIGURE 8

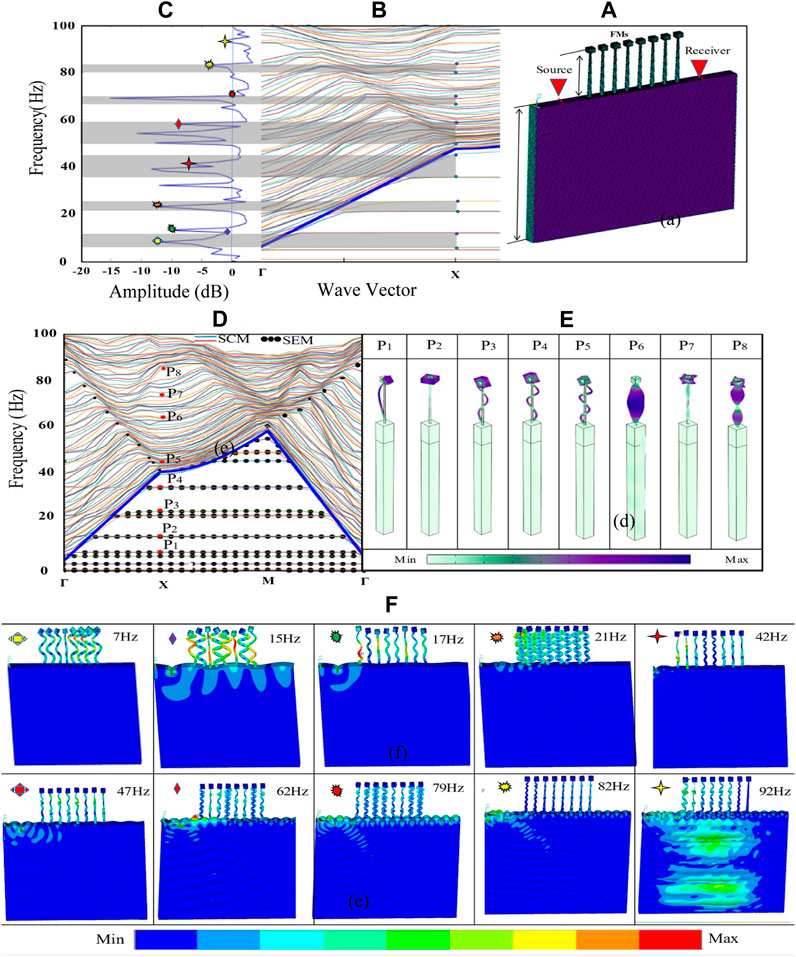
FIGURE 8. (A) Proposed model, (B) dispersion curve, (C) FRF plot, (D) dispersion curve, (E) vibration modes, and (F) distribution displacement.

The LR BGs are highlighted under the sound line. The exact ranges are 7.32–13.71 Hz, 21.18–26.32 Hz, and 37.17–46.62 Hz. In the actual process using the COMSOL Multiphysics 5.4a software, the vibration modes plotted in Figure 8D are integrated into EDM directly to achieve the related strain energy black dots in Figure 8E. The dispersion curves for moving surface waves in ΓXMΓ direction in the FMs with foliage in the internal curves of SCM are shown in the same figure, which are completely consistent with the elastic surface wave BGs determined in the figure. Some of the high-frequency surface wave modes are highlighted in gray regions. The simulation model also identifies some BS BGs for surface waves beyond the sound line in the ranges of 51.12–58.60 Hz, 74.22–79.24 Hz, and 80.06–84.24 Hz. The calculation methods in this case involve surface and bulk wave modes, revealing the changes in wave propagation in the upper part of forest trees. Therefore, through the presented intensive analysis and the calculation, it is determined the maximum percentage of the surface wave attenuation on soil and save the first 100 frequency bands. Furthermore, as shown in the simulation models, the effect of foliage appears not only for low bands of tens of hertz but also for the BGs at frequencies higher than 50 Hz.

The modes of vibration for unit cells indicate noticeable changes in vibration modes at points from P₁ to P₈ after damping the surface propagation of EW through the upper part of FMs. In the case of a foliage model, the increase in dimensions of foliage BG width declines. This case presents a detailed investigation into the effect of tree foliage and branches on ground vibration attenuation, particularly at low frequencies below 20 Hz. It demonstrates that these natural elements significantly contribute to the creation of Rayleigh wave band gaps, which are instrumental in reducing ground-borne vibrations. This finding emphasizes the potential of incorporating natural structures into seismic metamaterial design, offering ecological and effective solutions for vibration control. The inclusion of foliage, in particular, introduces vital band gaps at lower frequencies, enhancing the overall efficiency of vibration mitigation strategies. That is, the coupling of FMs and soil deteriorates with a negative effect, which means that the foliage can induce further noise when the incident wave interacts with the structure, especially in wind.

4.3 Gradually increasing FM height

In addition to the considerable influence of layered soil and treetops, another interesting feature appears, which may significantly affect the propagation of directed waves through forestation of FMs by increasing tree heights. In this case, FMs are arranged in a special periodic model, with an increase in FMs’ height from 4 times to 8 times the lattice constant. The FM parameters are as follows: the lattice is a = 2 m, the trunk radius at bottom is r = 0.3 m, the trunk radius at top is 0.5 r, and height changes from 8 m beside the wave sources to 15 m beside the recording point. The soil contains two layers with 4 and 26 m heights from up to down with the same parameters provided on Table 1. The metawall model includes eight rows of FMs, as shown in Figure 9A. The mechanical properties of the materials are listed in Section 2.1.

FIGURE 9

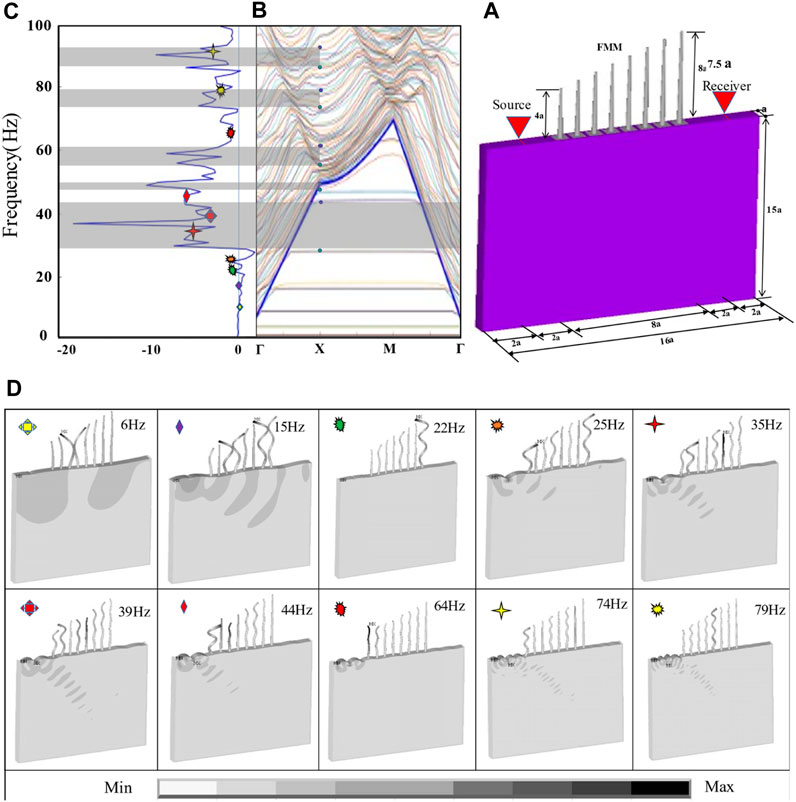
FIGURE 9. (A) Proposed model, (B) dispersion curve in the ΓX direction, (C) FRF curve, (D) distribution displacement corresponding.

As the height of FM increases, it interacts with the inducing surface wave, generating extremely wide BGs in the low frequency range of interest below 100 Hz. To determine the variant restrictions of the BGs in the 3D models of FMs, the dispersion curves based on SCM and EDM methods typically establish the BGs’ characteristics. The gradual change in FMs’ height effects results in deductive and eradicative intervention, causing a rise and minimizing the SW attenuation. The sound line divides the dispersion relations of FMs for medium heights into LR and BS BGs. The unit cell motion shows that the vibration is related to FM oscillations. The FMs show a large sinusoidal distortion in LR BGs in the ranges of 24.15–43.86 Hz and 47.18–51.62 Hz and a strong surface distortion, almost as strong as the ground movement of the surface wave below the sound line. On the contrary, such distortion is noticeably attenuated beyond the sound line to generate some of the BS BGs of periodic FMs in many ranges, such as the ranges of 56.21–61.46 and 64.4–79.12 Hz. The analysis finding in the case of gradually increasing FM height results in extremely wide BGs for LR and BS BGs. Although BGs do not appear at low frequencies below 20 Hz, the BGs produced by BS correspond to surface waves converting into shear waves in the deep layers of soil.

4.4 Gradually decreasing tree height

This case includes a numerical analysis of a model with varying heights of FMs and considers the cutoff frequency for the propagating wave with decreasing FM height from h_t = 15 m toward shorter trees, h_t = 8 m. The other parameters used in this case are the same as those presented in case (III). The analysis in this case is suitable to illustrate surface wave propagation along FMs with decreasing stem height, which becomes increasingly adapted to being converted into shear wave in deeper soil layers. The calculation methods here are limited to explaining the effect of gradually reducing FM height. The results show that when a tree reaches a certain height, coupled with the resonant frequency of the vector, it is converted into a common wave, not adapted to pass the cutoff frequency and thus simply reflected back to the lower layers of soil. This strongly asymmetric behavior of surface love waves was shown in a previous study by Maurel et al. (Maurel et al., 2018). Surface wave scattering and shifting are also observed in the “metawall” model. It is considered a point source outside a forest of eight trees, which generates a love spell in the surface layer of soil. FRF clearly shows the BGs of the proposed models to verify the effect of tree height change on the BGs, as shown in Figure 10B. The displacement distribution diagram in Figure 10D at points selected from the FRF shows the wave transformation inside and outside of BGs. The incident wave causes this coupling, and the periodic formation of trees acts constructively to produce a wide BG. The results show a strong attenuation of ground vibration because the first extremally large BG starts from 30.25 Hz to 47.5 Hz, expressed as LR BGs. The establishment of the bulk wave damping in the BS BGs is visible in the frequency range of 57.14–65.43 Hz.

FIGURE 10

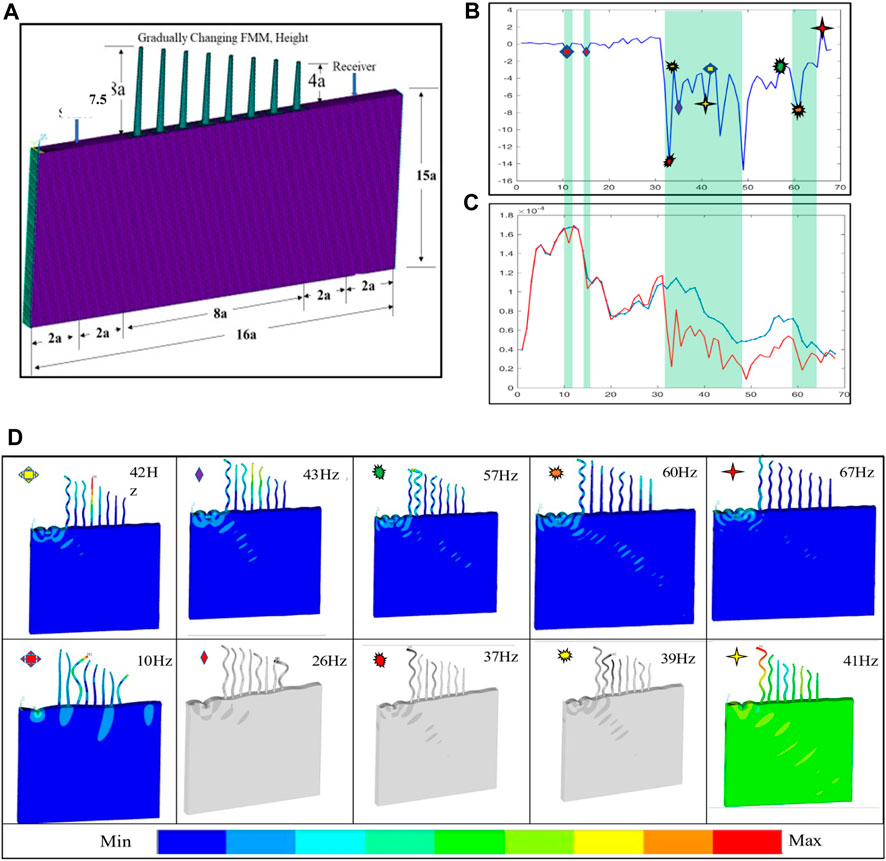
FIGURE 10. (A) Proposed model, (B) FRF curve, (C) comparison of the displacement distribution plot for the “metawall” model with (red line) and without (blue line) FMs, and (D) displacement distribution plot.

4.5 Gradually decreasing foliage height

In this case, the main concern is understanding how the attenuation effectiveness changes as surface waves move in the ΓXMΓ direction. As shown in Figure 11, on the top of the trees, the model includes a foliage effect as a vertical block load with dimensions of 1.5 m × 1.5 m × 1 m. Eight rows of forest trees are arranged, in which the height of FMs changes gradually from 15 m to 8 m. The other parameters of FMs are the same as in case (IV). Engineering FMs with altered stem height and foliage at the same time as actual tree planting has another effect. While foliage has a negative effect on increasing noise and low-frequency vibrations, it plays an important role in converting surface waves into bulk waves and generating wide BGs for LR and BS. When the foliage is presented with high trunk FMs, the reflection of Rayleigh wave remains almost constant throughout the considered high values. The coupling of strong SW modes creates great impedance through matching the resonance between FMs and the foliage fixed in the soil. As a result of this matching, BGs are generated at 22–31 Hz for LR BGs and 56–64 Hz for BS BGs. The negative effect of foliage disappears in the range of frequencies lower than 80 Hz, as depicted in Figure 11. The change in the mechanical properties of soil and FMs with foliage indicates the effects on the strength of wave mode coupling. Similarly, the band structure for foliage models achieves a strong response to absorb wave energy.

FIGURE 11

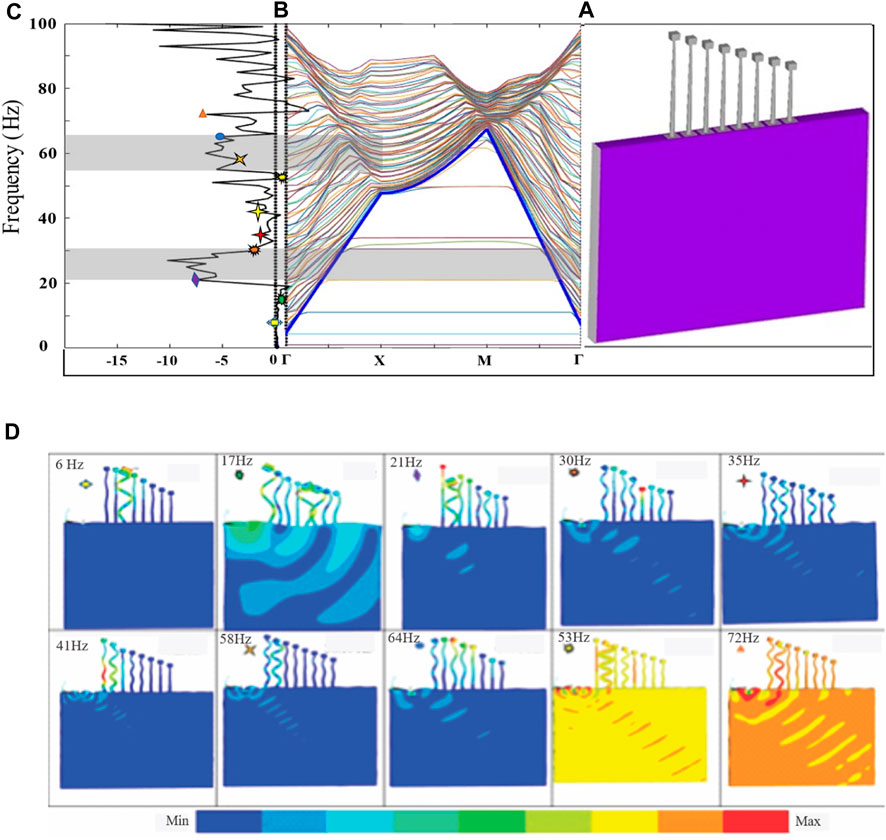
FIGURE 11. (A) Metawall model, (B) dispersion curves, (C) FRF plots, (D) total displacement distribution plots inside and outside BGs in the z direction.

5 Conclusion

This work concluded that FMs acted as a harvesting device for SWs through wide BGs, as evidenced by the hybridization phenomenon in numerical simulation. To this end, surface wave attenuation using FMs has been studied intensively on the basis of periodicity theory. The effects of various parameters, such as layered soil, foliage, and gradually changing tree height, have been comprehensively discussed. Conclusions are summarized as follows:

− The surface waves at low frequencies below 100 Hz are refracted and deflected in the unit cell and converted into shear waves, as proven through numerical simulations of different configurations of FMs in this work.

− The changes in BGs’ characteristics due to foliage are discernible. The results of additional characteristics are revealed in the case of the response of foliage in the low-frequency range of SWs, in which the first BGs start with small frequencies less than 10 Hz and show strong attenuation of the propagation of SWs. However, their effect becomes negative during wind waves, which causes further noise.

− According to the findings of this study, the wave propagation in layered soil results in refracted seismic surface waves at frequencies less than 50 Hz. Thus, the layered soil is believed to be the optimal damper median for surface waves because the waves are reflected multiple times as they travel in the various layers of soil.

− The gradual change in FMs’ height results in the rising the starting point of BGs, but it also generates wide BGs for LR and BS BGs.

− The local amplification of ground vibration control by FMs can be directly applied to the improvement of urban ecosystem functions and has extremely important application potential in urban ecological construction.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

QA-S: Conceptualization, Methodology, Writing–review and editing, Writing–original draft, Investigation. JH: Conceptualization, Methodology, Data curation, Writing–review and editing, Supervision, Project administration. MA: Writing–review and editing, Formal Analysis, Resources, Supervision, Project administration, Validation, Funding acquisition. SM: Formal Analysis, Resources, Writing–review and editing, Validation. AA: Conceptualization, Methodology, Formal Analysis, Writing–review and editing, Validation, MA-H: Writing–review and editing, Resources. YG: Writing–review and editing, Funding acquisition, Formal Analysis, Resources. HA: Formal Analysis, Writing–review and editing, Software, Visualization, Validation.

Funding

The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Acknowledgments

Authors gratefully acknowledge the Beijing Municipal Education Commission for their financial support through the Innovative Transdisciplinary Program “Ecological Restoration Engineering” and Peiyang Future Scholar Scholarship. The authors also appreciate the financial support given by the Islamic University of Madinah, Saudi Arabia.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Abbreviations

SW, Seismic wave; FM, Forest metamaterial; FEM, Finite element method; BG, Bandgap; EW, Elastic wave; LR, Local resonance; 3D, Three-dimension model; IBZ, Irreducible Brillouin Zone; SCM, Sound cone method; EDM, Energy density method; ARF, Amplitude reduction factor; FRF, Frequency response function.

References

An, N. M. N. (2022). Mitigation of ground vibration induced by high-speed trains using a periodic pile system 2022. Geotextiles and Geomembranes, 46,

Google Scholar

Aravantinos-Zafiris, N., and Sigalas, M. M. (2015). Large scale phononic metamaterials for seismic isolation. J. Appl. Phys. 118, 64901. doi:10.1063/1.4928405

CrossRef Full Text | Google Scholar

Atala, M., Aidelsburger, M., Barreiro, J. T., Abanin, D., Kitagawa, T., Demler, E., et al. (2013). Direct measurement of the zak phase in topological Bloch bands. Nat. Phys. 9, 795–800. doi:10.1038/nphys2790

CrossRef Full Text | Google Scholar

Audusse, E., Steinstraesser, J. G. C., Emerald, L., Heinrich, P., Paris, A., and Parisot, M. (2021). Comparison of models for the simulation of landslide generated tsunamis. ESAIM Proc. Surv. 70, 14–30. doi:10.1051/proc/202107002

CrossRef Full Text | Google Scholar

Azzouz, L. (2021). Development and characterisation of novel biocomposites fabricated using natural fibres and rapid prototyping Technology. University of Hertfordshire, Hatfield, UK,

Google Scholar

Barbuto, M. (2015). Design and implementation of metamaterial-inspired transmissive and radiating microwave components. University of Hertfordshire, Hatfield, UK,

Google Scholar

Brûlé, S., Javelaud, E. H., Enoch, S., and Guenneau, S. (2014). Experiments on seismic metamaterials: molding surface waves. Phys. Rev. Lett. 112, 133901. doi:10.1103/physrevlett.112.133901

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Ageeva, V., Smith, R. J., Clare, A., Patel, R., Clark, M., et al. (2017). Enhanced sensing and conversion of ultrasonic Rayleigh waves by elastic metasurfaces. Sci. Rep. 7, 6750–6759. doi:10.1038/s41598-017-07151-6

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Colquitt, D., Roux, P., Guenneau, S., and Craster, R. V. (2016b). A seismic metamaterial: the resonant metawedge. Sci. Rep. 6, 27717–27726. doi:10.1038/srep27717

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Roux, P., Guenneau, S., Gueguen, P., and Craster, R. V. (2016a). Forests as a natural seismic metamaterial: Rayleigh wave bandgaps induced by local resonances. Sci. Rep. 6, 19238–19247. doi:10.1038/srep19238

PubMed Abstract | CrossRef Full Text | Google Scholar

Colombi, A., Zaccherini, R., Aguzzi, G., Palermo, A., and Chatzi, E. (2020). Mitigation of seismic waves: metabarriers and metafoundations bench tested. J. Sound. Vib. 485, 115537. doi:10.1016/j.jsv.2020.115537

CrossRef Full Text | Google Scholar

Colquitt, D. J., Colombi, A., Craster, R. V., Roux, P., and Guenneau, S. R. L. (2017). Seismic metasurfaces: sub-wavelength resonators and Rayleigh wave interaction. J. Mech. Phys. Solids 99, 379–393. doi:10.1016/j.jmps.2016.12.004

CrossRef Full Text | Google Scholar

Cook, D. I., and Van Haverbeke, D. F. (1974). Tree-covered land-forms for noise control; forest service. U. S. Dep. Agric. 263.

Google Scholar

Dai, H., Liu, T., Jiao, J., Xia, B., and Yu, D. (2017). Double Dirac cone in two-dimensional phononic crystals beyond circular cells. J. Appl. Phys. 121. doi:10.1063/1.4979852

CrossRef Full Text | Google Scholar

Daradkeh, A. M., Hojat Jalali, H., and Seylabi, E. (2022). Mitigation of seismic waves using graded broadband metamaterial. J. Appl. Phys. 132, 54902. doi:10.1063/5.0089242

CrossRef Full Text | Google Scholar

Davis, B. L., and Hussein, M. I. (2014). Nanophononic metamaterial: thermal conductivity reduction by local resonance. Phys. Rev. Lett. 112, 055505. doi:10.1103/physrevlett.112.055505

PubMed Abstract | CrossRef Full Text | Google Scholar

Dijckmans, A., Coulier, P., Jiang, J., Toward, M. G. R., Thompson, D. J., Degrande, G., et al. (2015). Mitigation of railway induced ground vibration by heavy masses next to the track. Soil Dyn. Earthq. Eng. 75, 158–170. doi:10.1016/j.soildyn.2015.04.003

CrossRef Full Text | Google Scholar

Dong, Q. (2021). Acoustic-structural interaction: understanding and application in sensor development and metamaterials. Tokyo, Japan: Temple University libraries. doi:10.34944/dspace/6823

CrossRef Full Text | Google Scholar

Du, Q., Zeng, Y., Huang, G., and Yang, H. (2017). Elastic metamaterial-based seismic shield for both lamb and surface waves. AIP Adv. 7, 75015. doi:10.1063/1.4996716

CrossRef Full Text | Google Scholar

Du, Q., Zeng, Y., Xu, Y., Yang, H., and Zeng, Z. (2018). H-fractal seismic metamaterial with broadband low-frequency bandgaps. J. Phys. D. Appl. Phys. 51, 105104. doi:10.1088/1361-6463/aaaac0

CrossRef Full Text | Google Scholar

Gahlmann, T., and Tassin, P. (2022). Deep neural networks for the prediction of the optical properties and the free-form inverse design of metamaterials. https://arxiv.org/abs/2201.10387,

CrossRef Full Text | Google Scholar

Gao, G., Li, N., and Gu, X. (2015). Field experiment and numerical study on active vibration isolation by horizontal blocks in layered ground under vertical loading. Soil Dyn. Earthq. Eng. 69, 251–261. doi:10.1016/j.soildyn.2014.11.006

CrossRef Full Text | Google Scholar

Garg, N. (2022). “Environmental control strategies,” in Environmental noise control (Springer), Berlin, Germany, 277–344.

CrossRef Full Text | Google Scholar

He, C., Zhou, S., Li, X., Di, H., and Zhang, X. (2023). Forest trees as a natural metamaterial for surface wave attenuation in stratified soils. Constr. Build. Mater. 363, 129769. doi:10.1016/j.conbuildmat.2022.129769

CrossRef Full Text | Google Scholar

Hong, S.-W., Zhao, L., and Zhu, H. (2018). CFD simulation of airflow inside tree canopies discharged from air-assisted sprayers. Comput. Electron. Agric. 149, 121–132. doi:10.1016/j.compag.2017.07.011

CrossRef Full Text | Google Scholar

Huang, J., Liu, W., and Shi, Z. (2017). Surface-wave attenuation zone of layered periodic structures and feasible application in ground vibration reduction. Constr. Build. Mater. 141, 1–11. doi:10.1016/j.conbuildmat.2017.02.153

CrossRef Full Text | Google Scholar

Huang, J., Liu, Y., and Li, Y. (2019). Trees as large-scale natural phononic crystals: simulation and experimental verification. Int. Soil Water Conserv. Res. 7, 196–202. doi:10.1016/j.iswcr.2019.03.004

CrossRef Full Text | Google Scholar

Huang, J., and Shi, Z. (2013). Application of periodic theory to rows of piles for horizontal vibration attenuation. Int. J. Geomech. 10, 132–142. doi:10.1061/(asce)gm.1943-5622.0000193

CrossRef Full Text | Google Scholar

Huang, J., and Shi, Z. (2015). Vibration reduction of plane waves using periodic in-filled pile barriers. J. Geotech. Geoenvironmental Eng. 141, 4015018. doi:10.1061/(asce)gt.1943-5606.0001301

CrossRef Full Text | Google Scholar

Huang, T. T., Ren, X., Zeng, Y., Zhang, Y., Luo, C., Zhang, X. Y., et al. (2021). Based on auxetic foam: a novel type of seismic metamaterial for lamb waves. Eng. Struct. 246, 112976. doi:10.1016/j.engstruct.2021.112976

CrossRef Full Text | Google Scholar

Irschik, H., Bedford, A., and Drumheller, D. S. (1994). Introduction to elastic wave propagation. Hoboken, NJ, USA: John Wiley and Sons.

Google Scholar

Jia, G., and Shi, Z. (2010). A new seismic isolation system and its feasibility study. Earthq. Eng. Eng. Vib. 9, 75–82. doi:10.1007/s11803-010-8159-8

CrossRef Full Text | Google Scholar

Jiang, J., Toward, M. G. R., Dijckmans, A., Thompson, D. J., Degrande, G., and Lombaert, G., (2015). “Reducing railway induced ground-borne vibration by using trenches and buried soft barriers,” in Noise and vibration mitigation for rail transportation systems (Springer), Berlin, Germany, 555–562.

CrossRef Full Text | Google Scholar

Kaushik, M. V. (2023). Negative index materials: metamaterials. Review Feature, 9,

Google Scholar

Khelif, A., Achaoui, Y., Benchabane, S., Laude, V., and Aoubiza, B. (2010). Locally resonant surface acoustic wave band gaps in a two-dimensional phononic crystal of pillars on a surface. Phys. Rev. B 81, 214303. doi:10.1103/physrevb.81.214303

CrossRef Full Text | Google Scholar

Kim, S.-H. (2012). Seismic wave attenuator made of acoustic metamaterials. J. Acoust. Soc. Am. 131, 3292. doi:10.1121/1.4708309

CrossRef Full Text | Google Scholar

Li, B., Zhang, C., Peng, F., Wang, W., Vogt, B. D., and Tan, K. T. (2021). 4D printed shape memory metamaterial for vibration bandgap switching and active elastic-wave guiding. J. Mater. Chem. C 9, 1164–1173. doi:10.1039/d0tc04999a

CrossRef Full Text | Google Scholar

Li, G., Chen, Y., Chen, W., Liu, J., and He, H. (2022a). Local resonance–helmholtz lattices with simultaneous solid-borne elastic waves and air-borne sound waves attenuation performance. Appl. Acoust. 186, 108450. doi:10.1016/j.apacoust.2021.108450

CrossRef Full Text | Google Scholar

Li, S., Qiu, C., Huang, J., Guo, X., Hu, Y., Mugahed, A.-S. Q., et al. (2022b). Stability analysis of a high-steep dump slope under different rainfall conditions. Sustainability 14, 11148. doi:10.3390/su141811148

CrossRef Full Text | Google Scholar

Lim, C. W. (2019). Elastic waves propagation in thin plate metamaterials and evidence of low frequency pseudo and local resonance bandgaps. Phys. Lett. A 383, 2789–2796. doi:10.1016/j.physleta.2019.05.039

CrossRef Full Text | Google Scholar

Lim, C. W. (2021). Natural seismic metamaterials: the role of tree branches in the birth of Rayleigh wave bandgap for ground born vibration attenuation. Trees 35, 1299–1315. doi:10.1007/s00468-021-02117-8

CrossRef Full Text | Google Scholar

Lim, C. W., and Reddy, J. N. (2019). Built-up structural steel sections as seismic metamaterials for surface wave attenuation with low frequency wide bandgap in layered soil medium. Eng. Struct. 188, 440–451. doi:10.1016/j.engstruct.2019.03.046

CrossRef Full Text | Google Scholar

Liu, Y., Huang, J., Li, Y., and Shi, Z. (2019). Trees as large-scale natural metamaterials for low-frequency vibration reduction. Constr. Build. Mater. 199, 737–745. doi:10.1016/j.conbuildmat.2018.12.062

CrossRef Full Text | Google Scholar

Lombi, E., and Susini, J. (2009). Synchrotron-based techniques for plant and soil science: opportunities, challenges and future perspectives. Plant Soil 320, 1–35. doi:10.1007/s11104-008-9876-x

CrossRef Full Text | Google Scholar

Lott, M., Roux, P., Garambois, S., Guéguen, P., and Colombi, A. (2020). Evidence of metamaterial physics at the geophysics scale: the METAFORET experiment. Geophys. J. Int. 220, 1330–1339. doi:10.1093/gji/ggz528

CrossRef Full Text | Google Scholar

Mandal, P., and Somala, S. N. (2020). Periodic pile-soil system as a barrier for seismic surface waves. SN Appl. Sci. 2, 1184–1188. doi:10.1007/s42452-020-2969-8

CrossRef Full Text | Google Scholar

Marazzani, J., Cavalagli, N., and Gusella, V. (2021). Elastic properties estimation of masonry walls through the propagation of elastic waves: an experimental investigation. Appl. Sci. 11, 9091. doi:10.3390/app11199091

CrossRef Full Text | Google Scholar

Marigo, J.-J., and Maurel, A. (2017). Second order homogenization of subwavelength stratified media including finite size effect. SIAM J. Appl. Math. 77, 721–743. doi:10.1137/16m1070542

CrossRef Full Text | Google Scholar

Matthews, M. C., Hope, V. S., and Clayton, C. R. I. (1996). Rayleigh the use of surface waves in the determination of ground stiffness profiles. Proc. Inst. Civ. Eng. Eng. 119, 84–95. doi:10.1680/igeng.1996.28168

CrossRef Full Text | Google Scholar

Maurel, A., Marigo, J.-J., Pham, K., and Guenneau, S. (2018). Conversion of love waves in a forest of trees. Phys. Rev. B 98, 134311. doi:10.1103/physrevb.98.134311

CrossRef Full Text | Google Scholar

Mei, J., Liu, Z., Shi, J., and Tian, D. (2003). Theory for elastic wave scattering by a two-dimensional periodical array of cylinders: an ideal approach for band-structure calculations. Phys. Rev. B 67, 245107. doi:10.1103/physrevb.67.245107

CrossRef Full Text | Google Scholar

Miniaci, M., Krushynska, A., Bosia, F., and Pugno, N. M. (2016). Large scale mechanical metamaterials as seismic shields. New J. Phys. 18, 083041. doi:10.1088/1367-2630/18/8/083041

CrossRef Full Text | Google Scholar

Mir, F., Saadatzi, M. S., Ahmed, R. U., and Banerjee, S. (2018). The possibility of harvesting electrical energy from industrial noise barriers using meta-wall bricks. Proc. Sensors Smart Struct. Technol. Civ. Mech. Aerosp. Syst. 10598, 679–683. doi:10.1117/12.2296422

CrossRef Full Text | Google Scholar

Mu, D., Shu, H., Zhao, L., and An, S. (2020). A review of research on seismic metamaterials. Adv. Eng. Mater. 22, 1901148. doi:10.1002/adem.201901148

CrossRef Full Text | Google Scholar

Wu, T., and Lim, C. W. (2020). Forest trees as naturally available seismic metamaterials: low frequency Rayleigh wave with extremely wide bandgaps. Int. J. Struct. Stab. Dyn. 20, 2043014. doi:10.1142/s0219455420430142

CrossRef Full Text | Google Scholar

Oudich, M., and Badreddine Assouar, M. (2012). Surface acoustic wave band gaps in a diamond-based two-dimensional locally resonant phononic crystal for high frequency applications. J. Appl. Phys. 111. doi:10.1063/1.3673874

CrossRef Full Text | Google Scholar

Prati, E. (2006). Microwave propagation in round guiding structures based on double negative metamaterials. Int. J. Infrared Millim. Waves 27, 1227–1239. doi:10.1007/s10762-006-9134-3

CrossRef Full Text | Google Scholar

Pu, X., and Shi, Z. (2017). A novel method for identifying surface waves in periodic structures. Soil Dyn. Earthq. Eng. 98, 67–71. doi:10.1016/j.soildyn.2017.04.011

CrossRef Full Text | Google Scholar

Pu, X., and Shi, Z. (2018). Surface-wave attenuation by periodic pile barriers in layered soils. Constr. Build. Mater. 180, 177–187. doi:10.1016/j.conbuildmat.2018.05.264

CrossRef Full Text | Google Scholar

Qahtan, A. S., Huang, J., Amran, M., Qader, D. N., Fediuk, R., and Wael, A. D. (2022). Seismic composite metamaterial: a review. J. Compos. Sci. 6, 348. doi:10.3390/jcs6110348

CrossRef Full Text | Google Scholar

Roux, P., Bindi, D., Boxberger, T., Colombi, A., Cotton, F., Douste-Bacque, I., et al. (2018). Toward seismic metamaterials: the METAFORET project. Seismol. Res. Lett. 89, 582–593. doi:10.1785/0220170196

CrossRef Full Text | Google Scholar

Sánchez, P., Durda, D. D., Devaud, G., Fischer, A., Scheeres, D. J., and Dissly, R. (2021). Laboratory experiments with self-cohesive powders: application to the morphology of regolith on small asteroids. Planet. Space Sci. 207, 105321. doi:10.1016/j.pss.2021.105321

CrossRef Full Text | Google Scholar

Sang, S., Sandgren, E., and Wang, Z. (2018). Wave attenuation and negative refraction of elastic waves in a single-phase elastic metamaterial. Acta Mech. 229, 2561–2569. doi:10.1007/s00707-018-2127-1

CrossRef Full Text | Google Scholar

Schevenels, M., and Lombaert, G. (2017). Double wall barriers for the reduction of ground vibration transmission. Soil Dyn. Earthq. Eng. 97, 1–13. doi:10.1016/j.soildyn.2017.02.006

CrossRef Full Text | Google Scholar

Seive, L. (2019). Coding metamaterials, digital metamaterials and programmable metamaterials. Light Sci Appl 3, doi:10.1038/lsa.2014.99

CrossRef Full Text | Google Scholar

Sens-Schönfelder, C. (2008). Synchronizing seismic networks with ambient noise. Geophys. J. Int. 174, 966–970. doi:10.1111/j.1365-246x.2008.03842.x

CrossRef Full Text | Google Scholar

Sewar, Y. Y., Zhang, Z., Meng, X., Wahan, M. Y., Qi, H., Al-Shami, Q. M., et al. (2022). Mechanical properties and constitutive relationship of the high-durable parallel strand bamboo. J. Renew. Mater. 10, 219–235. doi:10.32604/jrm.2021.016013

CrossRef Full Text | Google Scholar

Thomes, R. L., Beli, D., and Junior, C. D. M. (2022). Space–time wave localization in electromechanical metamaterial beams with programmable defects. Mech. Syst. Signal Process. 167, 108550. doi:10.1016/j.ymssp.2021.108550

CrossRef Full Text | Google Scholar

Thompson, D. J., Kouroussis, G., and Ntotsios, E. (2019). Modelling, simulation and evaluation of ground vibration caused by rail vehicles. Veh. Syst. Dyn. 57, 936–983. doi:10.1080/00423114.2019.1602274

CrossRef Full Text | Google Scholar

Thompson, R. B., Margetan, F. J., Haldipur, P., Yu, L., Li, A., Panetta, P., et al. (2008). Scattering of elastic waves in simple and complex polycrystals. Wave Motion 45, 655–674. doi:10.1016/j.wavemoti.2007.09.008

CrossRef Full Text | Google Scholar

Uhlemann, S., Hagedorn, S., Dashwood, B., Maurer, H., Gunn, D., Dijkstra, T., et al. (2016). Landslide characterization using P-and S-wave seismic refraction tomography—the importance of elastic moduli. J. Appl. Geophys. 134, 64–76. doi:10.1016/j.jappgeo.2016.08.014

CrossRef Full Text | Google Scholar

Wang, M. Y., and Wang, X. (2013a). Frequency band structure of locally resonant periodic flexural beams suspended with force–moment resonators. J. Phys. D. Appl. Phys. 46, 255502. doi:10.1088/0022-3727/46/25/255502

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, C., Chen, W., Li, Z., Golub, M. V., and Fomenko, S. I. (2021). Precise and target-oriented control of the low-frequency lamb wave bandgaps. J. Sound. Vib. 511, 116367. doi:10.1016/j.jsv.2021.116367

CrossRef Full Text | Google Scholar

Wang, Y.-F., and Wang, Y.-S. (2013b). Multiple wide complete bandgaps of two-dimensional phononic crystal slabs with cross-like holes. J. Sound. Vib. 332, 2019–2037. doi:10.1016/j.jsv.2012.11.031

CrossRef Full Text | Google Scholar

Wei, W., Zhao, D., Xu, J., Wei, F., and Liu, G. (2015). P and S Wave tomography and anisotropy in northwest pacific and east asia: constraints on stagnant slab and intraplate volcanism. J. Geophys. Res. Solid Earth 120, 1642–1666. doi:10.1002/2014jb011254

CrossRef Full Text | Google Scholar

Woods, R. D., Barnett, N. E., and Sagesser, R. (1974). Holography—a new tool for soil dynamics. J. Geotech. Eng. Div. 100, 1231–1247. doi:10.1061/ajgeb6.0000121

CrossRef Full Text | Google Scholar

Xu, Y., and Peng, P. (2015). High quality broadband spatial reflections of slow Rayleigh surface acoustic waves modulated by a graded grooved surface. J. Appl. Phys. 117. doi:10.1063/1.4905948

CrossRef Full Text | Google Scholar

Yang, J., Qi, L., Li, B., Wu, L., Shi, D., Uqaili, J. A., et al. (2021). A terahertz metamaterial sensor used for distinguishing glucose concentration. Results Phys. 26, 104332. doi:10.1016/j.rinp.2021.104332

CrossRef Full Text | Google Scholar

Zeng, Y., Cao, L., Wan, S., Guo, T., Wang, Y.-F., Du, Q.-J., et al. (2022). Seismic metamaterials: generating low-frequency bandgaps induced by inertial amplification. Int. J. Mech. Sci. 221, 107224. doi:10.1016/j.ijmecsci.2022.107224

CrossRef Full Text | Google Scholar

Zhang, G., and He, B.-J. (2021). Towards green roof implementation: drivers, motivations, barriers and recommendations. Urban For. urban Green. 58, 126992. doi:10.1016/j.ufug.2021.126992

CrossRef Full Text | Google Scholar

Zhang, K., Luo, J., Hong, F., and Deng, Z. (2021). Seismic metamaterials with cross-like and square steel sections for low-frequency wide band gaps. Eng. Struct. 232, 111870. doi:10.1016/j.engstruct.2021.111870

CrossRef Full Text | Google Scholar