Historical review of mixed approach to passive damper optimization for building structures under earthquake loading

Takewaki, Izuru

doi:10.3389/fbuil.2024.1492802

REVIEW article

Front. Built Environ., 27 November 2024

Sec. Earthquake Engineering

Volume 10 - 2024 | https://doi.org/10.3389/fbuil.2024.1492802

This article is part of the Research Topic Advancing Energy Dissipation and Vibration-Control Systems for Structural Resilience View all articles

Historical review of mixed approach to passive damper optimization for building structures under earthquake loading

Izuru Takewaki*

Department of Architecture, Kyoto Arts and Crafts University, Kyoto, Japan

Passive dampers play a key role in the smart and reliable design of building structures under uncertain earthquake loading. Passive dampers enable structural designers to enhance the potential of their structural design techniques and acquire the powerful methodologies for more reliable structures under unpredictable uncertainties. While there exist many review articles on optimization of passive dampers, this review is aimed at introducing a new perspective that most passive damper algorithms can be classified based on the combination of several component approaches with different objectives. Mixed approaches considering input uncertainties are particularly highlighted. Research focused on comparison among different optimization methods is also investigated.

Introduction

Passive structural control has a long and successful history in mechanical and aerospace engineering with the support of applied mechanics. This rather new research field has been advanced together with innovative development of computer science and new material science in the latter half of the 20th century. However, in the field of civil engineering, it has a different background. Building and civil structures are often subjected to severe earthquake ground motions and wind disturbances with large uncertainties (Soong and Dargush, 1997; Soong and Constantinou, 2002; Christopoulos and Filiatrault, 2006; Takewaki, 2009; Lagaros et al., 2012). It is therefore required to take into account these uncertainties in a robust and reliable manner in the theory of structural control. Its application to actual structures is also important.

Professor Soong presented five important areas impacted by structural control in his seminal keynote lecture (Soong, 1998) in the second World Conference on Structural Control held in Kyoto, i.e., (a) systems approach, (b) deepening effect, (c) broadening effect, (d) experimental research and (e) creative engineering. Among these five areas, the broadening effect includes the effective use of passive dampers in building structures.

The early-stage development in the optimization of passive dampers was explained by Takewaki in his monograph (Takewaki, 2009). Then the general reviews including research works after his monograph were provided by Puthanpurayil et al. (2013), Whittle et al. (2013), De Domenico et al. (2019), Kookalani et al. (2021) and Takewaki and Akehashi. (2021), Zhu et al. (2022), El Ouni et al. (2022).

Figure 1 shows the role of dampers in the building structural design under load and model uncertainties. It is well known that energy dissipation by viscous, viscoelastic and hysteretic dampers can be performed stably compared to tuned-mass dampers under load and model uncertainties. Theoretical basis of effectiveness brought by passive control and energy dissipation via dampers can be provided from the classical viewpoint of earthquake input energy. If the classical earthquake input energy criterion, i.e., constant input energy (Housner, 1959; Takewaki, 2004; 2006; 2009; Takewaki and Fujita, 2009), holds regardless of the existence of supplemental dampers and the supplemental passive dampers can absorb the earthquake input energy as much as possible, the input energy to the frame can be reduced effectively.

Figure 1

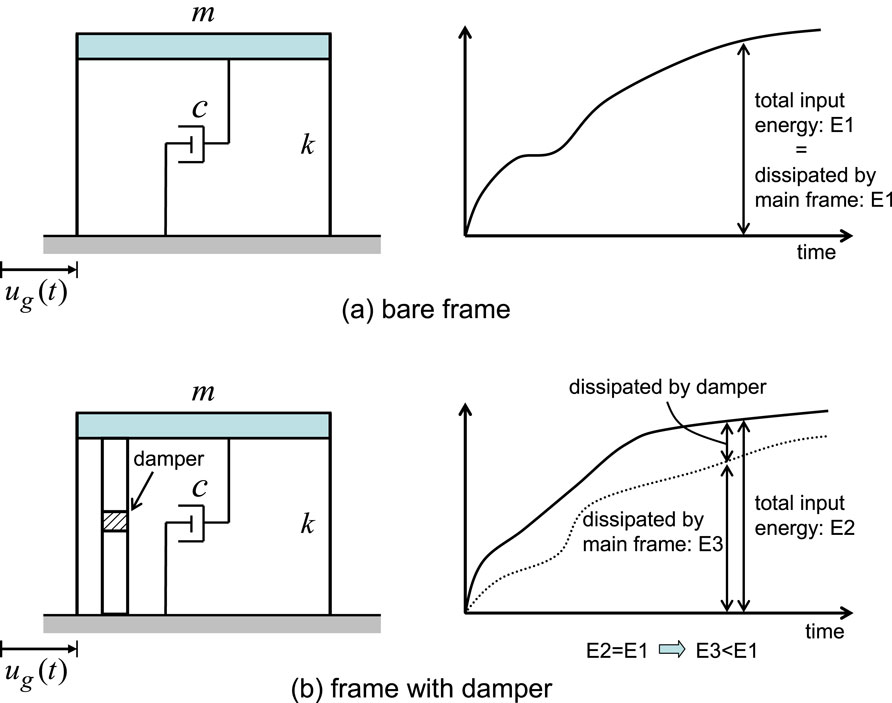
Figure 1. Theoretical basis of effectiveness of dampers, (A) Bare frame, (B) Frame with damper (Takewaki, 2009).

The original point of this review is the classification of optimization methods based on the combination of several component algorithms or approaches. For this reason, it is not intended to cite as many papers as possible in this review. Mixed approaches considering input uncertainties are particularly highlighted.

Various dampers

There are several kinds of dampers, i.e., oil dampers (fluid viscous), viscoelastic dampers, hysteretic dampers, friction dampers, mass dampers, inertial dampers (see Figure 2). Because inertial dampers have been developed rather recently and possess a peculiar characteristic, the mechanism of those dampers is shown in Figure 2 in detail. In some cases, these dampers are used simultaneously in a building structure and system.

Figure 2

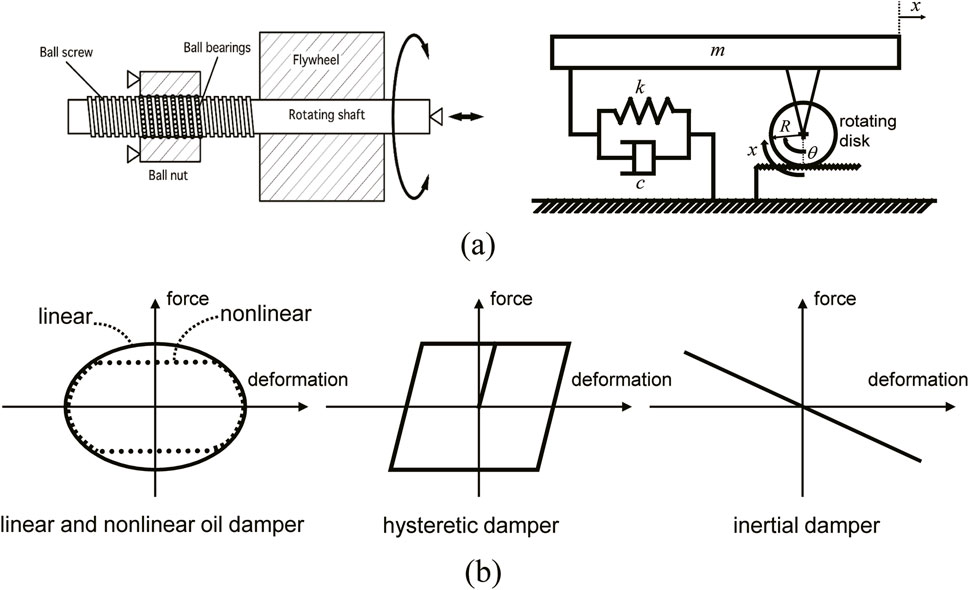
Figure 2. Various dampers, (A) Inertial damper, (B) Force-deformation relation of linear and nonlinear oil damper, hysteretic damper, inertial damper (Uemura et al., 2021).

In discussing their reliability, the dependence on temperature, the manufacturing precision issue, the aging issue, the resistance for high-speed loading, etc., should be remarked. Since many advanced systems are developed recently in each damper system, it seems difficult to classify these damper systems in terms of their reliability degree.

In view of economic implications, oil dampers, viscoelastic dampers, hysteretic dampers, friction dampers have almost the same cost performance to the identical damping performance approximately when used in building structures. Therefore, the selection of dampers is usually made from the viewpoint of functionalities, i.e., the reduction of deformation or acceleration.

Component algorithm

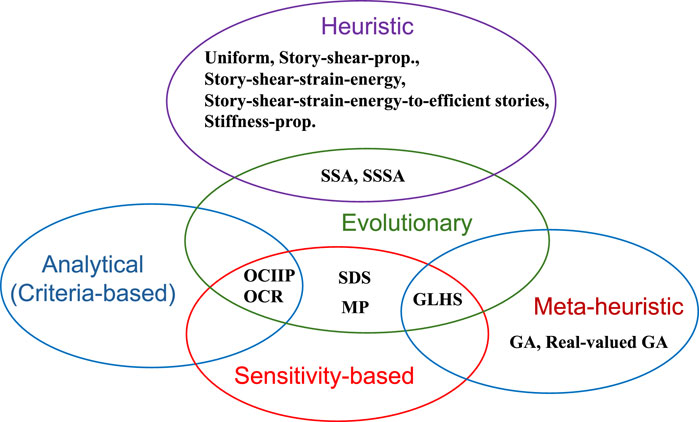
Since the original point of this review is to classify the methods of damper optimization from the viewpoint of mixed approaches of several component algorithms, the component algorithms are explained in the beginning. Figure 3 shows schematic diagrams of six component algorithms, i.e., (a) Evolutionary, (b) Heuristic, (c) Meta-heuristic, (d) Optimality criteria, (e) Sensitivity-based, (f) Input uncertainty.

Figure 3

Figure 3. Component algorithm, (A) Evolutionary, (B) Heuristic, (C) Meta-heuristic, (D) Optimality criteria, (E) Sensitivity-based, (F) Input uncertainty.

Evolutionary

Although ‘evolutionary’ is sometimes used for meta-heuristic approaches such as Genetic Algorithm, this is used in this review for variation of solutions with respect to damper quantity level (see Figure 3A). Through this algorithm, the characteristics of optimal solutions can be made clear or new original optimization algorithms can be developed.

Heuristic

Some methods were proposed as heuristic approaches. Story-shear-proportional, story-shear-strain energy-proportional, story-stiffness-proportional are well known (Hwang et al., 2013; De Domenico et al., 2019; Kookalani et al., 2021). The uniform distribution (UD) along height is the simplest one (see Figure 3B). Although UD does not seem to be strategic, there exist some reports that UD provides robust results for complex design conditions regardless of its simplicity (e.g., Del Gobbo et al., 2020).

Hwang et al. (2013) proposed and discussed several methods in detail. The story-shear-proportional-distribution (SSPD) was proposed by Pekcan et al. (1999) and Hwang et al. (2013). The so-called story-shear-strain-energy (SSSE) distribution was proposed by Hwang et al. (2013) who was motivated by the concept of composite damping ratio weighted by the element strain energy.

In addition, Hwang et al. (2013) presented the story-shear-strain-energy-to-efficient-stories (SSSEES) distribution formula. In this method, viscous dampers were located to the floors with higher level of shear strain energy in proportion to the normal story shear strain.

The stiffness proportional distribution (SPD) was proposed in view of the concept of usual ‘structural’ viscous damping. However, since the deformation of a part with large stiffness is small, it may not be effective to provide SPD for passive dampers.

Palermo et al. (2021) presented a model-comparing approach for designing dampers in a frame connected to an external strongback system. Various configurations of viscous dampers were investigated and an analytical derivation of the equivalent damping ratio was conducted for simple response evaluation.

Marra et al. (2023) proposed a five-step procedure dealing with the design (size) of fluid viscous dampers for the seismic retrofitting of existing frame buildings. The size of the uniformly distributed viscous damper was determined in several cases by considering the plastic-deformation demand level of elastic-plastic frames.

Meta-heuristic

GA, real-valued GA

After 1980s, a genetic algorithm (GA) was often and effectively used in the discrete optimal design of structural members and elements with the rapid advancement of computer processing capability. A combined use of damper designs at different generations may be possible (see Figure 3C).

Singh and Moreschi (2002) presented an optimal damper placement method using GA. Frequency-dependent and frequency-independent viscous and viscoelastic dampers were used. Numerical examples of distribution and size of different dampers were presented to achieve a desired level of reduction in the response or a performance index.

Wongprasert and Symans (2004) presented the application of GA for optimal damper distribution in a nonlinear seismic building.

Park K. S. et al. (2004) formulated a life-cycle-cost optimization problem by adopting structural sizing variables, locations and amount of viscoelastic damper as design variables. GA was used to find the optimum parameters of the system.

Silvestri and Trombetti (2007) aimed to identify the system of added viscous dampers which maximizes the dissipative properties under an equal total size constraint. A numerical approach (based upon the use of GA) and a physically based approach (based upon the properties of classically damped systems) were discussed.

Lavan and Dargush (2009) developed a multi-objective optimization algorithm of dampers using GA.

Apostolakis and Dargush (2010) proposed a computational framework for the optimal distribution and design of yielding metallic buckling restrained braces and/or friction dampers in steel moment-resisting frames. GA was used to solve the corresponding discrete optimization problem.

Bogdanovic and Rakicevic (2019) proposed an optimal damper placement method using a combined fitness function. Nine, previously defined, initial configurations were used as a starting point in the process of optimization. The desired performance was defined using the fitness function derived from the interstory drift and energy dissipated by dampers. The genetic algorithm was used as a tool of the optimization process and thirty optimal solutions were obtained.

Uemura et al. (2021) and Akehashi and Takewaki (2021) introduced the real-valued GA in the damper optimization problem. These works will be explained later.

Artificial bee colony algorithm, firefly algorithm, particle swarm algorithm

Sonmez et al. (2013) presented an optimal design method to find location and size of viscous dampers by using the artificial bee colony algorithm. They increased the resistance of frames under earthquakes.

Miguel et al. (2015) proposed a method to find the optimal design of placement and force of dampers in the footbridges. This method utilized the firefly algorithm.

Baei and Terzic (2022) proposed a method for the optimal design of viscous dampers in seismic applications utilizing the multi-objective particle swarm optimization (MOPSO) algorithm. The MOPSO, with its inherent metaheuristic approach and geographically-based adaptive grids, enabled the effective discovery of global and diverse non-convex solutions.

Optimality criteria

In every optimization problem, an objective function and constraints exist. By applying the Lagrange multiplier method, the optimality conditions can be derived. Once the optimality conditions are obtained, the optimality criteria approach can be developed (see Figure 3D). The first optimality criteria approach in the field of passive damper optimization may be the paper by Takewaki (Takewaki, 1997a).

Sensitivity-based

Once an optimal damper optimization problem including the objective function and the constraints is formulated, the sensitivities of the objective function and the constraints with respect to design variables can be obtained. These sensitivities are called design sensitivities and are used as indices for better damper designs (see Figure 3E). If the optimization problems include non-differentiable aspects, some other methods, for examples genetic algorithm, will be required.

Input uncertainty

It is well known that the optimal damper distribution depends on the input ground motions. One possibility is to find the active input ground motion which maximizes the response. However, the active input ground motion changes design by design. The most promising approach seems to be the introduction of the critical input ground motion which represents the worst case (see Figure 3F). It is remarkable that the critical input is obtained sequentially for the design with successively varying damper distribution. The optimal damper distribution exhibiting the optimal response reduction performance for the worst case may be desirable in the viewpoint of reliability.

Classification of optimization methods based on combination of different approaches

There exist many review articles on passive dampers after the year of 2000. In contrast to the previous ones, the original point of the present review is the introduction of a new perspective that most passive damper algorithms can be classified based on the combination of several approaches with different objectives, i.e., evolutionary, heuristic, meta-heuristic, analytical, sensitivity-based. Figure 4 shows the classification of optimization methods based on combination of different approaches.

Figure 4

Figure 4. Classification of optimization methods based on combination of different approaches.

Sequential search algorithm, simplified sequential search algorithm (SSA, SSSA) and related algorithm (evolutionary, heuristic)

Zhang and Soong (1992) proposed a seismic design method to find the optimal configuration of viscous dampers for a building with specified story stiffnesses, called the sequential search algorithm (SSA). Their algorithm seems to come from the concept in the active structural control. While their method is based upon an intuitive criterion that an additional damper should be placed sequentially on the story with the maximum interstory drift, it is pioneering.

Shukla and Datta (1999) developed an advanced version of SSA and evaluated responses in the frequency domain using the spectral analysis for narrow and broad band stationary random ground motions. They demonstrated that the scheme of the optimal placement of viscoelastic dampers provides more reduction in the response compared with other schemes of placement.

Lopez Garcia (2001) provided another simple method, called the simplified sequential search algorithm (SSSA), which modified the SSA by introducing another index including interstory velocities. Lopez Garcia and Soong (2002) applied SSSA to more practical building structures.

Adachi et al. (2013) proposed a sequential method for optimal design of nonlinear viscous oil dampers. Relief loads of the oil dampers were selected as key parameters for the algorithm.

Ishida and Takewaki (2021) developed an optimal design method for nonlinear frames with hysteretic-viscous hybrid dampers under the critical double impulse (will be discussed later in view of input uncertainty) simulating pulse-type ground motions. The interstory drifts and the top-story absolute acceleration were selected as the double response performance indices. The stiffness-proportional hysteretic damper stiffness (heuristic) and the gap were adopted as the design parameters for hysteretic dampers and the damping coefficients of viscous dampers were employed as the design parameter for the viscous dampers. Evolutionary treatment of the hysteretic damper stiffness ratio played a key role for the optimization.

Iguchi et al. (2023) developed a rapid discrete optimal design method of visco-elastic rubber dampers for elastic-plastic moment frames under the critical double impulse by extending the concept of SSA or SSSA to discrete design. To achieve a multi-objective damper design, interstory drifts and floor accelerations are considered in the indices which play a key role in the successive allocation of dampers with discrete dimensions.

Global-local hybrid search (GLHS) (meta-heuristic, sensitivity-based, evolutionary)

The conventional meta-heuristic approach is usually based on a discrete search and is not friendly with the sensitivity-based approach. Recently, some strategic attempts have been made to resolve this difficulty.

Uemura et al. (2021) developed a new algorithm for global simultaneous optimization of oil, hysteretic and inertial dampers using the real-valued genetic algorithm (GA) and local search including a sensitivity-based processing. The real-valued GA does not require a cumbersome processing of coding. It should be remarked that, the real-valued GA is superior for the global minimum search, the local search surpasses in the local minimum search.

Akehashi and Takewaki (2021) proposed a new technique including the real-valued GA for drawing an ideal drift response curve for robust optimal damper design for elastic-plastic MDOF structures under multi-level earthquakes. This approach also includes a sensitivity-based local search.

Optimality criteria method (including incremental inverse problem approach/OCIIP or redesign approach/OCR) (analytical, sensitivity-based, evolutionary)

The first paper dealing with the analytical and non-heuristic algorithm of optimal placement of dampers may be the work by Takewaki (1997a). It is called the optimality criteria method including the incremental inverse problem approach (OCIIP). A simple explanation was made by the keynote lecture by Soong (1998) in the second World Conference on Structural Control held in Kyoto. In that method, the damping coefficients of viscous dampers placed at every story were set as design variables and the story sum of the interstory transfer function amplitudes evaluated at the fundamental natural frequency of the structure was treated as the objective function for optimization. The optimality criteria were derived through the Lagrange multiplier method. Since the optimization problem satisfying the vibration governing equations and the optimality criteria is a highly nonlinear problem, it is difficult to obtain the optimal solution directly. To tackle this problem, an incremental inverse problem approach developed by Takewaki (1997b) and Takewaki (1997c) was applied between the initial structure with the uniform damper distribution and the optimal structure satisfying the optimality criteria. Figures 5A, B show the story-wise damper damping coefficient distributions for two different story stiffness distributions, one is the uniform distribution model and the other is the straight-line lowest mode model. The paper by Takewaki (1997a) has been cited many times as a pioneering work in the damper placement optimization.

Figure 5

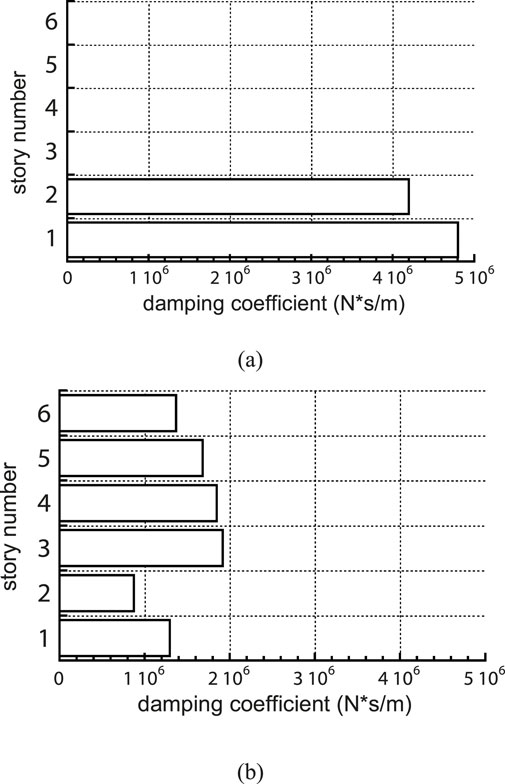
Figure 5. Distribution of optimal damping coefficients, (A) Model with uniform story stiffness distribution, (B) Model with straight-line lowest mode (Takewaki, 1997a).

After this work, the method was advanced for a multicriteria optimization problem (Takewaki, 1999) and a multi-modal optimization problem for multi-level earthquake input ground motions (Akehashi and Takewaki, 2022a).

Levy and Lavan (2006) proposed a fully stressed design based on the optimality condition and the redesign algorithm for design earthquake ground motions.

Steepest direction search method (SDS) and other methods (evolutionary, sensitivity-based)

SDS method

Although the work by Takewaki (1997a) is useful for the problem with a specified amount of dampers, it was desired to develop a method which is useful for a varied amount of dampers with a varied level of response reduction. To respond to this requirement, a new method called the steepest direction search method (SDS) was devised by Takewaki et al. (1999), Takewaki (2000).

Figure 6 indicates the representative schematic algorithm of the optimization procedure. In Figure 6, the initial design is a bare frame without supplemental dampers. Sensitivity analysis of the objective function with respect to a design variable (damping coefficient of damper) is performed first for this bare frame and the highest performance sensitivity is found. Then the damping coefficient of the damper is added to this story. This implies that the damper with the highest performance sensitivity can decrease the performance most effectively and the damping coefficient should be added in this damper. Again, sensitivity analysis is performed next for the frame with the allocated damper and the highest performance sensitivity is found. If the multiple stories show the highest performance sensitivity, then the damping coefficients of the corresponding dampers are added. Sensitivity analysis is subsequently performed next for the frame with such dampers and repeat the procedure explained above until the required total quantity of dampers is reached.

Figure 6

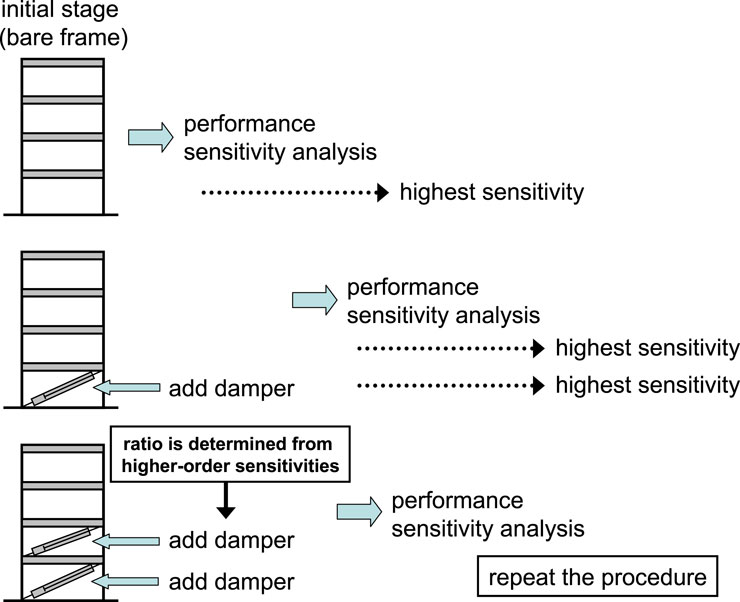
Figure 6. Representative schematic diagram of optimization procedures (Takewaki, 2009)

Since the computation of sensitivities of response quantities which are governed by the equations of motion and the optimality conditions is simple and straight-forward, the SDS method has a generality such that any kind of optimal damper placement problem and any kind of vibration model can be treated in a unified manner.

Figure 7 shows the comparison of the present SDS method with the steepest descent method which is often used in usual mathematical programming problems.

Figure 7

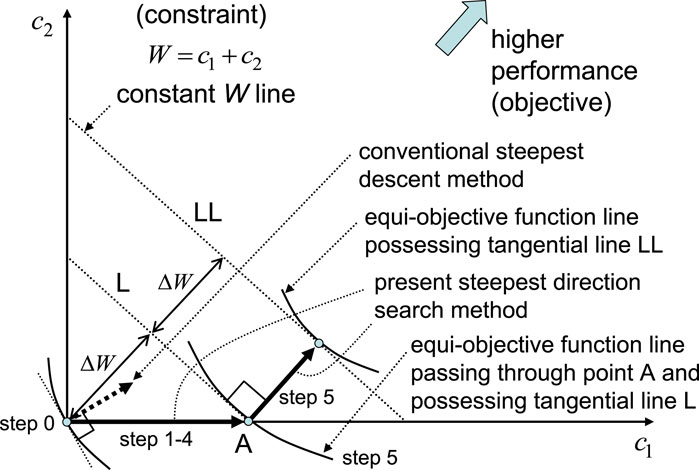
Figure 7. Comparison of the present steepest direction search method with the conventional steepest descent method (Takewaki, 2009).

The fundamental concept and algorithm of the present procedure are also summarized schematically in Figure 7. In step 0, all the added viscous dampers are initialized. In step 1, the first-order derivative $f_{, i}$ of the objective function f is computed. In Steps 2 and 3, the direction (k) which decreases the objective function f most effectively under the condition $\sum_{i = 1}^{n} Δ c_{i} = Δ W$ (n: number of stories, $c_{i}$ : damper damping coefficient, $W$ : total damper quantity) is searched and the design (the quantity of dampers) is updated in that direction (Point A). It is therefore appropriate to call the present algorithm explained above 'the steepest direction search algorithm’. In step 4, the first-order sensitivity $f_{, i}$ of the objective function by the linear approximation $f_{, i} + f_{, i k} Δ c_{k}$ is updated. In step 5, if there exists a damper of an index j such that the condition $- f_{, k} = \max_{j, j \neq k} \{- f_{, j}\}$ is satisfied in step 4, then stop. Step two to five is repeated until $\sum_{i = 1}^{n} c_{i} = \bar{W}$ is satisfied.

A simple numerical example of damping sensitivity of a performance (sum of transfer function amplitudes of interstory drifts) in a two-story shear building model is presented in the monograph by Takewaki (2009). This sensitivity example just corresponds to the gradient direction of the performance function at the origin in the schematic diagram shown in Figure 7. This algorithm may be similar to the conventional steepest descent method in the mathematical programming (see Figure 7). However, while the steepest descent method uses the gradient vector of the objective function as its redesign direction and does not utilize optimality criteria, the present algorithm takes advantage of the newly derived optimality criteria and does not adopt the gradient vector as its redesign direction. More specifically, the explained steepest direction search guarantees the automatic satisfaction of the optimality criteria. For example, if $Δ c_{k}$ is added to the kth added viscous damper in which $- f_{, k} = \max_{i} \{- f_{, i}\}$ is satisfied, then its damper $(c_{k} > 0)$ satisfies the optimality condition in equality and the other dampers $(c_{j} = 0, j \neq k)$ alternatively satisfy the optimality condition in inequality. It is important to note that a series of subproblems is introduced here tentatively in which the total damper capacity level $\bar{W}$ is increased gradually by $Δ W$ from null through the specified value.

Aydin et al. (2007) developed another SDS method following the Takewaki’s method for other transfer function indices at the fundamental natural frequency, i.e., top floor displacement, base shear.

De Domenico and Hajirasouliha (2021) proposed a method of multi-level performance-based design optimization for steel frames with nonlinear viscous dampers. Sensitivity analysis was performed to investigate the effects of initial height-wise damping distribution, convergence factor and uncertainty in design ground motion prediction on the optimization strategy.

Mathematical programming approach (evolutionary, sensitivity-based)

The general method to solve the problem of optimal damper placement may be the application of mathematical programming. Since a building frame and dampers are inter-connected and influence greatly each other, it may be rare to treat a design problem of dampers for a fixed frame dimension. On the other hand, because the dimensional types of dampers are usually limited, it may be realistic to design a building frame for a fixed set of dampers. Uetani et al. (2003) presented a practical application of mathematical programming to the realistic frame optimization for a fixed dimensional set of hysteretic and viscous dampers.

Singh and Moreschi (2001) presented a gradient-based mathematical programming approach (gradient projection method) to the optimal design problem of dampers. They also compared their results with the SSA results.

Park J. H. et al. (2004) presented a simultaneous optimization procedure for both viscoelastic dampers and supporting braces. The effect of supporting braces on the control efficiency of dampers was also investigated. A general gradient-based optimization algorithm was developed and the closed-form expressions for the gradients of the objective function and constraints were derived.

Levy and Lavan (2006) developed a fully stressed design method for framed structures with dampers.

Fujita et al. (2010) proposed an evolutionary algorithm for optimal damper placement to minimize the interstorey-drift transfer function in shear buildings. They presented a sensitivity-based evolutionary algorithm including a sequential quadratic programming.

Akehashi and Takewaki (2022b) presented a new reduced frame model including the effect of damping over a conventional static condensation model. They demonstrated the accuracy of the new model in the optimal design of viscous dampers.

Akehashi and Takewaki (2022c) proposed a new optimal design algorithm of dampers including linear programming by using inverse transformation from shear building models into frame models.

Lavan and Levy (2005) and Lavan and Levy (2006) proposed optimal design methods of supplemental viscous dampers for irregular shear frames and building frames by using a sensitivity-based mathematical programming approach.

Idels and Lavan (2020) presented a new sensitivity-based mathematical programming approach including a mixed-integer problem formulation for the simultaneous optimal design of main frames and dampers. They also used GA for the final member selection.

Agrawal and Yang (2000) proposed an optimal placement method of passive dampers on buildings using combinatorial optimization.

Other methods

Fujita and Takewaki (2012) proposed a robust passive damper design method using a sensitivity-based evolutionary approach for building structures under uncertain structural parameter environments.

Fujita et al. (2014) presented an optimal placement and design method using a sensitivity-based evolutionary approach for nonlinear dampers in building structures.

Murakami et al. (2013) proposed a sensitivity-based algorithm for simultaneous optimal damper placement using oil, hysteretic and inertial mass dampers. Since each damper possesses different response reduction characteristics and the cost issue is difficult to take into account, the proposed sensitivity-based algorithm seems to be quite useful for structural designers without sufficient experiences on each damper.

Kawamoto et al. (2016) presented a robust optimal damper placement method for structures with set-back and eccentricity using evolutionary sensitivity analysis for the integrated transfer function. The method includes a kind of heuristic approach, i.e., to add dampers to the place indicating the minimum objective function.

Tamura et al. (2017) proposed an optimal damper placement method in the hybrid control system of multiple isolation and building connection. Their method is a sensitivity-based evolutionary approach and includes a kind of heuristic approach, i.e., to add dampers to the place indicating the maximum sensitivity.

Terazawa et al. (2022) presented a two-stage (mixed placement and capacity distribution) optimization method for buckling-restrained braces in large metal spatial structures. They used a sensitivity-based evolutionary algorithm.

Mixed approach considering input uncertainty

Fujita et al. (2021) presented a new robust optimal damper placement method for nonlinear oil dampers with uncertainty using the critical double impulse. They proposed a new index for the robust design and used a sequential quadratic programming for optimization. GA was used for demonstrating the validity of the proposed method.

Akehashi and Takewaki (2019) presented a new method of the optimal viscous damper placement for elastic-plastic MDOF structures under the critical double impulse using a gradient-based technique. Since elastic-plastic MDOF structures exhibit complicated responses, this kind of design problems may be complex. Furthermore, the uncertainty in the selection of random earthquake ground motions was tackled by introducing the concept of the worst-case analysis in which the resonant double impulse was regarded as the worst-case input for resonant response.

Kondo and Takewaki (2019) proposed a method for optimal damper placement considering the critical fault rupture slip distribution. They used the stochastic Green’s function method based on a plane-source model of the fault rupture to produce ground motions (Makita et al., 2018).

Akehashi and Takewaki (2020b) developed an algorithm of simultaneous optimization of elastic-plastic building structures and viscous dampers under the critical double impulse. Since the behaviors of elastic-plastic MDOF building structures are sensitive to the building frame member design and the great variation of damper distribution is allowed, the simultaneous optimization of elastic-plastic building structures and viscous dampers is quite tough. They overcame the difficulty by introducing an efficient sensitivity-based design algorithm. It was made clear that the order of changes of structural stiffness and damper damping coefficient is critical to the achievement of reasonable designs.

Cetin et al. (2019) developed a method of optimal design and optimum distribution of viscous dampers for a shear building under the critical excitation by using the random vibration theory in the frequency domain.

Akehashi and Takewaki (2022d) proposed a new optimal damper placement method for a group of recorded ground motions by using the critical double impulse input. They introduced the earthquake input energy through the lowest eigemode to structures with dampers as a criterion to normalize the amplitude of recorded ground motions. It was demonstrated that the response to the critical double impulse can bound the maximum response to the group of recorded ground motions after normalization.

Hosoda and Fujita (2024) presented a robust optimal placement method based on a robustness index by using a sensitivity-based evolutionary algorithm. They used the critical double impulse and the corresponding resonant one-cycle sine wave as the uncertain input motion. They considered variation of elastoplastic design criteria and input level.

Research focused on comparison among different optimization methods

In some research works, the comparison of optimal damper placement methods was made. The following papers are those research works. Such comparison enables the clarification of the characteristics of proposed methods.

Lopez Garcia (2001) presented a comparison of the optimal dampers among the Takewaki’s approach (1997a) based on minimum transfer function, SSSA (Lopez Garcia, 2001) and the uniform distribution as shown in Figure 8. He used four recorded ground motions. He concluded that the efficiency of the damper configurations given by the SSSA is similar to the efficiency of the damper configuration given by the optimal placement for minimum transfer function. It should be noted that the story stiffness distribution used by Lopez Garcia may be the one with the straight lowest eigenmode in which the effect of damper placement seems small (see Figure 5). If other stiffness distributions are employed, e.g., the uniform stiffness distribution, the difference among these damper placements will become remarkable.

Figure 8

Figure 8. Comparison between the SSSA and optimal placement for minimum transfer functions: sum of interstory drifts for six-story structure (Lopez Garcia, 2001).

Trombetti and Silvestri (2004) showed a comparison among the MP (mass-proportional)-damping scheme, the SP (stiffness-proportional)-damping scheme and the Takewaki’s method (1997a). The models of MP and SP are shown in Figure 9. Figure 10 shows the comparison of the maximum structural displacements for three base acceleration inputs, i.e., Imperial Valley, 1940, El Centro record, NS component, Kern County, 1952, Taft Lincoln School record, EW, and Kobe, 1995, Kobe University record, NS component. Although the MP-damping scheme exhibits a remarkably good performance, its applicability to actual building structures may need more effort. In other aspect, it can be seen that the Takewaki’s method exhibits a preferable result against the SP-damping scheme.

Figure 9

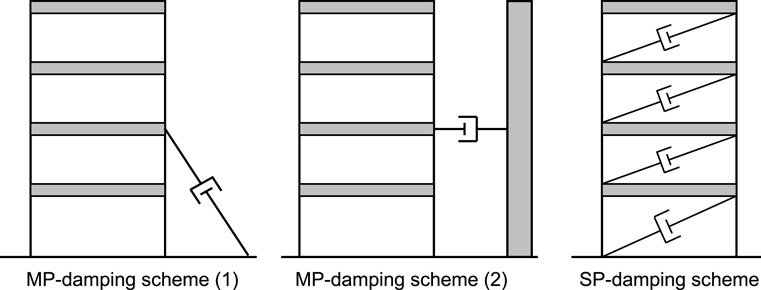
Figure 9. MP (mass-proportional)-damping scheme and SP (stiffness-proportional)-damping scheme (Takewaki, 2009).

Figure 10

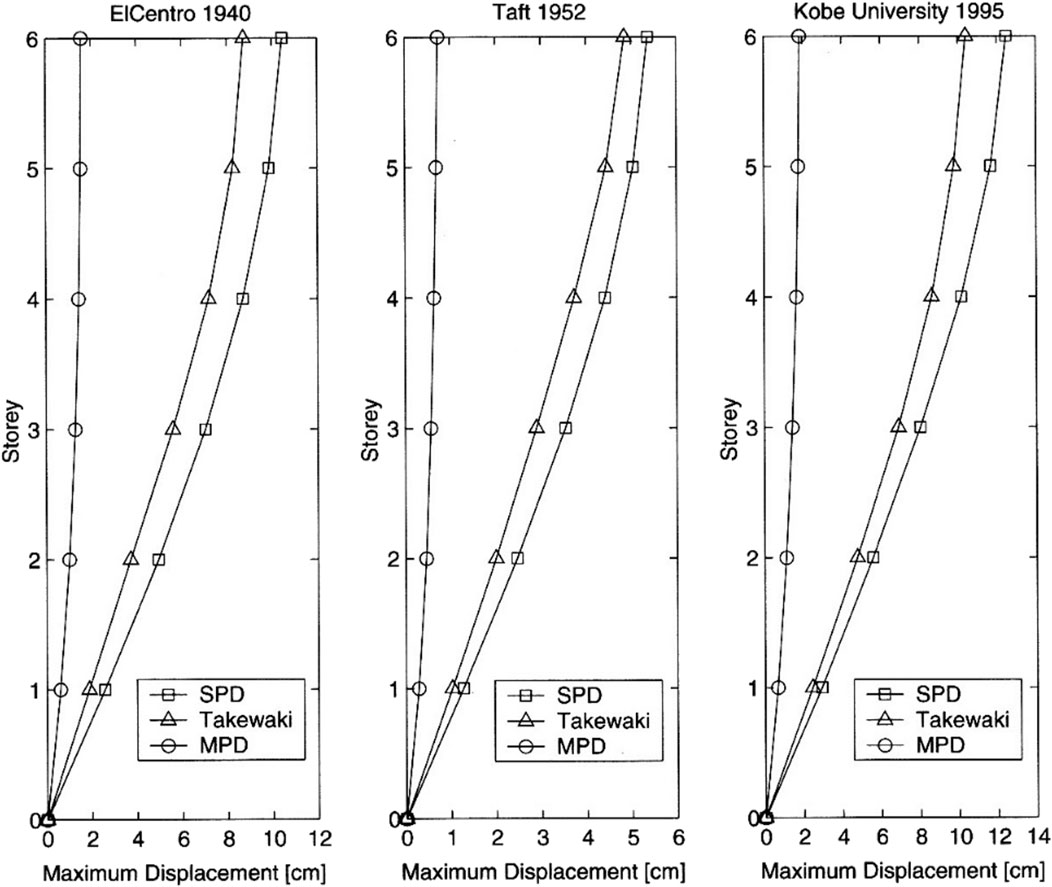
Figure 10. Maximum structural displacements for three base acceleration inputs: Imperial Valley, 1940, El Centro record, NS component, Kern County, 1952, Taft Lincoln School record, EW, and Kobe, 1995, Kobe University record, NS component (Trombetti and Silvestri, 2004).

Figure 11 shows the average percentage deflection reductions for six different damper placements in six damping systems in a 18-story structure and Figure 12 indicates the average percentage deflection reductions for six damping systems in six different damper placements in a 18-story structure (Marko et al., 2006). It can be observed from Figure 11 that the damper locations do not affect so much in some damping systems.

Figure 11

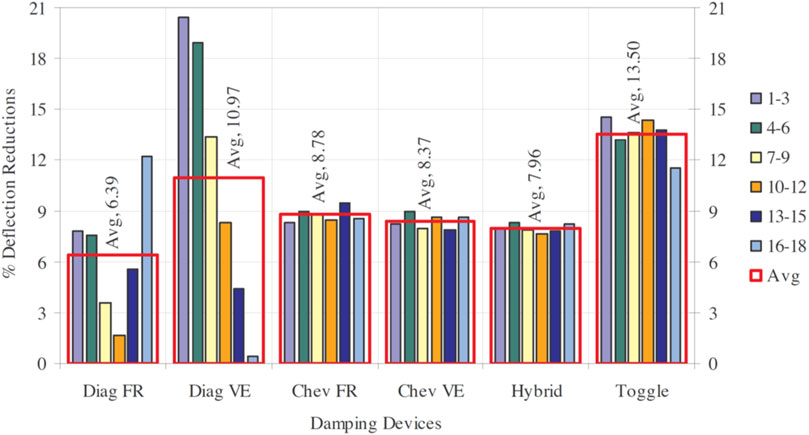
Figure 11. Average percentage deflection reductions for six different damper placements in six damping systems in 18-story structure (Marko et al., 2006).

Figure 12

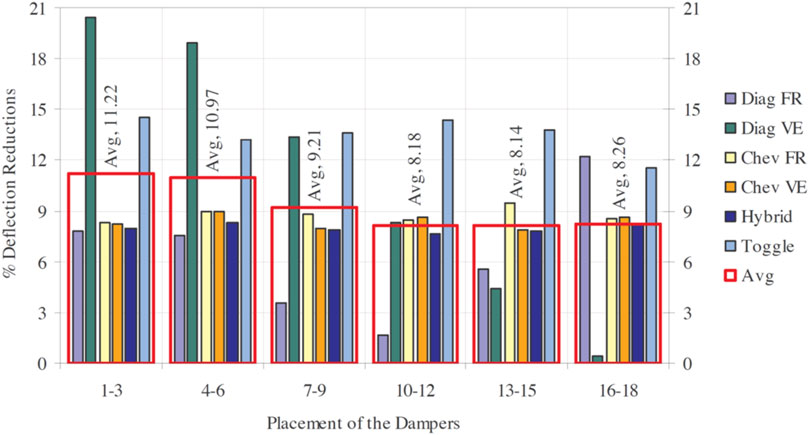
Figure 12. Average percentage deflection reductions for six damping systems in six different damper placements in 18-story structure (Marko et al., 2006).

Figure 13 presents the damping distributions by five approaches for a regular building and an irregular building (Whittle et al., 2012; 2013). Figure 14A illustrates the median of peak interstory drifts of the regular building under design basis earthquakes and the maximum considered earthquake (Whittle et al., 2012; 2013). On the other hand, Figure 14B indicates the median of peak interstory drifts of the irregular building under design basis earthquakes and the maximum considered earthquake (Whittle et al., 2012; 2013). It can be observed that the excessive interstory drifts in upper stories of the irregular building are controlled effectively by the passive dampers.

Figure 13

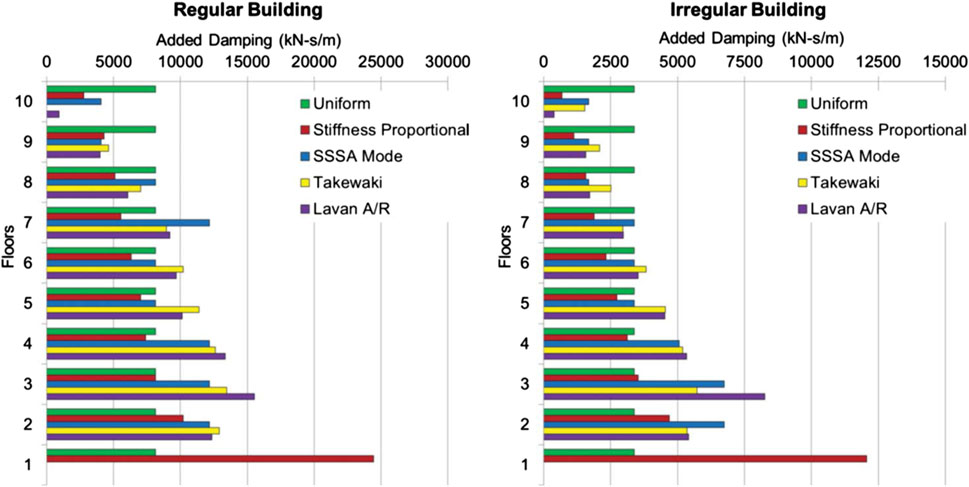
Figure 13. Damping distributions for regular building and irregular building (Whittle et al., 2012; 2013).

Figure 14

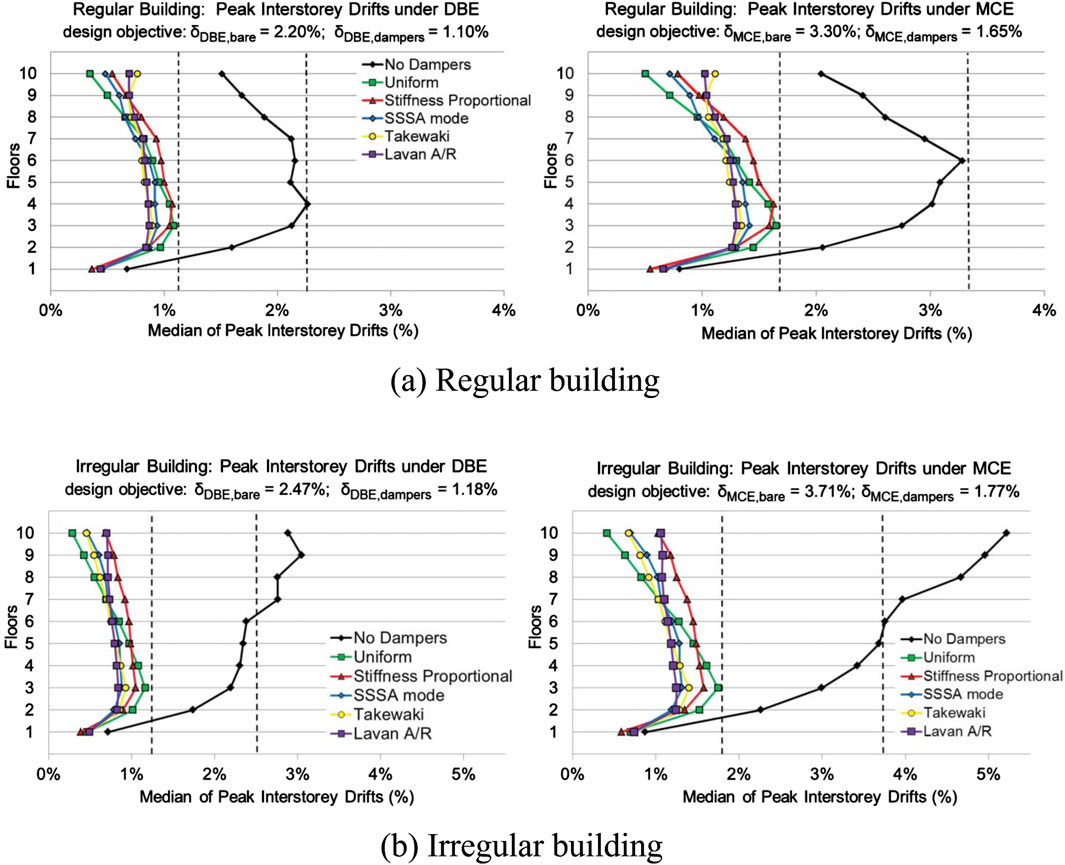
Figure 14. Median of peak interstory drifts of regular and irregular buildings under design basis earthquakes and maximum considered earthquake, (A) Regular building, (B) Irregular building (Whittle et al., 2012; 2013).

Figure 15 shows the comparative performance histograms of design methodologies of fluid viscous dampers (Uniform distribution, SSPD, SSSE, SSSEES, SPD, FEI/Filtered Energy Index) for three input motions, i.e., a) firm soil; b) soft soil; c) white-noise seismic input (De Domenico et al., 2019).

Figure 15

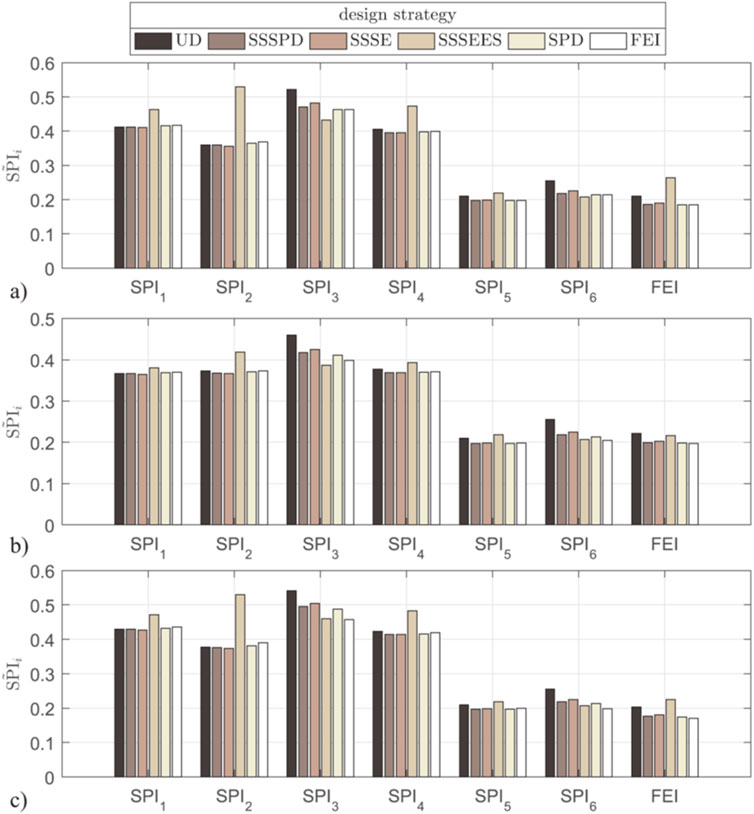
Figure 15. Comparative performance histograms of design methodologies of fluid viscous dampers: (A) firm soil; (B) soft soil; (C) white-noise seismic input (De Domenico et al., 2019) (SSSPD should be read as SSPD).

Akehashi and Takewaki (2020a) compared the optimization results between the transfer function method and the double impulse method.

Del Gobbo et al. (2020) compared six damper placement methods by paying attention to the condition that the total repair cost is limited. They demonstrated that the iterative methods can provide a greater total damping coefficient to the structures than the simple methods. This leads to a higher supplemental damping ratio and lower repair costs. They also showed that, if upfront funds are limited, or if architectural constraints prevent the placement of dampers in lower stories, then iterative methods provide the most favorable total-building seismic performance.

Damper optimization based on machine learning

Recently, machine learning is used extensively in the damper optimization following the advancement of computer technologies and neural-network sophisticated development. The following is some examples of recent development.

Li and Zhao (2019) developed machine learning methods using Support Vector Machine and Multilayer Perceptron to analyze the optimal damper distribution. For different building structures, a genetic algorithm-based optimization method was applied to determine optimal damper distributions that are used as training samples. The structural features, the objective function, the number of dampers, etc., were input features, and the distribution of dampers was taken as an output result.

Fang et al. (2022) proposed a general optimization framework for the optimal design of multi-parameter hybrid braced structures. The framework consists of selecting optimization parameters, establishing sample database, formulating machine learning strategy, conducting automatic design and cost calculation, and optimizing the multi-objective problem through the genetic algorithm.

Bekdaş and Nigdeli (2022) edited a book which summarizes the latest developments in the optimization of tuned mass dampers covering all classical approaches and new trends including metaheuristic algorithms. Artificial intelligence and machine learning methods were also included to reach optimum results by skipping long optimization processes.

Yang et al. (2023) proposed a method including two machine learning-based algorithms to optimize the natural frequency and damping ratio of a tuned-mass-damper (TMD) device for seismically excited building. The first algorithm represents the single-objective optimization of TMD parameters in a linear building structure based on physics-enhanced generative and adversarial network architecture. The second physics-enhanced machine learning algorithm was used for the multi-objective optimization of a TMD parameters in a nonlinear building structure under various seismic excitations.

Fu et al. (2024) proposed a machine learning-based hybrid optimization method where tuned mass dampers were optimized considering soil-structure interaction. A total of 200,000 time history analyses of the tuned mass damper-structure-soil system were conducted and the results were used to construct the database of six machine learning models. Three meta-heuristic algorithms were used for optimization.

Advantages and shortcomings of combined optimization methods

Although there are various advantages and shortcomings in the combined optimization methods, the principal ones are as follows.

The combined methods can broaden the degree of design spaces. For example, the combination of global-local search algorithms can reach a better optimal design with efficiency. On the other hand, too complicated algorithms may disturb the usage of the algorithms for practitioners who prefer simple ones. However, it is also true that the combination of some algorithms is inevitable to construct an optimization method which is robust for external disturbances.

As for other characteristics of various damper optimization algorithms, the readers can find something else in the review by Kookalani et al. (2021).

Conclusion

The optimization algorithms of passive dampers were classified in view of the types of mixture of algorithms. Six component algorithms were identified, i.e., (a) Evolutionary, (b) Heuristic, (c) Meta-heuristic, (d) Optimality criteria, (e) Sensitivity-based, (f) Input uncertainty. Then, the mixture of these component algorithms was discussed.

The first one is the sequential search algorithm (SSA) and its derivatives (evolutionary, heuristic). The second one is the optimality criteria method including the incremental inverse problem approach (OCIIP) or redesign approach (OCR) (analytical, sensitivity-based, evolutionary). The third one is the global-local hybrid search method (GLHS) (meta-heuristic, sensitivity-based, evolutionary). The fourth one is the steepest direction search method (SDS) and its derivatives such as mathematical programming (evolutionary, sensitivity-based). Except these four categories, the approach considering input uncertainty was discussed.

Finally, several researches focused on comparison among different optimization methods were discussed.

It is desired that the present review in terms of mixture types of algorithms will lead to a finding of new innovative approaches to more reliable and robust methods of damper optimization.

Author contributions

IT: Writing–original draft, Writing–review and editing.

Funding

The author(s) declare that no financial support was received for the research, authorship, and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adachi, F., Yoshitomi, S., Tsuji, M., and Takewaki, I. (2013). Nonlinear optimal oil damper design in seismically controlled multi-story building frame. Soil Dyn. Earthq. Eng. 44 (1), 1–13. doi:10.1016/j.soildyn.2012.08.010