Simplified design method for geocell-stabilized unpaved roads on weak subgrade

Geocells have been successfully used to stabilize granular bases for unpaved roads over weak subgrade subjected to traffic loading. Unfortunately, no well-accepted design method is available in the literature. This paper presents the development of a simplified design method for this application by modifying the simplified design method available for the geogrid-stabilized bases over weak subgrade. This design method was calibrated based on the test results from the large-scale cyclic plate loading tests and the moving wheel tests on geocell-stabilized granular bases over weak subgrade. The California Bearing Ratios of the subgrade and base course, the number loading cycles or wheel passes required for 50–75 mm permanent deformation, the height of geocell, and the thickness of the base course were the variables used for the calibration. The calibrated design method was used to verify the test results and yielded a good comparison. In addition, a design example is presented to illustrate how this method can be used in practice.

Introduction

An estimated 80% of all roads in the world are unpaved and a majority of them are low volume (Tingle and Jersey, 2007). While limited resources are available for repair, maintenance, and rehabilitation of low-volume roads, a sustainable option to overcome this problem is to develop an innovative stabilization technique with a sustainable solution that improves the overall structural capacity, reduces operational costs, and minimizes maintenance requirements. Geosynthetics are one of the established techniques of subgrade improvement and base stabilization for over 50 years (Giroud et al., 2023).

Since the 1970s, geosynthetics, mostly planar reinforcement (such as geogrid and woven geotextile), have been used to improve the performance of both paved and unpaved roads. For these applications, geosynthetic sheets are placed at the subgrade-base interface or within the base course to increase bearing capacity of subgrade or provide confinement to base courses. Geocells, in a form of three-dimensional interconnected honeycomb polymeric cells, are ideal for soil confinement. Based on a comprehensive literature review by Yuu et al. (2008), theories and design methods are far behind the applications of geocells in the field, especially for roadway applications, due to a lack understanding of mechanisms and influencing factors for geocell confinement.

Since then, significant research has been conducted to improve the understanding of these aspects. For example, Pokharel et al. (2010) investigated the factors influencing behavior of single geocell-stabilized bases under static loading, including shape, type, embedment, height of geocells, and quality of infill materials, while Thakur et al. (2017) investigated the factors influencing permanent and resilient deformations of recycled asphalt pavement (RAP) bases under cyclic loading, including geocell confinement, base course thickness, base course strength, and subgrade strength. Pokharel et al. (2011) and Yang et al. (2012) performed accelerated pavement testing of geocell-stabilized unpaved roads over weak subgrade. Han et al. (2011) assessed the performance of geocell-stabilized RAP bases over weak subgrade under full-scale moving wheel loading while Thakur et al. (2012) assessed the performance of geocell-stabilized RAP bases over weak subgrade under cyclic plate loading. Pokharel et al. (2018) conducted experimental evaluation of geocell-stabilized bases under repeated loading. Rahman et al. (2021) explored the equivalency of geocell-stabilized aggregate base to non-stabilized aggregate base over weak subgrade under static loading. Krishna and Latha (2023) provided an updated review of the evolution of geocells as sustainable support to transportation infrastructure.

Giroud et al. (2023) provided detailed explanations of the mechanisms associated with geosynthetics (including geocells) in improving the performance of roads. Figure 1 illustrates the mechanisms associated with geocells in improving the performance of unpaved roads while Figure 2 shows the benefits of geocells in unpaved roads. Due to the three-dimensional configuration, geocells can provide lateral confinement to granular materials (Figure 1a), which is equivalent to an increased confining stress under a vertical load, leading to an apparent cohesion (Figure 2a) as explained by Rajagopal et al. (1999). Geocell-stabilized granular bases prevent slip surfaces from occurring within the base course (Figure 1b) so that the stabilized granular base has a higher bearing capacity and elastic modulus than the non-stabilized base (Figure 2b) as found by Han et al. (2008) and Pokharel et al. (2011). Due to the increased modulus of the geocell-stabilized base, it enhances stress distribution on the weak subgrade by increasing the distribution angle (Figure 1c) as found by Han et al. (2011) and Rahman et al. (2021). Thakur et al. (2013) also found that geocell lateral confinement significantly reduced creep deformations of RAP aggregates (Figure 2c). Figure 1d shows that a geocell-stabilized base can serve as a surcharge to provide vertical confinement of the subgrade so that its heave is minimized and its bearing capacity is increased. Figure 1e shows that the geocell-stabilized base behaves as a tensioned membrane or stiffened slab as observed by Thakur et al. (2012). Under cyclic or moving wheel loading, geocell confinement can minimize the accumulation of permanent deformations of unpaved road (Figure 2d) as observed in several experimental or field studies, for example, Han et al. (2011), Thakur et al. (2012), and Pokharel et al. (2018). Liu et al. (2020) showed that geocell confinement minimized the breakage of ballast particles under cyclic loading as illustrated from the particle size distribution curves in Figure 2e.

Figure 1

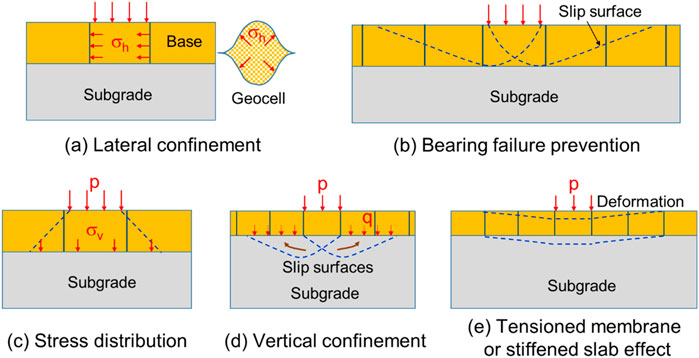
Figure 1. Mechanisms associated with geocell in improving unpaved roads. (a) Lateral confinement, (b) bearing failure prevention, (c) stress distribution, (d) vertical confinement, and (e) stiffened slab effect.

Figure 2

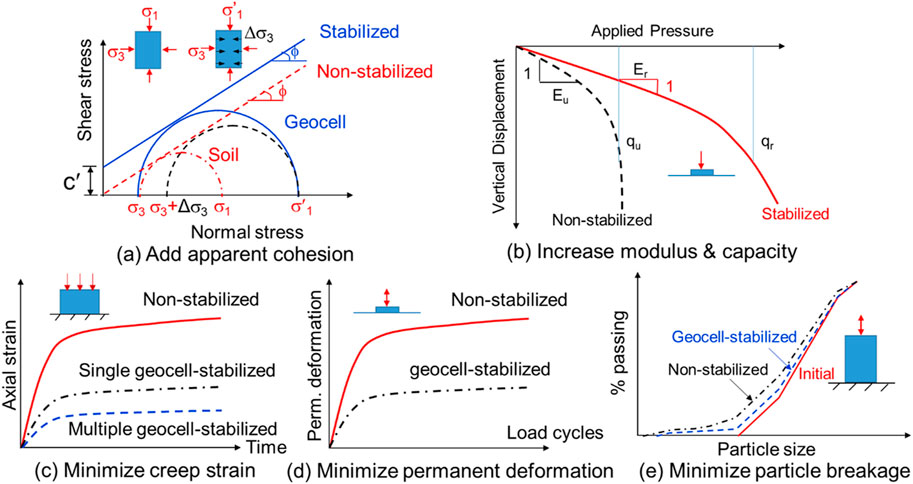
Figure 2. Benefits of geocell used in unpaved roads. (a) Add apparent cohesion, (b) increase modulus and capacity, (c) minimize creep strain, (d) minimize permanent deformation, and (e) Minimize particle breakage.

Even though significant advances have been made in the understanding of the mechanisms and benefits involving geosynthetics in unpaved roads in the past 2 decades, there is lack of well-accepted design methods for geocell-stabilized unpaved roads. Yang et al. (2013) proposed a three-dimensional mechanistic-empirical model for geocell-stabilized unpaved roads; however, this method requires three-dimensional numerical modeling and advanced testing for stress-dependent resilient modulus of granular base. As a result, this method is not well adopted in practice; therefore, a simplified method is needed.

Giroud and Han (2004) developed a simplified design method for geogrid-stabilized unpaved roads, which has been widely adopted in the practice. This method was developed based on the stress distribution angle from the base to the subgrade under static loading and then decreasing with the number of load cycles until reaching the bearing capacity of the subgrade. The benefits of a geogrid placed between an aggregate base and a weak subgrade are: (1) to increase the bearing capacity of the subgrade and (2) to reduce the rate of base deterioration, which slows down the reduction of stress distribution angle. Based on the test results in Gabr (2001), Giroud and Han (2004) established an empirical relationship between the reduction in the stress distribution angle due to base deterioration and the number of load cycles. Even though this method was developed for geogrid-stabilized unpaved roads, it can also be used for geotextile-stabilized unpaved roads (Giroud and Han, 2012) and has a generic formula as follows:

$h=\frac{\left\{0.868+\left(0.661-1.006{\mathrm{J}}^2\right){\left(\frac{r}{h}\right)}^{1.5}\right\}\log N}{\eta \left\{1+0.204\left[R_E-1\right]\right\}}\times \left(\sqrt{\frac{P}{\pi r^2\left(\frac{s}{f_s}\right)\left\{1-\xi \exp \left[-\omega {\left(\frac{r}{h}\right)}^n\right]\right\}{N}_c{c}_u}}-1\right)r(1)$

where η = the conversion factor between field and laboratory performance (0.689 for a laboratory condition under cyclic plate loading and 1.0 for a field condition under moving wheel loading); J = the aperture stability modulus, which is only suitable for geogrid and assumed to be 0 for non-stabilized and geotextile-stabilized roads); r = the radius of tire contact area (m); N = the number of passes or load cycles; P = the wheel load (kN); R_E = the modulus ratio of base to subgrade (limited to 5.0 for non-stabilized and planar geosynthetic-stabilized unpaved roads); c_u = undrained cohesion of the subgrade soil (kPa); ξ, ω, and n = the parameters determined as 0.9, 1.0, and 2.0, respectively; s = allowable rut depth (mm); f_s = the factor equal to 75 mm; and N_c is the bearing capacity factor (3.14 for non-stabilized roads, 5.71 for geogrid-stabilized roads, and 5.14 for geotextile-stabilized roads).

This method requires an important input parameter, J, the aperture stability modulus, which can be measured by the ASTM method for geogrids (ASTM, 2023). Giroud and Han (2012) suggested J = 0 for geotextiles. Unfortunately, the J value cannot be measured or determined for geocells; therefore, this method must be modified for geocells.

At the time of developing the simplified design method for geocell-stabilized unpaved roads over weak subgrade to be described later in this paper, there was limited research on this application. Experimental tests were needed to first understand geocell confinement mechanisms, and then steps were taken by modifying the Giroud and Han (2004) method using the test data to arrive at a reasonable design method for geocell-stabilized unpaved roads over weak subgrade. Pokharel (2010) explained the detailed procedure followed to establish this design method but a brief summary is provided herein. This research was started with single geocell-stabilized soil plate loading tests followed by multiple geocell tests under static loading to quantify modulus increase of base courses by geocell. Next step involved cyclic plate loading tests on base courses prepared on weak subgrade, followed by moving wheel tests under similar conditions. The Giroud and Han (2004) method started with a stress distribution angle under static loading, which is calculated based on the modulus ratio of base to subgrade under static loading. Then the distribution angle decreases with cyclic loading until subgrade bearing failure. The static plate loading tests were used to evaluate the modulus increase of base courses by geocell under static loading so that the modulus ratio of base to subgrade and the initial stress distribution angle under static loading could be calculated. The decrease of the stress distribution angle and the performance of unpaved roads were quantified by cyclic plate loading and moving wheel tests. Therefore, static and cyclic loading/moving wheel tests served different purposes during the development of this method. All the test data were used to determine a constant needed for geocell-stabilized bases as discussed later in this paper. This design method was verified at various road sections and validated in real projects by Pokharel et al. (2015).

Development of simplified design method for geocell-stabilized unpaved roads

As discussed above, Equation 1 was developed for geogrids and applicable to geotextiles, it needs to be modified for the design of three-dimensional geocell-stabilized unpaved roads. The reduction in the stress distribution angle with the number of load cycles was also observed in the testing of geocell-stabilized unpaved roads over weak subgrades (Pokharel, 2010; Thakur et al., 2012). Both studies show that geocells significantly slowed down the rate of deterioration in the base quality. This phenomenon is attributed to the geocell confinement of the base course to increase and maintain the modulus of the base course. A modulus improvement factor was proposed by Han et al. (2007) to account for the benefit of geocell confinement in the increased base modulus under static loading:

$I_f=\left(\frac{E_{bc\left(stabilized\right)}}{E_{bc\left(non-stabilized\right)}}\right)(2)$

where E_{bc (stabilized)} = the modulus of the stabilized base and E_{bc (non-stabilized)} = the modulus of the non-stabilized base.

The modulus ratio (R_E) given in Equation 1 was limited to a maximum limit of 5.0 for non-stabilized and planar geosynthetic-reinforced unpaved roads. Giroud and Han (2004) recommended this limit considering that base courses cannot be well compacted over soft subgrade. However, the three-dimensional confinement by geocells can overcome this problem and help the base course reach and maintain its higher modulus. Han et al. (2007) reported the geocell-stabilized bases had the modulus ratios ranging from 4.8 to 10.0. The calculated modulus ratios before cyclic plate loading tests and accelerated moving wheel tests in this study ranged from 3.4 to 7.6 and will be presented later in this paper. Therefore, it is reasonable to set the maximum limit of the modulus ratio to 7.6 for geocell-stabilized unpaved roads until more test data are available to justify a higher limit to be used. Considering the modulus improvement factor, the modulus ratio of the stabilized base to the subgrade can be modified from Giroud and Han (2004) as follows:

$R_E=I_f\frac{E_{bc}}{E_{sg}}=\mathit{Min}\left\{7.6,I_f\left(\frac{3.48CB{R}_{bc}^{0.3}}{CB{R}_{sg}}\right)\right\}(3)$

where E_bc = the resilient modulus of base course (MPa); E_sg = the resilient modulus of subgrade soil (MPa); CBR_bc = California Bearing Ratio (CBR) of base course; and CBR_sg = CBR of subgrade.

The bearing capacity mobilization coefficient (m) is given by Giroud and Han (2004) as follows:

$m=\left(\frac{s}{f_s}\right)\left\{1-0.9\exp \left[-{\left(\frac{r}{h}\right)}^2\right]\right\}=\left(\frac{s}{75mm}\right)\left\{1-0.9\exp \left[-{\left(\frac{r}{h}\right)}^2\right]\right\}(4)$

Since a nonwoven or woven geotextile sheet is commonly used below geocell-stabilized bases, the bearing capacity factor (N_c) for geocell-stabilized unpaved roads can be reasonably assumed to be equal to 5.14 (Giroud and Han, 2004).

Giroud and Han (2004) proposed a factor (k) that controls the rate of reduction in the stress distribution angle, which depends on the (r/h) ratio and the aperture stability modulus of a geogrid. Obviously, the aperture stability modulus is not suitable for geocells. A factor (k’) is proposed here to replace the term $\left(0.661-1.006J^2\right){\left(\frac{r}{h}\right)}^{1.5}$ in Equation 1 for the design of geocell-stabilized bases over weak subgrade as follows:

$h=\frac{\left(0.868+k^{\prime }\log N\right)}{\eta \left\{1+0.204\left(R_E-1\right)\right\}}\times \left(\sqrt{\frac{P}{\pi r^{2}m5.14c_u}}-1\right)r(5)$

The k’ factor will be calibrated in the next section using the data from the cyclic plate loading tests and the accelerated moving wheel tests in this study.

The undrained shear strength (c_u) is the property of subgrade soil and can be estimated by the following correlation:

$c_u=f_{c}CB{R}_{sg}(6)$

where ƒ_c = factor equal to 20.5 kPa for the subgrade used in the cyclic plate loading tests and 19.7 kPa in the moving wheel tests. The ƒ_c factors were obtained from the CBR tests and unconfined compression tests carried out on the subgrade materials, which were presented in Pokharel (2010).

Determination of k’ factor

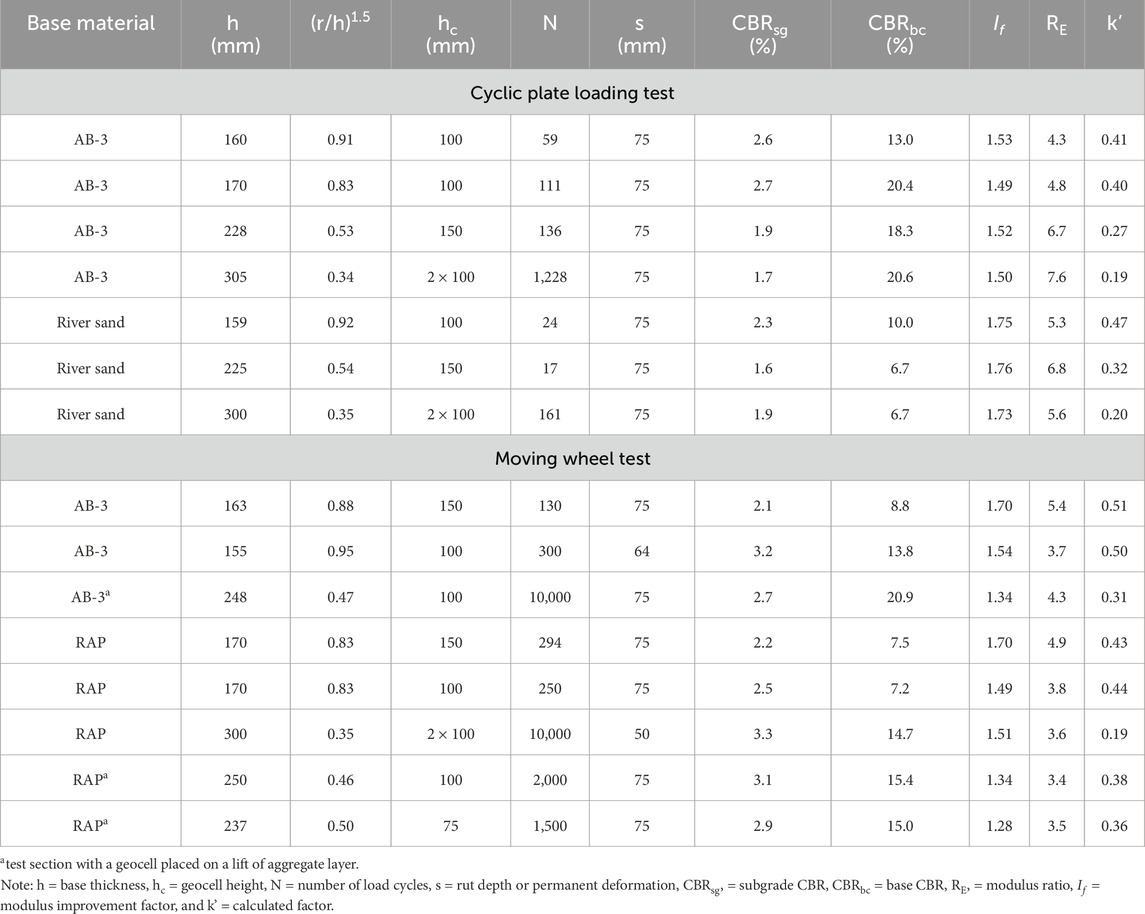
To determine the factor k’ in Equation 5, the data from the geocell-stabilized base tests, including seven cyclic plate loading tests in a large geotechnical box and eight moving wheel tests in a large test pit (Pokharel, 2010; Han et al., 2011; Pokharel et al., 2011) were used. The seven tests in the large box included four tests with an aggregate base (named AB-3 aggregate, commonly used in Kansas) and three tests with river sand base course materials while the eight moving wheel tests included three tests with a second aggregate base (AB-3 aggregate) and five tests with RAP base courses. The geocell used in this study was made of polymeric strips with a nano-composite alloy of polyester/polyamide nano-fibers, dispersed in polyethylene matrix. The novel polymeric alloy (NPA) is characterized by flexibility at low temperatures similar to HDPE with elastic behavior like engineering thermoplastic. The novel polymeric alloy geocell products, referred to as NPA geocells, have a lower thermal expansion coefficient and larger creep resistance, and higher tensile stiffness and strength than HDPE geocells. The geocell product used in this study had a tensile strength of 19.1 MPa and had two perforations of 100 mm² area each on each pallet. The heights of the geocells used in this study were 75, 100, and 150 mm. All geocells had wall thickness of 1.1 mm. The multiple geocell tests had a minimum of 13 cells in the medium size box. The big box contained a geocell panel with at least 127 cells while each section in the moving wheel tests had at least 216 cells. The frequency of cyclic loading was 0.77 Hz in the big box test while the frequency of moving wheel loading was 0.167 Hz (i.e., 6 s/pass). The wheels were run at a speed of 11.3 km/h.

The conversion factor (η) for the cyclic plate loading tests in the large box was taken as 0.689 as suggested by Giroud and Han (2004). Since the moving wheel tests are considered as field tests, a factor of 1.0 was assigned in the calculation.

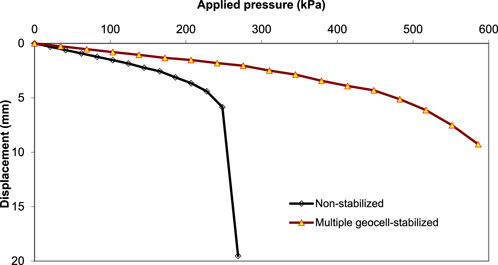
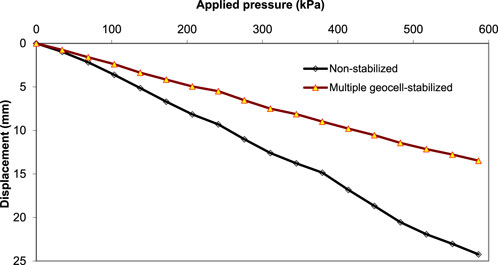
The modulus improvement factor (I_f) was calculated based on the static plate loading tests carried out on the medium-size geotechnical box with the procedures and equipment discussed in Pokharel (2010). The static plate loading tests with multiple geocells were carried out with AB-3, RAP and river sand materials separately and compared with the test with the same material under a non-stabilized condition. The respective stiffness values of non-stabilized and geocell-stabilized base courses were calculated to find the modulus improvement factor (I_f). Figure 3 presents the pressure-displacement curves from the static plate loading tests for river sand. Similarly Figures 4, 5 show the pressure-displacement curves for RAP and AB-3 bases, respectively. The ratio of the slope of the linear portion on the pressure-displacement curve of the stabilized section to that of the non-stabilized section was calculated as the modulus improvement factor ‘I_f’. The ‘I_f'’ values calculated from Figures 3–5 were 2.0 for river sand base courses and 1.7 for AB-3 and RAP base courses. These values are considered representative for all the river sand, AB-3, and RAP base courses and used in the calculation of k’. As these static tests were carried out with 20 mm cover over geocells, the modulus of the non-stabilized material was multiplied by ‘I_f’ for the thickness equal to the height of geocell plus 20 mm cover in each test stabilized section to estimate the modulus of the corresponding stabilized material. When the cover thickness was larger than 20 mm, the remaining cover thickness above 20 mm was considered as non-stabilized and no modulus improvement factor (i.e., I_f = 1.0) was applied. When the cover thickness was smaller than 20 mm (not recommended due to lack protection of geocell from wheel damage), the base course within the full thickness could be considered stabilized with the same I_f as the 20-mm cover. The final modulus was then calculated by taking the weighted average of the two values based on their thicknesses. For example, for a 230-mm thick RAP base section with a 150-mm high geocell, the modulus improvement factor can be calculated as follows: $I_f=\left[\frac{\left(150+20\right)\times 1.7+\left(230-150-20\right)\times 1.0}{230}\right]=1.52$.

Figure 3

Figure 3. Pressure-displacement curves of river sand under static loading.

Figure 4

Figure 4. Pressure-displacement curves of RAP under static loading.

Figure 5

Figure 5. Pressure-displacement curves of AB-3 aggregate under static loading.

The number of loading cycles (or passes in case of moving wheel tests) ‘N’ was directly obtained from the tests. The applied wheel load ‘P’ was 40 kN in all the tests and the radius of tire contact area (r) was 0.15 m. The CBR values of base and subgrade, CBR_bc and CBR_sg, were obtained from the Dynamic Cone Penetrometer (DCP) tests carried out on the test sections before cyclic loading or moving wheel tests. The ‘I_f’ factors and these CBR values used to calculate the modulus ratios ‘R_E’ in Equation 3 are reported in Table 1. It is shown that R_E ranged from 3.4 to 7.6. It should be noted here that most test sections had 50–80 mm thick well-graded aggregate material cover on top of the geocell. In case of the river sand as an infill material, the cover was AB-3 aggregate. There were three test sections with two layers of geocells labeled as 2 × 100 (i.e., each geocell height was 100 mm). For these test sections, the fill between two layers was within 20 mm thick; therefore, the combined thickness (the lower geocell layer + fill thickness + upper geocell layer +20 mm) could be taken as a composite single layer in the analysis.

Table 1

Table 1. Calculated k’ values based on test data.

The bearing capacity mobilization coefficient (m) was calculated using Equation 4. The allowable rut or permanent deformation (s) was taken as 75 mm, but in cases where the tests were stopped before reaching this limit the rut value at the final number of loading cycles (N) was taken as the final value of ‘s’. ‘c_u’ was calculated using Equation 6.

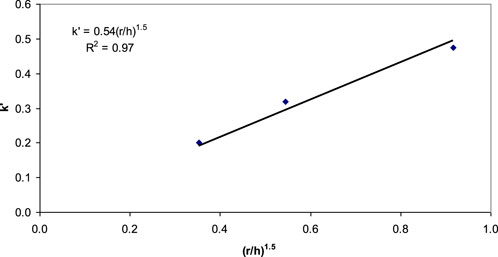
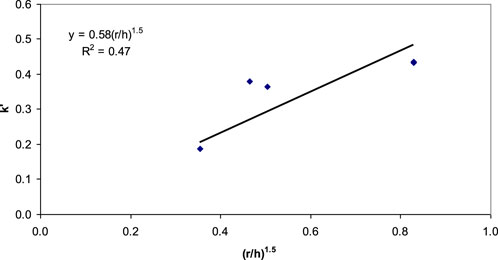
For all the fifteen geocell-stabilized tests with AB-3, RAP, and river sand, the values of k’ were calculated and provided in Table 1. The relationships between the calculated value of k’ and (r/h)^1.5 specifically for the river sand, RAP, and AB-3 base courses are given in Figures 6–8. A general relationship between the calculated value of k’ and (r/h)^1.5 for all types of granular base courses is given in Figure 9.

Figure 6

Figure 6. Relationship between k’ and (r/h)^1.5 for river sand base courses.

Figure 7

Figure 7. Relationship between k’ and (r/h)^1.5 for RAP base courses.

Figure 8

Figure 8. Relationship between k’ and (r/h)^1.5 for AB-3 base courses.

Figure 9

Figure 9. Relationship between k’ and (r/h)^1.5 for all granular base courses.

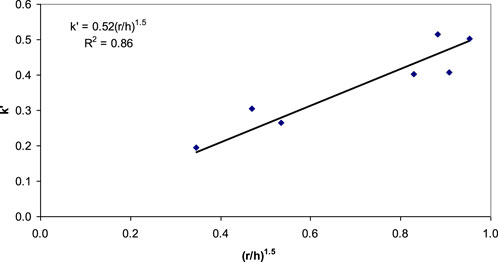
The relationship developed in Figure 9 includes two moving wheel test data using RAP and one using AB-3 that had different cross-sectional configurations from all the other tests. These three sections had a geocell placed on a lift of 100-mm thick aggregate. In other sections, however, geocells were placed above subgrade. The data from these three sections over-predicted the values of k’ as compared with all the other test sections. Therefore, further investigation to study the effect of geocell placement at different depths within the base courses is needed before including these three test data. After excluding these three sections, a generic relationship between k’ and (r/h)^1.5 for geocell-stabilized granular base courses with geocells placed above subgrade is plotted in Figure 10. A better correlation (R² = 0.94) is obtained.

Figure 10

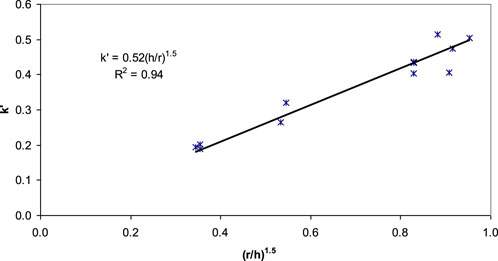
Figure 10. Generic relationship between k’ and (r/h)^1.5 for granular base courses stabilized with geocells above subgrade.

Therefore, the following generic formula is proposed to estimate k’ for geocell-stabilized granular bases over weak subgrade:

$k^{\prime }=0.52{\left[\frac{r}{h}\right]}^{1.5}(7)$

The formula to estimate the thickness of a geocell-reinforced base in field is as follows:

$h=\frac{\left(0.868+0.52{\left[\frac{r}{h}\right]}^{1·5}\log N\right)}{\left\{1+0.204\left(R_E-1\right)\right\}}\times \left(\sqrt{\frac{P}{\pi r^{2}m5.14c_u}}-1\right)r(8)$

It is important to point out that Equation 8 is only applicable to NPA geocell because the k’ value was obtained using NPA geocells. This k’ value may be different for other geocell products and should be calibrated using cyclic plate loading tests and/or moving wheel tests.

Comparison of calculated and measured base thicknesses

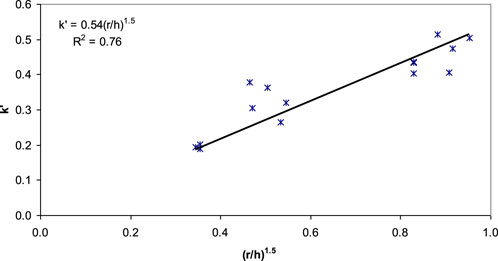
To verify the design formula presented in Equation 8, the actual base thicknesses (also referred as measured herein) are compared with the calculated ones in Figure 11. A good agreement (R² = 0.86) is obtained between the calculated and measured base thicknesses. This design method was also verified by Pokharel et al. (2015) and others in several field projects to be discussed later. For a demonstration purpose, Figure 12 shows the comparison of the calculated and measured base thicknesses with the three sections in which geocells were placed above 100 mm granular bases. This comparison clearly shows that a poorer correlation is obtained when the data of these three test sections are included. This demonstration shows that more research is needed to design geocell-stabilized bases over weak subgrade with geocell placed above granular materials.

Figure 11

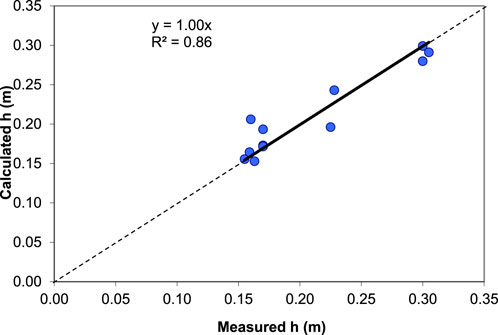
Figure 11. Comparison of the measured and calculated thicknesses of the base courses stabilized with geocells above subgrade.

Figure 12

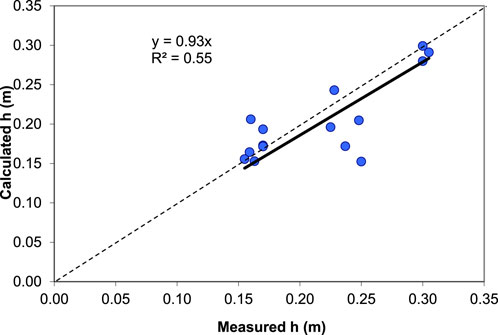
Figure 12. Comparison of the measured and calculated thicknesses of the base courses (all test sections included).

A separate check for the validity of Equation 1 for the design of non-stabilized sections was also made. The calculated and measured base thicknesses for the non-stabilized sections are plotted in Figure 13. Except for one test section, the plot shows a fair comparison between the measured and calculated base course thicknesses for the non-stabilized sections. The outlier point in the figure corresponds to a RAP control section of the moving wheel test with much better compaction.

Figure 13

Figure 13. Comparison of the measured and calculated thicknesses of non-stabilized base courses.

Design example

Design of a geocell-stabilized section

Based on the relationship given in Equation 8, a design example is worked out here to find the number of wheel passes for a 0.20-m thick unpaved AB-3 base course section stabilized with a 0.15-m high NPA geocell above a weak subgrade. The CBR values of the subgrade and the base course are 2% and 20%, respectively. The allowable rut is 75 mm. The design wheel load is 40 kN and the tire pressure is 552 kPa.

The radius of the equivalent tire contact area is:

$r={\left(\frac{P}{\pi p}\right)}^{0.5}={\left(\frac{40}{3.14\times 552}\right)}^{0·5}=0.15\mathrm{m}$

The modulus improvement factor (I_f) for AB-3 is 1.7 within the geocell and 20-mm cover and 1.0 for the remaining non-stabilized portion. The weighted average modulus improvement factor as explained above:

$I_f=\left[\frac{\left(150+20\right)\times 1.7+\left(200-150-20\right)\times 1.0}{200}\right]=1.59$

The conversion ƒ_c = 20.0 kPa is used here to estimate the undrained cohesion of the subgrade soil:

$c_u=f_{c}CB{R}_{sg}=20\times 2.0=40\text{\hspace{0.5em}kPa}$

The modulus ratio is:

$R_E=\mathit{Min}\left\{7.6,I_f\left(\frac{3.48CB{R}_{bc}^{0·3}}{CB{R}_{sg}}\right)\right\}=\mathit{Min}\left\{7.6,1.59\times \left(\frac{3.48\times {20}^{0·.3}}{2.0}\right)\right\}=6.81$

The bearing capacity mobilization coefficient is:

$\begin{array}{cc}\hfill m& =\frac{s}{75mm}\left\{1-0.9\exp \left[-{\left(\frac{r}{h}\right)}^2\right]\right\}\hfill \\ \hfill & =\frac{75}{75}\left\{1-0.9\exp \left[-{\left(\frac{0.15}{0.20}\right)}^2\right]\right\}=0.49\hfill \end{array}$

The factor k’ from Equation 7 is:

$k^{\prime }=0.52{\left[\frac{0.15}{0.20}\right]}^{1.5}=0.34$

Equation 8 is used to calculate the number of wheel passes:

$h=\frac{\left(0.868+k^{\prime }\log N\right)}{\eta \left\{1+0.204\left(R_E-1\right)\right\}}\times \left(\sqrt{\frac{P}{\pi r^{2}m5.14c_u}}-1\right)r$

$0.20=\frac{\left(0.868+0.34\times \log N\right)}{1\times \left\{1+0.204\left(6.81-1\right)\right\}}\times \left(\sqrt{\frac{40}{\pi {0.15}^2\times 0.49\times 5.14\times 40}}-1\right)\times 0.15$

$N=5500\text{\hspace{0.17em}cycles}.$

Design of non-stabilized section

The required thickness of a non-stabilized section corresponding to N = 5,500 passes for the geocell-stabilized section designed can be determined using Equation 1 developed by Giroud and Han (2004). For the non-stabilized section,

$I_f=1$

$R_E=1\times \left(\frac{3.48\times CB{R}_{bc}^{0.3}}{CB{R}_{sg}}\right)=\frac{3.48\times {20}^{0.3}}{2.0}=4.27$

$m=\frac{s}{75mm}\left\{1-0.9\exp \left[-{\left(\frac{r}{h}\right)}^2\right]\right\}=1-0.9\exp \left[-{\left(\frac{0.15}{h}\right)}^2\right]$

The equation for the non-stabilized case is:

$h=\frac{\left(0.868+0.661{\left(\frac{r}{h}\right)}^{1·5}\log N\right)}{\eta \left\{1+0.204\left(R_E-1\right)\right\}}\times \left(\sqrt{\frac{P}{\pi r^{2}m3.14c_u}}-1\right)r$

$\begin{array}{ll}\hfill h& =\frac{\left(0.868+0.661{\left(\frac{0.15}{h}\right)}^{1.5}\log 5500\right)}{1\times \left\{1+0.204\left(4.27-1\right)\right\}}\times \left(\sqrt{\frac{40}{\pi {0.15}^2\times \left[1-0.9{\mathrm{e}}^{-{\left(\frac{0.15}{h}\right)}^2}\right]\times 3.14\times 40}}-1\right)\hfill \\ \hfill & \times 0.15\hfill \end{array}$

$h=\frac{\left(0.868+2.47{\left(\frac{0.15}{h}\right)}^{1.5}\right)}{1.67}\times \left[\sqrt{\frac{4.57}{1-0.9{\mathrm{e}}^{-{\left(\frac{0.15}{h}\right)}^2}}}-1\right]\times 0.15$

Assume h = 0.46 m,

$h=\frac{\left(0.868+2.47{\left(\frac{0.15}{0.46}\right)}^{1.5}\right)}{1.67}\times \left[\sqrt{\frac{4.57}{\left[1-0.9{\mathrm{e}}^{\left[-{\left(\frac{0.15}{0.46}\right)}^2\right]}\right]}}-1\right]\times 0.15=0.46\mathrm{m}$

Therefore, the required thickness of the non-stabilized section is 0.46 m. There is a saving of 0.26 m AB-3 base course when a 0.15-m high NPA geocell is used in a 0.20-m thick AB-3 base course.

Han and Giroud (2012) suggested that a chart developed by the Hammitt (1970) should be used to assess the suitability of a base course for traffic on unpaved roads in terms of its strength expressed as a CBR value. An estimation of the coverages (i.e., passes) based on this design chart for the non-stabilized unpaved road section with a 20% CBR base shows more than 10,000 wheel passes of a 40-kN equivalent single-wheel load and 552 kPa tire pressure. The number of passes is much higher than that used in the design example; therefore, the base course is strong enough to sustain the traffic loading.

Applications and limitations of the design method

This method was first presented in the Ph.D. dissertation by Pokharel (2010) under the supervision of the first author. It has been used to design more than 200 NPA Geocell-stabilized roads (ranging from 100 m to 13 km) and pads that are in operation. Some of these applications have been documents in recent conference papers. For example, Yii et al. (2021) reported an unpaved access road utilizing polymeric geocell reinforcement over high water bearing muskeg, which leads to a Buffalo creek compressor station in Alberta, Canada. This 11.5-km road is still in good condition after 6 years of operation. Pokharel and Breault (2021) reported a 350-m long chip sealed gravel road designed using this method at Mitchel Beach, Alberta, Canada, which was problematic with a high water table and high maintenance cost before but has been maintenance free in the past 10 years Chatterjee et al. (2022) reported a 4.1-km long unpaved access road leading to a proposed compressor station in Blainville, Quebec, Canada for the construction of the station pad and future access.

The simplified design method presented herein for geocell-stabilized unpaved roads is generic as developed by Giroud and Han (2004) for geogrid and geotextile-stabilized unpaved roads on weak subgrade. It has some limitations due to the limited test conditions:

1. The I_f in Equation 2 and k’ value in Equation 7 were back-calculated against NPA geocell-stabilized base courses over weak subgrade; therefore, it is only applicable to NPA geocells. The back-calculation was performed based on unpaved road sections stabilized with a single layer of 75, 100, or 150-mm high geocell or double layers of two 100-mm high geocells. All the geocells were laid out in a near circular shape with the seam side of 250-mm long and the transverse side of 210-mm wide.

2. Equation 8 was developed based on the condition, in which geocells were placed directly above subgrade. Future research is needed for geocells placed at other locations.

3. All the tests in the large geotechnical box and the accelerated moving wheel facility were conducted with the standard highway traffic wheel load of 40 kN and tire pressure of 552 kPa.

4. The test data used for the back-calculation for the design method were based on the subgrade CBR values ranging from 1.7% to 3.3% and the base CBR values ranging from 7% to 21%. The subgrade used in this study had the conversion factor ƒ_c = 20 kPa between the undrained shear strength and the CBR value. Different conversion factors may exist for different subgrade.

5. Equation 8 was developed with base course thicknesses ranging from 150 mm to 300 mm.

6. Based on the present study, 20 mm is the minimum cover thickness required for this application. However, a 50–75 mm thick well-graded aggregate cover is recommended to minimize the damage of the geocell by moving wheels.

7. The value k’ was back-calculated for rut depths between 50 and 75 mm.

8. The number of loading cycles or passes used in the back-calculation ranged from 17 to 10,000.

This design method should be verified for conditions beyond the limits at which this study was carried out.

Summary

The design method developed in this paper derives its theoretical basis from Giroud and Han (2004). The factor (k’) for considering the stress distribution angle reduction rate depends on subgrade, granular base, and geocell was back-calculated based on the data from large-scale laboratory cyclic plate loading tests and full-scale moving wheel tests with NPA geocell-stabilized granular bases over weak subgrade. The design formula was verified by the test data and field studies. The design methodology is generic; however, the modulus improvement factors I_f and the distribution angle reduction factor k’ obtained in this study were based on NPA geocells. Calibrations are necessary if other geocell products are used.

An example was presented to demonstrate how to use this simplified method to design geocell-stabilized bases over weak subgrade. The design example demonstrated the benefit of geocell confinement in the reduction in base course thickness.

The limitations of the design method were discussed, which require further verifications of this design method if field conditions deviate from the test sections.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

JH: Conceptualization, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Supervision, Writing – original draft, Writing – review and editing. SP: Data curation, Formal Analysis, Investigation, Methodology, Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was jointly funded by the University of Kansas, Transportation Research Institute from Grant #DT0S59-06-G-00047, provided by the U.S. Department of Transportation - Research and Innovative Technology Administration and PRS Mediterranean, Inc. in Israel. The funders were not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Author SP was employed by company Stratum Logics Inc.

The remaining author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Author JH declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

ASTM (2023). ASTM D7864/D7864M-15 standard test method for determining the aperture stability modulus of geogrids. America. West Conshohocken, PA: American Society for Testing and Materials (ASTM) International.

Google Scholar

Chatterjee, A., Pokharel, S., and Breault, M. (2022). “Staged road construction in very weak subgrade using polymeric geocell,” in Innovations in Pavement Management, Engineering and Technologies TAC Conference & Exhibition 2022.

Google Scholar

Gabr, M. (2001). Cyclic Plate loading tests on geogrid reinforced roads. Research report to tensar earth technologies. Raleigh, NC: Inc., NC State University, 43.

Google Scholar

Giroud, J. P., and Han, J. (2004). Design method for geogrid-reinforced unpaved roads – Part I: development of Design Method. ASCE J. Geotech. Geoenviron. Eng. 130 (8), 776–786. doi:10.1061/(ASCE)1090-0241(2004)130:8(775)

CrossRef Full Text | Google Scholar

Giroud, J. P., and Han, J. (2012). The Giroud-Han design method for geosynthetic-reinforced unpaved roads. Part I. The method development and its calibration. Geosynthetics 30 (1), 40–49.

Google Scholar

Giroud, J. P., Han, J., Tutumluer, E., and Dobie, M. (2023). The use of geosynthetics in roads. Geosynth. Int. 30 (1), 47–80. doi:10.1680/jgein.21.00046

CrossRef Full Text | Google Scholar

Hammitt, G. M. (1970). Thickness requirements for unsurfaced roads and airfields: bare base support, project 3782-65. Vicksburg, MS: U.S. Army Engineer Waterways Experiment Station, CE, Vicksburg, Miss. Technical Report S-70-5.

Google Scholar

Han, J., and Giroud, J. P. (2012). The Giroud-Han design method for geosynthetic-reinforced unpaved roads. Part II Recommendations for the proper use of the method. Geosynthetics 30 (2), 44–52.

Google Scholar

Han, J., Pokharel, S. K., Yang, X., Manandhar, C., Leshchinsky, D., Halahmi, I., et al. (2011). Performance of geocell-reinforced RAP bases over weak subgrade under full-scale moving wheel loads. J. Mater. Civ. Eng. 23 (11), 1525–1534. doi:10.1061/(asce)mt.1943-5533.0000286

CrossRef Full Text | Google Scholar

Han, J., Yang, X., Parsons, R. L., and Leshchinsky, D. (2007). Design of geocell-reinforced bases. Internal report to PRS. Lawrence, KS: The University of Kansas.

Google Scholar

Han, J., Yang, X. M., Leshchinsky, D., and Parsons, R. L. (2008). Behavior of geocell-reinforced sand under a vertical load. J. Transp. Res. Board 2045, 95–101. doi:10.3141/2045-11

CrossRef Full Text | Google Scholar

Krishna, A., and Latha, G. M. (2023). Evolution of geocells as sustainable support to transportation infrastructure. Sustainability 15 (15), 11773. doi:10.3390/su151511773

CrossRef Full Text | Google Scholar

Liu, Y., Deng, A., and Jaksa, M. (2020). Three-dimensional discrete-element modeling of geocell-reinforced ballast considering breakage. Int. J. Geomech. 20 (4), 04020032. doi:10.1061/(asce)gm.1943-5622.0001552

CrossRef Full Text | Google Scholar

Pokharel, S. (2010). “Experimental study on geocell-reinforced bases under static and dynamic loading. Lawrence, KS: The University of Kansas, 316p. Ph.D. dissertation.

Google Scholar

Pokharel, S., and Breault, M. (2021). Polymeric Geocell-reinforced gravel base course for chip seal surfaced low volume road. GeoNiagara 2021.

Google Scholar

Pokharel, S., Han, J., Leshchinsky, D., and Parsons, R. L. (2018). Experimental evaluation of geocell-reinforced bases under repeated loading. Int. J. Pavement Res. Technol. 11 (2), 114–127. doi:10.1016/j.ijprt.2017.03.007

CrossRef Full Text | Google Scholar

Pokharel, S., Han, J., Leshchinsky, D., Parsons, R. L., and Halahmi, I. (2010). Investigation of factors influencing behavior of single geocell-reinforced bases under static loading. Geotext. Geomembr. 28 (6), 570–578. doi:10.1016/j.geotexmem.2010.06.002

CrossRef Full Text | Google Scholar

Pokharel, S. K., Han, J., Manandhar, C., Yang, X. M., Leshchinsky, D., Halahmi, I., et al. (2011). “Accelerated pavement testing of geocell-reinforced unpaved roads over weak subgrade”. Transp. Res. Rec. J. Transp. Res. Board Vol. 2, 67–75. doi:10.3141/2204-09

CrossRef Full Text | Google Scholar

Pokharel, S. K., Martin, I., Norouzi, M., and Breault, M. (2015). “Validation of geocell design for unpaved roads,” in Geosynthetics, Portland, Oregon, February 15-18, 2015.

Google Scholar

Rahman, M. R., Jawad, S., and Han, J. (2021). “Equivalency of geocell-stabilized aggregate base to non-stabilized aggregate base over weak subgrade under static loading,” in Proceedings of International Foundations Conference and Equipment Expo, Dallas, Texas, May 10-14, 530–540. doi:10.1061/9780784483411.050

CrossRef Full Text | Google Scholar

Rajagopal, K., Krishnaswamy, N. R., and Latha, G. M. (1999). Behaviour of sand confined with single and multiple geocells. Geotext. Geomembr. 17 (3), 171–184. doi:10.1016/s0266-1144(98)00034-x

CrossRef Full Text | Google Scholar

Thakur, J. K., Han, J., and Parsons, R. L. (2013). Creep behavior of geocell-reinforced recycled asphalt pavement (RAP) bases. ASCE J. Mater. Civ. Eng. 25 (10), 1533–1543. doi:10.1061/(ASCE)MT.1943-5533.0000705

CrossRef Full Text | Google Scholar

Thakur, J. K., Han, J., and Parsons, R. L. (2017). Factors influencing deformations of geocell-reinforced recycled asphalt pavement (RAP) bases under cyclic loading. ASCE J. Mater. Civ. Eng., 04016240. doi:10.1061/(ASCE)MT.1943-5533.0001760

CrossRef Full Text | Google Scholar

Thakur, J. K., Han, J., Pokharel, S. K., and Parsons, R. L. (2012). Performance of geocell-reinforced recycled asphalt pavement (RAP) bases over weak subgrade under cyclic plate loading. Geotext. Geomembr. 35, 14–24. doi:10.1016/j.geotexmem.2012.06.004

CrossRef Full Text | Google Scholar

Tingle, J. S., and Jersey, S. R. (2007). Empirical design methods for geosynthetic-reinforced low-volume roads. J. Transp. Res. Board 1989 (2), 91–101. doi:10.3141/1989-52

CrossRef Full Text | Google Scholar

Yang, X., Han, J., Leshchinsky, D., and Parsons, R. L. (2013). A three-dimensional mechanistic-empirical model for geocell-reinforced unpaved roads. Acta Geotech. 8 (2), 201–213. doi:10.1007/s11440-012-0183-6

CrossRef Full Text | Google Scholar

Yang, X., Han, J., Pokharel, S. K., Manandhar, C., Parsons, R. L., Leshchinsky, D., et al. (2012). Accelerated pavement testing of unpaved roads with geocell-reinforced sand bases. Geotext. Geomembr. 32, 95–103. doi:10.1016/j.geotexmem.2011.10.004

CrossRef Full Text | Google Scholar

Yii, T., Pokharel, S., Ali, M., and Breault, M. (2021). Unpaved access road utilizing polymeric geocell reinforcement over high water bearing muskeg. IFAI (ATA) Geosynth. Conf., 2021.

Google Scholar

Yuu, J., Han, J., Rosen, A., Parsons, R. L., and Leshchinsky, D. (2008). “Technical review of geocell-reinforced base courses over weak subgrade,” in Proceedings of the First Pan American Geosynthetics Conference and Exhibition, Cancún, Mexico, 2–5, March 2008, 1022–1030.

Google Scholar