Research on a risk assessment model for dense urban cable channels based on fuzzy mathematics

With the acceleration of urbanization, the safe and stable operation of dense urban cable channels is of great importance to the guarantee of urban power and communication systems. Cable channels face many sources of risk that bring great challenges to urban power supplies. Most existing risk assessment methods are based on accurate mathematical models, which require clear and deterministic boundaries of assessment indicators. These methods have difficulty in dealing with the fuzziness and uncertainty of cable channel risk factors, such as the challenge of determining the degree of aging of cable insulation or the degree of influence of external environmental factors that cannot be simply quantified. This paper presents a risk assessment model of a dense urban cable passage based on fuzzy mathematics. The model combines a membership function with a fuzzy comprehensive evaluation method to analyze and classify the risk factors of a dense urban cable passage. Eight risk factors were identified, including external damage, facility defects, and non-standard cable laying, and the importance of each factor was evaluated by constructing a membership matrix based on historical data and expert scoring methods. A typical dense cable trench and cable tunnel in actual operation in a region of China Southern Power Grid are analyzed, and the risk level is calculated by MATLAB 2021a programming. The results show that the model can effectively assess the level of risk and clearly show the impact of individual risk factors on the overall risk. For example, in the cable trench risk assessment, the model accurately identifies that external damage and cable overheating risk factors lead to moderate risk, and the remaining six factors are low risk. In the cable tunnel assessment, the corresponding risk level of each risk factor is also accurately determined. This indicates that the evaluation method based on fuzzy mathematics can not only quantify the uncertainty of risk factors but also improve the rationality of the evaluation results and provide a scientific decision basis for the safety management and maintenance of cable channels. The model has significant advantages over traditional evaluation methods.

1 Introduction

As an important infrastructure for urban power transmission, the safe and stable operation of dense urban cable channels is crucial to ensure the normal production and living order of cities (Kim et al., 2007; Liu J. et al., 2024; Liu F. et al., 2024). However, due to the complex and changeable environment and the influence of natural factors, human factors, and the equipment itself, cable channel failures occur from time to time, which bring great challenges to the urban power supply (Li et al., 2018; Zhang et al., 2023; Gilany et al., 2006; Das and Reddy, 2023).

In developed countries in Europe and in the United States, research on cable risk assessment started earlier and invested substantial human, material, and financial resources. It relied on the scientific research strength of universities and research institutions to carry out in-depth theoretical research. From the early construction of a simple risk assessment model based on probability theory and reliability theory, it has gradually developed to the integration of multidisciplinary knowledge and the introduction of artificial intelligence, machine learning, and other cutting-edge technologies to dynamically and accurately assess the risk of cable systems under complex working conditions. In contrast, although research in the field of cable risk assessment within China started a little later, it has developed rapidly in recent years. Universities and research institutes have gradually become the main force of research, focusing on cable aging mechanisms, fault diagnosis methods, risk assessment model construction, and other key issues to carry out in-depth research. Many Chinese universities have combined the operating conditions of China’s complex cable environment with a variety of traditional risk assessment methods.

Traditional risk assessment methods have many limitations when facing such a complex system as a dense urban cable channel. Chen et al. (2021) propose a fire risk analysis model in hybrid Bayesian networks to study the evolution of early cable fire risk induced by overloading, which can effectively assess the state of cables, explain the causes of fire risk, and can be used for early warning of fire. Zhu et al. (2024) propose a quantitative risk assessment method for fire in integrated cable corridors, which can identify the key hazards associated with fire in integrated cable corridors. Bai et al. (2024) proposed an energy-based coupled risk assessment model for urban underground integrated pipe corridors that can systematically identify interaction hazards and coupled accidents in integrated pipe corridors by introducing energy transfer and runaway theories. Lou et al. (2024) summarize the current plugging methods used for coalbed methane extraction boreholes, analyze the existing problems, and propose strategies to improve the plugging effect. Lou et al. (2025) developed a new type of dynamic fill material to solve the problem of crack sealing around boreholes for underground coal seam gas extraction. Dindar et al. (2018) summarized risk analysis techniques for railway switch systems, emphasizing the importance of identifying multidisciplinary risk analysis methods suitable for complex systems. By comparing and analyzing the existing methods, a comprehensive method suitable for railway switch systems is proposed. The study shows that the rail industry needs to pay special attention to monitoring and managing interconnected risks to improve public safety and operational reliability. The systematic thinking and diversified risk analysis methods proposed in this paper provide valuable guidance for risk management in the railway industry. Wang et al. (2024) used a multivariate linear regression model to detect the correlation between air pollution and α-synuclein levels in cerebrospinal fluid that can provide a reference for constructing cable channel monitoring signals and risk status.

Most of these methods are based on exact mathematical models, which require the assessment indicators to have clear boundaries and certainty; however, the cable passageway risk factors have strong ambiguity and uncertainty. Specifically, the degree of cable insulation aging is difficult to define with a precise value. Insulation aging is affected by a combination of factors, and different experts and operators have different judgment standards. In addition, the degree of influence of external environmental factors on the cable cannot be accurately measured by using quantitative data.

The emergence of fuzzy mathematics theory provides an effective way to solve this dilemma. Fuzzy mathematics can deal well with problems with vagueness and uncertainty by introducing the subordinate function and transforming fuzzy concepts into quantitative descriptions (Zhao et al., 2024; Xiong et al., 2024; Zeng et al., 2024; Khan et al., 2024). Applied to the field of risk assessment of dense urban cable channels, it can fully consider the fuzzy characteristics of various risk factors, synthesize the subjective opinions of different evaluators, and make the results of risk assessment more aligned with the actual situation to provide a more reliable basis for the maintenance and management decisions of the cable channels and guarantee the stable operation of the city’s electric power and communication systems (Ji et al., 2024; Ma et al., 2024; Qin et al., 2024; Jia, 2023).

Li (2019) proposes a building risk assessment and factor analysis based on multi-objective decision making and fuzzy mathematical modeling, and the risk analysis and control system based on fuzzy information processing theory can be widely used in the risk assessment of various systems to ensure safety. Liang et al. (2022) conducted risk assessment of urban gas pipelines by integrating the fuzzy TOPSIS model and cloud reasoning. This quantitative description of fuzziness can be more relevant to the actual situation because cable aging is difficult to define by a precise value but is affected by a combination of factors such as operating time, load size, ambient temperature, and humidity Expert opinions and judgment standards vary based on their own experience, and the affiliation function can integrate this fuzzy information (Zaman et al., 2024; Wang et al., 2023; Salari et al., 2024). Various methods used to determine the affiliation function are based on statistical data, expert experience, and fuzzy statistical tests. A method based on statistical data needs to collect a large amount of historical data, such as cable operation parameters and fault records, and fit the curve of the affiliation function through data analysis.

In the urban power transmission system, the safe and stable operation of a dense urban cable channel is the key to ensuring the normal operation of the city, but because of the complex risk factors, the traditional risk assessment method has limitations. Some studies use neural network methods to deal with uncertainty in power systems, but it is difficult to accurately define the risk grade boundary in dealing with the fuzziness of cable channel risk factors, resulting in poor accuracy of evaluation results. There are also studies using gray theory to assess the risk of complex systems. Although the uncertainty of some information is taken into account, the fuzzy relationship among multiple factors in the cable channel has not been properly dealt with.

The emergence of fuzzy mathematics theory provides an effective way to solve such problems. Introducing a membership function can transform fuzzy concepts into quantitative descriptions to deal with the uncertainty of risk factors effectively. For example, when evaluating the aging degree of cable insulation and the influence of external environmental factors, fuzzy mathematics can comprehensively consider a variety of factors, make up for the shortcomings of traditional accurate mathematical models, and make the evaluation results more realistic. In this study, the fuzzy mathematical theory is used to build a risk assessment model that can fully consider the fuzzy characteristics of various risk factors and integrate the subjective opinions of different assessors to provide a more reliable basis for the maintenance and management decisions of cable channels and effectively ensure the stable operation of urban power and communication systems.

A dense urban cable channel is located in a complex and changing environment, and many environmental factors pose potential threats to the long-term safe operation of cables. Aiming at the above problems, this paper constructs a risk assessment model of a dense urban cable channel by introducing fuzzy mathematical theory, comprehensively considers multiple risk factors, assesses the operational risk of the cable channel, and puts forward corresponding risk coping strategies. The study shows that the fuzzy mathematical theory can effectively deal with the problem of vagueness and uncertainty so that the risk assessment results are more in line with the actual situation, provide a more reliable basis for the maintenance and management decisions of the cable channel, and vigorously guarantee the stable operation of the urban electric power and communication system. Through fuzzy mathematics theory, this study fills the theoretical gap of ambiguity and uncertainty treatment in the risk assessment of dense urban cable passageways. Compared with traditional models and emerging machine learning methods, the proposed method has significant advantages in the following scenarios: (1) Reliable evaluation can be provided when data are scarce or of poor quality; (2) Strong interpretability, easy for operation and maintenance personnel to understand the source of risk; (3) Support dynamic updating of membership functions to meet the needs of the rapid development of urban power grids.

2 Risk state volume analysis of urban dense cable corridors

A dense urban cable channel is an important infrastructure for the various types of cables for urban electricity and communication. In modern cities, due to the growing demand for electricity and communication flow, the number of cables and dense distribution in such channels is increasing. These cable channels are like the city’s “meridian.” Any problem that occurs may lead to large-scale power outages, communication interruption, and other serious consequences, affecting the normal life of urban residents and the normal operation of the city. At the same time, the cable channel is faced with natural disasters, man-made destruction, technical failures, and other threatening risk factors, so a dense urban cable channel risk state volume classification and analysis can have great practical significance.

A 10-kV urban distribution network cable channel is divided according to the function and use. Risks include external damage risk, defective channel facilities, nonstandard cable laying, overcapacity of the channel, out-of-standard fire retardant, high voltage and low voltage lines in the same channel, overheating of cables, proximity to oil and gas pipelines, and eight kinds of volume risk. Risk factors for the operation of cable channels (ditches, tunnels, and integrated pipe corridors) are evaluated, and the hidden dangers are divided according to low risk, medium risk, and high risk. Collecting and organizing the historical fault data of different areas and types of cable channels in the city allows the frequency of various types of risk events to be understood.

Based on the existing risk assessment methods, the 10-kV distribution network cables channels and hidden dangers in a region of China Southern Power Grid in September 2024 were counted. The total number of urban distribution network cable channels counted was 1,052, of which 830 were low-risk channels, 202 were medium-risk channels, and 40 were high-risk channels. The details of this cable channel inventory are shown in Table 1.

Table 1

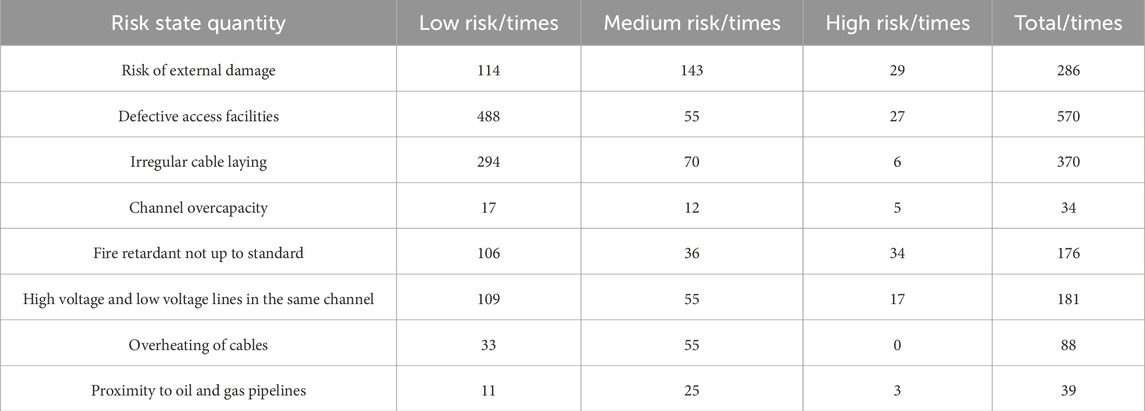
Table 1. The amount of cable channel risks by status and the number of occurrences of different risks.

In determining thresholds for low, medium, and high risk, we relied primarily on historical data trends and expert consensus. After collecting a large number of historical fault data from the 10-kV urban distribution network cable channels in different regions and types, we first carried out a statistical analysis of the data. For example, we calculated how often each risk event occurred at different levels of severity and plotted a frequency distribution curve. Taking “external damage risk” as an example, we found that when the number of failures caused by external damage in a certain area within a certain period of time is lower than a specific value, the cable channel in this area is less affected by external damage, and its operation is relatively stable, so this value range is divided into a low-risk range. With the increase in the number of failures, when the cable channel is in a certain middle range, there is a certain degree of security risks, but it has not reached the level of serious threats. This range is set as the medium-risk range. When the number of failures exceeds a certain high value, it indicates that the cable channel in the area is frequently damaged by external damage, posing a serious threat to the power supply security. This range is called the high-risk range.

We organized 10 senior experts from the power industry to conduct a seminar. These experts have rich experience in cable channel operation and maintenance, risk assessment, and other fields. They reviewed and adjusted the initial risk thresholds based on historical data in combination with actual work cases and industry standards. After several rounds of discussion and comprehensive evaluation, the low-, medium-, and high-risk thresholds suitable for this study were finally determined. This combination of historical data and expert experience ensures that risk thresholds are scientific and practical.

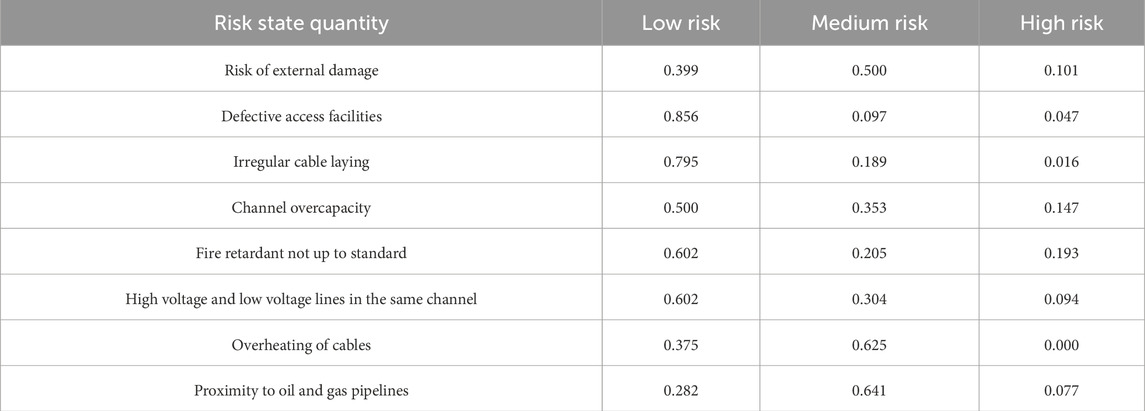
On this basis, the weights assigned to the number of occurrences of individual risk state quantities in low, medium, and high risk are calculated, and the results are shown in Table 2. In Table 2, the weights of different risk factors are determined by the analytic hierarchy process (AHP) combined with expert scoring. First, we built a hierarchical model of risk factors and set the target layer as the overall risk assessment of the cable channel. The criterion layer was the eight risk factors we identified, such as external damage and facility defects. Then, the 10 experts were invited to compare the relative importance of each risk factor pairwise and score it using the 1–9 scale method to construct the judgment matrix. For example, when comparing “risk of external damage” and “risk of facility defects,” experts give a score according to the importance of their impact on the safe operation of cable channels. Then, the maximum characteristic root of the judgment matrix and its corresponding eigenvector were calculated using a mathematical method, and the relative weight of each risk factor was obtained after normalization of the eigenvector. In order to ensure the accuracy and reliability of the weights, we also carried out a consistency test on the judgment matrix. If the consistency ratio (CR) was less than 0.1, the judgment matrix had satisfactory consistency, and the weight obtained was reasonable and reliable. If the CR was greater than 0.1, the judgment matrix was readjusted until the consistency requirements were met. In this way, we determined the weights of the risk factors in Table 2 under different risk levels.

Table 2

Table 2. Weights for the number of occurrences of individual risk state quantities.

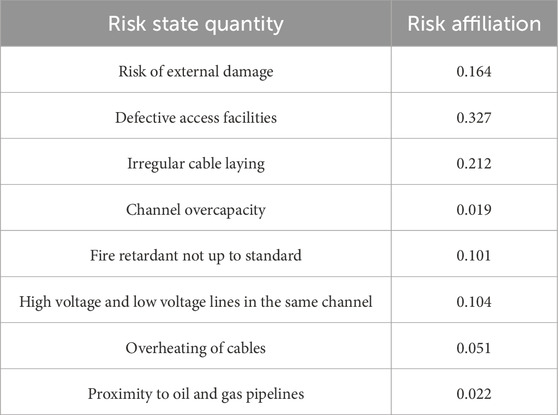
The risk affiliation of different risk state quantities is shown in Table 3.

Table 3

Table 3. Risk affiliation for different risk state quantities.

Table 3 shows the risk membership degree table of different risk states of a dense urban cable passage. The table clearly shows the degree of correlation between various risk state quantities and different risk levels. Each risk state quantity, such as “external damage risk,” “defective channel facility,” etc., corresponds to a specific risk membership value. These values are calculated by considering many factors comprehensively and using the theory and method of fuzzy mathematics. For example, “risk of external injury” has a risk membership of 0.164, which indicates that this risk is relatively low in the overall risk assessment. On the whole, the distribution of risk membership reflects the role of different risk states in the safe operation of cable channels. Some risk states, such as “defective channel facilities,” have a risk membership of 0.327, which is relatively high, indicating that this factor poses a greater threat to the security of cable channels. For example, the risk membership of “close to oil and gas pipeline risk” is only 0.022, indicating that this factor has a small impact on the overall risk in the current assessment model. Through the analysis of Table 3, we can have a deeper understanding of various risks faced by dense urban cable channels and provide an important basis for formulating targeted risk response strategies.

The fuzzy comprehensive risk assessment method is carried out according to the similarity of different eigenvalues and other relationships between individual state quantities. Specific implementation steps for analyzing the state quantities of cable lines. First, the risk state quantities corresponding to each component of cable lines are classified according to certain attributes. Second, each risk state quantity is comprehensively evaluated, and then the results of the evaluation of the cable channel are obtained, and a multilevel comprehensive evaluation is carried out.

3 Fuzzy mathematics-based risk assessment model for dense urban cable corridors

Fuzzy mathematics is a tool for dealing with vagueness and uncertainty, first proposed by American mathematician Lotfi A. Zadeh in 1965. Unlike traditional mathematics, which mainly studies deterministic problems, fuzzy mathematics aims to solve problems that cannot be described by precise definitions, especially in social sciences, engineering technology, and natural sciences with a wide range of applications. Cable channels face a variety of complex risk factors, such as natural disasters, external damage, and equipment aging, that seriously threaten the safe and stable operation of urban power systems. Therefore, this article introduces fuzzy mathematical theory and constructs a risk assessment model for a dense urban cable channel by comprehensively considering multiple risk factors.

3.1 First-level risk evaluation of cable channel based on fuzzy mathematics

Let the thesis domain be U. The fuzzy set μ_A refers to a mapping A of U to [0, 1]: U→[0, 1], and for any u∈U, μ_A(u) is called the degree of affiliation of u to A, which indicates the degree that u belongs to A. Assuming that there are m factors related to dense urban cable corridors, their set of risk factors is shown in Equation 1.

$U=\left\{U_1,U_2,\dots ,U_m\right\},(1)$

where U is the set of risk factors for dense urban cable corridors, and U_i (i = 1, 2, …, m) is a single factor in the factor set. The set of risk level rubrics is shown in Equation 2.

$Y=\left\{y_1,y_2,\dots ,y_n\right\},(2)$

where Y is the set of risk level rubrics, and y_i (i = 1, 2, …, n) is the i-th risk level. The affiliation degree r_ij of a dense urban cable channel to the risk level rubric y_i can be obtained by U_i, and then the set of r_i rubrics is obtained based on the obtained affiliation degree r_ij, as shown in Equation 3.

$r_i=\left(r_{i1},r_{i2},\dots ,r_{in}\right),(3)$

where r_i is a comprehensive set of dense urban cable channel level risk rubrics, that is, fuzzy subsets on Y.

Calculate the fuzzy set of the importance of each factor of a dense cable channel as shown in Equations 4, 5.

$D=\left(d_1,d_2,\dots ,d_n\right),(4)$

$d_i=\left(d_{i1},d_{i2},\dots ,d_{in}\right),(5)$

where D is the fuzzy set of single-factor importance of the risk of dense cable channel, d_i is the influence measure in the single-factor evaluation, and d_ii is the i-th influence measure in the single-factor evaluation. In this case, the eight factors related to dense urban cable channels and three risk levels, which can be obtained from Table 2, are expressed by Equations 6–13.

$d_1=\left(0.399,0.500,0.101\right),(6)$

$d_2=\left(0.856,0.097,0.047\right),(7)$

$d_3=\left(0.795,0.189,0.016\right),(8)$

$d_4=\left(0.500,0.353,0.147\right),(9)$

$d_5=\left(0.602,0.205,0.193\right),(10)$

$d_6=\left(0.602,0.304,0.094\right),(11)$

$d_7=\left(0.375,0.625,0.000\right),(12)$

$d_8=\left(0.282,0.641,0.077\right).(13)$

Among them, d₁ is the impact metric of external damage risk, d₂ is the impact metric of defective channel facilities, d₃ is the impact metric of cable laying irregularities, d₄ is the impact metric of overcapacity of the channel, d₅ is the impact metric of fire retardant failure, d₆ is the impact metric of high and medium voltage laying with the same channel, d₇ is the impact metric of overheating of cables, and d₈ is the impact metric of the proximity of oil and gas pipelines.

Then, the expert scoring method was used to construct a comprehensive judgment matrix for the first-level risk of dense urban cable corridors, as shown in Equation 14.

$R=\left(\begin{array}{cccc}{r}_{11}& r_{12}& \cdots & r_{1n}\\ r_{21}& r_{22}& \cdots & r_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ r_{m1}& r_{m2}& \cdots & r_{mn}\end{array}\right),(14)$

where R is a comprehensive risk evaluation matrix for the first level of dense urban cable corridors, which is derived from the set of m single-factor evaluations of the risk of dense cable corridors as the rows of the matrix. The fuzzy relation R_f∈ f (U × Y) of the matrix R is derived from the fuzzy value mapping f derived to Y.

The fuzzy set D of the importance of the risk factors and the fuzzy comprehensive judgment matrix R of the cable channel are known, and the linear fuzzy transformation is done by R to change D into a fuzzy subset on the risk level rubric Y of the cable channel.

$B_i=\left({b_i}_1,b_{i1},\dots ,b_{in}\right),(15)$

$b_{ii}=d_{in}·r_{in,}(16)$

where B_i is the comprehensive evaluation set of the first-level risk judgment of the i-th relevant factor of the dense urban cable channel, and b_ii is the i-th evaluation value of the i-th relevant factor of the dense urban cable channel. The comprehensive judgment result of the risk level y_i adopts the principle of maximum affiliation; that is, the y_i corresponding to the maximum value in B_i is selected as the comprehensive judgment result.

3.2 Fuzzy mathematics-based multilevel comprehensive risk assessment for cable passages

In this case, the risk factor set of a dense urban cable channel is U{U₁, U₂, …, U₈}, where U₁ is the risk factor of external damage, U₂ is the risk factor of defective channel facilities, U₃ is the risk factor of non-standardized cable laying, U₄ is the risk factor of overcapacity of the channel, U₅ is the risk factor of substandard fire-retardant, U₆ is the risk factor of high voltage and low voltage lines in the same channel, U₇ is the risk factor of cable overheating, and U₈ is the risk factor of adjacent oil and gas pipelines.

The second-level comprehensive judgment weights are constructed based on the fuzzy comprehensive judgment of the subset of risk factors based on Table 3, as shown in Equation 17.

$w=\left(0.164,0.327,0.212,0.019,0.101,0.104,0.051,0.022\right).(17)$

Construct the second-level fuzzy composite risk judgment matrix for the cable channel of U, as shown in Equation 18.

$A=\left(\begin{array}{cccc}{b}_{11}& b_{12}& \cdots & b_{1n}\\ b_{21}& b_{22}& \cdots & b_{2n}\\ ⋮& ⋮& \ddots & ⋮\\ b_{m1}& b_{m2}& \cdots & b_{mn}\end{array}\right).(18)$

This, in turn, results in a comprehensive evaluation set Z of the secondary fuzzy risk assessment of the cable channel of U, as shown in Equations 19, 20.

$Z=\left(z_1,z_2,\dots ,z_n\right).(19)$

$z_i=\frac{\left(w_1·b_{1i}+w_2·b_{2i}+\dots +w_m·b_{mi}\right)}{m}.(20)$

Most existing studies utilize the principle of maximum affiliation; that is, the largest z_i corresponding to the risk level rubric y_i is the best risk evaluation result. The biggest drawback of this evaluation result is that only the largest rubric is simply considered, while other rubric information is ignored. Consequently, the results obtained are not sufficiently comprehensive and accurate. In response to this shortcoming, a rank parameter synthesis judgment method is proposed. The grade parameter vector is constructed as shown in Equation 21.

$E={\left(e_1,{\mathrm{e}}_2,\dots ,e_n\right)}^T.(21)$

The cable channel risk level parameter judgment result p is calculated using the vector inner product to obtain a real number from 0 to 1 with Equation 22.

$p=Z·E={\displaystyle \sum _{i=1}^n}\left(z_i·e_i/{\displaystyle \sum _{j=1}^n}{e}_j\right).(22)$

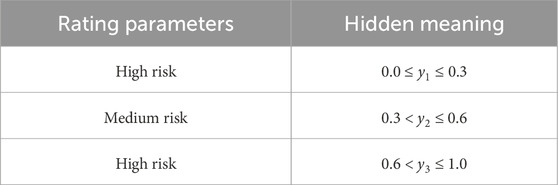
The result represents the degree of affiliation in the evaluation set; that is, the information represented by p is obtained by combining B and E. The values are assigned to the three class parameters of low, medium, and high risk involved in this case, as shown in Table 4.

Table 4

Table 4. Range of values assigned to the rank parameter.

Table 4 is the assignment table of cable channel risk level parameters and provides a clear standard and reference for evaluating the overall risk level. The table defines three risk levels, namely, high, medium, and low risk, and assigns a specific range of values to each level. For example, high risk ranges from 0.0 to 0.3, medium risk ranges from 0.3 to 0.6, and low risk ranges from 0.6 to 1.0. These numerical ranges are based on an in-depth study and analysis of cable channel risk characteristics. The basis of the assignment mainly considers the potential impact of risk factors on the safety of cable channels and actual engineering experience. By matching the risk assessment results with these rating parameters, the risk level of the cable channel can be quickly and intuitively judged.

In practical application, the value of Table 4 is that it provides clear guidance for the maintenance and management of cable channels. For example, when the evaluation results show that the cable channel is at a high-risk level, more stringent maintenance measures should be taken to strengthen monitoring and early warning to ensure its safe operation. Maintenance strategies for low-risk cable channels can be properly adjusted to reduce maintenance costs. The matrix of the corresponding rating parameters is given as 0.15 points for low risk, 0.45 points for medium risk, and 0.80 points for high risk. That is, E = (0.15, 0.45, and 0.80)^T.

4 Calculus analysis

In order to verify the effectiveness of the dense urban cable channel risk assessment model based on fuzzy mathematics constructed in this paper, a section of a typical dense cable trench operated in a region of China Southern Power Grid is selected for example analysis, and the cable channel risk level comment is calculated through MATLAB 2021a programming. Two experts in related fields, A and B, are invited to evaluate each risk factor, determine its affiliation to each evaluation level, and build the factor fuzzy evaluation matrices R_A and R_B as shown in Equations 23, 24.

Expert A has more work experience than Expert B. Therefore, the scoring results of the two experts are weighted, and the evaluation weights are 0.6 and 0.4, respectively. The comprehensive judgment matrix R combining the evaluation weights and opinions of the two experts is shown in Equation 25.

$R_A=\left(\begin{array}{ccc}0.45& 0.55& 0\\ \begin{array}{c}0.40\\ \begin{array}{c}0.91\\ 0.65\\ 0.55\\ 0.68\end{array}\\ 0.35\end{array}& \begin{array}{c}0.60\\ \begin{array}{c}0.09\\ 0.35\\ 0.43\\ 0.32\end{array}\\ 0.65\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0.02\\ 0\end{array}\\ 0\end{array}\\ 0.78& 0.22& 0\end{array}\right)(23)$

$R_B=\left(\begin{array}{ccc}0.48& 0.52& 0\\ \begin{array}{c}0.46\\ \begin{array}{c}0.77\\ 0.86\\ 0.82\\ 0.91\end{array}\\ 0.42\end{array}& \begin{array}{c}0.54\\ \begin{array}{c}0.23\\ 0.14\\ 0.18\\ 0.09\end{array}\\ 0.58\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\\ 0\end{array}\\ 0.88& 0.12& 0\end{array}\right)(24)$

$R=\left(\begin{array}{ccc}0.462& 0.538& 0\\ \begin{array}{c}0.424\\ \begin{array}{c}0.854\\ 0.734\\ 0.658\\ 0.772\end{array}\\ 0.378\end{array}& \begin{array}{c}0.576\\ \begin{array}{c}0.146\\ 0.266\\ 0.330\\ 0.228\end{array}\\ 0.622\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0.012\\ 0\end{array}\\ 0\end{array}\\ 0.820& 0.180& 0\end{array}\right)(25)$

Using Equations 15, 16 to calculate the typical dense cable trench-related factors of the first level of risk assessment comprehensive evaluation set, and based on the principle of maximum affiliation for risk assessment, the typical first level of risk assessment results are shown in Table 5.

Table 5

Table 5. First-level risk evaluation results of typical dense cable trench.

Table 5 shows the results of a typical dense cable trench based on a first-level risk assessment. Based on the principle of maximum membership degree, the risk is medium when the single-factor assessment is carried out using external damage risk factors and cable overheating risk factors. When the other six risk factors are assessed, the outcome trench is low risk. This result reflects that different risk factors have different effects on the risk level. External damage risk factors lead to the moderate-risk assessment result, which may be due to the frequent construction activities around the cable trench in this area or the existence of other external damage hazards that increase the possibility of external damage to the cable. For example, in actual operation, nearby road construction may use large machinery that may accidentally touch the cable trench during the operation, causing damage to the cable and increasing the risk level. The cable overheating risk factor is also assessed as medium risk that may be related to the load condition of the cable, heat dissipation conditions, and other factors. If the cable is in a state of high load operation for a long time, or the heat dissipation facilities in the cable trench are not perfect and the heat cannot be distributed fast enough, the cable can overheat, affecting its normal operation and increasing the probability of failure. In contrast, the remaining six risk factors are assessed as low risk, which indicates that the impact of these factors on the overall risk is relatively small in the current situation. Take the risk factor of non-standard cable laying as an example. Although there may be a non-standard situation, it may not have reached the degree of posing a serious threat to the safety of cable operation, so it is assessed as low risk. However, we cannot ignore these low-risk factors because they may interact under certain conditions, resulting in elevated risk levels.

In order to further support the data results in Table 5, we collected the on-site monitoring data of a typical dense cable trench during the evaluation period, including cable temperature and surrounding environmental conditions. For example, during the evaluation period, the temperature sensor installed in the cable trench monitored that the cable temperature was close to or even exceeded the normal operating temperature range in some periods, which echoed the result of the evaluation of the cable overheating risk factor as moderate risk, providing strong practical data support for the evaluation result. In addition, we consulted the historical fault records of the cable trench and found that slight cable damage caused by external construction had occurred in the past. Although no serious accident was caused, it indicated that there was indeed a risk of external damage to the cable in the area, which further confirmed the rationality of assessing the risk factor of external damage as medium risk.

Then, the cable trench is subjected to a two-level comprehensive risk assessment, taking into account the risk of external damage, lack of channel facilities, cable laying irregularities, channel overcapacity, substandard fire retardant, high voltage and low voltage lines in the same channel, overheating of cables, and the proximity of oil and gas pipelines, and constructing two-level comprehensive risk assessment matrix A, the specific expression is shown in Equation 26.

$A=\left(\begin{array}{ccc}0.184& 0.269& 0\\ \begin{array}{c}0.363\\ \begin{array}{c}0.679\\ 0.367\\ 0.396\\ 0.465\end{array}\\ 0.142\end{array}& \begin{array}{c}0.056\\ \begin{array}{c}0.028\\ 0.094\\ 0.068\\ 0.069\end{array}\\ 0.389\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0.002\\ 0\end{array}\\ 0\end{array}\\ 0.231& 0.115& 0\end{array}\right)(26)$

The comprehensive evaluation set Z of the two-level fuzzy risk evaluation of the cable channel for U is obtained, as shown in Equation 27.

$Z=\left(0.0501,0.0133,0\right)(27)$

According to the principle of maximum affiliation, the typical dense cable trench secondary risk assessment results in low risk, but the evaluation of low-risk and high-risk affiliation values is only a difference of 0.0368 if only the principle of maximum affiliation for the assessment is used, so it is also necessary to use the hierarchical parameter method for effective assessment. Using Equation 22, a rank parameter judgment overall score of 0.2129 can be obtained that reflects the overall low-risk evaluation results of the typical dense cable trench.

In order to further verify the effectiveness of the risk assessment model proposed in this paper, a cable tunnel with a poor operating environment in the region was selected for operational risk assessment. It was evaluated by experts A and B for each risk factor, and their affiliation to each evaluation level is determined to obtain the factor fuzzy evaluation matrices R_A1 and R_B1, as shown in Equations 28, 29.

$R_{\mathrm{A}1}=\left(\begin{array}{ccc}0.10& 0.90& 0\\ \begin{array}{c}0.15\\ \begin{array}{c}0.12\\ 0.11\\ 0.22\\ 0.21\end{array}\\ 0.23\end{array}& \begin{array}{c}0.85\\ \begin{array}{c}0.88\\ 0.89\\ 0.78\\ 0.79\end{array}\\ 0.77\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\\ 0\end{array}\\ 0.17& 0.83& 0\end{array}\right)(28)$

$R_{\mathrm{B}1}=\left(\begin{array}{ccc}0.24& 0.76& 0\\ \begin{array}{c}0.17\\ \begin{array}{c}0.26\\ 0.09\\ 0.05\\ 0.12\end{array}\\ 0.25\end{array}& \begin{array}{c}0.83\\ \begin{array}{c}0.74\\ 0.91\\ 0.95\\ 0.88\end{array}\\ 0.75\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\\ 0\end{array}\\ 0.14& 0.86& 0\end{array}\right)(29)$

The scoring results of the two experts are weighted, and the evaluation weights are 0.6 and 0.4, respectively. The comprehensive judgment matrix R₁ combining the evaluation weights and opinions of the two experts is shown in Equation 30.

$R_1=\left(\begin{array}{ccc}0.156& 0.844& 0\\ \begin{array}{c}0.158\\ \begin{array}{c}0.176\\ 0.102\\ 0.152\\ 0.174\end{array}\\ 0.238\end{array}& \begin{array}{c}0.842\\ \begin{array}{c}0.824\\ 0.898\\ 0.848\\ 0.826\end{array}\\ 0.762\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\\ 0\end{array}\\ 0.158& 0.842& 0\end{array}\right)(30)$

Using Equations 15, 16 to calculate the cable tunnel-related factors of the first level of risk assessment comprehensive evaluation set, and based on the principle of maximum affiliation risk assessment, the typical first level of risk assessment results are shown in Table 6.

Table 6

Table 6. First-level risk evaluation results of typical dense cable tunnels.

As seen in Table 6, based on the principle of maximum affiliation for the first-level comprehensive risk judgment, the passageway belongs to medium risk when the eight risk factors are evaluated in a single factor. The second-level comprehensive risk judgment matrix A₁ is constructed. The specific expression is shown in Equation 31.

$A_1=\left(\begin{array}{ccc}0.062& 0.422& 0\\ \begin{array}{c}0.135\\ \begin{array}{c}0.140\\ 0.051\\ 0.092\\ 0.105\end{array}\\ 0.089\end{array}& \begin{array}{c}0.082\\ \begin{array}{c}0.156\\ 0.317\\ 0.174\\ 0.251\end{array}\\ 0.476\end{array}& \begin{array}{c}0\\ \begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\\ 0\end{array}\\ 0.045& 0.540& 0\end{array}\right)(31)$

Then, the comprehensive evaluation set Z₁ of the two-stage fuzzy risk evaluation for a typical dense cable tunnel of U is obtained, as shown in Equation 32.

$Z_1=\left(0.0138,0.0268,0\right)(32)$

According to the principle of maximum affiliation, the result of a secondary risk assessment is medium risk. Equation 22 can be used to obtain a grade parameter judgment overall score of 0.3480. That is, the overall risk evaluation result of the typical dense cable tunnel is medium risk, consistent with the maximum affiliation principle judgment results.

5 Strategies for coping with different risks in urban dense cable corridors

5.1 Low-risk cable channel response strategies

Maintain regular inspections but extend the inspection cycle as appropriate. For example, the original weekly comprehensive inspection can be adjusted to once every 2 weeks. During the inspection, focus on minor changes in the operating status of the equipment, such as whether there is slight wear and tear on the cables and whether there are small fluctuations in the operating parameters of the ancillary equipment. Record minor equipment defects or potential hidden dangers in a timely manner and schedule them to be dealt with in the next maintenance program. Maintenance can focus on simple operations such as cleaning and tightening connection areas. For example, regularly cleaning the dust and debris in the cable channel will prevent its accumulation from adversely affecting the cables; checking whether the connecting bolts of the cable joints are loose, and tightening them in time if they are loose will prevent problems.

The identified low-risk factors and their relevant information, including the location where the risk occurs, the possible extent of the impact, etc., should be recorded in detail. For example, any section of cable that has some potential risk due to its proximity to a source of minor vibration (e.g., a small processing plant) should be noted, including its specific location and details of the source of vibration. The file information of the cable access equipment, including the equipment’s operating time, maintenance history, and so on, should be updated regularly. This information helps to analyze the performance trend of the equipment and provides a basis for subsequent maintenance decisions. For example, any changes in the insulation resistance test data of cable maintenance strategies should be recorded and used to evaluate the trend of cable insulation performance based on the data changes.

Regular basic training should be provided for operation and maintenance personnel, including basic knowledge of cable channels and the identification and treatment of simple faults. For example, training courses should be organized to explain the basic structure and working principles of cables so that operations and maintenance (O&M) personnel can better understand equipment operation and identify potential problems in a timely manner. Enhance O&M personnel’s safety awareness of low-risk factors that may cause faults through case sharing and other means. For example, sharing cases of ignoring minor equipment wear and tear that ultimately led to failures can help O&M personnel realize that even low-risk factors must be taken seriously.

5.2 Medium-risk cable channel response strategy

The depth and frequency of inspections should be increased, changing from comprehensive inspections to daily inspections of key areas and weekly inspections of other areas. Areas of higher risk, such as cable joints and sections of channels susceptible to external forces, should be focused on. For example, for cable passages passing near road construction areas, the appearance of the cables should be checked daily for signs of damage by construction equipment, and the laying status of the cables should be checked for normalcy. For medium-risk problems identified, a maintenance plan should be developed immediately and implemented as soon as possible. Maintenance measures can include operations such as partial replacement and performance enhancement of equipment. For example, if the insulation performance of cables is found to have a tendency to deteriorate but has not yet reached a serious level, the cables can be treated with insulation enhancement, such as spraying insulation paint. Real-time monitoring equipment, such as temperature sensors, humidity sensors, and partial discharge monitors, should be installed to monitor the operating status of the cable channel in real time. Once the monitoring data exceeds the set threshold, a timely alarm can be issued so that the operation and maintenance personnel can respond quickly. For example, when the temperature of the cable joint area exceeds the normal operating temperature range, the system can immediately alert the operation and maintenance personnel so that they can promptly check the joints for problems such as poor contact.

A detailed contingency plan for events that may result in moderate risk, such as localized external damage and localized equipment failure, should be developed. The plan should include the handling process of the incident, division of responsibilities, and resources required. For example, for the possible collision of vehicles with cable access facilities, a detailed handling process, including how to quickly isolate the faulty area, how to organize repair, and so on, should be developed. Regular emergency drills can test the feasibility and effectiveness of the emergency plan and improve the ability of operation and maintenance personnel to respond to emergencies. The drill can simulate a variety of medium-risk event scenarios, such as simulating a local short-circuit fault in a cable so that O&M personnel can operate in accordance with the emergency plan, including fault investigation, repair, and restoration of power supply.

Communication and coordination with external units such as municipal departments and construction units should be strengthened. Protective measures can be negotiated in advance before municipal construction and other activities that may affect the safety of cable channels. For example, before the construction of urban roads, a safety agreement should be signed with the construction unit, clarifying the responsibilities of both parties and requiring the construction unit to take the necessary cable protection measures during the construction process, such as setting warning signs and adopting non-excavation construction techniques. The collaboration between various specialties within the operation and maintenance department, such as cable specialties, communication specialties, automation specialties, and so on, can be strengthened. When dealing with medium-risk events, professionals can work together to improve processing efficiency. For example, when dealing with cable channel faults, cable professionals are responsible for fault investigation and repair, communication professionals are responsible for communication equipment inspection and recovery, and automation professionals are responsible for monitoring system maintenance and data recovery.

5.3 High-risk cable channel response strategy

Once a high-risk situation is detected, such as a serious fault in a cable or serious damage to a passageway, immediate measures should be taken to isolate the source of the risk and prevent the scope of the fault from expanding. For example, when a fire occurs in a cable, the power supply to the faulty cable should be cut and the firefighting system activated to extinguish the fire. A professional repair team can be organized to quickly carry out repair work. The repairers should have rich experience and professional skills and be able to repair the fault in the shortest possible time. For example, for cable breakage faults, repair personnel should carry a full range of tools and spare cables and quickly arrive at the scene for cable replacement or connection repair. During the period of emergency repair, depending on the actual situation, consider adopting temporary power supply measures, such as activating emergency power generators, in order to minimize the impact on users. For example, for important users, temporary power can be provided through emergency power generators to safeguard their basic power needs.

After the high-risk event has been dealt with, a comprehensive risk assessment of the entire cable corridor should be carried out, including an assessment of the degree of damage to the equipment and an assessment of the reliability of the remaining equipment. The assessment process should use advanced testing techniques and methods, such as non-destructive testing techniques for the internal structure of the cable. Based on the results of the risk assessment, a comprehensive rectification program will be developed. The rectification program may include large-scale replacement of equipment, reinforcement of the channel structure, and upgrading of protective facilities. For example, if the waterproofing facilities of a cable passageway are found to have been severely damaged in a high-risk event, a program for the complete renovation of the waterproofing facilities should be formulated, including measures such as re-laying the waterproofing layer and installing drainage pumps.

Planning for the upgrading of the entire cable channel system, including the use of more advanced cable materials, more reliable ancillary equipment, and so on, should be considered. For example, traditional cables can be replaced with new ones with higher insulation and anti-aging properties to enhance the long-term reliability of the system. A long-term risk prevention mechanism can be established, including strengthening cooperation with meteorological departments, geological departments, and other relevant organizations to obtain information on natural disasters and other risks in advance. Monitoring of the surrounding environment to prevent the recurrence of external damage should be improved. For example, an information-sharing platform can be established with the meteorological department to obtain timely warning information on meteorological disasters, such as rainstorms and typhoons, so that preparations can be made in advance for the protection of cable channels.

6 Conclusion

As the key infrastructure of modern urban power and communication systems, the security of a dense urban cable corridor is directly related to the stability of urban operation and the quality of life of residents. However, due to the complexity and diversity of risk factors faced by cable corridors, it is difficult for traditional assessment methods to fully and accurately reflect the actual risks. This study introduces fuzzy mathematics theory to build a risk assessment model that provides a new solution for the safety assessment of dense urban cable corridors. In the study, we systematically identified and classified key risk factors affecting the safety of cable channels, including external damage, equipment defects, and non-standard cable laying. Through the fuzzy membership function and the fuzzy comprehensive evaluation method, the quantitative description and comprehensive judgment of risk factors are realized, and the fuzziness and uncertainty of risk factors are effectively solved. In case studies of typical cable channels, the model not only accurately assessed the risk level but also clearly demonstrated the extent to which individual risk factors contributed to the overall risk. For example, in the assessment of typical dense cable trenches and cable tunnels, the risk levels under different risk factors were precisely determined, providing strong support for subsequent targeted risk response strategies.

The risk assessment model based on fuzzy mathematics can provide reasonable and scientific assessment results under an environment of high uncertainty and fuzziness and significantly improve the comprehensiveness and reliability of assessments. The application of this model is helpful in improving the safety of cable passage operations and provides an important decision basis for the maintenance and management of urban power systems. By adopting corresponding countermeasures for different risk levels of cable channels, such as reasonable adjustment of inspection cycle for low-risk channels, strengthening monitoring and making emergency plans for medium-risk channels, timely isolation of risks for high-risk channels, and comprehensive rectification, the stable operation of urban power and communication systems can be effectively guaranteed. In the future, we will further optimize the model, taking into account the impact of more complex factors, such as environmental differences in different regions and the dynamic process of cable aging, continue to improve the accuracy and adaptability of the model, and contribute more to the security of urban infrastructure.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material; further inquiries can be directed to the corresponding author.

Author contributions

YN: writing – original draft, writing – review and editing, and conceptualization. DC: conceptualization, writing – original draft, and writing – review and editing. SZ: methodology, writing – original draft, and writing – review and editing. XX: formal analysis, writing – original draft, and writing – review and editing. XW: funding acquisition, writing – original draft, and writing – review and editing. ZW: visualization, writing – original draft, and writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The authors declare that this study received funding from the China Southern Power Grid Company Limited’s Science and Technology Projects (YN-KJXM20240027). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors YN, DC, and XX were employed by Yunnan Power Grid Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, Y., Wu, J., Liu, K., Sun, Y., Shen, S., Cao, J., et al. (2024). Energy-based coupling risk assessment (CRA) model for urban underground utility tunnels. Reliab. Eng. Syst. Saf. 250, 110255. doi:10.1016/j.ress.2024.110255

CrossRef Full Text | Google Scholar

Chen, X., Huang, G., Gao, X., Ou, S., Li, Y., and Hezam, I. M. (2021). BN-RA: a hybrid model for risk analysis of overload-induced early cable fires. Appl. Sci. 11, 8922. doi:10.3390/app11198922

CrossRef Full Text | Google Scholar

Das, A., and Reddy, C. (2023). An analytical Approach to locate short circuit fault in a cable using Sweep frequency response analysis. IEEE Trans. Industrial Electron. 70, 5235–5244. doi:10.1109/tie.2022.3189080

CrossRef Full Text | Google Scholar

Dindar, S., Kaewunruen, S., and An, M. (2018). Identification of appropriate risk analysis techniques for railway turnout systems. J. Risk Res. 21, 974–995. doi:10.1080/13669877.2016.1264452

CrossRef Full Text | Google Scholar

Gilany, M., Ibrahim, D., and Eldin, E. (2006). Traveling-wave-based fault-location scheme for Multiend-Aged underground cable system. IEEE Trans. Power Deliv. 22, 82–89. doi:10.1109/TPWRD.2006.881439

CrossRef Full Text | Google Scholar

Ji, C., Wang, L., Hou, W., Huang, X., and Gao, M. (2024). Research on accident Prediction of cable tunnel based on FT-GS-SVR Algorithm. J. Electr. Eng. and Technol. 20, 889–902. doi:10.1007/s42835-024-01991-9

CrossRef Full Text | Google Scholar

Jia, Y. (2023). Research on fault location Algorithm of TPSS based on PSOA. PeerJ. Comput. Sci. 9, e1213. doi:10.7717/peerj-cs.1213

PubMed Abstract | CrossRef Full Text | Google Scholar

Khan, Y., Ashraf, S., and Shah, M. (2024). Determinants of Food security through statistical and fuzzy mathematical Synergy. Environ. Dev. Sustain. 26, 14981–14999. doi:10.1007/s10668-023-03231-y

CrossRef Full Text | Google Scholar

Kim, S., Kim, J., Cho, J., Sim, K., Lee, S., and Jang, H. (2007). Investigation on the stability of HTS power cable under fault current considering Stabilizer. IEEE Trans. Appl. Supercond. 17, 1676–1679. doi:10.1109/tasc.2007.899208

CrossRef Full Text | Google Scholar

Li, M., Zhou, C., Zhou, W., Wang, C., Yao, L., Su, M., et al. (2018). A novel fault location method for a Cross-Bonded HV cable system based on Sheath current monitoring. Sensors 18, 3356. doi:10.3390/s18103356

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, W. (2019). Fire risk assessment and factor analysis of buildings based on multi-target decision and fuzzy mathematical model. Appl. Eng. Technol. 37, 6337–6348. doi:10.3233/jifs-179214

CrossRef Full Text | Google Scholar

Liang, X., Ma, W., Ren, J., Dang, W., Wang, K., Nie, H., et al. (2022). An integrated risk assessment methodology based on fuzzy TOPSIS and cloud Inference for urban Polyethylene gas pipelines. J. Clean. Prod. 376, 134332. doi:10.1016/j.jclepro.2022.134332

CrossRef Full Text | Google Scholar

Liu, F., Zhang, J., Gu, M., Liu, Y., Sun, T., and Ye, L. (2024b). Simulation of damage caused by oil fire in cable passage to tunnel cable. Fire 7, 147. doi:10.3390/fire7040147

CrossRef Full Text | Google Scholar

Liu, J., Ma, M., Liu, X., and Xu, H. (2024a). High-voltage cable Buffer layer Ablation fault identification based on artificial intelligence and frequency domain Impedance Spectroscopy. Sensors 24, 3067. doi:10.3390/s24103067

PubMed Abstract | CrossRef Full Text | Google Scholar

Lou, Z., Wang, K., Kang, M., Zhao, W., Wei, G., Yue, J., et al. (2024). Plugging methods for underground gas extraction boreholes in coal seams: a review of Processes, challenges and strategies. Gas Sci. Eng. 122, 205225. doi:10.1016/j.jgsce.2024.205225

CrossRef Full Text | Google Scholar

Lou, Z., Wang, K., Yao, H., Zhao, W., Qin, H., Wu, Z., et al. (2025). A Novel dynamic filling material for plugging Fractures around underground gas extraction boreholes: experimental and engineering performances. Energy 314, 134202. doi:10.1016/j.energy.2024.134202

CrossRef Full Text | Google Scholar

Ma, Q., Liu, Y., Liu, Z., Li, W., Li, D., Liu, R., et al. (2024). Research on multi-physical field analysis and assessment technique of Virtual connection defects in Cluster cable joints based on Digital Twin technology. Front. Energy Res. 12, 1362361. doi:10.3389/fenrg.2024.1362361

CrossRef Full Text | Google Scholar

Qin, C., Zhu, X., Zhu, P., Lin, W., Liu, L., Che, C., et al. (2024). Partial discharge signal Pattern Recognition of composite insulation defects in Cross-Linked Polyethylene cables. Sensors 24, 3460. doi:10.3390/s24113460

PubMed Abstract | CrossRef Full Text | Google Scholar

Salari, S., Sadeghi-Yarandi, M., and Golbabaei, F. (2024). An integrated Approach to Occupational Health risk assessment of manufacturing nanomaterials using Pythagorean fuzzy AHP and fuzzy Inference system. Sci. Rep. 14, 180. doi:10.1038/s41598-023-48885-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, A., Hu, H., Sun, Y., Ou, Y., Ma, Y., Li, M., et al. (2024). Association between air pollution and Cerebrospinal Fluid Alpha-synuclein in urban Elders: the CABLE study. Front. Aging Neurosci. 16, 1422772. doi:10.3389/fnagi.2024.1422772

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, Y., Lyu, H., and Shen, S. (2023). Rapid Determination of fuzzy number in FAHP and assessment risk in coal mine Roof Fall. Geomatics, Nat. Hazards Risk 14, 2184670. doi:10.1080/19475705.2023.2184670

CrossRef Full Text | Google Scholar

Xiong, C., Fan, D., Zou, X., and Yu, W. (2024). Fuzzy mathematics-based evaluation method for comprehensive river Improvement Project Benefits. IEEE Access 12, 126344–126355. doi:10.1109/access.2024.3455320

CrossRef Full Text | Google Scholar

Zaman, N., Goldberg, D., Gruss, R., and Abrahams, A. (2024). A Semiautomated risk assessment method for Consumer products. Risk Anal. 44, 705–723. doi:10.1111/risa.14180

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, C., Zhou, Y., and Xu, X. (2024). Research on the ratio of similar materials in Water-Absorbent Mudstone based on fuzzy mathematics. Sci. Rep. 14, 4289. doi:10.1038/s41598-024-53409-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, P., Kong, L., Liang, R., Xu, B., and Peng, N. (2023). Fault location method for three-Core cable using Amplitude ratio of Shield-Grounding Wire currents. IEEE Trans. Industrial Inf. 19, 7456–7467. doi:10.1109/tii.2022.3194626

CrossRef Full Text | Google Scholar

Zhao, Z., Yang, Y., Dong, B., Zhang, R., Chen, G., Pan, Z., et al. (2024). Evaluation of Soil quality of Pingliang city based on fuzzy mathematics and Cluster analysis. Agronomy 14, 1205. doi:10.3390/agronomy14061205

CrossRef Full Text | Google Scholar

Zhu, X., Wu, J., Bai, Y., Wang, D., and Zhang, J. (2024). Integrating FBN and FDS for quantitative risk assessment of cable fire in utility tunnel. J. Loss Prev. Process Industries 88, 105266. doi:10.1016/j.jlp.2024.105266

CrossRef Full Text | Google Scholar