Heat extraction performance and formation cooling effect of borehole heat exchangers in high-temperature coal mines

High-temperature coal mines represent a promising but underexplored source of geothermal energy that can be harnessed for sustainable heating and cooling. This study evaluates the performance of borehole heat exchangers (BHEs) in active high-temperature coal mines, with a focus on their heat extraction capabilities and the associated formation cooling effects. A coupled three-dimensional numerical model is developed using OpenGeoSys to simulate heat transport processes within a network of five tunnel boreholes. The model is validated against analytical solutions and a one-dimensional wellbore simulator. Results show that the peripheral and central BHEs can reach a stable heat extraction rate of 7,975 and 7,950 W after 120 days, respectively, indicating that the heat extraction capacity is almost unaffected by thermal interactions between the tunnel boreholes in the short term. However, when colder water is injected into the tunnel wells, more heat can be extracted and the formation temperature will decrease faster, leading to a more significant thermal interaction between the well and a more pronounced cooling effect. Groundwater flow further alters these dynamics by redistributing heat within the subsurface and affecting the thermal interaction among boreholes. These findings highlight the dual potential of BHE systems in coal mines to both supply geothermal energy and mitigate underground heat hazards, providing practical insights for integrating such systems into district heating networks in mining regions.

1 Introduction

The growing global demand for energy and the imperative shift towards sustainable energy systems have highlighted the need for innovative solutions in renewable energy technologies (Fraser-Harris et al., 2022). Among them, geothermal energy has emerged as a stable, low-carbon, and underutilized resource. In particular, the extraction of geothermal heat from high temperature coal mines presents an innovative solution for both energy recovery and heat management (Chen et al., 2019; Chen et al., 2021; Cai et al., 2024; Chen et al., 2025a; Kolo et al., 2024). Coal mines, whether abandoned or operational, have extensive subsurface networks with high thermal gradients, which makes them suitable candidates for sustainable energy extraction. Furthermore, leveraging these resources not only enables efficient energy recovery, but also addresses environmental concerns associated with mine abandonment, such as flooding and accumulation of subsurface heat (Chen et al., 2024).

The utilization of geothermal energy from coal mines involves harnessing heat from abandoned or active mines to provide a sustainable energy source (Hall et al., 2011; Menéndez et al., 2019). This approach is gaining attention due to its potential for reducing carbon emissions and providing a reliable source of energy. The geothermal heat from the mines can be used for district heating, industrial processes, or power generation (Peralta Ramos et al., 2015). It is particularly attractive in areas with a history of mining, which may not have other renewable energy options. Additionally, this use can contribute to the economic revitalization of former mining areas, providing both energy and jobs (Loredo et al., 2016; Preene and Younger, 2014).

High-temperature coal mines located in historically intensive mining areas provide particularly favorable conditions for geothermal development (Sun et al., 2023). The considerable depth and connectivity of these mines facilitate the circulation of heat exchange fluids, effectively harnessing geothermal heat for diverse applications, including space heating, cooling, and industrial processes (Kelly and McDermott, 2022). Borehole heat exchangers (BHEs) are widely used for geothermal heating and cooling systems, providing a sustainable and energy-efficient method of transferring heat between the ground and buildings (Ciampi et al., 2018; Rosato et al., 2020a; Rosato et al., 2020b). When integrated into coal mines, BHEs can maximize thermal transfer efficiency while ensuring the structural and environmental integrity of the coal mine, which is critical to mitigating its operational risks (Xu et al., 2022).

Several studies have explored the feasibility of extracting geothermal energy from coal mines using BHEs. Vukelić and Šporin (2024) investigated the feasibility of utilizing shallow geothermal energy in a closed coal mine in Slovenia, focusing on both groundwater and borehole systems. Using Surfer software, the authors calculated that approximately 7.5 kW of thermal energy can be extracted from a 150-m-deep BHE. The research demonstrates that such systems can effectively provide heating and cooling for buildings near disused mines. Huang et al. (2023) assessed the long-term viability of parallel horizontal ground heat exchanger (pHGHE) system installed in backfilled stopes. Applied to the Anju coal mine in China, the model indicates that the system could deliver a total thermal capacity of 17 GWh per extraction cycle, sufficient to heat over 170,000 m²; of residential space. Sun et al. (2023) investigated the applicability of a BHE system designed for abandoned coal mines using coupled flow-heat mathematical models. Their findings indicate that increasing the angle of single-row boreholes improves heat transfer efficiency, with the optimal angle being no more than 30°. Moreover, to optimize system performance, the spacing between rows in multi-row configurations should exceed 4 m. Zhang et al. (2024) presented a comparative study on the performance of backfill heat exchangers (BFHEs) in various deep mine geological settings. The study finds that groundwater flow significantly enhances BFHE performance, while increasing the thermal conductivity of the backfill material improves heat extraction.

While these studies highlight the potential of utilizing abandoned or backfilled coal mines for geothermal applications, several research gaps remain. For example, the thermal interactions between BHEs, particularly under the influence of groundwater flow, are not yet fully understood, despite their potential impact on system efficiency and long-term performance. Moreover, the formation cooling effect resulting from thermal energy extraction—an important aspect of managing underground thermal environments—has received limited evaluation, especially in high-temperature and operating mining contexts. To address these gaps, this study investigates the performance and efficiency of geothermal heat extraction systems utilizing BHEs in high-temperature coal mines, with a specific focus on their formation cooling effects and overall energy efficiency. Through a combination of realistic field data and advanced simulation techniques, this research aims to: (1) elucidate the underlying mechanisms of heat transfer within coupled systems, (2) evaluate their one-heating-season performance, and (3) explore their potential for integration into district heating network. In addition, the cooling functionality of these systems as both geothermal energy sources and cooling mechanisms is examined, highlighting their significance in addressing heat management challenges in industrial and urban mining settings.

This study is among the first to systematically quantify the heat extraction capacity and formation cooling effects of BHEs in active high-temperature coal mines using a validated modeling framework. By applying numerical models implemented in the open source software OpenGeoSys (OGS) (Kolditz et al., 2012; Bilke et al., 2019), we not only reveal the dynamic thermal interactions within tunnel borehole arrays, but also demonstrate their practical feasibility for sustainable building heating in industrial settings. This integrated approach provides critical insights for repurposing coal mines as renewable energy hubs, addressing both energy demand and underground heat hazard mitigation.

2 Methods

2.1 The 3D borehole heat exchanger model

In this study, the heat pipe as a borehole heat exchanger (BHE) is used to extract heat to largely extract geothermal energy (as indicated by Kong et al. (2017); Chen C. et al. (2021)) from high-temperature surrounding rock formations to cool down the underground workplace. For the system shown in the reference of Chen C. et al. (2021) and Jiang et al. (2022), three governing equations have to be included to quantify the physical process in the borehole and surrounding formations, which correspond to the energy balance in each compartment.

In surrounding subsurface geological formations, with intrinsic soil/rock specific heat capacity $c_{\text{s}}$, intrinsic soil/rock density ${\rho }_{\text{s}}$ and soil/rock porosity $ϵ$, the evolution of soil/rock temperature $T_{\text{s}}$ is determined by the following governing Equation 2 considering both heat advection and conduction,

$\left[ϵ{\rho }_{\text{w}}{c}_{\text{w}}+\left(1-ϵ\right){\rho }_{\text{s}}{c}_{\text{s}}\right]\frac{\partial T_{\text{s}}}{\partial t}+{\rho }_{\text{w}}{c}_{\text{w}}{\mathbf{v}}_{\text{w}}\cdot \nabla T_{\text{s}}-\nabla \cdot \left({\mathrm{\Lambda }}_{\text{s}}\cdot \nabla T_{\text{s}}\right)=H_{\text{s}},(1)$

where $c_{\text{w}}$, ${\rho }_{\text{w}}$, and ${\mathbf{v}}_{\text{w}}$ refer to the specific heat capacity, density, and Darcy velocity of groundwater, respectively. ${\mathrm{\Lambda }}_{\text{s}}$ denotes the thermal hydrodynamic dispersion and $H_{\text{s}}$ represents the heat source and sink terms. The following Equation 2 then gives the heat flux between subsurface and the borehole,

$q_{\text{s}}=-{\mathrm{\Phi }}_{\text{gs}}\left(T_{\text{g}}-T_{\text{s}}\right)\mathrm{o}\mathrm{n}{\mathrm{\Gamma }}_{\text{s}},(2)$

where ${\mathrm{\Gamma }}_{\text{s}}$ is the boundary between soil/rock and borehole, ${\mathrm{\Phi }}_{\text{gs}}$ is the thermal resistance between the soil/rock and the grout inside the borehole, and $T_{\text{g}}$ is the grout temperature inside the borehole.

For the grout compartment surrounding the pipe inside the borehole, the heat transport process is dominated only by heat conduction as in Equations 3, 4,

${\rho }_{\text{g}}{c}_{\text{g}}\frac{\partial T_{\text{g}}}{\partial t}-\nabla \cdot \left({\lambda }_{\text{g}}\nabla T_{\text{g}}\right)=H_{\text{g}}(3)$

$\begin{array}{ccc}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{b}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{y}\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{d}\mathrm{i}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}(\mathrm{B}\mathrm{C}):\hfill & \hfill & \hfill \\ q_{\text{g}}=-{\mathrm{\Phi }}_{\text{gs}}\left(T_{\text{s}}-T_{\text{g}}\right)-{\mathrm{\Phi }}_{\text{fg}}\left(T_{\text{f}}-T_{\text{g}}\right)\mathrm{o}\mathrm{n}{\mathrm{\Gamma }}_{\text{g}}.\hfill & \hfill & \hfill \end{array}(4)$

The heat exchange term ${\mathrm{\Phi }}_{\text{fg}}$ is the thermal resistance between the circulation fluid $T_{\text{f}}$ and the grout $T_{\text{g}}$. Detailed calculations of the heat exchange coefficients ${\mathrm{\Phi }}_{\text{fg}}$ and ${\mathrm{\Phi }}_{\text{gs}}$ can be found in Diersch et al. (2011).

For the circulation fluid inside the pipe, the heat transport process is mainly dominated by the heat advection of the circulation fluid with a flow velocity of ${\mathbf{v}}_{\text{f}}$, as in Equations 5, 6

${\rho }_{\text{f}}{c}_{\text{f}}\frac{\partial T_{\text{f}}}{\partial t}+{\rho }_{\text{f}}{c}_{\text{f}}{\mathbf{v}}_{\text{f}}\cdot \nabla T_{\text{f}}-\nabla \cdot \left({\mathrm{\Lambda }}_{\text{f}}\cdot \nabla T_{\text{f}}\right)=H_{\text{f}}(5)$

$\begin{array}{ccc}\mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h}\mathrm{R}\mathrm{o}\mathrm{b}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{y}\mathrm{p}\mathrm{e}\mathrm{o}\mathrm{f}\mathrm{B}\mathrm{C}:\hfill & \hfill & \hfill \\ q_{\text{f}}=-{\mathrm{\Phi }}_{\text{fg}}\left(T_{\text{g}}-T_{\text{f}}\right)\mathrm{o}\mathrm{n}{\mathrm{\Gamma }}_{\text{f}},\hfill & \hfill & \hfill \end{array}(6)$

in which the hydrodynamic thermal dispersion can be written as in Equation 7

${\mathrm{\Lambda }}_{\text{f}}=\left({\lambda }_{\text{f}}+{\rho }_{\text{f}}{c}_{\text{f}}{\beta }_{\text{L}}\Vert {\mathbf{v}}_{\text{f}}\Vert \right)(7)$

where ${\lambda }_{\text{f}}$, ${\rho }_{\text{f}}$, $c_{\text{f}}$ denote the heat conductivity, density, and specific heat capacity of the circulation fluid. Finally, ${\beta }_{\text{L}}$ refers to the longitudinal heat dispersivity coefficient.

The numerical model was implemented in the OGS software using a dual-continuum approach (Chen C. et al., 2021; Diersch et al., 2011). The two heat transport equations inside the borehole are solved on 1D line elements, and the surrounding soil/rock heat transport equation is solved on 3D elements. The heat flux between each component inside the borehole and between the surrounding subsurface is calculated by the difference in temperature and the corresponding heat transfer coefficient. They are explicitly linked and solved together with the governing equations in the OGS numerical model (Chen, 2022). Compared to the fully discretized 3D model, the number of elements can be significantly reduced by implementing the model with DC-FEM technology (Al-Khoury et al., 2010). The implemented model has already been successfully verified against analytical solutions and documented in (Chen C. et al., 2021; Chen, 2022) in detail. More detailed documentation on benchmarks and tutorials for DBHE modeling features can be found on the official OpenGeoSys website (Bilke et al., 2020).

2.2 The 1D wellbore heat transport model

In a well with a constant cross-sectional area, the transient fluid flow in a two-phase, one-component geothermal well can be quantified using one-dimensional formulations of the mass, momentum, and energy balance. The one-dimensional coordinate $s$ runs along the axis of the well towards the top of the well. The specific governing equations are written as follows in Equations 8–10 (Akbar et al., 2016; Chen et al., 2025b):

$\frac{\partial {\rho }_{\text{m}}}{\partial t}=-\frac{\partial \left({\rho }_{\text{m}}{v}_{\text{m}}\right)}{\partial s}(8)$

$\frac{\partial \left({\rho }_{\text{m}}{v}_{\text{m}}\right)}{\partial t}=-\frac{\partial p}{\partial s}-\frac{\partial }{\partial s}\left({\rho }_{\text{m}}{v}_{\text{m}}^2+\gamma \right)-\frac{f{\rho }_{\text{m}}{v}_{\text{m}}|v_{\text{m}}|}{4r_{\text{i}}}(9)$

$\frac{\partial }{\partial t}\left[{\rho }_{\text{m}}{h}_{\text{m}}+\frac{{\rho }_{\text{m}}{v}_{\text{m}}^2}{2}-p\right]$

$=-\frac{\partial }{\partial s}\left[{\rho }_{\text{m}}{v}_{\text{m}}\left(h_{\text{m}}+\frac{1}{2}{v}_{\text{m}}^2\right)\right]+{\rho }_{\text{m}}{v}_{\text{m}}g\cos \theta +\frac{Q_{\text{wf}}}{\pi r_{\text{i}}^2}.(10)$

The primary variables are pressure $p$, mixture flow velocity $v_{\text{m}}$, and mixture-specific enthalpy $h_{\text{m}}$ that takes into account latent heat. ${\rho }_{\text{m}}$ refers to the density of the mixture that is averaged by the volume fraction of the steam $\alpha$. $\theta$ refers to the inclination angle of the wellbore. $r_{\text{i}}$ is the internal radius of the well. $f$ is the wall friction coefficient. The conductive heat flux exchanged between the well and the surrounding formation $(Q_{\text{wf}})$ can be approximated by the semi-analytical solution from Carslaw and Jaeger (1959) and Zhang et al. (2011), as in Equations 11, 12.

$Q_{\text{wf}}=2\pi k\left(T_{\text{well}}-T_{\text{r}}\right)\left[{\left(\pi t_{\text{d}}\right)}^{-0.5}+\frac{1}{2}-\frac{1}{4}\left(\frac{t_{\text{d}}}{\pi }\right)+\frac{1}{8}{t}_{\text{d}}\right]t_{\text{d}}<2.8(11)$

$Q_{\text{wf}}=4\pi k\left(T_{\text{well}}-T_{\text{r}}\right)\left[\frac{1}{\ln \left(4t_{\text{d}}\right)-2\beta }-\frac{\beta }{{\left(\ln \left(4t_{\text{d}}\right)-2\beta \right)}^2}\right]t_{\text{d}}\ge 2.8(12)$

where $t_{\text{d}}$ is the dimensionless time, $t_{\text{d}}=k_{\text{r}}t/({\rho }_{\text{r}}{c}_{\text{r}}{r}_{\text{i}}^2)$. $t$ is the real time. $\beta$ is the Euler’s constant, which equals 0.57722. The subscript $r$ refers to the geothermal reservoir.

The water equation of state in the 1D wellbore model is calculated based on the International Association for the Properties of Water and Steam (IAPWS-IF97) (Wagner and Kretzschmar, 2007). The detailed implementation of the 1D wellbore model can be referred to the reference (Chen et al., 2025b) and the source code can be found on the OGS Gitlab (https://gitlab.opengeosys.org/ogs/ogs).

2.3 Validation

To validate the numerical model used in this work, a 20-m well is drilled in a rock formation with an initial temperature of 55°C. Cold water with a constant inlet temperature of 20°C is continuously injected into the well for 30 days. All the properties used in the model are listed in Table 1. The simulated results of the BHE model have been compared with the analytical solution of wellbore heat transport proposed by Ramey (1962) and the two-phase wellbore simulator (Chen et al., 2025b).

Table 1

Table 1. Parameter values used in the validation case.

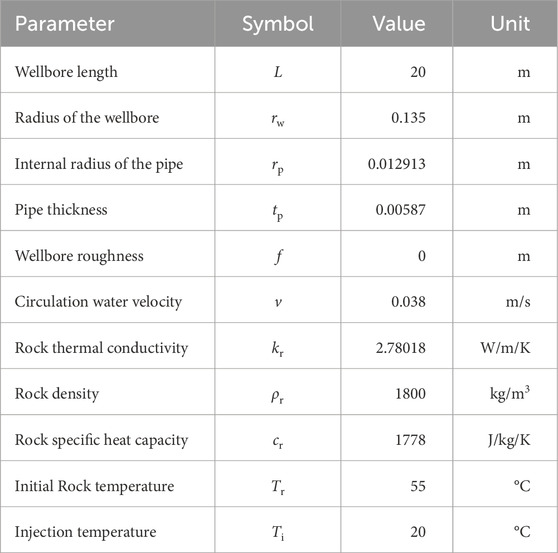
The results under the flow velocity in the tunnel of 0.038 and 0.076 m/s are compared and shown in Figure 1 for the change in outflow temperature over time. The results calculated by the BHE process and the wellbore simulator in OGS software can match the analytical solution very well, the relative difference decreases over the injection time. In the first 5 days, the wellbore simulator can have a better comparison with the analytical solution, especially for the case with very high velocity of 0.076 m/s. With increasing simulation time, the difference between the three models becomes minor. After 30 days, the relative difference between the BHE-1P process and the analytical solution is approximately 0.03%, between the wellbore simulator is approximately 0.01%.

Figure 1

Figure 1. Comparison of the 3D BHE model with the analytical solution proposed by Ramey (1962) and 1D wellbore model implemented by Chen et al. (2025b).

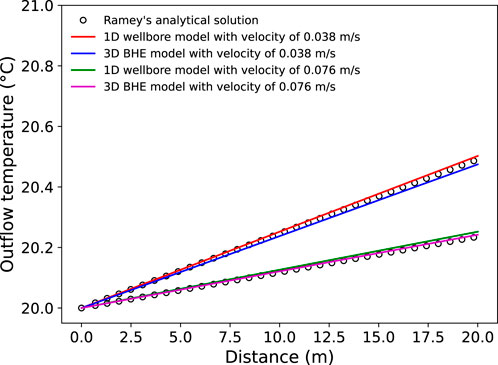
In Figure 2, the temperature distribution of the circulation fluid in the tunnel is additionally compared after injection of 30 days under the two flow velocities in the tunnel. The difference from the analytical solution in the lower velocity case of 0.038 m/s is greater than in the higher velocity case. The fluid temperature at the outlet point has a relative difference of approximately 0.08% against the analytical solution. In total, after the comparison of results among the three models, combining the previous validation results with the monitored data (Cai et al., 2024), the numerical model used in this study is accurate enough to simulate the long-term heat extraction performance of the tunnel network and its cooling effect for the high-temperature coal mines.

Figure 2

Figure 2. The comparison of the temperature distribution in the tunnel well after 30 days.

2.4 Model and scenarios setup

The numerical model in this study was constructed to simulate five horizontal tunnels to extract geothermal energy for the cooling of the coal mine workface. The tunnel length is 100 m and the inter-distance is set at 20, 10, and 5 m, respectively. The boundary BHE is marked as BHE#1, and the center BHE is marked as BHE#3. In order to ensure the accuracy of the model, the total length of the model is 200 m to avoid the thermal plume approaching the model boundary. There are 229,500 elements and 118,776 nodes in the model in total for the simulation by the OGS software.

The initial temperature of the surrounding formation is 55°C and the injection temperature is maintained at 20°C. The total simulation time is 120 days, which means that cold water will be continuously injected into the cooling tunnel for 120 days. The properties of the surrounding formation are the same as the parameters listed in Table 1. When there is groundwater flow in the surrounding formation, it is assumed that the flow velocity is $1\times 10^{-6}$ m/s during the operation.

3 Results

3.1 Base model results

In the base case with the distance between the boreholes of 20 m, the temperature distribution in the cross section of the five tunnels is shown in Figure 3. It can be seen that the thermal plumes generated by BHE heat extraction does not interfere with the model boundary, so that the total energy balance can be ensured. Addtionally, the thermal interaction between the tunnels are minor, as reflected by the temperature distribution.

Figure 3

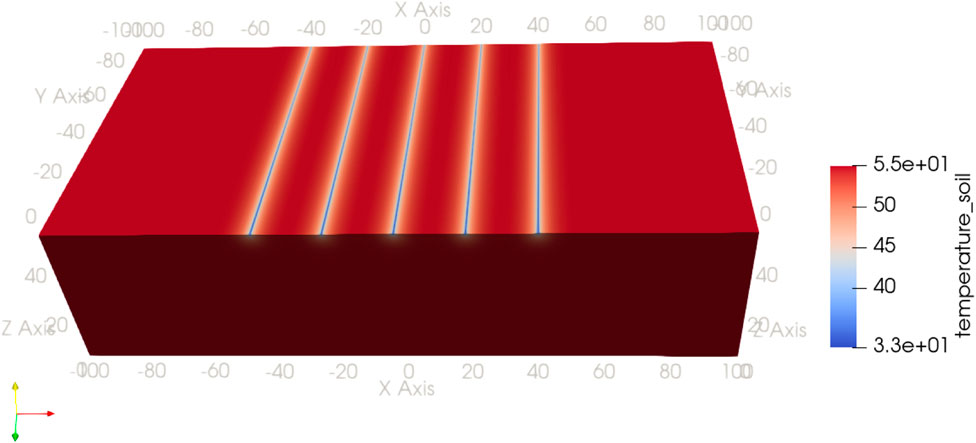
Figure 3. Temperature distribution in the surrounding formation after the heat extraction of 120 days, the inter-distance between BHEs is 20 m.

To further illustrate the temporal evolution of the thermal impacts, the temperature profile across the five tunnels (along the dashed line XX’ in Figure 3) after 10, 60, and 120 days of heat extraction is plotted in Figure 4. It can be observed that thermal interaction begins after approximately 120 days, as indicated by the overlapping thermal influence zones of neighboring BHEs. This indicates that with a well spacing of 20 m, the designed BHEs can provide stable heating for around 120 days—roughly equivalent to the duration of a typical heating season in northern China. Nevertheless, reduced thermal interaction also results in less temperature decrease in the area between tunnel boreholes, making it an ineffective strategy for cooling high-temperature coal mines.

Figure 4

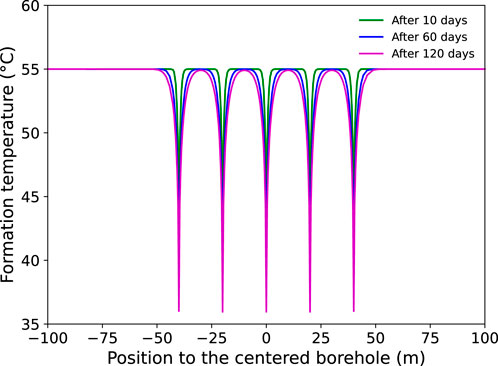
Figure 4. Temperature distribution profile of the surrounding formation crossing the middle position of the horizontal five-tunnel-borehole array.

3.2 Heat extraction rate

When looking at the heat supply capacity of the five tunnel boreholes to buildings in one heating season, the evolution of the outflow temperatures and the heat extraction rates of the boundary and center boreholes are shown in Figure 5. For the base case with a 20 m distance between tunnel boreholes, the outflow temperatures of BHE#1 and BHE#3 are almost identical, further confirming that thermal interaction between the boreholes is negligible across 120 days of heat extraction.

Figure 5

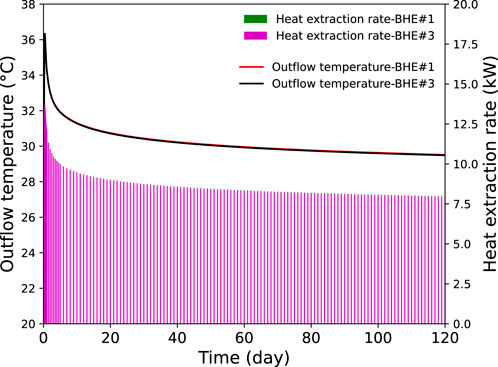
Figure 5. The evolution of outflow temperature from BHE#1 and BHE#3, as well as the heat extraction rate.

Furthermore, the evolution of heat extraction rates shows the same trend as the outflow temperatures, becoming stable after around 40 days. After 120 days, BHE#1 and BHE#3 can reach a stable heat extraction rate of 7,975 and 7950 W, respectively, indicating that the heat extraction capacities are almost unaffected by thermal interaction between neighboring boreholes. It is worth noting that if the heat extraction period extends beyond 120 days, the thermal interaction between boreholes is likely to significantly impact the heat extraction capacity of the BHEs, as more pronounced overlap of thermal influence zones is expected to occur beyond this duration (see Figure 4). In particular, the heat extraction rate of the central BHE (#3) will be most affected, with the greatest reduction in heat extraction capacity, as indicated in the reference (Chen et al., 2020; Chen et al., 2021).

It is worth mentioning that the heat extraction rate in this scenario is also limited by the injection temperature (Chen C. et al., 2021). If colder water is injected into the tunnel wellbores, more heat can be extracted and the formation temperature will decrease faster, leading to more significant thermal interaction between the tunnel boreholes, accompanied by a more pronounced cooling effect. This will pose a challenge from the engineering perspective on how to find a huge amount of cold water in the workface of a high-temperature coal mine.

3.3 Effect of borehole distance

Compared to the influence of injection temperature, the borehole distance could be more interesting to investigate because this will determine the amount of boreholes necessary in a single workface of a high-temperature coal mine to effectively extract geothermal energy and achieve sufficient cooling. Therefore, in this section, the influence of the borehole distance is investigated and three different scenarios are simulated with a borehole distance of 5, 10, and 20 m. The simulated temperature profile after 120 days across the medium depth of the borehole array is depicted in Figure 6.

Figure 6

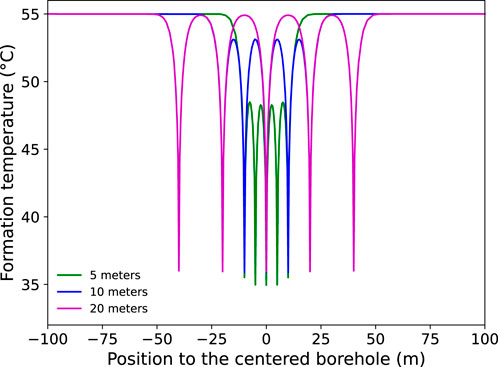
Figure 6. The formation temperature distribution for the three different inter-distance among the BHE after heat extraction of 120 days.

It can be seen from Figure 6 that the overall temperature in the area between boreholes decreases along with the decrease of borehole inter-distance. When the borehole distance is 20 m, the highest temperature in the area between boreholes (from $x=-40$ m to $x=40$ m) equals the initial formation temperature of 55°C, while the average temperature across this section is 52.9°C, equivalent to an average temperature decrease of 2.1°C. However, when the borehole distance is shortened to 5 m, the highest temperature in the area between boreholes (from $x=-10$ m to $x=10$ m) will decrease by approximately 7.2°C compared to the initial temperature (55°C), with an even lower average temperature. Meanwhile, the heat extraction capacity for the smaller distance scenario will decrease since the outflow temperature is expected to decrease (not shown). The lowest BHE outflow temperature in the 20-m distance scenario is 36.0°C (BHE#3), while this value decreases to 35.0°C (BHE#3) in the 5-m distance scenario. The outflow temperature decreases less significantly than the formation temperature in the area between boreholes, indicating that a more effective cooling effect can be achieved, albeit with a slight reduction in heat extraction capacity.

3.4 Effect of groundwater velocity

In this section, the influence of groundwater flow is considered, as groundwater is widely available and can be easily transported in the coal mine. The groundwater velocity is assumed to be $1\times 10^{-6}$ m/s (Huang et al., 2023) flowing from left to right and perpendicular to the direction of the borehole length. The formation temperature distribution after 120 days of the 5-m distance scenario is shown in Figure 7, with the impact of groundwater flow clearly visible at the downstream of the borehole array.

Figure 7

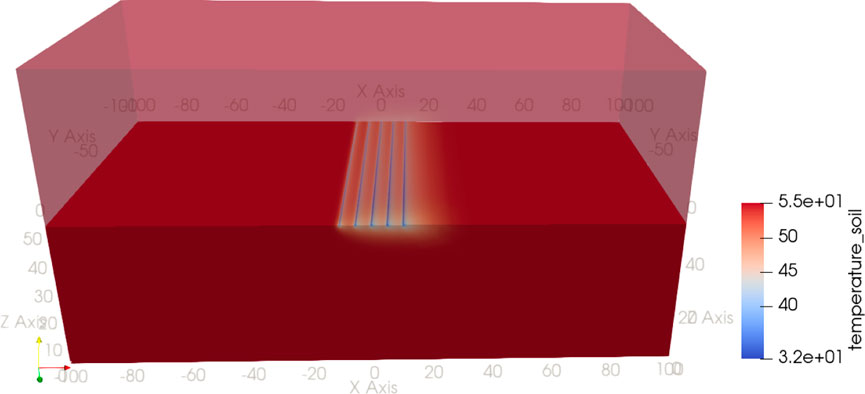
Figure 7. The formation temperature distribution for the borehole distance of 5 m after the heat extraction of 120 days, with the groundwater flow velocity of $1\times 10^{-6}$ m/s.

The detailed formation temperature profile across the BHE array for different borehole distances is depicted in Figure 8. For the cases with borehole spacing of 10 and 20 m, the thermal interaction are less prominent, as the groundwater flow appears to affect all BHEs almost equally. However, the effect of groundwater flow becomes significant when the borehole distance decreases to 5 m, as depicted by the non-uniform temperature profiles around different BHEs.

Figure 8

Figure 8. The formation temperature across the boreholes with the borehole inter-distance of 5, 10, and 20 m after the heat extraction of 120 days, with the groundwater flow velocity of $1\times 10^{-6}$ m/s.

This difference can be further visualized in Figure 9, which shows the temporal evolution of outflow temperatures of different BHEs and their corresponding heat extraction rates in the 5-m distance scenario. It can be seen that the outflow temperatures of BHE#1 and BHE#3 differs significantly after 120 days, reaching 1.6°C difference. Additionally, the heat extraction rate of BHE#1 is 9,250.5 W, whereas BHE#3 reaches only 7,940.8 W. The above differences are mainly due to the impact of groundwater flow, which induces thermal advection in the subsurface heat transport process (Equation 1). As a consequence, the thermal energy compensation of BHE#1 is the strongest since it locates in the most upstream of groundwater flow. The downstream BHEs receive less heat compensation due to the heat extraction of upstream ones, resulting in reduced heat extraction rates. This trend is further confirmed by the heat extraction rate of BHE#5, which is 7,777.2 W, even lower than BHE#3.

Figure 9

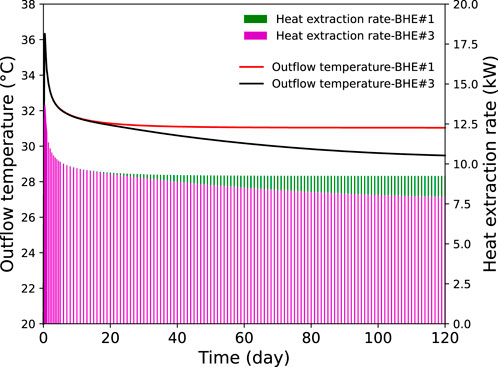
Figure 9. The evolution of outflow temperature from BHE#1 and BHE#3, as well as the heat extraction rate, under the influence of groundwater flow with a borehole distance of 5 m.

It should be noted that the relationship between heat extraction rates of the central and peripheral BHEs is different in scenarios without groundwater flow (Section 3.2 and here with groundwater flow. Also, the borehole distance plays a role. In general, fewer boreholes should be placed downstream when the borehole distance is small, so as to avoid negative thermal interaction between boreholes (Meng et al., 2019).

4 Discussion

4.1 Modeling approach

The 3D model shown in this study consumes more computational time than the 1D model (Akbar et al., 2016; Chen et al., 2025b). However, the 1D model cannot simulate the thermal interactions between boreholes and the influence of groundwater flow. As specified in Equations 11, 12, the 1D wellbore model uses the semi-analytical solution to quantify heat flux exchange with the virtual homogeneous surrounding formation, although the wellbore simulator has the advanced feature of modeling two-phase state.

4.2 Recommendations for sustainable operation

Although this study demonstrates that buried pipes generally exhibit good heat extraction performance in high-temperature coal mines, practical engineering applications often involve complex and variable geological conditions and BHE design requirements. Therefore, several recommendations are proposed to enhance the long-term sustainability and efficient operation of BHEs in coal mine settings.

As discussed in Sections 3.3, 3.4, the spacing between boreholes is a key factor influencing the formation temperature distribution and the heat extraction performance of BHEs (Gultekin et al., 2016). When boreholes are placed closer together, the surrounding temperature decreases more sharply; however, thermal interference between BHEs limits the amount of extractable heat. In contrast, wider borehole spacing generally results in higher average heat extraction rates and a larger cooled volume, despite less pronounced local temperature drops. Moreover, the positive effects of groundwater flow become more evident with increased borehole spacing. In practice, the borehole spacing should be carefully optimized based on the specific heating demand and acceptable formation cooling effects.

Additionally, although the influence of inlet temperature is not addressed in this study, it can be reasonably anticipated that lower inlet temperatures will intensify the cooling effect on the formation. To make practical use of this characteristic, the cascade utilization of mine geothermal heat is recommended, whereby the inlet temperature is progressively reduced through successive applications. Such a cascade system may include, for example, horticulture and fish farming following residential heating (Rubio-Maya et al., 2015).

4.3 Coupling with heat pump

Another discussion point is that the boundary condition of the BHEs is assuming a constant injection temperature in the model. As specified in Chen et al. (2025b), if a dynamic heat pump performance is considered, the total heat load will be redistributed between the heat pump and subsurface. In this case, subsurface heat extraction performance and its sustainability will be underestimated. The tunnel network model in this study can be easily coupled with the surface heat pump thermodynamic model. In real engineering applications, the subsurface heat exchanger must be coupled with the heat pump to further use the geothermal energy extracted for high-temperature coal mines. Whether extracted geothermal energy can be used for heating buildings or just wasted is dependent on the system’s techno-economic performance in the long term. That needs to have more detailed background information and an application case.

5 Conclusion

Based on the scenarios concerning the utilization of geothermal energy for building heating in high-temperature coal mines, a tunnel borehole array is modeled based on the OGS software. Then, a series of scenarios are simulated to investigate the heat extraction capacity and the formation cooling effect of the array. In addition, the influence of the borehole inter-distance and the groundwater flow on the heat extraction performance and the cooling effect is studied. The key findings are summarized below.

• For the base case with a well distance of 20 m, the thermal interaction starts to occur after 120 days. This system can provide stable heating for buildings during one heating season in typical northern China.

• BHE#1 and BHE#3 can reach a stable heat extraction rate of 7,975 and 7950 W, respectively, after 120 days. Their outlet temperatures and the heat extraction rates become stable after around 40 days.

• The mean temperature in the area between boreholes decreases along with the decrease of borehole inter-distance. When the borehole distance is reduced to 5 m, the temperature in the area between the boreholes will decrease by at least 7.2°C compared to the initial temperature 55°C.

• To achieve a better cooling effect, a certain level of thermal interaction between boreholes can be permitted, as the heat extraction capacity is not significantly compromised. However, in the presence of groundwater flow, it is advisable to place more boreholes upstream, especially when the borehole spacing is small (e.g., 5 m).

More techno-economic analysis will be performed in future case studies based on practical coal mines in northern China, so it could give more rational design suggestions for project implementation.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

JZ: Formal Analysis, Investigation, Visualization, Writing – original draft. DM: Formal Analysis, Software, Writing – original draft. XS: Formal Analysis, Software, Writing – original draft. WS: Data curation, Formal Analysis, Writing – original draft. QL: Data curation, Investigation, Writing – original draft. LC: Investigation, Visualization, Writing – original draft. CC: Conceptualization, Investigation, Methodology, Software, Formal analysis, Visualization, Writing – original draft. BM: Formal Analysis, Investigation, Methodology, Writing – review and editing. WC: Formal Analysis, Funding acquisition, Investigation, Methodology, Validation, Writing – review and editing. YK: Formal Analysis, Investigation, Methodology, Resources, Software, Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research is financially supported by the National Natural Science Foundation of China (No. 52306274).

Conflict of interest

Authors JZ, DM, XS, WS, QL, and LC were employed by Shandong Energy Group Xibei Mining Co., Ltd. Author BM was employed by Three Gorges Geotechnical Consultants Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akbar, S., Fathianpour, N., and Al Khoury, R. (2016). A finite element model for high enthalpy two-phase flow in geothermal wellbores. Renew. Energy 94, 223–236. doi:10.1016/j.renene.2016.03.034

CrossRef Full Text | Google Scholar

Al-Khoury, R., Kölbel, T., and Schramedei, R. (2010). Efficient numerical modeling of borehole heat exchangers. Comput. and Geosciences 36, 1301–1315. doi:10.1016/j.cageo.2009.12.010

CrossRef Full Text | Google Scholar

Bilke, L., Flemisch, B., Kalbacher, T., Kolditz, O., Helmig, R., and Nagel, T. (2019). Development of open-source porous media simulators: principles and experiences. Transp. porous media 130, 337–361. doi:10.1007/s11242-019-01310-1

CrossRef Full Text | Google Scholar

Bilke, L., Shao, H., Chen, S., and Cai, W. (2020). Opengeosys tutorial. Available online at: https://www.opengeosys.org/docs/userguide/basics/introduction/ (Accessed April 16, 2025).

Google Scholar

Cai, W., Wang, F., Zhang, Y., Jiang, J., Wang, Q., Shao, H., et al. (2024). Field test and long-term heat extraction performance evaluation of the deep u-type borehole heat exchanger system. Renew. Energy 240, 122171. doi:10.1016/j.renene.2024.122171

CrossRef Full Text | Google Scholar

Carslaw, H., and Jaeger, J. (1959). Conduction of heat in solids. second edition. Oxford, UK: Oxford University Press.

Google Scholar

Chen, C. (2022). Investigation on the heat extraction performance of deep closed-loop borehole heat exchanger system for building heating. Dissertation. Dresden: Technische Universität Dresden.

Google Scholar

Chen, C., Binder, M., Oppelt, L., Hu, Y., Engelmann, C., Arab, A., et al. (2024). Modeling of heat and solute transport in a fracture-matrix mine thermal energy storage system and energy storage performance evaluation. J. Hydrology 636, 131335. doi:10.1016/j.jhydrol.2024.131335

CrossRef Full Text | Google Scholar

Chen, C., Cai, W., Naumov, D., Tu, K., Zhou, H., Zhang, Y., et al. (2021a). Numerical investigation on the capacity and efficiency of a deep enhanced u-tube borehole heat exchanger system for building heating. Renew. Energy 169, 557–572. doi:10.1016/j.renene.2021.01.033

CrossRef Full Text | Google Scholar

Chen, C., Shao, H., Naumov, D., Kong, Y., Tu, K., and Kolditz, O. (2019). Numerical investigation on the performance, sustainability, and efficiency of the deep borehole heat exchanger system for building heating. Geotherm. Energy 7, 18. doi:10.1186/s40517-019-0133-8

CrossRef Full Text | Google Scholar

Chen, C., Witte, F., Taherdangkoo, R., Cai, W., Chen, S., Kong, Y., et al. (2025a). Thermal performance response and heat load redistribution mechanism of a deep u-type borehole heat exchanger in heating systems. Appl. Energy 382, 125216. doi:10.1016/j.apenergy.2024.125216

CrossRef Full Text | Google Scholar

Chen, C., Zhou, H., Nagel, T., Renaud, T., Naumov, D., Kolditz, O., et al. (2025b). Parametric analysis on the transient two-phase wellbore model applied to the yangyi high-temperature geothermal field. Geotherm. Energy 13 (1), 1. doi:10.1186/s40517-024-00322-5

CrossRef Full Text | Google Scholar

Chen, S., Cai, W., Witte, F., Wang, X., Wang, F., Kolditz, O., et al. (2021b). Long-term thermal imbalance in large borehole heat exchangers array–a numerical study based on the leicester project. Energy Build. 231, 110518. doi:10.1016/j.enbuild.2020.110518

CrossRef Full Text | Google Scholar

Chen, S., Witte, F., Kolditz, O., and Shao, H. (2020). Shifted thermal extraction rates in large borehole heat exchanger array–a numerical experiment. Appl. Therm. Eng. 167, 114750. doi:10.1016/j.applthermaleng.2019.114750

CrossRef Full Text | Google Scholar

Ciampi, G., Ciervo, A., Rosato, A., Sibilio, S., and Di Nardo, A. (2018). Parametric simulation analysis of a centralized solar heating system with long-term thermal energy storage serving a district of residential and school buildings in Italy. Adv. Model. and Analysis 55, 165–172. doi:10.18280/ama_a.550310

CrossRef Full Text | Google Scholar

Diersch, H.-J., Bauer, D., Heidemann, W., Rühaak, W., and Schätzl, P. (2011). Finite element modeling of borehole heat exchanger systems: Part 1. fundamentals. Comput. and Geosciences 37, 1122–1135. doi:10.1016/j.cageo.2010.08.003

CrossRef Full Text | Google Scholar

Fraser-Harris, A., McDermott, C. I., Receveur, M., Mouli-Castillo, J., Todd, F., Cartwright-Taylor, A., et al. (2022). The geobattery concept: a geothermal circular heat network for the sustainable development of near surface low enthalpy geothermal energy to decarbonise heating. Earth Sci. Syst. Soc. 3. doi:10.3389/esss.2022.10047

CrossRef Full Text | Google Scholar

Gultekin, A., Aydin, M., and Sisman, A. (2016). Thermal performance analysis of multiple borehole heat exchangers. Energy Convers. Manag. 122, 544–551. doi:10.1016/j.enconman.2016.05.086

CrossRef Full Text | Google Scholar

Hall, A., Scott, J. A., and Shang, H. (2011). Geothermal energy recovery from underground mines. Renew. Sustain. Energy Rev. 15, 916–924. doi:10.1016/j.rser.2010.11.007

CrossRef Full Text | Google Scholar

Huang, Y., Kong, Y., Cheng, Y., Zhu, C., Zhang, J., and Wang, J. (2023). Evaluating the long-term sustainability of geothermal energy utilization from deep coal mines. Geothermics 107, 102584. doi:10.1016/j.geothermics.2022.102584

CrossRef Full Text | Google Scholar

Jiang, J., Wang, F., Yang, X., Zhang, Y., Deng, J., Wei, Q., et al. (2022). Evaluation of the long-term performance of the deep u-type borehole heat exchanger on different geological parameters using the taguchi method. J. Build. Eng. 59, 105122. doi:10.1016/j.jobe.2022.105122

CrossRef Full Text | Google Scholar

Kelly, J. J., and McDermott, C. I. (2022). Numerical modelling of a deep closed-loop geothermal system: evaluating the eavor-loop. AIMS Geosci. 8, 175–212. doi:10.3934/geosci.2022011

CrossRef Full Text | Google Scholar

Kolditz, O., Bauer, S., Bilke, L., Böttcher, N., Delfs, J.-O., Fischer, T., et al. (2012). OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 67, 589–599. doi:10.1007/s12665-012-1546-x

CrossRef Full Text | Google Scholar

Kolo, I., Brown, C. S., Nibbs, W., Cai, W., Falcone, G., Nagel, T., et al. (2024). A comprehensive review of deep borehole heat exchangers (dbhes): subsurface modelling studies and applications. Geotherm. Energy 12, 19. doi:10.1186/s40517-024-00297-3

CrossRef Full Text | Google Scholar

Kong, Y., Chen, C., Shao, H., Pang, Z., Xiong, L., and Wang, J. (2017). Principle and capacity quantification of deep-borehole heat exchangers. Chin. J. Geophysics-Chinese Ed. 60, 4741–4752. doi:10.6038/cjg20171216

CrossRef Full Text | Google Scholar

Loredo, C., Roqueñí, N., and Ordóñez, A. (2016). Modelling flow and heat transfer in flooded mines for geothermal energy use: a review. Int. J. Coal Geol. 164, 115–122. doi:10.1016/j.coal.2016.04.013

CrossRef Full Text | Google Scholar

Menéndez, J., Ordóñez, A., Álvarez, R., and Loredo, J. (2019). Energy from closed mines: underground energy storage and geothermal applications. Renew. Sustain. Energy Rev. 108, 498–512. doi:10.1016/j.rser.2019.04.007

CrossRef Full Text | Google Scholar

Meng, B., Vienken, T., Kolditz, O., and Shao, H. (2019). Evaluating the thermal impacts and sustainability of intensive shallow geothermal utilization on a neighborhood scale: lessons learned from a case study. Energy Convers. Manag. 199, 111913. doi:10.1016/j.enconman.2019.111913

CrossRef Full Text | Google Scholar

Peralta Ramos, E., Breede, K., and Falcone, G. (2015). Geothermal heat recovery from abandoned mines: a systematic review of projects implemented worldwide and a methodology for screening new projects. Environ. Earth Sci. 73, 6783–6795. doi:10.1007/s12665-015-4285-y

CrossRef Full Text | Google Scholar

Preene, M., and Younger, P. (2014). Can you take the heat? geothermal energy in mining. Min. Technol. 123, 107–118. doi:10.1179/1743286314y.0000000058

CrossRef Full Text | Google Scholar

Ramey, H. J. (1962). Wellbore heat transmission. J. petroleum Technol. 14, 427–435. doi:10.2118/96-pa

CrossRef Full Text | Google Scholar

Rosato, A., Ciervo, A., Ciampi, G., Scorpio, M., and Sibilio, S. (2020a). Integration of micro-cogeneration units and electric storages into a micro-scale residential solar district heating system operating with a seasonal thermal storage. Energies 13, 5456. doi:10.3390/en13205456

CrossRef Full Text | Google Scholar

Rosato, A., Ciervo, A., Guarino, F., Ciampi, G., Scorpio, M., and Sibilio, S. (2020b). Dynamic simulation of a solar heating and cooling system including a seasonal storage serving a small Italian residential district. Therm. Sci. 24, 3555–3568. doi:10.2298/tsci200323276r

CrossRef Full Text | Google Scholar

Rubio-Maya, C., Díaz, V. A., Martínez, E. P., and Belman-Flores, J. M. (2015). Cascade utilization of low and medium enthalpy geothermal resources-a review. Renew. Sustain. Energy Rev. 52, 689–716. doi:10.1016/j.rser.2015.07.162

CrossRef Full Text | Google Scholar

Sun, Y., Zhang, X., Li, X., and Duan, C. (2023). A geothermal energy heat exchange system suitable for abandoned mines and its optimization. Heat Mass Transf. 59, 1749–1766. doi:10.1007/s00231-023-03364-w

CrossRef Full Text | Google Scholar

Vukelić, Ž., and Šporin, J. (2024). Groundwater potential for the utilisation of shallow geothermal energy from a closed coal mine. Water 16, 1572. doi:10.3390/w16111572

CrossRef Full Text | Google Scholar

Wagner, W., and Kretzschmar, H.-J. (2007). International steam tables - properties of water and steam based on the industrial formulation IAPWS-IF97. Berlin: Springer Science and Business Media.

Google Scholar

Xu, Y., Li, Z., Chen, Y., Jia, M., Zhang, M., and Li, R. (2022). Synergetic mining of geothermal energy in deep mines: an innovative method for heat hazard control. Appl. Therm. Eng. 210, 118398. doi:10.1016/j.applthermaleng.2022.118398

CrossRef Full Text | Google Scholar

Zhang, B., Zhan, R., Liu, L., Huan, C., Zhao, Y., and Zhang, X. (2024). A comparative analysis of the performance of backfill heat exchangers in deep mine geological environments. Appl. Therm. Eng. 239, 122092. doi:10.1016/j.applthermaleng.2023.122092

CrossRef Full Text | Google Scholar

Zhang, Y., Pan, L., Pruess, K., and Finsterle, S. (2011). A time-convolution approach for modeling heat exchange between a wellbore and surrounding formation. Geothermics 40, 261–266. doi:10.1016/j.geothermics.2011.08.003

CrossRef Full Text | Google Scholar