Use of steel slag and recycled concrete in GeoBarrier system for slope stabilization

Improving slope stability against rainfall-induced slope collapses is a current area of study interest in geotechnical structure design for climate change mitigation. The GeoBarrier system (GBS) concept used recycled concrete and steel slag to avoid these kinds of failures. The present study investigated the practicability of incorporating recycled concrete and steel slag, two types of recycled materials, into the GBS design. Extensive experimental investigations were conducted to determine the index properties and hydraulic characteristics, including permeability functions, soil-water characteristic curves (SWCCs), and unsaturated shear strength parameters of steel slag and recycled concrete. A finite element transient seepage analysis and limit equilibrium slope stability study were conducted to evaluate the impact of precipitation on the pore water pressure profile of the slope and its stability under rainfall circumstances, respectively. According to the findings, no breakthrough into the steel slag, a coarse-grained layer within the GBS, was observed. Based on the pore-water pressure profiles and the variation in the factor of safety (FOS) over time, steel slag and recycled concrete were found to be applicable for use as coarse- and fine-grained layers in the GBS, respectively. The incorporation of these waste materials facilitated the slope protection against infiltrated rainwater into the slope and increased the FOS for a slope with a height of 10 m and a slope angle of 70°.

1 Introduction

One of the significant contributors to worldwide climate change is the production of waste and its disposal (Chua et al., 2022). In the aftermath, extreme weather conditions, including the intensification of rainfall or its extended absence, referred to as a dry period, which often results in wildfires, are all meant by climate change (Tallar et al., 2025; Kristo et al., 2019). Cities, as hubs of rapid industrial development and growing populations, produce thousands of tons of waste daily, all of which must be properly managed (Rahardjo et al., 2016a). Globally, between seven and nine billion tonnes of waste products are generated annually (Wilson et al., 2015). On account of inadequate solid waste management, stemming from ineffective policies, limited transportation services, and a deficiency in proper waste treatment facilities, it will lead to the pollution of water, soil, and air that exposes both individuals and the environment to risk (Eawag, 2008). As environmental and public health issues mount, and as economic advancement prevails, the need to utilize these waste products as sustainable resources on a global scale is becoming ever more pressing (Rahardjo et al., 2013).

In practical terms, extreme weather events, such as heavy precipitation, induced by climate change may aggravate environmental hazards. For instance, landslides, which are prevalent worldwide, expose populations and infrastructure to substantial risk, often resulting in fatalities, injuries, and substantial socio-economic losses (Zhang and Li, 2018; Guzzetti et al., 2022). It occurs when stress conditions underneath the slopes exceed critical levels (Terzaghi, 1950; Guzzetti et al., 2022). In the process, rainfall plays a pivotal role, making alterations to groundwater dynamics and reducing slope stability, as the buildup of pore water pressure causes a reduction in negative pore water pressure (Terzaghi, 1962; Kim et al., 2022). Negative pore-water pressure, in other terms, is defined as soil suction (Ψ), and it is a key term in the domain of unsaturated soil mechanics (Zhai et al., 2021). A reduction in soil suction results in a corresponding decrease in shear strength of the soil, bringing about an increase in the likelihood of slope failure (Tsaparas et al., 2002). Other factors, such as steep slopes, seismic activity, and anthropogenic stresses, can further amplify the landslide risk, with mountainous regions being particularly vulnerable (Thurman, 2011). Thurman (2011) highlighted the susceptibility of Kazakhstan regions to landslides resulting from accelerated glacier melting and downpour events, which pose serious danger. Chepelianskaia and Sarkar-Swaisgood (2022) have specified that the landslide risk in the Southeast and East regions of Kazakhstan ranges from medium to high. To a large extent, understanding these factors and regional risks is crucial for implementing effective mitigation strategies for ensuring the safety of affected populations and infrastructure in those regions.

Preventive measures must be undertaken to reduce the possibility of slope failures caused by rainfall, protecting adjacent structures or community facilities. There are diverse varieties of slope stabilization methods that include horizontal drains, the capillary barrier system (CBS), and vegetation cover systems (Rahardjo et al., 2012a). Horizontal drains are widely employed for the stabilization of unsaturated residual soil slopes. Several parameters, including drain type, position, quantity, length, and spacing, are critical for the performance of a horizontal drainage system. A CBS is another preventative method that can be adopted to prevent rainfall infiltration. It is composed of a fine-grained layer placed on top of a coarse-grained layer of soil (Stormont, 1996; Chen et al., 2020). Additionally, CBS is incorporated into the GBS, which is a manufactured three-layered retaining structure that implements CBS principles and includes vegetation as a top layer (Rahardjo et al., 2019a; Chua et al., 2022). The demand for alternatives arises from the fact that the application of traditional slope stabilization methods can be costly, challenging to implement, and not necessarily meet the aesthetics of the location. Vegetative stabilization, or green technology, is an unconventional method for strengthening slope stability via integrating living biological elements with engineering design approaches (Rahardjo et al., 2019b; Aziz and Islam, 2022).

The field studies conducted by Rahardjo et al. (2012b), Rahardjo et al. (2007), Rahardjo et al. (2017a) demonstrated that the CBS effectively minimized rainfall infiltration, preserving slope stability up to around a 45° slope angle (Rahardjo et al., 2019c). However, when constructing slopes that are steeper than 45°, a retaining structure must be considered. The GBS, a retaining structure that combines CBS and vegetation, was later proposed by Rahardjo et al. (2015) (Rahardjo et al., 2019c). GBS is composed of fine- and coarse-grained layers that use recycled materials instead of natural materials, such as sand or gravel, hence promoting recycling as well. On top of that, GBS does not require materials, like concrete and steel, which makes it more environmentally safe and favorable for implementation in both countryside and city areas (Chua et al., 2022).

The retaining structure of GBS employs geosynthetics, such as geobags, which include geogrid reinforcement and are filled with fine-grained material to form reinforced walls (Rahardjo et al., 2018a). According to the research conducted by Rahardjo et al. (2018b), geobags placed between the fine- and coarse-grained components were not interfering with the CBS. Approved soil mixture (ASM) is a vegetative soil essential for the proper growth of the plants. To ease the introduction of deeply and widely rooted plants and trees in the framework of the wall facing, ASM had been enclosed in bags and installed up front, following the fine-grained component. The ASM bag is attached to the geogrid, reinforcing the system, and on account of this connection, the ASM bag contributes its role as facing within the retaining structure system as well (Rahardjo et al., 2019c). Figure 1 illustrates a schematic representation of GBS made of three primary components: a reinforced soil system (RSS), CBS, and ASM.

Figure 1

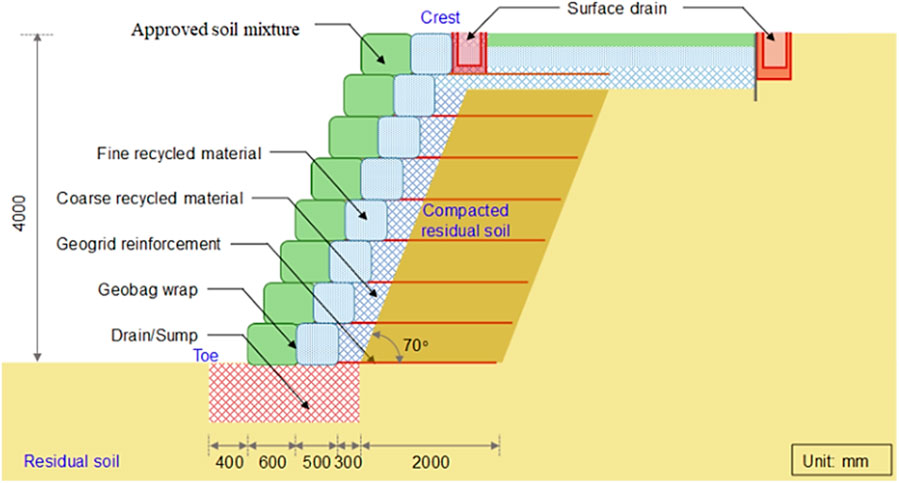
Figure 1. Schematic diagram of GBS (Chua et al., 2022).

On the basis of distinguishing unsaturated hydraulic characteristics, like soil-water characteristic curve (SWCC) and unsaturated permeability of the selected materials, GBS’s functioning is feasible, as in accordance with unsaturated conditions, the existing permeability contrast between fine- and coarse-grained layers restricts downward water flow via the effect of the capillary barrier. Compared to the fine-grained material, the coarse-grained material has a substantially lower coefficient of permeability at high suction ranges. In this scenario, water is unlikely to penetrate the coarse-grained layer. Capillary forces hold the penetrated water within the fine-grained material. The infiltrated water is eventually released via percolation into the drain at the slope’s toe, the lateral drainage system, and through evapotranspiration. Due to the capillary barrier effect, water is restricted from penetrating the slope until percolation (breakthrough) to the coarse-grained layer occurs (Rahardjo et al., 2016b).

According to the field study and numerical analyses results obtained by Rahardjo et al. (2017b), soil suction within the slope covered with GBS was maintained constant, whereas the suction in the soil inside the original slope dropped dramatically during the wet period. This demonstrated the efficacy of GBS as a retaining structure in reducing rainfall infiltration into the deeper soil layers (Rahardjo et al., 2017b). In another study by Rahardjo et al. (2020), GBS performance was evaluated on a slope with residual soil in Singapore. GBS was constructed for the slope with a 4 m height and a slope angle equal to 70°. The GBS was made up of eight layers of geobags that were placed atop one another and reinforced by 2.8 m of geogrid inside each layer of geobags. Eventually, GBS was capable of hindering raindrops from penetrating the underlying soil layers, consequently preserving slope stability that was unaffected by the infiltrated rain (Rahardjo et al., 2020). In this work, steel slag (SS) and recycled concrete (fine recycled concrete aggregate or FRCA) will be examined as capillary barrier materials inside the GBS for the slope protection against rainfall-triggered slope failures.

SS and recycled concrete are waste materials that have become in demand among many researchers around the world. SS is a by-product of the steel industry that is capable of providing properties applicable in different construction practices, contributing to sustainable development (Han et al., 2014; Rahardjo et al., 2013a). SS finds its application in road construction, creating aggregates comparable to natural ones owing to its high strength and durability (Motz and Geiseler, 2001), and in hydraulic construction due to its high abrasion and rough texture (Yi et al., 2012). A study by Rezaei-Hosseinabadi et al. (2022) investigated the use of SS as granular columns for treating problematic soils. When they introduced a SS or sand column in soil, its shear strength increased. Recycled crushed concrete, on the other hand, enhances soft soil’s characteristics, reducing swelling and compression while improving cohesiveness (Karkush and Yassin, 2019). In addition, recycled aggregates derived from construction and demolition waste demonstrated comparable drainage capacity to natural aggregates, enabling the construction of drainage structures (Roque et al., 2022). Recycled concrete aggregates have been used as a part of the GBS model in several studies, including Rahardjo et al. (2017b), Rahardjo et al. (2018a), Rahardjo et al. (2019c), Satyanaga et al. (2021) and Chua et al. (2022). On the whole, both materials offer viable solutions for sustainable construction practices, addressing environmental concerns while meeting construction needs.

In this work, GBS developed by Rahardjo et al. (2015) was proposed to protect a typical slope in the Almaty region of Kazakhstan by utilizing SS and FRCA, which have not previously been implemented together in the design model, especially considering the fact that SS in general is not commonly used for slope protection. It is crucial to minimize rainfall infiltration to maintain the safety of local slopes and, at the same time, preserve natural materials, which can be accomplished by the application of GBS. The principal goal is to investigate the characteristics of SS and FRCA for protecting slopes against rainfall-triggered landslides. To accomplish this goal, the following objectives have been established: 1) examine the physical and hydraulic characteristics of waste materials and perform seepage and stability analyses; 2) evaluate the effectiveness of SS and FRCA as capillary barrier materials inside the GBS.

2 Materials and methods

The present study includes laboratory testing procedures to evaluate the saturated and unsaturated properties of SS, FRCA, and ASM, as well as finite element seepage and slope stability analyses, which can be seen in more detail in the flowchart (Figure 2). Soil parameters obtained from experimental tests were incorporated in numerical analyses whose results were used to assess the performance of GBS using the studied materials, which were SS, FRCA, and ASM (see Figure 3). Since a vegetative soil layer is required in GBS analyses, ASM properties were also determined by conducting laboratory tests.

Figure 2

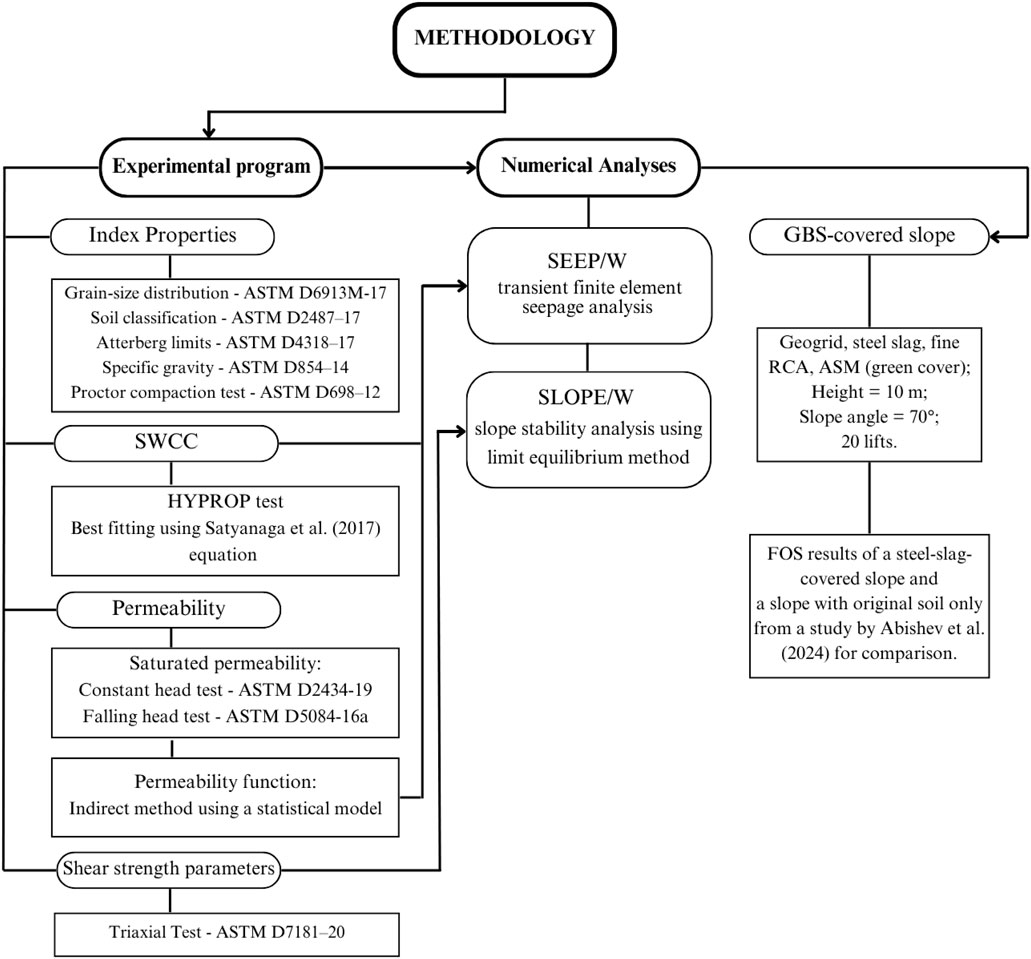
Figure 2. A flow chart of methodology including experimental program and numerical analyses using SEEP/W and SLOPE/W.

Figure 3

Figure 3. (A) Steel Slag (SS), (B) recycled concrete–Fine Recycled Concrete Aggregate (FRCA), (C) soil for vegetation–approved soil mixture (ASM) used in the study.

The current study focused on the typical slope in Almaty because this region has experienced a significant amount of slope collapses in the past. Given that there are no samples of the original soil to be studied, to define shear strength parameters of the original soil, properties of a clayey loam containing 5% fine pebbles were assigned, as reported in a study by Sharipov et al. (2023): cohesion (c′) = 33 kPa, friction angle (φ′) = 19°, and unit weight (γ) = 17 kN/m³. The shear strength parameters were incorporated in the subsequent slope stability analyses. In accordance with the guidelines provided by Mercer et al. (2019), the USCS classification of original soil was used to create the SWCC. While the permeability function was estimated using the SWCC and saturated permeability, following the statistical method outlined by Satyanaga et al. (2022). The SWCC and the permeability function of the original soil were incorporated into the seepage analysis and presented in Figures 6, 7, respectively.

2.1 Experimental program

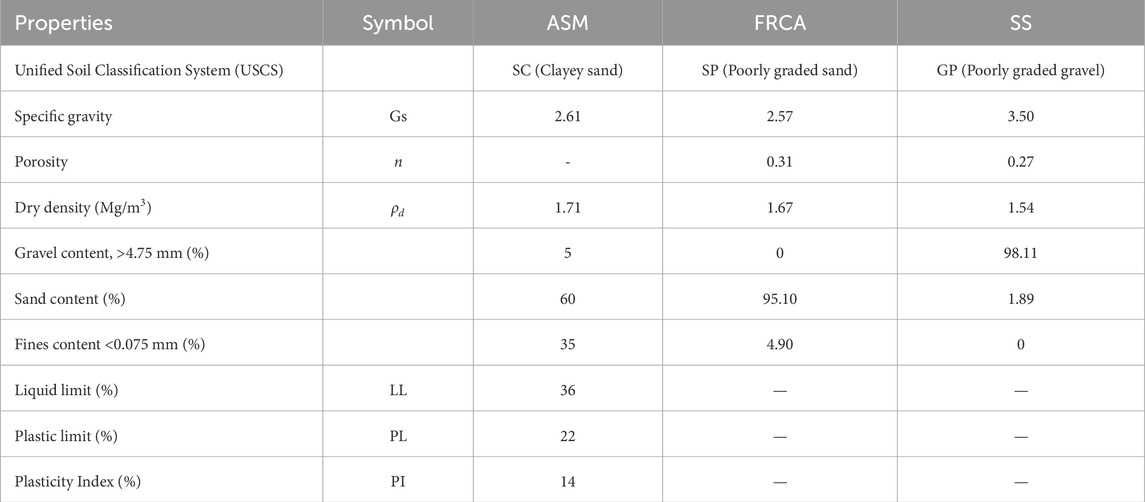
Grain-size distribution (GSD) tests of SS, FRCA, and ASM were performed following ASTM D6913M-17. For this part of the work, sieve analysis of waste materials and the ASM were conducted to obtain the desired soil particle size, coarse or fine, and to classify the soil according to ASTM D2487–17. GSD and the pore size distribution of soils are closely related; therefore, GSD is deeply connected to the SWCC (Perera et al., 2005). To accomplish the index properties of SS, FRCA, and ASM, other tests like Atterberg limits, specific gravity, and Proctor compaction tests were carried out following ASTM D4318–17, ASTM D854–14; ASTM D698–12, respectively.

SWCC can be measured using various methods, including the Tempe Cell Test and Pressure Plate equipment or HYPROP equipment. Compared to the Tempe cell test, HYPROP is a more accurate and, of greater importance, quicker approach for determining SWCC. The method is based on Wind, (1968) evaporation approach, which is optimized by Schindler, (1980) model (METER Group AG, 2018; Satyanaga et al., 2019). In this case, SWCC had been measured using HYPROP equipment. The procedures for SWCC testing using HYPROP equipment consist of the following steps: soil collection and saturation of the soil sample; setup of the measuring equipment; assembly of the specimen within the device; and commencement of measurement and analysis of the measured data using HYPROP-FIT.

The material was arranged to match the capacity of a sample ring and compacted within five layers, achieving a total height of 5 cm for the sample ring, with a total of 25 blows applied to each 1 cm layer (ASTM D698–12). In the subsequent step, the compacted specimen in the sample ring was immersed in a bowl of water to be saturated. At the same time tensiometers with ceramic tips were inserted in a beaker containing deionized water. Following saturation, holes were bored into the soil with a tension shaft auger. Drill holes were filled with water during assembly to prevent air from being driven into the soil sample. The holes in the sensor unit were filled bubble-free using a droplet syringe, after which the tensiometers were secured in the openings. Following the careful placement of the sensor unit on the soil sample, the entire test setup was inverted. After removing the saturation plate and nonwoven cloth, the sample ring and clips were carefully cleaned and dried. After the soil sample was prepared, measurements were initiated (METER Group AG, 2018). To complete the variation of soil suction with water content, HYPROP test results were best fitted using the equation for the unimodal SWCC developed by Satyanaga et al. (2017), whose parameters have physical meaning.

Saturated permeabilities (k_s) of the SS and FRCA specimens were identified using the constant head test according to ASTM D2434–19. Since the examined materials were granular soils with less than 10% passing the 75-micron (No. 200) sieve, the constant head test method was chosen. The saturated permeability of ASM was identified using the falling head permeability test method based on ASTM D5084–16a because this method is commonly used for less permeable soils, like silt and clay. The permeability functions (k_w) of the materials were measured by an indirect method using a statistical model. While Darcy’s law is generally used to characterize water flow in saturated conditions, it can still apply to flow in unsaturated soils. Though unlike saturated soils, the permeability of unsaturated soils changes with the soil suction. Therefore, it is required to treat the permeability in unsaturated soils as a function rather than a constant (Fredlund and Rahardjo, 1993). However, it can be challenging to measure it directly, therefore, theoretical methods—which are regarded as indirect methods—are usually used to estimate this parameter. To determine the permeability function, one known approach is to incorporate SWCC (Fredlund and Rahardjo, 1993). Using the given method, the following Equation (1) can be used to estimate the permeability function, represented by $k_w$:

$k_w{\left(\theta \right)}_i=\frac{k_s}{k_{sc}}{A}_d{\displaystyle \sum _{j=i}^m}\left[\left(2j+1-2i\right){{\left(u_a-u_w\right)}_j}^{-2}\right],i=1,2,\dots ,m(1)$

Where: $k_w{\left(\theta \right)}_i$ = estimated permeability coefficient at the $i$ th interval for a given volumetric water content ${\theta }_i$ (m/s); $i$ = interval number that decreases as water content increases (e.g., on the experimental SWCC, $i=m$ indicates the final interval near the lowest volumetric water content (${\theta }_L$), and $i=1$ indicates the initial interval near the saturated water volumetric content (${\theta }_s$)); $A_d$ = adjustment factor [i.e., (${T_s}^2{\rho }_{w}g/2v_w$) (${{\theta }_s}^p$/$N^2$) (m⋅ $s^{-1}·{kPa}^2$)]; $k_{sc}$ = estimated saturated permeability coefficient (m/s); $T_s$ = surface tension of water (kN/m); ${\rho }_w$ = density of water (kg/m³); $g$ = acceleration due to gravity (m/s²); $v_w$ = absolute viscosity of water (Ns/m²); $p$ = constant that addresses the interaction of pores of varying sizes; $m$ = total number of intervals between ${\theta }_s$ and ${\theta }_L$ on the experimental SWCC; $N$ = total number of intervals computed between ${\theta }_s$ and zero water content, i.e., $\theta$ = 0 (note: $N$ = $m$ [${\theta }_s$/ $\left({\theta }_s-{\theta }_L\right)$], $m$ ≤ $N$, and $m$ = $N$ when ${\theta }_L$ = $0$).

The permeability of unsaturated soil can be indirectly measured using the SWCC data. In order to account for SI units and substitute soil suction for the pore-water pressure head, Fredlund et al. (1994) modified the Kunze et al. (1968) model. The relationship between volumetric water content and soil suction is divided into m equal intervals according to water content for computational purposes. The soil suction value at each segment’s midpoint is then used to calculate the permeability coefficient.

The triaxial test was performed following ASTM D7181–20, and it consisted of three stages: saturation, consolidation, and shearing. The main purpose of the triaxial test was to measure effective cohesion (c′) and effective friction angle (φ′). Out of three different types of triaxial tests, the consolidated-drained (CD) triaxial test was conducted since this test is suitable for the coarse-grained material used in this study. In this case, the drainage valve was open during all the stages of the test to consolidate the specimen under a selected confining pressure and avoid excess pore pressure when the deviator stress was applied during the shearing stage (Bishop and Henkel, 1962).

The starting point was to place a triaxial cell on top of a cylinder-shaped soil sample covered with a rubber membrane. When setting up the soil specimen, first, a metal split mold with an internal diameter of 7.1 cm was sealed with a 1 mm-thick rubber membrane. Filter paper and a porous stone were used to line the base of the membrane, which was secured to the pedestal using O-rings. After that, the soil mixture was placed in layers, each of the layers being hammered 50 times to reach a height of 14 cm. The specimen was left to stand unsupported after the air in the membrane was removed with a hand vacuum. Another filter paper and porous stone were placed on top, and the membrane was sealed with additional O-rings. The triaxial cell was then filled with water.

Before consolidation, saturation was verified by measuring the pore water pressure response (Δu) to a change in cell pressure (Δσ_c). A B-value of one denoted full saturation. Back pressure was raised to release trapped air if it could not be reached (Powrie, 2004). Following saturation, the specimen was consolidated under a predetermined confining pressure (σ₃) while an open-valve system tracked changes in water volume. When no more volume change was observed, equilibrium was achieved. Under drained conditions, shearing had taken place at a strain rate of 0.01 mm/min. A volume change transducer was used to record the volume change during shearing. The shearing process was stopped when the maximum deviator stress was attained. In multistage tests, the procedures for the consolidation and shearing were repeated at varying confining pressures. Each stage proceeded with zero deviator stress, adjusted by releasing axial load. Shearing at each stage stopped near the peak stress, except in the final stage, where higher strain levels were allowed.

2.2 Numerical analyses

Numerical analyses are used to analyze the behavior of the GBS to actual rainfall, allowing the numerical model to anticipate the performance of the GBS slope under various soil characteristics and flux boundary conditions. The stability and behavior of unsaturated soil slopes under different loading situations can be studied using GeoStudio software (Abishev et al., 2025). It is commonly used by many researchers throughout the world (Mohammad et al., 2024; Zhong et al., 2023; Gao et al., 2023) This software is able to incorporate SWCC and permeability functions to accurately analyze water seepage through unsaturated soil, while other software has limited functions related to unsaturated soil mechanics principles (Fredlund et al., 2012). Thereby, the numerical analyses were conducted using GeoStudio software, in particular using SEEP/W for transient finite element seepage analysis and SLOPE/W for slope stability analysis by the limit equilibrium method. SEEP/W can examine seepage and flow and mimic the movement of water through unsaturated soil (Abishev et al., 2025). It delivers a series of preserved timesteps, each with its own pore water pressure distribution determined by stated material properties, boundary conditions, and recharge parameters (Camera et al., 2011). To assess the combined effects of rainfall infiltration and slope stability, SEEP/W analysis data can be input into SLOPE/W slope stability analysis (Abishev et al., 2025). SLOPE/W may be used to predict how soil suction with water content would change in response to rainfall and how these changes will affect slope stability (Lee et al., 2009).

The governing partial differential equation of seepage enables the analysis of water infiltration through saturated and unsaturated soil in both steady and transient conditions. The solution is discovered through the application of numerical modeling techniques, including finite difference and finite element methodologies (Fredlund et al., 2012). The finite element method is utilized to address two-dimensional transient seepage issues, integrating Equations (2) and (3) for saturated and unsaturated soils, respectively. Unsteady state seepage equations:

$\text{Saturated}:\hspace{0.17em}{k}_s\left(\frac{{{\partial }^{2}h}_w}{\partial x^2}\right)+k_s\frac{\partial }{\partial y}\left(\frac{{{\partial }^{2}h}_w}{\partial y^2}\right)=m_v{\rho }_{w}g\frac{\partial h_w}{\partial t}(2)$

$\text{Unsaturated}:\hspace{0.17em}\frac{\partial }{\partial x}\left(k_w\frac{\partial h_w}{\partial x}\right)+\frac{\partial }{\partial y}\left(k_w\frac{\partial h_w}{\partial y}\right)={m_2}^w{\rho }_{w}g\frac{\partial h_w}{\partial t}(3)$

where: $k_s$ = saturated coefficient of permeability; $m_v$ = the coefficient of volume change for saturated soils; $k_w$ = permeability function; $\frac{\partial h_w}{\partial x}$ = hydraulic head gradient in the x-direction; $\frac{\partial h_w}{\partial y}$ = hydraulic head gradient in the y-direction; ${m_2}^w$ = water storage modulus (the coefficient of water volume change); ${\rho }_w$ = density of water; $g$ = acceleration due to gravity; t = time.

The limit equilibrium method is used to conduct a slope stability analysis. There are two FOS equations used to determine two types of equilibrium: horizontal force and moment equilibrium (Fredlund et al., 2012). Assuming an atmospheric air pressure ($u_a$ = 0), the following FOS equations with respect to force equilibrium for saturated (Equation 4) and unsaturated (Equation 5) soils are obtained:

$\text{Saturated}:\hspace{0.17em}{\mathit{F}}_{\mathit{f}}=\frac{\sum \left[{\mathit{c}}^{\prime }\mathit{\beta }\mathit{}\mathit{cos}\mathit{}\mathit{\alpha }+\left\{\mathit{N}-{\mathit{u}}_{\mathit{w}}\mathit{\beta }\right\}\mathit{tan}\mathit{}{\mathit{\phi }}^{\prime }\mathit{}\mathit{cos}\mathit{}\mathit{\alpha }\right]}{\sum \mathit{Nsin}\mathit{\alpha }}(4)$

$\text{Unsaturated}:\hspace{0.17em}{\mathit{F}}_{\mathit{f}}=\frac{\sum \left[{\mathit{c}}^{\prime }\mathit{\beta }\mathit{cos}\mathit{}\mathit{\alpha }+\left\{\mathit{N}-{\mathit{u}}_{\mathit{w}}\mathit{\beta }\frac{\mathit{tan}\mathit{}{\mathit{\phi }}^{\mathit{b}}}{\mathit{tan}\mathit{}{\mathrm{\phi }}^{\prime }}\right\}\mathit{tan}\mathit{}{\mathit{\phi }}^{\prime }\mathit{}\mathit{cos}\mathit{}\mathit{\alpha }\right]}{\sum \mathit{Nsin}\mathit{\alpha }}(5)$

where: $F_f$ = FOS with respect to force equilibrium; $c^{\prime }$ = effective cohesion; ${\phi }^{\prime }$ = effective friction angle; ${\phi }^b$ = angle indicating the rate of increase in shear strength with respect to a change in suction; $u_w$ = pore-water pressure; N = total normal force on the base of the slice; α = angle between the tangent to the center of the base of each slice and the horizontal (when the angle slopes in the same direction as the overall slope of the geometry, α is positive, and vice versa); β = sloping distance across the base of a slice.

For moment equilibrium with zero pore-air pressure, the FOS equations for saturated (Equation 6) and unsaturated (Equation 7) conditions:

$\text{Saturated}:\hspace{0.17em}{F}_m=\frac{\sum \left[c^{\prime }\beta R+\left\{N-u_w\beta \right\}Rtan{\phi }^{\prime }\right]}{\sum Wx-\sum Nf}(6)$

$\text{Unsaturated}:\hspace{0.17em}{\mathit{F}}_{\mathit{m}}=\frac{\sum \left[{\mathit{c}}^{\prime }\mathit{\beta }\mathit{R}+\left\{\mathit{N}-{\mathit{u}}_{\mathit{w}}\mathit{\beta }\frac{\mathit{tan}\mathit{}{\mathit{\phi }}^{\mathit{b}}}{\mathit{tan}\mathit{}{\mathit{\phi }}^{\prime }}\right\}\mathit{Rtan}{\mathit{\phi }}^{\prime }\right]}{\sum \mathit{Wx}-\sum \mathit{Nf}}(7)$

Where: $F_m$ = FOS with respect to moment equilibrium; $c^{\prime }$ = effective cohesion, ${\phi }^{\prime }$ = effective friction angle; ${\phi }^b$ = angle indicating the rate of increase in shear strength with respect to a change in suction; $u_w$ = pore-water pressure; N = total normal force on the base of the slice; β = sloping distance across the base of a slice; R = radius for a circular slip surface, or the moment arm corresponding to the mobilized shear force Sm​ for slip surfaces of any shape; W = total weight of the slice of width b and height h, or shortly the slice weight; x = horizontal distance from the centerline of each slice to the center of rotation; f = perpendicular offset of the normal force from the center of rotation.

According to the regional data in Almaty, the groundwater table level is between 3 and 10 m below the ground surface (King et al., 1999). Therefore, the average value of the groundwater table was taken as 5 m beneath the ground surface at the slope’s toe for a 10 m-high slope. For the numerical analyses, based on the climatic conditions in Kazakhstan, a daily rainfall not exceeding 20 mm was adopted (Chepelianskaia and Sarkar-Swaisgood, 2022). Rainfall was distributed in the form of a flux boundary condition, and its intensity was set to 20 mm/day on the ground surface of the numerical model. To properly introduce the groundwater table, constant total heads were also applied to both the left and right sides of the model as boundary conditions. These boundary conditions were assigned to avoid the impact of the side boundary condition on the examined slope (Gasmo et al., 2000). The boundary conditions and main components of GBS can be seen in Figure 4.

Figure 4

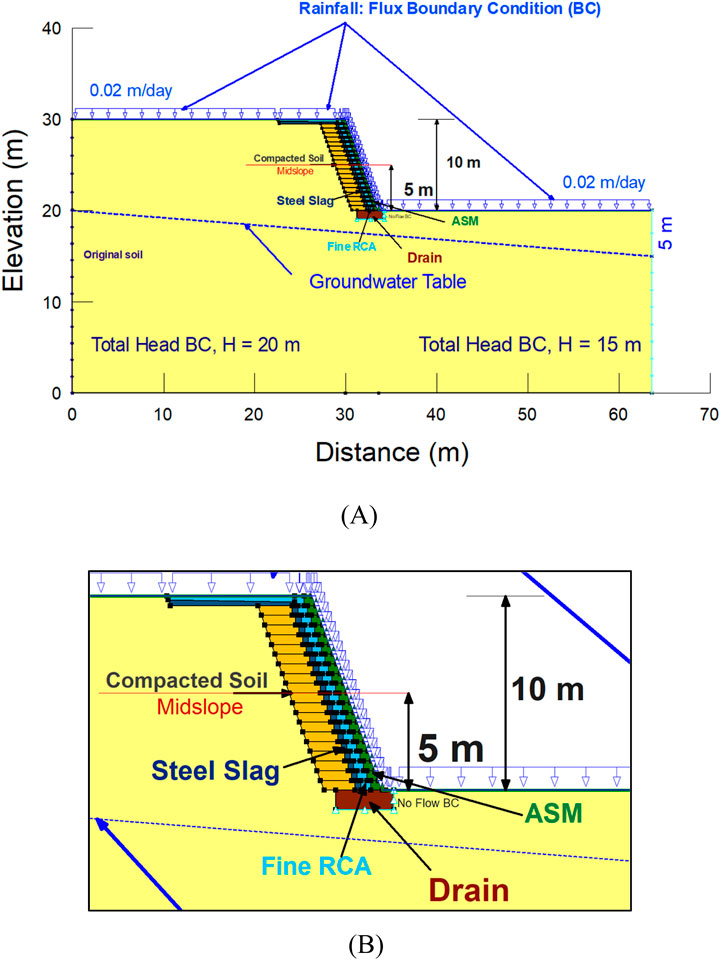
Figure 4. (A) A numerical model for seepage analyses: GBS for a slope with a 10 m height and a 70° inclination. (B) The enlarged figure of GBS components.

The element size used in the finite element study was 0.1 m as adopted from a study by Chua et al. (2022). A numerical model of GBS was constructed for a steep slope with a 10 m height and a 70° inclination. The thicknesses of each of the GBS components were assigned according to the model developed by Rahardjo et al. (2015). The GBS was made up of compacted soil, geogrid reinforcement, SS and FRCA for the CBS, and ASM for the green cover. All the components of GBS are summarized in Table 1. For a 10 m-high slope, GBS consisted of 20 lifts (bag height is 50 cm), where the top lift was extended to about 7 m, as according to the design criteria of the model, it was required to have an extension of 70% of the slope height from the facing of GBS. The SWCC and permeability functions of each of the GBS materials were incorporated into the SEEP/W model to generate pore-water pressure profiles for various time periods.

Table 1

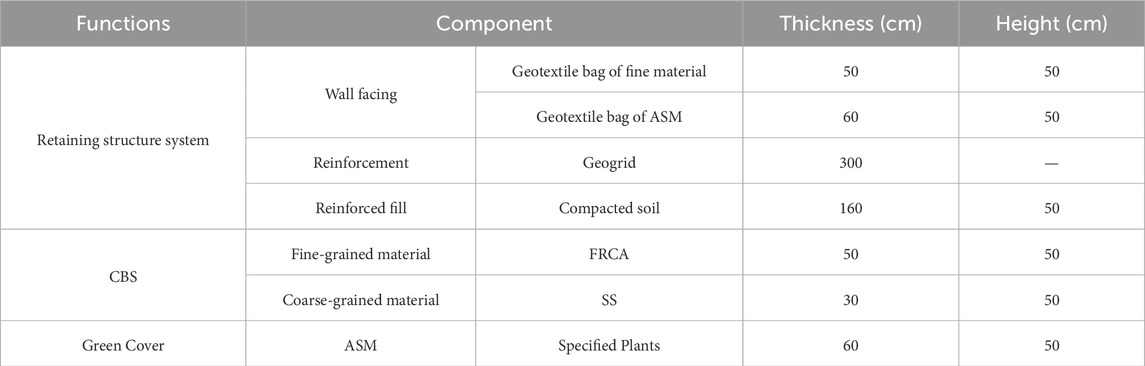
Table 1. Dimensions and main functions of GBS components (Rahardjo et al., 2015).

The pore-water pressure changes from seepage analyses were integrated into the slope stability analyses. To carry out slope stability analyses, the slice-based limit equilibrium method was used. The Morgenstern-Price approach was selected for determining FOS as both moment and force equilibrium are satisfied. The analysis was performed by setting up the Mohr-Coulomb material model and inputting the appropriate shear strength parameters. This model is an extended version of Mohr-Coulomb that is applicable for unsaturated soils as it incorporates the suction component in the analysis (Oh and Vanapalli, 2010). In SLOPE/W, the grid and radius method—both of which were created by trial and error—were utilized for searching the slip surface. In slope stability analyses, reinforcement needed to be assigned as it is part of the GBS design model. It was accomplished by using reinforcement loads in the define stage. To support 20 layers of geobags stacked atop each other, 20 geogrid reinforcements were assigned to the slope. The geogrid’s length was determined to be 3 m following Rahardjo et al. (2019a). In reinforcement loads, geogrid was chosen to be geosynthetic, and pullout resistance was calculated from the material properties; specifically, interface adhesion was 0 kPa, interface shear angle, which is referred to as compacted soil’s effective friction angle, was 19°, surface area factor was 1, and resistance reduction factor was 2. Other design considerations include the tensile capacity of a geogrid, which was equal to 46 kN, and a reduction factor of 2 (Chua et al., 2022). To evaluate the effectiveness of GBS, the FOS results were compared with the SS-covered slope and a slope with original soil identified in a previous study by (Abishev et al., 2024).

3 Results

3.1 Experimental results

Table 2 lists the soil classifications according to the Unified Soil Classification System (USCS) and index properties of SS, FRCA, and ASM. SS, FRCA, and ASM were classified as “poorly graded gravel” (GP), “poorly graded sand” (SP), and “clayey sand” (SC), respectively. Figure 5 depicts the GSD curves of SS, FRCA, and ASM, showing that each of the materials was found within the classified range, correspondingly. 98.11% of the gravel content larger than 4.75 mm was found in SS, while FRCA consisted of 95.1% sand content. It means that based on the particle size of the materials, the use of SS as a coarse-grained layer and, similarly, FRCA as a fine-grained layer is acceptable. When it comes to ASM, it was mostly composed of sand content, which was 60%, and fine particles (35%). The dry densities (ρd) of SS and FRCA were 1.54 mg/m³ and 1.67 mg/m³, respectively. The required dry density (ρd) for the coarse-grained layer is between 1.53 and 1.57 mg/m³, and for the fine-grained layer, the required dry density (ρd) ranges from 1.62 to 1.67 mg/m³ (Rahardjo et al., 2019c). The dry densities of both materials complied with the above criteria. Furthermore, ASM had the highest dry density of 1.71 mg/m³, and its plasticity index was 14% when the liquid limit was 36% and the plastic limit was 22%.

Table 2

Table 2. Index properties of SS, FRCA and ASM.

Figure 5

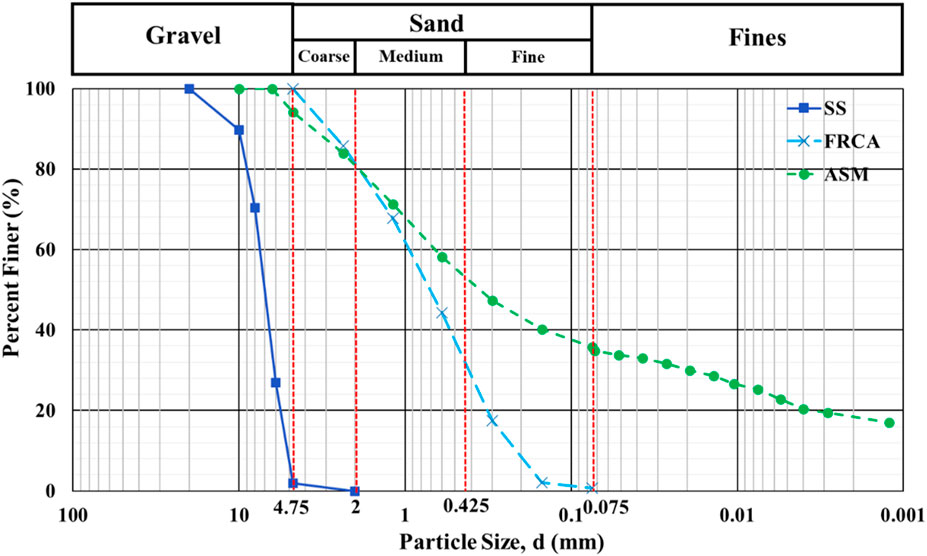
Figure 5. Grain size distribution (GSD) curves of steel slag (SS), fine recycled concrete aggregate (FRCA), and approved soil mixture (ASM).

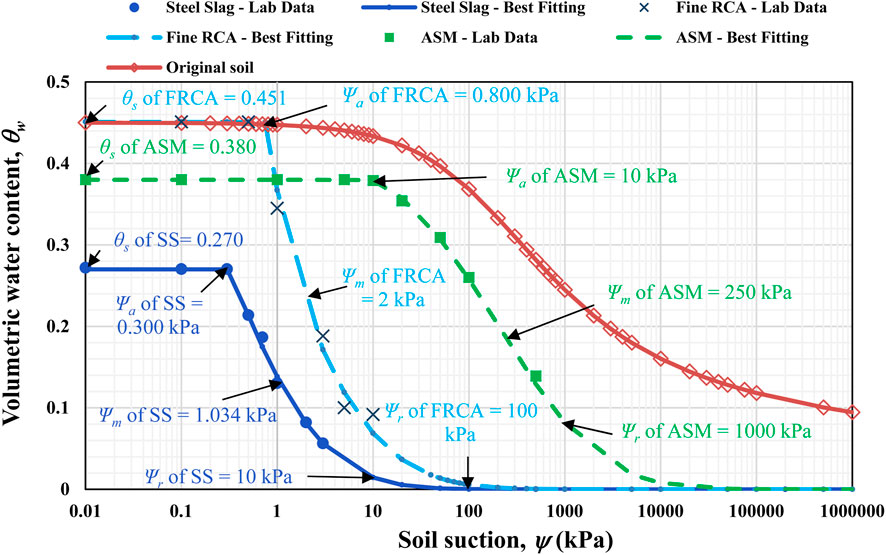
The HYPROP test results were used to create SWCCs of SS, FRCA, and ASM. Accordingly, the relationship between volumetric water content and soil suction, including all major SWCC parameters, was finalized and can be observed in Figure 6. The experimental data of SWCC was best fitted using the unimodal fitting equation by Satyanaga et al. (2017). The best-fitting parameters are demonstrated in Table 3. In order to use the Satyanaga et al. (2017) fitting equation for modeling SWCC, each parameter requires a valid initial value. To accurately match the SWCC experimental data, all the parameters can be adjusted using an iterative non-linear regression method available in the Microsoft Excel software (Satyanaga et al., 2019; Dodge and Stinson, 2007).

Figure 6

Figure 6. SWCCs of SS, FRCA, and ASM.

Table 3

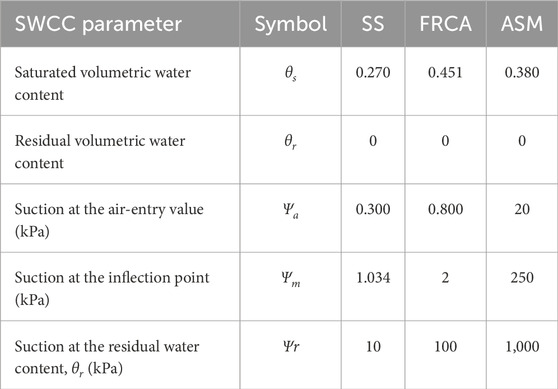
Table 3. Summary of SWCC parameters [Satyanaga et al. (2017) equation].

The SWCCs of both waste materials were very similar in shape; however, the corresponding parameters differed. The saturated volumetric water content (θs) of SS was 0.27, while FRCA had a higher value, which was equal to 0.451. In the same way, the air-entry value (Ψa) of SS was 0.3 kPa, and it was lower than the air-entry value of FRCA, which was 0.8 kPa. The GSD of soil has a significant impact on its air-entry value (Fredlund et al., 2012). It can be observed that coarser particles typically have lower air-entry values compared to finer particles. Having the largest air-entry value of 20 kPa, ASM had a saturated volumetric content of 0.38. Suctions at the inflection point of SS, FRCA, and ASM were found to be 1.034, 2, and 250 kPa, respectively; meanwhile, residual suctions were equal to 10, 100, and 1,000 kPa, respectively. The SWCC data were eventually applied in the subsequent seepage analyses.

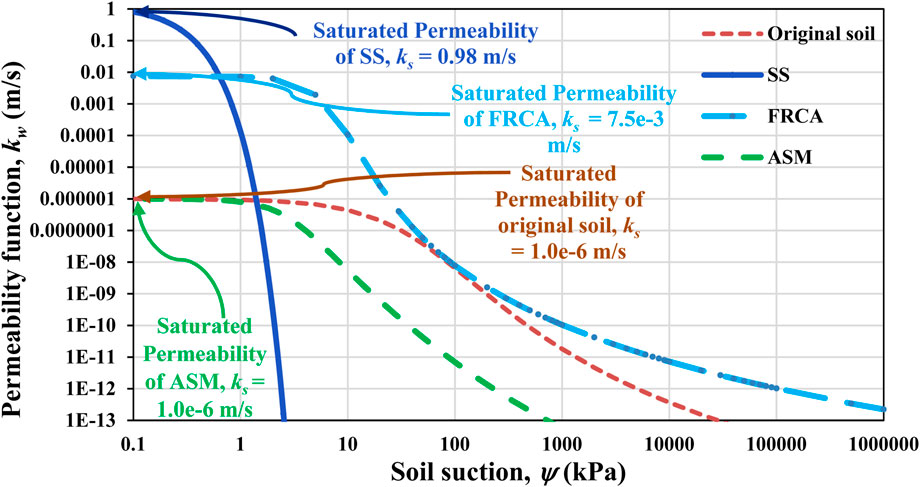
The permeability functions of SS, FRCA, and ASM were derived from saturated permeability and SWCC using the statistical method outline in the procedure described by Satyanaga et al. (2022). Figure 7 shows that SS has significantly lower coefficient of permeability at high suction ranges compared to the FRCA. This contrast in permeability between fine- and coarse-grained layers develops a capillary barrier effect, which means that there will be no water penetration into the SS. SWCCs and permeability functions of SS and FRCA indicate that the aforementioned waste materials are capable of providing a capillary barrier effect. In addition, ASM had the lowest permeability due to the higher presence of fines. Its saturated permeability was equal to 1.0 × 10⁻⁶ m/s. Lastly, the permeability functions were also included in the numerical analysis along with the best-fitted SWCC data.

Figure 7

Figure 7. Permeability functions of SS, FRCA, and ASM.

From the triaxial test results, the effective internal friction angles of SS, FRCA, and ASM were 42°, 45°, and 30°, respectively. Unsaturated shear strength angles (φ^b) were assumed to be half of the effective internal friction angles (Fredlund and Rahardjo, 1993). Effective cohesions of both waste materials were zero since, to have a capillary barrier effect, non-cohesive soils were required (Rahardjo et al., 2020). Meanwhile, the effective cohesion of ASM was equal to 10 kPa. According to Rahardjo et al. (2020), original soil is used as a compacted material behind GBS. Therefore, the properties of compacted soil are equivalent to the original soil. All the materials’ shear strength parameters are presented in Table 4.

Table 4

Table 4. Summary of shear strength parameters used in slope stability analyses.

3.2 Numerical analysis results

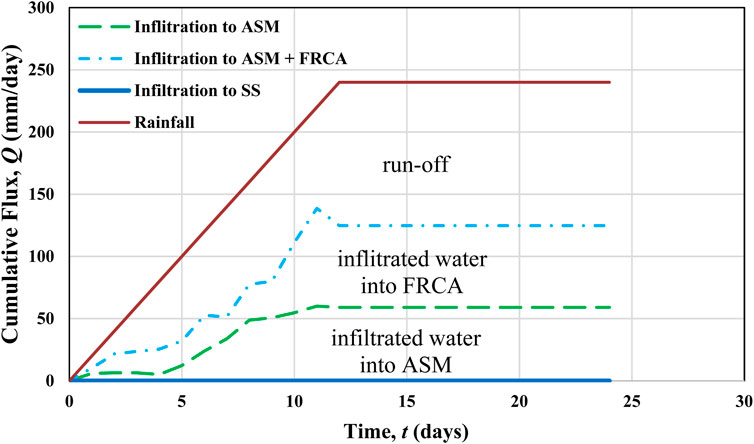
Firstly, seepage analyses using SEEP/W were performed under rainfall loading for a slope with a 10 m height and a 70° slope angle. As a result, pore-water pressure changes in soils below the slope with GBS were obtained. Figure 8 illustrates the pore-water pressure profiles for two different periods, wet and dry, at the middle of GBS, specifically 5 m from the slope’s crest. From the pore-water pressure profiles, it is clearly seen that there is only a slight increase in pore-water pressure within the SS layer for both periods, which suggests that the rainwater was infiltrated only into the ASM and FRCA layers, where rainfall resulted in increased pore-water pressures. It is verified by Figure 9, which demonstrates the amount of rainfall infiltration into the GBS layers.

Figure 8

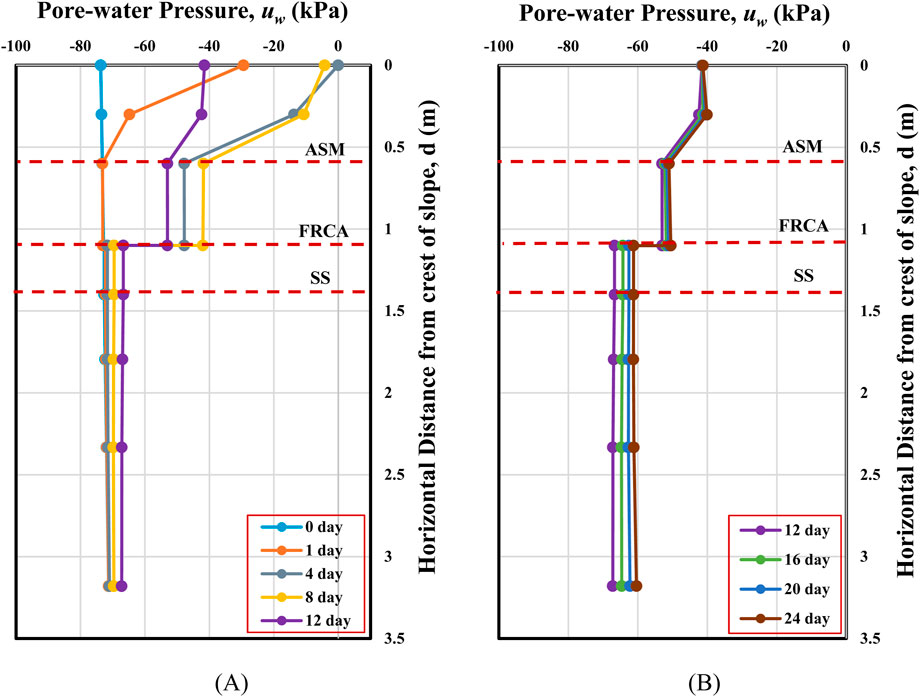
Figure 8. (A) Pore-water pressure profiles during rainfall at the middle of GBS – 5 m depth from the slope’s crest with a height of 10 m and a 70° inclination. (B) Pore-water pressure profiles during dry periods at the middle of GBS – 5 m depth from the slope’s crest with a height of 10 m and a 70° inclination.

Figure 9

Figure 9. Rainfall infiltration into the layers of GBS.

It is possible to assess the efficacy of GBS in reducing rainwater infiltration (Figure 9). Considering the specified rainfall intensity of 20 mm/day, about 52% of rainwater was infiltrated into ASM and FRCA combined, while the remaining rainwater was discharged as run-off. Another important notice from Figure 9 is that there was no infiltration into SS, which implies that there was no breakthrough into the coarse-grained layer of CBS and the system worked well. It proves that GBS is effective in minimizing rainfall infiltration and can be employed using SS and FRCA as capillary barrier materials.

The FOS against time graph created using the SLOPE/W analysis showed the positive influence of GBS cover on the FOS of a slope when compared with a slope covered with and without SS, as can be seen in Figure 10. From previous discussions, it was found that SS is not competent to be used as the cover for steeper slopes. The FOS of the original soil was higher than the minimum FOS; however, on day 12, it marginally appeared below 1.5, which suggested that there was a need for protective measures against rainfall infiltration. Meanwhile, the FOS of a slope incorporating GBS improved the FOS of the original soil, and it was nearly constant throughout all 24 days. The reason for the increased FOS arises from the fact that GBS was successful in reducing the amount of rainwater that seeps into the slope during wet periods.

Figure 10

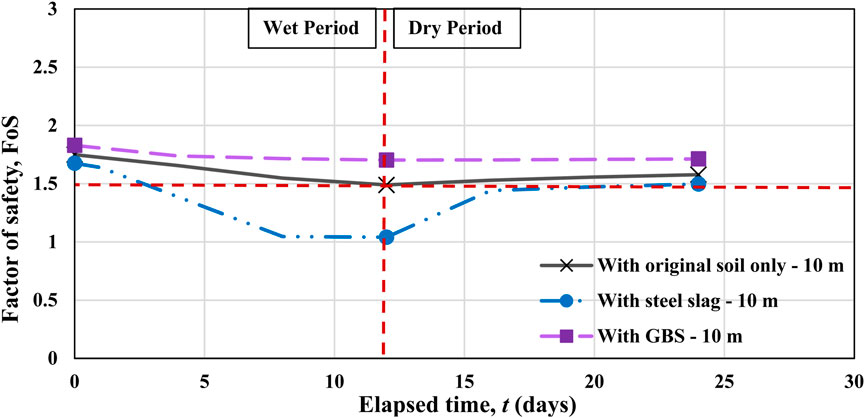
Figure 10. Comparison of FOS between the slopes covered with SS, GBS, and a slope with original soil when a slope height = 10 m and a slope angle = 70°.

4 Discussion

One of the key things to be examined to verify the eligibility of SS and FRCA as capillary barrier materials is the GSD of the mentioned materials. Statistically, it should be comparable to the original materials (either sand or gravel). According to the study of Satyanaga et al. (2021), the lower and upper bounds for a coarse-grained layer were set in the range of medium to coarse gravel, exactly from 4.75 mm to 40 and 25 mm, respectively. SS was mostly found within the specified range and corresponded to the gravel size. For the fine-grained layer, it was sand material, where the lower and upper bounds ranged from 0.075 to 4.75 mm and 0.05–2 mm, respectively. The FRCA range was almost the same as the lower bound limits, covering 0.075–4.75 mm in size. Overall, the GSDs of FRCA and SS were comparable to the GSDs of the original materials, and they can be used to replace sand and gravel in GBS.

The next significant points to be discussed are the SWCC and permeability functions of the materials investigated in comparison with the original materials. Regarding the original materials, the studies conducted by Li et al. (2021) will be used as the reference source, where natural aggregates, like granite chips (gravel) and fine sand, were used in the construction of CBS as coarse- and fine-grained layers, respectively. For the comparison, key SWCC parameters will be evaluated. Normally, saturated volumetric content (θs) of fine-grained material (fine sand = 0.41) should be higher than that of a coarse-grained material (granite chip = 0.34), which was confirmed by waste materials: the value of FRCA (θs = 0.451) was higher than SS (θs = 0.27). At the same time, the air-entry value (Ψa) of fine-grained material (fine sand = 0.8 kPa) should be greater than that of a coarse-grained material (granite chip = 0.07 kPa), and it also happened in the cases of FRCA (Ψa = 0.8 kPa) and SS (Ψa = 0.3 kPa). Correspondingly, suction at the inflection point (Ψm) of a fine-grained soil (fine sand = 1.4 kPa) was greater than that of a coarse-grained soil (granite chips = 0.16 kPa); it was also applicable for FRCA (Ψm = 2 kPa) and SS (Ψm = 1.034 kPa). On top of that, the residual suction (Ψr) of a coarse-grained material (granite chips = 0.6 kPa) was lower than that of a fine-grained material (fine sand = 2.75 kPa); similarly, the residual suction of a SS (Ψr = 10 kPa) was lower than that of a FRCA (Ψr = 100 kPa).

The saturated permeability (ks) of a fine material (fine sand = 2.7 × 10⁻⁴ m/s) is much lower than that of a coarse material (granite chip = 5.1 × 10⁻¹ m/s). The following contrast appeared in the case of waste materials as well, where the saturated permeability of FRCA (ks = 7.5 × 10⁻³ m/s) was lower than that of SS (ks = 9.8 × 10⁻¹ m/s). In both waste and natural materials, in contrast to fine-grained materials, coarse-grained materials (either SS or granite chips) had a much lower coefficient of permeability at high suction ranges. Their permeability functions suggested that the capillary barrier effect was achievable. Ultimately, it can be summarized that the SWCC and permeability functions of the SS and FRCA were analogous to those of the fine sand and granite chips, which proved that the substitution of natural materials with the examined waste materials is realistic.

Furthermore, it is required to compare the shear strengths of FRCA and SS with those of original or natural materials. Effective cohesions of both natural and waste materials were equal to zero, since for a normal GBS or CBS, it was essential to have non-cohesive soils. Apart from the effective cohesion, there were two more shear strength parameters, namely, the effective friction angle (φ′) and the unsaturated shear strength angle (φb). The effective friction angles of fine sand and granite chip were 34° and 36°, respectively (Li et al., 2021), whereas SS and FRCA had effective friction angles of 42° and 45°, respectively. Meantime, unsaturated shear strength angles of fine sand and granite chip were 15° and 17°, respectively (Li et al., 2021), while unsaturated shear strength angles of SS and FRCA were 21° and 22.5°, respectively. Accordingly, from the effective friction and unsaturated shear strength angles, it can be stated that both SS and FRCA had greater shear strength than natural materials. Hence, in terms of shear strength, it is preferable to use SS and FRCA instead of the original materials.

According to the numerical results, before the rainfall, the FOS of the GBS slope was 4.36% higher than that of the original slope, 12.54% higher at the end of the rainfall, and 7.88% higher by the end of day 24. Evidently, FOS would decrease once rainfall had been infiltrated into the slope; this was confirmed in this numerical study since, during the wet period, the changes in FOS of a slope covered with SS, original soil, and GBS were −37.91%, −14.84%, and −6.88%, respectively. It can be noted that the GBS slope had the smallest change in FOS. On the whole, the FOS of GBS slopes was fairly constant; however, the reason why it was reduced during the wet period is that rainwater mostly infiltrated into the ASM and FRCA layers. The change in pore-water pressure at these layers in the mid-slope of GBS was 43.66% and 27.26%, respectively; however, rainfall infiltration into these layers was considered in GBS design, more importantly, to avoid breakthrough into the layer of a SS. In this case, the change in pore-water pressure in the SS layer was 8.15%, which is reasonable. Owing to the contrast in SWCC and permeability functions between FRCA and SS, changes in pore-water pressure were identified as acceptable; consequently, FOS remained relatively constant throughout the entire duration.

5 Summary and conclusions

The characteristics of steel slag and recycled concrete for slope protection against rainfall-induced landslides were investigated as part of GBS materials. Comprehensive experimental tests were performed to identify the index properties and hydraulic characteristics, such as permeability functions, SWCCs, and unsaturated shear strength parameters of SS, FRCA, and ASM. According to the results, SS and FRCA had the same properties as natural gravel and sand, respectively. The incorporation of these waste materials in GBS was evaluated by performing numerical analyses using GeoStudio software, particularly SEEP/W and SLOPE/W. Furthermore, the FOS results were compared with the original slope and the slope covered with steel slag only, which was obtained from a previous study. Since SS appeared to be ineffective as a slope cover for maintaining the stability of steeper slopes, GBS was recommended as an alternative due to its retaining features. The results from the seepage analyses revealed that negative pore water pressures, or suctions, were almost maintained within the SS layer during both wet and dry periods, as the rainwater was hindered by this layer and no breakthrough had occurred. Slope stability analyses showed that GBS improved FOS in comparison to the slope with original soil. The FOS of the GBS slope was higher than that of the original slope and the slope covered only with SS for the studied geometry. This numerical study confirmed that the FOS decreases once rainwater penetrates the slope. During the wet period, the variations in FOS for slopes covered with SS, original soil, and GBS were found to be smaller than those observed after rainfall. However, the GBS slope showed the smallest change in FOS. Accordingly, it was concluded that the application of GBS would be a successful protection method against rainfall-triggered landslides. Utilization of SS and FRCA was discovered to be feasible and suitable for fine- and coarse-grained layers of GBS with a slope height of 10 m and a slope angle equal to 70°. Nevertheless, there are some limitations and recommendations to be addressed. One of the limitations is the absence of deformation analysis to see the deformation characteristics of planting geobags. Furthermore, the existing slope profiles are rather simplistic. In fact, the variability of materials can be influenced by sediment deposition and stratification. To enhance the credibility of the analysis, non-uniform soil profiles should be taken into account in the model. In addition, as the parameters of the original soil were based on the literature review, it is also recommended to get original soil from the site to have its real properties and perform field tests with monitoring to further validate the results obtained in this study. Moreover, the original GBS design was proposed for construction in a tropical climate; however, it was mentioned in the studies that it is not confined to tropical nations and can be applied in other regions as well, contingent upon more research for adaptation to cold climates. Due to the extreme continental climate of Kazakhstan, it is recommended to check the effect of freezing and thawing as future work. Finally, an environmental aspect, like the toxicity of the waste materials, which has not been part of the present work, should also be studied.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

RA: Validation, Formal Analysis, Data curation, Investigation, Writing – original draft. AS: Conceptualization, Writing – original draft, Project administration, Methodology, Supervision, Funding acquisition. MG: Investigation, Data curation, Writing – review and editing, Formal Analysis, Validation. AL: Writing – review and editing, Validation, Funding acquisition, Supervision. JK: Writing – review and editing, Project administration, Funding acquisition, Supervision.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This research was funded by the research project AP23486953 from the Ministry of Higher Education and Science of the Republic of Kazakhstan Nazarbayev University, Faculty Development Competitive Research Grants Program (FDCRGP) Grant No. 20122022FD4133.

Acknowledgments

This research was funded by the research project AP23486953 from the Ministry of Higher Education and Science of the Republic of Kazakhstan Nazarbayev University, Faculty Development Competitive Research Grants Program (FDCRGP) Grant No. 20122022FD4133. The authors are grateful for this support. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Nazarbayev University.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abishev, R., Satyanaga, A., Moon, S.-W., and Kim, J. (2025). “GeoBarrier system incorporating recycled concrete and steel slag for slope protection,” in EGU General Assembly 2025, Vienna, Austria, 27 Apr – 2 May 2025, EGU25-616. doi:10.5194/egusphere-egu25-616

CrossRef Full Text | Google Scholar

Abishev, R., Satyanaga, A., Pernebekova, G., Rahardjo, H., Zhai, Q., Shon, C. S., et al. (2024). Stability of soil slope in Almaty covered with steel slag under the effect of rainfall. Sci. Rep. 14 (1), 7711. doi:10.1038/s41598-024-58364-5

PubMed Abstract | CrossRef Full Text | Google Scholar

ASTM D6913M-17 (2017). Standard test methods for particle-size distribution (gradation) of soils using sieve analysis. West Conshohocken: ASTM International.

Google Scholar

ASTM D2434–19 (2019). Standard test method for permeability of granular soils. West Conshohocken: ASTM International.

Google Scholar

ASTM D2487–17 (2017). Standard practice for classification of soils for engineering purposes (unified soil classification system). West Conshohocken: ASTM International.

Google Scholar

ASTM D4318–17 (2017). Standard test methods for liquid limit, plastic limit, and plasticity index of soils. West Conshohocken: ASTM International.

Google Scholar

ASTM D5084-16a (2016). Standard test methods for measurement of hydraulic conductivity of saturated porous materials using a flexible wall permeameter. West Conshohocken: ASTM International.

Google Scholar

ASTM D698–12 (2012). Standard test methods for laboratory compaction characteristics of soil using standard effort. West Conshohocken: ASTM International.

Google Scholar

ASTM D7181–20 (2020). Standard test method for consolidated drained triaxial compression test for soils. West Conshohocken: ASTM International.

Google Scholar

ASTM D854–14 (2014). Standard test methods for specific gravity of soil solids by water pycnometer. West Conshohocken: ASTM International.

Google Scholar

Aziz, S., and Islam, M. S. (2022). Mechanical effect of vetiver grass root for stabilization of natural and terraced hill slope. Geotechnical Geol. Eng. 40, 3267–3286. doi:10.1007/s10706-022-02092-y

CrossRef Full Text | Google Scholar

Bishop, A., and Henkel, D. (1962). The measurement of soil properties in the tri-axial test. London: Edward Arnold.

Google Scholar

Camera, C., Apuani, T., and Masetti, M. (2011). Parametrization of a dry retaining wall on a terraced slope in Valtellina (Northern Italy) and stability analysis. Paper presented at the 8th conference Field Measurements in GeoMechanics held in Berlin in 2011.

Google Scholar

Chen, Y., Gao, Y., and Ng, C. W. W. (2020). A new capillary barrier system for retaining wall backfilled with fine-grained soil. Comput. Geotech. 118, 103324. doi:10.1016/j.compgeo.2019.103324

CrossRef Full Text | Google Scholar

Chepelianskaia, O., and Sarkar-Swaisgood, M. (2022). Kazakhstan climate change and disaster risk profile. Bangkok, Thailand: United Nations ESCAP, IDD.

Google Scholar

Chua, Y. S., Rahardjo, H., and Satyanaga, A. (2022). Structured soil mixture for solving deformation issue in GeoBarrier System. Transp. Geotech. 33, 100727. doi:10.1016/j.trgeo.2022.100727

CrossRef Full Text | Google Scholar

Dodge, M., and Stinson, C. (2007). Microsoft office Excel 2007 inside out. USA: Microsoft Press.

Google Scholar

Eawag, C. H. (2008). Global waste challenge situation in developing countries. Dübendorf, Switzerland: Sandec, Swiss Federal Institute of Aquatic Science and Technology.

Google Scholar

Fredlund, D. G., and Rahardjo, H. (1993). Soil mechanics for unsaturated soils. New York: John Wiley and Sons, Inc. doi:10.1002/9780470172759

CrossRef Full Text | Google Scholar

Fredlund, D. G., Rahardjo, H., and Fredlund, M. D. (2012). Unsaturated soil mechanics in engineering practice. Hoboken, New Jersey: John Wiley & Sons, Inc.

Google Scholar

Fredlund, D. G., Xing, A., and Huang, S. Y. (1994). Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotechnical J. 31 (4), 533–546. doi:10.1139/t94-062

CrossRef Full Text | Google Scholar

Gao, Y., Zhang, Y., Ma, C., Zheng, X., Li, T., Zeng, P., et al. (2023). Failure process and stability analysis of landslides in Southwest China while considering rainfall and supporting conditions. Front. Environ. Sci. 10, 1084151. doi:10.3389/fenvs.2022.1084151

CrossRef Full Text | Google Scholar

Gasmo, J. M., Rahardjo, H., and Leong, E. C. (2000). Infiltration effects on stability of a residual soil slope. Comput. Geotech. 26, 145–165. doi:10.1016/s0266-352x(99)00035-x

CrossRef Full Text | Google Scholar

Guzzetti, F., Gariano, S. L., Peruccacci, S., Brunetti, M. T., and Melillo, M. (2022). Rainfall and landslide initiation. In Rainfall: Modeling, Measurement and Applications, ed. Renato Morbidelli Netherlands: Elsevier., 427–450.

CrossRef Full Text | Google Scholar

Han, B., Yu, X., and Ou, J. (2014). Self-sensing concrete in smart structures. Oxford: Elsevier Butterworth-Heinemann.

Google Scholar

Karkush, M. O., and Yassin, S. (2019). Improvement of geotechnical properties of cohesive soil using crushed concrete. Civ. Eng. J. (Iran) 5, 2110–2119. doi:10.28991/cej-2019-03091397

CrossRef Full Text | Google Scholar

Kim, Y., Rahardjo, H., Nistor, M. M., Satyanaga, A., Leong, E. C., and Sham, A. W. L. (2022). Assessment of critical rainfall scenarios for slope stability analyses based on historical rainfall records in Singapore. Environ. Earth Sci. 81, 39. doi:10.1007/s12665-021-10160-4

CrossRef Full Text | Google Scholar

King, S. A., Khalturin, V. I., and Tucker, B. E. (1999). Seismic hazard and building vulnerability in post-soviet central Asian Republics. Netherlands: Springer.

Google Scholar

Kristo, C., Rahardjo, H., and Satyanaga, A. (2019). Effect of hysteresis on the stability of residual soil slope. Int. Soil Water Conservation Res. 7, 226–238. doi:10.1016/j.iswcr.2019.05.003

CrossRef Full Text | Google Scholar

Kunze, R. J., Uehara, G., and Graham, K. (1968). Factors important in the calculation of hydraulic conductivity. Soil Sci. Soc. Am. J. 32 (6), 760–765. doi:10.2136/sssaj1968.03615995003200060020x

CrossRef Full Text | Google Scholar

Lee, L. M., Gofar, N., and Rahardjo, H. (2009). A simple model for preliminary evaluation of rainfall-induced slope instability. Eng. Geol. 108 (3–4), 272–285. doi:10.1016/j.enggeo.2009.06.011

CrossRef Full Text | Google Scholar

Li, Y., Satyanaga, A., and Rahardjo, H. (2021). Characteristics of unsaturated soil slope covered with capillary barrier system and deep-rooted grass under different rainfall patterns. Int. Soil Water Conservation Res. 9, 405–418. doi:10.1016/j.iswcr.2021.03.004

CrossRef Full Text | Google Scholar

Mercer, K., Rahardjo, H., and Satyanaga, A. (2019). Unsaturated soils guidelines–volume 1: soil-water characteristic curves for materials classified according to the unified soil classification system. Crawley, Western Australia: Australian Center for Geomechanics. University of Western Australia.

Google Scholar

METER Group AG (2018). Operation manual HYPROP 2. Munich, Germany: UMS GmbH.

Google Scholar

Mohammad, A. S., Satyanaga, A., Abilev, Z., Bello, N., Nadezhda, K., Zhai, Q., et al. (2024). The influence of rainfall patterns on factor of safety for clayey soil slopes. Front. Built Environ. 10, 1376585. doi:10.3389/fbuil.2024.1376585

CrossRef Full Text | Google Scholar

Motz, H., and Geiseler, J. (2001). Products of steel slags an opportunity to save natural resources. Waste Manag. 21, 285–293. doi:10.1016/s0956-053x(00)00102-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Oh, W. T., and Vanapalli, S. K. (2010). Influence of rain infiltration on the stability of compacted soil slopes. Comput. Geotech. 37, 649–657. doi:10.1016/j.compgeo.2010.04.003

CrossRef Full Text | Google Scholar

Perera, Y. Y., Zapata, C., Houston, W. N., and Houston, S. (2005). Prediction of the soil-water characteristic curve based on grain-size-distribution and index properties. Geotechnical Special Publication 130-142. 49–60.

Google Scholar

Powrie, W. (2004). Soil mechanics: concepts and applications. 2nd ed. London: Spon Press.

Google Scholar

Rahardjo, H., Choon Leong, E., Professor, A., Looi Wang, C., and Liang Heng Wong, J. (2019c). Geobarrier system for protection against rainfall-induced slope failure. ISSMGE Int. J. Geoengin. Case Hist. © 5, 26–42. doi:10.4417/IJGCH-05-01-03

CrossRef Full Text | Google Scholar

Rahardjo, H., Gofar, N., and Satyanaga, A. (2018b). Effect of geobags on water flow through capillary barrier system. Geotechnical Eng. J. SEAGS and AGSSEA 49, 73–78. doi:10.14456/seagj.2018.10

CrossRef Full Text | Google Scholar

Rahardjo, H., Gofar, N., Satyanaga, A., Leong, E. C., Wang, C. L., and Johnny Wong, L. H. (2019a). Effect of rainfall infiltration on deformation of geobarrier wall. Geotechnical Geol. Eng. 37, 1383–1399. doi:10.1007/s10706-018-0693-6

CrossRef Full Text | Google Scholar

Rahardjo, H., Kim, Y., Gofar, N., Leong, E. C., Wang, C. L., and Wong, J. L. H. (2018a). Field instrumentations and monitoring of GeoBarrier System for steep slope protection. Transp. Geotech. 16, 29–42. doi:10.1016/j.trgeo.2018.06.006

CrossRef Full Text | Google Scholar

Rahardjo, H., Kim, Y., Gofar, N., and Satyanaga, A. (2020). Analyses and design of steep slope with GeoBarrier system (GBS) under heavy rainfall. Geotext. Geomembranes 48, 157–169. doi:10.1016/j.geotexmem.2019.11.010

CrossRef Full Text | Google Scholar

Rahardjo, H., Kim, Y., and Satyanaga, A. (2019b). Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Engineering 10, 8. doi:10.1186/s40703-019-0104-8

CrossRef Full Text | Google Scholar

Rahardjo, H., Qian, Z., Satyanaga, A., Leong, E. C., Wang, C. L., and Wong, J. L. H. (2016b). “Field instrumentation for performance assessment of Geobarrier System,” in E3S Web of Conferences. Les Ulis, France: EDP Sciences 9. 15006. doi:10.1051/e3sconf/20160915006

CrossRef Full Text | Google Scholar

Rahardjo, H., Santoso, V. A., Leong, E. C., Ng, Y. S., and Hua, C. J. (2012b). Performance of an instrumented slope covered by a capillary barrier system. J. Geotechn. Geoenviron. Eng. 138, 481–490. doi:10.1061/(asce)gt.1943-5606.0000600

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., Harnas, F. R., and Leong, E. C. (2016a). Use of dual capillary barrier as cover system for a sanitary landfill in Singapore. Indian Geotechnical J. 46, 228–238. doi:10.1007/s40098-015-0173-3

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., and Leong, E. C. (2012a). Unsaturated soil mechanics for slope stabilization. Geotech. Eng. 43, 48–58. doi:10.14456/seagj.2012.33

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., Leong, E. C., Ng, Y. S., Foo, M. D., and Wang, C. L. (2007). “Slope failures in Singapore due to rainfall,” in Proceedings of 10th Australia New Zealand conference on geomechanics common Ground,” 21–24 October (Brisbane, Australia), 704–709.

Google Scholar

Rahardjo, H., Satyanaga, A., Leong, E.-C., and Noh, O. (2017a). Performance of residual soil as cover system for a sanitary landfill in Singapore. J. Perform. Constr. Facil. 31, D4016004. doi:10.1061/(asce)cf.1943-5509.0000926

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., Leong, E. C., and Wang, J. Y. (2013). Unsaturated properties of recycled concrete aggregate and reclaimed asphalt pavement. Eng. Geol. 161, 44–54. doi:10.1016/j.enggeo.2013.04.008

CrossRef Full Text | Google Scholar

Rahardjo, H., Zhai, Q., Satyanaga, A., Leong, E. C., Wang, C. L., and Wong, J. L. H. (2017b).Numerical analyses for assessment of geobarrier system performance. Geotechnical Special Publication. Reston, Virginia, USA: American Society of Civil Engineers (ASCE). 300 132–148.

CrossRef Full Text | Google Scholar

Rahardjo, H., Zhai, Q., Satyanaga, A., Leong, E. C., Wang, C. L., and Wong, L. H. (2015). “Geo-Barrier System as a retaining structure,” in 6th Asia-Pacific Conference on Unsaturated Soil Mechanics from Theory to Practice, AP-UNSAT 2015 (Lei- den, The Netherlands: CRC Press/Balkema), 871–876.

CrossRef Full Text | Google Scholar

Rezaei-Hosseinabadi, M. J., Bayat, M., Nadi, B., and Rahimi, A. (2022). Sustainable utilisation of steel slag as granular column for ground improvement in geotechnical projects. Case Stud. Constr. Mater. 17, e01333. doi:10.1016/j.cscm.2022.e01333

CrossRef Full Text | Google Scholar

Roque, A. J., da Silva, P. F., and de Almeida, R. P. M. (2022). Recycling of crushed concrete and steel slag in drainage structures of geotechnical works and road pavements. J. Mater Cycles Waste Manag. 24, 2385–2400. doi:10.1007/s10163-022-01486-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Satyanaga, A., Bairakhmetov, N., Kim, J. R., and Moon, S. W. (2022). Role of bimodal water retention curve on the unsaturated shear strength. Appl. Sci. Switz. 12, 1266. doi:10.3390/app12031266

CrossRef Full Text | Google Scholar

Satyanaga, A., Rahardjo, H., Koh, Z. H., and Mohamed, H. (2019). Measurement of a soil-water characteristic curve and unsaturated permeability using the evaporation method and the chilled-mirror method. J. Zhejiang Univ. Sci. A 20, 368–374. doi:10.1631/jzus.A1800593

CrossRef Full Text | Google Scholar

Satyanaga, A., Rahardjo, H., and Zhai, Q. (2017). Estimation of unimodal water characteristic curve for gap-graded soil. Soils Found. 57, 789–801. doi:10.1016/j.sandf.2017.08.009

CrossRef Full Text | Google Scholar

Satyanaga, A., Zhai, Q., Rahardjo, H., Gitirana Jr, G. de F. N., Moon, S.-W., and Kim, J. (2021). Performance of capillary barrier as a sustainable slope protection. MATEC Web Conf. 337, 03021. doi:10.1051/matecconf/202133703021

CrossRef Full Text | Google Scholar

Schindler, U. (1980). Ein schnellverfahren zur messung der wasserleitfähigkeit im teilgesättigten boden an stechzylinderproben.

Google Scholar

Sharipov, A., Satyanaga, A., Abishev, R., Moon, S. W., Taib, A. M., and Kim, J. (2023). Influence of slope geometry on stability of clayey soil slopes. Geotechnical Geol. Eng. 41, 2939–2950. doi:10.1007/s10706-023-02438-0

CrossRef Full Text | Google Scholar

Stormont, J. C. (1996). The effectiveness of two capillary barriers on a 10% slope. Geotechnical & Geological Engineering 14, 243–267.

CrossRef Full Text | Google Scholar

Tallar, R. Y., Joelin, G. C., Suen, J. P., Mauregar, G. G., Anugrah, O., Romulo, M., et al. (2025). “Examining the role of land use change as an ecosystem service on watershed management,” in Proceedings of the International Conference on Social Science, Environment and Technology Development, 49–55.

Google Scholar

Terzaghi, K. (1950). Mechanisms of landslides. Berkeley: Geotechnical Society of America, 83–125.

Google Scholar

Terzaghi, K. (1962). Stability of steep slopes on hard unweathered rock. Geotechnique 12, 251–270. doi:10.1680/geot.1962.12.4.251

CrossRef Full Text | Google Scholar

Thurman, M. (2011). Natural disaster risks in central asia: a synthesis.

Google Scholar

Tsaparas, I., Rahardjo, H., Toll, D. G., and Leong, E. C. (2002). Controlling parameters for rainfall-induced landslides. Comput. Geotech. 29, 1–27. doi:10.1016/s0266-352x(01)00019-2

CrossRef Full Text | Google Scholar

Wilson, D. C., Rodic, L., Modak, P., Soos, R., Carpintero, A., Velis, K., et al. (2015). Global waste management outlook. Nairobi, Kenya: United Nations Environment Programme (UNEP).

Google Scholar

Wind, G. P. (1968). Capillary conductivity data estimated by a simple method. Water in the unsaturated zone 1, 181–191.

Google Scholar

Yi, H., Xu, G., Cheng, H., Wang, J., Wan, Y., and Chen, H. (2012). An overview of utilization of steel slag. Procedia Environ. Sci. 16, 791–801. doi:10.1016/j.proenv.2012.10.108

CrossRef Full Text | Google Scholar

Zhai, Q., Rahardjo, H., Satyanaga, A., Zhu, Y., Dai, G., and Zhao, X. (2021). Estimation of wetting hydraulic conductivity function for unsaturated sandy soil. Eng. Geol. 285, 106034. doi:10.1016/j.enggeo.2021.106034

CrossRef Full Text | Google Scholar

Zhang, J., and Li, J. (2018). Delay failure mechanism of rainfall-caused shallow landslide. Geotechnical Geol. Eng. 36, 2293–2304. doi:10.1007/s10706-018-0462-6

CrossRef Full Text | Google Scholar

Zhong, L., Wang, B., Zhao, X., Liu, F., Miao, M., and Pu, C. (2023). Study on rainfall infiltration characteristic parameters of unsaturated soil. Front. Ecol. Evol. 11, 1251765. doi:10.3389/fevo.2023.1251765

CrossRef Full Text | Google Scholar