Study on physical and mechanical properties and freeze-thaw damage models of granite under freeze-thaw cycles

Introduction: To describe the evolution of freeze-thaw damage in rocks and quantitatively analyze the degree of damage, a freeze-thaw damage model based on continuum damage mechanics and thermodynamics is proposed.

Methods: Taking granite as the research object, its physical and mechanical properties, acoustic emission characteristics, and failure modes were studied through freeze-thaw cycling, uniaxial compression, acoustic emission detection, and CT scanning experiments, and the validity of the model was verified.

Results: The results show that with the increase in the number of freeze-thaw cycles, the porosity of the specimens significantly increases, while the uniaxial compressive strength, elastic modulus, and wave velocity of granite decrease exponentially. During uniaxial compression, the cumulative acoustic emission ring counts and energy increase in a stepwise manner. In the early stage of loading, the signals are few, but as the stress increases and the cracks propagate, the signals significantly increase and reach a maximum at the stress peak. An increase in the number of freeze-thaw cycles leads to a decrease in the rate of increase of ring counts and energy in the early stage of loading and a reduction in their cumulative values. The failure mode changes from “X”-shaped shear failure to conical shear failure, with the shear triangle gradually increasing and shifting upward, and the number of main cracks decreasing.

Discussion: The experimental results are consistent with the theoretical model, indicating that the model can accurately describe the mechanical behavior and damage evolution of rocks under freeze-thaw cycling.

1 Introduction

With the implementation of major national strategies such as the “Belt and Road Initiative” and the “West-East Power Transmission Project”, China has constructed numerous hydraulic engineering projects in cold regions. These areas experience significant diurnal temperature variations and intense freeze-thaw cycling. The pore water and fissure water within rock masses undergo repeated cycles of freezing and thawing due to temperature fluctuations, leading to the rapid development and expansion of pores and fractures in rocks. Consequently, this process reduces the strength of rock materials and destabilizes geotechnical structures, resulting in frequent challenges in geotechnical engineering for hydraulic projects across alpine regions. Therefore, research on the physico-mechanical properties of rocks under freeze-thaw cycling is of significant theoretical and practical value for the design, construction, and operation of hydraulic engineering in cold regions.

In recent years, scholars and experts worldwide have conducted extensive theoretical and experimental research on the physico-mechanical properties of various rocks under freeze-thaw cycles as well as image recognition technologies, achieving significant research outcomes (Momeni et al., 2016; Park et al., 2015; Li et al., 2018; Li et al., 2019; Zheng et al., 2024; Zhu et al., 2025). Kolay and Ersin (Kolay, 2016; Del Roa et al., 2005) conducted freeze-thaw experiments on rocks and established the variation patterns of multiple physical parameters with respect to the number of freeze-thaw cycles. Chen et al., (2021) found that with the increase of freeze-thaw times, the peak strength and elastic modulus of sandstone decreased significantly, the porosity increased, and the failure mode changed from splitting failure to shear failure. Zhang and Yang, (2013) found that freeze-thaw cycles significantly reduce the mechanical properties of rocks, such as elastic modulus and compressive strength. Sandstone, due to its higher porosity and water content, exhibits a more sensitive freeze-thaw damage response, primarily characterized by particle spalling and fracture modes. In contrast, shale, with its dense structure, mainly experiences crack propagation and demonstrates relatively stronger freeze-thaw durability. Luo et al. (2020) confirmed through dynamic impact compression tests that freeze-thaw cycles significantly reduce the dynamic compressive strength and elastic modulus of sandstone, and the strength degradation follows an exponential decay model that takes into account the coupling effects of freeze-thaw cycles and strain rate. Wang et al. (2016) proposed a decay model to predict the dynamic mechanical degradation of sedimentary rocks under freeze-thaw cycles, The dynamic compressive strength and deformation modulus of red-sandstone decrease significantly after freeze-thaw cycles, with the degradation rate slowing down as the number of cycles increases. Mutlutürk et al. (2004) proposed an exponential decay model that indicates the integrity loss of rocks under freeze-thaw or thermal cycling follows a first-order process, and its decay constant and half-life can serve as quantitative indicators of durability. Gao et al. (2019) proposed a novel piecewise constitutive model that integrates statistical compaction theory with statistical damage mechanics, effectively characterizing the stress-strain behavior of freeze-thaw weathered rocks. Hou et al., (2025) proposed a freeze-thaw rock damage constitutive model incorporating damage threshold and residual strength, establishing a damage evolution equation under triaxial compression conditions through statistical damage mechanics theory. Shi S. et al. (2024) established a statistical damage constitutive equation capable of accurately characterizing the complete stress-strain curve of freeze-thaw damaged rocks by integrating macro-micro damage analysis with energy dissipation theory, including the nonlinear deformation characteristics during the compaction stage. Jia et al. (2024) established a mesoscopic damage constitutive model for granite under freeze-thaw cycles by integrating porosity and fractal dimension, demonstrating that the first 20 FTCs account for 50% of total damage, which is critical for stability assessment in seasonal frozen regions. Li et al. (2024) developed a damage constitutive model for rock shear strength degradation based on the Weibull distribution and Mohr-Coulomb criterion, demonstrating that increasing freeze-thaw cycles significantly reduce rock porosity, P-wave velocity, and mechanical properties. In terms of acoustic emission (AE) testing, (Cao et al., 2024) combined with AE monitoring, revealing that the mechanical properties of mixed granite exhibit nonlinear degradation with increasing freeze-thaw cycles. Additionally, the internal crack types transitioned from shear-dominated to tensile-dominated failure mechanisms. Barkat et al. (Ullah et al., 2023) investigated the effects of freeze-thaw cycles on the mechanical properties of various rocks (sandstone, marble, and granite), predicting rock failure through acoustic emission signals and energy evolution patterns, while analyzing the characteristics of microcrack development. Yu et al. (2024) demonstrated through AE monitoring and scanning electron microscopy (SEM) analysis that freeze-thaw cycling induces a progressive transition in sandstone’s failure mode from shear-dominated to tensile-dominated fracture. Shi C. D. et al. (2024) revealed that freeze-thaw led to the decrease of granite intensity, the decrease of P-wave velocity, and the change of the frequency characteristics and energy release mode of the AE signal. In terms of image recognition, In terms of image recognition, Ruiz et al. (1999) employed computed tomography (CT) to scan Laspra dolomite specimens, analyzing the evolutionary patterns of pore structures under freeze-thaw cycling conditions. Wang et al. (2021), Chen et al. (2023), Wang et al. (2022) utilized X-ray penetration techniques for internal structure characterization, enabling precise delineation of rock microstructural features including mineral distribution and pore network architectures. Qiu et al. (2024) investigated the microstructural deterioration mechanisms of sandstone under freeze-thaw cycles with varying water saturation conditions using X-ray computed tomography (CT) technology. Zhang et al. (2014) conducted CT scanning investigations on pre-fractured sandstone to elucidate pore structure expansion and evolution patterns under freeze-thaw cycling, revealing a significant frost-driven increase in macroporosity proportion. Wu et al. (2025) employed X-ray computed tomography (CT) scanning to unveil the meso-damage evolution mechanisms in artificially frozen sandy gravel, achieving quantitative characterization of damage zones through advanced four-color image processing techniques.

In conclusion, although abundant research achievements have been made regarding the changes in Physical and mechanical parameters and damage evolution laws of rocks under freeze-thaw action, there remains room for further investigation. Most existing freeze-thaw damage models primarily describe the changes in macroscopic mechanical properties induced by freeze-thaw cycles, without considering the internal microscopic characteristics of rocks. The model parameters are mostly determined directly through fitting methods, failing to reflect the regulatory changes of different damage variables and lacking actual physical significance. Moreover, there are few reports on applying appropriate freeze-thaw damage models to examine mechanical damage characteristics.

In response to the issue that previous research has not sufficiently considered the impact of the compaction stage on rock deformation and the effects of pore compaction, this paper establishes a freeze-thaw damage evolution model based on the theory of continuum damage mechanics, which characterizes the evolution laws of different damage variables. To validate the reliability of the model, this study focuses on granite as the research object and simulates actual environmental effects through freeze-thaw cycle tests. Additionally, uniaxial compression tests are conducted to obtain the complete stress-strain curves. Using acoustic emission monitoring and CT scanning technologies, the physical and mechanical properties of granite, the laws of damage evolution, and the failure modes are systematically analyzed from both macroscopic and microscopic perspectives. The comparative analysis of the experimental results and the theoretical model indicates that the established model can accurately describe the damage accumulation and failure process of granite under freeze-thaw cycles, providing a theoretical basis for the long-term stability assessment of rock engineering in cold regions.

2 Rock freeze-thaw damage model

Previous studies have primarily concentrated on macroscopic scales, characterizing rock damage variables through macroscopic mechanical parameters such as elastic modulus, strength, and wave velocity. However, these models fail to capture the internal microscale damage evolution processes, whereas microstructural damage is the fundamental cause of rock mechanical property deterioration. To comprehensively investigate the degradation process and mechanisms of rock damage under freeze-thaw loading, it is essential to select appropriate damage variables at both macroscopic and microscopic scales for the establishment of damage evolution equations.

Based on the principles of Continuum Damage Mechanics (CDM), damage can be conceptualized as an irreversible, energy-dissipative evolution process of a material’s internal structural state, governed by the laws of irreversible thermodynamics. Consequently, the damage variable D_FT can be defined as an internal state variable (hereafter referred to as an internal variable) that quantifies the macroscopic degradation of material properties. Its conjugate thermodynamic force is the damage energy dissipation rate Y (or damage energy release rate), where their product represents the damage dissipation energy (Jia et al., 2019). Due to their conjugate relationship, the evolution of D_FT is controlled by Y.

Based on the normal rheological laws of internal variables, the general expression of the damage evolution equation can be formulated as:

${\dot{D}}_{FT}=\frac{\mathrm{\partial }{\psi }^{*}}{\mathrm{\partial }Y}(1)$

Where: ${\dot{D}}_{FT}$ denotes the time derivative of the damage function tensor (D_FT); ${\psi }^{*}$ represents the dissipation potential. As evident from Equation 1, the damage evolution model can be derived once a specific dissipation potential is defined.

For rocks with high porosity and well-connected pore structures, such as sandstone, shale, and conglomerate, several theoretical frameworks have been proposed to describe freeze-thaw (FT) damage mechanisms. These include the volume expansion theory (Murton et al., 2006), hydrostatic pressure theory (Powers, 1945), ice segregation theory (Taber, 1930), capillary stress theory (Everett, 1961), and crystallization pressure theory (Scherer, 1999). However, none of these theories fully account for all observed FT-induced degradation phenomena.

The volume expansion theory is widely accepted for rocks containing closed pore spaces (or closed systems where ice expansion occurs). During freezing, water undergoes approximately 9% volumetric expansion. If freezing occurs within rigidly confined closed pores, the restricted volume increase generates elevated ice pressure. Upon thawing, ice contraction reduces pore pressure, allowing partial recovery of pore deformation. Nevertheless, irreversible deformation persists in the rock matrix due to FT cycling. As the number of FT cycles increases, cumulative irreversible deformation progressively accumulates, ultimately leading to material damage and failure. Mechanistically, the freezing phase acts analogously to fatigue loading, while thawing corresponds to fatigue unloading.

Based on the work of Zhang et al. (2018), the energy dissipation potential characterizing material fatigue was adopted:

${\psi }^{*}\left(Y,T,D_{FT},\sigma \right)=\frac{b}{S_0+1}{\left(\frac{-Y}{b}\right)}^{S_0+1}\dot{Y}(2)$

Where: Y denotes the damage conjugate thermodynamic force of the material; T represents the material temperature; b and S₀ are material constants. Although temperature fluctuates during freeze-thaw (FT) cycles, the temperature gradient remains consistent across each cycle, implying identical FT-induced damage per cycle. Consequently, the influence of FT temperature T on damage evolution is neglected. Substituting Equation 2 into Equation 1, the FT damage rate can be expressed as:

${\dot{D}}_{FT}=\frac{\mathrm{\partial }{\psi }^{*}}{\mathrm{\partial }Y}={\left(\frac{-Y}{b}\right)}^{S_0}\left(-\dot{Y}\right)(3)$

Assuming no coupling between plastic dissipation and damage dissipation, and that FT damage progression occurs as a gradual isothermal process, the damage conjugate thermodynamic force Y can be expressed as (Yu et al., 2022):

$Y=-\frac{{\sigma }_{eq}^2}{2E_0{\left(1-D_{FT}\right)}^2}{\mathrm{R}}_{\mathrm{v}}(4)$

Where: ${\sigma }_{eq}$ represents the von Mises equivalent stress; E₀ is the elastic modulus of the material; R_v denotes the triaxiality function. The R_v expression is shown in Equation 5:

${\mathrm{R}}_{\mathrm{v}}=\frac{2\left(1+\mu \right)}{3}+3\left(1-2\mu \right){\left(\frac{{\sigma }_H}{{\sigma }_{eq}}\right)}^2(5)$

Where: μ is the Poisson’s ratio of the rock; ${\sigma }_{ij}^D$ denotes the deviatoric stress, as shown in Equation 6; ${\sigma }_H$ represents the hydrostatic pressure.

${\sigma }_{ij}^D={\sigma }_{ij}-{\delta }_{ij}{\sigma }_H,{\sigma }_H=\frac{1}{3}{\sigma }_{kk}(6)$

Where: ${\delta }_{ij}$ is the Kronecker delta, defined as ${\delta }_{ij}$ = 1 if i = j, and ${\delta }_{ij}$ = 0 otherwise; ${\sigma }_{ij}$ denotes the stress tensor; ${\sigma }_{kk}$ is the trace of the stress tensor. Differentiating Y with respect to time yields:

$\dot{Y}=-\frac{{\sigma }_{eq}{\mathrm{R}}_{\mathrm{v}}}{E_0{\left(1-D_{FT}\right)}^2}{\dot{\sigma }}_{eq}(7)$

By substituting Equation 4 and Equation 7 into Equation 3, the damage evolution equation can be determined as follows:

${\dot{D}}_{FT}={\left(\frac{{\sigma }_{eq}^2{\mathrm{R}}_{\mathrm{v}}}{2E_{0}b{\left(1-D_{FT}\right)}^2}\right)}^{S_0}\frac{2{\sigma }_{eq}{\mathrm{R}}_{\mathrm{v}}}{2E_0{\left(1-D_{FT}\right)}^2}{\dot{\sigma }}_{eq}=\frac{2{\sigma }_{eq}^{2S_0+1}{\mathrm{R}}_{\mathrm{v}}^{S_0+1}}{{\left(2E_0\right)}^{S_0+1}{b}^{S_0}{\left(1-D_{FT}\right)}^{2S_0+2}}{\dot{\sigma }}_{eq}(8)$

As mentioned above, the damage to rock induced by freeze-thaw cycles is a continuously accumulating process. It is assumed that the cumulative damage caused by freezing and thawing effects during each freeze-thaw cycle is a constant value, and the damage increment can be expressed as $\frac{\delta D_{FT}}{\delta N}$. Under proportional loading conditions, R_v is considered constant. Consequently, the damage per freeze-thaw cycle can be derived from Equation 8 as:

$\begin{array}{l}\frac{\delta D_{FT}}{\delta N}={\int }_{cycle}{\dot{D}}_{FT}dt\\ =2{\int }_{{\sigma }_{\min }}^{{\sigma }_{\max }}\frac{2{\mathrm{R}}_{\mathrm{v}}^{S_0+1}}{{\left(2E_0\right)}^{S_0+1}{b}^{S_0}{\left(1-D_{FT}\right)}^{2S_0+2}}{\sigma }^{2S_0+1}d\sigma \\ =2{\int }_{{\sigma }_{\min }}^{{\sigma }_{\max }}\frac{B{\sigma }^{2S_0+1}}{{\left(1-D_{FT}\right)}^{2S_0+2}}d\sigma \end{array}(9)$

Where: $B=\frac{2{\mathrm{R}}_{\mathrm{V}}^{S_0+1}}{{\left(2E_0\right)}^{S_0+1}{b}^{S_0}}$. As mentioned above, During a single freeze-thaw cycle, the frost-induced expansive stress decays to zero upon thawing. By integrating Equation 9 over the cycle duration, we obtain:

$\frac{\delta D_{FT}}{\delta N}=\frac{B\Delta {\sigma }^{2S_0+2}}{\left(S_0+1\right){\left(1-D_{FT}\right)}^{2S_0+2}}(10)$

Where: $\Delta \sigma$ denotes the variation in frost-heave pressure. Thus, the cumulative damage after N freeze-thaw cycles can be determined by Equation 10:

$D_{FT}=1-{\left[1-\frac{B\left(2S_0+3\right)}{\left(S_0+1\right)}\Delta {\sigma }^{2S_0+2}N\right]}^{\frac{1}{2S_0+3}}(11)$

The experimental results indicate that porous media materials undergo failure after a certain number of freeze-thaw cycles (Khanlari et al., 2015; Ruedrich et al., 2011). From this, it can be inferred that specific rock materials must have a critical threshold of freeze-thaw cycles. When the number of freeze-thaw cycles exceeds this critical value, the rock will experience failure. According to damage theory, the damage variable for material failure equals 1. Thus, the critical value of freeze-thaw cycles N_f can be expressed as:

$N_f=\frac{\left(S_0+1\right)}{B\left(2S_0+3\right)\Delta {\sigma }^{2S_0+2}}(12)$

From Equation 12, it can be observed that the frost damage life of rock is related to the intrinsic properties of the rock material and is also constrained by the frost heave force induced by freeze-thaw conditions. The greater the frost heave force per freeze-thaw cycle, the shorter the frost damage life of the rock. By substituting the defined frost damage life expression (Equation 12) into Equation 11, the evolution of frost damage with freeze-thaw cycles can be shown in Equation 13.

$D_{FT}=1-{\left[1-\frac{N}{N_f}\right]}^{\frac{1}{2S_0+3}}(13)$

It should be noted that in actual laboratory test results, the freeze-thaw damage value of porous rock subjected to Nf freeze-thaw cycles is significantly less than 1. Furthermore, the determination of Dc depends on the definition of the damage variable. When the damage variable is defined based on strength, mass, or porosity, its value may vary. Inspired by Bai et al. (Bai et al., 2022)’s research on concrete, the freeze-thaw damage evolution model can be modified as:

$D_{FT}=D_c\left[1-{\left(1-\frac{N}{N_f}\right)}^{\frac{1}{2S_0+1}}\right](14)$

Where: D_c denotes the critical freeze-thaw damage threshold, determinable under laboratory conditions; N_f represents the critical freeze-thaw cycle count at which failure occurs. Equation 14 constitutes a damage evolution model formulated by integrating Continuum Damage Mechanics (CDM) with thermodynamic theory.

3 Test overview

3.1 Test materials

The rock samples used in the experiment were all taken from the same mining area in Jining City, Shandong Province. To eliminate the influence of rock heterogeneity, the samples were extracted from the same rock block. After field core sampling, indoor cutting, and polishing, the samples were processed into standard rock specimens with a diameter of 50 mm and a height of 100 mm, conforming to the sample preparation requirements of the International Society for Rock Mechanics (ISRM). The granite samples were divided into five groups, corresponding to 0, 50, 100, 150, and 200 freeze-thaw cycles, totaling 25 rock samples, as shown in Figure 1. The processed granite samples and the results of X-ray diffraction (XRD) spectrum analysis of the mineral composition of the samples are shown in Figure 2 (Yang et al., 2024). The basic physical parameters of the rock samples are listed in Table 1.

Figure 1

Figure 1. Granite sample.

Figure 2

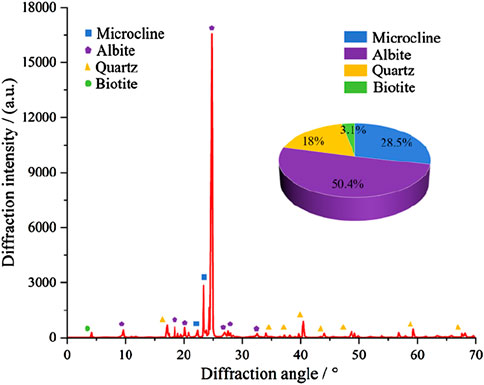
Figure 2. Mineral composition of granite (Yang et al., 2024).

Table 1

Table 1. The basic physical and mechanical parameters of granite.

3.2 Test program and experimental Equipment

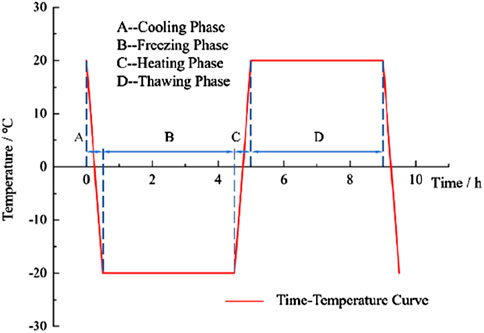
This study strictly followed the DZ/T 0276.8-2015“Testing Procedures for the Physical and Mechanical Properties of Rocks” to conduct freeze-thaw cycle tests. All rock samples were dried at 105°C for 24 h before undergoing vacuum saturation treatment (with a vacuum degree of 0.1 MPa for 4 h). They were then completely immersed in the distilled water tank of the freeze-thaw testing machine for cyclic testing. Each freeze-thaw cycle consists of two stages: freezing at −20°C for 4 h and thawing at 20°C for 4 h, with the temperature change rate controlled at 1.5 °C/min. During the testing process, a freeze-thaw testing machine with a temperature control accuracy of ±0.5°C was used to ensure temperature stability. Additionally, the pH value of the distilled water was regularly monitored (maintained between 6.5 and 7.5), and the distilled water was replaced every five cycles to ensure water quality. Preliminary experiments confirmed that a 4-h freezing time was sufficient to completely freeze the samples, with the mass change rate after thawing being less than 0.1%, validating the adequacy of the freezing process. The experimental setup is illustrated in Figure 3a, and the detailed cycling path is shown in Figure 4.

Figure 3

Figure 3. Rock mechanics equipments: (a) JCD-40 Concrete Building Material Freeze-Thaw Testing Machine; (b) TAJW-1000 Multi-Functional Shear Rheometer; (c) DS5 Full-Information Acoustic Emission Signal Analyzer; (d) nanoVoxel 5,500 High-Energy Holographic Scanning Imaging Analyzer.

Figure 4

Figure 4. Freeze-thaw cycle path.

The test loading system used is the TAJW-1000 multifunctional shear rheometer, as ill in Figure 3b, this equipment has a maximum axial force capacity of 1,000 kN and a stiffness of 10 GN, it can apply a maximum test load of 1,000 kN in the horizontal direction, with a measurement accuracy for the test force of less than ±0.5%. The resolution for deformation and displacement measurements is 0.001 mm. As shown in Figure 3c, the device supports up to 32 channels of AE signal detection, and the data throughput rate can reach up to 262 MB/s, which can completely collect AE signals. For the uniaxial compression test, loading was controlled by displacement at a rate of 0.02 mm/min, and four AE sensors were installed at 30 mm and 70 mm from the bottom of the rock sample, as shown in Figure 3a couplant was applied between the sensor and the surface of the rock sample to ensure that the sensor was in good contact with the rock sample, and the loading continued until the loading was stopped when the specimen was broken. At the end of the uniaxial compression test, a CT scan of each specimen was performed using the nanoVoxel 5,500 high-energy holographic scanning imaging analyzer (Figure 3d).

4 Test results and analysis

4.1 Law of physical property variation

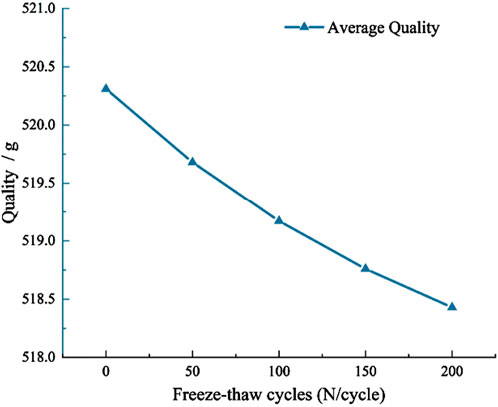
Figure 5 shows the relationship between the mass of granite and the number of freeze-thaw cycles. With the increase in the number of freeze-thaw cycles, the mass exhibits a continuous decline. At 50 cycles, the mass decreases to 519.68 g; at 100 cycles, it drops to 519.17 g; at 150 cycles, it is approximately 518.76 g; and finally, at 200 cycles, it reaches about 518.43 g, resulting in a total mass loss of approximately 1.98 g (with a loss rate of about 0.38%). This trend clearly reflects the progressive damage effect of freeze-thaw cycles on granite. The initial mass loss is quite significant, likely due to the frost heave stress causing rapid spalling of surface mineral particles. In the later stages, the rate of mass loss slows down but remains steadily decreasing, indicating that internal microcracks continue to expand, albeit at a more gradual pace. This characteristic of mass change is primarily attributed to the tensile stress generated by the repeated frost heave of pore water, as well as the weakening of the bonding strength between mineral particles due to thermal fatigue effects.

Figure 5

Figure 5. Relationship curve between quality and freeze-thaw cycles.

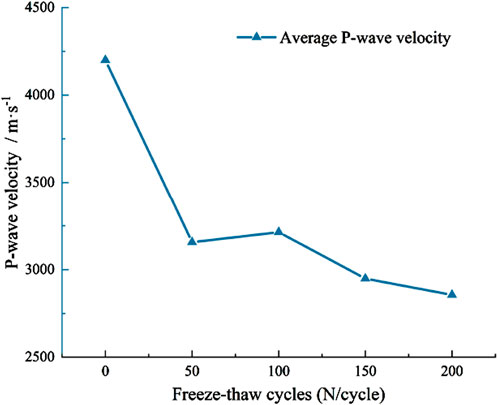
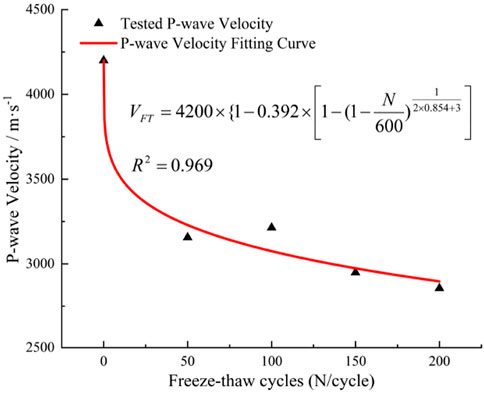
Wave velocity is an effective indicator of the compactness within specimens (Liu et al., 2015). Figure 6 illudtrates the changes in P-wave velocity of granite samples subjected to varying numbers of freeze-thaw cycles. The P-wave velocities of granite were measured using the DS5 full-information acoustic emission signal analyzer, obtaining the following results: 4,200 m/s, 3,156 m/s, 3,213 m/s, 2,949 m/s, and 2,856 m/s, with corresponding change rates of −24.86%, +1.81%, −8.22%, and −3.15%. From these results, it is evident that the P-wave velocity of granite exhibits an overall decreasing trend with an increase in the number of freeze-thaw cycles. This decline can be attributed to the rapid development of micro-pores during the freeze-thaw process, which leads to an increase in porosity. As the internal compactness of the granite decreases, the time required for P-wave propagation increases, resulting in a gradual reduction of the P-wave velocity.

Figure 6

Figure 6. Relationship curve between P-wave velocity and freeze-thaw cycles.

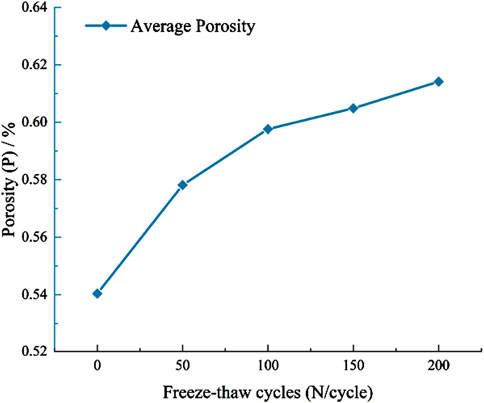
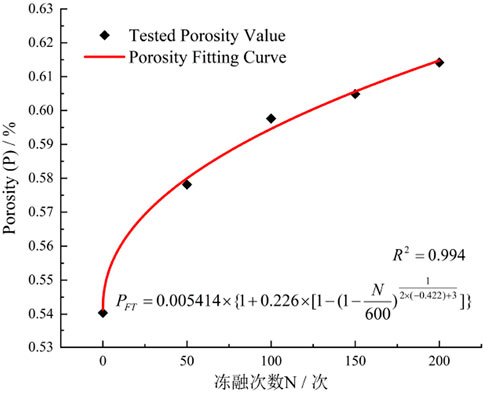
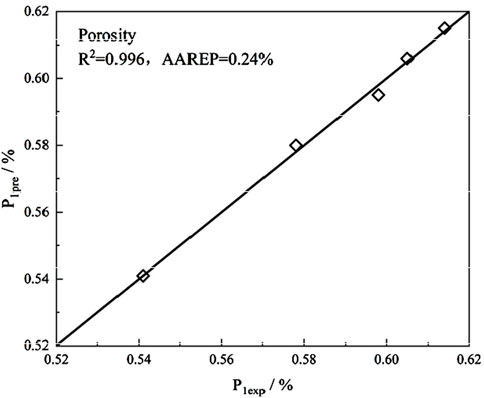
Figure 7 illustrates the relationship curve between porosity and the number of freeze-thaw cycles. As the number of freeze-thaw cycles increases, the porosity of the rock gradually increases, while the rate of porosity change gradually decreases with increasing freeze-thaw cycles. This phenomenon can be explained by the following factors: (1) The rock is composed of multiple minerals, and the expansion degrees of different minerals during freeze-thaw processes are inconsistent, leading to deformation differences. As freeze-thaw cycles proceed, pores and microcracks gradually develop. 2) At low temperatures, water in the rock’s internal pores freezes and expands by approximately 9% in volume. However, the pore space is limited, so the expansion of ice is constrained, generating frost heave pressure that promotes the expansion of pores and microcracks. When temperature rises, the ice melts and water fills the pores and microcracks. (3) With increasing freeze-thaw cycles, the repeated frost heave pressure continuously compresses the rock’s initial pores, causing further expansion of pores and microcracks. This reduces the compactness of the rock’s internal structure and increases porosity.

Figure 7

Figure 7. Relationship curve between porosity and freeze-thaw cycles.

4.2 Law of mechanical property variation

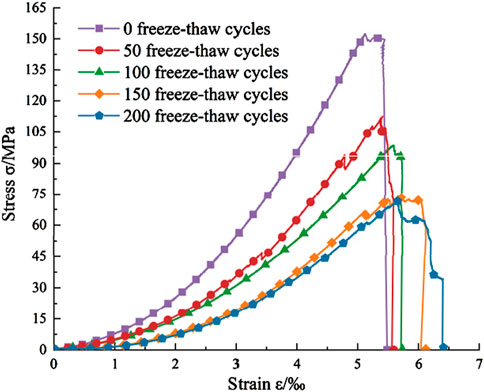
Figure 8 presents the stress-strain curves of the whole process of uniaxial compression of granite under different freeze-thaw cycles. As can be seen from the figure, the curve can be divided into four stages: (1) pore compaction stage: the initial pores in the granite gradually close during the application of pressure, and show an upward concave shape in the stress-strain curve; (2) Elastic deformation stage: the stress-strain curve is linearly and roughly linear; (3) Elastoplastic stage: In this stage, tiny cracks begin to appear in the granite. With the increase of stress, the number of microcracks increases, and the internal failure is gradual. (4) Failure stage: the stress continues to increase, the granite is rapidly damaged, the axial strain changes are small, and the axial stress decreases rapidly. With the increase in the number of freeze-thaw cycles, the strain associated with brittle failure of the rock sample decreases, and the slope of the stress-strain curve decreases, signifying a reduction in elastic modulus, and the peak point of the curve also decreases, indicating that the freeze-thaw cycles significantly weaken the strength of granite.

Figure 8

Figure 8. Uniaxial compression stress-strain curves of granite with different freeze-thaw cycles.

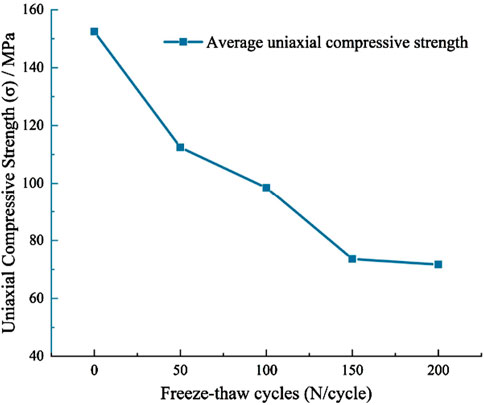
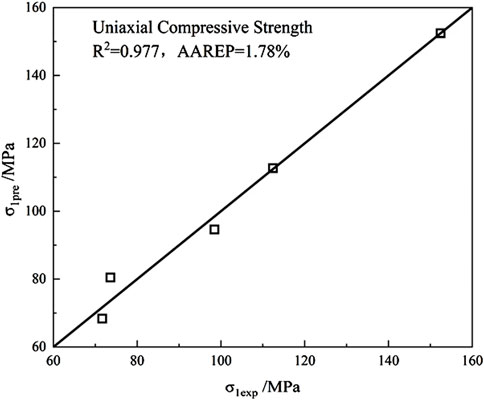
As can be seen from Figure 9, the uniaxial compressive strength of granite varies with the number of freeze-thaw cycles. With an increasing number of freeze-thaw cycles, the uniaxial compressive strength gradually decreases, but the variation law is not linear, which is due to the influence of the strength of the rock itself and the number of internal pores and fractures. After the freeze-thaw cycle, the rates of change in uniaxial compressive strengthwere recoeded as follows: 26.25%, 35.42%, 51.71% and 52.98%, respectively, indicating that the expansion of water and the formation of ice during the freeze-thaw process led to cracks and damage in the rock, the porosity increased and the degree of compactness decreased, thereby weakening the compressive strength of the rock and deteriorating its macroscopic mechanical properties.

Figure 9

Figure 9. Relationship curve between uniaxial compressive strength and freeze-thaw cycles.

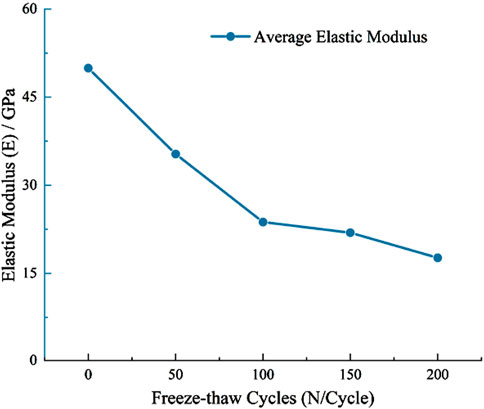
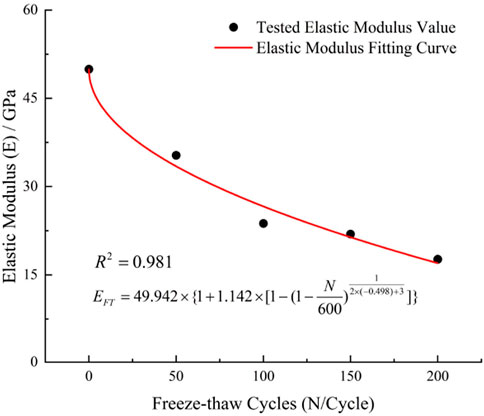
Figure 10 illustrates the change of the elastic modulus of granite under different freeze-thaw cycles, and the change rates of the elastic modulus after the freeze-thaw cycles are recorded as 29.31%, 32.79%, 7.63% and 19.46%, respectively. It is evident that during the first 100 freeze-thaw cycles, the elastic modulus decreases at a faster rate compared to the subsequent 100 cycles, showing an exponential downward trend, and the rate of change of the elastic modulus decreases from 100 to 150 freeze-thaw cycles. This may be due to the influence of heterogeneity and anisotropy of granite materials (Man, 2022). The results indicate that the elastic modulus of granite decreases gradually as the number of freeze-thaw cycles increases, however, the rate of this decrease becomes less pronounced with additional cycles.

Figure 10

Figure 10. Relationship curve between elastic modulus and freeze-thaw cycles.

4.3 Study on acoustic emission (AE) characteristics

Studies on the acoustic emission (AE) characteristics during rock fracture processes demonstrate that stress waves, manifested in the form of AE signals, can effectively reveal the energy dissipation mechanisms during crack initiation and propagation (Wang et al., 2018; Sagar and Rao, 2014). In this study, the AE ring-down count and energy were selected for analysis, as their evolutionary patterns can characterize the rock failure process. The relationships among AE ring-down count, stress, and time for granite under uniaxial compression, as well as the correlations between AE energy, stress, and strain, are presented in Figures 11, 12, respectively.

Figure 11

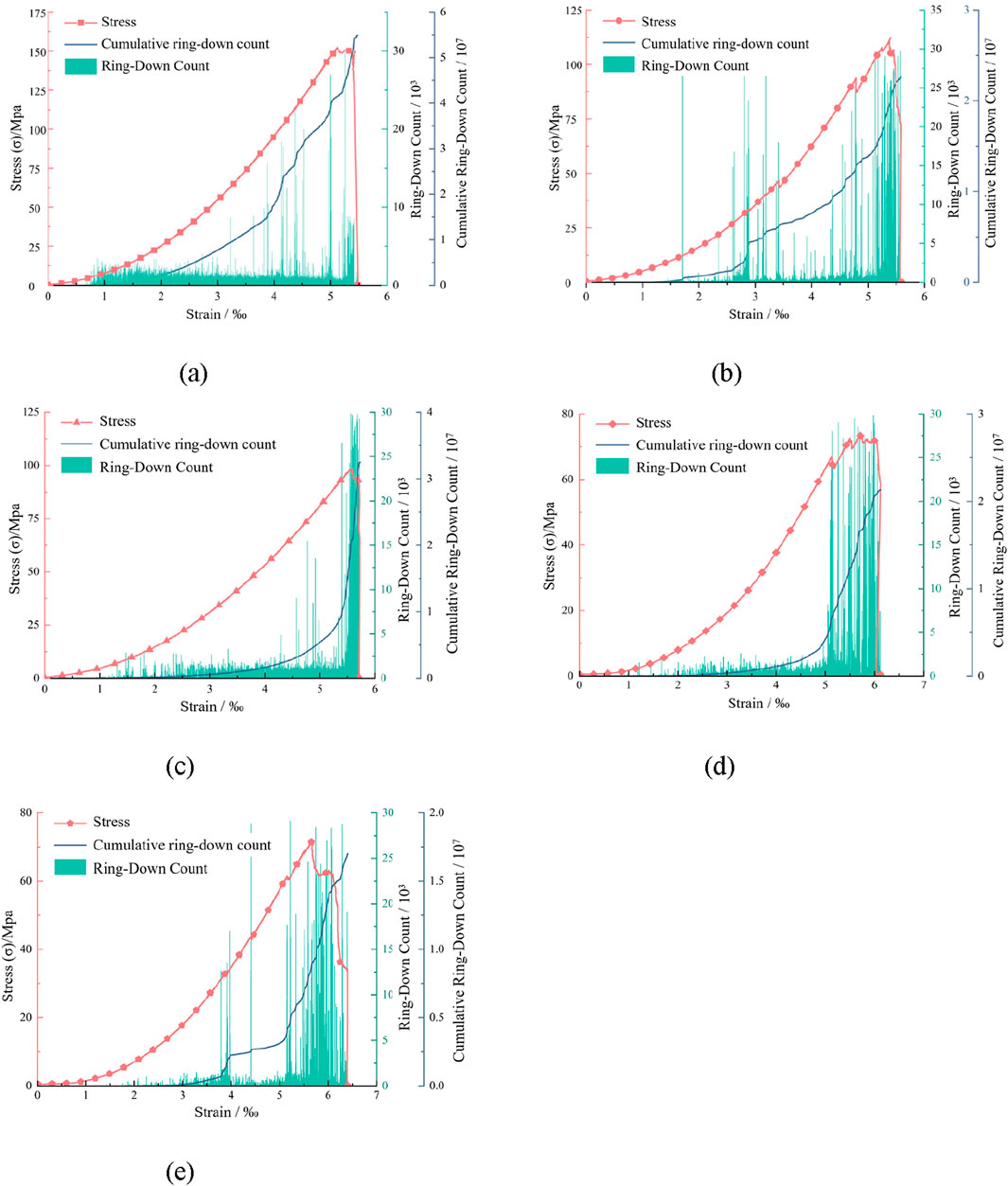
Figure 11. Relationship Curves between Acoustic Emission Ringing Count, Stress, and Strain under Uniaxial Compression Load for Granite. (a) 0 cycles (b) 50 cycles (c) 100 cycles (d) 150 cycles (e) 200 cycles.

Figure 12

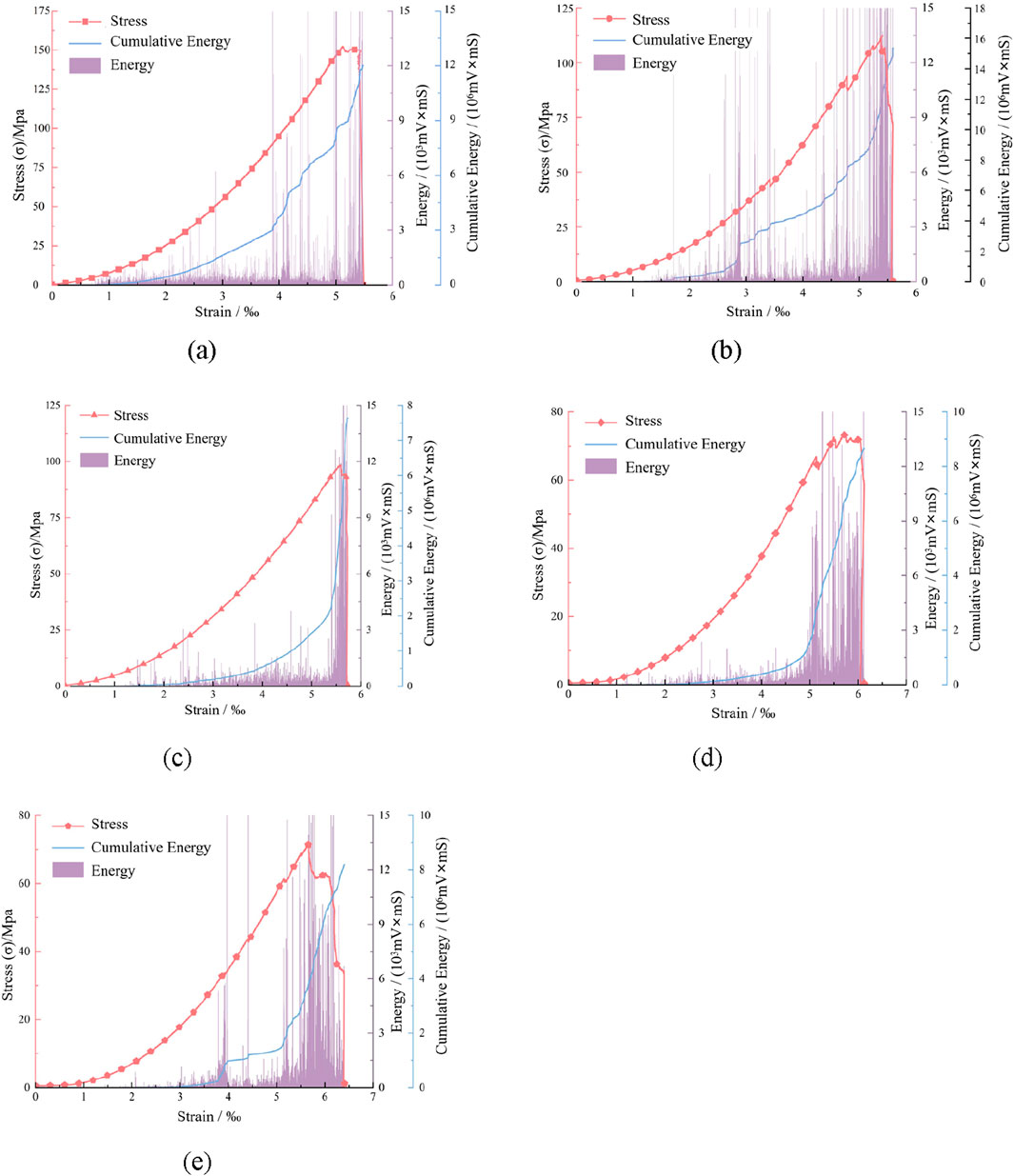
Figure 12. Relationship Curves between Acoustic Emission Energy, Stress, and Strain under Uniaxial Compression Load for Granite. (a) 0 cycles (b) 50 cycles (c) 100 cycles (d) 150 cycles (e) 200 cycles.

From the stress-strain curve, it can be observed that both the cumulative AE ring-down counts and energy exhibit a stepwise growth pattern. This phenomenon arises because, during the axial stress increase process, internal cracks within the rock sample progressively propagate, leading to abrupt changes in AE signals. During the stages of pore compaction and elastic deformation, when stress levels remain relatively low, AE activity is minimal or even non-existent. In this phase, the compaction of pores enhances the integrity of the internal structure of the rock sample, creating conditions that are unfavorable for significant AE activity. As stress continues to increase, newly formed cracks begin to propagate, leading to greater deformation of the specimen. This is accompanied by a notable increase in AE signals. When approaching peak stress, AE activity intensifies, with both ring-down counts and energy reaching their maximum values. At this critical juncture, internal cracks become interconnected, leading to the macroscopic fractures on the specimen’s surface, ultimately resulting in complete failure, after which AE activity ceases entirely.

Comparative analysis of AEdata under different freeze-thaw cycles reveals that both cumulative AE counts and energy exhibit a gradual decreasing trend as the number of cycles increases. This phenomenon can be mechanistically explained by the fact that freeze-thaw cycling promotes the development of pores and microcracks within the rock, increasing the initial damage level of the material and reducing the number of structural units available for fracture during compression. Further analysis demonstrates that specimens subjected to fewer freeze-thaw cycles show a rapid increase in AE activity during the early loading stages, while those undergoing more cycles exhibit slower initial growth but a sudden surge at failure. This characteristic evolution patternindicates that, as the number of freeze-thaw cycles accumulates, the progressive increase in initial damage reduces the number of fracture-capable units during early loading, consequently leading to an overall weakening trend in AE activity.

In the process of uniaxial compressive failure of rocks, the AE ringing count shows a closely related co-evolution characteristic with AE energy. The effect of freeze-thaw cycles significantly alters the proportional relationship between the two. As the number of freeze-thaw cycles increases, the initial damage to the rock intensifies, leading to a reduction in the number of fracture-prone units. This results in a decreased growth rate of the ringing count. Meanwhile, the networking of cracks causes energy release to become more concentrated in a few macro-cracks, which is reflected in the relatively decreased ringing count and the increased amplitude of single energy events. This transition from high-frequency, low-energy emissions to low-frequency, high-energy emissions illustrate the significant impact of freeze-thaw damage on the fracture mode of rocks.

4.4 CT scanning results and analysis of granite failure modes

CT scanning of granite specimens after uniaxial compression failure was conducted using the nanoVoxel 5,500 high-energy holographic imaging system, which clearly revealed the size, quantity and distribution of internal cracks in the rock, thereby enabling analysis of their failure modes as shown in Figure 13. The results indicate significant differences in failure patterns among specimens subjected to varying numbers of freeze-thaw cycles.

Figure 13

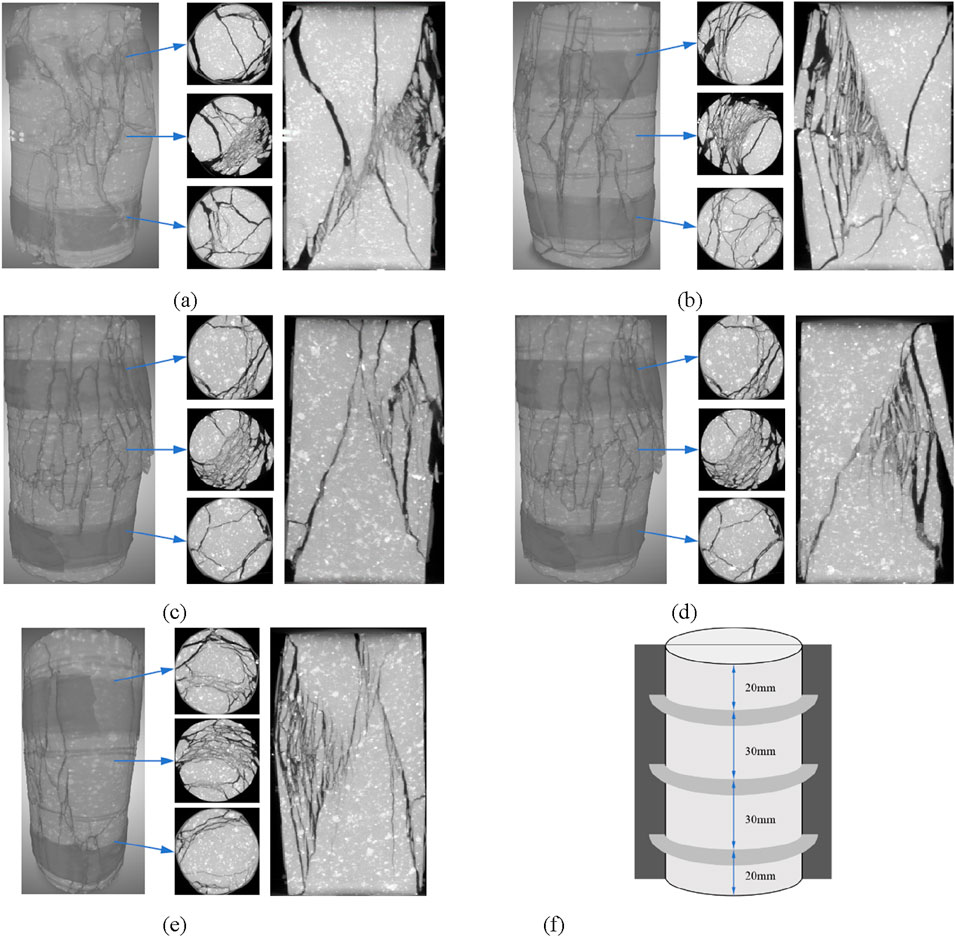
Figure 13. Reconstruction Model and Slice Image of Granite by CT Scanning under Different Freeze-Thaw Cycles. (a) 0 cycles (b) 50 cycles (c) 100 cycles (d) 150 cycles (e) 200 cycles (f) Schematic Diagram of Section Location.

The specimens that underwent no freeze-thaw cycles exhibited intact structures prior to loading. Under uniaxial compression, the granite showed microcrack initiation and propagation, leading to thedevelopment of penetrating fractures on both left and right sides. The lateral surfaces displayed outward deformation and spalling, particularly in the upper-right section, where microcrack development and coalescence were observed, resulting in a distinct “X”-shaped shear failure pattern. In specimens subjected to 50 freeze-thaw cycles, multiple fragmented sections appeared on the left side due to the propagation and coalescence of microcracks, showing significant flake spalling while maintaining an overall “X”-shaped shear failure, though with upward migration of the shear triangle apex. After 100 cycles, two penetrating cracks propagated diagonally from the central top toward both bottom sides, with further upward displacement of the shear triangle apex and partial spalling on the right side, demonstrating a characteristic conical shear failure. The 150 cycle developed a single penetrating crack extending from the top-right to the bottom-left, demonstrating typical conical shear failure with extensive spalling on the right side. At 200 cycles, axial loading produced a dominant diagonal crack that propagated from the central top to the bottom-right, with significant fragment accumulation on the left side, indicating progressive evolution toward conical shear failure. With increasing freeze-thaw cycles, the failure mode transitioned from “X”-shaped to conical shear, accompanied by gradual enlargement of the shear triangle, upward apex migration, and reduction in main fracture quantity. This transition likely results from freeze-thaw induced pore and microcrack development, which reduces granite’s brittleness while enhancing ductility, ultimately leading to rapid failure through dominant fracture formation along zones of maximum microcrack concentration.

5 Validation of rock freeze-thaw damage model under cyclic freezing-thawing conditions

5.1 Fitting results of freeze-thaw damage model

According to Equation 14, under freeze-thaw cycling, the freeze-thaw damage variable D_FT of rock is a function of material characteristic parameter S₀, critical freeze-thaw damage value D_c, key freeze-thaw parameter N_f indicating rock failure, and number of freeze-thaw cycles N. Once the critical freeze-thaw cycle number N_f is determined, the specific material parameters can be obtained through fitting. Granite demonstrates a stronger resistance to freeze-thaw damage due to its dense crystalline structure, high quartz content, and excellent mechanical properties. Its critical freeze-thaw cycle number is significantly higher than that of sandstone, which is 345 cycles (Zheng et al., 2024), and concrete, which is 450 cycles (Liu et al., 2018). Therefore, in this study, the critical freeze-thaw cycle number N_f for all granite samples is set to 600 cycles to verify the accuracy of the freeze-thaw damage model proposed in this paper.

Using the aforementioned model parameters, the nonlinear prediction equation for rock physico-mechanical parameters can be determined as:

$X=X_0\left\{1-D_c\left[1-{\left(1-\frac{N}{600}\right)}^{\frac{1}{2S_0+3}}\right]\right\}(15)$

To verify the feasibility of the rock freeze-thaw damage model under cyclic freezing-thawing conditions, the experimental results mentioned above were substituted into Equation 15 to calculate the model-predicted values. Comparative curves between experimental data and predicted values were then plotted, as shown in Figures 14–17.

Figure 14

Figure 14. Comparison curve between experimental and fitted values of P-wave velocity.

Figure 15

Figure 15. Comparison curve between experimental and fitted values of porosity.

Figure 16

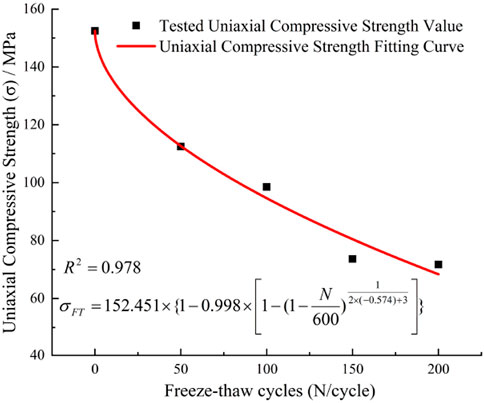
Figure 16. Comparison curve between experimental and fitted values of uniaxial compressive strength.

Figure 17

Figure 17. Comparison curve between experimental and fitted values of elastic modulus.

The fitted correlation coefficients for wave velocity, porosity, uniaxial compressive strength, and elastic modulus are 0.969, 0.994, 0.978, and 0.981, respectively. The parameters of their predictive curve equations are summarized in Table 2.

Table 2

Table 2. Model parameters of nonlinear prediction equations of rock physical and mechanical parameters.

5.2 Evaluation metrics for fitting results and their Assessment​

Inspired by Zheng et al., (2022), three error metrics were adopted to evaluate the fitting results of the freeze-thaw damage model against experimental uniaxial compression test data of rocks. The first error metric is the goodness-of-fit R²:

$R^2=1-\frac{{\sum }_{i=1}^N{\left(X_{1\exp }-X_{1pre}\right)}^2}{{\sum }_{i=1}^N{\left(X_{1\exp }-{\overline{X}}_{1\exp }\right)}^2}(16)$

where N is the number of data points; X_1exp and X_1pre were the uniaxial compression test values and the fitting values of the freeze-thaw damage model, respectively. It is the average value of the uniaxial compression test value of the rock.

The second error index is the single-point data error D_p,i:

$D_{p,i}=\frac{X_{1pre}-X_{1\exp }}{X_{1\exp }}\times 100\%(17)$

The third error indicator is the mean absolute error AAREP:

$\text{AAREP}=\frac{{\sum }_{i-1}^N\left|D_{p,i}\right|}{N}\times 100\%(18)$

From Equations 16–18, it can be seen that: The larger the R² value, the smaller the AAREP value, the closer the predicted values of the rock freeze-thaw damage model are to the experimental values, The better the fitting performance.

The fitting effectiveness of the freeze-thaw damage model for rock physico-mechanical properties was evaluated using the three aforementioned evaluation indices, with their correlation relationships illustrated in Figures 18–21.

Figure 18

Figure 18. Diagram of correlation between theoretical and experimental values of P-wave velocity.

Figure 19

Figure 19. Correlation diagram between theoretical and experimental values of porosity.

Figure 20

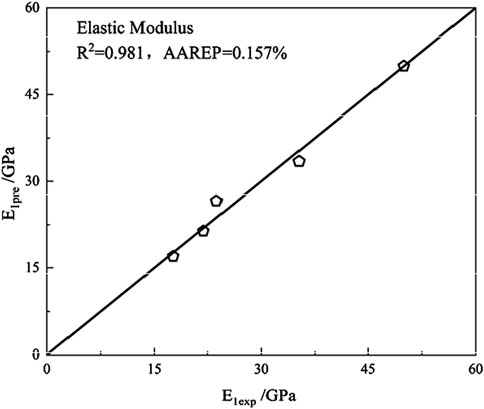
Figure 20. Diagram of correlation between theoretical and experimental values of uniaxial compressive strength.

Figure 21

Figure 21. Graph of correlation between theoretical and experimental values of elastic modulus.

The proposed freeze-thaw damage model demonstrates an average goodness-of-fit (R²) = 0.983 and an average absolute relative error percentage (AAREP) < 2%, demonstrating excellent agreement between predicted and experimental values. The model effectively captures the evolution patterns of various damage variables, thereby validating its feasibility and effectiveness. These results highlight the model’s practical significance for geotechnical engineering applications in cold-region hydraulic projects.

6 Conclusion

This study establishes a novel rock freeze-thaw damage model based on continuum damage mechanics and thermodynamics to characterize the damage evolution in various rock types under cyclic freeze-thaw conditions. Through laboratory freeze-thaw tests, AE monitoring, and uniaxial compression experiments, the physico-mechanical properties of granite were systematically investigated to validate the model’s applicability. The main conclusions are as follows.

(1) With increasing freeze-thaw cycles, the internal fractures in granite progressively develop, resulting in a decreasing trend in UCS, elastic modulus, and wave velocity, while the porosity exhibits an increasing trend.

(2) Under uniaxial compressive loading, internal cracks in rock samples progressively propagate, with AE signals demonstrating a stepwise increasing trend. As stress intensifies, crack propagation accelerates, accompanied by enhanced AE activity. Approaching peak stress, rock failure becomes most pronounced, characterized by intense AE events and maximum AE signal amplitudes.

(3) As the number of freeze-thaw cycles increases, the cumulative AE ring-down counts and energy gradually decrease. This trend indicates that freeze-thaw action accelerates the development of pores and microcracks, which in turn increase the initial damage in rocks and reduces the number of fracture units during compression. Concurrently, the enhanced initial rock damage leads to fewer fracture units in the early loading stage, resulting in weakened AE activity during the initial loading phase.

(4) With the increase in freeze-thaw cycles, the failure mode of granite transitions from “X”-shaped shear failure to conical shear failure, characterized by upward migration of the shear triangle apex and gradual reduction of major fractures. This transition likely occurs because progressive freeze-thaw action promotes the propagation of pores and microcracks within the rock specimen. Once a significant penetrating fracture develops at the location with the highest concentration of microcracks and pores, rapid failure is triggered.

(5) The proposed rock freeze-thaw damage model exhibits excellent predictive capability, evidenced by an average goodness-of-fit (R²) of 0.983 and AAREP consistently below 2%. These metrics confirm a strong agreement between model‘s predictions and the experimental results, highlighting the model’s effectiveness in characterizing the evolution patterns of various damage variables under cyclic freeze-thaw conditions.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

SX: Writing – review and editing, Writing – original draft, Methodology, Investigation. YH: Writing – review and editing, Writing – original draft, Investigation, Validation. CJ: Validation, Writing – review and editing, Supervision. LW: Conceptualization, Supervision, Writing – review and editing, Funding acquisition.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The grant support from the National Natural Science Foundation of China (Grant No. 52378421) is acknowledged.

Conflict of interest

Author SX was employed by Hunan Baige Water Conservancy Construction Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. During the preparation of this work the authors used Deepseek in order to improve language. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bai, J., Zhao, Y., Shi, J., and He, X. (2022). Damage degradation model of aeolian sand concrete under freeze–thaw cycles based on macro-microscopic perspective. Constr. Build. Mater 327, 126885. doi:10.1016/j.conbuildmat.2022.126885

CrossRef Full Text | Google Scholar

Cao, J., Hu, J., Wang, X., Yang, B., Xia, Z., Wang, H., et al. (2024). Mechanical properties and acoustic emission characteristics of mixed granite after different numbers of freeze–thaw cycles. Sci. Rep. 14, 14074. doi:10.1038/s41598-024-65008-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, L., Li, K., Song, G., Zhang, D., and Liu, C. (2021). Effect of freeze–thaw cycle on physical and mechanical properties and damage characteristics of sandstone. Sci. Rep. 11, 12315. doi:10.1038/s41598-021-91842-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X. C., Wang, G., Chen, H., and Wang, S. (2023). Analysis of the effects of coal facture shape factor on water seepage based on computerized tomography (CT) 3D reconstructed artificial fractures. Fuel 348, 128571. doi:10.1016/j.fuel.2023.128571

CrossRef Full Text | Google Scholar

Del Roa, L. M., Lopez, F., Esteban, F. J., Tejado, J., Mota, M., Gonzalez, I., et al. (2005). Ultrasonic study of alteration processes in granites caused by freezing and thawing. IEEE Ultrason. Symp. 1, 415–418. doi:10.1109/ULTSYM.2005.1602882

CrossRef Full Text | Google Scholar

Everett, D. H. (1961). The thermodynamics of frost damage to porous solids. Trans. Faraday Soc. 57:1541–1551. doi:10.1039/TF9615701541

CrossRef Full Text | Google Scholar

Gao, F., Xiong, X., Xu, C. S., and Zhou, K. (2019). Mechanical property deterioration characteristics and a new constitutive model for rocks subjected to freeze-thaw weathering process. Int. J. Rock Mech. Min. Sci. 140, 104642. doi:10.1016/j.ijrmms.2021.104642

CrossRef Full Text | Google Scholar

Hou, C., Wang, C., and Dias, D. (2025). Damage constitutive model for freeze-thawed rock: considering damage threshold and residual strength. Geotech. Geol. Eng. 43, 21. doi:10.1007/s10706-024-03030-w

CrossRef Full Text | Google Scholar

Jia, C., Xu, W., Wang, S., Wang, R., and Yu, J. (2019). Experimental analysis and modeling of the mechanical behavior of breccia lava in the dam foundation of the Baihetan Hydropower Project. Bull. Eng. Geol. Environ. 78, 2681–2695. doi:10.1007/s10064-018-1228-3

CrossRef Full Text | Google Scholar

Jia, S., Yu, Q., Yin, H., Dai, Z., Yin, S., Kong, Y., et al. (2024). Analysis of damage evolution and study on mesoscopic damage constitutive model of granite under freeze–thaw cycling. Bull. Eng. Geol. Environ. 83, 236. doi:10.1007/s10064-024-03741-7

CrossRef Full Text | Google Scholar

Khanlari, G., Sahamieh, R. Z., and Abdilor, Y. (2015). The effect of freeze–thaw cycles on physical and mechanical properties of Upper Red Formation sandstones, central part of Iran. Arab. J. Geosci. 8, 5991–6001. doi:10.1007/s12517-014-1653-y

CrossRef Full Text | Google Scholar

Kolay, E. (2016). Modeling the effect of freezing and thawing for sedimentary rocks. Environ. Earth Sci. 75, 210. doi:10.1007/s12665-015-5005-3

CrossRef Full Text | Google Scholar

Li, J. L., Kaunda, R. B., and Zhou, K. P. (2018). Experimental investigations on the effects of ambient freeze-thaw cycling on dynamic properties and rock pore structuredeterioration of sandstone. Cold Reg. Sci. Technol. 154, 133–141. doi:10.1016/j.coldregions.2018.06.015

CrossRef Full Text | Google Scholar

Li, X. P., Qu, D. X., Luo, Y., Ma, R. Q., Xu, K., and Wang, G. (2019). Damage evolution model of sandstone under coupled chemical solution and freeze-thaw process. Cold Reg. Sci. Technol. 162, 88–95. doi:10.1016/j.coldregions.2019.03.012

CrossRef Full Text | Google Scholar

Li, Y., Wang, Z., Cao, H., and Wu, T. (2024). Constitutive characteristics of rock damage under freeze–thaw cycles. Appl. Sci. 14, 4627. doi:10.3390/app14114627

CrossRef Full Text | Google Scholar

Liu, Y. L., Chu, D. H., Liu, J. J., and Zhong, X.(2015). Comparative study on calculation formula of crack load for reinforced concrete beam. Build. Struct. 45(6), 14–17. doi:10.19701/j.jzjg.2015.06.003

CrossRef Full Text | Google Scholar

Liu, F., You, Z., Yang, X., and Wang, H. (2018). Macro-micro degradation process of fly ash concrete under alternation of freeze-thaw cycles subjected to sulfate and carbonation. Constr. Build. Mater. 181, 369–380. doi:10.1016/j.conbuildmat.2018.06.037

CrossRef Full Text | Google Scholar

Luo, Y., Qu, D., Wang, G., Li, X., and Zhang, G. (2020). Degradation model of the dynamic mechanical properties and damage failure law of sandstone under freeze-thaw action. Soil dynam. earthg. Eng. 132, 106094. doi:10.1016/j.soildyn.2020.106094

CrossRef Full Text | Google Scholar

Man, L. E. I. (2022). Study on the meso-mechanical properties and mechanism of granite under combined action of hydrochemistry and freeze-thaw cycle based on nanoindentation test. Sch. Civ. Eng. Archit. doi:10.27398/d.cnki.gxalu.2022.001756

CrossRef Full Text | Google Scholar

Momeni, A., Abdilor, Y., Khanlari, G. R., Heidari, M., and Sepahi, A. A. (2016). The effect of freeze–thaw cycles on physical and mechanical properties of granitoid hard rocks. Bull. Eng. Geol. Environ. 75, 1649–1656. doi:10.1007/s10064-015-0787-9

CrossRef Full Text | Google Scholar

Murton, J. B., Peterson, R., and Ozouf, J. C. (2006). Bedrock fracture by ice segregation in cold regions. Science314 314, 1127–1129. doi:10.1126/science.1132127

PubMed Abstract | CrossRef Full Text | Google Scholar

Mutlutürk, M., Altindag, R., and Türk, G. (2004). A decay function model for the integrity loss of rock when subjected to recurrent cycles of freezingethawing and heatingecooling. Int. J. Rock Mech. Min. 41 (2), 237e244. doi:10.1016/S1365-1609(03)00095-9

CrossRef Full Text | Google Scholar

Park, J., Hyun, C. U., and Park, H. D. (2015). Changes in microstructure and physical properties of rocks caused by artificial freeze–thaw action. Bull. Eng. Geol. Environ. 74, 555–565. doi:10.1007/s10064-014-0630-8

CrossRef Full Text | Google Scholar

Powers, T. C. (1945). A working hypothesis for further studies of frost resistance of concrete, 41. J. of the American Concrete Institute, 245–272. doi:10.14359/8684

CrossRef Full Text | Google Scholar

Qiu, B., Fan, L., and Du, X. (2024). Microstructure deterioration of sandstone under freeze-thaw cycles using CT technology: the effects of different water immersion conditions. J. Rock Mech. Geotech. Eng. 17 (3), 1599–1611. doi:10.1016/j.jrmge.2024.02.002

CrossRef Full Text | Google Scholar

Ruedrich, J., Kirchner, D., and Siegesmund, S. (2011). Physical weathering of building stones induced by freeze–thaw action: a laboratory long-term study. Environ. Earth Sci. 63, 1573–1586. doi:10.1007/s12665-010-0826-6

CrossRef Full Text | Google Scholar

Ruiz, V. G., Rey, R. A., Clorio, C., Suárez del Río, L. M., Calleja, L., and Llavona, J. (1999). Characterization by computed X-ray tomography of the evolution of the pore structure of a dolomite rock during freeze-thaw cyclic tests. Phys. Chem. Earth 7 (24), 633–637. doi:10.1016/S1464-1895(99)00092-7

CrossRef Full Text | Google Scholar

Sagar, V. R., and Rao, M. (2014). An experimental study on loading rate effect on acoustic emission based b -values related to reinforced concrete fracture. Constr. Build. Mater., 70460–70472. doi:10.1016/j.conbuildmat.2014.07.076

CrossRef Full Text | Google Scholar

Scherer, G. W. (1999). Crystallization in pores. Cem. Concr. Res. 29, 1347–1358. doi:10.1016/S0008-8846(99)00002-2

CrossRef Full Text | Google Scholar

Shi, C. D., Nie, W., Ma, G. W., He, M., and Chen, Y. (2024b). Effects of freeze-thaw cycles on granite failure using acoustic emission test. Rock Mech. Geotech. Eng. doi:10.1016/j.jrmge.2024.11.021

CrossRef Full Text | Google Scholar

Shi, S., Zhu, F. J., and Hu, H. Q. (2024a). Investigation on the damage model of rock subjected to freeze-thaw cycles considering its fracture voids compaction. Cold Reg. Sci. Tech. 223, 104222. doi:10.1016/j.coldregions.2024.104222

CrossRef Full Text | Google Scholar

Taber, S. (1930). The mechanics of frost heaving. J. Geol. 38:303–317. doi:10.1086/623720

CrossRef Full Text | Google Scholar

Ullah, B., Zhou, Z., Cai, X., Lu, J., and Zhao, C. C. (2023). Failure prediction and microcracks development based on acoustic emission and energy evolution for different rocks treated with freeze–thaw weathering. Bull. Eng. Geol. Environ. 82, 471. doi:10.1007/s10064-023-03485-w

CrossRef Full Text | Google Scholar

Wang, P., Xu, J. Y., Liu, S., Liu, S. H., and Wang, H. Y. (2016). A prediction model for the dynamic mechanical degradation of sedimentary rock after a long-term freeze-thaw weathering: considering the strain-rate effect. Cold Reg. Sci. Technol. 131, 16–23. doi:10.1016/j.coldregions.2016.08.003

CrossRef Full Text | Google Scholar

Wang, Y., Li, C. H., and Hu, Y. Z. (2018). Experimental investigation on the fracture behaviour of black shale by acoustic emission monitoring and CT image analysis during uniaxial compression. Geophys. J. Int. 213 (1), 660–675. doi:10.1093/gji/ggy011

CrossRef Full Text | Google Scholar

Wang, G., Chen, X. C., Wang, S. B., and Chen, H. (2022). Influence of fracture connectivity and shape on water seepage of low-rank coal based on CT 3D reconstruction. J. Nat. Gas Sci. Eng. 102, 104584. doi:10.1016/j.jngse.2022.104584

CrossRef Full Text | Google Scholar

Wang, G., Qin, X. J., Han, D. Y., and Liu, Z. (2021). Study on seepage and deformation characteristics of coal microstructure by 3D reconstruction of CT images at high temperatures. Int. J. Min. Sci. Technol. 31 (2), 175–185. doi:10.1016/j.ijmst.2020.11.003

CrossRef Full Text | Google Scholar

Wu, W., Yan, Q., Li, Y., Zhang, J., Ding, Z., and Xu, C. (2025). Investigation on mechanism and variation of mesoscopic damage in artificial frozen sandy gravels by X-ray CT scanning. Bull. Eng. Geol. Environ. 84, 188. doi:10.1007/s10064-025-04183-5

CrossRef Full Text | Google Scholar

Yang, H., Wang, K. H., Zhou, G., Li, M., Wu, H. J., and Dai, X. H. (2024). Dynamic mechanical properties and anti-penetration performance of granite with different weathering degrees. Explos. Shock Waves 44 (10), 101403-1-101403–18. doi:10.11883/bzycj-2024-0017

CrossRef Full Text | Google Scholar

Yu, C., Huang, S., Li, J., Wu, X., Tian, Y., and Bao, X. (2024). Study on the failure process and acoustic emission characteristics of freeze–thawed sandstone under cyclic loading and unloading. Buildings 14, 1264. doi:10.3390/buildings14051264

CrossRef Full Text | Google Scholar

Yu, Y., Huang, X., Wang, Y., and Yang, Z. (2022). Experiment and simulation of high-cycle corrosion fatigue damage evolution and corrosion pit tolerance analysis of crack nucleation. Fatigue Fract. Eng. Mater Struct. 45, 1435–1447. doi:10.1111/ffe.13671

CrossRef Full Text | Google Scholar

Zhang, H. M., and Yang, G. S. (2013). Experimental study of damage deterioration and mechanical properties for freezing thawing rock. J. China Coal Soc. 38 (10), 1756–1762. doi:10.13225/j.cnki.jccs.2013.10.020

CrossRef Full Text | Google Scholar

Zhang, W., Jiang, W., Zhao, X., and Tu, S. T. (2018). Fatigue life of a dissimilar welded joint considering the weld residual stress: experimental and finite element simulation. Int. J. Fatigue 109, 182–190. doi:10.1016/j.ijfatigue.2018.01.002

CrossRef Full Text | Google Scholar

Zhang, X., Luo, X., He, X., and Niu, S. (2014). Pore structure expansion and evolution in sandstone with prefabricated crack under freeze-thaw cycles based on CT scanning. Front. Earth Sci. 12. doi:10.3389/feart.2024.1394731

CrossRef Full Text | Google Scholar

Zheng, Y., Jia, C., Lei, M., Huang, J., and Shi, C. (2024). Investigation of the constitutive damage model of rock under the coupled effect of freeze–thaw cycles and loading. Rock Mech. Rock Eng. 57, 1861–1879. doi:10.1007/s00603-023-03627-2

CrossRef Full Text | Google Scholar

Zheng, Y., Zang, Q., Zhang, S., Jia, C., and Lei, M. (2022). Yield criterion research on intact rock transverse isotropy based on Hoek-Brown citerion. Rock Soil Mech. 43 (1), 139–151. doi:10.16285/j.rsm.2021.0821

CrossRef Full Text | Google Scholar

Zhu, T., Shi, C., Zhu, Z., Peng, Z., and Lou, Y. (2025). Analysis of defects in measurement of cement slurry with a high water-cement ratio and optimization of error correction. IEEE Trans. Instrum. Meas. 74, 1–9. doi:10.1109/TIM.2025.3551850

CrossRef Full Text | Google Scholar