- Department of Earth Sciences, Uppsala University, Uppsala, Sweden
This Mini Review provides a focused and up-to-date summary of recent advancements in 3D discrete fracture network (DFN) modelling for simulating coupled thermo-hydro-mechanical-chemical processes in fractured rocks, which are crucial for various geotechnical engineering-related challenges. Particular emphasis is placed on recent developments in 3D DFN modelling technologies, which have enabled more realistic and detailed representations of fracture topologies, interactions, and multiphysics couplings. We highlight key advances in simulating complex multiphysical processes and phenomena in 3D fractured geological media such as flow channelling, stress fluctuation, fracture interaction, and anomalous transport. Despite these advances, significant challenges remain—especially in multiscale representation, mesh generation, model calibration, computational efficiency, and integration with field observational data. The review concludes by identifying current research gaps and proposing future directions aimed at enhancing model realism, advancing the simulation of multiscale multiphysical processes, and expanding the applicability of DFN models to real-world geological and geotechnical engineering challenges.
1 Introduction
1.1 Background
Fractures such as joints and faults are prevalent geological features, forming hierarchical networks of discontinuities in crustal rocks (Ouillon et al., 1996; Bonnet et al., 2001; Lei and Wang, 2016). They play a critical role in various subsurface processes such as stress transfer, pressure diffusion, heat transport, and chemical dissolution (Tsang, 1991; Rutqvist and Stephansson, 2003; Viswanathan et al., 2022; Vaezi et al., 2026), which are highly relevant for many geotechnical engineering-related problems, such as civil infrastructure development, geothermal energy exploitation, critical mineral extraction, nuclear waste disposal, underground energy storage, and geohazard risk management. It is therefore essential to advance both our capability to model these ubiquitous discontinuity structures and our understanding of their influence on subsurface processes under complex geological and geotechnical conditions.
To address the need for modelling complex fracture systems, the discrete fracture network (DFN) approach has been developed since the early 1980s, with initial efforts focusing on fluid flow (Long et al., 1982; Long et al., 1985) and later extended to thermo-hydro-mechanical-chemical processes (Lei et al., 2017; Viswanathan et al., 2022). Unlike continuum approaches, the DFN method requires no a priori assumption of a representative elementary volume, making it particularly suited for modelling hierarchical fractured rocks that may lack a characteristic length scale (Ouillon et al., 1996; Bonnet et al., 2001; Lei and Wang, 2016). Over the past decades, the DFN method has evolved to become a cornerstone in modelling fractured geological media. In the following subsection, a concise overview of the DFN method is presented, outlining its fundamental concepts, key assumptions, and general workflow.
1.2 Overview of the DFN method
The DFN method treats fractures as distinct features by explicitly representing the geometry and behaviour of each individual fracture within a fracture system. Fractures are modelled as discrete, lower-dimensional objects—typically lines in 2D or discs/ellipses in 3D—embedded within the host rock (Dershowitz and Einstein, 1988). Each fracture is characterised by properties such as orientation, size, aperture, roughness, and mechanical/hydraulic attributes, which are often assigned specific values or sampled from probability distributions.
The workflow of DFN modelling typically involves four major steps: (1) statistical characterisation of fracture systems using field data; (2) stochastic or deterministic generation of fracture networks informed by these statistics; (3) mesh generation followed by process-based simulations; and (4) validation and calibration of DFN models against observational data, if available. In step (1), various fracture properties may be sampled from scanline surveys, outcrop mapping, and borehole logs, with their underlying statistical distributions inferred. In step (2), the DFN generation process can be either stochastic, where fracture properties are sampled from the inferred statistical distributions, or deterministic, where observed fractures are explicitly embedded within the model domain. In step (3), mesh generation creates a computational grid, enabling detailed process-based simulations of thermo-hydro-mechanical-chemical processes. In step (4), validation and calibration involve adjusting model parameters and comparing simulation results with observational data, such as hydraulic/tracer tests and microseismic/deformation measurements, to evaluate model accuracy and reduce uncertainties.
A key challenge of applying the DFN approach for practical engineering problems is realistically representing subsurface fracture systems, given the typically limited site characterisation data from outcrops, boreholes, and/or tunnel walls. Substantial efforts have been made to infer fracture statistics from geological mapping and use them to constrain fracture network generation (Andersson and Dverstorp, 1987; Dershowitz and Einstein, 1988; Kulatilake et al., 1993; Priest, 1993) as well as calibrate DFN models based on available field measurement data (Dverstorp and Andersson, 1989; Dverstorp et al., 1992). In addition, the computational cost of 3D simulations and the difficulty of upscaling fine-scale DFN results to field scales remain critical challenges for the broader application of the DFN method.
1.3 Scope of the review
Over the past decades, extensive studies employing 2D DFNs have been performed to study different physical processes such as geomechanical deformation, seismic attenuation, fluid flow, solute transport, heat transfer, and chemical dissolution as well as their couplings in fractured geological media (Min et al., 2004; Lei et al., 2014; Lei et al., 2015; Lei et al., 2020; Lei et al., 2021; Lei and Gao, 2018; Lei and Gao, 2019; Kang et al., 2019; Hu and Rutqvist, 2020; Sun et al., 2020; Sun et al., 2021; Lei and Sornette, 2021b; Lei and Sornette, 2021a; Wang et al., 2021; Zhao et al., 2021; Zhao et al., 2022; Jiang et al., 2022; Jiang et al., 2024; Steefel and Hu, 2022; Cao et al., 2024). However, important 3D effects associated with fracture network configuration and multiphysical processes cannot be adequately captured in 2D models. Consequently, significant efforts in recent years have been devoted to the development and implementation of 3D DFN models to more accurately represent these complexities and gain deeper insights into the behaviour of fractured media in 3D space. While previous studies have provided comprehensive reviews of DFN methods and applications (Lei et al., 2017; Berre et al., 2019; Viswanathan et al., 2022; Vaezi et al., 2026), this Mini Review highlights recent advances with particular emphasis on 3D DFN modelling as well as further discusses current gaps and future prospects in the field. Detailed discussions of multiphysics coupling methods are beyond the scope of this paper; readers are referred to more comprehensive reviews (Lei et al., 2017; Viswanathan et al., 2022; Vaezi et al., 2026).
2 Recent advances
2.1 3D DFN-based multiphysics simulations
Substantial progress has been made in recent years on 3D DFN modelling of multiphysical processes in fractured geological media. For instance, 3D DFN models have been extensively applied to investigate fluid flow and solute transport in 3D fracture networks, demonstrating that the structural configuration and associated geometrical/topological properties (e.g., fracture density, length, and connectivity) play a critical role in driving the emergence of flow channelling and anomalous transport phenomena (Figure 1a) (Hyman et al., 2019; Hyman, 2020; Kang et al., 2020; Yoon et al., 2023; Davy et al., 2024). More advanced 3D models that incorporate aperture variation within individual fractures have further revealed that fracture-scale heterogeneity exerts a significant influence on flow and transport properties at the network scale (Zou and Cvetkovic, 2020; 2021; Hyman et al., 2021; Sweeney et al., 2023; Osuji et al., 2025). Inspired by observed flow channelling phenomena, graph-based reduction models or channel network models have been developed to represent the flow in 3D fracture networks using interconnected 1D conductance channels, significantly reducing computational demand while preserving the essential characteristics of dominant flow structures (Viswanathan et al., 2018; Berrone et al., 2020; Doolaeghe et al., 2020; Dessirier et al., 2023). Geomechanical simulations based on 3D DFNs have also been performed to study the relationship between fracture network properties (e.g., density, length, and connectivity) and the overall mechanical properties of rock masses (e.g., Young’s modulus, Poisson’s ratio, and stress heterogeneity) (Davy et al., 2018; Lavoine et al., 2024). Advanced geomechanics models have been developed to simulate fracture propagation and interaction in 3D rock masses (Paluszny and Zimmerman, 2011; Wang et al., 2018; Paluszny et al., 2020; Sun et al., 2024). Notably, 3D DFN models have been recently applied to investigate earthquake rupture and associated geomechanical responses in 3D fracture networks (Figure 1b) (Pan et al., 2023; Pan et al., 2024; Gabriel et al., 2024; Palgunadi et al., 2024). Coupled hydro-mechanical simulations have also been conducted to investigate the impact of stress on fluid flow and solute transport (Lang et al., 2018; Sweeney and Hyman, 2020; Darcel et al., 2024) as well as to derive bulk hydro-mechanical properties such as equivalent Biot and Skempton coefficients (De Simone et al., 2023b). Additionally, heat transport in fractured rocks has been simulated using 3D DFNs, with the results highlighting the strong influence of flow velocity heterogeneity and matrix diffusion on thermal behaviour (De Simone et al., 2021; De Simone et al., 2023a). Recent advances have also enabled coupled hydro-chemical simulations of reactive transport in 3D fracture networks, shedding light on the interplay between fluid flow, solute transport, and chemical reaction (Hyman et al., 2022; Hyman et al., 2024; Andrews et al., 2023). Furthermore, 3D DFN models have been applied to a range of geoengineering problems, including fluid injection-induced seismicity (Ucar et al., 2017; Ucar et al., 2018), nuclear waste disposal (Pan et al., 2023; Pan et al., 2024; Leone et al., 2025), slope stability (Bonilla-Sierra et al., 2015), and tunnel excavation (Wang and Cai, 2025) in fractured rock masses. Compared to their 2D counterparts, these 3D DFN models reveal significantly richer physical behaviours of fractured media in 3D space and offer deeper insights into 3D effects associated with structural configurations, fracture interactions, stress fluctuations, aperture variations, and flow channelling, which cannot be adequately captured by 2D models.
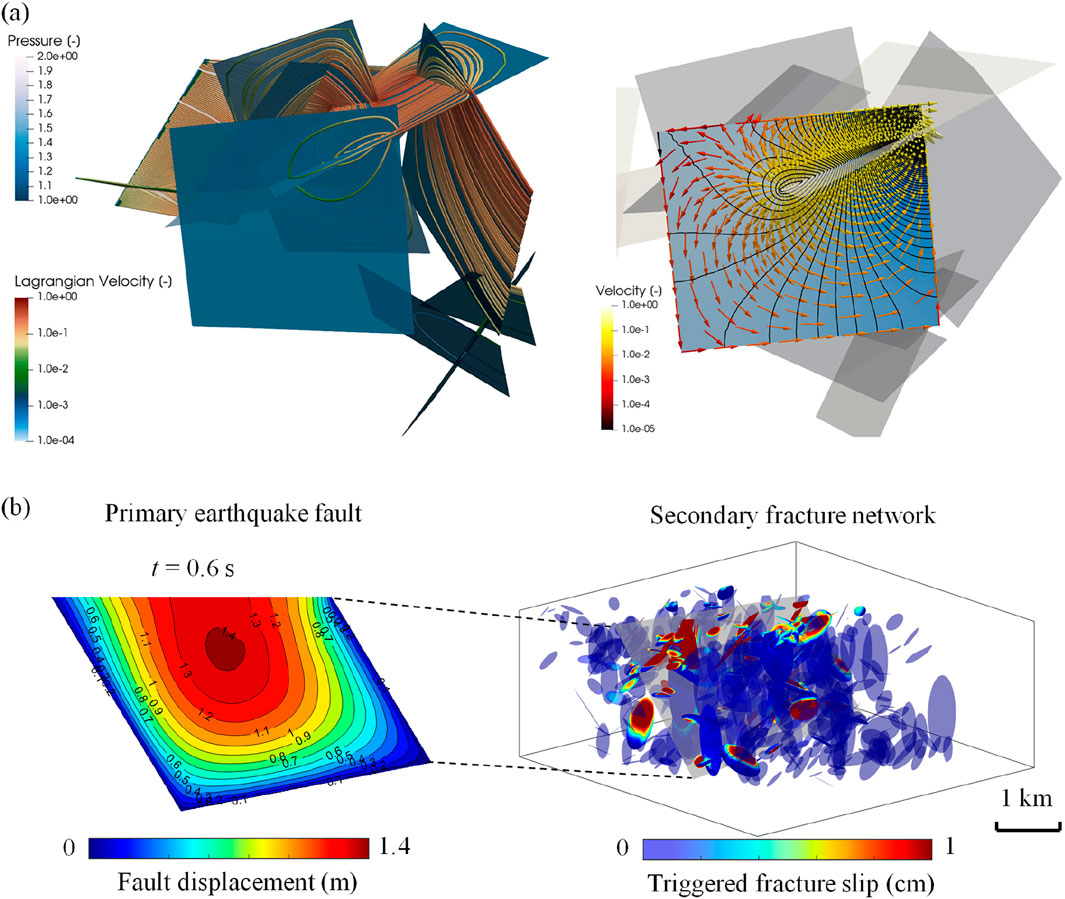
Figure 1. 3D DFN simulations of (a) fluid flow and solute transport (Kang et al., 2020), and (b) earthquake rupture and triggered shear displacements (Pan et al., 2023) in 3D fracture networks.
2.2 3D DFN model validation and calibration
While substantial efforts have been made to incorporate site characterisation data to inform or parameterise 3D DFN models, the validation and calibration of 3D DFN-based multiphysics simulations using field monitoring data remain limited, with only a few recent attempts addressing this gap. For example, Zhao et al. (2023) conducted a comprehensive case study of the Gotthard Base Tunnel—a 57 km long, up to 2.5 km deep high-speed railway tunnel in the Swiss Alps. During the tunnel construction, significant ground surface displacements up to ∼10 cm occurred, threatening the nearby critical infrastructures like concrete arch dams. To understand the causal mechanism of these decimetre-scale displacements, a 3D DFN-based computational model has been developed (Figure 2a) to realistically represent the heterogeneous ground conditions constrained by extensive laboratory/site characterization datasets and mechanistically compute the coupled processes of fluid flow, ground deformation, and fault slip at the site scale. The simulation results showed an excellent match to the in-situ monitoring data (Figures 2b,c), illuminating that the surface displacements originate from tunnelling-induced water drainage and rock mass consolidation in the deep subsurface. In addition, efforts have been made to integrate 3D DFN models with field experiments from underground research laboratories, e.g., the Mont Terri Rock Laboratory (Zhao et al., 2024), the Grimsel Rock Laboratory (Ringel et al., 2021), the ONKALO Demonstration Area (Hartley et al., 2018), and the Äspö Hard Rock Laboratory (Cvetkovic and Frampton, 2010). These studies demonstrate the validity and broad applicability of the DFN method across diverse geological settings, including both crystalline and sedimentary formations. They also highlight the significant value of integrating 3D DFN models with field observational data, enabling model validation and calibration to assess performance and build confidence, while elucidating the multiphysical mechanisms underlying complex phenomena observed at the site scale.
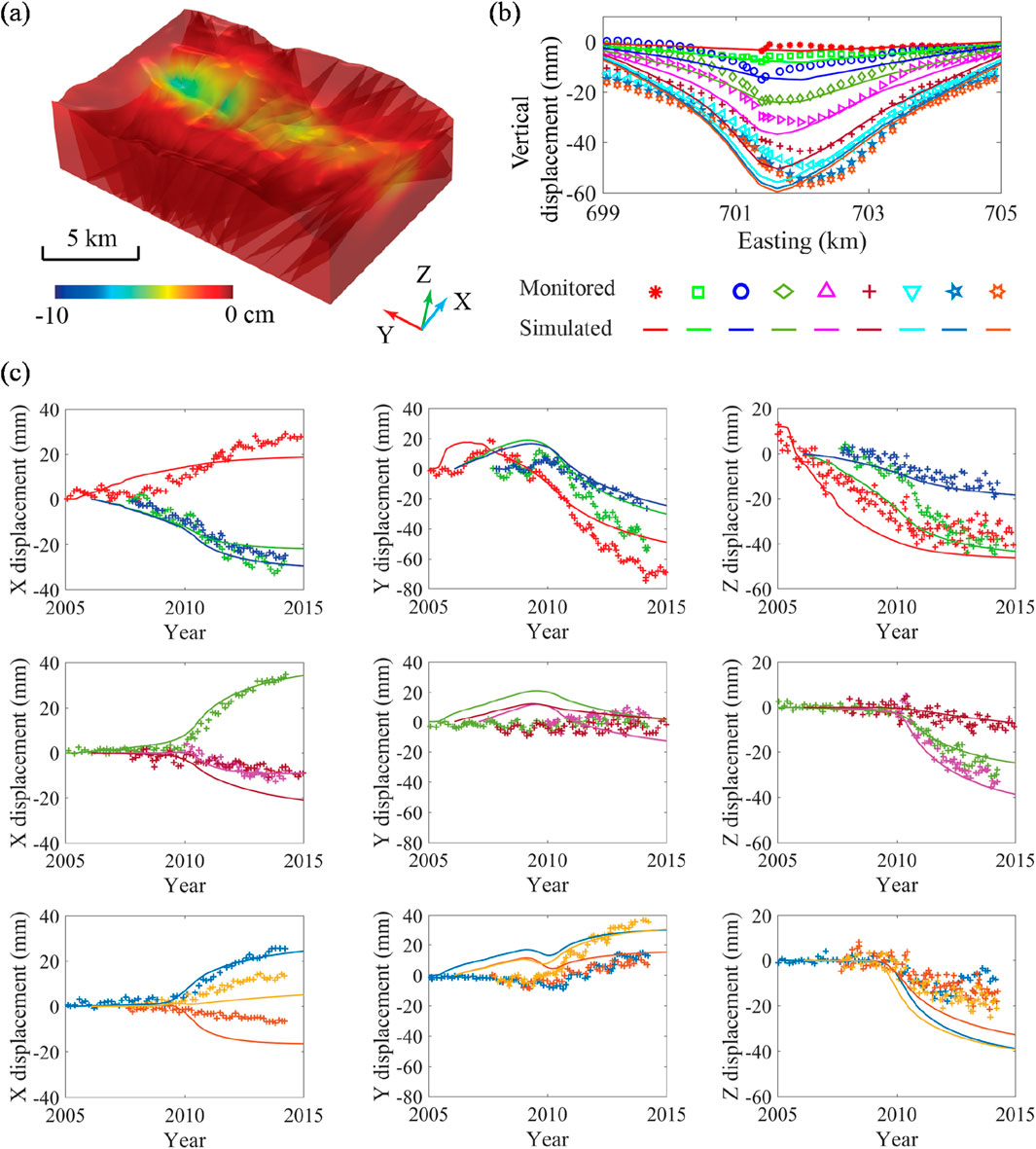
Figure 2. 3D DFN-based multiphysical simulation of Gotthard Base Tunnel-induced ground surface displacements (Zhao et al., 2023): (a) simulated ground settlement; (b) comparison of simulated ground settlement profiles (lines) with levelling measurements (markers); (c) comparison of simulated ground surface displacements (lines) with measurement data recorded by different GPS stations (markers).
3 Future prospects
3.1 Tackling computational challenges
Over the past years, various 3D DFN generators and simulators have been developed by different research groups (Davy et al., 2013; Hyman et al., 2015; Alghalandis, 2017; Paluszny et al., 2020; Keilegavlen et al., 2021; Zhu et al., 2022; Pan et al., 2023; Im and Avouac, 2024; Palgunadi et al., 2024), each with a distinct emphasis on some specific aspects. Recently, those teams that originally focused on different aspects are now increasingly working towards a common goal—developing 3D DFN models capable of capturing an expanding range of multiphysical processes, such as mechanical deformation, fracture propagation, fluid flow, heat transport, and chemical reactions. A major obstacle to this endeavour is the multifaceted computational challenge posed by 3D multiphysics simulations. This difficulty is rooted in the DFN modelling concept itself, which aims to explicitly represent individual fractures and their associated multiphysical processes in a complex network, given that fractures in rock are inherently multiscale geological features that span a broad range of length scales. This challenge becomes even more pronounced when attempting to couple different physical processes, such as seismic slip, fluid flow, and chemical reaction, which operate across vastly different time scales. Compromised solutions may need to be developed, such as hierarchical modelling of fracture networks, where the effects of small-scale fractures are incorporated into equivalent matrix properties, and sequential coupling, where different physical processes are simulated over separate time steps and then coupled. Apart from the multiscale complexity, this challenge also partly stems from the difficulty of automated mesh generation for stochastically generated 3D DFNs, which involve a wide range of fracture sizes and exhibit complex topologies. Algorithms should be developed to optimise 3D DFN geometries during model construction, aiming to eliminate features such as tiny dead-ends, narrow intersection angles, and closely spaced fractures, which can degrade mesh quality and lead to numerical instability.
3.2 Improving model realism and practical use
Owing to the significant computational challenges associated with 3D DFN multiphysics simulations, various simplifications and assumptions are often introduced in previous work to reduce model complexity and ensure computational feasibility. For example, the matrix is usually neglected in many 3D modelling studies, assuming that flow and transport primarily occur through interconnected fractures (Hyman et al., 2019; Hyman et al., 2021; Kang et al., 2020; Zou and Cvetkovic, 2020; Zou and Cvetkovic, 2021; Sweeney et al., 2023; Yoon et al., 2023; Davy et al., 2024). Local stresses on individual fractures in 3D fracture networks have often been calculated by simply projecting far-field stresses onto local fracture planes (Ucar et al., 2017; Ucar et al., 2018; Sweeney and Hyman, 2020), without accounting for fracture interaction-induced local stress fluctuations. Furthermore, fracture constitutive behaviour has often been modelled using simplified formulations, such as linear elastic or perfectly elasto-plastic models (Davy et al., 2018; Ucar et al., 2018; Sweeney and Hyman, 2020; Darcel et al., 2024), which do not account for the strongly non-linear deformational responses of rough fractures under normal and shear stress loadings (Lei and Barton, 2022). These simplifications can significantly influence the calculation of fracture shear dilations, which play a critical role in the formation of flow channelling and the emergence of anomalous transport behaviour. Future efforts are needed to assess how these simplifications affect the processes we aim to model and capture, especially in the context of multiphysics coupling, while continuously advancing the realism of 3D DFN models through more refined assumptions and enhanced computational capacity and efficiency.
Most existing 3D DFN modelling studies have focused on theoretical or conceptual investigations aimed at uncovering the complex multiphysical processes in fractured geological media. However, a significant gap remains in translating these advances into practical engineering applications. Bridging this gap requires reliably conditioning 3D DFN models using limited site characterization data and rigorously calibrating them against comprehensive field observations. Common calibration methods include parameter sensitivity analysis, inverse modelling, and Bayesian inference (Dverstorp and Andersson, 1989; Somogyvári et al., 2017; Ringel et al., 2021; Jiang et al., 2023), which enable probabilistic updating of model parameters based on observed data. Data assimilation techniques, such as the Ensemble Kalman Filter, may also be applied to integrate real-time monitoring data with DFN simulations (Elahi and Jafarpour, 2018). A major challenge arises from the large number of input parameters for DFN modelling, which often exhibit complex correlations and nonlinear effects on model outputs. Differentiating epistemic uncertainty (due to incomplete knowledge) from aleatoric uncertainty (due to inherent variability) is essential for meaningful uncertainty quantification (Murph et al., 2024). Machine learning techniques can be employed to accelerate calibration and facilitate uncertainty quantification (Srinivasan et al., 2018; Srinivasan et al., 2021), thereby enhancing the practical applicability of DFN models.
3.3 Emerging challenges and opportunities
Looking ahead, future DFN modelling research may expand along several other avenues. First, significant knowledge gaps remain regarding chemo-mechanical coupling in fracture networks, particularly in understanding how chemical reactions influence the mechanical properties of individual fractures (e.g., stiffness, friction coefficient) and bulk rock masses (e.g., modulus, strength). Addressing this issue will require integrated efforts combining numerical simulations with laboratory experiments. Secondly, while much of the existing DFN research focuses on quasi-static simulations of multiphysical processes, considering inertial effects becomes crucial when addressing problems related to earthquake triggering, seismic slip, and wave propagation. Significant efforts are needed to address the challenge of simultaneously modeling these transient dynamic processes alongside other more quiescent ones like fluid flow and chemical reaction. Thirdly, fracture systems in crustal rocks often exhibit hierarchical structures, such as large-scale fault zones with numerous subsidiary fractures (Faulkner et al., 2010). Investigating how the collective behaviour of these structures governs larger-scale phenomena could provide valuable insights into developing hierarchical modelling strategies, which may be further inspired by the renormalisation group concept (Sornette, 2006), to address the multiscale challenges inherent in DFN modelling. Lastly, modelling fracture propagation in 3D complex fractured media under coupled multiphysical conditions remains a key challenge and warrants further investigation.
Although DFN models have witnessed significant advances in recent years, longstanding criticisms remain and are likely to persist, concerning their complexity, representativeness, and the challenges associated with model parameterisation and calibration, which in turn raise questions about their reliability for practical use. This stems from the inherent dilemma of studying fractured media, which exhibit varying degrees of complexity across multiple scales. The multiscale nature of fractured media arises from two aspects: (i) presence of fractures spanning multiple length scales and (ii) emergent behaviour at the system level resulting from interactions among numerous components. In this context, “small-scale” refers to either features of limited spatial extent or the level of individual components, while “large-scale” denotes either broader spatial domains or the collective behaviour emerging at the system level. At one end, understanding small-scale details, including numerous fractures and masses, requires navigating a high degree of complexity. At the other, practical applications usually require predictions of only a few large-scale properties, such as modulus, strength, permeability, breakthrough, and reaction rate, for which reducing complexity is key. To address this dilemma, a hierarchical modelling strategy should be adopted, integrating models across complexity levels, from high-to intermediate- and low-complexity models. DFN-based multiphysics simulations fall in the category of high-complexity models that resolve detailed physical processes at high spatial and temporal resolutions, with significant computational and data requirements, providing deep insights into the mechanisms. Intermediate-complexity models, such as graph-based reduction approaches, simplify some of these processes to focus on key phenomena, lowering computational costs and data demands while still capturing essential system dynamics, which makes them particularly suitable for uncertainty analyses and Monte Carlo simulations. Low-complexity models, such as statistical or surrogate models, rely on highly simplified representations to capture general trends, offering rapid predictions and enabling robust calibration. Used in a complementary manner, these models offer a pathway to balance complexity and utility: to unravel the intricacies of fractured media while enabling practical, real-world applications. Lastly, it is worth reaffirming the spirit of the adage that “all models are wrong, but some are useful.” DFN models, despite their inherent complexities and uncertainties, can be extremely useful, especially in combination with other models of intermediate/low-complexity, for both gaining mechanistic understanding and informing engineering decisions. Extensive efforts are required to establish such a hierarchical framework to effectively reconciles model predictions with real-world observations, ultimately enhancing the reliability of DFN models for practical applications.
Author contributions
QL: Writing – original draft, Writing – review and editing, Conceptualization, Funding acquisition, Resources, Visualization.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. Swedish Radiation Safety Authority (SSM) Swedish Transport Administration (Trafikverket) Swedish Rock Engineering Research Foundation (BeFo).
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alghalandis, Y. F. (2017). ADFNE: open source software for discrete fracture network engineering, two and three dimensional applications. Comput. Geosciences 102, 1–11. doi:10.1016/j.cageo.2017.02.002
Andersson, J., and Dverstorp, B. (1987). Conditional simulations of fluid flow in three-dimensional networks of discrete fractures. Water Resour. Res. 23, 1876–1886. doi:10.1029/WR023i010p01876
Andrews, E. M., Hyman, J. D., Sweeney, M. R., Karra, S., Moulton, J. D., and Navarre-Sitchler, A. (2023). Fracture intensity impacts on reaction front propagation and mineral weathering in three-dimensional fractured media. Water Resour. Res. 59, e2022WR032121. doi:10.1029/2022WR032121
Berre, I., Doster, F., and Keilegavlen, E. (2019). Flow in fractured porous media: a review of conceptual models and discretization approaches. Transp. Porous Med. 130, 215–236. doi:10.1007/s11242-018-1171-6
Berrone, S., Hyman, J. D., and Pieraccini, S. (2020). Multilevel Monte Carlo predictions of first passage times in three-dimensional discrete fracture networks: a graph-based approach. Water Resour. Res. 56, e2019WR026493. doi:10.1029/2019WR026493
Bonilla-Sierra, V., Scholtès, L., Donzé, F. V., and Elmouttie, M. K. (2015). Rock slope stability analysis using photogrammetric data and DFN–DEM modelling. Acta Geotech. 10, 497–511. doi:10.1007/s11440-015-0374-z
Bonnet, E., Bour, O., Odling, N. E., Davy, P., Main, I., Cowie, P., et al. (2001). Scaling of fracture systems in geological media. Rev. Geophys. 39, 347–383. doi:10.1029/1999RG000074
Cao, W., Durucan, S., Shi, J.-Q., Korre, A., Ratouis, T., and Hjörleifsdóttir, V. (2024). Geothermal fluid extraction and injection-related fracture slip susceptibility and seismicity in naturally fractured rocks. Int. J. Rock Mech. Min. Sci. 183, 105939. doi:10.1016/j.ijrmms.2024.105939
Cvetkovic, V., and Frampton, A. (2010). Transport and retention from single to multiple fractures in crystalline rock at Äspö (Sweden): 2. Fracture network simulations and generic retention model. Water Resour. Res. 46, 2009WR008030. doi:10.1029/2009WR008030
Darcel, C., Le Goc, R., Lavoine, E., Davy, P., Mas Ivars, D., Sykes, E., et al. (2024). Coupling stress and transmissivity to define equivalent directional hydraulic conductivity of fractured rocks. Eng. Geol. 342, 107739. doi:10.1016/j.enggeo.2024.107739
Davy, P., Darcel, C., Le Goc, R., and Mas Ivars, D. (2018). Elastic properties of fractured rock masses with frictional properties and power law fracture size distributions. JGR Solid Earth 123, 6521–6539. doi:10.1029/2017JB015329
Davy, P., Le Goc, R., and Darcel, C. (2013). A model of fracture nucleation, growth and arrest, and consequences for fracture density and scaling. JGR Solid Earth 118, 1393–1407. doi:10.1002/jgrb.50120
Davy, P., Le Goc, R., Darcel, C., Pinier, B., Selroos, J.-O., and Le Borgne, T. (2024). Structural and hydrodynamic controls on fluid travel time distributions across fracture networks. Proc. Natl. Acad. Sci. U.S.A. 121, e2414901121. doi:10.1073/pnas.2414901121
Dershowitz, W. S., and Einstein, H. H. (1988). Characterizing rock joint geometry with joint system models. Rock Mech. Rock Engng 21, 21–51. doi:10.1007/BF01019674
De Simone, S., Bour, O., and Davy, P. (2023a). Impact of matrix diffusion on heat transport through heterogeneous fractured aquifers. Water Resour. Res. 59, e2022WR033910. doi:10.1029/2022WR033910
De Simone, S., Darcel, C., Kasani, H. A., Mas Ivars, D., and Davy, P. (2023b). Equivalent Biot and Skempton poroelastic coefficients for a fractured rock mass from a DFN approach. Rock Mech. Rock Eng. 56, 8907–8925. doi:10.1007/s00603-023-03515-9
De Simone, S., Pinier, B., Bour, O., and Davy, P. (2021). A particle-tracking formulation of advective–diffusive heat transport in deformable fracture networks. J. Hydrol. 603, 127157. doi:10.1016/j.jhydrol.2021.127157
Dessirier, B., Sharma, K. M., Pedersen, J., Tsang, C., and Niemi, A. (2023). Channel network modeling of flow and transport in fractured rock at the Äspö HRL: data-worth analysis for model development, calibration and prediction. Water Resour. Res. 59, e2022WR033816. doi:10.1029/2022WR033816
Doolaeghe, D., Davy, P., Hyman, J. D., and Darcel, C. (2020). Graph-based flow modeling approach adapted to multiscale discrete-fracture-network models. Phys. Rev. E 102, 053312. doi:10.1103/PhysRevE.102.053312
Dverstorp, B., and Andersson, J. (1989). Application of the discrete fracture network concept with field data: possibilities of model calibration and validation. Water Resour. Res. 25, 540–550. doi:10.1029/WR025i003p00540
Dverstorp, B., Andersson, J., and Nordqvist, W. (1992). Discrete fracture network interpretation of field tracer migration in sparsely fractured rock. Water Resour. Res. 28, 2327–2343. doi:10.1029/92WR01182
Elahi, S. H., and Jafarpour, B. (2018). Dynamic fracture characterization from tracer-test and flow-rate data with ensemble Kalman filter. SPE J. 23, 449–466. doi:10.2118/189449-PA
Faulkner, D. R., Jackson, C. A. L., Lunn, R. J., Schlische, R. W., Shipton, Z. K., Wibberley, C. A. J., et al. (2010). A review of recent developments concerning the structure, mechanics and fluid flow properties of fault zones. J. Struct. Geol. 32, 1557–1575. doi:10.1016/j.jsg.2010.06.009
Gabriel, A.-A., Garagash, D. I., Palgunadi, K. H., and Mai, P. M. (2024). Fault size–dependent fracture energy explains multiscale seismicity and cascading earthquakes. Science 385, eadj9587. doi:10.1126/science.adj9587
Hartley, L., Appleyard, P., Baxter, S., Mosley, K., Williams, T., and Fox, A. (2018). Demonstration Area discrete fracture network modelling at olkiluoto [posiva Report 2017-31]. Eurajoki: Posiva Oy.
Hu, M., and Rutqvist, J. (2020). Numerical manifold method modeling of coupled processes in fractured geological media at multiple scales. J. Rock Mech. Geotechnical Eng. 12, 667–681. doi:10.1016/j.jrmge.2020.03.002
Hyman, J. D. (2020). Flow channeling in fracture networks: characterizing the effect of density on preferential flow path formation. Water Resour. Res. 56, e2020WR027986. doi:10.1029/2020WR027986
Hyman, J. D., Dentz, M., Hagberg, A., and Kang, P. K. (2019). Linking structural and transport properties in three-dimensional fracture networks. JGR Solid Earth 124, 1185–1204. doi:10.1029/2018JB016553
Hyman, J. D., Karra, S., Makedonska, N., Gable, C. W., Painter, S. L., and Viswanathan, H. S. (2015). dfnWorks: a discrete fracture network framework for modeling subsurface flow and transport. Comput. Geosciences 84, 10–19. doi:10.1016/j.cageo.2015.08.001
Hyman, J. D., Navarre-Sitchler, A., Andrews, E., Sweeney, M. R., Karra, S., Carey, J. W., et al. (2022). A geo-structurally based correction factor for apparent dissolution rates in fractured media. Geophys. Res. Lett. 49, e2022GL099513. doi:10.1029/2022GL099513
Hyman, J. D., Navarre-Sitchler, A., Sweeney, M. R., Pachalieva, A., Carey, J. W., and Viswanathan, H. S. (2024). Quartz dissolution effects on flow channelization and transport behavior in three-dimensional fracture networks. Geochem Geophys Geosyst 25, e2024GC011550. doi:10.1029/2024GC011550
Hyman, J. D., Sweeney, M. R., Frash, L. P., Carey, J. W., and Viswanathan, H. S. (2021). Scale-bridging in three-dimensional fracture networks: characterizing the effects of variable fracture apertures on network-scale flow channelization. Geophys. Res. Lett. 48, e2021GL094400. doi:10.1029/2021GL094400
Im, K., and Avouac, J.-P. (2024). Quake-DFN: a software for simulating sequences of induced earthquakes in a discrete fault network. Bull. Seismol. Soc. Am. 114, 2341–2358. doi:10.1785/0120230299
Jiang, C., Roubinet, D., Lei, Q., Wang, Y., and Wang, X. (2024). Anomalous transport and upscaling in critically-connected fracture networks under stress conditions. J. Hydrol. 630, 130661. doi:10.1016/j.jhydrol.2024.130661
Jiang, C., Wang, X., Zhang, F., Deng, K., and Lei, Q. (2022). Fracture activation and induced seismicity during long-term heat production in fractured geothermal reservoirs. Rock Mech. Rock Eng. 55, 5235–5258. doi:10.1007/s00603-022-02882-z
Jiang, Z., Ringel, L. M., Bayer, P., and Xu, T. (2023). Fracture network characterization in reservoirs by joint inversion of microseismicity and thermal breakthrough data: method development and verification. Water Resour. Res. 59, e2022WR034339. doi:10.1029/2022WR034339
Kang, P. K., Hyman, J. D., Han, W. S., and Dentz, M. (2020). Anomalous transport in three-dimensional discrete fracture networks: interplay between aperture heterogeneity and injection modes. Water Resour. Res. 56, e2020WR027378. doi:10.1029/2020WR027378
Kang, P. K., Lei, Q., Dentz, M., and Juanes, R. (2019). Stress-induced anomalous transport in natural fracture networks. Water Resour. Res. 55, 4163–4185. doi:10.1029/2019WR024944
Keilegavlen, E., Berge, R., Fumagalli, A., Starnoni, M., Stefansson, I., Varela, J., et al. (2021). PorePy: an open-source software for simulation of multiphysics processes in fractured porous media. Comput. Geosci. 25, 243–265. doi:10.1007/s10596-020-10002-5
Kulatilake, P. H. S. W., Wathugala, D. N., and Stephansson, O. (1993). Joint network modelling with a validation exercise in Stripa mine, Sweden. Int. J. Rock Mech. Min. Sci. Geomechanics Abstr. 30, 503–526. doi:10.1016/0148-9062(93)92217-E
Lang, P. S., Paluszny, A., Nejati, M., and Zimmerman, R. W. (2018). Relationship between the orientation of maximum permeability and intermediate principal stress in fractured rocks. Water Resour. Res. 54, 8734–8755. doi:10.1029/2018WR023189
Lavoine, E., Davy, P., Darcel, C., Mas Ivars, D., and Kasani, H. A. (2024). Assessing stress variability in fractured rock masses with frictional properties and power law fracture size distributions. Rock Mech. Rock Eng. 57, 2407–2420. doi:10.1007/s00603-023-03683-8
Lei, Q., and Barton, N. (2022). On the selection of joint constitutive models for geomechanics simulation of fractured rocks. Comput. Geotechnics 145, 104707. doi:10.1016/j.compgeo.2022.104707
Lei, Q., and Gao, K. (2018). Correlation between fracture network properties and stress variability in geological media. Geophys. Res. Lett. 45, 3994–4006. doi:10.1002/2018GL077548
Lei, Q., and Gao, K. (2019). A numerical study of stress variability in heterogeneous fractured rocks. Int. J. Rock Mech. Min. Sci. 113, 121–133. doi:10.1016/j.ijrmms.2018.12.001
Lei, Q., Gholizadeh Doonechaly, N., and Tsang, C.-F. (2021). Modelling fluid injection-induced fracture activation, damage growth, seismicity occurrence and connectivity change in naturally fractured rocks. Int. J. Rock Mech. Min. Sci. 138, 104598. doi:10.1016/j.ijrmms.2020.104598
Lei, Q., Latham, J., Tsang, C., Xiang, J., and Lang, P. (2015). A new approach to upscaling fracture network models while preserving geostatistical and geomechanical characteristics. JGR Solid Earth 120, 4784–4807. doi:10.1002/2014JB011736
Lei, Q., Latham, J.-P., and Tsang, C.-F. (2017). The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks. Comput. Geotechnics 85, 151–176. doi:10.1016/j.compgeo.2016.12.024
Lei, Q., Latham, J.-P., Xiang, J., Tsang, C.-F., Lang, P., and Guo, L. (2014). Effects of geomechanical changes on the validity of a discrete fracture network representation of a realistic two-dimensional fractured rock. Int. J. Rock Mech. Min. Sci. 70, 507–523. doi:10.1016/j.ijrmms.2014.06.001
Lei, Q., and Sornette, D. (2021a). Anderson localisation and reentrant delocalisation of tensorial elastic waves in two-dimensional fractured media. EPL 136, 39001. doi:10.1209/0295-5075/ac225d
Lei, Q., and Sornette, D. (2021b). Transport and localization of elastic waves in two-dimensional fractured media: consequences on scattering attenuation. JGR Solid Earth 126, e2020JB021178. doi:10.1029/2020JB021178
Lei, Q., and Wang, X. (2016). Tectonic interpretation of the connectivity of a multiscale fracture system in limestone. Geophys. Res. Lett. 43, 1551–1558. doi:10.1002/2015GL067277
Lei, Q., Wang, X., Min, K.-B., and Rutqvist, J. (2020). Interactive roles of geometrical distribution and geomechanical deformation of fracture networks in fluid flow through fractured geological media. J. Rock Mech. Geotechnical Eng. 12, 780–792. doi:10.1016/j.jrmge.2019.12.014
Leone, R. C., Mariner, P. E., Stein, E. R., Hyman, J. D., Thiedau, J., Guevara Morel, C. R., et al. (2025). Comparison of performance assessment models and methods in crystalline rock: task F1 DECOVALEX-2023. Geomechanics Energy Environ. 41, 100629. doi:10.1016/j.gete.2024.100629
Long, J. C. S., Gilmour, P., and Witherspoon, P. A. (1985). A model for steady fluid flow in random three-dimensional networks of disc-shaped fractures. Water Resour. Res. 21, 1105–1115. doi:10.1029/WR021i008p01105
Long, J. C. S., Remer, J. S., Wilson, C. R., and Witherspoon, P. A. (1982). Porous media equivalents for networks of discontinuous fractures. Water Resour. Res. 18, 645–658. doi:10.1029/WR018i003p00645
Min, K.-B., Rutqvist, J., Tsang, C.-F., and Jing, L. (2004). Stress-dependent permeability of fractured rock masses: a numerical study. Int. J. Rock Mech. Min. Sci. 41, 1191–1210. doi:10.1016/j.ijrmms.2004.05.005
Murph, A. C., Strait, J. D., Moran, K. R., Hyman, J. D., Viswanathan, H. S., and Stauffer, P. H. (2024). Sensitivity analysis in the presence of intrinsic stochasticity for discrete fracture network simulations. J. Geophys. Res. Mach. Learn. Comput. 1, e2023JH000113. doi:10.1029/2023JH000113
Osuji, N. I., Niemi, A., Tsang, C.-F., Jiang, C., and Lei, Q. (2025). Impact of multiscale anisotropy on flow and transport in three-dimensional fracture networks. Hydrogeol. J.
Ouillon, G., Castaing, C., and Sornette, D. (1996). Hierarchical geometry of faulting. J. Geophys. Res. 101, 5477–5487. doi:10.1029/95JB02242
Palgunadi, K. H., Gabriel, A., Garagash, D. I., Ulrich, T., and Mai, P. M. (2024). Rupture dynamics of cascading earthquakes in a multiscale fracture network. JGR Solid Earth 129. doi:10.1029/2023jb027578
Paluszny, A., Thomas, R. N., Saceanu, M. C., and Zimmerman, R. W. (2020). Hydro-mechanical interaction effects and channelling in three-dimensional fracture networks undergoing growth and nucleation. J. Rock Mech. Geotechnical Eng. 12, 707–719. doi:10.1016/j.jrmge.2020.04.004
Paluszny, A., and Zimmerman, R. W. (2011). Numerical simulation of multiple 3D fracture propagation using arbitrary meshes. Comput. Methods Appl. Mech. Eng. 200, 953–966. doi:10.1016/j.cma.2010.11.013
Pan, W., Zhang, Z., Wang, S., and Lei, Q. (2023). Earthquake-induced fracture displacements and transmissivity changes in a 3D fracture network of crystalline rock for spent nuclear fuel disposal. J. Rock Mech. Geotechnical Eng. 15, 2313–2329. doi:10.1016/j.jrmge.2023.07.001
Pan, W., Zhang, Z., Wang, S., and Lei, Q. (2024). Slip-weakening friction controls coseismic displacements in a 3D fracture network: implications for the long-term safety of nuclear waste repositories. Geomechanics Energy Environ. 38, 100551. doi:10.1016/j.gete.2024.100551
Priest, S. D. (1993). Discontinuity analysis for rock engineering. Dordrecht: Springer Netherlands. doi:10.1007/978-94-011-1498-1
Ringel, L. M., Jalali, M., and Bayer, P. (2021). Stochastic inversion of three-dimensional discrete fracture network structure with hydraulic tomography. Water Resour. Res. 57, e2021WR030401. doi:10.1029/2021WR030401
Rutqvist, J., and Stephansson, O. (2003). The role of hydromechanical coupling in fractured rock engineering. Hydrogeology J. 11, 7–40. doi:10.1007/s10040-002-0241-5
Somogyvári, M., Jalali, M., Jimenez Parras, S., and Bayer, P. (2017). Synthetic fracture network characterization with transdimensional inversion. Water Resour. Res. 53, 5104–5123. doi:10.1002/2016WR020293
Sornette, D. (2006). Critical phenomena in natural sciences - chaos, fractals, selforganization and disorder: concepts and tools. Berlin/Heidelberg: Springer. doi:10.1007/3-540-33182-4
Srinivasan, G., Hyman, J. D., Osthus, D. A., Moore, B. A., O’Malley, D., Karra, S., et al. (2018). Quantifying topological uncertainty in fractured systems using graph theory and machine learning. Sci. Rep. 8, 11665. doi:10.1038/s41598-018-30117-1
Srinivasan, S., O’Malley, D., Mudunuru, M. K., Sweeney, M. R., Hyman, J. D., Karra, S., et al. (2021). A machine learning framework for rapid forecasting and history matching in unconventional reservoirs. Sci. Rep. 11, 21730. doi:10.1038/s41598-021-01023-w
Steefel, C. I., and Hu, M. (2022). Reactive transport modeling of mineral precipitation and carbon trapping in discrete fracture networks. Water Resour. Res. 58, e2022WR032321. doi:10.1029/2022WR032321
Sun, Y., Fei, F., Wong, L. N. Y., and Choo, J. (2024). Intermediate principal stress effects on the 3D cracking behavior of flawed rocks under true triaxial compression. Rock Mech. Rock Eng. 57, 4607–4634. doi:10.1007/s00603-024-03777-x
Sun, Z., Jiang, C., Wang, X., Lei, Q., and Jourde, H. (2020). Joint influence of in-situ stress and fracture network geometry on heat transfer in fractured geothermal reservoirs. Int. J. Heat Mass Transf. 149, 119216. doi:10.1016/j.ijheatmasstransfer.2019.119216
Sun, Z., Jiang, C., Wang, X., Zhou, W., and Lei, Q. (2021). Combined effects of thermal perturbation and in-situ stress on heat transfer in fractured geothermal reservoirs. Rock Mech. Rock Eng. 54, 2165–2181. doi:10.1007/s00603-021-02386-2
Sweeney, M. R., and Hyman, J. D. (2020). Stress effects on flow and transport in three-dimensional fracture networks. JGR Solid Earth 125, e2020JB019754. doi:10.1029/2020JB019754
Sweeney, M. R., Hyman, J. D., O’Malley, D., Santos, J. E., Carey, J. W., Stauffer, P. H., et al. (2023). Characterizing the impacts of multi-scale heterogeneity on solute transport in fracture networks. Geophys. Res. Lett. 50, e2023GL104958. doi:10.1029/2023GL104958
Tsang, C. (1991). Coupled hydromechanical-thermochemical processes in rock fractures. Rev. Geophys. 29, 537–551. doi:10.1029/91RG01832
Ucar, E., Berre, I., and Keilegavlen, E. (2017). Postinjection normal closure of fractures as a mechanism for induced seismicity. Geophys. Res. Lett. 44, 9598–9606. doi:10.1002/2017GL074282
Ucar, E., Berre, I., and Keilegavlen, E. (2018). Three-dimensional numerical modeling of shear stimulation of fractured reservoirs. JGR Solid Earth 123, 3891–3908. doi:10.1029/2017JB015241
Vaezi, I., Yoshioka, K., Simone, S., Gómez, B., Paluszny, A., Jalali, M., et al. (2026). A review on thermo-hydro-mechanical modeling of coupled processes in fractured rock: a continuum to discontinuum perspective. J. Rock Mech. Geotechnical Eng. 18.
Viswanathan, H. S., Ajo-Franklin, J., Birkholzer, J. T., Carey, J. W., Guglielmi, Y., Hyman, J. D., et al. (2022). From fluid flow to coupled processes in fractured rock: recent advances and new frontiers. Rev. Geophys. 60, e2021RG000744. doi:10.1029/2021RG000744
Viswanathan, H. S., Hyman, J. D., Karra, S., O’Malley, D., Srinivasan, S., Hagberg, A., et al. (2018). Advancing graph-based algorithms for predicting flow and transport in fractured rock. Water Resour. Res. 54, 6085–6099. doi:10.1029/2017WR022368
Wang, H., Dyskin, A., Pasternak, E., Dight, P., and Sarmadivaleh, M. (2018). Effect of the intermediate principal stress on 3-D crack growth. Eng. Fract. Mech. 204, 404–420. doi:10.1016/j.engfracmech.2018.10.024
Wang, M., and Cai, M. (2025). Simulation of time-dependent response of jointed rock masses using the 3D DEM-DFN modeling approach. Int. J. Rock Mech. Min. Sci. 188, 106062. doi:10.1016/j.ijrmms.2025.106062
Wang, X., Aliouache, M., Wang, Y., Lei, Q., and Jourde, H. (2021). The role of aperture heterogeneity in incipient karst evolution in natural fracture networks: insights from numerical simulations. Adv. Water Resour. 156, 104036. doi:10.1016/j.advwatres.2021.104036
Yoon, S., Hyman, J. D., Han, W. S., and Kang, P. K. (2023). Effects of dead-end fractures on non-fickian transport in three-dimensional discrete fracture networks. JGR Solid Earth 128, e2023JB026648. doi:10.1029/2023JB026648
Zhao, C., Lei, Q., Zhang, Z., and Loew, S. (2023). Causal mechanism of Gotthard Base Tunnel-induced ground deformation: insights from 3D fully-coupled hydro-mechanical simulation and comparison to field measurements. Int. J. Rock Mech. Min. Sci. 170, 105515. doi:10.1016/j.ijrmms.2023.105515
Zhao, C., Lei, Q., Ziegler, M., and Loew, S. (2024). Structurally-controlled failure and damage around an opening in faulted Opalinus Clay shale at the Mont Terri Rock Laboratory: in-situ experimental observation and 3D numerical simulation. Int. J. Rock Mech. Min. Sci. 180, 105812. doi:10.1016/j.ijrmms.2024.105812
Zhao, C., Zhang, Z., and Lei, Q. (2021). Role of hydro-mechanical coupling in excavation-induced damage propagation, fracture deformation and microseismicity evolution in naturally fractured rocks. Eng. Geol. 289, 106169. doi:10.1016/j.enggeo.2021.106169
Zhao, C., Zhang, Z., Wang, S., and Lei, Q. (2022). Effects of fracture network distribution on excavation-induced coupled responses of pore pressure perturbation and rock mass deformation. Comput. Geotechnics 145, 104670. doi:10.1016/j.compgeo.2022.104670
Zhu, W., Khirevich, S., and Patzek, T. W. (2022). HatchFrac: a fast open-source DFN modeling software. Comput. Geotechnics 150, 104917. doi:10.1016/j.compgeo.2022.104917
Zou, L., and Cvetkovic, V. (2020). Inference of transmissivity in crystalline rock using flow logs under steady-state pumping: impact of multiscale heterogeneity. Water Resour. Res. 56, e2020WR027254. doi:10.1029/2020WR027254
Keywords: fracture network, multiphysics simulation, coupled processes, rock mass, model calibration
Citation: Lei Q (2025) 3D discrete fracture network modelling of multiphysical processes in fractured media: recent advances and future prospects. Front. Built Environ. 11:1611025. doi: 10.3389/fbuil.2025.1611025
Received: 13 April 2025; Accepted: 21 May 2025;
Published: 30 May 2025.
Edited by:
Jie Han, University of Kansas, United StatesReviewed by:
Jinhyun Choo, Korea Advanced Institute of Science and Technology (KAIST), Republic of KoreaXiaoyu Meng, China University of Petroleum, China
Copyright © 2025 Lei. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Qinghua Lei, cWluZ2h1YS5sZWlAZ2VvLnV1LnNl
 Qinghua Lei
Qinghua Lei