Variable-order fractional constitutive model for triaxial fatigue behavior of freeze-thaw double-fractured red sandstone

To explore the fatigue behavior of freeze-thaw fractured rocks, triaxial incremental cyclic loading tests were performed on double-fractured red sandstone under three freeze-thaw cycle conditions. A fatigue deformation constitutive model incorporating variable-order fractional derivatives was proposed. Results show that with increasing freeze-thaw cycles, peak stress under static and cyclic loads decreases linearly, while peak strain increases linearly. The fatigue failure process of freeze-thaw double-fractured sandstone follows the static full-process curve. The failure strain exceeds the static peak strain but remains below the control point strain. After multiple freeze-thaw cycles, rock samples exhibited triaxial fatigue failure with extensive and complex surface cracking. Surface deterioration resulted in particle detachment and powdering without fragment dispersion, indicating that freeze-thaw cycling softens the rock and enhances ductility. The fatigue strength of freeze-thaw double-fractured sandstone can be accurately determined by an incremental fatigue loading scheme, averaging the final two cycle stress values, and utilizing the fatigue threshold stress ratio from axial deformation. By modifying the Nishihara model’s third-stage Abel viscoelastic model to a variable-order fractional-order viscous pot, performing cyclic load equivalent substitution and introducing freeze-thaw damage variables can better reflect the three-stage deformation of double-fractured red sandstone under freeze-thaw and cyclic loading. These findings advance constitutive modeling of sandstone fatigue failure and support safety assessments of fractured rock masses in cold regions.

1 Introduction

Geotechnical projects in cold regions, such as railroads, tunnels, and slope stabilization (Yu et al., 2020; Tan et al., 2014), frequently face freeze-thaw hazards. These hazards manifest as tunnel lining cracks or landslides (Shen et al., 2022; Mateos et al., 2011). The freeze-thaw process alters rock physical properties and induces structural damage, particularly in cold climates. Understanding rock mechanics under freeze-thaw conditions is crucial for engineering stability.

Over the past century, scholars have explored a great deal about the freeze-thaw damage mechanisms of large pore materials such as rocks. The main damage polarization forces include ice expansion, hydraulic stress from unfrozen water, and crystal growth-induced internal stress (Stöcke et al., 1941; Deprez et al., 2020; Steiger, 2005). Through laboratory experiments, scholars have examined the effects of key factors on rock freeze-thaw damage, including saturation, porosity, pH, confining pressure, and freeze-thaw cycles on rock damage (Liu et al., 2019; Qu et al., 2018; Chen et al., 2020). To study the microscopic damage of rocks in more depth, many studies have also combined advanced tools such as CT scanning, MRI, and SEM have been utilized to analyze rock microdamage (Song et al., 2021a; Wang et al., 2020; Yun et al., 2025). Studies confirm that increasing freeze-thaw cycles reduces uniaxial compressive strength, elastic modulus, and other mechanical properties (Li et al., 2017).

Recent studies on fractured rocks under freeze-thaw conditions have gained attention, as natural rock masses inherently contain fractures. Freezing water in cracks induces crack propagation and accelerates rock deterioration (Zhang et al., 2020; Maji and Murton, 2021). In terms of theoretical studies, scholars have predicted the freeze-thaw damage of rocks by establishing an intrinsic model. Some of the studies focus on the evolution of damage variables and consider the influence of elastic modulus, pore structure, and ultrasonic wave velocity (Huang et al., 2018; Huang et al., 2022; Yun et al., 2024).

Geotechnical projects in cold regions also face fatigue deformation due to construction disturbances and cyclic loads. Freeze-thaw cycling combined with cyclic loading exacerbates rock degradation, threatening project stability (Song et al., 2021b). As a result, rock fatigue behavior has become a critical research topic. Researchers have examined key fatigue parameters such as loading frequency, stress amplitude, upper stress limit, and waveform (Peng et al., 2019). In addition, the fatigue threshold theory has gained broad acceptance as a fundamental damage criterion (Ge and Lu, 1992). There is also some progress in fatigue intrinsic modeling. For example, Li et al. explored the damage law of rocks under cyclic loading by investigating the dissipated energy (Li et al., 2020); Liu et al. proposed an intrinsic model for the fatigue deformation of rocks by analogizing the fatigue deformation of rocks to the long-time creep (Liu et al., 2020).

However, existing research predominantly focuses on the isolated effects of either freeze-thaw cycles or cyclic loading, with their coupling effects remaining inadequately explored. Furthermore, many studies rely on conventional uniaxial compression tests, lacking comprehensive investigation into the mechanical properties and failure mechanisms of rocks under triaxial stress conditions. For this reason, in this study, under the action of freeze-thaw cycle and triaxial cyclic loading, the freeze-thaw cycle test and triaxial cyclic loading test were carried out by using double-fractured red sandstone as the research object. By comparing and analyzing the static properties of the sandstone, the influence law of the number of freezing and thawing on the fatigue damage strength of the rock is explored, and the fatigue deformation intrinsic model of the rock is established based on the variable-order fractional-order derivatives, and finally, the reasonableness and accuracy of the model are verified by the test.

2 Experimental materials and methods

2.1 Specimen preparation

According to ISRM (Chau and Wong, 1996), standard cylindrical rock specimens (ϕ50 mm × 100 mm) were prepared. Artificially prefabricated fractures simulated the jointed rock mass. According to Sagong et al.'s research (Sagong and Bobet, 2002), the prefabricated fractures features a 45° inclination, 20 mm length, and 1 mm aperture. The rock bridge inclined at 120° with a length of 28.28 mm. Figure 1a illustrates the rock sample’s geometric parameters.

Figure 1

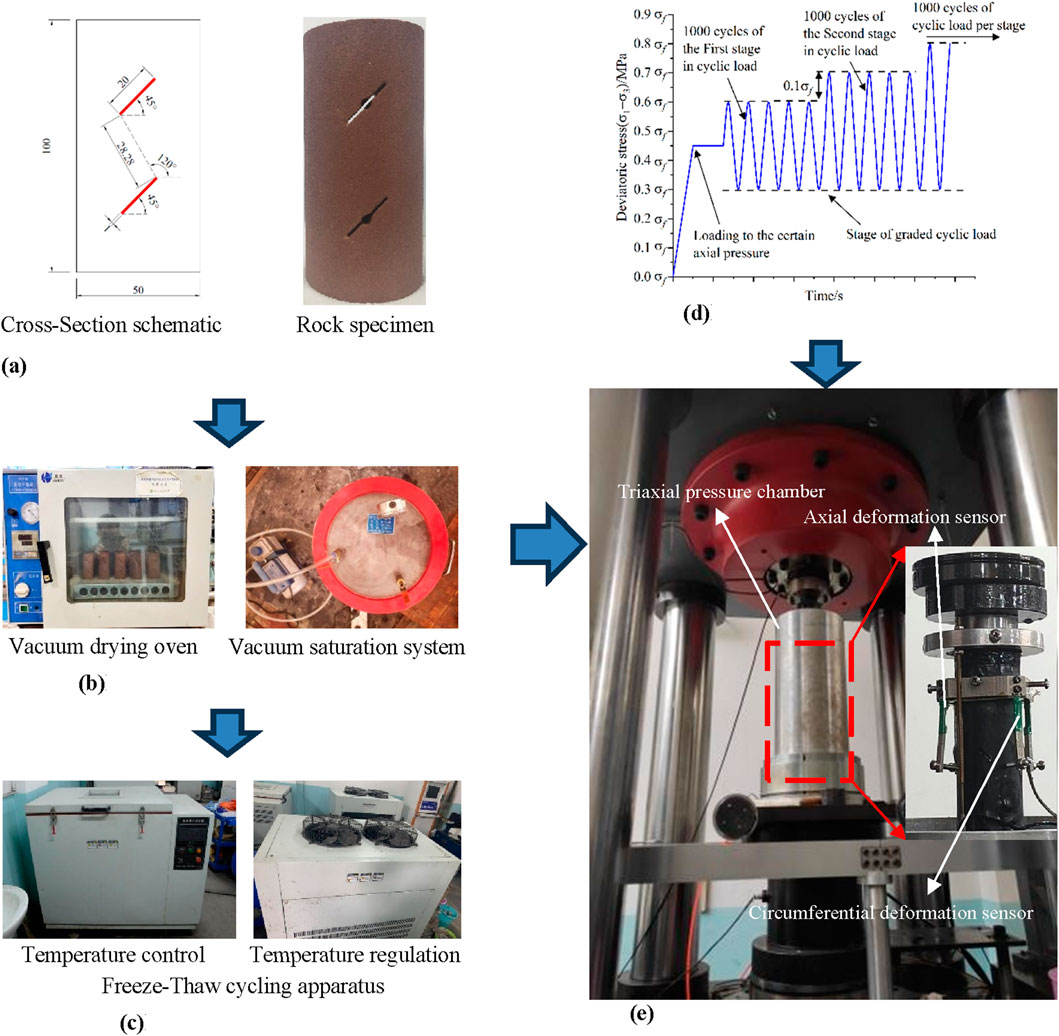
Figure 1. Flowchart of stepwise cyclic loading test. (a) Basic geometric parameters of rock samples (b) Experimental preparation phase (c) Freeze-Thaw cycling (d) Fatigue loading protocol (e) Triaxial rock high pressure dynamic test system.

2.2 Test method

Prior to testing, all rock samples underwent quality assessment and ultrasonic longitudinal wave velocity testing (The test results are shown in Table 1). Specimens with abnormal wave velocities were excluded to maintain sample consistency. The selected samples were then divided into three groups, totaling 18 specimens. A repeatability test with three specimens for each experimental condition was subsequently conducted as follows.

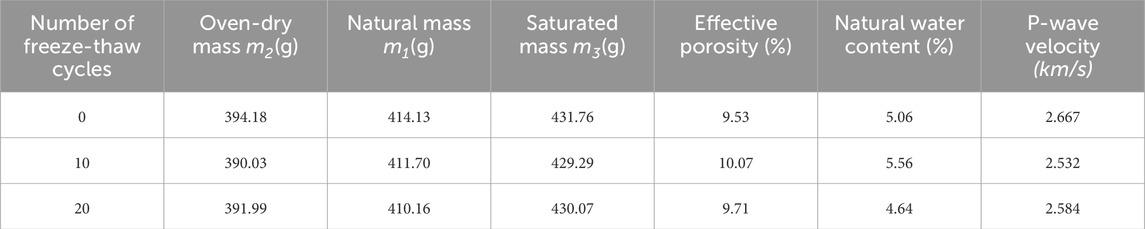
(1) Test Preparation Stage: The rock samples were placed in a DZF-type vacuum drying oven at 105°C for 24 h. After drying, they were transferred to a drying tray and allowed to cool naturally to room temperature, followed by measuring their dry weight. The samples were then placed in a ZK-270 vacuum saturation device with air pressure maintained at 0.001 MPa. After 24 h of vacuum pumping and saturation, the samples were left to soak naturally for over 4 h. Upon removal, surface moisture was wiped off, and the saturated mass and porosity of the samples were measured.

(2) Freeze-Thaw Cycle Test: The vacuum-saturated rock samples were placed in a freeze-thaw cycle tester. The freezing temperature was set to −30°C for 12 h, followed by thawing at 20°C for another 12 h. Three freeze-thaw cycle conditions were designed: 0 cycles (room temperature), 10 cycles, and 20 cycles.

(3) Triaxial Static Loading Test: As illustrated in Figure 1e, the DTAW-8000 triaxial high-pressure dynamic test system, co-developed by Xi’an University of Science and Technology and Changchun Chaoyang Experimental Company, was used for the loading tests. This system supports static and dynamic loading under various control modes, including displacement, strain, and stress, and allows real-time data display and automatic data collection throughout the entire loading process. After completing the designated freeze-thaw cycles, the rock samples underwent triaxial static loading with an enclosing pressure of 3 MPa. The loading process consisted of two stages: In the first stage, the enclosing pressure was increased uniformly to 3 MPa at a rate of 0.01 MPa/s. In the second stage, while maintaining the enclosing pressure constant, axial loading was applied at a deformation-controlled rate of 0.001 mm/s until the samples failed.

(4) Triaxial Cyclic Loading Test: As shown in Figure 1d, the cyclic loading employed a sinusoidal waveform with a frequency of 1 Hz, following a graded loading approach. Similar to step (2), an initial confining pressure of 3 MPa was applied. After maintaining the confining pressure, axial deviatoric stress was increased to 0.45 σf [where σf is the axial peak strength determined in step (3)] at a deformation-controlled rate of 0.001 mm/s. The lower stress limit for each loading level was set at 0.3 σf, while the upper stress limit for the first level was set at 0.6 σf. Every 1,000 cycles, the upper stress limit was incrementally increased by 0.1 σf until the rock sample ultimately failed at a specific level and cycle.

Table 1

Table 1. Measured physical properties of double-fractured red sandstone before freeze-thaw cycles.

3 Test results

3.1 The results of the three-axis static load test

Table 2 presents the triaxial static mechanical parameters of double-fractured red sandstone under three different freeze-thaw cycles. The initiation stress σ_ci of the rock is the dividing point between the elastic deformation stage and the stable crack propagation stage in the stress-strain curve. As shown in Figure 2, the stress-strain curve of 0 freeze-thaw cycles shows a steep elastic segment, with σ_ci/σ_f = 0.63. After 20 cycles, the curve loses linearity, and σ_ci/σ_f drops to 0.31, indicating earlier crack nucleation. The initiation stress σ_ci indicates the beginning of crack nucleation within the rock and can serve as a reference for the fatigue strength threshold value in the cyclic loading test (Wang, 2019). The ratio of the dilatancy stress σ_cd to the peak stress σ_f represents the speed of irreversible expansion of the double-fractured red sandstone from the beginning of expansion to the stage when it enters the cracks. Figure 2 shows that σ_cd/σ_f decreases from 0.88 (0 cycles) to 0.60 (20 cycles), with the curve exhibiting gradual crack growth and fluctuations in the ascending segment, reflecting weakened crack propagation resistance due to freeze-thaw damage. The larger the value is, the later the rock undergoes expansion (Xue et al., 2013). As shown in Table 2, with the increase in the number of freeze-thaw cycles, both the initiation stress σ_ci value and the Dilatancy stress σ_cd value decrease, and the axial peak stress σ_f levels of both also decline accordingly.

Table 2

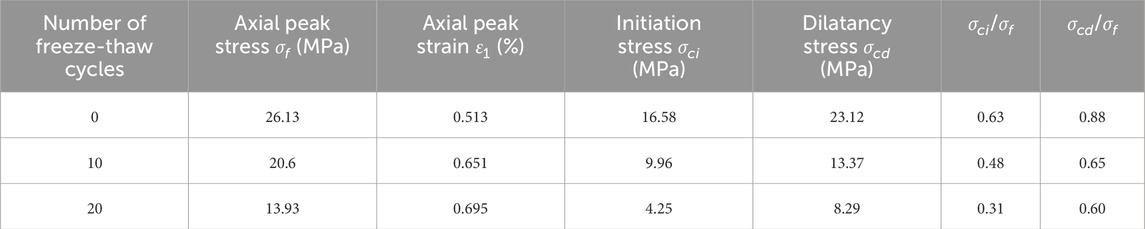
Table 2. Mechanical parameters of triaxial compression tests on double-fractured red sandstone samples.

Figure 2

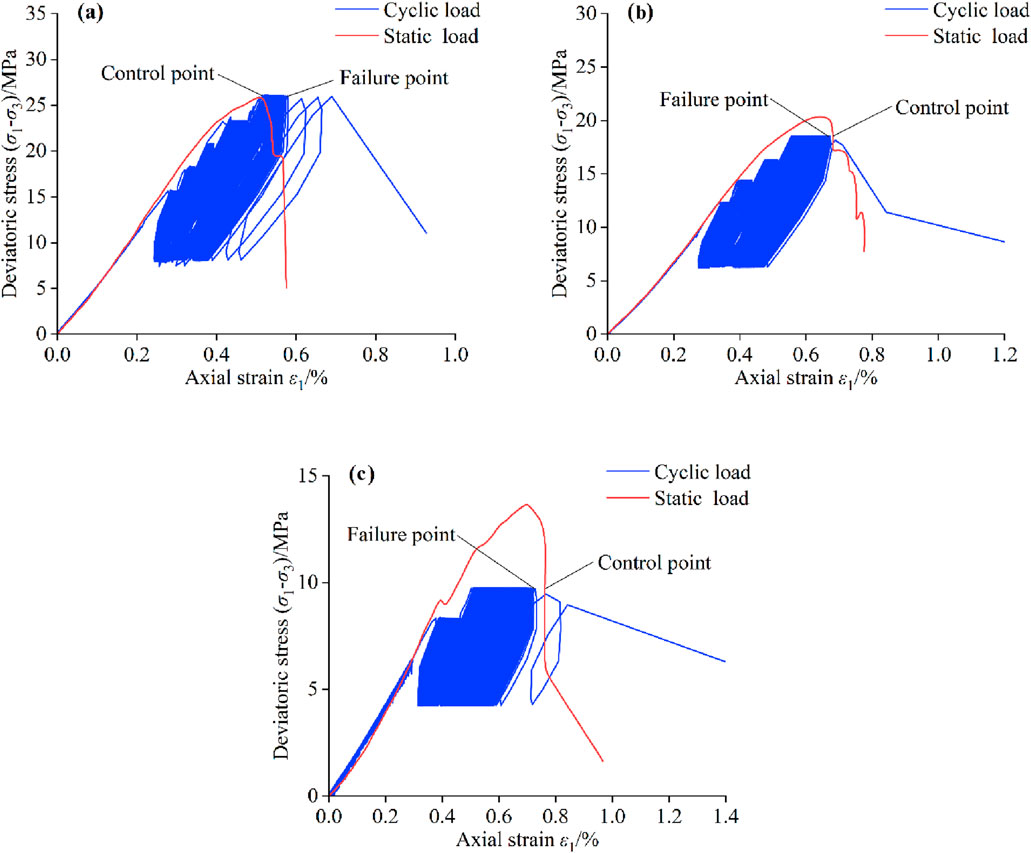
Figure 2. Triaxial static load and cyclic load stress-strain curves of double-fractured red sandstone after freeze-thawing (a-c). The number of freezing and thawing cycles are 0, 10, and 20 times, respectively). (a) F-T=0 (b) F-T=10 (c) F-T=20.

3.2 The test results of the three-axis cyclic loading

3.2.1 Typical stress-strain curve

Figure 2 illustrates the stress-strain relationship of double-fractured sandstone under cyclic loading after varying freeze-thaw (F-T) cycles. The fatigue limit strength of double-fractured sandstone decreases with an increasing number of freeze-thaw cycles due to freeze-thaw damage. Due to stress control in the cyclic loading test, rock samples experience brittle failure upon reaching ultimate irreversible deformation, causing a rapid stress drop and the transition from the hysteresis loop to a normal stress-strain curve. Under confining pressure, samples with 0 and 20 freeze-thaw cycles exhibited a sudden increase in axial deformation near the failure point, but stress did not immediately drop. Instead, samples continued cycling before failure, suggesting that confining pressure restrains brittle damage.

Based on Wang et al.'s study (Wang et al., 2021b), the average of the last two cyclic loading stresses closely approximates the true fatigue damage strength of double-fractured red sandstone. Table 3 presents the fatigue strength parameters of triaxial cyclic loading tests on double-fractured red sandstone after freeze-thaw cycles. With increasing freeze-thaw cycles N, axial strain ε_d1 at failure increases, while average fatigue strength decreases almost linearly. Ge et al. found that the threshold value is the dividing point B between the linear and nonlinear phases of the whole process curve of the rock (Ge and Lu, 1992). For the double-fractured red sandstone after freezing and thawing, the fatigue threshold value is closer to the dilatancy stress ratio, so it can be used as a certain reference.

Table 3

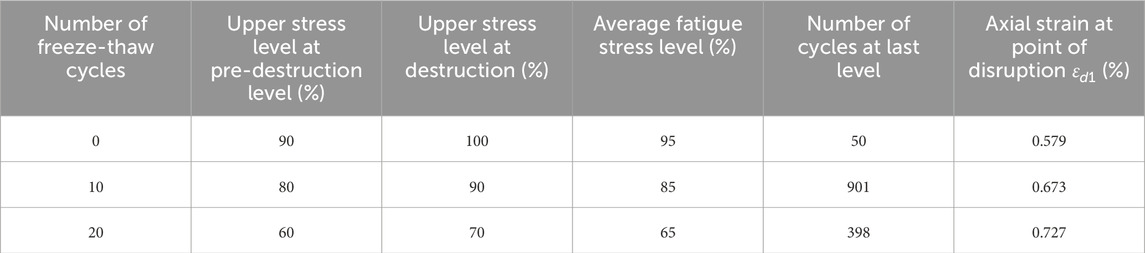
Table 3. Fatigue strength characteristics of double-fractured red sandstone under triaxial graded cyclic loading.

Ge et al. define the “failure point” as the peak of the previous cycle when the rock sample’s bearing capacity fails to reach the preset upper stress limit (Ge et al., 2003). The “control point” is the strain point after the peak in the triaxial stress-strain curve, corresponding to the upper limit stress of cyclic loading. The positions of the damage and control points in the graded cyclic loading test are shown in Figure 2. Table 3 shows that the strain values at the “failure point” for double-fractured red sandstone follows a consistent pattern across various freeze-thaw cycles. As shown in Figure 2, these strain values are higher than the peak strains under static loading but lower than those at the “control point”. Since the sample with 0 cycles of freezing and thawing has only been loaded for 1,000 cycles at the upper stress limit of 0.9σ_f, according to Figure 6, it can be seen that the sample will be damaged if the loading is continued, and at the last loading level, the sample can only withstand 50 cycles and the axial strain increases dramatically, so the strain value at the “failure point” is larger than the strain value corresponding to the “control point”.

3.2.2 Fracture damage characteristics

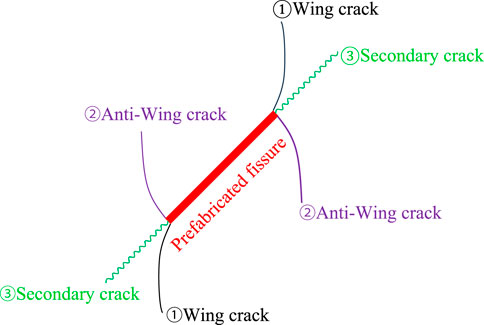
New cracks at the ends of preformed fractures include two types: wing cracks and secondary cracks. Wing cracks are tensile cracks formed by tensile forces at the ends of preformed fractures. Secondary cracks are shear cracks that are coplanar with the preformed fractures and subjected to shear forces. According to Yang’s research (Yang et al., 2021), Anti-wing cracks appear and expand rapidly at or near the ends of preformed fractures when axial pressure approaches the rock’s peak strength, The failure mode is dominated by anti-wing cracks. Numerical simulations show that anti-wing cracks often form under combined tensile-shear or compressive-shear stresses (Wang et al., 2021a). The crack propagation mode is illustrated in Figure 3.

Figure 3

Figure 3. Schematic diagram of crack expansion pattern.

The pre-prepared macroscopic fractures alter the stress field of the originally uniform damaged medium. The ends of pre-prepared cracks are prone to stress concentration. The rock sample’s tensile strength is much lower than its compressive strength. Therefore, tensile wing cracks are typically the first to emerge, with rapid propagation and long extension distances. When subjected to sufficient shear force, shear cracks are generated. Shear cracks are usually oriented in the same direction as the pre-prepared cracks. Under high confining pressure, the rock sample is prone to shear failure, with powder particles forming near the failure surface. Anti-wing cracks will be produced when the pressure on the rock sample reaches a certain value, usually sprouting in the compressive stress zone between multiple fissures and generally appearing less frequently and with a lag.

The triaxial cyclic load fracture failure characteristics of double-fractured red sandstone after freeze-thaw are presented in Figure 4. During the triaxial compression test, the rock sample remained compressed, causing internal pores and cracks to close. The test duration was short, limiting the expansion of micro-cracks, and accumulated strain energy was released through several large fissures. The instability failure in the triaxial compression test originated from the connection of several large fissures, resulting in relatively mild failure with few small fragments.

Figure 4

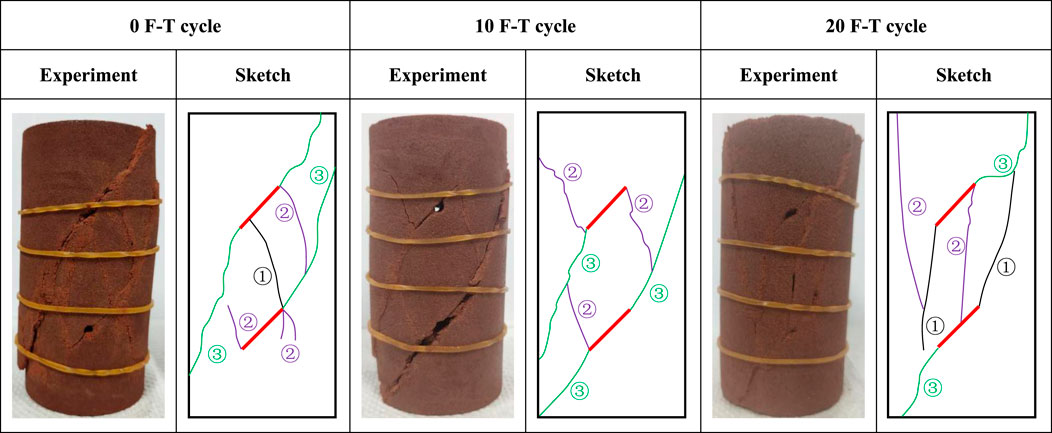
Figure 4. Failure situation diagram of cyclic load test of double-fractured red sandstone under different freeze-thaw cycles.

Comparison of the physical images and sketches of rock sample failure shows that double-fractured red sandstone undergoes fatigue failure under 3 MPa confining pressure. Two types of main fracture surfaces are observed: (1) the fracture surface consists of two wing cracks developed from the ends of pre-existing fissures, or a combination of pre-existing fissures, secondary cracks, and wing cracks. (2) the co-planarity of secondary cracks and pre-existing fissures is typical of shear cracks. Under 3 MPa confining pressure, shear and tensile stresses at the tips of pre-existing fissures cause the crack to extend from parallel to the fissures to the height direction of the rock sample. After 20 freeze-thaw cycles, the rock sample exhibits a large number of complex surface cracks under cyclic loading. This phenomenon is attributed to the crystallization pressure generated by ice nucleation in microscopic pores (Steiger, 2005), which transforms local strain energy into distributed microcrack propagation while enhancing the rock’s ductility, thereby contributing to the complexity of crack networks in rock samples. The expansion is evident, with increased surface particles and powders, but no small fragments have fallen. This suggests that freeze-thaw cycles have softened the rock and enhanced its ductility.

4 Fatigue deformation constitutive model of double-fractured sandstone after freeze-thaw cycles

4.1 The establishment of constitutive models

Ge et al. suggest that both the creep and cyclic loading curves exhibit a similar three-stage linear pattern, governed by a common stress intensity criterion (Ge et al., 2003). Therefore, the existing creep model can be replaced by an equivalent cyclic loading model, incorporating the freeze-thaw damage variable to develop the fatigue constitutive model under cyclic loading.

4.1.1 Nonlinear creep constitutive model

Han et al. argue that the variable-order fractional viscoelastic model more accurately describes the relationship between viscosity coefficient and fractional order, and its deformation rate better aligns with dynamic changes, compared to the Abel viscoelastic model (Han et al., 2021). As shown in Figure 5, the Nishihara model consists of a Hooke elastic body, a Kelvin viscoelastic body, and a variable-order fractional viscoplastic body. Modifying the Abel viscoelastic model in the third part of the Nishihara model to a variable-order fractional viscoplastic model yields a one-dimensional nonlinear creep constitutive model (Equation 1) (Gao and Yin, 2021; Liu et al., 2021):

$\left\{\begin{array}{l}\mathit{\epsilon }={\mathit{\epsilon }}_{\mathit{e}}+{\mathit{\epsilon }}_{\mathit{v}\mathit{e}}=\frac{\mathit{\sigma }}{{\mathit{E}}_{\mathbf{1}}}+\frac{\mathit{\sigma }}{{\mathit{E}}_{\mathbf{2}}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{E}}_{\mathbf{2}}}{{\mathit{\eta }}_{\mathbf{1}}}\mathit{t}\right)\right]\left(\mathit{\sigma }\le {\mathit{\sigma }}_{\mathit{s}}\right)\\ \mathit{\epsilon }={\mathit{\epsilon }}_{\mathit{e}}+{\mathit{\epsilon }}_{\mathit{v}\mathit{e}}+{\mathit{\epsilon }}_{\mathit{v}\mathit{p}}\left(\mathit{t}\right)\left(\mathit{\sigma }>{\mathit{\sigma }}_{\mathit{s}}\right)\\ =\frac{\mathit{\sigma }}{{\mathit{E}}_{\mathbf{1}}}+\frac{\mathit{\sigma }}{{\mathit{E}}_{\mathbf{2}}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{E}}_{\mathbf{2}}}{{\mathit{\eta }}_{\mathbf{1}}}\mathit{t}\right)\right]+\frac{\mathit{\sigma }-{\mathit{\sigma }}_{\mathit{s}}}{{\mathit{\eta }}_{\mathbf{2}}}{\left({\mathit{t}}_{\mathbf{2}}-{\mathit{t}}_{\mathbf{1}}\right)}^{{\mathit{\xi }}_{\mathbf{2}}}{\mathit{E}}_{\mathbf{1},{\mathit{\xi }}_{\mathbf{2}}}\left(\mathit{\kappa }{\mathit{t}}_{\mathbf{2}}\right)\end{array}\right.(1)$

Figure 5

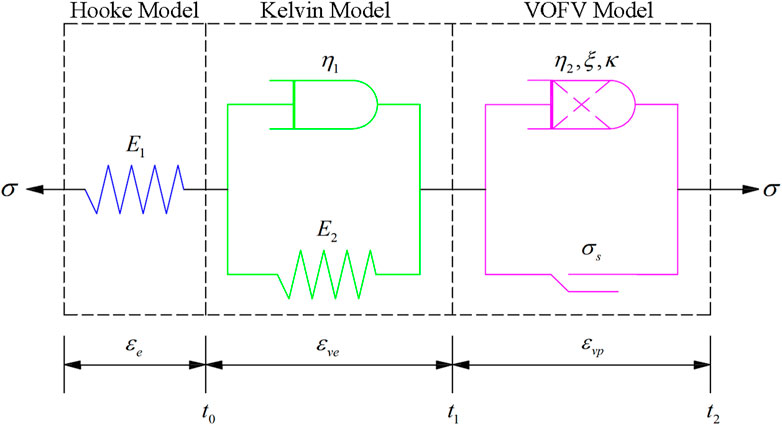
Figure 5. Schematic diagram of creep constitutive model based on fractional derivative of varying order.

In the formula, ε represents the total strain; ε_e is the elastic strain of pure elasticity; ε_ve is the viscoelastic strain of the material; ε_vp is the viscoplastic strain of the material; σ is the total stress; E₁ is the elastic modulus of the Hooke elastic body; E₂ is the elastic modulus of the Kelvin viscoelastic body; η₁ is the viscosity coefficient of the Kelvin viscoelastic body; t is the total creep time; σ_s is the long-term strength of the double-fractured sandstone; η₂ is the viscosity coefficient of the variable-order fractional viscoplastic body; t₁ is the critical moment when the viscoelastic stage (constant-rate creep stage) transitions to the viscoplastic stage (accelerated creep stage); t₂ is the critical moment when the viscoplastic stage (accelerated creep stage) transitions to the ultimate failure; ξ₂ is the ξ(t₂) value corresponding to the moment t₂, that is, the order of the fractional order; κ is the viscosity variable of the variable-order fractional viscoplastic body (VOFV Model), E_1,ξ2 (κt₂) is the Mittag–Leffler function.

4.1.2 Fatigue deformation constitutive model

Wang et al. propose that cyclic loads can be decomposed into static and alternating loads (Equation 2) (Wang et al., 2021b). Thus, the stress state of double-fractured red sandstone under three-dimensional cyclic loading is:

${\mathit{\sigma }}_{\mathit{i}\mathit{j}}\left(\mathit{t}\right)=\left[\begin{array}{ccc}{\mathit{\sigma }}_{\mathbf{1}}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& {\mathit{\sigma }}_{\mathbf{2}}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& {\mathit{\sigma }}_{\mathbf{3}}\end{array}\right]+\left[\begin{array}{ccc}{\mathit{\sigma }}_{\mathit{d}}\mathit{sin}\left(\mathit{\omega }\mathit{t}\right)& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\\ \mathbf{0}& \mathbf{0}& \mathbf{0}\end{array}\right](2)$

In the formula, σ₁= (σ_max+σ_min)/2 represents the static load, σ_dsin(ωt) = [(σ_max-σ_min)/2]sin(ωt) represents the alternating load; σ₂ and σ₃ are constant confining pressures; ω is the circular frequency, ω = 2πf; f is the frequency of the periodic load, and in this paper, it is 1 Hz.

The strain of the red sandstone under cyclic loading (Equation 3) can be decomposed into static strain ε_s(N) and dynamic strain ε_d(N):

$\mathit{\epsilon }\left(\mathit{t}\right)={\mathit{\epsilon }}_{\mathit{d}}\left(\mathit{t}\right)+{\mathit{\epsilon }}_{\mathit{s}}\left(\mathit{t}\right)={\mathit{\epsilon }}_{\mathit{d}}\left(\mathit{N}\right)+{\mathit{\epsilon }}_{\mathit{s}}\left(\mathit{N}\right)(3)$

In the formula, N represents the number of cycles of the periodic load, and t = N/f.

Based on the study by Wu et al., the model stress tensor for double-fractured red sandstone under three-dimensional stress comprises the deviatoric stress tensor S_ij and the ball stress tensor σ_m (Wu et al., 2020). Correspondingly, the resulting strain consists of the deviatoric strain tensor e_ij and the ball strain tensor ε_m. Combined with the knowledge of tensor mechanics, the following equations are derived.

(1) According to the generalized Hooke’s law, the expression for the elastic stage of static load under three-dimensional stress (Equations 4-6) is:

${\mathit{\epsilon }}_{\mathit{e},\mathit{i}\mathit{j}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{H}}}{\mathit{S}}_{\mathit{i}\mathit{j}}+\frac{\mathbf{1}}{\mathbf{3}{\mathit{K}}_{\mathit{H}}}{\mathit{\sigma }}_{\mathit{m}}{\mathit{\delta }}_{\mathit{i}\mathit{j}}(4)$

${\mathit{G}}_{\mathit{H}}=\frac{{\mathit{E}}_{\mathit{H}}}{\mathbf{2}\left(\mathbf{1}+{\mathit{\mu }}_{\mathit{H}}\right)}(5)$

${\mathit{K}}_{\mathit{H}}=\frac{{\mathit{E}}_{\mathit{H}}}{\mathbf{3}\left(\mathbf{1}-\mathbf{2}{\mathit{\mu }}_{\mathit{H}}\right)}(6)$

In the formula, ε_e,ij represents the strain tensor of the Hooke body under three-dimensional static load; G_H represents the shear modulus of the Hooke body; K_H represents the bulk modulus of the Hooke body, δ_ij represents the Kronecker delta function, which is usually a unit matrix in three-dimensional stress.

According to the relevant theories of viscoelasticity mechanics, the storage compliance or the loss compliance can be calculated by the parameters of constitutive equations (Equation 7) (Lakes, 1998).

The elastic-stage constitutive relationship of alternating loads under three-dimensional stress expressed by the storage compliance or the loss compliance is:

$\frac{{\mathit{\epsilon }}_{\mathit{d}\mathit{e}}}{{\mathit{\sigma }}_{\mathit{d}}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{H}}}={\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{1}}-\mathit{i}{\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{2}}(7)$

In the formula, ε_de represents the strain of the Hooke body under three-dimensional alternating loads; i is the imaginary unit; the storage compliance J_de1 of the Hooke body under three-dimensional alternating loads is 1/2G_H; and the loss compliance J_de2 of the Hooke body under three-dimensional alternating loads is 0.

(2) The spherical stress tensor has a relatively small influence on the viscous deformation of sandstone and can thus be neglected. The three-dimensional static constitutive equation of the viscoelastic Kelvin body (Equation 8) is:

${\mathit{\epsilon }}_{\mathit{v}\mathit{e},\mathit{i}\mathit{j}}\left(\mathit{N}\right)=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{K}}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{G}}_{\mathit{K}}}{{\mathit{\eta }}_{\mathit{K}}}\frac{\mathit{N}}{\mathit{f}}\right)\right]{\mathit{S}}_{\mathit{i}\mathit{j}}(8)$

In the formula, G_K represents the shear modulus of the Kelvin body under three-dimensional stress, and η_K represents the viscosity coefficient of the Kelvin body under three-dimensional stress.

The constitutive relationship of viscoelasticity in the viscoelastic stage under alternating loads in three-dimensional stress (Equation 9) can be expressed by using the storage compliance or the loss compliance:

$\begin{array}{ll}\hfill & \hfill \frac{{\mathit{\epsilon }}_{\mathit{d}\mathit{v}\mathit{e}}}{{\mathit{\sigma }}_{\mathit{d}}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{K}}+\mathbf{2}\mathit{i}{\mathit{\eta }}_{\mathit{K}}\mathit{\omega }}=\frac{{\mathit{G}}_{\mathit{K}}}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}-\mathit{i}\frac{{\mathit{\eta }}_{\mathit{K}}\mathit{\omega }}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}\\ \hfill & \hfill ={\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{1}}-\mathit{i}{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{2}}\end{array}(9)$

In the formula, ε_dve represents the strain of the Kelvin body under three-dimensional alternating loads; the storage compliance of the Kelvin viscoelastic body under three-dimensional alternating loads is $J_{dve1}=\frac{G_K}{2G_K^2+2{\left({\eta }_K\omega \right)}^2}$; the loss compliance of the Kelvin viscoelastic body under three-dimensional alternating loads is $J_{dve2}=\frac{{\eta }_K\omega }{2G_K^2+2{\left({\eta }_K\omega \right)}^2}$.

(3) The expression of the viscoplastic stage under three-dimensional static stress (Equation 10) is:

${\mathit{\epsilon }}_{\mathit{v}\mathit{p},\mathit{i}\mathit{j}}\left(\mathit{t}\right)=\frac{\mathit{F}}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}}\frac{\mathit{\partial }\mathit{Q}}{\mathit{\partial }{\mathit{\sigma }}_{\mathit{i}\mathit{j}}}{\left({\mathit{t}}_{\mathbf{2}}-{\mathit{t}}_{\mathbf{1}}\right)}^{{\mathit{\xi }}_{\mathbf{2}}}{\mathit{E}}_{\mathbf{1},{\mathit{\xi }}_{\mathbf{2}}}\left(\mathit{\kappa }{\mathit{t}}_{\mathbf{2}}\right)(10)$

In the formula, ε_vp,ij(t) represents the strain of the variable-order fractional viscoplastic body under three-dimensional static stress; η_V is the viscosity coefficient of the variable-order fractional viscoplastic body; Q is the plastic potential function of the red sandstone; F is the yield function (Equation 11), whose expression is:

$\mathit{F}=\sqrt{{\mathit{J}}_{\mathbf{2}}}-\frac{{\mathit{\sigma }}_{\mathit{t}\mathit{h}}}{\sqrt{\mathbf{3}}}(11)$

In the formula, J₂ represents the second invariant of the stress deviator, and $J_2=\frac{1}{6}\left[{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_1-{\sigma }_3\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2\right]$; σ_th is the critical stress amplitude of the double-fractured sandstone, which is determined by the fatigue strength threshold.

The constitutive relationship of the viscoplastic behavior of three-dimensional stress under alternating loads expressed (Equation 12) by the storage compliance or the loss compliance is:

$\frac{{\mathit{\epsilon }}_{\mathit{d}\mathit{v}\mathit{p}}}{{\mathit{\sigma }}_{\mathit{d}}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}{\left(\mathit{i}\mathit{\omega }\right)}^{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)}{\mathit{e}}^{-\mathit{\kappa }\frac{\mathit{N}}{\mathit{f}}}}={\mathit{J}}_{\mathit{d}\mathit{v}\mathit{p}\mathbf{1}}-\mathit{i}{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{p}\mathbf{2}}(12)$

Introducing Euler’s formula $i^n=\mathit{cos}\left(n\pi /2\right)+i\times \mathit{sin}\left(n\pi /2\right)$, and reorganizing Equation 12 yields (Equation 13) (Pu et al., 2020):

$\frac{{\mathit{\epsilon }}_{\mathit{d}\mathit{v}\mathit{p}}}{{\mathit{\sigma }}_{\mathit{d}}}=\frac{\mathit{cos}\left(\frac{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)\mathit{\pi }}{\mathbf{2}}\right)}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}{\mathit{\omega }}^{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)}{\mathit{e}}^{-\mathit{\kappa }\frac{\mathit{N}}{\mathit{f}}}}-\mathit{i}\frac{\mathit{sin}\left(\frac{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)\mathit{\pi }}{\mathbf{2}}\right)}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}{\mathit{\omega }}^{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)}{\mathit{e}}^{-\mathit{\kappa }\frac{\mathit{N}}{\mathit{f}}}}={\mathit{J}}_{\mathit{d}\mathit{v}\mathit{p}\mathbf{1}}-\mathit{i}{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{p}\mathbf{2}}(13)$

In the formula, ε_dvp represents the strain under three-dimensional alternating loads of Kelvin body; the storage compliance of the variable-order fractional viscoplastic body is $J_{dvp1}=\frac{\mathit{cos}\left(\xi \left(\frac{N}{f}\right)\pi /2\right)}{2{\eta }_V{\omega }^{\xi \left(\frac{N}{f}\right)}{e}^{-\kappa \frac{N}{f}}}$, and the loss compliance of the variable-order fractional viscoplastic body is $J_{dvp2}=\frac{\mathit{sin}\left(\xi \left(\frac{N}{f}\right)\pi /2\right)}{2{\eta }_V{\omega }^{\xi \left(\frac{N}{f}\right)}{e}^{-\kappa \frac{N}{f}}}$.

Therefore, the expressions for the storage compliance and the loss compliance work quantities of the constitutive model under three-dimensional (Equations 14, 15) stress are as follows:

$\begin{array}{l}{\mathit{J}}_{\mathit{d}\mathit{a}\mathbf{1}}={\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{1}}+{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{1}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{H}}}+\frac{{\mathit{G}}_{\mathit{K}}}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}\\ {\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{1}}={\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{2}}+{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{2}}=\frac{{\mathit{\eta }}_{\mathit{K}}\mathit{\omega }}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}\end{array}\left({\mathit{\sigma }}_{\mathit{d}}\le {\mathit{\sigma }}_{\mathit{t}\mathit{h}}\right)(14)$

$\begin{array}{l}{\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{1}}={\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{1}}+{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{1}}+{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{p}\mathbf{1}}=\frac{\mathbf{1}}{\mathbf{2}{\mathit{G}}_{\mathit{H}}}+\frac{{\mathit{G}}_{\mathit{K}}}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}\\ +\frac{\mathit{cos}\left(\frac{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)\mathit{\pi }}{\mathbf{2}}\right)}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}{\mathit{\omega }}^{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)}{\mathit{e}}^{-\mathit{\kappa }\frac{\mathit{N}}{\mathit{f}}}}\left({\mathit{\sigma }}_{\mathit{d}}>{\mathit{\sigma }}_{\mathit{t}\mathit{h}}\right)\\ {\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{2}}={\mathit{J}}_{\mathit{d}\mathit{e}\mathbf{2}}+{\mathit{J}}_{\mathit{d}\mathit{v}\mathit{e}\mathbf{2}}=\frac{{\mathit{\eta }}_{\mathit{K}}\mathit{\omega }}{\mathbf{2}{\mathit{G}}_{\mathit{K}}^{\mathbf{2}}+\mathbf{2}{\left({\mathit{\eta }}_{\mathit{K}}\mathit{\omega }\right)}^{\mathbf{2}}}+\frac{\mathit{sin}\left(\frac{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)\mathit{\pi }}{\mathbf{2}}\right)}{\mathbf{2}{\mathit{\eta }}_{\mathit{V}}{\mathit{\omega }}^{\mathit{\xi }\left(\frac{\mathit{N}}{\mathit{f}}\right)}{\mathit{e}}^{-\mathit{\kappa }\frac{\mathit{N}}{\mathit{f}}}}\end{array}(15)$

In the formula, J_a1 and J_a2 represent the storage compliance and the loss compliance, respectively, of the constitutive model in the stable stage under three-dimensional alternating loads. J_b1 and J_b2 represent the storage compliance and the loss compliance, respectively, in the acceleration deformation stage under three-dimensional alternating loads.

Since the confining pressure σ₂ = σ₃ was adopted in the triaxial compression test of this paper, therefore:

$\left\{\begin{array}{l}{\mathit{\sigma }}_{\mathit{m}}=\frac{\mathbf{1}}{\mathbf{3}}\left({\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}\right)\\ {\mathit{S}}_{\mathit{i}\mathit{j}}={\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathit{m}}=\frac{\mathbf{2}}{\mathbf{3}}\left({\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}\right)\\ \sqrt{{\mathit{J}}_{\mathbf{2}}}=\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\sqrt{\mathbf{3}}}\end{array}\right.(16)$

Substituting Equation 16 into Equations 4, 8, 10, the response strain of the static load under three-dimensional stress (Equations 17, 18) can be obtained:

When σ_d ≤σ_th:

${\mathit{\epsilon }}_{\mathit{s}}=\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{H}}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{9}{\mathit{K}}_{\mathit{H}}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{K}}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{G}}_{\mathit{K}}}{{\mathit{\eta }}_{\mathit{K}}}\frac{\mathit{N}}{\mathit{f}}\right)\right](17)$

When σ_d >σ_th:

$\begin{array}{c}{\mathit{\epsilon }}_{\mathit{s}}=\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{H}}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{9}{\mathit{K}}_{\mathit{H}}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{K}}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{G}}_{\mathit{K}}}{{\mathit{\eta }}_{\mathit{K}}}\frac{\mathit{N}}{\mathit{f}}\right)\right]+\\ \frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}-{\mathit{\sigma }}_{\mathit{t}\mathit{h}}}{\mathbf{3}{\mathit{\eta }}_{\mathit{V}}}{\left(\frac{{\mathit{N}}_{\mathbf{2}}}{{\mathit{f}}_{\mathbf{2}}}-\frac{{\mathit{N}}_{\mathbf{1}}}{{\mathit{f}}_{\mathbf{1}}}\right)}^{{\mathit{\xi }}_{\mathbf{2}}}{\mathit{E}}_{\mathbf{1},{\mathit{\xi }}_{\mathbf{2}}}\left(\mathit{\kappa }\frac{{\mathit{N}}_{\mathbf{2}}}{{\mathit{f}}_{\mathbf{2}}}\right)\end{array}(18)$

According to Wang et al. research (Wang et al., 2019), the dynamic strain response of the constitutive model under uniaxial stress (Equations 19, 20) is:

$\begin{array}{l}{\mathit{\epsilon }}_{\mathit{f}}\left(\mathit{t}\right)={\mathit{\epsilon }}_{\mathbf{0}}\mathit{sin}\left(\mathit{\omega }\mathit{t}+\mathit{\phi }\right)\\ =\left[\frac{{\mathit{\sigma }}_{\mathit{max}}-{\mathit{\sigma }}_{\mathit{min}}}{\mathbf{2}}\right]\sqrt{{\mathit{J}}_{\mathit{a}\mathbf{1}}^{\mathbf{2}}+{\mathit{J}}_{\mathit{a}\mathbf{2}}^{\mathbf{2}}}\times \mathit{sin}\left[\mathit{\omega }\left(\frac{\mathit{N}}{\mathit{f}}\right)+\mathit{arctan}\left(\frac{{\mathit{J}}_{\mathit{a}\mathbf{1}}}{{\mathit{J}}_{\mathit{a}\mathbf{2}}}\right)\right]\left({\mathit{\sigma }}_{\mathit{d}}\le {\mathit{\sigma }}_{\mathit{t}\mathit{h}}\right)\end{array}(19)$

$\begin{array}{l}{\mathit{\epsilon }}_{\mathit{f}}\left(\mathit{t}\right)={\mathit{\epsilon }}_{\mathbf{0}}\mathit{sin}\left(\mathit{\omega }\mathit{t}+\mathit{\phi }\right)\\ =\left[\frac{{\mathit{\sigma }}_{\mathit{max}}-{\mathit{\sigma }}_{\mathit{min}}}{\mathbf{2}}\right]\sqrt{{\mathit{J}}_{\mathit{b}\mathbf{1}}^{\mathbf{2}}+{\mathit{J}}_{\mathit{b}\mathbf{2}}^{\mathbf{2}}}\times \mathit{sin}\left[\mathit{\omega }\left(\frac{\mathit{N}}{\mathit{f}}\right)+\mathit{arctan}\left(\frac{{\mathit{J}}_{\mathit{b}\mathbf{1}}}{{\mathit{J}}_{\mathit{b}\mathbf{2}}}\right)\right]\left({\mathit{\sigma }}_{\mathit{d}}>{\mathit{\sigma }}_{\mathit{t}\mathit{h}}\right)\end{array}(20)$

In the formula, ε₀ represents the corresponding strain amplitude under unidirectional alternating loading; φ is the residual angle of the energy dissipation angle.

According to the macroscopic phenomenological damage mechanics concept proposed (Zhang et al., 2020), the elastic modulus can be obtained through the response of the macroscopic physical properties of rocks, and it can represent the deterioration degree of the material inside. Therefore, the freeze-thaw damage variable (Equation 21) can be expressed as:

${\mathit{D}}_{\mathit{n}}=\mathbf{1}-\frac{{\mathit{E}}_{\mathit{n}}}{{\mathit{E}}_{\mathbf{0}}}(21)$

In the formula, D_n represents the variable of freeze-thaw damage, E_n is the elastic modulus of double-fractured sandstone after n freeze-thaw cycles, and E₀ is the initial elastic modulus of double-fractured sandstone.

To sum up, substituting Equations 14, 15 into Equations 19, 20 yields the strain responses under alternating loads. By adding the strain responses under static loads and static stress in three-dimensional to the strain responses under alternating loads, and introducing the variable 1-D_n for freeze-thaw damage, a three-dimensional fatigue constitutive model for double-fractured red sandstone under freeze-thaw and cyclic loads (Equations 22, 23) is obtained:

When σ_d ≤σ_th:

$\begin{array}{l}\mathit{\epsilon }={\mathit{\epsilon }}_{\mathit{s}}+{\mathit{\epsilon }}_{\mathit{f}}\\ =\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{H}}^{*}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{9}{\mathit{K}}_{\mathit{H}}^{*}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{K}}^{*}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{G}}_{\mathit{K}}^{*}}{{\mathit{\eta }}_{\mathit{K}}^{*}}\frac{\mathit{N}}{\mathit{f}}\right)\right]\\ +\left(\frac{{\mathit{\sigma }}_{\mathit{max}}-{\mathit{\sigma }}_{\mathit{min}}}{\mathbf{2}}\right)\times \sqrt{{\left({\mathit{J}}_{\mathit{d}\mathit{a}\mathbf{1}}^{*}\right)}^{\mathbf{2}}+{\left({\mathit{J}}_{\mathit{d}\mathit{a}\mathbf{2}}^{*}\right)}^{\mathbf{2}}}\times \mathit{sin}\left[\mathit{\omega }\left(\frac{\mathit{N}}{\mathit{f}}\right)+\mathit{arctan}\left(\frac{{\mathit{J}}_{\mathit{d}\mathit{a}\mathbf{1}}^{*}}{{\mathit{J}}_{\mathit{d}\mathit{a}\mathbf{2}}^{*}}\right)\right]\end{array}(22)$

When σ_d >σ_th:

$\begin{array}{l}\mathit{\epsilon }={\mathit{\epsilon }}_{\mathit{s}}+{\mathit{\epsilon }}_{\mathit{f}}\\ =\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{H}}^{*}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}+\mathbf{2}{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{9}{\mathit{K}}_{\mathit{H}}^{*}}+\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}}{\mathbf{3}{\mathit{G}}_{\mathit{K}}^{*}}\left[\mathbf{1}-\mathit{exp}\left(-\frac{{\mathit{G}}_{\mathit{K}}^{*}}{{\mathit{\eta }}_{\mathit{K}}^{*}}\frac{\mathit{N}}{\mathit{f}}\right)\right]\\ +\frac{{\mathit{\sigma }}_{\mathbf{1}}-{\mathit{\sigma }}_{\mathbf{3}}-{\mathit{\sigma }}_{\mathit{t}\mathit{h}}}{\mathbf{3}{\mathit{\eta }}_{\mathit{V}}^{*}}{\left(\frac{{\mathit{N}}_{\mathbf{2}}}{{\mathit{f}}_{\mathbf{2}}}-\frac{{\mathit{N}}_{\mathbf{1}}}{{\mathit{f}}_{\mathbf{1}}}\right)}^{{\mathit{\xi }}_{\mathbf{2}}}{\mathit{E}}_{\mathbf{1},{\mathit{\xi }}_{\mathbf{2}}}\left(\mathit{\kappa }\frac{{\mathit{N}}_{\mathbf{2}}}{{\mathit{f}}_{\mathbf{2}}}\right)\\ +\left(\frac{{\mathit{\sigma }}_{\mathit{max}}-{\mathit{\sigma }}_{\mathit{min}}}{\mathbf{2}}\right)\times \sqrt{{\left({\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{1}}^{*}\right)}^{\mathbf{2}}+{\left({\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{2}}^{*}\right)}^{\mathbf{2}}}\times \mathit{sin}\left[\mathit{\omega }\left(\frac{\mathit{N}}{\mathit{f}}\right)+\mathit{arctan}\left(\frac{{\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{1}}^{*}}{{\mathit{J}}_{\mathit{d}\mathit{b}\mathbf{2}}^{*}}\right)\right]\end{array}(23)$

In the formula, the variables with asterisks as superscripts all represent the variables after freeze-thaw, ${G*}_H=G_H\left(1-D_n\right)$; ${K*}_H=K_H\left(1-D_n\right)$; ${G*}_K=G_K\left(1-D_n\right)$; ${\eta *}_K={\eta }_K\left(1-D_n\right)$; ${\eta *}_V={\eta }_V\left(1-D_n\right)$; ${J*}_{\mathit{da1}}=J_{da1}\left({G*}_H,{G*}_K,{\eta *}_K\right)$; ${J*}_{\mathit{da2}}=J_{da2}\left({G*}_K,{\eta *}_K\right)$; ${J*}_{\mathit{db1}}=J_{db1}\left({G*}_H,{G*}_K,{\eta *}_K,{\eta *}_V\right)$; ${J*}_{\mathit{db2}}=J_{db2}\left({G*}_K,{\eta *}_K,{\eta *}_V\right)$.

4.2 The establishment of constitutive models

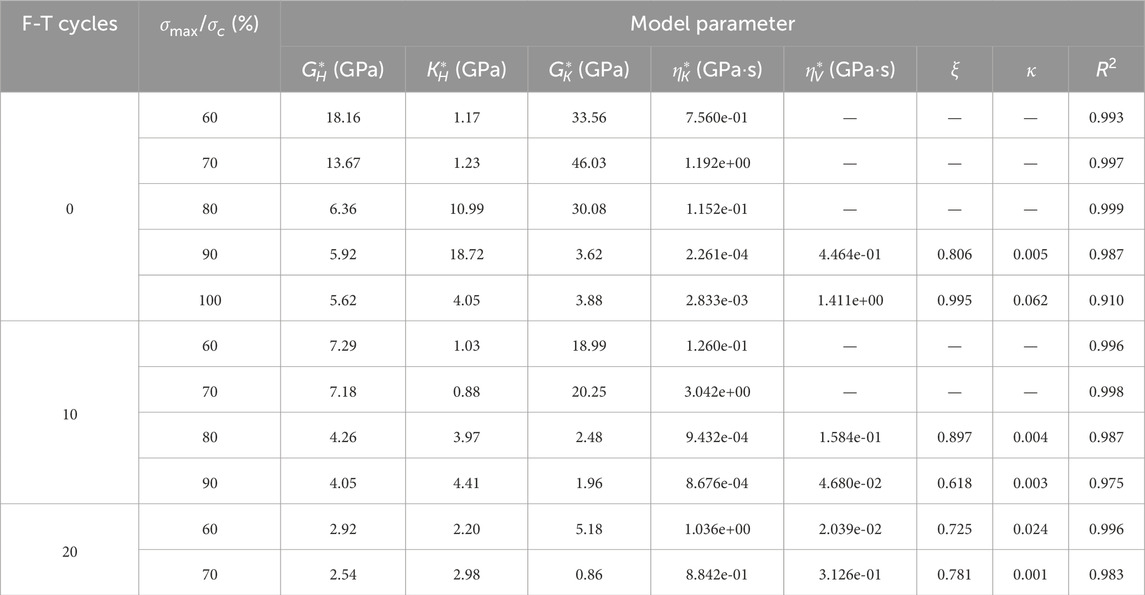
The fatigue constitutive model parameters for double-fractured red sandstone under freeze-thaw and cyclic loading were fitted using the Levenberg-Marquardt least squares method, with 1stOpt mathematical software. In the cyclic loading test, the maximum and minimum axial strains (i.e., irreversible axial strain) clearly reflect the three stages of the rock’s fatigue process. Thus, the cyclic loading test parameters were inverted. By comparing the test and fitting results under three types of freeze-thaw cycles (Figure 6), the model parameters (${G*}_H$, ${K*}_H$, ${G*}_K$, ${\eta *}_K$, ${\eta *}_V$, $\kappa$) are obtained, as shown in Table 4.

Figure 6

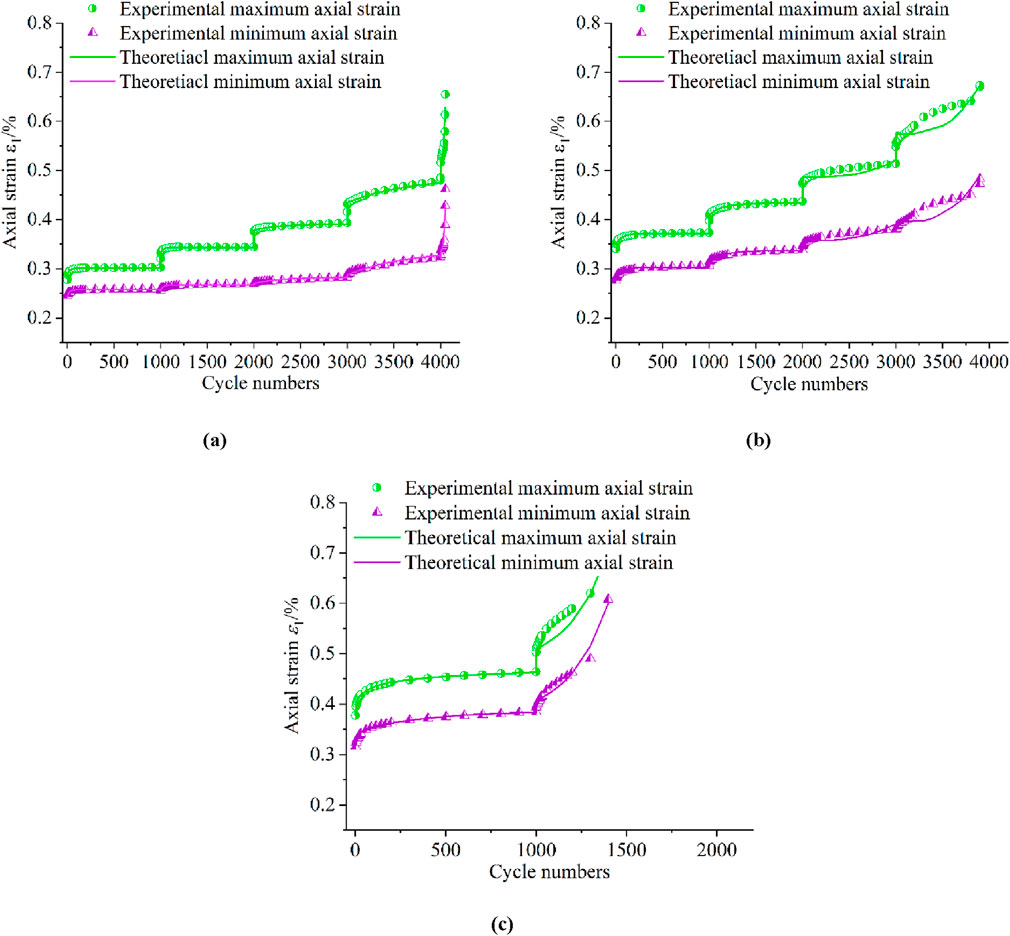
Figure 6. Fitting results of cyclic load tests after different number of freeze-thaw cycles (a-c. The number of freeze-thaw cycles are 0, 10, and 20 respectively). (a) F-T=0 (b) F-T=10 (c) F-T=20.

Table 4

Table 4. Parameter fitting results of fatigue constitutive model.

As shown in Figure 6, the curve development of the fatigue constitutive model for double-fractured red sandstone under freeze-thaw and cyclic loading closely matches the test values. The correlation coefficients for all working conditions in Table 4 exceed 0.9. Therefore, the model can better describe the axial strain evolution of double-fractured red sandstone with increasing number of cycles in cyclic loading tests.

5 Discussion

Ge et al. adapted the creep concept to classify the irreversible axial deformation development during the fatigue process of rocks into three stages: the initial stage, the steady-rate stage, and the accelerated stage (Ge et al., 2003), as illustrated in Figure 7b. As shown in Figure 7a, irreversible axial deformation development curves can be categorized into three types:

(a) When the upper limit stress is below the fatigue strength threshold, the axial deformation curve follows type a. The deformation increases first, and after a certain number of cycles, the deformation no longer increases with the number of cycles, or the increase is extremely slow, and fatigue damage of the rock may not occur.

(b) When the upper limit stress slightly exceeds the fatigue strength threshold, the axial deformation curve is of type b, which follows a common three-stage development pattern. The steady-rate stage during the isokinetic phase dominates the fatigue life yet constitutes only approximately one-third of the total deformation.

(c) When the upper stress limit approaches the peak compressive strength, the axial deformation curve of the rock exhibits type c behavior, leading to failure after very few cycles. This phenomenon is commonly observed in brittle rocks subjected to high upper stress levels.

Figure 7

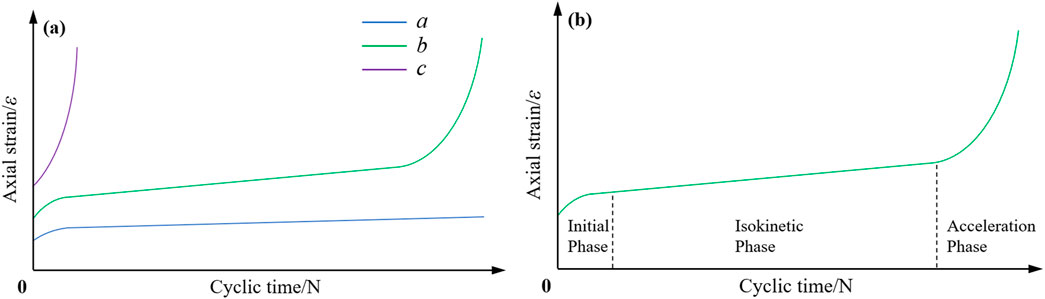
Figure 7. The irreversible axial deformation development curve of the rock fatigue process. (a) The irreversible axial deformation development curves of the three types; (b) The universal three-stage type curve).

As shown in Figure 6, for the double-fractured sandstone with no freeze-thaw cycles, the axial strain remains relatively constant after a significant initial increase, with the deformation curve following type a. At the last two stages, the curve transitions to types b and c, indicating that with more cycles, the rock samples under 3 MPa peripheral pressure can be damaged at a stress level of 90%. After 10 freeze-thaw cycles, the double-fractured sandstone can be damaged at an 80% stress level. After 20 freeze-thaw cycles, the same holds true for a 70% stress level in the double-fractured sandstone. The fatigue strength threshold defines whether rock samples are fatigued under a given stress state. The lowest value from both the upper limit stress and axial strain criteria is selected to ensure a safety margin for rock engineering in cold regions under cyclic loading. Combined with the average fatigue damage strengths in Table 3 (95%, 85%, and 65%), the fatigue strength thresholds can be determined: for unfrozen double-fractured red sandstone, it is approximately 90% of the peak strength from the triaxial compression test; after 10 freeze-thaw cycles, it is about 80%, and after 20 cycles, it is around 65%. Thus, the fatigue strength threshold stress ratio decreases with increasing freeze-thaw cycles.

For geotechnical projects in cold regions affected by long-term cyclic loads, such as construction, traffic, and small earthquakes, the fatigue strength of the fractured rock should be carefully considered. An early warning value for the surrounding rock should be developed based on the dilatancy stress from static loading tests, considering the actual geological conditions and the duration of cyclic loading, ensuring that the stress on the rock body remains below its fatigue strength threshold. Simultaneously, real-time monitoring of stress magnitude and deformation patterns in areas affected by cyclic loading should be conducted for safety assessment of the fractured rock engineering in cold regions.

The variable-order fractional derivative fatigue model developed in this study offers substantial advantages over traditional constitutive frameworks. In contrast to the classic Nishihara model (Gao and Yin, 2021), which employs a fixed fractional-order parameter, this model introduces a dynamically adjustable fractional-order parameter ξ₂ to accommodate freeze-thaw damage evolution, enabling precise characterization of three-stage fatigue deformation. This adaptability is validated by the model’s excellent fit to the experimental data presented in Figure 6. Additionally, by integrating the freeze-thaw damage variable D_n to modify viscoelastic parameters, the model explicitly bridges micro-damage with macro-fatigue behavior—a capability lacking in most energy-based or uniaxial-focused models (Li et al., 2020; Yun et al., 2024). These features empower the model to accurately capture complex fracture evolution and stress-dependent fatigue life in freeze-thaw fractured sandstone, providing a more reliable framework for coupled damage analysis. It should be noted that the proposed fatigue constitutive model is established based on indoor experimental sandstone specimens. However, its adaptability to hard rocks such as granite is poor due to the significant differences in mechanical properties and failure mechanisms between sandstone and hard rocks. Additionally, the current indoor experiments are conducted on small-scale specimens, and the size effect leads to notable discrepancies in mechanical parameters between small-scale specimens and large-scale rock masses in practical engineering. Therefore, the parameters related to large-scale rock engineering still require further investigation, including expanding the application scope to various hard rock types and conducting in-depth studies on size effect through large-scale field tests and numerical simulations. This will help improve the universality and engineering applicability of the model in practical geotechnical projects.

6 Conclusion

To investigate the fatigue damage strength and deformation behavior of fractured red sandstone under freeze-thaw and cyclic loading, triaxial cyclic loading tests were conducted on rock samples subjected to 0, 10, and 20 freeze-thaw cycles. The results indicate that with increasing freeze-thaw cycles, both the peak triaxial static load strength and average fatigue strength decreased, while the strain at failure increased. The fatigue damage process is governed by the full-range static stress-strain curves, with the strain at the “failure point” consistently exceeding the peak strain under static loading but generally remaining below the strain at the “control point.” Under high confining pressure, the freeze-thawed sandstone primarily undergoes shear failure, characterized by crack interconnection, granular powder accumulation near the failure surface, and relatively mild fragmentation. The complexity and quantity of surface cracks increase with freeze-thaw cycles, indicating enhanced ductility. By integrating the average fatigue damage stress ratio with the axial strain evolution, the fatigue strength thresholds for 0, 10, and 20 freeze-thaw cycles were determined to be approximately 90%, 80%, and 65% of the peak strength in triaxial static compression tests, respectively. Given the significant influence of cyclic loading on fractured rock masses in cold regions, real-time monitoring of stress magnitude and deformation patterns is essential for predicting fatigue damage. Furthermore, a fatigue deformation intrinsic model based on variable-order fractional derivatives was developed, effectively capturing the three-stage deformation process demonstrating its applicability in modeling the fatigue behavior of freeze-thawed fractured sandstone.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JH: Writing – original draft, Conceptualization, Investigation, Methodology, Writing – review and editing. YG: Data curation, Supervision, Methodology, Writing – original draft, Writing – review and editing. JR: Funding acquisition, Validation, Visualization, Writing – review and editing. FY: Writing – original draft, Funding acquisition, Resources. CZ: Writing – review and editing, Supervision, Resources, Formal Analysis. XM: Project administration, Funding acquisition, Supervision, Writing – review and editing. SF: Investigation, Methodology, Resources, Writing – review and editing, Formal Analysis.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work has been supported by the National Natural Science Foundation of China (5230090704, 5207090840), China Postdoctoral Science Foundation (2022MD723827), and the Xi’an Association for Science and Technology Youth Talent Support Program (959202413072).

Conflict of interest

Authors JH, FY, CZ, and XM were employed by Shenmu Zhangjiamao Mining Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that Generative AI was used in the creation of this manuscript. The author(s) verify and take full responsibility for the use of generative AI in the preparation of this manuscript. Generative AI was used During the preparation of this work the authors used Deepseek in order to improve language. After using this tool/service, the authors reviewed and edited the content as needed and take full responsibility for the content of the publication.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Chau, K. T., and Wong, R. H. C. (1996). Uniaxial compressive strength and point load strength of rocks. Int. J. Rock Mech. Min. Sci. 33 (2), 183–188. doi:10.1016/0148-9062(95)00056-9

CrossRef Full Text | Google Scholar

Chen, L., Wu, P., Chen, Y., and Zhang, W. (2020). Experimental study on physical-mechanical properties and fracture behaviors of saturated yellow sandstone considering coupling effect of freeze-thaw and specimen inclination. Sustainability 12 (3), 1029. doi:10.3390/su12031029

CrossRef Full Text | Google Scholar

Deprez, M., De Kock, T., De Schutter, G., and Cnudde, V. (2020). A review on freeze-thaw action and weathering of rocks. Earth-Sci. Rev. 203, 103143. doi:10.1016/j.earscirev.2020.103143

CrossRef Full Text | Google Scholar

Gao, Y., and Yin, D. (2021). A full-stage creep model for rocks based on the variable-order fractional calculus. Appl. Math. Model. 95, 435–446. doi:10.1016/j.apm.2021.02.020

CrossRef Full Text | Google Scholar

Ge, X., and Lu, Y. (1992). Discussion on fatigue failure and irreversible deformation of rock under cyclic loading. J. Geotechnical Eng. 14 (3), 56–60. Available online at: https://cgejournal.com/article/id/9580.

Google Scholar

Ge, X. R., Jiang, Y., and Lu, Y. D. (2003). Testing study on fracture deformation law of rock under cyclic loading. Chin. J. Rock Mech. Eng. 22 (10), 1581–1585. doi:10.3321/j.issn:1000-6915.2003.10.001

CrossRef Full Text | Google Scholar

Han, C., Liu, X., Li, D., and Shao, Y. (2021). Constitutive modeling of rock materials based on variable-order fractional theory. Mech. Time-Depend. Mater 26 (2), 485–498. doi:10.1007/s11043-021-09497-x

CrossRef Full Text | Google Scholar

Huang, S., Liu, Q., Cheng, A., and Liu, Y. (2018). A statistical damage constitutive model under freeze-thaw and loading for rock and its engineering application. Cold Reg. Sci. Technol. 145, 142–150. doi:10.1016/j.coldregions.2017.10.015

CrossRef Full Text | Google Scholar

Huang, S., Yu, S., Ye, Y., Ye, Z., and Cheng, A. (2022). Pore structure change and physico-mechanical properties deterioration of sandstone suffering freeze-thaw actions. Constr. Build. Mat. 330, 127200. doi:10.1016/j.conbuildmat.2022.127200

CrossRef Full Text | Google Scholar

Lakes, R. S. (1998). Viscoelastic solids. London: CRC Press.

Google Scholar

Li, J., Zhou, K., Liu, W., and Zhang, Y. (2017). Analysis of the effect of freeze–thaw cycles on the degradation of mechanical parameters and slope stability. Bull. Eng. Geol. Environ. 77 (2), 573–580. doi:10.1007/s10064-017-1013-8

CrossRef Full Text | Google Scholar

Li, T., Pei, X., Guo, J., Meng, M., and Huang, R. (2020). An energy-based fatigue damage model for sandstone subjected to cyclic loading. Rock Mech. Rock Eng. 53 (11), 5069–5079. doi:10.1007/s00603-020-02209-w

CrossRef Full Text | Google Scholar

Liu, J., Pu, S., and Rao, J. (2020). Visco-Elastoplastic constitutive fatigue model for rocks. Adv. Civ. Eng. 2020 (1), 4292043. doi:10.1155/2020/4292043

CrossRef Full Text | Google Scholar

Liu, J., Wu, F., Zou, Q., Chen, J., Ren, S., and Zhang, C. (2021). A variable-order fractional derivative creep constitutive model of salt rock based on the damage effect. Geomech. Geophys. Geo-Energy Geo-Resour. 7 (2), 46. doi:10.1007/s40948-021-00241-w

CrossRef Full Text | Google Scholar

Liu, Y., Cai, Y., Huang, S., Guo, Y., and Liu, G. (2019). Effect of water saturation on uniaxial compressive strength and damage degree of clay-bearing sandstone under freeze-thaw. Bull. Eng. Geol. Environ. 79 (4), 2021–2036. doi:10.1007/s10064-019-01686-w

CrossRef Full Text | Google Scholar

Maji, V., and Murton, J. B. (2021). Experimental observations and statistical modeling of crack propagation dynamics in limestone by acoustic emission analysis during freezing and thawing. J. Geophys. Res.:Earth Surf. 126 (7). doi:10.1029/2021jf006127

CrossRef Full Text | Google Scholar

Mateos, R. M., García-Moreno, I., and Azañón, J. M. (2011). Freeze–thaw cycles and rainfall as triggering factors of mass movements in a warm Mediterranean region: the case of the Tramuntana Range (Majorca, Spain). Landslides 9 (3), 417–432. doi:10.1007/s10346-011-0290-8

CrossRef Full Text | Google Scholar

Peng, K., Zhou, J., Zou, Q., and Song, X. (2019). Effect of loading frequency on the deformation behaviours of sandstones subjected to cyclic loads and its underlying mechanism. Int. J. Fatigue. 131, 105349. doi:10.1016/j.ijfatigue.2019.105349

CrossRef Full Text | Google Scholar

Pu, S., Zhu, Z., Song, L., Song, W., and Peng, Y. (2020). Fractional-order visco-elastoplastic constitutive model for rock under cyclic loading. Arab. J. Geosci. 13 (9), 326. doi:10.1007/s12517-020-05288-9

CrossRef Full Text | Google Scholar

Qu, D., Li, D., Li, X., Luo, Y., and Xu, K. (2018). Damage evolution mechanism and constitutive model of freeze-thaw yellow sandstone in acidic environment. Cold Reg. Sci. Technol. 155, 174–183. doi:10.1016/j.coldregions.2018.07.012

CrossRef Full Text | Google Scholar

Sagong, M., and Bobet, A. (2002). Coalescence of multiple flaws in a rock-model material in uniaxial compression. Int. J. Rock Mech. Min. Sci. 2 (39), 229–241. doi:10.1016/S1365-1609(02)00027-8

CrossRef Full Text | Google Scholar

Shen, Y., Luo, T., Wei, X., Li, X., Jin, L., Wen, L., et al. (2022). Mechanism analysis of the influence of freeze-thaw on the damage and debonding evolution of sandstone-concrete interface. Geofluids 2022 (1), 1–13. doi:10.1155/2022/3550597

CrossRef Full Text | Google Scholar

Song, Y., Tan, H., Yang, H., Chen, S., Che, Y., and Chen, J. (2021a). Fracture evolution and failure characteristics of sandstone under freeze-thaw cycling by computed tomography. Eng. Geol. 294, 106370. doi:10.1016/j.enggeo.2021.106370

CrossRef Full Text | Google Scholar

Song, Z., Wang, Y., Konietzky, H., and Cai, X. (2021b). Mechanical behavior of marble exposed to freeze-thaw-fatigue loading. Int. J. Rock Mech. Min. Sci. 138, 104648. doi:10.1016/j.ijrmms.2021.104648

CrossRef Full Text | Google Scholar

Steiger, M. (2005). Crystal growth in porous materials—I: the crystallization pressure of large crystals. J. Cryst. Growth 282 (3-4), 455–469. doi:10.1016/j.jcrysgro.2005.05.007

CrossRef Full Text | Google Scholar

Stöcke, K., Weise, F., Kieslinger, A., Eissner, W., Walz, K., and de Quervain, F. (1941). “Die Prüfung der natürlichen Bausteine,” in Die Prüfung nichtmetallischer Baustoffe. Handbuch der Werkstoffprüfung. Editor E. Brenner (Berlin, Heidelberg: Springer), 138–223.

Google Scholar

Tan, X., Chen, W., Yang, D., Dai, Y., Wu, G., Yang, J., et al. (2014). Study on the influence of airflow on the temperature of the surrounding rock in a cold region tunnel and its application to insulation layer design. Appl. Therm. Eng. 67 (1-2), 320–334. doi:10.1016/j.applthermaleng.2014.03.016

CrossRef Full Text | Google Scholar

Wang, F., Cao, P., Wang, Y., Hao, R., Meng, J., and Shang, J. (2020). Combined effects of cyclic load and temperature fluctuation on the mechanical behavior of porous sandstones. Eng. Geol. 266, 105466. doi:10.1016/j.enggeo.2019.105466

CrossRef Full Text | Google Scholar

Wang, S.-R., Chen, Y.-L., Ni, J., Zhang, M.-D., and Zhang, H. (2019). Influence of freeze-thaw cycles on engineering properties of tonalite: examples from China. Adv. Civ. Eng. 2019 (1), 3418134. doi:10.1155/2019/3418134

CrossRef Full Text | Google Scholar

Wang, Y., Yang, H., Han, J., and Zhu, C. (2021a). Insight into the fracture evolution behavior of pre-flawed hollow-cylinder granite under multi-stage increasing-amplitude cyclic loads: a lab-scale testing. Fatigue Fract. Eng. Mat. Struct. 45 (1), 285–301. doi:10.1111/ffe.13601

CrossRef Full Text | Google Scholar

Wang, Z. (2019). Study on the fatigue damage characteristics of sandstone and stability of rock slope under cyclic dynamic loading. [dissertation]. [Chongqing (CHN)]. Chongqing University.

Google Scholar

Wang, Z., Li, Y., Cai, W., Zhu, W., Kong, W., Dai, F., et al. (2021b). Crack propagation process and acoustic emission characteristics of rock-like specimens with double parallel flaws under uniaxial compression. Theor. Appl. Fract. Mech. 114, 102983. doi:10.1016/j.tafmec.2021.102983

CrossRef Full Text | Google Scholar

Wu, F., Liu, J., Zou, Q., Li, C., Chen, J., and Gao, R. (2020). A triaxial creep model for salt rocks based on variable-order fractional derivative. Mech. TIME-DEPEND Mat. 25 (1), 101–118. doi:10.1007/s11043-020-09470-0

CrossRef Full Text | Google Scholar

Xue, L., Qin, S., Sun, Q., Wang, Y., Lee, L. M., and Li, W. (2013). A study on crack damage stress thresholds of different rock types based on uniaxial compression tests. Rock Mech. Rock Eng. 47 (4), 1183–1195. doi:10.1007/s00603-013-0479-3

CrossRef Full Text | Google Scholar

Yang, S.-Q., Zhao, Y., Liu, X., Huang, Y. H., and Yang, J. (2021). An experimental study on failure mechanical behavior and cracking mechanism of rectangular solid sandstone containing two non-coplanar fissures under conventional triaxial compression. Theor. Appl. Fract. Mech. 114, 102975. doi:10.1016/j.tafmec.2021.102975

CrossRef Full Text | Google Scholar

Yu, W., Zhang, T., Lu, Y., Han, F., Zhou, Y., and Hu, D. (2020). Engineering risk analysis in cold regions: state of the art and perspectives. Cold Reg. Sci. Technol. 171, 102963. doi:10.1016/j.coldregions.2019.102963

CrossRef Full Text | Google Scholar

Yun, M., Ren, J., Song, Y., Zhang, L., Sun, C., Chang, P., et al. (2024). Fracture mechanism and damage constitutive model of freeze-thaw fissured granite subjected to fatigue loading. Appl. Sci. 14 (14), 6324. doi:10.3390/app14146324

CrossRef Full Text | Google Scholar

Yun, M., Ren, J., Tan, M. F., and Song, J. W. (2025). Fractal evolution of sandstone material under combined thermal and mechanical action: microscopic pore structure and macroscopic fracture characteristics. Mat. Lett. 389, 138388. doi:10.1016/j.matlet.2025.138388

CrossRef Full Text | Google Scholar

Yun, M., Ren, J., Zhang, L., and Zhang, K. (2024). Research on triaxial compressive mechanical properties and damage constructive model of post-thawing double-fractured quasi-sandstones with different angles. Heliyon 10 (14), e34268. doi:10.1016/j.heliyon.2024.e34268

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhang, G., Chen, G., Xu, Z., Yang, Y., and Lin, Z. (2020). Crack failure characteristics of different rocks under the action of frost heaving of fissure water. Front. Earth Sci. 8 (13). doi:10.3389/feart.2020.00013

CrossRef Full Text | Google Scholar

Zhang, H., Meng, X., and Yang, G. (2020). A study on mechanical properties and damage model of rock subjected to freeze-thaw cycles and confining pressure. Cold Reg. Sci. Technol. 174, 103056. doi:10.1016/j.coldregions.2020.103056

CrossRef Full Text | Google Scholar