Neural network based active control of base isolated structure considering isolator nonlinearity

Introduction: Hybrid control systems combining passive and active strategies have emerged as effective solutions to enhance structural resilience during earthquakes. Recent advancements in smart structures integrate active tuned mass dampers (ATMDs) for precise dynamic response control and seismic hazard mitigation. Simultaneously, artificial intelligence (AI), particularly machine learning algorithms, has opened new frontiers in structural control.

Methods: This study proposes a novel AI-based approach for structures equipped with nonlinear base isolation and an ATMD. An artificial neural network (ANN) is employed, trained via supervised learning using the Levenberg-Marquardt backpropagation algorithm to minimize displacement demands during strong earthquakes. The ANN-driven controller aims to achieve significant response reduction with fewer sensors than traditional algorithms while enhancing robustness against signal time delays and white noise contamination. For validation, an ATMD is installed at the base isolation layer of an 8-story benchmark building. The ANN controller's performance is evaluated under near-field and far-field seismic excitations and compared with a conventional linear quadratic regulator (LQR)-controlled ATMD and a classical tuned mass damper (TMD). Robustness tests include time delays and white noise in input signals.

Results: The results demonstrate that the ANN-driven ATMD controller notably reduces key dynamic response parameters, including peak base acceleration, displacement, velocity, inter-story drift, maximum drift, and base shear, under both near-field and far-field earthquake scenarios. Furthermore, the ANN controller maintains high performance even when subjected to signal time delays and white noise contamination, underscoring its robustness. Importantly, these improvements are attained while utilizing fewer sensors than the LQR controller, highlighting the practicality and cost-effectiveness of the proposed method.

Discussion: The proposed ANN controller achieves performance comparable to the full-state LQR controller but requires fewer sensors, enhancing practicality and cost-effectiveness for real-world applications. This approach demonstrates superior robustness against signal imperfections while maintaining high seismic response mitigation efficacy.

1 Introduction

In the field of civil engineering, mitigating structural damage caused by seismic and wind actions is of critical importance. Earthquakes, in particular, pose significant threats to the stability of buildings and infrastructure, making the development and implementation of advanced control systems essential for enhancing structural resilience (El Ouni et al., 2022; Elias et al., 2025).

Control systems are generally classified into four categories: passive, active, semi-active, and hybrid (Fisco and Adeli, 2011a; Fisco and Adeli, 2011b). Passive control systems play a key role in seismic protection, particularly in the area of base isolation. These systems, such as base isolation (BI), tuned mass dampers (TMDs), and energy dissipation devices, operate without the need for external energy sources (Djerouni et al., 2020; Elia et al., 2017; Mazza et al., 2024; Mazza et al., 2023).

Base Isolation Systems (BIS) function by decoupling the superstructure’s dynamic response from that of the ground. This is achieved through the introduction of a laterally flexible isolation layer between the foundation and the superstructure. The effectiveness of BIS has been extensively investigated in the literature (Sapountzakis et al., 2024; Skinner et al., 1993; Naeim and Kelly, 1999; Charrouf et al., 2024; Mazza and Labernarda, 2022). Despite their proven reliability and simplicity, these techniques are inherently limited by their passive nature, which prevents them from adapting to seismic events not considered during the design stage. To overcome these limitations, hybrid control systems, which can combine passive and active/semi-active control mechanisms, have been proposed as a more adaptable and effective solution in certain scenarios (Djedoui et al., 2017; Banerjee and Matsagar, 2023; Cheng and Jiang, 1998; Zahedin Labaf et al., 2023). Given the often nonlinear behavior of many passive devices, hybrid systems are particularly valuable for actively managing nonlinearities and inelastic hysteretic responses (Yang et al., 1992; Li et al., 2021). The integration of active control elements into base-isolated systems can help mitigate some of the drawbacks associated with nonlinear BIS, especially the large displacements that may occur under severe earthquake excitations (Heertjes and van de Wouw, 2006; Lee and Kawashima, 2007; Subasri et al., 2013; Gu et al., 2017).

Active control systems utilize sensors, actuators, and sophisticated control algorithms to dynamically respond to seismic forces, adjusting the structural response in real-time. One of the most used devices is the active tuned mass damper (ATMD), which has emerged as a viable solution for reducing unwanted vibrations in multistory buildings during seismic events (Sabetahd et al., 2022; Chang and Soong, 1980; Ümütlü et al., 2021). Researchers such as Li et al. (Linderman and Spencer, 2016) have demonstrated the effectiveness of AMDs in high-rise buildings, while Linderman and Spencer have explored their integration with wireless sensor networks in civil structures (Linderman and Spencer, 2016). Control force requirements for ATMD systems can be substantial. To address this challenge, various algorithms have been developed to optimize the control effort and enhance overall system performance. Among the most widely used are proportional-integral-derivative (PID) controllers (Djedoui et al., 2016; Ulusoy et al., 2021) and the linear quadratic regulator (LQR), first introduced in the 1960s (Kalman, 1960). This method has since been widely applied in active and semi-active control systems (Amezquita-Sanchez et al., 2014; Elias et al., 2023; Hashemi et al., 2022). The main goal of the LQR approach is to determine an optimal control law that minimizes a predefined quadratic cost function, which typically balances the system’s performance and the energy required for control. By systematically weighing the relative importance of state deviations and control efforts, the LQR provides a feedback gain matrix that ensures efficient performance with constrained energy input, making it especially suitable for real-time structural control applications. LQR is pivotal in controlling multiple-input multiple-output (MIMO) systems (Islam et al., 2003; Phillips and Sahin, 2014; Pandey and Laxmi, 2015). However, its practical application is challenged by the considerable sensor requirements, often limited by real-world constraints on sensor availability (Ghanemi et al., 2024).

Integrating hybrid control for a multi-degree-of-freedom (MDOF) structure equipped with BIS offers a promising solution for reducing excessive seismic displacement at the base isolation level (Shin et al., 2020). However, in this context, a significant challenge is the necessity for nonlinear adaptive control strategies to account for the hysteresis or friction mechanism typically introduced by the base-isolation system. Classical control methods, such as PID and LQR controllers, have shown limitations in effectively managing time-varying and nonlinear systems. To address these challenges, a novel approach involving artificial intelligence (AI) control methods is proposed.

In recent decades, researchers have made significant strides in AI, which has greatly enhanced the performance of structural systems in areas such as monitoring, controlling, evaluating, and response mitigation. Lu et al. (2012) performed a survey examining various AI techniques, such as evolutionary computation, fuzzy logic, neural networks, and swarm intelligence. Aldwaik and Adeli (2014) presented a multiparadigm learning approach, showing that integrating neural networks, genetic algorithms, fuzzy sets, and parallel processing can significantly boost performance. Mardani et al. (2015) reviewed the uses and approaches of fuzzy multi-criteria decision-making methods, while Zhang and Xue (2023) examined the latest developments in optimizing high-rise buildings. Moreover, studies have explored the application of random forests for safeguarding structures from external disturbances (Smarra et al., 2020; Di Girolamo et al., 2020).

One of the most widely used AI techniques is Artificial Neural Networks (ANN). The utilization of ANN models in managing seismic responses has led to notable progress, particularly in mitigating structural oscillations (Jhang et al., 2018; Yang et al., 2006). A fundamental aspect of ANN controllers is their precision in approximating nonlinear functions, rendering them well-suited for intricate systems like multistory buildings (Conte et al., 1994; Blachowski and Pnevmatikos, 2018). For instance, ANNs have been used to develop intelligent systems that adapt in real-time (Jamil et al., 2021), Chang and Sung evaluated enhanced vibration mitigation in a nonlinear building using a neuro-controller (Chang and Sung, 2019), and Liut et al. (1999) developed a neural network controller, trained through a force-matching technique, to operate a tuned-mass damper confirming its functionality. The use of ANN in assessing bridge risks has been thoroughly investigated (Ying et al., 2009; Neves et al., 2017). Additionally, ANN has been employed to mitigate structural responses to seismic risks (Ghanemi et al., 2024; Ghanemi et al., 2023; Blachowski and Pnevmatikos, 2018; Radmard Rahmani et al., 2019; Brancati et al., 2020). Furthermore, Sanad and Saka (2001) applied ANNs to predict the maximum shear strength of reinforced concrete beams. The time delay method is widely used for training ANNs (Chen and Chien, 2020), yet its specific effects on structural responses remain largely unexplored. This gap highlights the need for research that examines how these methods influence the overall performance of the system’s response.

The primary focus of this study is the development of an AI-based controller aimed at enhancing the functionality of nonlinear base-isolated structures while simultaneously reducing sensor requirements and improving robustness against external disturbances. Specifically, the proposed approach integrates an ANN controller with an ATMD to mitigate the seismic response of a base-isolated structure. The ANN controller is trained using data generated by an LQR based on one earthquake signal, enabling it to replicate near-optimal control strategies while significantly reducing the need for full-state observation. Unlike conventional LQR controllers, which typically require a large number of sensors to monitor all state variables, the ANN controller operates effectively using fewer sensors, directly addressing concerns about ATMD implementation complexity and cost by minimizing hardware requirements. In addition to performance under ideal conditions, the proposed ANN-driven ATMD system is also evaluated under signal time delays and white noise contamination to proactively resolve feasibility challenges and verify its robustness in realistic operating environments. This dual focus on sensor reduction and delay/noise tolerance ensures practical viability without compromising control efficacy. The methodology is applied to an 8-story nonlinear base-isolated benchmark building subjected to both near-field and far-field earthquake records. The performance of the ANN-based controller is systematically compared with that of a classical TMD and a conventional LQR-controlled ATMD. Furthermore, to validate the generalizability of the proposed approach, the ANN controller is tested under six additional earthquake records beyond the one adopted in the training phase. By demonstrating consistent performance across diverse seismic events while mitigating implementation barriers, this work establishes a balanced framework for intelligent vibration control systems.

The remainder of the paper is organized as follows. Section 2 presents the mathematical modeling of the system, describing both the LQR controller and the ANN training process. Section 3 details the numerical study, including the description of the benchmark building model, the tuning of the ATMD, the properties of the base-isolated system, the tuning processes for both the LQR and ANN controllers, and the earthquake dataset used for validation. Section 4 discusses the results, highlighting the effectiveness of the proposed controller and analyzing the impact of time delay and noise on the system’s performance. Finally, Section 5 concludes the paper, summarizing the main findings and suggesting directions for future research.

2 Mathematical model

Let’s consider an n-DOF structure equipped with a nonlinear BIS combined with an ATMD (Figure 1) exposed to earthquake ground acceleration. The BIS is modeled as a rigid mass $m_b$, with horizontal displacement $x_b$ and base isolators. The restoring force $F_b\left(t\right)$ exerted by the isolators accounts for both linear and nonlinear behavior modeled as reported in Yang et al. (1994) as it can be seen in Equation 1:

$F_b\left(t\right)={c_b{\dot{x}}_b\left(t\right)+\alpha }_b{k}_b{x}_b\left(t\right)+\left(1-{\alpha }_b\right)k_b{D}_{yb}{\upsilon }_b\left(t\right)(1)$

where $c_b$ and k_b respectively represent the BIS viscous damping coefficient and elastic stiffness, ${\alpha }_b$ is the ratio between the post-yielding to pre-yielding stiffness, $D_{yb}$ signifies the yield deformation and ${\upsilon }_b$ symbolizes the non-dimensional variable describing the hysteretic component of the deformation according to Bouc-Wen law (Wen, 1976; Wen, 1989; Ismail et al., 2009) the first derivative of ${\upsilon }_b$ is shown in Equation 2 as follow:

${\dot{\upsilon }}_b=D_{yb}^{-1}\left[A_b{\dot{x}}_b-{\beta }_b\left|{\dot{x}}_b\right|{\left|{\upsilon }_b\right|}^{{\eta }_b-1}{\upsilon }_b-{\gamma }_b{\dot{x}}_b{\left|{\upsilon }_b\right|}^{{\eta }_b}\right](2)$

where the overdot denotes the derivative with respect to time. The parameter ${\eta }_b$ influences the smoothness of the force-deformation curve, while the parameters $A_b,{\beta }_b,\mathrm{a}\mathrm{n}\mathrm{d}{\gamma }_b$ control both the scale and the shape of the hysteresis loop.

Figure 1

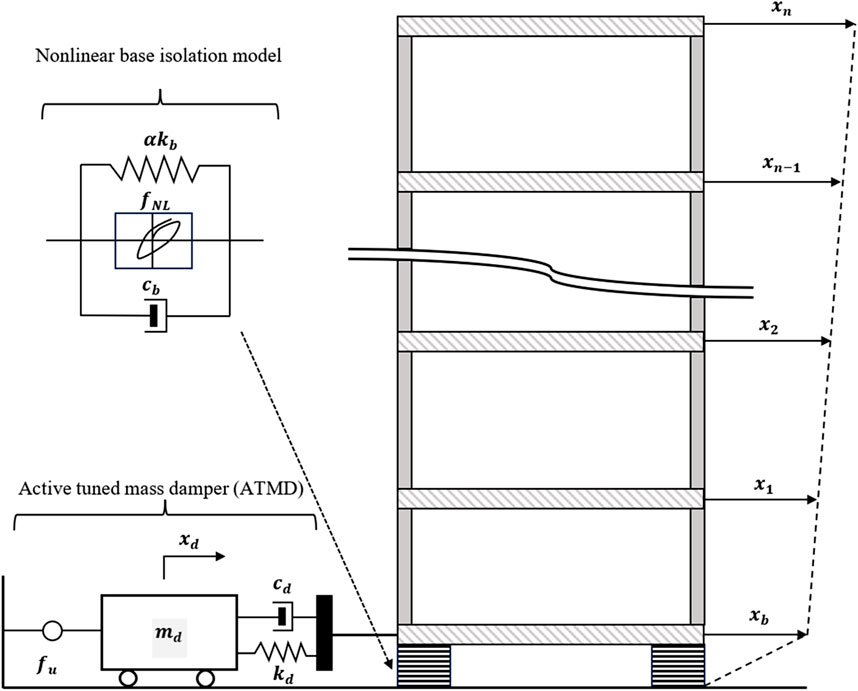
Figure 1. Structural model of MDOF story building equipped with the hybrid control system including BIS and ATMD.

It is possible to decompose the restoring force $F_b\left(t\right)$ (Equation 3) into two distinct components, characterized by a linear segment $f_L\left(t\right)$ (Equation 4) and a nonlinear segment $f_{NL}\left(t\right)$ (Equation 5):

$F_b\left(t\right)=f_L\left(t\right)+f_{NL}\left(t\right)(3)$

$f_L\left(t\right)=c_b{\dot{x}}_b\left(t\right)+{\alpha }_b{k}_b{x}_b\left(t\right)(4)$

$f_{NL}\left(t\right)=\left(1-{\alpha }_b\right)k_b{D}_{yb}{\upsilon }_b\left(t\right)(5)$

In order to minimize the BIS displacement, an ATMD with mass $m_d$ and horizontal displacement $x_d$ is attached to it. The ATMD mass is connected at one side to the BIS through an elastic stiffness $k_d$ and a viscous damping coefficient $c_d$, and at the other side to the actuator, which exerts its active control force $f_u$. The active control force impacts the structure by directly influencing its own response, which, in turn, modifies the BIS motion to enhance overall stability. By managing the isolator’s motion, it can effectively control the response of the entire superstructure.

Equation 6 shows the equation of motion that governs the resultant $\left(n+2\right)$-DOF system is expressed as:

$\mathit{M}{\ddot{\mathit{x}}}_{\mathit{t}}+\mathit{L}{\dot{\mathit{x}}}_{\mathit{t}}+\mathit{K}{\mathit{x}}_{\mathit{t}}+f_{NL}\left(t\right)\mathit{H}=-\mathit{M}\mathit{r}{\ddot{x}}_g+\mathit{d}{f}_u(6)$

${\mathit{x}}_t={\left\{\begin{array}{cccccc}{x}_b& x_1& x_2& \cdots & x_n& x_d\end{array}\right\}}^T$ represents the displacement vector, whereas M, L, and K respectively represent the system mass, damping, and stiffness matrix as it can be seen in Equations 7–9. $\mathit{r}$ is the influence vector that captures the effect of ground acceleration ${\ddot{x}}_g$. The vector $\mathit{d}$ (Equation 10) specifies the location where the control force $f_u$ is applied, note that a null $\mathit{d}$ will result in the mathematical formulation of a classical TMD. Meanwhile, H (Equation 10) represents the distribution of the base isolation force on the structure.

Matrices M, L, and K have the following expressions:

$\mathit{M}=\left[\begin{array}{ccccccc}{m}_b& 0& 0& 0& 0& 0& 0\\ 0& m_1& 0& 0& 0& 0& 0\\ 0& 0& m_2& 0& 0& 0& 0\\ 0& 0& 0& \ddots & 0& 0& 0\\ 0& 0& 0& 0& m_{n-1}& 0& 0\\ 0& 0& 0& 0& 0& m_n& 0\\ 0& 0& 0& 0& 0& 0& m_d\end{array}\right](7)$

$\mathit{L}=\left[\begin{array}{ccccccc}{c}_b+c_1+c_d& -c_1& 0& 0& 0& 0& -c_d\\ -c_1& c_1+c_2& -c_2& 0& 0& 0& 0\\ 0& -c_2& c_2+c_3& -c_3& 0& 0& 0\\ 0& 0& -c_3& \ddots & \ddots & 0& 0\\ 0& 0& 0& \ddots & c_{n-1}+c_n& -c_n& 0\\ 0& 0& 0& 0& -c_n& c_n& 0\\ -c_d& 0& 0& 0& 0& 0& c_d\end{array}\right](8)$

$\mathit{K}=\left[\begin{array}{ccccccc}{{\alpha }_{b}k}_b+k_1+k_d& -k_1& 0& 0& 0& 0& -k_d\\ -k_1& k_1+k_2& -k_2& 0& 0& 0& 0\\ 0& -k_2& k_2+k_3& -k_3& 0& 0& 0\\ 0& 0& -k_3& \ddots & \ddots & 0& 0\\ 0& 0& 0& \ddots & k_{n-1}+k_n& -k_n& 0\\ 0& 0& 0& 0& -k_n& k_n& 0\\ -k_d& 0& 0& 0& 0& 0& k_d\end{array}\right](9)$

vectors d and H, of ((n+2)×1) dimensions, assume the form:

$\mathit{d}=\left\{\begin{array}{c}0\\ 0\\ ⋮\\ 0\\ 0\\ 1\end{array}\right\},\mathit{H}=\left\{\begin{array}{c}1\\ 0\\ ⋮\\ 0\\ 0\\ -1\end{array}\right\}(10)$

Let’s note that the linear component of the BIS restoring force $f_L\left(t\right)$ is collected in the matrices L and K. The second-order nonlinear (Equation 6) can be transformed into a first-order nonlinear equation (Equation 11), known as the state-space representation in the following manner:

$\left\{\begin{array}{c}\dot{\mathit{z}}\left(t\right)=\mathit{A}\mathit{z}\left(t\right)+\mathit{B}\mathit{u}\left(t\right)\\ \mathit{y}\left(t\right)=\mathit{C}\mathit{z}\left(t\right)+\mathit{D}\mathit{u}\left(t\right)\end{array}\right.(11)$

$\mathit{z}\left(t\right)={\left[{\dot{\mathit{x}}}_t\left(t\right){\mathit{x}}_{\mathit{t}}\left(t\right)\right]}^T$ represents the full state of the system, encompassing velocity and displacement vectors, $\mathit{u}\left(t\right)={\left[f_u\left(t\right){\ddot{x}}_g\left(t\right)\right]}^T$ is the input vector collecting the ATMD force and the seismic acceleration, $\mathit{y}\left(t\right)$ is the output vector. Matrices A and B correspond to the state and the input matrix (Equations 12, 13), respectively defined as:

$\mathit{A}=\left[\begin{array}{cc}-{\mathit{M}}^{-\mathbf{1}}\mathit{L}& -{\mathit{M}}^{-\mathbf{1}}\mathit{K}\\ \mathit{E}& \mathbf{0}\end{array}\right](12)$

$\mathit{B}=\left[\begin{array}{cc}-{\mathit{M}}^{-\mathbf{1}}\mathit{d}& \mathit{E}\\ \mathbf{0}& \mathbf{0}\end{array}\right](13)$

C and D are the output matrix and the feedthrough matrix, respectively, and can vary depending on the choice of the output vector.

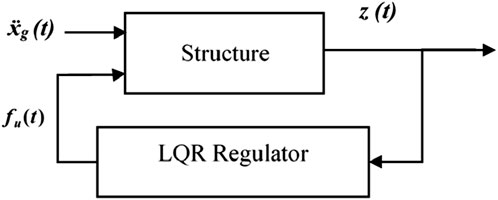
2.1 The trainer controller LQR

LQR controller is one of the most widely used classical control algorithms for active control (Moghaddasie and Jalaeefar, 2019). Since its inception, LQR has evolved to address complex challenges in structural dynamics, enhancing the ability to mitigate vibrations and improve the stability of structures under various dynamic loads. The LQR controller aims to minimize the quadratic performance index (J) (Equation 14) defined as:

$J=\frac{1}{2}{\displaystyle \underset{0}{\overset{t_f}{\int }}}\left({\mathit{z}}^T\left(t\right)\mathit{Q}\mathit{z}\left(t\right)+{\mathit{f}}_u^T\left(t\right)\mathit{R}{\mathit{f}}_u\left(t\right)\right)dt(14)$

where Q and R (Q ≥ 0), (R > 0), are two weighting matrices that weight the system state $\mathit{z}$ and the active control force vector ${\mathit{f}}_u$. The effectiveness of LQR depends on the proper selection of the weighting matrices Q and R, which determine the trade-off between system performance and control effort. The matrix Q imposes a penalty on the system response, where larger values lead to greater response reduction but require higher control forces. Conversely, the matrix R penalizes the control effort, where larger values result in lower control forces, potentially limiting the reduction in structural response. The dimensions and shape of the R depend essentially on the number of actuators and their location on the structure (Moghaddasie and Jalaeefar, 2019). Matrix Q (Equation 15) is detailed below:

$\mathit{Q}=\left[\begin{array}{cccc}{q}_{1,1}& & & \\ & q_{2,2}& & \\ & & \ddots & \\ & & & q_{2n+2,2n+2}\end{array}\right](15)$

The matrix R in this study is a scalar due to the use of a single actuator acting only on the movable mass of the ATMD while being grounded at its second end.

The resulting actuator optimal control force (Equation 16) is evaluated by:

$f_u\left(t\right)=\mathit{G}\mathit{z}\left(t\right)(16)$

where G (Equation 18) is the gain matrix determined by solving the Riccati equation (Equation 17) as:

$\mathit{P}\mathit{A}+{\mathit{A}}^{\mathit{T}}\mathit{P}+\mathit{Q}-\mathit{P}\mathit{B}{\mathit{R}}^{-\mathbf{1}}{\mathit{B}}^{\mathit{T}}\mathit{P}=0(17)$

$\mathit{G}={\mathit{R}}^{-\mathbf{1}}{\mathit{B}}^{\mathit{T}}\mathit{P}(18)$

The block diagram of the LQR controller is illustrated in Figure 2.

Figure 2

Figure 2. LQR control diagram.

2.2 ANN controller training

ANN controllers play a pivotal role in structural control systems, offering a robust approach to optimize control strategies using active and semi-active dampers (Kim, 2020). Their application in managing seismic responses has led to significant advancements, particularly in reducing structural oscillations and enhancingare two weighting matricesthat weight the system state overall system performance. A key strength of ANN controllers is their ability to accurately approximate nonlinear functions, making them ideally suited for complex systems like multistory buildings. ANNs enable the training of controllers to adapt to varying conditions, thereby minimizing dynamic responses during seismic events.

In this study, the developed ANN model is designed to predict the active control force $f_u\left(t\right)$ replicating the behavior of an ideal LQR controller, where the main goal is to drive the ATMD to reduce the structural response at the base level of the isolated MDOF structure. The ANN achieves this prediction by learning the relationship between selected input variables and the corresponding control force through a training process. This involves adjusting internal weights, biases, and activation functions to minimize the prediction error.

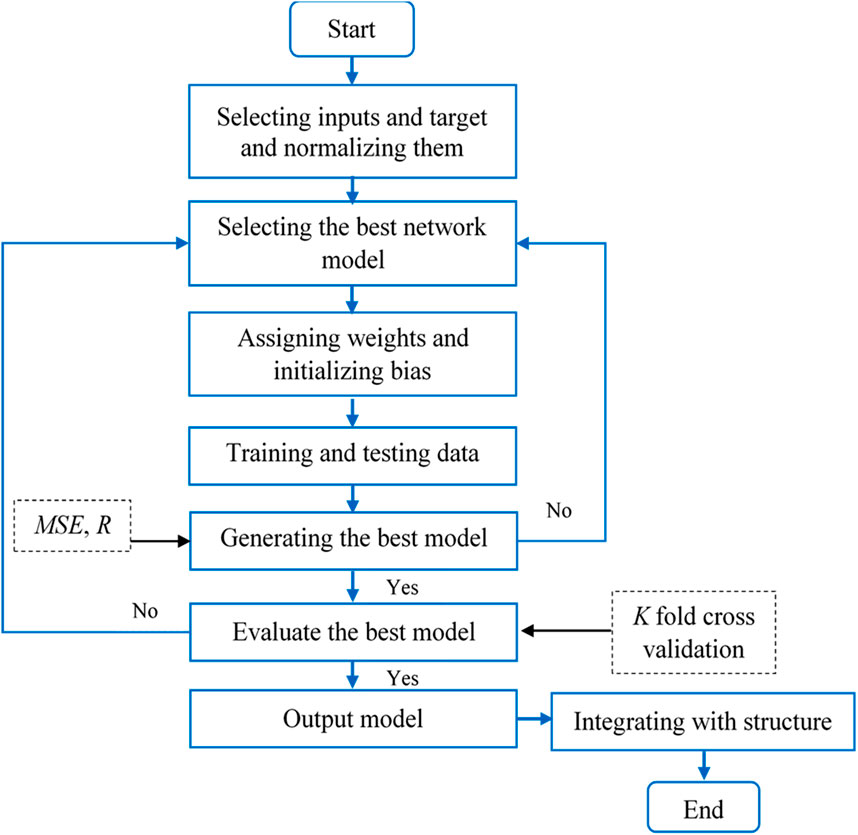
The process of training and deploying the ANN model for driving the ATMD can be summarized as follows:

1. Architecture Definition: select the optimal ANN architecture by determining the number of hidden layers and neurons per layer.

2. Data Preparation: identify relevant input and output variables and normalize all input and target output data to improve convergence during training.

3. Model Initialization: initialize the ANN model with randomly assigned weights and biases.

4. Forward Propagation - Hidden Layer: compute the activations of the hidden layer by applying an activation function to the weighted sum of inputs plus biases.

5. Forward Propagation - Output Layer: using the output of the hidden layer to compute the final output of the network, again applying weights, biases, and an appropriate activation function.

6. Training and optimization: adjust weights and biases through a learning algorithm, minimizing the loss function.

7. Model Evaluation: Assess model performance using suitable statistical metrics. If the model does not perform well, readjust the weights and biases and iterate; otherwise, finalize the weights and compute the final output.

8. Cross-Validation: perform K-fold cross-validation to verify the generalization capability of the model and check whether overfitting or underfitting occurs. If either is detected, the model is retrained.

9. Model Selection and Deployment: finalize the trained ANN model based on the best-performing configuration. Integrate the trained model into the control loop of the ATMD system for real-time prediction of the control force.

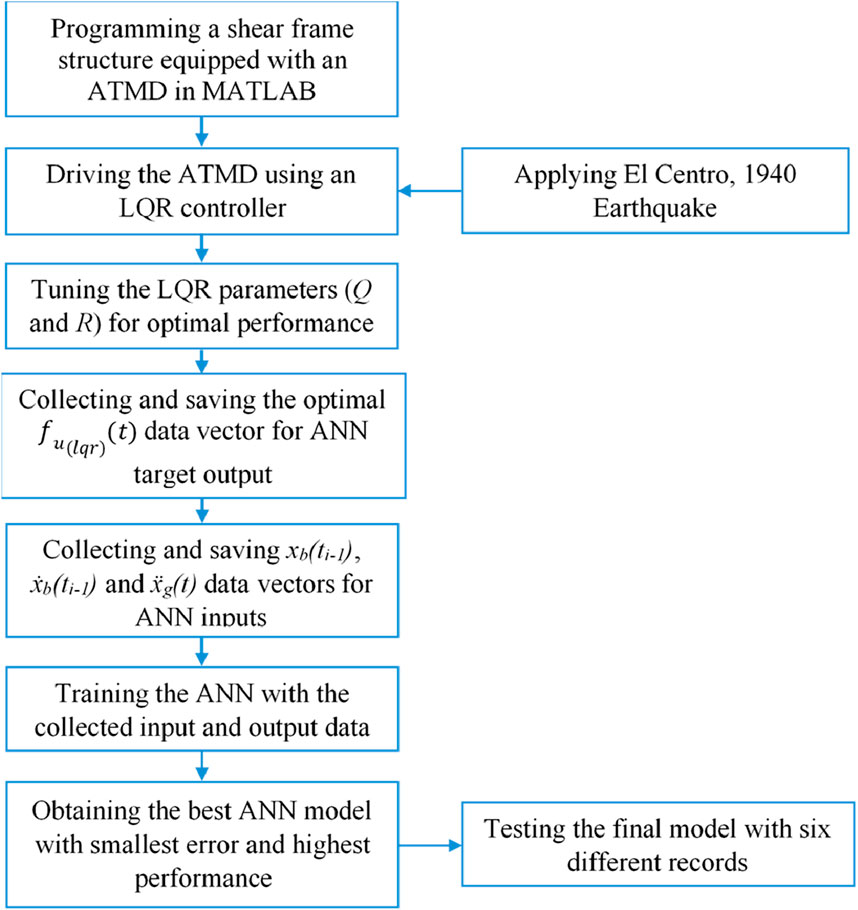
A flowchart detailing the major steps of the procedure can be seen in Figure 3.

Figure 3

Figure 3. Flow chart of the considered ANN model.

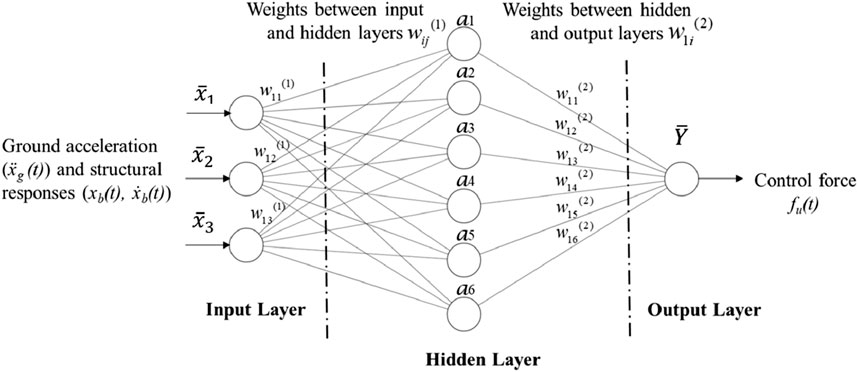
The current study employed a multilayer ANN architecture, visually represented in Figure 4, structured with three layers: an input layer, a hidden layer, and an output layer.

Figure 4

Figure 4. Optimal ANN model’s architecture.

The input data utilized in the input layer include the base displacement and its velocity, respectively $x_b\left(t\right)\text{and\hspace{0.17em}}{\dot{x}}_b\left(t\right),$ and the ground motion acceleration $\ddot{x_g}\left(t\right)$ taken from an earthquake record characterized by a wide frequency range. Optimized over iterations, the hidden layer has six nodes, and the output layer has one node $\left(\overline{Y}\right)$ representing the LQR control force $f_u\left(t\right)$ trained with target data of an optimal LQR control force. Therefore, the model is represented as Fisco and Adeli (2011a), Fisco and Adeli (2011b), Djerouni et al. (2020) and Elia et al. (2017). The layers in the neural network are interconnected by weights, which are adjusted during the training process to minimize the error between the ANN model’s output and the desired target LQR control force. The connections between the input and hidden layers are represented by weight terms $w_{ij}^{\left(1\right)}$, where i corresponds to the index of the hidden neuron and j to the input neuron. Similarly, the connections between the hidden and output layers are defined by the weight terms $w_{1i}^{\left(2\right)}$, where i denotes the hidden neuron index. The hidden layer consists of activation neurons $a_i$, which processes the weighted sum of the inputs through a nonlinear activation function $f\left({\overline{g}}_i\right)$, enhancing the network’s ability to capture complex relationships in the data. This architecture allows the ANN to learn and replicate the control strategy of the LQR controller effectively.

For training and optimization, the network configuration implemented the backpropagation algorithm, a widely used technique for training neural networks, in conjunction with the TANSIG (hyperbolic tangent sigmoid) activation function (Sibi et al., 2013). These choices were pivotal in the model’s ability to effectively learn and adapt to the complexities of the dataset under investigation. The equation of the activation (Equation 19) function is written as follows:

$f\left({\overline{g}}_i\right)=\frac{2}{\left(1+e^{-2{\overline{g}}_i}\right)}-1(19)$

The output of the first layer is obtained by applying the activation function (Equation 20):

$a_i=f\left({\overline{g}}_i\right)=f\left({\displaystyle \sum _{j=1}^3}{w}_{ij}^{\left(1\right)}{\overline{x}}_j+b_i^{\left(1\right)}\right)(20)$

Finally, the final output is determined as (Equation 21):

$\overline{Y}={\displaystyle \sum _{i=1}^6}{w}_{1i}^{\left(2\right)}{a}_i+b^{\left(2\right)}(21)$

In this scenario, $\overline{x_j}$ represents the input features, while $w^{\left(1\right)}$ and $w^{\left(2\right)}$ correspond to the weights associated with the first and hidden layers, respectively. Similarly, $b^{\left(1\right)}$ and $b^{\left(2\right)}$ denote the biases for the first and second layers.

To guarantee the robustness of the model during the training phase, the dataset was divided into training and validation subsets, with 80% dedicated to training the neural network. This allowed for effective pattern recognition. The remaining 20% was used for validation, providing an evaluation of the model’s accuracy on new data. The Levenberg-Marquardt backpropagation technique (trainlm) (Reynaldi et al., 2012) from MATLAB’s Neural Network Toolbox was selected for its proficiency in optimizing parameters and reducing training errors.

According to the model training process, the mean squared error (MSE) (Equation 22) and the correlation coefficient $\left(R\right)$ (Equation 23) are utilized as performance metrics and evaluated as:

$MSE=\frac{1}{N}{\displaystyle \sum _{i=1}^N}{\left(Y_{tar,i}-Y_{out,i}\right)}^2\left(0<MSE<\infty \right)(22)$

$R=\frac{{\displaystyle {\sum }_{i=1}^N}\left(\left(Y_{tar,i}-\overline{Y_{tar}}\right)\left(Y_{out,i}-\overline{Y_{out}}\right)\right)}{\sqrt{{\displaystyle {\sum }_{i=1}^N}\left({\left(Y_{tar,i}-\overline{Y_{tar}}\right)}^2{\left(Y_{out,i}-\overline{Y_{out}}\right)}^2\right)}}\left(-1<R<1\right)(23)$

where $Y_{tar,i},{Y_{out}}_{,i}$, $\overline{Y_{tar}}$, $\overline{Y_{out}}$ correspond to the target, output, mean target, and mean output, respectively, whereas N represents the dataset size to measure the performance of the model and assess the error for each split. According to Smith (1986), the evaluation criteria for $\left(R\right)$ include the following limit:

• $\left|R\right|<0.2$ Weak correlation.

• $0.2\le \left|R\right|<0.8$ Correlation exists.

• $\left|R\right|\ge 0.8$ Strong Correlation.

Following the selection of the optimal model with the optimal node’s number according to statistical performance, the K-fold cross-validation approach (Kohavi, 1995) was employed to assess the model’s capability prediction. K-fold cross-validation is a method used to evaluate a machine learning model’s performance by dividing the dataset into k equally sized subsets. The model is trained k times, each time using $\left(k-1\right)$ folds for training and the remaining fold for validation. This ensures that each fold serves as the validation set exactly once.

In this study, 5-fold cross-validation was adopted, as it offers a good compromise between computational efficiency, bias, and variance, making it a standard choice for model evaluation.

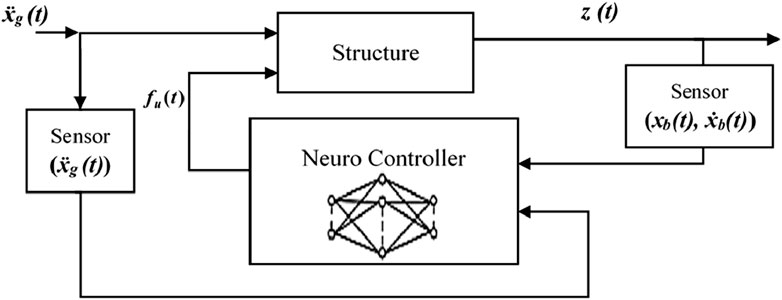
Figure 5 illustrates the active control feedback, in which the ANN controller actuates the ATMD to mitigate structural vibrations. The system comprises three primary sensors: one measuring the base layer displacement, another measuring the base layer velocity, and a third measuring the ground acceleration. The sensor data are fed into the ANN controller, which processes the inputs and determines the appropriate control force. This control force is applied to the structure to counteract the vibrations. The structure’s response is continuously monitored and fed back into the neuro controller, creating a closed-loop system. The ANN controller dynamically adjusts the damping force based on real-time feedback, ensuring optimal vibration suppression and enhancing structural stability and performance under various dynamic conditions. The ANN controller dynamically adjusts the damping force in real-time based on feedback, ensuring effective vibration suppression and enhancing structural stability and performance under various dynamic loading conditions.

Figure 5

Figure 5. ANN control diagram using ATMD.

3 Numerical study

3.1 Benchmark building model

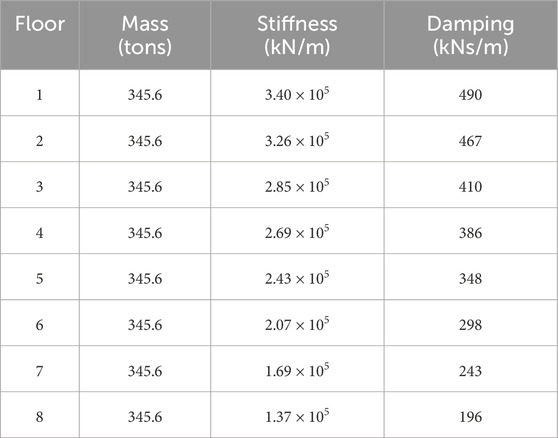
An 8-story benchmark isolated building, proposed by Yang et al. (1994), is utilized to implement the hybrid control system. The structure is equipped with a lead core rubber-bearing isolation system and an ATMD located on the base floor. The structural properties of each floor are summarized in Table 1.

Table 1

Table 1. Dynamic parameters of the structure.

3.2 ATMD tuning

An ATMD was coupled to the BIS to enhance its performance during seismic events and reduce structural vibrations, specifically the base isolation layer displacement. The tuning parameters for the passive part of the ATMD are determined using equations provided by Sadek et al. (1997) in terms of the non-dimensional parameters (Equation 24):

$\mathrm{\mu }=\frac{m_d}{M_T},\gamma =\frac{1}{1+\mu }\left[1-{\xi }_s\sqrt{\frac{\mu }{1+\mu }}\right],{\xi }_d={\xi }_s\frac{1}{1+\mu }+\sqrt{\frac{\mu }{1+\mu }}(24)$

$m_d=\mu M_T(25)$

$c_d=2{\xi }_d{m}_d{\omega }_d(26)$

$k_d={\omega }_d^2{m}_d(27)$

where $\mu$ is the mass ratio between the ATMD mass, $m_s$, and the structure’s total mass, $M_T$ , $\gamma =\frac{{\omega }_d}{{\omega }_s}$ is the frequency ratio between the TMD and the structure’s first frequency and ${\xi }_d$ is the TMD damping ratio calculated with respect to the structure damping ratio ${\xi }_s=5\%$. Being the total mass of the adopted base-isolated structure equal to $M_T=3214.8\text{\hspace{0.17em}tons}$, while its first natural frequency is ${\omega }_s=2.2\text{\hspace{0.17em}rad}/\mathrm{s},$ having assumed a mass ratio $\mu =0.05$, the TMD proprieties (Equations 25–27) are: $m_d=160.74\text{\hspace{0.17em}tons}$, $k_d=694.59\text{\hspace{0.17em}kN}/\mathrm{m}$, and $c_d=177.62\text{\hspace{0.17em}kNs}/\mathrm{m}$. It is worth noticing that the assumed mass ratio is in accordance with typical values adopted in literature for conventional TMD systems (Djedoui et al., 2016).

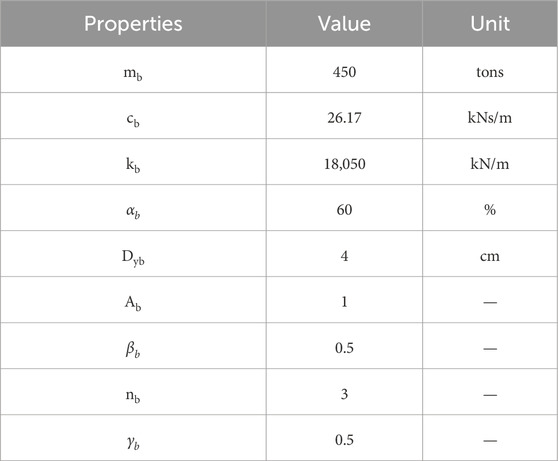
3.3 Base isolated system properties

The properties of the BIS are taken from Yang et al. (1994) and are detailed in Table 2.

Table 2

Table 2. BIS parameters.

3.4 LQR tuning

The inputs to the Artificial Neural Network (ANN) are derived from the structural response generated by a Linear Quadratic Regulator (LQR) controller, which requires the definition of the weighting matrices Q and R. These matrices play a crucial role in shaping the control performance by penalizing deviations in system states and excessive control effort, respectively. n this study, the system includes a single actuator associated with the ATMD. Consequently, the R matrix is reduced to a scalar. A value of R = 10⁻³ was selected to ensure a suitable trade-off between minimizing the control effort and achieving effective vibration mitigation.

The weighting matrix Q is used to penalize deviations in selected state variables. Since the ATMD is directly connected to the BIS, the base displacement $x_b\left(t\right)$ and base velocity ${\dot{x}}_b\left(t\right)$ are key states to be regulated. To emphasize their importance in the control design, the diagonal elements corresponding to these variables, specifically $q_{1,1}$ and $q_{11,11}$, were set to 10³. This choice reflects the objective of reducing base motion without completely constraining it, consistent with the dynamic behavior expected in seismically isolated systems.

The values of Q and R were fine-tuned through an iterative trial-and-error process. Multiple numerical simulations were performed to assess the effectiveness of different combinations of weights. The configuration yielding the best compromise between vibration reduction and control effort was selected. The optimal control forces computed through the tuned LQR controller were then used as reference outputs for training the ANN model, enabling it to emulate the LQR behavior in real-time without relying on an explicit dynamic model during operation.

3.5 ANN tuning

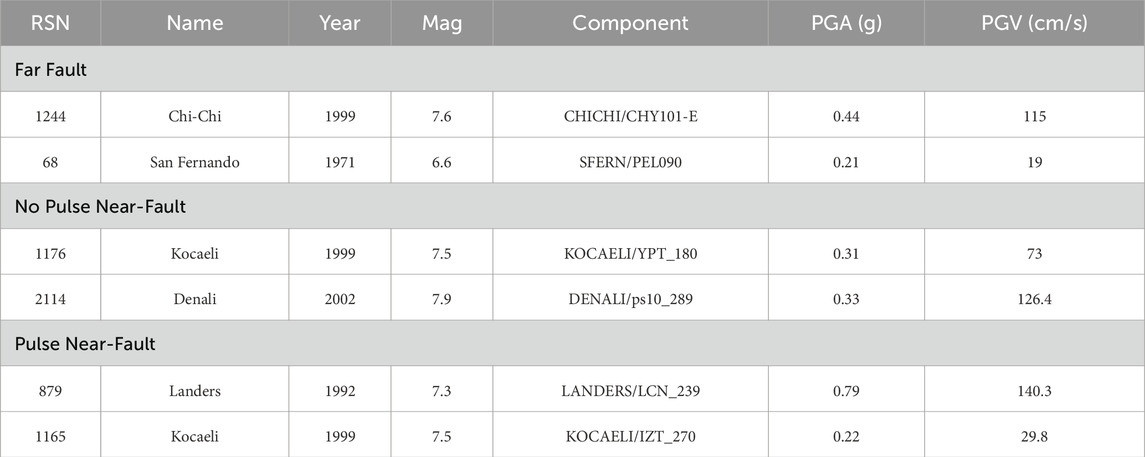
The ANN-based controller is designed to regulate the ATMD system in real-time, with the objective of improving the seismic performance of an eight-story nonlinear base-isolated structure. The network is trained using data derived exclusively from a single natural earthquake record. Specifically, the ground motion from the 1940 El Centro earthquake was recorded at the Imperial Valley station, with a peak ground acceleration (PGA) of 0.32 g measured on the North/South component. The El Centro record was selected due to its broadband frequency content, which makes it a representative and widely adopted benchmark for training purposes. Once the optimal ANN model was identified through training, its generalization capability and robustness were evaluated by subjecting the structure to six additional earthquake records. These included both far-field and near-field events, with and without velocity pulses, to comprehensively assess the model’s performance under a diverse range of seismic scenarios.

The process is illustrated in Figure 6, which outlines the step-by-step development and validation of the ANN-based controller. The procedure begins with programming a shear frame structure in MATLAB and applying an LQR controller, where the weighting matrices (Q and R) are optimized for improved performance. The ANN is then trained using the collected data, and the best-performing model is selected based on accuracy and error minimization. Finally, the trained ANN model is tested with six different earthquake records to evaluate its generalization and effectiveness. Training with historical earthquake data allows the ANN to learn, adjust, and reduce the differences between the LQR control force and the desired one, thereby enabling the ANN to approximate the optimal control strategy for which the LQR is known.

Figure 6

Figure 6. Flowchart of the ANN training process adopted in this study.

To assess the effectiveness of the ANN and ensure its emulation to the LQR, its structural response will be compared with that of the LQR controller itself, as well as with scenarios where no active control is applied.

3.6 Earthquakes data set

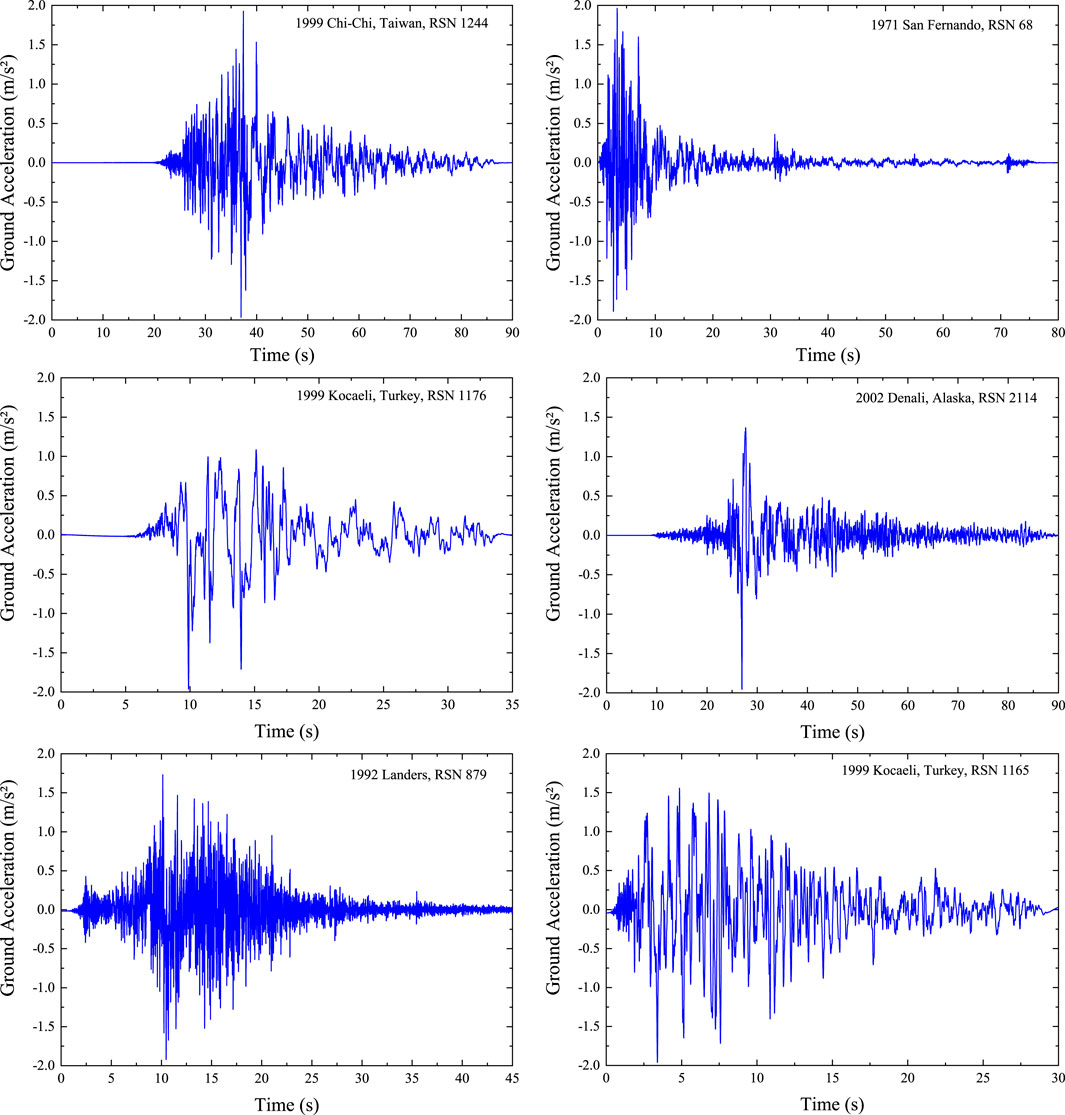
The effectiveness of the ANN model within the hybrid system is evaluated by assessing it with six different real seismic recordings, each featuring diverse frequency components and peak accelerations. The seismic data for these six earthquakes, as sourced from the Federal Emergency Management Agency (FEMA) P659 (Council, 2009), are presented in Table 3. To keep the structural behavior within a reasonable range, all the used records were scaled to a PGA of 0.2 g, as seen in Figure 7.

Table 3

Table 3. FEMA unscaled ground motion records.

Figure 7

Figure 7. Scaled earthquake records used in the simulation.

The utilized ground acceleration records are depicted in Figure 7.

4 Results and discussion

4.1 ANN model training results

In this section, the evaluation of the ANN model’s performance is made, employing the two key statistical metrics defined in Equations 22, 23 the MSE and the correlation coefficient R, are evaluated. Furthermore, the model’s predictive capability is assessed through the implementation of K-fold cross-validation.

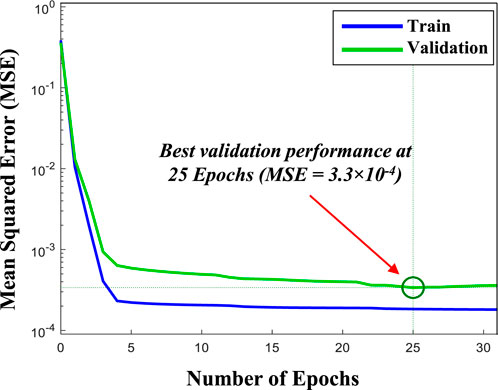
Figure 8 shows the MSE over 31 epochs, which highlights the model’s accuracy and error dynamics. Initially, the MSE decreases sharply across training and validation datasets, indicating a reduction in prediction error as the model learns from the data. The close alignment of MSE values across datasets underscores the model’s robustness. The best validation performance is observed at epoch 25, where the MSE reaches its minimum value of ${3.3·10}^{-4}$. This epoch represents the point at which the model generalizes best to unseen data, striking an optimal balance between underfitting and overfitting, ensuring maximum predictive performance and minimal error between the output and the target. Beyond this point, MSE slightly increases, which may lead to overfitting.

Figure 8

Figure 8. Train and validation performance of the ANN model.

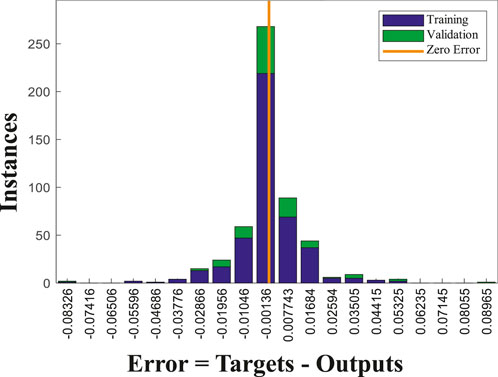
Figure 9 shows the error histogram from the simulation of the optimal ANN model. The green bars indicate validation data, and the blue bars represent training data. Errors between the output and target values can be observed to lie within the range of −0.04 to 0.04.

Figure 9

Figure 9. Error histogram of the most appropriate ANN model (3 6 1) with 20 Bins.

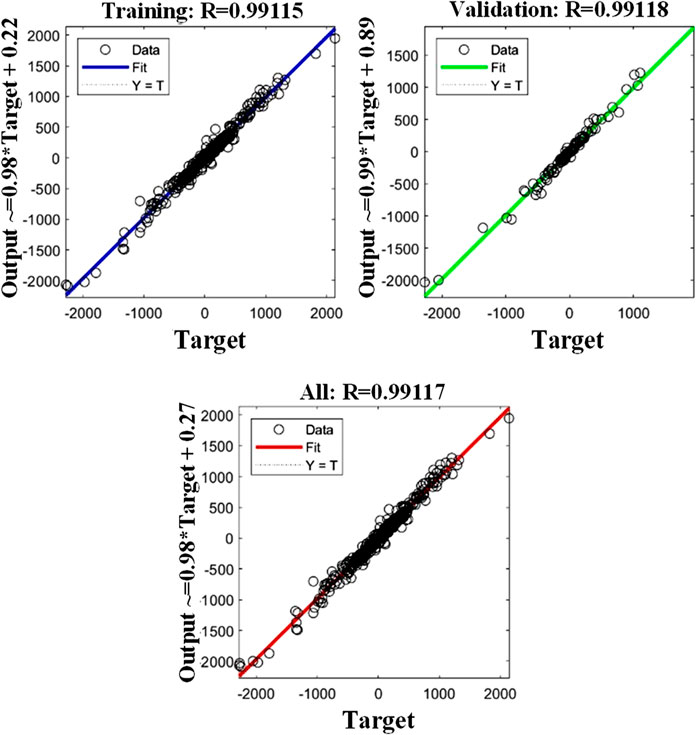
As defined in Equation 23, the correlation coefficient R measures the strength and direction of the linear relationship between predicted and actual values, with higher values closer to 1 indicating stronger correlation and better predictive performance. Figure 10 displays scatter plots comparing the output and the target values of the control force in the optimal ANN model in the training phase, validation phase, and both phases. The results show strong correlation coefficients, with R values of 0.99115 for training and 0.99118 for validation, which demonstrates the effective learning capability of the model.

Figure 10

Figure 10. Scatter plots between predicted and measured $f_u$ in the optimal ANN model (3 6 1).

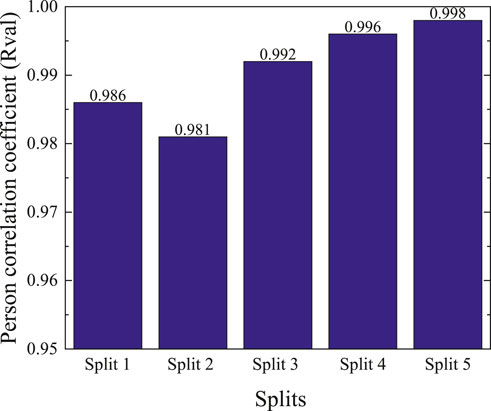
The performance measures of the best ANN model are shown in Figure 11, revealing an R range of 0.98–0.99, where each column in the figure corresponds to a different fold in the K-fold cross-validation process, representing the model’s performance across multiple training-validation splits. This underscores the success of K-fold cross-validation in showcasing the model’s robustness. The model consistently performs well across all five folds, effectively mitigating overfitting and underfitting risks, showcasing its remarkable ability to learn from training data and generate new data.

Figure 11

Figure 11. Performance measures of the ANN model using the K-fold cross-validation, with K = 5.

4.2 Performance assessment of ANN controller

After identifying the most effective neural network training model, it is utilized to control the ATMD through a feedback loop. This will enable computing the required control force to mitigate the effect of seismic activity on several ground motions to evaluate and validate the performance of the ANN model in adapting to new seismic conditions. For this purpose, the six ground motion records from the FEMA database not utilized during the training phase are selected (Table 3; Figure 7).

Various control strategies are considered to assess the performance of the ANN-driven ATMD. The control strategies adopted are:

• The base-isolated structure is equipped with a classical TMD, where the actuator force is set to null; this strategy is denoted BIS + TMD.

• The base-isolated structure is equipped with an ATMD driven by a LQR controller, denoted BIS + ATMD (LQR).

• The base-isolated structure is equipped with an ATMD driven by an ANN controller, denoted BIS + ATMD (ANN).

The first one has been compared with a hybrid control system employing only passive strategies. The performances of each control strategy are compared with those of BIS considered alone, and the results are reported in terms of reduction rate.

The dynamical parameters of interest investigated are the peak base floor displacement, the root mean square (RMS) of the base displacement, the peak control device stroke, the base floor acceleration, velocity and displacement time histories, the maximum drift and inter-story drift of all the floors and the hysteresis loops of the nonlinear isolator.

Table 4 presents the peak base displacement and the base displacement RMS for each control strategy under each earthquake, along with their respective reduction rate (RR) percentages evaluated across the six different earthquake scenarios. The passive TMD system provides moderate displacement reductions, ranging from 17% to 36%, showing its ability to mitigate vibrations to a certain extent. The active control strategy using LQR shows a more substantial improvement, reducing displacements by 63%–81%. Notably, the ANN-based ATMD demonstrates the highest effectiveness, consistently achieving displacement reductions between 81% and 87%, indicating its effectiveness and successful learning from the LQR controller. Further, the passive TMD system achieves moderate reductions in RMS values, ranging from 27% to 52%, indicating its limited yet consistent damping capacity. The ANN demonstrates reduction rates ranging from 91% to 94%, surpassing LQR’s rates of 86%–92%. Similar to peak base displacement results, the ANN highlights its ability to learn from and surpass LQR’s performance.

Table 4

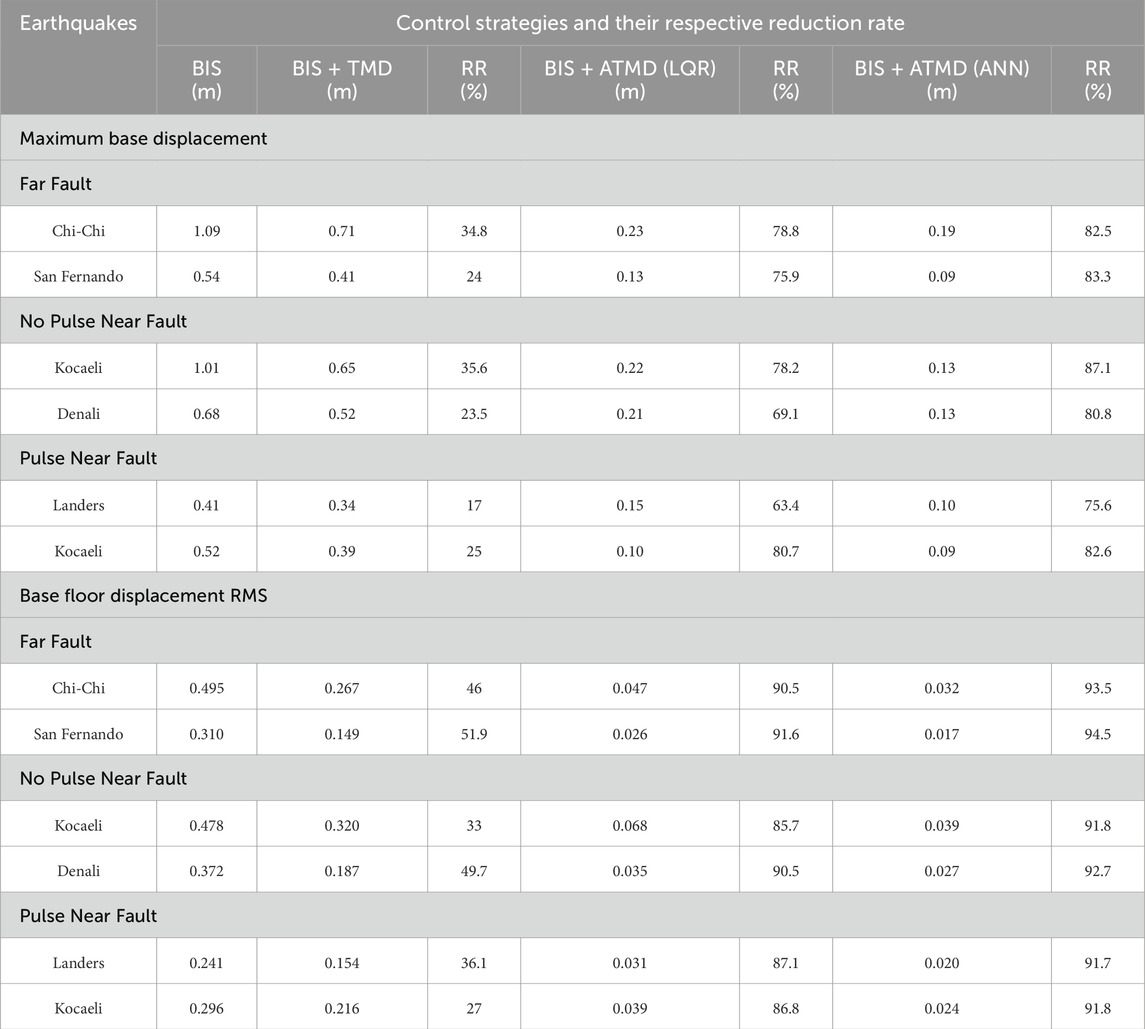
Table 4. Maximum base displacements and base floor displacement RMS under different control strategies and their reduction rate (RR).

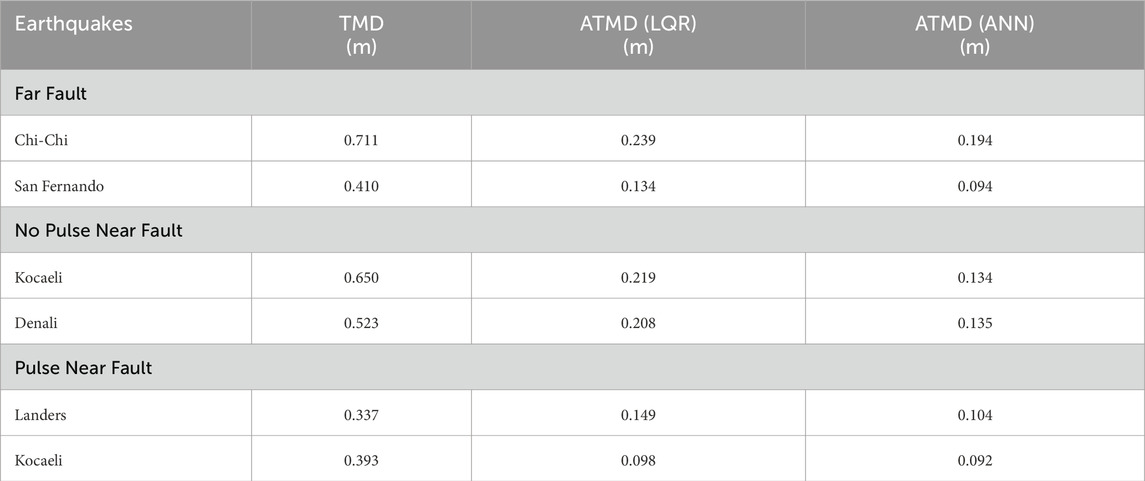
In addition to displacement and RMS evaluations, it is crucial to assess the stroke response of the damper systems to ensure their practical applicability. The stroke, defined as the peak displacement of the damper mass, determines the device’s required motion range. Excessive stroke demands may render a control system impractical despite its effectiveness in reducing vibrations. Therefore, Table 5 presents a comparative analysis of the peak stroke displacements for the TMD, the LQR-controlled ATMD, and the ANN-controlled ATMD under the various earthquake records, offering insights into their mechanical feasibility alongside their control performance.

Table 5

Table 5. Peak damper stroke for TMD, ATMD-LQR, and ATMD-ANN.

As shown in Table 5, the TMD system exhibits the highest stroke demands across all earthquake records, with peak values reaching up to 0.711 m. In contrast, the LQR-controlled ATMD significantly reduces the required stroke, and the ANN-based ATMD achieves even lower stroke values in most cases. This demonstrates not only the superior control capability of the ATMD systems but also their mechanical efficiency. Notably, the ANN consistently maintains a lower stroke than LQR, confirming its intelligent control ability and practical feasibility.

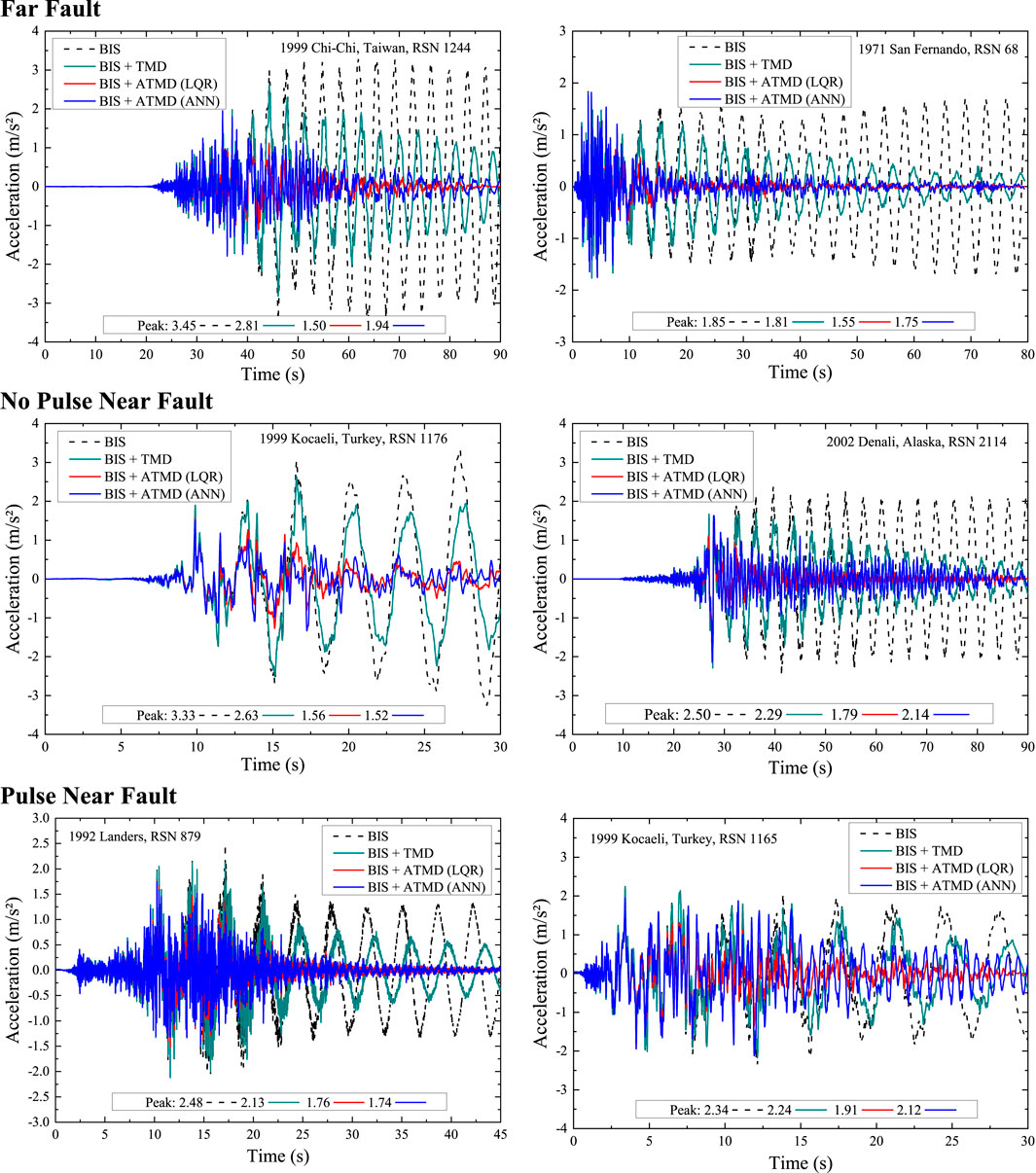
Figure 12 illustrates for the six ground motions the base acceleration response of the nonlinear base-isolated structure comparing four scenarios: BIS, BIS and TMD, BIS and ATMD driven by the LQR controller, BIS and ATMD trained with the ANN controller. Applying TMD to the BIS is able to reduce the response better for far fault earthquakes than near fault ones. The graph reveals that the response can be further decreased by adopting the ATMD: a close performance between the ANN system and the LQR system in mitigating structural vibration for all the records is observed.

Figure 12

Figure 12. Time history of base floor acceleration.

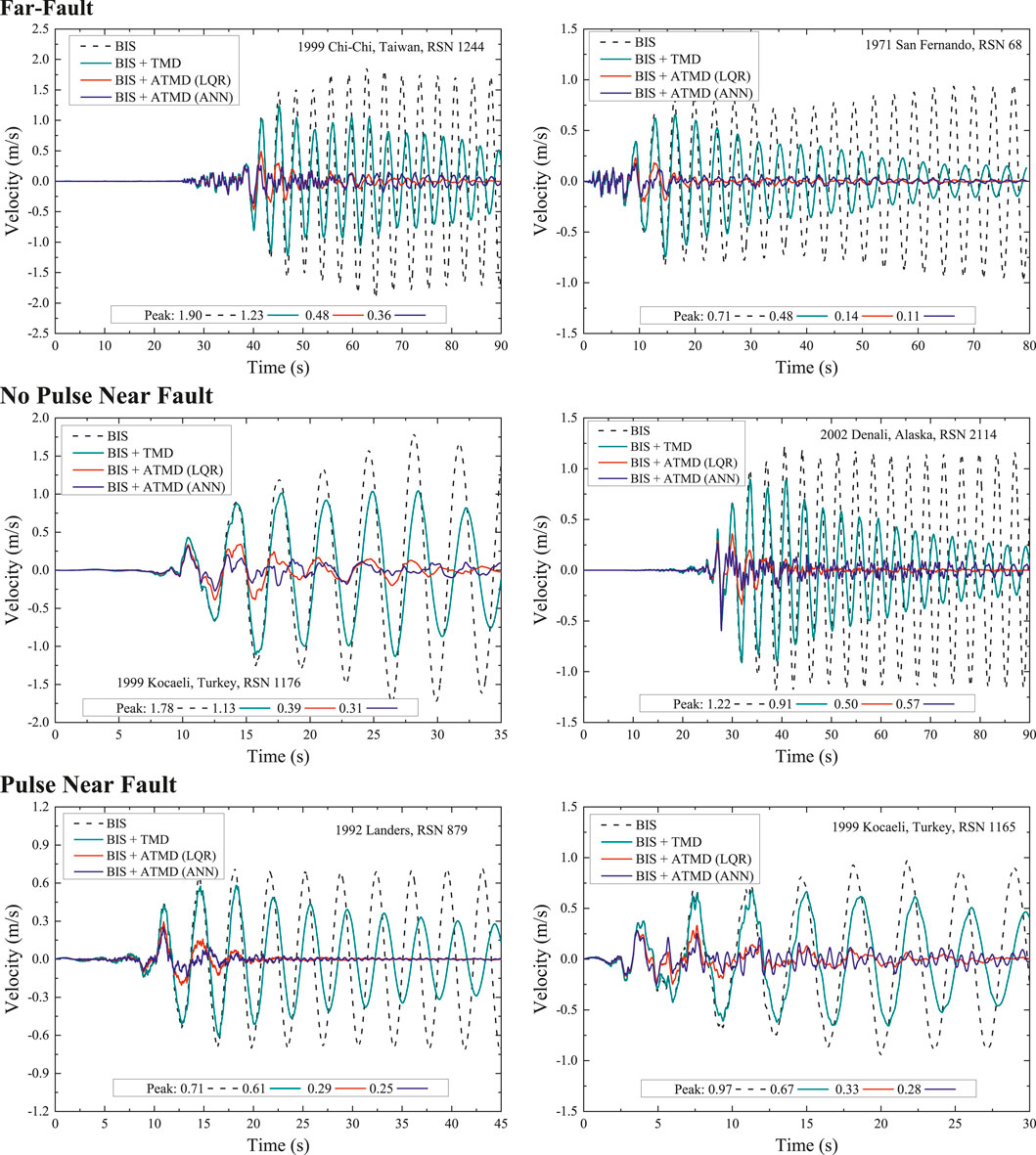
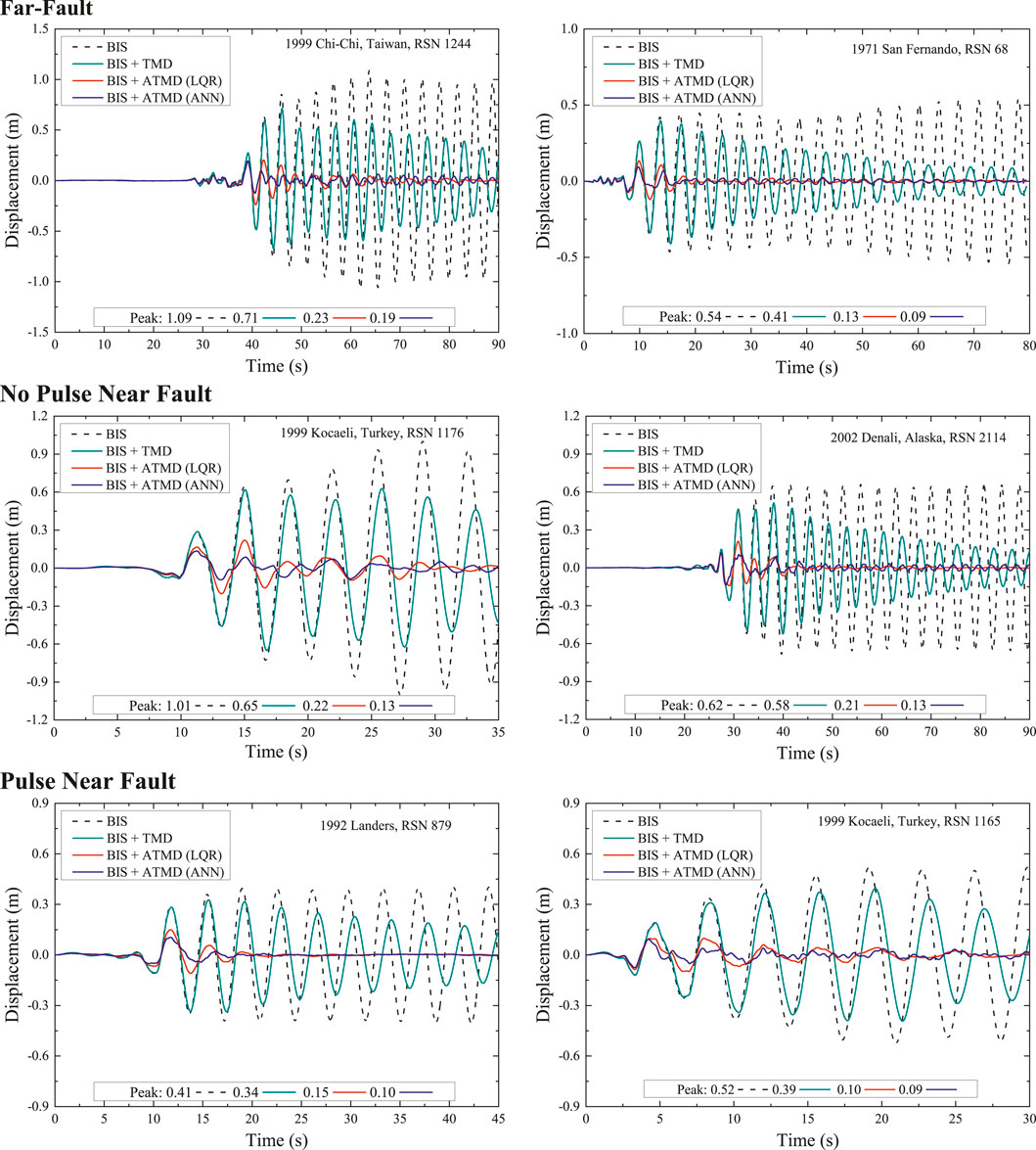
Figures 13, 14 illustrate the time history of base velocity and base displacement, respectively; it is evident that the ANN control system consistently achieves lower peak responses than the LQR control system; the adjustments of the control action in real time make this strategy more effective than applying only a TMD to limit base displacement and velocity. The response reductions occur across a wide range of earthquakes with different intensities and frequencies, which indicates that the ANN effectively adapts to the nonlinear behavior of the structure, providing better damping and stability.

Figure 13

Figure 13. Time history of base floor velocity.

Figure 14

Figure 14. Time history of base floor displacement.

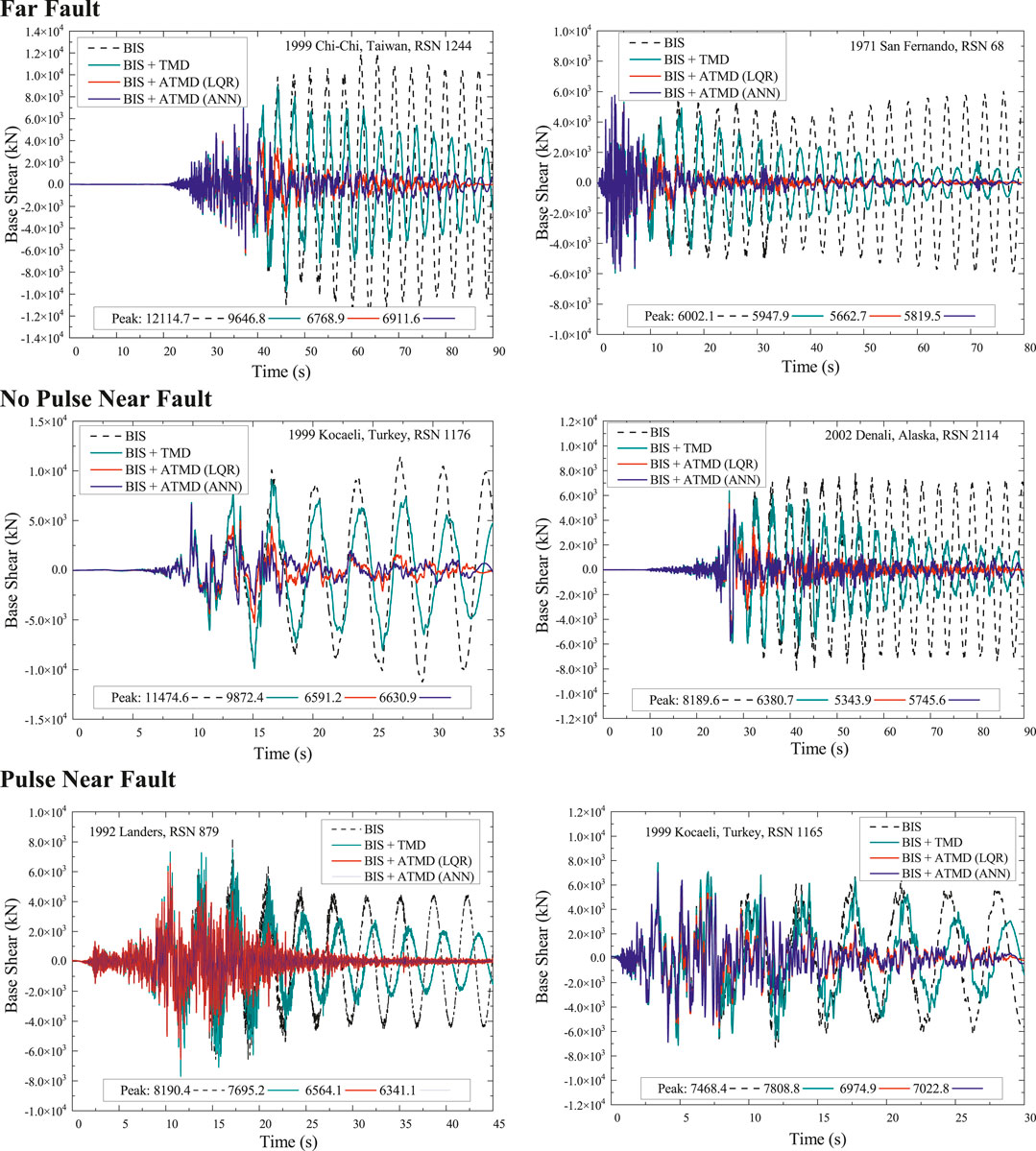
The base shear force is shown in Figure 15 for the cases examined. The reduction observed with the hybrid control with ATMD helps to decrease seismic forces, thereby minimizing stress on structural components and reducing the risk of failure. Figure 15 illustrates how well active control methods are capable of minimizing the base shear across all seismic events and how this performance increases, especially for near fault earthquakes, compared to classical passive TMD. Notably, the ANN control exhibited nearly identical behavior to that of the LQR control, with only a slight increase observed in the maximum peak levels.

Figure 15

Figure 15. Time history of base shear response.

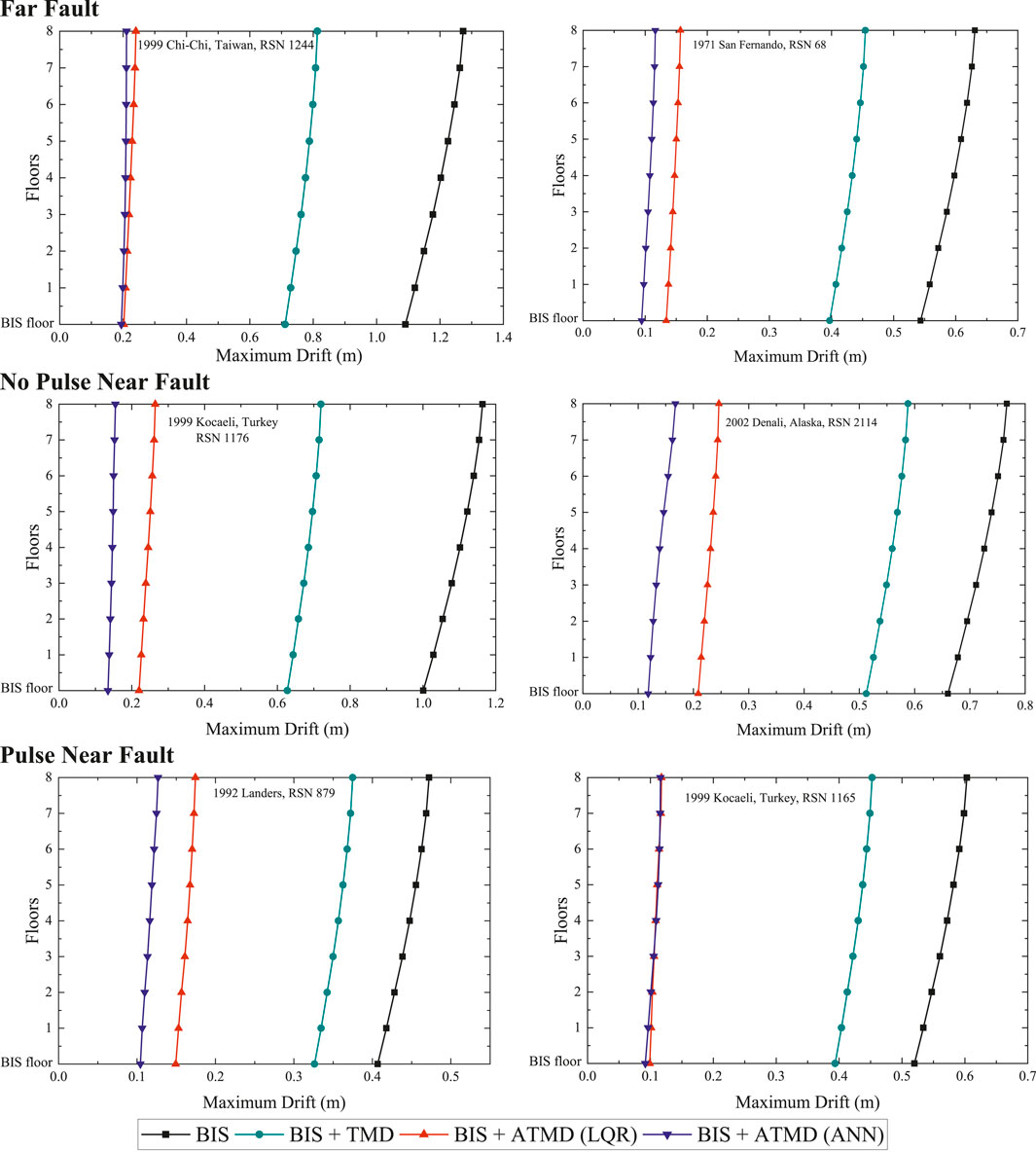
Figure 16 presents the maximum drift at all floors. The isolated structure exhibits significant drift for some earthquakes (Chi Chi, and Kocaeli earthquakes), indicating high susceptibility to seismic forces and potential structural damage. Applying a TMD to the base isolation layer can reduce the response to some extent; however, the LQR system shows markedly improved performance. ANN system performs even better, highlighting its superior efficiency in managing seismic responses. This reduced drift implies less structural damage and better protection.

Figure 16

Figure 16. Maximum floor drift.

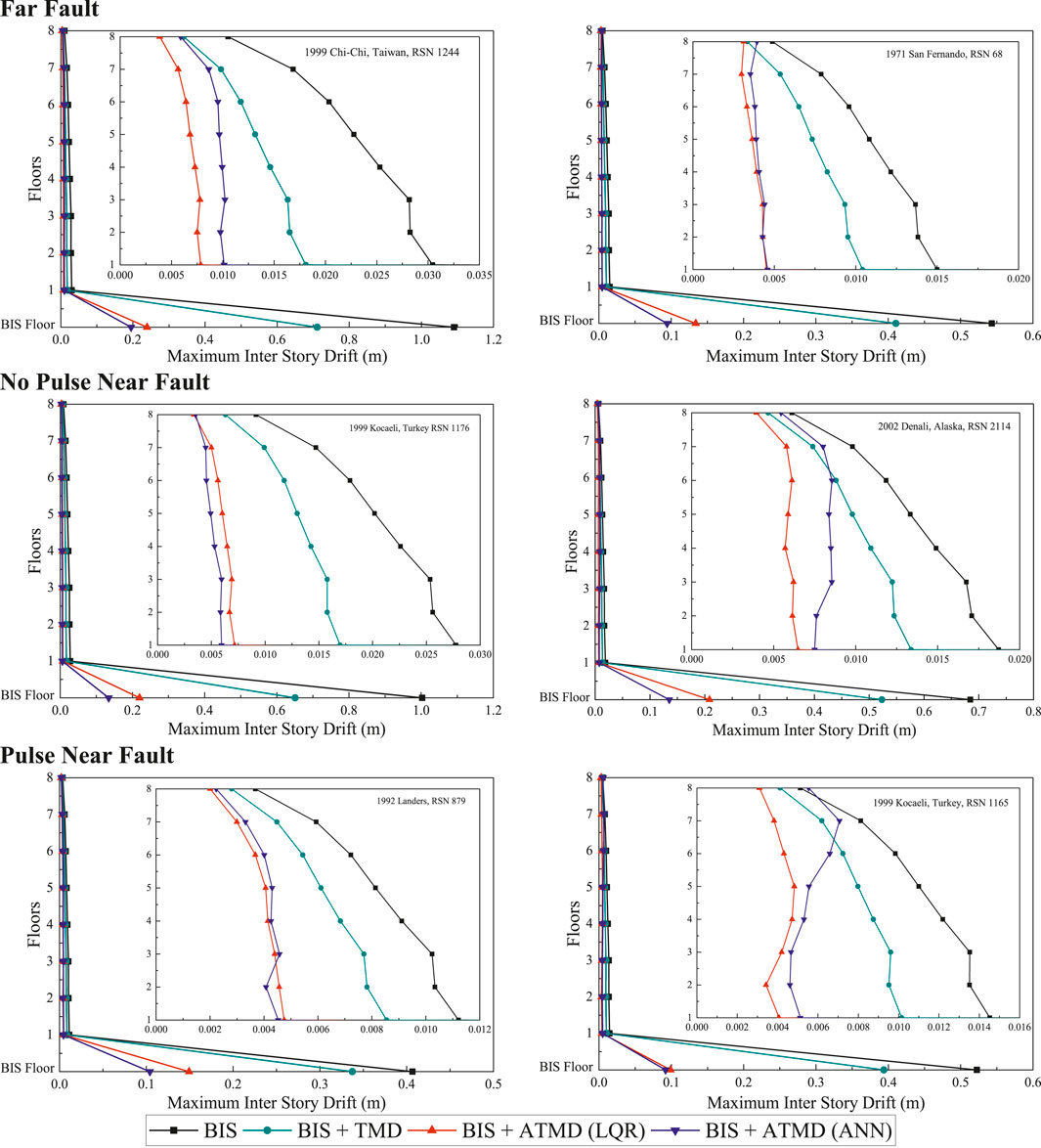
The inter-story drift, depicted in Figure 17, shows that, again, both control methods based on ATMD effectively reduce the responses, especially at the lower floors, where the inter-story drift values are significantly minimized. While the LQR system shows superior performance, the ANN system also achieves notable reductions, closely miming the behavior of the LQR. This underscores the potential of ANN as a viable control strategy also compared to passive control with TMD.

Figure 17

Figure 17. Inter-story drift.

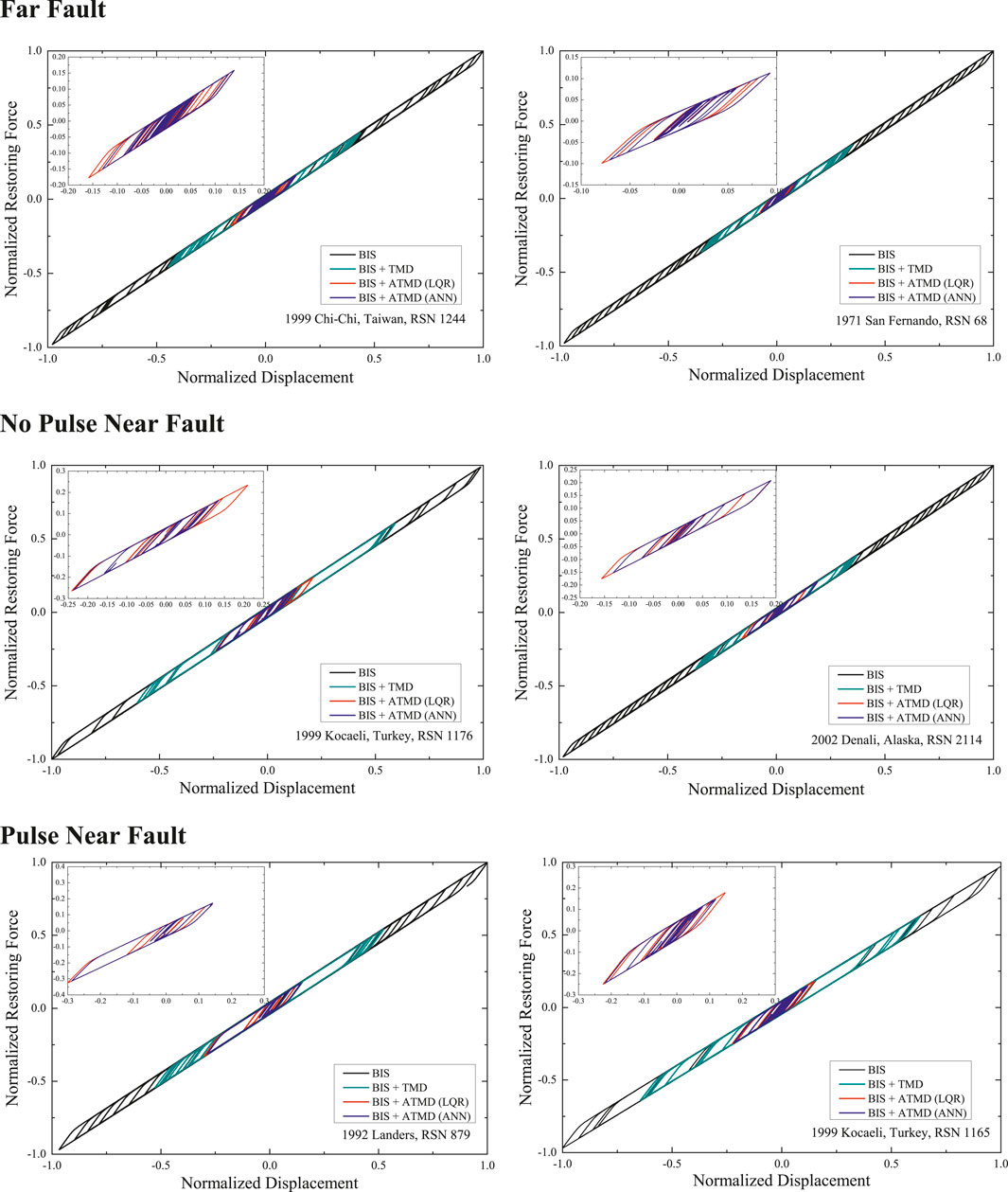
Figure 18 illustrates the normalized restoring force of the BIS versus the normalized base displacement for the control strategies under six different testing earthquakes. Normalization is performed by dividing all the values by the maximum absolute value of the reference BIS responses, namely the restoring force and the base displacement. The addition of an ATMD to the BIS significantly reduces the energy dissipated by the isolator compared to the case where a classical TMD is added. This reduction is evident from the smaller peaks in the restoring force for both LQR and ANN controllers compared to the isolated structure. The decrease in the restoring force indicates lower hysteretic energy dissipation during seismic events, highlighting the ATMD’s effectiveness in minimizing the relative motion between the building and its foundation.

Figure 18

Figure 18. BIS normalized restoring force versus normalized displacement.

Moreover, the ANN controller exhibits relatively smaller restoring force values, suggesting that it provides a more adaptive and efficient control strategy compared to the LQR controller. The ANN’s ability to learn from data and predict optimal control actions allows it to handle the nonlinear behavior of the base isolation system more effectively.

4.3 Time delay effect on the response reduction

In order to emulate real-world conditions more accurately in the model, time delays were incorporated into the control loop of the model. Specifically, the structural responses sent to both LQR and ANN-based controllers were delayed by a one-time step. Additionally, the control forces generated by each controller were delayed by a one-time step before being applied via the actuator. This configuration resulted in an overall delay of two time steps within the control loop, effectively emulating the inherent delays present in practical applications.

The introduction of these delays revealed marked differences between the LQR and ANN approaches. When operating with a delayed full-state vector, the LQR encountered significant challenges in producing an effective control force. This difficulty highlighted concerns about the LQR’s robustness and reliability in environments characterized by time delays, as the delayed response compromised its ability to maintain optimal control performance. The inherent limitations of the LQR in handling time delays emphasize the need for alternative control strategies that can better cope with such conditions.

Conversely, the ANN demonstrated an excellent adaptability to time delays, consistently generating effective control forces and swiftly responding to mitigate structural responses. The ANN’s performance remained robust despite the delays, showcasing its ability to adapt and learn from the delayed input data. This adaptability is attributed to the ANN’s inherent capability to model complex, nonlinear relationships and its flexibility in handling dynamic changes within the system. The ANN’s superior performance in the presence of time delays underscores its potential as a more reliable and effective control strategy in scenarios where delays are inevitable. These findings are confirmed in Table 6, which presents the root mean square (RMS) displacement results.

Table 6

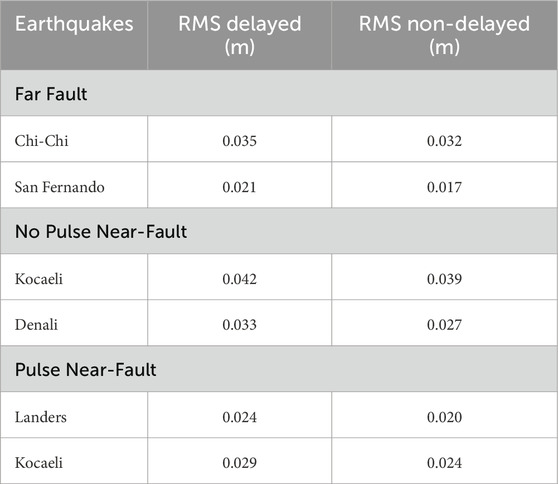
Table 6. Base floor displacement RMS values for the system controlled with ANN with and without delay.

These findings underscore the potential advantages of employing ANN control strategies in scenarios where time delays are a critical factor. The adaptability and resilience of the ANN in the face of delays suggest that it can maintain high levels of control performance due to its natural ability to detect and react to nonlinearities, offering a significant improvement over traditional LQR methods. Therefore, incorporating ANN-based controllers in systems where time delays are prevalent could lead to more robust and efficient control solutions, ultimately enhancing the overall stability and performance of nonlinear systems.

4.4 Noise effect on the response reduction

Accurate measurement of dynamic response parameters such as base peak displacement, acceleration, velocity, inter-story drift, maximum drift, and base shear is critical for effective structural control. However, in real-world applications, sensor data is often contaminated with noise, which can compromise the accuracy and reliability of the measurements.

To address this challenge, this study investigates the impact of noise contamination on the performance of both the ANN controller and the LQR controller. A white noise disturbance (Chen and Xu, 2008; Abdeddaim et al., 2017) is randomly generated and then integrated to obtain velocity and displacement signals. The obtained signals are summed with the displacement and velocity data during both the LQR simulation and the testing phase of the ANN to simulate noise contamination in sensors. The white noise peak acceleration is set to be 30 times less than the PGA of the earthquake.

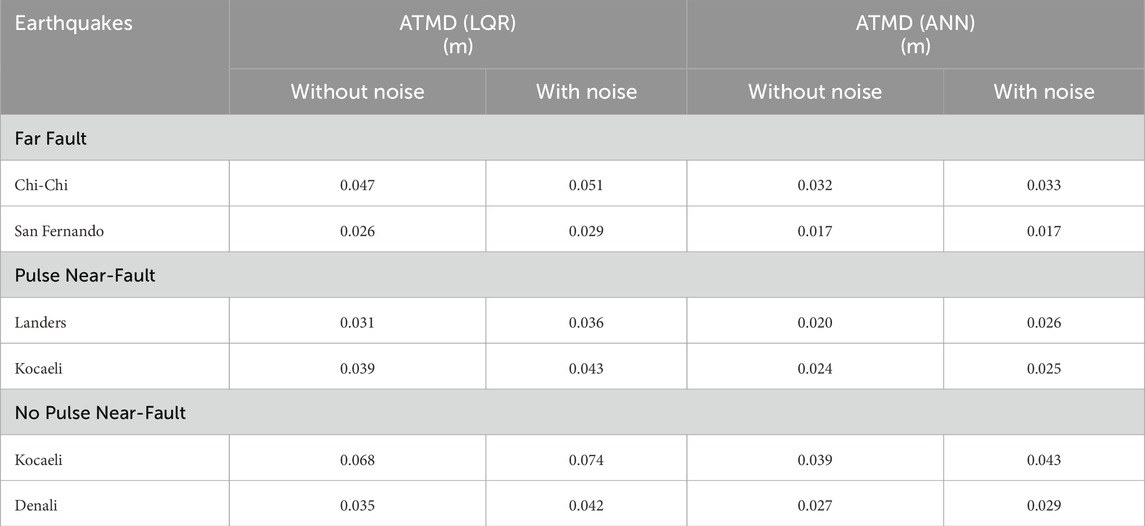
The noise-affected responses were fed into both the LQR and ANN control systems within the feedback loop. Table 7 presents the base floor root mean square (RMS) under both LQR and ANN controllers with and without noise contamination for all the used records.

Table 7

Table 7. Base floor displacement RMS with and without noise.

After introducing noise, a slight increase in the RMS displacement response was observed for both the LQR and ANN control methods. However, it was found that an effective solution to mitigate this increase is to adjust the control force. The robustness of the ANN controller was evaluated based on its ability to maintain control performance despite the presence of noise. Finally, this consistent effectiveness across different responses underscores ANN’s potential to enhance structural resilience against seismic impacts.

5 Conclusion

This study aimed to enhance the seismic performance of nonlinear base-isolated structures by developing an AI-based hybrid control strategy that combines BIS with ATMDs, applying an ANN controller. The main objective was to design a control system capable of achieving effective seismic response mitigation with a limited number of sensors, thus improving practicality and cost-efficiency compared to conventional methods.

The methodology involved training an ANN controller using data generated from an LQR controller under seismic excitation with one ground motion data. The ANN model was trained to replicate the optimal control action of the LQR while addressing the nonlinear hysteretic behavior of the base-isolated structure. The controller’s performance was validated through numerical simulations on an 8-story nonlinear base-isolated benchmark building subjected to various near-field and far-field earthquakes, including additional unseen earthquake records to assess generalization capabilities.

The major findings from the case study can be summarized as follows:

1. The ANN controller successfully captured the nonlinear behavior of the base isolators and structural responses, leading to more effective mitigation of seismic-induced vibrations compared to classical passive control (provided with classical TMD).

2. A reduction of over 80% in the base isolator displacement was achieved with the ATMD trained by the ANN, alongside a significant decrease in the RMS values of structural responses.

3. The ANN-based system demonstrated robustness against signal time delays and white noise contamination, ensuring reliable performance under realistic data conditions.

4. Effective control was achieved with only three sensors, highlighting a significant advantage over the conventional LQR controller, which requires full-state observation.

5. The ANN controller exhibited strong generalization capabilities, effectively mitigating structural responses during seismic events not included in the initial training dataset.

6. The ANN-driven control system provided real-time response capabilities, enabling immediate and adaptive adjustments to maintain structural integrity during earthquakes.

Moreover, the integration of BIS with ATMD further enhanced the energy dissipation capacity of the structure, leading to improved overall robustness against seismic events.

In conclusion, the proposed ANN-driven hybrid control approach demonstrated considerable potential for practical implementation by achieving comparable or superior performance to classical control methods while significantly reducing the complexity and cost associated with sensor deployment. Future research will focus on exploring more advanced ANN architectures, such as deep learning models, and conducting experimental validations on larger-scale structures to further assess the applicability of AI-based adaptive control in real-world scenarios. Additionally, the versatility of ANN-driven hybrid control strategies could be investigated in broader engineering contexts beyond seismic resilience.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

NG: Visualization, Formal Analysis, Data curation, Writing – original draft, Investigation, Software. MA: Writing – review and editing, Validation, Methodology, Supervision, Conceptualization. AO: Validation, Supervision, Writing – review and editing, Conceptualization. MB: Funding acquisition, Writing – review and editing, Supervision, Validation, Conceptualization, Investigation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study has been supported by Universitas Mercatorum of Rome, Italy, under Grant No. 24-FIN/RIC (financial framework 2024).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdeddaim, M., Ounis, A., Shrimali, M. K., and Datta, T. K. (2017). Retrofitting of a weaker building by coupling it to an adjacent stronger building using MR dampers. Struc Eng. Mech. 62 (2), 197–208. doi:10.12989/sem.2017.62.2.197

CrossRef Full Text | Google Scholar

Aldwaik, M., and Adeli, H. (2014). Advances in optimization of highrise building structures. Struct. Multidiscip. Optim. 50, 899–919. doi:10.1007/s00158-014-1148-1

CrossRef Full Text | Google Scholar

Amezquita-Sanchez, J. P., Dominguez-Gonzalez, A., Sedaghati, R., de Jesus Romero-Troncoso, R., and Osornio-Rios, R. A. (2014). Vibration control on smart civil structures: a review. Mech. Adv. Mater. Struct. 21 (1), 23–38. doi:10.1080/15376494.2012.677103

CrossRef Full Text | Google Scholar

Banerjee, S., and Matsagar, V. (2023). Hybrid vibration control of hospital buildings against earthquake excitations using unbonded fiber-reinforced elastomeric isolator and tuned mass damper. Buildings 13 (7), 1724. doi:10.3390/buildings13071724

CrossRef Full Text | Google Scholar

Blachowski, B., and Pnevmatikos, N. (2018). Neural network based vibration control of seismically excited civil structures. Period. Polytech. Civ. Eng. 62 (3), 620–628. doi:10.3311/ppci.11601

CrossRef Full Text | Google Scholar

Brancati, R., Di Massa, G., Pagano, S., Petrillo, A., and Santini, S. (2020). A combined neural network and model predictive control approach for ball transfer unit–magnetorheological elastomer–based vibration isolation of lightweight structures. J. Vib. Control 26 (19-20), 1668–1682. doi:10.1177/1077546320902316

CrossRef Full Text | Google Scholar

Chang, J. C., and Soong, T. T. (1980). Structural control using active tuned mass dampers. J. Eng. Mech. Div. 106 (6), 1091–1098. doi:10.1061/jmcea3.0002652

CrossRef Full Text | Google Scholar

Chang, S., and Sung, D. (2019). Modal-energy-based neuro-controller for seismic response reduction of a nonlinear building structure. Appl. Sci. 9 (20), 4443. doi:10.3390/app9204443

CrossRef Full Text | Google Scholar

Charrouf, M. E., Ounis, A., Djedoui, N., and Abdeddaim, M. (2024). Analyzing seismic performance of optimized base isolation systems with soil–structure interaction: an analytical and numerical approach. Pract. Periodical Struct. Des. Constr. 29 (3), 04024032. doi:10.1061/ppscfx.sceng-1479

CrossRef Full Text | Google Scholar

Chen, B., and Xu, Y. L. (2008). Integrated vibration control and health monitoring of building structures using semi-active friction dampers: Part II—numerical investigation. Eng. Struct. 30 (3), 573–587. doi:10.1016/j.engstruct.2007.03.006

CrossRef Full Text | Google Scholar

Chen, P.-C., and Chien, K.-Y. (2020). Machine-learning based optimal seismic control of structure with active mass damper. Appl. Sci. 10 (15), 5342. doi:10.3390/app10155342

CrossRef Full Text | Google Scholar

Cheng, F. Y., and Jiang, H. (1998). Hybrid control of seismic structures with optimal placement of control devices. J. Aerosp. Eng. 11 (2), 52–58. doi:10.1061/(asce)0893-1321(1998)11:2(52)

CrossRef Full Text | Google Scholar

Conte, J. P., Durrani, A. J., and Shelton, R. O. (1994). Seismic response modeling of multi-story buildings using neural networks. J. intelligent material Syst. Struct. 5 (3), 392–402. doi:10.1177/1045389x9400500312

CrossRef Full Text | Google Scholar

Council, A. T. (2009). Quantification of building seismic performance factors. Redwood City, CA: US Department of Homeland Security, FEMA.

Google Scholar

Di Girolamo, G. D., Smarra, F., Gattulli, V., Potenza, F., Graziosi, F., and D'Innocenzo, A. (2020). Data-driven optimal predictive control of seismic induced vibrations in frame structures. Struct. Control Health Monit. 27 (4). doi:10.1002/stc.2514

CrossRef Full Text | Google Scholar

Djedoui, N., Ounis, A., and Abdeddaim, M. (2016). Active vibration control for base-isolated structures using a PID controller against earthquakes. Int. J. Eng. Res. Afr. 26, 99–110. doi:10.4028/www.scientific.net/jera.26.99

CrossRef Full Text | Google Scholar

Djedoui, N., Ounis, A., Pinelli, J., and Abdeddaim, M. (2017). Hybrid control systems for rigid buildings structures under strong earthquakes. Asian J. Civ. Eng. 18, 893–909.

Google Scholar

Djerouni, S., Ounis, A., Athamnia, B., Charrouf, M. E., Abdeddaim, M., and Djedoui, N. (2020). Optimal seismic response using a passive tuned mass damper inerter (TMDI). J. Build. Mater. Struct. 7 (1), 51–59. doi:10.34118/jbms.v7i1.208

CrossRef Full Text | Google Scholar

Elias, S., Beer, M., and Chen, J. (2025). Assessing seismic vulnerability of modular buildings under earthquake ground motions. Eng. Struct. 331, 120002. doi:10.1016/j.engstruct.2025.120002

CrossRef Full Text | Google Scholar

Elias, S., Djerouni, S., De Domenico, D., Abdeddaim, M., and El Ouni, M. H. (2023). Seismic response control of building structures under pulse-type ground motions by active vibration controller. J. Low Freq. Noise, Vib. Act. Control 42 (1), 345–367. doi:10.1177/14613484221130192

CrossRef Full Text | Google Scholar

Elias, S., and Matsagar, V. (2017). Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 44, 129–156. doi:10.1016/j.arcontrol.2017.09.015

CrossRef Full Text | Google Scholar

El Ouni, M. H., Abdeddaim, M., Elias, S., and Kahla, N. B. (2022). Review of vibration control strategies of high-rise buildings. Sensors 22 (21), 8581. doi:10.3390/s22218581

PubMed Abstract | CrossRef Full Text | Google Scholar

Fisco, N. R., and Adeli, H. (2011a). Smart structures: Part I—active and semi-active control. Sci. Iran. 18 (3), 275–284. doi:10.1016/j.scient.2011.05.034

CrossRef Full Text | Google Scholar

Fisco, N. R., and Adeli, H. (2011b). Smart structures: Part II — hybrid control systems and control strategies. Sci. Iran. 18 (3), 285–295. doi:10.1016/j.scient.2011.05.035

CrossRef Full Text | Google Scholar

Ghanemi, N. E., Abdeddaim, M., and Ounis, A. (2024). Artificial intelligence-driven active tuned mass damper for enhanced seismic resilience of shear frame smart structures. J. Vib. Eng. and Technol. 12, 1577–1599. doi:10.1007/s42417-024-01491-0

CrossRef Full Text | Google Scholar

Ghanemi, N. E., Abdeddaim, M., and Ounis, A. (2023). “Seismic response reduction using an active tuned mass damper driven by an artifical neural network controller,” in 9th international conference on computational methods in structural dynamics and earthquake engineering methods in structural dynamics and earthquake Engineering, 1227–1235.

Google Scholar

Gu, X., Yu, Y., Li, J., and Li, Y. (2017). Semi-active control of magnetorheological elastomer base isolation system utilising learning-based inverse model. J. Sound Vib. 406, 346–362. doi:10.1016/j.jsv.2017.06.023

CrossRef Full Text | Google Scholar

Hashemi, A., Jang, J., and Hosseini-Hashemi, S. (2022). Smart active vibration control system of a rotary structure using piezoelectric materials. Sensors 22 (15), 5691. doi:10.3390/s22155691

PubMed Abstract | CrossRef Full Text | Google Scholar

Heertjes, M., and van de Wouw, N. (2006). Nonlinear dynamics and control of a pneumatic vibration isolator. J. Vib. Acoust. 128, 439–448. doi:10.1115/1.2128642

CrossRef Full Text | Google Scholar

B. Islam, N. Ahmed, D. Bhatti, and S. Khan (2003). “Controller design using fuzzy logic for a twin rotor MIMO system,” 7th international multi topic conference, 2003 INMIC 2003 (IEEE).

Google Scholar

Ismail, M., Ikhouane, F., and Rodellar, J. (2009). The hysteresis Bouc-Wen model, a survey. Archives Comput. methods Eng. 16, 161–188. doi:10.1007/s11831-009-9031-8

CrossRef Full Text | Google Scholar

Jamil, M., Khan, M. N., Rind, S. J., Awais, Q., and Uzair, M. (2021). Neural network predictive control of vibrations in tall structure: an experimental controlled vision. Comput. and Electr. Eng. 89, 106940. doi:10.1016/j.compeleceng.2020.106940

CrossRef Full Text | Google Scholar

S.-S. Jhang, H.-J. Lee, C.-N. Kim, C.-H. Song, and W.-K. Yu (2018). “ANN control for damping low-frequency oscillation using deep learning,” Australasian universities power engineering conference (AUPEC) (IEEE).

Google Scholar

Kalman, R. E. (1960). Contributions to the theory of optimal control. Bol. Soc. Mat. Mex. 5 (2), 102–119.

Google Scholar

Kim, H.-S. (2020). Development of seismic response simulation model for building structures with semi-active control devices using recurrent neural network. Appl. Sci. 10 (11), 3915. doi:10.3390/app10113915

CrossRef Full Text | Google Scholar

Kohavi, R. (1995). A study of cross-validation and bootstrap for accuracy estimation and model selection. International joint conference on Artifical Intelligence (IJCAI). Montreal, QC.

Google Scholar

Lee, T.-Y., and Kawashima, K. (2007). Semiactive control of nonlinear isolated bridges with time delay. J. Struct. Eng. 133 (2), 235–241. doi:10.1061/(asce)0733-9445(2007)133:2(235)

CrossRef Full Text | Google Scholar

Li, C., Chang, K., Cao, L., and Huang, Y. (2021). Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn. Earthq. Eng. 143, 106589. doi:10.1016/j.soildyn.2021.106589

CrossRef Full Text | Google Scholar

Linderman, L. E., and Spencer, Jr B. (2016). Decentralized active control of multistory civil structure with wireless smart sensor nodes. J. Eng. Mech. 142 (10), 04016078. doi:10.1061/(asce)em.1943-7889.0001126

CrossRef Full Text | Google Scholar

Liut, D., Matheu, E., Singh, M., and Mook, D. (1999). Neural-network control of building structures by a force-matching training scheme. Earthq. Eng. Struct. Dyn. 28 (12), 1601–1620. doi:10.1002/(sici)1096-9845(199912)28:12<1601::aid-eqe884>3.0.co;2-g

CrossRef Full Text | Google Scholar

Lu, P., Chen, S., and Zheng, Y. (2012). Artificial intelligence in civil engineering. Math. Problems Eng. 2012, 1–22. doi:10.1155/2012/145974

CrossRef Full Text | Google Scholar

Mardani, A., Jusoh, A., and Zavadskas, E. K. (2015). Fuzzy multiple criteria decision-making techniques and applications–Two decades review from 1994 to 2014. Expert Syst. Appl. 42 (8), 4126–4148. doi:10.1016/j.eswa.2015.01.003

CrossRef Full Text | Google Scholar

Mazza, F., Donnici, A., and Labernarda, R. (2023). Seismic vulnerability of fixed-base and base-isolated hospitals: blind comparison between shaking table and numerical tests. Procedia Struct. Integr. 44, 147–154. doi:10.1016/j.prostr.2023.01.020

CrossRef Full Text | Google Scholar

Mazza, F., Donnici, A., and Labernarda, R. (2024). Structural and non-structural numerical blind prediction of shaking table experimental tests on fixed-base and base-isolated hospitals. Earthq. Eng. Struct. Dyn. 53 (10), 2961–2987. doi:10.1002/eqe.4146

CrossRef Full Text | Google Scholar

Mazza, F., and Labernarda, R. (2022). Effects of near-fault acceleration and non-acceleration pulses on pounding between in-plan irregular fixed-base and base-isolated buildings. Struct. Control Health Monit. 29 (9), e2992. doi:10.1002/stc.2992

CrossRef Full Text | Google Scholar

Moghaddasie, B., and Jalaeefar, A. (2019). Optimization of LQR method for the active control of seismically excited structures. Smart Struct. Syst. 23 (3), 243–261. doi:10.12989/sss.2019.23.3.243

CrossRef Full Text | Google Scholar

Naeim, F., and Kelly, J. M. (1999). Design of seismic isolated structures: from theory to practice. John Wiley and Sons.

Google Scholar

Neves, A. C., Gonzalez, I., Leander, J., and Karoumi, R. (2017). Structural health monitoring of bridges: a model-free ANN-based approach to damage detection. J. Civ. Struct. Health Monit. 7, 689–702. doi:10.1007/s13349-017-0252-5

CrossRef Full Text | Google Scholar

Pandey, S. K., and Laxmi, V. (2015). “Optimal control of twin rotor MIMO system using LQR technique,” in Computational intelligence in data mining-volume 1 (New Delhi: Springer), 11–21.

CrossRef Full Text | Google Scholar

A. Phillips, and F. Sahin (2014). “Optimal control of a twin rotor MIMO system using LQR with integral action,” 2014 world automation congress (WAC) (IEEE).

Google Scholar

Radmard Rahmani, H., Chase, G., Wiering, M., and Könke, C. (2019). A framework for brain learning-based control of smart structures. Adv. Eng. Inf. 42, 100986. doi:10.1016/j.aei.2019.100986

CrossRef Full Text | Google Scholar

A. Reynaldi, S. Lukas, and H. Margaretha (2012). Backpropagation and levenberg-marquardt algorithm for training finite element neural network. 2012 sixth UKSim/AMSS European symposium on computer modeling and simulation (IEEE).

Google Scholar

Sabetahd, R., Mousavi Ghasemi, S. A., Vafaei Poursorkhabi, R., Mohammadzadeh, A., and Zandi, Y. (2022). Response attenuation of a structure equipped with ATMD under seismic excitations using methods of online simple adaptive controller and online adaptive type-2 neural-fuzzy controller. Comput. Intell. Neurosci. 2022, 1–25. doi:10.1155/2022/5832043

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadek, F., Mohraz, B., Taylor, A. W., and Chung, R. M. (1997). A method of estimating the parameters of tuned mass dampers for seismic applications. Earthq. Eng. Struct. Dyn. 26 (6), 617–635. doi:10.1002/(sici)1096-9845(199706)26:6<617::aid-eqe664>3.0.co;2-z

CrossRef Full Text | Google Scholar

Sanad, A., and Saka, M. (2001). Prediction of ultimate shear strength of reinforced-concrete deep beams using neural networks. J. Struct. Eng. 127 (7), 818–828. doi:10.1061/(asce)0733-9445(2001)127:7(818)

CrossRef Full Text | Google Scholar

Sapountzakis, E., Florakis, G., and Kapasakalis, K. (2024). Design and performance assessment of base isolated structures supplemented with vibration control systems. Buildings 14 (4), 955. doi:10.3390/buildings14040955

CrossRef Full Text | Google Scholar

Shin, J.-H., Kwak, M. K., Kim, S.-M., and Baek, K.-H. (2020). Vibration control of multi-story building structure by hybrid control using tuned liquid damper and active mass damper. J. Mech. Sci. Technol. 34 (12), 5005–5015. doi:10.1007/s12206-020-1105-4

CrossRef Full Text | Google Scholar

Sibi, P., Jones, S. A., and Siddarth, P. (2013). Analysis of different activation functions using back propagation neural networks. J. Theor. Appl. Inf. Technol. 47 (3), 1264–1268.

Google Scholar

Skinner, R. I., Robinson, W. H., and McVerry, G. H. (1993). An introduction to seismic isolation.

Google Scholar

Smarra, F., Girolamo, G. D. D., Gattulli, V., Graziosi, F., and D’Innocenzo, A. (2020). Learning models for seismic-induced vibrations optimal control in structures via random forests. J. Optim. Theory Appl. 187 (3), 855–874. doi:10.1007/s10957-020-01698-7

CrossRef Full Text | Google Scholar

Smith, G. N. (1986). “Probability and statistics in civil engineering,” in Collins professional and technical books, 244.

Google Scholar

R. Subasri, A. Natarajan, S. Sundaram, and W. Jianliang (2013). Neural aided discrete PID active controller for non-linear hysteretic base-isolation building. 2013 9th Asian Control Conference ASCC (IEEE).

Google Scholar

Ulusoy, S., Bekdaş, G., Nigdeli, S. M., Kim, S., and Geem, Z. W. (2021). Performance of optimum tuned PID controller with different feedback strategies on active-controlled structures. Appl. Sci. 11 (4), 1682. doi:10.3390/app11041682

CrossRef Full Text | Google Scholar

Ümütlü, R. C., Ozturk, H., and Bidikli, B. (2021). A robust adaptive control design for active tuned mass damper systems of multistory buildings. J. Vib. Control 27 (23-24), 2765–2777. doi:10.1177/1077546320966236

CrossRef Full Text | Google Scholar

Wen, Y. (1989). Methods of random vibration for inelastic structures. Appl. Mech. Rev. 42, 39–52. doi:10.1115/1.3152420

CrossRef Full Text | Google Scholar

Wen, Y.-K. (1976). Method for random vibration of hysteretic systems. J. Eng. Mech. Div. 102 (2), 249–263. doi:10.1061/jmcea3.0002106

CrossRef Full Text | Google Scholar

Yang, J., Li, Z., Danielians, A., and Liu, S. (1992). Aseismic hybrid control of nonlinear and hysteretic structures I. J. Eng. Mech. 118 (7), 1423–1440. doi:10.1061/(asce)0733-9399(1992)118:7(1423)

CrossRef Full Text | Google Scholar

Yang, J., Li, Z., and Vongchavalitkul, S. (1994). Generalization of optimal control theory: linear and nonlinear control. J. Eng. Mech. 120 (2), 266–283. doi:10.1061/(asce)0733-9399(1994)120:2(266)

CrossRef Full Text | Google Scholar

Yang, S.-M., Chen, C.-J., and Huang, W. (2006). Structural vibration suppression by a neural-network controller with a mass-damper actuator. J. Vib. Control 12 (5), 495–508. doi:10.1177/1077546306064269

CrossRef Full Text | Google Scholar

Ying, W., Chong, W., Hui, L., and Renda, Z. (2009). “Artificial neural network prediction for seismic response of bridge structure,” in 2009 international conference on artificial intelligence and computational Intelligence, 503–506.

Google Scholar

Zahedin Labaf, D., De Angelis, M., and Basili, M. (2023). Multi-objective optimal design and seismic assessment of an inerter-based hybrid control system for storage tanks. Bull. Earthq. Eng. 21 (3), 1481–1507. doi:10.1007/s10518-022-01457-1

CrossRef Full Text | Google Scholar

Zhang, J., and Xue, Y. (2023). Intelligent control method research for high rise building vibration by integrating genetic algorithm and LSTM. IEEE Access 12, 9810–9821. doi:10.1109/access.2023.3348145

CrossRef Full Text | Google Scholar