Optimal placement and design of M-STLCDs in n-story buildings: a comparative study with M-TMDs and M-TLCDs

This study proposes a novel optimization procedure for the seismic vibration control of multi-degree-of-freedom systems incorporating Multiple Sliding Tuned Liquid Column Dampers (M-STLCDs). Unlike conventional compliant liquid-based devices, the proposed system consists of multiple translating U-shaped liquid containers, each independently tuned to a specific structural mode, enabling multi-modal control, particularly suited for stiff structures and not previously explored in the literature. The procedure can optimize and install one device at a time while accounting for the modifications introduced by prior installations, ensuring a progressive adaptation of the control system to the dynamic characteristics of the structure. For each single STLCD, the procedure considers both the optimal location in the building and the fundamental mode to be controlled. More specifically, for each STLCD, the procedure detects the optimal floor where the device should be placed and optimizes the damping and the natural frequency of the spring-dashpot unit, the head-loss coefficient and the natural frequency characterizing the liquid. To prove the effectiveness of the optimal placement of the devices, the optimization procedure was applied on two different types of shear-type structures, i.e., on a three-story and a six-story structure, subjected to a broadband and zero-mean white noise process. Moreover, the control performance of the device was evaluated both in the time and the frequency domain and under recorded seismic events, in comparison with optimized configurations of traditional devices, such as Multiple Tuned Mass Dampers (M-TMDs) and Multiple Tuned Liquid Column Dampers (M-TLCDs).

1 Introduction

In structural engineering, passive vibration control devices are widely used to enhance the capacity of structures to withstand dynamic events such as earthquakes and winds. Among these devices, the Tuned Mass Damper (TMD) was the first to be introduced and extensively studied (Den Hartog, 1956). A TMD consists of a secondary mass attached to a structure via a spring-damper system, designed to oscillate out of phase with the primary structure, dissipating vibrational energy and reducing structural response. Initially, research on TMDs primarily focused on the use of a single TMD device for mitigating vibrations (Ayorinde and Warburton, 1980; Randall et al., 1981; Warburton, 1982; Argenziano et al., 2022; Faiella et al., 2022). In this respect, the literature and real-world applications proved the effectiveness of TMDs in controlling both long-period, slender structures and short-period, stiff structures under several types of dynamic excitations. Given its efficacy, researchers started to examine the potential benefits of several TMDs installed within the same structure, exploring multi-unit configurations in both single-degree-of-freedom (SDOF) and multi-degree-of-freedom (MDOF) structures. One of the first approaches pursued in the development of multiple TMD configurations involved installing several TMD units on the same floor, all optimally tuned to the same frequency, typically corresponding to the fundamental mode of the target structure (Yamaguchi and Harnpornchai, 1993; Xu and Igusa, 1992; Abé and Fujino, 1994; Kareem and Kline, 1995; Joshi and Jangid, 1997; Jangid, 1999; Bakre and Jangid, 2004; Park and Reed, 2001; Li, 2000; Li, 2002; Shetty et al., 2017; Kim and Lee, 2018). This strategy presents both performance-related and practical advantages. From a control standpoint, its slight frequency spacing among the TMD units enhances the robustness of the system, reducing sensitivity to detuning effects and improving the overall vibration mitigation efficiency. Additionally, from an installation and maintenance perspective, dividing the overall TMD system into multiple, smaller units simplifies handling, placement, and upkeep, making it a more feasible solution in real-world applications. However, despite the benefits of improved robustness and practical implementation, this configuration, like the single TMD, primarily targeted the fundamental mode, consequently limiting its effectiveness in mitigating the influence of higher modes on the structural response. To address this limitation, two approaches were mainly explored in the literature. One approach maintained the concept of multiple TMDs installed on the same level while extending their functionality to target different modes of the MDOF structure (Mohebbi et al., 2013; Zak et al., 2024). This improvement, achieved through optimization algorithms of the TMDs’ parameters, enabled broader modal control and effectively enhanced the capabilities of the configuration beyond its initial limitation to the fundamental mode. As a result, these multiple TMD configurations achieved more effective vibration mitigation across a broader frequency range, making them suitable for controlling the complex dynamics of MDOF structures.

Meanwhile, other researchers focused on a second approach, implying the distribution of the devices across multiple levels (Clark, 1988), laying the groundwork for further advancements. In this manner, this approach retained practical advantages by dividing the system into smaller units, simplifying installation and maintenance. Additionally, distributing devices across multiple floors reduced spatial constraints at any single level, avoiding excessive concentration of mass and minimizing floor space requirements. Building on this concept, in (Chen, 1996), a Multi-Stage Tuned Mass Damper (MSTMD) strategy was introduced, specifically designed to reduce coupling effects that can arise in MDOF structures controlled by TMDs. The configuration consisted of multiple TMDs, each tuned to the first fundamental mode and each one installed on a separate floor, effectively minimizing coupling effects and leading to a reduction in structural accelerations. Then, further advances in this field were achieved in (Chen and Wu, 2001) where authors introduced the Multi-Tuned Mass Damper (M-TMD), a configuration aimed at enhancing the mitigation of higher mode contributions and improving the overall effectiveness of vibration control systems. Extending the previous concept of distributing TMDs across multiple floors, the M-TMD configuration further enhanced multi-modal control by allowing each TMD to be tuned to different vibration modes. As part of their work (Chen and Wu, 2001), the authors developed a numerical sequential optimization procedure that expanded the range of optimal tuning solutions for each device while simultaneously identifying the most effective floor for the installation. This advancement led to notable reductions in structural response, demonstrating both its effectiveness and adaptability across different seismic excitations and site-specific installation requirements. The concept of the M-TMD was further explored in the literature from multiple perspectives, including optimization strategies, structural uncertainties, and mass distribution effects, to enhance its effectiveness in multi-modal vibration control, particularly under seismic excitations (Lewandowski and Grzymisławska, 2009; Elias et al., 2016; Elias et al., 2019; Fadel Miguel et al., 2016; Suresh and Mini, 2019; Vellar et al., 2019; Zhang et al., 2022), also considering different types of structures. Another prominent example of passive control systems is the Tuned Liquid Column Damper (TLCD), which gained widespread recognition for its effectiveness and advantageous features in attenuating structural vibrations (Sakai et al., 1989; Gao et al., 1997; Ziegler, 2007; Di Matteo et al., 2016; Fei et al., 2019). The TLCD consists of a container, which can be U-shaped or V-shaped, partially filled with fluid, and fixed to the main structure. Clearly, the TLCD offers a more environmentally friendly solution, as the majority of its required mass is composed of the contained liquid, leading to lower construction and maintenance costs. Additionally, the contained liquid, typically water, can serve as a reservoir for several purposes, enhancing the overall practicality of the system. Further numerical and experimental investigations into the TLCD explored its potential to meet diverse structural demands through the exploration of advanced configurations and the use of innovative materials (Adam et al., 2017; Di Matteo et al., 2018; Di Matteo et al., 2019; Furtmüller et al., 2019; Konar and Ghosh, 2023). For instance, the use of different liquids can optimize the device’s performance by tailoring its dynamic properties to the specific needs of the structure (Ocak et al., 2022). Additionally, sealed TLCDs, incorporating gas chambers, can improve control efficiency and extend the range of tunability (Hochrainer and Ziegler, 2006). Multi-cell TLCDs, though conceptually distinct from multiple control solutions, offer some adaptability through internal tuning to specific dynamic characteristics (Kim et al., 2012). TLCDs have been implemented in various real-world structures to address specific performance requirements (Konar and Ghosh, 2023). Similarly to the TMD, with the aim of obtaining an enhanced structural control solution, many studies investigated a control solution consisting of several TLCDs having closely spaced natural frequencies. For instance (Sadek et al., 1998; Gao et al., 1999), investigated the characteristics of closely spaced TLCDs in suppressing structural vibrations, showing enhanced performance when tuned to a single mode. As demonstrated both theoretically and experimentally, configurations involving multiple TLCDs can also be employed to reduce the dynamic response of structures subjected to torsional vibrations (Shum and Xu, 2002; Xu and Shum, 2003), or to mitigate lateral displacements in wind-prone high-rise buildings (Min et al., 2005). In (Mohebbi et al., 2015) the design of multiple TLCDs was optimized for seismic applications in MDOF structures, demonstrating their effectiveness in reducing seismic responses. Similarly, in (Zhu et al., 2017) real-time hybrid simulations were employed to assess the performance of full-scale multiple TLCDs in controlling higher-order modal responses, underlining their adaptability in mitigating vibrations across multiple modes. In contrast to TMDs, TLCDs have demonstrated effectiveness primarily in long-period structures (Adam et al., 2017; Di Matteo et al., 2018; Di Matteo et al., 2019; Furtmüller et al., 2019; Hochrainer and Ziegler, 2006; Kim et al., 2012; Min et al., 2005; Mohebbi et al., 2015; Balendra et al., 1995) since optimizing the TLCD for short-period structures results in parameter values that are challenging to achieve in real applications. In fact, as determining the optimal TLCD frequency depends on the total length of the liquid column contained in the reservoir, geometrical and structural constraints arise. In this regard, to extend the use of the TLCD to different structural categories, another liquid-based device, the Sliding Tuned Liquid Column Damper (STLCD), has lately gained relevant attention. Such a device is a variant of the TLCD in which the container is not directly attached to the structure to be controlled, but it is free to translate on a sliding support and connected to the structure through a system of springs and dampers (Ghosh and Basu, 2004). By making it possible to adjust the damping and the stiffness parameters in a more flexible manner due to the presence of the spring-dashpot unit, the STLCD device extends the use of liquid devices to short-period structures, while maintaining both comparable performance to the TMD and the eco-sustainability features inherent in the TLCD, such as reduced fabrication costs and the possible reuse of the water. It is worth noting that compared to previous studied compliant liquid devices (Pandey et al., 2019), which typically omit the vertical column, the present model retains the classical TLCD column-based configuration, preserving the gravity-driven restoring force while enhancing tunability through added compliance. Further numerical and experimental investigations on the potential of the device examined its use as a hybrid solution in combination with base isolation and by streamlining the design process by means of statistical linearization techniques (Masnata and Pirrotta, 2024; Masnata et al., 2024a; Masnata et al., 2024b). However, to the best of the authors’ knowledge, although some studies have investigated the use of a single STLCD for the control of MDOF structures (Masnata and Pirrotta, 2024; Masnata et al., 2024a; Masnata et al., 2024b), also referred to as Tuned Liquid Column Mass Dampers (TLCMDs) (Wei and Zhao, 2020), no research has yet explored structural vibration control using a multiple-control system composed of several STLCD units. In particular, there are no studies addressing the coordinated operation and the optimization of these devices while maintaining their nonlinear behavior for multi-modal control. Such an investigation could contribute to a deeper comprehension of the effectiveness of these devices when interacting with real-world structures, which are generally n-story structures. Moreover, it would allow for an assessment of their performance in protecting both flexible and rigid systems from dynamic events. Based on these considerations, this study introduces a novel control configuration, comprising multiple sliding liquid column containers installed on different floors and tuned to distinct modes, which is defined herein as the Multi-Sliding Tuned Liquid Column Damper (M-STLCD). Hence, as a first contribution of this study, a numerical optimization procedure is proposed for the determination of the optimal parameters of the M-STLCD, aiming at reducing structural responses in MDOF structures subjected to different base excitations. In particular, the proposed procedure is iterative as it can install and optimize one STLCD unit per iteration while accounting for the modifications introduced by prior installations. More specifically, for each STLCD unit, the procedure targets the optimal values of the spring-dashpot unit, in terms of damping and natural frequency, and the optimal values of the liquid inside the container, in terms of head-loss coefficient and natural frequency. In addition, the procedure identifies the optimal floor for the installation of each unit, ensuring that the overall structural response is effectively minimized. In contrast to widely used metaheuristic methods, such as Genetic Algorithms (GA) (Goldberg and Holland, 1988), Particle Swarm Optimization (PSO) (Perez and Behdinan, 2007), Artificial Bee Colony (ABC), Simulated Annealing (SA) (Chen et al., 2012), Mouth Brooding Fish (MBF) (Roozbahan et al., 2025), and multi-objective approaches like NSGA-II (Ma et al., 2023), known for addressing complex optimization tasks with global solutions, the proposed algorithm operates in a discrete search space using a sequential strategy. In this manner, this approach addresses some of limitations of metaheuristics (Almufti et al., 2023; Vié, 2020; Aote et al., 2013), especially in engineering contexts where parameter transparency, solution reproducibility, and alignment with practical implementation constraints are essential. The algorithm’s reliability is demonstrated through numerical analyses and comparison with global PSO on two planar shear-type stiff structures (as defined in (American Society of Civil Engineers, 2022)), in contrast to the long-period structures typically considered in TLCD-related literature. The first model is a three-story frame, purposely constructed to explore the effectiveness of the proposed control strategy. The second is a well-established six-story frame, previously analyzed in (Chen and Wu, 2001), serving as a reference case in the field of seismic vibration control. In addition, to the best of the Authors’ knowledge, the existing literature does not provide sequential methodologies that address both the strategic placement of multiple TLCD units within n-story structures and their optimization for higher-mode control. Therefore, given the lack of similar studies using TLCDs, and for a comprehensive comparison on the performance of the M-STLCD, the implementation of the same optimization procedure for the control solution composed of multiple TLCDs distributed across different floors, here referred to as the Multi-Tuned Liquid Column Damper (M-TLCD), and the Multi-Tuned Mass Damper (M-TMD) is presented. Numerical comparisons among the response reduction achievable by these three control strategies were performed in both the time and frequency domains, using the uncontrolled structure as a reference, under different base accelerations.

The structure of the paper is organized as follows. Section 2 introduces the mathematical modeling for M-STLCD-controlled n-story structures. Section 3 describes the excitation model used for numerical simulations throughout the paper. In Section 4, some preliminary analyses are presented to investigate the effects of a single STLCD placed on an MDOF structure with respect to the different modes of the structure. The proposed sequential optimization procedure for M-STLCD-controlled n-story structures follows in Section 5. The results of the optimization in terms of device parameters for each iteration as well as the evaluation of the control performance in comparison with common control strategies (M-TMD and M-TLCD), are discussed in Sections 6, 7, focusing on the frequency and time domains, respectively. Finally, conclusions are drawn in Section 8.

2 Mathematical modeling

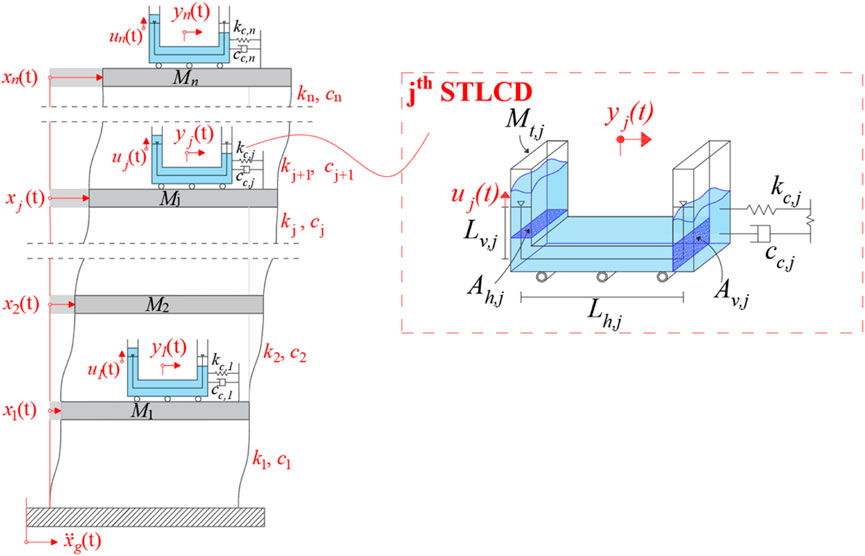
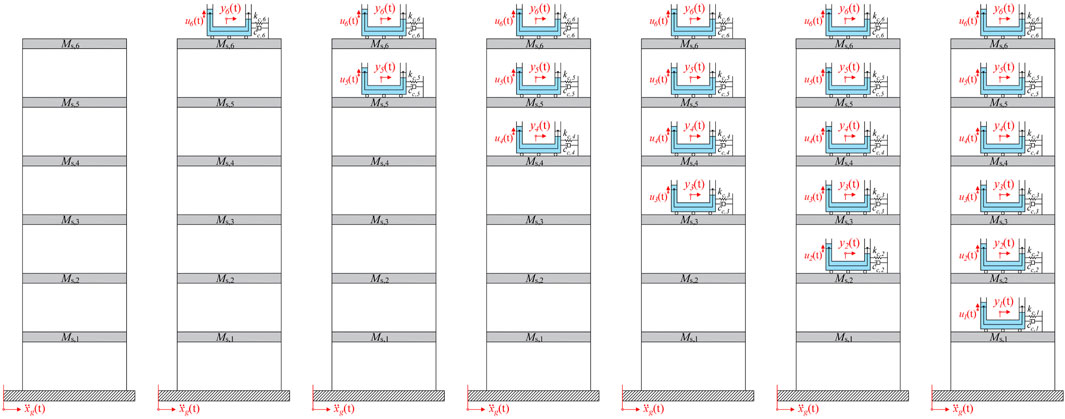
Let us consider the system shown in Figure 1, subjected to the ground acceleration ${\ddot{x}}_g\left(t\right)$. The main structure is a shear-type planar frame with n stories. Hence, the main structure has n dynamic DOF, represented by the ground-relative displacements of the n story masses $M_j$ (j = 1, … , n), which are collected in the n × 1 array ${\mathbf{x}}_s\left(t\right)=\left[{\mathrm{x}}_1\left(t\right);{\mathrm{x}}_2\left(t\right);\dots ;{\mathrm{x}}_n\left(t\right)\right]$. Aiming at reducing the structural responses, an M-STLCD control system, composed of $\overline{n}$ STLCD units (with $\overline{n}\le n$) is introduced. Each unit is a translational U-shaped column container, filled with liquid and connected to the floor by a spring-dashpot system (Figure 1).

Figure 1

Figure 1. M-STLCD-controlled n-story structure.

In the close up of the generic jth (with j = 1,… $\overline{n}$) STLCD unit in Figure 1, installed at the jth floor, $L_{v,j}$ and $L_{h,j}$ represent the height of the liquid in a single column at rest and the length of the horizontal segment of the container, respectively, with the total length of the jth liquid column expressed as $L_j=2L_{v,j}+L_{h,j}$. The horizontal and vertical cross-sectional areas of the jth container are denoted as $A_{h,j}$ and $A_{v,j}$, respectively, and the area ratio is defined as $r_j=A_{h,j}/A_{v,j}$. The jth unit has a total mass $M_{t,j}$ which is composed of both the container mass, $m_{c,j}$ and the liquid mass, $m_{l,j}=2\rho A_{h,j}{L}_{v,j}+\rho A_{v,j}{L}_{h,j}$, with $\rho$ representing the density of the liquid, which is assumed the same for all the devices. Dissipative phenomena experienced by the liquid mass during the motion are accounted for through the head-loss coefficient ${\xi }_j$. The damping and the stiffness parameters of the spring-dashpot unit are denoted by $c_{c,j}$ and $k_{c,j}$, respectively. The horizontal displacement of the jth STLCD unit relative to the floor on which the unit is installed is described by ${\mathrm{y}}_j\left(t\right)$,while ${\mathrm{u}}_j\left(t\right)$, represents the vertical displacements of the liquid inside the jth container relative to its equilibrium position at rest. In the final configuration, when all the devices are placed in the structure, the displacements of all the STLCD units are collected in the n × 1 vectors $\mathit{y}\left(t\right)=\left[{\mathrm{y}}_1\left(t\right);{\mathrm{y}}_2\left(t\right);...;{\mathrm{y}}_n\left(t\right)\right]$ and $\mathit{u}\left(t\right)=\left[{\mathrm{u}}_1\left(t\right);{\mathrm{u}}_2\left(t\right);...;{\mathrm{u}}_n\left(t\right)\right]$, respectively. Hence, the M-STLCD has 2n DOF, n regarding the vertical motion of the liquid and n regarding the translational motion of each unit. The equations of motion for the M-STLCD-controlled n-story structure, obtained using the Euler-Lagrange approach (Pandey et al., 2019), are given in a compact form as follows:

$\mathbf{M}\ddot{\mathbf{x}}\left(t\right)+\mathbf{C}\dot{\mathbf{x}}\left(t\right)+\mathbf{K}\mathbf{x}\left(t\right)=-\stackrel{\sim }{\mathbf{M}}{\ddot{x}}_g\left(t\right)(1)$

where $\mathbf{x}\left(t\right)=\left[\begin{array}{ccc}{\mathbf{x}}_s{\left(t\right)}_{\left[nx1\right]};& \mathbf{y}{\left(t\right)}_{\left[nx1\right]};& \mathbf{u}{\left(t\right)}_{\left[nx1\right]}\end{array}\right]$ is the 3n × 1 vector that collects the structural and device responses, while $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ defined in Equations 2–4 represent the 3n × 3n mass, the damping and the stiffness matrices of the entire M-STLCD-controlled MDOF system, respectively. Each of these matrices is organized into submatrices that group terms associated with the main structure separately from those related to the M-STLCD device, following a subdivision based on recurring patterns observed in the elements describing the system’s dynamics as follows:

${\mathbf{M}}_{\left[3nx3n\right]}=\left[\begin{array}{ccc}{{\mathbf{M}}_s}_{\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}\\ {{\mathbf{M}}_c}_{\left[nxn\right]}& {{\mathbf{M}}_c}_{\left[nxn\right]}& {{\mathbf{M}}_{c,l}}_{\left[nxn\right]}\\ {{\mathbf{M}}_{c,l}}_{\left[nxn\right]}& {{\mathbf{M}}_{c,l}}_{\left[nxn\right]}& {{\mathbf{M}}_l}_{\left[nxn\right]}\end{array}\right](2)$

${\mathbf{C}}_{\left[3nx3n\right]}=\left[\begin{array}{ccc}{\mathbf{C}}_{s\left[nxn\right]}& -{\mathbf{C}}_{c\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}\\ {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{C}}_{c\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}\\ {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{C}}_{l\left[nxn\right]}\end{array}\right](3)$

${\mathbf{K}}_{\left[3nx3n\right]}=\left[\begin{array}{ccc}{\mathbf{K}}_{s\left[nxn\right]}& -{\mathbf{K}}_{c\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}\\ {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{K}}_{c\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}\\ {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{0}}_{\left[nxn\right]}& {\mathbf{K}}_{l\left[nxn\right]}\end{array}\right](4)$

Finally, $\stackrel{\sim }{\mathbf{M}}$ is a 3n × 1 vector that accounts for the inertial contributions due to the ground acceleration, which can be expressed as follows in Equation 5:

${\stackrel{\sim }{\mathbf{M}}}_{\left[3nx1\right]}=\left[\begin{array}{l}{{\mathbf{M}}_s}_{\left[nxn\right]}{\mathbf{\tau }}_{\left[nx1\right]}\\ {{\mathbf{M}}_c}_{\left[nxn\right]}{\mathbf{\tau }}_{\left[nx1\right]}\\ {{\mathbf{M}}_{c,l}}_{\left[nxn\right]}{\mathbf{\tau }}_{\left[nx1\right]}\end{array}\right](5)$

In this regard, ${\mathbf{M}}_s$, ${\mathbf{C}}_s$ and ${\mathbf{K}}_s$ are, respectively, the mass, damping and stiffness matrices associated with the main structure, considered as a classically damped system and $\mathbf{0}$ is a matrix of zeros. It is worth noting that, in the present study, the main structure is assumed to behave linearly. The M-STLCD-related submatrices are denoted as ${\mathbf{M}}_{c,l}$, ${\mathbf{M}}_c$ and ${\mathbf{M}}_l$, while $\mathbf{\tau }=\left[1;1;...;1\right]$ is a n × 1 vector of ones. Specifically, ${\mathbf{M}}_{c,l}$, ${\mathbf{M}}_c$ and ${\mathbf{M}}_l$ are diagonal submatrices expressed below in Equation 6:

${\mathbf{M}}_{c,l\left[nxn\right]}=\lceil \rho A_{h,j}{L}_{h,j}\rfloor ;{\mathbf{M}}_{c\left[nxn\right]}=\lceil \rho A_{h,j}\left(2L_{v,j}+\frac{1}{r_j}{L}_{h,j}\right)+m_{c,j}\rfloor {\mathbf{M}}_{l\left[nxn\right]}=\lceil \rho A_{h,j}\left(2L_{v,j}+r_j{L}_{h,j}\right)\rfloor (6)$

${\mathbf{C}}_c$ and ${\mathbf{C}}_l$, contained in the damping matrix $\mathbf{C}$, are the diagonal damping matrices related to the M-STLCD. In particular, ${\mathbf{C}}_c$ contains the damping terms of each STLCD unit, while ${\mathbf{C}}_l$ contains the damping terms of the liquid as expressed in Equation 7:

${\mathbf{C}}_{c\left[nxn\right]}=\lceil c_{c,j}\rfloor ;{\mathbf{C}}_{l\left[nxn\right]}=\lceil \frac{1}{2}\rho A_{h,j}{r}_j{\xi }_j\left|{\dot{u}}_j\left(t\right)\right|\rfloor (7)$

The liquid behavior is herein considered as nonlinear, as can be seen from the dependence of the jth damping term on the absolute value of the liquid’s vertical velocity $\left|{\dot{u}}_j\left(t\right)\right|$. Similarly, ${\mathbf{K}}_c$ and ${\mathbf{K}}_l$ comprise the stiffness properties related to each STLCD unit as follows in Equation 8:

${\mathbf{K}}_{c\left[nxn\right]}=\lceil k_{c,j}\rfloor ;{\mathbf{K}}_{l\left[nxn\right]}=\lceil 2\rho A_{h,j}g\rfloor (8)$

where g indicates the gravitational acceleration. It should be emphasized that, although the nonlinearity in the present formulation arises exclusively from the liquid dynamics, via the velocity-dependent head-loss term, the coupled interaction between structure and fluid renders the entire system nonlinear. Importantly, this localized nonlinearity does not compromise the generalizability of the formulation, which remains valid and applicable regardless of the source or distribution of nonlinear effects within the system.

To normalize and generalize the analyses, a set of dimensionless parameters that describe the system dynamic characteristics crucial for achieving optimal control performance are introduced. One of the most relevant is the tuning ratio of the jth STLCD unit, defined as ${\nu }_{c,j}={\omega }_{c,j}/{\omega }_j$ where ${\omega }_{c,j}=\sqrt{k_{c,j}/M_{t,j}}$ represents the natural frequency of the jth device and ${\omega }_j$ is the jth fundamental frequency of the structure. Moreover, the damping ratio of the jth STLCD unit is ${\zeta }_{c,j}=c_{c,j}/2M_{t,j}{\omega }_{c,j}$. Similarly, the influence of the ground’s dynamic properties can be described through the ground tuning ratio ${\nu }_{g,j}={\omega }_g/{\omega }_j$ where ${\omega }_g$ is the fundamental frequency of the ground. Moreover, the geometric and mass-related properties of the system also play a crucial role in defining its response. In this respect, ${\alpha }_j=L_{h,j}/L_j$ defines the length ratio, while the liquid column length directly influences the natural frequency of the liquid column ${\omega }_{l,j}$ through the relation ${\omega }_{l,j}=\sqrt{2g/L_j}$. Additionally, the mass of the jth STLCD is divided into the liquid and the container mass contributions, both of which are expressed as ratios relative to the total structural mass: ${\mu }_{l,j}=m_{l,j}/M_{tot}$ and ${\mu }_{c,j}=m_{c,j}/M_{tot}$, being $M_{tot}={\sum }_{j=1}^n{M}_j$. Hence, the mass ratio of the jth STLCD unit relative to the total structural mass can be defined as ${\mu }_{t,j}={\mu }_{l,j}+{\mu }_{c,j}$ or, equivalently, as ${\mu }_{t,j}=M_{t,j}/M_{tot}$.

3 Base excitation generation and response descriptors

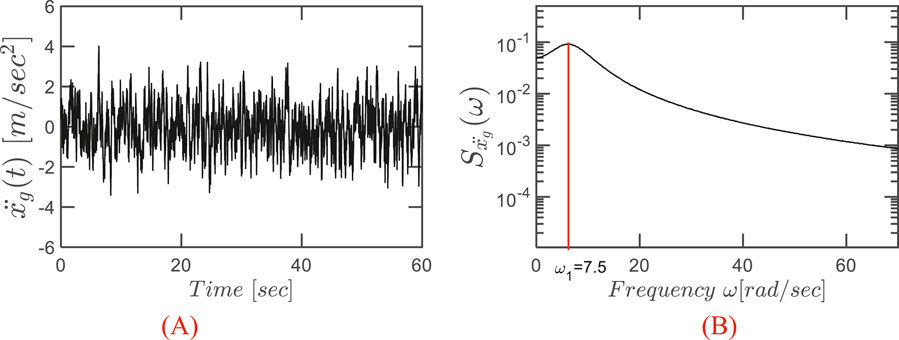
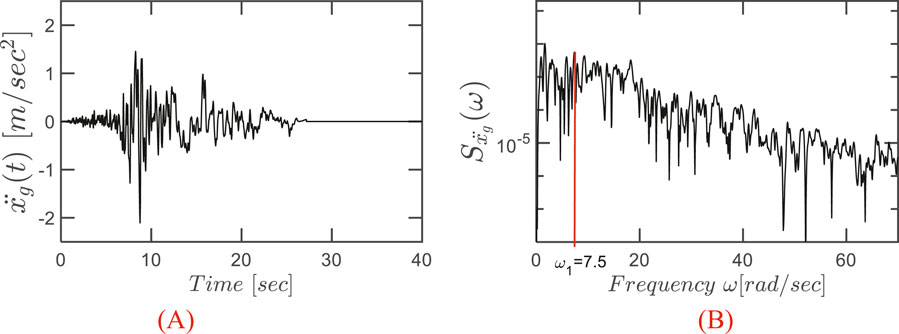
In order to effectively design and optimize the vibration control system, it is essential to accurately characterize the seismic excitation acting on the structure. This section describes the generation of the ground acceleration used as input at the base of the structure and establishes the main response descriptors, which will serve as the basis for the successive sections focusing on both the preliminary analyses on a single STLCD and the subsequent optimization of multiple STLCD devices. In this respect, seismic ground motions are often modeled as stochastic processes to account for their inherently random nature. One of the most widely used representations for characterizing the frequency content of earthquake-induced ground accelerations is the Kanai-Tajimi power spectral density (PSD) function (Chen and Wu, 2001). This widely used formulation accounts for the filtering effects of local soil conditions on seismic waves and is expressed as:

$S_{{\ddot{x}}_g}\left(\omega \right)=S_0\frac{{{\omega }_g}^4+4{{\zeta }_g}^2{{\omega }_g}^2{\omega }^2}{{\left({{\omega }_g}^2-{\omega }^2\right)}^2+4{{\zeta }_g}^2{{\omega }_g}^2{\omega }^2}(9)$

In Equation 9, ${\omega }_g$ and ${\zeta }_g$ denote the natural frequency and damping ratio of the ground, respectively, while $S_0$ represents the peak amplitude of the PSD. Starting from Equation 9, to generate a time-domain representation of the seismic excitation, a single deterministic realization of the ground acceleration ${\ddot{x}}_g\left(t\right)$ can be obtained using Shinozuka’s method (Chen and Wu, 2001). This is achieved by summing a series of harmonic waves with the generic pth wave corresponding to a precise frequency interval having spacing equal to $\Delta \omega$ and central frequency ${\omega }_p=p\Delta \omega$. In particular, ${\ddot{x}}_g\left(t\right)$ is given by:

${\ddot{x}}_g\left(t\right)={\displaystyle \sum _{p=1}^{N_{\omega }}}\sqrt{2S_{{\ddot{x}}_g}\left({\omega }_p\right)\Delta \omega }\sin \left(\left({\omega }_p+\delta {\omega }_p\right)t+{\theta }_p\right)(10)$

In this equation, $N_{\omega }={\omega }_{\max }/\Delta \omega$ is defined as the ratio between the maximum angular frequency ${\omega }_{\max }$ and the frequency step $\Delta \omega$, and represents the total number of discrete frequency components used in the summation. Additionally, $\delta {\omega }_p$ and ${\theta }_p$ represent the generic random variations in frequency and phase associated with the pth wave, respectively, and $2S_{{\ddot{x}}_g}\left({\omega }_p\right)$ denotes the amplitude, at the pth frequency interval, of the two-sided PSD of the stochastic process.

Given the PSD of the input, the structural response can be described by the displacement variance ${\sigma }_{x,j}^2$ and the absolute acceleration variance ${\sigma }_{{\ddot{x}}_a,j}^2$ at the jth floor, respectively expressed as follows in Equations 11a, 11b:

${\sigma }_{x,j}^2={\displaystyle \underset{0}{\overset{\infty }{\int }}}{\left|H_{x,j}\left(\omega \right)\right|}^2{S}_{{\ddot{x}}_g}\left(\omega \right)d\omega (\mathrm{11a})$

${\sigma }_{{\ddot{x}}_a,j}^2={\displaystyle \underset{0}{\overset{\infty }{\int }}}{\left|H_{{\ddot{x}}_a,j}\left(\omega \right)\right|}^2{S}_{{\ddot{x}}_g}\left(\omega \right)d\omega (\mathrm{11b})$

where $H_{x,j}\left(\omega \right)$ and $H_{{\ddot{x}}_a,j}\left(\omega \right)$ correspond to the Frequency Response Functions (FRFs) of the displacement and absolute acceleration ${\ddot{x}}_{a,j}\left(t\right)={\ddot{x}}_j\left(t\right)+{\ddot{x}}_g\left(t\right)$ at the jth floor. These response descriptors serve as fundamental criteria for evaluating the effectiveness of the STLCD placement and optimization strategies in controlling structural vibrations. However, it is worth noting that the calculation of FRFs in this case involves an n-story structure and nonlinear terms, particularly related to the liquid behavior, making a closed-form solution difficult to obtain (Bilello et al., 2002). Therefore, a numerical approach is considered by computing the FRFs in terms of displacement and total acceleration as $H_{x,j}\left(\omega \right)=\mathfrak{I}\left[x_j\left(t\right)\right]/\mathfrak{I}\left[{\ddot{x}}_g\left(t\right)\right]$ and $H_{{\ddot{x}}_a,j}\left(\omega \right)=\mathfrak{I}\left[{\ddot{x}}_{a,j}\left(t\right)\right]/\mathfrak{I}\left[{\ddot{x}}_g\left(t\right)\right]$, being $\mathfrak{I}$ the Fourier Transform. As usual in the literature (Pandey et al., 2019), two performance indicators are introduced to quantify the effectiveness of each STLCD on the structural response:

${{\eta }_{{\ddot{x}}_a}}_{,j}=\frac{{{\sigma }_{{\ddot{x}}_a}^2}_{,j}}{{{\sigma }_{{\ddot{x}}_{a0}}^2}_{,j}}(\mathrm{12a})$

${\eta }_{x,j}=\frac{{\sigma }_{x,j}^2}{{\sigma }_{x_0,j}^2}(\mathrm{12b})$

where ${{\sigma }_{{\ddot{x}}_a}^2}_{,j}$ and ${\sigma }_{x,j}^2$ represent the variance of absolute acceleration and displacement at the jth floor, respectively. Each of these values is compared to the corresponding variance of the uncontrolled structure, which is distinguished by the subscript 0, i.e., ${{\sigma }_{{\ddot{x}}_{a0}}^2}_{,j}$ and ${\sigma }_{x_0,j}^2$, respectively. These two indicators measure the reduction in the structural response achieved by adding the device at the jth floor, with values below one signifying effective vibration mitigation. Clearly, the mathematical formulation introduced in Equation 1 holds even for a number of STLCD units $\overline{n}$ lower than the degrees-of-freedom of the structural system ($\overline{n}<n$).

4 Preliminary analyses: effect of a single STLCD on n-story structures

This Section presents preliminary analyses on the effectiveness of a single STLCD ($\overline{n}=1$) installed at the top of an MDOF structure before extending the study on M-STLCD. The numerical analyses presented here focus on a parametric study, systematically varying key STLCD parameters to assess their individual influence on the structural response. By conducting these multi-parametric preliminary analyses on a benchmark structure, the parameters having the most significant impact on different modes are identified, providing insights into the overall effectiveness of this device. The three-story structure used for these analyses was deliberately defined to construct a representative testbed to assess the extended applicability of liquid-based damping solutions to structures typically considered outside the traditional TLCD target domain, rather than replicating a specific real-world structure. In particular, the model allows for the investigation of control effectiveness in short-period buildings, where geometric constraints limit the feasibility of TLCDs, and where modal contributions vary significantly due to non-uniform damping ratios across modes, as generally observed in real and experimental structures, where damping is rarely uniform across modes (Basili and Angelis, 2022). Specifically, the structure consists of three floors having different lumped masses $M_1$ = 6.0 × 10⁴ kg, $M_2$ = 4.5 × 10⁴ kg and $M_3$ = 3.0 × 10⁴ kg, respectively, while the interstory stiffness values are $k_1$ = 4.0 × 10⁷ N/m, $k_2$ = 2.1 × 10⁷ N/m and $k_3$ = 2.0 × 10⁶ N/m. The damping ratios are equal to 5% for the 1^st mode, 2% for the 2^nd mode, and 3% for the 3^rd mode, and the natural frequencies are ${\omega }_j=\left[7.50,17.23,35.23\right]$ rad/sec, denoting a relatively stiff system (according to (American Society of Civil Engineers, 2022)). Although the natural periods of this structure do not fall into the extremely short range typical of most three-story buildings, they are still significantly lower than those of the more flexible structures where TLCDs are traditionally most effective. This makes the case particularly challenging and of interest for assessing M-TLCD and M-STLCD performance outside of conventional application ranges. As widely documented in the literature, the optimal placement of a single vibration control device is typically at the uppermost floors (Chen and Wu, 2001; Elias et al., 2016; Elias et al., 2019; Fadel Miguel et al., 2016; Suresh and Mini, 2019; Vellar et al., 2019), as the 1^st mode, generally the most dominant, exhibits the largest displacements at these levels. Given the importance of the 1^st mode, the tuning ratio of the single STLCD was selected with respect to the 1^st mode as the primary variable to be varied in the parametric analyses, as it is typically the most influential factor in vibration mitigation. Since this section focuses on a single STLCD device all variables formerly denoted with the subscript j have been simplified by omitting the subscript. Accordingly, the tuning ratio is defined as ${\nu }_c={\omega }_c/{\omega }_1$. In each analysis, ${\nu }_c$ varied together with one additional STLCD parameter at a time: the liquid column length $L$, the head-loss coefficient $\xi$ and the container damping ratio ${\zeta }_c$. One additional analysis specifically explores the influence of the ground tuning ratio with respect to the 1^st fundamental mode, ${\nu }_g={\omega }_g/{\omega }_1$. Parameters such as the liquid and container mass ratios relative to the total structural mass, ${\mu }_l=m_l/M_{tot}$ and ${\mu }_c=m_c/M_{tot}$ are kept constant in this Section, as configurations with increased mass ratios are explored later in the study. Similarly, the horizontal-to-total length ratio $\alpha$ is fixed to a value consistent with previous studies on STLCD systems (Ghosh and Basu, 2004). To quantify the effectiveness of a single STLCD, the two dimensionless performance indicators in Equations 12a, b were computed as ${{\eta }_{{\ddot{x}}_a}}_{,3}={{\sigma }_{{\ddot{x}}_a}^2}_{,3}/{{\sigma }_{{\ddot{x}}_{a0}}^2}_{,3}$ and ${\eta }_{x,3}={\sigma }_{x,3}^2/{\sigma }_{x_0,3}^2$, where ${{\sigma }_{{\ddot{x}}_a}^2}_{,3}$ and ${\sigma }_{x,3}^2$ represent the variance of absolute acceleration and displacement at the top floor, each compared to the corresponding variance in the uncontrolled structure, i.e., ${{\sigma }_{{\ddot{x}}_{a0}}^2}_{,3}$ and ${\sigma }_{x_0,3}^2$, respectively. These two indicators measure the reduction in the structural response achieved by adding one device on the 3^rd floor, with values below one signifying effective vibration mitigation. Each two-parameter analysis is summarized in Figure 2 through graphs illustrating the relationship between ${\nu }_c$ (reported in x-axis) and the selected performance indicator, ${{\eta }_{{\ddot{x}}_a}}_{,3}$ or ${\eta }_{x,3}$ (reported in y-axis), while varying one additional parameter at a time (${\nu }_g$, $L$, $\xi$ , ${\zeta }_c$ and ${\mu }_l$) and keeping the remaining parameters fixed (with reference set $L=20m$, ${\mu }_l=0.5\%$, ${\mu }_c=0.5\%$, $\xi =10$, ${\zeta }_c=0.05$ and $\alpha =0.85$). In addition, ${\nu }_g=3$, $S_0=0.05$ m²/s³ and ${\zeta }_g=0.6$ are used in Equation 9 to generate the broadband base excitation. As can be seen in Figure 2A, the STLCD unit allows for a reduction of the response for values of ${\nu }_c$ approaching 0.9. In addition, as ${\nu }_g$ increases, a further reduction in response becomes evident when ${\nu }_c$ approaches the 2^nd mode. This result highlights the importance of extending the optimization beyond the fundamental mode to higher structural modes, ensuring a more comprehensive mitigation across the diverse frequency contents of the input excitation. On the other hand, the curves in Figure 2B suggest that, in terms of displacements, the response reduction is mainly achieved for the 1^st mode, since the 2^nd mode does not appear to benefit from the presence of the STLCD across the investigated values of ${\nu }_g$. The same trend observed in Figures 2A,B can also be noted in Figures 2C–L, where different values of $L$, $\xi$, ${\zeta }_c$ , and ${\mu }_l$ are explored. As expected, Figures 2I–L show that increasing the mass ratio improves control efficiency, particularly for higher modes. However, as noted in both literature and practice, varying the mass ratio may require different container sizes, which is often impractical. Therefore, the mass ratio is typically kept constant across devices and floors to enhance practical feasibility and limit added structural weight. For this reason, while the following analyses assume a fixed mass for all devices, some scenarios with increased, but still uniform, mass ratios will also be considered in subsequent sections to explore scalability and performance trends. In general, as can be deduced from Figure 2, tuning the STLCD device to the 2^nd mode provides a reduction in the acceleration response, improvement which is not appreciable in terms of displacement response. Hence, rather than targeting displacements, the subsequent studies will focus on optimizing the control strategy with the aim of reducing absolute accelerations, as this has a more direct impact even on occupant comfort.

Figure 2

Figure 2. Effect of a single STLCD on the structural response at the top floor for various tuning ratios ${\nu }_c$, expressed in terms of: (A,C,E,G,I) normalized acceleration variance ${{\eta }_{{\ddot{x}}_a}}_{,3}$ and (B,D,F,H,J) normalized displacement variance ${\eta }_{x,3}$, each plotted against ground tuning ratio ${\nu }_g$, liquid column length $L$, head loss coefficient $\xi$, damping ratio ${\zeta }_c$, and liquid mass ratio ${\mu }_l$, respectively.

5 Sequential optimization strategy for M-STLCD in n-story structures

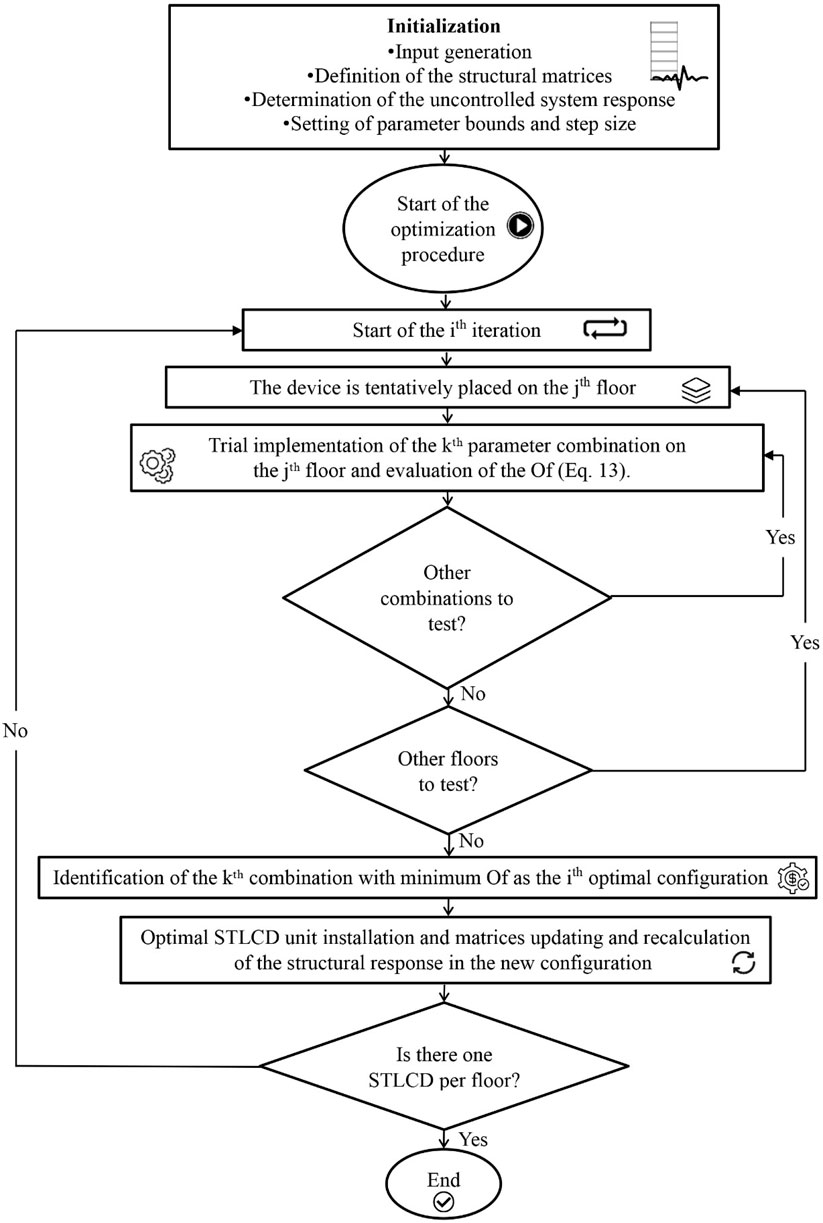
This Section proposes an optimization procedure developed to design the M-STLCD in order to enhance the dynamic performance in n-story structures. Since the M-STLCD is composed of several STLCD units, the goal is to determine the optimal set of parameters and optimal positioning of each device within the structure to achieve an overall reduction in the structural response. Notably, the optimization follows a sequential approach, where STLCD units are installed progressively, one per iteration, ensuring that each unit adapts to the evolving dynamic characteristics of the structure. It is worth emphasizing that, to date, existing literature has not proposed any sequential optimization methodology for the coordinated design and placement of multiple nonlinear STLCD devices across multi-story structures. The proposed optimization strategy installs one STLCD at a time, excluding previously selected floors from subsequent consideration. However, analogously to (Chen and Wu, 2001), a single optimized device can later be interpreted as a set of equivalent dampers distributed across multiple floors in a subsequent phase of the analysis. While the restriction of one device per floor may limit the exploration of more synergistic configurations, such as deploying multiple devices on the same floor, the framework is inherently flexible and can be adapted to support such scenarios if desired.

Unlike most metaheuristic algorithms that operate in a “global” optimization mode, seeking the best overall solution by considering all devices simultaneously, often under a static structural configuration, the proposed method integrates the evolving structural dynamics at each iteration. It accounts for the fact that installing a single damper modifies the dynamic properties of the structure, thereby influencing the optimal parameters of subsequent devices. Although the algorithm can be readily extended to perform global optimization if required, the present study deliberately focuses on understanding the effect of each installation step rather than pursuing a globally optimal configuration. This allows for the isolated evaluation of each damper’s influence, providing ease of interpreting intermediate outcomes and clearer insight into the physical mechanisms involved and the interdependencies between design variables. Additionally, given its sequential nature, the procedure allows earlier termination if satisfactory results are achieved, or based on specific practical criteria, significantly reducing potential implementation costs. This structured, step-by-step approach thus offers a flexible and practical framework, aligned with how design and installation often evolve in real engineering practice, guiding the selection of design variables to be optimized at each stage. In this respect, as is common in optimization procedures, certain parameters are generally optimized as they significantly influence the effectiveness of the control strategy, while others remain fixed due to structural constraints or geometric limitations. For instance, ${\alpha }_j$ is typically predefined to ensure practical feasibility, while mass ratios ${\mu }_{l,j}$ and ${\mu }_{c,j}$ are kept constant to prevent excessive loading on the structure. Moreover, $A_{h,j}$ and $A_{v,j}$ are set equal in this study. However, since it is acknowledged that holding certain parameters constant may limit the generalizability of the findings, future studies could extend this work by systematically varying additional parameters, enabling a more comprehensive exploration of the system’s response. The algorithm is fully extendable to include any additional variables as needed. Such an approach would be particularly valuable in scenarios requiring precise calibration of the protective methodology to address site-specific conditions or unique structural configurations. Consequently, for the purpose of this study, for the generic jth STLCD unit, the natural frequency ${\omega }_{c,j}$ and the damping coefficient ${\zeta }_{c,j}$ of the container, the natural frequency ${\omega }_{l,j}$ (or equivalently the total liquid lengths $L_j$ since ${\omega }_{l,j}=\sqrt{2g/L_j}$) and the head-loss coefficient ${\xi }_j$ of the liquid, are identified as the key design variables to be optimized within the control algorithm. Each parameter is selected from a predefined discrete search space, bounded by lower and upper limits and explored with a fixed step size. Unlike common implementations of metaheuristic algorithms (Almufti et al., 2023), which operate in a “quasi-continuous” domain and make it difficult to enforce strict step sizes on design variables, the proposed method provides complete control over the resolution of each decision parameter. By working within a fully discrete, user-defined search space, the procedure enhances both the traceability and interpretability of the optimization process. Moreover, this step-wise approach yields realistic and practically implementable solutions that align with construction constraints, where device parameters (e.g., column lengths in TLCD/STLCD systems) often correspond to standardized, pre-manufactured components (such as liquid containers) that cannot be adjusted with arbitrary precision. It is worth noting that the procedure is fully automated, sequential and transparent, requiring only basic structural and excitation data, pre-defined parameter bounds, and the choice of an Objective function ($Of$). It simplifies interpretation by directly associating results with physical parameters, facilitating controlled adjustments during simulations. This contrasts with metaheuristic algorithms, which typically involve multiple internal tuning parameters, not directly linked to the physical behavior of the structure (e.g., mutation and crossover rates in GA or inertia weights and social/cognitive coefficients in PSO), whose optimal settings are often unknown and must be selected arbitrarily or by trial-and-error (Vié, 2020; Aote et al., 2013). Such sensitivity of heuristic algorithms can lead to significant variability in the solution quality and often results in convergence to suboptimal or non-reproducible configurations unless multiple runs, parameter studies and comparative assessments with several algorithms are conducted. Moreover, although the current implementation assumes linear behavior for the primary structure, the proposed optimization can be arranged for models incorporating other material or geometric nonlinearities. Indeed, since the procedure relies exclusively on the updated structural response at each iteration, regardless of whether the system behaves linearly or nonlinearly, it requires no modifications to the core algorithm. This makes the proposed method particularly attractive for practical applications involving different structural behaviors, without requiring fundamental changes to the optimization strategy.

Based on the insights gained from the preliminary analyses, the $Of$ is formulated to capture the progressive reduction in absolute acceleration variance across all floors, as higher-mode peaks are predominantly evident in this context, as observed in Figure 2. Following established approaches in the literature (Chen and Wu, 2001), the square root of the sum of absolute acceleration variances at each floor is chosen as $Of$ since it is a representative quantity of the structural dynamic response. Clearly, at the initial stage (state 0), the variance ${\sigma }_{{\ddot{x}}_{a0},j}^2$ in terms of absolute accelerations of each floor of the uncontrolled structure is first computed, serving as a reference. As the optimization starts, the variance at each iteration is normalized relative to the corresponding value in the previous configuration. In detail, the $Of$ is defined as in Equation 13.

$O{f}_i=\sqrt{{\displaystyle \sum _{j=1}^n}\frac{{\sigma }_{{\ddot{x}}_{a}i,j}^2}{{\sigma }_{{\ddot{x}}_a\left(i-1\right),j}^2}}\text{\hspace{0.17em}with\hspace{0.17em}}i=1,\dots ,n(13)$

where i is the ith iteration varying from one to the number of DOF. The optimal configuration at the ith iteration corresponds to the combination of the installation floor and the set of parameters that minimizes the $Of$. The optimization procedure, which can be implemented in any computational environment (e.g., MatLab), can be summarized in the following steps:

1. Initialization: The algorithm generates the structural base acceleration input, defines the matrices of the uncontrolled structure, and evaluates the structural response of the nonlinear system in Equation 1 in terms of absolute acceleration variances ${\sigma }_{{\ddot{x}}_{a0},j}^2$ at each floor. At this stage, no STLCD units are attached. Then, the algorithm defines the system matrices and establishes the search vectors for the optimal parameters. The procedure accounts for system matrices, as defined in Equation 1, with their maximum possible dimension, i.e., 3n × 3n for $\mathbf{M}$, $\mathbf{C}$ and $\mathbf{K}$ and 3n × 1 for $\stackrel{\sim }{\mathbf{M}}$, where all STLCD-related terms are initially set to zero. These matrices will serve as a restore-point configuration for the 1^st iteration.

2. 1^st iteration (placement of the 1^st STLCD): The algorithm starts the 1^st iteration. The 1^st STLCD unit is tentatively placed on the lowest floor, removing the zero rows and columns associated with inactive STLCD degrees-of-freedom from the restore-point matrices. The $Of$ in Equation 13 is evaluated for every possible combination of parameters at that floor until there are no more combinations left to be assessed.

• The process is repeated for each successive floor up to the top floor, until all possible combinations of the single unit across different floors have been thoroughly explored.

• The combination of parameters, including the floor and the STLCD properties, that leads to the minimum of the $O{f}_1$ is identified as the optimal configuration for the 1^st optimal STLCD unit, which is installed on the detected floor. This floor is then excluded from the installation of additional units in subsequent iterations.

• After installing the 1^st optimal STLCD unit, the algorithm updates the full-size restore-point matrices accordingly and recalculates the nonlinear structural response for the new configuration. Both the updated mathematical model and the associated structural response then serve as the new baseline for the next iteration.

3. Subsequent iterations (placement of STLCD units on remaining floors): Once the 1^st iteration has been completed, the algorithm proceeds to execute the subsequent iterations, similarly retracing the aforementioned steps (clearly excluding the initialization steps). The process continues until each single, optimally tuned STLCD unit has been placed on each floor.

An overview of the sequential optimization process is provided in the flowchart shown in Figure 3.

Figure 3

Figure 3. Flowchart of the sequential optimization process.

6 Sequential optimization outcomes

This section presents the results of the proposed optimization procedure applied to the M-STLCD system in multi-story structures, focusing on optimal parameters, placement, and the resulting reductions in structural response. To ensure a comprehensive analysis, two types of structures were examined: one with three stories and the other with six stories, both modeled as shear-type planar frames. For both structures, the outcomes of the optimization procedure are analyzed in terms of the optimal parameters determined for each STLCD, in terms of the iterative variance reduction and FRF peak reductions at a specific floor, as well as the variance reduction achieved across all floors upon completion of the optimization procedure using a broadband base excitation generated as described in Section 3. Furthermore, to provide a comprehensive examination of the procedure, the M-STLCD control strategy is compared with common strategies incorporating the M-TMD and the M-TLCD, optimized by adopting the same sequential optimization procedure as the M-STLCD. Thus, in each iteration of these procedures, one optimal unit is determined along with its corresponding installation floor. For each TMD unit, the parameters to be determined through the optimization procedure are the natural frequency and the damping ratio denoted as ${\omega }_{d,j}$ and ${\zeta }_{d,j}$, respectively, while for each TLCD unit, the parameters to be optimized are the natural frequency ${\omega }_{l,j}$ and the liquid head-loss coefficient ${\xi }_j$. It is worth noting that compared to previous studies on TLCDs and STLCDs (Pandey et al., 2019; Masnata and Pirrotta, 2024; Masnata et al., 2024a), which employ linearization techniques and optimize an equivalent damping ratio rather than the head loss coefficient, this optimization is conducted considering the nonlinearities characterizing the liquid behavior. Regarding the mass ratios, a mass equal to 1% of the total structural mass is assigned to each device for consistency across comparisons. Specifically, the solid mass of each TMD and the liquid mass of each TLCD unit are set to 1% of the structural mass. For consistency, each STLCD unit maintains the same total mass ratio of 1%, equally distributed between the sliding container (0.5%) and the liquid (0.5%), ensuring a fair comparison with the other devices. In this manner, the cumulative mass ratios attained at the end of the optimization for each strategy (≈3% for the three-story model and ≈6% for the six-story model) remain well within the ranges reported in literature and adopted in full-scale installations of vibration control devices (Elias et al., 2017). For both the M-TLCD and M-STLCD, ${\alpha }_j$ = 0.85, which represents an intermediate value among those most adopted (Gao et al., 1997; Ziegler, 2007; Di Matteo et al., 2016; Fei et al., 2019; Adam et al., 2017). More specifically, for the two investigated structures, the parameter constraints were defined based on practical considerations and established references and are summarized in Table 1 along with the corresponding value ranges, fixed values, optimized variables, and step sizes. Frequency-related bounds were expressed as multiples of the lowest and highest fundamental frequencies of the uncontrolled structure, denoted as ${\omega }_{\min }$ and ${\omega }_{\max }$, respectively (Chen and Wu, 2001). Hence, for the M-STLCD control strategy ${\omega }_{c,j}\in \left[0.64{\omega }_{\min },1.36{\omega }_{\max }\right]$ and, similarly, for M-TMD ${\omega }_{d,j}\in \left[0.64{\omega }_{\min },1.36{\omega }_{\max }\right]$. For both M-TMD and M-STLCD strategies, the damping ratios were constrained to values typical of underdamped systems (i.e., ${\zeta }_{c,j}$ < 1), generally slightly below 10%, in line with prior studies (Chen and Wu, 2001). Liquid column lengths for M-TLCDs and M-STLCDs were selected within a realistic range, reflecting standard room dimensions and ensuring that a sufficient quantity of liquid can be accommodated, typically between 1% and 5% of the total structural mass, to achieve meaningful vibration reductions. While shorter columns shift the device frequency upward, benefiting higher-mode control, the selected range reflects practically feasible scenarios, particularly when considering large-scale applications (Balendra et al., 1995). Unlike classical damping ratios, head-loss coefficients can reach much higher values, often exceeding unity; while some numerical studies report extremely high values (>1000) (Wang et al., 2020), experimental data typically remain below 80 (Gao et al., 1997; Di Matteo et al., 2016; Min et al., 2005; Wu et al., 2005), so the selected range was chosen to align more closely with actual applications. It is also worth noting that excessively high head-loss coefficients can significantly restrict fluid motion, causing STLCDs to resemble TMDs. Despite this convergence in behavior, as outlined in the Introduction, the fluid-based system retains some intrinsic advantages over solid-mass devices. Additionally, a comparison with M-TMD strategies is presented in the following section to illustrate the relative effectiveness of both approaches. During the optimization with an assigned unit mass of 1%, the broadband noise excitation was generated considering ${\omega }_g=7.62$ rad/sec, $S_0=0.05$ m²/s³ and ${\zeta }_g=0.6$ in Equation 9. The time history and corresponding PSD of the excitation are shown in Figure 4, with the PSD clearly indicating that the maximum spectral amplitude occurs near the structure’s natural frequency. At this exploratory stage, the excitation was chosen following the methodology in (Chen and Wu, 2001) to provide a preliminary analysis basis and ensure consistency with previous studies.

Table 1

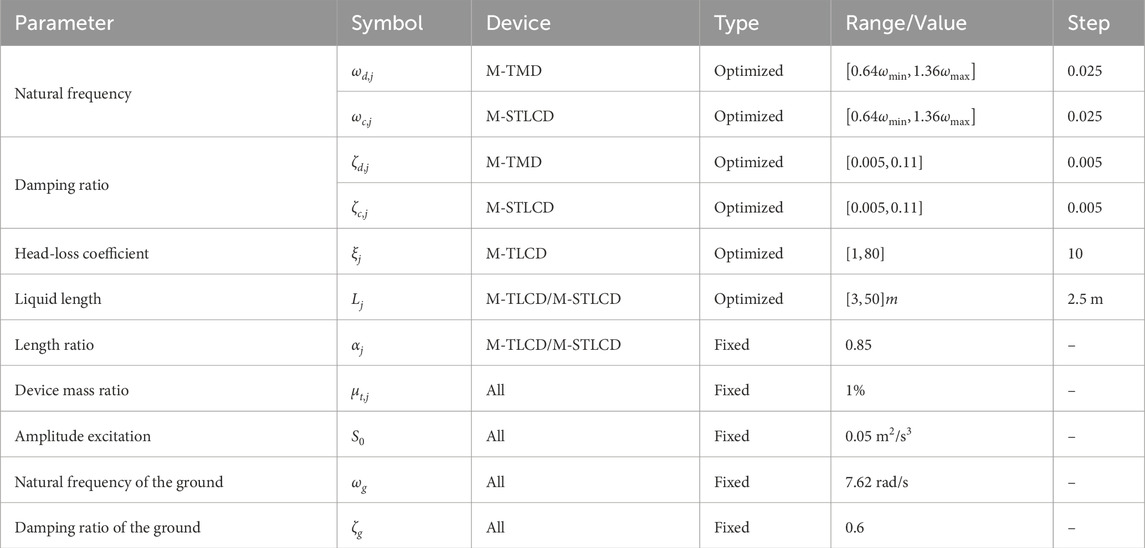
Table 1. Parameter definitions and design constraints for the damping devices and excitation used in the multi-story optimization procedure.

Figure 4

Figure 4. Broadband noise-based base excitation: (A) time history; (B) PSD.

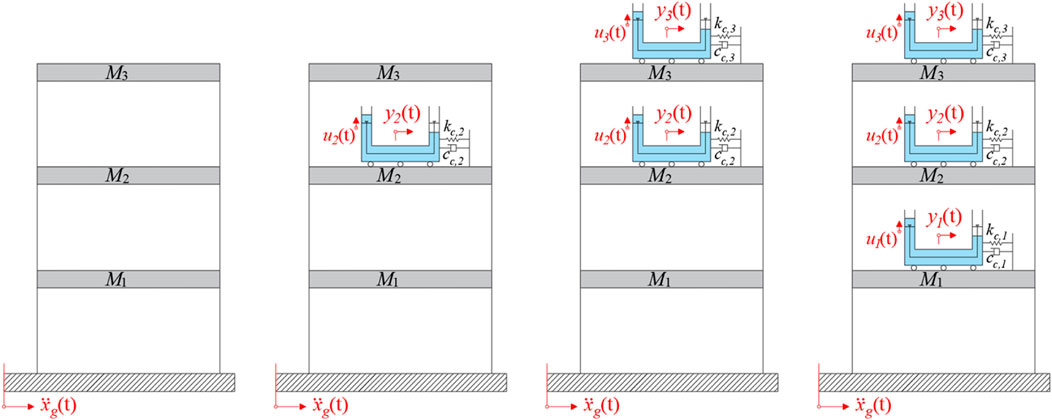
6.1 Case study 1: three-story structure

This Section reports the optimization results for the three-story structure previously introduced in Section 4. In particular, the results are provided in terms of optimized parameters, installation floors, and the vibration modes targeted by the optimization procedure for the M-STLCD-controlled three-story structure. An intuitive representation of the optimal installation floors is provided in Figure 5, while detailed results are listed in Table 2, which shows the outcomes of each iteration of the proposed procedure. For each entry, a comparison with the global PSO algorithm, implemented using the default MATLAB package, is included by reporting, in round parentheses next to the proposed values, the corresponding PSO results in terms of both device parameters and normalized variances obtained for the M-STCLD strategy. It is important to note that, unlike the sequential nature of the proposed approach, PSO results refer to the final configuration obtained by optimizing all devices simultaneously, rather than iteratively. As can be observed, the 1^st STLCD unit is tuned to the 2^nd mode from the very 1^st iteration and placed on the 2^nd floor. The tuning decision is likely influenced by the strong contribution of the 2^nd mode, partly due to its low damping ratio, while the placement is driven by the largest component of the 2^nd mode at the 2^nd floor, making that level the most effective location for the 1^st installations to achieve optimal control performance. At the 2^nd iteration, the 2^nd STLCD is installed on the 3^rd floor and tuned to the 1^st mode. In the 3^rd and final iteration, the last device is placed on the 1^st floor and tuned to the 2^nd mode. As can be deduced from Table 2, although the parameters obtained via PSO differ significantly from those identified by the proposed sequential algorithm, the resulting acceleration variances are practically equivalent. At the upper two floors, the PSO approach achieves slightly lower variances, whereas at the 1^st floor, the proposed method provides a marginally better reduction, highlighting how PSO’s effectiveness depends on careful tuning of internal parameters. Despite its simplicity, the proposed method delivers competitive, and sometimes superior, results without requiring extensive calibration. In any case, the maximum discrepancy is limited to 1.92% at the 2^nd floor. This close agreement in performance confirms the effectiveness of the proposed sequential strategy, despite its simpler and more interpretable optimization process. The results for the other M-TMD and M-TLCD control strategies are also listed in Table 2. The M-TMD follows a similar trend to the M-STLCD. The M-TLCD, however, does not exhibit the same clear pattern of mode and floor selection, suggesting that its physically realizable lengths were insufficient to properly target the 2^nd mode. This deviation, compared to the other devices, stems from constraints on the liquid length, imposed to ensure the practical feasibility of the M-TLCD, which shifts the liquid frequency either too far above or too far below the structural frequency. The effectiveness of these three strategies is compared in Figure 6, where the normalized variances of absolute acceleration and displacement are shown, respectively. Figure 6 illustrates the evolution of the normalized acceleration variance at each floor of the three-story structure throughout the optimization process. A clear trend of progressive variance reduction is observed for the M-STLCD, showing performance closely aligned with the M-TMD across all iterations. In contrast, the M-TLCD exhibits higher variance levels throughout the procedure, failing to match the effectiveness of the other strategies. Similarly, Figure 7 presents the evolution of the normalized displacement variance at each floor in the final configuration. For the M-STLCD, a comparison is included with results obtained via a global PSO to highlight the effect of simultaneous optimization across all devices through a metaheuristic approach. As shown in Figure 7A, in terms of acceleration variance, PSO exhibits essentially the same performance. On the other hand, regarding displacement response (Figure 7B), although it was not directly included in the objective function, the PSO algorithm yields slightly better results. This can be attributed to the global nature of the PSO strategy, which simultaneously adjusts all device parameters in a way that may indirectly favor improved displacement performance. Despite not being explicitly targeted, such outcomes suggest that the broader search space exploration characteristic of PSO may occasionally capture favorable trade-offs among multiple dynamic response quantities. Nonetheless, the proposed sequential discrete procedure yields comparable performance, especially in terms of acceleration reduction, as seen in Figure 7A, while offering significant advantages in terms of implementation simplicity and transparency of the optimization process. It is deterministic, less sensitive to algorithmic tuning, and requires substantially fewer resources. These characteristics make it particularly suitable for practical civil engineering applications, where robustness, reproducibility, feasibility, parameter traceability, step size control, and sequential installation might outweigh marginal performance gains. Again, the M-STLCD progressively reduces displacement variances at all floors with results comparable to the M-TMD. Figure 7 presents the final variance values across all floors in terms of normalized absolute accelerations (Figure 7A) and displacements (Figure 7B). In Figure 7A, the M-STLCD closely matches the M-TMD at the 3^rd floor, while the M-TMD achieves slightly lower variances at the 1^st and 2^nd floors. In contrast, Figure 7B shows that the M-STLCD attains slightly lower displacement variance at the 3^rd floor (∼0.57), and comparable performance across all levels. The M-TLCD, on the other hand, remains the least effective solution in both acceleration and displacement responses.

Figure 5

Figure 5. Installation floors for the M-STLCD-controlled three-story structure.

Table 2

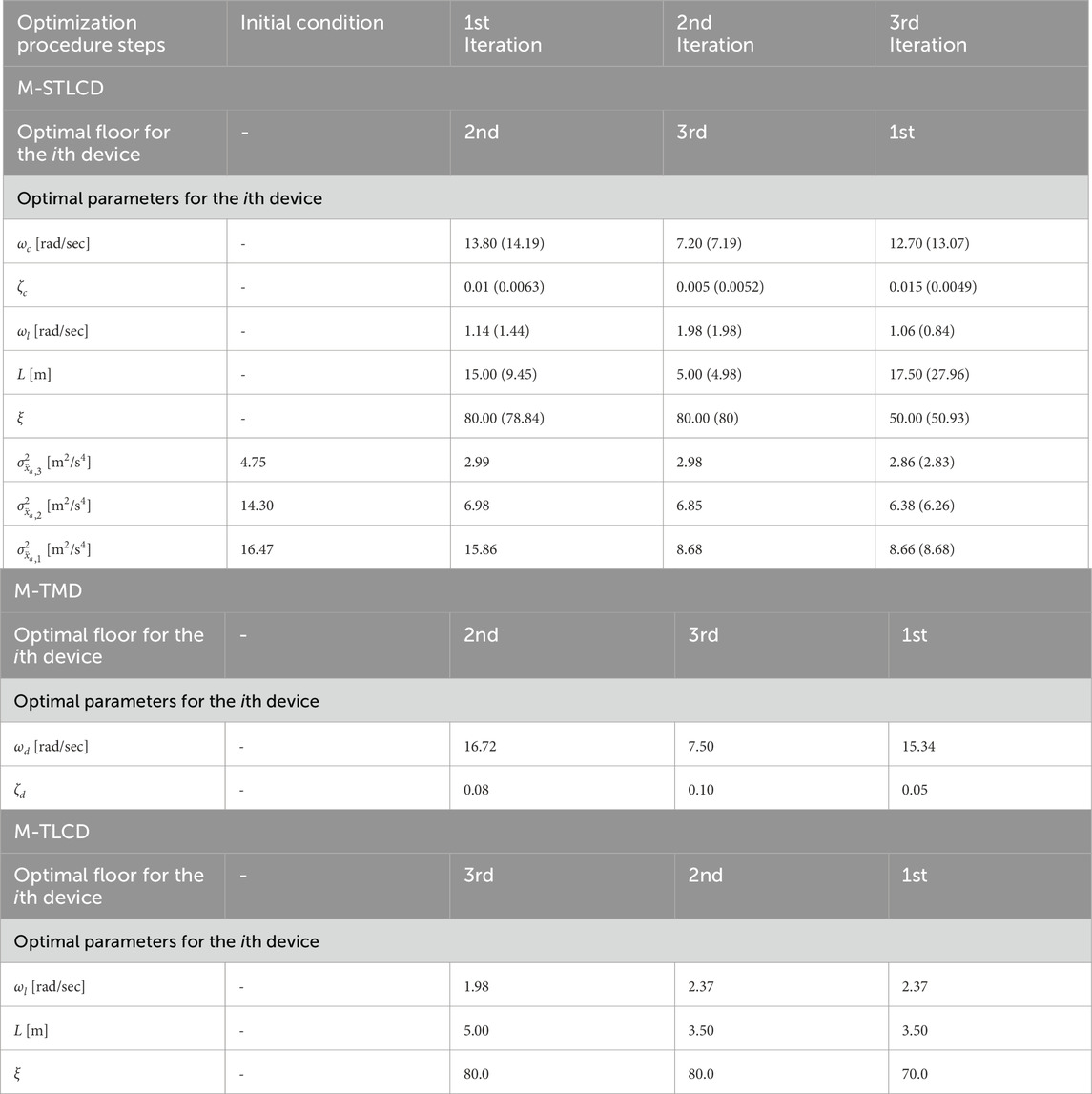
Table 2. Optimized parameters, installation floors, and tuned modes for the M-STLCD, M-TMD, M-TLCD controlled three-story structure.

Figure 6

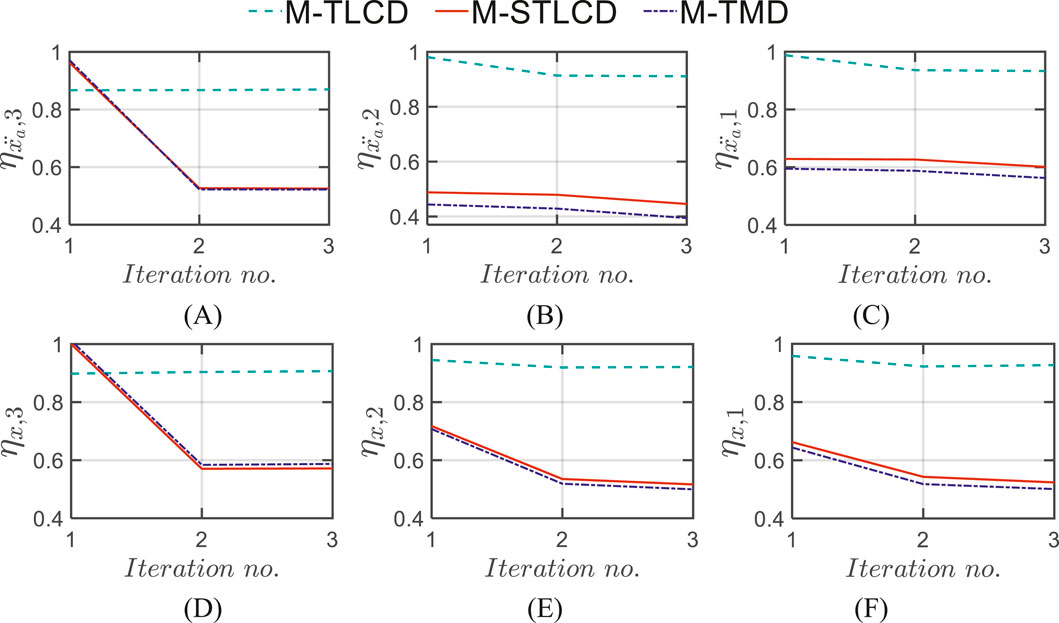
Figure 6. Normalized acceleration variance (top row) at the: (A) 3^rd; (B) 2^nd; (C) 1^st floor, and normalized displacement variance (bottom row) at the: (D) 3^rd; (E) 2^nd; (F) 1^st floor of the three-story structure for each iteration: M-STLCD vs. M-TMD and M-TLCD.

Figure 7

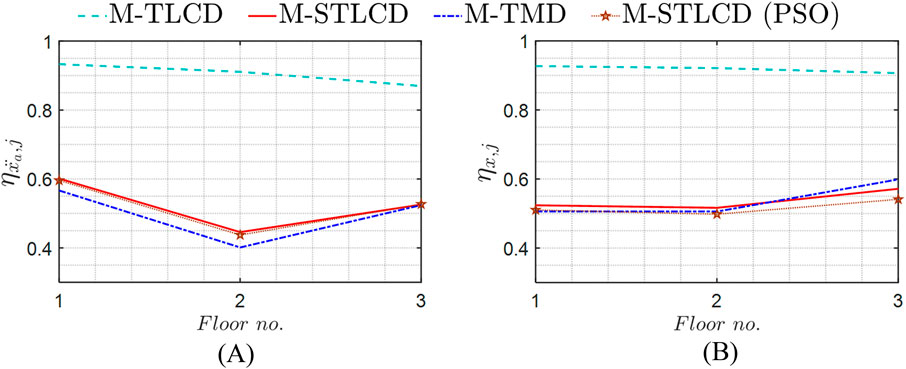
Figure 7. Normalized variance in the final configuration in terms of (A) acceleration ${\eta }_{{\ddot{x}}_a,j}$; (B) displacement ${\eta }_{x,j}$ for each floor of the three-story structure: M-STLCD (optimized through the proposed procedure or the PSO (pentagram markers)) vs. M-TMD and M-TLCD.

Figure 8 illustrates the iterative evolution of the FRFs for the three-story structure, comparing the M-STLCD-controlled system with the uncontrolled case, in terms of absolute acceleration for the 1^st, 2^nd, and 3^rd floors, shown in panels (A)-(C), respectively. As can be seen, the device sequentially targets the 2^nd mode in the 1^st iteration, then the 1^st mode, and finally refines the 2^nd mode again. In particular, the influence of the first STLCD on the subsequent devices is evident from Figure 8A. The first STLCD is placed on the 2^nd floor to target the 2^nd vibration mode, which exhibits a dominant peak in the uncontrolled structure, particularly evident in Figure 8B. This device is effectively tuned to reduce the 2^nd mode’s contribution, leading to a significant attenuation of the corresponding peak of 65.44%, 61.74%, and 62.14% at the 3^rd, 2^nd, and 1^st floors, respectively. Once the 2^nd mode is mitigated, the 1^st mode becomes the most critical contributor to the structural response. Consequently, the second STLCD, selected in the following iteration, is tuned closer to the first natural frequency to suppress the now-dominant 1^st mode, resulting in further attenuation of the lower-frequency peak by 55.48%, 27.64%, and 15.95% at the 3^rd, 2^nd, and 1^st floors. In the 3^rd iteration, the optimizer refines the response further by addressing residual contributions from the 2^nd mode, achieving additional reductions of 67.50%, 64.26%, and 63.87%, respectively. This iterative pattern highlights how the optimization strategy adapts to the evolving modal content. The influence of each previously installed STLCD is inherently accounted for, as the system matrices are updated after each iteration. Although the process is sequential, inter-device interactions are implicitly captured, and each new device responds to the residual dynamics left unaddressed by earlier ones. The consistent peak attenuation across all floors confirms the effectiveness of the M-STLCD approach. Finally, Figure 9 compares the FRFs in the final configuration (last iteration) among the M-STLCD, M-TLCD and M-TMD strategies. From this comparison, it emerges that the M-TLCD consistently underperforms in mitigating the peak responses; by contrast, both the M-STLCD and the M-TMD effectively suppress the 1^st and 2^nd modes. Specifically, the M-STLCD achieves a higher peak reduction of the 1^st mode at the 3^rd floor (56.07% for M-STLCD vs. 54.51% M-TMD), and the M-TMD provides higher peak attenuations of the 2nd mode at lower floors (64.26% M-STLCD vs. 72.37% M-TMD at the 2nd floor, and 63.87% M-STLCD vs. 72.25% M-TMD at the 1st floor).

Figure 8

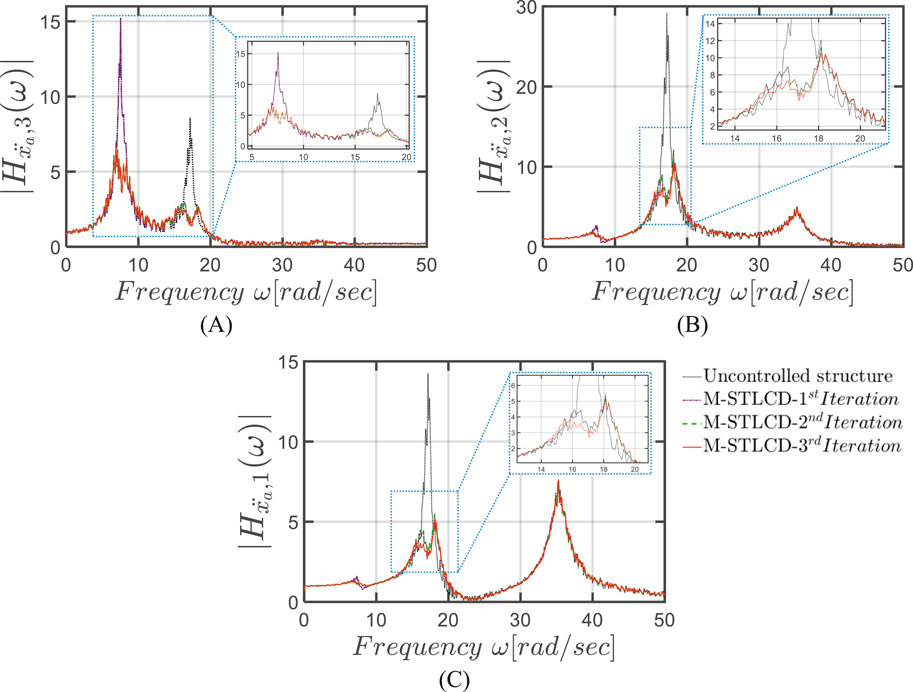
Figure 8. FRFs in terms of absolute accelerations at the: (A) 3^rd; (B) 2^nd; (C) 1^st floor, for each iteration of the optimization procedure for the M-STLCD-controlled three-story structure.

Figure 9

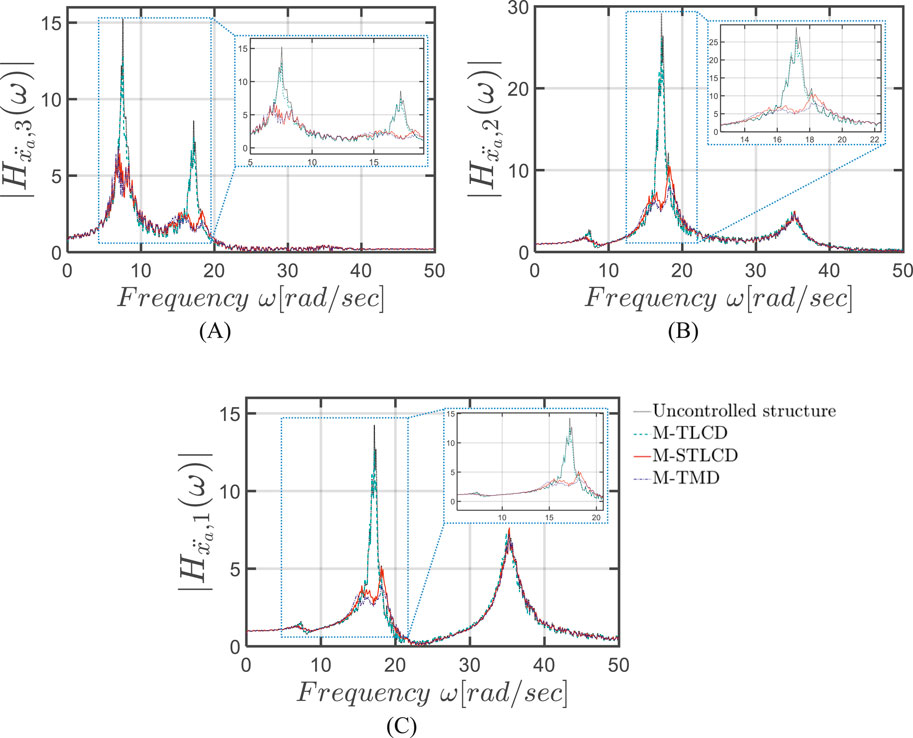
Figure 9. FRFs in terms of absolute accelerations in the final configuration at the: (A) 3^rd; (B) 2^nd; (C) 1^st floor, of the three-story structure: M-STLCD vs. M-TMD and M-TLCD.

6.2 Case study 2: six-story structure

To demonstrate the generalization capability of the proposed optimization procedure across different structural configurations, this section presents the optimization results for the six-story reference structure, which has already been investigated in the literature for multi-modal control via TMDs (Chen and Wu, 2001). The reference structure consists of six floors having identical lumped masses $M_j$ = 4.3 × 10⁴ kg (j = 1, … ,6) and uniform interstory stiffness values $k_j$ = 4.0 × 10⁷ N/m (j = 1, … ,6). A modal damping ratio of 3% was assumed for all modes, and the natural frequencies are ${\omega }_j=\left[7.62,22.43,35.93,47.34,56.00,61.41\right]$ rad/sec.

Figure 10 depicts the results of the optimization procedure in terms of the installation floors for each iteration, while Table 3 presents the details of the results of the optimization procedures for the M-STLCD-controlled six-story structure. Unlike the three-story structure, each STLCD here is installed sequentially from the top to the bottom floor, almost always targeting the 1^st structural mode and switching its tuning to the 2^nd mode only at the 5^th iteration as a consequence of the primary influence of the fundamental mode in early iterations. In contrast to the 3-DOF case, the acceleration variances obtained through the PSO algorithm are unexpectedly higher than those achieved by the proposed sequential method highlighting the sensitivity of global optimization algorithms to the choice of their internal parameters (such as population size, inertia weight, and acceleration coefficients) which, if not properly tuned, may lead to suboptimal results. These findings further reinforce the fact that, despite its simplicity and lack of global coordination, the proposed algorithm is capable of delivering competitive, and in some cases superior, performance without the need for extensive parameter calibration. As shown in Table 3, which also includes results for the M-TMD and M-TLCD, similar trends are observed for the M-TMD. In contrast, detecting the target mode is challenging for the M-TLCD, as the identified frequencies often deviate from the fundamental ones of the uncontrolled structure, underscoring its inadequacy for this type of short-period structure. Figure 11 illustrates the variation in normalized acceleration variance at each floor of the six-story structure over the course of the optimization process, comparing the performance of the M-STLCD, M-TLCD, and M-TMD. Overall, both the M-STLCD and the M-TMD achieve comparable reductions in variance, while the M-TLCD consistently underperforms. From the 6^th down to the 3^rd floor (Figures 11A–D), the M-STLCD and the M-TMD progressively reduce the structural response. A similar trend is observed at the lower levels (Figures 11E,F), where the steeper drop between the 4^th and 5^th iterations highlights the effectiveness of the 5^th unit, installed on the second floor and tuned to the 2^nd mode, in mitigating local accelerations. A similar trend is observed in terms of normalized displacement variance at all floors over the course of the optimization process (Figure 12), with the M-STLCD and M-TMD demonstrating comparable effectiveness, while the M-TLCD continues to show limited effectiveness in mitigating displacements. Figure 13A illustrates the final normalized variance in terms of absolute accelerations across all floors for each control strategy in the final configuration. As can be seen in Figure 13A, and as already evident from Table 3, in terms of normalized acceleration variance, PSO exhibits essentially the same performance, albeit slightly lower. While the M-TLCD remains the least effective, the M-STLCD shows progressive improvement, ultimately approaching the performance of the M-TMD at the upper floors. Notably, the M-TMD matches or even exceeds the performance of the M-STLCD in terms of normalized displacement variance at all levels (Figure 13B), while the M-TLCD proves to be the least effective. Again, as in the case of the three-story structure, the PSO algorithm yields slightly better results.

Figure 10

Figure 10. Installation floors for the M-STLCD-controlled six-story structure.

Table 3

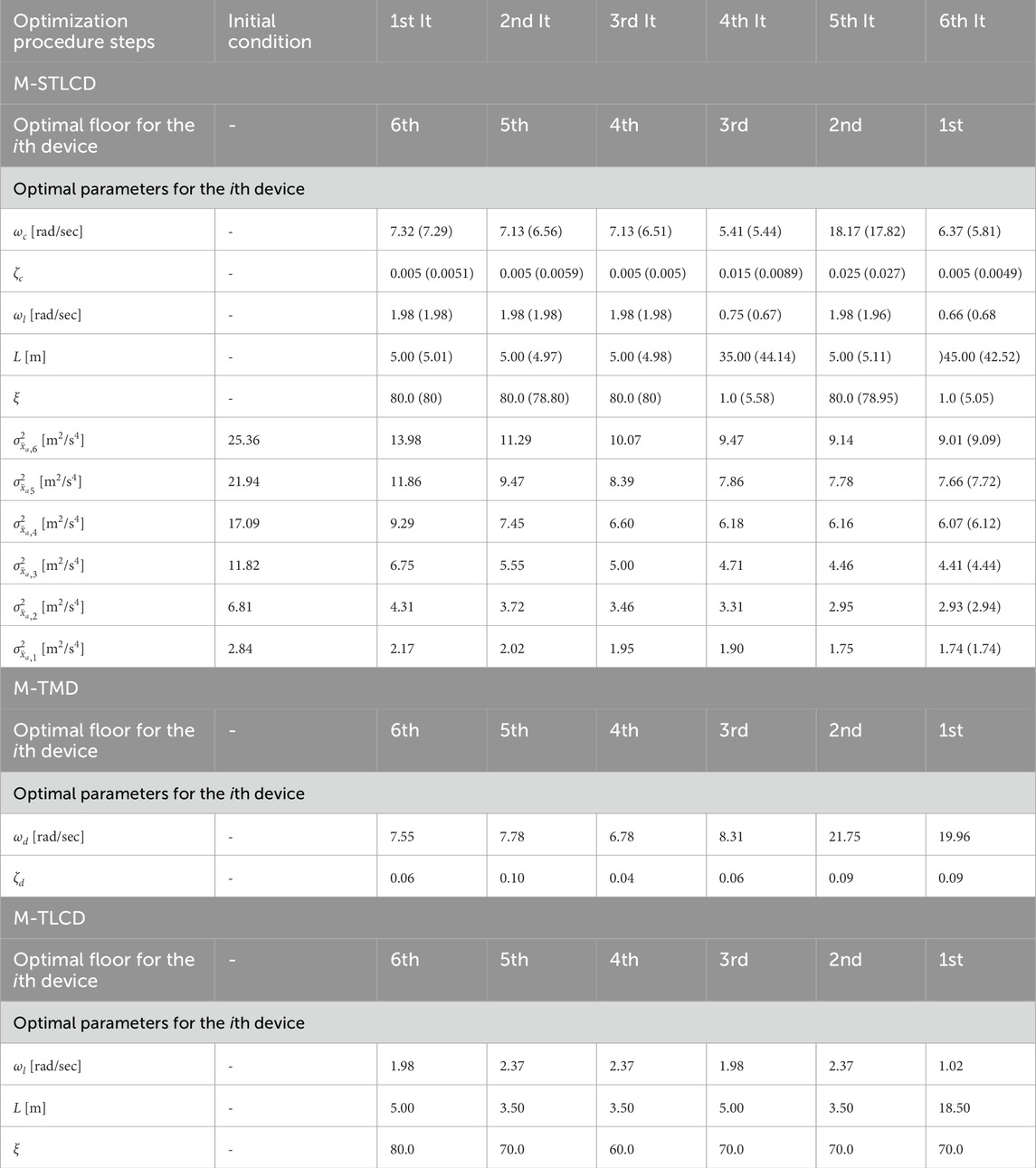
Table 3. Optimized parameters, installation floors, and tuned modes for the M-STLCD, M-TMD, M-TLCD-controlled six-story structure.

Figure 11

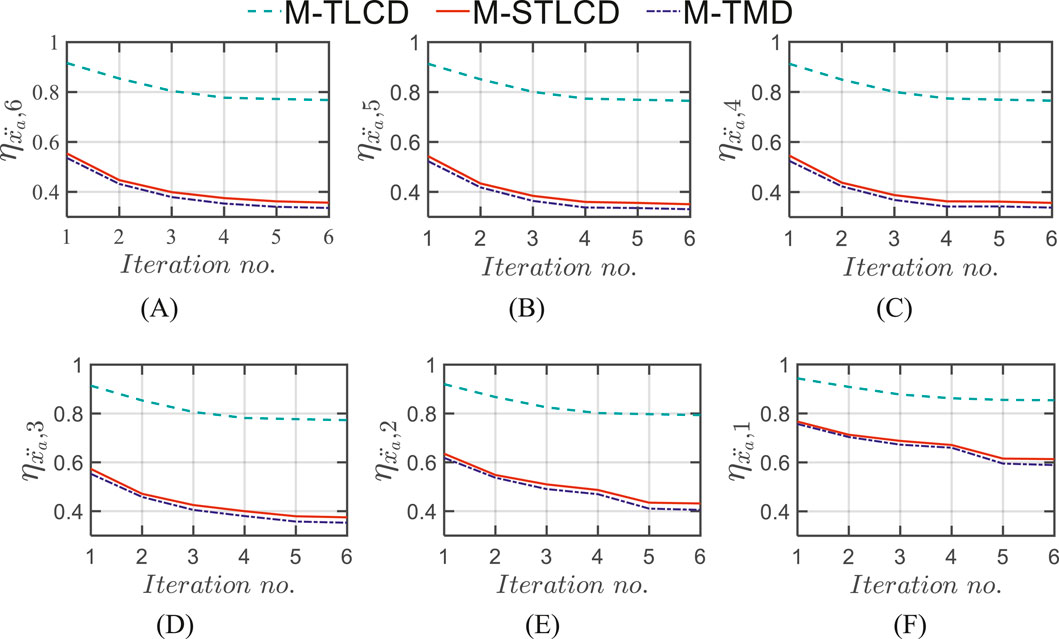
Figure 11. Normalized acceleration variance ${\eta }_{{\ddot{x}}_a,j}$ at the: (A) 6^th; (B) 5^th; (C) 4^th; (D) 3^rd; (E) 2^nd; (F) 1^st floor of the six-story structure for each iteration: M-STLCD vs. M-TMD and M-TLCD.

Figure 12

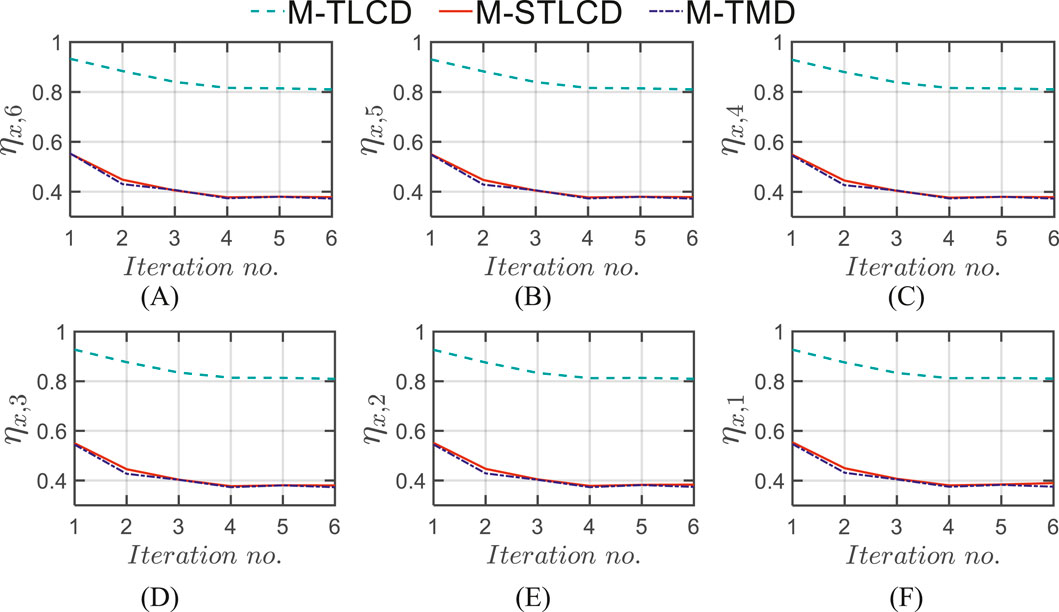
Figure 12. Normalized displacement variance ${\eta }_{x,j}$ at the: (A) 6^th; (B) 5^th; (C) 4^th; (D) 3^rd; (E) 2^nd; (F) 1^st floor of the six-story structure for each iteration: M-STLCD vs. M-TMD and M-TLCD.

Figure 13

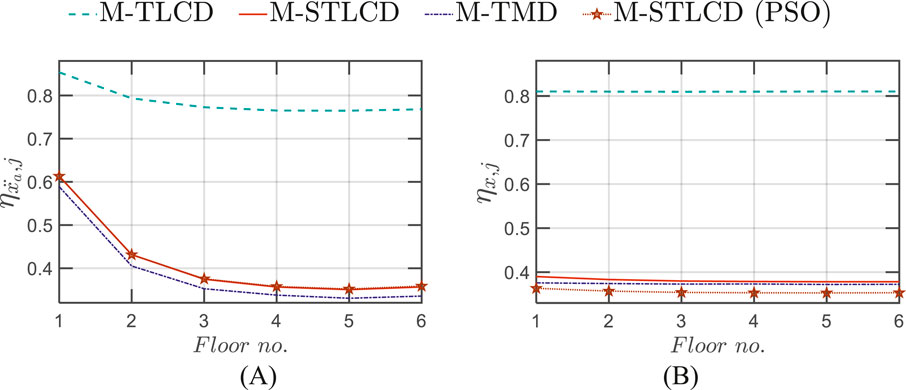
Figure 13. Normalized variance in the final configuration in terms of: (A) acceleration ${\eta }_{{\ddot{x}}_a,j}$; (B) displacement ${\eta }_{x,j}$ for each floor of the six-story structure: M-STLCD (optimized through the proposed procedure or the PSO (pentagram markers)) vs. M-TMD and M-TLCD.

Figure 14 illustrates the iterative evolution of FRFs in terms of absolute accelerations for the M-STLCD control strategy compared to the uncontrolled structure. The uncontrolled structure exhibits a dominant 1^st mode, with progressively lower magnitudes from the 6^th to the 1^st floors. At the 2^nd and 1^st floors, however, the contribution of the 2^nd mode becomes significant and, due to the reduced amplitude of the 1^st mode at these levels, the two modes exhibit comparable magnitudes. From the 1^st iteration, the initial STLCD unit substantially reduces the 1^st mode across all floors, achieving a peak reduction of 57.69% at the 6^th floor. The attenuation continues in iterations 2 and 3, albeit with diminishing impact, while the 4^th iteration further refines the 1^st mode’s reduction, leading to 71.96% peak reduction. A significant shift occurs in the 5^th iteration, which specifically targets the 2^nd mode, leading to a marked attenuation of the 2^nd peak across all floors, reaching 52.79% at the 6^th floor. Finally, Figure 15 highlights the M-STLCD’s performance relative to alternative approaches, showing that the M-STLCD and the M-TMD demonstrate comparable reductions in the 1^st mode (72.21% for M-STLCD vs. 76.07% for M-TMD at the 6^th floor), as well as in the 2^nd mode (52.22% for M-STLCD vs. 54.22% for M-TMD at the 6^th floor). In contrast, the M-TLCD achieves only modest reductions in both modes, confirming its limitations in addressing higher-mode contributions in short-period structures.

Figure 14

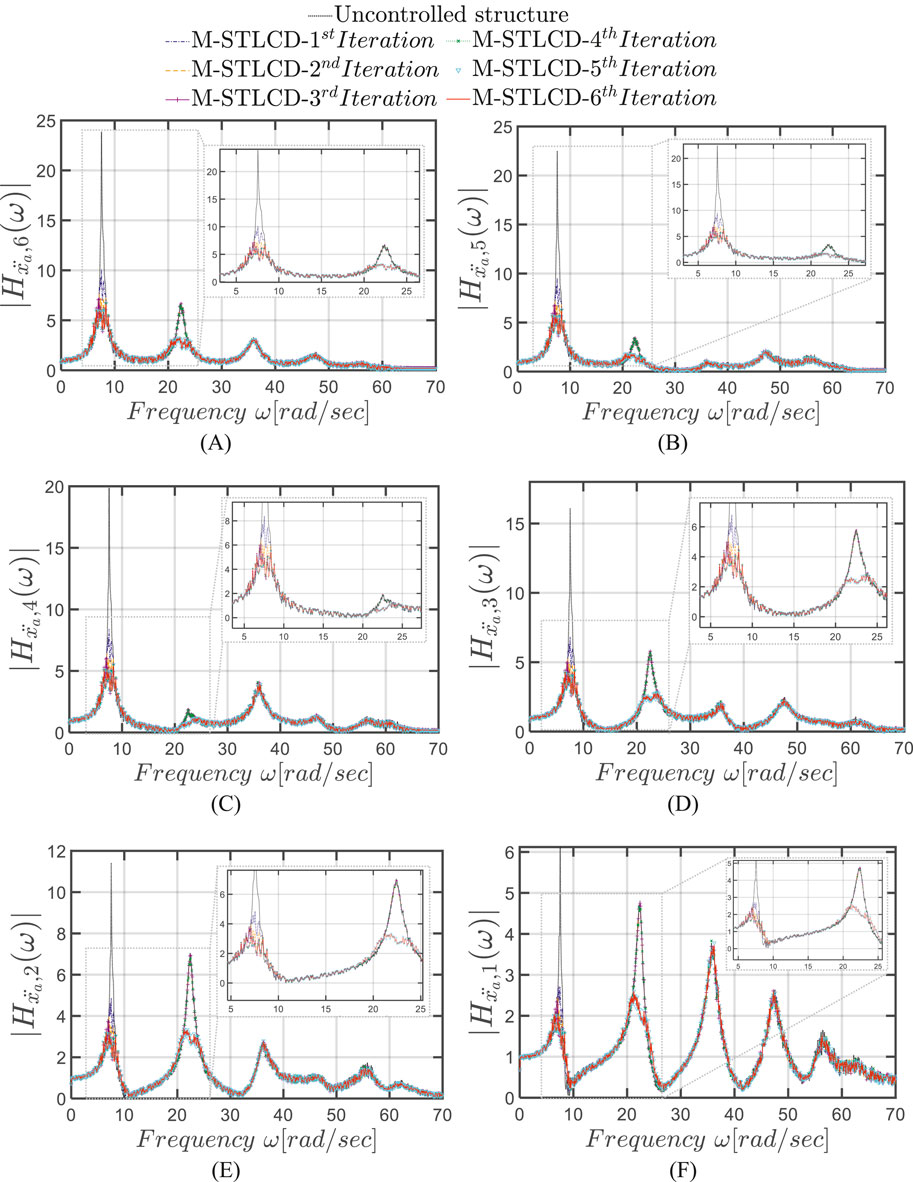
Figure 14. FRFs in terms of absolute accelerations for each iteration at the: (A) 6^th; (B) 5^th; (C) 4^th; (D) 3^rd; (E) 2^nd; (F) 1^st floor for each iteration of the optimization procedure for the M-STLCD-controlled six-story structure.

Figure 15

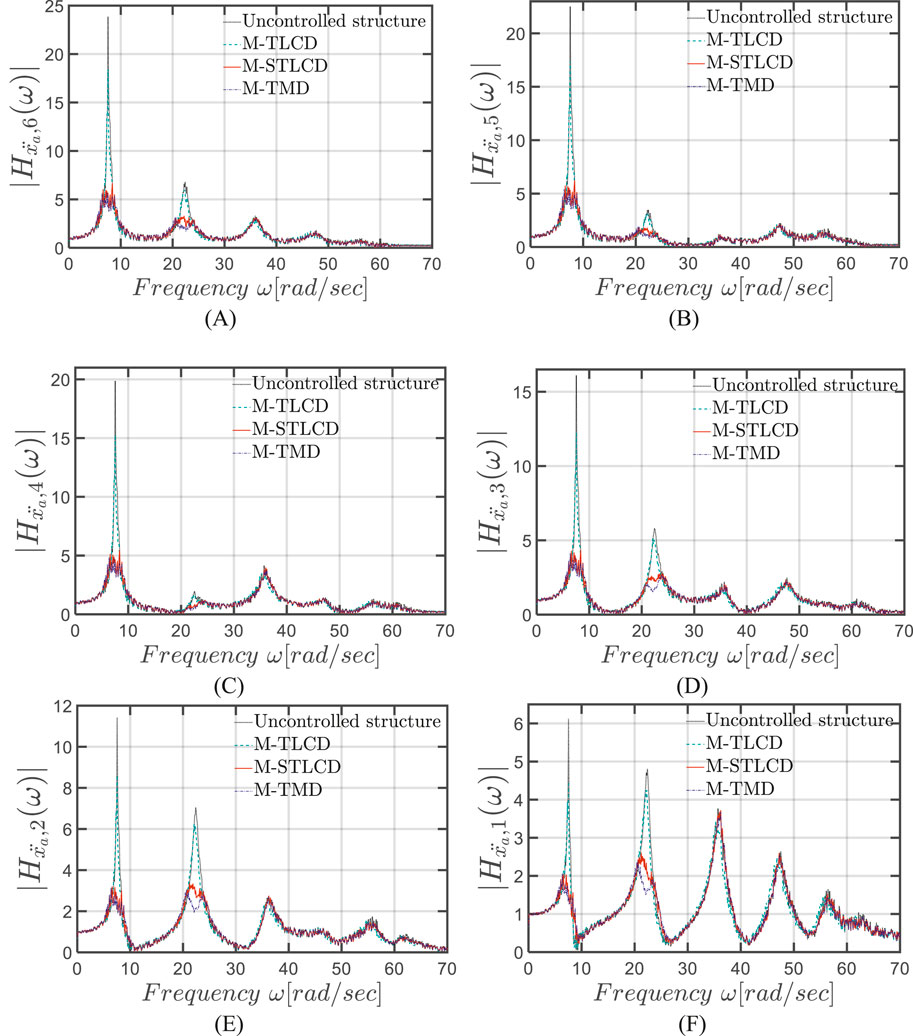
Figure 15. FRFs in terms of absolute accelerations in the final configuration at the: (A) 6^th; (B) 5^th; (C) 4^th; (D) 3^rd; (E) 2^nd; (F) 1^st floor of the six-story structure: M-STLCD vs. M-TMD and M-TLCD.

7 Time-history analyses of final M-STLCD-optimized configurations

This Section evaluates the control performance of the optimized M-STLCD in n-story structures through numerical simulations in the time domain in comparison with the corresponding optimal M-TLCD and M-TMD solutions. As in Section 6, results are presented separately for the three-story and six-story structures. First, time-domain assessment has been carried out under the same broadband excitation described in Section 6. The broadband noise excitation adopted for the time-history analyses has been calibrated to match the amplitude range associated with severe seismic events in seismically active regions (Joshi et al., 2019). Generated numerically through Equations 9, 10, it features a predominant frequency ${\omega }_g=7.62$ rad/sec that deliberately falls within the resonance bandwidth of the case-study structures. This configuration places both the three-story and six-story structures in a resonant or near-resonant first-mode condition, further amplifying the structural response and posing an even more demanding scenario for vibration control. Following the device design phase outlined in Section 6, each damper unit is initially assigned a mass equal to 1% of the total structural mass. To further explore the scalability of the sequential tuning procedure, a second set of simulations has been conducted with increased unit mass ratios for each M-STLCD, M-TMD, and M-TLCD unit: 4% for the three-story structure and 2% for the six-story structure. In both cases, the resulting total control mass amounts to 12%, which remains within the practical range typically recommended in the literature (Elias et al., 2017). Finally, further analyses have been performed by subjecting both structures to a real seismic event. In this respect, to evaluate the M-STLCD control strategy under realistic seismic conditions, the increased-mass configurations have been tested using the 1999 Kocaeli earthquake in Turkey, characterized by a pronounced impulsive content, whose corresponding time history and PSD function are shown in Figure 16. Importantly, for both increased mass excitation scenarios, the broadband noise and the recorded earthquake, all sequential optimization procedures for the M-STLCD, M-TLCD, and M-TMD were re-executed to ensure a consistent evaluation of each control strategy under specific input conditions and to confirm the adaptability of the optimization framework to site-specific structural demands. The results for three-story and six-story structures are presented in dedicated subsections comparing the M-STLCD, M-TLCD, M-TMD, and the uncontrolled structure as the baseline. The results are presented in terms of peak values, as these are particularly important since peak accelerations can affect occupant comfort or damage sensitive equipment, while excessive interstory displacements are directly linked to increased demands on both structural and non-structural components. Additionally, time-history plots are provided to demonstrate the temporal evolution of structural accelerations and interstory drifts throughout the seismic events.

Figure 16

Figure 16. Kocaeli earthquake: (A) time history; (B) PSD.

7.1 Case study 1: three-story structure

The first set of results pertains to the peak responses of the three-story structure under a broadband noise excitation. In this regard, the peak absolute accelerations at all floors ${\ddot{x}}_{k,peak}=\max \left[{\ddot{x}}_k\left(t\right)\right]$ and interstory drifts $\Delta {x_k}_{,k-1,peak}=\max \left[x_k\left(t\right)-x_{k,k-1}\left(t\right)\right]$ (with k = 1,2,…,ndof) are reported in Figures 17A,B, while Figures 17C,D illustrates the corresponding percentage reductions, denoted as ${\epsilon }_{{\ddot{x}}_{k,peak}}$ and ${\epsilon }_{\Delta {x_k}_{,k-1,peak}}$, achieved by each control strategy, M-STLCD, M-TMD, and M-TLCD, relative to the uncontrolled case in both acceleration and drift compared to the uncontrolled case. Results are presented for two damper mass ratios: 1% and 4% of the total structural mass. Importantly, the control strategies were not simply scaled in mass; rather, all sequential optimization procedures, for the M-STLCD, the M-TLCD, and the M-TMD, were re-executed under the structural input to reflect the updated design requirements. As can be seen from Figure 17C, M-STLCD and M-TMD outperform M-TLCD in both acceleration and drift reductions, particularly at higher mass ratios. At 4% mass ratio, the M-STLCD strategy achieves the highest peak acceleration reduction (46.66%) and significant drift reduction (25.41%), comparable to the M-TMD which provides the best drift reduction (29.21%) and strong acceleration mitigation (47.83%).

Figure 17

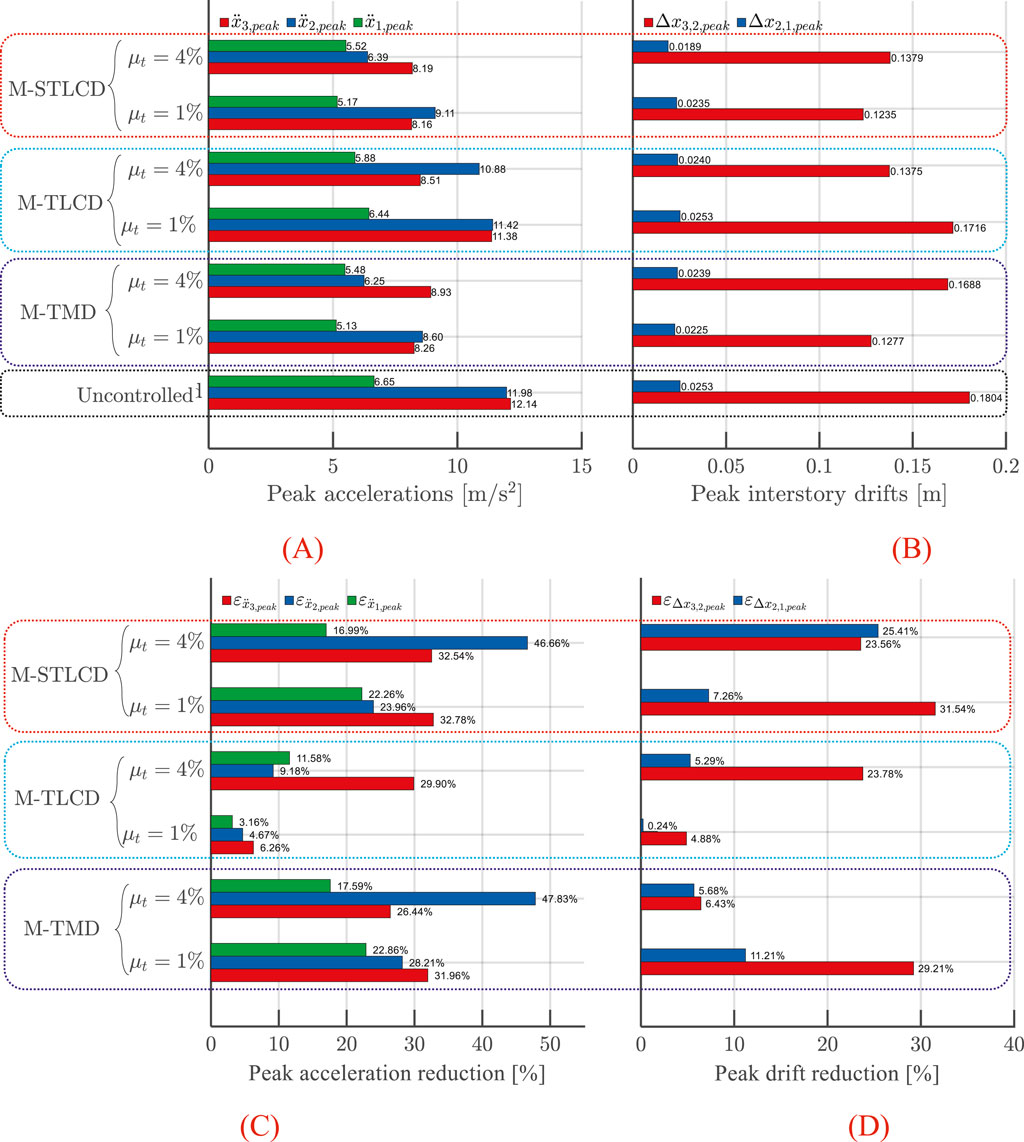
Figure 17. (A) Peak floor accelerations; (B) interstory drifts; (C) acceleration reduction; (D) drift reduction in the three-story structure: M-STLCD vs. M-TMD and M-TLCD control strategies under broadband noise excitation.

These trends are clearly illustrated in the time-history plots shown in Figure 18, which refers to the case with a 4% mass ratio. Specifically, Figures 18A,B display the time-history responses of the top floor acceleration and the interstory drift between the upper floors, respectively. In both cases, the M-STLCD demonstrates robust and consistent performance, effectively reducing the structural response throughout the event. The M-TMD shows comparable overall performance, though it occasionally exceeds the uncontrolled response in localized instances. In contrast, the M-TLCD performs the worst among the three strategies.

Figure 18

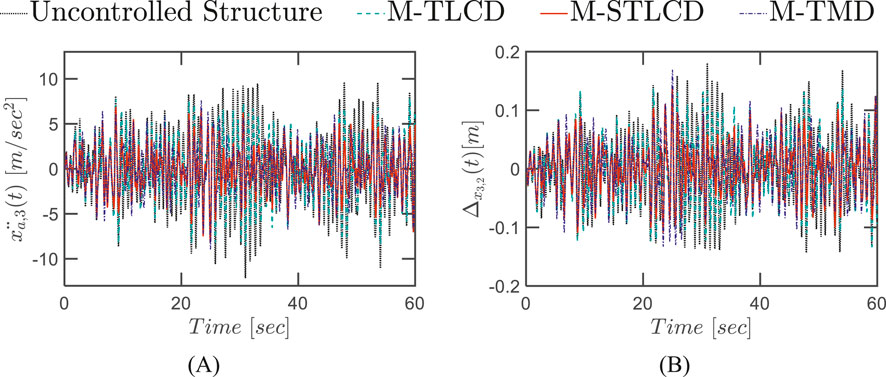
Figure 18. Time-history response of the three-story structure equipped with M-STLCD, M-TMD, and M-TLCD, each having a mass equal to 4% of the total structural mass, subjected to broadband noise excitation: (A) top floor absolute accelerations; (B) interstory drift.

Finally, similar trends are observed in Figure 19, which illustrates the structural response to the real accelerogram recorded during the 1999 Kocaeli earthquake. At the 3^rd floor, the M-TMD achieves the greatest peak acceleration reduction (Figure 19A), reaching 37%, while the M-STLCD remains highly competitive with a 26% reduction. In contrast, the M-TLCD consistently delivers lower effectiveness, showing limited reductions across all floors and highlighting its reduced suitability for impulsive seismic inputs. In terms of interstory drift (Figure 19B), the M-STLCD achieves a 14% reduction between the 3^rd and 2^nd floors, while the M-TMD shows a more substantial reduction of 21%. Notably, the M-TLCD performs poorly, slightly exceeding the uncontrolled response at this interstory level. Overall, the M-STLCD exhibits robust and consistent performance, maintaining effective response reduction even under the challenging, impulsive nature of real earthquake excitation. Its results remain competitive with the M-TMD and clearly superior to the M-TLCD strategy. Clearly, if the goal is to assess whether the system remains within linear limits under these severe earthquake scenarios, the proposed procedure can be applied using specific structural models, alongside standard structural codes. Indeed, the current procedure is based on mass, damping, and stiffness matrices with numerical values that are detached from specific material or geometric information, which is essential for directly verifying linearity. While this aspect can be effectively addressed in a subsequent design phase, involving experiments and tailored protection strategies, the present formulation offers a solid and flexible foundation upon which more detailed, application-driven assessments can be systematically developed. Moreover, only a sample of real earthquakes has been investigated, which is, of course, not exhaustive. Nonetheless, the same procedure can be extended to a wide range of excitation scenarios using comprehensive ground motion data tailored to specific locations and seismic code requirements.

Figure 19

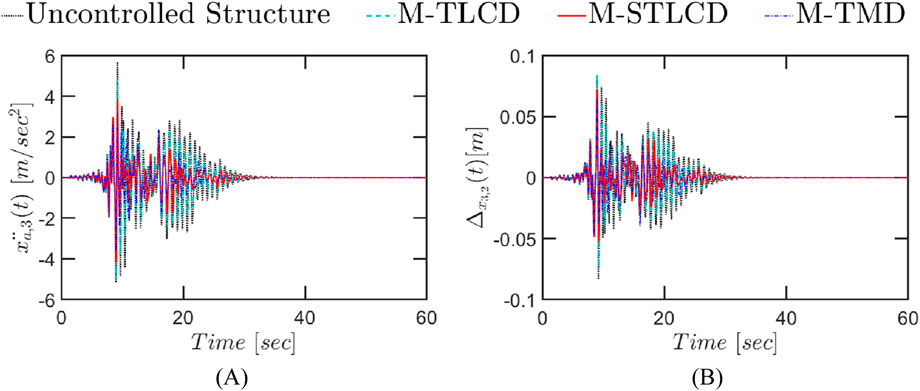
Figure 19. Time-history response of the three-story structure equipped with M-STLCD, M-TMD, and M-TLCD, each having a mass equal to 4% of the total structural mass, subjected to a real earthquake record (1999 Kocaeli): (A) top floor absolute accelerations; (B) interstory drifts.

7.2 Case study 2: six-story structure

This subsection, dedicated to the six-story structure, presents the peak values of absolute accelerations and interstory drifts across all floors, along with time-history responses under both broadband noise and real earthquake base excitations. Specifically, Figure 20 summarizes peak structural responses and corresponding reductions for the six-story structure subjected to the broadband noise excitation, comparing damper units set at 1% and 2%. Concerning absolute accelerations (Figures 20A–C), the M-STLCD strategy effectively reduces the peak responses at all floors. At the top floor, where accelerations are highest, the M-STLCD achieves a 43% reduction in peak acceleration (with mass ratio 1%) comparable to the M-TMD, while the M-TLCD lags significantly with only a 9% reduction. A similar trend continues across the lower floors: both M-STLCD and M-TMD provide consistent reductions in acceleration, with nearly equivalent performance throughout. When increasing the damper mass ratio from 1% to 2%, the M-STLCD shows further improvement, achieving the highest peak acceleration (up to 49.8%) and drift reductions (up to 47.6%), outperforming its own results at lower mass and surpassing the M-TMD at all floors which reaches 43.2% acceleration and 43.6% drift reduction. M-TLCD remains the least effective, with maximum reductions around 25% (acceleration) and 22% (drift). Increasing the mass ratio yields only minor changes for the M-STLCD, which maintains consistent drift reductions across all interstories. In contrast, the M-TMD exhibits a systematic performance decline at almost all levels compared to the 1% case, highlighting the advantage of the proposed M-STLCD configuration.

Figure 20

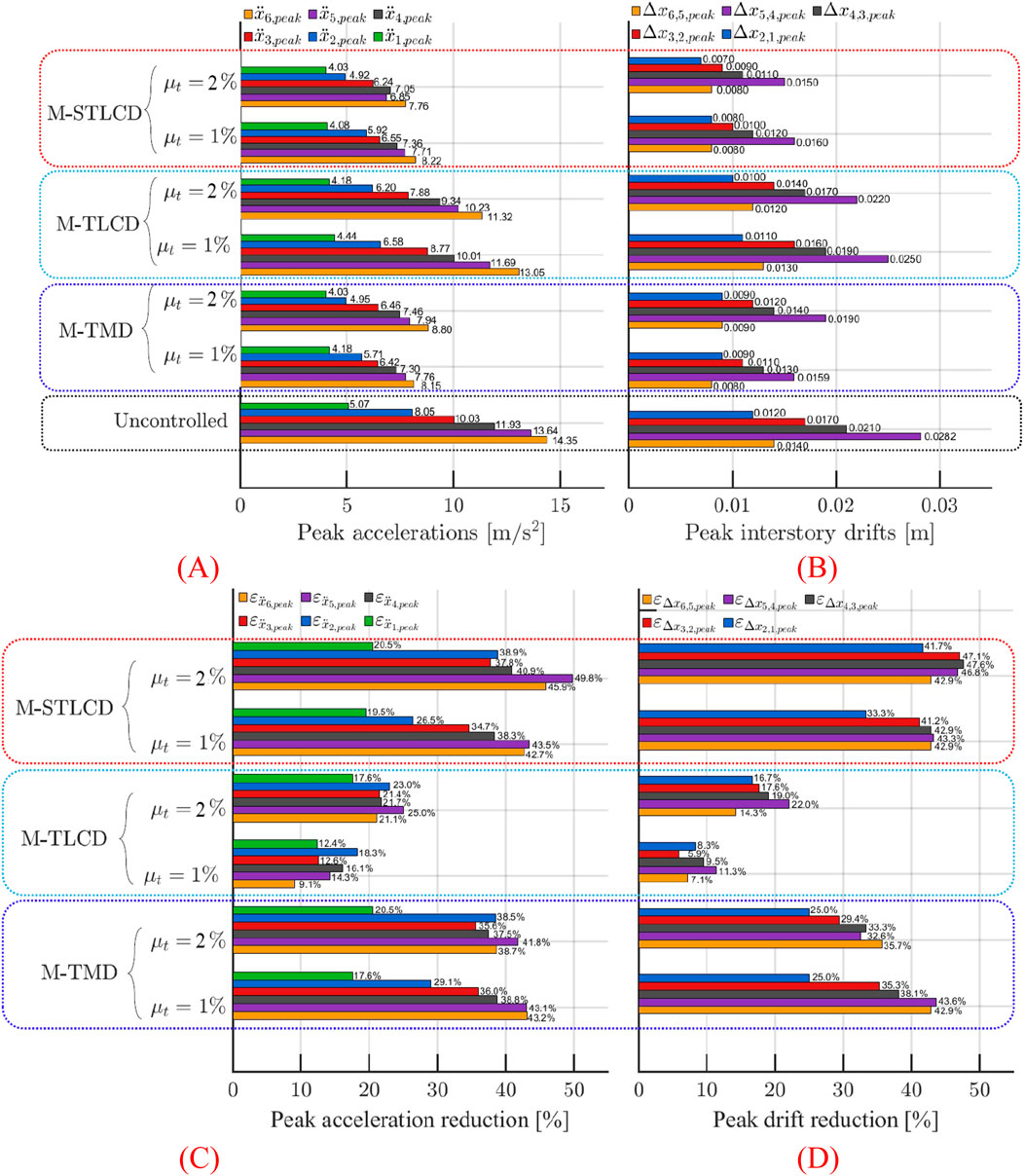
Figure 20. (A) Peak floor accelerations; (B) interstory drifts; (C) acceleration reduction; (D) drift reduction in the six-story structure: M-STLCD vs. M-TMD and M-TLCD control strategies under broadband noise excitation.

The substantial reductions are evident in Figure 21, illustrating M-STLCD’s consistent and stable performance along the seismic event for both absolute accelerations and interstory drifts, when employing an increased unit mass ratio of 2%, performing on par with, or in some cases even surpassing, the M-TMD. Conversely, the M-TLCD exhibits limited improvement, barely reducing the structural response relative to the uncontrolled baseline.

Figure 21

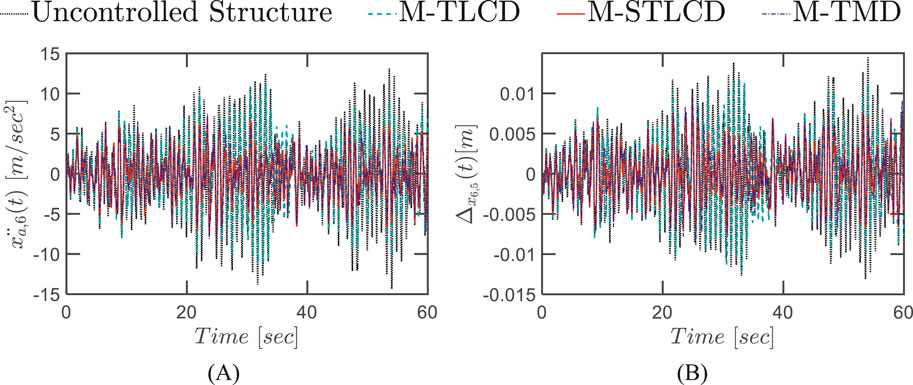
Figure 21. Time-history response of the six-story structure equipped with M-STLCD, M-TMD, and M-TLCD, each having a mass equal to 2% of the total structural mass, subjected to broadband noise excitation: (A) top floor absolute accelerations; (B) interstory drifts.

Finally, Figure 22 illustrates the effectiveness of the M-STLCD under the Kocaeli earthquake in reducing both absolute accelerations and interstory drifts throughout the time-domain response, when employing an increased unit mass ratio of 2%. The M-STLCD exhibits notably robust performance, especially considering the impulsive nature of the Kocaeli record, reducing peak acceleration at the top floor from 5.26 m/s² (uncontrolled) to 4.85 m/s² (8% reduction), nearly identical to M-TMD’s performance (4.86 m/s²). In terms of interstory drifts (Figure 22B), both the M-STLCD and M-TMD show slight increases in peak values compared to the uncontrolled case. This behavior aligns with the optimization objective, which prioritizes the reduction of absolute accelerations, often at the expense of drift performance, a well-known trade-off in passive control systems. If the goal is to suppress the initial transient response, it is important to note that the first acceleration peak, often inadequately controlled by passive systems, can be more effectively mitigated using active or hybrid control strategies, which are commonly employed to address this inherent limitation of passive devices. Nevertheless, the M-STLCD proves highly effective in attenuating the structural response over time, delivering sustained and stable performance throughout the remainder of the event. Additionally, compared to the other devices, it offers additional advantages, such as reduced solid mass requirements and the potential use of readily available water resources for damping.

Figure 22

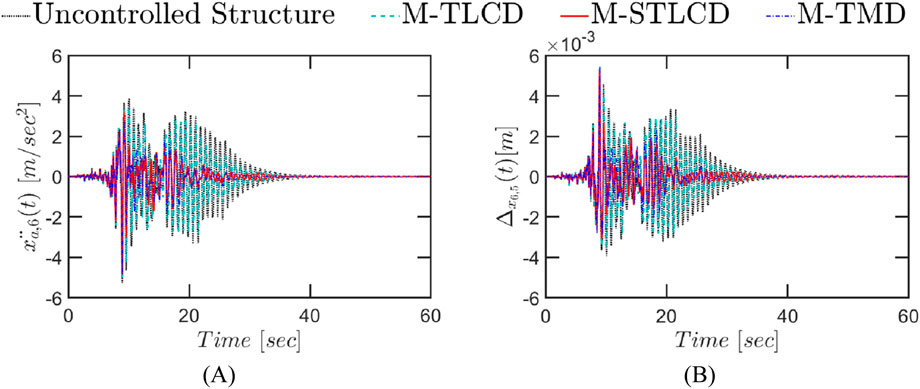
Figure 22. Time-history response of the six-story structure equipped with M-STLCD, M-TMD, and M-TLCD, each having a mass equal to 2% of the total structural mass, subjected to a real earthquake record (1999 Kocaeli): (A) top floor absolute accelerations; (B) interstory drifts.

8 Conclusion

This study proposes a novel vibration control system composed of multiple Sliding Tuned Liquid Column Damper (STLCD) units, collectively referred to as the M-STLCD, for mitigating seismic-induced vibrations in multi-story, stiff structures. Given its modular and distributed design, multiple STLCD units, consisting of mobile U-shaped liquid containers, can be easily integrated throughout the structural layout. Specifically, a sequential optimization procedure, structured in iterative steps, has been developed to progressively identify an optimal configuration tailored to the dynamic properties of the structure and the characteristics of the input seismic excitation. At each iteration, the procedure optimizes a single STLCD unit by determining the optimal parameters and installation floor for each damper unit. Based on preliminary analyses carried out on a three-story building, the proposed optimization focuses on minimizing absolute accelerations. To evaluate the response in terms of control performance, in addition to the three-story structure, a six-story building has also been considered as a benchmark. For comparative purposes, analogous sequential optimization procedures have also been developed and applied to multiple Tuned Mass Damper (M-TMD) and multiple Tuned Liquid Column Damper (M-TLCD) systems. The proposed optimization framework has been initially assessed in the frequency domain by subjecting the two benchmark structures to a broadband noise excitation. Results demonstrate the M-STLCD’s ability to effectively target first vibration modes, consistently lowering response variances across all floors matching the performance of M-TMD and outperforming M-TLCD, which exhibits clear limitations in tuning to stiff structures. Subsequently, the effectiveness of the M-STLCD control strategy is further assessed in the time domain, considering both structures equipped with optimal device configurations subjected to a broadband noise excitation and a real seismic event. An increased mass configuration is also explored to evaluate performance under varying control mass conditions. Results confirm the M-STLCD’s control capabilities across these diverse inputs, achieving peak acceleration reductions of up to 47% under the broadband noise excitation and up to 39% under the recorded seismic event. Notably, the M-STLCD consistently exhibits performance comparable to M-TMD systems while offering additional advantages, such as reduced solid mass requirements and the potential use of available water resources for damping. Unlike M-TLCD systems, typically unsuitable for short-period structures, the M-STLCD effectively extends the applicability of liquid-based devices to stiff buildings characterized by shorter periods, thus presenting a robust, scalable, and promising solution for vibration mitigation in multi-story structures.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

CM: Methodology, Writing – review and editing, Writing – original draft, Supervision, Data curation, Conceptualization, Formal Analysis. SD: Writing – original draft, Investigation, Software. SR: Writing – review and editing. AP: Supervision, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Funded by the European Union - Next-Generation EU, Mission 4 Component 1 CUP B53D23006220006. The authors gratefully acknowledge financial support from the Italian Ministry of Education, University and Research (MIUR) under the P.R.I.N. 2022 National Grant ‘‘Innovative metamaterial components and absorbers for vibration mitigation (METAVIBRA)’’ (Project Code 2022LA43E2_001; University of Palermo Research Unit). AP gratefully acknowledges the support received from the project SiciliAn MicronanOTecH Research And Innovation CEnter’’SAMOTHRACE‘‘(MUR, PNRR-M4C2, ECS_00000022), spoke 3-Universita’ degli Studi di Palermo’’ S2-COMMs-Micro and Nanotechnologies for Smart and Sustainable Communities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

The author(s) declared that they were an editorial board member of Frontiers, at the time of submission. This had no impact on the peer review process and the final decision.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abé, M., and Fujino, Y. (1994). Dynamic characterization of multiple tuned mass dampers and some design formulas. Earthq. Eng. and Struct. Dyn. 23, 813–835. doi:10.1002/eqe.4290230802

CrossRef Full Text | Google Scholar

Adam, C., Di Matteo, A., Furtmüller, T., and Pirrotta, A. (2017). Earthquake excited base-isolated structures protected by tuned liquid column dampers: design approach and experimental verification. Procedia Eng. 199, 1574–1579. doi:10.1016/j.proeng.2017.09.060

CrossRef Full Text | Google Scholar

Almufti, S., Shaban, A., Ali, R., Jayson, F., and A. Dela Fuente, J. (2023). Overview of metaheuristic algorithms. Polaris Glob. J. Sch. Res. Trends 2, 10–32. doi:10.58429/pgjsrt.v2n2a144

CrossRef Full Text | Google Scholar

American Society of Civil Engineers (2022). Minimum design loads and associated criteria for buildings and other structures (ASCE/SEI 7-22). Reston, VA: ASCE.

Google Scholar

Aote, S., Raghuwanshi, M. M., and Malik, L. (2013). A brief review on particle swarm optimization: Limitations and future directions. Int. J. Comput. Sci. Eng. 14 (1), 196–200.

Google Scholar

Argenziano, M., Faiella, D., Carotenuto, A. R., Mele, E., and Fraldi, M. (2022). Generalization of the den Hartog model and rule-of-thumb formulas for optimal tuned mass dampers. J. Sound Vib. 538, 117213. doi:10.1016/j.jsv.2022.117213

CrossRef Full Text | Google Scholar

Ayorinde, E. O., and Warburton, G. B. (1980). Minimizing structural vibrations with absorbers. Earthq. Eng. and Struct. Dyn. 8, 219–236. doi:10.1002/eqe.4290080303

CrossRef Full Text | Google Scholar

Bakre, S. V., and Jangid, R. S. (2004). Optimum multiple tuned mass dampers for base-excited damped main System. Int. J. Struct. Stab. Dyn. 04, 527–542. doi:10.1142/S0219455404001367

CrossRef Full Text | Google Scholar

Balendra, T., Wang, C. M., and Cheong, H. F. (1995). Effectiveness of tuned liquid column dampers for vibration control of towers. Eng. Struct. 17, 668–675. doi:10.1016/0141-0296(95)00036-7

CrossRef Full Text | Google Scholar

Basili, M., and Angelis, M. D. (2022). Experimental dynamic response of a multi-story frame structure equipped with non-conventional TMD implemented via inter-story isolation. Appl. Sci. 12 (18), 9153. doi:10.3390/app12189153

CrossRef Full Text | Google Scholar

Bilello, C., Di Paola, M., and Pirrotta, A. (2002). Time delay induced effects on control of non-linear systems under random excitation. Meccanica 37, 207–220. doi:10.1023/A:1019659909466

CrossRef Full Text | Google Scholar

Chen, G. (1996). “Multi-stage tuned mass dampers,” in Proceedings of the 11th world conference on earthquake engineering. Acapulco, Mexico, 1–8.

Google Scholar

Chen, G., and Wu, J. (2001). Optimal placement of multiple tune mass dampers for seismic structures. J. Struct. Eng. 127, 1054–1062. doi:10.1061/(ASCE)0733-9445(2001)127:9(1054)

CrossRef Full Text | Google Scholar

Chen, S. M., Sarosh, A., and Dong, Y. F. (2012). Simulated annealing based artificial bee colony algorithm for global numerical optimization. Appl. Math. Comput. 219 (8), 3575–3589. doi:10.1016/j.amc.2012.09.052

CrossRef Full Text | Google Scholar

Clark, A. J. (1988). “Multiple passive tuned mass dampers for reducing earthquake induced building motion,” in Proceedings of the 9th world conference on earthquake engineering, 779–784.

Google Scholar

Den Hartog, J. P. (1956). Mechanical vibrations. New York: McGraw-Hill.

Google Scholar

Di Matteo, A., Di Paola, M., and Pirrotta, A. (2016). Innovative modeling of tuned liquid column damper controlled structures. Smart Struct. Syst. 18, 117–138. doi:10.12989/sss.2016.18.1.117

CrossRef Full Text | Google Scholar

Di Matteo, A., Furtmüller, T., Adam, C., and Pirrotta, A. (2018). Optimal design of tuned liquid column dampers for seismic response control of base-isolated structures. Acta Mech. 229, 437–454. doi:10.1007/s00707-017-1980-7

CrossRef Full Text | Google Scholar

Di Matteo, A., Masnata, C., and Pirrotta, A. (2019). Hybrid passive control strategies for reducing the displacements at the base of seismic isolated structures. Front. Built Environ. 5, 132. doi:10.3389/fbuil.2019.00132

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2016). Effectiveness of distributed tuned mass dampers for multi-mode control of chimney under earthquakes. Eng. Struct. 124, 1–16. doi:10.1016/j.engstruct.2016.06.006

CrossRef Full Text | Google Scholar

Elias, S., and Matsagar, V. (2017). Research developments in vibration control of structures using passive tuned mass dampers. Annu. Rev. Control 44, 129–156. doi:10.1016/j.arcontrol.2017.09.015

CrossRef Full Text | Google Scholar

Elias, S., Matsagar, V., and Datta, T. K. (2019). Distributed tuned mass dampers for multi-mode control of benchmark building under seismic excitations. J. Earthq. Eng. 23, 1137–1172. doi:10.1080/13632469.2017.1351407

CrossRef Full Text | Google Scholar

Fadel Miguel, L. F., Lopez, R. H., Miguel, L. F. F., and Torii, A. J. (2016). A novel approach to the optimum design of MTMDs under seismic excitations. Struct. Control Health Monit. 23, 1290–1313. doi:10.1002/stc.1845

CrossRef Full Text | Google Scholar

Faiella, D., Argenziano, M., and Mele, E. (2022). Improving the seismic response of tall buildings: from diagrid to megastructures and mega-subcontrol systems. Open Constr. and Build. Technol. J. 16 (1), e187483682201030. doi:10.2174/18748368-v16-e2201030

CrossRef Full Text | Google Scholar

Fei, Z., Jinting, W., Feng, J., and Liqiao, L. (2019). Control performance comparison between tuned liquid damper and tuned liquid column damper using real-time hybrid simulation. Earthq. Eng. Eng. Vib. 18, 695–701. doi:10.1007/s11803-019-0530-9

CrossRef Full Text | Google Scholar

Furtmüller, T., Di Matteo, A., Adam, C., and Pirrotta, A. (2019). Base-isolated structure equipped with tuned liquid column damper: an experimental study. Mech. Syst. Signal Process. 116, 816–831. doi:10.1016/j.ymssp.2018.06.048

CrossRef Full Text | Google Scholar

Gao, H., Kwok, K. C. S., and Samali, B. (1997). Optimization of tuned liquid column dampers. Eng. Struct. 19, 476–486. doi:10.1016/S0141-0296(96)00099-5

CrossRef Full Text | Google Scholar

Gao, H., Kwok, K. S. C., and Samali, B. (1999). Characteristics of multiple tuned liquid column dampers in suppressing structural vibration. Eng. Struct. 21, 316–331. doi:10.1016/S0141-0296(97)00183-1

CrossRef Full Text | Google Scholar

Ghosh, A., and Basu, B. (2004). Seismic vibration control of short period structures using the liquid column damper. Eng. Struct. 26, 1905–1913. doi:10.1016/j.engstruct.2004.07.001

CrossRef Full Text | Google Scholar

Goldberg, D. E., and Holland, J. H. (1988). Genetic algorithms and machine learning. Mach. Learn. 3, 95–99. doi:10.1023/a:1022602019183

CrossRef Full Text | Google Scholar

Hochrainer, M. J., and Ziegler, F. (2006). Control of tall building vibrations by sealed tuned liquid column dampers. Struct. Control Health Monit. 13, 980–1002. doi:10.1002/stc.90

CrossRef Full Text | Google Scholar

Jangid, R. S. (1999). Optimum Multiple Tuned Mass Dampers for base-excited undamped system. Earthq. Eng. and Struct. Dyn. 28, 1041–1049. doi:10.1002/(SICI)1096-9845(199909)28:9<1041::AID-EQE853>3.0.CO;2-E

CrossRef Full Text | Google Scholar

Joshi, A. S., and Jangid, R. S. (1997). Optimum parameters of multiple tuned mass dampers for base-excited damped systems. J. Sound Vib. 202, 657–667. doi:10.1006/jsvi.1996.0859

CrossRef Full Text | Google Scholar

Joshi, A., Devi, S., Kumar, P., Sah, S. K., Lal, S., et al. (2019). Strong motion generation area modelling of the 2008 Iwate earthquake, Japan using modified semi-empirical technique. J. Earth Syst. Sci. 128, 202. doi:10.1007/s12040-019-1221-7

CrossRef Full Text | Google Scholar

Kareem, A., and Kline, S. (1995). Performance of multiple mass dampers under random loading. J. Struct. Eng. 121, 348–361. doi:10.1061/(ASCE)0733-9445(1995)121:2(348)

CrossRef Full Text | Google Scholar

Kim, S.-Y., and Lee, C.-H. (2018). Optimum design of linear multiple tuned mass dampers subjected to white-noise base acceleration considering practical configurations. Eng. Struct. 171, 516–528. doi:10.1016/j.engstruct.2018.06.002

CrossRef Full Text | Google Scholar

Kim, D.-I., Min, K.-W., Park, J.-H., Lee, H.-R., Kim, J.-K., Hwang, K.-S., et al. (2012). Tunable tuned liquid column dampers with multi-cells for wind vibration control of tall buildings. Proc. SPIE 8345, 83452L–1. doi:10.1117/12.914452

CrossRef Full Text | Google Scholar

Konar, T., and Ghosh, A. (2023). A review on various configurations of the passive tuned liquid damper. J. Vib. Control 29, 1945–1980. doi:10.1177/10775463221074077

CrossRef Full Text | Google Scholar

Lewandowski, R., and Grzymisławska, J. (2009). Dynamic analysis of structures with multiple tuned mass dampers. J. Civ. Eng. Manag. 15, 77–86. doi:10.3846/1392-3730.2009.15.77-86

CrossRef Full Text | Google Scholar

Li, C. (2000). Performance of multiple tuned mass dampers for attenuating undesirable oscillations of structures under the ground acceleration. Earthq. Eng. and Struct. Dyn. 29, 1405–1421. doi:10.1002/1096-9845(200009)29:9<1405::AID-EQE976>3.0.CO;2-4

CrossRef Full Text | Google Scholar

Li, C. (2002). Optimum multiple tuned mass dampers for structures under the ground acceleration based on DDMF and ADMF. Earthq. Eng. and Struct. Dyn. 31, 897–919. doi:10.1002/eqe.128

CrossRef Full Text | Google Scholar

Ma, H., Zhang, Y., Sun, S., Liu, T., and Shan, Y. (2023). A comprehensive survey on NSGA-II for multi-objective optimization and applications. Artif. Intell. Rev. 56 (12), 15217–15270. doi:10.1007/s10462-023-10526-z

CrossRef Full Text | Google Scholar

Masnata, C., and Pirrotta, A. (2024). Optimal control of base-isolated systems with sliding TLCD under stochastic process. Eng. Struct. 318, 118754. doi:10.1016/j.engstruct.2024.118754

CrossRef Full Text | Google Scholar

Masnata, C., Di Matteo, A., Adam, C., and Pirrotta, A. (2024a). Sliding TLCD for vibration control of base-isolation systems: experimental comparison with traditional TLCD and TMD. J. Phys. Conf. Ser. 2647, 172005. doi:10.1088/1742-6596/2647/17/172005

CrossRef Full Text | Google Scholar

Masnata, C., Adam, C., and Pirrotta, A. (2024b). Optimal design of short-period structures equipped with sliding tuned liquid column damper and numerical and experimental control performance evaluation. Acta Mech. 235, 1603–1622. doi:10.1007/s00707-023-03832-8

CrossRef Full Text | Google Scholar

Min, K.-W., Kim, H.-S., Lee, S.-H., Kim, H., and Kyung Ahn, S. (2005). Performance evaluation of tuned liquid column dampers for response control of a 76-story benchmark building. Eng. Struct. 27, 1101–1112. doi:10.1016/j.engstruct.2005.02.008

CrossRef Full Text | Google Scholar

Mohebbi, M., Shakeri, K., Ghanbarpour, Y., and Majzoub, H. (2013). Designing optimal multiple tuned mass dampers using genetic algorithms (GAs) for mitigating the seismic response of structures. J. Vib. Control 19, 605–625. doi:10.1177/1077546311434520

CrossRef Full Text | Google Scholar

Mohebbi, M., Dabbagh, H. R., and Shakeri, K. (2015). Optimal design of multiple tuned liquid column dampers for seismic vibration control of MDOF structures. Period. Polytech. Civ. Eng. 59, 543–558. doi:10.3311/PPci.7645

CrossRef Full Text | Google Scholar

Ocak, A., Bekdaş, G., Nigdeli, S. M., Kim, S., and Geem, Z. W. (2022). Optimization of tuned liquid damper including different liquids for lateral displacement control of single and multi-story structures. Buildings 12, 377. doi:10.3390/buildings12030377

CrossRef Full Text | Google Scholar

Pandey, D. K., Sharma, M. K., and Mishra, S. K. (2019). A compliant tuned liquid damper for controlling seismic vibration of short period structures. Mech. Syst. Signal Process. 132, 405–428. doi:10.1016/j.ymssp.2019.07.002

CrossRef Full Text | Google Scholar

Park, J., and Reed, D. (2001). Analysis of uniformly and linearly distributed mass dampers under harmonic and earthquake excitation. Eng. Struct. 23, 802–814. doi:10.1016/S0141-0296(00)00095-X

CrossRef Full Text | Google Scholar

Perez, R. E., and Behdinan, K. (2007). Particle swarm approach for structural design optimization. Comput. Struct. 85 (19), 1579–1588. doi:10.1016/j.compstruc.2006.10.013

CrossRef Full Text | Google Scholar

Randall, S. E., Halsted, D. M., and Taylor, D. L. (1981). Optimum vibration absorbers for Linear damped systems. J. Mech. Des. 103, 908–913. doi:10.1115/1.3255005

CrossRef Full Text | Google Scholar

Roozbahan, M., Masnata, C., Turan, G., and Pirrotta, A. (2025). Efficiency evaluation of optimal TLCD and TMD for the seismic response reduction of buildings considering soil-structure interaction effect. Meccanica. doi:10.1007/s11012-025-01981-9

CrossRef Full Text | Google Scholar

Sadek, F., Mohraz, B., and Lew, H. S. (1998). Single- and multiple-tuned liquid column dampers for seismic applications. Earthq. Eng. and Struct. Dyn. 27, 439–463. doi:10.1002/(SICI)1096-9845(199805)27:5<439::AID-EQE730>3.0.CO;2-8

CrossRef Full Text | Google Scholar

Sakai, F., Takeda, S., and Tamaki, T. (1989). “Tuned liquid column damper—new type device for suppression of building vibrations,” in Proceedings of the international conference on highrise buildings. Nanjing, China, 926–931.

Google Scholar

Shetty, K. K., Krishnamoorthy, A., and Nayak, G.Dhanalakshmi (2017). The effect of multiple tuned mass dampers on response control of base isolated multi-storey space frame structure. Int. J. Struct. Eng. 8, 148–168. doi:10.1504/IJSTRUCTE.2017.084650

CrossRef Full Text | Google Scholar

Shum, K. M., and Xu, Y. L. (2002). Multiple-tuned liquid column dampers for torsional vibration control of structures: experimental investigation. Earthq. Eng. and Struct. Dyn. 31, 977–991. doi:10.1002/eqe.133

CrossRef Full Text | Google Scholar

Suresh, L., and Mini, K. M. (2019). Effect of multiple tuned mass dampers for vibration control in high-rise buildings. Pract. Periodical Struct. Des. Constr. 24, 04019031. doi:10.1061/(ASCE)SC.1943-5576.0000453

CrossRef Full Text | Google Scholar

Vellar, L. S., Ontiveros-Pérez, S. P., Miguel, L. F. F., and Fadel Miguel, L. F. (2019). Robust Optimum design of multiple tuned mass dampers for vibration control in buildings subjected to seismic excitation. Shock Vib. 2019, 9273714. doi:10.1155/2019/9273714

CrossRef Full Text | Google Scholar

Vié, A. (2020). Qualities, challenges and future of genetic algorithms: a literature review. arXiv Neural Evol. Comput. Available online at: http://export.arxiv.org/pdf/2011.05277.

Google Scholar

Wang, Q., Tiwari, N. D., Qiao, H., and Wang, Q. (2020). Inerter-based tuned liquid column damper for seismic vibration control of a single-degree-of freedom structure. Int. J. Mech. Sci. 184, 105840. doi:10.1016/j.ijmecsci.2020.105840

CrossRef Full Text | Google Scholar

Warburton, G. B. (1982). Optimum absorber parameters for various combinations of response and excitation parameters. Earthq. Eng. and Struct. Dyn. 10, 381–401. doi:10.1002/eqe.4290100304

CrossRef Full Text | Google Scholar

Wei, X., and Zhao, X. (2020). Vibration suppression of a floating hydrostatic wind turbine model using bidirectional tuned liquid column mass damper: vibration suppression of a floating HWT using BTLCMD. Wind Energy 23, 1887–1904. doi:10.1002/we.2524

CrossRef Full Text | Google Scholar

Wu, J.-C., Shih, M.-H., Lin, Y.-Y., and Shen, Y.-C. (2005). Design guidelines for tuned liquid column damper for structures responding to wind. Eng. Struct. 27 (13), 1893–1905. doi:10.1016/j.engstruct.2005.05.009

CrossRef Full Text | Google Scholar

Xu, K., and Igusa, T. (1992). Dynamic characteristics of multiple substructures with closely spaced frequencies. Earthq. Eng. and Struct. Dyn. 21, 1059–1070. doi:10.1002/eqe.4290211203

CrossRef Full Text | Google Scholar

Xu, Y. L., and Shum, K. M. (2003). Multiple-tuned liquid column dampers for torsional vibration control of structures: theoretical investigation. Earthq. Eng. and Struct. Dyn. 32, 309–328. doi:10.1002/eqe.227

CrossRef Full Text | Google Scholar

Yamaguchi, H., and Harnpornchai, N. (1993). Fundamental characteristics of Multiple Tuned Mass Dampers for suppressing harmonically forced oscillations. Earthq. Eng. and Struct. Dyn. 22, 51–62. doi:10.1002/eqe.4290220105

CrossRef Full Text | Google Scholar

Zakian, P., and Bakhshpoori, T. (2024). Optimal design of multiple tuned mass dampers for controlling the earthquake response of randomly excited structures. Acta Mech. 235, 511–532. doi:10.1007/s00707-023-03749-2

CrossRef Full Text | Google Scholar

Zhang, X., Han, Q., Bi, K., and Du, X. (2022). An improved multi-mode seismic vibration control method using multiple tuned mass dampers. Adv. Struct. Eng. 25, 804–819. doi:10.1177/13694332211050977

CrossRef Full Text | Google Scholar

Zhu, F., Wang, J.-T., Jin, F., and Lu, L.-Q. (2017). Real-time hybrid simulation of full-scale tuned liquid column dampers to control multi-order modal responses of structures. Eng. Struct. 138, 74–90. doi:10.1016/j.engstruct.2017.02.004

CrossRef Full Text | Google Scholar

Ziegler, F. (2007). The tuned liquid column damper as a cost-effective alternative for the mechanical damper in civil engineering structures. Int. J. Acoust. Vib. 12, 25–39. doi:10.20855/ijav.2007.12.1207

CrossRef Full Text | Google Scholar