Climate change impacts on geotechnical infrastructure: role of unsaturated soil mechanics for adaptation

Climate change has intensified rainfall variability, droughts, and temperature extremes, amplifying the risks of instability and deformation in geotechnical infrastructure. Traditional saturated soil frameworks are inadequate to capture these effects, whereas unsaturated soil mechanics (USM) offers a more realistic basis for understanding soil behavior under fluctuating hydro-climatic conditions. This paper reviews the critical role of USM in advancing climate-resilient geotechnical engineering. Key challenges include the complexity of soil–atmosphere exchanges, hydraulic hysteresis, scaling from laboratory to field, and uncertainty in climate projections. Concurrently, opportunities are emerging through advanced monitoring, innovative experimental techniques, computational modeling, climate integration, and reliability-based design. By extending classical bearing capacity models, this study integrates USM to more accurately predict geostructure performance. Analytical insights, supported by case studies, demonstrate the influence of rainfall-induced infiltration on slope stability, shallow foundation capacity, and column-supported embankments. Results reveal that suction enhances soil strength but may diminish rapidly during infiltration, heightening failure risk. The study advocates embedding USM into design codes, modeling frameworks, and early-warning systems to move from reactive to proactive resilience. Bridging theory and practice, it provides a pathway for adapting geotechnical systems to climate variability and ensuring long-term infrastructure durability.

1 Introduction

Climate change is reshaping the frequency, intensity, and duration of weather events globally. In many regions, particularly those under tropical climates with residual soils, slope failures are increasingly triggered by climate-driven events such as prolonged droughts, extreme rainfall, and rising temperatures, which are no longer isolated anomalies but part of an increasingly volatile climate system (Vardon, 2015; Yasuhara and Bergado, 2022; Costa et al., 2023; Kandalai et al., 2023; Bridges, 2024). For example, climate change has significantly altered rainfall patterns, leading to more intense storms occurring less frequently. This shift, coupled with increased atmospheric temperatures and moisture capacity, results in extreme rainfall events that greatly affect slope stability (Au, 1998; Toll et al., 2008; Loveridge et al., 2010; Rahimi et al., 2011; Scaringi and Loche, 2022). Specifically, in tropical regions, intense rainfall infiltration reduces matric suction in residual soils, diminishing shear strength and making slopes more prone to failure. In contrast, arid and semi-arid regions face challenges associated with collapsible or dispersive soils, where wetting after prolonged droughts can induce sudden settlement or erosion. These diverse regional contexts highlight the universal applicability of unsaturated soil mechanics while underscoring the need for tailored design and adaptation strategies. These phenomena significantly affect the behavior and performance of geotechnical infrastructures (Salimi and Al-Ghamdi, 2020; Pantoja Porro et al., 2025).

Understanding how these regional processes translate into soil-scale mechanisms is crucial. The degree of infiltration and suction loss is strongly influenced by soil properties such as permeability, water retention characteristics, and hydraulic conductivity. These factors control how quickly pore-water pressures fluctuate during wetting and drying cycles. In climates with pronounced dry and wet seasons, this leads to frequent instability in areas composed of unsaturated soils. At the core of this challenge lies the unsaturated zone of the soil, often overlooked in traditional design but critical in modern geotechnical engineering. This vadose zone, located between the ground surface and the water table, comprises partially saturated soils commonly found beneath slopes, embankments, pavements, and shallow foundations. The hydro-mechanical properties of these unsaturated soils make them highly responsive to climate-driven changes in moisture and temperature, posing risks to stability, deformation, and serviceability (Jardine, 2020; Culligan et al., 2019; Rouainia et al., 2020; Illés and Nagy, 2022; Ng et al., 2024; Pham et al., 2024).

These challenges highlight the importance of reviewing the state-of-the-art in unsaturated soil mechanics, where significant advances have been made in theory, experimentation, and modeling, yet important gaps remain in applying these insights to climate-resilient infrastructure. Research in unsaturated soil mechanics (USM) has advanced considerably over the past 3 decades, establishing a robust theoretical framework for linking matric suction, effective stress, and mechanical behavior (Fredlund and Rahardjo, 1993; Lu and Likos, 2004; Alonso and Olivella, 2006; Mancuso et al., 2012). Building upon these theoretical foundations, research has increasingly moved toward experimental and computational innovations that capture the complex response of unsaturated soils under climate stressors. Novel laboratory methods such as high-capacity tensiometers, TDR-based suction monitoring, and microfabricated devices for pore-scale observation have improved our ability to observe suction and moisture dynamics with greater accuracy (Ridley and Burland, 1993; Haghighi et al., 2012; Ng and Menzies, 2014; Cardoso et al., 2017; Najdi et al., 2023; Pham et al., 2023a). At the same time, computational approaches have become increasingly sophisticated, from constitutive modeling of hydraulic hysteresis (Khalili et al., 2022) to the integration of data-driven techniques such as physics-informed machine learning (Haruzi and Moreno, 2023; Ajdari et al., 2025; Yang et al., 2025). These advances provide powerful tools to capture the coupled thermo-hydro-mechanical response of soils under climate stressors.

Nevertheless, several gaps still remain. Challenges persist in scaling laboratory measurements to field conditions, accounting for hysteresis in soil-water retention, and applying USM concepts across diverse climatic contexts. For example, while tropical regions emphasize rainfall-induced slope failures, arid and semi-arid areas highlight the potential for collapse and erosion following wet conditions after droughts (Salimi and Al-Ghamdi, 2020; Ng et al., 2024). More recent studies have emphasized the importance of soil–atmosphere interaction under changing climatic conditions, particularly rainfall infiltration and evaporation processes that govern suction fluctuations (Rahardjo et al., 2019). A number of reviews have synthesized these developments, notably Tang et al. (2018), who provided an extensive synthesis of atmosphere–vegetation–soil interactions, with particular emphasis on eco-hydrological processes under climate change. Similarly, Siemens (2018) highlighted the broader context of climate–soil interactions, calling for resilience-based frameworks in geotechnical practice. Bridging these diverse contexts requires more integrative frameworks that link fundamental mechanics with region-specific case studies and long-term monitoring strategies.

Given the growing impact of climate variability on geotechnical systems, there is an urgent need to integrate unsaturated soil mechanics into engineering design and risk management. Understanding the coupled interactions between soil suction, moisture content, permeability, and temperature under climate stressors is vital (Toll et al., 2012; Vahedifard et al., 2018; Likos et al., 2019; Siemens, 2018; Rahardjo et al., 2019; Houston, 2024; Shwan, 2024). These relationships dictate how infrastructure responds to climate-induced loading conditions, from pore pressure buildup during intense rainfall to desiccation and cracking under drought (Figure 1). Therefore, a climate-responsive approach to geotechnical engineering must begin with a re-evaluation of the role of unsaturated soil mechanics. This includes not only understanding the principles of effective stress and shear strength in unsaturated conditions but also acquiring reliable data on matric suction, soil-water retention characteristics, and hydraulic conductivity.

Figure 1

Figure 1. A representative example of climate-induced slope instability.

Although several review studies of climate change on infrastructure exist in the literature, they have approached the subject from different perspectives. These contributions are highly valuable; however, the present paper adopts a complementary perspective by placing unsaturated soil mechanics at the core of climate-adaptive geotechnical design. The emphasis here is on the physical foundations of suction, soil–water retention, and hydro-mechanical coupling, and on how these principles can be directly translated into climate-resilient infrastructure solutions. In doing so, this paper bridges the gap between theoretical advances in USM and their practical application in designing, monitoring, and adapting geotechnical systems under climate variability.

2 Physical foundation of unsaturated soil mechanics

The importance of unsaturated soil mechanics stems from its crucial role in understanding and mitigating the impacts of climate change, particularly in response to rainfall variability and extreme weather events (Fredlund, 2006; Fredlund, 2014; Houston, 2019; Lu, 2020). As shown in Figures 2a, as patterns of precipitation and evaporation shift, soils are subjected to more frequent wetting–drying cycles, leading to fluctuations in matric suction, effective stress, and shear strength. These changes significantly influence the stability and performance of slopes, foundations, and earth structures. Since unsaturated conditions dominate the vadose zone—where climate-sensitive hydrological and geotechnical processes interact—integrating unsaturated soil behavior into design and risk assessment is essential for ensuring climate-resilient infrastructure.

Figure 2

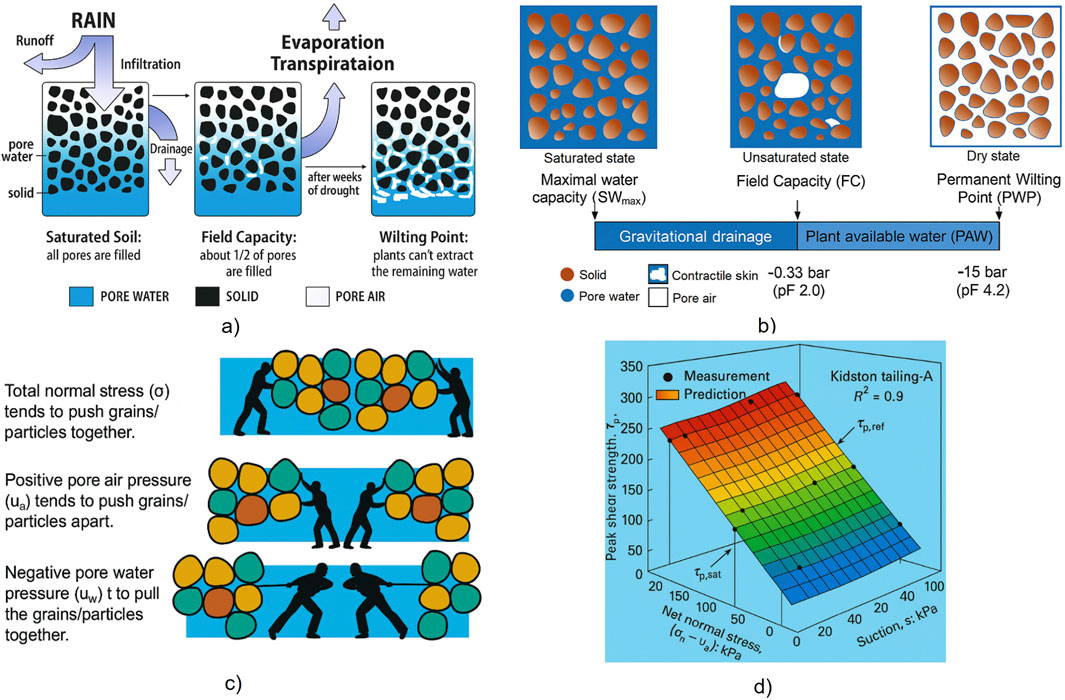
Figure 2. Physical foundation of unsaturated soil mechanics: (a) infiltration-evaporation mechanism; (b) water status in unsaturated soils; (c) view of stress state of unsaturated soil (adapted from Houston, 2019); (d) shear strength suction relationship.

Unsaturated soil is a complex multiphase system generally comprising three principal phases—solid particles, pore water, and pore air—and a fourth interfacial phase known as the contractile skin act like an elastic membrane that binds soil particles, creating additional strength (Terzaghi, 1943; Fredlund and Morgenstern, 1977; Fredlund et al., 1978; Rahardjo et al., 2019; Pham et al., 2025). This additional phase represents the curved air–water interface at the pore scale and plays a crucial role in defining suction stress and mechanical behavior in unsaturated conditions. This interfacial tension imparts cohesion to the soil matrix, particularly at low water contents, and must be considered in a comprehensive analysis of the overall state of stress in unsaturated soils.

To characterize the water status in unsaturated soils, soil water constants are used (Figure 2b). These refer to the water content at defined water potential values, capturing the energy state of water and its availability to plants or its role in mechanical behavior (Scanlon et al., 2002). The maximal water capacity (SW_max) refers to the upper limit of water content, occurring at or near full saturation when all pore spaces are filled with water. At this point, water movement is driven predominantly by gravitational forces, particularly through macropores. Following saturation, the field capacity (FC) defines the amount of water retained in the soil after gravitational drainage has mostly ceased (typically 2–3 days post-irrigation or rainfall). In soil physics, FC is conventionally associated with a matric suction of approximately −0.33 bar (≈33 kPa, pF 2.0), particularly for medium-textured soils (Filipović et al., 2016). This value originates from experimental studies on soil moisture constants (e.g., Richards and Weaver, 1943) and has since been widely adopted in soil physics and agronomy texts as a standard reference point (Livingston and Topp, 1993; Scanlon et al., 2002). At this suction, water is primarily stored within micro- and mesopores and remains relatively mobile and accessible to plants. At the drier end of the spectrum, the permanent wilting point (PWP) is reached. PWP is defined as the soil water content at which plants can no longer extract sufficient water to sustain growth, and permanent wilting occurs even under favorable atmospheric conditions. This threshold is conventionally associated with a matric suction of approximately −15 bar (≈1,500 kPa, pF 4.2) (Hillel, 1998; Filipović et al., 2016). At this stage, the remaining water is tightly bound to soil particles and predominantly inaccessible to plant roots.

The plant available water (PAW) is defined as the difference between FC and PWP. PAW thus represents the fraction of soil water that is accessible for plant growth, predominantly held in micro- and mesopores under suctions between about −0.33 bar and −15 bar (Hillel, 1998; Kirkham, 2023). This concept is widely used in agronomy, hydrology, and soil physics to quantify the biologically active water storage capacity of soils.

In unsaturated soils, the physical meaning of effective stress remains fundamentally aligned with that in saturated soils: it represents the portion of total stress transmitted through the soil skeleton, governing its deformation and strength behavior. However, the presence of a pore-air phase and the contractile skin (the curved air–water interface within soil pores) necessitates additional considerations. Two critical stress-related factors arise in unsaturated conditions:

• Pore-air pressure ($u_a$) – This pressure, exerted through the air-filled pores, influences the soil’s response to external loads and can act antagonistically to pore-water pressure

• Matric suction ($\psi =u_a-u_w$) – Defined as the difference between pore-air pressure $\left(u_a\right)$ and pore-water pressure $\left(u_w\right)$, this suction plays a pivotal role in controlling shear strength, volume change, and hydraulic behavior in unsaturated soils.

As illustrated in Figure 2c, pore-air pressure tends to push soil particles apart, whereas negative pore-water pressure and net total stress tend to pull particles together via capillary and surface tension forces. The combined effect of these forces governs the internal stability of soil fabric. Over the years, various formulations have been proposed to incorporate these stress components into meaningful and measurable stress variables. Matyas and Radhakrishna (1968) and Fredlund and Morgenstern (1977) demonstrated that three stress components—total stress, pore-air pressure, and pore-water pressure—can be reorganized into two independent net stress variables that can be both measured and externally controlled in laboratory and field conditions (Fredlund et al., 1978; Fredlund and Rahardjo, 1993; Khalili et al., 2004).

One of the most widely adopted formulations is Bishop’s effective stress equation (Bishop, 1959), which extends Terzaghi’s classical effective stress concept to unsaturated conditions by introducing a suction-dependent stress term. This approach has gained prominence due to its simplicity, interpretability, and ability to reflect unsaturation effects on soil strength and stiffness (Bishop and Blight, 1963; Lu and Likos, 2004; Baker and Frydman, 2009; Lu et al., 2010; Nikooee et al., 2012; Pham, 2022). The effective shear stress equation of unsaturated soils is written as Equation 1:

${\sigma }^{\prime }=\left(\sigma -u_a\right)+\chi \left(u_a-u_w\right)=\left(\sigma -u_a\right)+{\sigma }^s(1)$

where ${\sigma }^{\prime }$ is the effective stress, $\sigma$ is the total stress, ${\sigma }^s$ is the suction stress, $\left(\sigma -u_a\right)$ is the net normal stress, $\psi =\left(u_a-u_w\right)$ is the matric suction, and $\chi$ is the suction weighting coefficient that represents the influence of matric suction on effective stress. The parameter $\chi$ serves as a bridge between mechanical behavior and hydraulic state by quantifying how much of the matric suction contributes to the effective stress. Its value typically depends on the degree of saturation (S) of the soil:

• $\chi$ = 0 corresponds to a dry state (no contribution from suction),

• $\chi$ = 1 corresponds to a fully saturated state (all suction contributes to stress).

Numerous empirical and theoretical models have been proposed to describe the relationship between $\chi$ and S, reflecting the influence of pore-size distribution, soil fabric, and interfacial forces. The exact form of this relationship is soil-specific and affects how suction influences both shear strength and deformation behavior (Khalili and Khabbaz, 1998; Garven and Vanapalli, 2006; Hamid and Miller, 2009; Pham and Sutman, 2022a; Pham et al., 2023a). To capture this variability, common assumptions are typically made regarding the definition of Equation 2:

$\chi ={\eta }_{\psi }{S}_e={\eta }_{\psi }·\frac{S-S_r}{1-S_r}(2)$

where $S$ is the degree of saturation, $S_e$ is the effective degree of saturation, $S_r$ is the residual degree of saturation, and ${\eta }_{\psi }$ is a suction correction factor introduced to account for the transitional behavior in shear strength mobilization. Specifically, ${\eta }_{\psi }$ reflects the fact that the mobilization of suction-induced strength does not occur simultaneously with the mobilization of frictional strength during shearing. Due to differences in the deformation mechanisms at the pore scale, suction effects typically require larger displacements to fully mobilize compared to frictional resistance along particle contacts. Therefore, ${\eta }_{\psi }$ serves as a weighting function or delay factor that modulates the contribution of matric suction to shear strength as a function of displacement or strain level, enhancing the accuracy of constitutive models for unsaturated soil behavior.

Another core concept in unsaturated soil mechanics is the Soil–Water Retention Curve (SWRC), which defines the relationship between soil suction and water content. The SWRC captures critical hydraulic transitions, such as the air-entry value (AEV)—the point at which air invades the largest pores—and the residual suction, beyond which further water removal is minimal (Figure 3a). These properties reflect the soil’s pore structure and significantly influence hydraulic conductivity, shear strength, stiffness, and deformation behavior (Fredlund et al., 1994; Fredlund et al., 1996; Kim and Borden, 2011; Vanapalli and Oh, 2010; Zhai et al., 2019; Cavalcante and Mascarenhas, 2021; Mahmoodabadi and Bryson, 2021; Pham et al., 2023b). The degree of saturation form of the SWRC is widely favored, as it aligns with pore-size distribution and facilitates integration into constitutive models for mechanical analysis. These properties are essential inputs to models that simulate geotechnical response under climate variability.

Figure 3

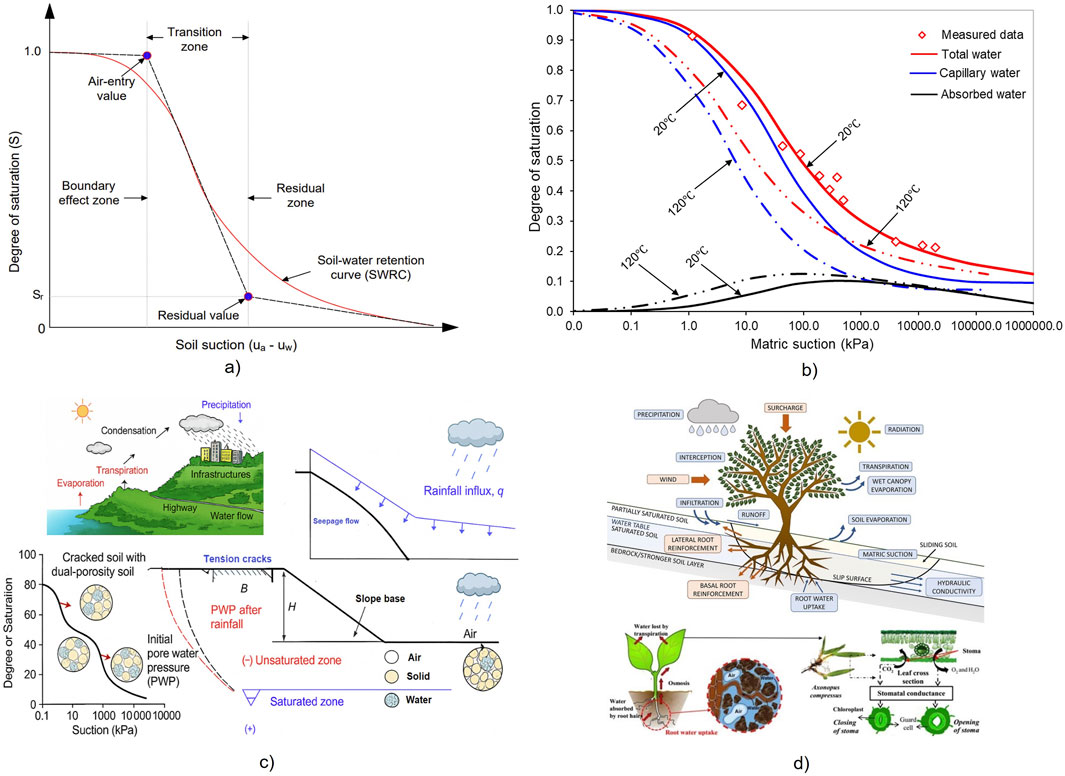
Figure 3. Soil-Water Retention Curve: (a) Important characteristics of SWRC; (b) Effect of temperature on SWRC (data extracted from Pham et al., 2025); (c) Pore-water pressure after rainfall; (d) Principal effects in climate–vegetation–soil interactions (modified from Garg et al., 2020; DiBiagio et al., 2024).

Importantly, temperature has a notable impact on the SWRC, and an example is as shown in Figure 3b. As temperature increases, surface tension and viscosity of water decrease, leading to a reduction in matric suction for a given water content. This shift can flatten the SWRC, lower the AEV, and reduce the suction range over which water is retained. Moreover, thermal expansion of water and soil minerals can alter pore geometry, further modifying retention behavior. These temperature-dependent changes are crucial for modeling thermal-hydro-mechanical (THM) interactions, especially in climates experiencing seasonal or extreme temperature variations (Hopmans and Dane, 1986; Bachmann et al., 2002; Salager et al., 2010; Schneider and Goss, 2011; Gao and Shao, 2015; Pham and Sutman, 2023a; Pham et al., 2023c; Pham et al., 2023d; Peipei et al., 2024).

Matric suction in unsaturated soils is highly dynamic, responding directly to environmental conditions (Figure 3c). During intense rainfall, infiltration reduces suction, diminishing shear strength and increasing the risk of slope failures or foundation instability (Bashir et al., 2015). Conversely, extended drought conditions elevate suction levels, which may enhance strength temporarily but often induce shrinkage, cracking, and volumetric deformation, especially in expansive soils. These fluctuations highlight the critical need to understand and quantify unsaturated soil behavior. As infrastructure systems age and climate extremes become more frequent, integrating unsaturated soil mechanics into design and risk assessment is not merely beneficial—it is essential for resilience and long-term performance.

3 Climate-unsaturated soil interaction: Challenges and opportunities

The intersection of unsaturated soil mechanics and climate change presents both formidable challenges and transformative opportunities (Likos et al., 2019; Lu, 2020). On one hand, uncertainties in suction dynamics, hysteresis, and scaling from laboratory to field hinder reliable prediction of soil behavior under evolving hydro-climatic stresses. On the other hand, advances in experimental sensing, numerical modeling, and data-driven approaches provide unprecedented capacity to capture the coupled thermo-hydro-mechanical response of soils. Harnessing these tools within integrative frameworks offers the opportunity not only to mitigate climate-induced risks but also to reimagine geotechnical design as inherently adaptive and resilient. Thus, the future of climate-resilient infrastructure will be inseparable from continued innovation in unsaturated soil mechanics. Figure 3d illustrates an example of climate–soil–vegetation interactions, highlighting the principal processes and effects on water balance, suction, and stability.

3.1 Challenges

Despite significant progress in unsaturated soil mechanics, applying these principles under climate variability presents several challenges. Complex soil–atmosphere interactions, scale effects, and uncertainties in climatic drivers continue to limit predictive reliability and practical implementation. Several key challenges are as follows.

3.1.1 Complexities of soil water potential

Total soil water potential represents the work required to transfer an infinitesimal quantity of pure water from a reference state to a given point in the soil, under isothermal and reversible conditions (Bolt, 1976). It arises from multiple force fields, including gravity, hydrostatic pressure, capillarity, solute concentration, and air pressure, and can be expressed as Equation 3:

$\psi ={\psi }_g+{\psi }_p+{\psi }_o+{\psi }_m+{\psi }_a(3)$

where ${\psi }_g,{\psi }_p,{\psi }_o,{\psi }_m,{\psi }_a$ denote the gravitational, pressure, osmotic, matric, and air potentials, respectively. Gravitational potential (${\psi }_g$) reflects the energy difference per unit volume or weight between standard water and soil water due to gravity due to elevation relative to a reference level. Pressure potential (${\psi }_p$) arises from the hydrostatic pressure of overlying free water. Osmotic potential (${\psi }_o$) represents the reduction in energy caused by dissolved solutes. Matric potential (${\psi }_m$) captures the effects of capillarity and adsorption at the soil–water interface. Air potential (${\psi }_a$) accounts for the influence of pore-air pressure on soil water. In most geotechnical applications, osmotic and air potentials are negligible (Fredlund, 2006).

While the concept of water potential has proven useful, its application in soil mechanics has sometimes deviated from rigorous physical principles. Barbour (1998) noted that the assumption of linear additivity of all reported potentials (e.g., gravitational, osmotic, vapor, matric, hydrostatic, and overburden) is misleading. In classical soil mechanics, saturated water flow is strictly described by hydraulic head, consisting only of pressure and gravitational components acting in the vertical direction. Other processes—such as air flow associated with matric suction or chemical gradients—respond to their own independent driving forces and should not be simply superimposed onto the hydraulic framework.

This highlights a key challenge: while soil water potential provides a unifying framework, not all “potentials” contribute equally or linearly to water movement. Careful distinction between governing mechanisms is essential, particularly in unsaturated soils where climate-induced variations in suction, pore-air pressure, and solute concentration complicate the interaction between soil and water.

3.1.2 Soil–atmosphere interaction complexity

Modeling infiltration, evaporation, and suction fluctuations under variable climates remains highly nonlinear and site-specific. This is typically expressed using Richards’ equation (Equation 4),

$\frac{\partial \theta \left(\psi \right)}{\partial t}=\nabla ·\left[K\left(\theta \right)\left(\nabla \psi +e_z\right)\right](4)$

where $\theta \left(\psi \right)$ is volumetric water content as a function of matric suction/head, $\psi$ is soil water potential (matric suction, pressure head), $K\left(\theta \right)$ is hydraulic conductivity as a function of water content, $e_z$ is unit vector in the vertical (gravity) direction, $t$ is time. With surface boundary fluxes for rainfall and evaporation, the equation captures the atmosphere–soil interface, but prediction accuracy suffers due to highly path-dependent infiltration and drying.

3.1.3 Hydraulic hysteresis

Soil-water retention curves are not unique, showing path-dependent wetting–drying (d/w) responses that challenge parameterization. This is often represented by van Genuchten functions with distinct drying/wetting parameters (Equation 5),

$S_e^{\left(d/w\right)}={\left[1+{\left({\mathit{\alpha }}_{d/w}/\psi \right)}^{n_{d/w}}\right]}^{{-m}_{d/w}}(5)$

where $S_e^{\left(d/w\right)}$ is effective saturation, ${\mathit{\alpha }}_{d/w}$, $n_{d/w}$, $m_{d/w}$ ​are fitting parameters. Differences between drying and wetting curves create hysteresis, complicating prediction of suction and permeability under cyclic wetting–drying. Ignoring hysteresis can lead to significant errors in suction and permeability estimates (Lechman et al., 2006; Likos et al., 2014). Capturing scanning curves is computationally demanding and often infeasible in practical design. This limits the reliable application of laboratory SWRC data to real-world cyclic conditions.

3.1.4 Scaling from laboratory to field

Controlled laboratory tests provide valuable insights but rarely capture the heterogeneity of field soils. Effective hydraulic properties must be upscaled, often using statistical expressions such as Equation 6,

$K_{eff}\approx \mathit{exp}\left({\mu }_{lnK}+\frac{1}{2}{\mathit{\sigma }}_{\mathit{l}\mathit{n}\mathit{K}}^{\mathbf{2}}\right)(6)$

where $K_{eff}$ is the effective field conductivity, ${\mu }_{lnK}$ is the mean log-conductivity, and ${\mathit{\sigma }}_{\mathit{l}\mathit{n}\mathit{K}}^{\mathbf{2}}$ is its variance. This expression highlights which show how variability in hydraulic conductivity leads to higher field-scale values than laboratory estimates. Vegetation, preferential flow, and climate variability further widen this scale gap.

3.1.5 Coupled processes

Soils exposed to climate stresses experience simultaneous hydraulic, thermal, and mechanical influences. The effective stress can be extended to include suction and thermal contributions (Equation 7),

${\sigma }^{\prime }=\left(\sigma -u_{a}I\right)+\chi \psi I-C_T\Delta T(7)$

where $I$ is identity tensor, $C_T$ is thermal coefficient, and $\Delta T$ is temperature change. This shows that suction and temperature alter strength and deformation. Capturing these thermo-hydro-mechanical interactions (e.g., rainfall + temperature + desiccation cracking) into models remains a major challenge for practice.

3.1.6 Uncertainty under climate variability

Future rainfall, drought, and temperature regimes carry significant uncertainty, complicating risk-based design. Reliability-based frameworks evaluate the probability of failure (Equation 8),

$P_f=P\left\{g\left(X\right)<0\right\},\text{and}\beta =-{\mathrm{\Phi }}^{-1}\left(P_f\right)(8)$

where $g\left(X\right)$ is the limit-state function with random inputs X, $P_f$ is probability of failure, $\beta$ is the reliability index, and ${\mathrm{\Phi }}^{-1}$ the inverse normal distribution. This framework shows how uncertain climate inputs propagate into geotechnical risks. These approaches highlight how uncertain climatic drivers propagate into slope stability, foundation capacity, and embankment performance.

3.1.7 Monitoring limitations

Field measurements of suction and moisture are still limited by sensor cost, durability, and calibration issues. State estimation techniques, such as the Kalman filter (Equation 9),

$x_{k\mid k}=x_{k\mid k-1}+K_k\left(z_k-H{x}_{k\mid k-1}\right)(9)$

where $x_{k\mid k}$ is the updated state, $x_{k\mid k-1}$ is prediction, $K_k$ is Kalman gain, $z_k$ is measurement, and $H$ is observation matrix. While powerful, these methods are technically demanding, limiting their broad field adoption. Without robust long-term monitoring, model calibration and validation remain restricted.

3.1.8 Regional diversity

Different climates produce distinct soil–climate challenges: rainfall-induced failures in the tropics, collapsible soils in arid regions, and freeze–thaw in temperate zones. These differences can be framed using indices such as the aridity ratio $\left(\text{AR}\right)$ (Equation 10),

$\text{AR}=\frac{PRT}{P},PAW=\theta \left(\psi =-0.33\right)-\theta \left(\psi =-15\right)(10)$

where potential evapotranspiration (PET) and plant available water (PAW) highlight regional contrasts. Such variability demands tailored frameworks instead of one-size-fits-all designs.

3.2 Opportunities

At the same time, rapid advances in monitoring, modeling, and design frameworks are opening new opportunities. These innovations provide powerful tools to translate unsaturated soil mechanics into climate-resilient solutions for geotechnical infrastructure.

3.2.1 Advanced monitoring technologies

High-frequency suction and moisture data from tensiometers, TDR probes, and remote sensing enable early warning. Real-time fluxes can be derived using a simple water balance (Equation 11),

$q_s\left(t\right)\approx P\left(t\right)-E\left(t\right)-\frac{d}{dt}{\int }_{z_1}^{z_2}\theta \left(z,t\right)dz(11)$

linking rainfall, evapotranspiration, and soil water storage. Where $q_s\left(t\right)$ is vertical flux, $P\left(t\right)$ is precipitation, $E\left(t\right)$ is evapotranspiration, and $\theta \left(z,t\right)$ is water content between depths $z_1$ and $z_2$. These advances improve hazard detection and enable early-warning systems. These advances improve hazard detection and early-warning systems.

3.2.2 Innovative experimental methods

Micro-sensors, pore-scale imaging, and centrifuge tests now allow detailed exploration of soil–water interactions. Their outputs are often interpreted via inverse modeling (Equation 12),

$\underset{\theta }{\min }{\displaystyle \sum _i}{\left[{\psi }_i^{obs}-{\psi }_i^{sim}\left(\theta \right)\right]}^2(12)$

where ${\psi }_i^{obs}$ is observed suction, and ${\psi }_i^{sim}$ is simulated values. Such methods extract accurate soil retention parameters beyond traditional lab tests. Which estimates soil-water retention parameters. These tools provide deeper mechanistic insights that cannot be captured by traditional testing alone.

3.2.3 Computational advances

Coupled THM models, probabilistic methods, and machine learning expand predictive capacity. Physics-informed neural networks integrate governing equations with sparse data through a loss function (Equation 13),

$L={‖{\partial }_t\theta -\nabla ·\left[K\left(\theta \right)\left(\nabla \psi +e_z\right)\right]‖}^2\parallel \parallel 2+\lambda {‖{\partial }_t\theta -\nabla ·\left(\psi -{\psi }^{data}\right)‖}^2(13)$

where $L$ is loss, ${\psi }^{data}$, and $\lambda$ is weighting factor. This framework enhances extrapolation under novel climate stresses. Producing models that are both data-efficient and mechanistically consistent.

3.2.4 Integration with climate models

Downscaled climate scenarios can drive unsaturated soil models to project future risks. For example, suction evolution can be written as (Equation 14),

$\psi \left(z,t;\omega \right)=R\left(P_{\omega }\left(t\right),T_{\omega }\left(t\right),{PET}_{\omega }\left(t\right)\right)(14)$

where $\psi \left(z,t;\omega \right)$ is suction at depth $z$, time $t$, under climate scenario $\omega$, with drivers $P_{\omega }$ (rainfall), $T_{\omega }$ (temperature), and ${PET}_{\omega }$ (evapotranspiration). This integration bridges climate science and geotechnical design. $\omega$ denotes climate scenarios. This integration bridges climate science and geotechnical engineering, enabling scenario-based resilience analysis.

3.2.5 Reliability-based design

Incorporating suction variability into design frameworks enhances resilience. Partial factor methods link design checks to reliability targets (Equation 15),

${\gamma }_Q{Q}_k\le \frac{R_k}{{\gamma }_R},\beta \ge {\beta }_T(15)$

where loads $Q_k$ and resistances $R_k$ are adjusted to achieve a target reliability index ${\beta }_T$. This provides a structured way to address climate uncertainty in codes.

3.2.6 Region-specific solutions

Tailored design frameworks acknowledge regional differences in soil and climate. Soil-water characteristic curves can be parameterized for each climate zone (Equation 16),

$S_e={\left[1+{\left({\alpha }_r/\psi \right)}^{n_r}\right]}^{{-m}_r}rϵ\left\{tropical,arid,temperate\right\},(16)$

allowing models to capture regional hydro-mechanical responses more accurately.

3.2.7 Sustainability and adaptation

Embedding unsaturated soil mechanics in lifecycle analysis supports climate adaptation. A cost–risk optimization framework (Equation 17),

$\underset{d}{\min }{C}_{cap}\left(d\right)+E\left[{\displaystyle \sum _{t=1}^T}{C}_{maint}\left(d,t\right)+C_{fail}{I}_{\left\{gt\left(d\right)<0\right\}}\right](17)$

balances initial construction, maintenance, and failure costs. Such approaches ensure infrastructure remains robust and economical under uncertain future climates.

4 Applications for unsaturated soil mechanics in engineering practice

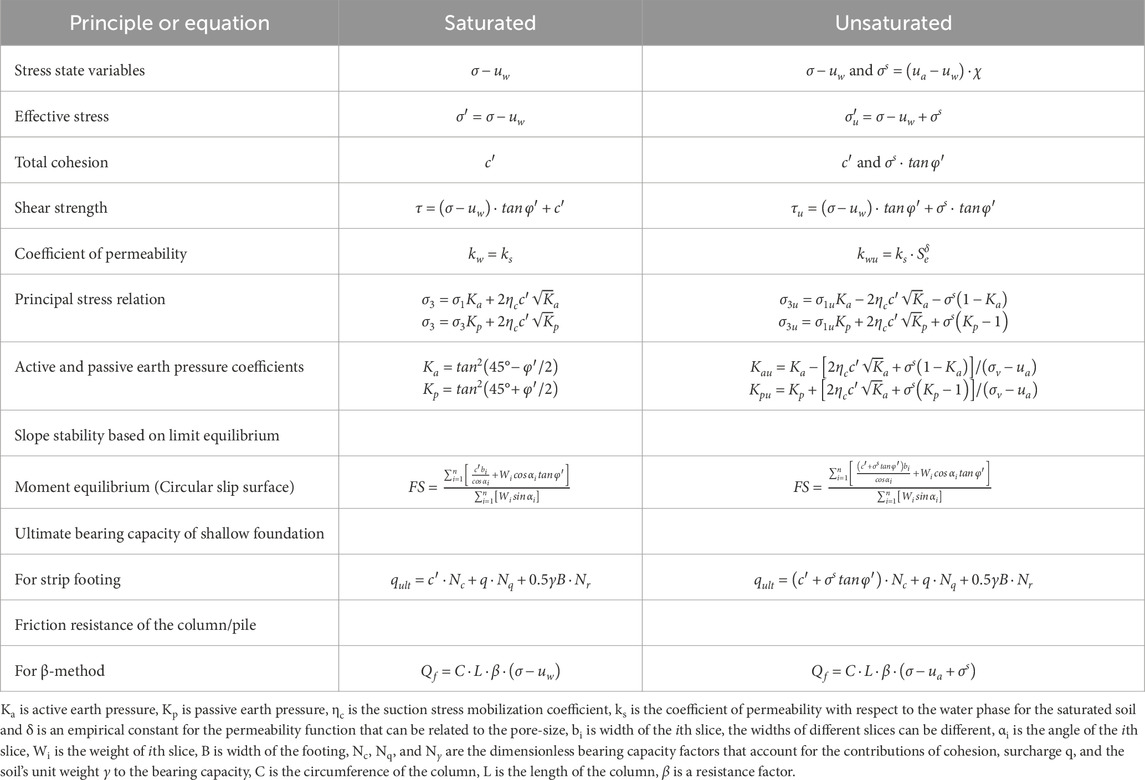
The influence of unsaturated soil mechanics on infrastructure design and performance becomes particularly significant under climate-induced moisture fluctuations. In this study, four case studies are investigated and presented. Table 1 summarizes the fundamental differences between saturated and unsaturated soils and introduces extended formulations for selected engineering applications in geotechnical engineering.

Table 1

Table 1. Equations for saturated and unsaturated soil mechanics.

4.1 Case study 1 – Rainfall-induced slope instability

Rainfall-induced slope instability provides one of the most direct illustrations of the role of unsaturated soil mechanics. In residual soils with permeability on the order of 10⁻⁶–10^–7 m/s, antecedent suctions of 20–100 kPa are often recorded prior to rainfall events (Rahardjo et al., 2019; Pham et al., 2023b). Intense tropical storms can rapidly infiltrate and reduce matric suction to zero, leading to a sharp drop in shear strength and slope stability. Numerical back-analyses of rainfall-induced landslides have shown that the factor of safety may decrease from values above 1.3 in dry conditions to below unity within hours of infiltration (Ng et al., 2003; Rahimi et al., 2011; Toll et al., 2012; Rahardjo et al., 2011). This is especially critical in cut slopes or embankments with low permeability. To illustrate this effect, a case of slope instability in Belgrade, Serbia, is selected for discussion, with input parameters and details as reported by Hadži-Niković et al. (2015).

The study area is a loess complex in hilly terrain where urbanization has modified natural morphology through excavations, slope cuts, and fills. Loess deposits up to 15 m thick consist of layered and clayey horizons overlying deluvial clays and marls at 15–18 m depth. Groundwater monitoring (2010–2013) indicated an average depth of 10 m, with fluctuations of 2.4–3.9 m. The soils were unsaturated, with 18%–20% water content, 75%–80% saturation, PL = 23%, PI = 18%, and CI classification. Unit weights ranged from 15 to 19.5 kN/m³. Shear strength parameters were c′ = 15 kPa, φ′ = 24°, and matric suction = 60 kPa. These properties informed slope stability analyses under rainfall-induced fluctuations.

Stability analyses were conducted using SLOPE/W software. Initially, an average matric suction of 60 kPa (degree of saturation, S_r = 0.80) was equivalent to a cohesion of 19.5 kPa. The corresponding factor of safety (Fs) increased from 1.249 (zero suction) to 1.476 — an improvement of approximately 19% (see Figure 4a). Slope stability was further assessed under varying groundwater table (GWT) conditions, as shown in Figure 4b. The results show that:

• With average GWT: Fs = 1.25

• Lowest GWT (12.0 m): Fs = 1.29 → 3% increase in factor of safety

• Highest GWT (8.0 m): Fs = 1.15 → 8% decrease in factor of safety

Figure 4

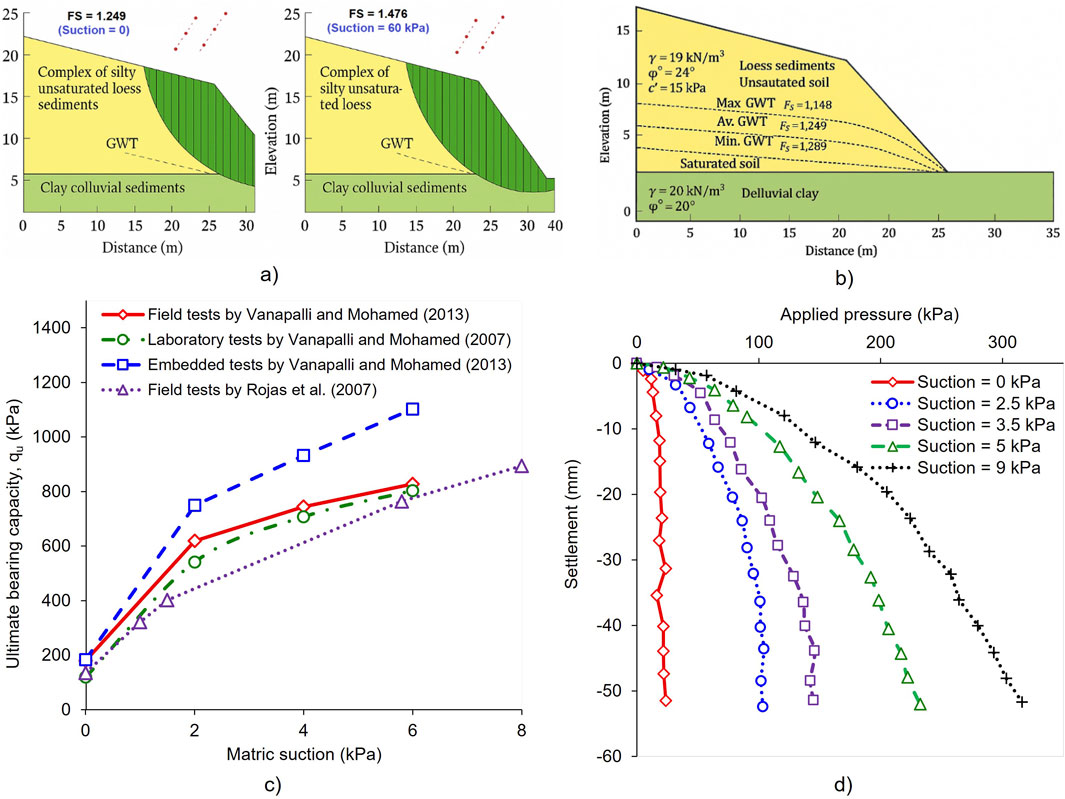
Figure 4. Analytical results of two case studies illustrating the impact of rainfall-induced infiltration: (a) Effect of decreasing suction on the factor of safety of a slope (adapted from Hadži-Niković et al. (2015); (b) Effect of rising groundwater table on FS of a slope (adapted from Hadži-Niković et al. (2015); (c) Influence of matric suction on the stability of a shallow foundation; (d) Influence of matric suction on the stability of stone columns.

These findings emphasize the role of suction and GWT fluctuations in slope stability under rainfall conditions.

4.2 Case study 2 – Stability of shallow foundation under infiltration

Shallow foundations in arid and semi-arid regions also demonstrate the critical role of suction. One key factor influencing this capacity is the mobilized cohesion at the interface between the footing and the underlying soils. In collapsible loess or dispersive soils, bearing capacity is often enhanced by suction during prolonged droughts, with field observations suggesting suction can contribute 20%–40% of total resistance (Vanapalli and Mohamed, 2007; Zimbardo et al., 2020). However, sudden wetting following intense rainfall or irrigation can collapse the soil structure, leading to differential settlement and loss of capacity. Case studies from semi-arid environments highlight that neglecting suction variation can underestimate settlement risk, compromising the reliability of shallow foundation design.

As shown in Figure 4c, several experimental studies (Vanapalli and Mohamed, 2007; 2013; Rojas et al., 2007; Pham and Sutman, 2022b) have demonstrated that the ultimate bearing capacity of shallow foundations increases with increasing matric suction. However, infiltration from rainfall or a rising groundwater table tends to reduce suction, which in turn can lead to a decrease in bearing capacity.

4.3 Case study 3 – Stability of column-supported embankment

The performance of a column-supported embankment was analyzed by incorporating the role of matric suction in the soil, according to Mohammed et al. (2025). Figure 4d shows the relationship between normalized settlement (s/B) and bearing pressure at different suction levels ($\psi$). Both experimental and numerical results consistently demonstrate that matric suction significantly enhances soil stiffness and load-bearing capacity. For example, compared to the saturated condition ($\psi$ = 0), the soil under $\psi$ = 7.5 kPa sustains substantially higher bearing pressures at the same settlement level, delaying the onset of large deformations. This highlights suction as a stabilizing mechanism, particularly relevant for embankment fills where moisture fluctuations are frequent.

However, the results also reveal a strong sensitivity to suction loss. When suction reduces from $\psi$ = 7.5 kPa to near-saturation ($\psi$ = 0), the bearing capacity drops by more than half for the same settlement threshold. This demonstrates how rainfall infiltration or groundwater rise can rapidly diminish stability, concentrating stresses on the columns and potentially inducing excessive settlement or lateral spreading. Importantly, the close agreement between experimental and numerical results validates the use of suction-dependent constitutive models for predicting embankment performance.

This case emphasizes two key insights into the application of USM in engineering practice: i) Stabilization by suction–Under unsaturated conditions, suction contributes directly to shear strength and stiffness, improving load distribution between soil and columns, thereby reducing settlement. ii) Vulnerability to climate events–Rainfall infiltration reduces suction, eroding these benefits and highlighting the need for suction monitoring and adaptive design strategies in embankment systems.

5 Summary of findings

In conclusion, these contrasting regional cases emphasize the universal applicability of USM while highlighting the need for climate-tailored solutions. Tropical regions require attention to rapid suction loss and rainfall infiltration, while arid regions demand careful consideration of collapse potential and wetting-induced settlement. All examples demonstrate that climate-responsive geotechnical design must explicitly incorporate unsaturated soil mechanics, supported by monitoring and predictive modeling, to ensure resilience across diverse climatic contexts.

In addition to the three representative case studies discussed above, there are numerous infrastructure systems whose performance is significantly affected by climate-induced moisture fluctuations. For instance, road and railway embankments are highly vulnerable to seasonal wetting and drying cycles, which induce shrink-swell behavior in the underlying subgrade soils (Clarke et al., 2006). Another example is buried infrastructure, such as pipelines and utility conduits, which may experience uplift or deformation due to swelling pressures, or energy geostructures are also involved in unsaturated soils due to water evaporation (Pham and Sutman, 2023b).

6 Emerging solutions

Incorporating unsaturated soil mechanics into design codes and analysis frameworks is critical. This includes moving beyond conventional saturated models and accounting for partial saturation, suction variation, and coupled flow-deformation processes. The integration of unsaturated soil mechanics into climate-resilient geotechnical design involves both analytical advancements and field instrumentation:

• Design Code Evolution: Some modern codes have begun to consider unsaturated conditions, but widespread adoption remains limited. Incorporating SWRC-based design charts, suction envelopes, and moisture sensitivity classifications into national and international codes can bridge this gap.

• Numerical Modeling Advances: Software platforms such as PLAXIS, SEEP/W, and CODE_BRIGHT offer capabilities to simulate transient seepage, suction-dependent strength, and Thermal-hydro-mechanical (THM) coupling. These tools are essential for climate-aware geotechnical simulations.

• Field Monitoring and Early Warning: Suction sensors, time-domain reflectometry (TDR) probes, and remote sensing tools are increasingly used to monitor moisture variation and matric suction in situ. Coupled with weather forecasts, these systems support real-time risk assessment and early warning for infrastructure managers.

• Cost–Benefit Considerations for Monitoring Systems: From a practical standpoint, cost–benefit analysis plays an important role in adopting USM-based monitoring systems. While advanced suction sensors, TDR probes, and remote sensing technologies can involve higher initial installation costs, the benefits often outweigh the expenses. Their ability to deliver early warning, reduce maintenance cycles, and prevent catastrophic failures provides substantial long-term economic advantages. Integrating such systems into infrastructure management strategies ensures that resilience measures are not only technically robust but also economically viable.

• Data-Driven Approaches: Machine learning and AI-based models, trained on historical performance data and climate inputs, can provide rapid assessment tools for infrastructure vulnerability under unsaturated conditions.

• Climate-Integrated Planning: Multiscale models that incorporate regional climate projections, soil-atmosphere interactions, and land use can inform the long-term adaptation of critical infrastructure.

7 Conclusion

Climate change has magnified the vulnerabilities of geotechnical infrastructure, exposing the limitations of traditional saturated soil frameworks. This study demonstrates that unsaturated soil mechanics (USM) provides not only a more realistic description of soil behavior under fluctuating moisture and temperature conditions but also a critical pathway toward climate-resilient infrastructure. By linking matric suction, soil–water retention, and hydro-mechanical coupling, USM offers a framework that captures the transient processes driving instability, settlement, and loss of serviceability across diverse climatic regions.

The challenges remain formidable: nonlinear soil–atmosphere exchanges, hydraulic hysteresis, scale effects, and climate uncertainty continue to complicate predictions and design. Yet these very challenges also present opportunities. Advances in monitoring technologies, data-driven modeling, and climate-integrated risk frameworks are rapidly expanding the ability to capture, predict, and adapt to unsaturated soil behavior. The case studies discussed in this paper—from rainfall-induced slope failures to shallow foundation performance and column-supported embankments—underscore both the stabilizing role of suction and the fragility of this benefit under climate extremes.

Moving forward, the integration of USM into geotechnical practice must extend beyond research frontiers to design codes, infrastructure monitoring, and policy frameworks. Proactive adoption of suction-aware models, reliability-based design, and region-specific adaptation strategies will be vital. By embedding USM into the lifecycle of geotechnical systems, engineers can move from reactive responses to a proactive paradigm of resilience.

Ultimately, unsaturated soil mechanics represent more than a refinement of geotechnical theory—it is a cornerstone for safeguarding infrastructure in a climate-uncertain future. Harnessing its principles will allow societies not only to withstand climate extremes but also to adapt infrastructure systems in ways that are scientifically robust, economically viable, and environmentally sustainable.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to YXRwaGFtQGt0aC5zZQ==.

Author contributions

TP: Conceptualization, Data curation, Formal Analysis, Funding acquisition, Investigation, Methodology, Project administration, Resources, Software, Supervision, Validation, Visualization, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ajdari, M., Vahedifard, F., and Amirlatifi, A. (2025). Physics-informed data-driven modeling of unsaturated soils under thermo-hydro-mechanical loading conditions. J. Geotechnical Geoenvironmental Eng. 151 (10), 04025108. doi:10.1061/JGGEFK.GTENG-13239

CrossRef Full Text | Google Scholar

Alonso, E. E., and Olivella, S. (2006). Unsaturated soil mechanics applied to geotechnical problems. Unsaturated Soils 2006, 1–35. doi:10.1061/40802(189)1

CrossRef Full Text | Google Scholar

Au, S. W. C. (1998). Rain-induced slope instability in Hong Kong. Eng. Geol. 51 (1), 1–36. doi:10.1016/S0013-7952(98)00038-6

CrossRef Full Text | Google Scholar

Bachmann, J., Horton, R., Grant, S. A., and Van der Ploeg, R. R. (2002). Temperature dependence of water retention curves for wettable and water-repellent soils. Soil Sci. Soc. Am. J. 66 (1), 44–52. doi:10.2136/sssaj2002.4400

CrossRef Full Text | Google Scholar

Baker, R., and Frydman, S. (2009). Unsaturated soil mechanics: critical review of physical foundations. Eng. Geol. 106 (1-2), 26–39. doi:10.1016/j.enggeo.2009.02.010

CrossRef Full Text | Google Scholar

Barbour, S. L. (1998). Nineteenth Canadian Geotechnical Colloquium: the soil-water characteristic curve: a historical perspective. Can. Geotechnical J. 35 (5), 873–894. doi:10.1139/cgj-35-5-873

CrossRef Full Text | Google Scholar

Bashir, R., Sharma, J., and Stefaniak, H. (2015). Effect of hysteresis of soil-water characteristic curves on infiltration under different climatic conditions. Can. Geotechnical J. 53 (2), 273–284. doi:10.1139/cgj-2015-0004

CrossRef Full Text | Google Scholar

Bishop, A. W. (1959). The principle of effective stress: teknisk Ukeblad, 39.

Google Scholar

Bishop, A. W., and Blight, G. E. (1963). Some aspects of effective stress in saturated and partly saturated soils. Geotechnique 13 (3), 177–197. doi:10.1680/geot.1963.13.3.177

CrossRef Full Text | Google Scholar

Bolt, G. H. (1976). Soil physics terminology. Bull. Int. Soc. Soil Sci. 49, 26–36.

Google Scholar

Bridges, C. A. (2024). “Climate change impacts on geotechnical infrastructure,” in Geotechnical engineering challenges to meet current and emerging needs of society (London, United Kingdom: CRC Press), 2838–2841.

CrossRef Full Text | Google Scholar

Cardoso, R., Sarapajevaite, G., Korsun, O., Cardoso, S., and Ilharco, L. (2017). Microfabricated sol-gel relative humidity sensors for soil suction measurement during laboratory tests. Can. Geotechnical J. 54 (8), 1176–1183. doi:10.1139/cgj-2016-0419

CrossRef Full Text | Google Scholar

Cavalcante, A. L. B., and Mascarenhas, P. V. S. (2021). Efficient approach in modeling the shear strength of unsaturated soil using soil water retention curve. Acta Geotech. 16 (10), 3177–3186. doi:10.1007/s11440-021-01144-6

CrossRef Full Text | Google Scholar

Clarke, G. R. T., Hughes, D. A. B., Barbour, S. L., and Sivakumar, V. (2006). “The implications of predicted climate changes on the stability of highway geotechnical infrastructure: a case study of field monitoring of pore water response,” in 2006 IEEE EIC Climate Change Conference, Ottawa, ON, Canada, 10-12 May 2006 (IEEE), 1–10.

Google Scholar

Costa, S., Robert, D., and Kodikara, J. (2023). “Climate change and geo-infrastructures: assessment and challenges,” in Sustainable Civil engineering (London, United Kingdom: CRC Press), 217–233.

CrossRef Full Text | Google Scholar

Culligan, P. J., Whittle, A. J., and Mitchell, J. K. (2019). “The role of geotechnics in addressing new world problems,” in Geotechnical fundamentals for addressing new world challenges (Cham: Springer International Publishing), 1–27.

CrossRef Full Text | Google Scholar

DiBiagio, A., Capobianco, V., Oen, A., and Tallaksen, L. M. (2024). State-of-the-art: parametrization of hydrological and mechanical reinforcement effects of vegetation in slope stability models for shallow landslides. Landslides 21 (10), 2417–2446. doi:10.1007/s10346-024-02300-1

CrossRef Full Text | Google Scholar

Filipović, V., Ondrašek, G., and Filipović, L. (2016). “Modelling water dynamics, transport processes and biogeochemical reactions in soil vadose zone,” in Groundwater—contaminant and resource management. Editor M. S. Javaid (Rijeka, Croatia: Intech), 133–162.

CrossRef Full Text | Google Scholar

Fredlund, D. G. (2006). Unsaturated soil mechanics in engineering practice. J. Geotechnical Geoenvironmental Eng. 132 (3), 286–321. doi:10.1061/(ASCE)1090-0241(2006)132:3(286)

CrossRef Full Text | Google Scholar

Fredlund, D. G. (2014). The emergence of unsaturated soil mechanics. Can. Geotechnical J. 51 (12), ix–x. doi:10.1139/cgj-2014-0095

CrossRef Full Text | Google Scholar

Fredlund, D. G., and Morgenstern, N. R. (1977). Stress state variables for unsaturated soils. J. Geotechnical Eng. Div. 103 (5), 447–466. doi:10.1061/AJGEB6.000042

CrossRef Full Text | Google Scholar

Fredlund, D. G., and Rahardjo, H. (1993). Soil mechanics for unsaturated soils. New York: John Wiley and Sons.

Google Scholar

Fredlund, D. G., Morgenstern, N. R., and Widger, R. A. (1978). The shear strength of unsaturated soils. Can. Geotechnical J. 15 (3), 313–321. doi:10.1139/t78-029

CrossRef Full Text | Google Scholar

Fredlund, D. G., Xing, A., and Huang, S. (1994). Predicting the permeability function for unsaturated soils using the soil-water characteristic curve. Can. Geotechnical J. 31 (4), 533–546. doi:10.1139/t94-062

CrossRef Full Text | Google Scholar

Fredlund, D. G., Xing, A., Fredlund, M. D., and Barbour, S. L. (1996). The relationship of the unsaturated soil shear strength to the soil-water characteristic curve. Can. Geotechnical J. 33 (3), 440–448. doi:10.1139/t96-065

CrossRef Full Text | Google Scholar

Gao, H., and Shao, M. (2015). Effects of temperature changes on soil hydraulic properties. Soil Tillage Res. 153, 145–154. doi:10.1016/j.still.2015.05.003

CrossRef Full Text | Google Scholar

Garg, A., Bordoloi, S., Ganesan, S. P., Sekharan, S., and Sahoo, L. (2020). A relook into plant wilting: observational evidence based on unsaturated soil–plant-photosynthesis interaction. Sci. Rep. 10 (1), 22064. doi:10.1038/s41598-020-78893-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Garven, E. A., and Vanapalli, S. K. (2006). “Evaluation of empirical procedures for predicting the shear strength of unsaturated soils,” in Unsaturated soils 2006, 2570–2592. doi:10.1061/40802(189)219

CrossRef Full Text | Google Scholar

Hadži-Niković, G., Rakić, D., and Djoković, K. (2015). Effect of changes in matric suction on slope stability in natural unsaturated soil. doi:10.1680/ecsmge.60678

CrossRef Full Text | Google Scholar

Haghighi, A., Medero, G. M., Marinho, F. A., Mercier, B., and Woodward, P. K. (2012). Temperature effects on suction measurement using the filter paper technique. Geotechnical Test. J. 35 (1), 83–90. doi:10.1520/GTJ103575

CrossRef Full Text | Google Scholar

Hamid, T. B., and Miller, G. A. (2009). Shear strength of unsaturated soil interfaces. Can. Geotechnical J. 46 (5), 595–606. doi:10.1139/T09-002

CrossRef Full Text | Google Scholar

Haruzi, P., and Moreno, Z. (2023). Modeling water flow and solute transport in unsaturated soils using physics-informed neural networks trained with geoelectrical data. Water Resour. Res. 59 (6), e2023WR034538. doi:10.1029/2023WR034538

CrossRef Full Text | Google Scholar

Hillel, D. (1998). Environmental soil physics. San Diego, CA: Academic Press.

Google Scholar

Hopmans, J. W., and Dane, J. H. (1986). Temperature dependence of soil water retention curves. Soil Sci. Soc. Am. J. 50 (3), 562–567. doi:10.2136/sssaj1986.03615995005000030004x

CrossRef Full Text | Google Scholar

Houston, S. L. (2019). It is time to use unsaturated soil mechanics in routine geotechnical engineering practice. J. Geotechnical Geoenvironmental Eng. 145 (5), 02519001. doi:10.1061/(ASCE)GT.1943-5606.0002044

CrossRef Full Text | Google Scholar

Houston, S. L. (2024). Unsaturated soil mechanics topics for all geotechnical engineers. Indian Geotechnical J., 1–17. doi:10.1007/s40098-024-01102-5

CrossRef Full Text | Google Scholar

Illés, Z., and Nagy, L. (2022). Effect of climate change on earthworks of infrastructure: statistical evaluation of the cause of dike pavement cracks. Geoenvironmental Disasters 9 (1), 20. doi:10.1186/s40677-022-00221-6

CrossRef Full Text | Google Scholar

Jardine, R. J. (2020). Geotechnics, energy and climate change: the 56th Rankine Lecture. Géotechnique 70 (1), 3–59. doi:10.1680/jgeot.18.RL.001

CrossRef Full Text | Google Scholar

Kandalai, S., John, N. J., and Patel, A. (2023). Effects of climate change on geotechnical infrastructures—state of the art. Environ. Sci. Pollut. Res. 30 (7), 16878–16904. doi:10.1007/s11356-022-24788-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Khalili, N., and Khabbaz, M. H. (1998). A unique relationship for χ for the determination of the shear strength of unsaturated soils. Geotechnique 48 (5), 681–687. doi:10.1680/geot.1998.48.5.681

CrossRef Full Text | Google Scholar

Khalili, N. G. F. A., Geiser, F., and Blight, G. E. (2004). Effective stress in unsaturated soils: review with new evidence. Int. J. Geomechanics 4 (2), 115–126. doi:10.1061/(ASCE)1532-3641(2004)4:2(115)

CrossRef Full Text | Google Scholar

Khalili, N., Romero Morales, E. E., and Marinho, F. A. (2022). “State of the art report. Advances in unsaturated soil mechanics: constitutive modelling, experimental investigation, and field instrumentation,” in Proceedings of twentieth international conference on soil mechanics and geotechnical engineering (ICSMGE 2022): a geotechnical discovery down under, sydney, new South wales (Australia), 297–348.

Google Scholar

Kim, W. S., and Borden, R. H. (2011). Influence of soil type and stress state on predicting shear strength of unsaturated soils using the soil-water characteristic curve. Can. Geotechnical J. 48 (12), 1886–1900. doi:10.1139/t11-082

CrossRef Full Text | Google Scholar

Kirkham, M. B. (2023). Principles of soil and plant water relations. Elsevier.

Google Scholar

Lechman, J., Lu, N., and Wu, D. (2006). Hysteresis of matric suction and capillary stress in monodisperse disk-shaped particles. J. Eng. Mech. 132 (5), 565–577. doi:10.1061/(ASCE)0733-9399(2006)132:5(565

CrossRef Full Text | Google Scholar

Likos, W. J., Lu, N., and Godt, J. W. (2014). Hysteresis and uncertainty in soil water-retention curve parameters. J. Geotechnical Geoenvironmental Eng. 140 (4), 04013050. doi:10.1061/(ASCE)GT.1943-5606.000107

CrossRef Full Text | Google Scholar

Likos, W. J., Song, X., Xiao, M., Cerato, A., and Lu, N. (2019). “Fundamental challenges in unsaturated soil mechanics,” in Geotechnical fundamentals for addressing new world challenges (Cham: Springer International Publishing), 209–236.

CrossRef Full Text | Google Scholar

Livingston, N. J., and Topp, G. C. (1993). Soil water potential. Soil sampling and methods of analysis. London, United Kingdom: Canadian Society of Soil Sciences, 559–567.

Google Scholar

Loveridge, F. A., Spink, T. W., O'Brien, A. S., Briggs, K. M., and Butcher, D. (2010). The impact of climate and climate change on infrastructure slopes, with particular reference to southern England. Geol. Soc. Lond. 43, 461–472. doi:10.1144/1470-9236/09-050

CrossRef Full Text | Google Scholar

Lu, N. (2020). Unsaturated soil mechanics: fundamental challenges, breakthroughs, and opportunities. J. Geotechnical Geoenvironmental Eng. 146 (5), 02520001. doi:10.1061/(ASCE)GT.1943-5606.0002233

CrossRef Full Text | Google Scholar

Lu, N., and Likos, W. J. (2004). Unsaturated soil mechanics. Hoboken, NJ: John Wiley and Sons.

Google Scholar

Lu, N., Godt, J. W., and Wu, D. T. (2010). A closed-form equation for effective stress in unsaturated soil. Water Resour. Res. 46 (5). doi:10.1029/2009WR008646

CrossRef Full Text | Google Scholar

Mahmoodabadi, M., and Bryson, L. S. (2021). Direct application of the soil–water characteristic curve to estimate the shear modulus of unsaturated soils. Int. J. Geomechanics 21 (1), 04020243. doi:10.1061/(ASCE)GM.1943-5622.000189

CrossRef Full Text | Google Scholar

C. Mancuso, C. Jommi, and F. D'Onza (2012). Unsaturated soils: research and applications (Berlin: Springer), 1.

Google Scholar

Matyas, E. L., and Radhakrishna, H. S. (1968). Volume change characteristics of partially saturated soils. Geotechnique 18 (4), 432–448. doi:10.1680/geot.1968.18.4.432

CrossRef Full Text | Google Scholar

Mohammed, S. A., Rathod, D., and Vanapalli, S. K. (2025). Experimental and numerical studies on geosynthetic encased stone columns in saturated and unsaturated soils. Transp. Geotech. 52, 101566. doi:10.1016/j.trgeo.2025.101566

CrossRef Full Text | Google Scholar

Najdi, A., Encalada, D., Mendes, J., Prat, P. C., and Ledesma, A. (2023). Evaluating innovative direct and indirect soil suction and volumetric measurement techniques for the determination of soil water retention curves following drying and wetting paths. Eng. Geol. 322, 107179. doi:10.1016/j.enggeo.2023.107179

CrossRef Full Text | Google Scholar

Ng, C. W. W., and Menzies, B. (2014). Advanced unsaturated soil mechanics and engineering. London, United Kingdom: CRC Press.

Google Scholar

Ng, C. W. W., Zhan, L. T., Bao, C. G., Fredlund, D. G., and Gong, B. W. (2003). Performance of an unsaturated expansive soil slope subjected to artificial rainfall infiltration. Geotechnique 53 (2), 143–157. doi:10.1680/geot.2003.53.2.143

CrossRef Full Text | Google Scholar

Ng, C. W. W., Wang, Y., Zhang, S., and Zhang, Q. (2024). Effects of climate change on soil embankments for transport infrastructure. Transp. Geotech. 48, 101324. doi:10.1016/j.trgeo.2024.101324

CrossRef Full Text | Google Scholar

Nikooee, E., Habibagahi, G., Hassanizadeh, S. M., and Ghahramani, A. (2012). “The effective stress in unsaturated soils: insights from thermodynamics. Unsaturated Soils Res. Appl. 2, 5–11. doi:10.1007/978-3-642-31343-1_1

CrossRef Full Text | Google Scholar

Pantoja Porro, R., Li, Z., and O’Donovan, J. (2025). The impact of climate change on underground transport infrastructure: a review. Geotechnical Res. 12 (2), 85–101. doi:10.1680/jgere.24.00047

CrossRef Full Text | Google Scholar

Peipei, C., Ming, J., Huanwei, Z., Zhiguang, G., Bing, B., and Ruisong, Z. (2024). Thermal-hydro-mechanical coupling response characteristics of unsaturated soil under complex temperature paths. J. Basic Sci. Eng. 32 (5), 1294–1306. doi:10.16058/j.issn.1005-0930.2024.05.007

CrossRef Full Text | Google Scholar

Pham, T. A. (2022). Micromechanical-based shear strength equation considering the stress-state effect for unsaturated soils. Int. J. Geomechanics 22 (9), 06022022. doi:10.1061/(ASCE)GM.1943-5622.0002495

CrossRef Full Text | Google Scholar

Pham, T. A., and Sutman, M. (2022a). An analytical model for predicting the shear strength of unsaturated soils. Proc. Institution Civ. Engineers-Geotechnical Eng. 176 (4), 369–387. doi:10.1680/jgeen.21.00135

CrossRef Full Text | Google Scholar

Pham, T. A., and Sutman, M. (2022b). Disturbed state concept and non-isothermal shear strength model for unsaturated soils. Bull. Eng. Geol. Environ. 81 (5), 202. doi:10.1007/s10064-022-02688-x

CrossRef Full Text | Google Scholar

Pham, T. A., and Sutman, M. (2023a). Modeling the combined effect of initial density and temperature on the soil–water characteristic curve of unsaturated soils. Acta Geotech. 18 (12), 6427–6455. doi:10.1007/s11440-023-01920-6

CrossRef Full Text | Google Scholar

Pham, T. A., and Sutman, M. (2023b). A simplified method for bearing-capacity analysis of energy piles integrating temperature-dependent model of soil–water characteristic curve. J. Geotechnical Geoenvironmental Eng. 149 (9), 04023080. doi:10.1061/JGGEFK.GTENG-11095

CrossRef Full Text | Google Scholar

Pham, T. A., Hashemi, A., Sutman, M., and Medero, G. M. (2023a). Effect of temperature on the soil–water retention characteristics in unsaturated soils: analytical and experimental approaches. Soils Found. 63 (3), 101301. doi:10.1016/j.sandf.2023.101301

CrossRef Full Text | Google Scholar

Pham, T. A., Sutman, M., and Medero, G. M. (2023b). Validation, reliability, and performance of shear strength models for unsaturated soils. Geotechnical Geol. Eng. 41 (7), 4271–4309. doi:10.1007/s10706-023-02520-7

CrossRef Full Text | Google Scholar

Pham, T. A., Sutman, M., and Medero, G. M. (2023c). Density-dependent model of soil–water characteristic curves and application in predicting unsaturated soil–structure bearing resistance. Int. J. Geomechanics 23 (4), 04023017. doi:10.1061/IJGNAI.GMENG-7504

CrossRef Full Text | Google Scholar

Pham, T. A., Medero, G. M., and Sutman, M. (2023d). Thermo-hydro-mechanical coupling model of elastic modulus characteristic curve for unsaturated soils. Comput. Geotechnics 162, 105704. doi:10.1016/j.compgeo.2023.105704

CrossRef Full Text | Google Scholar

Pham, T. A., Nadimi, S., and Sutman, M. (2024). Critical review of physical-mechanical principles in geostructure-soil interface mechanics. Geotechnical Geol. Eng. 42 (8), 6757–6808. doi:10.1007/s10706-024-02954-7

CrossRef Full Text | Google Scholar

Pham, T. A., Sutman, M., and Nadimi, S. (2025). Capillary-based nonisothermal suction stress and nonlinear shear strength criteria for unsaturated compacted soils. Int. J. Geomechanics 25 (5), 04025061. doi:10.1061/IJGNAI.GMENG-10364

CrossRef Full Text | Google Scholar

Rahardjo, H., Santoso, V. A., Leong, E. C., Ng, Y. S., and Hua, C. J. (2011). Numerical analyses and monitoring performance of residual soil slopes. Soils Found. 51 (3), 471–482. doi:10.3208/sandf.51.471

CrossRef Full Text | Google Scholar

Rahardjo, H., Kim, Y., and Satyanaga, A. (2019). Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Engineering 10 (1), 8. doi:10.1186/s40703-019-0104-8

CrossRef Full Text | Google Scholar

Rahimi, A., Rahardjo, H., and Leong, E. C. (2011). Effect of antecedent rainfall patterns on rainfall-induced slope failure. J. Geotechnical Geoenvironmental Eng. 137 (5), 483–491. doi:10.1061/(ASCE)GT.1943-5606.0000451

CrossRef Full Text | Google Scholar

Richards, L. A., and Weaver, L. R. (1943). Fifteen-atmosphere percentage as related to the permanent wilting percentage. Soil Sci. 56 (5), 331–340. doi:10.1097/00010694-194311000-00002

CrossRef Full Text | Google Scholar

Ridley, A. M., and Burland, J. B. (1993). A new instrument for the measurement of soil moisture suction. Géotechnique 43 (2), 321–324. doi:10.1680/geot.1993.43.2.321

CrossRef Full Text | Google Scholar

Rojas, J. C., Salinas, L. M., and Sejas, C. (2007). “Plate-load tests on an unsaturated lean clay,” in Experimental unsaturated soil mechanics (Berlin, Heidelberg: Springer Berlin Heidelberg), 445–452.

CrossRef Full Text | Google Scholar

Rouainia, M., Helm, P., Davies, O., and Glendinning, S. (2020). Deterioration of an infrastructure cutting subjected to climate change. Acta Geotech. 15 (10), 2997–3016. doi:10.1007/s11440-020-00965-1

CrossRef Full Text | Google Scholar

Salager, S., El Youssoufi, M. S., and Saix, C. (2010). Effect of temperature on water retention phenomena in deformable soils: theoretical and experimental aspects. Eur. J. soil Sci. 61 (1), 97–107. doi:10.1111/j.1365-2389.2009.01204.x

CrossRef Full Text | Google Scholar

Salimi, M., and Al-Ghamdi, S. G. (2020). Climate change impacts on critical urban infrastructure and urban resiliency strategies for the Middle East. Sustain. Cities Soc. 54, 101948. doi:10.1016/j.scs.2019.101948

CrossRef Full Text | Google Scholar

Scanlon, B. R., Andraski, B. J., and Bilskie, J. (2002). 3.2. 4 Miscellaneous methods for measuring matric or water potential. Methods Soil Analysis Part 4 Phys. Methods 5, 643–670. doi:10.2136/sssabookser5.4.c23

CrossRef Full Text | Google Scholar

Scaringi, G., and Loche, M. (2022). A thermo-hydro-mechanical approach to soil slope stability under climate change. Geomorphology 401, 108108. doi:10.1016/j.geomorph.2022.108108

CrossRef Full Text | Google Scholar

Schneider, M., and Goss, K. U. (2011). Temperature dependence of the water retention curve for dry soils. Water Resour. Res. 47 (3). doi:10.1029/2010WR009687

CrossRef Full Text | Google Scholar

Shwan, B. J. (2024). Drought-induced stability reduction in unsaturated geotechnical applications. Model. Earth Syst. Environ. 10 (3), 4513–4523. doi:10.1007/s40808-024-02039-7

CrossRef Full Text | Google Scholar

Siemens, G. A. (2018). Thirty-ninth canadian geotechnical colloquium: unsaturated soil mechanics—bridging the gap between research and practice. Can. Geotechnical J. 55 (7), 909–927. doi:10.1139/cgj-2016-0709

CrossRef Full Text | Google Scholar

Tang, A. M., Hughes, P. N., Dijkstra, T. A., Askarinejad, A., Brenčič, M., Cui, Y. J., et al. (2018). Atmosphere–vegetation–soil interactions in a climate change context; impact of changing conditions on engineered transport infrastructure slopes in Europe. Q. J. Eng. Geol. Hydrogeology 51 (2), 156–168. doi:10.1144/qjegh2017-103

CrossRef Full Text | Google Scholar

Terzaghi, K. (1943). Theoretical soil mechanics. John Wiley and Sons.

CrossRef Full Text | Google Scholar

Toll, D. G., Mendes, J., Augarde, C. E., Karthikeyan, M., Phoon, K. K., Gallipoli, D., et al. (2008). “Effects of climate change on slopes for transportation infrastructure,” in Advances in transportation geotechnics (London, United Kingdom: CRC Press), 521–528.

Google Scholar

Toll, D. G., Mendes, J., Hughes, P. N., Glendinning, S., and Gallipoli, D. (2012). Climate change and the role of unsaturated soil mechanics. Geotechnical Eng. J. SEAGS and AGSSEA 43 (1), 76–82. doi:10.14456/seagj.2012.35

CrossRef Full Text | Google Scholar

Vahedifard, F., Williams, J. M., and AghaKouchak, A. (2018). Geotechnical engineering in the face of climate change: role of multi-physics processes in partially saturated soils. IFCEE 2018, 353–364. doi:10.1061/9780784481585.035

CrossRef Full Text | Google Scholar

Vanapalli, S. K., and Mohamed, F. M. (2007). “Bearing capacity of model footings in unsaturated soils,” in Experimental unsaturated soil mechanics (Berlin, Heidelberg: Springer Berlin Heidelberg), 483–493.

CrossRef Full Text | Google Scholar

Vanapalli, S. K., and Mohamed, F. M. (2013). Bearing capacity and settlement of footings in unsaturated sands. Geomate J. 5 (9), 595–604.

Google Scholar

Vanapalli, S., and Oh, W. (2010). A model for predicting the modulus of elasticity of unsaturated soils using the soil-water characteristic curve. Int. J. Geotechnical Eng. 4 (4), 425–433. doi:10.3328/IJGE.2010.04.04.425-433

CrossRef Full Text | Google Scholar

Vardon, P. J. (2015). Climatic influence on geotechnical infrastructure: a review. Environ. Geotech. 2 (3), 166–174. doi:10.1680/envgeo.13.00055

CrossRef Full Text | Google Scholar

Yang, H. Q., Shi, C., and Zhang, L. (2025). Ensemble learning of soil–water characteristic curve for unsaturated seepage using physics-informed neural networks. Soils Found. 65 (1), 101556. doi:10.1016/j.sandf.2024.101556

CrossRef Full Text | Google Scholar

Yasuhara, K., and Bergado, D. T. (2022). “Climate change-induced geotechnical hazards in Asia: impacts, assessments, and responses,” in Sustainable geo-technologies for climate change adaptation (Singapore: Springer Nature Singapore), 197–224.

CrossRef Full Text | Google Scholar

Zhai, Q., Rahardjo, H., Satyanaga, A., and Dai, G. (2019). Estimation of unsaturated shear strength from soil–water characteristic curve. Acta Geotech. 14 (6), 1977–1990. doi:10.1007/s11440-019-00785-y

CrossRef Full Text | Google Scholar

Zimbardo, M., Ercoli, L., Mistretta, M. C., Scaffaro, R., and Megna, B. (2020). Collapsible intact soil stabilisation using non-aqueous polymeric vehicle. Eng. Geol. 264, 105334. doi:10.1016/j.enggeo.2019.105334

CrossRef Full Text | Google Scholar