Data-driven models for human–structure interaction based on MLP and NARX neural networks

Structural design often neglects the dynamic effects induced by human activities. Excessive vibrations in structures such as pedestrian bridges, grandstands, slabs, and stairways have highlighted the analysis as dynamic systems of humans interacting with structures. This phenomenon, commonly referred to as “human–structure interaction” (HSI), is investigated in this study using experimental records obtained from a cantilever steel frame specially constructed to represent a variety of structures susceptible to the HSI phenomenon. This study aims to develop and evaluate artificial neural network (ANN) models capable of representing subjects in the passive condition of HSI using only simple anthropometric parameters. Two models—Nonlinear Auto-Regressive with eXogenous input (NARX) and MultiLayer Perceptron (MLP) —are implemented and compared with a conventional Mass-Spring-Damper (MSD) model. The results show that the ANN models significantly outperform the MSD model, achieving lower Normalized Mean Square Error (NMSE) values both in time-response prediction (20.23% for NARX and 25.07% for MLP vs. 30.19% for MSD) and frequency-response prediction (16.00% for NARX and 17.05% for MLP vs. 26.01% for MSD). These findings demonstrate that the proposed ANN-based models can predict the dynamic response of individual subjects using only simple anthropometric parameters such as mass and height. This approach provides a practical and efficient tool for modeling HSI in civil engineering applications.

1 Introduction

In recent decades, slender structures such as slabs, footbridges, staircases, and grandstands have revealed problems with excessive vibrations induced by human activities (Dang and Živanović, 2015; Shahabpoor et al., 2016; Gomez et al., 2018; Lin et al., 2020). Structural advances have significantly increased the strength of building materials, optimizing them while decreasing construction costs. However, the materials’ stiffness increment has been at a different rate than their strength (Connor and Laflamme, 2014). The combination of these two aspects and the trend in structural design to build more flexible and slender structures have reflected significant changes in the dynamic properties of structures, generating the potential for unexpected structural vibration (Wei and Živanović, 2018). Therefore, the serviceability load conditions due to human activities have drastically influenced the design of these structures (Živanović et al., 2005; Dang and Živanović, 2016).

Structures with serviceability issues due to human activities reflect a phenomenon known in the literature as “human–structure interaction” (HSI). Ahmadi et al. (2019) defined HSI as the bidirectional dynamic effect between humans and structures. HSI encompasses three main effects: (1) dynamic forces exerted by individuals on a structure; (2) the impact of structural vibrations on the human body; (3) alterations in the dynamic properties of a structure due to the presence of people. This interaction is especially significant when the walking frequency of individuals aligns with the structure’s fundamental frequency, leading to resonance. However, even stationary individuals can influence a structure’s response. When they sense discomfort from vibrations, people instinctively exert counteracting forces to stabilize themselves, which in turn affects the overall behavior of the structure. Thus, the HSI phenomenon may occur with a person or group of people in active (jogging, walking, or running) or passive (standing, sitting, or static position) conditions on a structure where the dynamic response is modified (Salyards and Noss, 2014; Ahmadi et al., 2018; Ortiz and Caicedo, 2019).

Different models have been proposed to represent humans in HSI that encompass their active and passive conditions. For instance, Sim et al. (2007), Hashim et al. (2020), and others have employed Mass-Spring-Damper (MSD) models to represent a standing human, aiming to identify the fundamental parameters of the human body in vibrating structures. Others have proposed representing humans using different dynamic models, such as feedback systems (Ortiz and Caicedo, 2019; Alzubaidi and Caicedo, 2021) and inverted pendulum (Bocian et al., 2013; Qin et al., 2013; Cruise et al., 2017). These models brought new perspectives and possibilities to understanding HSI.

Traditionally, researchers have used conventional deterministic MSD models to represent HSI. These models relied on one or more degrees of freedom (DOF) and were considered linear time-invariant systems. However, further research has demonstrated that this assumption is only valid in specific cases (Subashi et al., 2006; Martínez-García et al., 2021). Despite their simplicity of implementation, MSD models have limitations that make it challenging to represent subjects with different biodynamic characteristics (Gomez et al., 2020). For example, they require the stiffness and damping coefficients of the person to operate; these are more complicated to measure than anthropometric characteristics such as mass and height. Another disadvantage of deterministic MSD models is that they only include biodynamic parameters for one subject at a time. Therefore, each subject needs its own deterministic MSD model. Additionally, deterministic MSD models do not consider important factors such as weight, height, age, and gender, which may significantly affect the HSI (Bierbaum et al., 2010; Cruise et al., 2017). These limitations reveal a research gap, as most existing models fail to provide a practical and generalizable approach to represent human occupants in HSI using parameters that are simple to obtain.

Alternative models to MSD have been employed to address problems similar to HSI. For instance, artificial neural networks (ANNs) have been successfully used in solving the vehicle–bridge interaction (VBI) problem. ANNs can offer advantages based on self-learning capabilities that deterministic models cannot consider. ANNs have been used to predict system responses in VBI phenomena (Luo et al., 2020; Li et al., 2021). Other research has also used deep ANNs such as long short-term memory (LSTM) and convolutional neural networks (CNN) to predict human-induced force predictions in different scientific applications (Johnson et al., 2019; Peláez-Rodríguez et al., 2024).

Significant technological advances related to several artificial intelligence branches have been developed for decades. ANNs, for example, are particularly noteworthy for their ability to imitate the biological neuron’s structure and functioning (Norgaard et al., 2000). ANNs learn and generalize complex linear and nonlinear relationships based on experience. Several ANN architectures are available, but our study focused on ANNs tailored to time series and dynamic system identification (Norgaard et al., 2000; Khodabandehlou and Fadali, 2019; Li et al., 2021). The ability of ANNs to learn and generalize temporal signal behavior, together with their capacity to integrate external parameters into training, makes them a powerful tool for representing interaction phenomena between dynamic systems, including HSI. These advantages position ANN-based models as a viable alternative to conventional approaches for representing humans in HSI. This study leverages these learning and generalization capabilities of ANNs—qualities often missing in deterministic models and many conventional approaches used to represent humans in HSI. Accordingly, we introduce novel ANN-based models specifically designed to represent humans in the HSI phenomenon, utilizing the nonlinear autoregressive with eXogenous inputs (NARX) and multilayer perceptron (MLP) architectures.

This study aims to demonstrate that ANN-based models can effectively represent the human body in HSI while also demonstrating their robustness to variations in subjects’ anthropometric parameters under passive conditions. To achieve this, the models are trained and validated using experimental data collected from structures occupied by individual subjects.

The organization of this paper is as follows. The “Methodology” section describes the procedure used to obtain the test data, the mathematical model representing the test structure, and the ANN-based models representing the human in HSI. In “Results and Discussion”, the results of the developed models are shown. Finally, “Conclusions” contains the main findings of this study and outlines essential considerations for future research.

2 Methodology

2.1 Test structure

The cantilever steel frame used in this study was built at the University of South Carolina and comprises two fixed supports and two sliding supports that facilitate adjustments to the cantilever’s length and, thus, its stiffness. Concrete blocks can be added to the structure to increase its mass. With the modification of mass and structural stiffness, the test structure can represent a range of frequencies in which some structures are susceptible to HSI. The experimental data used in this study were obtained from Ortiz (2016). The cantilever length was 2.54 m, and the concrete blocks were located 1.9 m from the fixed support. The test structure used in the experimental program is shown in Figure 1, where, in the HSI tests, the subject stands in an upright (vertical) and natural position on the center of the concrete block located at the end of the cantilever.

Figure 1

Figure 1. Experimental structure, initially proposed by Salyards and Noss (2014), modified and constructed at the University of South Carolina to evaluate structural responses in the 3–10 Hz frequency range.

The tests involved exciting the structure through a vertical impact using a 096D50 PCB hammer applied at the center of the concrete block at the cantilever’s end. This method is commonly used to stimulate a broad range of frequencies in the test structure, including those associated with both vertical and horizontal vibration modes. The structure was instrumented with PCB 333B50 accelerometers, which recorded the vertical and horizontal accelerations of the experimental structure with a sampling frequency of 1,652 Hz. The frequency range of interest for this study is below 10 Hz; thus, the data were resampled to 128 Hz to satisfy the Nyquist theorem, allowing for accurate representation of frequencies up to 64 Hz. A low-pass filter was then applied to each signal to remove high-frequency noise unrelated to HSI, ensuring that only relevant frequencies contributed to model fitting. This preprocessing step was critical in avoiding interference from extraneous frequencies that could otherwise compromise the accuracy of the models. Initially, the empty structure was excited to carry out the system identification process of the test structure. Subsequently, the procedure was repeated with different subjects on the structure. The vibration levels exerted on the structure were large enough for humans to perceive the vibration and generate a response action on the structure. Figure 2 depicts the experimental HSI set-up, where $y_v$ and $y_h$ refer to the vertical and horizontal DOF of the structure, respectively. $K_v$ is the structural stiffness associated with the vertical DOF, and $C_v$ is the structural damping coefficient related to the vertical DOF. Similarly, $K_h$ and $C_h$ are the stiffness and damping associated with the horizontal DOF of the structure, respectively. $P$ is the force produced by the impact of a hammer on the structure. The human is modeled as a single DOF system in the vertical direction, with $s_p$ as the relative vertical displacement between the human and the structure. It is important to highlight that temperature control measures were implemented during the tests within a laboratory environment, ensuring a constant temperature of approximately 21 °C. The experiments were conducted under these controlled temperature conditions, with each subject’s test lasting approximately 3 min. Therefore, we can affirm that the thermal effects on the test structure were constant during the tests.

Figure 2

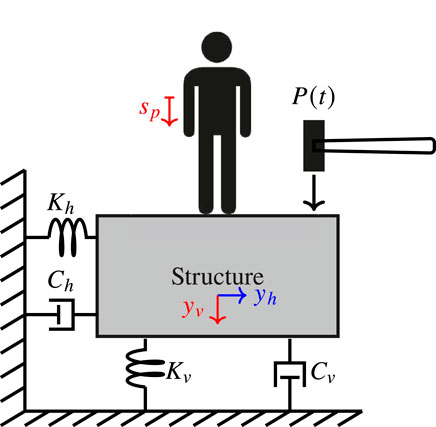
Figure 2. Experimental HSI set-up representation where the structure is modeled as a two-DOF system, while the subject is expressed as a single-DOF system with its effect on the vertical DOF. The structure is impacted with a hammer in the center of the concrete block at the end of the cantilever in the vertical direction.

2.2 Participants

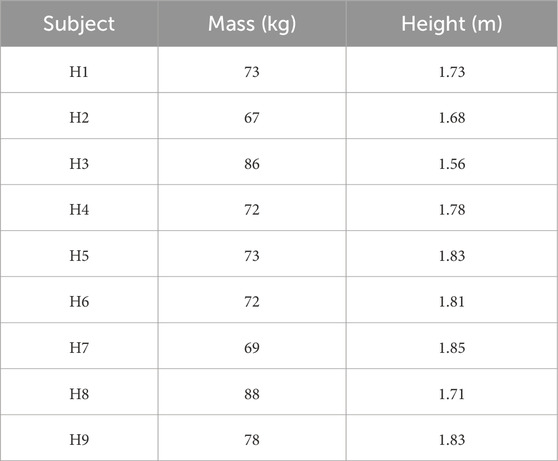
Nine test subjects (three females) participated in the study. The sample size (n = 9) was defined according to the practical constraints of the experimental campaign, including volunteer availability, laboratory scheduling, and instrumentation requirements. Participants were recruited from available volunteers to provide variation in anthropometric characteristics relevant to model development under passive HSI. All participants confirmed through self-report that they had no conditions affecting their standing posture. Informed consent was obtained from all subjects, with approval from the University of South Carolina Institutional Review Board. Anthropometric parameters for each subject are presented in Table 1.

Table 1

Table 1. Anthropometric characteristics of test subjects.

2.3 Dataset

During the experiment, the impact force $P$ and accelerations ${\ddot{y}}_v$ and ${\ddot{y}}_h$ of the structure were recorded over time. We obtained 27 records for the occupied structure, with three measured for each of the nine participants. Additionally, three records were obtained for the empty structure. The models followed a standard ANN training and validation data distribution (80% training—20% validation). Data from seven out of the nine subjects were used for training, while the third record of each training subject served as additional validation data for the models. In this regard, the occupied structure dataset was split into two parts: (1) the training dataset, comprising the first two records of participants H1–H7, and (2) the validation dataset, including the third record of participants H1–H7 and all records of participants H8 and H9. It is important to clarify that each dataset includes the time signals of the hammer’s impact on the structure, the vertical and horizontal accelerations of the structure, and the mass and height of the analyzed subject. Table 2 presents the organization of the data used in this study, which is used to feed and validate all the human models.

Table 2

Table 2. Dataset organization for the occupied structure.

2.4 Structural model

The current study represents the structure as a two-DOF state-space model, accounting for both vertical and horizontal movements. The model incorporates the effect of the human on the structure through the vertical force generated by the subject’s location. Equations 1, 2 give the equation of motion (EOM) of the empty structure as

$\ddot{\mathbf{q}}+\mathbf{Z}\dot{\mathbf{q}}+{\mathbf{\Omega }}^{\mathbf{2}}\mathbf{q}={\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }P+{\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }{F}_p(1)$

with

$\mathbf{Z}=2\left[\begin{array}{cc}\hfill {\zeta }_1{\omega }_1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\zeta }_2{\omega }_2\hfill \end{array}\right],{\mathbf{\Omega }}^{\mathbf{2}}=\left[\begin{array}{cc}\hfill {\omega }_1^2\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\omega }_2^2\hfill \end{array}\right],\mathbf{\Gamma }=\left[\begin{array}{c}\hfill 1\hfill \\ \hfill 0\hfill \end{array}\right](2)$

where $\ddot{\mathbf{q}}$, $\dot{\mathbf{q}}$, and $\mathbf{q}$ are the generalized acceleration, velocity, and displacement of the structure in the vertical and horizontal DOF, respectively. ${\zeta }_1$ and ${\omega }_1$ respectively represent the damping ratio and the natural frequency associated with the first vibration mode. Similarly, ${\zeta }_2$ and ${\omega }_2$ respectively correspond to the damping ratio and the natural frequency associated with the second vibration mode. ${\mathbf{\Omega }}^{\mathbf{2}}$ is the spectral matrix, $\mathbf{\Phi }$ is the modal matrix normalized with respect to the mass, and $\mathbf{\Gamma }$ is the vector defining the DOF where the inputs are applied—in this case, the hammer impact force and the human force are applied at the same place. $P$ refers to the impact force of the hammer on the structure, and $F_p$ is the force generated by the human on the structure. It is important to note that when the structure is empty, $F_p$ is equal to zero. Using the state-space model, the EOM of the structural model is described by Equations 3, 4 as

$\begin{array}{c}\hfill {\dot{\mathbf{X}}}_s={\mathbf{A}}_s{\mathbf{X}}_s+{\mathbf{B}}_s{\mathbf{u}}_s\\ \hfill \ddot{\mathbf{y}}={\mathbf{C}}_s{\mathbf{X}}_s+{\mathbf{D}}_s{\mathbf{u}}_s\end{array}(3)$

with

$\begin{array}{cccc}\hfill {\mathbf{A}}_s& ={\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{I}\hfill \\ \hfill -{\mathbf{\Omega }}^{\mathbf{2}}\hfill & \hfill -\mathbf{Z}\hfill \end{array}\right]}_{4\mathit{x}4},\hfill & \hfill {\mathbf{B}}_s& ={\left[\begin{array}{cc}\hfill \mathbf{0}\hfill & \hfill \mathbf{0}\hfill \\ \hfill {\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }\hfill & \hfill {\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }\hfill \end{array}\right]}_{4\mathit{x}2},\hfill \\ \hfill \\ \hfill {\mathbf{C}}_s& =\mathbf{\Phi }{\left[\begin{array}{cc}\hfill {-\mathbf{\Omega }}^{\mathbf{2}}\hfill & \hfill -\mathbf{Z}\hfill \end{array}\right]}_{2\mathit{x}4},\hfill & \hfill {\mathbf{D}}_s& =\mathbf{\Phi }{\left[\begin{array}{cc}\hfill {\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }\hfill & \hfill {\mathbf{\Phi }}^{\mathbf{T}}\mathbf{\Gamma }\hfill \end{array}\right]}_{2\mathit{x}2}\hfill \end{array}(4)$

where ${\mathbf{X}}_s$ is the state vector ${[\mathbf{q}\dot{\mathbf{q}}]}^T$ of the structure. The vector ${\mathbf{u}}_s$ includes the inputs of the structure corresponding to the hammer impact and the human force, and $\mathbf{I}$ is the identity matrix. The structure’s frequency response is obtained from the relationship between the hammer impact $P$ as the input and the vertical ${\ddot{y}}_v$ and horizontal ${\ddot{y}}_h$ accelerations of the structure as the outputs. This analysis enables us to estimate the transfer function that describes the system in the frequency domain. The empty structure has natural frequencies at 3.49 Hz and 3.92 Hz with associated damping ratios of 0.62% and 0.32%, respectively.

2.5 Human as an MSD model

The human being may be considered a dynamic system due to its biomechanical characteristics, with the ability to modify the behavior of a structure. Thus, the HSI effect occurs from the interaction between two dynamic systems: the human and the structure. When an occupied structure is excited by an impact, the human exerts a controlling force on the structure, modifying the structural response. Multiple models have been proposed to represent the human in the HSI phenomenon. Traditionally, simplified models have been used, such as linear deterministic MSD models, with one or multiple degrees of freedom. These models have been widely employed under the justification that the human, in addition to contributing mass, also contributes stiffness and damping to the coupled system.

An MSD model of a single DOF (reference MSD model) was developed to compare the ANN-based models proposed in this study with a model traditionally used to represent a human being in HSI. Equation 5 describes the EOM of the reference MSD model human model as

${\ddot{s}}_p+2{\zeta }_p{\omega }_p{\dot{s}}_p+{\omega }_p^2{s}_p=-{\ddot{y}}_v(5)$

where ${\ddot{s}}_p$, ${\dot{s}}_p$, and $s_p$ are the relative acceleration, velocity, and displacement between the structure and the center of gravity (COG) of the subject, respectively. ${\zeta }_p$ and ${\omega }_p$ are the respective damping ratio and natural frequency of the test subject in the vertical direction. Equations 6, 7 show the state space model of the reference MSD model interacting with the structure as

$\begin{array}{cc}\hfill {\dot{\mathbf{X}}}_p& ={\mathbf{A}}_p{\mathbf{X}}_p+{\mathbf{B}}_p{\ddot{y}}_v\hfill \\ \hfill F_{\mathit{msd}}& ={\mathbf{C}}_p{\mathbf{X}}_p\hfill \end{array}(6)$

with

${\mathbf{A}}_p=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill -{\omega }_p^2\hfill & \hfill -2{\zeta }_p{\omega }_p\hfill \end{array}\right],{\mathbf{B}}_p=\left[\begin{array}{c}\hfill 0\hfill \\ \hfill -1\hfill \end{array}\right],{\mathbf{C}}_p=\left[\begin{array}{cc}\hfill K_p\hfill & \hfill C_p\hfill \end{array}\right](7)$

where ${\mathbf{X}}_p$ is the state vector ${[s_p{\dot{s}}_p]}^T$ of the human model, and $K_p$ and $C_p$ are the stiffness and damping coefficients of the human, respectively. The prediction of the MSD-SDOF model for the force produced by the human is denoted as $F_{\mathit{msd}}$.

The mass value of the reference model is obtained by calculating the arithmetical average of the mass of subjects H1–H7, resulting in a value of 73.1 kg. The experimental data corresponding to the training dataset described in the section dataset are linked consecutively to determine the damping and stiffness values. After joining and aligning the training dataset, the damping and stiffness values of the reference MSD model are optimized, resulting in values of 1,652 kg$\cdot {\text{s}}^{-1}$ and 72,074 kg$\cdot {\text{s}}^{-2}$, respectively. Considering the fixed mass value mentioned above and the damping and stiffness values found, the natural frequency and damping ratio values are calculated, resulting in 5 Hz and 36%, respectively. The natural frequency and damping ratio obtained agree with the results in the literature for standing subjects (Wei and Živanović, 2018). Figure 3 compares the experimental frequency responses of the empty and occupied structure. It is observed that the interaction between human and structure modifies its natural frequency and provides damping to the system.

Figure 3

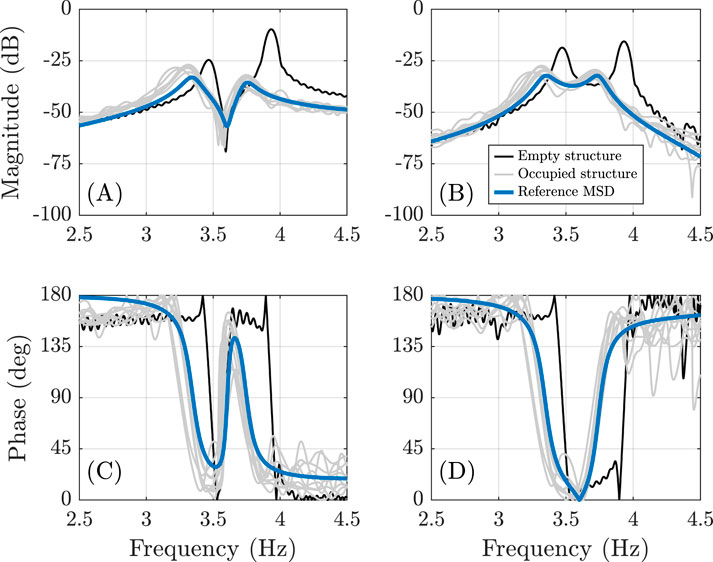
Figure 3. Frequency responses of the empty structure, occupied structure, and reference MSD model prediction. (A) and (C) show the vertical response in magnitude and phase, respectively. (B) and (D) present the horizontal response in magnitude and phase, respectively.

2.6 HSI models with ANNs

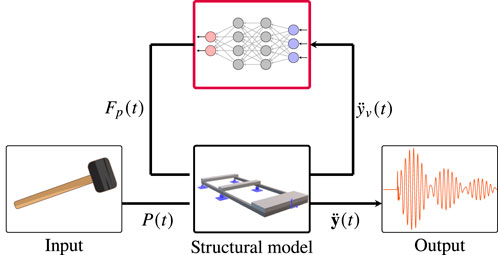
The HSI models presented in this study utilize dynamic substructuring to capture the bidirectional interaction between the structural model and the ANN-based models representing human behavior. By simulating the coupled models, the prediction of the response of the test structure interacting with subjects of different masses and heights is obtained. This response varies according to the anthropometric parameters of the human under consideration. The structural model and the ANN-based models described below provide a single model that considers the effect of each model on the other (Figure 4).

Figure 4

Figure 4. Interaction between the structural and human model represented by ANNs.

Closed-loop diagram representing the interaction between humans and structures, the humans are represented by an artificial neural network. The input is the impact of the hammer “P(t)” that excites the coupled system. The arrows indicate the process that leads, through a neural network represented by connected nodes. The human exerts a force “Fp(t)” on the structure, and the output of the coupled system is the recorded acceleration “y(t)”.

2.7 Human as a NARX model

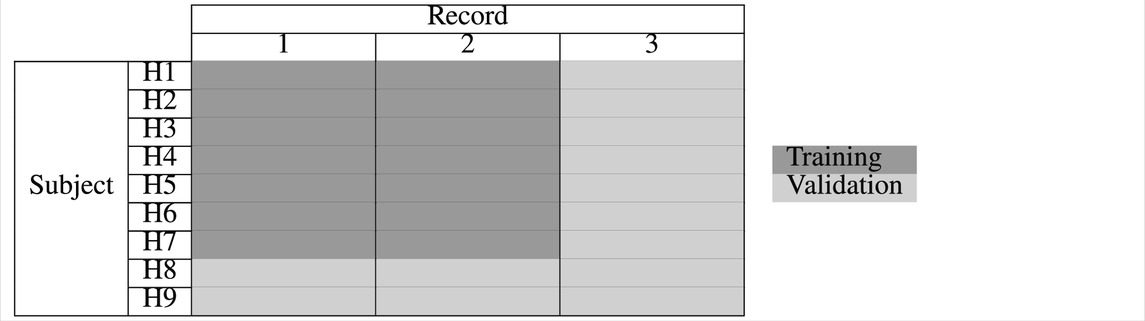
The first human model proposed in this study represents the human as a NARX-type ANN. The NARX model is a recurrent ANN based on the ARX configuration and is typically used for time series problems. Research indicates that this type of ANN has a better response to long time series and a better generalization capability than conventional ANNs due to the implementation of delays in its architecture (Lin et al., 1996). NARX models can represent almost any nonlinear function using backpropagation in the gradient descent process for ANN parameter updating (Ruslan et al., 2014). As shown in Table 2, the first two records from subjects H1–H7 are used for model training, while the third record for subjects H1–H7 and all records for subjects H8 and H9 are used for model validation. As the force exerted by the human was not measured in the experiment, the force generated by an independent MSD model for each subject is used as the starting point for training the NAXR model. The NARX model, coupled with the structural model, then continues the training to minimize the error between the prediction of the structural response and the experimental data. To incorporate differences between subjects in the ANN’s learning, additional inputs, such as the anthropometric parameters of mass and height, are included in the NARX model. Figure 5 illustrates the architecture described by Equation 8 to represent the NARX model, as

$F_{\mathit{narx}}=f\left(F_{\mathit{narx}}\left(t-1\right),F_{\mathit{narx}}\left(t-2\right),\mathbf{u}\left(t-1\right),\mathbf{u}\left(t-2\right)\right)(8)$

where $\mathbf{u}$ is the input vector containing the training dataset’s mass, height, and vertical acceleration. $f$ is a nonlinear function representing the relationship between inputs and output. The prediction of the force produced by the human at each instant of time $t$ is denoted by $F_{\mathit{narx}}$. $F_{\mathit{narx}}(t-1)$ and $F_{\mathit{narx}}(t-2)$ are the past values of $F_{\mathit{narx}}$, which are used as autoregressive inputs to the model; likewise $\mathbf{u}(t-1)$ and $\mathbf{u}(t-2)$ are the past values of the exogenous characteristics used as exogenous inputs to the model. This model incorporates past input values to detect variations in model parameters attributed to external factors. Therefore, implementing memory through delays is crucial in such models (Chen et al., 1990; Argyropoulos et al., 2016). The training process employed the Levenberg–Marquardt backpropagation algorithm, a statistical optimization method widely used for nonlinear least-squares problems. This algorithm was selected because it combines the rapid convergence properties of the Gauss–Newton method with the stability of gradient descent, making it particularly effective for system identification tasks with relatively small to medium-sized datasets, such as the present experimental campaign. Model evaluation was conducted using a five-fold cross-validation procedure, ensuring that the dataset was partitioned into five subsets, with each serving once as the validation set while the remaining four were used for training.

Figure 5

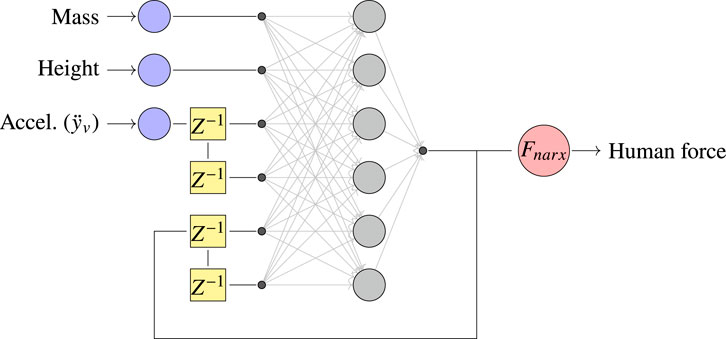
Figure 5. NARX architecture models the human in HSI. In addition to the vertical structural acceleration input, the model considers the mass and height of the subjects, while the output of the model is the prediction of the force generated by the subject on the structure.

2.8 Human as an MLP model

The second human model proposed in this study represents the human as an MLP-type ANN performing point-to-point response prediction. The model takes a set of past data and successively predicts a future value until the output signal is complete. Two ANNs are pre-trained to feed the MLP model, with each ANN corresponding to one of the analyzed systems. The first pre-trained ANN is designed to represent the human. It is trained with mass, height, and vertical structural acceleration inputs. The force generated by an independent MSD model for each subject is the output target of the pre-training ANN. The second pre-trained ANN represents the experimental structure, and it is trained using the hammer force and the force generated by each independent MSD model as inputs, with the vertical structural acceleration as the output.

An MLP model is implemented in this study with two hidden layers, using transfer learning to incorporate the properties of pre-trained ANNs (Figure 6). The first layer of the MLP model integrates the characteristics of the pre-trained ANN for the human, while the second layer integrates the characteristics of the pre-trained ANN for the structure. Each layer consists of fully connected neurons, and the learning process requires updating of the synaptic weights $W$ and biases $\theta$ using the backpropagation algorithm. The model’s training is conducted using the first two records of subjects H1–H7, while the third record for H1–H7 and all records for H8 and H9 are used for model validation. Equation 9 describes the mathematical representation of the MLP model as

${\ddot{y}}_o=f_o\left(\sum {\mathbf{W}}_{jo}{\mathbf{I}}_h+{\mathit{\theta }}_o\right)(9)$

where ${\mathbf{W}}_{jo}$ is the synaptic weight of the node $j$ in the layer $o$, ${\mathbf{I}}_h$ is the output of the hidden layer $h$, while ${\mathit{\theta }}_o$ corresponds to the bias of the layer $o$. The layers $h$ and $o$ are hidden and output layers, respectively. ${\ddot{y}}_o$ is the prediction of the vertical acceleration of the structure, and $f_o$ is the hyperbolic tangent activation function as recommended by Pinkus (1999). The model jointly represents the human and the structure to achieve an experimental fit. The prediction of the force generated by the human on the structure is denoted as $F_{\mathit{mlp}}$.

Figure 6

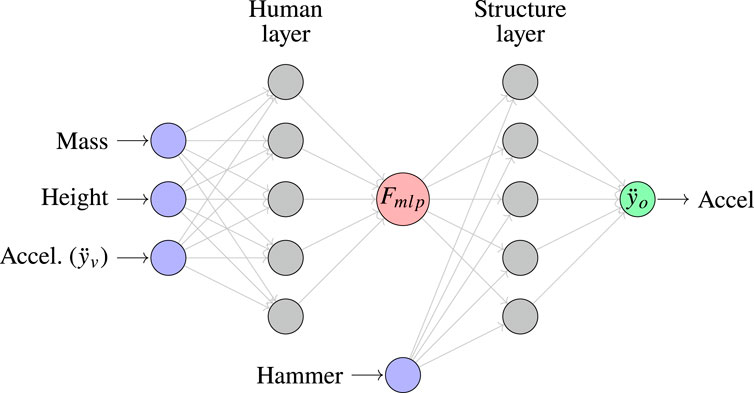
Figure 6. MLP architecture represents the human and structural systems together in HSI. The subject’s mass, height, and vertical acceleration are provided as inputs to the human layer. The output of the human layer is denoted by $F_{\mathit{mlp}}$, which is then used as an input along with the impact of the hammer for the structure layer. The output of the structure layer is the prediction of the vertical acceleration of the structure.

The training loop developed to improve the performance of the MLP model involves fitting the parameters of the layer representing the structural model. In contrast, the layer’s parameters representing the human are fixed. This procedure uses 100 epochs or early stopping criteria to enhance the overall performance of the MLP model by updating the layer representing the structural model. In the second phase of the loop, the layer’s parameters representing the structure are fixed, and the layer’s parameters representing the human are updated with five epochs. The entire procedure is repeated until the error criterion in the experimental fit has minimal changes with a tolerance of two decimal places. After the coupled human–structure system is modeled and the training process is completed, the layer representing the human is separated from the MLP model to build a hybrid interaction model with the structural model described in Section 2.4. The training process of the MLP model employed the Bayesian regularization backpropagation algorithm, a statistical optimization method that introduces a regularization term into the error function to balance model complexity and fitting accuracy. This approach was selected because it mitigates the risk of overfitting, which is especially important when working with relatively small experimental datasets and neural network architectures of moderate complexity, such as in this study. The MLP model was evaluated using a 5-fold cross-validation procedure, where the dataset was divided into five equal parts. In each iteration, one subset was used for validation while the remaining four were used for training, ensuring a balanced assessment of the model’s generalization capability.

3 Results and discussion

The performance of HSI models with ANNs (NARX and MLP) was evaluated by comparing the structural acceleration of the coupled models with experimental measurements. In both cases, HSI models with ANNs could predict the structural response by modifying the mass and height of the test subjects. Figures 7–10 show the comparison between the prediction of the ANN-based models and the experimental response of the structure due to the impact of the hammer while the structure is occupied by one subject at a time—H8 and H9. It is important to note that the NARX and MLP models are not trained using the parameters of these subjects, making these results an adequate assessment of the robustness of the models. The results presented here are fundamental for validating the models and evaluating their ability to predict the structural response in HSI for different subjects.

Figure 7

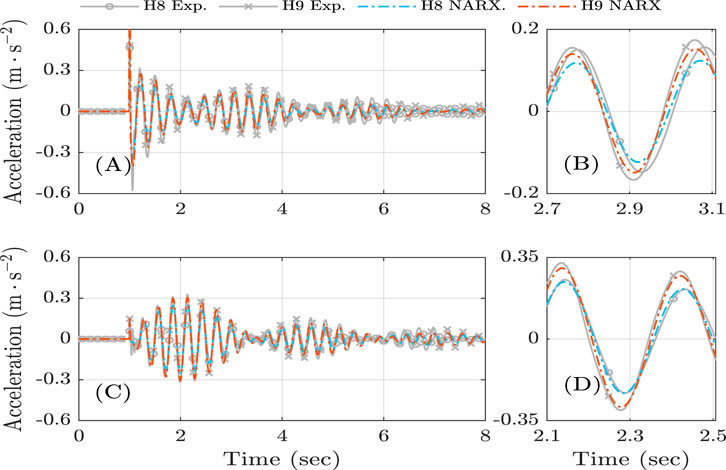
Figure 7. Experimental time response and NARX model prediction for H8 (88 kg, 1.71 m) and H9 (78 kg, 1.83 m). (A,C) present the responses in the vertical and horizontal directions, respectively. (B,D) provide enlarged views of the results shown in (A,C), respectively.

Figure 8

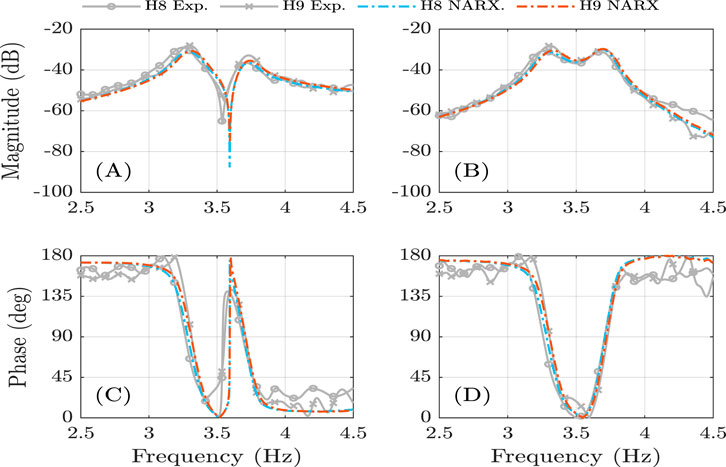
Figure 8. Experimental frequency response and NARX model prediction for H8 (88 kg, 1.71 m) and H9 (78 kg, 1.83 m). (A) and (C) show the vertical response in magnitude and phase, respectively. (B) and (D) present the horizontal response in magnitude and phase, respectively.

Figure 9

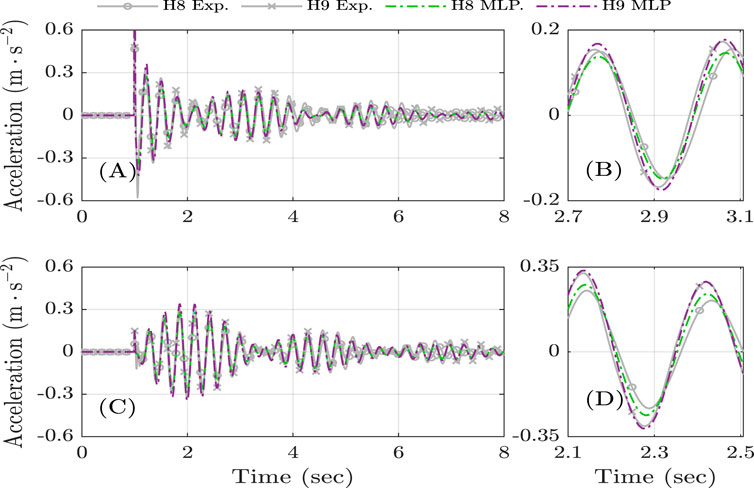
Figure 9. Experimental time response and MLP model prediction for H8 (88 kg, 1.71 m) and H9 (78 kg, 1.83 m). (A,C) present the responses in the vertical and horizontal directions, respectively. (B,D) provide enlarged views of the results shown in (A,C), respectively.

Figure 10

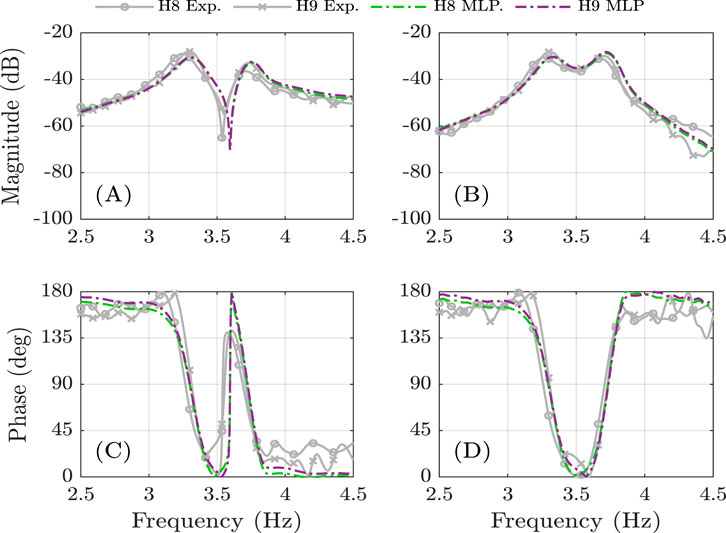
Figure 10. Experimental frequency response and MLP model prediction for H8 (88 kg, 1.71 m) and H9 (78 kg, 1.83 m). (A,C) show the vertical response in magnitude and phase, respectively. (B,D) present the horizontal response in magnitude and phase, respectively.

3.1 NARX model results

Figures 7, 8 present the performance of the NARX model for subjects H8 and H9, incorporating their anthropometric parameters. The comparison includes both vertical and horizontal structural responses in the time and frequency domains, with enlarged views provided to highlight details of the predictions against the experimental data.

Overall, the results demonstrate that the NARX model is capable of accurately predicting the structural response under passive HSI when the anthropometric characteristics of different individuals are considered. The time-domain responses show close agreement with the experimental measurements, while the frequency-domain analysis confirms that the model adequately captures both magnitude and phase behavior. These findings highlight the robustness of the NARX model in adapting to variations in subject mass and height.

3.2 MLP model results

Figures 9, 10 illustrate the performance of the MLP model for subjects H8 and H9, considering their respective anthropometric parameters. The results include both vertical and horizontal responses in the time and frequency domains, with detailed views provided to highlight differences between experimental measurements and model predictions.

The comparison shows that the MLP model can successfully reproduce the structural response under passive HSI, adapting to variations in subject characteristics. In the time domain, the model predictions closely match the experimental responses, while the frequency-domain results confirm that the MLP model effectively captures both magnitude and phase behavior. These findings confirm the model’s ability to generalize across subjects and highlight its suitability as an alternative representation of humans in HSI.

Figure 11 presents the vertical force predictions obtained from the NARX and MLP models for subjects H8 and H9. Both models consistently indicate that H8 exerts greater forces on the structure than H9, highlighting the ability of the ANN-based approaches to capture inter-subject variability. These results confirm that the models not only reproduce the structural response but also provide meaningful insights into individual human contributions within the HSI phenomenon.

Figure 11

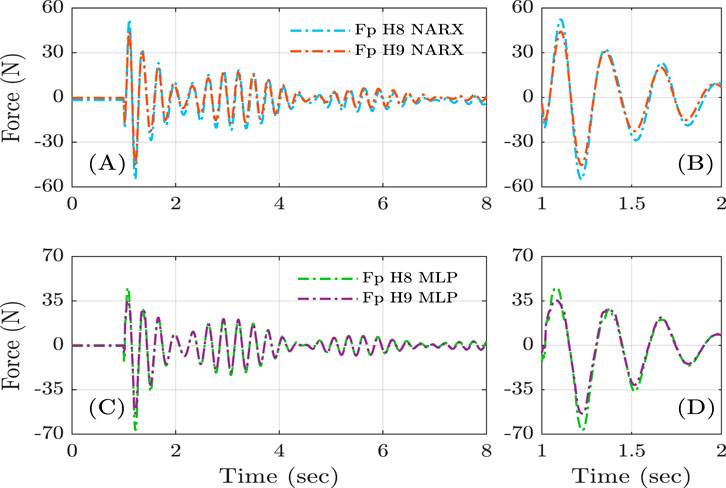
Figure 11. NARX and MLP model prediction for the force exerted by H8 (mass = 88 kg, height = 1.71 m) and H9 (mass = 78 kg, height = 1.83 m) on the structure. (A) and (C) present the force prediction of the NARX and MLP models, respectively. (B) and (D) show an enlarged view of the results presented in (A) and (C), respectively.

3.3 Overall results

The models developed consider the influence of the human on the vertical DOF of the test structure. The Normalized Mean Square Error (NMSE) is a statistical measure that normalizes the mean square error (MSE) by the variance of the experimental data. This normalization allows for direct comparison between predicted and experimental signals and enhances interpretability across different scales and datasets. This metric was selected because it is scale-independent and accounts for the variability of the experimental signals, making it more suitable than absolute error measures for comparing structural vibration data. For this reason, the NMSE is used to calculate the error obtained by the reference MSD, NARX, and MLP models concerning the structural vertical response. Equation 10 describes the NMSE as

$\mathrm{N}\mathrm{M}\mathrm{S}\mathrm{E}=\frac{\Vert x_{\mathit{exp}}-x_{\mathit{sim}}{\Vert }^2}{\Vert x_{\mathit{exp}}-\mathrm{m}\mathrm{e}\mathrm{a}\mathrm{n}\left(x_{\mathit{exp}}\right){\Vert }^2}(10)$

where $x_{\mathit{exp}}$ is the vertical component experimental response in the time or frequency domain for each subject, and $x_{\mathit{sim}}$ is the prediction of the response in the same domain from the model under consideration. Figure 12 shows the NMSE values obtained by the reference MSD, NARX, and MLP models for the vertical component response in the time (Figure 12A) and frequency (Figure 12B) domains. It can be observed that the NARX and MLP models obtain a better prediction of the structural response than the reference MSD model when a subject occupies the structure. Averaging the obtained values, the NARX and MLP models achieve NMSEs of 20.23% and 25.07% in the time domain, respectively, while the reference MSD model has a higher NMSE of 30.19%. For frequency response prediction, the NARX and MLP models achieve NMSEs of 16.00% and 17.05%, respectively, outperforming the reference MSD model, which has a higher NMSE of 26.01%. In both domains, the ANN-based models outperform the reference model. This result shows that ANN-based models are a promising alternative to represent humans in the HSI phenomenon due to the adaptation of the response to the input parameters, which correspond to human mass and height.

Figure 12

Figure 12. NMSE obtained by the NARX and MLP models in the vertical DOF. (A) NMSE value prediction of the models in the time domain. (B) NMSE value prediction of the models in the frequency domain.

It is noteworthy that subjects H3 and H8 exhibit significant variations in their anthropometric parameters compared to other participants. Interestingly, the NARX model predicts the structural response better than the MLP model in these cases. However, in cases when the subject has mass and height values near those of training, the MLP model performs better. This suggests that the NARX model might be implemented to predict subjects’ responses with mass and height values farther away from the training data. Conversely, the MLP model may better predict the structural response for data close to the training dataset.

To quantify the uncertainty of human force predictions in the developed models, a Monte Carlo approach was applied with 100 iterations, perturbing the input data by 5% relative to the maximum value of each variable. The mean and standard deviation of the NMSE were calculated. For the NARX model, the average NMSE was 3.03% with a standard deviation of $2.94\times 10^{-3}$, indicating the variability of predictions around the mean value. For the MLP model, equivalent analyses yielded an average NMSE of 10.60% with a standard deviation of $2.91\times 10^{-3}$. These results provide a quantitative assessment of prediction uncertainty for both models under input variability. In addition, 95% confidence intervals (CI) were computed to further assess uncertainty. For the NARX model, the CI ranged from 2.97% to 3.09%, whereas for the MLP model it spanned 10.54%–10.66%. These results provide a robust quantitative assessment of predictive reliability under input variability, highlighting the superior consistency of the NARX model compared to the MLP.

In practical terms, the ANN-based models can support engineers by providing fast tools for predicting the vibration levels induced by different individuals, which can be integrated into structural health monitoring systems. These models may also guide design adjustments in slabs and grandstands by accounting for variability in user mass and height. From a policy perspective, adopting such data-driven approaches could inform serviceability criteria in building codes, ensuring that human-induced vibrations are evaluated not only through simplified deterministic models but also through adaptive predictive tools.

3.4 Sensitivity analysis

A sensitivity analysis was conducted to improve the interpretability of the ANN models. This analysis quantifies the relative influence of each input variable on the model’s output. To do so, a 5% multiplicative perturbation was applied to one input variable at a time, and the resulting change in model performance was recorded; the procedure was repeated for all input variables.

The results presented in Figure 13 indicate that the height of each subject is the most influential variable in the models, providing a clearer understanding of the neural network’s decision-making process and highlighting the importance of considering subjects’ anthropometric parameters in the HSI phenomenon.

Figure 13

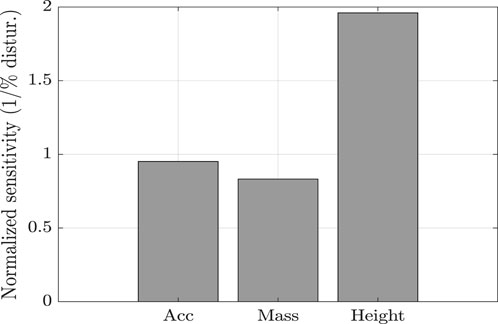
Figure 13. Average normalized sensitivity analysis of ANN-based models. The relative contribution of each input variable to the model output is shown.

3.5 Validation results

According to the data organization described in Table 2, the model validation may be performed using any data from subjects H8 and H9 or the third record from any subject. Thus, the third record from H3, H8, and H9 is chosen. Figure 14 shows the errors obtained by the reference MSD, NARX, and MLP models for the third record of the selected subjects.

Figure 14

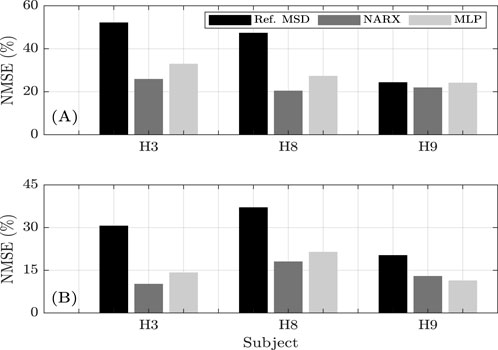
Figure 14. Validation of the NARX and MLP models, considering the anthropometric parameters of H7, H8, and H9. (A) NMSE values prediction of the models for the time domain. (B) NMSE values prediction of the models for the frequency domain.

As shown in Figure 14, the ANN models outperform the reference MSD model with validation data, with NARX exhibiting the best adaptability to anthropometric variations. Trained on multiple subjects, these models effectively generalize human responses in human–structure interaction (HSI) scenarios, dynamically adjusting to individual differences.

The findings of this study demonstrate that ANNs can adapt to changing input patterns and learn to generalize from the training data to make predictions on new data. Specifically, the ANN-based models exhibit exceptional adaptability for subjects with higher mass, such as H8 and H3. Interestingly, the reference MSD model’s error increases for these subjects, even after being carefully optimized using data from all the participants. These results highlight the limitations of deterministic models like the reference MSD model in capturing the complexity of human behavior in HSI scenarios. In contrast, ANN-based models effectively adapt to inter-subject variations in anthropometric parameters, providing more accurate predictions of the HSI response.

Several recent studies have explored alternative representations of HSI beyond the traditional MSD. Equivalent models have been proposed that translate human effects into adjusted modal properties (Van Nimmen et al., 2021), as well as convolution-based formulations for passive and active components (Lucà et al., 2022). More recently, control-based approaches have been introduced to model humans within HSI (Calonge et al., 2023; Lopez et al., 2025). The ANN-based models proposed in this study align with current trends that seek alternatives to traditional physical and deterministic models. The results reinforce the idea that it is possible to achieve more accurate approximations than conventional approaches using adaptive methodologies. Unlike analytical simplifications or control formulations, ANN-based models prioritize adaptability and predictive accuracy by learning nonlinear relationships directly from the data without relying on predefined structures or parameters.

4 Conclusion

This study highlights the contribution of ANN-based models, specifically MLP and NARX, as powerful alternatives to classical MSD representations for capturing human–structure interaction. A key contribution is the ability of these models to adapt to easily measurable anthropometric parameters, such as mass and height, while maintaining high accuracy in predicting individual responses. Compared with the MSD model, the ANN models, particularly the NARX, significantly reduced prediction error, thereby offering a practical and accessible tool for engineers and researchers. The implications of these findings extend to enhancing safety and comfort in civil structures, as they provide a reliable method for incorporating human variability into the design and analysis of structural systems.

Some real applications of the developed models can focus analyzing and designing structures where humans are in a passive posture, such as grandstands and classrooms. By more accurately representing the impact of humans on these structures, ANN models can be used to predict and mitigate problems related to comfort and structural stability. From a computational perspective, the proposed MLP and NARX models feature relatively simple architectures and low computational cost, with per-sample inference times in the millisecond range for datasets sampled at 128 Hz. These characteristics indicate that real-time execution is feasible on standard computing platforms and potentially on embedded hardware, especially if ported to lightweight languages such as Python or C++. This makes the models suitable for integration into structural health monitoring systems or adaptive control frameworks, where rapid and continuous assessment of HSI is required. Future research may include testing the performance of the proposed models in real-time scenarios. In addition, the proposed models could serve as a basis for developing more advanced systems to predict the response of multiple humans or differentiate between individuals by incorporating additional anthropometric parameters that are easily measurable.

However, it is important to note that the ANN models employed in this study use supervised learning, which relies on labeled input–output data. Improvements in the availability of human-generated force data and a larger dataset might enhance the prediction accuracy of the models. Future research may also focus on increasing the number of easily measurable parameters in test subjects to enhance the accuracy of individual responses. The ANN models developed here have the potential to be applied in different system types as long as the human is in a standing (passive) condition and the structure is influenced by excitations that affect the same DOF where the human is. An example of such an application may be individuals standing passively on grandstands. The proposed ANN-based models are not restricted to representing only passive human conditions in HSI. With appropriate retraining using data from moving subjects, they can capture active interactions, such as pedestrian–bridge dynamics, and can be extended to other contexts, including vehicle–structure interactions. To unlock their full potential, future research should prioritize the development of a broader and more diverse database, incorporating a greater number of easily measurable anthropometric parameters. Such an effort would strengthen model accuracy, enhance generalization, and expand its applicability to a broader range of HSI scenarios. Overall, this study provides a solid foundation for further research on the use of ANN models to represent humans as dynamic systems in HSI.

This study focuses exclusively on the passive condition of the HSI phenomenon. However, active human conditions, such as walking, jogging, or jumping, generate complex and significant dynamic interactions in structures susceptible to HSI. As part of future research, we propose extending the current framework to include these active conditions by acquiring experimental data in controlled environments using instrumented platforms that record forces induced by human gait and other dynamic activities. Simultaneously, the developed neural network models, such as NARX and MLP, will be adapted to process non-stationary inputs, capturing the inherent variability of active HSI. This approach enables the evaluation of the generalization and robustness of the models under active HSI conditions, supporting broader applications of AI-based modeling in structural dynamics analysis.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found at https://github.com/mena-sanchezdaniel/Data-driven-models-for-human-structure-interaction-based-on-MLP-and-NARX-neural-networks.

Ethics statement

The studies involving humans were approved by University of South Carolina Institutional Review Board. The studies were conducted in accordance with local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.

Author contributions

DM-S: Conceptualization, Formal analysis, Methodology, Software, Validation, Writing – original draft. NG-T: Formal analysis, Methodology, Writing – review and editing. WA: Conceptualization, Formal analysis, Methodology, Software, Validation, Writing – review and editing. AO: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Resources, Writing – review and editing. DG: Conceptualization, Formal analysis, Funding acquisition, Methodology, Project administration, Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was financially supported by the Universidad del Valle, Colombia (Grant No. 21125: Feedback control theory for modeling human-structure interaction). The authors would also like to acknowledge Professor Juan Caicedo from the University of South Carolina (United States) for providing the steel platform used in this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmadi, E., Caprani, C., Živanović, S., Evans, N., and Heidarpour, A. (2018). A framework for quantification of human-structure interaction in vertical direction. J. Sound Vib. 432, 351–372. doi:10.1016/j.jsv.2018.06.054

CrossRef Full Text | Google Scholar

Ahmadi, E., Caprani, C., Živanović, S., and Heidarpour, A. (2019). Assessment of human-structure interaction on a lively lightweight GFRP footbridge. Eng. Struct. 199, 109687. doi:10.1016/j.engstruct.2019.109687

CrossRef Full Text | Google Scholar

Alzubaidi, A. T., and Caicedo, J. M. (2021). “Modeling human jumping force on a flexible structure using control models,” in Dynamics of Civil Structures, Volume 2: Proceedings of the 38th IMAC, A Conference and Exposition on Structural Dynamics 2020 (Springer), 241–249.

Google Scholar

Argyropoulos, D., Paraforos, D. S., Alex, R., Griepentrog, H. W., and Müller, J. (2016). NARX neural network modelling of mushroom dynamic vapour sorption kinetics. IFAC-PapersOnLine 49, 305–310. doi:10.1016/j.ifacol.2016.10.056

CrossRef Full Text | Google Scholar

Bierbaum, S., Peper, A., Karamanidis, K., and Arampatzis, A. (2010). Adaptational responses in dynamic stability during disturbed walking in the elderly. J. Biomechanics 43, 2362–2368. doi:10.1016/j.jbiomech.2010.04.025

PubMed Abstract | CrossRef Full Text | Google Scholar

Bocian, M., Macdonald, J. H. G., and Burn, J. F. (2013). Biomechanically inspired modeling of pedestrian-induced vertical self-excited forces. J. Bridge Eng. 18, 1336–1346. doi:10.1061/(ASCE)BE.1943-5592.0000490

CrossRef Full Text | Google Scholar

Calonge, J. D., Gomez, D., and Ortiz, A. R. (2023). Robust feedback models with structured uncertainties for human–structure interaction. Mech. Syst. Signal Process. 202, 110681. doi:10.1016/j.ymssp.2023.110681

CrossRef Full Text | Google Scholar

Chen, S., Billings, S. A., and Grant, P. M. (1990). Non-linear system identification using neural networks. Int. J. Control 51, 1191–1214. doi:10.1080/00207179008934126

CrossRef Full Text | Google Scholar

Connor, J., and Laflamme, S. (2014). Structural motion engineering. one edn. Springer Cham. doi:10.1007/978-3-319-06281-5

CrossRef Full Text | Google Scholar

Cruise, D. R., Chagdes, J. R., Liddy, J. J., Rietdyk, S., Haddad, J. M., Zelaznik, H. N., et al. (2017). An active balance board system with real-time control of stiffness and time-delay to assess mechanisms of postural stability. J. Biomechanics 60, 48–56. doi:10.1016/j.jbiomech.2017.06.018

PubMed Abstract | CrossRef Full Text | Google Scholar

Dang, H. V., and Živanović, S. (2015). Experimental characterisation of walking locomotion on rigid level surfaces using motion capture system. Eng. Struct. 91, 141–154. doi:10.1016/j.engstruct.2015.03.003

CrossRef Full Text | Google Scholar

Dang, H. V., and Živanović, S. (2016). Influence of low-frequency vertical vibration on walking locomotion. J. Struct. Eng. 142, 04016120. doi:10.1061/(asce)st.1943-541x.0001599

CrossRef Full Text | Google Scholar

Gomez, D., Dyke, S. J., and Rietdyk, S. (2018). Experimental verification of a substructure-based model to describe pedestrian-bridge interaction. J. Bridge Eng. 23, 04018013–04018019. doi:10.1061/(ASCE)BE.1943-5592.0001204

CrossRef Full Text | Google Scholar

Gomez, D., Dyke, S. J., and Rietdyk, S. (2020). Structured uncertainty for a pedestrian-structure interaction model. J. Sound Vib. 474, 115237. doi:10.1016/j.jsv.2020.115237

CrossRef Full Text | Google Scholar

Hashim, R., Ji, T., Mandal, P., Zhang, Q., and Zhou, D. (2020). Human-structure interaction experiments to determine the dynamic properties of the standing human body in vertical vibration. Structures 26, 934–946. doi:10.1016/j.istruc.2020.04.040

CrossRef Full Text | Google Scholar

Johnson, W. R., Alderson, J., Lloyd, D., and Mian, A. (2019). Predicting athlete ground reaction forces and moments from spatio-temporal driven cnn models. IEEE Trans. Biomed. Eng. 66, 689–694. doi:10.1109/TBME.2018.2854632

PubMed Abstract | CrossRef Full Text | Google Scholar

Khodabandehlou, H., and Fadali, M. (2019). “Nonlinear system identification using neural networks and trajectory-based optimization,” Proceedings 16th International Conference Inf. Control, Automation Robotics. Editor O. Gusikhin, K. Madani, and J. Zaytoon (Czech Republic) 1. 579–586. doi:10.5220/0007772605790586

CrossRef Full Text | Google Scholar

Li, H., Wang, T., and Wu, G. (2021). Dynamic response prediction of vehicle-bridge interaction system using feedforward neural network and deep long short-term memory network. Structures 34, 2415–2431. doi:10.1016/j.istruc.2021.09.008

CrossRef Full Text | Google Scholar

Lin, T., Horne, B. G., Tino, P., and Giles, C. L. (1996). Learning long-term dependencies in NARX recurrent neural networks. IEEE Trans. Neural Netw. 7, 1329–1338. doi:10.1109/72.548162

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, B., Zhang, Q., Fan, F., and Shen, S. (2020). A damped bipedal inverted pendulum for human–structure interaction analysis. Appl. Math. Model. 87, 606–624. doi:10.1016/j.apm.2020.06.027

CrossRef Full Text | Google Scholar

Lopez, S. A., Gomez, D., Ortiz, A. R., and Villamizar, S. (2025). Integrating feedback control for improved human-structure interaction analysis. Front. Built Environ. 10, 1524027. doi:10.3389/fbuil.2024.1524027

CrossRef Full Text | Google Scholar

Lucà, F., Berardengo, M., Manzoni, S., Vanali, M., and Drago, L. (2022). Human-structure interaction: convolution-based estimation of human-induced vibrations using experimental data. Mech. Syst. Signal Process. 167, 108511. doi:10.1016/j.ymssp.2021.108511

CrossRef Full Text | Google Scholar

Luo, Z., Zheng, X., Yuan, H., and Niu, X. (2020). Dynamic coupling analysis of vehicle-bridge system for long-span suspension bridge based on backpropagation neural network method. Adv. Civ. Eng. 2020, 5878426. doi:10.1155/2020/5878426

CrossRef Full Text | Google Scholar

Martínez-García, M., Zhang, Y., and Gordon, T. (2021). Memory pattern identification for feedback tracking control in human–machine systems. Hum. Factors 63, 210–226. doi:10.1177/0018720819881008

PubMed Abstract | CrossRef Full Text | Google Scholar

Norgaard, M., Ravn, O., Poulsen, N. K., and Hansen, L. K. (2000). Neural networks for modelling and control of dynamic systems. Springer London. doi:10.1007/978-1-4471-0453-7

CrossRef Full Text | Google Scholar

Ortiz, A. R. (2016). Modeling human-structure interaction using a controller system. Doctoral dissertation. Columbia, United States: University of South Carolina.

Google Scholar

Ortiz, A. R., and Caicedo, J. M. (2019). Modeling the effects of a human standing on a structure using a closed loop–control system. J. Eng. Mech. 145, 04019025. doi:10.1061/(asce)em.1943-7889.0001583

CrossRef Full Text | Google Scholar

Peláez-Rodríguez, C., Álvaro, M., Terán, J. M. G., Pérez-Aracil, J., Salcedo-Sanz, S., and Lorenzana, A. (2024). An iterative neural network approach applied to human-induced force reconstruction using a non-linear electrodynamic shaker. Heliyon 10, e32858. doi:10.1016/j.heliyon.2024.e32858

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinkus, A. (1999). Approximation theory of the MLP model in neural networks. Acta Numer. 8, 143–195. doi:10.1017/S0962492900002919

CrossRef Full Text | Google Scholar

Qin, J. W., Law, S. S., Yang, Q. S., and Yang, N. (2013). Pedestrian-bridge dynamic interaction, including human participation. J. Sound Vib. 332, 1107–1124. doi:10.1016/j.jsv.2012.09.021

CrossRef Full Text | Google Scholar

Ruslan, F. A., Samad, A. M., Zain, Z. M., and Adnan, R. (2014). “Flood water level modeling and prediction using NARX neural network: case study at kelang river,” in 2014 IEEE 10th international colloquium on signal processing and its applications, 204–207. doi:10.1109/CSPA.2014.6805748

CrossRef Full Text | Google Scholar

Salyards, K. A., and Noss, N. C. (2014). Experimental evaluation of the influence of human-structure interaction for vibration serviceability. J. Perform. Constr. Facil. 28, 458–465. doi:10.1061/(asce)cf.1943-5509.0000436

CrossRef Full Text | Google Scholar

Shahabpoor, E., Pavic, A., and Racic, V. (2016). Identification of mass-spring-damper model of walking humans. Structures 5, 233–246. doi:10.1016/j.istruc.2015.12.001

CrossRef Full Text | Google Scholar

Sim, J., Blakeborough, A., and Williams, M. (2007). Modelling of joint crowd-structure system using equivalent reduced-dof system. Shock Vib. 14, 261–270. doi:10.1155/2007/498081

CrossRef Full Text | Google Scholar

Subashi, G. H. M. J., Matsumoto, Y., and Griffin, M. J. (2006). Apparent mass and cross-axis apparent mass of standing subjects during exposure to vertical whole-body vibration. J. Sound Vib. 293, 78–95. doi:10.1016/j.jsv.2005.09.007

CrossRef Full Text | Google Scholar

Van Nimmen, K., Pavic, A., and Van den Broeck, P. (2021). A simplified method to account for vertical human-structure interaction. 32, 2004, 2019. doi:10.1016/j.istruc.2021.03.090

CrossRef Full Text | Google Scholar

Wei, X., and Živanović, S. (2018). Frequency response function-based explicit framework for dynamic identification in human-structure systems. J. Sound Vib. 422, 453–470. doi:10.1016/j.jsv.2018.02.015

CrossRef Full Text | Google Scholar

Živanović, S., Pavic, A., and Reynolds, P. (2005). Vibration serviceability of footbridges under human-induced excitation: a literature review. J. Sound Vib. 279, 1–74. doi:10.1016/j.jsv.2004.01.019

CrossRef Full Text | Google Scholar