Soil-water characteristic curve and permeability function of concrete waste

The soil-water characteristic curve (SWCC) and permeability function are critical parameters for understanding the hydraulic behavior of unsaturated soils and are increasingly relevant in evaluating alternative materials for geotechnical and environmental applications. While recycled materials like concrete waste hold promise as substitutes for natural soil, limited research has been conducted to systematically characterize their unsaturated hydraulic properties. In particular, previous studies have largely overlooked the influence of grain size distribution on the SWCC and permeability of concrete waste, resulting in a gap in data necessary for practical application. This study addresses that gap by directly measuring the SWCC and saturated permeability (k_s) of concrete waste with varying grain size distributions—a novel approach not widely explored in earlier research. The SWCC was determined using a Tempe cell, and saturated permeability was measured using a constant head test. Results showed that three of the five samples exhibited relatively low k_s values, while the remaining two displayed significantly higher permeability. In terms of saturated volumetric water content, In terms of saturated volumetric water content, poorly graded sand demonstrated a greater capacity to retain water, whereas sandy gravel and well-graded sand had much lower water retention, indicating poor drainage. These findings reveal that the hydraulic behavior of concrete waste is highly variable and dependent on its particle size composition and internal structure. By providing new empirical data, this study contributes original insights into the feasibility of using concrete waste as an engineered fill or barrier material in soil-related applications, where understanding unsaturated hydraulic properties is essential for modeling groundwater flow and assessing environmental impact.

1 Introduction

As the largest archipelagic nation with a tropical climate, Indonesia faces a high degree of vulnerability to the impacts of climate change. Increased temperatures and intensified rainfall patterns contribute to a greater likelihood of slope failure, particularly in areas underlain by residual soils. These soils, commonly found in tropical regions, are inherently heterogeneous, with grain-size distributions that are highly variable and often unpredictable (Murthy, 2002). From a geotechnical perspective, understanding the behavior of such soils under changing moisture conditions requires the application of unsaturated soil mechanics. Key to this understanding is the role of soil suction, especially in the vadose zone, where it mitigates excess pore water pressure caused by flux boundary changes like infiltration and evaporation (Rahardjo et al., 2019a).

Soil suction, defined as the difference between air pressure and pore water pressure (u_a – u_w), typically simplifies to negative pore-water pressure under field conditions where air pressure is atmospheric (Briaud, 2023). During rainfall events, the infiltration of water into the unsaturated zone forms a perched water table, causing an increase in pore water pressure and shifting the stress state depending on the depth of wetting. In Indonesia, slope failures—largely associated with residual soils—commonly occur during the rainy season due to this mechanism.

Several studies have emphasized the role of rainfall-induced infiltration and the application of capillary barrier systems (CBS) in reducing slope instability (Rahayu et al., 2024). While these studies have established the conceptual viability of CBS in minimizing infiltration and excess pore pressure (Li et al., 2021), limitations remain. Most prior research has been conducted using conventional soil materials, with little focus on sustainable alternatives such as construction and demolition waste. Furthermore, limited data exists on the hydraulic behavior of waste concrete under unsaturated conditions, particularly in configurations relevant to CBS design. The variability in grain size distribution in waste-derived materials also introduces complexities that have not been sufficiently explored in relation to their effect on unsaturated hydraulic properties.

To address these gaps, this research presents a novel investigation into the use of waste concrete as a non-cohesive material for capillary barrier systems. The originality of this study lies in its focus on characterizing the unsaturated hydraulic behavior of recycled concrete materials with varying particle size distributions—an area previously underexplored in tropical slope stability research. Previous studies on unsaturated hydraulic properties, such as the soil-water characteristic curve (SWCCs) and the permeability function, have largely focused on natural soils (Li et al., 2011; Wijaya et al., 2024; Yao et al., 2021; Zhang et al., 2017; Zhou et al., 2014). Previous works also demonstrated that SWCC behavior is affected by sample size, plasticity, and fines content (Raghuram et al., 2020; Raghuram et al., 2023; Raghuram et al., 2024), highlighting the importance of material-specific investigations. Recent study also highlighted significant progress in suction measurement methods, including the development of high-suction polymer tensiometer (Liu et al., 2024). Studies on recycled concrete materials have given little consideration to the unsaturated hydraulic properties (Ito et al., 2022; Rahardjo et al., 2013).

The main objective of this research is to determine the hydraulic characteristics of waste concrete as a non-cohesive material under unsaturated conditions. Five different grain-size distributions are tested. The soil-water characteristic curve (SWCCs) of the samples are determined using the Tempe Cell method, and the hydraulic properties are derived through saturated permeability tests and fitted statistical models. These unsaturated parameters are essential for future research aiming to optimize the configuration of fine- and coarse-grained layers within a capillary barrier system.

2 Methods

2.1 Material properties

The material used in this research is concrete waste. Recycled concrete aggregate (RCA) is prepared the same as soil but is pulverized using a rock hammer after being collected from waste materials that are no longer in use. The concrete waste used in this study was collected from construction debris originating in Bandung, West Java, Indonesia. All samples were prepared by compacting manually the concrete waste aggregates using a pestle with each layer tamped uniformly. This procedure was selected to minimize excessive particle crushing while ensuring uniform density across samples. Based on the grain size distribution, sample one contains 90 percent coarse sand. Sample two contains 95 percent medium sand. Sample three contains 95 percent medium sand. Sample four contains 50 percent gravel and 28 percent coarse sand and 22 percent medium sand. sample five contains 10 percent medium sand and 50 percent medium sand.

2.2 Soil-water characteristic curve

In this research, laboratory tests under unsaturated conditions were performed on disturbed of concrete waste (CW) samples. The initial conditions of the CW samples were determined prior to testing. Table 1 shows the values of initial void ratio (e), gravimetric water content (w), and volumetric water content (θ). These parameters provide the initial reference in the determination of unsaturated permeability function. Suction measurements were performed using the Tempe Cell (Rahardjo et al., 2019b). The Tempe Cell comprises four main components, including a base cap, a porous ceramic plate, a brass cylinder, and a top cap. The component dimensions of the specimen cylinder are 2.12 inches (5.38 cm) and a length of 2.36 inches (6.00 cm). The maximum capacity of soil suction that occurs on porous ceramic plates (high AEV) is only 100 kPa. To ensure that soil suction measurements can run optimally, the porous ceramic plate must first be saturated by submerging it inside a container filled with distilled and de-aired water.

Table 1

Table 1. Initial condition of CW samples.

The working principle of the Tempe Cell is that the amount of air pressure applied is the same as that of soil suction that occurs on the porous ceramic plate. When air pressure is applied, the water molecules in the specimen cylinder can flow out into the porous ceramic plate. The time required to reach equilibrium conditions in soil suction measurements is highly dependent on the thickness and permeability of the soil specimen being tested. Measurement of water content was carried out by weighing the concrete waste sample in the specimen cylinder along with the Tempe Cell after reaching equilibrium conditions in the soil suction. After performing the final measurement of soil suction by applying the highest air pressure of 100 kPa, the CW sample was removed and dried in an oven for approximately 24 h. The final measurement results of water content and weight changes in the previous concrete waste sample were used to recalculate the water mass in accordance with the soil suction value in stages. Next, the soil suction values ​​and water content (gravimetric, volumetric, and degree of saturation) can be plotted on a graph, ultimately producing a SWCC curve.

The water characteristic curve consists of three conditions that represent the desaturation zone in a type of soil, including boundary conditions, transition conditions, and residual conditions (Rahardjo et al., 2019a). Specifically, the Air-entry value (AEV) is defined as the point at which there is a sufficiently large pressure difference between the air and water so that water molecules can be displaced by the air from the soil pore space. Meanwhile, residual suction is defined as a point where there is a further increase in matrix suction that fails to remove large amounts of water. The best fitting of the soil-water characteristic curve in this study includes six parameters fitting curve based on a non–linear regression function utilizing Equation 1 proposed by Satyanaga et al. (2017):

${\theta }_w=\left(1-\frac{\ln \left(1+\frac{\psi }{{\psi }_r}\right)}{\ln \left(1+\frac{{10}^6}{{\psi }_r}\right)}\right)\times \left[{\theta }_r+\left\{\left({\theta }_s-{\theta }_r\right)\left(-\left(\beta \right)erfc\right)\left(\frac{\ln \left(\frac{{\psi }_a-\psi }{{\psi }_a-{\psi }_m}\right)}{s}\right)\right\}\right](1)$

where: $\beta$ = 0 when $\psi \le {\psi }_a;$ $\beta$ = 1 when $\psi \ge {\psi }_a$; ${\theta }_w$ = calculated volumetric water content; ${\theta }_s$ = saturated volumetric water content; $\psi$ = matric suction under consideration (kPa); ${\psi }_a$ = parameter representing the air-entry value of the soil (kPa); ${\psi }_m$ = parameter representing the matric suction at the inflection point of the SWCC (kPa); ${\psi }_r$ = suction corresponding to the residual water content, ${\theta }_r$ ; $s$ = parameter representing the geometric standard deviation of the SWCC; ${\theta }_r$ = parameter representing the residual volumetric water content.

2.3 Permeability function

The constant-head (CH) permeameter method is widely used in pervious concrete permeability coefficient test at the laboratory (Zhang et al., 2020). The Constant head permeability test follows the principle of Darcy’s Law. The coefficient of water permeability was calculated by Equation 2:

$K_T=\frac{QL}{AHt}(2)$

Where: $K_T$ is the water permeability coefficient at water temperature of T °C (cm/s); Q is the quantity of water collected over time $t$ (s); $L$ (cm) is thickness of sample; $A$ is the cross-sectional area of the sample (cm²); $H$ is the water head above the specimen (cm); $t$ is the time of the water collected after the water flow from the over flow port stabilizes (s).

The constant head consists of a plastic soil specimen, two porous stones, two rubber stoppers, one spring, one constant head chamber, a large funnel, a stand, a scale, three clamps, and some plastic tubes (Das, 2004). The constant head permeability test was conducted on cylindrical specimens with a diameter of 63.2 mm and a length of 140 mm. A hydraulic gradient was applied by maintaining a constant head difference equivalent to the specimen length. The detailed experimental setup and procedure followed those adopted in previous study by Adinegara et al. (2025).

In unsaturated soil mechanics, the permeability function can be determined from the soil-water characteristic curve (Fredlund and Xing, 1994). The soil-water characteristic curve describes the behavior and ability of soil to store or drain water, which is highly dependent on the grain size distribution of soil. The permeability function reflects the relationship between the coefficient of permeability (k_w) and soil suction (ψ_s). The determination of the permeability function was conducted using statistical methods following the procedure explained in (Fredlund et al., 2012). To estimate the soil permeability function based on the three parameters in the SWCC curve, it can be analyzed using Equation 3 (Fredlund and Xing, 1994):

$k_w=k_{sat}·\frac{{\displaystyle {\int }_{\ln \psi }^{\ln {\psi }_r}}\frac{{\theta }_s\left(e^y\right)-{\theta }_s\left(\psi \right)}{e^y}{{\theta }_s}^{\prime }\left(e^y\right)dy}{{\displaystyle {\int }_{\ln {\psi }_{AEV}}^{\ln {\psi }_r}}\frac{{\theta }_s\left(e^y\right)-{\theta }_s\left({\psi }_{AEV}\right)}{e^y}{{\theta }_s}^{\prime }\left(e^y\right)dy}(3)$

Where k_w is the relative coefficient of permeability, k_sat is the saturated coefficient of permeability, and θ_s is the volumetric water content. ψ is soil suction, ψ_aev is the suction at the lower limit of integration, commonly taken as the air-entry value (AEV), and ψ_r is the soil suction at the upper limit of integration, commonly taken as residual soil suction.

3 Results and discussion

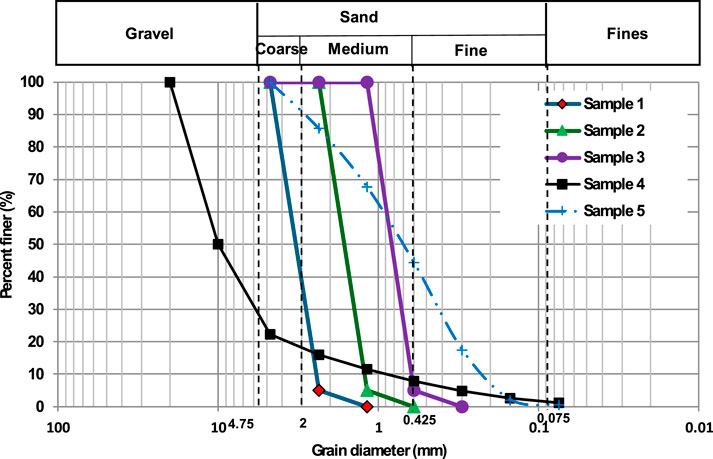
The grain-size distributions (GSDs) of the investigated concrete waste are presented in Figure 1. It shows that Sample four consists of around 79% gravel and 31% sand size particles. Samples 1, two and three present the uniform particle size since the shape of their GSD is classified as poorly graded sand. Sample five is classified as well-graded sand with 10% coarse sand, 45% medium sand, and 45% fine sand.

Figure 1

Figure 1. Grain-size distribution of concrete waste.

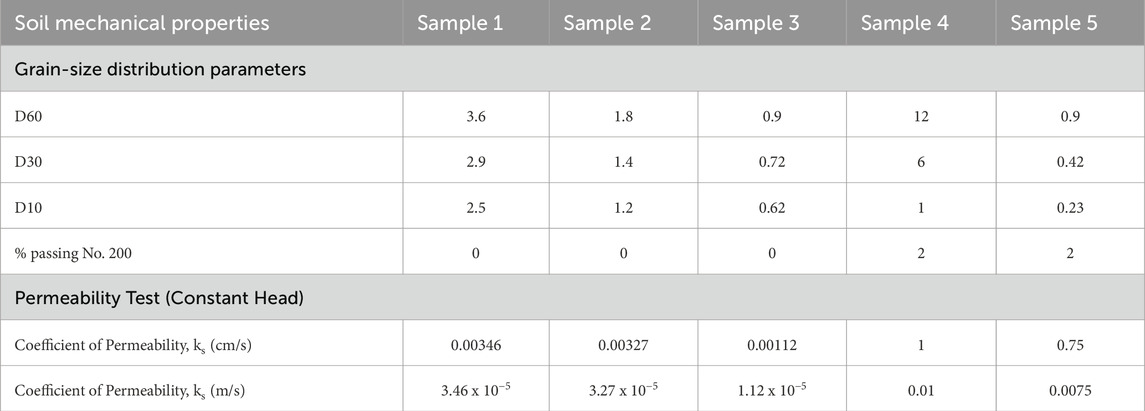
Table 2 lists the saturated permeability of concrete waste material used in this study. Specifically, Samples 3, 2, and one have a uniform grain size distribution pattern and are classified as poorly graded sand. The saturated permeability (k_s) in each sample has a relatively very small value, namely, 1.12 x 10⁻⁵ m/s, 3.27 x 10⁻⁵ m/s, and 3.46 x 10⁻⁵ m/s. Sample 5 has a diverse grain size distribution pattern and is classified as well-graded sand, with a relatively high saturated permeability (k_s), namely, 750 x 10⁻⁵ m/s. Sample 4 has a very diverse grain size distribution pattern and is classified as sandy gravel, with a relatively very high saturated permeability (k_s), namely, 1,000 x 10⁻⁵ m/s. As is known, grain size distribution plays a quite important role, especially in terms of groundwater flow. The smaller and more uniform the grain size of a soil type, the smaller the saturated permeability value (Rotz, 2021).

Table 2

Table 2. Saturated permeability of CW material.

In a typical procedure, the Tempe cell test was started with a saturation process. Based on the concrete waste saturation process, there is an increase in water content with each addition of water molecules. The saturation process for the concrete waste sample was carried out for 7 days until reaching a fully saturated condition, which was characterized by stability in the weight of the Tempe Cell and the sample in the specimen cylinder.

Figure 2 shows the lab data on the measurement results from soil suction data obtained using the Tempe Cell. The best-fitting curve was performed after determining the appropriate initial values for the six parameters for the SWCC curve unimodally using a non–linear regression function (Satyanaga et al., 2017). The procedure for applying the non–linear regression function has been repeatedly provided in Microsoft Excel software.

Figure 2

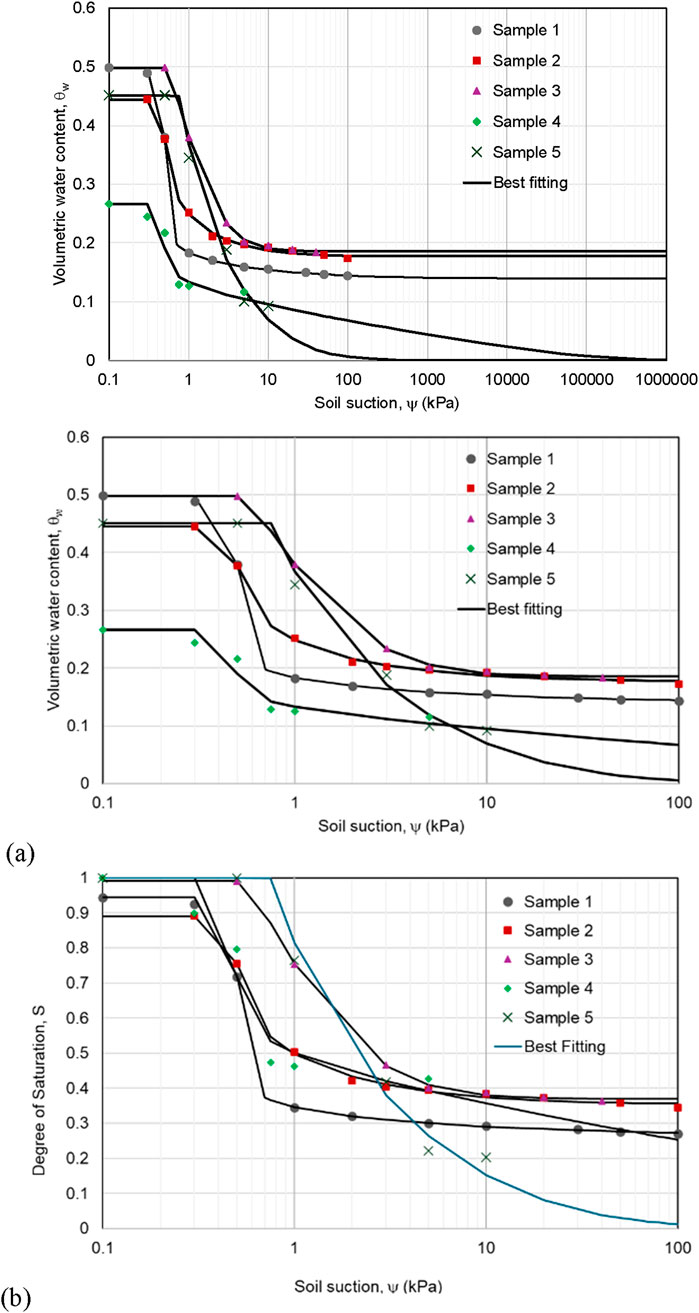
Figure 2. Modeling and plotting best fit curve (SWCC). (a) Relationship between volumetric water content and soil suction. (b) Relationship between degree of saturation and soil suction.

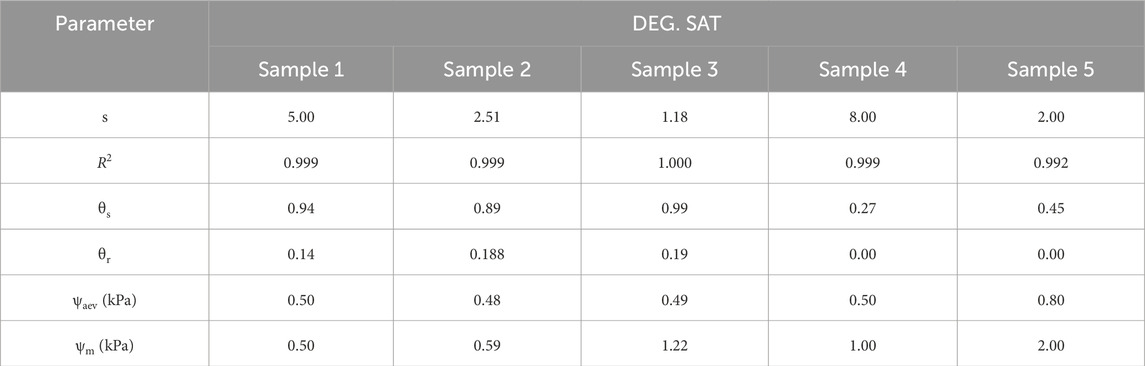
The relationship between the volumetric water content and soil suction of the investigated concrete waste are presented in Figure 2a. The volumetric water content is defined as the comparison value between the volume of water and the total volume of the specimen cylinder expressed as a percent (Leong and Wijaya, 2023). The saturated volumetric water content (θ_s) describes the behavior and ability of the soil to store water. Samples one and three have a very high storage capacity, with a saturated volumetric water content (θ_s) value of 0.495 or 50%. Samples two and five have high storage capacities, with respective saturated volumetric water content (θ_s) values of 0.445 or 45%, and 0.455 or 46%. Sample 4 has a low storage capacity, with a saturated volumetric water content (θ_s) of 0.265 or 27%. Meanwhile, the residual volumetric water content (θ_r) describes the behavior and ability of the soil to drain water. Sample 4 has a low drainage capacity, with a residual volumetric water content (θ_r) of 0.145 or 15%. Samples 5, 1, and three have relatively moderate drainage capacities, with respective residual volumetric water content (θ_r) values of 0.175 or 18%, 0.195 or 20%, and 0.205 or 21%. Sample 2 has a high drainage capacity, with a residual volumetric water content (θ_r) of 0.275 or 28%.

The relationship between the saturated water content and soil suction of the investigated concrete waste are presented in Figure 2b. Degree of saturation is defined as the ratio of water volume to void volume, which is also expressed as a percentage. Sample one and Sample two exhibit moderate degrees of saturation with respective values of 0.943 or 94%, and 0.89 or 89%. Sample 3, four and Sample five have a relatively high degree of saturation with respective values of 0.99 or 99%.

Based on Figures 2a,b, soil suction consists of three conditions, including boundary conditions (ψ_aev), transition conditions (ψ_m), and residual conditions (ψ_r). The AEV (ψ_aev) quantity describes the existence of a large enough pressure difference between air and water so that water molecules can be moved by air from the soil pore space. Samples 2, 3, 4, and one have relatively moderate AEV (ψ_aev) magnitudes, with values of around 0.5 kPa. Sample 5 has a high AEV (ψ_aev), with a value of 0.8 kPa. The suction inflection point (ψ_m) represents a brief increase in matrix suction which is correlated with the desaturation speed (δ_s). Samples one and two have low suction inflection points (ψ_m), with values of 0.50 kPa and 0.59 kPa respectively. Samples four and three have relatively moderate suction inflection points (ψ_m), with values of 1 kPa and 1.2 kPa respectively. Sample 5 has a high suction inflection point (ψ_m), with a value of 2 kPa. For more details, the best-fitting parameters of the water characteristic curve of concrete waste can be shown in Table 3.

Table 3

Table 3. Best Fitting Parameters of water characteristic curve of concrete waste.

As is known, grain size distribution is greatly influenced by the amount of soil suction that occurs. The smaller the grain size contained in a type of soil, the greater the air–entry value (ψ_aev) into the soil pores (Leong, 2019).

Figure 2 shows that conversion and graph plotting are performed on the modeling results, along with the best fit for the water characteristic curve (SWCC). It is worth noting that the test data for the saturated permeability of CW material were used to determine the permeability function. The saturated permeability (k_s) was found to be 1.12 x 10⁻⁵ m/s in Sample 3, 3.27 x 10⁻⁵ m/s in Sample 2, 3.46 x 10⁻⁵ m/s in Sample 1, 750 x 10⁻⁵ m/s in Sample 5, and 1,000 x 10⁻⁵ m/s in Sample 4. In terms of application, the permeability function can be analyzed using Equation 2.2, based on three parameters from the best fit on the SWCC. Generally, the permeability function reflects the relationship between the coefficient of permeability (k_w) and soil suction (ψ_s).

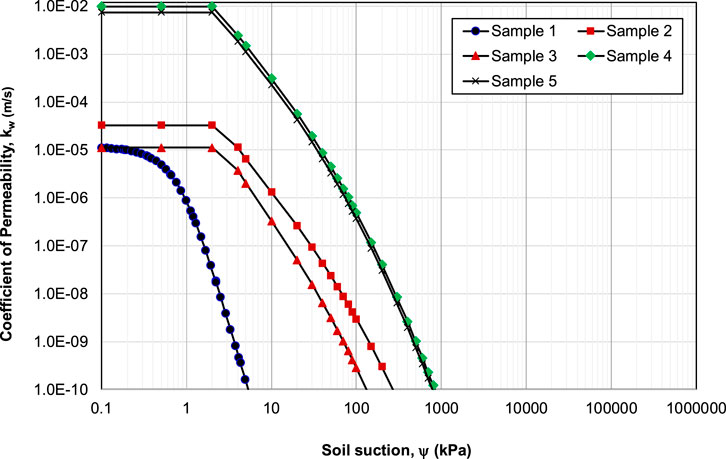
Figure 3 shows conversion and graph plotting for the permeability function of CW. The coefficient of permeability (k_w) in CW material, especially in boundary conditions (ψ_aev), has a value of 5.43 x 10⁻⁴ m/s in Sample 3, 1.57 x 10⁻³ m/s in Sample 2, 1.73 x 10⁻³ m/s in Sample 1, 4.95 x 10⁻¹ m/s in Sample 4, and 6.00 x 10⁻¹ m/s in Sample 5. Meanwhile, the coefficient of permeability (k_w) in CW material, especially in transition conditions (ψ_m), has a value of 1.37 x 10⁻³ m/s in Sample 3, 1.73 x 10⁻³ m/s in Sample 1, 1.92 x 10⁻³ m/s in Sample 2, 1.000 m/s in Sample 4, and 1.500 m/s in Sample 5. As is known, grain size distribution plays a crucial role, especially in understanding the behavior of groundwater flow. Fine grained soil generally retain water through adsorption and capillarity, with adsorption being dominant in clay due to the high specific surface area (D.G. Fredlund and Rahardjo, 1993; Lu, 2016; Lu and Likos, 2004). However, since the concrete waste examined in this study contains no clay particles, adsorption is negligible. The unsaturated hydraulic behavior is therefore governed primarily by capillarity and pore-size distribution, which explains the observed differences in SWCC and permeability among the samples.

Figure 3

Figure 3. Permeability function.

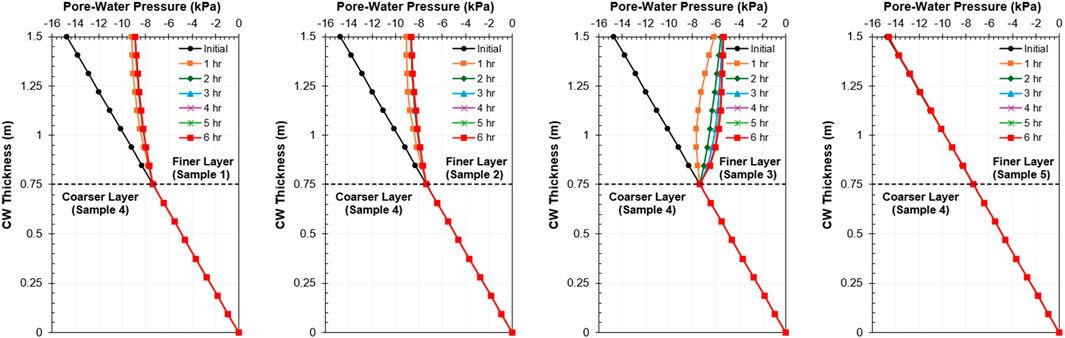
To further evaluate the effectiveness of concrete waste (CW) as a capillary barrier material, a one-dimensional seepage model was conducted using the seepage finite element program SEEP/W. This seepage analysis consisted of evaluating different finer layer materials (Samples 1,2,3,5) combined with Sample 4 as the coarser layer. The model configuration consisted of a finer CW layer (thickness of 0.75 m) overlying a coarser CW layer (Sample 4 with a thickness of 0.75 m). Sample four was selected as the coarser layer because it showed the highest saturated permeability. A constant rainfall infiltration rate of 150 mm/day was applied for 6 h at the top of the model. The boundary conditions specified zero pressure at the bottom of the model and no-flow along the sides to ensure that water movement occurred only in the vertical direction.

The initial matric suction at the top of the finer layer was approximately 15 kPa. At this suction, the unsaturated permeability of the finer materials differs significantly. At a matric suction of approximately 15 kPa, Samples one and 2 (uniformly graded with moderate θ_s) showed higher unsaturated permeability, on the order of 10⁻⁵ – 10⁻⁶ m/s, compared with the other samples, resulting in fast wetting. At matric suction of approximately 15 kPa, Sample three shows moderate unsaturated permeability values relative to the other finer materials. This behavior reflects the broader transition zone in its SWCC between the air-entry value and the suction inflection point. In contrast, Sample four shows significantly lower permeability (around 10⁻⁷ m/s) at the same suction level, reflecting stronger resistance to infiltration. The more gradual increase in unsaturated permeability observed in Sample four corresponds to its higher air-entry value and greater suction at the inflection point, allowing the material to maintain low permeability over a wider suction range.

Figure 4 shows the time-dependent pore-water pressure distribution of concrete waste (finer and coarser layers) under 150 mm/day rainfall. For Samples one to three used as the finer layer, the infiltration zone progresses downward more quickly, as indicated by the reduction of suction with time. In the case of Sample 4, changes in pore-water pressure are insignificant, reflecting its limited permeability under unsaturated conditions. This opposing behavior is governed by the air-entry value (AEV) and suction inflection point of each material. Samples one to three, with lower AEV values (around 0.50 kPa), allow earlier water entry and faster increase in permeability, which explains the quicker wetting response. In contrast, Sample 4 has a higher AEV and a delayed inflection point, which delays water entry and maintains lower permeability under rainfall infiltration.

Figure 4

Figure 4. Pore-water pressure profiles of CW under 150 mm/day rainfall.

4 Conclusion

The hydraulic properties of soil are a determining factor in understanding the behavior of groundwater flow and are largely influenced by the grain size distribution of the soil type. The smaller the grain size of a type of soil, the higher the soil’s ability to absorb and store groundwater. However, this is inversely proportional to the relatively low ability of groundwater to flow. CW (Concrete Waste) material can be used as an alternative to prevent slope collapse during the rainy season because this material has quite high-water drainage capabilities. The CW material is installed as a cover at the bottom of the slope surface, which functions as a preventer of rainwater infiltration and reduces excessive increases in pore water pressure, especially in unsaturated soil zones. The finer CW material is placed over the coarser CW material to prevent rainwater infiltration into the slope. The upper layer, finer CW absorbs and holds rainwater, causing it to drain horizontally down the slope. Simultaneously, the underlying coarse-grained layer remains unsaturated, functioning as a capillary barrier that retains water from penetrating deeper. This barrier remains effective unless a critical saturation point is reached.

The one-dimensional seepage analysis demonstrates that the hydraulic performance of concrete waste in a capillary barrier depends on the choice of finer material. Samples one to three, with lower AEV values, allow earlier water entry and reach higher permeability at relatively low suction, which explains their rapid wetting behavior. In contrast, Sample 4 has a higher AEV and an inflection point at greater suction, which delays water entry and maintains lower permeability during rainfall infiltration.

To extend the findings of this research, further studies are planned to conduct an infiltration box test incorporating sensors to directly monitor pore-water pressure. This approach will provide experimental validation of the numerical simulations, which in the present study were based only on laboratory-derived parameters. The combination of sensor-based infiltration tests and numerical modeling is expected to strengthen the reliability of using concrete waste as a capillary barrier material. Following this stage, a full-scale field application can be considered to evaluate the performance of concrete waste layers as a capillary barrier under real rainfall and slope conditions.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

FS: Conceptualization, Formal Analysis, Methodology, Writing – original draft, Investigation. AH: Funding acquisition, Data curation, Writing – original draft, Conceptualization, Methodology. GA: Data curation, Writing – original draft, Software, Methodology. MW: Conceptualization, Supervision, Writing – original draft, Methodology. WP: Conceptualization, Investigation, Supervision, Writing – review and editing, Project administration. WR: Methodology, Supervision, Writing – review and editing, Resources, Visualization. ED: Methodology, Software, Investigation, Writing – review and editing, Formal Analysis. AS: Investigation, Writing – review and editing, Validation, Supervision.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. Directorate of Research and Development, Universitas Indonesia—Hibah PUTI 2024 (Grant No. NKB-457/UN2.RST/HKP.05.00/2024).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Adinegara, A. W., Ramadhan, R. I., Hamdany, A. H., and Sagitaningrum, F. H. (2025). Pengukuran langsung kurva Karakteristik Air – tanah (SWCC) Pada Limbah Beton Dengan Metode Tempe cell. J. Tek. Sipil 32 (1), 29–34. doi:10.5614/jts.2025.32.1.4

CrossRef Full Text | Google Scholar

Briaud, J.-L. (2023). Geotechnical engineering: unsaturated and saturated soils. John Wiley and Sons, Inc.

CrossRef Full Text | Google Scholar

Das, B. M. (2004). “Soil mechanics,” in The engineering handbook. Second Edition.

Google Scholar

Fredlund, D. G., and Rahardjo, H. (1993). Soil mechanics for unsaturated soils. New York: Wiley.

Google Scholar

Fredlund, D. G., and Xing, A. (1994). Equations for the soil-water characteristic curve. Can. Geotechnical J. 31 (4), 521–532. doi:10.1139/t94-061

CrossRef Full Text | Google Scholar

Fredlund, D. G., Rahardjo, H., and Fredlund, M. D. (2012). Unsaturated soil mechanics in Engineering practice. Hoboken, New Jersey: John Wiley and Sons, Inc.

Google Scholar

Ito, R., Kato, A., Matsuno, A., and Kawamoto, K. (2022). “Characterization of water retention and unsaturated hydraulic conductivity for recycled road-base materials,” in Paper presented at the ICSBE 2020. Singapore.

Google Scholar

Leong, E.-C. (2019). Soil-water characteristic curves - determination, estimation and application. Jpn. Geotech. Soc. Spec. Publ. 7 (2), 21–30. doi:10.3208/jgssp.v07.003

CrossRef Full Text | Google Scholar

Leong, E. C., and Wijaya, M. (2023). Laboratory tests for unsaturated soils. Boca Raton, United States: CRC Press.

CrossRef Full Text | Google Scholar

Li, J. H., Zhang, L. M., and Li, X. (2011). Soil-water characteristic curve and permeability function for unsaturated cracked soil. Can. Geotechnical J. 48 (7), 1010–1031. doi:10.1139/t11-027

CrossRef Full Text | Google Scholar

Li, Y., Satyanaga, A., and Rahardjo, H. (2021). Characteristics of unsaturated soil slope covered with capillary barrier system and deep-rooted grass under different rainfall patterns. Int. Soil Water Conservation Res. 9 (3), 405–418. doi:10.1016/j.iswcr.2021.03.004

CrossRef Full Text | Google Scholar

Liu, H., Hamdany, A. H., and Rahardjo, H. (2024). Laboratory investigation of osmotic tensiometers filled with cross-linked polyacrylamide. Transp. Geotech. 44, 101173. doi:10.1016/j.trgeo.2023.101173

CrossRef Full Text | Google Scholar

Lu, N. (2016). Generalized soil water retention equation for adsorption and capillarity. J. Geotechnical Geoenvironmental Eng., 142 (10), 04016051. doi:10.1061/(ASCE)GT.1943-5606.0001524

CrossRef Full Text | Google Scholar

Lu, N., and Likos, W. J. (2004). Unsaturated soil mechanics, c2004. Hoboken, N.J.: J. Wiley.

Google Scholar

Murthy, V. N. S. (2002). Geotechnical engineering, principles and practices of soil mechanics and foundation engineering. Marcel Dekker AG.

Google Scholar

Raghuram, A. S. S., Basha, B. M., and Moghal, A. A. B. (2020). Effect of fines content on the hysteretic behavior of water-retention characteristic curves of reconstituted soils. J. Mater. Civ. Eng. 32 (4), 04020057. doi:10.1061/(ASCE)MT.1943-5533.0003114

CrossRef Full Text | Google Scholar

Raghuram, A. S. S., Mounika, N., Basha, B. M., and Moghal, A. A. B. (2023). Soil water characteristic curves of soils exhibiting different plasticity. Int. J. Geosynth. Ground Eng. 9 (3), 25. doi:10.1007/s40891-023-00444-z

CrossRef Full Text | Google Scholar

Raghuram, A. S. S., Negi, P. S., Basha, B. M., and Moghal, A. A. B. (2024). Effect of sample size, dry unit weight, and hysteresis of expansive soil on SWCC and finite Slope stability. Int. J. Geosynth. Ground Eng. 10 (2), 18. doi:10.1007/s40891-024-00531-9

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., Leong, E.-C., and Wang, J.-Y. (2013). Unsaturated properties of recycled concrete aggregate and reclaimed asphalt pavement. Eng. Geol. 161, 44–54. doi:10.1016/j.enggeo.2013.04.008

CrossRef Full Text | Google Scholar

Rahardjo, H., Kim, Y., and Satyanaga, A. (2019a). Role of unsaturated soil mechanics in geotechnical engineering. Int. J. Geo-Engineering 10 (1), 8. doi:10.1186/s40703-019-0104-8

CrossRef Full Text | Google Scholar

Rahardjo, H., Satyanaga, A., Mohamed, H., Yee Ip, S. C., and Shah, R. S. (2019b). Comparison of soil–water characteristic curves from conventional testing and combination of small-scale centrifuge and dew point methods. Geotechnical Geol. Eng. 37 (2), 659–672. doi:10.1007/s10706-018-0636-2

CrossRef Full Text | Google Scholar

Rahayu, W., Ramadhan, R. I., Adinegara, A. W., Adiguna, G. A., Hamdany, A. H., Wijaya, M., et al. (2024). Effect of slope protection using concrete waste on slope stability during rainfall. Results Eng. 24, 103244. doi:10.1016/j.rineng.2024.103244

CrossRef Full Text | Google Scholar

Rotz, R. (2021). Hydrogeologic properties of Earth materials and principles of groundwater flow. Groundwater 59, 320–321. doi:10.1111/gwat.13085

CrossRef Full Text | Google Scholar

Satyanaga, A., Rahardjo, H., and Zhai, Q. (2017). Estimation of unimodal water characteristic curve for gap-graded soil. Soils Found. 57 (5), 789–801. doi:10.1016/j.sandf.2017.08.009

CrossRef Full Text | Google Scholar

Wijaya, M., Lim, A., Rahardjo, P. P., Satyanaga, A., Hamdany, A. H., and Adiguna, G. A. (2024). Determination of soil–water characteristic curves by using a polymer tensiometer. J. Mech. Behav. Mater., 33, 20240007(1). doi:10.1515/jmbm-2024-0007

CrossRef Full Text | Google Scholar

Yao, Y., Ni, J., and Li, J. (2021). Stress-dependent water retention of granite residual soil and its implications for ground settlement. Comput. Geotechnics 129, 103835. doi:10.1016/j.compgeo.2020.103835

CrossRef Full Text | Google Scholar

Zhang, F., Wilson, G. W., and Fredlund, D. G. (2017). Permeability function for oil sands tailings undergoing volume change during drying. Can. Geotechnical J. 55 (2), 191–207. doi:10.1139/cgj-2016-0486

CrossRef Full Text | Google Scholar

Zhang, Y., Li, H., Abdelhady, A., and Yang, J. (2020). Comparative laboratory measurement of pervious concrete permeability using constant-head and falling-head permeameter methods. Constr. Build. Mater. 263, 120614. doi:10.1016/j.conbuildmat.2020.120614

CrossRef Full Text | Google Scholar

Zhou, W.-H., Yuen, K.-V., and Tan, F. (2014). Estimation of soil–water characteristic curve and relative permeability for granular soils with different initial dry densities. Eng. Geol. 179 (0), 1–9. doi:10.1016/j.enggeo.2014.06.013

CrossRef Full Text | Google Scholar