- 1School of Mathematics and Data Science, Shaanxi University of Science and Technology, Xi’an, China
- 2State Key Laboratory for Strength and Vibration, Xi’an Jiaotong University, Xi’an, China
Collective behavior is among the most fascinating complex dynamics in coupled networks with applications in various fields. Recent works have shown that higher-order interactions widely exist in complex systems. Both positive couplings among nodes, as the majority of studies have assumed, and negative couplings are very common in real-world systems, like physiological networks. Positive coupling (excitatory coupling) promotes synchronization and drives excitatory synaptic transmission between neurons. Meanwhile, negative coupling (inhibitory coupling) inhibits synchronization and sustains inhibitory synaptic transmission between neurons. Since high-order coupling patterns and different coupling patterns strongly affect the synchronous performance of complex systems, this article develops a globally coupled higher-order oscillatory system model that incorporates both positive and negative couplings. It is shown that, in the case of positive couplings, a second-order interaction has a negligible impact on the synchronization capability of a network within a certain range. In contrast, a higher-order network with purely negative couplings exhibits asynchronous states for any values of the second-order interactions. However, the synchronous region gradually shrinks with the increase of the negative coupling in the case of mixed couplings. This indicates a prominent role of coupling patterns on the onset of globally higher-order network synchronization.
1 Introduction
Both power networks and neuronal networks featuring synaptic plasticity describe real-world complex systems of critical importance in modern times (Parshani and Stanley, 2011). The majority of our infrastructure and activities crucially depend on a reliable supply of electric power. Hence, various real-world networks have been successfully modeled as coupled dynamical systems with many interacting units. In general, complex dynamic networks can be regarded as ensembles of nodes with various dynamics connected by links, where the connections denote pairwise interactions (Grzybowski et al., 2016; Gomes-Gardenes et al., 2007; Fan et al., 2018). The majority of previous studies have focused on analyzing networks with pairwise interactions, thereby neglecting the higher-order interactions that can exist between these networks. Indeed, pairwise interactions fall short when describing any realistic process responses and fail to describe practical situations.
Researchers have developed a general method for analyzing the attribution of symmetry breaking. Their findings give the first demonstration of symmetry breaking in power grids (Nishikawa and Motter, 2021). Instead, higher-order interactions among nodes have been discussed in the context of the characteristics of complex system structures and dynamics. Specifically, higher-order interactions (Battiston et al., 2020; Boccaletti et al., 2023) contain hypergraphs and simplicial complexes (Zhang et al, 2023; Xu et al., 2021). Recent studies have revealed that the presence of higher-order interactions plays a significant role in the dynamics of networked systems (Dai et al., 2021; Bairey et al., 2016; Zhang et al., 2023; Skardal and Arenas, 2020a). The higher-order interaction plays a critical role in shaping complex systems and their collective behaviors. It is well known that the performance of the dynamic behavior of networks has been significantly influenced by coupling patterns (Gambuzza et al., 2021; Tlaie et al., 2019). In recent years, some efforts have been devoted to studying the dynamic behaviors of complex networks with higher-order structures because of this special characteristic being more accurate while analyzing dynamic behaviors for real-world complex networks (Estrada and Ross, 2018; Battiston et al., 2020; Grilli et al., 2017; Benson et al., 2016; Witthaut et al., 2016).
Researchers have also investigated the optimization of collective behavior in networks with higher-order interactions encoded in clique complexes. This work demonstrates that strengthening higher-order couplings enhances collective behavior and broadens the range of possible dynamics, with an ideal balance between pairwise and higher-order interactions yielding the strongest collective behavior (Skardal et al., 2021). In particular, synchronous behavior is a phenomenon appearing in many real complex systems. The majority of systems exhibit striking similarities in their behavior when passing from a disordered to an ordered state. Many researchers have investigated the relationship between coupling patterns and synchronized states. Self-organized synchronization in physiological networks can potentially lead to epilepsy, cardiac arrhythmias, or immune dysregulation. Gaining a deeper understanding of these synchronization mechanisms offers targets for disease intervention strategies. Kuramoto oscillators describe phase synchronization and are applicable to the study of the rhythmic coordination within neuronal populations. Authors investigated the dynamics of Kuramoto oscillators with higher-order structures and found the emergence of explosive synchronization (Rodrigues et al., 2016). Fatemeh et al. (2022) studied the effects of pairwise and three-body interactions on the emergence of synchronization in Hindmarsh–Rose neurons. Their results indicated that the overall synchronization cost is reduced due to the introduction of three-body interactions. Additionally, Skardal and Arenas studied the dynamics of phase oscillators with higher-order interactions. They found that the higher-order structure may cause self-organized features and achieve synchronization of the overall system (Skardal and Arenas, 2020a).
Power systems are one of the most critical infrastructures in the real world. These systems can be modeled as complex networks that contain generations, electricity consumers, and transmission lines (Schäfer et al., 2018; Yang et al., 2023; Mandal and Banerjee, 2016; Witthaut et al., 2022). All of these components are linked by various interactions. The majority of existing results focused only on power systems with single connectivity, which does not take into account the effects of higher-order structures in the real power system. In fact, there exist pairwise and higher-order interactions among elements simultaneously. However, the crucial role of higher-order structures is still unclear in the coupled oscillatory power systems. Hence, it is necessary to investigate the relationship between higher-order structures and complex dynamics in power systems.
The second-order swing equation provides a standard dynamical model of the power system (Filatrella et al., 2008). This model has stimulated further studies in the field of power systems (Berner et al., 2021; Frasca and Gambuzza, 2021; Nauck et al., 2022). For instance, Berner, Yanchuk, and Schöll offered profound insights into the fundamental relationship between power grid networks and neuronal networks. Their findings proved that phase oscillator models with inertia were applicable to more general categories of power grid models. Moreover, they uncovered a plethora of multicluster states for phase oscillators with inertia (Berner et al., 2021). León et al. (2024) studied a globally coupled identical oscillator model, revealing the important role of higher-order interactions in synchronization transitions and multistability by introducing a three-body interaction with a phase lag. Particularly, when the coupling strength or phase lag varies, the system exhibits different synchronized, incoherent, and two-cluster states. Higher-order structures are ubiquitous in such networks and profoundly influence their dynamic behaviors.
Synchronization is among the most important collective behaviors in coupled oscillatory systems. In 1977, Hermann Haken investigated how biological networks spontaneously organize into ordered structures through the collective interactions of subsystems. His work demonstrated that even disordered systems can transition to a state of coherence via order parameters, which dominate the macroscopic behavior of the networks. This framework has become foundational for modeling networks in neuroscience and power systems (Haken, 1977). Most importantly, this behavior plays a vital role in the reliable operation process of power systems (Rohden et al., 2012; Menck et al., 2014; Schäfer et al., 2015). The robust operation of a power system relates to the synchronization of all elements from the perspective of a complex network. Therefore, due to the importance of synchronization emergence in real-world complex networks, many researchers have been motivated to study the mathematical aspects of synchronization and its influential factors. For example, Wilson et al. (2018) discussed the synchronous behavior of coupled oscillators with weak and strong coupling. They derived the expression of upper bounds on the critical coupling strength of networks under different perturbations and predicted synchronization using graph theoretical techniques. Taher H. et al. investigate the synchronization and stability of power grids using the Kuramoto model with inertia, focusing on time-delayed feedback control strategies to achieve synchronization and Lyapunov stability across different network configurations and models (Taher et al., 2019). Costa et al. (2024) combined external periodic forcing and higher-order interactions in the Kuramoto model, revealing a rich bifurcation scenario that produced 11 distinct asymptotic states and demonstrated the competition between forced and spontaneous synchronization. The dynamics of coupled oscillator networks with higher-order interactions and their ability to store information have been studied in recent works. For instance, Skardal and Arenas (2020b) propose a stability criterion to identify stable states in such systems while also exploring how these systems switch between stable states under random perturbations. In an extension of the Kuramoto model, Xu and Skardal (2021) explore three-way simplicial interactions, revealing novel dynamical properties such as clustering, multistability, and abrupt desynchronization transitions, while providing a rigorous spectral analysis of the stability of multicluster states in the thermodynamic limit. Additionally, researchers have demonstrated that phase frustration in networks of phase-frustrated coupled oscillators with higher-order interactions can unexpectedly promote explosive synchronization, a result explained through a low-dimensional model and bifurcation analysis (Dutta et al., 2023).
Later, researchers investigated synchronization of Kuramoto oscillators for power grids with general connectivity and damping (Choi and Li, 2019). Results are given as an estimate for a synchronous basin in a power system with general damping. Tang et al. investigated synchronous performance in a multilayer network. They proposed an approximation method of enhancing the predictive power for stable synchronization in multilayer networks (Tang et al., 2022). In 2023, Chen et al. revealed that the power system has higher-order connectivity features and studied the influence of topology structure on stability and construction cost (Liu et al., 2023). As power grids become more complex due to renewable energy integration and large-scale expansions, maintaining synchronization and preventing cascading failures are major challenges. Totz et al. (2020) introduced a two-layer control scheme for power grids, where the first layer represents the grid itself and the second layer manages frequency synchronization. Their study shows that a control strategy minimizing frequency differences between nodes can effectively handle various perturbations. Olmi et al. (2024) expanded on this by proposing a multilayer network control system to address node failures and cascading line failures. Their study of an Italian high-voltage grid demonstrates that distributed proportional and integral control laws can stabilize the grid even under extreme conditions. Schäfer et al. (2022) explored Braess’ paradox in power grids, showing that adding transmission lines can sometimes reduce system performance and cause blackouts. Their work emphasizes the importance of considering network topology when expanding grid capacity.
Despite many theoretical advances, little attention has so far been given to the performance of higher-order power systems with multiple coupling patterns. In reality, coupled oscillators are subjected to a mixture of both positive and negative couplings. From an energy perspective, multiple couplings are more beneficial for power transmission. Therefore, it is of great interest to study the collective dynamics of real-world networks with multiple coupling types, as this interaction substantially impacts the system’s critical phenomena.
In light of these concerns, this article addresses the scenario in which positive and negative interactions coexist in a high-order power system. Moreover, we further analyze the complex behaviors of the proposed model. Specifically, the synchronous solution is derived through theoretical analysis, and the influence of higher-order structures on synchronous stability is discussed.
The remainder of this article is organized as follows. First, we present a globally coupled higher-order oscillatory power system model with mixed coupling types in Section II. Then, in Section III, stability analysis for the condition of the synchronous solutions of a globally coupled higher-order oscillatory network system is investigated. In Section IV, we test our theory on higher-order coupled networks and perform numerical simulations to analyze the influence of coupling patterns. Section V concludes the article.
2 Mathematical model
To study the dynamics of a power system with coupled oscillators, we assume that the oscillators evolve through first- and second-order interactions. Then, the general mathematical model can be described by the following Equation 1:
where
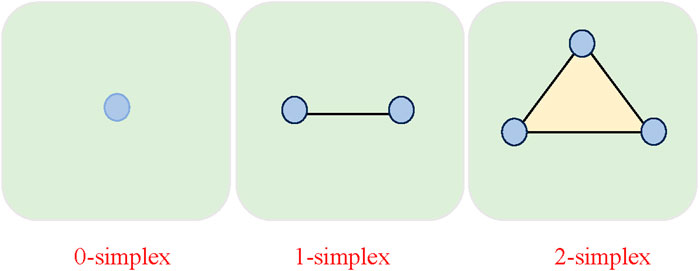
Figure 1. The building blocks of the higher-order interactions consist of nodes (0-simplices), edges (1-simplices), and triangles (2-simplices).
Therefore, the values of
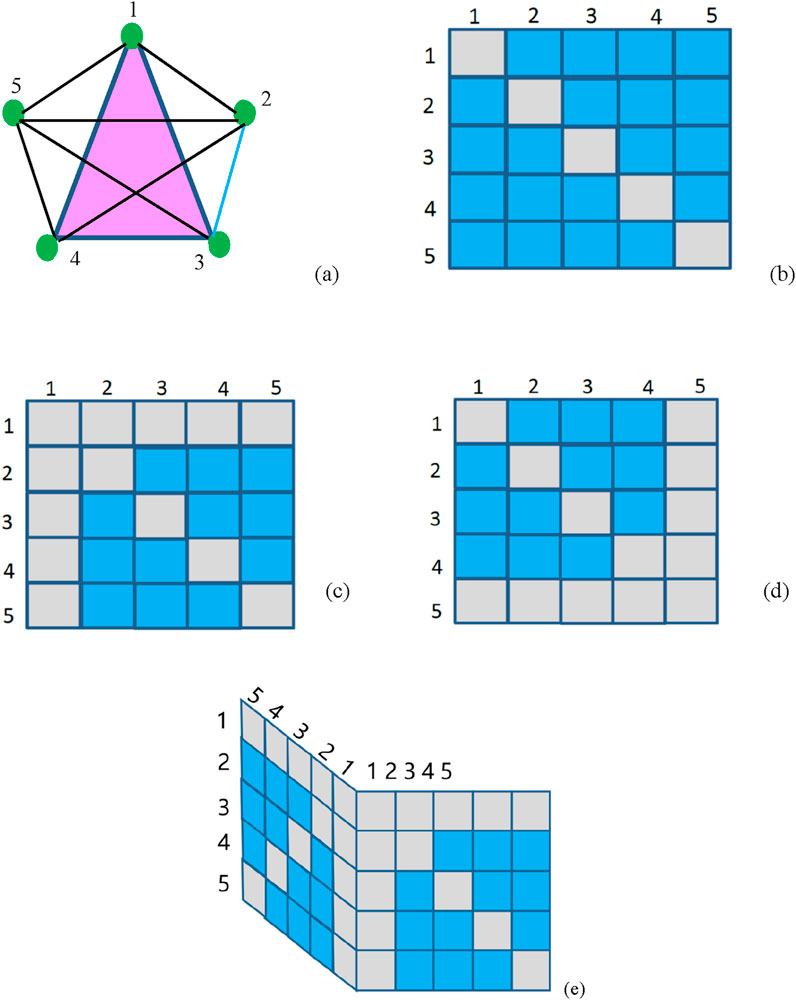
Figure 2. (a) Schematic illustration of a five-node network with global coupling. A first-order (blue) and a second-order (triangle) of the network are described by blue and pink colors as an example. (b) The corresponding adjacency matrix
As we know, the Kuramoto-like model (Rodrigues et al., 2016; Acebrón et al., 2005) is regarded as a standard reduced model that characterizes the collective phenomena, which is of great interest in power systems. Before proceeding, we represent the power system as a network of generators and consumers connected by transmission lines. The starting point of our analysis is coupled second-order oscillators:
for
In what follows, we focus on a higher-order coupled power system with mixed coupling patterns. First, the synchronous stability of the power system is studied for first- and second-order coupling strengths. Here, we focus on the first-order interaction of the oscillator is diffusive, that is
For simplicity, we neglect Ohmic effects and assume that the oscillators have the same dissipative coefficients and the same moments of inertia. Under these approximations, we rewrite Equation 2 in the form of a dynamical system of first-order ordinary differential equations (ODEs) and consider a second-order connection:
To measure the synchronization transition of the power system, the following complex order parameter is introduced (see Equation 4):
which is considered the average sum of the unit vectors associated with the phases of each oscillator in the complex plane. Here, the modulus of the resulting complex number is the order parameter, given by Equation 5
In this way,
3 Stability analysis of synchronous solutions
In this section, we aim to derive the synchronous solution of a power system with high-order interactions. The corresponding synchronized solution is
According to Equation 3, one can obtain Equation 6
It is found that variables
So Equation 7 becomes
Suppose that
Afterwards, the value of the parameter
Because the power system is symmetric, we can then obtain Equation 11.
Subsequently, Equation 10 can be rewritten as Equation 12.
where
In the following, to assess the linear stability of the synchronization, the linear stability analysis is developed on a general network model with the first- and second-order interactions by considering a small perturbation to the synchronous manifold
where
Moreover, we have that
Here, a tensor
According to the above definition, Equation 15 can be rewritten as
Based on the symmetric of the tensor T, Equation 17 becomes Equation 18
where
Matrix K is the diagonal matrix with the degree of the nodes, and
Let us rewrite Equation 18 in block form by introducing the stack vector
We assume that the eigenvectors of the classic Laplacian matrix
The following equations can be derived:
where
Thus, the stability of the coupled oscillators can be reduced by solving Equation (24) and calculate the maximum transverse Lyapunov exponents. We note that the necessary condition for the stability of a synchronous solution requires that the maximum transverse Lyapunov exponents be negative.
4 Numerical simulations
In this section, numerical simulations are performed under different types of interactions coexisting within the same system to better understand the dynamics that emerge in the higher-order power system above. Here, we take Figure 1 as an example. In this work, we address the scenario of a network with first-order and second-order interactions. In each of the following cases, the maximum Lyapunov exponents of the linearized equation for
4.1 Purely positive interconnections
For the sake of illustration, we start BY considering the case of purely positive coupling,
According to Figure 3, we find that with increasing
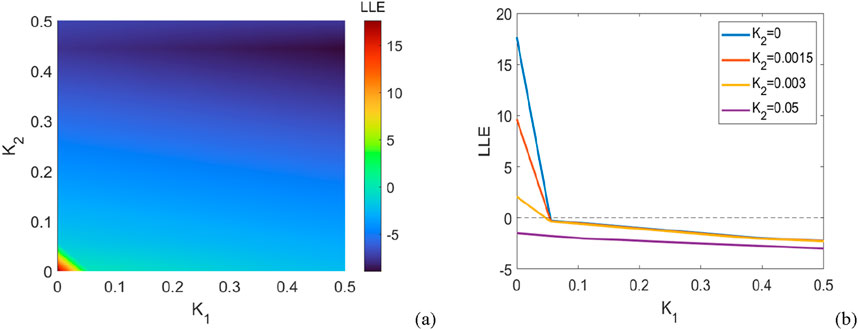
Figure 3. System parameters: number of oscillators, showing the regions of synchronous and asynchronous states for coupled oscillators with purely positive couplings. (a) The maximum Lyapunov exponent of the linearized Equation 23 in the parameter plane
4.2 Purely negative interconnections
Then, we restrict our attention to the case of purely negative couplings,
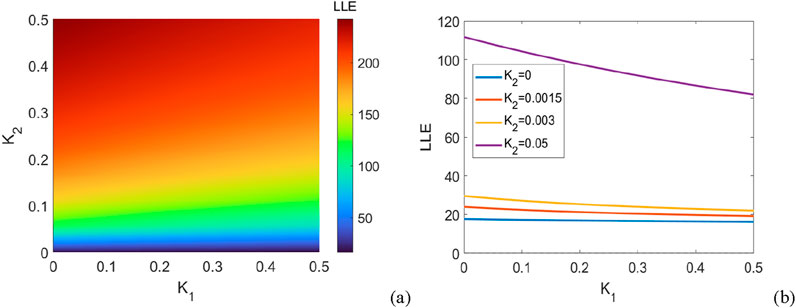
Figure 4. The system consists of
From Figure 4, first, it can be observed that in the absence of second-order interactions (
Figure 5 also shows the evolution of the order parameter for the entire network under different coupling types. Here, for simplicity, we assume the coupling strengths of the first-, second-, and higher-order couplings are equal; thus, the parameter
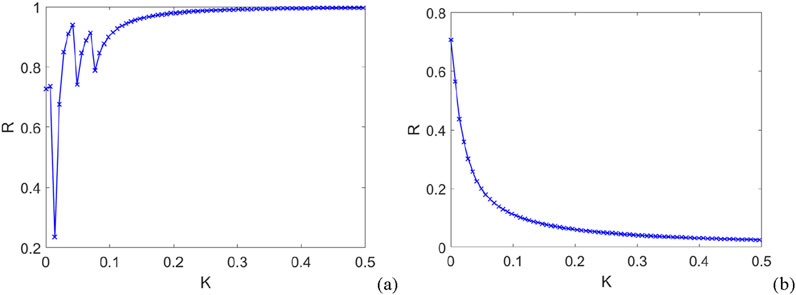
Figure 5. The evolution curves of the order parameter of a high-order oscillatory network with different coupling patterns. (a) purely positive coupling; (b) purely negative coupling.
4.3 Mixed positive and negative couplings
Here, we consider cases in which interactions can be either positive or negative. Figures 6a–f show the regions of synchronous and asynchronous states for coupled oscillators with mixed positive and negative couplings. It can be found that for a small
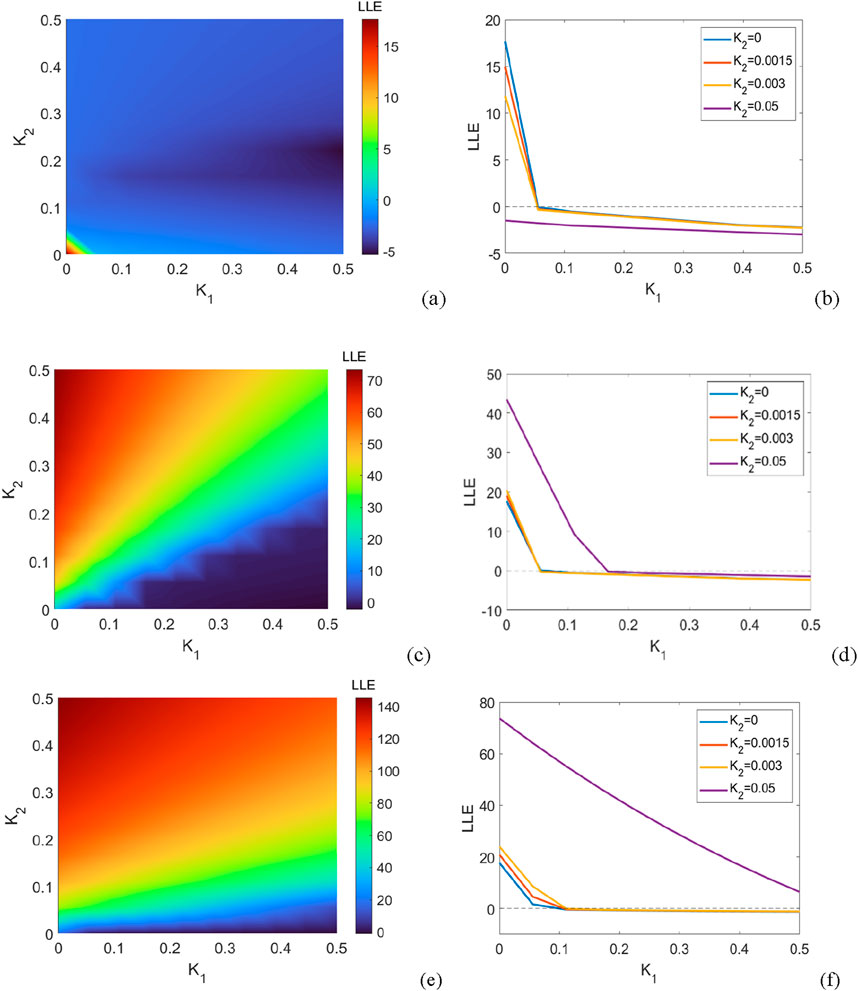
Figure 6. The regions of synchronous and asynchronous states for coupled oscillators with mixed negative and positive couplings. (a,b)
Based on the numerical results presented in Figure 6, when second-order interactions are taken into account, purely positive couplings lead to a synchronous state, while purely negative couplings can impede synchronization. Additionally, both the coupling strength and the ratio of the two types of couplings jointly shape the collective behaviors of the oscillatory network. It is important to note that the above-mentioned phenomena are derived from the global coupling of all oscillators. In other words, these numerical results are in line with those of conventional networks with either purely positive or purely negative couplings. Consequently, in small-scale oscillatory power systems, the impact of second-order interactions on the synchronous state is restricted.
The results presented above allow us to reach several conclusions about how different coupling patterns affect the synchronous stability of higher-order coupled oscillatory networks. In particular, we note that these networks are restricted to hybrid coupling types, which include binary interactions and higher-order interactions among the units. Finally, we explore the relationship between synchronizability and the coupling patterns in globally coupled networks. Here, we assume that all the couplings are positive. In what follows, simulation results are presented to illustrate the impact of first- and second-order interactions on synchronous performance.
A smaller value of the maximum Lyapunov exponent implies better synchronizability; that is, a smaller coupling strength is required to realize synchronization. Here, we examine a network of 10 nodes consisting of all-to-all coupled oscillators. We estimate the synchronizability by measuring the maximum Lyapunov exponent, taking into account both pairwise and second-order interactions. Figure 7 displays the differences in the stability of the coupled network under different coupling patterns.
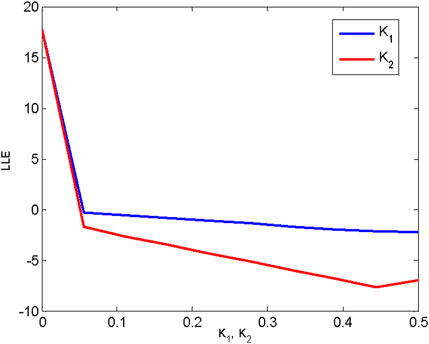
Figure 7. The maximum Lyapunov exponent of all-to-all coupled oscillators under different interaction patterns.
Figure 7 shows that a coupled network with fully second-order interactions exhibits better synchronizability than the case of first-order interactions. That is, second-order interactions enhance synchronization with respect to first-order interactions.
5 Conclusion
High-order networks are a powerful framework for characterizing real-world complex systems. Taking into account second-order interactions, we explore the synchronous performance of a globally higher-order network and derive the synchronous solutions of the model. In contrast to previous oscillatory models where nodes typically had uniform coupling patterns, in our model, the coupled oscillators interact according to a common pattern, which can be either positive or negative. According to the presented model, we analyze the impact of higher-order interactions on synchronous performance under different circumstances. Our findings disclose that the synchronization capability of a network with purely positive couplings is not influenced by the second-order interactions. However, the network with purely negative coupling exhibits asynchronous states for any different values of second-order interactions. In addition, with the increase of the negative coupling, the region of synchrony gradually diminishes. In summary, the coupling pattern plays a crucial role in shaping collective dynamics within globally higher-order networks. Especially for physiological networks, collective behaviors are crucial for maintaining vital life functions such as heartbeat, respiration, and cognition. The research not only reveals the principles of the robustness of living systems but also provides theoretical support for the treatment of diseases and the design of bionic systems.
Consequently, the proposed network model, along with the synchronous analysis, offers valuable perspectives for the design of more resilient real-world systems. As future work, we intend to integrate real-world data with the topological structures of networks featuring higher-order interactions to explore complex dynamic behaviors.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
LY: formal analysis, methodology, and writing – original draft. ML: software and writing – review and editing. JJ: writing – review and editing, funding acquisition, supervision, and validation.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by the National Natural Science Foundation of China (NSFC) under grants No. 12172267 and 11702195.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fnetp.2025.1582297/full#supplementary-material
References
Acebrón, J. A., Bonilla, L. L., Pérez Vicente, C. J., Ritort, F., and Spigler, R. (2005). The Kuramoto model: a simple paradigm for synchronization phenomena. Rev. Mod. Phys. 77, 137–185. doi:10.1103/RevModPhys.77.137
Bairey, E., Kelsic, E. D., and Kishony, R. (2016). High-order species interactions shape ecosystem diversity. Nat. Commun. 7, 12285. doi:10.1038/ncomms12285
Battiston, F., Cencetti, G., Iacopini, I., Latora, V., Lucas, M., Patania, A., et al. (2020). Networks beyond pairwise interactions: structure and dynamics. Phys. Rep. 874, 1–92. doi:10.1016/j.physrep.2020.05.004
Benson, A. R., Gleich, D. F., and Leskovec, J. (2016). Higher-order organization of complex networks. Science 353, 163–166. doi:10.1126/science.aad9029
Berner, R., Yanchuk, S., and Schöll, E. (2021). What adaptive neuronal networks teach us about power grids. Phys. Rev. E 103, 042315. doi:10.1103/PhysRevE.103.042315
Boccaletti, S., De Lellis, P., Del Genio, C. I., Alfaro-Bittner, K., Criado, R., Jalan, S., et al. (2023). The structure and dynamics of networks with higher order interactions. Phys. Rep. 1018, 1–64. doi:10.1016/j.physrep.2023.04.002
Choi, Y. P., and Li, Z. C. (2019). Synchronization of nonuniform Kuramoto oscillators for power grids with general connectivity and dampings. Nonlinearity 32, 559–583. doi:10.1088/1361-6544/aaec94
Costa, G. S., Novaes, M., and de Aguiar, M. A. (2024). Bifurcations in the Kuramoto model with external forcing and higher-order interactions. Chaos 34, 123133. doi:10.1063/5.0239011
Dai, X., Kovalenko, K., Molodyk, M., Wang, Z., Li, X., Musatov, D., et al. (2021). D-dimensional oscillators in simplicial structures: odd and even dimensions display different synchronization scenarios. Chaos Solit. Fractals 146, 110888. doi:10.1016/j.chaos.2021.110888
Dutta, S., Mondal, A., Kundu, P., Khanra, P., Pal, P., and Hens, C. (2023). Impact of phase lag on synchronization in frustrated Kuramoto model with higher-order interactions. Phys. Rev. E 108, 034208. doi:10.1103/PhysRevE.108.034208
Estrada, E., and Ross, G. J. (2018). Centralities in simplicial complexes. Applications to protein interaction networks. J. Theor. Biol. 438, 46–60. doi:10.1016/j.jtbi.2017.11.003
Fan, C., Huang, J., Rong, Z., and Zhou, T. (2018). Coupling diversity across human behavior spaces. Europhys. Lett. 124, 48001. doi:10.1209/0295-5075/124/48001
Fatemeh, P., Mahtab, M., Karthikeyan, R., Jafari, S., and Perc, M. (2022). Synchronization in Hindmarsh–Rose neurons subject to higher-order interactions. Chaos 32, 013125. doi:10.1063/5.0079834
Filatrella, G., Nielsen, A. H., and Pedersen, N. F. (2008). Analysis of a power grid using a Kuramoto-like model. Eur. Phys. J. Condensed Matter Complex Syst. 61, 485–491. doi:10.1140/epjb/e2008-00098-8
Frasca, M., and Gambuzza, L. V. (2021). Control of cascading failures in dynamical models of power grids. Chaos, Solit. Fractals 153, 111460. doi:10.1016/j.chaos.2021.111460
Gambuzza, L. V., Di Patti, F., Gallo, L., Lepri, S., Romance, M., Criado, R., et al. (2021). Stability of synchronization in simplicial complexes. Nat. Commun. 12, 1255. doi:10.1038/s41467-021-21486-9
Gomes-Gardenes, J., Moreno, Y., and Arenas, A. (2007). Paths to synchronization on complex networks. Phys. Rev. Lett. 98, 034101. doi:10.1103/PhysRevLett.98.034101
Grilli, J., Barabás, G., Michalska-Smith, M. J., and Allesina, andS. (2017). Higher-order interactions stabilize dynamics in competitive network models. Nature 548, 210–213. doi:10.1038/nature23273
Grzybowski, J. M. V., Macau, E. E. N., and Yoneyama, T. (2016). On synchronization in power-grids modelled as networks of second-order Kuramoto oscillators. Chaos 26, 113113. doi:10.1063/1.4967850
Haken, H. (1977). Synergetics: an Introduction: nonequilibrium phase transitions and self-organization in physics, chemistry, and biology. Berlin, Heidelberg: Springer-Verlag. doi:10.1007/978-3-642-88338-5
León, I., Muolo, R., Hat, S., and Nakao, H. (2024). Higher-order interactions induce anomalous transitions to synchrony. Chaos 34, 1. doi:10.1063/5.0176748
Liu, H., Chen, X., Huo, L., and Niu, C. (2023). Power network uniqueness and synchronization stability from a higher-order structure perspective. Phys. D. 443, 133557. doi:10.1016/j.physd.2022.133557
Mandal, K., and Banerjee, S. (2016). Synchronization phenomena in interconnected power electronic systems. IEEE Trans. Circuits Syst. II, Exp. Briefs 63, 221–225. doi:10.1109/TCSII.2015.2498299
Menck, P. J., Heitzig, J., Kurths, J., and Joachim Schellnhuber, H. (2014). How dead ends undermine power grid stability. Nat. Commun. 5, 3969. doi:10.1038/ncomms4969
Nauck, C., Lindner, M., Schürholt, K., Zhang, H., Schultz, P., Kurths, J., et al. (2022). Predicting basin stability of power grids using graph neural networks. New J. Phys. 24, 043041. doi:10.1088/1367-2630/ac54c9
Nishikawa, F. M. T., and Motter, A. E. (2021). Asymmetry underlies stability in power grids. Nat. Commun. 12, 1457. doi:10.1038/s41467-021-21290-5
Olmi, S., Gambuzza, L. V., and Frasca, M. (2024). Multilayer control of synchronization and cascading failures in power grids. Chaos, Solit. and Fractals 180, 114412. doi:10.1016/j.chaos.2023.114412
Parshani, R., and Stanley, H. E. (2011). Critical effect of dependency groups on the function of networks. Proc. Natl. Acad. Sci. U.S.A. 108, 3. doi:10.1073/pnas.1008404108
Rodrigues, F. A., Peron, T. K. D., Ji, P., and Kurths, J. (2016). The Kuramoto model in complex networks. Phys. Rep. 610, 1–98. doi:10.1016/j.physrep.2015.10.008
Rohden, M., Sorge, A., Timme, M., and Witthaut, D. (2012). Self-organized synchronization in decentralized power grids. Phys. Rev. Lett. 109, 064101. doi:10.1103/PhysRevLett.109.064101
Schäfer, B., Matthiae, M., Timme, M., and Witthaut, D. (2015). Decentral smart grid control. New J. Phys. 17, 015002. doi:10.1088/1367-2630/17/1/015002
Schäfer, B., Pesch, T., Manik, D., Gollenstede, J., Lin, G., Beck, H. P., et al. (2022). Understanding braess' paradox in power grids. Nat. Commun. 13, 5396. doi:10.1038/s41467-022-32917-6
Schäfer, B., Witthaut, D., Timme, M., and Latora, V. (2018). Dynamically induced cascading failures in power grids. Nat. Commun. 9, 1975. doi:10.1038/s41467-018-04287-5
Skardal, P. S., and Arenas, A. (2020a). Higher order interactions in complex networks of phase oscillators promote abrupt synchronization switching. Commun. Phys. 3, 218. doi:10.1038/s42005-020-00485-0
Skardal, P. S., and Arenas, A. (2020b). Memory selection and information switching in oscillator networks with higher-order interactions. J. Phys. Complex. 2, 015003. doi:10.1088/2632-072X/abbd4c
Skardal, P. S., Arola-Fernández, L., and Taylor, D. (2021). Higher-order interactions can better optimize network synchronization. Phys. Rev. Res. 3, 043193. doi:10.1103/PhysRevResearch.3.043193
Taher, H., Olmi, H. S., and Schöll, E. (2019). Enhancing power grid synchronization and stability through time-delayed feedback control. Phys. Rev. E 100, 062306. doi:10.1103/PhysRevE.100.062306
Tang, L. K., Smith, K., Daley, K., and Belykh, I. (2022). When multilayer links exchange their roles in synchronization. Phys. Rev. E 106, 024214. doi:10.1103/PhysRevE.106.024214
Tlaie, A., Leyva, I., and Sendiña-Nadal, I. (2019). High-order couplings in geometric complex networks of neurons. Phys. Rev. E 100, 052305. doi:10.1103/PhysRevE.100.052305
Totz, C. H., Olmi, S., and Schöll, E. (2020). Control of synchronization in two-layer power grids. Phys. Rev. E 102, 022311. doi:10.1103/PhysRevE.102.022311
Wilson, D., Faramarzi, S., Moehlis, J., Tinsley, M. R., and Showalter, K. (2018). Synchronization of heterogeneous oscillator populations in response to weak and strong coupling. Chaos 28, 123114. doi:10.1063/1.5049475
Witthaut, D., Kurths, J., Kettemann, S., Meyer-Ortmanns, H., Timme, M., and Kurths, F. (2022). Collective nonlinear dynamics and self-organization in decentralized power grids. Rev. Mod. Phys. 94, 015005. doi:10.1103/RevModPhys.94.015005
Witthaut, D., Rohden, M., Zhang, X., Hallerberg, S., and Timme, M. (2016). Critical links and nonlocal rerouting in complex supply networks. Rev. Lett. 116, 138701. doi:10.1103/PhysRevLett.116.138701
Xu, C., and Skardal, P. S. (2021). Spectrum of extensive multiclusters in the Kuramoto model with higher-order interactions. Phys. Rev. Res. 3, 013013. doi:10.1103/PhysRevResearch.3.013013
Xu, C., Wang, X., Zheng, Z. G., and Cai, Z. (2021). Stability and bifurcation of collective dynamics in phase oscillator populations with general coupling. Phys. Rev. E 103, 032307. doi:10.1103/PhysRevE.103.032307
Yang, L. X., Dang, Y. C., He, P. Y., and Jiang, J. (2023). Exploring the effect of voltage amplitude and phase difference on resilient ability for power network with third-order model. Int. J. Electr. Power Energy Syst. 150, 109109. doi:10.1016/j.ijepes.2023.109109
Keywords: complex network, higher-order interactions, network physiology, synchronous behavior, coupling patterns
Citation: Yang L, Li M and Jiang J (2025) Collective behavior of higher-order globally coupled oscillatory networks in response to positive and negative couplings. Front. Netw. Physiol. 5:1582297. doi: 10.3389/fnetp.2025.1582297
Received: 24 February 2025; Accepted: 19 June 2025;
Published: 22 July 2025.
Edited by:
Eckehard Schöll, Technical University of Berlin, GermanyReviewed by:
Yong Xu, Northwestern Polytechnical University, ChinaAnna Zakharova, Humboldt University of Berlin, Germany
Copyright © 2025 Yang, Li and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Jun Jiang, anVuLmppYW5nQHhqdHUuZWR1LmNu
 Lixin Yang
Lixin Yang Mengjiao Li
Mengjiao Li Jun Jiang
Jun Jiang