- 1 PMB Intelligence LLC, West Lafayette, IN, USA
- 2 State Key Laboratory of Non-linear Mechanics, Institute of Mechanics, Chinese Academy of Sciences, Beijing, China
- 3 Mechanical and Materials Engineering, Wright State University, Dayton, OH, USA
- 4 Affymetrix, Inc., Santa Clara, CA, USA
- 5 Department of Earth and Atmospheric Sciences, Purdue University, West Lafayette, IN, USA
- 6 Electrical Engineering, Wright State University, Dayton, OH, USA
Physiological signals often are highly non-stationary (i.e., mean and variance change with time) and multiscaled (i.e., dependent on the spatial or temporal interval lengths). They may exhibit different behaviors, such as non-linearity, sensitive dependence on small disturbances, long memory, and extreme variations. Such data have been accumulating in all areas of health sciences and rapid analysis can serve quality testing, physician assessment, and patient diagnosis. To support patient care, it is very desirable to characterize the different signal behaviors on a wide range of scales simultaneously. The Scale-Dependent Lyapunov Exponent (SDLE) is capable of such a fundamental task. In particular, SDLE can readily characterize all known types of signal data, including deterministic chaos, noisy chaos, random 1/fα processes, stochastic limit cycles, among others. SDLE also has some unique capabilities that are not shared by other methods, such as detecting fractal structures from non-stationary data and detecting intermittent chaos. In this article, we describe SDLE in such a way that it can be readily understood and implemented by non-mathematically oriented researchers, develop a SDLE-based consistent, unifying theory for the multiscale analysis, and demonstrate the power of SDLE on analysis of heart-rate variability (HRV) data to detect congestive heart failure and analysis of electroencephalography (EEG) data to detect seizures.
1. Introduction
Complex systems, such as physiological systems, usually are comprised of multiple subsystems that exhibit both highly non-linear deterministic, as well as, random characteristics, and are regulated hierarchically. These systems generate signals that exhibit complex characteristics such as sensitive dependence on small disturbances, long memory, extreme variations, and non-stationarity (i.e., mean and variance change with time). Examples of such signals in physiology are abundant (Bassingthwaighte et al., 1994). An example of heart-rate variability (HRV) data for a normal young subject (Physionet, 2011) is shown in Figure 1. Evidently, the signal is highly non-stationary and multiscaled (i.e., dependent on the spatial or temporal interval lengths), appearing oscillatory for some period of time (Figures 1B,D), and then varying as a 1/f process for another period of time (Figures 1C,E).
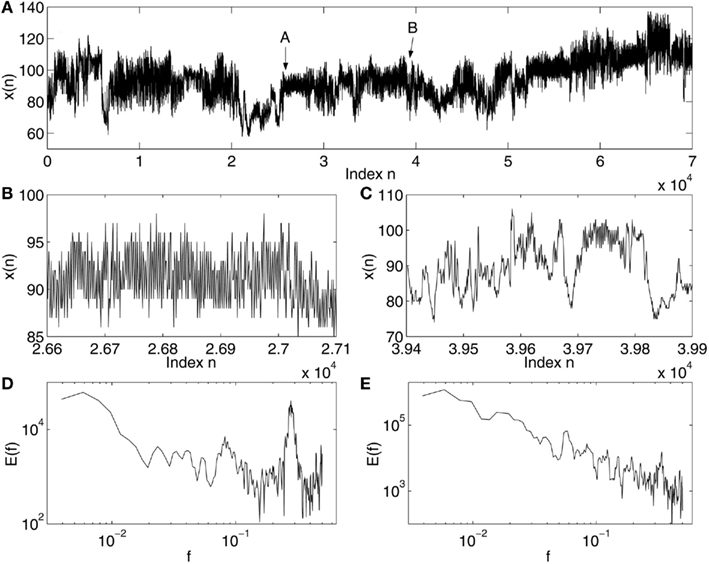
Figure 1. Non-stationarity in HRV data: (A) The HRV data for a normal subject; (B,C) the segments of signals indicated as A and B in (A); (D,E) power spectral density E(f) vs. frequency f for the signals shown in (B,C).
While the multiscale nature of signals such as shown in Figure 1 cannot be fully characterized by existing methods, the non-stationarity of the data is even more troublesome, because it prevents direct application of spectral analysis, or methods based on chaos theory and random fractal theory. For example, in order to reveal that the HRV data is of 1/f nature (Akselrod et al., 1981; Kobayashi and Musha, 1982) with anti-persistent long-range correlations (i.e., algebraically decaying autocorrelation function; Peng et al., 1993; Ashkenazy et al., 2001) and multifractality (i.e., multiple power-law behavior; Ivanov et al., 1999), time series such as shown in Figure 1A has to be pre-processed to remove components (such as the oscillatory ones) that do not conform to fractal scaling analysis. However, automated segmentation of complex biological signals to remove undesired components is a significant open problem, since it is closely related to the challenging task of accurately detecting transitions from normal to abnormal states in physiological data.
Rapid accumulation of complex data in all areas of natural and health sciences has made it increasingly important to be able to analyze multiscale and non-stationary data. Since multiscale signals behave differently, depending upon the temporal and spatial scale at which the data are examined, it is of fundamental importance to develop measures that explicitly incorporate the concept of scale so that different data behaviors on varying scales can be simultaneously characterized.
Straightforward multiscale analysis include short-time Fourier transform based time-frequency analysis, wavelet analysis (Strang and Nguyen, 1997; Mallat, 2008), and time-domain adaptive filtering (Gao et al., 2011b; Tung et al., 2011). Multiscale analysis can also be based on chaos theory and random fractal theory (Gao et al., 2007). In many instances, the latter two theories are more appealing, since measures from chaos or fractal theories can be associated with the complexity of the signal and the underlying physiological system, and thus can stimulate researchers to ask whether the complexity of the signal may change when certain pathology of the physiological system progresses, and if so, how. Indeed, they have been used extensively in physiology (Goldberger and West, 1987; Kaplan and Goldberger, 1991; Garfinkel et al., 1992; Peng et al., 1993; Bassingthwaighte et al., 1994; Fortrat et al., 1997; Ivanov et al., 1999; Kaneko and Tsuda, 2000; Ashkenazy et al., 2001; Gao et al., 2007, 2011b).
The key element of random fractal theory is scale-invariance, i.e., the statistical behavior of the signal is independent of a spatial or temporal interval length. With scale-invariance, only one or a few parameters are sufficient to describe the complexity of the signal across a wide range of scales where the fractal scaling laws hold. Because of the small number of parameters, fractal analyses are among the most parsimonious multiscale approaches. Chaos theory also provides a few multiscale approaches, including ε-entropy (Gaspard and Wang, 1993; where entropy is a way of measuring uncertainty), the finite size Lyapunov exponent (FSLE; Torcini et al., 1995; Aurell et al., 1996, 1997), multiscale entropy (MSE; Costa et al., 2005), and the scale-dependent Lyapunov exponent (SDLE; Gao et al., 2006b, 2007). FSLE and SDLE are in fact closely related – conceptually SDLE is partially inspired by FSLE. The algorithm for computing SDLE, which is derived from that for computing time-dependent exponent curves and will be defined shortly (Gao and Zheng, 1993, 1994a,b; Gao, 1997), is completely different from that for computing FSLE. This leads to a few important differences between FSLE and SDLE: (1) FSLE assumes the underlying dynamics to be divergent, and thus is positive; SDLE, however, is assumption-free, and therefore, can assume any value. Consequentially, SDLE possesses a unique scale separation property, i.e., different types of dynamics manifesting themselves on different scales. This allows SDLE to readily detect intermittent chaos and detect fractal structures from non-stationary signals, while FSLE does not. (2) It is much easier to analytically derive and numerically verify scaling laws for SDLE than for FSLE for various types of processes.
In this article, we aim to present SDLE in such a way that it can be readily understood and implemented by non-mathematically oriented researchers1. We shall focus on its capabilities that are not shared by other popular chaos or fractal analysis methods, such as detecting intermittent chaos, detecting fractal structures from non-stationary data, and characterizing fractal scaling laws for stochastic limit cycles. We shall also consider detection of epileptic seizures from electroencephalography (EEG) and certain cardiac disease from heart-rate variability (HRV) data, for the purposes of (1) shedding new light on the interpretation of complexity of physiological data, and (2) illustrating SDLE’s clinical relevance.
The remainder of the paper is organized as follows. In Section 2, we first define SDLE, then apply it to characterize low-dimensional chaos, noisy chaos, and random 1/fα processes, and show how SDLE can readily detect intermittent chaos and deal with non-stationarity. As real world applications, in Section 3, we apply SDLE to characterize EEG and HRV data for detecting epileptic seizures and certain cardiac disease. Finally, in Section 4, we make a few concluding remarks, including a discussion of best practices for experimental data analysis using the SDLE approach.
2. SDLE: Definitions and Fundamental Properties
Chaos theory is a mathematical analysis of irregular behaviors of complex systems generated by non-linear deterministic (i.e., future behavior described by the initial conditions) interactions of only a few degrees of freedom without concern of noise or intrinsic randomness. Random fractal theory, on the other hand, assumes that the dynamics of the system are inherently random. One of the most important classes of random fractals is 1/fα processes with long-range correlations, where 1 < α < 3. Therefore, the foundations of chaos theory and random fractal theory are entirely different. Consequentially, different conclusions may be drawn depending upon which theory is utilized to analyze a data set. In fact, much of the research in the past has been devoted to determining whether a complex time series is generated by a chaotic or a random system (Grassberger and Procaccia, 1983a,b; Wolf et al., 1985; Sugihara and May, 1990; Kaplan and Glass, 1992; Gao and Zheng, 1994a,b; Pei and Moss, 1996; Gaspard et al., 1998; Dettmann and Cohen, 2000; Poon and Barahona, 2001; Hu et al., 2005). From past research, 1/fα processes have distinguished themselves as providing counter examples that invalidate commonly used tests for chaos (Osborne and Provenzale, 1989; Provenzale and Osborne, 1991; Hu et al., 2005). In fact, the two research communities, one favoring chaos theory, the other random fractal theory, often assume two polar positions, either rarely communicating or constantly debating with each other as to the applicability of their theories2. While this classic issue, distinguishing chaos from noise, is still important, the authors believe that chaos and random fractal theories should be used synergistically in order to comprehensively characterize the behaviors of signals over a wide range of scales. Based on this belief, we aim to develop a complexity measure that cannot only effectively distinguish chaos from noise, but also aptly extract the crucial or the defining parameters of a process generating the data, be it chaotic or random. SDLE is a measure that has these capabilities.
SDLE stems from two important concepts, the time-dependent exponent curves (Gao and Zheng, 1993, 1994a,b; Gao, 1997) and the finite size Lyapunov exponent (Torcini et al., 1995; Aurell et al., 1996, 1997). SDLE was first introduced by (Gao et al., 2006b, 2007), and has been further developed in (Gao et al., 2009, in press) and applied to characterize EEG (Gao et al., 2011a), HRV (Hu et al., 2009a, 2010), Earth’s geodynamo (Ryan and Sarson, 2008), and non-autonomous Boolean chaos (Blakely et al., under review). To better understand SDLE, it is beneficial to consider an ensemble forecasting framework. An example is shown in Figure 2, where we observe that 2500 close by initial conditions rapidly evolve to fill the entire attractor. A fundamental question is, how do we characterize such evolutions?
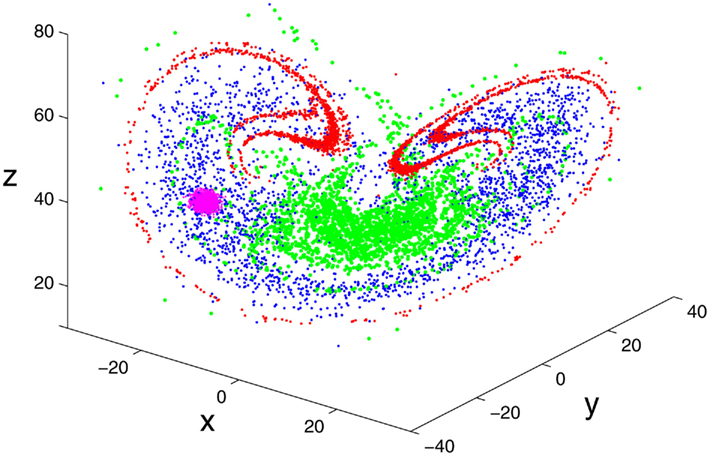
Figure 2. Error growth in the chaotic Lorenz system (Lorenz, 1963) illustrated using an ensemble forecasting framework, where 2500 initial conditions, initially represented by the pink color, evolve to those represented by the red, green, and blue colors at t = 2, 4, and 6 units.
SDLE is a concept derived from a high-dimensional phase space. Assume that all that is known is a scalar time series x[n] = x(1), x(2), …, x(n). How can we obtain a phase space? This can be achieved by the time delay embedding technique (Packard et al., 1980; Takens, 1981; Sauer et al., 1991). This technique is perhaps the most significant contribution of chaos theory to practical data analysis, since non-trivial dynamical systems usually involve many state variables, and therefore, have to be described by a high-dimensional state (or phase) space. The embedding technique consists of creating vectors of the form:
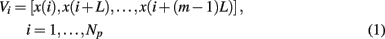
where Np = n − (m− 1)L is the total number of reconstructed vectors, and the embedding dimension m and the delay time L are chosen according to certain optimization criteria (Gao et al., 2007). Specifically, L alone may be determined by computing the first zero of the autocorrelation or the first minimal point of mutual information (Fraser and Swinney, 1986), while joint determination of m and L may be achieved using false nearest neighbor method (Liebert et al., 1991; Kennel et al., 1992), which is a static geometrical method, or time-dependent exponent method (Gao and Zheng, 1993, 1994b), which is a dynamical method. Note that when the time series is random, the embedding procedure transforms the self-affine (i.e., x and t have to be stretched differently in order to make the curve look “similar,” since the units for x and t are different) stochastic process into a self-similar (i.e., part of the curve in the high-dimensional space looks similar to another part or the whole when it is magnified or shrinked, since all the axes have the same unit) process in phase space. In this case, the specific value of m is not important, so long as m > 1.
After a proper phase space is re-constructed, we consider an ensemble of trajectories. We denote the initial separation between two nearby trajectories by ε0, and their average separation at time t and t + Δt by εt and εt + Δt, respectively. The trajectory separation is schematically shown in Figure 3. We can then examine the relation between εt and εt + Δt, where Δt is small. When Δt → 0, we have,
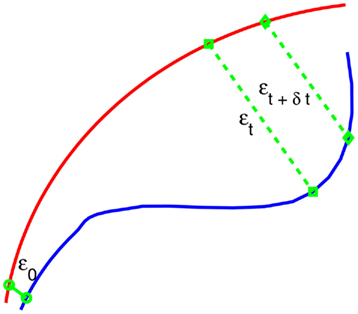
Figure 3. A schematic showing 2 arbitrary trajectories in a general high-dimensional space, with the distance between them at time 0, t, and t + δt being ε0, εt, and εt + δt, respectively.

where λ(εt) is the SDLE given by

Equivalently, we can express this as,

Given a time series data, the smallest Δt possible is the sampling time τ.
Note that the classic algorithm of computing the Lyapunov exponent λ1 (Wolf et al., 1985) amounts to assuming  and estimating λ1 by (ln εt − ε0)/t. Depending on ε0, this may not be the case even for truly chaotic systems, such as shown in Figure 2. This is emphasized in the schematic of Figure 3 – εt + δt could in fact be smaller than εt. A greater difficulty with such an assumption is that for any type of noise, λ1 can always be greater than 0, leading to misclassifying noise as chaos. This is because εt will be closer to the most probable separation so long as ε0 is small (for a more quantitative discussion of this issue, see Gao and Zheng, 1994b). On the other hand, Eq. 2 does not involve any assumptions, except that Δt is small. As we will see, chaos amounts to λ(ε) being almost constant over a range of ε.
and estimating λ1 by (ln εt − ε0)/t. Depending on ε0, this may not be the case even for truly chaotic systems, such as shown in Figure 2. This is emphasized in the schematic of Figure 3 – εt + δt could in fact be smaller than εt. A greater difficulty with such an assumption is that for any type of noise, λ1 can always be greater than 0, leading to misclassifying noise as chaos. This is because εt will be closer to the most probable separation so long as ε0 is small (for a more quantitative discussion of this issue, see Gao and Zheng, 1994b). On the other hand, Eq. 2 does not involve any assumptions, except that Δt is small. As we will see, chaos amounts to λ(ε) being almost constant over a range of ε.
To compute SDLE, we check whether pairs of vectors (Vi, Vi) defined by Eq. 1 satisfy the following Inequality,
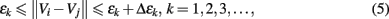
where εk and Δεk are arbitrarily chosen small distances, and
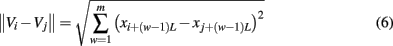
Geometrically, Inequality (5) defines a high-dimensional shell (which reduces to a ball with radius Δεk when εk = 0; in a 2-D plane, a ball is a circle described by (x − a)2 + (y − b)2 = r2, where (a, b) is the center of the circle, and r is the radius). We then monitor the evolution of all such vector pairs (Vi, Vj) within a shell and take the ensemble average over indices i, j. Since we are most interested in exponential or power-law functions, we assume that taking logarithm and averaging can be exchanged, then Eq. 3 can be written as
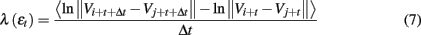
where t and Δt are integers in units of the sampling time, the angle brackets denote the average over indices i, j within a shell, and
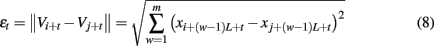
Note that the initial set of shells for computing SDLE serve as initial values of the scales; through evolution of the dynamics, the scales will automatically converge to the range of inherent scales – which are the scales that define Eqs 3 and 4. This point will be clearer after we introduce the notion of characteristic scale below.
Also note that when analyzing chaotic time series, the condition

needs to be imposed when finding pairs of vectors within a shell, where tuncorrelated denotes a time scale beyond which the two vectors Vi and Vj are no longer along the tangential motions (i.e., close orbital motions similar to two cars driving in the same lane, one following the other closely) of the same trajectory (Gao and Zheng, 1994b). Often tuncorrelated > (m − 1)L is sufficient to ensure the elimination of the effects of tangential motions and the convergence of initial scales to the inherent scales (Gao et al., 2007).
Finally, we note that
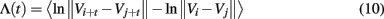
is called the time-dependent exponent curves by Gao and Zheng(1993, 1994a,b). Since Λ(t) = ln εt − ln ε0, we immediately see that SDLE amounts to the local slopes of such curves vs.

With this realization, the algorithm for computing SDLE can be summarized by the following pseudo code (the actual Fortran, C, and Matlab codes are available from the authors, or at http://www.gao.ece.ufl.edu/GCTH_Wileybook/programs/lambda_k_curves/):
(1) (More or less arbitrarily) choose the scale parameters εk, Δεk, k = 1, 2, 3, …; properly choose m and L to reconstruct a suitable phase space from a scalar time series using Eq. 1; also choose tuncorrelated. These are the basic parameters needed for lambda.m in step (2).
(2) Compute the time-dependent exponent Λ(t) curves:
for i = 1:Np − tuncorrelated – Tmax
for j = i + tuncorrelated:NP – Tmax
check Inequality (5); if valid,
save Λ(t) = ln ||Vi + t − Vj + t||, t = 0, 1, …, Tmax
end
end
(3) Estimate SDLE as the local slopes of Λ(k). Specifically, at time t = kδt, where δt is the sampling time, the scale parameter εt is given by Eq. 11, while the local slope of Λ(k) may be estimated by
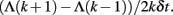
Equivalently, the local slope may be estimated based on ln εt, where εt is given by Eq. 11. To improve estimation of the local slope of Λ(k), filtering may be used to suppress local variations.
2.1. Scaling Laws for SDLE
SDLE has distinctive scaling laws for chaotic signals and 1/fα processes. First we analyze the chaotic Lorenz system (shown in Figure 2) with stochastic forcing:
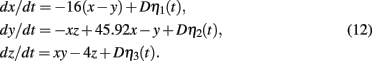
where ηi(t), i = 1, 2, 3 are independent Gaussian noise forcing terms with zero mean and unit variance. When D = 0, the system is clean. Figure 4 (top) shows a few Λ(t) curves for the clean Lorenz system; the bottom of the Figure shows five SDLE curves, for the cases with D = 0, 1, 2, 3, 4. The computations are done with 10000 points and m = 4, L = 2. We observe the following interesting features:
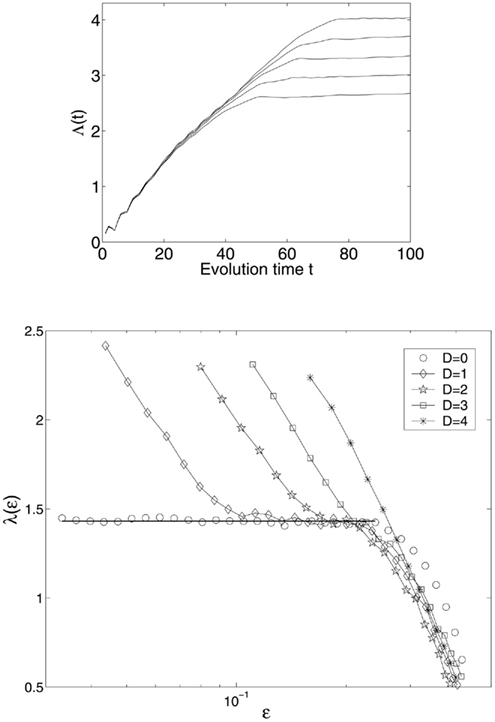
Figure 4. Top: Λ(t) curves for the clean Lorenz system; bottom: SDLE λ(ε) curves for clean and noisy Lorenz systems.
(1) For the clean chaotic signal, λ(ε) fluctuates slightly around a constant. As is expected, this constant is the very largest positive Lyapunov exponent, λ1,

The small fluctuation in λ(ε) is due to the fact that the divergence (i.e., expansion) rate on the Lorenz attractor is not uniform (i.e., varies from one region to another). This non-uniform divergence is the origin of multifractality in chaotic systems.
(2) When there is stochastic forcing, λ(ε) is no longer a constant when ε is small, but diverges to infinity as ε → 0 according the following scaling law,

where γ is a coefficient controlling the speed of loss of information (i.e., defined as the measure of uncertainty involved in predicting the value of a random variable). This feature suggests that entropy generation is infinite when the scale ε approaches zero.
(3) When the noise is increased, the part of the curve with λ(ε) ∼ − γ ln ε shifts to the right. In fact, the plateau (i.e., the chaotic signature) can no longer be identified when D is increased beyond 3.
To facilitate practical applications, we emphasize that there are two features that are important in real data analysis: (i) the location of the −γ ln ε curve; this includes the slope and the position of the “transition” point from −γ ln ε curve to the plateau scaling; and (ii) the width of the plateau.
Note that similar results to those shown in Figure 4 have been observed in other model chaotic systems, such as the Mackey-Glass delay differential equation with multiple positive Lyapunov exponents (Mackey and Glass, 1977). Also note that Eq. 14 characterizes various types of noise, including independent identically distributed random variables, or noise with correlations (including long-range correlation) for time scale up to the embedding window, (m − 1)L. This means SDLE is close to zero if Inequality (9) is imposed when it is computed.
At this point, it is beneficial to introduce a concept, characteristic scale, or limiting scale, ε∞, which is defined as the scale where SDLE is close to 0. In terms of the Λ(t) curves, this amounts to where the curves are flat, as shown in the top plot of Figure 4. If one starts from ε0 ≪ ε∞, then, regardless of whether the data is deterministically chaotic or simply random, εt will initially increase with time and gradually settle around ε∞. Consequentially, λ(εt) will be positive before εt reaches ε∞. On the other hand, if one starts from ε0 ≫ ε∞, then εt will simply decrease, yielding negative λ(εt), again regardless of whether the data are chaotic or random. When ε0 ∼ ε∞, then λ(εt) will stay around 0. For stationary noise processes, the only scale available after t > (m − 1)L would be this limiting scale, since SDLE will always close to 0. In other words, for noise, the only scale resolvable is ε∞. Note however, for some dynamical systems, ε∞ may not be a single point, but a function of time, such as a periodic function of time. When this is the case, the motion can be said to have large scale coherent motions. This is often the case for physiological data.
Next we consider 1/fα processes. Such type of processes is ubiquitous in science and engineering (see Gao et al., 2007 and references therein). Two important prototypical models for such processes are fractional Brownian motion (fBm) process (Mandelbrot, 1982) and ON/OFF intermittency with power-law distributed ON and OFF periods (Gao et al., 2006a). For convenience, we introduce the Hurst parameter 0 < H < 1 through a simple equation,

Depending on whether H is smaller than, equal to, or larger than 1/2, the process is said to have anti-persistent correlation, short-range correlation, and persistent long-range correlation (Gao et al., 2006a). Note that D = 1/H is the fractal dimension of such processes, and Kolmogorov’s 5/3 law for the energy spectrum of fully developed turbulence (Frisch, 1995) corresponds to H = 1/3.
It is well-known that the variance of such stochastic processes increases with t as t2H. Translating this into the average distance between nearby trajectories, we immediately have

To obtain SDLE from Eq. 16, we can use the defining Eq. 3 to obtain λ(εt) ∼ H/t. Expressing t by εt, we obtain

Equation 17 can be readily verified by calculating λ(εt) from such processes. Therefore, SDLE offers a new means of estimating H. In fact, SDLE improves analysis over commonly used fractal analysis methods in two important situations: (i) in some non-stationary environments where commonly used fractal analysis methods fail to detect fractal structures from the data, SDLE may still be able to; this will be shown shortly; and (ii) Eq. 17 also characterizes stochastic limit cycles. This is true for many model systems (Gao et al., 1999a,b, 2006b; Hwang et al., 2000), as well as essential and Parkinsonian tremors (Gao and Tung, 2002).
SDLE also has distinct scaling laws for random Levy processes, and complex motions with multiple scaling laws on different scale ranges. For the details, we refer to Gao et al. (2006b, 2007).
2.2. Detecting Intermittent Chaos by SDLE
Intermittent chaos is a type of complex motion where regular (i.e., periodic) and chaotic motions alternate. It is a crucial ingredient of the intermittent route to chaos, one of the most famous and universal routes to chaos (Gao et al., 2007). One can envision that intermittent chaos may be associated with the physiological transitions from normal to abnormal states, and vice versa. Therefore, studying intermittent chaos can be very important for physiology in general and pathology in particular. Since intermittent chaos is a universal phenomena to many dynamical systems, without loss of generality and to ease repeatability, we examine the logistic map

with a = 3.8284. An example of the time series is shown in Figure 5A. We observe that time intervals exhibiting chaos are very short compared with those exhibiting periodic motions. Traditional methods for computing Lyapunov exponent, being based on global average, is unable to quantify chaos in such intermittent situations, since the laminar phase dominates. Neither can FSLE, since it requires that divergence dominates most of the time. Interestingly, the SDLE curve shown in Figure 5B clearly indicates existence of chaotic motions, since the plateau region extends almost one decade in the scale (see arrow A in the Figure).
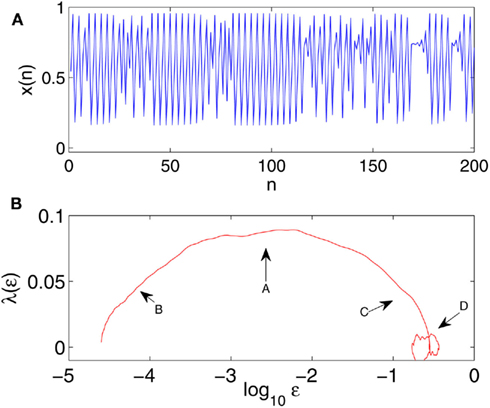
Figure 5. (A) An intermittent time series generated by the logistic map with a = 3.8284. (B) The SDLE curve for a time series of 10000 points, with m = 4, L = 1, and a shell size of (2−13.5, 2−13). A plateau, indicated by arrow A, is clearly visible. Regions indicated by arrows B and C are due to transitions between periodic and chaotic motions, and arrow D indicates the region of oscillatory motions.
One might wonder why Figure 5B is more complicated than Figure 4 (bottom), even though the model system is a simpler logistic map. The reason is that the motion now is intermittent. Realizing intermittent transitions, we can readily understand all the features in Figure 5B: the scale regions indicated by arrows B and C in Figure 5B are due to the transitions from periodic to chaotic motions, and vice versa. To understand the transition, consider two very close trajectories in the laminar region. So far as they stay in the laminar region, ε will remain small. When both trajectories enter the chaotic region, the distance between them will become greater – this divergence becomes stronger when the trajectories get deeper into the chaotic region, till it stabilizes at the plateau region, after it is fully within the chaotic region. This argument is equally valid when the motion gets out of the chaotic region.
The discussion above can be readily extended to understand the circular structure, indicated as arrow D, in Figure 5B. This structure is caused by the large scale laminar flows (i.e., oscillatory motions). Region D is an example of a limiting scale being not a constant. Such a feature can often arise in physiological data, as we will see shortly in Section 4.
In summary, we conclude that the oscillatory part of the data only affects the scale range where λ(ε) ∼ 0. It cannot affect the positive portion of λ(ε). Therefore, SDLE has a unique scale separation property such that different motions are manifested on different scales.
2.3. Detecting Fractal Structure from Non-Stationarity Data
The HRV data shown in Figure 1A motivates us to consider complicated processes generated by the following two scenarios. One is to randomly concatenate 1/f 2H + 1 and oscillatory components. Another is to superimpose oscillatory components on 1/f 2H + 1 processes at randomly chosen time intervals. Either scenario generates signals that appear quite similar to that shown in Figure 1A. The λ(ε) curves for such processes are shown in Figure 6, for a wide range of the H parameter instances. We observe well-defined power-law relations, consistent with Eq. 17, when λ(ε) > 0.02. Figure 6 clearly shows that oscillatory components in the signals can only affect the SDLE where λ(ε) is close to 0. The effects of oscillatory components on SDLE observed in these scenarios is another manifestation of SDLE’s scale separation property. It is most important to emphasize that none of other commonly used fractal analysis methods are able to detect fractal structure from such non-stationary data.
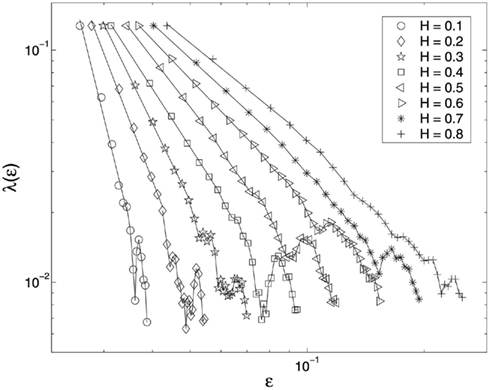
Figure 6. SDLE λ(ε) vs. ε curves for the simulation data. Eight different H values are considered. To put all the curves on one plot, the curves for different H values (except the smallest one considered here) are arbitrarily shifted rightward.
Now, let us ask: when we perturb chaotic data by similar procedures, will we still be able to detect chaos? The answer is yes. In fact, the intermittent chaos discussed above may be viewed as an example of such a procedure.
We are now ready to fully understand why the SDLE can deal with the types of non-stationary data constructed here. One type of non-stationarity causes shifts of the trajectory in phase space – the greater the non-stationarity, the larger the shifts. SDLE, however, cannot be significantly affected by trajectory shifts, especially large ones, since it is based on the co-evolution of pairs of vectors within chosen small shells. The other type is related to oscillatory components. The oscillatory components only affect SDLE where it is close to zero, therefore, will not alter the distinct scaling for chaos and fractal processes.
3. Applications: Biological Data Analysis
As we have mentioned, the popularity of chaos and fractal theories in modeling physiology is closely related to the desire of learning whether a healthy brain, heart, etc., may be associated with greater complexity, greater chaoticity, or greater adaptability due to properties such as long-range correlations. While such complexity interpretations are very appealing, one has to envision that the reality is more difficult, since disease diagnosis is complicated by many factors where the cause is unknown. For example, as man-made chemicals are designed and used, it has yet to know how they affect the body. To (1) shed new light on the interpretation of complexity of physiological data, and (2) illustrate SDLE’s clinical relevance, in this section, we apply SDLE to examine two types of physiological data, HRV and EEG. As we shall see, the most relevant scaling law for these data is Eq. 14, which cannot be obtained by standard chaos or conventional random fractal analysis. Due to space limitations, we shall only briefly describe a complexity measure, when it is used for comparison with SDLE.
3.1. EEG Analysis
EEG signals provide a wealth of information about brain dynamics, especially related to cognitive processes and pathologies of the brain such as epileptic seizures. To understand the nature of brain dynamics as well as to develop novel methods for the diagnosis of brain pathologies, a number of complexity measures have been used in the analysis of EEG data. These include the Lempel-Ziv (LZ) complexity (Lempel and Ziv, 1976), the permutation entropy (Cao et al., 2004), the Lyapunov exponent (LE; Wolf et al., 1985), the Kolmogorov entropy (Grassberger and Procaccia, 1983b), the correlation dimension D2 (Grassberger and Procaccia, 1983a; Martinerie et al., 1998), and the Hurst parameter (Peng et al., 1994; Hwa and Ferree, 2002; Robinson, 2003). Since foundations of information theory, chaos theory, and random fractal theory are different, and brain dynamics are complicated, involving multiple spatial-temporal scales, it is natural and important for us to ask whether there exist relations among these complexity measures, and if so, how to understand those relations.
The EEG signals analyzed here were measured intracranially by the Shands hospital at the University of Florida (Gao et al., 2011a). Such EEG data are also called depth EEG and are considered cleaner and more free of artifacts than scalp (or surface) EEG. Altogether, we have analyzed 7 patients’ multiple channel EEG data, each with a duration of a few hours, with a sampling frequency of 200 Hz. When analyzing EEG for epileptic seizure prediction/detection, it is customary to partition a long EEG signal into short windows of length W points, and calculate the measure of interest for each window. The criterion for choosing W is such that the EEG signal in each window is fairly stationary, is long enough to reliably estimate the measure of interest, and is short enough to accurately resolve localized activities such as seizures. Since seizure activities usually last about 1–2 min, in practice, one often chooses W to be about 10 sec. When applying methods from random fractal theory such as detrended fluctuation analysis (DFA) (Peng et al., 1994), it is most convenient when the length of a sequence is a power of 2. Therefore, we have chosen W = 2 × 1024 = 2048 when calculating various measures. We have found, however, that the variations of these measures with time are largely independent of the window size W. The relations among the measures studied here are the same for all the 7 patients’ EEG data, so we illustrate the results based on only one patient’s EEG signals.
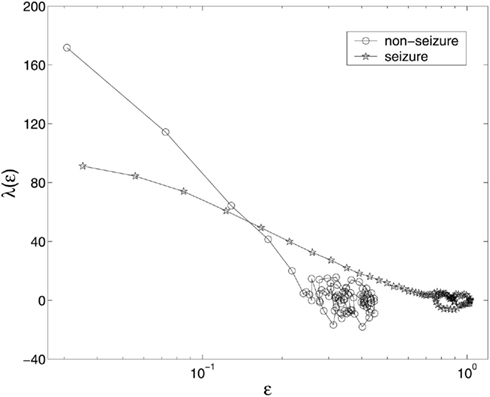
We have examined the variation of λ(ε) with ε is for each segment of the EEG data. Two representative examples for seizure and non-seizure segments are shown in Figure 7. We observe that on a specific scale ε*, the two curves cross. Loosely, we may term any ε < ε* as small scale, while any ε > ε* as large scale. Therefore, on small scales, λ(ε) is smaller for seizure than for non-seizure EEG, while on large scales, the opposite is true. The variations of λsmall − ε and λlarge − ε with time for this patient’s data, where small − ε and large − ε stand for (more or less arbitrarily) chosen fixed small and large scales, are shown in Figures 8A,B, respectively. We observe two interesting features: (i) the pattern of variation of λsmall − ε(t) is reciprocal of that of λlarge − ε(t). This result can be expected from Figure 7. (ii) The variations in λsmall − ε(t) and λlarge − ε(t) clearly indicate the two seizure events. Therefore, either λsmall − ε(t) or λlarge − ε(t) can be used to accurately detect epileptic seizures.
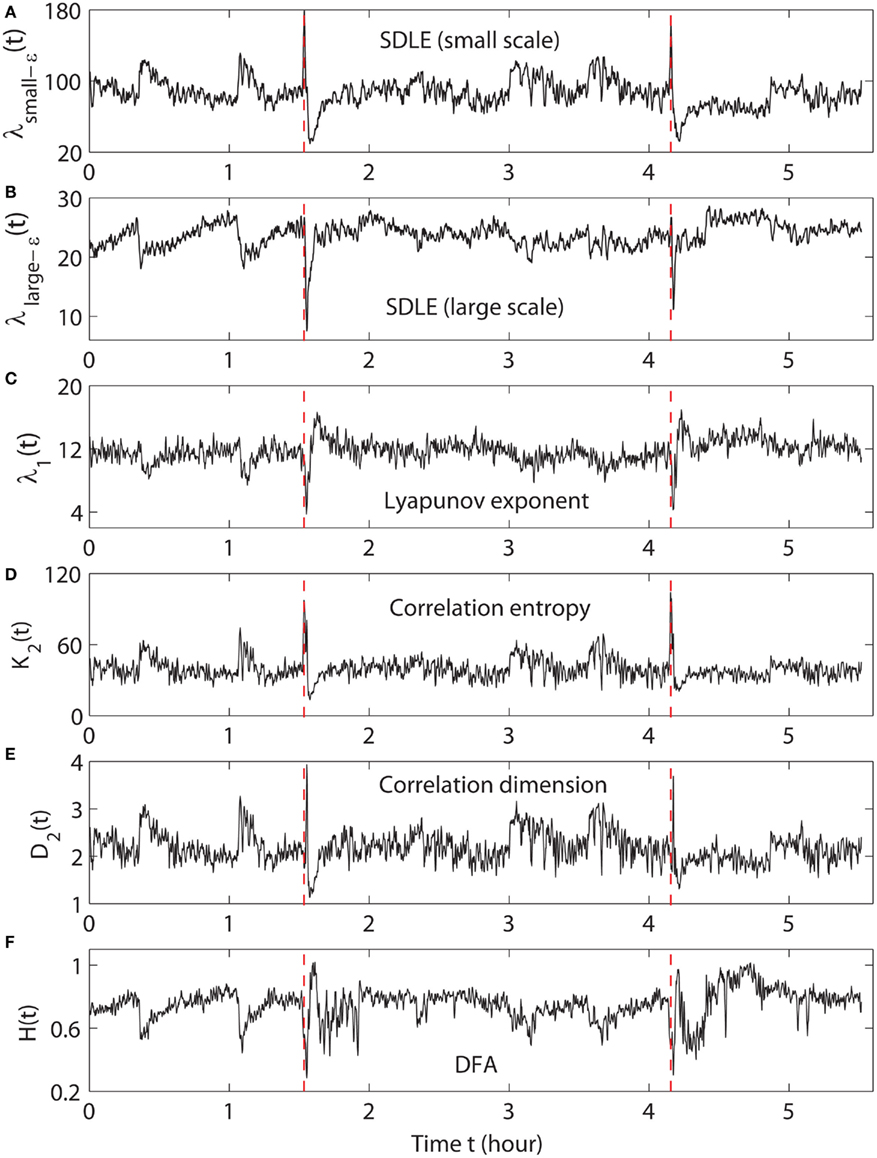
Figure 8. The variation of (A) λsmall − ε, (B) λlarge − ε, (C) the LE, (D) the K2 entropy, (E) the D2, and (F) the Hurst parameter with time for EEG signals of a patient. The vertical dashed lines in (A–F) indicate seizure occurrence times determined by medical experts.
We now compare the SDLE with three commonly used measures from chaos theory, the largest positive Lyapunov exponent (LE), which we have discussed earlier; the correlation entropy (Grassberger and Procaccia, 1983b), and the correlation dimension (Grassberger and Procaccia, 1983a). We also choose one measure from random fractal theory, the Hurst parameter. We discuss the three measures from chaos theory first.
As we have discussed, LE is a dynamic quantity, characterizing the exponential growth of an infinitesimal line segment,  . For truly chaotic signals, 1/λ1 gives the prediction time scale of the dynamics. Also, it is well-known that the sum of all the positive Lyapunov exponents in a chaotic system equals the Kolmogorov-Sinai (KS) entropy. The KS entropy characterizes the rate of creation of new information (or loss of prior knowledge) in a system. It is zero, positive, and infinite for regular, chaotic, and random motions, respectively. However, it is difficult to compute. Therefore, one usually computes the correlation entropy K2, which is a tight lower bound of the KS entropy. Similarly, the box-counting dimension, which is a geometrical quantity characterizing the minimal number of variables that are needed to fully describe the dynamics of a motion, is difficult to compute, and one often calculates the correlation dimension D2 instead. Again, D2 is a tight lower bound of the box-counting dimension. For in-depth discussions of K2 and D2, we refer to Gao et al. (2012).
. For truly chaotic signals, 1/λ1 gives the prediction time scale of the dynamics. Also, it is well-known that the sum of all the positive Lyapunov exponents in a chaotic system equals the Kolmogorov-Sinai (KS) entropy. The KS entropy characterizes the rate of creation of new information (or loss of prior knowledge) in a system. It is zero, positive, and infinite for regular, chaotic, and random motions, respectively. However, it is difficult to compute. Therefore, one usually computes the correlation entropy K2, which is a tight lower bound of the KS entropy. Similarly, the box-counting dimension, which is a geometrical quantity characterizing the minimal number of variables that are needed to fully describe the dynamics of a motion, is difficult to compute, and one often calculates the correlation dimension D2 instead. Again, D2 is a tight lower bound of the box-counting dimension. For in-depth discussions of K2 and D2, we refer to Gao et al. (2012).
From the above brief descriptions, one would expect that λ1(t) and K2(t) are similar, while D2(t) has little to do with either λ1(t) or K2(t). Surprisingly, from Figures 8C,D,E, we observe that this is not the case: λ1(t) is similar to D2(t), but reciprocal of K2(t). In a moment, we shall explain how these puzzling relations may be understood based on λsmall − ε(t) and λlarge − ε(t).
Next we consider the calculation of the Hurst parameter H. As pointed out earlier, H characterizes the long-term correlations in a time series. There are many different ways to estimate H. We have chosen DFA (Peng et al., 1994), since it is more reliable (Gao et al., 2006a), and has been used to study EEG data (Hwa and Ferree, 2002; Robinson, 2003).
Figure 8F shows H(t) for our EEG data. We observe that the pattern of H(t) is very similar to that of λ1(t), but reciprocal to K2(t) and D2(t). Such relations cannot be readily understood intuitively, since the foundations for chaos theory and random fractal theory are entirely different.
Let us now resolve all of the curious relations observed between λ1(t), K2(t), D2(t), and H(t).
(1) Generally, entropy measures the randomness of a dataset. This pertains to small scale. Therefore, K2(t) should be similar to λsmall − ε(t). This is indeed the case. We should point out that we have also calculated other entropy-related measures, such as the Lempel-Ziv complexity (Lempel and Ziv, 1976), which is closely related to the Shannon entropy, and the permutation entropy (Cao et al., 2004), and observed similar variations. Therefore, we can conclude that the variation of the entropy is represented by λsmall − ε(t), regardless of how entropy is defined.
(2) To understand why λ1(t) calculated by the algorithm of Wolf et al. (1985) corresponds to λlarge − ε(t), we note that the algorithm of Wolf et al. (1985) involves a scale parameter that whenever the divergence between a reference and a perturbed trajectory exceeds this chosen scale, a renormalization procedure is performed. When the algorithm of Wolf et al. (1985) is applied to a time series with only a few thousand points, in order to obtain a well-defined LE, a fairly large scale parameter has to be chosen. This is the reason that the LE and λlarge − ε are similar. In fact, the scale we have chosen to calculate λ1(t) is even larger than that for calculating λlarge − ε(t). This is the reason that the value of λ1(t) shown in Figure 8C is smaller than that of λlarge − ε(t) shown in Figure 8B.
(3) It is easy to see that if one fits the λ(ε) curves shown in Figure 7 by a straight line, then the variation of the slope with time should be similar to λsmall − ε(t) but reciprocal of λlarge − ε(t). Such a pattern will be preserved even if one takes the logarithm of λ(ε) first and then does the fitting. Such a discussion makes it clear that even if EEG is not ideally of the 1/f2H + 1 type, qualitatively, the relation λ(ε) ∼ ε−1/H holds. This in turn implies D2 ∼ 1/H. With these arguments, it is clear that the seemingly puzzling relations among the measures considered here can be readily understood by the λ(ε) curves. More importantly, we have established that commonly used complexity measures can be related to the values of the SDLE at specific scales.
As we have pointed out, around the characteristic scale ε∞, λ(ε) is always close to 0. The pattern of λ(ε) around ε∞ is governed by the structured components in the data, such as the α, γ, β, and δ brain waves. From Figure 7, we observe that the patterns for seizure and non-seizure EEG segments are very different. In particular, the pattern of the limiting scale for seizure EEG resembles that of the intermittent chaos indicated by arrow D in Figure 5. Since the brain dynamics on this scale are different from those on smaller scales, such information is clearly helpful in preliminary detection or prediction of seizures. However, we shall not pursue this issue further here, as further use of the SDLE methods for seizure forewarning would require coordination with clinical verification.
3.2. HRV Analysis
HRV is an important dynamical variable of the cardiovascular function. Its most salient feature is the spontaneous fluctuation, even when the environmental parameters are maintained constant and no perturbing influences can be identified. Since the observation that HRV is related to various cardiovascular disorders (Hon and Lee, 1965), a number of methods have been proposed to analyze HRV data. They include methods based on simple statistics from time and frequency domain analyses (see Malik, 1996 and references therein), as well as those derived from chaos theory and random fractal theory (Kobayashi and Musha, 1982; Goldberger and West, 1987; Babyloyantz and Destexhe, 1988; Kaplan and Goldberger, 1991; Pincus and Viscarello, 1992; Bigger et al., 1996; Ho et al., 1997). We shall now show that the SDLE can readily characterize the hidden differences in the HRV under healthy and diseased conditions, and shed new light on the dynamics of the cardiovascular system.
We examine two types of HRV data, one for healthy subjects, and another for subjects with the congestive heart failure (CHF), a life-threatening disease. The data were downloaded from the (Physionet, 2011). There are 18 healthy subjects and 15 subjects with CHF. Part of these datasets were analyzed by random fractal theory. In particular, 12 of the 15 CHF datasets were analyzed by wavelet based multifractal analysis (Ivanov et al., 1999), for the purpose of distinguishing healthy subjects from CHF patients. For ease of comparison, we take the first 3 × 104 points of both groups of HRV data for analysis. In Figures 9A,B, we have shown two typical λ(ε) vs. ε curves, one for a healthy subject, and another for a patient with CHF. We observe that for the healthy subject, λ(ε) linearly decreases with ln ε before λ reaches around 0, or, before ε settles around the characteristic scale, ε∞. Recall that this is a characteristic of noisy dynamics (Figure 4). For the CHF case plotted in Figure 9B, we observe that the λ(ε) is oscillatory, with its value always close to 0, and hence, the only scale resolvable is around ε∞. Since the length of the time series used in our analysis for the healthy and the CHF subjects is the same, the inability of resolving the λ(ε) behavior on scales much smaller than ε∞ for patients with CHF strongly suggests that the dimension of the dynamics of the cardiovascular system for CHF patients is considerably higher than that for healthy subjects.
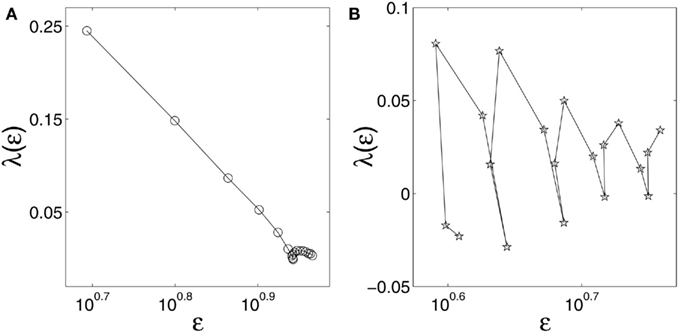
Figure 9. λ(ε) (per beat) vs. ε (in semi-log scale) for HRV data of (A) a healthy subject and (B) a subject with CHF.
We now discuss how to distinguish between healthy subjects and patients with CHF from HRV analysis. We have devised two simple measures, or features. The first feature characterizes how well the linear relation between λ(ε) and ln ε can be defined. We have quantified this by calculating the error between a fitted straight line and the actual λ(ε) vs. ln ε plots of Figures 9A,B. The second feature is to characterize how well the characteristic scale ε∞ is defined. This is quantified by the ratio between two scale ranges, one is from the 2nd to the 6th point of the λ(ε) curves, and another is from the 7th to the 11th point of the λ(ε) curves. Now each subject’s data can be represented as a point in the feature plane, as shown in Figure 10. We observe that for healthy subjects, feature 1 is generally very small, but feature 2 is large, indicating that the dynamics of the cardiovascular system is like a non-linear system with stochasticity, (i.e., with resolvable small scale behaviors and well-defined characteristic scale ε∞). The opposite is true for the patients with CHF: feature 1 is large, but feature 2 is small, indicating that not only small scale behaviors of the λ(ε) curves cannot be resolved, but also that the characteristic scale ε∞ is not well-defined. Very interestingly, these two simple features separate completely the normal subjects from patients with CHF. The results show that no formal methods of statistical clustering are needed and that presentation of the feature space can be readily usable for diagnostics. In fact, each feature alone can almost perfectly separate the two groups of subjects studied here.
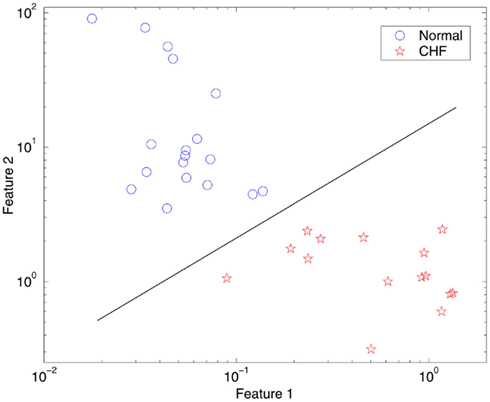
Figure 10. Feature plane separating normal subjects from subjects with CHF, where Feature 1 quantifies the goodness-of-fit of Eq. 14 to the actual SDLE curve, and Feature 2 is related to how well the characteristic scale ε∞ is defined.
It is interesting to note that for the purpose of distinguishing normal HRV from CHF HRV, the features derived from SDLE are much more effective than other metrics including the Hurst parameter, the sample entropy, and multiscale entropy. For the details of the comparisons, we refer to Hu et al. (2010).
Finally, we emphasize that the results presented here should not be interpreted as 100% accurate in distinguishing normal from CHF patients, since only 18 normal and 15 CHF HRV data sets were available to us and analyzed here. It merits noting, however, that other approaches, such as wavelet based multifractal analysis (Ivanov et al., 1999), are not able to achieve the classification rate of SDLE, when all these data were used. The preliminary analysis demonstrates that SDLE could be used over collected HRV data as a first indication of possible non-healthy cardiovascular issues. The use of SDLE could provide valuable complementary information in patient testing.
4. Concluding Remarks
In this paper, we have discussed a multiscale complexity measure, the SDLE. We have shown that it can readily (1) characterize low-dimensional chaos, random 1/f α processes, and stochastic limit cycles, (2) detect intermittent chaos, and (3) conveniently deal with non-stationarity, especially to detect fractal from non-stationary data. Furthermore, we have shown that SDLE can accurately detect epileptic seizures from EEG and distinguish healthy subjects from patients with CHF from HRV. More importantly, we have established that commonly used complexity measures for EEG can be related to the value of the SDLE at specific scales, and that the pattern of the SDLE around the characteristic scale ε∞ contains a lot of useful information on the structured components of the data that may greatly help detect significant patterns. Because of the ubiquity of chaos-like motions and 1/fα-type processes and the complexity of HRV and EEG data, our analyses strongly suggest that the SDLE is potentially important for clinical practice, and provides a comprehensive characterization of complex data arising from a wide range of fields in science and engineering.
Our analyses have a number of important implications.
(1) To comprehensively characterize the complexity of complicated data such as HRV or EEG data, a wide range of scales has to be considered, since the complexity may be different on different scales. For this purpose, the entire λ(ε) curve, where ε is such that λ(ε) is positive, provides a good solution. Using the entire λ(ε) curve is particularly important when one wishes to compare the complexity between two signals – the complexity for one signal may be higher on some scales, but lower on other scales. The situation shown in Figure 7 may be considered one of the simplest.
(2) For detecting important events such as epileptic seizures, λsmall − ε and λlarge − ε appear to provide better defined features than other commonly used complexity measures. This may be due to the fact that λsmall − ε and λlarge − ε are evaluated at fixed scales, while other measures are not. In other words, scale mixing may blur the features for events being detected, such as seizures.
(3) In recent years, there has been much effort in searching for cardiac chaos (Goldberger and West, 1987; Babyloyantz and Destexhe, 1988; Kaplan and Goldberger, 1991; Garfinkel et al., 1992; Fortrat et al., 1997; Kaneko and Tsuda, 2000). Due to the inability of unambiguously distinguishing deterministic chaos from noise by calculating the largest positive Lyapunov exponent and the correlation dimension, it is still unclear whether the control mechanism of cardiovascular system is truly chaotic or not. Our analysis here highly suggests that if cardiac chaos does exist, it is more likely to be identified in healthy subjects than in pathological groups. This is because the dimension of the dynamics of the cardiovascular system appears to be lower for healthy than for pathological subjects. Intuitively, such an implication makes sense, because a healthy cardiovascular system is a tightly coupled system with coherent functions, while components in a malfunctioning cardiovascular system are somewhat loosely coupled and function incoherently.
As example applications, we have focused on the analyses of HRV and EEG data here. It is evident that SDLE will be useful for other kinds of physiological data analyses. While much of the past as well as current research has been focused on determining whether some experimental data are chaotic or not, the scaling laws of SDLE suggest that it is often feasible to obtain the defining parameters of the data under study, without a focus on assessing the chaotic nature of the data. While in principle, SDLE is able to do so without pre-processing of the data under study, suitable detrending and denoising may help. A particularly simple and versatile procedure is the smooth adaptive filter developed by the authors, which has been successfully applied to recover chaos in an extremely noisy environment (Hu et al., 2009b; Gao et al., 2010, 2011b; Tung et al., 2011).
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work is supported in part by U.S. NSF grants CMMI-1031958 and 0826119 as well as by the State Key Laboratory of Non-linear Mechanics (LNM), Institute of Mechanics, Chinese Academy of Sciences, Beijing, People’s Republic of China. We also thank Dr. Jay Holden and two anonymous reviewers, for their many constructive comments which have considerably improved the manuscript.
Footnotes
References
Akselrod, S., Gordon, D., Ubel, F., Shannon, D., Barger, M., and Cohen, R. (1981). Power spectrum analysis of heart rate fluctuation: a quantitative probe of beat-to-beat cardiovascular control. Science 213, 220–222.
Ashkenazy, Y., Ivanov, P., Havlin, S., Peng, C., Goldberger, A., and Stanley, H. (2001). Magnitude and sign correlations in heartbeat fluctuations. Phys. Rev. Lett. 86, 1900–1903.
Aurell, E., Boffetta, G., Crisanti, A., Paladin, G., and Vulpiani, A. (1996). Growth of non-infinitesimal perturbations in turbulence. Phys. Rev. Lett. 77, 1262.
Aurell, E., Boffetta, G., Crisanti, A., Paladin, G., and Vulpiani, A. (1997). Predictability in the large: an extension of the concept of Lyapunov exponent. Physica A 30, 1–26.
Babyloyantz, A., and Destexhe, A. (1988). Is the normal heart a periodic oscillator? Biol. Cybern. 58, 203–211.
Bassingthwaighte, J., Liebovitch, L., and West, B. (1994). Fractal Physiology. New York: Oxford University Press.
Bigger, J., Steinman, R., Rolnitzky, L., Fleiss, J., Albrecht, P., and Cohen, R. (1996). Power law behavior of rr-interval variability in healthy middle-aged persons, patients with recent acute myocardial infarction, and patients with heart transplants. Circulation 93, 2142–2151.
Cao, Y., Tung, W., Gao, J., Protopopescu, V., and Hively, L. (2004). Detecting dynamical changes in time series using the permutation entropy. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70, 046217.
Costa, M., Goldberger, A., and Peng, C. (2005). Multiscale entropy analysis of biological signals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 71, 021906.
Fortrat, J., Yamamoto, Y., and Hughson, R. (1997). Respiratory influences on non-linear dynamics of heart rate variability in humans. Biol. Cybern. 77, 1–10.
Fraser, A., and Swinney, H. (1986). Independent coordinates for strange attractors from mutual information. Phys. Rev. A 33, 1134–1140.
Gao, J., Cao, Y., Tung, W., and Hu, J. (2007). Multiscale Analysis of Complex Time Series – Integration of Chaos and Random Fractal Theory, and Beyond. Hoboken, NJ: Wiley.
Gao, J., Chen, C., Hwang, S., and Liu, J. (1999a). Noise-induced chaos. Int. J. Mod. Phys. B 13, 3283–3305.
Gao, J., Hwang, S., and Liu, J. (1999b). When can noise induce chaos? Phys. Rev. Lett. 82, 1132–1135.
Gao, J., Hu, J., Mao, X., and Tung, W. (in press). Detecting Low-Dimensional Chaos by the “Noise Titration” Technique: Possible Problems and Remedies. Chaos, Solitons, & Fractals.
Gao, J., Hu, J., and Tung, W. (2011a). Complexity measures of brain wave dynamics. Cogn. Neurodyn. 5, 171–182.
Gao, J., Hu, J., and Tung, W. (2011b). Facilitating joint chaos and fractal analysis of biosignals through nonlinear adaptive filtering. PLoS ONE 6, e24331.
Gao, J., Hu, J., and Tung, W. (2012). Entropy measures for biological signal analysis. Nonlinear Dyn.
Gao, J., Hu, J., Tung, W., Cao, Y., Sarshar, N., and Roychowdhury, V. (2006a). Assessment of long range correlation in time series: how to avoid pitfalls. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 73, 016117.
Gao, J., Hu, J., Tung, W., and Cao, Y. (2006b). Distinguishing chaos from noise by scale-dependent Lyapunov exponent. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 74, 066204.
Gao, J., Sultan, H., Hu, J., and Tung, W. (2010). Denoising nonlinear time series by adaptive filtering and wavelet shrinkage: a comparison. IEEE Signal Process. Lett. 17, 237–240.
Gao, J., and Tung, W. (2002). Pathological tremors as diffusional processes. Biol. Cybern. 86, 263–270.
Gao, J., Tung, W., and Hu, J. (2009). Quantifying dynamical predictability: the pseudo-ensemble approach (in honor of Professor Andrew Majda’s 60th birthday). Chi. Ann. Math. Series B 30, 569–588.
Gao, J., and Zheng, Z. (1993). Local exponential divergence plot and optimal embedding of a chaotic time series. Phys. Lett. A 181, 153–158.
Gao, J., and Zheng, Z. (1994a). Direct dynamical test for deterministic chaos. Europhys. Lett. 25, 485–490.
Gao, J., and Zheng, Z. (1994b). Direct dynamical test for deterministic chaos and optimal embedding of a chaotic time series. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 49, 3807–3814.
Garfinkel, A., Spano, M., Ditto, W., and Weiss, J. (1992). Controlling cardiac chaos. Science 257, 1230–1235.
Gaspard, P., Briggs, M., Francis, M., Sengers, J., Gammons, R., Dorfman, J., and Calabrese, R. (1998). Experimental evidence for microscopic chaos. Nature 394, 865–868.
Gaspard, P., and Wang, X. (1993). Noise, chaos, and (ε,τ)-entropy per unit time. Phys. Report. 235, 291–343.
Goldberger, A., and West, B. (1987). Applications of nonlinear dynamics to clinical cardiology. Ann. N. Y. Acad. Sci. 504, 155–212.
Grassberger, P., and Procaccia, I. (1983a). Characterization of strange attractors. Phys. Rev. Lett. 50, 346–349.
Grassberger, P., and Procaccia, I. (1983b). Estimation of the Kolmogorov entropy from a chaotic signal. Phys. Rev. A 28, 2591–2593.
Ho, K., Moody, G., Peng, C., Mietus, J., Larson, M., Levy, D., and Goldberger, A. (1997). Predicting survival in heart failure cases and controls using fully automated methods for deriving nonlinear and conventional indices of heart rate dynamics. Circulation 96, 842–848.
Hon, E., and Lee, S. (1965). Electronic evaluations of the fetal heart rate patterns preceding fetal death: further observations. Am. J. Obstet. Gynecol. 87, 814–826.
Hu, J., Gao, J., and Tung, W. (2009a). Characterizing heart rate variability by scale-dependent Lyapunov exponent. Chaos 19, 028506.
Hu, J., Gao, J., and Wang, X. (2009b). Multifractal analysis of sunspot time series: the effects of the 11-year cycle and Fourier truncation. J. Stat. Mech..
Hu, J., Gao, J., Tung, W., and Cao, Y. (2010). Multiscale analysis of heart rate variability: a comparison of different complexity measures. Ann. Biomed. Eng. 38, 854–864.
Hu, J., Tung, W., Gao, J., and Cao, Y. (2005). Reliability of the 0-1 test for chaos. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72, 056207.
Hwa, R., and Ferree, T. (2002). Scaling properties of fluctuations in the human electroencephalogram. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 66, 021901.
Hwang, S., Gao, J., and Liu, J. (2000). Noise-induced chaos in an optically injected semiconductor laser. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 61, 5162–5170.
Ivanov, P., Amaral, L., Goldberger, A., Havlin, S., Rosenblum, M., Struzik, Z., and Stanley, H. (1999). Multifractality in human heartbeat dynamics. Nature 399, 461–465.
Kaplan, D., and Glass, L. (1992). Direct test for determinism in a time-series. Phys. Rev. Lett. 68, 427–430.
Kaplan, D., and Goldberger, A. (1991). Chaos in cardiology. J. Cardiovasc. Electrophysiol. 2, 342–354.
Kennel, M., Brown, R., and Abarbanel, H. (1992). Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 45, 3403–3411.
Kobayashi, M., and Musha, T. (1982). 1/f fluctuation of heart beat period. IEEE Trans. Biomed. Eng. 29, 456–457.
Lempel, A., and Ziv, J. (1976). On the complexity of finite sequences. IEEE Trans. Inform. Theory 22, 75–81.
Liebert, W., Pawelzik, K., and Schuster, H. (1991). Optimal embedding of chaotic attractors from topological considerations. Europhys. Lett. 14, 521–526.
Mackey, M., and Glass, L. (1977). Oscillation and chaos in physiological control-systems. Science 197, 287–288.
Malik, M. (1996). Task force of the European society of cardiology and the North American society of pacing and electrophysiology: heart rate variability: standards of measurement, physiological interpretation, and clinical use. Circulation 93, 1043–1065.
Martinerie, J., Adam, C., Quyen, M., Baulac, M., Clemenceau, S., Renault, B., and Varela, F. (1998). Epileptic seizures can be anticipated by non-linear analysis. Nat. Med. 4, 1173–1176.
Osborne, A., and Provenzale, A. (1989). Finite correlation dimension for stochastic-systems with power-law spectra. Physica D 35, 357–381.
Packard, N., Crutchfield, J., Farmer, J., and Shaw, R. (1980). Geometry from time-series. Phys. Rev. Lett. 45, 712–716.
Pei, X., and Moss, F. (1996). Characterization of low-dimensional dynamics in the crayfish caudal photoreceptor. Nature 379, 618–621.
Peng, C., Buldyrev, S., Havlin, S., Simons, M., Stanley, H., and Goldberger, A. (1994). On the mosaic organization of DNA sequences. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 49, 1685–1689.
Peng, C., Mietus, J., Hausdorff, J., Havlin, S., Stanley, H., and Goldberger, A. (1993). Long-range anticorrelations and non-Gaussian behavior of the heartbeat. Phys. Rev. Lett. 70, 1343–1346.
Physionet. (2011). MIT-BIH normal sinus rhythm database and BIDMC congestive heart failure. Available at: http://www.physionet.org/physiobank/database/#ecg
Pincus, S., and Viscarello, R. (1992). Approximate entropy: a regularity statistic for fetal heart rate analysis. Obstet. Gynecol. 79, 249–255.
Poon, C., and Barahona, M. (2001). Titration of chaos with added noise. Proc. Natl. Acad. Sci. U.S.A. 98, 7107–7112.
Provenzale, A., and Osborne, A. (1991). Convergence of the k2 entropy for random noises with power law spectra. Physica D 47, 361–372.
Robinson, P. (2003). Interpretation of scaling properties of electroencephalographic fluctuations via spectral analysis and underlying physiology. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67, 032902.
Ryan, D., and Sarson, G. (2008). The geodynamo as a low-dimensional deterministic system at the edge of chaos. Europhys. Lett. 83, 49001.
Sugihara, G., and May, R. (1990). Nonlinear forecasting as a way of distinguishing chaos from measurement error in time series. Nature 344, 734–741.
Takens, F. (1981). “Detecting strange attractors in turbulence,” in Dynamical Systems and Turbulence, Lecture Notes in Mathematics, eds D. A. Rand, and L. S. Young (New York, NY: Springer-Verlag), 366.
Torcini, A., Grassberger, P., and Politi, A. (1995). Error propagation in extended chaotic systems. J. Phys. A Math. Gen. 28, 4533.
Tung, W., Gao, J., Hu, J., and Yang, L. (2011). Recovering chaotic signals in heavy noise environments. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 83, 046210.
Keywords: multiscale analysis, chaos, random fractal, scale-dependent Lyapunov exponent, EEG, heart-rate variability, intermittent chaos, non-stationarity
Citation: Gao J, Hu J, Tung W-w and Blasch E (2012) Multiscale analysis of biological data by scale-dependent Lyapunov exponent. Front. Physio. 2:110. doi: 10.3389/fphys.2011.00110
Received: 11 November 2011; Accepted: 08 December 2011;
Published online: 24 January 2012.
Edited by:
John Holden, University of Cincinnati, USAReviewed by:
Michael A. Riley, University of Cincinnati, USAJohn Holden, University of Cincinnati, USA
Damian Stephen, Harvard University, USA
Copyright: © 2012 Gao, Hu, Tung and Blasch. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Jianbo Gao, PMB Intelligence LLC, PO Box 2077, West Lafayette, IN 47996, USA. e-mail:amJnYW8ucG1iQGdtYWlsLmNvbQ==

 Jing Hu4
Jing Hu4