- 1 Center for Non-linear Science, Department of Physics, University of North Texas, Denton, TX, USA
- 2 Department of Physics, La Sierra University, Riverside, CA, USA
- 3 Information Science Directorate, United States Army Research Office, Durham, NC, USA
- 4 Istituto di Fisiologia Clinica del Consiglio Nazionale delle Ricerche, Pisa, Italy
According to an increasing number of researchers intelligence emerges from criticality as a consequence of locality breakdown and long-range correlation, well known properties of phase transition processes. We study a model of interacting units, as an idealization of real cooperative systems such as the brain or a flock of birds, for the purpose of discussing the emergence of long-range correlation from the coupling of any unit with its nearest neighbors. We focus on the critical condition that has been recently shown to maximize information transport and we study the topological structure of the network of dynamically linked nodes. Although the topology of this network depends on the arbitrary choice of correlation threshold, namely the correlation intensity selected to establish a link between two nodes; the numerical calculations of this paper afford some important indications on the dynamically induced topology. The first important property is the emergence of a perception length as large as the flock size, thanks to some nodes with a large number of links, thus playing the leadership role. All the units are equivalent and leadership moves in time from one to another set of nodes, thereby insuring fault tolerance. Then we focus on the correlation threshold generating a scale-free topology with power index ν ≈ 1 and we find that if this topological structure is selected to establish consensus through the linked nodes, the control parameter necessary to generate criticality is close to the critical value corresponding to the all-to-all coupling condition. We find that criticality in this case generates also a third state, corresponding to a total lack of consensus. However, we make a numerical analysis of the dynamically induced network, and we find that it consists of two almost independent structures, each of which is equivalent to a network in the all-to-all coupling condition. This observation confirms that cooperation makes the system evolve toward favoring consensus topological structures. We argue that these results are compatible with both Hebbian learning and fault tolerance.
Introduction
The issue of defining a robust performance measure (Boccaletti et al., 2006; Qiang and Nagurney, 2008) to assess network efficiency is one of the main problems of the emerging field of complex networks. As noted in Qiang and Nagurney (2008), problems akin to network vulnerability, which are linked to events such as 9/11, hurricane Katrina and the biggest blackout in North America (8/14/03), cannot be satisfactorily addressed without a measure of global network efficiency. Network efficiency was originally studied in connection with topological structure (Boccaletti et al., 2006), and more recently with measures capturing the flow of information to determine the criticality of nodes and links (Qiang and Nagurney, 2008).
In the last few years increasing attention has been devoted to discussing the connection between synchronization and topology (Arenas et al., 2006, 2008; Gómez-Gardeñes et al., 2007; Díaz-Guilera, 2008; Liang et al., 2009). Using sociological perspective (Castellano et al., 2009) synchronization can be thought of as a form of consensus. Consequently the efficiency of a network can be expressed as a quantity inversely proportional the critical value of the control parameter KC, at which a phase transition of the network to an organized state occurs. Herein that organized state is identified as consensus, where most of the nodes of the network are found to share the same opinion. Simultaneously, expressing network efficiency through consensus has the effect of establishing a close connection between network topology and the ubiquitous natural phenomenon of synchronization. In this way a number of investigators have concluded that topology plays an important role in biology, ecology, climatology, and sociology (Pikovsky et al., 2001; Arenas et al., 2008; West et al., 2008; Castellano et al., 2009).
Some investigators (Arenas et al., 2006) employ a local order parameter to determine that synchronization can be used to detect communities. More recent work (Liang et al., 2009) follows a similar path, using the response of the surrounding nodes to a weak signal generated by a given node of the network. The paper of Gómez-Gardeñes et al. (2007) uses synchronization as a way to compare the efficiency of a scale-free network to the random network of Erdos and Renyi. All this is extensively discussed in an excellent review paper by Arenas et al. (2008) showing very interesting comparisons of Erdos–Renyi networks and scale-free networks as a function of the control parameter K. The influence of complex network topology on synchronization has been studied (Restrepo et al., 2006) and these authors found that although the heterogeneous network is less efficient than the all-to-all coupled network, the phase transition remains sharp, thereby qualitatively confirming the results of earlier work (Moreno and Pacheco, 2004). The latter authors studied the Kuramoto model (Kuramoto, 1984) embedded in a scale-free network and found that, quite surprisingly, a phase transition emerges at a critical value of the control parameter K with no need to use all-to-all coupling. Another interesting result (Moreno and Pacheco, 2004) is that single nodes, with k links, regress to synchronization with the mean time 〈τ〉 ∝ 1/k, thereby making the hubs very stable. This observation led those authors to conjecture that the scale-free condition may be a consequence of an optimization mechanism. As a main result of this paper, we substantiate this conjecture with an example where the hubs have a dynamical origin.
A limitation of the earlier work on the connection between global efficiency and topological complexity, with one exception (Moreno and Pacheco, 2004), is that the dynamical origin of topological complexity is not addressed. We examine this connection between topology and dynamics herein as follows: (a) We distinguish between a resting and a dynamic network; the former being the network where the constitutive units are at rest, and the latter being the network generated by the self-organization of the units located on the structure of the resting network. (b) We explore the possible benefits of the dynamic network by using it as a resting network on which to activate our cooperation model. (c) We argue that these results establish a connection between criticality and the famous Donald Hebb’s neurophysiological postulate (Hebb, 1949).
Materials and Methods
We adopt a decision making model (DMM; Bianco et al., 2008; Turalska et al., 2009), which uses a social paradigm of decision makers who choose between “yes” (+) and “no” (−) at each point in time. Note that the DMM is expected to have a range of application that is not limited to social processes. In fact, the DMM is usefully applied to account for the phenomenon of intermittency of colloidal quantum dots (Frantsuzov et al., 2009). In DMM the dynamics of each node si is determined by the following master equation

The cooperation among the units in the network is realized by setting the coupling coefficients to the time-dependent form

and

Here M denotes the total number of nearest neighbors, and M1(t) and M2(t) are the count of nearest neighbors who are making the decision “yes” and “no,” respectively. The single individuals change opinion, and as a consequence M1(t) and M2(t) are fluctuating in time variables, while, of course, the total number of nearest neighbors is conserved: M1(t) + M2(t) = M. The single unit in isolation, K = 0, would fluctuate between “yes” and “no,” with the rate g. Once the value of the coupling increases, K > 0, single in the state “yes” (“no”) is less and less independent and makes transition to the state “no” (“yes”) faster or slower according to whether M2 > M1 (M1 > M2) or M2 < M1 (M1 < M2), respectively. We define the global fluctuation ξ(t) ≡ (N1(t) − N2(t))/N, where N is the total number of nodes, and N1(t) and N2(t) are the units in the state “yes” and “no” at time t, respectively. Additionally, we use the time average ξeq= 〈|ξ(t)|〉 as a measure of the global majority.
It is important to note that the master equation of each site is a fluctuating master equation. This property emerges from the fact that the transition rates g12(t) (g21(t)) depend on the stochastic evolution of each unit’s environment. Only in the thermodynamical condition when the number of nodes creating the network is infinite, N = ∞, and all nodes are directly connected with each other, M = ∞, the ratios M1(t)/M and M2(t)/M are equivalent to the probabilities p1(t) and p2(t) (Turalska et al., 2009). However, this correspondence is violated once the number of nodes is finite or the structure of the network departures from all-to-all coupling. Both those conditions introduce randomness into the dynamic evolution of a single unit. In the most general case this stochastic fluctuations can be realized as a difference between the estimate of a random walker position after finite number of steps (what corresponds to given number of neighbors each node has) and the position obtained after an infinite time.
Here we consider a topology of a simple two-dimensional regular lattice, where each node is coupled to four nearest neighbors, thereby setting M = 4. We call this structure a resting network. The numerical calculations were performed on a lattice of N = 100 × 100 nodes with periodic boundary conditions. At the initial time, t = 0, the state of each node was assigned randomly to be either +1 or −1, symbolizing decision in “yes” and “no,” respectively. Next, in a single time step a run over the whole lattice is performed and for every unit si the transition rate of Eqs 2 or 3 is calculated according to which a node is given the possibility to change its state. After initial 106 time steps the time average is taken over the same number of consecutive steps of the model to evaluate the global majority measure ξeq.
Results
As expected, the global order parameter ξeq shows a transition to the organized state with the respect to the coupling constant K. The critical value of the coupling constant KC can be found analytically in the case of N = ∞ (McCoy and Wu, 1973) and yields 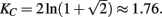 On Figure 1 we present the phase transition curve obtained for a finite square lattice of 10,000 nodes. We observe that the transition into the organized phase occurs at the critical value of KC ≈ 1.70, which is significantly larger than the value of the all-to-all coupling case with an infinite number of units (Bianco et al., 2008; Turalska et al., 2009), KC= 1.
On Figure 1 we present the phase transition curve obtained for a finite square lattice of 10,000 nodes. We observe that the transition into the organized phase occurs at the critical value of KC ≈ 1.70, which is significantly larger than the value of the all-to-all coupling case with an infinite number of units (Bianco et al., 2008; Turalska et al., 2009), KC= 1.
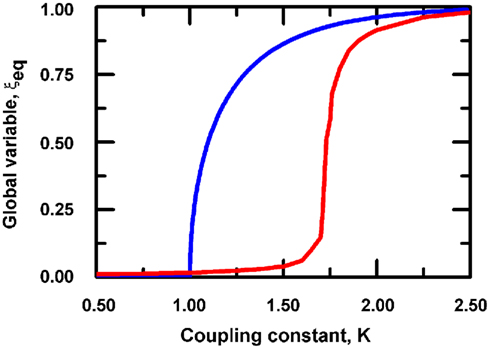
Figure 1. The phase diagram for global variable ξeq. Solid blue line corresponds to the equilibrium states obtained in the case of fully connected, infinite network N = ∞. Red line corresponds to the global states observed for two-dimensional regular lattice (N = 100 × 100) and setting g = 0.01.
To study the dynamically induced network topology, we consider the DMM with the critical value of the coupling, KC= 1.70. After initial 106 time steps, we record lattice configurations over 2000 time step windows, registering the dynamics of each node {si(t)} over that time interval. In the next step we evaluate the linear correlation coefficient between the i-th and the j-th node (Fraiman et al., 2009):
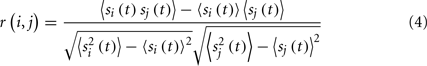
where 〈…〉 denotes time average. If the correlation intensity between nodes i and j of the square lattice is larger than the arbitrarily chosen threshold value Θ = 0.61, we consider them connected by a link in the dynamically induced topology. The Figure 2 serves as an illustration of this process.
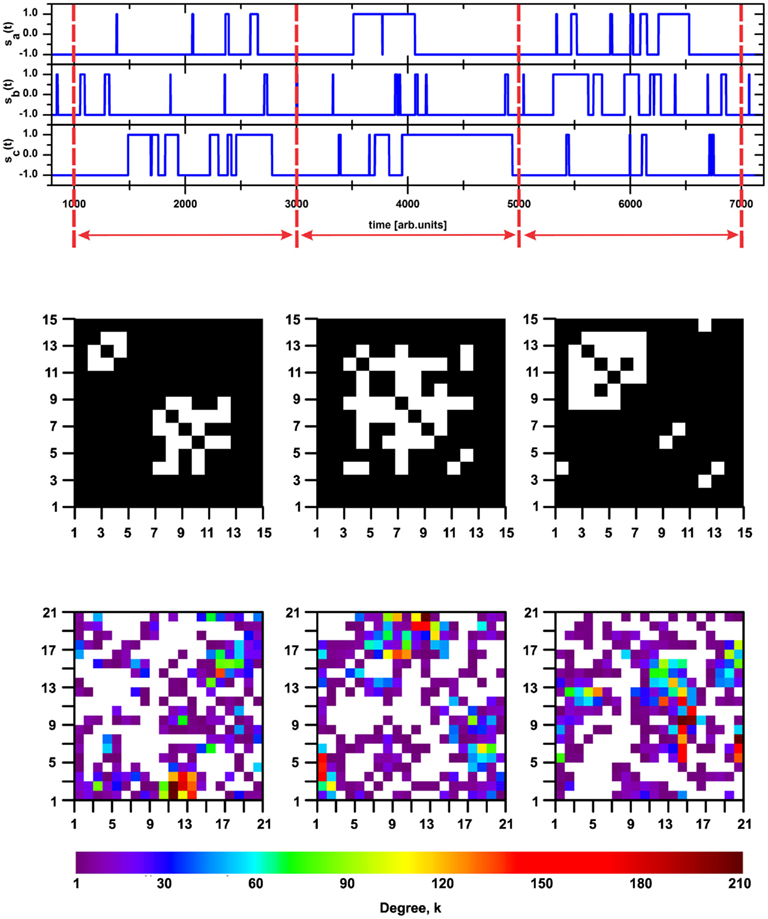
Figure 2. Consecutive steps that lead to the dynamical topology. Top panel shows time evolution of three randomly selected nodes of the square lattice. Arrows denote time intervals over which the correlation index of Eq. 4 is calculated. Middle panel illustrates the fragment of an adjacency matrix of the dynamically created network. It originates by the application of a threshold Θ to the values of correlation all nodes of square lattice. Full size of this adjacency matrix is N2 × N2. White squares denote the case when the correlation between unit i and j is larger than threshold and they correspond to the link between node i and j in the dynamical network. Lower panel presents fragment of the dynamical topology that arises from above adjacency matrix. Here a single square is a node of the dynamical network. Full dimension of this matrix is N × N. The color scheme denotes the degree of a node. As in the case of the adjacency matrix, this representation confirms that the dynamical network is very sparse when overlaid on the original square lattice (white squares represent nodes of the square lattice that are not a part of the dynamical network). The clarity of figures presented on middle and bottom panels are the only reason for showing fragments of matrices, rather them whole.
This newly created topology clearly depends both on selected value of the coupling and the threshold value applied to the set of obtained correlation coefficients. If one would consider the dynamics of the system in the subcritical phase, K < KC, where the randomness dominates over the cooperation between units, as a result observed values of r(i, j) would be small, as expected for two independent variables. In the opposite case, when K > KC, strong coupling reduces the variability of a state of a single unit in time, and due to the definition of r(i, j) also leads to small correlation values. In both cases, the distribution created from a set of obtained r(i, j) values is centered at zero, and has very fast decreasing tails. However, once the dynamics approaches criticality, K ≈ KC, the coupling between units is just enough to balance the stochasticity. This condition leads to dynamical coupling between units that are not directly connected, and results in much wider distribution of values of r(i, j) than in two previous cases.
In all discussed cases adoption of a low threshold would include most of the correlation pairs r(i, j) and would result in highly connected networks, where almost all nodes are connected to each other. As the threshold Θ increases less and less pairs of nodes would be included in the newly created topology. Since for K < KC and K > KC the distribution of correlations decreases much faster than for K ≈ KC, the increase of Θ leads to the destruction of the giant component, thus no new structure can be identified. Close to the criticality, the transition between the fully connected structure obtained for low threshold and its destruction into separate modules is more subtle. In this condition, the Dirac-like degree distribution, obtained for low Θ when almost all nodes are directly connected, starts to present a tail once Θ is increased, signifying that some links are eliminated and nodes with degree smaller than the average appear. Even further increase in the value of threshold eliminates enough links to distribute nodes degree as an inverse power law. The inclusion of correlations even higher than this special value leads to the disruption of the giant component.
As mentioned in the previous paragraph, above prescription generates a scale-free network, with the inverse power index ν ≈ 1, as shown in Figure 3, thereby supporting the observation of Moreno and Pacheco (2004), that the scale-free structure is the result of an optimization process, which is, in the case of this Letter, the realization of a consensus condition. We also evaluate the distribution density p(l) of the Euclidian distance l between two linked nodes and find that the average distance is of the order of 50, namely, of the size of the two-dimensional network 100 × 100. This average distance implies the emergence of long-range links, essential to realize the fast transfer of information over a complex network (Kleinberg, 2000; Boguñá and Krioukov, 2009; Boguñá et al., 2009; Li et al., 2010).
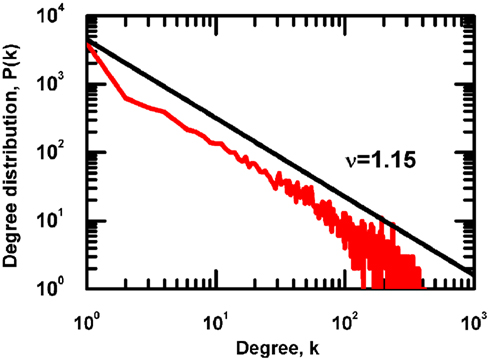
Figure 3. The degree distribution for correlation network created by examining the dynamics of nodes placed on two-dimensional, regular lattice. Examined network had N = 6740 nodes and the parameters of DMM were g = 0.01 and K = 1.70.
Now let us turn the dynamically induced network into a resting network, called a dynamically generated resting (DGR) network and let us study its efficiency running the DMM on it. We find it convenient to compare its cooperative behavior with another seemingly equivalent scale-free networks with the same ν ≈ 1. We realize this latter scale-free network using the probabilistic algorithm (Kalisky et al., 2004) and we refer to it as an ad hoc network, and run the DMM on it as well as on the DGR network. The phase transition diagrams of the DGR and ad hoc networks are illustrated in Figure 4, and Figure 5B, respectively. We see that the phase transition occurs on both networks at K = 1, namely, at the same critical value corresponding to the all-to-all coupling condition. However, in Figure 4 a new phenomenon is observed, that being the emergence of both a consensus and a non-consensus state. The new state emerges because the self-organization process generates two weakly coupled identical clusters (Figure 4B), each cluster being equivalent to an ad hoc network with ν ≈ 1. These two networks are virtually independent from one another, thereby yielding the states ++; −−; +−; −+ with equal probability. The states +− and −+ are the non-consensus state. To support this interpretation we generate two identical ad hoc networks with ν = 1 and couple them with a single link. The resulting phase diagram, shown in Figure 5A, is very similar to that depicted on the Figure 4, thereby establishing that DGR networks may lead to coexistence of communities with conflicting opinions, reminiscent of recent results obtained by others (Shao et al., 2009).
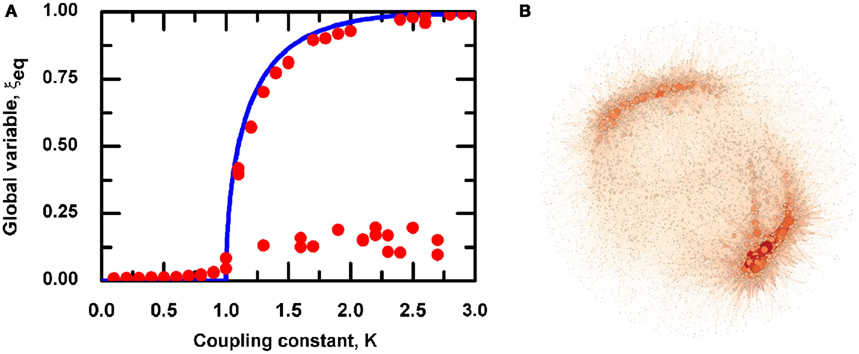
Figure 4. (A) Shows the phase diagram for global variable ξeq. Solid blue line corresponds to the equilibrium states obtained in the case of fully connected, infinite network (N = ∞). Dots correspond to the equilibrium states obtained by evaluating the dynamics of the decision making model on the DGR correlation network with g = 0.01. (B) Presents graphic depiction of the dynamical network prepared with the help of open-source graph visualization software, Gephi (Bastian et al., 2009).
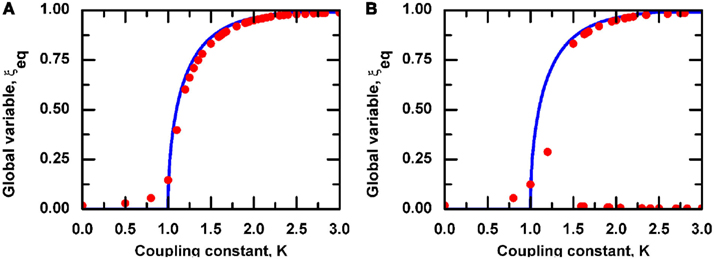
Figure 5. The phase diagram for global variable ξeq. Solid blue line corresponds to the equilibrium states obtained in the case of fully connected, infinite network (N = ∞). (A) Dots show the phase diagram for a scale-free ad hoc network with N = 2000 nodes and scaling exponent of degree distribution ν = 1. (B) Dots correspond to the equilibrium states obtained by evaluating the dynamics of the decision making model on a system of two scale-free ad hoc networks, each having N = 1000 nodes and scaling exponent ν = 1. Those networks are coupled with only one randomly created link. In both cases scale-free ad hoc networks were generated according to the probabilistic algorithm of Kalisky et al., 2004.
Discussion
Note that the scale-free network generated by the mechanism of cooperation is observed in the brain dynamics of neuronal networks (Fraiman et al., 2009). Although these authors use the two-state nodes of the Ising model to explain the source of the scale-free neuronal network, the Ising and the DMM model are essentially equivalent as far as dynamically generated scale-free topology is concerned. This paper, inspired in part by Fraiman et al. (2009), yields the additional discovery that the emergence of consensus produces long-rage links as well scale-free topology, thereby establishing a possible connection between the brain dynamics and the navigation in complex networks (Kleinberg, 2000; Boguñá and Krioukov, 2009; Boguñá et al., 2009; Li et al., 2010).
Fault Tolerance
Let us address the problem of network efficiency and vulnerability. The scale-free topologies are universally judged to be robust against an external random attack, since the key nodes (hubs) are rare and their annihilation is expected to be highly improbable. However, if a unit with a large number of links is annihilated, the efficiency of the network is drastically reduced. Thus, a scale-free network is robust against a random attack but not against an intelligent attack whose targets are the hubs of the network (Albert et al., 2000; Cohen et al., 2000; Gallos et al., 2005).
Now, as illustrated on Figure 4, if we consider the emergence of consensus on a DGR scale-free topology two scenarios arise: one in which the evaluation of DMM leads to a state of non-consensus and one in which the consensus depends on the structure of the DGR network. An annihilation of a hub in the latter case would cause disruption of network dynamics and could affect the consensus state. This paper shows that it may be convenient to run the DMM on the original regular network, with M = 4, even if the self-organization process would require a higher critical parameter, KC= 1.70 rather than KC= 1.00. The regular network, although dynamically less efficient, is less vulnerable than the scale-free network, either the one dynamically generated or the ad hoc network. To substantiate this prediction, let us imagine an intelligent attack annihilating a highly connected hub in the dynamical topology, which action affects the organization state. Since targeted node simultaneously is one of the units of regular lattice, we observe the consequence of the attack also in the regular network, from which dynamical topology emerge. In this case the damage provoked by the intelligent attack is the generation of a defect, and consequently of a network of N − 1 nodes, with all of them having four links but four of them that have three links. We expect that for N → ∞ the self-organization process is not severely damaged. To paraphrase, if the flag bearer, guiding a large number of fighters, falls in the battle another fighter will pick up the fallen flag and carry it forward. According to Singer (2005) this property is shared by the brain and is depicted by him as an orchestra with no conductor.
Hebbian Learning
Hebb (1949) proposed the following neurophysiological postulate: “When an axon of cell A is near enough to excite a cell B and repeatedly or persistently takes part in firing it, some growth process or metabolic change takes place in one or both cells such that A’s efficiency, as one of the cells firing b, is increased,” according to which persistence or repetition of neural activity induces lasting cellular changes. We interpret the results of this paper in the light of this fundamental postulate.
First, we notice that at criticality the system of cooperating units reaches consensus but the consensus time duration is finite (Turalska et al., 2011). Vanni et al. (2011) have proved that the function of a system of cooperating units benefits from the occurrence of organizational collapses, allowing single units to recover the free-will condition that they have in the absence of cooperation. The consensus time duration TC is the distance between two consecutive organizational collapses. Using the same procedure as that adopted in the recent work of Turalska et al. (2011), Vanni et al. (2011) find that TC is proportional to the size of the system. Thus, since dynamically induced links are established on the basis of a temporal measure (Eq. 4), we assume that they correspond to cellular changes lasting for an extended, but not infinite time. Consecutively, we make the conjecture that according to Hebb’s postulate, after a number of organizational collapses, reoccurring dynamical links are turned into resting links. This leads to an iterative procedure; where the initial resting network evolves into a dynamical structure (DGR1) which after certain time is used as the resting topology. Evaluation of the DMM on this new topology leads to the generation of a new dynamical network (DGR2), which then can be considered as a starting point.
It is worth noticing that this model for evolutionary network is rather crude, since the DGR2 network is established dynamically only on the basis of positive correlations between the units of the DGR1 network. A more realistic model would imply a random growth of connections, with a selection driven not purely by reinforcing Hebb’s rule. However, from the results of this paper, we eventually expect the emergence of a complex network out of any evolution scheme. If we make the plausible hypothesis that increasing the complexity of the network also the dynamics becomes more complex, this evolution has been experimentally established by a recent paper (Smit et al., 2011) by looking at how scale-free indexes in electroencephalograms evolve with brain maturation in children and adolescent.
Herein we proved that, while dynamically induced links evolve into resting links, the thermodynamics of the system change, and the critical coupling significantly decreases. When a resting scale-free network evolves, with the topology herein studied, the coupling coefficient becomes indistinguishable from the minimal possible value, corresponding to all-to-all coupling. This means that the system (the brain) has efficiently decreased the resources necessary to keep working at criticality, both in terms of wiring (number of synapses) and coupling (amount of neurotransmitters). We may conjecture that the hypothesis that the brain works at criticality (Allegrini et al., 2010; Chialvo, 2010; Werner, 2010), or, better, that remains critical while exploring a continuity of different critical states (Longo and Montévil, 2011) is more fundamental than the Hebb’s rule itself. In other words, Hebb’s rule may have been evolutionary selected due to the cost-saving mechanisms herein suggested.
What about fault tolerance? Apart from the fault tolerance properties exposed in the previous subsection, that characterize the scale-free structure evolving from the Hebb’s rule, Hebb’s rule also provides network plasticity, so that even hub-oriented attacks can be effectively dealt with. Within our crude evolutionary model, due to the probabilistic nature of the process, it is expected that the links generated dynamically by DGRn do not coincide with its resting nodes, although many DGRn leaders may remain leaders at the DGR(n + 1) level. Thus we conclude that the discovery of this paper that topological complexity may be dynamically generated is not incompatible with fault tolerance. This is again in accordance with Hebb and his followers, who prevent all synapses from increasing indefinitely by assuming that synaptic effectiveness is reduced when the simultaneous firing of post-abs pre-synaptic impulse does not occur.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Malgorzata Turalska, Elvis Geneston, and Paolo Grigolini thankfully acknowledge financial support from ARO through Grant #W911NF1110478.
References
Albert, R., Jeong, H., and Barabasi, A.-L. (2000). Error and attack tolerance of complex networks. Nature 406, 378–382.
Allegrini, P., Paradisi, P., Menicucci, D., and Gemignani, A. (2010). Fractal complexity in spontaneous EEG metastable-state transitions: new vistas on integrated neural dynamics. Front. Physiol. 1:128. doi:10.3389/fphys.2010.00128
Arenas, A., Díaz-Guilera, A., Kurths, J., Moreno, Y., and Zhou, C. (2008). Synchronization in complex networks. Phys. Rep. 469, 93–153.
Arenas, A., Díaz-Guilera, A., and Pérez-Vincente, C. (2006). Synchronization reveals topological scales in complex networks. Phys. Rev. Lett. 96, 114102.
Bastian, M., Heymann, S., and Jacomy, M. (2009). “Gephi: an open source software for exploring and manipulating networks,” in Third International AAAI Conference on Weblogs and Social Media, San Jose.
Bianco, S., Geneston, E., Grigolini, P., and Ignaccolo, M. (2008). Renewal aging as emerging property of phase synchronization. Phys. A 387, 1387–1392.
Boccaletti, S., Latora, V., Moreno, Y., Chavez, M., and Hwang, D.-U. (2006). Complex networks: structure and dynamics. Phys. Rep. 424, 175–308.
Boguñá, M., and Krioukov, D. (2009). Navigating ultrasmall worlds in ultrashort time. Phys. Rev. Lett. 102, 058701.
Boguñá, M., Krioukov, D., and Claffy, K. C. (2009). Navigability of complex networks. Nat. Phys. 5, 74–80.
Castellano, C., Fortunato, S., and Loreto, V. (2009). Statistical physics of social dynamics. Rev. Mod. Phys. 81, 591–646.
Cohen, R., Erez, K., ben-Avraham, D., and Havlin, S. (2000). Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628.
Díaz-Guilera, A. (2008). Dynamics towards synchronization in hierarchical networks. J. Phys. A Math. Theor. 41, 224007.
Fraiman, D., Balenzuela, P., Foss, J., and Chialvo, D. R. (2009). Ising-like dynamics in large-scale functional brain networks. Phys. Rev. E 79, 061922.
Frantsuzov, P. A., Volkán-Kacsó, S., and Jankó, B. (2009). Model of fluorescence intermittency of single colloidal semiconductor quantum dots using multiple recombination centers. Phys. Rev. Lett. 103, 207402.
Gallos, L. K., Cohen, R., Argyrakis, P., Bunde, A., and Havlin, S. (2005). Stability and topology of scale-free networks under attack and defense strategies. Phys. Rev. Lett. 94, 188701.
Gómez-Gardeñes, J., Moreno, Y., and Arenas, A. (2007). Paths to synchronization on complex networks. Phys. Rev. Lett. 98, 034101.
Kalisky, T., Cohen, R., ben-Avraham, D., and Havlin, S. (2004) Tomography and stability of complex networks. Lect. Notes Phys. 650, 3–34.
Li, G., Reis, S. D. S., Moreira, A. A., Havlin, S., Stanley, H. E., and Andrade, J. S. (2010). Towards design principles for optimal transport networks. Phys. Rev. Lett. 104, 018701.
Liang, X., Liu, Z., and Li, B. (2009). Weak signal transmission in complex networks and its application in detecting connectivity. Phys. Rev. E 80, 046102.
Longo, G., and Montévil, M. (2011). From physics to biology by extending criticality and symmetry breakings. Prog. Biophys. Mol. Biol. 106, 340–347.
McCoy, B. M., and Wu, T. T. (1973). The Two – Dimensional Ising Model. Cambridge: Harvard University Press.
Moreno, Y., and Pacheco, A. F. (2004). Synchronization of Kuramoto oscillators in scale-free networks. Europhys. Lett. 68, 603–609.
Pikovsky, A., Rosenblum, M., and Kurths, J. (2001). Synchronization: A Universal Concept in Nonlinear Science. Cambridge: Cambridge University Press.
Qiang, Q., and Nagurney, A. (2008). A unified network performance measure with importance identification and the ranking of network components. Optim. Letters 2, 127–142.
Restrepo, J. G., Ott, E., and Hunt, B. R. (2006). Characterizing the dynamical importance of network nodes and links. Phys. Rev. Lett. 97, 094102.
Shao, J., Havlin, S., and Stanley, H. E. (2009). Dynamic opinion model and invasion percolation. Phys. Rev. Lett. 103, 018701.
Smit, D. J. A., de Geus, E. J. C., van de Nieuwenhuijzen, M. E., van Beijsterveldt, C. E. M., van Baal, G. C. M., Mansvelder, H. D., Boomsma, D. I., and Linkenkaer-Hansen, K. (2011). Scale-free modulation of resting-state neuronal oscillations reflects prolonged brain maturation in humans. J. Neurosci. 31, 13128–13136.
Turalska, M., Lukovic, M., West, B. J., and Grigolini, P. (2009). Complexity and synchronization. Phys. Rev. E 80, 021110.
Turalska, M., West, B. J., and Grigolini, P. (2011). Temporal complexity of the order parameter at the phase transition. Phys. Rev. E 83, 061142.
Vanni, F., Lukovic, M., and Grigolini, P. (2011) , Criticality and transmission of information in a swarm of cooperative units. Phys. Rev. Lett. 107, 078103.
Werner, G. (2010). Fractals in the nervous system: conceptual implications for theoretical neuroscience. Front. Physiol. 1:15. doi:10.3389/fphys.2010.00015
Keywords: criticality, cooperation, complex topology, inverse power law
Citation: Turalska M, Geneston E, West BJ, Allegrini P and Grigolini P (2012) Cooperation-induced topological complexity: a promising road to fault tolerance and hebbian learning. Front. Physio. 3:52. doi: 10.3389/fphys.2012.00052
Received: 27 October 2011; Paper pending published: 09 December 2011;
Accepted: 26 February 2012; Published online: 16 March 2012.
Edited by:
Bruce J. West, United States Army Research Office, USAReviewed by:
Mauro Bologna, Universitdad de Tarapacá-Casilla, ChileVadim Uritsky, Catholic University of America at NASA Goddard Space Flight Center, USA
Copyright: © 2012 Turalska, Geneston, West, Allegrini and Grigolini. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Paolo Allegrini, Istituto di Fisiologia Clinica (IFC-CNR), Via Moruzzi 1, 56124 Pisa, Italy. e-mail:YWxsZWdyaXBAZGYudW5pcGkuaXQ=




