- 1 Center for Nonlinear Science, University of North Texas, Denton, TX, USA
- 2 Centro EXTREME, Scuola Superiore Sant’Anna, Pisa, Italy
- 3 Istituto di Fisiologia Clinica-CNR, Pisa, Italy
- 4 Department of Physics, La Sierra University, Riverside, CA, USA
- 5 Information Science Directorate, US Army Research Office, Durham, NC, USA
We address the issue of criticality that is attracting the attention of an increasing number of neurophysiologists. Our main purpose is to establish the specific nature of some dynamical processes that although physically different, are usually termed as “critical,” and we focus on those characterized by the cooperative interaction of many units. We notice that the term “criticality” has been adopted to denote both noise-induced phase transitions and Self-Organized Criticality (SOC) with no clear connection with the traditional phase transitions, namely the transformation of a thermodynamic system from one state of matter to another. We notice the recent attractive proposal of extended criticality advocated by Bailly and Longo, which is realized through a wide set of critical points rather than emerging as a singularity from a unique value of the control parameter. We study a set of cooperatively firing neurons and we show that for an extended set of interaction couplings the system exhibits a form of temporal complexity similar to that emerging at criticality from ordinary phase transitions. This extended criticality regime is characterized by three main properties: (i) In the ideal limiting case of infinitely large time period, temporal complexity corresponds to Mittag-Leffler complexity; (ii) For large values of the interaction coupling the periodic nature of the process becomes predominant while maintaining to some extent, in the intermediate time asymptotic region, the signature of complexity; (iii) Focusing our attention on firing neuron avalanches, we find two of the popular SOC properties, namely the power indexes 2 and 1.5 respectively for time length and for the intensity of the avalanches. We derive the main conclusion that SOC emerges from extended criticality, thereby explaining the experimental observation of Plenz and Beggs: avalanches occur in time with surprisingly regularity, in apparent conflict with the temporal complexity of physical critical points.
1. Introduction
Bridging psychology and neurophysiology is a challenging issue of the twenty-first century whose origin traces back to the middle nineteenth century. In fact, as pointed out by Kinouchi and Copelli (2006) the work of Weber and Fechner in the middle of the nineteenth century, on how physical stimuli turn into psychological sensation is a fundamental mind-brain problem, which has influenced the foundation of psychology by James (Hawkins, 2011). Kinouchi and Copelli (2006) show that synchronization and global oscillations allow the coding of information spanning several orders of magnitude and claim that this mechanism could provide a microscopic neural basis for psychophysical laws. The basic idea behind the work of Kinouchi and Copelli (2006) is that in biological complex systems the optimal information processing is found near phase transitions, and that the efficiency of biologically relevant processes is optimized at criticality. Criticality of phase transition is one of the most important achievements of the twentieth century physics, thereby implying a transition from the middle nineteenth century to the second half of the twentieth century.
Chialvo (2010) points out that, although understanding the brain is still certainly a challenge (Chialvo, 2010), there are spatiotemporal brain data with which to confront theories, provided that criticality is taken into due account. Criticality is a concept that is attracting a fastly increasing number of researchers in the field of Complexity, with applications ranging from neurophysiology (Levina et al., 2009) to stock-price fluctuations (Kiyono et al., 2006). The term criticality, however, remains not quite clearly defined. In addition to the classical second-order phase transition, where temperature is the control parameter, the term criticality has been used to denote processes as different as noise-induced phase transitions (Van den Broeck et al., 1994) and Self-Organized Criticality (SOC), whereas the identification of the occurrence of criticality through the observation of time series is considered to be a challenging task requiring special techniques (Varotsos et al., 2011) holding true for both the 2D Ising model and SOC.
More recently, it has been pointed out (Bailly and Longo, 2011) that moving from physical to biological systems may require an extension of the concept of criticality, namely, the adoption of Extended Criticality (EC). These authors point out that in physics phase transitions are treated as “singular events,” corresponding to a specific well-defined value of the control parameter. When this singular event occurs, the fluctuations are enhanced and their correlation length becomes as large as the system’s size (Stanley, 1999). In biology, these “coherent critical structures” are “extended” and organized in such a way that they persist in space and time. Living matter organizes itself in a sequence of phase transitions, beyond the punctual edge of chaos that seems to be shared by all forms of phase transitions in physics, from noise-induced to self-organized criticality.
Where does the transition from physical to extended criticality occur? Is it possible that complex physical systems may show signs of EC? In the last few years the researchers of the Pisa lab of professor Leone Fronzoni (Fronzoni and Allegrini, 2009; Silvestri et al., 2009; Allegrini et al., 2010) have studied the weak turbulence on liquid crystals and have found that as an effect of the cooperative interaction between defects, annihilation, and creation of coherent structures take place through the occurrence of crucial events, namely, the distance between two consecutive events, denoted by the symbol τ, does not have memory of the earlier distances and has a distribution density ψ(τ) with the form ψ(τ) ∝ 1/τμ and 1 < μ < 3. These authors defined the control parameter ε = V/V0 − 1, where V0 is a threshold voltage at which convective instability emerges, and found that the phase transition to temporal complexity, rather than being restricted to a single value of ε is extended to a wide interval of values of ε.
In this article we study the statistical properties of a model for neuron dynamics recently proposed by Geneston and Grigolini (2011). We shall show that this model generates experimental avalanches of the same kind as those revealed by the experimental work of Beggs and Plenz(2003, 2004), interpreted by Chialvo (2010) as a SOC property, thereby suggesting that this model may produce SOC criticality.
The time distance between two consecutive avalanches is described by a waiting time distribution density ψ(τ) that has to be compared to the distribution density of time distances between two consecutive liquid crystal crucial events. We shall focus our attention on the function Ψ(τ) defined by
namely, the probability that no new avalanche occurs up to a time distance τ from an earlier avalanche.
We shall find properties similar to those experimentally observed through the liquid crystals of the lab of professor Fronzoni. The neurons of the model interact through a cooperation parameter K generating different values of a complexity parameter α, which is related to the temporal complexity of the liquid crystals through μ = 1 + α. The parameter α is frequently adopted to denote the Mittag-Leffler (ML) relaxation process. As pointed out by Metzler and Klafter (2002), the important property of the ML function is the establishment of a bridge between stretched exponential and inverse-power law relaxation. To point out the importance of ML complexity, let us notice that the temporal complexity of liquid crystals is described by a distribution density of inter-event times
and by the corresponding survival probability
In equation 2 the parameter T is introduced for the main purpose of eliminating the unphysical short-time divergencies and ensuring the proper normalization condition, thereby making it possible for us to focus on the long-time regime. Thus, the short-time regime remains essentially unknown and T only plays the limited role of effective parameter. In other words, T defines the time scale of the microscopic regime where the collective properties generated by the interaction between the system’s units do not appear yet. In the case of ML complexity, on the contrary, the short-time relaxation is described by the stretched exponential exp(−(λt)α), with α < 1. The term short-time scale is not appropriate to describe the stretched exponential portion of the ML relaxation. In fact, the deviation from the ordinary exponential relaxation mirrors collective properties, closely related to the temporal complexity emerging at later times, which is the inverse-power law 1/τα. The term of intermediate asymptotics coined by Barenblatt (1996) is more appropriate to denote the time scale of the stretched exponential relaxation. At the intermediate asymptotics level scaling already appears, in a form that is not yet affected by physical limitations such as boundary conditions. In the case of the model discussed in this article the emergence of the inverse-power law 1/τα is accompanied by the first signs of periodicity that for large values of the cooperation parameter K yields an abrupt truncation of the inverse-power law regime.
The ML complexity settles the controversy between the advocates of complexity as being characterized by relaxation departing from the usual exponential form through a stretched exponential structure and the advocates of inverse-power laws as the most significant signature of complexity. In fact, the long-time regime of the ML relaxation is described by a power law with index α = μ − 1 that makes the far asymptotic time regime of the ML relaxation identical to that of the survival probability of equation 3. Thus, even if statistical inaccuracy, time series finiteness, and other possible reasons may make it difficult to reveal the inverse-power law nature of the long-time regime, the temporal complexity of the ML relaxation is of the same nature as the temporal complexity of the form of equation 3.
These interesting properties generate the question of which is the form of criticality emerging from the neuron cooperation. We shall come back to this interesting problems in the last Section of this article.
2. Materials and Methods
2.1. Mittag-Leffler Temporal Complexity
As mentioned in the Introduction, the temporal complexity emerging from the extended criticality of our model of interacting neurons is given by the Mittag-Leffler (ML) function. A convenient way to illustrate this form of temporal complexity rests on the use of Laplace representation. In this article we adopt for the Laplace transform of the function f(τ) the notation
Using this notation, if we assign to Ψ(τ) the ML form, we have
Via inverse Laplace transformation we get
where Eα(z) is the ML function expressed with respect to time. The series expansion of Eα(z) is
It is known that for α > 1, this function can become oscillatory. We shall restrict our use of the form of temporal complexity to 0 < α ≤ 1, where the ML function is positive and strictly monotonically decreasing.
It is important to stress, as already mentioned in the Introduction, that in the short-time regime τ < 1/λ the ML function has the form of the stretched exponential function
It is important to reiterate an observation made in the earlier work by Geneston and Grigolini (2011). This has to do with the long-time truncation of the ML survival probability. Usually, the long-time truncation of inverse-power laws is thought to be a consequence of the statistical inaccuracy due to the finite sizes of the systems under study. For instance, Failla et al. (2004) and Bianco et al. (2007) adopted the form
with α < 1. In the case Γt= 0 this is the Laplace transform of the ML function of equation 5. However, the experimental observation has forced these authors to introduce the parameter Γt> 0. The experimental results are explained by setting 1/Γt of the order of 1/λ and both much larger than the unit time step: in this case equation 5 generates a function Ψ(t) indistinguishable from a stretched exponential function. In conclusion, in the earlier work the ML complexity is violated in the large time limit by environmental fluctuations that make the system fall in the exponential regime. In the case of this article, on the contrary, as already pointed out by Geneston and Grigolini (2011), the breakdown of the ML condition is due to the same cooperative effect as that making the ML function emerge in the first place.
In this article we observe quakes, namely events corresponding to one or more neurons firing. The physical meaning of the survival probability Ψ(τ) is defined by referring ourselves to the occurrence of a quake as time origin. Given that a quake occurs at the time origin, what is the probability that no new quake occurs up to time τ? The probability of no quake occurrence is the survival probability Ψ(τ). In the absence of cooperation
In this case α = 1 and λ = G. The quantity corresponding to the magnetization of the Ising model is
At criticality λα = G begins departing from the vanishing value. In practice, we observe numerically the quantity
and we use it to establish the critical value of K at which phase-transition occurs.
2.2. Stochastic Version of the Model of Mirollo and Strogatz
This is a model originally proposed by Mirollo and Strogatz (1990) that Geneston and Grigolini (2011) generalized by adding a stochastic fluctuation. Therefore we shall refer to it as Stochastic Mirollo and Strogatz (SMS) model.
The SMS model is based on the dynamics of Ntot neurons. In the absence of cooperation, the dynamics of each neuron are described by the simplest model of a leaky integration-and-fire neuron:
where the natural number t denotes the discrete time, and the leakage factor γ is taken γ ≪ 1 so as to make the integer time virtually continuous when γt ≈ 1. The variable x moves from the initial condition x = 0, therefore the term S > 0, favoring its motion toward threshold x = 1 describes the average neural activity of afferent connections (coming from outside the system of interest); ξ(t) is a random variable getting either the value of 1 or −1, with equal probability, with no memory of the earlier values, and the quantity σ is the noise intensity. The role of the term σξ is that of describing the fluctuations of the afferent neural activity. At the threshold, the neuron fires and resets back to the initial value x = 0.
When σ = 0, it is straightforward to prove that the time necessary for the neuron to reach the threshold is given by
We assume, with Mirollo and Strogatz (1990), that the neurons cooperate, namely, that when one neuron fires all the other neurons make a step ahead by the quantity K < 1 which is the cooperation strength. This condition is equivalent to assume that each neuron interacts with all the other neurons, and it will be referred to as All-To-All coupling condition. This model is very close to the one used by Levina et al. (2010). These authors consider both inhibition and excitation links between neurons. The model of this paper can be derived from that of Levina et al. (2010) by eliminating the inhibition links. Notice that All-To-All condition (or almost All-To-All) and the absence of inhibitory control are here considered as a simplifying approximation. However, they may also be of importance in describing specific pathological conditions, like the Morvan’s syndrome (Liguori et al., 2001).
Mirollo and Strogatz (1990) found the exact solution of this problem when σ = 0 and proved that, after a transient, all the neurons fire at the same time, with time period TMS of equation 14, the MS time.
As an effect of noise, it may take a time either shorter or longer than TMS for a neuron to fire. Furthermore, the time distance between two consecutive firings may be much shorter than TMS. When K = 0, even if we assign to all the neurons the same initial condition, x = 0, due to stochastic fluctuations the neurons fire at different times so that the system eventually reaches a steady state with a constant firing rate G given by
where 〈τ〉 denotes the mean time between two consecutive firings of the single neuron. For σ ≪ 1, 〈τ〉 ≈ TMS. From the condition of constant rate G we immediately derive the Poisson survival probability
We shall see hereby that this heuristic argument agrees very well with numerical results. For the numerical simulation we select the condition
yielding
thereby realizing the time scale of interest for this paper, which is much shorter than the MS time. It is evident that the condition of non-interacting neurons fits equation 5 with α = 1 and
For our numerical calculations we adopt the values σ = 0.001, Ntot= 100, γ = 0.0001, and S = 0.00019. We have assessed numerically that 〈τ〉 = 7431 thereby yielding, thanks to equation 15, G = 0.0135, and TMS= 7472.14. Throughout the paper the time units are expressed in terms of the number of the discrete time steps of the numerical model. The connection with physical times can in principle be established via the connection of TMS with the periodic rhythm under study. However, the scope of the paper is to explore at a theoretical level a possible interplay between criticality and periodicity in cooperative systems. We therefore believe it is premature to adopt at this stage the usage of physical units (e.g., seconds).
Finally, it is important to point out that for larger values of Ntot the same properties are observed as long as the condition (17) is applied.
3. Results
We begin the illustration of the numerical results with Figure 1, which shows the number of firing per unit of time moving from an initial condition where all the neurons are assigned a random value x in the interval (0, 1).
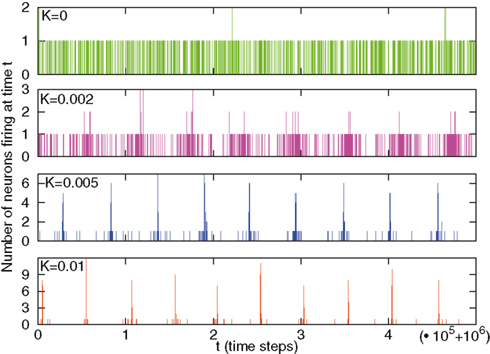
Figure 1. This figure shows the number of firings moving from initial conditions xi taken randomly in the interval (0,1). A very large time (one million time steps) is waited so that memory of initial conditions is completely lost. Different panels refer to different values of the cooperation parameter K. We observe a change in behavior from no coupling (K = 0, upper panel) to larger values of K. For K = 0, for each time, only one or, rarely, two neurons are firing, and the firing times are homogeneous, following a Poisson statistics. For K = 0.002 (second panel) we see some sporadic events with three neurons firing, tending to take place in periodical patterns; non-Poisson “holes” of silence, with large duration variability, emerge in between. For K = 0.005 (third panel) we see events with higher numbers of neurons concurrently firing, and longer silence durations. For K = 0.01 (lower panel) the system is almost periodic, and silence durations can be as long as the distance between major peaks.
We see that for small values of K the number of firings is almost constant in time. Increasing K has the effect of generating a more complex time structure, which in the limiting case of very large values of K is expected to fit the periodicity of the original model of Mirollo and Strogatz.
We are in the presence of a situation more complex than that corresponding to the ordinary renewal condition (Turalska et al., 2011). When the ordinary criticality condition applies, namely the phase-transition generated by a single value of the control parameter is realized, organizational collapses occur (Vanni et al., 2011), and they are proved to be renewal events (Turalska et al., 2011). In the case of the SMS model, as already suggested by Figure 1, the emergence of criticality is accompanied by signs of periodicity that become predominant at large values of the control parameter K.
Let us now move to discuss the statistical properties of firing avalanches. First of all we study the time distance between two consecutive avalanches. We are interested in the time asymptotic properties of the survival probability Ψ(τ). For this reason we do not have to define the minimal distance between two consecutive avalanches, as we shall have to do to study the avalanche time duration. We limit ourselves to record the time distance between two consecutive firings, regardless of the number of neurons contributing to them. This allows us to define ψ(τ). Then, using equation 1 we determine the survival probability Ψ(τ), illustrated in Figure 2. Figure 2 is helpful to evaluate with theoretical arguments the surprising mixture of time complexity and time periodicity that is suggested by Figure 1. We see, in fact, that increasing K has the effect of turning the Poisson statistics of the condition with no cooperation (see the insert) into a form of exact periodicity, as shown by the fifth curve (the upper one, denoted by K = 0.1) of this Figure, where the abrupt jump to 0 of the survival probability corresponds to all the neurons firing together with the time period of equation 14.
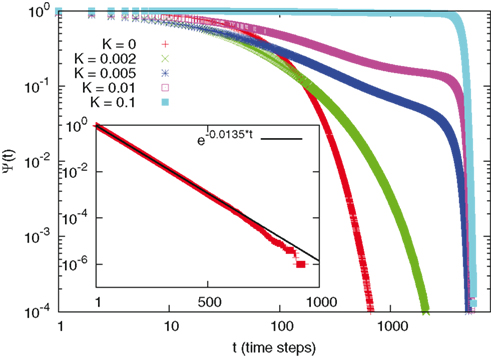
Figure 2. Survival probability for different values of K. As we move from K = 0 (lower curve) to higher values of K we see the passage from Poisson behavior (shown in the insert as a straight line in semi-log scale) to a step-like function at the highest vale of K (K = 0.1) here reported, signaling complete periodicity. For intermediate values complex non-Poisson decays are visible, followed by abrupt cutoffs, due to periodicity.
Figure 3 illustrates the fitting procedure adopted to prove the emergence of the cooperation-induced ML complexity. At variance with the earlier analysis of Geneston and Grigolini (2011), we fitted directly the numerical Laplace transforms of the experimental survival probabilities with the Mittag-Leffler function in the Laplace representation, given by equations 6 and 7. For this purpose we selected a suitable interval for u. From the parameters α and λ obtained via the fitting procedure, the stretched exponential (8) has been visually superimposed to the survival probability data in the time representation, in the early regime, and a slope α + 1 has been superimposed to an intermediate regime, before the cutoff, as shown in the inset of Figure 3. As a result, the quality of fit has been excellent for all values of coupling parameter K, with very slight deviations only at the critical value K = 0.002.
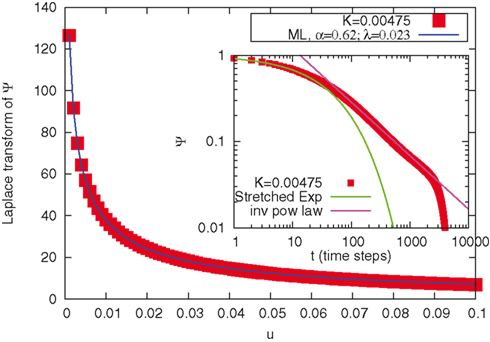
Figure 3. Illustration of the fitting procedure adopted to prove the cooperation-induced emergence of the ML complexity. In the main figure the numerical Laplace transform of the Survival probability is plotted, for K = 0.00475 (squares). The solid line represent the fitted ML function, in the Laplace representation. The resulting fitting parameters are in this example α = 0.62 and λ = 0.023. In the insert we plot the same survival probability, but this time in the time domain. A stretched exponential exp[ − (λt)α] is superimposed in the shorter time regime, called intermediate asymptotic regime; an inverse-power law constant/tα is superimposed in the far asymptotic regime. We notice the good agreement in both the Laplace and the time representation.
It is possible to see the emergence of a clear trend, illustrated in Figure 4. The temporal complexity parameter α at K = 0 has the value α = 1, corresponding to μ = 2, which is, in fact, the boundary with the ergodic regime. The inverse-power law component drops to zero, and the stretched exponential function becomes an ordinary exponential function. As soon as we switch on the cooperation parameter, temporal complexity emerges with α < 1 and μ < 2. While for K < 0.002 α slowly decreases with increasing K, at K ≈ 0.002 it undergoes a fast drop and remains close to α ≈ 0.6 for an extended range. The parameter λ shows a steep increase at K = 0.002, reaches a maximum around k = 0.00275 and decreases for larger values of K. The complexity indicator λα increases slowly from the value of G at K = 0 to larger values at about K = 0.002 where it undergoes a faster increase that Geneston and Grigolini (2011) interpreted as a form of ordinary transition rounded by finite size effects. Actually this parameter does not saturate for increasing values of K, since for values larger than K ≈ 0.0035 it tends to slowly decrease. On the basis of the fitting procedure of this article we are inclined to interpret all this as a form of extended criticality rather than an ordinary criticality corresponding to the single value K ≈ 0.002.
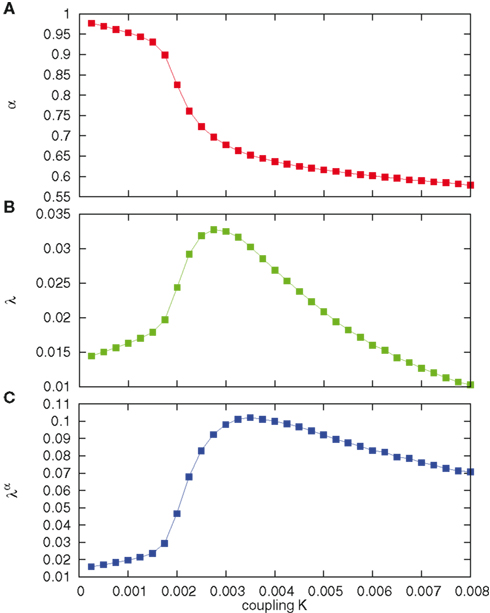
Figure 4. (A) Complexity fractal index α as a function of the cooperation parameter K. Notice the change in the steepness of descent near K = 0.002. (B) Temporal parameter λ reaches a maximum for K = 0.00275. Notice again a change in the steepness near K = 0.002. (C) The order parameter λα, as a function K, shows a behavior similar to second-order phase transition, but with rounded increase at K = 0.002 and slow decay after a maximum.
Finally, Figures 5–7 refer to the neural avalanches that have been the focus of the research work of Beggs and Plenz (2004). Chialvo (2010) considers the avalanches experimentally revealed by Beggs and Plenz to be a striking manifestation of SOC (Zapperi et al., 1995; De Arcangelis et al., 2006). Figure 5 shows the intensity of avalanches as a function of the cooperation parameter K. Some caution has to be exerted in defining the avalanche: Due to finite statistics and discrete time, it happens that actual avalanches may present “holes,” namely times within the avalanche where no neuron is firing. This makes it difficult to operatively define an avalanche starting from the data. As in the original work of Beggs and Plenz (2004) we defined a tolerance time Δt: Avalanches are thus defined as patterns of neuron firing separated from one another of at least Δt time steps. In other words, the starting of an avalanche is the first time step following a silence period lasting at least Δt time steps. Results not herein reported show that the analysis of avalanche size, duration, and mean shape depend on the choice of Δt. We choose Δt = 5 time steps, because we saw that numerically the inverse-power law indexes of the probability densities for avalanche size and duration would not change with further increasing that value, for all values of K herein reported.
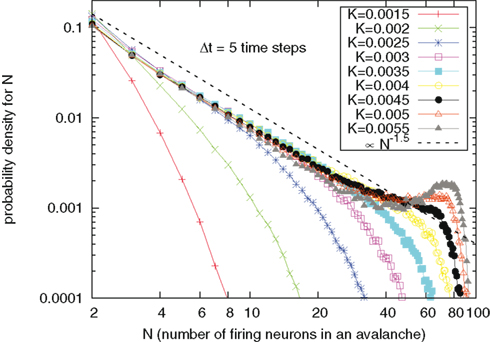
Figure 5. Probability density for N, the number of neurons within an avalanche, as a function of N, for different values of cooperation parameter K. The dashed line is a guide to the eye, signaling an inverse-power law decay ∝N−1.5. For K > 0.002 there is an accumulation of curves on a straight line parallel to the eye guide.
We see that in the case of no coupling the avalanche’s intensity falls down exponentially upon increasing their intensity. With increasing the cooperation parameter K there is an accumulation of curves around an inverse-power law with index ζ = 1.5 as K overcomes the critical value. With further increase of K the inverse-power law does not change, but a peak becomes predominant at large times. This is a manifestation of the tendency for the system to recover the periodicity of the model of Mirollo and Strogatz.
The analysis of the distribution of time duration of the avalanches generates, as shown in Figure 6, results similar to those concerning the intensity distribution, thereby suggesting a correspondence between intensity and duration.
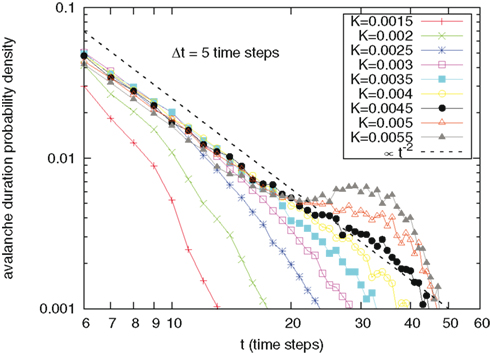
Figure 6. Probability density for avalanche durations t, namely the time difference between an avalanche starting and a silence period of at least Δt = 5 time steps, for different values of cooperation parameter K. The dashed line is a guide to the eye, signaling an inverse-power law decay ∝t−2. Again, for K > 0.002 there is an accumulation of curves on a straight line parallel to the eye guide.
It is interesting to notice that the theoretical value of ζ = 1.5 for avalanche sizes and ν = 2 for avalanche durations experimentally observed by Beggs and Plenz (2003) are realized in our model, even in a region that is strongly influenced by periodicity. We remind that although these SOC critical signatures are conserved in this broad region, the fractal statistics of inter-avalanche times, corresponding to Figure 4, change. In particular, the fractal index α continuously varies from the value α = 1, for independent neurons, to smaller values, of the order of 1/2 for large choices of cooperation parameter K. All this thereby suggests a significant departure from the condition of temporal complexity corresponding to the conventional criticality (Turalska et al., 2011), corresponding in turn to a single value of the control parameter.
We have also adopted the procedure of Levina et al. (2007) to determine the avalanche’s shape. This is described by Figure 7. We have considered the times at which avalanches begin as the time origin. Then, for any time larger than Δt we have evaluated the mean number of firing neurons, as an average over all the avalanches. We have recovered an interesting effect found by Levina et al. (2007). In the correspondence of a cooperation parameter so large as to make periodicity predominant, K = 0.007, we see that the decay of the avalanche’s shape is not monotonic, and that the avalanche’s intensity increases, reaches a maximum, and it decays again. This is a consequence of the avalanche’s periodicity (Beggs and Plenz, 2004). Adopting a Gibbs’ ensemble representation, we can state that in this regime the events signaling that an avalanche begins can be interpreted as precursors of big avalanches occurring later.
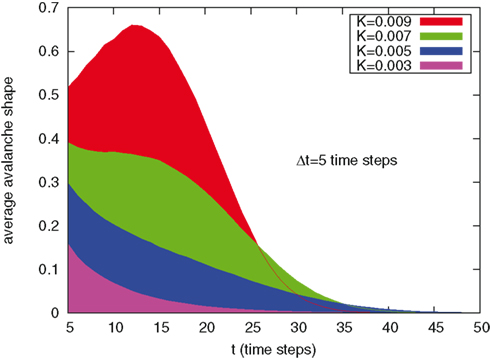
Figure 7. Avalanche mean shape, i.e. average number of firing neurons after t time steps form the avalanche starting, for different values of K.
4. Discussion
4.1. Criticality of Neural Networks
The SMS model generates neural avalanches: for many values of K it yields the value of ζ = 1.5 for avalanche size and ν = 2 for avalanche durations, in accordance with the experimental observations by Beggs and Plenz (2003). According to Chialvo (2010) these are typical SOC signatures, thereby generating the impression that the SMS model may be a form of SOC. However, Aschwanden (2011) has recently pointed out that there are “three necessary and (perhaps) sufficient criteria” to establish if a system is a SOC system. These are: Statistical Independence, Non-linear Coherent Growth, and Random Duration of Rise Time. We think that none of these properties is obeyed by the SMS model of this paper. Therefore we are inclined to believe that its criticality is not a SOC. This makes us conclude that the SOC theoretical framework is not the only one explaining the main properties of neural avalanches.
The next question to answer is as to whether the cooperation-induced temporal complexity is of the same kind as that produced by the phase-transition processes. Interesting examples of this form of criticality are given by the recent papers of Turalska et al. (2011) and Vanni et al. (2011). These authors show that at phase transition a metastable consensus condition occurs, with abrupt organizational collapses. The survival probability, namely the probability that no organizational collapse occurs, has the inverse-power law structure of equation 3. This property is limited to a singular value of the cooperation parameter K. With the SMS model, as clearly shown by Figure 4, changing K has the effect of changing temporal complexity. We are therefore inclined to believe that the SMS model is a form of extended criticality, whose temporal complexity in the intermediate asymptotic condition is characterized by stretched exponential relaxation.
In the far asymptotic regime the fat tail of the survival probability Ψ(τ) is truncated by a periodicity-induced fast drop, thereby breaking the renewal ML complexity (Metzler and Klafter, 2002). Is this a biological property compatible with the concept of EC? According to Bailly and Longo, EC signals the transition from physics to biology, and the SMS model is a model introduced for the specific purpose of interpreting neural dynamics. Although it may be questionable as all models that are currently proposed to shed light into complexity, the SMS model generates a form of periodicity that agrees qualitatively with the experimental observation (Beggs and Plenz, 2004). Furthermore, we have to keep in mind the natural periodicity of biological systems, evident in the concept itself of the ubiquitous “biological clock” (Winfree, 2000), and this does in fact support the view that periodicity reinforces rather than weakens the biological nature of a model. These arguments strengthen our conviction that the SMS model is compatible with the concept of extended criticality of Bailey and Longo.
We note that the theoretical interpretation of the experimental results on liquid crystals (Silvestri et al., 2009; Allegrini et al., 2010), although sharing with EC the condition that the control parameter is not a singular value, is based on the concept of renewal aging that implies the occurrence of quakes or organizational collapses (Vanni et al., 2011). These organizational collapses reset to zero the system’s memory, thereby creating a condition incompatible with the temporal precision of activity patterns (Beggs and Plenz, 2004). We therefore expect that the SMS model of this paper should stimulate theoretical progress to extend the concept of temporal criticality so as to make it compatible with the complexity of the far asymptotics.
4.2. Criticality and the Brain
The intriguing issue as to which form of criticality is obeyed by the brain has been debated in the earlier work by Allegrini et al. (2010). These authors found that the index ζ of the distribution of avalanches intensity is 1.92, and thus significantly different from the SOC prediction ζ = 1.5. On the other hand, the statistical analysis made by Allegrini and co-workers seems to be more compatible with the standard concept of phase-transition induced criticality. These authors find that the temporal complexity of the events corresponding to the simultaneous occurrence of bursts in different channels is different from the temporal complexity of the single channels. The analysis of the single channels (Ignaccolo et al., 2010) discloses the emergence of a coherent behavior that may be related to the time periodicity addressed in this article, thereby leading to the conclusion that the global behavior of the brain may correspond to the phase-transition induced criticality, triggered by the cooperation among different brain components, while the dynamics of the single channels may correspond to a different kind of criticality, compatible with coherent dynamics. This form of criticality might be the extended criticality of Bailly and Longo (2011).
It is important to keep in mind that there is a deep difference between the brain, thought of as network of networks, and the dynamics of its components, namely neural networks that may be adequately described by the SMS model of this paper. The recent model proposed by Kello et al. (2011) is an attempt at understanding the global properties of the brain and the 1/f scaling of this model fits the observation of Allegrini et al. (2009b) who interpret the brain as a source of ideal 1/f noise.
4.3. Complexity Management: A Challenge
A further issue generated by the result of this article is the extension of the Fluctuation Dissipation Theorem of first kind (Allegrini et al., 2009a) and of the Complexity Management (Aquino et al., 2010, 2011). To understand the conceptual difficulty of this important issue, we must recall that Fluctuation Dissipation Theorem in statistical physics has a long history, ranging from the 1905 Einstein paper on Brownian motion and Onsagers regression hypothesis to the more recent work of Kubo et al. (1985), whose linear response theory (LRT) is in fact considered by Lee (2007) to be the basic theoretical tool for the ergodic condition produced by Hamiltonian systems. In the case of the dynamics of the brain this traditional approach cannot be adopted, because of the lack of ergodicity condition, not to speak about the lack (or the impossibility) of a Hamiltonian treatment. The dynamical Fluctuation Dissipation Theorem proposed by Allegrini et al. (2007) is the first attempt at establishing a LRT for a system driven by renewal events violating the ergodic condition. The Complexity Management (or Complexity Matching) proposed by Aquino et al. (2011) rests on the surprising discovery that information can be transmitted by a complex network to another via an extremely weak coupling provided that a form of resonance exists between the complexity of the perturbed system and the complexity of the perturbing one.
The coexistence of temporal complexity and periodicity raises the question of whether the Fluctuation Dissipation Theorem and the related complexity management can be extended so as to deal with this more complex condition.
4.4. Conjectures and Plan for Future Research Work
One of the most important issues concerning the brain function is as to whether the brain does or does not compute. Werner made a strong warning against the adoption of the computer paradigm to explain the brain function (Werner, 2011). Neurons do not compute and function at meso- and macroscopic levels through a process of self-organization that makes significant their collective dynamics and irrelevant the behavior of single neurons as computational units. According to Werner the role of computer simulation is that of affording an epistemic access to their ontological states. This is an important warning that must be taken into a proper account. It seems to us that this warning may fit Varela’s principles (Varela, 1979), in the form recently advocated by Mira and Delgado García (2007). These authors developed an “extended computation paradigm” whose main aim is to avoid contamination between the “External Observer Domain” and the “Own Domain.” We freely interpret the External Observer Domain and the Own Domain of Mira and Delgado as the epistemic level and ontological levels of Werner, respectively.
We notice that the role of the neuron cooperation is also recognized by Soares et al. (2011) who propose the creation of coupled networks to make a significant progress toward the creation of intelligent systems.
The interaction between different neuron networks may account for the apparent conflict between the observation of coherence (Ignaccolo et al., 2010) and the observation of ordinary criticality at the level of global behavior of the brain (Allegrini et al., 2009b). A theoretical result based on the interaction between different neural networks would reinforce the perspective that to shed light into consciousness it is necessary to move from the action of the single neurons or group of neurons to the interaction and probably cooperative behavior of neural networks interpreted as complex systems by their own.
Research work in this direction is possible thanks to significant technological advances with neuron cultures done in the last 30 years (Gross et al., 1982). It is interesting to notice that there exists a gap between these experimental advances and the theoretical understanding. The results of this article suggest research directions that should fill this gap. We should move from the All-To-All condition to the adoption of a more proper topology. This is closely connected to the issue of how “information” is transferred from one to another network. As earlier stated, this requires the extension of Complexity Management to the case where temporal complexity and time periodicity coexist. Furthermore, although the assumption of extremely weak stimuli makes it possible the adoption of analytical treatments, it is necessary to go beyond it while maintaining the extremely useful suggestion that complexity matching may be the crucial ingredient for information transmission.
Finally, we want to stress that if the kind of criticality operating at the level of the model adopted in this article, is really a form of EC (Bailly and Longo, 2011) the arguments of these authors can be adopted to support our conviction that we are operating at a genuinely biological level.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Elisa Lovecchio and Paolo Grigolini thankfully acknowledge financial support from ARO through Grant No. W911NF-08-1-0177.
References
Allegrini, A., Bologna, M., Grigolini, P., and West, B. J. (2007). Fluctuation-dissipation theorem for event-dominated processes. Phys. Rev. Lett. 99, 010603.
Allegrini, P., Bologna, M., Fronzoni, L., Grigolini, P., and Silvestri, L. (2009a). Experimental quenching of harmonic stimuli: universality of linear response theory. Phys. Rev. Lett. 103, 030602.
Allegrini, P., Menicucci, D., Bedini, R., Fronzoni, L., Gemignani, A., Grigolini, P., West, B. J., and Paradisi, P. (2009b). Spontaneous brain activity as a source of ideal 1/f noise. Phys. Rev. E 80, 061914.
Allegrini, P., Paradisi, P., Menicucci, D., and Gemignani, A. (2010). Fractal complexity in spontaneous EEG metastable-state transitions: new vistas on integrated neural dynamics. Front. Physiol. 1:128. doi:10.3389/fphys.2010.00128
Aquino, G., Bologna, M., Grigolini, P., and West, B. J. (2010). Beyond the death of linear response: 1/f optimal information transport. Phys. Rev. Lett. 105, 040601.
Aquino, G., Bologna, M., West, B. J., and Grigolini, P. (2011). Transmission of information between complex systems: 1/f resonance. Phys. Rev. E 83, 051130.
Aschwanden, M. (2011). Self-Organized Criticality in Astrophysics: The Statistics of Nonlinear Processes in the Universe. Berlin: Springer.
Bailly, F., and Longo, G. (2011). Mathematics and the Natural Sciences. The Physical Singularity of Life. Singapore: Imperial College Press/World Scientific [preliminary version, in French: Hermann, Paris, 2006].
Barenblatt, G. I. (1996). Scaling, Self-Similarity, and Intermediate Asymptotics: Dimensional Analysis and Intermediate Asymptotics. Cambridge Texts in Applied Mathematics. Cambridge: Cambridge UniversityPress.
Beggs, J. M., and Plenz, D. (2003). Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177.
Beggs, J. M., and Plenz, D. (2004). Neuronal avalanches are diverse and precise activity patterns that are stable for many hours in cortical slice cultures. J. Neurosci. 24, 5216–5229.
Bianco, S., Ignaccolo, M., Rider, M. S., Ross, M. J., Winsor, P., and Grigolini, P. (2007). Brain, music, and non-Poisson renewal processes. Phys. Rev. E 75, 061911.
De Arcangelis, L., Perrone-Capano, C., and Herrmann, H. J. (2006). Self-organized criticality model for brain plasticity. Phys. Rev. Lett. 96, 028107.
Failla, R., Grigolini, P., Ignaccolo, M., and Schwettmann, A. (2004). Random growth of interfaces as a subordinated process. Phys. Rev. E 70, 010101.
Fronzoni, L., and Allegrini, P. (2009). Movies of the Defects Dynamics, with Relative Description. Available at: http://mail.df.unipi.it/∼allegrip/liquid_crystal.html
Geneston, E., and Grigolini, P. (2011). “Quakes in complex systems as a signature of cooperation,” in World Scientific, Studies of Nonlinear Phenomena in Life Science, Singapore, Vol. 15, 135–160.
Gross, G. W., Williams, A. N., and Lucas, J. H. (1982). Recording of spontaneous activity with photoetched microelectrode surfaces from mouse spinal neurons in culture. J. Neurosci. Methods 5, 13–22. [For a recent review see: G. W. Gross, Multielectrode arrays. Scholarpedia 6, 5749 (2011)].
Hawkins, S. (2011). William James, Gustav Fechner, and early psychophysics. Front. Physiol. 2:68. doi:10.3389/fphys.2011.00068
Ignaccolo, M., Latka, M., Jernajczyk, W., Grigolini, P., and West, J. B. (2010). Dynamics of electroencephalogram entropy and pitfalls of scaling detection. Phys. Rev. E. 81, 031909.
Kello, C. T., Kerster, B., and Johnson, E. (2011). “Critical branching neural computations, neuronal avalanches, and 1/f scaling,” in Proceeddings of the 33rd Annual Conference of the Cognitive Science Society. Available at: http://cogmech.ucmerced.edu/pubs/KelloETAL11-cogsciproc.pdf
Kinouchi, O., and Copelli, M. (2006). Optimal dynamical range of excitable networks at criticality. Nat. Phys. 2, 348–352.
Kiyono, K., Struzik, Z. R., and Yamamoto, Y. (2006). Criticality and phase transition in stock-price fluctuations. Phys. Rev. Lett. 96, 068701.
Kubo, R., Toda, M., and Hashitsume, N. (1985). Statistical Physics II: Nonequilibrium Statistical Mechanics. Berlin: Springer-Verlag.
Lee, M. H. (2007). Birkhoff’s theorem, many-body response functions, and the ergodic condition. Phys. Rev. Lett. 98, 110403.
Levina, A., Ernst, U., and Hermann, J. M. (2007). Criticality of avalanche dynamics in adaptive recurrent networks. Neurocomputing 70, 1877–1881.
Levina, A., Hermann, J. M., and Geisel, T. (2010). Dynamical synapses causing self-organized criticality in neural networks. Nat. Phys. 3, 857–860.
Levina, A., Herrmann, J. M., and Geisel, T. (2009). Phase transitions towards criticality in a neural system with adaptive interactions. Phys. Rev. Lett. 102, 118110.
Liguori, R., Vincent, A., Clover, L., Avoni, P., Plazzi, G., Cortelli, P., Baruzzi, A., Carey, T., Gambetti, P., Lugaresi, E., and Montagna, P. (2001). Morvan’s syndrome: peripheral and central nervous system and cardiac involvement with antibodies to voltage-gated potassium channels. Brain 124, 2417–2426.
Metzler, R., and Klafter, J. (2002). From stretched exponential to inverse-power law: fractional dynamics, cole-cole relaxation processes, and beyond. J. Non Cryst. Solids 305, 81–87.
Mira, J., and Delgado García, A. E. (2007). On how the computational paradigm can help us to model and interpret the neural function. Nat. Comput. 6, 211–240.
Mirollo, R. E., and Strogatz, S. H. (1990). Synchronization of pulse-coupled biological oscillators. SIAM J. Appl. Math. 50, 1645–1662.
Silvestri, L., Fronzoni, L., Grigolini, P., and Allegrini, P. (2009). Event-driven power-law relaxation in weak turbulence. Phys. Rev. Lett. 102, 014502.
Soares, G. E., Borges, H. E., Gomes, R. M., Zeferino, G. M., and Braga, A. P. (2011). Emergence of synchronicity in a self-organizing spiking neuron networks: an approach via genetic algorithms. Nat. Comput. doi: 10.1007/s11047-011-9288-3
Stanley, H. E. (1999). Scaling, universality, and renormalization: Three pillars of modern critical phenomena. Rev. Mod. Phys. 71, S358–S366.
Turalska, M., West, B. J., and Grigolini, P. (2011). Temporal complexity of the order parameter at the phase transition. Phys. Rev. E 83, 061142.
Van den Broeck, C., Parrondo, J. M. R., and Toral, R. (1994). Noise-induced nonequilibrium phase transition. Phys. Rev. Lett. 73, 3395.
Vanni, F., Lukovic, M., and Grigolini, P. (2011). Criticality and transmission of information in a swarm of cooperative units. Phys. Rev. Lett. 107, 078103.
Varela, F. (1979). Principles of Biological Autonomy. The North Holland Series in General Systems Research. New York: North Holland.
Varotsos, P., Sarlis, N. V., Skordas, E. S., Uyeda, S., and Kamogawa, M. (2011). Natural time analysis of critical phenomena. Proc. Natl. Acad. Sci. U.S.A. 108, 11361–11364.
Werner, G. (2011). Letting the brain speak for itself. Front. Fractal Physiol. 2:60 doi:10.3389/fphys.2011.00060
Keywords: SOC, extended criticality, neural networks, cooperation
Citation: Lovecchio E, Allegrini P, Geneston E, West BJ and Grigolini P (2012) From self-organized to extended criticality. Front. Physio. 3:98. doi: 10.3389/fphys.2012.00098
Received: 24 October 2011; Accepted: 30 March 2012;
Published online: 26 April 2012.
Edited by:
Zbigniew R. Struzik, The University of Tokyo, JapanReviewed by:
Zbigniew R. Struzik, The University of Tokyo, JapanFred Hasselman, Radboud University Nijmegen, Netherlands
Klaus Linkenkaer-Hansen, Center for Neurogenomics and Cognitive Research, Netherlands
Copyright: © 2012 Lovecchio, Allegrini, Geneston, West and Grigolini. This is an open-access article distributed under the terms of the Creative Commons Attribution Non Commercial License, which permits non-commercial use, distribution, and reproduction in other forums, provided the original authors and source are credited.
*Correspondence: Paolo Allegrini, Istituto di Fisiologia Clinica-CNR, Via Moruzzi 1, 56124 Pisa, Italy. e-mail:YWxsZWdyaW5pQGlmYy5jbnIuaXQ=; Paolo Grigolini, Center for Nonlinear Science, University of North Texas, Denton, TX 76203-1427, USA. e-mail:Z3JpZ29AdW50LmVkdQ==




