- 1Division of Public Administration, Center for Research and Teaching in Economics (CIDE), Aguascalientes, Mexico
- 2Institute for Technology Assessment, Massachusetts General Hospital, Boston, MA, United States
- 3Decision and Infrastructure Sciences Division, Argonne National Laboratory, Argonne, IL, United States
- 4Consortium for Advanced Science and Engineering, University of Chicago, Chicago, IL, United States
- 5Division of Health Policy and Management, University of Minnesota School of Public Health, Minneapolis, MN, United States
Background: We evaluated the implications of different approaches to characterize the uncertainty of calibrated parameters of microsimulation decision models (DMs) and quantified the value of such uncertainty in decision making.
Methods: We calibrated the natural history model of CRC to simulated epidemiological data with different degrees of uncertainty and obtained the joint posterior distribution of the parameters using a Bayesian approach. We conducted a probabilistic sensitivity analysis (PSA) on all the model parameters with different characterizations of the uncertainty of the calibrated parameters. We estimated the value of uncertainty of the various characterizations with a value of information analysis. We conducted all analyses using high-performance computing resources running the Extreme-scale Model Exploration with Swift (EMEWS) framework.
Results: The posterior distribution had a high correlation among some parameters. The parameters of the Weibull hazard function for the age of onset of adenomas had the highest posterior correlation of −0.958. When comparing full posterior distributions and the maximum-a-posteriori estimate of the calibrated parameters, there is little difference in the spread of the distribution of the CEA outcomes with a similar expected value of perfect information (EVPI) of $653 and $685, respectively, at a willingness-to-pay (WTP) threshold of $66,000 per quality-adjusted life year (QALY). Ignoring correlation on the calibrated parameters’ posterior distribution produced the broadest distribution of CEA outcomes and the highest EVPI of $809 at the same WTP threshold.
Conclusion: Different characterizations of the uncertainty of calibrated parameters affect the expected value of eliminating parametric uncertainty on the CEA. Ignoring inherent correlation among calibrated parameters on a PSA overestimates the value of uncertainty.
Background
Decision models (DMs) are commonly used in cost-effectiveness analysis where uncertainty in the parameters is inherent (Kuntz et al., 2017). The impact of parameter uncertainty can be assessed with a probabilistic sensitivity analysis (PSA) to characterize decision uncertainty (i.e., the probability of a strategy being cost-effective) (Briggs et al., 2012; Sculpher et al., 2017) and to quantify the value of potential future research by determining the potential consequences of a decision with value of information (VOI) analysis (Schlaifer, 1959; Raiffa and Schlaifer, 1961).
The parameters of DMs can be split into two categories, those obtained from the literature or estimated from available data (i.e., external parameters) and those that need to be estimated through calibration (i.e., calibrated parameters). External parameters are estimated either from individual-level or aggregated data that directly inform the parameters of interest. There are recommendations on the type of distributions that characterize their uncertainty based on the characteristics of the parameters or the statistical model used to estimate them (Briggs et al., 2012). For example, a probability could be modeled with a beta distribution and a relative risk with a lognormal distribution (Briggs et al., 2002). For calibrated parameters, no such data exist that can directly inform their uncertainty because a research study hasn’t been conducted or is unfeasible to conduct, or because the parameters reflect unobservable phenomena, as is often the case in natural history models of chronic diseases (Welton and Ades, 2005; Karnon et al., 2007; Rutter et al., 2009; Rutter et al., 2011) or in infectious disease dynamic models (Enns et al., 2017). The choice of distribution for these parameters is often less clear. One option is to define uniform distributions with wide bounds or generate informed distributions based on moments of the calibrated parameters, such as the mean and standard error. However, the impact of these approaches to characterize the uncertainty of calibrated parameters on decision uncertainty and the VOI on reducing that uncertainty has not been studied.
Model calibration is the process of estimating unobserved or unobservable parameters by matching model outputs to observed clinical or epidemiological data (known as calibration targets) (Kennedy and O’Hagan, 2001; Stout et al., 2009; Kuntz et al., 2017). While there are several approaches for searching the parameter space in the calibration process, most approaches are insufficient to characterize the uncertainty in the calibrated model parameters because they do not provide interval estimates. For example, direct-search optimization algorithms like Newton-Raphson Nelder-Mead (Nelder and Mead 1965) simulated annealing or genetic algorithms (Kong et al., 2009) treat the calibration targets as if they were known with certainty, so are primarily useful when identifying a single or a set of parameters that yield good fit to the targets (Kennedy and O’Hagan, 2001).
A sample of calibrated parameter sets that correctly characterizes the uncertainty of the calibration target data is obtained from their joint distribution, conditional on the calibrated targets. To obtain the joint distribution, calibration could be specified as a statistical estimation problem under at least two different frameworks, through maximum likelihood (ML) or Bayesian methods. ML can fail in obtaining interval estimates by not being able to estimate the Hessian matrix when the likelihood is intractable or computationally intensive to simulate and when the calibration problem is non-identifiable (Gustafson, 2005; Alarid-Escudero et al., 2018); thus, we focus on Bayesian methods (Romanowicz et al., 1994; Kennedy and O’Hagan, 2001; Oakley and O’Hagan, 2004; Gustafson, 2005; Kaipio and Somersalo, 2005; Oden et al., 2010; Gustafson, 2015; Alarid-Escudero et al., 2018).
Despite their suitability to correctly characterize the uncertainty of calibrated model parameters, Bayesian methods are generally computationally expensive because they require evaluating the model thousands and sometimes millions of times. The computational burden of Bayesian methods does not seem to be an impediment when calibrating non-computationally intensive DMs (e.g., Markov cohort models, difference equations, relatively small systems of differential equations, etc.) (Whyte et al., 2011; Hawkins-Daarud et al., 2013; Jackson et al., 2016; Menzies et al., 2017). Still, they become more challenging to apply to DMs that could be computationally intensive to solve, such as models that simulate underlying stochastic processes (Iskandar, 2018) (e.g., microsimulation, discrete-event simulation, and agent-based models), limiting their use to only a few of such models (Rutter et al., 2009).
However, the increasing availability of high-performance computing (HPC) systems in an academic, national laboratory and commercial settings enables such systems for model calibration and model exploration of microsimulation DMs at a large scale to a broader audience. HPC resources allow running large numbers of DMs concurrently, allowing calibration algorithms to generate large batches of parameters simultaneously, such as the incremental mixture importance sampling (IMIS) described below, to be run efficiently. In many cases, particularly in the academic and national laboratory settings, computing allocations can be obtained through proposals with no cost to researchers (e.g., the Advanced Scientific Computing Research (ASCR) Leadership Computing Challenge (ALCC), https://science.osti.gov/ascr/Facilities/Accessing-ASCR-Facilities/ALCC). However, implementing dynamic calibration algorithms for HPC resources has generally proved difficult, requiring specialized knowledge across various disciplines. The Extreme-scale Model Exploration with Swift (EMEWS) framework was designed to facilitate large-scale model calibration and exploration on HPC resources (Ozik et al., 2016a) to a broad community. EMEWS can run very large, highly concurrent ensembles of microsimulation DMs of varying types with a broad class of calibration algorithms, including those increasingly available to the community via. Python and R libraries, using HPC workflows. EMEWS workflows provide interfaces for plugging in DMs (and any other simulation or black box model) and algorithms, through an inversion of control scheme (Ozik et al., 2018), to control the dynamic execution of those DMs for calibration and other heuristics for “model exploration” purposes. These interfaces help reduce the need for an in-depth understanding of how task coordination and inter-task dependencies are implemented for HPC resources. The general use of EMEWS can be seen on the EMEWS website (https://emews.github.io), which includes links to tutorials.
The purpose of our study is threefold. First, to use recently developed HPC capabilities to characterize the uncertainty of calibrated parameters of a microsimulation model of the natural history of colorectal cancer (CRC). Second, to explore the impact of different approaches to characterize the uncertainty of calibrated parameters on decision uncertainty, and third, to use VOI analysis to quantify the value of eliminating parameter uncertainty when assessing the cost-effectiveness of CRC screening.
Methods
We developed a microsimulation model of the natural history of CRC and calibrated it using a Bayesian approach. We then overlaid a simple CRC screening strategy onto the natural history model and conducted a cost-effectiveness analysis (CEA) of screening, including a PSA. Instead of using the posterior means to represent the best estimates of each calibrated parameter, we obtained the posterior distribution using a Bayesian approach that represents the joint uncertainty of all the calibrated parameters that can then be used in a PSA. We then evaluated the impact of different approaches to characterize the uncertainty of calibrated parameters on the joint distribution of incremental costs and incremental effects of the screening strategy compared with no screening through a PSA while also accounting for the uncertainty of the external parameters (e.g., test characteristics, costs, etc.). Finally, we quantified the amount of money that a decision maker should be willing to spend to eliminate all parameter uncertainty (i.e., the expected value of perfect information (EVPI)).
Microsimulation Model of the Natural History of CRC
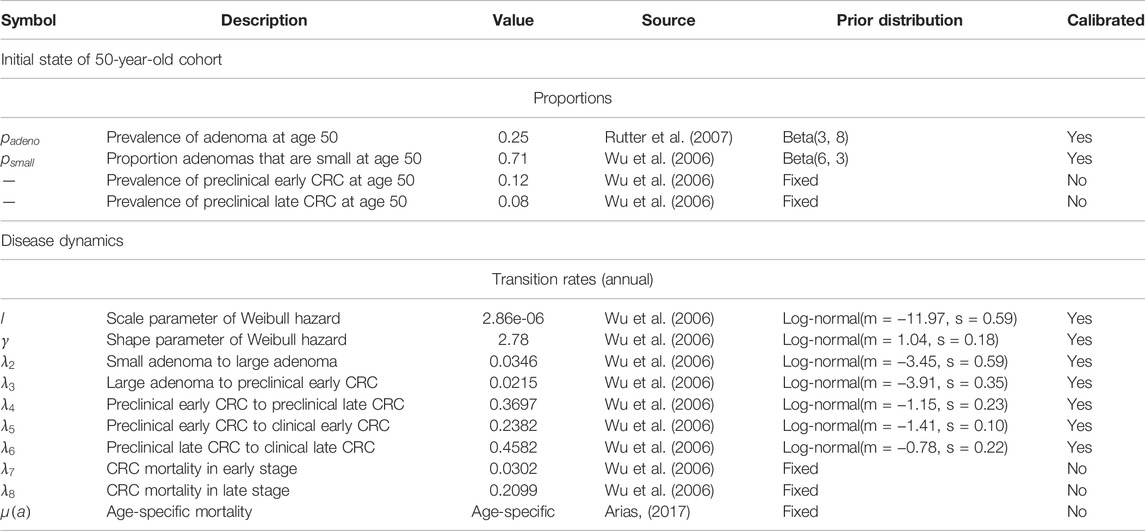
We developed a state-transition microsimulation model of the natural history of CRC implemented in R (Krijkamp et al., 2018) based on a previously developed model (Alarid-Escudero et al., 2018). The progression between health states follows a continuous-time age-dependent Markov process. There are two age-dependent transition intensities (i.e., transition rates),
where
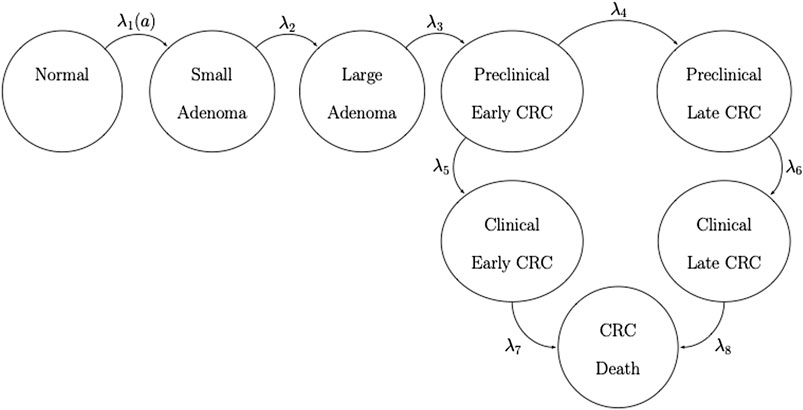
FIGURE 1. State-transition diagram of the nine-state microsimulation model of the natural history of colorectal cancer. Individuals in all health states face an age-specific mortality of dying from other causes (state not shown) (Jalal et al., 2021).
The continuous-time age-dependent Markov process of this natural history model of CRC can be represented by an age-dependent
where
We simulated a hypothetical cohort of 50-year-old women in the United States over a lifetime. The cohort starts the simulation with a prevalence of adenoma of
Calibration Targets
We used the microsimulation model of the natural history of CRC to generate synthetic calibration targets by selecting a set of parameter values based on plausible estimates from the literature (Table 1) (Wu et al., 2006; Rutter et al., 2007). We simulated four different age-specific synthetic targets, including adenoma prevalence, the proportion of small adenomas, and CRC incidence for early and late stages, which resemble commonly used calibration targets for this type of model (Rutter et al., 2009; Whyte et al., 2011; Frazier et al., 2000; Kuntz et al., 2011). To simulate the calibration targets, we ran the microsimulation model 100 times to get a stable estimate of the standard errors (SEs) using the fixed values in Table 1. We then aggregated each outcome across all 100 model replications to compute their mean and SE. To account for different levels of uncertainty across targets given the amount of data to estimate their summary measures, we simulated various targets based on cohorts of different sizes (Rutter et al., 2009). Adenoma-related targets were based on a cohort of 500 individuals, and cancer incidence targets were based on 100,000 individuals.
Calibration of the Microsimulation Model of the Natural History
To state the calibration of the microsimulation model as an estimation problem (Alarid-Escudero et al., 2018), we define
To calibrate
where
To conduct the Bayesian calibration, we used the incremental mixture importance sampling (IMIS) algorithm (Steele et al., 2006; Raftery and Bao, 2009), which has been previously used to calibrate health policy models (Menzies et al., 2017; Ryckman et al., 2020). We ran the IMIS algorithm on the Midway2 cluster at the University of Chicago Research Computing Center (https://rcc.uchicago.edu/resources/high-performance-computing). Midway2 is a hybrid cluster, including both central processing unit (CPU) and graphics processing unit (GPU) resources. For this work, we used the CPU resources. Midway2 consists of 370 nodes of Intel E5-2680v4 processors, each with 28 cores and 64 GB of RAM. Using EMEWS, we developed a workflow that parallelized the likelihood evaluations over 1,008 processes using 36 compute nodes. In other words, we reduced the computation time approximately by 250 had the analysis been conducted in a laptop with four processing cores.
Consistent with previous analyses, we deemed that convergence had occurred when the target effective sample size (ESS) got as close as 5,000 (Rutter et al., 2019; DeYoreo et al., 2022). An advantage of IMIS over other Monte Carlo methods, such as Markov chain Monte Carlo, is that with IMIS, we parallelize the evaluation of the likelihood for different sampled parameter sets, making its implementation perfectly suitable for an HPC environment using EMEWS. IMIS requires defining and computing the likelihood, which we could do with our model. However, when computing the likelihood is intractable, modelers could use the incremental mixture approximate Bayesian computation (IMABC) algorithm (Rutter et al., 2019), which an approximate Bayesian version of IMIS.
Propagation of Uncertainty
We sampled 5,000 parameter sets from the IMIS joint posterior distribution for the nine calibrated model parameters. To compare the outputs of the calibrated model against the calibration targets, we propagated the uncertainty of the calibrated parameters through the microsimulation model of the natural history of CRC. We simulated a cohort of 100,000 (i.e., the largest cohort size used to generate the targets). We generated the model-predicted adenoma and cancer outcomes for each of the 5,000 calibrated parameter sets drawn from their joint posterior distribution. We computed the 95% posterior predicted interval (PI), defined as the estimated range between the 2.5th and 97.5th percentiles of the model-predicted posterior outputs to quantify the uncertainty limit model outputs.
Cost-Effectiveness Analysis of Screening for CRC
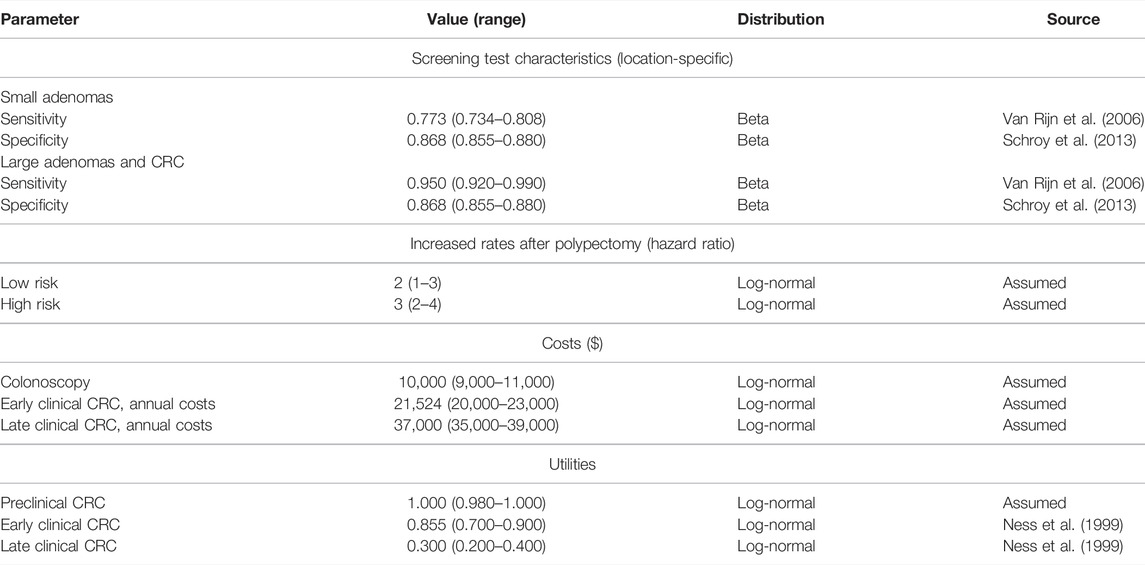
With the calibrated microsimulation model of the natural history of CRC, we assessed the cost-effectiveness of 10-yearly colonoscopy screening starting at age 50 years compared to no screening. For adenomas detected with colonoscopy, a polypectomy was performed during the procedure. Individuals diagnosed with a small or large adenoma underwent surveillance with colonoscopy every 5 or 3 years, respectively. We assumed screening or surveillance continued until 85 years of age. Individuals with a history of polyp diagnosis had higher recurrence rates after polypectomy, that is, a higher transition rate from normal to small adenoma (i.e.,
Uncertainty Quantification
We performed four different approaches to quantify the uncertainty of the two types of parameters—calibrated parameters and external (i.e., CEA) parameters. The first approach for uncertainty quantification considers uncertainty in both types of parameters, with uncertainty of the calibrated parameters characterized by their joint posterior distribution obtained from the IMIS algorithm. The second approach only considers uncertainty in the external parameters while fixing the calibrated parameters at the maximum-a-posteriori (MAP) estimate, defined as the parameter with the highest posterior density. The third approach considers uncertainty only in the calibrated parameters characterized by their joint posterior distribution and no uncertainty in the external parameters, fixed at their mean values. The fourth approach considers uncertainty in both types of parameters, but instead of using the IMIS posterior distribution of the calibrated parameters, we constructed distributions based solely on the IMIS posterior moments (i.e., means and standard deviations) and the type of calibrated parameters ignoring correlations.
We conducted a PSA to evaluate the impact of uncertainty in model parameters on the cost-effectiveness of 10-years colonoscopy screening vs. no screening for CRC. A separate PSA was performed for the four different approaches to quantify the uncertainty of the two types of parameters. We used EMEWS to distribute the samples of each PSA across HPC resources.
Value of Information Analysis
We quantified the theoretical value of eliminating uncertainty in the external and calibrated model parameters using VOI analysis. VOI measures the losses (i.e., foregone benefits) from choosing a strategy given imperfect information (Raiffa and Schlaifer, 1961), providing the amount of resources a decision maker should be willing to spend to obtain information that would reduce the uncertainty. Specifically, we estimated the value of eliminating parametric uncertainty (i.e., the EVPI) in the cost-effectiveness of a 10-years colonoscopy screening strategy. This entailed computing the difference in net benefit between perfect information and current information (Oostenbrink et al., 2008). The EVPI was calculated across a wide range of willingness-to-pay (WTP) thresholds (Eckermann et al., 2010). We repeated this VOI analysis for the different approaches to characterize the uncertainty of the calibrated and external parameters.
Results
We sampled 5,000 parameter sets from the posterior distribution using IMIS, including 3,241 unique parameter sets with an expected sample size (ESS) of 2,098. With the sample from the posterior distribution, we estimated posterior means and standard deviations, MAP estimates, and 95% credible intervals (CrI) for all calibrated parameters (Table 3). The posterior means of the calibrated parameter were similar to the prior means (Table 3). Still, the major contrast is that the width of the posterior distributions shrunk, meaning that the calibration targets informed the calibrated parameters through a Bayesian updating (Figure 2).
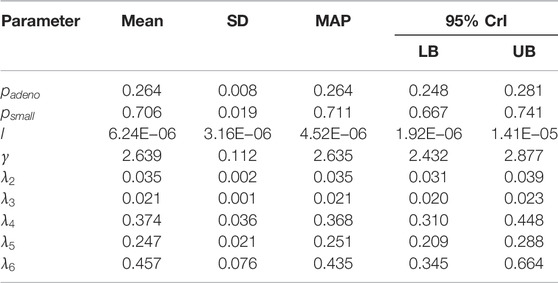
TABLE 3. Posterior means, standard deviations, maximum-a-posteriori (MAP) estimate and 95% credible interval (CrI) of calibrated parameters of the microsimulation model of the natural history of CRC.
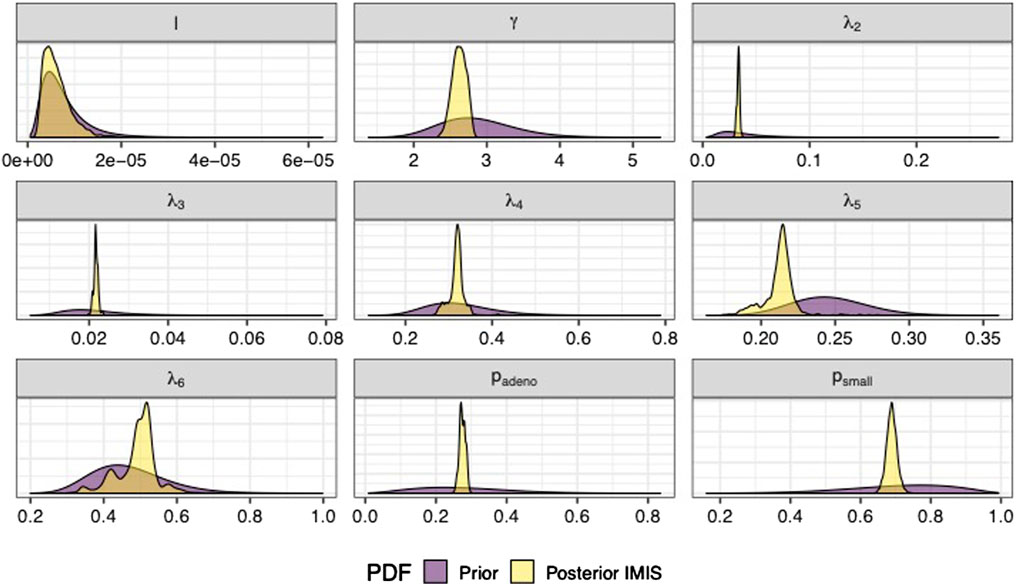
FIGURE 2. Prior and posterior marginal distributions of calibrated parameters of the microsimulation model of the natural history of CRC.
The Bayesian calibration also correlated the parameters, showing the dependency among some of them (Figure 3). There are pairs of parameters with high correlation. The scale and shape parameters of the Weibull hazard function for the age of onset of adenomas,
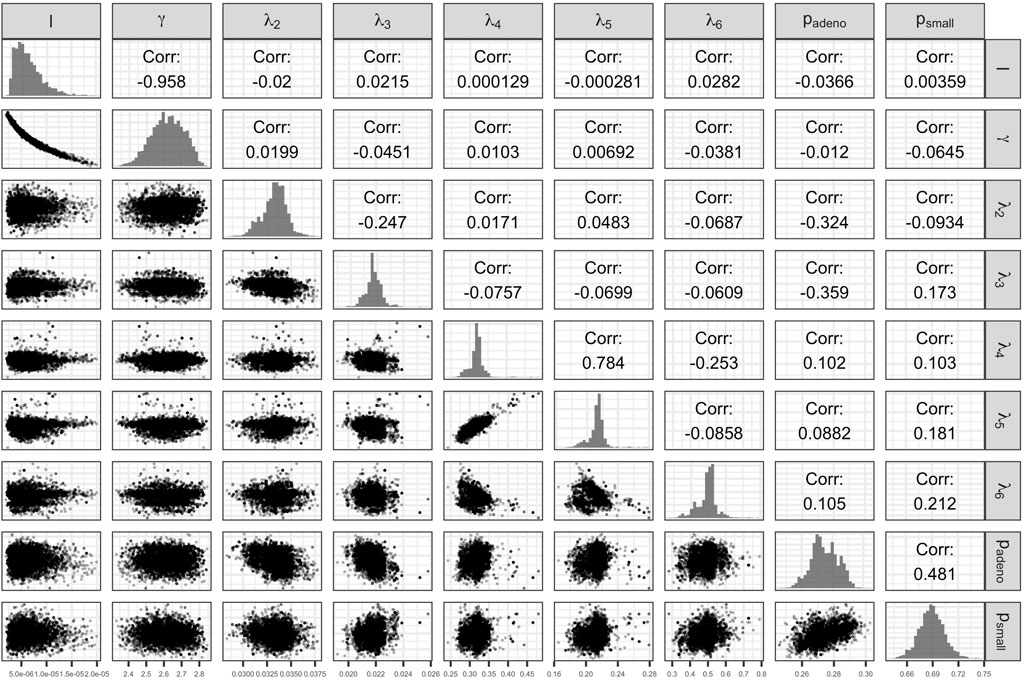
FIGURE 3. Scatter plot of pairs of deep model parameters with correlation coefficient and posterior marginal distributions.
The calibrated model accurately predicted the calibration targets for both the means and the uncertainty intervals. Figure 4 shows the internal validation of the calibrated model by comparing calibration targets with their 95% confidence interval (CI) and the model-predicted posterior means together with their 95% posterior PI.
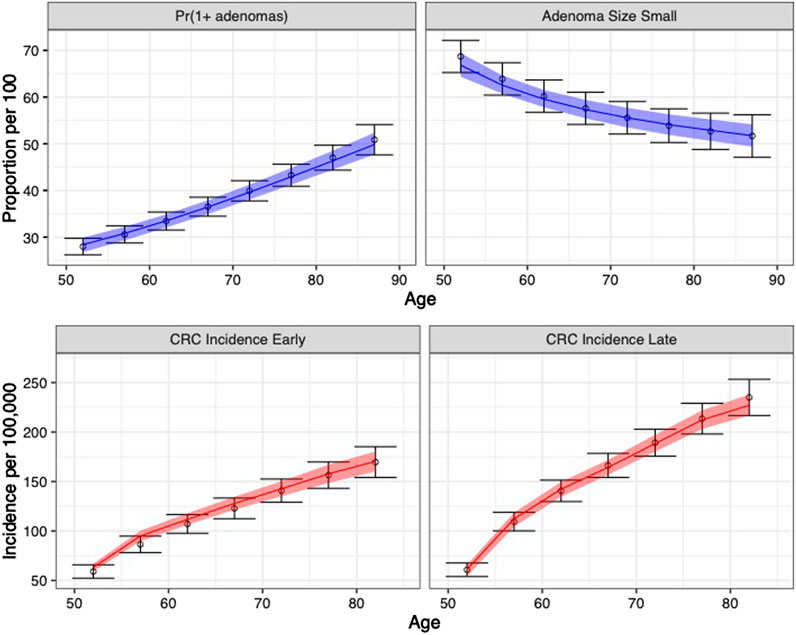
FIGURE 4. Comparison between posterior model-predicted outputs and calibration targets. Calibration targets with their 95% CI are shown in black. The shaded area shows the 95% posterior model-predictive interval of the outcomes and colored lines shows the posterior model-predicted mean based on 5,000 simulations using samples from the posterior distribution. Upper panel refers to adenoma-related targets and lower panel refers to CRC incidence targets by stage.
The joint distribution of the incremental quality-adjusted life years (QALYs) and incremental costs of the 10 years colonoscopy screening strategy vs. the no-screening strategy resulting from the PSA for the four uncertainty quantification approaches of the calibrated parameters are shown in Figure 5. When accounting for the uncertainty on the external parameters, there is little difference in the spread of the CEA outcomes when considering the joint distribution of the calibrated parameters vs. using only the MAP estimates (approaches 1 and 2 on the top row of Figure 5, respectively). The joint distribution of the outcomes is slightly wider when considering uncertainty on all parameters compared to when fixing the calibrated parameters at their MAP estimate. The third approach reflects the impact of only varying the calibrated parameters on the joint distribution of incremental QALYS and incremental costs, which is much narrower than approaches 1 and 2. The fourth approach, which characterizes uncertainty of the calibrated parameters using the method of moments without accounting for correlation, has the widest spread on the distribution of the outcomes.
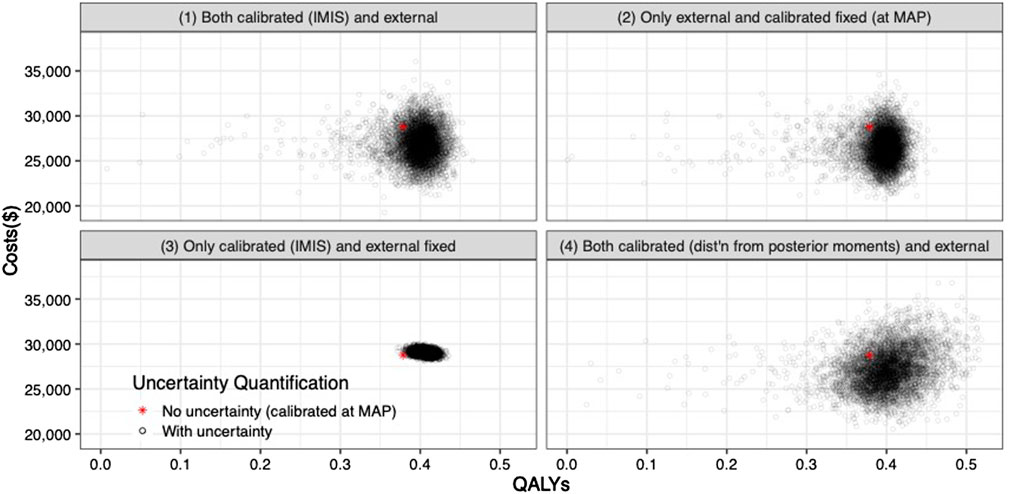
FIGURE 5. Incremental costs and incremental QALYs of 10-years colonoscopy screening vs. no screening under different assumptions of characterization of the uncertainty of both calibrated and external parameters. The red star corresponds to the incremental costs and incremental QALYs evaluated at the maximum-a-posteriori estimate of the calibrated parameters and the mean values of the external parameters.
For the VOI analysis, we found value in eliminating uncertainty by having a positive EVPI in the parameters of the CEA of the 10-years colonoscopy screening strategy (Figure 6). However, the value varies by uncertainty quantification and WTP threshold. The first and second approaches to uncertainty quantification had similar EVPI, reaching their maximum of $653 and $685, respectively, at a $66,000/QALY WTP threshold. For WTP thresholds greater than $66,000/QALY, the first approach had a higher EVPI than the second approach. When we consider only the uncertainty for the calibrated parameters (approach 3), the EVPI is the lowest across all WTP thresholds with an EVPI of $0.1 at a WTP threshold of $66,000/QALY and reaching its highest of $212 at a WTP threshold of $71,000/QALY. The fourth approach reaches a maximum of $809 at a WTP threshold of $66,000/QALY and is the highest compared to the other approaches up to a WTP threshold of $81,000/QALY, at which the first approach has the highest EVPI.
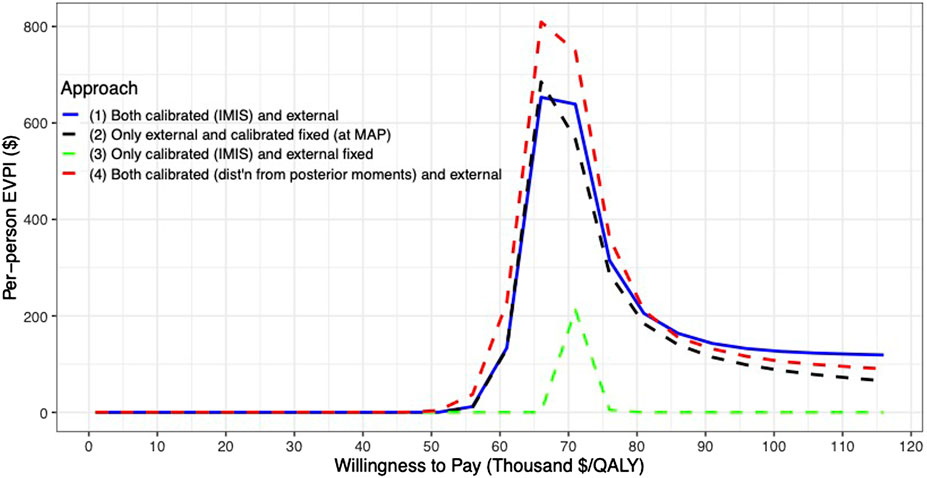
FIGURE 6. Per-patient EVPI of 10-year colonoscopy screening vs no screening under different approaches to characterize the uncertainty of both the calibrated and external parameters.
Discussion
In this study, we characterized the uncertainty of a realistic microsimulation model of the natural history of CRC by calibrating its parameters to different targets with varying degrees of uncertainty using a Bayesian approach on an HPC environment using EMEWS. We also quantified the value of the uncertainty of the calibrated parameters on the cost-effectiveness of a 10-year colonoscopy screening strategy with a VOI analysis. EMEWS has been previously used to calibrate other microsimulation DMs (Rutter et al., 2019; Rutter et al., 2019) but has not been previously used to conduct a PSA with the calibrated parameters and calculate the VOI. Although Bayesian calibration can be a computationally intensive task, we reduce the computation time by evaluating the likelihood of different parameter sets in multiple cores simultaneously on an HPC setup, which IMIS allows.
We found that different characterizations of the uncertainty of calibrated parameters affect the expected value of reducing uncertainty on the CEA. Ignoring inherent correlation among calibrated parameters on a PSA overestimates the value of uncertainty. When the full posterior distribution of the calibrated parameters is not readily available, the MAP could be considered the best parameter set. In our example, not considering the uncertainty of calibrated parameters on the PSA did not seem to have a meaningful impact on the uncertainty of the CEA outcomes and the EVPI of the screening strategy. The uncertainty associated with the natural history was less valuable than the uncertainty of the external parameters. However, these results should be taken with caution because this analysis is conducted on a fictitious model with simulated calibrated targets. Modelers should analyze the impact of a well-conducted characterization of the uncertainty of calibrated parameters on CEA outcomes and VOI measures on a case-by-case basis.
There are examples of calibrated parameters being included in a PSA. For instance, by taking a certain number of good-fitting parameter sets (Kim et al., 2007; Kim et al., 2009), bootstrapping with equal probability good-fitting parameter sets obtained through directed search algorithms (e.g., Nelder-Mead) (Taylor et al., 2012), or conducting a Bayesian calibration, which produces the joint posterior distribution of the calibrated parameters (Menzies et al., 2017). However, this is the first manuscript to conduct a PSA and VOI analysis using distributions of calibrated microsimulation DM parameters that accurately characterize their uncertainty.
Currently, Bayesian calibration of microsimulation DMs might not be feasible on regular desktops or laptops. To circumvent current computational limitations from using Bayesian methods in calibrating microsimulation models, surrogate models -often called metamodels or emulators-have been proposed (O’Hagan et al., 1999; O’Hagan, 2006; Oakley and Youngman, 2017). Surrogate models are statistical models like Gaussian processes (Sacks et al., 1989a; Sacks et al., 1989b; Oakley and O’Hagan, 2002) or neural networks (Hauser et al., 2012; Jalal et al., 2021) that aim to replace the relationship between inputs and outputs of the original microsimulation DM (Barton et al., 1992; Kleijnen, 2015), which, once fitted, are computationally more efficient to run than the microsimulation DM. Constructing an emulator might not be a straightforward task because the microsimulation DM still needs to be evaluated at different parameter sets, which could also be computationally expensive. Furthermore, the statistical routines to build the emulator may not be readily available in the programming language in which the microsimulation DM is coded. These are situations where EMEWS can be used to construct metamodels efficiently; however, this is a topic for further research.
Researchers might actively avoid questions that would require HPC due to the perceived difficulties involved or make do with less-than-ideal smaller-scale analyses (e.g., choosing the maximum likelihood estimate or a small set of parameters instead of the posterior distribution for uncertainty quantification) and the robustness of the conclusions can suffer as a result.
In this article, we showed that EMEWS could facilitate the use of HPC to implement computationally demanding Bayesian calibration routines to correctly characterize the uncertainty of the calibrated parameters of microsimulation DMs and propagate it in the evaluation of CEA of screening strategies and quantify their value of information. This study’s methodology and results could guide a similar VOI analysis on CEAs using microsimulation DMs to determine where more research is needed and guide research prioritization.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
FA-E contributed to the conceptualization, data curation, formal analysis, funding acquisition, investigation, methodology, project administration, resources, software, supervision, validation, visualization, and writing of the original draft and of reviewing and editing; AK contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, validation, and writing of the original draft and of reviewing and editing; JO contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, validation, and writing of the original draft and of reviewing and editing; NC contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, validation, and writing of the original draft and of reviewing and editing; KK contributed to the conceptualization, formal analysis, funding acquisition, investigation, methodology, resources, validation, and writing of the original draft and of reviewing and editing.
Funding
Financial support for this study was provided in part by a grant from the National Council of Science and Technology of Mexico (CONACYT) and a Doctoral Dissertation Fellowship from the Graduate School of the University of Minnesota as part of Dr. Alarid-Escudero’s doctoral program. All authors were supported by grants from the National Cancer Institute (U01- CA-199335 and U01-CA-253913) as part of the Cancer Intervention and Surveillance Modeling Network (CISNET). The work was supported in part by the U.S. Department of Energy, Office of Science, under contract (No. DE- AC0206CH11357). The funding agencies had no role in the study’s design, interpretation of results, or writing of the manuscript. The content is solely the authors’ responsibility and does not necessarily represent the official views of the National Institutes of Health. The funding agreement ensured the authors’ independence in designing the study, interpreting the data, writing, and publishing the report. This research was completed with resources provided by the Research Computing Center at the University of Chicago (Midway2 cluster).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Alarid-Escudero F., MacLehose R. F., Peralta Y., Kuntz K. M., Enns E. A. (2018). Nonidentifiability in Model Calibration and Implications for Medical Decision Making. Med. Decis. Mak [Internet] 38 (7), 810–821. doi:10.1177/0272989x18792283
Barton R. R. (1992). “Metamodels for Simulation Input-Output Relations,” in Winter Simulation Conference. Editors J. J. Swain, D. Goldsman, R. C. Crain, and J. R. Wilson, 289–299. doi:10.1145/167293.167352
Briggs A. H., Goeree R., Blackhouse G., O'Brien B. J. (2002). Probabilistic Analysis of Cost-Effectiveness Models: Choosing between Treatment Strategies for Gastroesophageal Reflux Disease. Med. Decis. Mak 22, 290–308. doi:10.1177/027298902400448867
Briggs A. H., Weinstein M. C., Fenwick E. A. L., Karnon J., Sculpher M. J., Paltiel A. D. (2012). Model Parameter Estimation and Uncertainty Analysis. Med. Decis. Making 32 (5), 722–732. doi:10.1177/0272989x12458348
DeYoreo M., Rutter C. M., Ozik J., Collier N. (2022). Sequentially Calibrating a Bayesian Microsimulation Model to Incorporate New Information and Assumptions. BMC Med. Inform. Decis. Mak [Internet]. Biomed. Cent. 22 (1), 12. doi:10.1186/s12911-021-01726-0
Eckermann S., Karnon J., Willan A. R. (2010). The Value of Value of Information: Best Informing Research Design and Prioritization Using Current Methods. Pharmacoeconomics 28 (9), 699–709. doi:10.2165/11537370-000000000-00000
Enns E. A., Kao S. Y., Kozhimannil K. B., Kahn J., Farris J., Kulasingam S. L. (2017). Using Multiple Outcomes of Sexual Behavior to Provide Insights into Chlamydia Transmission and the Effectiveness of Prevention Interventions in Adolescents. Sex. Transm. Dis. 44 (10), 619–626. doi:10.1097/olq.0000000000000653
Frazier A. L., Colditz G. A., Fuchs C. S., Kuntz K. M. (2000). Cost-effectiveness of Screening for Colorectal Cancer in the General Population. JAMA 284 (15), 1954–1961. doi:10.1001/jama.284.15.1954
Gustafson P. (2015). Bayeisan Inference for Partially Identified Models: Exploring the Limits of Limited Data. Boca Raton, FL: CRC Press.
Gustafson P. (2005). On Model Expansion, Model Contraction, Identifiability and Prior Information: Two Illustrative Scenarios Involving Mismeasured Variables. Stat. Sci. [Internet] 20 (2), 111–129. doi:10.1214/088342305000000098
Hauser T., Keats A., Tarasov L. (2012). Artificial Neural Network Assisted Bayesian Calibration of Climate Models. Clim. Dyn. 39 (1–2), 137–154. doi:10.1007/s00382-011-1168-0
Hawkins-Daarud A., Prudhomme S., van der Zee K. G., Oden J. T. (2013). Bayesian Calibration, Validation, and Uncertainty Quantification of Diffuse Interface Models of Tumor Growth. J. Math. Biol. 67 (6–7), 1457–1485. doi:10.1007/s00285-012-0595-9
Iskandar R. (2018). A Theoretical Foundation of State-Transition Cohort Models in Health Decision Analysis. PLoS One 13 (12), e0205543. doi:10.1371/journal.pone.0205543
Jackson C. S., Oman M., Patel A. M., Vega K. J. (2016). Health Disparities in Colorectal Cancer Among Racial and Ethnic Minorities in the United States. J. Gastrointest. Oncol. 7 (Suppl. 1), 32–43. doi:10.3978/j.issn.2078-6891.2015.039
Jalal H., Trikalinos T. A., Alarid-Escudero F. (2021). BayCANN: Streamlining Bayesian Calibration with Artificial Neural Network Metamodeling. Front. Physiol. 12, 1–13. doi:10.3389/fphys.2021.662314
Kaipio J., Somersalo E. (2005). Statistical and Computational Inverse Problems. New York, NY: Springer.
Karnon J., Goyder E., Tappenden P., McPhie S., Towers I., Brazier J., et al. (2007). A Review and Critique of Modelling in Prioritising and Designing Screening Programmes. Health Technol. Assess. (Rockv). 11 (52), 1–145. doi:10.3310/hta11520
Kennedy M. C., O’Hagan A. (2001). Bayesian Calibration of Computer Models. J. R. Stat Soc Ser B Stat. Methodol. 63 (3), 425–464. doi:10.1111/1467-9868.00294
Kim J. J., Kuntz K. M., Stout N. K., Mahmud S., Villa L. L., Franco E. L., et al. (2007). Multiparameter Calibration of a Natural History Model of Cervical Cancer. Am. J. Epidemiol. 166 (2), 137–150. doi:10.1093/aje/kwm086
Kim J. J. P., Ortendahl B. S. J., Goldie S. J. M. (2009). Cost-Effectiveness of Human Papillomavirus Vaccination and Cervical Cancer Screening in Women Older Than 30 Years in the United States. Ann. Intern. Med. 151 (8), 538–545. doi:10.7326/0003-4819-151-8-200910200-00007
Kleijnen J. P. C. (2015). Design and Analysis of Simulation Experiments. 2nd ed. New York, NY: Springer International Publishing.
Kolmogorov A. N. (1963). On the Representation of Continuous Functions of Several Variables by Superposition of Continuous Functions of One Variable and Addition. Am. Math. Soc. Transl Ser. 28, 55–59. doi:10.1090/trans2/028/04
Kong C. Y., McMahon P. M., Gazelle G. S. (2009). Calibration of Disease Simulation Model Using an Engineering Approach. Value Heal 12 (4), 521–529. doi:10.1111/j.1524-4733.2008.00484.x
Krijkamp E. M., Alarid-Escudero F., Enns E. A., Jalal H. J., Hunink M. G. M., Pechlivanoglou P. (2018). Microsimulation Modeling for Health Decision Sciences Using R: A Tutorial. Med. Decis. Mak [Internet] 38 (3), 400–422. doi:10.1177/0272989x18754513
Kuntz K. M., Lansdorp-Vogelaar I., Rutter C. M., Knudsen A. B., van Ballegooijen M., Savarino J. E., et al. (2011). A Systematic Comparison of Microsimulation Models of Colorectal Cancer: the Role of Assumptions about Adenoma Progression. Med. Decis. Mak 31, 530–539. doi:10.1177/0272989x11408730
Kuntz K. M., Russell L. B., Owens D. K., Sanders G. D., Trikalinos T. A., Salomon J. A. (2017). “Decision Models in Cost-Effectiveness Analysis,” in Cost-Effectiveness in Health and Medicine. Editors P. J. Neumann, G. D. Sanders, L. B. Russell, J. E. Siegel, and T. G. Ganiats (New York, NY: Oxford University Press), 105–136.
Menzies N. A., Soeteman D. I., Pandya A., Kim J. J. (2017). Bayesian Methods for Calibrating Health Policy Models: A Tutorial. Pharmacoeconomics 25 (6), 613–624. doi:10.1007/s40273-017-0494-4
Nelder J. A., Mead R. (1965). A Simplex Method for Function Minimization. Comput. J. 7 (4), 308–313. doi:10.1093/comjnl/7.4.308
Ness R. M., Holmes A. M., Klein R., Dittus R. (1999). Utility Valuations for Outcome States of Colorectal Cancer. Am. J. Gastroenterol. 94 (6), 1650–1657. doi:10.1111/j.1572-0241.1999.01157.x
Oakley J., O’Hagan A. (2002). Bayesian Inference for the Uncertainty Distribution of Computer Model Outputs. Biometrika 89 (4), 769–784. doi:10.1093/biomet/89.4.769
Oakley J., O’Hagan A. (2004). Probabilistic Sensitivity Analysis of Complex Models: a Bayesian Approach. J. R. Stat. Soc. Ser. B (Statistical Methodol. [Internet] 66 (3), 751–769. doi:10.1111/j.1467-9868.2004.05304.x
Oakley J. E., Youngman B. D. (2017). Calibration of Stochastic Computer Simulators Using Likelihood Emulation. Technometrics 59 (1), 80–92. doi:10.1080/00401706.2015.1125391
Oden T., Moser R., Ghattas O. (2010). Computer Predictions with Quantified Uncertainty. Austin. TX: The Institute for Computational Engineering and Sciences.
O’Hagan A. (2006). Bayesian Analysis of Computer Code Outputs: A Tutorial. Reliab Eng. Syst. Saf. [Internet] 91 (10--11), 1290–1300. doi:10.1016/j.ress.2005.11.025
O’Hagan A., Kennedy M. C., Oakley J. E. (1999). Uncertainty Analysis and Other Inference Tools for Complex Computer Codes. Bayesian Staistics 6: Proceedings of the Sixth Valencia International Meeting. Editors J. M. Bernardo, J. O. Berger, A. P. Dawid, and A. F. M. Smith. Oxford, United Kingdom: Clarendon Press, 503–24.
Oostenbrink J. B., Al M. J., Oppe M., Rutten-van Mölken M. P. M. H. (2008). Expected Value of Perfect Information: An Empirical Example of Reducing Decision Uncertainty by Conducting Additional Research. Value Heal [Internet]. Int. Soc. Pharmacoeconomics Outcomes Res. (Ispor) 11 (7), 1070–1080. doi:10.1111/j.1524-4733.2008.00389.x
Ozik J., Collier N. T., Wozniak J. M., Macal C. M., An G. (2018). Extreme-scale Dynamic Exploration of a Distributed Agent-Based Model with the EMEWS Framework. IEEE Trans. Comput. Soc. Syst. IEEE 5 (3), 884–895. doi:10.1109/tcss.2018.2859189
Ozik J., Collier N. T., Wozniak J. M., Spagnuolo C. (2016a). “From Desktop to Large-Scale Model Exploration with Swift/T,” in Proceedings of the 2016 Winter Simulation Conference. Editors T. M. K. Roeder, P. I. Frazier, R. Szechtman, E. Zhou, T. Huschka, and S. E. Chick (IEEE Press), 206–220. doi:10.1109/wsc.2016.7822090
Raftery A. E., Bao L. (2009). Estimating and Projecting Trends in HIV/AIDS Generalized Epidemics Using Incremental Mixture Importance Sampling. Biometrics 66, 1162–1173. doi:10.1111/j.1541-0420.2010.01399.x
Raiffa H., Schlaifer R. O. (1961). Applied Statistical Decision Theory. Cambridge, MA: Harvard Business School.
Romanowicz R. J., Beven K. J., Tawn J. A. (1994). Evaluation of Predictive Uncertainty in Nonlinear Hydrological Models Using a Bayesian Approach. Stat. Environ. 2 Water Relat. Issues. Editors V. Barnett, and K. F. Turkman. Hoboken, NJ: John Wiley & Sons (February), 297–317.
Rutter C. M., Ozik J., DeYoreo M., Collier N. (2019). Microsimulation Model Calibration Using Incremental Mixture Approximate Bayesian Computation. Ann. Appl. Stat. [Internet 13 (4), 2189–2212. doi:10.1214/19-aoas1279
Rutter C. M., Yu O., Miglioretti D. L. (2007). A Hierarchical Non-homogenous Poisson Model for Meta-Analysis of Adenoma Counts. Stat. Med. 26 (1), 98–109. doi:10.1002/sim.2460
Rutter C. M., Miglioretti D. L., Savarino J. E. (2009). Bayesian Calibration of Microsimulation Models. J. Am. Stat. Assoc. 104 (488), 1338–1350. doi:10.1198/jasa.2009.ap07466
Rutter C. M., Zaslavsky A. M., Feuer E. J. (2011). Dynamic Microsimulation Models for Health Outcomes. Med. Decis. Making 31 (1), 10–18. doi:10.1177/0272989x10369005
Ryckman T., Luby S., Owens D. K., Bendavid E., Goldhaber-Fiebert J. D. (2020). Methods for Model Calibration under High Uncertainty: Modeling Cholera in Bangladesh. Med. Decis. Mak 40 (5), 693–709. doi:10.1177/0272989x20938683
Sacks J., Schiller S. B., Welch W. J. (1989). Designs for Computer Experiments. Technometrics 31 (1), 41–47. doi:10.1080/00401706.1989.10488474
Sacks J., Welch W. J., Mitchell T. J., Wynn H. P. (1989). Design and Analysis of Computer Experiments. Stat. Sci. 4 (4), 409–423. doi:10.1214/ss/1177012413
Schlaifer R. O. (1959). Probability and Statistics for Business Decisions. New York, NY: McGraw-Hill.
Schroy P. C., Coe A., Chen C. A., O’Brien M. J., Heeren T. C. (2013). Prevalence of Advanced Colorectal Neoplasia in White and Black Patients Undergoing Screening Colonoscopy in a Safety-Net Hospital. Ann. Intern. Med. 159 (1), 13. doi:10.7326/0003-4819-159-1-201307020-00004
Sculpher M. J., Basu A., Kuntz K. M., Meltzer D. O. (2017). “Reflecting Uncertainty in Cost-Effectiveness Analysis,” in Cost-Effectiveness in Health and Medicine. Editors PJ Neumann, GD. Sanders, L. B. Russell, J. E. Siegel, and T. G. Ganiats (New York, NY: Oxford University Press), 289–318.
Steele R. J., Raftery A. E., Emond M. J. (2006). Computing Normalizing Constants for Finite Mixture Models via Incremental Mixture Importance Sampling (IMIS). J. Comput. Graph Stat. 15 (3), 712–734. doi:10.1198/106186006x132358
Stout N. K., Knudsen A. B., Kong C. Y., Mcmahon P. M., Gazelle G. S. (2009). Calibration Methods Used in Cancer Simulation Models and Suggested Reporting Guidelines. Pharmacoeconomics 27 (7), 533–545. doi:10.2165/11314830-000000000-00000
Taylor D. C., Pawar V., Kruzikas D. T., Gilmore K. E., Sanon M., Weinstein M. C. (2012). Incorporating Calibrated Model Parameters into Sensitivity Analyses: Deterministic and Probabilistic Approaches. Pharmacoeconomics 30 (2), 119–126. doi:10.2165/11593360-000000000-00000
Van Rijn J. C., Reitsma J. B., Stoker J., Bossuyt P. M., Van Deventer S. J., Dekker E. (2006). Polyp Miss Rate Determined by Tandem Colonoscopy: A Systematic Review. Am. J. Gastroenterol. 101 (2), 343–350. doi:10.1111/j.1572-0241.2006.00390.x
Welton N. J., Ades A. E. (2005). Estimation of Markov Chain Transition Probabilities and Rates from Fully and Partially Observed Data: Uncertainty Propagation, Evidence Synthesis, and Model Calibration. Med. Decis. Making 25, 633–645. doi:10.1177/0272989x05282637
Whyte S., Walsh C., Chilcott J. (2011). Bayesian Calibration of a Natural History Model with Application to a Population Model for Colorectal Cancer. Med. Decis. Mak 31 (4), 625–641. doi:10.1177/0272989x10384738
Keywords: microsimulation models, uncertainty quantification, calibration, Bayesian, value of information analysis, decision-analytic models, high-performance computing, EMEWS
Citation: Alarid-Escudero F, Knudsen AB, Ozik J, Collier N and Kuntz KM (2022) Characterization and Valuation of the Uncertainty of Calibrated Parameters in Microsimulation Decision Models. Front. Physiol. 13:780917. doi: 10.3389/fphys.2022.780917
Received: 22 September 2021; Accepted: 04 April 2022;
Published: 09 May 2022.
Edited by:
Nicole Y. K. Li-Jessen, McGill University, CanadaReviewed by:
Daniele E. Schiavazzi, University of Notre Dame, United StatesRowan Iskandar, sitem-insel, Switzerland
Copyright © 2022 Alarid-Escudero, Knudsen, Ozik, Collier and Kuntz. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fernando Alarid-Escudero, ZmVybmFuZG8uYWxhcmlkQGNpZGUuZWR1
 Fernando Alarid-Escudero
Fernando Alarid-Escudero Amy B. Knudsen
Amy B. Knudsen Jonathan Ozik
Jonathan Ozik Nicholson Collier3,4
Nicholson Collier3,4 Karen M. Kuntz
Karen M. Kuntz