A framework for heart-lung interaction and its application to prone position in the acute respiratory distress syndrome

While both cardiac output (Q_circulatory) and right atrial pressure (P_RA) are important measures in the intensive care unit (ICU), they are outputs of the system and not determinants. That is to say, in a model of the circulation wherein venous return and cardiac function find equilibrium at an ‘operating point’ (OP, defined by the P_RA on the x-axis and Q_circulatory on the y-axis) both the P_RA and Q_circulatory are, necessarily, dependent variables. A simplified geometrical approximation of Guyton’s model is put forth to illustrate that the independent variables of the system are: 1) the mean systemic filling pressure (P_MSF), 2) the pressure within the pericardium (P_PC), 3) cardiac function and 4) the resistance to venous return. Classifying independent and dependent variables is clinically-important for therapeutic control of the circulation. Recent investigations in patients with acute respiratory distress syndrome (ARDS) have illuminated how P_MSF, cardiac function and the resistance to venous return change when placing a patient in prone. Moreover, the location of the OP at baseline and the intimate physiological link between the heart and the lungs also mediate how the P_RA and Q_circulatory respond to prone position. Whereas turning a patient from supine to prone is the focus of this discussion, the principles described within the framework apply equally-well to other more common ICU interventions including, but not limited to, ventilator management, initiating vasoactive medications and providing intravenous fluids.

Introduction

Though evidence of benefit has existed for placing patients with moderate-to-severe acute respiratory distress syndrome (ARDS) in the prone position for some time, the coronavirus pandemic raised clinical awareness of this maneuver (Guérin et al., 2020). Guidelines currently recommend prone position for patients with ARDS and a partial pressure-to-fraction of inspired oxygen (P_aO₂/F_iO₂) ratio of not more than 150 mmHg (Papazian et al., 2019). Furthermore, with this ARDS severity, patients should maintain the prone position for at least 12 h per day for optimal benefit (Guérin et al., 2013).

Turning a patient from the supine to prone position has salutary benefits on gas exchange as oxygenation and carbon dioxide elimination are both enhanced (Guérin et al., 2020). The mechanisms by which the prone position exerts its salubrious effects are manifold. When the dorsal, de-gassed ‘sponge lung’ (Bone, 1993) is no longer gravity-dependent, it is recruited and the surface area for gas exchange increased. Critically, the newly-enlisted alveoli see no significant change in pulmonary blood flow (Henderson et al., 2013); as a consequence, the burden of low ventilation-to-perfusion (V/Q) lung units is reduced. In addition to alveolar recruitment, shifting to the prone position improves ‘shape matching’ between the pulmonary parenchyma and the chest wall (Gattinoni et al., 2013). In total, the result is that there is less pulmonary inhomogeneity (Cressoni et al., 2014; Cressoni et al., 2015) and, therefore, fewer ‘stress-raisers’ (Mead et al., 1970) that amplify radial traction forces upon the lungs and pulmonary vasculature (Broccard et al., 1998; Marini et al., 2003; Repessé et al., 2016). Furthermore, stiffening the chest wall with improved pulmonary compliance diminishes trans-pulmonary pressure (P_TP) as the pleural pressure is raised for any given airway pressure (Marini and Gattinoni, 2021). This reduces the mechanical power applied to the pulmonary parenchyma and mitigates West zone 1 and 2 conditions (Gattinoni and Quintel, 2016). All of the aforementioned changes in pulmonary physiology (i.e., improved oxygenation and carbon dioxide elimination, optimized perivascular pulmonary mechanics, diminished P_TP) minimize the afterload experienced by the right ventricle (RV), giving weight to the motto: ‘what’s good for the lung is good for the RV (Repessé et al., 2016).’

While the literature is replete with elegant investigations into the mechanical pulmonary pathophysiology of ARDS in both supine and prone positions, comparatively little is known about the hemodynamic effects. With a recent investigation exploring the determinants of venous return in the prone position (Lai et al., 2021) and an excellent related review (Lai et al., 2023), this overview will expand upon relevant concepts in clinical hemodynamics, propose a simplified geometrical model clarifying the determinants of cardiac output and right atrial pressure and then relate this to what is currently known about prone position in the ARDS patient (Table 1).

TABLE 1

TABLE 1. Key messages by section.

Guyton primer

Many excellent reviews connecting Guyton’s model of the circulatory system to critical-illness are available (Sylvester et al., 1983; Bressack and Raffin, 1987; Fessler, 1997; Jacobsohn et al., 1997; Magder, 2004; Gelman, 2008; Parkin and Leaning, 2008; Feihl and Broccard, 2009a; Feihl and Broccard, 2009b; Magder, 2012; Berlin and Bakker, 2015; Berger and Takala, 2018; Persichini et al., 2022). Though this model has been criticized and debated (Brengelmann, 2003; Beard and Feigl, 2011; Moller et al., 2017; Berger et al., 2019; Brengelmann, 2019; Werner-Moller et al., 2020; Kenny, 2021), these controversies are beyond the scope of this review. Guyton’s contributions to hemodynamics are many and may be parsed into: 1.) the explication of venous return (Guyton et al., 1955) and 2.) the graphical superposition of the venous return and Starling-Sarnoff curves (Guyton, 1955).

Venous return

The determinants of venous return from the peripheral circulation are, from Guyton’s experiments: 1.) the mean circulatory filling pressure (P_MCF), 2.) right atrial pressure (P_RA) and 3.) the resistance to venous return (R_VR) (Guyton, 1955; Sylvester et al., 1983; Jacobsohn et al., 1997; Feihl and Broccard, 2009a). Together the P_MCF and the P_RA define the pressure gradient for venous return.

The pressure gradient for venous return

If blood flow were ceased, arterial pressure would fall and venous pressure would rise to a weighted recoil pressure reflecting the portion of the circulation with greatest blood volume (Sylvester et al., 1983; Jacobsohn et al., 1997). As the small veins and venules comprise this circulatory segment, the P_MCF is a ‘pivot pressure’ found downstream of the capillary beds but upstream from the larger veins (Magder, 2012). The ‘pivot pressure’ description arises from the sense that when the heart recommences circulatory flow, pressure in the arteries rise up from the P_MCF while the pressure in the downstream veins fall below it; thus, the P_MCF acts as a quasi-static ‘pivot’ around which pressures upstream and downstream rise and fall, respectively (Broccard, 2012). As discussed below, the P_MCF is similar, but not equivalent to, the mean systemic filling pressure (P_MSF). The P_MSF excludes the contributions of intrathoracic blood volume and compliance.

The P_MCF (or P_MSF) is determined by two related–and often confused–biophysical properties: capacitance and compliance (Rothe, 1986; Rothe, 1993; Tyberg, 2002). To understand capacitance, the reader must appreciate that the total circulatory volume is comprised of two distinct (though dynamic) ‘types’ of volume–the unstressed (V_US) and stressed (V_S) volumes (Gelman, 2008; Magder, 2012). The V_US does not create a vascular elastic recoil pressure while the V_S does. As an analogy, filling a waterbed requires water volume before the walls are stretched (i.e., the V_US); further volume generates a recoil pressure from the elastic walls (i.e., the V_S). As compared to a water balloon, a waterbed has a much larger capacitance because its V_US is greater than the V_US of the balloon. Compliance and its inverse, elastance, describe the relationship between changing vascular volume and changing recoil pressure (Rothe, 1993). It follows that compliance (or elastance) pertain to the V_S; the V_US, by definition, generates no change in pressure (i.e., the V_US has infinite compliance or zero elastance). Continuing with the analogy above, were the waterbed made from a poorly elastic (i.e., stiff) material, it would have a large capacitance, but low compliance (or high elastance). If the water balloon was made of a highly elastic material, it would have a low capacitance, but high compliance (or low elastance). Mathematically, the P_MCF is determined by the volume of blood generating a recoil pressure (i.e., the V_S, which is determined by total vascular volume and capacitance) divided by the vascular compliance (Tyberg, 2002; Magder, 2012) (Figure 1).

FIGURE 1

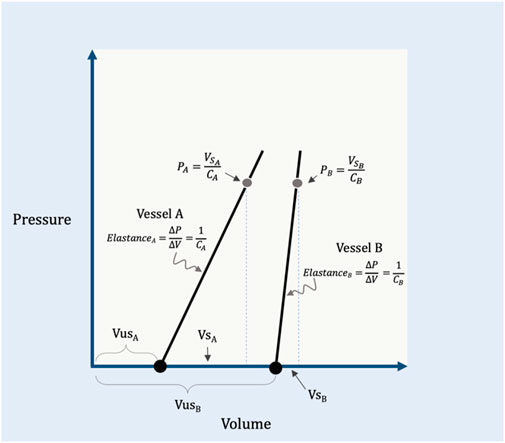
FIGURE 1. Illustration of capacitance and compliance. Vessel A has a relatively small capacitance because its unstressed volume (V_USA) is small. The compliance of the vessel (C_A) is the inverse of elastance on this graph; by rearrangement, the recoil pressure generated in this vessel (P_A) is equal to its stressed volume (V_SA) divided by its compliance. Vessel B shows a larger capacitance, but an increased elastance (i.e., reduced compliance, C_B) relative to vessel A. Vessel A and B are analogous to the ‘water balloon’ and ‘waterbed,’ respectively, described within the text. V_SB is the stressed volume, V_USB is the unstressed volume and P_B is the recoil pressure of vessel B.

As noted above, the P_MCF includes the cardiac and pulmonary vascular volumes and compliances (i.e., the total circulation) while the P_MSF measures only the extra-thoracic, systemic, circulation (Rothe, 1993); they are very similar in value and often used interchangeably. In clinical practice, the methods for estimating this static, ‘pivot pressure’ reflect the systemic pressure (i.e., P_MSF) and this measure will be used throughout this review (Berger et al., 2016). For patients, there are three methods to estimate the P_MSF: 1.) extrapolation to zero flow of the P_RA–cardiac output relationship altered by ventilator-hold maneuvers (Pinsky, 1984; Maas et al., 2009), 2.) extremely rapid cuff insufflation on the arm with an ipsilateral arterial line (Maas et al., 2012) and 3.) mathematical modelling by the method of Parkin and Leaning (Parkin and Leaning, 2008). Though beyond the scope of this discussion, the ventilator-hold and arm-occlusion methods over-estimate P_MSF (Maas et al., 2012; Berger et al., 2016) for a variety of reasons (Moller and Berger, 2023) whereas the mean systemic filling pressure analogue (P_MSA) (i.e., the method of Parkin and Leaning) accurately estimated absolute and changing values of P_MSF in a porcine model (Werner-Moller et al., 2022). Because it is simply calculated from P_RA, cardiac output and mean arterial pressure (Parkin and Leaning, 2008; Moller and Parkin, 2022), the P_MSA is an attractive tool for guiding both prospective and retrospective research as well as clinical therapy (Moller and Parkin, 2022; Moller and Berger, 2023). Given the above, the importance of understanding and, arguably, measuring the P_MSF is that it is a hemodynamic variable the clinician can target therapeutically. For example, a low P_MSF intimates low V_S which could be due to diminished total blood volume (e.g., hypovolemia, hemorrhage) and/or high venous capacitance (e.g., venodilation, sepsis). The clinician might rectify these pathological states by giving volume and/or administering alpha-agonists, respectively (Parkin and Leaning, 2008). Thus, the P_MSF and its determinants are independent variables that can be adjusted for therapeutic control of the circulation; increasing P_MSF raises venous return for any given right atrial pressure (P_RA) (Figure 2).

FIGURE 2

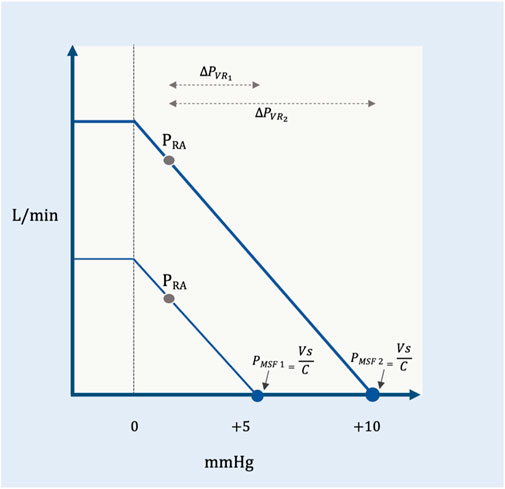
FIGURE 2. Pressure gradient for venous return. The effect of changing mean systemic filling pressure (in millimeters of mercury, mmHg) from a low (P_MSF1) to a higher value (P_MSF2) (e.g., volume infusion, decreased capacitance). The slope of the venous return curve is constant between the two curves meaning that the resistance to venous return is constant (see below). For a given right atrial pressure (P_RA), the lower P_MSF1 (i.e., reduced pressure gradient for venous return, $∆$ P_VR1) causes a diminished venous return on the y-axis (liters per minute, L/min). The same P_RA in a system with P_MSF2 (i.e., increased pressure gradient for venous return, $∆$ P_VR2) results in a higher venous return on the y-axis. The P_MSF is the pressure in the right atrium at zero flow (i.e., the x-intercept). V_S and C are the stressed volume and average compliance, respectively, of the systemic vasculature. The flattening of the venous return curve is where the great veins collapse; this creates a maximal venous return in each state.

Downstream from the P_MSF is the P_RA. In Guyton’s original experimental set-up, P_RA was studied as an independent variable, altered via the height of a collapsible tube (Guyton et al., 1957). Guyton observed that the P_RA was inversely related to venous return; in other words, decreasing P_RA increased venous return, linearly (Figure 2). Consequently, the difference between P_MSF and P_RA is the pressure gradient for venous return ($∆$ P_VR); the value of this gradient is directly proportional to blood return to the right heart (Equation 1). More concretely, an increase in P_MSF and/or decrease in P_RA will augment venous return and vice versa (Magder, 2012).

The resistance to venous return

Guyton began with a mathematical approximation of the circulation, modeled after a system of distensible tubes (Jacobsohn et al., 1997). In this representation, the forces that resist total blood flow back to the heart are termed the ‘resistance to venous return’ (R_VR). While the R_VR is often considered to be a purely Poiseuillean description of the venous circulation, this is not correct. The R_VR, like the P_MSF, is a weighted average of the system (i.e., including arterial components) (Jacobsohn et al., 1997). Each vascular bed faces a downstream resistance and has a unique compliance; the R_VR is a summation of the downstream resistance encountered by each vascular bed, multiplied by its individual compliance relative to the total compliance of the system (Figure 3).

FIGURE 3

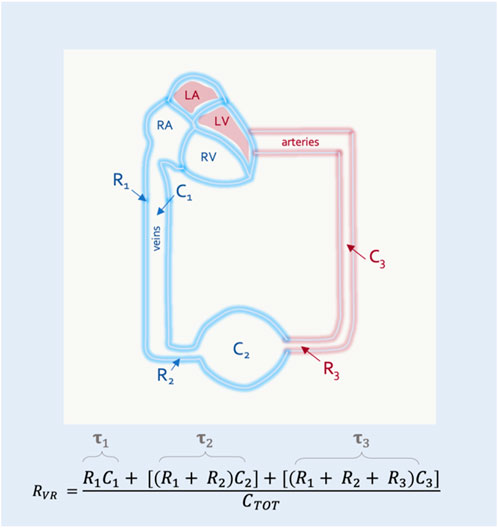
FIGURE 3. The resistance to venous return (R_VR). R_VR is composed of resistances (R_x) and compliances (C_x) for the entire circulation. This simplified model shows 3 vascular segments in series. The R_VR is the sum of the resistance and compliance for each segment divided by the total compliance of the circulatory system (C_TOT). Resistance multiplied by compliance is the time constant ($\tau$).

In this way the R_VR can also be described by the time constant (i.e., the resistance multiplied by the compliance) of each vascular segment (Magder, 2016). This is clinically-important because diverting blood volume towards or away from a vascular bed with a long time constant (e.g., the splanchnic circulation) will increase or decrease the R_VR, respectively (Caldini et al., 1974). The converse is true for vascular beds with a short time constant (e.g., kidneys, muscle) (Magder, 2016) (Figure 4). Accordingly, should an intervention in the ICU (e.g., prone position) alter the fraction of flow to vascular beds of differing time constants, R_VR will be affected.

FIGURE 4

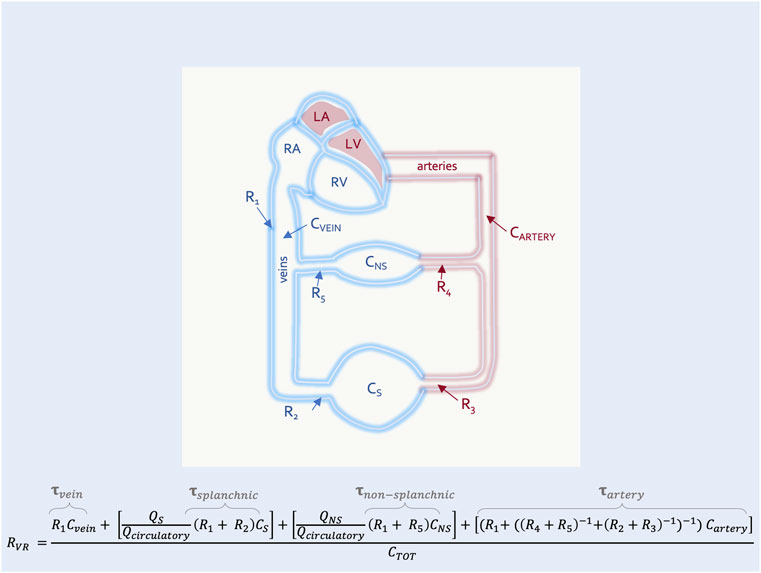
FIGURE 4. The resistance to venous return with high and low time-constant segments in parallel. This is an expansion of Figure 3 with two representative segments in parallel–the non-splanchnic (NS) (i.e., low time constant, $\left.\tau \right)$ and splanchnic (S) (i.e., high $\left.\tau \right)$ segments. Here the fraction of total circulatory flow (Q_circulatory) to the splanchnic (i.e., Q_S/Q_circulatory) versus non-splanchnic (i.e., Q_NS/Q_circulatory) segments determines the R_VR. If all blood diverted to the splanchnic segment (i.e., Q_S/Q_circulatory = 1.0; Q_NS/Q_circulatory = 0.0), its higher compliance (C_S) increases R_VR. If all blood diverted to the non-splanchnic segment (i.e., Q_S/Q_circulatory = 0.0; Q_NS/Q_circulatory = 1.0), its lower compliance (C_NS) decreases R_VR (assuming all other resistances remain equal). C_TOT is the total compliance of the system.

On the venous return curve, change in the R_VR alters the slope for a given pressure gradient (Figure 5). An increase in R_VR reduces the slope, while a decrease in R_VR steepens the slope.

FIGURE 5

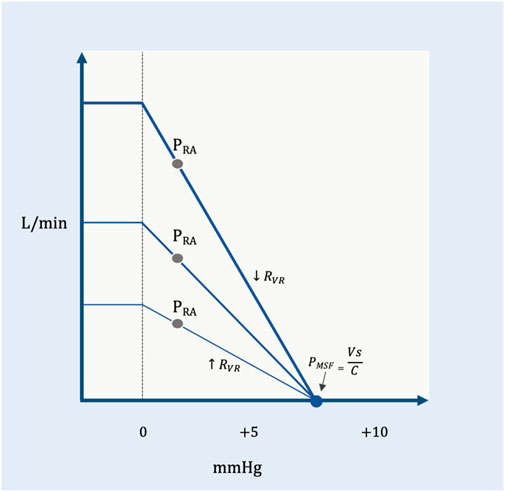
FIGURE 5. The R_VR and the venous return curve. P_MSF is constant, but the resistance to venous return changes. The shallow curve is a higher resistance ($\uparrow$ R_VR) the steeper curve is a lower resistance ($\downarrow$ R_VR). At the same P_RA, lower resistance and higher resistance generate increased and decreased flow (L/min), respectively. V_S and C are the stressed volume and average compliance, respectively, of the systemic vasculature. The flattening of the venous return curve is where the great veins collapse; this creates a maximal venous return in each state.

In summary, venous return is directly proportional to the P_MSF less the P_RA and indirectly proportional to the R_VR. If the P_MSF increases and/or P_RA falls, then venous return rises (Figure 2). Similarly, decreased R_VR facilitates blood return to the heart and vice versa (Figure 5). The Ohmic representation of this relationship is as follows (Berger and Takala, 2018):

$venousreturn=\frac{P_{MSF}-P_{RA}}{R_{VR}}(1)$

Venous return and cardiac function: the Guyton diagram

In addition to detailing the peripheral vascular determinants of blood returning to the heart, Guyton expanded our understanding of hemodynamics by adding to his analysis the cardiac determinants of blood flow from the heart. He did so by superimposing the venous return and Starling-Sarnoff curves (Guyton, 1955); this depiction is commonly referred to as the ‘Guyton diagram.’ These curves can be placed over each other because they both have P_RA on the x-axis and blood flow on the y-axis (Figure 6). Though it will be developed in more detail below, the Guyton diagram introduces an important distinction between intravascular and transmural pressures. The P_RA and P_MSF measured on the Guyton diagram are intravascular pressures. Thus, the pressure gradient for venous return is directly related to the difference between the intravascular P_MSF and P_RA (Equation 1). The Starling mechanism, however, is related to right atrial transmural pressure which is the pressure within the right atrium less its ambient pressure (i.e., the pericardial pressure). The transmural right atrial pressure is a static pressure that determines cardiac myocyte stretch which servo-controls the ejected stroke volume to match the venous return inflow.

FIGURE 6

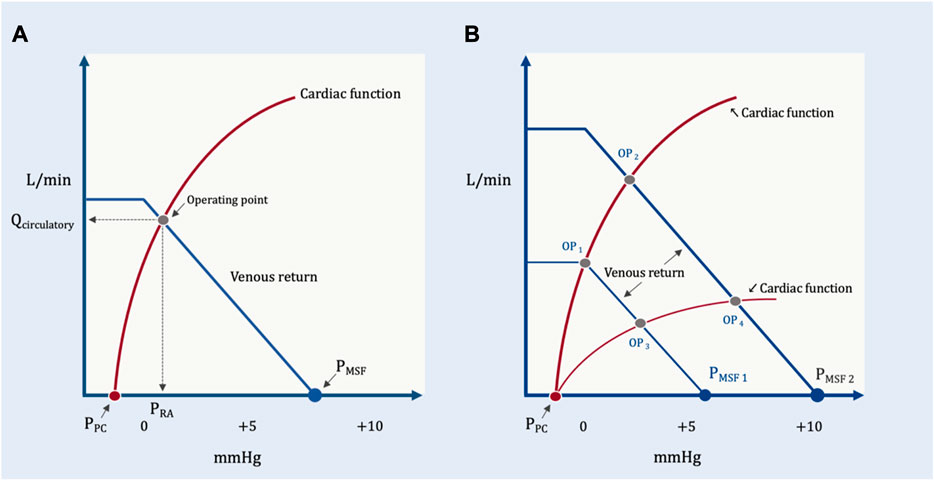
FIGURE 6. The Guyton diagram. (A) The circulation in its resting state; as in Figure 2, the x-axis is right atrial pressure in millimeters of mercury (mmHg) and y-axis is total blood flow in liters per minute (L/min). The P_MSF is approximately 8 mmHg at the x-intercept of the venous return curve (in blue). The Starling-Sarnoff (or cardiac function) curve is in red in a normal, upright position; its x-intercept is the pressure around the right atrium, the pericardial pressure (P_PC). In this model, the dependent variable is the operating point, at the intersection of the venous return and cardiac function curves at equilibrium. Accordingly, both the x- (i.e., P_RA) and y- (i.e., Q_circulatory) coordinates defined by the operating point are also dependent variables. (B) How the P_RA and Q_circulatory are determined by the system. Normal cardiac function but diminished P_MSF1 (e.g., volume loss, venodilation) results in operating point 1 (OP₁), diminished P_RA and Q_circulatory. Normal cardiac function with increased P_MSF2 (e.g., volume expansion, decreased venous capacitance from adrenergic agents) causes OP₂ (i.e., increased P_RA and Q_circulatory). Reduced P_MSF and diminished cardiac function (e.g., acute cor pulmonale with tricuspid regurgitation) leads to OP₃. Elevated P_MSF with reduced cardiac function leads to OP₄. Both Q_circulatory and P_RA are dependent variables in this system. The independent variables are reflected in the position and slopes of the venous return and cardiac function curves.

Like any model, the value of the Guyton diagram is that it makes explicit the system’s independent and dependent variables. Independent variables are those things the clinician can change or control (e.g., vascular volume and capacitance, airway pressure), whereas dependent variables are what the clinician wants to predict or study (e.g., cardiac output) by manipulating the independent variables. These distinctions are critical when considering the effects of any intervention in the ICU (e.g., prone position).

Nestled within the venous return curve are some of the independent variables of the circulatory system touched upon above: 1.) vascular capacitance, 2.) total vascular volume and 3.) the R_VR. Thus, increasing total vascular volume via intravenous fluids and/or decreasing vascular capacitance via alpha-agonists both augment the V_S and, therefore, P_MSF. On the Guyton diagram, raising P_MSF right-shifts the venous return curve such that there is increased blood flow to the heart for any given P_RA. Similarly, beta-agonists (Green, 1977) and/or shunting blood from long to short time-constant vascular beds decreases the R_VR (Caldini et al., 1974); this also enhances venous return for any given P_RA. On the Guyton diagram, diminished R_VR is manifested by an increased slope of the venous return curve (Figure 6). The converse also holds, diminished blood volume, increased capacitance and/or increased R_VR all reduce venous return for any given P_RA. One clinically-important scenario wherein vascular capacitance rises (i.e., which decreases P_MSF) is reduced adrenergic tone (e.g., sedation, anesthesia, relief of hypoxemia) (Bressack and Raffin, 1987).

Found within the cardiac function curve are additional independent variables: heart rate, rhythm, valve function, afterload, inotropic and lusitropic states (Feihl and Broccard, 2009a; Feihl and Broccard, 2009b). Consequently, rate and rhythm control (e.g., cardioversion), afterload reduction (e.g., vasodilator therapy, pulmonary vascular recruitment), enhanced contractility and improved relaxation (e.g., epinephrine infusion) all increase the slope of the Starling-Sarnoff curve. With this, blood flow from the heart is enhanced for any given P_RA. The converse also holds, for example, rapid atrial dysrhythmia coupled with torrential tricuspid regurgitation and severe pulmonary arterial hypertension decreases the slope of the cardiac function curve, that is to say, reduce cardiac output for any given P_RA (Figure 6).

But what about the P_RA itself? Is it an independent variable? In Guyton’s experimental work on venous return, P_RA was studied as an independent variable. However, on the Guyton diagram, which considers both venous return and cardiac function simultaneously, P_RA is not independent. This was clearly stated by Guyton in his initial proposal: “right atrial pressure is not one of the primary determinants of cardiac output but, instead, is itself determined simultaneously with cardiac output” (Guyton, 1955). Later, Fiehl and Broccard expanded upon P_RA as a dependent variable in their excellent review (Feihl and Broccard, 2009a). Accordingly, when analyzing venous return and cardiac function simultaneously, the dependent variable is the equilibrium formed at their intersection–the operating point. Thus, both the x- (i.e., P_RA) and y- (i.e., cardiac output) Cartesian coordinates are equally dependent upon the system. This may be counterintuitive given the convention of placing the independent variable on the x-axis, however, with the Guyton diagram this is a vestige of his initial work on venous return. When it is understood that the operating point is the dependent variable, the circular and specious reasoning that the concept of venous return is incorrect because ‘raising P_RA reduces venous return per Guyton but augments cardiac output by Starling’ becomes moot. Rather, at any given time (or in response to an intervention, such as the prone position) there are characteristics of the peripheral circulation and heart that, in tandem, produce a unique cardiac output and P_RA (Guyton, 1955). To clarify this, a modified Guyton model is proposed below to disclose the clinically-relevant independent variables.

A geometrical model

This is a simplified geometric approximation of the principles discussed above. If we consider the intersection of cardiac function and venous return as two directly-opposed right triangles, then we can solve for the height of their shared apex at equilibrium (i.e., cardiac output or venous return presently identified as Q_circulatory) as a function of their bases and hypotenuse slopes (Figure 7). Q_circulatory is numerically equivalent to cardiac output and/or venous return. It is used in the geometrical model to emphasize that total blood flow (i.e., Q_circulatory) is determined by the operating point–the intersection of both peripheral venous and cardiac function. This avoids the confusion that sometimes arises when ‘cardiac output’ is thought to be determined only by cardiac factors or when ‘venous return’ is thought entirely due to peripheral factors; ‘Q_circulatory’ circumvents this ambiguity.

FIGURE 7

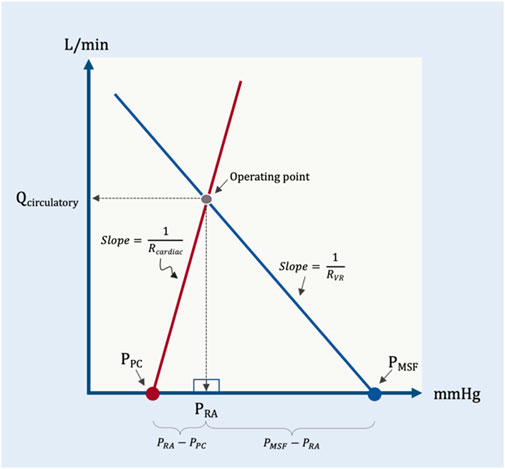
FIGURE 7. Simplified geometrical model. This model borrows from the Guyton diagram where the red line represents cardiac function and the blue line venous return. Two right triangles are formed as described in the text; the operating point is the apex of the two right triangles. Note that the slope (change in flow per unit pressure) is conductance, G. The inverse of conductance is resistance. As in previous figures, P_PC is pericardial pressure, P_MSF is mean systemic filling pressure, R_cardiac and R_VR are cardiac and venous resistance, respectively. Q_circulatory is blood flow of the system with right atrial pressure (P_RA) in millimeters of mercury (mmHg) on the x-axis and blood flow in liters per minute (L/min) on the y-axis.

The base of the left triangle rests on the x-axis and is defined by the pressure immediately surrounding the heart, within the pericardium (i.e., the P_PC) and the P_RA; this is the transmural pressure of the right atrium. The slope (i.e., hypotenuse) of this triangle is the change in cardiac output per mmHg of transmural right atrial pressure, or cardiac conductance (G_cardiac). This value is estimated to be 35 mL/min/kg per 1 mmHg (Rothe, 1993). Multiplying the base of this triangle (i.e., P_RA–P_PC) by the slope of the hypotenuse (G_cardiac) gives the height of this triangle (i.e., total circulatory flow, Q_circulatory).

$Q_{circulatory}={\mathrm{G}}_{cardiac}x\left(P_{RA}-P_{PC}\right)(2)$

Equation 2 is solved for P_RA

$P_{RA}=\frac{Q_{circulatory}}{{\mathrm{G}}_{cardiac}}+P_{PC}(3)$

Similarly, the base of the rightmost triangle is defined by the P_MSF and the P_RA; this is the pressure gradient for venous return (the difference between two intravascular pressures along a hypothetical length of vessel), as above. The slope of this triangle is the change in cardiac output per the gradient for venous return, or venous conductance (G_VR). Based on a P_MSF of 8 mmHg, this value is estimated to be 10 mL/kg/min per 1 mmHg. Multiplying the base of this triangle (i.e., P_MSF–P_RA) by the slope of its hypotenuse (G_VR) gives the height of this triangle, which is also total circulatory flow, Q_circulatory.

$Q_{circulatory}={\mathrm{G}}_{VR}x\left(P_{MSF}-P_{RA}\right)(4)$

Equation 4 is solved for P_RA

$P_{RA}=P_{MSF}-\frac{Q_{circulatory}}{{\mathrm{G}}_{VR}}(5)$

Setting equation 3 equal to equation 5, we can reduce the equation to Q_circulatory as follows:

$P_{MSF}-\frac{Q_{circulatory}}{{\mathrm{G}}_{VR}}=\frac{Q_{circulatory}}{{\mathrm{G}}_{cardiac}}+P_{PC}(6)$

$\frac{P_{MSF}}{{\mathrm{Q}}_{circulatory}}-\frac{1}{{\mathrm{G}}_{VR}}=\frac{Q_{circulatory}}{{\mathrm{G}}_{cardiac}}+P_{PC}(7)$

$\frac{P_{MSF}-P_{PC}}{{\mathrm{Q}}_{circulatory}}=\frac{1}{{\mathrm{G}}_{cardiac}}+\frac{1}{{\mathrm{G}}_{VR}}(8)$

${\mathrm{Q}}_{circulatory}=\frac{P_{MSF}-P_{PC}}{\frac{1}{{\mathrm{G}}_{cardiac}}+\frac{1}{{\mathrm{G}}_{VR}}}(9)$

Because the inverse of conductance, G, is resistance, this equation can be written as:

${\mathrm{Q}}_{circulatory}=\frac{P_{MSF}-P_{PC}}{R_{cardiac}+R_{VR}}(10)$

Accordingly, in this model the shared apex of the two triangles (i.e., the operating point, which defines Q_circulatory) is a function of the total base of the two triangles (i.e., P_MSF less P_PC) and the inverse of the slopes of their respective hypotenuses (i.e., R_VR and R_cardiac). More concretely, if R_VR and R_cardiac remain constant, increased P_MSF and/or decreased pressure surrounding the heart (P_PC) raise the height of their shared apex (Figure 8). A concomitant decrease in R_cardiac (i.e., increased slope of the Starling-Sarnoff curve) or R_VR (i.e., increased slope of the venous return curve) would further elevate their shared apex (Figure 8).

FIGURE 8

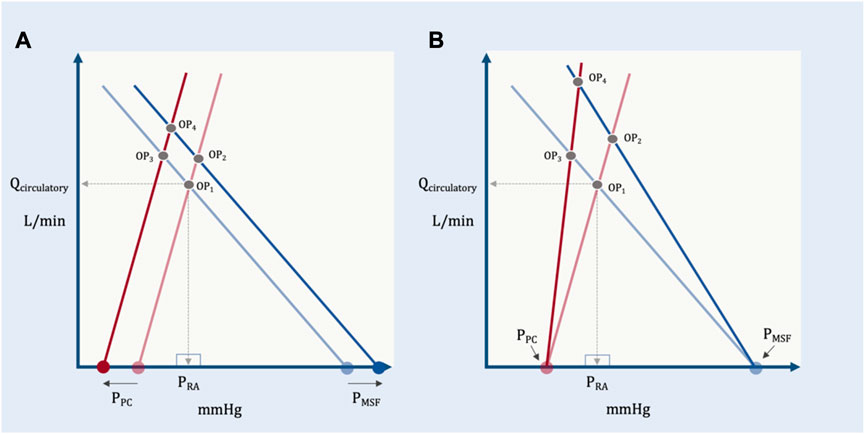
FIGURE 8. The independent and dependent variables of the geometric model. (A) The effect of changing the independent variables, P_PC and P_MSF on the dependent variable (operating point, OP). OP₁ depicts baseline conditions, its x- (P_RA) and y-(Q_circulatory) coordinates are shown. A solitary increase in P_MSF (e.g., volume infusion) results in OP₂, that is, increased P_RA and Q_circulatory. A selective decrease in P_PC (e.g., spontaneous inspiration) leads to OP₃ which increases Q_circulatory, but decreases P_RA. If P_MSF rises and P_PC falls, the result is OP₄, increased Q_circulatory at a slightly reduced P_RA relative to baseline. (B) The effect of changing the independent variables, R_VR and R_cardiac on the dependent variable (operating point, OP). A selective decrease in venous resistance (e.g., shunting blood away from the splanchnic circulation) leads to OP₂ (i.e., both P_RA and Q_circulatory rise). A selective decrease in cardiac resistance (i.e., improving cardiac function by, for example, reducing pulmonary vascular resistance) leads to OP₃ (i.e., P_RA falls, while Q_circulatory rises). Reducing venous and cardiac resistance together leads to OP₄ (i.e., little P_RA change with large Q_circulatory augmentation).

In this model, P_RA plays no role in cardiac output because the operating point (i.e., the shared apex) is the dependent variable; Q_circulatory and P_RA both fall out from this equilibrium (Feihl and Broccard, 2009a). The equations above could have equally been solved for P_RA instead of Q_circulatory; P_RA, nevertheless, would still be dependent upon P_MSF, P_PC, R_cardiac and R_VR.

To further develop this model with an emphasis on heart-lung interaction, the determinants of P_PC are included. Doing so reveals additional, clinically-relevant independent variables when placing an ARDS patient in the prone position. The P_PC is the x-intercept of the hypotenuse defined by R_cardiac (i.e., the cardiac function curve) (Magder, 2004; Feihl and Broccard, 2009a). As originally hypothesized by Guyton (Feihl and Broccard, 2009a) and demonstrated by Marini and colleagues (Marini et al., 1981), increasing P_PC initiates a parallel, right-shift of the cardiac function curve. Consequently, increased P_PC decreases the shared apex (i.e., the operating point) and Q_circulatory is diminished but only if there is no simultaneous change in P_MSF, R_cardiac or R_VR.

Given that the P_PC is a summation of: 1.) pleural pressure (P_PL), 2.) pressure added by mechanical ventilation (i.e., estimated as the mean airway pressure, P_AW, multiplied by the ratio of the chest wall to respiratory system elastances, E_CW/E_RS) (Gattinoni et al., 2004) and 3.) the elastic recoil pressure of the pericardium (P_PCEL) (Cabrera et al., 1989), we can expand equation 10 above.

${\mathrm{Q}}_{circulatory}=\frac{\left.P_{MSF}-{\left[P\right.}_{PL}+\left(P_{AW}\bullet \frac{E_{CW}}{E_{RS}}\right)+P_{{PC}_{EL}}\right]}{R_{cardiac}+R_{VR}}(11)$

Accordingly, increased pleural (e.g., thoracic supports) and/or elastic recoil pressure from the pericardium (e.g., right ventricular dilatation in acute cor pulmonale), raise the pressure surrounding the heart, P_PC. Furthermore, elevated P_AW (e.g., increasing positive end-expiratory pressure, PEEP) or a stiffened chest wall (e.g., prone position increases the E_CW/E_RS ratio) both amplify P_PC; from equation 11, we see that increasing P_PC reduces Q_circulatory but only if P_MSF, R_cardiac and R_VR are constant. It should not escape the reader’s attention that including P_PC in this model is a crucial link between cardiac and respiratory physiologies.

Cardiac limitation

While the proposed model is meant to illuminate the clinically-relevant independent variables determining Q_circulatory, equation 11 has important caveats (Magder, 2012). The most important is that it is predicated upon the intersection of two hypotenuses; in vivo, both the venous return and cardiac function curves have portions that flatten out. When the operating point falls upon the flat portion of the cardiac function curve, Q_circulatory depends only upon the independent variables of cardiac function: P_PC, the right atrial pressure at which the cardiac function curve begins to plateau, P_RAplat and the R_cardiac (Figure 9).

${\mathrm{Q}}_{circulatory}=\frac{P_{{RA}_{plat}}-P_{PC}}{R_{cardiac}}(12)$

FIGURE 9

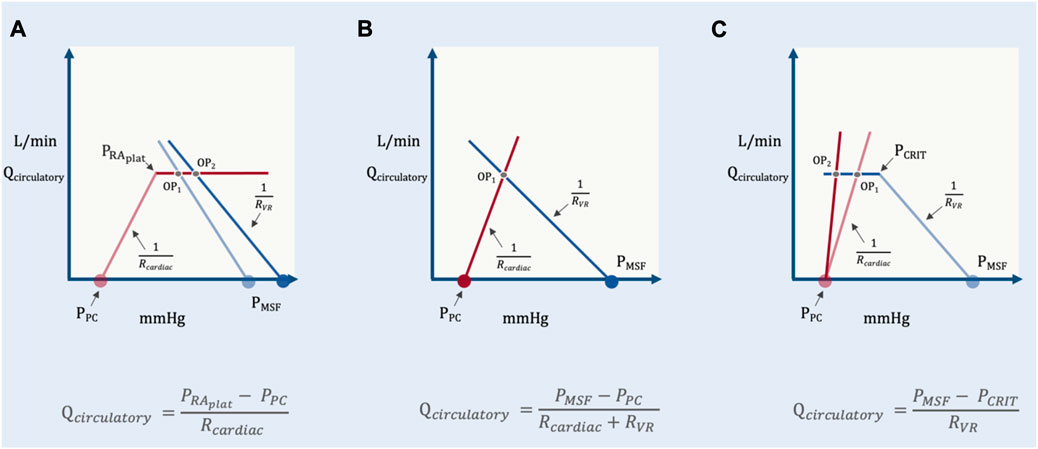
FIGURE 9. Operating point positions in the geometrical model. (A) reveals cardiac limitation where the operating point (OP) is on the flat portion of the cardiac function curve. Change in P_MSF or R_VR change only P_RA and not Q_circulatory (OP₁ versus OP₂). (B) is when the system is neither venous nor cardiac limited. Q_circulatory is changed by P_MSF, P_PC, R_cardiac and R_VR (see Figure 5). (C) shows venous limitation or ‘waterfall’ physiology. Changes in cardiac function alter only P_RA and not Q_circulatory (OP₁ versus OP₂).

Fundamentally, this equation relays that Q_circulatory is no longer determined by peripheral factors when the operating point is above the P_RAplat. Changing P_MSF or R_VR only alter P_RA with fixed Q_circulatory.

Venous limitation

In a manner similar to cardiac function, the venous return curve also flattens when the P_RA falls below venous collapse pressure, P_CRIT (Magder, 2012). This is the formation of a Starling resistor when the great veins enter the thorax and is observed with ultrasound as collapse of the great veins. This phenomenon is also termed ‘waterfall’ physiology because the pressure below P_CRIT has no bearing on flow, just as the height of a waterfall does not mediate its flow (Permutt and Riley, 1963). Consequently, when the operating point lies to the left of P_CRIT (i.e., on the “flat portion” of the venous return curve) Q_circulatory becomes independent of cardiac function or P_PC; the independent variables are P_CRIT, P_MSF and R_VR (Figure 9).

${\mathrm{Q}}_{circulatory}=\frac{P_{MSF}-P_{CRIT}}{R_{VR}}(13)$

In other words, when venous limited, reducing R_cardiac (i.e., improving cardiac function) or changing P_PC has no bearing on Q_circulatory; only changing P_MSF, R_VR or P_CRIT might alter total flow.

Implications for the prone position

With a Guyton-based circulatory model proposed above, anticipating the change in Q_circulatory follows the independent variables of the system: P_MSF, P_PC, R_cardiac and R_VR. At present there are three key studies that have elucidated interactions between the circulation and prone position in ARDS (Vieillard-Baron et al., 2007; Jozwiak et al., 2013; Lai et al., 2021). Much of the discussion below is taken from these investigations.

Mean systemic filling pressure

Recently, Lai and colleagues studied the effect of prone position on the determinants of venous return (Lai et al., 2021). They measured P_MSF by extrapolating to zero flow a series of P_RA–cardiac output pairings in response to increasing airway pressure. Though this method overestimated P_MSF in a porcine model (Berger et al., 2016), this observation was restricted to euvolemic conditions which are less likely in ARDS patients in the ICU. Nevertheless, considering the discussion on P_MSF measurement above, a retrospective calculation of P_MSA would be of great interest given that the average P_MSF measured by Lai et al. was clinically quite high, especially in the prone position. Irrespective of absolute values, Lai and colleagues observed that P_MSF increased significantly from the semi-recumbent to prone position; they hypothesized that this was due to increased intra-abdominal pressure (IAP). However, the baseline value and change in IAP had no bearing on P_MSF behavior. This is unsurprising given what is known about the mechanisms by which PEEP increase P_MSF. Initially, it was also hypothesized that IAP mediated P_MSF augmentation with PEEP application and/or stiffening of the chest wall (i.e., akin to prone position) in early canine models (Scharf et al., 1977). However, IAP had no role in raising P_MSF, instead, adrenergic reflexes (i.e., changing vascular capacitance) and redistribution of blood volume from the central to peripheral circulation were the main drivers of P_MSF rise (Scharf and Ingram, 1977; Fessler, 1995; Fessler, 1997). Accordingly, central blood volume, adrenergic reserve and exogenous vasoactive agents all undoubtedly mediate the change in P_MSF upon pronation, rather than IAP. Parenthetically, this could also explain hemodynamic differences noted between elective surgical and critically-ill ARDS patients when prone position is employed (Edgcombe et al., 2008). The latter are more likely to be on vasoactive agents and volume-loaded, while the former more likely euvolemic; as well, anesthetic agents may blunt reflexive changes in vascular capacitance which would limit P_MSF rise in the operating room. As described above, P_MSF is directly related to Q_circulatory when the patient is not cardiac limited and without concurrent changes in P_PC, R_cardiac or R_VR.

Pericardial pressure

There are no known direct measurements of P_PC in humans with ARDS placed in the prone position. Yet, inferences can be made given the mathematical approximation of P_PC presented above. The prone position increases the elastance (i.e., stiffness) of the chest wall (E_CW) (Pelosi et al., 1998). To the extent that pronation also decreases the elastance (i.e., improves compliance) of the lungs by alveolar recruitment, the E_CW relative to the elastance of the respiratory system (i.e., the lungs and the chest wall together, E_RS) rises. Multiplying the mean airway pressure generated by mechanical ventilation by the E_CW/E_RS ratio approximates P_PC augmentation when a patient is passive with the ventilator. For example, if the mean airway pressure is 10 mmHg with an E_CW/E_RS ratio of 0.3 in the supine position, then 3 mmHg is added to the P_PC. If mean airway pressure remains constant and prone position increases the E_CW/E_RS ratio to 0.5, then 5 mmHg is added to the P_PC.

Additionally, pericardial restraint could play an important role determining P_PC, especially if there is comorbid acute cor pulmonale (ACP). Typically, when right atrial volume is low (i.e., estimated by a transmural pressure below 5 mmHg (Hamilton et al., 1994)), there is little recoil pressure generated by the pericardium around it. As atrial volume increases beyond this, the pericardial sac is engaged and moves up its volume-pressure relationship. This leads to an increasingly large elastic recoil pressure from the pericardium, which raises the P_PC. Elevated P_PC, therefore, restricts right ventricular filling and ‘protects’ from overdistention; however, this blunts Q_circulatory by narrowing the P_MSF–P_PC gradient.

In the setting of ACP, often seen in moderate-to-severe ARDS (Guérin and Matthay, 2016; Mekontso Dessap et al., 2016), pericardial recoil may play an important role upon prone position. With ACP, co-existent right atrial distension elevates P_PC by pericardial recoil; this is especially true with P_RA above 10–12 mmHg (Hamilton et al., 1994). While prone position is expected to further increase P_PC (i.e., by increasing P_PL), to the extent that the elevated P_PL shrinks cardiac volume, P_PC may remain constant, or even fall, as the elastic recoil pressure imparted by the pericardium is reduced. More simply, the rising P_PL experienced by the pericardial space is offset by falling recoil pressure of the pericardium. This was originally observed in models of continuous positive airway pressure in heart failure (Huberfeld et al., 1995). Were this to occur upon prone position in a patient with ACP, P_PC would remain constant or fall. Taken with the effect of prone position on P_MSF noted above, the P_MSF–P_PC gradient would be maintained (or enhanced) and so too would Q_circulatory if R_cardiac and R_VR remain constant.

Finally, some have argued for the execution of prone position with thoracoabdominal supports that allow the abdomen to hang freely (Chiumello et al., 2006). These supports are typically placed mid-sternum and below the pelvis. Chiumello and colleagues compared these supports to the abdomen flush with the bed in prone ARDS patients (Chiumello et al., 2006). They found that the supports accentuated local pressure without any benefit to gas exchange while diminishing stroke volume. Given support placement directly at the sternum, it is possible that P_PC is accentuated, reducing the P_MSF–P_PC gradient and Q_circulatory barring a concomitant decrease in R_cardiac or R_VR.

Cardiac resistance

While not a commonly-employed term within the sphere of clinical hemodynamics, ‘cardiac resistance’ (R_cardiac) is analogous to R_VR. Graphically and mathematically, R_cardiac is simply the inverse slope of the cardiac function curve. A decrease in R_cardiac (i.e., a steeper slope of the cardiac function curve) represents improved cardiac function and raises the operating point (i.e., Q_circulatory) unless the system is venous limited. In an elegant ultrasonographic study, Vieillard-Baron and colleagues illuminated the salubrious effects on the RV prompted by prone position (Vieillard-Baron et al., 2007). In 21 patients with P_aO₂/F_iO₂ ratio of less than 100 mmHg and ACP defined as RV enlargement and septal dyskinesia, 18 h of prone position led to a significant reduction in heart rate and increase in cardiac output. Furthermore, RV end-diastolic area fell while LV end-diastolic area increased and tricuspid regurgitation was reduced. Taken together, the rise in cardiac output with diminished RV size strongly implies reduced R_cardiac as a mechanism of improved Q_circulatory, at least in patients with ACP. The mechanism for this improvement (detailed at the outset of this review and by others (Repessé et al., 2016)) was reduced pulmonary vascular impedance to flow facilitating RV ejection (Jardin and Vieillard-Baron, 2003; Vieillard-Baron et al., 2007) which improves stroke volume and cardiac output for any given P_RA.

Recent studies also imply reduced R_cardiac. Ruste and colleagues investigated the hemodynamic effects of prone position in over 100 patients (Ruste et al., 2018). 25% of prone sessions led to significantly increased cardiac output, while 23% had a significant decrease; the remainder showed no change. Importantly, of those sessions where cardiac output rose, 56% had no change or a decrease in global end-diastolic volume (GEDV) measured by transpulmonary thermodilution. Rising cardiac output without an increase in end-diastolic volume infers reduced R_cardiac. Importantly, static GEDV with prone position could signify a shrinking RV end diastolic volume with enlarging LV end diastolic volume consistent with the reduced RV-to-LV end-diastolic area ratio observed with echocardiography by Vieillard-Baron et al. (Vieillard-Baron et al., 2007). Finally, Boesing and colleagues recently published on different PEEP titration strategies and their interaction with prone position (Boesing et al., 2022). In this study, esophageal pressure (P_ES) was used as a surrogate for P_PL. Curiously, the PEEP titration strategy that led to the greatest increase in cardiac output from supine to prone was associated with the smallest rise in transmural P_RA (i.e., P_RA less P_ES), in other words, the least preload augmentation. Similar to the observations by Ruste and colleagues, this finding suggests, but does not prove, enhanced cardiac function (i.e., reduced R_cardiac).

Resistance to venous return

In the study of Lai and colleagues (Lai et al., 2021), the R_VR was calculated from semi-recumbent to prone position in ARDS patients. In total, R_VR increased in the vast majority, though there were a few with stable or slightly diminished R_VR. Like P_MSF, the change in R_VR was not related to IAP and like P_MSF, this is unsurprising given the foundational work of Takata and Robotham (Takata et al., 1990). In their original model, Takata and Robotham proposed that the relationship between great vein pressure and IAP would behave analogously to West zones in the lung. That is, if the IAP is much greater than inferior vena cava (IVC) pressure (i.e., zone 2), then venous return is impaired when the abdomen is pressurized by diaphragmatic descent and, in theory, prone position. However, if IAP is much less than IVC pressure (i.e., zone 3), then increased IAP generated by diaphragmatic descent (or prone position) enhances venous return. Their initial work confirmed this model, however, they later found that the model held even with an open abdomen and evisceration, that is, constant IAP (Takata and Robotham, 1992). Thus, the ambient pressure of import was more likely focal subcostal, crural, or intra-hepatic pressure, rather than general IAP. This was observed by Decramer and colleagues (Decramer et al., 1984) and explored further by Brienza et al. in a porcine model (Brienza et al., 1995) and Jellinek et al. in humans (Jellinek et al., 2000). Accordingly, diaphragmatic shape-matching between the liver and upper abdomen, active versus passive diaphragm displacement, intra-hepatic compliance (e.g., intrinsic liver disease) and the use of focal thoracoabdominal supports, among other factors might affect hepatic pressure (P_hepatic) upon pronation. Diminished venous pressure (e.g., hypovolemia, venodilation) relative to P_hepatic might increase R_VR. By contrast, elevated venous pressure (e.g., high blood volume, low venous capacitance) relative to P_hepatic might blunt a rise in R_VR with prone positioning.

Another possible mechanism for increased R_VR with prone position follows that of P_MSF. As described above, reflex sympathetic tone is a key mediator of increased P_MSF. However, when alpha agonists act upon veins to increase the V_S, resistance necessarily rises. This is because change in volume is proportional to the second power of vessel diameter but resistance is related to the fourth power. More concretely, if the diameter of a vein falls by 20% from its baseline, its volume is diminished by 36% (i.e., this reduces its capacitance, increases P_MSF) but its resistance rises by 244% (Rothe, 1993). Because the splanchnic circulation is a crucial reservoir for venous blood, the rise in resistance in response to V_S recruitment can be offset by beta-agonism (Green, 1977) in the hepatic veins, or redistribution of blood flow to short time constant vascular beds, as noted above (Magder, 2016) (Figure 4). Nevertheless, hepatosplanchnic blood flow during prone position in ARDS changes little (Hering et al., 2002; Matejovic et al., 2002). Interestingly, one study found decreased renal blood flow (Hering et al., 2001)—a fast time-constant bed; diversion of blood in this manner contributes to increased R_VR. A final, potential mechanism for R_VR augmentation with prone position lies in the superior vena cava (SVC). Fessler found that the rise in total R_VR following PEEP application was predominantly due to the veins draining into the SVC rather than the IVC (Fessler et al., 1992). Because P_PL is the pressure that surrounds SVC and prone tends to raise P_PL for any given P_AW (see equation 11 above), it is possible that mechanical compression of the SVC contributes to R_VR (Lansdorp et al., 2014; Berger et al., 2016). Regardless of the mechanism, R_VR is a critical determinant of Q_circulatory (Pinsky, 2021).

Knowing the limits

Taking the above into consideration, a key factor when predicting the hemodynamic response to prone position is the location of the operating point whilst semi-recumbent; is the operating point ‘cardiac limited’, ‘venous limited’ or ‘unlimited’ (Figure 6) (Magder, 2012)? Knowing this focuses the clinician on the independent variables most likely affecting Q_circulatory. For instance, if the operating point is cardiac limited (Figure 6) we see that changes in P_MSF and R_VR play no role, while changes in cardiac characteristics (e.g., R_cardiac) mediate Q_circulatory. Of course, this depends on how close the operating point is to the P_RA at which the cardiac function curve flattens out, but this is, nevertheless, a reasonable clinical heuristic. Jozwiak and colleagues studied 18 ARDS patients with elevated right ventricular-to-left ventricular end-diastolic areas (RVEDA/LVEDA), but without ACP (Jozwiak et al., 2013). Prior to prone position, the change in cardiac output in response to a passive leg raise was evaluated. By the model above, ‘cardiac limitation’ is detected when a patient is preload unresponsive. In this state, only improved cardiac function during pronation (i.e., reduced R_cardiac) increases Q_circulatory; changes in P_MSF and R_VR shift the operating point along the x-axis, but not the y-axis. In other words, P_RA changes but not blood flow. Jozwiak and colleagues found that in ‘cardiac limited’ patients, prone position significantly reduced pulmonary vascular resistance and the RVEDA/LVEDA which should diminish R_cardiac and improve Q_circulatory. However, these patients were also found to have depressed left ventricular ejection fraction. Furthermore, in the face of prone position, systemic afterload increased; total R_cardiac, therefore, did not improve.

When patients are not ‘cardiac limited,’ the operating point may be either ‘unlimited’ or ‘venous limited.’ In the study of Jozwiak and colleagues, imaging of the great veins was not reported, but those patients who were preload responsive were unlikely to have great vein collapse (i.e., venous ‘waterfall’) given that their average, baseline P_RA was relatively high (i.e., 15 mmHg) with increased RVEDA/LVEDA ratios. Thus, based on equation 11 above, the change in Q_circulatory was probably subject to all of: P_MSF, P_PC, R_cardiac and R_VR. Given what we know from Lai and colleagues, prone position likely increased P_MSF; P_PC may have increased less than the rise in P_PL because of reduced pericardial restraint and R_cardiac fell due to diminished pulmonary vascular resistance. Each of these effects raise Q_circulatory, presumably offsetting heightened R_VR with prone (Figure 10).

FIGURE 10

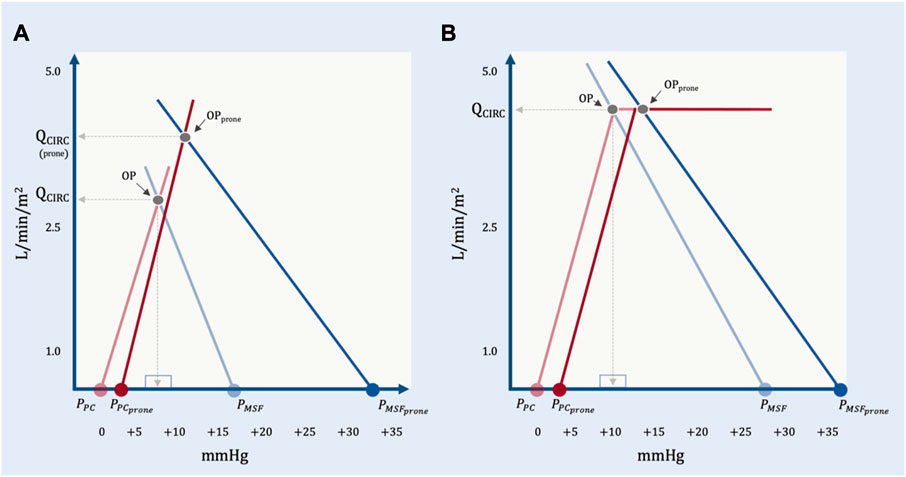
FIGURE 10. The geometrical model applied to representative data from Lai et al. (A) The effect of prone position on a preload responsive patient. At baseline, P_PC is estimated by assuming a mean airway pressure of 15 mmHg, an E_CW/E_RS ratio of 0.2 and a pleural pressure (P_PL) at functional residual capacity of—2.5 mmHg. With prone position, the P_MSF rises much more than P_PC. There is an increase in R_VR and an assumed decrease in R_cardiac due to reduced pulmonary vascular resistance. The operating point with prone position (OP_prone) leads to an increase in total blood flow (Q_CIRC) and increased right atrial pressure (P_RA). By this model, P_RA does not determine Q_CIRC; both P_RA and Q_CIRC are determined by P_MSF, P_PC, R_cardiac and R_VR. (B) Prone position in a preload unresponsive patient at baseline. P_PC in prone is estimated by assuming a mean airway pressure of 15 mmHg, and E_CW/E_RS ratio of 0.5 and a P_PL at functional residual capacity of—2.5 mmHg. With cardiac limitation, only a significant change in R_cardiac would increase Q_CIRC.

It is also possible for preload responsive patients to be ‘venous limited’ as described by equation 13 above. When the operating point lies on the flat portion of the venous return curve (i.e., below P_CRIT) then R_cardiac ceases to affect Q_circulatory. Said another way, blood flow is determined solely by peripheral venous factors. When ‘venous limited’, volume status is likely a crucial determinant of the hemodynamic response to prone position based on the model of Takata and Robotham described above (Takata et al., 1990). A zone 3 abdomen might have a stable or enhanced P_MSF relative to P_CRIT and blunt any increase in R_VR (i.e., stable or increased Q_circulatory), while a zone 2 abdomen would diminish P_MSF relative to P_CRIT and favour elevated R_VR (i.e., stable or reduced Q_circulatory). There is little data on ‘venous limited’ ARDS patients being placed in prone. In the study by Lai and colleagues, there were four ‘preload responsive’ patients who had no change (n = 3) or a decrease (n = 1) in Q_ciculatory when placed in prone position. These patients may have been venous limited, but this data was not collected. Given that at low trans-mural pressure, the great veins are very compliant (Bodson and Vieillard-Baron, 2012), generation of a hemodynamically-significant Starling resistor, i.e., ‘venous limitation,’ should lead to great vein collapse throughout most of the respiratory cycle. In a patient passive with the ventilator, collapse is an inspiratory event for the SVC and expiatory event for the IVC. Collecting this data with ultrasound before and after pronation could help delineate this hemodynamic phenotype.

Finally, it is possible to be both venous and cardiac limited simultaneously, in other words, the operating point is on both the flat portion of the venous return and cardiac function curves concurrently. This might happen in states of high P_CRIT (e.g., high PEEP, high subdiaphragmatic pressure) coupled with depressed cardiac function. In the setting of ARDS, this could be a syndrome of alveolar over-distension (Jardin and Vieillard-Baron, 2003). Prone position in such a patient might reduce Q_circulatory, especially if the patient is hypovolemic. Managing this hemodynamic phenotype might involve PEEP titration to reduce P_CRIT and enhance cardiac function as this could move the operating point onto steep portions of the venous return and cardiac function curves.

Conclusion

At equilibrium, the intersection of venous return and cardiac function generates the hemodynamic operating point. The operating point and both of its coordinates (i.e., P_RA and Q_circulatory) are dependent variables. The independent variables of the system are the P_MSF, resistance to venous return, cardiac function and the pressure surrounding the right atrium. These are not new principles; however, clinical physiology can be muddied in terms of how dependent and independent variables are discussed. A simplified geometrical model was presented to clarify the mechanisms of blood flow at equilibrium founded on Guyton’s model of the circulation; this focuses the clinician on how interventions in the ICU (e.g., prone position) might affect hemodynamics. Recent mechanistic investigations into the circulatory consequences of prone position have been reported. These findings were incorporated into the simplified geometrical model with emphasis on the link between cardiac and respiratory physiologies. The pericardial pressure is one nexus binding the heart and the lungs; so too are changes in cardiac function from pulmonary vascular recruitment. Measuring ‘preload responsiveness’ locates the system’s operating point; this helps predict the hemodynamic response to any intervention in the ICU, including the decision to prone a patient with ARDS.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Acknowledgments

Pietro Verrecchia for review of Figures 3 and 4.

Conflict of interest

J-ESK is the cofounder and Chief Medical Officer of Flosonics Medical.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Beard, D. A., and Feigl, E. O. (2011). Understanding Guyton's venous return curves. Am. J. Physiol. Heart Circ. Physiol. 301 (3), H629–H633. doi:10.1152/ajpheart.00228.2011

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, D., Moller, P. W., and Takala, J. (2019). Reply to "Is the Guytonian framework justified in explaining heart lung interactions?" and "Venous return, mean systemic pressure and getting the right answer for the wrong reason. Ann. Transl. Med. 7 (8), 186. doi:10.21037/atm.2019.04.50

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, D., Moller, P. W., Weber, A., Bloch, A., Bloechlinger, S., Haenggi, M., et al. (2016). Effect of PEEP, blood volume, and inspiratory hold maneuvers on venous return. Am. J. physiology-heart circulatory physiology 311 (3), H794–H806. doi:10.1152/ajpheart.00931.2015

PubMed Abstract | CrossRef Full Text | Google Scholar

Berger, D., and Takala, J. (2018). Determinants of systemic venous return and the impact of positive pressure ventilation. Ann. Transl. Med. 6 (18), 350. doi:10.21037/atm.2018.05.27

PubMed Abstract | CrossRef Full Text | Google Scholar

Berlin, D. A., and Bakker, J. (2015). Starling curves and central venous pressure. Crit. Care 19 (1), 55. doi:10.1186/s13054-015-0776-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Bodson, L., and Vieillard-Baron, A. (2012). Respiratory variation in inferior vena cava diameter: Surrogate of central venous pressure or parameter of fluid responsiveness? Let the physiology reply. Crit. Care 16 (6), 181. doi:10.1186/cc11824

PubMed Abstract | CrossRef Full Text | Google Scholar

Boesing, C., Graf, P. T., Schmitt, F., Thiel, M., Pelosi, P., Rocco, P. R. M., et al. (2022). Effects of different positive end-expiratory pressure titration strategies during prone positioning in patients with acute respiratory distress syndrome: A prospective interventional study. Crit. Care 26 (1), 82. doi:10.1186/s13054-022-03956-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Bone, R. C. (1993). The ARDS lung. New insights from computed tomography. Jama 269 (16), 2134–2135. doi:10.1001/jama.269.16.2134

PubMed Abstract | CrossRef Full Text | Google Scholar

Brengelmann, G. L. (2003). A critical analysis of the view that right atrial pressure determines venous return. J. Appl. Physiol. (1985) 94 (3), 849–859. doi:10.1152/japplphysiol.00868.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

Brengelmann, G. L. (2019). Venous return and the physical connection between distribution of segmental pressures and volumes. Am. J. Physiol. Heart Circ. Physiol. 317 (5), H939–h953. doi:10.1152/ajpheart.00381.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

Bressack, M. A., and Raffin, T. A. (1987). Importance of venous return, venous resistance, and mean circulatory pressure in the physiology and management of shock. Chest 92 (5), 906–912. doi:10.1378/chest.92.5.906

PubMed Abstract | CrossRef Full Text | Google Scholar

Brienza, N., Ayuse, T., O'Donnell, C. P., Permutt, S., and Robotham, J. L. (1995). Regional control of venous return: Liver blood flow. Am. J. Respir. Crit. care Med. 152 (2), 511–518. doi:10.1164/ajrccm.152.2.7633700

PubMed Abstract | CrossRef Full Text | Google Scholar

Broccard, A. F. (2012). Cardiopulmonary interactions and volume status assessment. J. Clin. Monit. Comput. 26 (5), 383–391. doi:10.1007/s10877-012-9387-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Broccard, A. F., Hotchkiss, J. R., Kuwayama, N., Olson, D. A., Jamal, S., Wangensteen, D. O., et al. (1998). Consequences of vascular flow on lung injury induced by mechanical ventilation. Am. J. Respir. Crit. care Med. 157 (6), 1935–1942. doi:10.1164/ajrccm.157.6.9612006

PubMed Abstract | CrossRef Full Text | Google Scholar

Cabrera, M. R., Nakamura, G. E., Montague, D. A., and Cole, R. P. (1989). Effect of airway pressure on pericardial pressure. Am. Rev. Respir. Dis. 140 (3), 659–667. doi:10.1164/ajrccm/140.3.659

PubMed Abstract | CrossRef Full Text | Google Scholar

Caldini, P., Permutt, S., Waddell, J. A., and Riley, R. L. (1974). Effect of epinephrine on pressure, flow, and volume relationships in the systemic circulation of dogs. Circulation Res. 34 (5), 606–623. doi:10.1161/01.res.34.5.606

PubMed Abstract | CrossRef Full Text | Google Scholar

Chiumello, D., Cressoni, M., Racagni, M., Landi, L., Li Bassi, G., Polli, F., et al. (2006). Effects of thoraco-pelvic supports during prone position in patients with acute lung injury/acute respiratory distress syndrome: A physiological study. Crit. Care 10 (3), R87. doi:10.1186/cc4933

PubMed Abstract | CrossRef Full Text | Google Scholar

Cressoni, M., Cadringher, P., Chiurazzi, C., Amini, M., Gallazzi, E., Marino, A., et al. (2014). Lung inhomogeneity in patients with acute respiratory distress syndrome. Am. J. Respir. Crit. care Med. 189 (2), 149–158. doi:10.1164/rccm.201308-1567OC

PubMed Abstract | CrossRef Full Text | Google Scholar

Cressoni, M., Chiurazzi, C., Gotti, M., Amini, M., Brioni, M., Algieri, I., et al. (2015). Lung inhomogeneities and time course of ventilator-induced mechanical injuries. Anesthesiology 123 (3), 618–627. doi:10.1097/ALN.0000000000000727

PubMed Abstract | CrossRef Full Text | Google Scholar

Decramer, M., De Troyer, A., Kelly, S., Zocchi, L., and Macklem, P. T. (1984). Regional differences in abdominal pressure swings in dogs. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 57 (6), 1682–1687. doi:10.1152/jappl.1984.57.6.1682

PubMed Abstract | CrossRef Full Text | Google Scholar

Edgcombe, H., Carter, K., and Yarrow, S. (2008). Anaesthesia in the prone position. Br. J. Anaesth. 100 (2), 165–183. doi:10.1093/bja/aem380

PubMed Abstract | CrossRef Full Text | Google Scholar

Feihl, F., and Broccard, A. F. (2009a). Interactions between respiration and systemic hemodynamics. Part I: Basic concepts. Intensive Care Med. 35 (1), 45–54. doi:10.1007/s00134-008-1297-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Feihl, F., and Broccard, A. F. (2009b). Interactions between respiration and systemic hemodynamics. Part II: Practical implications in critical care. Intensive Care Med. 35 (2), 198–205. doi:10.1007/s00134-008-1298-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Fessler, H. E., Brower, R. G., Wise, R. A., and Permutt, S. (1992). Effects of positive end-expiratory pressure on the canine venous return curve. Am. Rev. Respir. Dis. 146 (1), 4–10. doi:10.1164/ajrccm/146.1.4

PubMed Abstract | CrossRef Full Text | Google Scholar

Fessler, H. E. (1995). Effects of CPAP on venous return. J. Sleep. Res. 4 (S1), 44–49. doi:10.1111/j.1365-2869.1995.tb00185.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Fessler, H. E. (1997). Heart-lung interactions: Applications in the critically ill. Eur. Respir. J. 10 (1), 226–237. doi:10.1183/09031936.97.10010226

PubMed Abstract | CrossRef Full Text | Google Scholar

Gattinoni, L., Chiumello, D., Carlesso, E., and Valenza, F. (2004). Bench-to-bedside review: Chest wall elastance in acute lung injury/acute respiratory distress syndrome patients. Crit. Care 8 (5), 350–355. doi:10.1186/cc2854

PubMed Abstract | CrossRef Full Text | Google Scholar

Gattinoni, L., and Quintel, M. (2016). How ARDS should be treated. Crit. Care 20, 86. doi:10.1186/s13054-016-1268-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Gattinoni, L., Taccone, P., Carlesso, E., and Marini, J. J. (2013). Prone position in acute respiratory distress syndrome. Rationale, indications, and limits. Am. J. Respir. Crit. care Med. 188 (11), 1286–1293. doi:10.1164/rccm.201308-1532CI

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelman, S. (2008). Venous function and central venous pressure: A physiologic story. Anesthesiology 108 (4), 735–748. doi:10.1097/ALN.0b013e3181672607

PubMed Abstract | CrossRef Full Text | Google Scholar

Green, J. F. (1977). Mechanism of action of isoproterenol on venous return. Am. J. Physiol. 232 (2), H152–H156. doi:10.1152/ajpheart.1977.232.2.H152

PubMed Abstract | CrossRef Full Text | Google Scholar

Guérin, C., Albert, R. K., Beitler, J., Gattinoni, L., Jaber, S., Marini, J. J., et al. (2020). Prone position in ARDS patients: Why, when, how and for whom. Intensive Care Med. 46 (12), 2385–2396. doi:10.1007/s00134-020-06306-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Guérin, C., and Matthay, M. A. (2016). Acute cor pulmonale and the acute respiratory distress syndrome. Intensive Care Med. 42 (5), 934–936. doi:10.1007/s00134-015-4197-z

PubMed Abstract | CrossRef Full Text | Google Scholar

Guérin, C., Reignier, J., Richard, J. C., Beuret, P., Gacouin, A., Boulain, T., et al. (2013). Prone positioning in severe acute respiratory distress syndrome. N. Engl. J. Med. 368 (23), 2159–2168. doi:10.1056/NEJMoa1214103

PubMed Abstract | CrossRef Full Text | Google Scholar

Guyton, A. C. (1955). Determination of cardiac output by equating venous return curves with cardiac response curves. Physiol. Rev. 35 (1), 123–129. doi:10.1152/physrev.1955.35.1.123

PubMed Abstract | CrossRef Full Text | Google Scholar

Guyton, A. C., Lindsey, A. W., Abernathy, B., and Richardson, T. (1957). Venous return at various right atrial pressures and the normal venous return curve. Am. J. Physiol. 189 (3), 609–615. doi:10.1152/ajplegacy.1957.189.3.609

PubMed Abstract | CrossRef Full Text | Google Scholar

Guyton, A. C., Lindsey, A. W., and Kaufmann, B. N. (1955). Effect of mean circulatory filling pressure and other peripheral circulatory factors on cardiac output. Am. J. Physiol. 180 (3), 463–468. doi:10.1152/ajplegacy.1955.180.3.463

PubMed Abstract | CrossRef Full Text | Google Scholar

Hamilton, D. R., Dani, R. S., Semlacher, R. A., Smith, E. R., Kieser, T. M., and Tyberg, J. V. (1994). Right atrial and right ventricular transmural pressures in dogs and humans. Effects of the pericardium. Circulation 90 (5), 2492–2500. doi:10.1161/01.cir.90.5.2492

PubMed Abstract | CrossRef Full Text | Google Scholar

Henderson, A. C., Sá, R. C., Theilmann, R. J., Buxton, R. B., Prisk, G. K., and Hopkins, S. R. (2013). The gravitational distribution of ventilation-perfusion ratio is more uniform in prone than supine posture in the normal human lung. J. Appl. Physiol. (1985) 115 (3), 313–324. doi:10.1152/japplphysiol.01531.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

Hering, R., Vorwerk, R., Wrigge, H., Zinserling, J., Schröder, S., von Spiegel, T., et al. (2002). Prone positioning, systemic hemodynamics, hepatic indocyanine green kinetics, and gastric intramucosal energy balance in patients with acute lung injury. Intensive Care Med. 28 (1), 53–58. doi:10.1007/s00134-001-1166-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Hering, R., Wrigge, H., Vorwerk, R., Brensing, K. A., Schröder, S., Zinserling, J., et al. (2001). The effects of prone positioning on intraabdominal pressure and cardiovascular and renal function in patients with acute lung injury. Anesth. analgesia 92 (5), 1226–1231. doi:10.1097/00000539-200105000-00027

PubMed Abstract | CrossRef Full Text | Google Scholar

Huberfeld, S. I., Genovese, J., Tarasiuk, A., and Scharf, S. M. (1995). Effect of CPAP on pericardial pressure and respiratory system mechanics in pigs. Am. J. Respir. Crit. care Med. 152 (1), 142–147. doi:10.1164/ajrccm.152.1.7599813

PubMed Abstract | CrossRef Full Text | Google Scholar

Jacobsohn, E., Chorn, R., and O'Connor, M. (1997). The role of the vasculature in regulating venous return and cardiac output: Historical and graphical approach. Can. J. Anaesth. 44 (8), 849–867. doi:10.1007/BF03013162

PubMed Abstract | CrossRef Full Text | Google Scholar

Jardin, F., and Vieillard-Baron, A. (2003). Right ventricular function and positive pressure ventilation in clinical practice: From hemodynamic subsets to respirator settings. Intensive Care Med. 29 (9), 1426–1434. doi:10.1007/s00134-003-1873-1

PubMed Abstract | CrossRef Full Text | Google Scholar

Jellinek, H., Krenn, H., Oczenski, W., Veit, F., Schwarz, S., and Fitzgerald, R. D. (2000). Influence of positive airway pressure on the pressure gradient for venous return in humans. J. Appl. Physiol. (1985) 88 (3), 926–932. doi:10.1152/jappl.2000.88.3.926

PubMed Abstract | CrossRef Full Text | Google Scholar

Jozwiak, M., Teboul, J. L., Anguel, N., Persichini, R., Silva, S., Chemla, D., et al. (2013). Beneficial hemodynamic effects of prone positioning in patients with acute respiratory distress syndrome. Am. J. Respir. Crit. care Med. 188 (12), 1428–1433. doi:10.1164/rccm.201303-0593OC

PubMed Abstract | CrossRef Full Text | Google Scholar

Kenny, J. S. (2021). Letter to the editor: The venous circulation actively alters flow: A brief evolutionary perspective. Am. J. Physiol. Heart Circ. Physiol. 320 (1), H469–h470. doi:10.1152/ajpheart.00862.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, C., Adda, I., Teboul, J. L., Persichini, R., Gavelli, F., Guérin, L., et al. (2021). Effects of prone positioning on venous return in patients with acute respiratory distress syndrome. Crit. Care Med. 49 (5), 781–789. doi:10.1097/CCM.0000000000004849

PubMed Abstract | CrossRef Full Text | Google Scholar

Lai, C., Monnet, X., and Teboul, J. L. (2023). Hemodynamic implications of prone positioning in patients with ARDS. Crit. Care 27 (1), 98. doi:10.1186/s13054-023-04369-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Lansdorp, B., Hofhuizen, C., van Lavieren, M., van Swieten, H., Lemson, J., van Putten, M. J., et al. (2014). Mechanical ventilation-induced intrathoracic pressure distribution and heart-lung interactions*. Crit. Care Med. 42 (9), 1983–1990. doi:10.1097/CCM.0000000000000345

PubMed Abstract | CrossRef Full Text | Google Scholar

Maas, J. J., Geerts, B. F., van den Berg, P. C., Pinsky, M. R., and Jansen, J. R. (2009). Assessment of venous return curve and mean systemic filling pressure in postoperative cardiac surgery patients. Crit. Care Med. 37 (3), 912–918. doi:10.1097/CCM.0b013e3181961481

PubMed Abstract | CrossRef Full Text | Google Scholar

Maas, J. J., Pinsky, M. R., Geerts, B. F., de Wilde, R. B., and Jansen, J. R. (2012). Estimation of mean systemic filling pressure in postoperative cardiac surgery patients with three methods. Intensive Care Med. 38 (9), 1452–1460. doi:10.1007/s00134-012-2586-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Magder, S. (2012). Bench-to-bedside review: An approach to hemodynamic monitoring--Guyton at the bedside. Crit. Care 16 (5), 236. doi:10.1186/cc11395

PubMed Abstract | CrossRef Full Text | Google Scholar

Magder, S. (2004). Clinical usefulness of respiratory variations in arterial pressure. Am. J. Respir. Crit. care Med. 169 (2), 151–155. doi:10.1164/rccm.200211-1360CC

PubMed Abstract | CrossRef Full Text | Google Scholar

Magder, S. (2016). Volume and its relationship to cardiac output and venous return. Crit. Care 20 (1), 271. doi:10.1186/s13054-016-1438-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Marini, J. J., Culver, B. H., and Butler, J. (1981). Effect of positive end-expiratory pressure on canine ventricular function curves. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 51 (6), 1367–1374. doi:10.1152/jappl.1981.51.6.1367

PubMed Abstract | CrossRef Full Text | Google Scholar

Marini, J. J., and Gattinoni, L. (2021). Improving lung compliance by external compression of the chest wall. Crit. Care 25 (1), 264. doi:10.1186/s13054-021-03700-8

PubMed Abstract | CrossRef Full Text | Google Scholar

Marini, J. J., Hotchkiss, J. R., and Broccard, A. F. (2003). Bench-to-bedside review: Microvascular and airspace linkage in ventilator-induced lung injury. Crit. Care 7 (6), 435–444. doi:10.1186/cc2392

PubMed Abstract | CrossRef Full Text | Google Scholar

Matejovic, M., Rokyta, R., Radermacher, P., Krouzecky, A., Sramek, V., and Novak, I. (2002). Effect of prone position on hepato-splanchnic hemodynamics in acute lung injury. Intensive Care Med. 28 (12), 1750–1755. doi:10.1007/s00134-002-1524-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Mead, J., Takishima, T., and Leith, D. (1970). Stress distribution in lungs: A model of pulmonary elasticity. J. Appl. Physiol. 28 (5), 596–608. doi:10.1152/jappl.1970.28.5.596

PubMed Abstract | CrossRef Full Text | Google Scholar

Mekontso Dessap, A., Boissier, F., Charron, C., Bégot, E., Repessé, X., Legras, A., et al. (2016). Acute cor pulmonale during protective ventilation for acute respiratory distress syndrome: Prevalence, predictors, and clinical impact. Intensive Care Med. 42 (5), 862–870. doi:10.1007/s00134-015-4141-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Moller, P. W., and Berger, D. C. (2023). Commentary: Feasibility to estimate mean systemic filling pressure with inspiratory holds at the bedside. Front. Physiology 14, 1135769. doi:10.3389/fphys.2023.1135769

CrossRef Full Text | Google Scholar

Moller, P. W., and Parkin, W. G. (2022). Correct calculation of the mean systemic pressure analogue. Intensive Care Med. 48 (11), 1679–1680. doi:10.1007/s00134-022-06862-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Moller, P. W., Winkler, B., Hurni, S., Heinisch, P. P., Bloch, A., Sondergaard, S., et al. (2017). Right atrial pressure and venous return during cardiopulmonary bypass. Am. J. Physiol. Heart Circ. Physiol. 313 (2), H408–h420. doi:10.1152/ajpheart.00081.2017

PubMed Abstract | CrossRef Full Text | Google Scholar

Papazian, L., Aubron, C., Brochard, L., Chiche, J. D., Combes, A., Dreyfuss, D., et al. (2019). Formal guidelines: Management of acute respiratory distress syndrome. Ann. Intensive Care 9 (1), 69. doi:10.1186/s13613-019-0540-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Parkin, W. G., and Leaning, M. S. (2008). Therapeutic control of the circulation. J. Clin. Monit. Comput. 22 (6), 391–400. doi:10.1007/s10877-008-9147-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Pelosi, P., Tubiolo, D., Mascheroni, D., Vicardi, P., Crotti, S., Valenza, F., et al. (1998). Effects of the prone position on respiratory mechanics and gas exchange during acute lung injury. Am. J. Respir. Crit. care Med. 157 (2), 387–393. doi:10.1164/ajrccm.157.2.97-04023

PubMed Abstract | CrossRef Full Text | Google Scholar

Permutt, S., and Riley, R. L. (1963). Hemodynamics of collapsible vessels with tone: The vascular waterfall. J. Appl. Physiol. 18, 924–932. doi:10.1152/jappl.1963.18.5.924

PubMed Abstract | CrossRef Full Text | Google Scholar

Persichini, R., Lai, C., Teboul, J. L., Adda, I., Guérin, L., and Monnet, X. (2022). Venous return and mean systemic filling pressure: Physiology and clinical applications. Crit. Care 26 (1), 150. doi:10.1186/s13054-022-04024-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinsky, M. R. (2021). Cardiovascular effects of prone positioning in acute respiratory distress syndrome patients: The circulation does not take it lying down. Crit. Care Med. 49 (5), 869–873. doi:10.1097/CCM.0000000000004858

PubMed Abstract | CrossRef Full Text | Google Scholar

Pinsky, M. R. (1984). Instantaneous venous return curves in an intact canine preparation. J. Appl. Physiol. Respir. Environ. Exerc Physiol. 56 (3), 765–771. doi:10.1152/jappl.1984.56.3.765

PubMed Abstract | CrossRef Full Text | Google Scholar

Repessé, X., Charron, C., and Vieillard-Baron, A. (2016). Acute respiratory distress syndrome: The heart side of the moon. Curr. Opin. Crit. Care 22 (1), 38–44. doi:10.1097/MCC.0000000000000267

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothe, C. F. (1993). Mean circulatory filling pressure: Its meaning and measurement. J. Appl. Physiol. (1985) 74 (2), 499–509. doi:10.1152/jappl.1993.74.2.499

PubMed Abstract | CrossRef Full Text | Google Scholar

Rothe, C. F. (1986). Physiology of venous return. An unappreciated boost to the heart. Arch. Intern Med. 146 (5), 977–982. doi:10.1001/archinte.146.5.977

PubMed Abstract | CrossRef Full Text | Google Scholar

Ruste, M., Bitker, L., Yonis, H., Riad, Z., Louf-Durier, A., Lissonde, F., et al. (2018). Hemodynamic effects of extended prone position sessions in ARDS. Ann. Intensive Care 8 (1), 120. doi:10.1186/s13613-018-0464-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Scharf, S. M., Caldini, P., and Ingram, R. H. (1977). Cardiovascular effects of increasing airway pressure in the dog. Am. J. Physiol. 232 (1), H35–H43. doi:10.1152/ajpheart.1977.232.1.H35

PubMed Abstract | CrossRef Full Text | Google Scholar

Scharf, S. M., and Ingram, R. H. (1977). Influence of abdominal pressure and sympathetic vasoconstriction on the cardiovascular response to positive end-expiratory pressure. Am. Rev. Respir. Dis. 116 (4), 661–670. doi:10.1164/arrd.1977.116.4.661

PubMed Abstract | CrossRef Full Text | Google Scholar

Sylvester, J. T., Goldberg, H. S., and Permutt, S. (1983). The role of the vasculature in the regulation of cardiac output. Clin. Chest Med. 4 (2), 333–348. doi:10.1016/s0733-8651(18)30629-5

PubMed Abstract | CrossRef Full Text | Google Scholar

Takata, M., and Robotham, J. L. (1992). Effects of inspiratory diaphragmatic descent on inferior vena caval venous return. J. Appl. Physiol. (1985) 72 (2), 597–607. doi:10.1152/jappl.1992.72.2.597

PubMed Abstract | CrossRef Full Text | Google Scholar

Takata, M., Wise, R. A., and Robotham, J. L. (1990). Effects of abdominal pressure on venous return: Abdominal vascular zone conditions. J. Appl. Physiol. (1985) 69 (6), 1961–1972. doi:10.1152/jappl.1990.69.6.1961

PubMed Abstract | CrossRef Full Text | Google Scholar

Tyberg, J. V. (2002). How changes in venous capacitance modulate cardiac output. Pflugers Arch. 445 (1), 10–17. doi:10.1007/s00424-002-0922-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Vieillard-Baron, A., Charron, C., Caille, V., Belliard, G., Page, B., and Jardin, F. (2007). Prone positioning unloads the right ventricle in severe ARDS. Chest 132 (5), 1440–1446. doi:10.1378/chest.07-1013

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner-Moller, P., Berger, D., and Takala, J. (2020). Letter to the Editor: Venous return and the physical connection between distribution of segmental pressures and volumes. Am. J. Physiol. Heart Circ. Physiol. 318 (1), H203–h204. doi:10.1152/ajpheart.00698.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

Werner-Moller, P., Heinisch, P. P., Hana, A., Bachmann, K. F., Sondergaard, S., Jakob, S. M., et al. (2022). Experimental validation of a mean systemic pressure analog against zero-flow measurements in porcine VA-ECMO. J. Appl. Physiology 132 (3), 726–736. doi:10.1152/japplphysiol.00804.2021

CrossRef Full Text | Google Scholar