Formal Models of Bitcoin Contracts: A Survey

1. Introduction

Smart contracts were originally conceived in Szabo (1997) as agreements among two or more parties, that can be enforced automatically without a trusted intermediary. The recent surge of applications like Bitcoin and Ethereum has revived the idea of smart contract, because of the possibility of creating and transferring crypto-assets in a decentralized way. These applications are run by a peer-to-peer network of nodes, which collectively maintain a public, append-only data structure, called blockchain. The basic usage of the blockchain is to record transactions of crypto-assets between users. In Bitcoin, one can exploit some advanced features of transactions to extend this basic usage: at an abstract level, transactions can be interpreted as updates to the global state of a contract, and the sequence of transactions on the blockchain determines the state of each contract—and, accordingly, the crypto-assets owned by each user. In Ethereum this mechanism is made more explicit, as transactions are calls to procedures of contracts.

The first proposal to implement smart contracts on Bitcoin dates back at least to Bitcoin wiki (2012), when simple contracts were proposed that delegate an external entity (like an oracle or an escrow service) to regulate transfers of bitcoins. Going beyond these basic contracts, Andrychowicz et al. (2014c) demonstrated how to exploit some advanced features of Bitcoin transactions to implement the timed commitment protocol. This is a contract which allows a participant to commit to a secret, ensuring that either she reveals the secret before a certain deadline, or she pays a penalty to another participant. The time commitment protocol is the basic building block of more sophisticated contracts, like lotteries and other gambling games, since it allow players to choose their moves independently through a public channel, ensuring non-repudiation. In particular, multi-player lotteries in Bitcoin have been thoroughly investigated, starting from the version in Andrychowicz et al. (2014c), which requires each player to deposit a quadratic collateral in the number of players, to the versions in Bartoletti and Zunino (2017) and Miller and Bentov (2017), which enable lotteries without collaterals using Bitcoin extensions. More general forms of fair multiparty computations were proposed in Andrychowicz et al. (2014a), Bentov and Kumaresan (2014), and Kumaresan and Bentov (2014). Contingent payments contracts, allowing users to trade solutions of a class of NP problems, were proposed in Banasik et al. (2016) and Maxwell (2016).

All the works mentioned above share a common trait: they describe smart contracts in an informal manner, by using protocol narrations where, besides the usual actions of cryptographic protocols (e.g., sending and signing messages, computing hashes, verifying signatures), participants can also read and append transactions to the Bitcoin blockchain. Transactions, as well, are expressed informally, relying upon a simplified intuition of their behavior in Bitcoin. The lack of formal models of Bitcoin contracts is an obstacle to their verification. The current practice in the scientific literature is that each time a new contract is proposed, it is accompanied by a paper-and-pencil proof of correctness. Besides being a time-consuming task, doing these proofs by hand is error-prone, since for complex contracts is it quite likely to miss some corner cases, or to misinterpret the behavior of some Bitcoin transactions. This is a critical issue: since smart contracts cannot be changed after deployment, and they may handle the ownership of valuable crypto-assets, attackers may be tempted to exploit their vulnerabilities to steal or tamper with these assets. Automatic verification tools for Bitcoin contracts would help to overcome these issues.

Starting from Andrychowicz et al. (2014b), a few formal models of Bitcoin contracts have been proposed in the scientific literature. They are based on different modeling techniques, ranging from timed automata to process algebras and λ-calculi, and pursue different goals: some works are focused on contracts that can actually be run on Bitcoin, while some others propose extensions of Bitcoin; some works enable the verification of contract properties, while some others just provide an executable semantics.

In this paper, we survey the existing formal models of Bitcoin contracts, applying them to a common basic use case: the timed commitment. We start in section 2 by providing the needed background on Bitcoin; then, in sections 3–7 we illustrate the models, and in section 8 we compare them along various directions: expressiveness, usability, and suitability for verification. This comparison can help programmers to choose the right model for their decentralized application. In section 9 we also briefly overview a parallel research direction, that is the study of formal models contracts in other blockchain platforms, like Ethereum.

2. Background

In this section we give a minimalistic introduction to Bitcoin (Nakamoto, 2008), focusing on the aspects related to contracts; see (Bonneau et al., 2015) for a broader overview. Bitcoin is a decentralized infrastructure to securely transfer currency (the bitcoins, ) between users. Transfers of bitcoins are represented as transactions, and the history of all transactions is stored in a public, append-only, distributed data structure called blockchain. The blockchain is maintained by the nodes of the Bitcoin network; a subset of them, called miners, gather the transactions sent by users, aggregate them in blocks, and try to append these blocks to the blockchain. A consensus protocol based on moderately-hard “proof-of-work” puzzles is used to resolve conflicts that may happen when different miners concurrently try to extend the blockchain, or when some miner attempts to append a block with invalid transactions. The security of the consensus protocol relies on the assumption that miners are rational (i.e., that following the protocol is more convenient than trying to attack it). To make this assumption hold, miners receive some economic incentives for performing the time-consuming computations required to solve the puzzles. Part of these incentives is given by the fees paid by users upon each transaction.

To illustrate how transfers of bitcoins work, we consider two transactions ${\text{T}}_0$ and ${\text{T}}_1$, which we represent graphically as follows:

The transaction ${\text{T}}_0$ contains v₀ Satoshis (1 bitcoin = 10⁸ Satoshis). A user can redeem this amount by publishing another transaction (e.g., ${\text{T}}_1$), whose in field contains the identifier of ${\text{T}}_0$ (its hash), and whose in-script field makes the out-script of ${\text{T}}_0$ evaluate to true. When this happens, the value of ${\text{T}}_0$ is transferred to the new transaction ${\text{T}}_1$, and ${\text{T}}_0$ becomes unredeemable. In the example above, the two transactions are using a pattern called Pay to public key (P2PK). Namely, executing the output script starts with a signature sigA on top of an evaluation stack, and then proceeds by pushing also pubKeyA. Then, the opcode $\text{OP\_CHECKSIG}$ verifies, using the public key pubKeyA, if sigA is a valid signature of ${\text{T}}_1$. If this check succeeds, and v₁ ≤ v₀, then ${\text{T}}_1$ can be appended to the blockchain, specifying a new condition for redeeming v₁ Satoshis. For instance, if the output script of ${\text{T}}_1$ is pubKeyB $\text{OP\_CHECKSIG}$, then ${\text{T}}_1$ is effectively moving v₁ Satoshis from the user with public key pubKeyA to that with key pubKeyB. Further, the difference v₀−v₁ Satoshis is transferred from the user with key pubKeyA to the miner which has appended the block enclosing ${\text{T}}_1$ to the blockchain.

The previous example shows the simple case of transactions with only one input and one output. In general, transactions can have multiple inputs and outputs, and can specify more complex redeeming conditions. A transaction with multiple inputs redeems all the (outputs of) transactions in its in fields, by providing a suitable in-script for each of them. Transactions with multiple outputs may have only some of them redeemed by a subsequent transaction; each output has its own value, and the sum of the values of all the outputs must be greater than or equal to the sum of the values of the inputs. Other transaction fields can be used to specify time constraints on when a transaction can appear on the blockchain.

An informal presentation of the Bitcoin scripting language is in Antonopoulos (2017), while an executable formalization of a significant fragment of this language is in Klomp and Bracciali (2018). In this paper we do not investigate the actual Bitcoin scripting language: rather, we focus on the higher-level languages that can be used to model Bitcoin contracts.

3. Balzac

Balzac (for “Bitcoin Abstract Language, analyZer and Compiler”) is a formal model and a toolchain for Bitcoin contracts, composed by a transaction model, and an endpoint protocol model. The transaction model is an abstraction layer over the Bitcoin transactions sketched in section 2: it features a modeling language for transactions, with a formal semantics (Atzei et al., 2018b) and an online tool (https://blockchain.unica.it/balzac/) that translates Balzac transactions into standard Bitcoin transactions. The endpoint protocol model (Atzei et al., 2018a) specifies the behavior of the participants involved in the smart contract, allowing them to exchange messages, to inspect the blockchain, and to append transactions. We now briefly illustrate the two models, by applying them to formalize the timed commitment protocol. The protocol involves two participants: a committer $\text{A}$ who chooses a secret, and promises to reveal it within a given deadline, and a receiver $\text{B}$ who will either know the secret, or otherwise obtain 1.

Overall, the protocol uses three transactions: $\text{Commit}$ and $\text{Reveal}$ specified by $\text{A}$ (in Figure 1, left), and $\text{Timeout}$ specified by $\text{B}$ (in Figure 1, right). The committer $\text{A}$ uses $\text{Commit}$ to commit to her secret, and to deposit the reward for $\text{B}$, which is taken from an unspent transaction $\text{FundsA}$. Committing to a secret s is obtained by appending to the blockchain $\text{Commit}$ (h,sigAc) where h = sha256(s) is the SHA256 hash of s, and sigAc is a signature of $\text{A}$ on $\text{Commit}$. This signature is needed to authorize the transfer of currency from $\text{FundsA}$ to $\text{Commit}$. Since the hash h occurs in $\text{Commit}$ $.\text{output}$, it becomes public, but the secret s is not revealed. As specified in its $\text{output}$ field, $\text{Commit}$ can be redeemed in two ways: either by revealing the secret and providing $\text{A}$'s signature, or by providing $\text{B}$'s signature after the deadline.

FIGURE 1

Figure 1. Balzac transactions for the timed commitment protocol.

Once $\text{Commit}$ is on the blockchain, $\text{A}$ can append $\text{Reveal}$ (h,s,sigAr) to redeem it. For this to succeed, h must be the hash specified within $\text{Commit}$, and s must be one of its preimages. Instead, sigAr must be a signature by $\text{A}$ on $\text{Reveal}$. Appending $\text{Reveal}$ to the blockchain makes the witnesses in its $\text{input}$ field public: in particular, $\text{B}$ will know the secret s. Note that, after $\text{Commit}$ is on the blockchain, $\text{A}$ cannot change her secret: indeed, trying to append a transaction $\text{Reveal}$ (h,s2,sigAr) with sha256(s2) ≠ h would fail. Appending $\text{Reveal}$ transfers the balance back to $\text{A}$, since its $\text{output}$ field is only satisfied by a witness x which is $\text{A}$'s signature on the redeeming transaction. We remark that Balzac exploits the SegWit feature of Bitcoin (Lombrozo et al., 2015): this is why the $\text{input}$ field of $\text{Reveal}$ refers to $\text{Commit}$ (h,_), i.e., the transaction $\text{Commit}$ with only the parameter h specified. Indeed, the second parameter is only used within the witnesses of $\text{Commit}$, so it does not contribute to its identifier according to SegWit.

Finally, $\text{Timeout}$ can be used by $\text{B}$ to punish $\text{A}$ if she does not reveal her secret before the deadline. More specifically, $\text{Timeout}$ (h) redeems $\text{Commit}$ (h,_) after the deadline, using $\text{B}$'s signature sig(kB) on $\text{Timeout}$ as a witness in $\text{Timeout}$ $.\text{input}$. The $\text{absLock}$ field prevents $\text{Timeout}$ to appear on the blockchain earlier than the deadline, ensuring that $\text{A}$ has enough time to reveal her secret by using $\text{Reveal}$. Note that $\text{B}$ might attempt to violate this time constraint by choosing a lower value for the $\text{absLock}$ field before computing his signature sig(kB); however, doing so would make $\text{Commit}$ $.\text{output}$ fail, since $\text{checkDate}$ deadline ensures that the $\text{absLock}$ field of the redeeming transaction (in our case, $\text{Timeout}$) does not refer to an earlier time. Once $\text{Timeout}$ is on the blockchain, it can be redeemed using $\text{B}$'s signature, only: so, $\text{Timeout}$ effectively allows $\text{B}$ to claim $\text{A}$'s funds as his own, as a compensation for $\text{A}$'s misbehavior. We remark that this version of $\text{Timeout}$ slightly differs from the one in Atzei et al. (2018a), where also $\text{A}$'s signature was used. Here, the use of $\text{checkDate}$ makes this additional signature unneeded.

Note that the transactions in Figure 1 are not enough to completely specify the protocol, as they do not describe the actual behavior of participants. For instance, the transactions do not describe whether $\text{A}$ chooses to reveal the secret or not, and they do not say whether $\text{B}$ will eventually opt to use $\text{Timeout}$.

A natural behavior for $\text{A}$ could be to commit to the secret, and then reveal it before the deadline. We formalize this behavior using the Balzac endpoint protocol language, as follows:

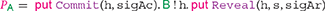
The prefix $\text{put}$ $\text{Commit}$(h, sigAc) appends $\text{Commit}$ to the blockchain, provided that the transaction $\text{FundsA}$ occurs unredeemed on the blockchain. Note that sigAc is $\text{A}$'a signature on $\text{Commit}$ (h,_): neglecting the second parameter is possible because this parameter would only affect the witnesses of $\text{Commit}$, and witnesses are not covered by Bitcoin signatures (indeed, were signatures also covering witnesses, it would be unfeasible to include a signature as a witness, since it would need to sign itself). The prefix $\text{B}$ ! h sends to $\text{B}$ the hash of chosen secret. Then, $\text{put}$ $\text{Reveal}$ (h, s, sigAr) appends $\text{Reveal}$ to the blockchain, revealing the secret. Note that this specification does not impose time constraints on actions: in particular, it does not ensure that $\text{Reveal}$ is appended before the deadline. Modeling this behavior would be possible by extending the language with urgent operators, as in Nicollin and Sifakis (1991).

A possible behavior of the receiver $\text{B}$ is specified by the following protocol $Q_{\text{B}}$, where the subprotocols $Q_{ok}$ and $Q_{nok}$ are left unspecified:

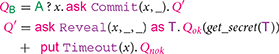
In this protocol, $\text{B}$ first receives from $\text{A}$ (and saves in x) the hash committed to within the transaction $\text{Commit}$. The prefix $\text{ask}$ $\text{Commit}$ (x, _) waits until a transaction of the form $\text{Commit}$(x, y) is indeed on the blockchain, for some value of y (while x is fixed, and it corresponds to the hash received from $\text{A}$). Then, $\text{B}$ proceeds by executing $Q\prime$, a guarded choice between two actions. The leftmost guard is satisfied when a transaction of the form $\text{Reveal}$(x, y, z) is on the blockchain, for some y and z. If the leftmost prefix is fired, the variable $\text{T}$ is bound to the actual $\text{Reveal}$ transaction on the blockchain: from there, $\text{B}$ extracts the secret, and uses it in the continuation $Q_{ok}$. The rightmost guard is enabled only when the transaction $\text{Timeout}$ can be appended to the blockchain, i.e., after the deadline. Firing the prefix $\text{put}$ $\text{Timeout}$(x) appends $\text{Timeout}$ to the blockchain, allowing $\text{B}$ to get his reward, and to continue with $Q_{nok}$.

The overall behavior of the participants involved in a contract is defined in Atzei et al. (2018a) as an LTS between systems. A system is the parallel composition of the protocols of all participants, written $\text{A}[P_{\text{A}}]|\text{B}[Q_{\text{B}}]|\cdots$, and the blockchain, written as a pair ($\text{B}$, t), where $\text{B}$ is a sequence of timestamped transactions (${\text{T}}_i$, t_i), and t is the current time (greater than the time of all transactions in $\text{B}$). For instance, we show a trace of our timed commitment specification, starting from a system $S=\text{A}[P_{\text{A}}]|\text{B}[Q_{\text{B}}]|$ ($\text{B}$, t), where the blockchain $\text{B}$ contains an unredeemed $\text{FundsA}$, and t < deadline − 1. We have the trace:

where $\text{B}\text{'}$ = $\text{B}$($\text{Commit}$(h, sigAc), t)($\text{Reveal}$(h, s, sigAr),)deadline − 1)

Note that the time advances at the fifth step of the computation, but, at the subsequent step, $\text{A}$ manages to append $\text{Reveal}$ before the deadline, withdrawing her deposit. After that, the receiver $\text{B}$ obtains the secret s, and uses it within the continuation $Q_{ok}$(s).

4. Ivy

Ivy (https://ivy-lang.org/bitcoin) is an abstraction layer over Bitcoin scripts, featuring a compiler from its abstract language to standard Bitcoin scripts. We exemplify Ivy by modeling the timed commitment protocol in Figure 2. The $\text{contract}$ $\text{Commit}$ describes the two redeeming conditions for the first transaction (corresponding to the output script within the transaction $\text{Commit}$ in section 3). Each condition is specified by a $\text{clause}$ construct. The reveal clause requires a preimage of the hash h, and a signature by Alice verifiable with her public key kApub. This clause can be redeemed by a transaction using the script within $\text{contract}$ $\text{Reveal}$ (the witnesses of this transaction are not included in the Ivy contract). The $\text{Timeout}$ clause can be satisfied only after the deadline, and it requires Bob to provide his signature, verifiable with kBpub. This is done by a transaction using the script within $\text{contract}$ $\text{Timeout}$.

FIGURE 2

Figure 2. Ivy scripts for the timed commitment protocol.

Each Ivy $\text{contract}$ describes only the output script, while there are no constructs to model the other parts of the transactions—they can be programmed in Javascript when using Ivy as a Javascript library. For instance, Ivy does not specify that the transaction using $\text{contract}$ $\text{Timeout}$ should have $\text{contract}$ $\text{Commit}$ as its input, nor that it should have an absLock field set to deadline (or later) in order to correctly redeem $\text{contract}$ $\text{Commit}$. By contrast, Balzac includes all this information in its transaction code, allowing the tool to perform some sanity checks on the whole set of transactions, e.g., that each witness correctly redeems its own input. Such kind of checks have to be done in Ivy in an interactive way, by testing the code in its web playground. This requires to provide explicit parameters to each $\text{contract}$, as well as the absLock.

5. Simplicity

Simplicity (O'Connor, 2017) is an alternative language for Bitcoin scripts, aimed at replacing the Bitcoin scripting language with a more easily analyzable one, neglecting backward compatibility with Bitcoin. Technically, it is a first-order simply-typed λ-calculus. Its types include a unit type 1, product types A × B, and sum types A + B, but no function types. More complex types are defined in terms of these basic ones: for instance, the type of booleans is defined as 2 = 1 + 1, while fixed-length bitstring types are defined e.g., as Hash256 = 2²⁵⁶ = 2×2 × ⋯ . By construction, each type is inhabited by finitely many values. Because of this, Simplicity can be proven to be universal, i.e., its combinators allow to define any function f : A ⊢ B between types A and B.

Among the primitive combinators, we find pair a b : C ⊢ A × B which constructs a pair with the outputs of functions a : C ⊢ A and b : C ⊢ B. Dually, take t : A × B ⊢ C applies t : A ⊢ C to the first component of the input pair, while drop s : A × B ⊢ C applies s : B ⊢ C to the second component. Values in sum types can be eliminated using case s t:(A+B) × C ⊢ D, which checks whether its first input is a “left” value of type A or a “right” value of type B. In the former case, case s t applies s : A × C ⊢ D to the inputs, otherwise it applies t : B × C ⊢ D. Note that case generalizes the usual “if-then-else” expression, which only operates on booleans. Simplicity features an identity combinator iden : A ⊢ A, and a composition combinator s; t : A ⊢ C which sequences the combinators s : A ⊢ B and t : B ⊢ C. Finally, the combinator unit : A ⊢ 1 discards any value of any type A, while fail : A ⊢ 1 causes the program to abort unsuccessfully, making the transaction redemption fail.

To showcase how Simplicity can be used in modeling Bitcoin contracts, we replace the $\text{output}$ scripts in the Balzac transactions of the timed commitment protocol (Figure 1) with equivalent Simplicity programs. Note that all the other fields of the transactions remain unchanged, since Simplicity does not feature a model of transactions (this is because O'Connor, 2017 focuses on scripts, without detailing how to use them to formalize multi-transaction smart contracts like the timed commitment).

We start by modeling some constant values. These are combinators that can take as input a value of any type A, and return a constant value (neglecting the input). More precisely, we assume the following:

•     kApub : A ⊢ PubKey models the public key of $\text{A}$ (similarly, kBpub : A ⊢ PubKey for $\text{B}$);

•     deadline : A ⊢ Date models the deadline before which $\text{A}$ should reveal her secret;

•     h : A ⊢ Hash256 models the hash of the secret committed by $\text{A}$.

Simplicity also features combinators that operate on the (implicit) redeeming transaction. For instance, txHash : 1 ⊢ Hash256 returns the hash of such a transaction (to keep our treatment simple, here we neglect the signature modifiers, affecting which parts of a transactions are considered). The combinator txHash is often used together with versig : Signature × (PubKey × Hash256) ⊢ 2, which verifies a given signature against a public key and the hash of the signed message. The result of versig is a boolean, denoting whether the verification succeeded or not. In our example we also use the combinators equal : Hash256 × Hash256 ⊢ 2, which checks whether two hashes are equal, and $\text{checkDate}$:Date ⊢ 1, which verifies that the $\text{absLock}$ field in the (implicit) redeeming transaction contains a later date than the one provided as input, failing in the other case. Further, the combinator witness extracts the witness from the (implicit) redeeming transaction.

We start by describing the $\text{output}$ script of the $\text{Reveal}$ transaction, since it is the simplest one (it is just a signature verification on the redeeming transaction). The Simplicity program is the following:

     (pair witness (pair kApub txHash) ; pair versig

     unit ; case fail unit)

Here, witness : 1 ⊢ Signature denotes a signature provided by the redeeming transaction. It is used to form a triple with the public key of $\text{A}$ and the hash of the redeeming transaction. This triple is then fed to versig for verification. If the signature verification fails, the combinator fail aborts the program preventing $\text{Reveal}$ to be redeemed. Otherwise, if the verification succeeds, unit is used to allow the redemption. The output script used in the $\text{Timeout}$ transaction is similar.

The $\text{Commit}$ transaction is more complex, since its output script involves two conditions, which can be satisfied by witnesses of two forms: either a pair containing $\text{A}$'s signature and her secret, or $\text{B}$'s signature (but only after the deadline). We uniformly represent these cases by assuming that witness has a sum type, witness : 1 ⊢ (Signature × Secret256) + Signature. Then, the output script is the following program:

     (pair witness unit ; case (take SA) (take SB))

The program above checks whether the witness is of the “left” form Signature × Secret256 or of the “right” form Signature. In the first case, the program applies SA to the pair at hand, while in the second case it applies SB to the signature.

The subprograms SA : Signature × Secret256 ⊢ 1 and SB : Signature ⊢ 1 are as follows:

    SA = (pair

         (drop (pair sha256 h ; pair equal unit ;

          case fail unit))

         (take (pair iden (pair kApub txHash) ;

          pair versig unit ; case fail unit))

         ; unit)

    SB = (pair iden (pair kBpub txHash)

         ; pair versig unit

         ; case fail (take (deadline ; checkDate)))

Intuitively, SA constructs a pair 1 × 1 and then discards it using the final unit. The value of the pair is indeed immaterial, but the evaluation of its components verifies the witnesses. Indeed, in the first component we compute the hash of the provided secret using sha256 and we compare it with the committed hash h. If these hashes are equal, the combinator case evaluates unit, resulting in a success; otherwise, if they differ, case evaluates fail, causing a failure. Instead, the second component verifies the signature in the witness against the public key of $\text{A}$ and the hash of the (implicit) redeeming transaction. This program is analogous to the one used for the $\text{Reveal}$ transaction.

The program SB verifies a signature in a similar way, except that when the verification succeeds, instead of simply evaluating unit and succeed, we evaluate deadline ; checkDate to check that the absLock field of the redeeming transaction is correct.

6. Uppaal

Andrychowicz et al. (2014b) model Bitcoin contracts in Uppaal (Behrmann et al., 2004), a model checking framework based on Timed Automata (TA; Alur and Dill, 1994). The idea is that the behavior of each participant in a contract (including the adversary) is modeled as a TA, and the overall system is the network obtained by composing these TAs, plus a TA which models the Bitcoin network.

The overall system state is given by the current location of each TA, the values of all the clocks used in the TAs, and the values of a set of global variables. Transitions between locations are guarded by a predicate on the global variables and the clocks, and can trigger an update of the global variables. Each location has an invariant (true by default), which must be satisfied as long as the TA stays in that location. Both predicates and updates are defined through a C-like procedural language. A network of TAs can be model-checked, using a simplified version of TCTL (timed computation tree logic) to express queries.

We illustrate this modeling technique by slightly adapting the timed commitment contract in Andrychowicz et al. (2014b), to make it coherent with the models in the previous sections (in particular, to avoid using $\text{A}$'s signature in $\text{Timeout}$). This model exploits global variables to represent the current state of the Bitcoin network (e.g., which transactions have been sent or confirmed), as well as the knowledge of the participants (e.g., private keys and secrets). The initial knowledge is set by the procedure init_prot (see Figure 4, lines $19$–$24$).

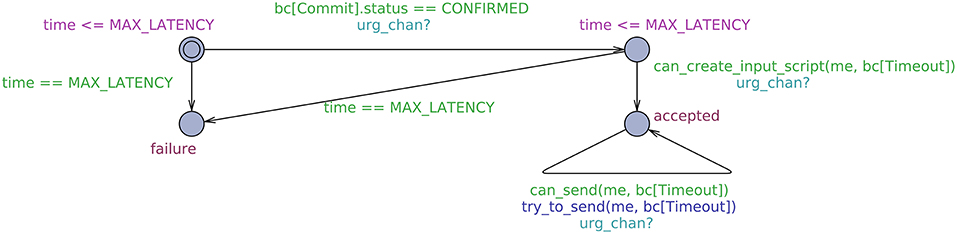
We show in Figure 3 (left) the TA modeling the Bitcoin network. Essentially, the transition labeled init_bc() initializes the state of all the needed transactions, calling the procedure init_bc to update the state (see Figure 4, lines $1$–$8$). Besides the four protocol transactions (an initial deposit, $\text{Commit}$, $\text{Reveal}$, and $\text{Timeout}$), init_bc creates four additional transactions, used by the adversary to attempt to disrupt the contract by redeeming the protocol transactions. After init_bc, the TA waits until the participants broadcasts some transaction (is_waiting), and fulfills such requests (try_to_confirm). The invariant on the rightmost location ensures that each transaction is confirmed within MAX_LATENCY of sending it. Moreover, the TA also sets the flag timelock_passed on all the transactions when the time specified by their timelock field is reached, so that they can now be appended.

FIGURE 3

Figure 3. Uppaal timed automata for the blockchain network (Left) and for the adversary (Right).

FIGURE 4

Figure 4. Snippet of Uppaal code for the timed commitment contract.

The TA modeling the adversary has a single location, with a self-loop (Figure 4, right). This TA simply tries to append to the blockchain any transaction, in a non-deterministic fashion (try_to_append). Before modifying the state of the blockchain, the procedure try_to_append verifies that the adversary can indeed satisfy the output scripts of the input transactions. This is checked by can_create_input_script (see Figure 5, lines $10$–$16$). This procedure deals separately with standard and non-standard output scripts. Standard output scripts are dealt with by know_signature, which checks that either the signature or the private key are known. Non-standard output scripts are hard-coded within can_create_input_script : in our example, this only happens for the script in $\text{Commit}$, which is detected by o.script == 0 at line $13$. The script is satisfied either by $\text{A}$'s signature (using C_KEY) and the secret, or by $\text{B}$'s signature (using R_KEY) when the timelock is after the deadline. Note that the implementation of can_create_input_script strictly depends on the contract at hand, in particular on all the non-standard output scripts used by the contract.

FIGURE 5

Figure 5. Uppaal timed automaton for an honest receiver B.

Finally, in Figure 5 we show the TA describing the behavior of an honest receiver $\text{B}$. The TA initially waits for a confirmed $\text{Commit}$ transaction. If that transaction is not confirmed within MAX_LATENCY, $\text{B}$ does not accept the commitment, and moves to location failure. Otherwise, $\text{B}$ checks that he can construct the input script for $\text{Timeout}$ (this is always true, since $\text{B}$ knows R_KEY) and then accepts the commitment. After that, $\text{B}$ simply tries to append the $\text{Timeout}$ transaction as soon as it is enabled (try_to_send).

Uppaal can be used to verify that the given model behaves as expected. For instance, when $\text{A}$ is impersonated by the adversary, an expected property is that in all runs where $\text{B}$ does not reject the commitment (failure), after time DEADLINE+MAX_LATENCY either $\text{B}$ knows the committed secret (know_secret[0]) or he earns a reward (hold_bitcoins). This property is formalized by the following TCTL formula, which is verified as true by Uppaal:

  A[] (not BobTA.failure and time >=

   DEADLINE+MAX_LATENCY) imply

      (parties[BOB].know_secret[0] or

      hold_bitcoins(parties[BOB]) == 1)

7. BitML

Bartoletti and Zunino (2018) express Bitcoin contracts through a simple process calculus, named BitML. The workflow of BitML contracts consists of three phases. First, participants can broadcast a contract advertisement, which specifies the actual contract and the preconditions to its execution (e.g., depositing given amounts of bitcoins). Then, participants can accept some contract by fulfilling all the required preconditions. When all the needed participants have fulfilled the preconditions, the contract is stipulated and can be executed. Executing the contract will eventually result in a transfer of the bitcoins deposited by participants, according to the logic defined by the contract.

A contract advertisement is modeled as a term of the form {$G$}$C$, where $C$ is the contract, specifying the rules to transfer bitcoins, while $G$ is the set of preconditions. Preconditions (Figure 6, left) may require participants to deposit some , or to commit to some secret. For instance, our timed commitment contract requires the following preconditions:

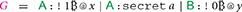
This means that $\text{A}$ must put a persistent deposit (named x) of 1, and must commit to a secret a before the contract starts. Instead, $\text{B}$ puts a null deposit, named y (here, for simplicity we have omitted the transaction fees). Once the two deposit has been used for stipulating the contract, either $\text{A}$ or $\text{B}$ will redeem 1 by executing the contract.

FIGURE 6

Figure 6. Syntax of BitML contracts and preconditions.

A contract is a guarded choice of branches, with the syntax in Figure 6, right. For instance, with the precondition $G$ above, we can model the timed commitment contract in BitML as follows:

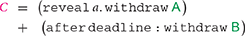
Contract $C$ is a guarded choice between two branches, separated by the + operator. The first branch reveal a. withdraw $\text{A}$ can be taken only by $\text{A}$, by revealing the previously committed secret a. After that, anyone can execute withdraw $\text{A}$, which transfers the 1 deposit back to $\text{A}$. Instead, the second branch after deadline : withdraw $\text{B}$ can be taken only after the deadline. Its execution causes the deposit to be transferred to $\text{B}$. Intuitively, stipulating $C$ in BitML corresponds, in Balzac, to appending the transaction $\text{Commit}$ to the blockchain. Further, taking the first branch of $C$ corresponds to appending $\text{Reveal}$, while taking the second branch corresponds to appending $\text{Timeout}$. In spite of this similarity, BitML uses higher level code, which does not directly describe the Bitcoin transactions, but rather focuses on how the bitcoins are transferred.

We remark that a BitML contract only specifies which moves may be taken by participants, while their actual behavior must be specified separately from the contract, through strategies. Strategies roughly play the same role as Balzac endpoint protocols, even if in Bartoletti and Zunino (2018) they are simply modeled as algorithms, and not expressed in a specific formal language.

The semantics of BitML is a labeled transition system between configurations, which are the parallel composition of terms of the following form:

•     {$G$}$C$, representing an advertisement of contract $C$ with preconditions $G$;

•     〈$C$, v〉_x, representing a stipulated contract, holding a current balance of v. The name x uniquely identifies the contract in a configuration;

•     〈$\text{A}$, v〉_x representing a fund of v owned by $\text{A}$, and with unique name x;

•     $\text{A}$[χ], representing $\text{A}$'s authorization to perform some operation χ;

•     {$\text{A}$ : a#N}, representing that $\text{A}$ has committed to a random secret a with (secret) length N;

•     $\text{A}$ : a#N, representing that $\text{A}$ has revealed her secret a (with its length N);

•     t ∈ ℕ is a global time (can only occur once in a configuration).

Once stipulated, contracts start their execution with a balance, initially set to the sum of the persistent deposits required by the preconditions. Running a contract will affect its balance, when participants deposit/withdraw funds to/from the contract. Back to our timed commitment contract, let the initial configuration be Γ = 〈$\text{A}$, 1〉_x ∣ 〈$\text{B}$, 0〉_y ∣ t, with t < deadline. A possible computation where $\text{A}$ reveals her secret and then redeems the deposit is the following:

Step (1) advertises {$G$}$C$, which refers to the deposits x and y, available in the initial configuration Γ. At step (2), $\text{A}$ commits to a secret a, with length N. The term $\text{A}$[# ▹ {$G$}$C$] witnesses that $\text{A}$'s secrets have been committed to. Similarly, at step (3) $\text{B}$ adds the term $\text{B}$[# ▹ {$G$}$C$]. At steps (4)–(5), $\text{A}$ and $\text{B}$ give their authorization to stipulate $C$, by providing their authorizations to spend the deposits x and y, respectively. At step (6) the contract is stipulated, transferring the deposits x and y to the contract. At step (7), $\text{A}$ reveals her secret. After that, the action reveal a is performed at step (8), reducing the contract to withdraw $\text{A}$, and discarding the after branch. Finally, step (9) performs the withdraw $\text{A}$ action, producing a fresh deposit x₃ with 1 redeemable by $\text{A}$.

We also show a computation where $\text{A}$ does not reveal her secret, and $\text{B}$ waits until t′ > deadline to redeem $\text{A}$'s deposit. Starting from 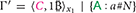at time t, we have the following steps:

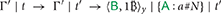
The first step lets the time pass, making the deadline expire. In the second step, $\text{B}$ fires the prefix withdraw $\text{B}$ within the after, and in this way he collects 1.

Bartoletti and Zunino (2018) also introduce a compiler from BitML contracts into standard Bitcoin transactions. In this way, participants can effectively execute BitML contracts on the Bitcoin network, by appending the obtained transactions according to their strategies. The compiler enjoys a computational soundness property, which basically ensures that computational attacks to compiled contracts at the Bitcoin level are also observable at the BitML level. In practice, this result can be exploited to prove the correctness of static analyses on BitML contracts, like the one for liquidity presented in Bartoletti and Zunino (2019).

8. Discussion

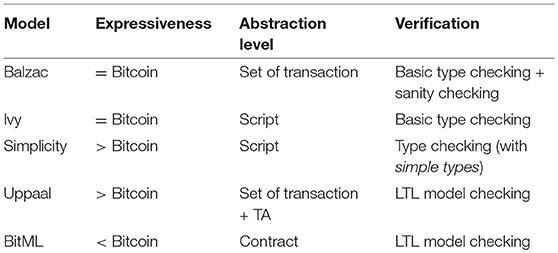
The works we have discussed in this survey serve different purposes, and consequently the formal models they introduce have substantial differences. Uppaal and Simplicity are the models which allow more expressiveness, not being constrained to be translated into actual Bitcoin transactions. On the other side, Balzac, Ivy and BitML can be compiled into Bitcoin, and so they suffer from the limitations of the Bitcoin scripting language—although in a different way. Balzac covers most of the features of Bitcoin, including Segregated Witnesses, signature modifiers, and temporal constraints. Similarly, Ivy seems to cover most of the features of Bitcoin scripts. So, Balzac and Ivy seem suitable to specify any contract actually realizable on top of Bitcoin. BitML poses some limits to expressiveness, which however are exploited for verification purposes, as we will discuss below. For instance, BitML cannot exploit signature modifiers besides all-inputs / all-outputs, and it requires participants to sign all the transactions potentially used in a contract before stipulation. As a consequence of these limitations, BitML cannot express e.g., infinite-state crowdfunding contracts, which instead are expressible as Balzac endpoint protocols (Atzei et al., 2018a), where signatures can be provided at any moment. Since this kind of contracts are inherently infinite-state (because the set of participants is not known a priori), modeling them in Uppaal seems unfeasible as well. Notwithstanding the limitations, BitML can express a wide variety of common contracts, as discussed in Bartoletti et al. (2018).

The higher level of abstraction featured by BitML allows for expressing complex contracts more succinctly than in the other models. For instance, a slight variant of the timed commitment contract where both participants are both committers and receivers can be specified in 3 lines of BitML (Bartoletti and Zunino, 2018), while it requires 9 transactions (18, also considering those for the adversary) in Uppaal (Andrychowicz et al., 2014b), as well as in the other transaction-based models. Another advantage of BitML is that it allows programmers to focus on high-level behaviors (revealing secrets, providing authorizations, checking deadlines, …), rather than struggling with the low-level details of Bitcoin transactions (hashes, signatures, scripts, …). Simplicity provides an alternative language for Bitcoin output scripts based on algebraic types, which, compared with Bitcoin scripts, can help the protocol designer to structure the data in a more rigorous way than using bare bit-strings. In this way, Simplicity also enables type checking, which helps to reduce programming errors. On the other hand, Simplicity differs from many declarative languages by using a point-free notation, which can be rather inconvenient to use directly, without leveraging a transformation from a more human-friendly point-full language (as in Cunha and Pinto 2005). Ivy follows an imperative paradigm, allowing the user to specify the redeeming condition as a block of statements to be executed. Instead, Balzac output scripts are boolean expressions. Ivy allows multiple clauses within a contract, which are instead modeled as a disjunction in Balzac output scripts. Compared with Simplicity, Balzac and Ivy scripts are more restrictive, as they are bound to be encodable to Bitcoin scripts; instead, Simplicity scripts are meant as a replacement of Bitcoin ones. Among the models we have discussed, Uppaal is the only one which features a procedural language, which is used to define the various components of the Bitcoin network (including the participants in the contract). On the one hand, this language is quite flexible, as it could be used to model Bitcoin extensions; on the other hand, contract designers must pay special attention to craft models that can actually be executed in Bitcoin.

All the models presented in this paper (except Ivy) feature a formal semantics, and they all implement some form of checks on the code. Both Ivy and Balzac perform some basic type checking; further, since Balzac provides a view of all the transactions composing a contract, it also performs some complex sanity checks, e.g., whether the witnesses satisfy the predicates of the input transactions. Also Simplicity performs type checking, but with richer types; further, it features a static analysis to predict an upper bound to the memory consumption of the execution of scripts. BitML and Uppaal can also verify complex contract properties expressed in LTL, by model-checking the state space of the contract. Although this state space is potentially infinite for BitML, verification is possible through the finite-state abstraction in Bartoletti and Zunino (2019). Verification of Uppaal models is possible through the Uppaal model checker (http://www.uppaal.org); a tool for verifying BitML contracts is available (Atzei et al., 2019). There also exists a formalization of BitML in Agda (https://github.com/omelkonian/formal-bitml), which allows for verifying properties of BitML contracts through a proof assistant.

A summary of the comparison between the models is in Table 1.

TABLE 1

Table 1. Comparison between the models of Bitcoin contracts.

9. Conclusions

In this paper we have compared the various languages and models for Bitcoin contracts. The need for formal modeling of Bitcoin contracts is motivated by the surprising complexity that these contracts may exhibit: for instance, the literature reports the use of Bitcoin to implement financial services, auctions, timed commitments, lotteries, and a variety of other gambling games (Atzei et al., 2018a, 2019). Our survey aims to help programmers to choose the right model for their contracts, based on the required expressiveness and available verification tools.

A parallel line of research is that on formal models of smart contracts running on alternative blockchains. Currently, the main target of this research is Ethereum, the most widespread platform for smart contracts so far. Driven by the proliferation of vulnerabilities of Ethereum contracts (Atzei et al., 2017) which have caused major money losses, many researchers have studied models and verification techniques to make Ethereum contracts more secure (Miller et al., 2018). Several papers focus on EVM, the bytecode language interpreted by Ethereum clients, as well as the target of the compilation of high-level contract languages, like Solidity. Luu et al. (2016) give a partial formalization of the semantics of EVM, and exploit symbolic execution to detect some common vulnerability patterns of EVM contracts. Grishchenko et al. (2018b) and Hildenbrandt et al. (2018) formalize executable semantics of EVM, validated against the official Ethereum test suite; these semantics are the basis of static verifiers of EVM contracts, like e.g., Grishchenko et al. (2018a). Bhargavan et al. (2016) translate EVM into F^*, and uses its verification tools to detect vulnerabilities. Hirai (2017) uses the Isabelle/HOL proof assistant (Nipkow et al., 2002) to verify the EVM code obtained by compiling a fragment of the Ethereum Name Service. Sergey et al. (2018) propose a strongly typed intermediate language for contracts, which are modeled as Communicating Automata; this richer structure (compared to EVM) simplifies formal reasoning, making contracts more amenable to verification.

Author Contributions

RZ and MB equally contributed to all parts of the paper.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

MB is partially supported by Aut. Reg. of Sardinia projects Sardcoin and Smart Collaborative Engineering. RZ is partially supported by MIUR PON Distributed Ledgers for Secure Open Communities.

References

Alur, R., and Dill, D. L. (1994). A theory of timed automata. Theor. Comput. Sci. 126, 183–235. doi: 10.1016/0304-3975(94)90010-8

CrossRef Full Text | Google Scholar

Andrychowicz, M., Dziembowski, S., Malinowski, D., and Mazurek, L. (2014a). “Fair two-party computations via Bitcoin deposits,” in Financial Cryptography Workshops Vol. 8438 of LNCS (Christ Church: Springer), 105–121. doi: 10.1007/978-3-662-44774-1_8

CrossRef Full Text | Google Scholar

Andrychowicz, M., Dziembowski, S., Malinowski, D., and Mazurek, Ł. (2014b). “Modeling Bitcoin contracts by timed automata,” in International Conference on Formal Modeling and Analysis of Timed Systems (FORMATS), Vol. 8711 of LNCS (Florence: Springer), 7–22. doi: 10.1007/978-3-319-10512-3_2

CrossRef Full Text | Google Scholar

Andrychowicz, M., Dziembowski, S., Malinowski, D., and Mazurek, L. (2014c). “Secure multiparty computations on Bitcoin,” in IEEE Symposium on Security and Privacy (Berkeley, CA) 443–458. doi: 10.1109/SP.2014.35

CrossRef Full Text | Google Scholar

Antonopoulos, A. M. (2017). Mastering Bitcoin: Programming the Open Blockchain, 2nd Edn. (Sebastopol, CA: O'Reilly Media, Inc.).

Google Scholar

Atzei, N., Bartoletti, M., and Cimoli, T. (2017). “A survey of attacks on Ethereum smart contracts (SoK),” in POST, Vol. 10204 of LNCS (Uppsala: Springer), 164–186. doi: 10.1007/978-3-662-54455-6_8

CrossRef Full Text | Google Scholar

Atzei, N., Bartoletti, M., Cimoli, T., Lande, S., and Zunino, R. (2018a). “SoK: unraveling Bitcoin smart contracts,” in POST, Vol. 10804 of LNCS (Thessaloniki: Springer), 217–242. doi: 10.1007/978-3-319-89722-6

CrossRef Full Text

Atzei, N., Bartoletti, M., Lande, S., Yoshida, N., and Zunino, R. (2019). “Developing secure Bitcoin contracts with BitML,” in ESEC/FSE (Tallinn). doi: 10.1145/3338906.3341173

CrossRef Full Text | Google Scholar

Atzei, N., Bartoletti, M., Lande, S., and Zunino, R. (2018b). “A formal model of Bitcoin transactions,” in Financial Cryptography and Data Security, Vol. 10957 of LNCS (Santa Barbara: Springer). doi: 10.1007/978-3-662-58387-6

CrossRef Full Text | Google Scholar

Banasik, W., Dziembowski, S., and Malinowski, D. (2016). “Efficient zero-knowledge contingent payments in cryptocurrencies without scripts,” in ESORICS, Vol. 9879 of LNCS (Heraklion: Springer), 261–280. doi: 10.1007/978-3-319-45741-3_14

CrossRef Full Text | Google Scholar

Bartoletti, M., Cimoli, T., and Zunino, R. (2018). “Fun with bitcoin smart contracts,” in ISoLA (Limassol), 432–449. doi: 10.1007/978-3-030-03427-6_32

CrossRef Full Text | Google Scholar

Bartoletti, M., and Zunino, R. (2017). “Constant-deposit multiparty lotteries on Bitcoin,” in Financial Cryptography Workshops, Vol. 10323 of LNCS (Sliema: Springer). doi: 10.1007/978-3-319-70278-0

CrossRef Full Text | Google Scholar

Bartoletti, M., and Zunino, R. (2018). “BitML: a calculus for Bitcoin smart contracts,” in ACM CCS (New York, NY: ACM). doi: 10.1145/3243734.3243795

CrossRef Full Text | Google Scholar

Bartoletti, M., and Zunino, R. (2019). “Verifying liquidity of bitcoin contracts,” in POST, Vol. 11426 of LNCS (Cham: Springer).

Google Scholar

Behrmann, G., David, A., and Larsen, K. G. (2004). “A tutorial on Uppaal,” in Formal Methods for the Design of Real-Time Systems, Vol. 3185 of LNCS (Bertinoro: Springer), 200–236. doi: 10.1007/978-3-540-30080-9_7

CrossRef Full Text | Google Scholar

Bentov, I., and Kumaresan, R. (2014). “How to use Bitcoin to design fair protocols,” in CRYPTO, Vol. 8617 of LNCS (Santa Barbara, CA: Springer), 421–439. doi: 10.1007/978-3-662-44381-1_24

CrossRef Full Text | Google Scholar

Bhargavan, K., Delignat-Lavaud, A., Fournet, C., Gollamudi, A., Gonthier, G., Kobeissi, N., et al. (2016). “Formal verification of smart contracts,” in PLAS (Vienna).

Google Scholar

Bitcoin wiki (2012). Bitcoin wiki- Contracts. Available online at: https://en.bitcoin.it/wiki/Contract

Google Scholar

Bonneau, J., Miller, A., Clark, J., Narayanan, A., Kroll, J. A., and Felten, E. W. (2015). “SoK: Research perspectives and challenges for Bitcoin and cryptocurrencies,” in IEEE Symposium on Security and Privacy (San Jose, CA), 104–121. doi: 10.1109/SP.2015.14

CrossRef Full Text | Google Scholar

Cunha, A., and Pinto, J. S. (2005). Point-free program transformation. Fundam. Inform. 66, 315–352. Available online at: https://content.iospress.com/articles/fundamenta-informaticae/fi66-4-02

Google Scholar

Grishchenko, I., Maffei, M., and Schneidewind, C. (2018a). “Foundations and tools for the static analysis of Ethereum smart contracts,” in CAV, Vol. 10981 of LNCS (Oxford, UK: Springer), 51–78. doi: 10.1007/978-3-319-96145-3_4

CrossRef Full Text | Google Scholar

Grishchenko, I., Maffei, M., and Schneidewind, C. (2018b). “A semantic framework for the security analysis of ethereum smart contracts,” in POST, Vol. 10804 of LNCS (Thessaloniki: Springer), 243–269. doi: 10.1007/978-3-319-89722-6_10

CrossRef Full Text | Google Scholar

Hildenbrandt, E., Saxena, M., Rodrigues, N., Zhu, X., Daian, P., Guth, D., et al. (2018). “KEVM: A complete formal semantics of the Ethereum Virtual Machine,” in IEEE Computer Security Foundations Symposium (CSF) (Oxford, UK: IEEE Computer Society), 204–217. doi: 10.1109/CSF.2018.00022

CrossRef Full Text | Google Scholar

Hirai, Y. (2017). “Defining the Ethereum Virtual Machine for interactive theorem provers,” in Financial Cryptography Workshops, Vol. 10323 of LNCS (Sliema: Springer), 520–535. doi: 10.1007/978-3-319-70278-0_33

CrossRef Full Text | Google Scholar

Klomp, R., and Bracciali, A. (2018). “On symbolic verification of Bitcoin's script language,” in Workshop on Cryptocurrencies and Blockchain Technology (CBT), Vol. 11025 of LNCS (Barcelona: Springer), 38–56. doi: 10.1007/978-3-030-00305-0_3

CrossRef Full Text | Google Scholar

Kumaresan, R., and Bentov, I. (2014). “How to use Bitcoin to incentivize correct computations,” in ACM CCS (Scottsdale, AZ), 30–41. doi: 10.1145/2660267.2660380

CrossRef Full Text | Google Scholar

Lombrozo, E., Lau, J., and Wuille, P. (2015). Segregated Witness (Consensus Layer) BIP 141. Available online at: https://github.com/bitcoin/bips/blob/master/bip-0141.mediawiki

Google Scholar

Luu, L., Chu, D.-H., Olickel, H., Saxena, P., and Hobor, A. (2016). “Making smart contracts smarter,” in ACM CCS (Vienna), 254–269. doi: 10.1145/2976749.2978309

CrossRef Full Text | Google Scholar

Maxwell, G. (2016). The First Successful Zero-Knowledge Contingent Payment. Available online at: https://bitcoincore.org/en/2016/02/26/zero-knowledge-contingent-payments-announcement/

Miller, A., and Bentov, I. (2017). “Zero-collateral lotteries in Bitcoin and Ethereum,” in EuroS&P Workshops (Paris), 4–13. doi: 10.1109/EuroSPW.2017.44

CrossRef Full Text | Google Scholar

Miller, A., Cai, Z., and Jha, S. (2018). “Smart contracts and opportunities for formal methods,” in ISoLA, Vol. 11247 of LNCS (Cham: Springer), 280–299. doi: 10.1007/978-3-030-03427-6_22

CrossRef Full Text | Google Scholar

Nakamoto, S. (2008). Bitcoin: A Peer-to-Peer Electronic Cash System. Available online at: https://bitcoin.org/bitcoin.pdf

Google Scholar

Nicollin, X., and Sifakis, J. (1991). “An overview and synthesis on timed process algebras,” in CAV (Aalborg), 376–398. doi: 10.1007/3-540-55179-4_36

CrossRef Full Text | Google Scholar

Nipkow, T., Paulson, L. C., and Wenzel, M. (2002). Isabelle/HOL: A Proof Assistant for Higher-Order Logic, Vol. 2283 (Berlin: Springer Science & Business Media).

Google Scholar

O'Connor, R. (2017). “Simplicity: A new language for blockchains,” in PLAS (Sliema). doi: 10.1145/3139337.3139340

CrossRef Full Text | Google Scholar

Sergey, I., Kumar, A., and Hobor, A. (2018). Scilla: a smart contract intermediate-level language. CoRR abs/1801.00687

Google Scholar

Szabo, N. (1997). Formalizing and securing relationships on public networks. First Monday 2. Available online at: https://firstmonday.org/ojs/index.php/fm/article/view/548/469-publisher=First

Google Scholar