- RMIT Blockchain Innovation Hub, RMIT University, Melbourne, VIC, Australia
In this paper we introduce a new zero-intelligence framework to analyse price formation in a cryptocurrency decentralised exchange (DEX) combining agent-based modelling and real trading history. We shuffle real Uniswap order event data and replay back into the automatic market maker (AMM) matching mechanism. We study how decomposing real markets down from bounded rationality to zero-intelligence markets in a controlled experiment affects liquidity provider’s impermanent loss, trade slippage and price efficiency.
1 Introduction
Decentralised Finance (DeFi) has recently shown phenomenal growth in the blockchain and cryptocurrency space. Recognised as an alternative and potential disruptor to traditional centralised finance, DeFi offers the prospect of higher levels of financial access allowing the ability for a suite of financial products to be built on permissionless distributed blockchains. This allows financial products and services to be deployed as code and users can interact with each other through smart contracts that operates as self-executing code on the blockchain. Participants thus can interact with each other cutting out the middleman of financial institutions who traditionally provided the service of intermediation. In addition to providing alternative access to traditional financial products, DeFi also offers the possibility of unique financial architecture to be added piecemeal as “money legos” to the financial ecosystem. A novel product that has seen increasing success are DEXs (decentralised exchanges) that allow users to supply and source liquidity by interacting through protocols coded as an algorithm that provides an automated market making function. The study of user behaviour and effects of strategic interaction with the automated market maker (AMM) mechanism in DeFi is still in a nascent stage as the DEX space is emerging.
Behavioral finance has highlighted many examples which cast doubt on the assumption that agents make trading and investing decisions in financial markets with perfect rationality [Hirshleifer (2001); Barberis and Thaler (2003)]. This has led to alternative modelling paradigms, such as agent-based modelling, in which the detailed nuances of less-than-perfect decision making are incorporated into models which attempt to tackle the messiness of real-world markets by taking a bottom-up approach to the modelling problem. One radical approach to modelling rationality is to drop it entirely from the model. Surprising as it may seem, such zero-intelligence models are often able to account for empirical features of actual market data, suggesting that many regularities in economic time-series data can arise from the environment in which agents trade—i.e., the market microstructure, rather than the particulars of the trading decisions themselves (Gode and Sunder, 1993).
A typical approach to building a zero-intelligence model of a financial market is to build a simple random simulation model of the order-submission process; in the simplest case, we can use arbitrary distributions from which to draw i. i.d. random variables such as the size and sign of orders. A more subtle approach is to calibrate the statistical model of order-flow against the statistical properties of empirical data.
In this paper we present a novel version of a calibrated zero-intelligence model. We do this by simply taking existing order flow and shuffling its ordering and then simulating back through the AMM matching mechanism. We make some adjustments to liquidity removal actions to ensure liquidity pools can never go negative. The output of many shuffles is then analysed using two main market quality metrics used in the AMM space such as impermanent loss and slippage along with a price efficiency metric well known in traditional finance. Our simulations show that a zero-intelligence AMM model has lower impermanent loss, higher slippage and lower deviation from a random walk (suggesting higher price efficiency).
For the rest of this section we give a background to the DEX space within DeFi and related work in the zero-intelligence literature. In Section 2 we describe the Uniswap V1 protocol along with the open-source cadCAD Uniswap model that sources the underlying empirical dataset and digital-twin simulation platform used before describing how this data is shuffled. In Section 3 we describe and analyse metrics on impermanent loss, slippage and price efficiency. Finally we conclude in Section 4 discussing the results and outlying future work.
1.1 Decentralised Exchanges, Automatic Market Makers, and Cryptofinance
Cryptocurrencies are digital currencies that do not rely on a central authority such as a central bank or government. The global cryptocurrency market capitalization is currently $2.29 USD trillion1. Since the maturing of Bitcoin the first peer to peer cryptocurrency on the bitcoin blockchain, there has been a rapid growth in decentralised finance (DeFi) applications built on the Ethereum permissionless blockchain. These DeFi applications make use of smart contracts that allow pre-existing computer code to determine the terms between counterparties and be recorded on the blockchain. The amount of assets or total value locked (TVL) held in DeFi applications has grown in the last year from roughly $20.21 USD Billion to $74.63 Billion USD2. The biggest components of DeFi are lending protocols such as Aave and Compund and decentralised exchanges (DEXs) such as Uniswap and Balancer. DEXs offer an alternative way for buyers and sellers to trade cryptocurrency without going through a centralised exchange. Traditionally financial exchanges operate using a limit order book mechanism to match buy offers with sell offers. Centralised cryptocurrency exchanges such as Coinbase and Binance also use this mechanism where liquidity is provided by limit orders and consumed by market orders. In a dealer market, registered market makers will buy and sell stock regularly continuously at publicly quoted prices. In these markets the bid-ask spread compensates the liquidity provision.
The most popular DEXs use an automatic market maker (AMM) protocol whereby users can stake and remove liquidity and interact with users who want to swap one cryptocurrency for another. A user of an AMM like Uniswap, can swap token A for token B by depositing token A into the AMM’s liquidity pool and remove token B. The counterparty is thus the AMM liquidity pools, which consist of the funds of the tokenised assets (in this case the fictitious tokens A and B) seeded by a community of liquidity providers who consist of individuals and institutions staking their assets. These assets are converted into a smart contract and the pricing of the tokens are algorithmically determined that allows traders to transact 24/7. In return for staking their assets, liquidity providers are issued with liquidity tokens by the protocol. These liquidity tokens act like an accounting unit to a claim on their share of the liquidity pool balances which will benefit from accrued fees paid by users looking to swap tokens.
Automatic market makers (AMMs) thus offer an automated way for buyers and sellers to interact. Indeed in more mature equity and fixed-income markets, algorithmic trading market making strategies are already a big part of high-frequency trading. AMMs have been extensively studied as a method of information discovery in thin prediction markets since it was introduced by Hanson (2003). In building a blockchain automated market maker, a smart contract designer sets up a price function that will buy and sell to all comers at that price. Prices move when trades occur. Thus market makers do not adjust prices but rather are dependant on arbitrageurs (typically arbitrage bots) to trade and readjust token balances to bring prices back to equilibrium. Any user can be a liquidity provider and stake tokens in a liquidity pool. Other users can access that liquidity and exchange tokens based on a pricing function dictated by their relative availability in the pool. The AMM protocol thus, offers a simplified decentralised way to automate trading and has the advantage of being cheaper and faster than an order book to store on a smart contract. It does have however potential drawbacks of being more at risk from front-running by miners who validate transactions on the blockchain (Harvey et al., 2021). In an orderbook, liquidity provision is compensated by earning the bid-ask spread and faces the risk of adverse selection. In an AMM, liquidity providers (LPs) are compensated by fees paid when users looks to exchange or swap one cryptocurrency token for another. LPs however run the risk of impermanent loss i.e. the price ratio of staked assets in a pool changes at the time of withdrawing them from the pool.
1.2 Zero-Intelligence Models
For a comprehensive review of agent based modelling and zero-intelligence (ZI) modelling in finance see Chakraborti et al. (2011). In this section we give a an overview of the lineage of ZI models of financial markets that lead to this work. Early work in computational economics modelled order flow in a continuous double-auction market using various types of zero-intelligence traders which place orders with prices drawn iid. at random from exogenously-specified marginal supply and demand functions [Gode and Sunder (1993); Cliff and Bruten (1997)]. This was extended to a financial markets by Ladley and Schenk-Hoppé (2009) who showed that a similar model could replicate several of the empirically-observed stylized facts of financial time-series. Within econophysics this approach has been extended to incorporate the entire life-cycle of an order on a typical exchange in which both market orders and limit orders are taken into account, moreover the limit-order cancellation process is also modelled [Challet and Stinchcombe (2001); Maslov (2000); Tóth et al. (2010)]3. This interplay of random cancellation and random order-submission is modelled as an evaporation-deposition process which is able to reproduce fat-tailed return distributions, long-range correlations and a non-trivial Hurst exponent of the price signal [Maslov (2000); Preis et al. (2006, 2007)].
Mike and Farmer (2008) was one of the first models to introduce calibration of zero-intelligence models using market data. Using London Stock Exchange (LSE) order placement and cancellation data to calibrate parameters of their model, they managed to reproduce realistic spread and volatility dynamics for a group of LSE stocks. Palit et al. (2012) introduced a zero-intelligence model where the probability of different event categories, classified according to their aggressiveness, was calibrated against empirically estimated conditional-probabilities. Brandouy et al. (2012) revisited the zero-intelligence paradigm and found to get a quantitatively realistic model (i.e. replication of stylised facts) more and more constraints had to placed on zero-intelligence traders, and thus concluded although these models had insights into market microstructure, behavioural considerations were needed for useful financial engineering and predictive power. In our ZI approach we look not to replicate stylised facts to show what can be attributed to the market microstructure, but rather how market quality metrics are affected by strategic behaviour when it is removed.
Another strand of financial agent based models look at “weak-intelligence” models that model the interaction of different types of strategies for example chartist, noise and fundamental strategies [LeBaron and Yamamoto (2007, 2008); Chiarella et al. (2009)]. In the cryptocurrency space, Cocco et al. (2017) show calibrated simulated interaction between chartists and ZI traders on an order book can mimic Bitcoin prices. Angeris et al. (2021) simulate arbitrageurs, convenience traders and LPs interacting through the Uniswap V1 mechanism and show protocol prices track reference external prices in a stable manner through a range of market conditions. In this paper we take an alternative approach which is to shuffle existing order data and replay in the matching mechanism. The advantage of this very simple approach is that it enables a like-for-like comparison between the zero-intelligence data and the empirical data. By directly using empirical data as the underlying data from which to generate the zero-intelligence dataset and not drawing from preset distributions, we attempt to avoid making any unwarranted assumptions and play back realistically calibrated data into the automatic market maker (AMM) matching mechanism. We study how decomposing real markets down to zero-intelligence markets in a controlled experiment affects metrics on the profitability of liquidity providers, slippage of trades and price efficiency.
2 Simulation, Data, and Shuffling Methodology
2.1 The Uniswap Decentralised Finance Protocol
Uniswap is a constant product AMM smart contract on the Ethereum blockchain. Uniswap created by Hayden Adams, launched November 2018 and provides certain liquidity and price discovery for ERC-20 tokens. ERC-20 is the main Ethereum based standard that allows fungibility across all tokens. This standard is a set of commands that allows integration and interoperability with other ERC-20 token compliant contracts, wallets and marketplaces.
Instead of an orderbook, Uniswap operates its’ own AMM with a constant product market built on Ethereum. The constant product follows the following formula:
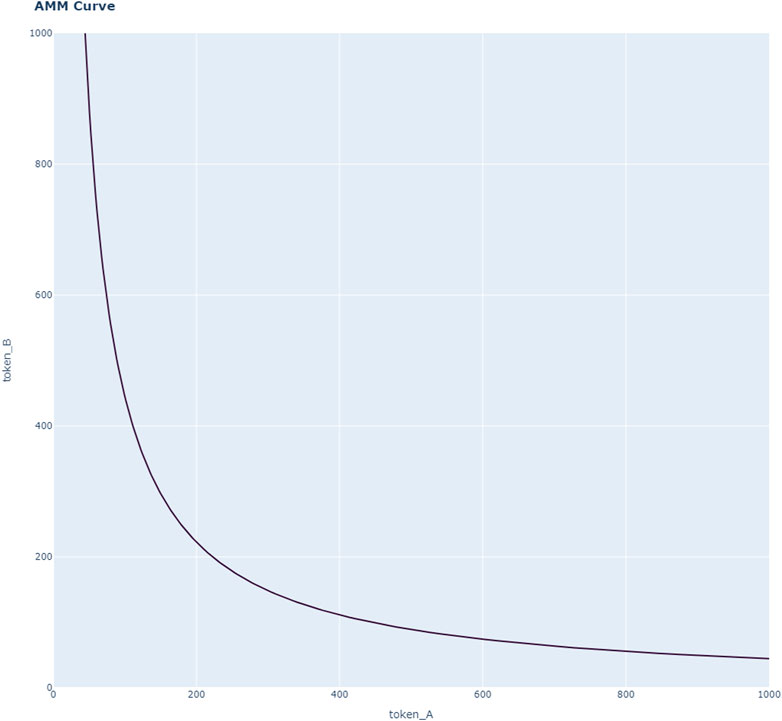
where x represents the amount of token A in the pool and y represents the amount of token B in the pool. The constant product k is termed the invariant which determines the price of A in terms of B (and vice versa) dependant on the volume wanting to be traded. This price formula graphed below in Figure 1 shows these prices change depending on the amount of a token being bought. The slope of the curve can be thought of as the spot price assuming an infinitesimally small amount is bought (or swapped as the other token is deposited or sold). However as the amount bought increases the per unit cost increases at an increasing rate to ensure that Eq. 1 holds. The constant product of the token balance thus should always equal the invariant. The term invariant is actually a misnomer as the invariant always changes slightly every trade as fees are charged for every swap. For Uniswap V1, 0.3% fees are charged. Also the invariant k increases when liquidity providers add liquidity to the AMM (i.e add quantities of both tokens to the pool) and decreases when they remove their liquidity (withdraw quantities of both tokens from the pool). Thus liquidity providers add/remove liquidity to/from both pools and liquidity takers remove liquidity in one pool in exchange for adding to another. Although Uniswap V1 and V2 is a constant product market maker (CPMM), its V3 instance launched May 2021 adds extra features e.g. the ability to submit liquidity within custom ranges that are similar to limit orders in an orderbook (Adams et al., 2020). Indeed other AMMs use variations such as constant mean market maker (CMMM), constant sum marker maker (CSMM) and constant product market maker (CPMM) pricing. This opens the door to AMMs functioning using a myriad of various hybrids amongst these pricing functions. Mohan (2022) shows these different pricing functions and various permutations can be unified in a framework as a homogeneous family of pricing functions.
2.2 Simulations of Uniswap in cadCAD
Our simulations are run in cadCAD a Python package designed by BlockScience to experiment with the interaction of complex systems and agent behaviours4. We make use of their cadCAD Uniswap model that imports real data and replicates the mechanics of a real-world smart contract by replicating the smart contract Uniswap V1 Vyper code into Python. Thus the open source cadCAD model can be described as a Python “Digital Twin” representation of Uniswap that allows experimenting with historical and/or synthetic transactions5.
In our cadCAD model we make use of the open-source digital twin repository and use it as a base for our own “Shuffled Replay” model. Essentially we take the historical data, shuffle the dataset and replay it back into the Uniswap smart contract. The state output variables at each event timestep such as ETH tokens, DAI tokens, UNI supply and invariants can be analysed in each of our simulation runs. In each of the 100 Monte-Carlo simulations we shuffle the dataset with a new seed and match the output to the original timestamps. For all results from the shuffled model, we present a mean value of the calculated metric over the 100 Monte-Carlo simulations runs in Section 3. We then compare from the output of the “Digital Twin” model as our representation of the real-world metrics. We choose to use the “Digital Twin” as the original dataset exhibits many swaps (trades) with negative slippage when many events share the timestamp. Timestamps are only granular to the 1s level i.e. ‘hh:mm:ss’ format. Using the “Digital Twin” processed data, instances of negative slippage disappear.
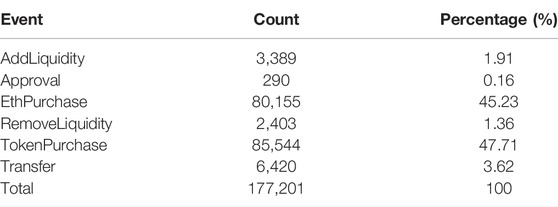
Our model uses data from 2 November 2018 to 31 March 2020 extracted using an ETL (extraction, transformation and loading) Google big query of ETHDAI Uniswap smart contract data from the Ethereum Blockchain6. Ether (ETH) is the native cryptocurrency of the Ethereum platform. DAI is a stablecoin cryptocurrency which is engineered to keep its value as close to $1USD. In strategy performance metrics calculated later in Section 3 we convert to DAI to compare performance. With a Uniswap ETHDAI pool, liquidity providers deposit ETH and DAI tokens in the liquidity pool. In exchange they mint UNI tokens - “shares” of that Uniswap instance. Not to be confused with the Uniswap governance token, UNI here refers to the token that liquidity providers receive when they add liquidity to the pool - i.e. an accounting unit that represents pool ownership. So there are three token pools that are maintained ETH, DAI and UNI at each timestep with a balance and a delta (change from the previous timestep). Table 1 below shows the breakdown of the 177,201 different events in the dataset with their absolute counts of occurrences and their percentage share of all events during the period.
An EthPurchase removes ETH from the ETH pool and adds an amount of token DAI in exchange to the DAI pool. In the cadCAD setups (both digital twin and shuffled replay), the variable taken from the historical dataset is the DAI delta i.e. how many tokens were sold and added to the DAI pool. This goes through the Uniswap pricing function and the appropriate amount (also taking into account of 0.3% fee which reduces the quantity purchased) of ETH is removed from the pool. Analogously for TokenPurchase events, the models take the historical ETH delta i.e. how many ETH were sold and added to the ETH pool, removing the appropriate amounts of DAI from the DAI pool.
For an AddLiquidity event, the simulation takes the historical ETH delta and deposits that to the ETH pool. That same quantity is converted to DAI (price is the ratio of DAI and ETH balances states) and is also added to the DAI pool. The same occurs with the UNI pool and the same amount (ETH delta converted to UNI tokens again as a ratio of the UNI and ETH current balance states) is added or rather “minted” (as technically they hitherto did not exist) to the UNI pool. In the original real data this is represented with two events: an AddLiquidity event that adds to the ETH and DAI balances and a Transfer event that mints and adds the UNI tokens to the UNI pool. In the simulations (both original digital twin and shuffled ZI) this is all done in the same step when replaying an AddLiquidity event.
For a RemoveLiquidity event, in the real data both ETH and DAI are removed from their respective pools. Then a corresponding Transfer event removes or rather “burns” (as these coins are technically destroyed) UNI from the pool. In the simulation models, RemoveLiquidity events are processed when there is a Transfer event with a negative UNI delta. The amount of this delta is converted to ETH and DAI amounts which are also removed from the pool. In the cadCAD “digital twin” simulations, this is implemented by converting the UNI delta to a percentage burned amount as a function of the existing UNI supply. This percentage of ETH and DAI (and UNI) are removed from the pool. In the Shuffled Replay model, the simulation maintains a pointer to the original data to access the historical percentage of liquidity removed i.e. the historical UNI delta as a percentage of UNI supply at the original timestep. This percentage liquidity removed is “replayed” (albeit at its simulated shuffled event timestep) and accordingly UNI, ETH and DAI balances are removed according to that historical percentage. This ensures the simulation doesn’t go into a state of negative balances (i.e. liquidity is removed that is not there due to the shuffling) as it is always a percentage of available liquidity that is removed. The total amount of AddLiquidity and RemoveLiquidity events in the real data is 5,792 events (3,389 + 2,403). There is always a Transfer event for each of these events. There are 6,420 Transfer events. For the remaining 628 (6,420–5,792) Transfer events and 290 Approval events the real data shows 0 changes or deltas for ETH, DAI and UNI balances in the historical data so both in the real data and simulations there are essentially ineffectual and the simulation does not change any balances or prices when encountering these events.To give an idea of the level of arbitrageur strategic behaviour in the real trading activity we use an algorithm that attempts to classify Uniswap trades between convenience and arbitrage trades based on the precision of the amount of coin sold (DAI for EthPurchase and ETH for TokenPurchase). As ETH protocol dictates the minimum ETH denomination is one WEI, which is equivalent to 1E10-18 ETH.7 So the more precision the traders sells tokens with i.e. specifying more ETH up to a maximum 18 numbers the more likely the trader is an arbitrage trader as opposed to a convenience trader. The classifying algorithm we use use is a rule of four i.e. if the trader ETH or DAI delta is in the range we 1E10-1 to 1E10-4 (resp. 1E10-5 to 1E10-18) we classify the trade as a convenience (resp. arbitrage) trader.8 In Table 2 our estimates show that roughly 35% of events are convenience trades, 58% are arbitrage trades and 7% are other non swap events (i.e., either AddLiquidity, Approval or Transfer events). In Figure 2, we show the counts and percentages on the historical data per block on the Ethereum blockchain. It shows the level of arbitrage activity increasing from roughly 40–80% during the sample period. This is the type of strategic behaviour that is destroyed by our shuffling experiment and thus we can see the effect it has when removed. It is worth bearing in mind that it is not just swap/trade events (EthPurchase and TokenPurchases) that are shuffled but also liquidity providing events as well (AddLiquidity and Remove Liquidity). Thus both liquidity taking and provision roles are now acting with ZI traders9.
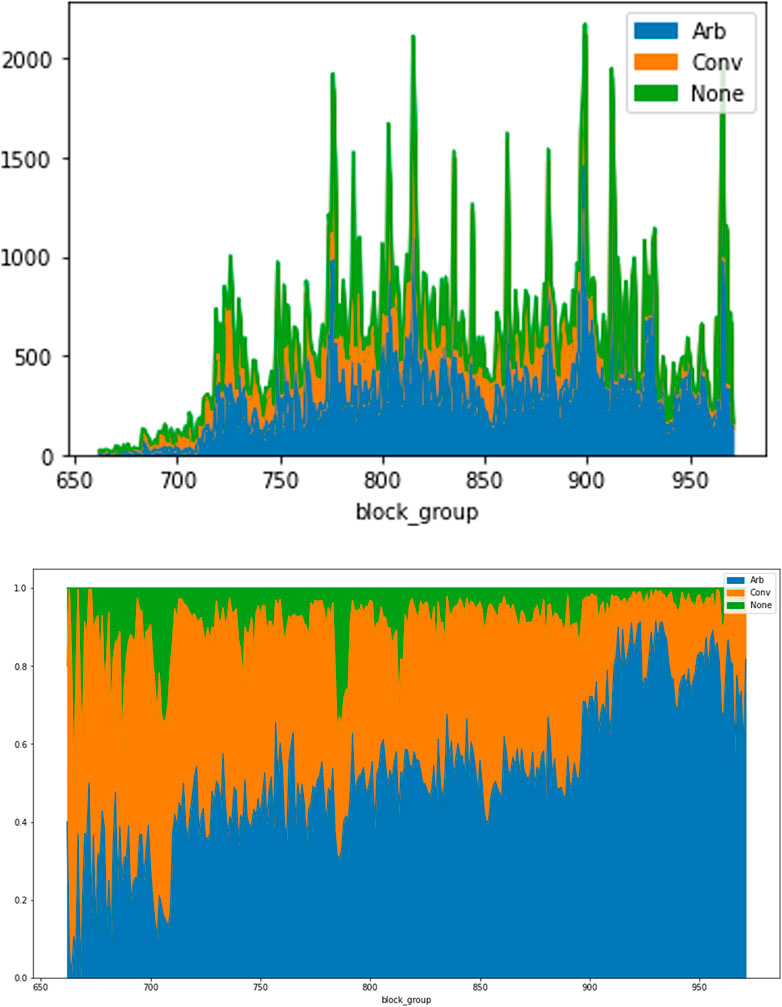
FIGURE 2. Uniswap Trade Classifier Estimation, Retail Precision (4dp) of Convenience and Arbitrage trades in counts and percentages per block.
3 Results
3.1 Liquidity Providers’ Impermanent Loss
We first show some statistical results of three different strategies measured in token DAI in Table 3. ETH Hodler is calculated by the price of ETH (in DAI) at every hour and the prices are sampled every hour and converted into annualized returns by taking the difference of logarithms of this timeseries and multiplying by 252*24. The same is done for the UNI price and a 50:50 strategy whose price is equal weighted between ETH (in DAI) and DAI. Table 3 shows higher returns in the shuffled ZI treatment possibly due to less value drain from arbitrageurs. The value of the UNI coin which can be seen as a proxy for the returns from liquidity provision are much higher. The ZI returns are much more volatile, positively skewed and non-Gaussian.
Table 4 shows the token and invariant percentage growth from first event to last event. The real data shows phenomenal growth as can be expected as more people staked liquidity in DeFi during this period. This shuffled treatment shows an even higher growth rate again suggesting bigger liquidity pools and less value drain from arbitrageurs. With 100 Monte-Carlo simulations runs we can not only calculate a mean metric but a 95% confidence interval. As the real growth rates in Table 4 are always lower than the lowest bound in the 95% confidence interval range the result of higher token growth in the ZI model is robust.
In Table 5 we show the first to last event returns for the three strategies UNI hodler, 50:50 hodler, ETH hodler along with the impermanent loss as measured by:
where price ratio represents the ratio of the price of ETH, UNI or 50:50 ETH:DAI (in DAI) at the end divided by the price at the start [see Pintail (2019)]. Table 5 shows much higher performance in the shuffled treatment for all strategies especially from UNI hodling. Even the ETH hodling strategy which lost -34.05% only loses on average -3.07% in the shuffled experiments. The shuffled treatment shows lower impermanent loss which is in line with the higher profitability of liquidity provision in a ZI AMM.
3.2 Slippage
We now investigate slippage as measured as a percentage by which the effective price exceeds the spot price. It can be calculated as a function of the amountIn traded (Ai) i.e. the amount of DAI (resp. ETH) deposited for a EthPurchase (resp. DAIPurchase) as these two quantities make up the effective price.
We use formulas for slippage used by Martinelli (2020):
where
where the effective price is the ratio of amount of tokens trader deposited (amountIn: Ai) divided by the amount of the other token they bought in return (amountOut: Ao) i.e. essentially the average price that was actually paid. Note as we are using ETH and DAI deltas from data already calculated from the trades run through the protocol (either real or simulated) this already takes into account the 0.3% fees.
which is the ratio of amount of ETH (resp. DAI) pool balance divided by the amount DAI (resp. ETH) pool balance for TokenPurchases (resp. EthPurchases) adjusted up by the 0.3% fee. Table 6 shows that in the digital twin slippage for TokenPurchase and EthPurchases (around 0.12%) was lower than the ZI model slippage (around 0.20%). The slippage metrics again fall outside the shuffled treatment 95% confidence levels again showing this difference is significant. This intuitively makes sense as with the lack of strategic behaviour in the ZI model, traders are no longer conditioning their trading decision on the available liquidity and their immediate price impact. Although in the Shuffled Replay some trades in the simulation may benefit from randomly larger pools, the results show on average traders pay higher slippage.
3.3 Pricing Efficiency
Finally in Table 7 we use a common variance ratio (VR) measure for informational efficiency [see e.g. Comerton-Forde et al. (2019); Schwartz (2021)]:
where
Of course, we cannot say our ZI model is more informationally efficient as we are not incorporating information or any fundamental value in a ZI simulation, but it shows evidence in the real AMM market that the effect of strategic behaviour also adds noise and inefficiency to the prices even though in an AMM, the strategic behaviour of arbitrageurs is assumed primarily to make prices more informationally efficient. We leave the study of DEX arbitrageurs on cryptocurrency price discovery for future work.
4 Conclusion
In this paper we have developed a novel type of zero-intelligence (ZI) model that involves shuffling historical data and feeding it back into the market matching mechanism. In this case we have used it to analyse an Automatic Market Maker (AMM) in the cryptofinance space. ZI analysis allows us to investigate effects of the mechanism design without strategic behaviour. Traditionally in the ZI literature replicating realism e.g., observed stylised facts, is a methodology to link certain attributes of financial markets to the mechanism design or considerations beyond strategic behaviour. In the past ZI models have had some success in replicating some stylised facts. In a universe of a large set of agents with heterogeneous strategies and responses, the collective trade generating behaviour could indeed be random. However, it is intuitive to assume trade actions by specific agents are typically done in response to specific prices. This is especially so in cryptocurrency AMMs dependant on arbitrageurs for price discovery. By showing statistically significant differences between our ZI model and the real data (i.e. what realism is removed) we can highlight the effect of strategic behaviour on important market quality metrics. We have shown evidence that strategic behaviour/interaction (between LPs, arbitrageurs, and convenience traders) reduces LP returns, reduces slippage/price impact and decreases price efficiency.
Extensions to this work could include adding arbitrageur agents interacting with a historical oracle centralised exchange (CEX) ETH-USD price feed to analyse in a structured way their value-drain on an AMM. These arbitrage agents could strategically enter swaps with calculated amount sizes to move prices back to a reference price signal. Other extensions could be to restrict shuffling locally within blockchain blocks or to apply to other AMM protocols such as a Balancer pool which might have an uneven weighted (e.g. 80:20) and/or multi-coin pool structure. The baseline ZI model presented here could also be used to incorporate a simulation parameter sweep of different fees or intelligent agents. This could be in the form of genetic algorithms or reinforcement-learning agents to model the effect of intelligent agents on the same metrics of impermanent loss, slippage and price efficiency studied in this paper.
Data Availability Statement
The code analysed for this study can be found in the cadCAD open source Github repository. [https://github.com/cadCAD-org/demos/tree/master/demos/Multiscale/uniswap]. The dataset analysed for this study can be found using the following link (last accessed on 11th October 2021). [https://www.kaggle.com/markusbkoch/uniswap-ethdai-exchange/data].
Author Contributions
This paper was conceptualized, executed and written by IP.
Funding
IP gratefully acknowledges funding from the Australian Research Council (ARC DP200101808).
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
The author thanks colleagues at the RMIT Blockchain Innovation Hub and fellow participants in the Token Engineering Academy x Balancer Simulations Research Group for valuable feedback and thought-provoking discussions.
Footnotes
1See https://coinmarketcap.com, accessed on 11 October 2021.
2See https://defipulse.com, accessed on 11 October 2021.
3Market orders are scheduled for immediate execution at best prices. In contrast limit-orders are queued on the exchange until a counter-party can be found who is willing to trade at the pre-specified price limit.
5Open source Github repository with code and datatset can be accessed here: https://github.com/cadCAD-org/demos/tree/master/demos/Multiscale/uniswap.
6The dataset used in this study can be found here: https://www.kaggle.com/markusbkoch/uniswap-ethdai-exchange/data, accessed on 11 October 2021.
7Written as a full number up to the full 18 decimal places instead of scientific format one WEI = 0.000000000000000001 ETH.
8The algorithm we use can be found here: https://github.com/neo-empresarial/uniswap/blob/arbitrage/trade-classification-tests.ipynb - accessed 1 July 2021. The analysis shows on the same historical dataset that a classifying value of four is an appropriate value. We thank the developer for making the code open-source.
9To examine whether our shuffled order flow results are sensitive to the shuffling of liquidity events, we repeat the analysis in this paper comparing unshuffled (Digital Twin) and shuffled (Shuffled Replay) with every liquidity event (AddLiquidity, RemoveLiquidity, Transfer) switched off in the simulations (both Digital Twin or Shuffled Replay). This means when a liquidity event is encountered, all token balances are unaltered (ETH, DAI and UNI deltas are zero) and UNI token supply remains constant throughout. These Supplementary Tables show economically similar results and are available on request. We thank a reviewer for suggesting this robustness check.
References
Adams, H., Zinsmeister, N., Salem, M., Keefer, R., and Robinson, D. (2021). Uniswap V3 Core. Available at: https://uniswap.org/whitepaper-v3.pdf.
Angeris, G., Kao, H.-T., Chiang, R., Noyes, C., and Chitra, T. (2021). An Analysis of Uniswap Markets. Cryptoeconomic Syst. 1. doi:10.21428/58320208.c9738e64
Barberis, N., and Thaler, R. (2003). “Chapter 18 A Survey of Behavioral Finance,” in Handbook of the Economics of Finance. Editors G. Constantinides, M. Harris, and R. M. Stulz. 1 edn (Elsevier), 1, 1053–1128. Part 2chap. 18. doi:10.1016/s1574-0102(03)01027-6
Bouchaud, J.-P., Farmer, J. D., and Lillo, F. (2009). “Chapter 2 - How Markets Slowly Digest Changes in Supply and Demand,” in Handbook of Financial Markets: Dynamics and Evolution. Editors T. Hens, and K. R. Schenk-Hoppé (San Diego: North-Holland), 57–160. Handbooks in Finance. doi:10.1016/B978-012374258-2.50006-3
Brandouy, O., Corelli, A., Veryzhenko, I., and Waldeck, R. (2012). A Re-examination of the "zero Is Enough" Hypothesis in the Emergence of Financial Stylized Facts. J. Econ. Interact. Coord. 7, 223–248. doi:10.1007/s11403-012-0099-0
Chakraborti, A., Toke, I. M., Patriarca, M., and Abergel, F. (2011). Econophysics Review: II. Agent-Based Models. Quant. Finance 11, 1013–1041. doi:10.1080/14697688.2010.539249
Challet, D., and Stinchcombe, R. (2001). Analyzing and Modeling 1+1d Markets. Phys. A Stat. Mech. its Appl. 300, 285–299. doi:10.1016/s0378-4371(01)00335-1
Chiarella, C., Iori, G., and Perelló, J. (2009). The Impact of Heterogeneous Trading Rules on the Limit Order Book and Order Flows. J. Econ. Dyn. Control 33, 525–537. doi:10.1016/j.jedc.2008.08.001
Cliff, D., and Bruten, J. (1997). Minimal-Intelligence Agents for Bargaining Behaviors in Market-Based Environments. Bristol: Hewlett-Packard Laboratories. Tech. Rep. HPL-97-91.
Cocco, L., Concas, G., and Marchesi, M. (2017). Using an Artificial Financial Market for Studying a Cryptocurrency Market. J. Econ. Interact. Coord. 12, 345–365. doi:10.1007/s11403-015-0168-2
Comerton-Forde, C., Grégoire, V., and Zhong, Z. (2019). Inverted Fee Structures, Tick Size, and Market Quality. J. Financial Econ. 134, 141–164. doi:10.1016/j.jfineco.2019.03.005
Daniels, M. G., Farmer, J. D., Gillemot, L., Iori, G., and Smith, E. (2003). Quantitative Model of Price Diffusion and Market Friction Based on Trading as a Mechanistic Random Process. Phys. Rev. Lett. 90, 108102. doi:10.1103/physrevlett.90.108102
Gode, D. K., and Sunder, S. (1993). Allocative Efficiency of Markets with Zero-Intelligence Traders: Market as a Partial Substitute for Individual Rationality. J. Political Econ. 101, 119–137. doi:10.1086/261868
Hanson, R. (2003). Combinatorial Information Market Design. Inf. Syst. Front. 5, 107–119. doi:10.1023/a:1022058209073
Harvey, C. R., Ramachandran, A., and Santoro, J. (2021). DeFi and the Future of Finance. John Wiley & Sons.
Hirshleifer, D. (2001). Investor Psychology and Asset Pricing. J. Finance 56, 1533–1597. doi:10.1111/0022-1082.00379
Ladley, D., and Schenk-Hoppé, K. R. (2009). Do stylised Facts of Order Book Markets Need Strategic Behaviour? J. Econ. Dyn. Control 33, 817–831. doi:10.1016/j.jedc.2008.09.005
LeBaron, B., and Yamamoto, R. (2007). Long-memory in an Order-Driven Market. Phys. A Stat. Mech. its Appl. 383, 85–89. doi:10.1016/j.physa.2007.04.090
LeBaron, B., and Yamamoto, R. (2008). The Impact of Imitation on Long Memory in an Order-Driven Market. East. Econ. J. 34, 504–517. doi:10.1057/eej.2008.32
Martinelli, F. (2020). Calculating Value, Impermanent Loss and Slippage for Balancer Pools. Medium.com.
Maslov, S. (2000). Simple Model of a Limit Order-Driven Market. Phys. A Stat. Mech. its Appl. 278, 571–578. doi:10.1016/s0378-4371(00)00067-4
Mike, S., and Farmer, J. D. (2008). An Empirical Behavioral Model of Liquidity and Volatility. J. Econ. Dyn. Control 32, 200–234. doi:10.1016/j.jedc.2007.01.025
Mohan, V. (2022). Automated Market Makers and Decentralized Exchanges: a DeFi Primer. Financ. Innov. 8. doi:10.1186/s40854-021-00314-5
Palit, I., Phelps, S., and Ng, W. L. (2012). “Can a Zero-Intelligence Plus Model Explain the Stylized Facts of Financial Time Series Data?,” in Proceedings of the 11th International Conference on Autonomous Agents and Multiagent Systems (AAMAS), Valencia, Spain, 653–660.
Pintail (2019). Uniswap: A Good Deal for Liquidity Providers?. Available at: https://pintail.medium.com/uniswap-a-good-deal-for-liquidity-providers-104c0b6816f2.
Preis, T., Golke, S., Paul, W., and Schneider, J. J. (2006). Multi-agent-based Order Book Model of Financial Markets. Europhys. Lett. 75, 510–516. doi:10.1209/epl/i2006-10139-0
Preis, T., Golke, S., Paul, W., and Schneider, J. J. (2007). Statistical Analysis of Financial Returns for a Multiagent Order Book Model of Asset Trading. Phys. Rev. E 76, 016108. doi:10.1103/physreve.76.016108
Schwartz, R. A. (2021). A Market Microstructure View of the Informational Efficiency of Security Prices. Jpm 47, 75–84. doi:10.3905/jpm.2021.1.268
Smith, E., Farmer, J. D., Gillemot, L., and Krishnamurthy, S. (2003). Statistical Theory of the Continuous Double Auction. Quant. Finance 3, 481–514. doi:10.1088/1469-7688/3/6/307
Keywords: cryptofinance, decentralised finance, automatic market makers, zero-intelligence, agent-based simulation
Citation: Palit I (2022) A Shuffled Replay of Events on Uniswap. Front. Blockchain 5:745101. doi: 10.3389/fbloc.2022.745101
Received: 21 July 2021; Accepted: 03 June 2022;
Published: 11 July 2022.
Edited by:
Diego Valiante, University of Bologna, ItalyReviewed by:
Daniel Liebau, Erasmus University Rotterdam, NetherlandsHugo E. Benedetti, University of Los Andes, Chile
Copyright © 2022 Palit. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Imon Palit, aW1vbi5wYWxpdEBybWl0LmVkdS5hdQ==
 Imon Palit
Imon Palit