- Department of Mathematics, National Institute of Technology Rourkela, Rourkela, India
In this article, free vibration of the variable cross-section (non-uniform) single-layered graphene nano-ribbons (SLGNRs) is investigated by using the Differential Quadrature Method (DQM). Here width of the cross-section is assumed to vary exponentially along the length of the nano-ribbon. Euler–Bernoulli beam theory is considered in conjunction with the nonlocal elasticity theory of Eringen. Step by step procedure is included and MATLAB code has been developed to obtain the numerical results for different scaling parameters as well as for four types of boundary conditions. Convergence study is carried out to illustrate the efficiency of the method and obtained results are validated with known results in special cases showing good agreement. Further, numerical as well as graphical results are depicted to show the effects of the nonuniform parameter, nonlocal parameter, aspect ratio and edge conditions on the frequency parameters.
Introduction
Application of nanomaterials has expanded in the area of physics, chemistry, engineering, and nanotechnology because of their special properties like mechanical, electrical and electronic (Dai et al., 1996). As a result of these properties, nanomaterials play very significant roles in various nano-mechanical systems and nanomaterials. These materials include nanowires, nanoparticles, nanoribbons, nanotubes etc. Various applications concerning CNT reinforced structure like reinforced beam, plate etc. can be found in the literatures (Tornabene et al., 2016, 2017; Banic et al., 2017; Fantuzzi et al., 2017). One may also get detail information about nanobeams and nanoplates in the book (Chakraverty and Behera, 2016). Among these nanostructures, single-layered graphene nano-ribbons viz. nanobeams attract more attention due to their great potential in engineering applications. Graphene nanoribbons (Geim and Novoselov, 2007; Geim, 2009; Novoselov et al., 2012) are graphene nanostrip with width less than 50 nm. For the first time, Mitsutaka Fujita and coauthors introduced Graphene ribbons as a theoretical model to examine the edge and nanoscale size effect in graphene (Fujita et al., 1996; Nakada et al., 1996; Wakabayashi et al., 1999). Reddy et al. (2006) investigated equilibrium configuration and continuum elastic properties of finite sized graphene. GNRs possess additional advantages over graphene sheets. These advantages include high aspect ratio, ultra-thin width, and opening band gap. So, one must have appropriate knowledge about the mechanical behaviors for accurate prediction of vibration characteristics. So far, many researchers have developed various nonclassical continuum theories such as couple stress theory, strain gradient theory, micropolar theory, and nonlocal elasticity theory. Out of these nonclassical continuum theories, nonlocal elasticity theory developed by Eringen (1972), has been extensively used in the vibration.
Non-uniformity of nanomaterials is very useful in designing of many nanoelectromechanical systems (NEMS) devices such as oscillators, clocks, and sensor devices. In order to make a NEMS device more efficient, nanobeams with non-uniform cross-sections should be used. To be able to use non-uniform nanobeams, mechanical behaviors in both static and dynamic conditions should be known. So, vibration analysis is important for many NEMS devices. Aydogdu et al. (2018) investigated vibration of axially functionally graded nanorods and beams with a variable nonlocal parameter and these variations are assumed in the material properties viz. elasticity modulus, density, and nonlocal parameter. Ece et al. (2007) investigated the vibration of an isotropic beam with an exponentially varying width along the length of the beam. Mirzabeigy (2014) studied free vibration analysis of variable cross-section beams resting on elastic foundation and under axial force by using a semi-analytical approach. Transverse vibration of beam of linearly variable depth with edge crack was Modeled of Chaudhari and Maiti (1999). Attarnejad and Shahba (2011) used dynamic basic displacement functions for free vibration analysis of centrifugally stiffened tapered beams. A nonlocal version of Euler-Bernoulli beam in conjunction with Eringen's nonlocal elasticity was studied by Peddieson et al. (2003). Wang et al. (2007) investigated analytical solutions for vibration of nonlocal Euler-Bernoulli and Timoshenko nanobeams. Application of nonlocal theories for bending, buckling and vibration of beams can be seen in Reddy (2007) and Aydogdu (2009) and vibration analysis of Euler-Bernoulli nanobeams by using finite element method can be found in Eltaher et al. (2013). Hosseini Hashemi and Bakhshi Khaniki (2016) investigated an analytical solution for free vibration of a variable cross-section nonlocal nanobeam. The free transverse vibration of cracked Euler- Bernoulli nanobeams based on nonlocal elasticity model was studied by Loya et al. (2009). Beni et al. (2014) studied the transverse vibration of cracked nano-beam based on modified couple stress theory. Further, Bagdatli (2015) presented the non-linear vibration of nanobeams. Now, literature related to development of various approaches of Differential Quadrature (DQ) method have also been briefly mentioned herein.
For the first time, Bellman and Casti (1971) introduced the Differential Quadrature (DQ) method in the year 1971. Therefore, this powerful technique is being used for solving linear and nonlinear differential equations arising in various dynamic problems. Later, Bert et al. (1988) used this method for solving the dynamical problem arising in the field of structural dynamics. Since then, this method is applied by various researchers for solving different types of structural problems such as linear or nonlinear. Different authors introduced various procedures to use edge conditions in the DQ method. In this regard, for the first time, Bert et al. (Jang et al., 1989) proposed δ technique to use edge conditions. In this case (Shu, 2000), one may observe that one edge condition is used at the boundary point whereas other edge condition is at a distance δ from the boundary point. This δ technique may be suitable for the C-C edge but this is not useful for S-S and S-C edge conditions. In order to eradicate the shortcomings of the above approach, Bert further presented a new technique in applying edge conditions which may be found in Bert et al. (1993, 1994), Wang and Bert (1993), Wang et al. (1993), Bert and Malik (1996). In this technique, one just needs to implement one boundary condition numerically while the other edge condition can be obtained from the DQ weighting coefficient matrices. Similarly, Tornabene et al. surveyed several methods under the heading of strong formulation finite element method (SFEM) which can be found in Tornabene et al. (2015).
To the best of the present authors' knowledge, this article provides first time the frequency parameters of the variable cross-section (non-uniform) single-layered graphene nano-ribbons (SLGNRs) by using Differential Quadrature Method (DQM). In this article, Euler-Bernoulli beam theory in conjunction with nonlocal elasticity theory has been considered to illustrate the effects of the nonuniform parameter, nonlocal parameter, aspect ratio and edge condition on the frequency parameter.
Review of Nonlocal Elastic Theory
Nonlocal stress tensor σ at a given point x in conjunction to nonlocal elasticity theory can be expressed as Murmu and Adhikari (2010)
where τ is the classical stress tensor, K(|x′ − x|, α) the nonlocal modulus, and |x′ − x| the Euclidean distance. One may note that the volume integral is considered over the region V. Here α is the material constant and it depends on both external and internal characteristic lengths.
From Hooke's law, one may have
where C is the fourth order elasticity tensor, ε is the classical strain tensor and: denotes double dot product.
It may be noted that Equation (1) is the integral constitutive relation and it is very complicated to solve. Hence we need an equivalent form of this equation which may be expressed as Murmu and Adhikari (2010)
where ∇2 is the Laplace operator, e0 is a material constant, a is an internal characteristic length and L is the external characteristic length of the nanostructure. Here e0a is the nonlocal parameter which shows scale effect on the nanostructures.
Mathematical Formulation of the Proposed Model
In this study, the Euler–Bernoulli beam theory along with the nonlocal elasticity theory of Eringen (1972) has been considered for the investigation. In this regard, one must have adequate knowledge about energies. Strain energy U for local elasticity may express as
where σxx is the normal stress, L is the length and A is the cross-section area. The strain-displacement relation is given as
where εxx is the normal strain and w is the deflection function. Substituting Equation (5) in Equation (4), one may obtain
where , is the bending moment. In this study, the free harmonic motion is considered viz. we take w = w0(x) sin ωt, where ω is the natural frequency of vibration. Using free harmonic motion in Equation (6), we may obtain the strain energy U as
The kinetic energy T is given as
where ρ is the mass density and A is the area.
Using Hamilton's principle and setting the co-efficient of δw0 to zero, one may obtain the governing equation as
Based on Eringen's nonlocal elasticity theory, the nonlocal constitutive relation for EBT may be expressed as
where μ is the nonlocal parameter which can be expressed as with e0 and a denoting material constant and internal characteristic length respectively, I is the second moment of area and E is Young's modulus. By using Equation (9) and Equation (10), M may be expressed as
Structural members with variable cross section play very significant role in civil, mechanical, and aeronautical engineering. Since we have considered the width of the cross-section is varied exponentially along the length of the nanoribbon, so we will have (Hosseini Hashemi and Bakhshi Khaniki, 2016)
where, n is the non-uniform parameter, I0 and A0 are the second moment of area and cross-section of nanoribbon respectively. Using Equation (11) along with Equation (12) in Equation (9), one may obtain the governing equation in terms of displacement as
Let us introduce the following non-dimensional terms
= Dimensionless co-ordinate
= Dimensionless transverse displacement
= Frequency parameter
= Dimensionless non-local parameter
η = nL = Dimensionless non-uniform parameter.
Using the above non-dimensional terms in Equation (13), we obtain the nondimensionalized form of the governing differential equation as Hosseini Hashemi and Bakhshi Khaniki (2016)
Next, we introduce an overview of the differential quadrature method.
Differential Quadrature Method
In this investigation, Quan and Chang (1989) approach is taken into consideration along with Chebyshev-Gauss-Lobatto grid points which are expressed as
One may express the derivatives of displacement function W(X) at a given discrete point i as Behera and Chakraverty (2015)
where i = 1, 2, …, N and N is the number of discrete grid points.
Here Aij, Bij, Cij, and Dij are the weighting coefficients of the first, second, third and fourth derivatives respectively.
Determination of Weighting Coefficients
Computation of weighting coefficient matrix A = (Aij) plays significant role in DQ method. As per Quan and Chang 's approach, the matrix A = (Aij) can be computed by the following procedure.
For i≠j
For i = j
After weighting coefficients of first-order derivatives are computed, one may easily get the weighting coefficients of higher order derivatives by simple matrix multiplication which is given as
Application of Boundary Conditions
Four classical boundary conditions such as SS, CS, CC, and CF are taken into consideration in the present study where the letters S, C, and F denote simply supported, clamped and free edge conditions respectively.
Let us now denote
The weighting coefficients of higher order derivatives for different edge conditions are given below.
Simply Supported-Simply Supported
where or
Clamped-Simply Supported
Clamped-Clamped
Clamped-Free
Substituting the expression of Equation (16) into Equaion (14), one may obtain generalized eigenvalue problem as
where S is the stiffness matrix and T is the mass matrix.
Numerical Results and Discussions
Equaion (22) is solved by using a MATLAB program which is developed by the authors and frequency parameters have been obtained. DQ method has been implemented along with the boundary conditions in the coefficient matrix. Following parameters (Reddy et al., 2006) are taken for the computational purpose.
Validation
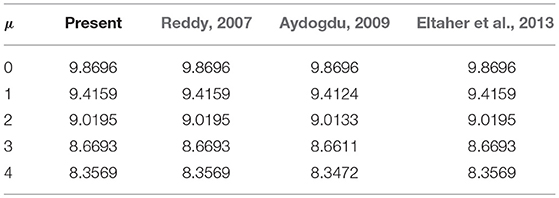
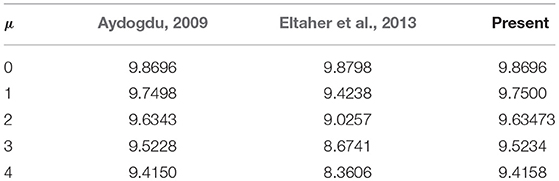
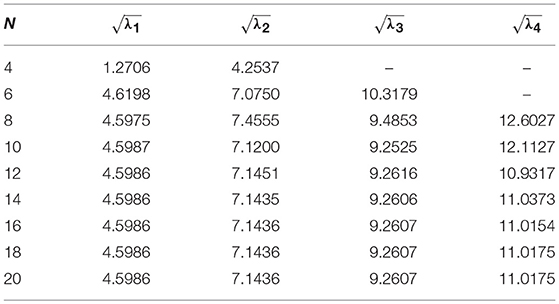
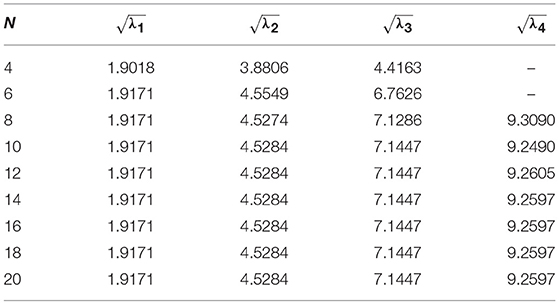
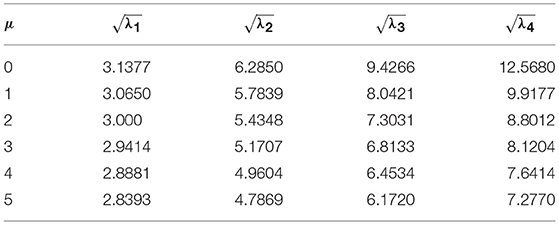
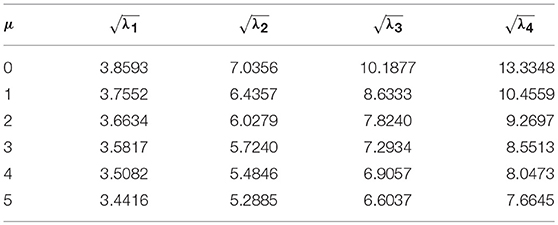
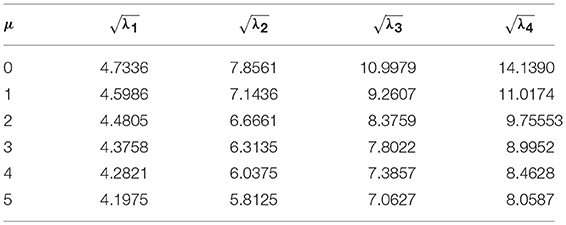
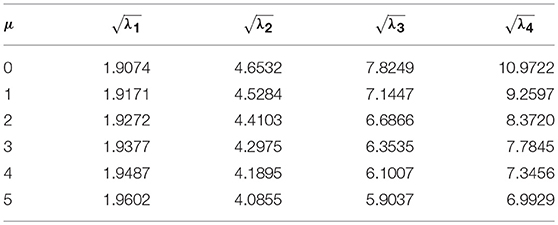
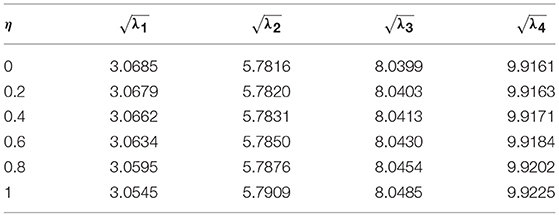
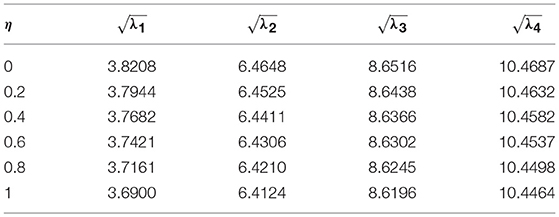
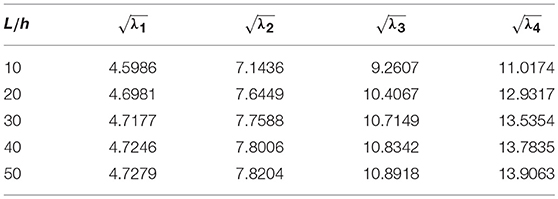
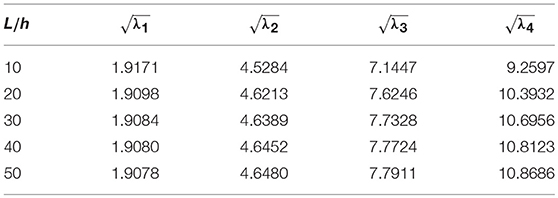
For validation of present method, we consider a nanobeam with uniform cross-section viz. results of fundamental frequency parameter (λ) are then compared with (Reddy, 2007; Aydogdu, 2009; Eltaher et al., 2013) for different nonlocal parameters (μ) which are presented in Tables 1, 2. In Table 1, aspect ratio (L/h) is taken as 10. Similarly, in Table 2, fundamental frequency parameter (λ) for SS nanobeam is compared with (Aydogdu, 2009; Eltaher et al., 2013) with an aspect ratio (L/h) as 20. Again results are compared with (Wang et al., 2007) for different which are presented in Tables 3–6. From these Tables 1–6, one may observe close agreement of results with those available in the literature.
Convergence
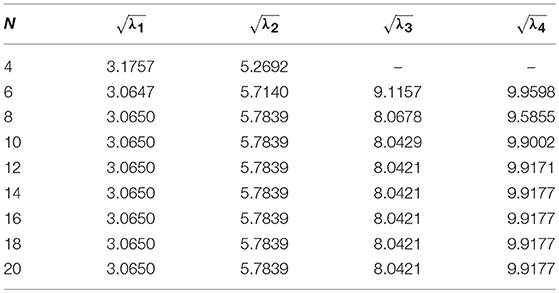
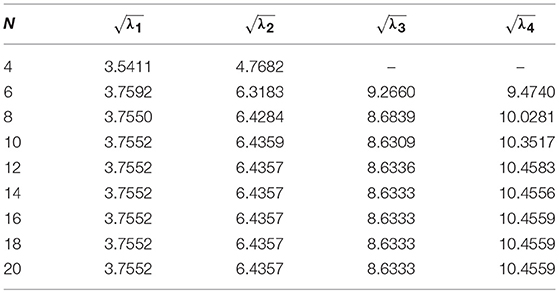
A minimum number of grid points have been obtained by studying convergence to obtain the final results. In order to show how the solution is affected by the grid points, variations of the frequency parameters with number of grid points (N) are shown in Figure 1 and in Tables 7–10 for SS, CS, CC, and CF cases respectively. Here, we have considered L = 10, η = 0.5 and μ = 1. From this figure, one may note that with an increase in number of grid points, the convergence is achieving fast. One may also observe that 12 grid points are sufficient to get the converged results.
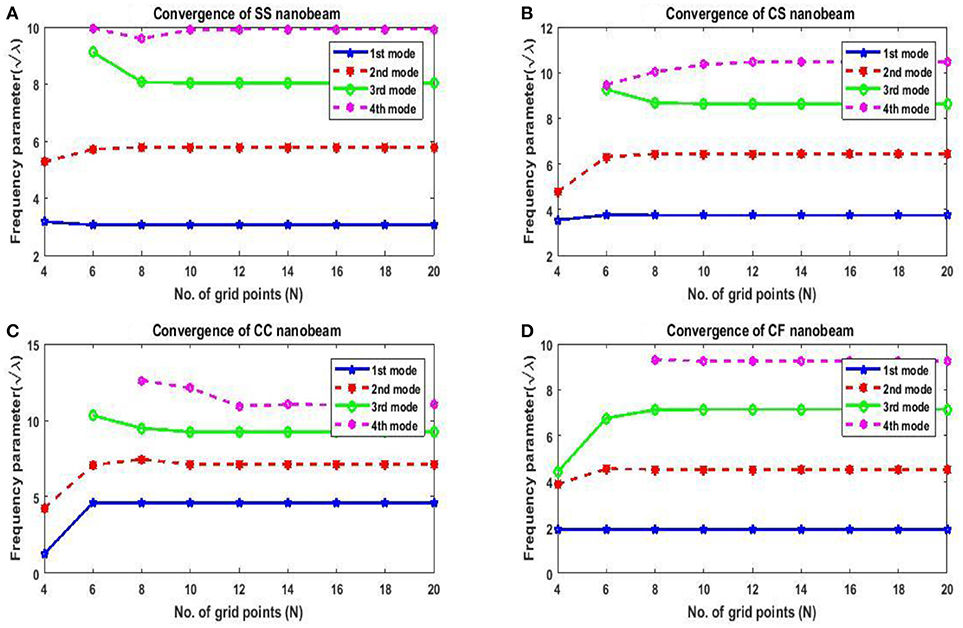
Figure 1. Variation of frequency parameters with number of terms for SS, CS, CC, and CF conditions. (A) Convergence of SS Nanobeam. (B) Convergence of CS Nanobeam. (C) Convergence of CC Nanobeam. (D) Convergence of CF Nanobeam.
Effect of Nonlocal Parameter
In this subsection, the first four frequency parameters of nanobeam are obtained for different nonlocal parameters. We have taken the values of nonlocal parameter as 0, 1, 2, 3, 4, 5nm2. In this study, classical boundary conditions such as SS, CS, CC, and CF are considered for investigation. Both tabular and graphical results are depicted by taking other parameters such as non-uniform parameter (η) as 0.5 and L = 10 nm. First four frequency parameters of SS, CS, CC, and CF edges for different nonlocal parameters are presented in Tables 11–14. From these tables, one may observe that frequency parameters decrease with increase in nonlocal parameter except first fundamental frequency parameter of CF nanobeams. One may also notice that frequency parameters increase with increase in mode number. Here one important point is to note that CC nanobeams are having highest frequency parameters than other set of boundary conditions. Figure 2 shows variation of frequency parameters with nonlocal parameters for different edge conditions such as SS, CS, CC, and CF.
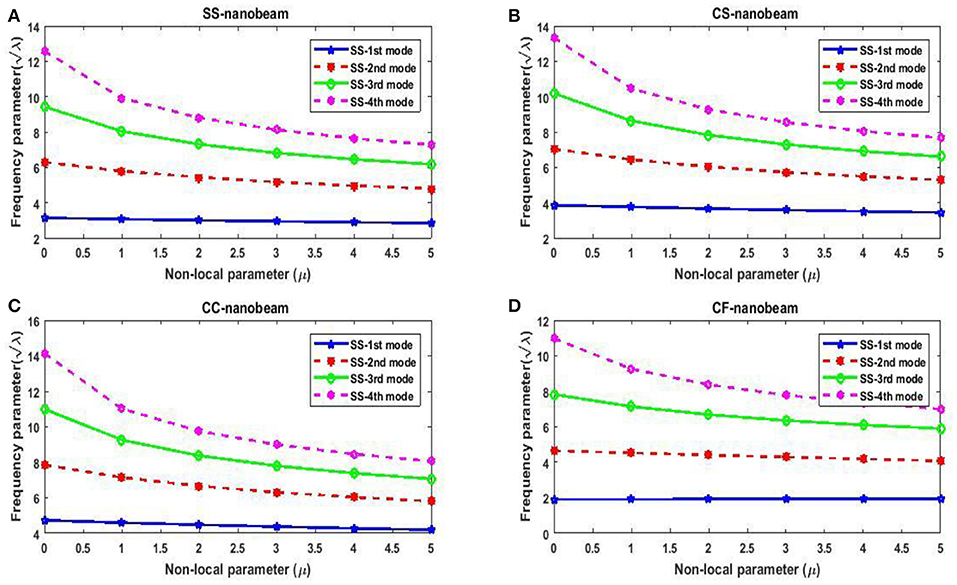
Figure 2. Variation of frequency parameter with nonlocal parameter. (A) Variation of Nonlocal parameter for SS Nanobeam. (B) Variation of Nonlocal parameter for CS Nanobeam. (C) Variation of Nonlocal parameter for CC Nanobeam. (D) Variation of Nonlocal parameter for CF Nanobeam.
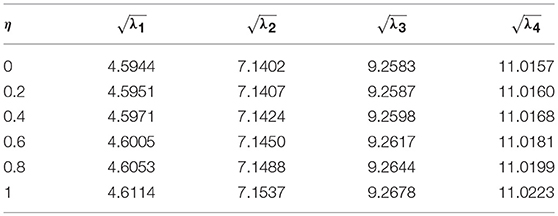
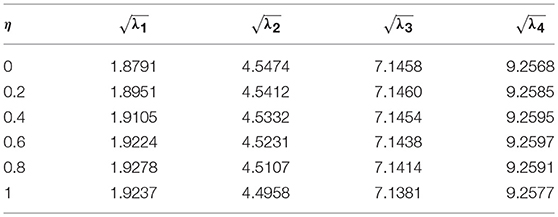
Effect of Non-uniform Parameter
Effect of the non-uniform parameter η on first four frequency parameters is analyzed by taking non-uniform parameter η as 0, 0.2, 0.4, 0.6, 0.8, and 1. Tables 15–18 depict frequency parameters of SS, CS, CC, and CF edges for different non-uniform parameters and Figure 3 illustrates the variation of frequency parameters with non-uniform parameter η for classical boundary conditions SS, CS, CC, and CF. Here, computation is done with nonlocal parameter μ = 1nm2 and L = 10. It is evident from the Figure 3 and Tables 15–18 that the frequency parameters decrease with increase in the non-uniform parameter for the fundamental frequency of SS condition while other modes are increasing. With the increase in non-uniform parameter, frequency parameters decrease for all mode of CS edge whereas this is exactly opposite in case of CC nanoribbons. For the CF case, fundamental frequency increases, second mode decreases, and other modes show random behavior with increase in the non-uniform parameter.
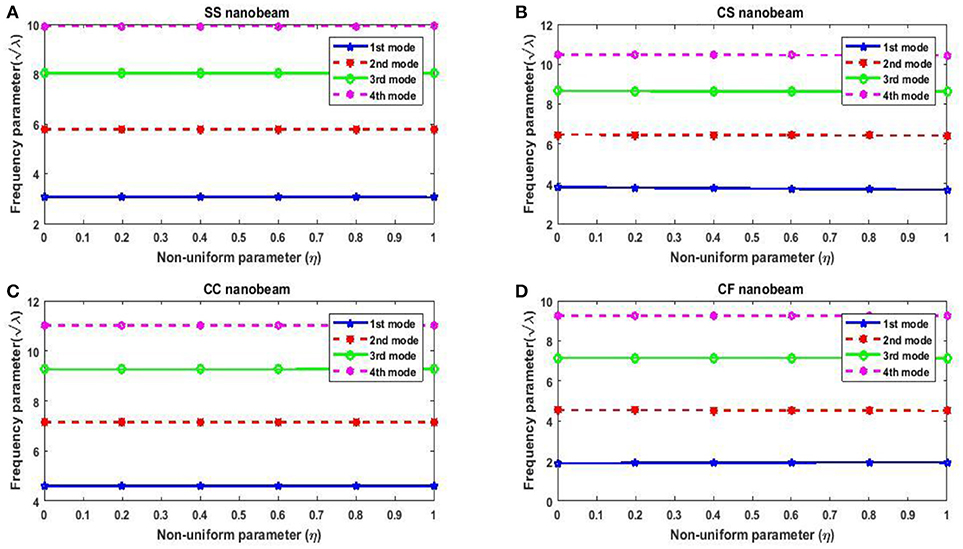
Figure 3. Variation of frequency parameter with non-uniform parameter. (A) Variation of Non-uniform parameter for SS Nanobeam. (B) Variation of Non-uniform parameter for CS Nanobeam. (C) Variation of Non-uniform parameter for CC Nanobeam. (D) Variation of Non-uniform parameter for CF Nanobeam.
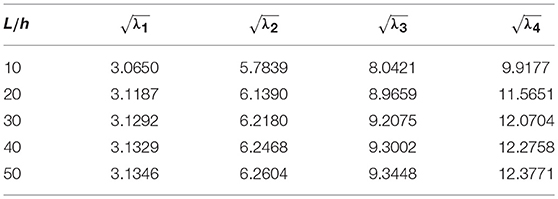
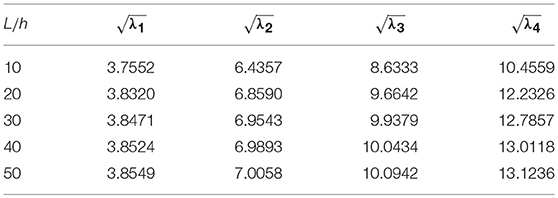
Effect of Length-to-Height Ratio
In this subsection, the effect of length-to-height ratio (L/h) on the first four frequency parameters has been analyzed for the classical boundary conditions such as SS, CS, CC, and CF. First four frequency parameters of nanobeam are given in Tables 19–22 for different L/h (10, 20, 30, 40, 50). Here, computation is done with μ = 1nm2 and η = 0.5. Graphical results are presented in Figure 4, where variation of first four frequency parameters with L/h has been shown. From these tables, one may observe that frequency parameters increase with increase in length-to-height ratio except fundamental frequency parameter of CF nanobeams.
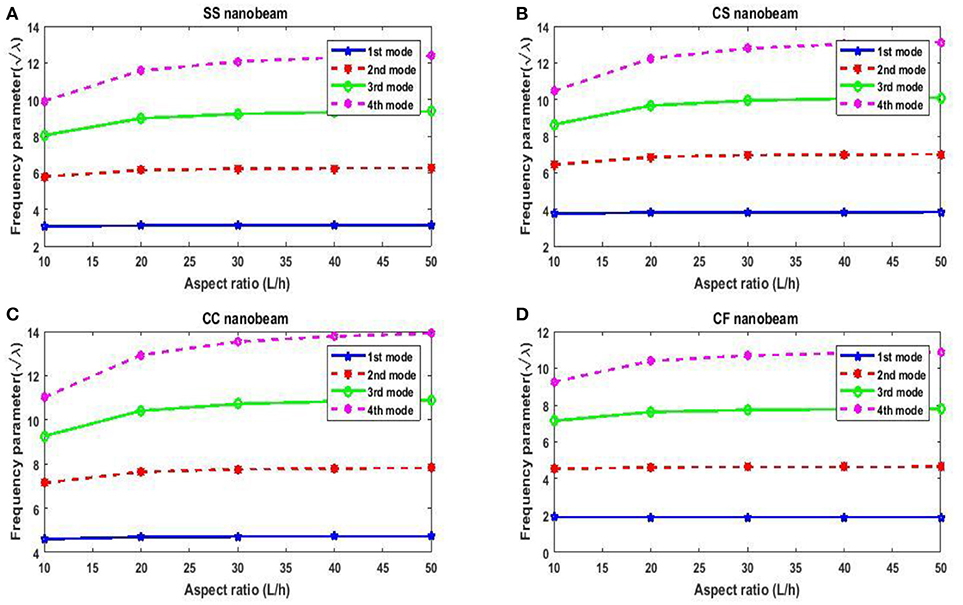
Figure 4. Variation of frequency parameter with length-to-height ratio. (A) Variation of L/h for SS Nanobeam. (B) Variation of L/h for CS Nanobeam. (C) Variation of L/h for CC Nanobeam. (D) Variation of L/h for CF Nanobeam.
Effect of Boundary Conditions
One need to have adequate knowledge about boundary conditions for designing engineering structures. It helps designers to gather important information without carrying out detail experimental investigation. Therefore, it is quite important to study the effect of boundary conditions on frequency parameter. Figure 5 illustrates variation of frequency parameter with nonlocal parameter for different boundary conditions. The values of other parameters are taken as L = 10nm and η = 0.5. One may observe from the figure that CC nanobeams are having highest frequency parameter whereas CF nanobeams possess the lowest frequency parameter.
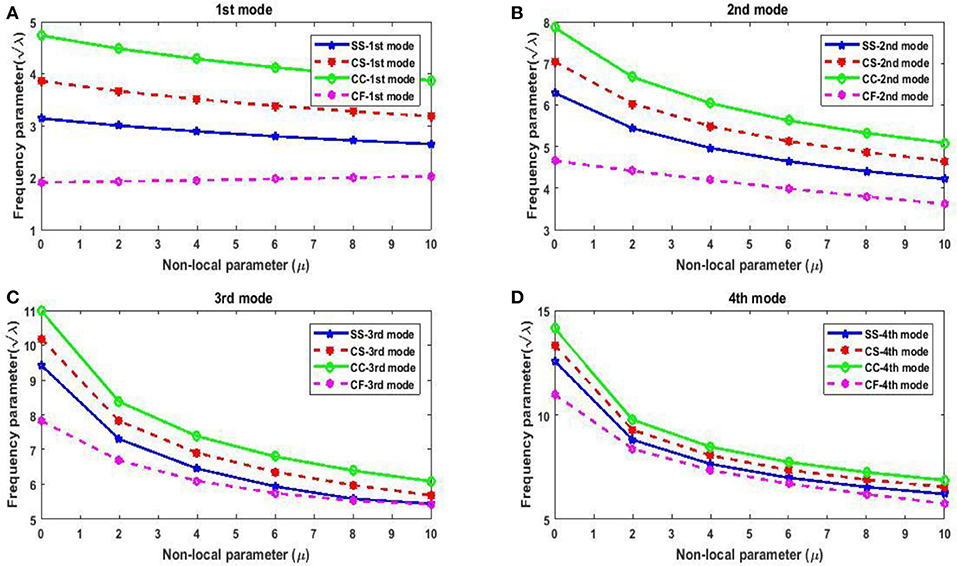
Figure 5. Variation of frequency parameter with boundary condition. (A) Variation of boundary condition for 1st mode. (B) Variation of boundary condition for 2nd mode. (C) Variation of boundary condition for 3rd mode. (D) Variation of boundary condition for 4th mode.
Conclusions
Free vibration of the variable cross-section (non-uniform) single-layered graphene nano-ribbons (SLGNRs) is investigated using the Differential Quadrature Method (DQM). Euler–Bernoulli beam theory is considered in conjunction with the nonlocal elasticity theory of Eringen. In this study, width of the cross-section is varying exponentially along the length of the nano-ribbon while other parameters are kept constant. Complete procedure of Differential Quadrature Method (DQM) is depicted clearly including application of boundary conditions and MATLAB code has been developed to obtain the numerical results for different scaling parameters as well as for four types of boundary conditions. Numerical as well as graphical results are presented to show the effects of the nonlocal parameter, non-uniform parameter, aspect ratio and the boundary conditions on the frequency parameters. one may observe that the effect of the nonlocal parameter is more in higher modes and another interesting observation is that fundamental frequency (1st mode) parameter of the cantilever (CF) nanobeam does not decrease with increase in nonlocal parameters whereas frequency parameters of other modes of nanobeam decrease with increase in nonlocal parameters. Frequency parameters decrease with increase in the non-uniform parameter for the fundamental frequency of SS condition while other modes are increasing. With the increase in non-uniform parameter, frequency parameters decrease for all mode of CS edge whereas this is exactly opposite in case of CC nanoribbons. For the CF case, fundamental frequency increases, second mode decreases, and other modes show random behavior with increase in the non-uniform parameter. One may also conclude that frequency parameters increase with increase in length-to-height ratio (aspect ratio) except fundamental frequency parameter of CF nanobeam. Moreover, it is also found that clamped (CC) case possesses highest frequency parameters and cantilever (CF) nanobeam possesses the lowest among all other types of boundary conditions.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors are thankful to Defence Research & Development Organization(DRDO), Ministry of Defence, New Delhi, India (Sanction Code: DG/TM/ERIPR/GIA/17-18/0129/020) for the funding to carry out the present research work.
References
Attarnejad, R., and Shahba, A. (2011). Dynamic basic displacement functions in free vibration analysis of centrifugally stiffened tapered beams; a mechanical solution. Meccanica 46, 1267–1281. doi: 10.1007/s11012-010-9383-z
Aydogdu, M. (2009). A general nonlocal beam theory: its application to nanobeam bending, buckling and vibration. Phys. E 41, 1651–1655. doi: 10.1016/j.physe.2009.05.014
Aydogdu, M., Arda, M., and Filiz, S. (2018). Vibration of axially functionally graded nanorods and beams with a variable nonlocal parameter. Adv. Nano Res. 6, 257–278. doi: 10.12989/anr.2018.6.3.257
Bagdatli, S. M. (2015). Non-linear vibration of nanobeams with various boundary condition based on nonlocal elasticity theory. Composites Part B. Eng. 80, 43–52. doi: 10.1016/j.compositesb.2015.05.030
Banic, D., Bacciocchi, M., Tornabene, F., and Ferreira, A. J. M. (2017). Influence of winkler-pasternak foundation on the vibrational behavior of plates and shells reinforced by agglomerated carbon nanotubes. Appl. Sci. 7, 1–55. doi: 10.3390/app7121228
Behera, L., and Chakraverty, S. (2015). Application of Differential Quadrature method in free vibration analysis of nanobeams based on various nonlocal theories. Comput. Math. Appl. 69, 1444–1462. doi: 10.1016/j.camwa.2015.04.010
Bellman, R., and Casti, J. (1971). Differential quadrature and long-term integration. J. Math. Anal. Appl. 34, 235–238. doi: 10.1016/0022-247X(71)90110-7
Beni, Y. T., Jafaria, A., and Razavi, H. (2014). Size effect on free transverse vibration of cracked nano-beams using couple stress theory. Int. J. Eng. Trans. B Appl. 28, 296–305. doi: 10.5829/idosi.ije.2015.28.02b.17
Bert, C., Wang, X., and Striz, A. (1994). Static and free vibrational analysis of beams and plates by differential quadrature method. Acta Mech. 102, 11–24. doi: 10.1007/BF01178514
Bert, C. W., Jang, S. K., and Striz, A. G. (1988). Two new approximate methods for analyzing free vibration of structural components. AIAA J. 26, 612–618. doi: 10.2514/3.9941
Bert, C. W., and Malik, M. (1996). The differential quadrature method for irregular domains and application to plate vibration. Int. J. Mech. Sci. 38, 589–606. doi: 10.1016/S0020-7403(96)80003-8
Bert, C. W., Xinwei, W., and Striz, A. G. (1993). Differential quadrature for static and free vibration analyses of anisotropic plates. Int. J. Solids Struct. 30, 1737–1744.
Chakraverty, S., and Behera, L. (2016). Static and Dynamic Problems of Nanobeams and Nanoplates, 1st Edn. Singapore: World Scientific Publishing Co.
Chaudhari, T., and Maiti, S. (1999). Modelling of transverse vibration of beam of linearly variable depth with edge crack. Eng. Fract. Mech. 63, 425–445. doi: 10.1016/S0013-7944(99)00029-6
Dai, H., Hafner, J. H., Rinzler, A. G., Colbert, D. T., and Smalley, R. E. (1996). Nanotubes as nanoprobes in scanning probe microscopy. Nature 384, 147–150. doi: 10.1038/384147a0
Ece, M. C., Aydogdu, M., and Taskin, V. (2007). Vibration of a variable cross-section beam. Mech. Res. Commun. 34, 78–84. doi: 10.1016/j.mechrescom.2006.06.005
Eltaher, M. A., Alshorbagy, A. E., and Mahmoud, F. F. (2013). Vibration analysis of Euler-Bernoulli nanobeams by using finite element method. Appl. Math. Model. 37, 4787–4797. doi: 10.1016/j.apm.2012.10.016
Eringen, A. C. (1972). Nonlocal polar elastic continua. Int. J. Eng. Sci. 10, 1–16. doi: 10.1016/0020-7225(72)90070-5
Fantuzzi, N., Tornabene, F., Bacciocchi, M., and Dimitri, R. (2017). Free vibration analysis of arbitrarily shaped Functionally Graded Carbon Nanotube-reinforced plates. Composites Part B 115, 384–408. doi: 10.1016/j.compositesb.2016.09.021
Fujita, M., Wakabayashi, K., Nakada, K., and Kusakabe, K. (1996). Peculiar localized state at zigzag graphite edge. J. Phys. Soc. Jpn. 65, 1920–1923.
Geim, A. K. (2009). Graphene: status and prospects. Science 324, 1530–1534. doi: 10.1126/science.1158877
Geim, A. K., and Novoselov, K. S. (2007). The rise of graphene. Nat. Mat. 6, 183–191. doi: 10.1038/nmat1849
Hosseini Hashemi, S., and Bakhshi Khaniki, H. (2016). Analytical solution for free vibration of a variable cross-section nonlocal nanobeam. Int. J. Eng. 29, 688–696. doi: 10.5829/idosi.ije.2016.29.05b.13
Jang, S. K., Bert, C. W., and Striz, A. G. (1989). Application of differential quadrature to static analysis of structural components. Int. J. Num. Methods Eng. 28, 561–577. doi: 10.1002/nme.1620280306
Loya, J., Lopez-Puente, J., Zaera, R., and Fernández-Sáez, J. (2009). Free transverse vibrations of cracked nanobeams using a nonlocal elasticity model. J. Appl. Phys. 105, 78–86. doi: 10.1063/1.3068370
Mirzabeigy, A. (2014). Semi-analytical approach for free vibration analysis of variable cross-section beams resting on elastic foundation and under axial force. Int. J. Eng. Trans. C Aspects 27, 455–463. doi: 10.5829/idosi.ije.2014.27.03c.05
Murmu, T., and Adhikari, S. (2010). Nonlocal transverse vibration of double-nanobeam-systems. J. Appl. Phys. 108:083514. doi: 10.1063/1.3496627
Nakada, K., Fujita, M., Dresselhaus, G., and Dresselhaus, M. S. (1996). Edge state in graphene ribbons: nanometer size effect and edge shape dependence. Phys. Rev. B 54:17954. doi: 10.1103/PhysRevB.54.17954
Novoselov, K. S., Fal'ko, V. I., Colombo, L., Gellert, P. R., Schwab, M. G., and Kim, K. A. (2012). Roadmap for graphene. Nature 490, 192–200. doi: 10.1038/nature11458
Peddieson, J., Buchanan, G. R., and McNitt, R. P. (2003). Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 41, 305–312. doi: 10.1016/S0020-7225(02)00210-0
Quan, J., and Chang, C. (1989). New insights in solving distributed system equations by the quadrature method— Analysis, I. Comput. Chem. Eng. 13, 779–788. doi: 10.1016/0098-1354(89)85051-3
Reddy, C. D., Rajendran, S., and Liew, K. M. (2006). Equilibrium configuration and continuum elastic properties of finite sized graphene. Nanotechnology 17, 864–870. doi: 10.1088/0957-4484/17/3/042
Reddy, J. (2007). Nonlocal theories for bending, buckling and vibration of beams. Int. J. Eng. Sci. 45, 288–307. doi: 10.1016/j.ijengsci.2007.04.004
Shu, C. (2000). Differential Quadrature and its Application in Engineering. Singapore: Springer. doi: 10.1007/978-1-4471-0407-0
Tornabene, F., Fantuzzi, N., and Bacciocchi, M. (2017). Linear static response of nanocomposite plates and shells reinforced by agglomerated carbon nanotubes. Composites Part B 115, 449–476. doi: 10.1016/j.compositesb.2016.07.011
Tornabene, F., Fantuzzi, N., Bacciocchi, M., and Viola, E. (2016). Effect of agglomeration on the natural frequencies of functionally graded carbon nanotube-reinforced laminated composite doubly-curved shells. Composites Part B 89, 187–218. doi: 10.1016/j.compositesb.2015.11.016
Tornabene, F., Fantuzzi, N., Ubertini, F., and Viola, E. (2015). Strong formulation finite element method based on differential quadrature: a survey. Appl. Mech. Rev. 67:020801. doi: 10.1115/1.4028859
Wakabayashi, K., Fujita, M., Ajiki, H., and Sigrist, M. (1999). Electronic and magnetic properties of nanographite ribbons. Phys. Rev. B 59:8271. doi: 10.1103/PhysRevB.59.8271
Wang, C., Zhang, Y., and He, X. (2007). Vibration of nonlocal timoshenko beams. Nanotechnology 18, 105–113. doi: 10.1088/0957-4484/18/10/105401
Wang, X., and Bert, C. (1993). A new approach in applying differential quadrature to static and free vibrational analyses of beams and plates. J. Sound Vib. 162, 566–572. doi: 10.1006/jsvi.1993.1143
Keywords: SLGNR, euler-bernoulli beam theory, DQM, vibration, variable cross-section
Citation: Jena SK and Chakraverty S (2018) Free Vibration Analysis of Variable Cross-Section Single-Layered Graphene Nano-Ribbons (SLGNRs) Using Differential Quadrature Method. Front. Built Environ. 4:63. doi: 10.3389/fbuil.2018.00063
Received: 30 August 2018; Accepted: 11 October 2018;
Published: 30 October 2018.
Edited by:
Vagelis Plevris, OsloMet – Oslo Metropolitan University, NorwayReviewed by:
Ahmad Partovi Meran, Necmettin Erbakan University, TurkeyFrancesco Tornabene, Università degli Studi di Bologna, Italy
Metin Aydogdu, Trakya University, Turkey
Copyright © 2018 Jena and Chakraverty. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Subrat Kumar Jena, c2plbmE0MzBAZ21haWwuY29t
Snehashish Chakraverty, c25lX2NoYWtAeWFob28uY29t
 Subrat Kumar Jena
Subrat Kumar Jena Snehashish Chakraverty
Snehashish Chakraverty