Voronoi-Like Grid Systems for Tall Buildings

In the context of innovative patterns for tall buildings, Voronoi tessellation is certainly worthy of interest. It is an irregular biomimetic pattern based on the Voronoi diagram, which derives from the direct observation of natural structures. The paper is mainly focused on the application of this nature-inspired typology to load-resisting systems for tall buildings, investigating the potential of non-regular grids on the global mechanical response of the structure. In particular, the study concentrates on the periodic and non-periodic Voronoi tessellation, describing the procedure for generating irregular patterns through parametric modeling and illustrates the homogenization-based approach proposed in the literature for dealing with unconventional patterns. To appreciate the consistency of preliminary design equations, numerical and analytical results are compared. Moreover, since the mechanical response of the building strongly depends on the parameters of the microstructure, the paper focuses on the influence of the grid arrangement on the global lateral stiffness, therefore on the displacement constraint, which is an essential requirement in the design of tall buildings. To this end, five case studies, accounting for different levels of irregularity and relative density, are generated and analyzed through static and modal analysis in the elastic field. In addition, the paper focuses on the mechanical response of a pattern with gradual rarefying density to evaluate its applicability to tall buildings. Displacement based optimizations are carried out to assess the adequate member cross sections that provide the maximum contribution in restraining deflection with the minimum material weight. The results obtained for all the models generated are compared and discussed to outline a final evaluation of the Voronoi structures. In addition to the wind loading scenario, the efficiency of the building model with varying density Voronoi pattern, is tested for seismic ground motion through a response spectrum analysis. The potential applications of Voronoi tessellation for tall buildings is demonstrated for both regions with high wind load conditions and areas of high seismicity.

Introduction

In the last few decades, tall buildings have become a world architectural phenomenon. The modern tendency toward lightweight and best performing designs has led, in recent years, to innovative structural systems for skyscrapers, able to integrate aesthetic and engineering aspects. Traditional structural systems have been progressively abandoned in favor of more efficient structures that allow new “design challenges,” such as the search for increasing heights.

In the design of tall buildings, the outer skin assumes a more significant role than any other type of building. As a matter of fact, the tallness of the building causes greater vulnerability to wind forces. Following this line of reasoning, Khan (1969) suggested the adoption of the so-called exterior tubular structures: perimeter load-resisting systems, able to provide a great contribution in terms of global structural efficiency.

These structures are based on the concept of a continuous perforated tube along the height of the building, obtained by moving the structural members toward the perimeter to increase the moment of inertia of the building, and as a consequence its strength and stiffness.

The introduction of tubular systems offers the possibility of achieving high efficiency and architectural potential. The elimination of intermediate supports, indeed, positively contributes to the definition of large spaces, without intermediate supports, with great benefits on the flexibility of architectural planning. From an engineering point of view, a perimeter system involves greater stiffness and resistance to vertical and lateral loads. In fact, if one considers the tall building as a large cantilever beam fixed at the base (where the height of the building is equivalent to the length of the beam), moving the resistant parts from the neutral axis, outwards, is comparable to increase the wing area of a beam, with a consequent increase of the moment of inertia. This is a desirable requirement in the design of tall buildings in order to achieve stiffer structures against wind loads and earthquakes.

The last generation of tubular systems are perimeter grid tubes with geometric patterns.

According to their configuration they can be distinguished as: Diagrid (Figure 1A), PentaGrid (Figure 1B), HexaGrid (Figure 1C), OctaGrid (Figure 1D) and the so-called Voronoi grid (Figure 1E).

FIGURE 1

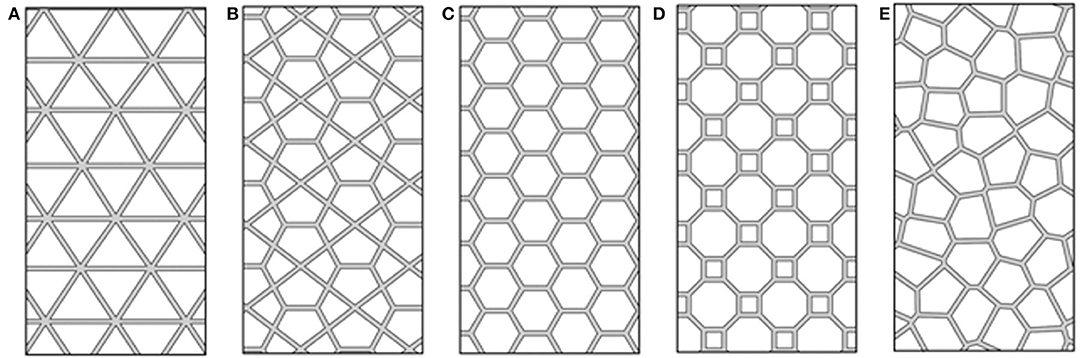
Figure 1. Grid examples: (A) Diagrid, (B) Pentagrid, (C) Hexagrid, (D) Octagrid, and (E) Voronoi grid.

Diagrid structural systems have been widely adopted for high-rise buildings in the last decades, due to their structural and aesthetic efficiency.

In the last decades, several well-known diagrid examples have been built, such as the Poly International Plaza tower in Beijing, the Hearst Tower in New York, the 30 St. Mary Ax in London, the Capital Gate Tower in Abu Dhabi and many others.

An important contribution to the state of the art of Diagrid is provided by Moon, starting from 2007, with the study of optimal diagonal inclination and the formulation of a preliminary stiffness-based design methodology (Moon et al., 2007). Moon proved that for diagrid heights ranging from 20 to 60 stories, the optimal angle is about 53°-76°, where “optimal” means the lighter and most economical solution in terms of material usage (Moon, 2010).

In recent developments, the diagrid system has evolved into other innovative patterns for tall buildings. Nature-inspired patterns, i.e., geometric patterns that can be observed in nature, represent a source of inspiration for a new generation of tessellated tubes.

Such biomimetic patterns are derived by the arrangement of regular or irregular unit cells, in order to create aesthetically attractive façades.

The PentaGrid structural pattern is generated by the arrangement of pentagons with different orientations. Its irregular arrangement is strictly related to technical considerations, in order to increase the global stiffness toward the shear and bending moment. In particular, Pentagrid takes advantage of an equitable distribution of stresses, with a predominantly axial behavior in the members.

HexaGrid systems are inspired by honeycomb structures, made up of several hexagons. The regular angle of 120° between consecutive cells, determines a uniform distribution of the stresses but a relatively low global stiffness.

Taranath et al. (2014) demonstrated that Pentagrid systems are more efficient in containing lateral deflection when compared to Hexagrids, reducing the displacements by 27–34% for 40-story height buildings and 26–35% for 60-story height.

In 2012, de Meijer (2012) analyzed the mechanical performances of tall building models with outer tubes discretized using triangular, hexagonal and trihexagonal patterns. The comparison showed that hexagrid structures exhibit a lower stiffness than a triangular diagrid or a trihexagonal grid. In particular, the stiffness of the hexagrid structures strictly depends on the slenderness ratio of the members composing the grid, e.g., when the ratio decreases, the difference between the two systems also decreases.

Further developments on the behavior of hexagrid structures have been made by Montuori et al. (2015), who investigated the mechanical properties of horizontal hexagrid patterns, to evaluate their applicability on tall buildings, and compared their potential efficiency with diagrid systems. As outlined by the authors, the hexagrids, being bending-dominated structures, are inherently less stiff, and consequently, less efficient in terms of weight than diagrids that are stretch-dominated structures.

In the context of innovative patterns for tall buildings, Voronoi tessellation is certainly worthy of interest. It is an innovative and irregular pattern that derives from the observation of natural structures, as they are visible in nature in the ribs of the leaves, in the motifs of giraffe fur or circulatory system of insect wings, etc.

Although diagrid and hexagrid have been widely applied in recent designs and much has been said in the literature, studies on alternative non-conventional patterns are still an open topic, given their geometric complexity. Considering the potential application of Voronoi tessellation and the interest of scholars to the topic, this paper mainly focuses on the application of this nature-inspired typology for tall buildings, investigating the efficiency of non-regular grids on the global mechanical response. In particular, the study focuses on the periodic and non-periodic Voronoi tessellation.

In paragraph 2 the state of the art on the tessellated Voronoi systems is exhaustively outlined and the geometric definition of the Voronoi diagram is presented. In particular, this section deals with the homogenization-based approach, proposed in the literature, to take into account the discrete nature of the micro-structure during the preliminary design of the tall building.

Finally, in section Voronoi pattern for tall buildings the design of five irregular Voronoi-grid structures using parametric modeling is described. The paper analyzes the mechanical behavior of periodic and non-periodic grid buildings with varying degrees of irregularity and density coefficients, in order to define the most suitable geometry that satisfies the stiffness requirements. To appreciate the consistency of preliminary design equations, numerical, and analytical results are compared. Moreover, since the mechanical response of the building strongly depends on the parameters of the microstructure, the paper focuses on the influence of the grid arrangement on the global lateral stiffness, thus on the displacement constraint, which is an essential requirement in the design of tall buildings. To this end, five case studies, accounting for different levels of irregularity and relative density, are generated and analyzed through static and modal analysis in the elastic field.

In addition, the paper focuses on the mechanical response of a pattern with gradual rarefying density to evaluate its applicability to tall buildings with Voronoi-like grids. Displacement-based optimizations are carried out to assess the member cross sections that provide the maximum contribution in limiting the top deflection with the minimum material weight. Results obtained for all the models generated are compared and discussed to outline a final evaluation of the Voronoi structures.

In addition to the wind loading scenario, the efficiency of the building model with varying density Voronoi pattern, is tested, in section Seismic behavior of the Voronoi grid, for a Turkish seismic ground motion through a response spectrum analysis. Applications of the Voronoi tessellations for tall buildings are investigated for both regions with high wind load conditions and areas of high seismicity, in order to demonstrate the potential of the innovative Voronoi patterns as an alternative to conventional regular grids.

The Voronoi Tessellation: Geometrical and Mechanical Properties

The tendency of modern designs toward optimal structures often leads to high performance and aesthetically appealing structures, accounting for a multitude of multi-disciplinary requirements. Making an efficient use of material, i.e., building lighter structures able to satisfy loading conditions, is a recurrent topic for designers and researchers. To this end, recent developments in architectural design are strongly inspired by biological processes through the use of mathematical models.

The evolution of living organisms through genetic selection and the organization of unit cells on biological structures represent a continuous source of inspiration for researchers.

The improvement of the computational tools has allowed, in the last decades, the possibility to investigate new design fashions and innovative solutions with affordable times and costs, using mathematical methods. The Voronoi tessellation (Voronoi, 1908) is an example of this concept, representing a geometric diagram that reproduces non-regular biomimetic cells easily observable in nature, e.g., on the wings of the dragonflies, the shells of the turtles and others.

Due to its ability of mathematically describing natural models, Voronoi tessellation has gained a growing interest spanning in many fields of science from biology to architectural design. Recent applications have been addressed toward material engineering for modeling cellular materials (Silva and Gibson, 1997; Vajjhala et al., 2000) and material science for representing polycrystalline microstructures (Wigner and Seitz, 1933). In the context of structural engineering, applications of the Voronoi tessellation has been proposed by Beghini et al. (2014), eVolo¹ and LAVA².

Despite the lack of available literature, in the last years, significant developments have been made in the adoption of tubular systems with innovative patterns for skyscrapers. Recently, indeed, Montuori et al. (2016) investigated the mechanical potentials of non-regular tessellations for tall buildings. In particular, through the definition of appropriate correction factors, the authors described the behavior of the Voronoi structure starting from that of a regular hexagrid pattern.

Voronoi Diagram Definition

The decomposition of the metric space, determined by the distances with respect to a certain set of discrete elements is the basis of the Voronoi tessellation, which makes it possible to transpose these biomimetic forms to the design environment. Voronoi tessellation can be applied both to two-dimensional and three-dimensional configurations, allowing several applications in architectural and urban planning because the use of non-conventional patterns in the configuration of tubular structures offers numerous benefits, e.g., allows to have irregular and non-repetitive façades.

Since the mechanical properties of the Voronoi pattern are mainly influenced by its geometrical characteristics, to fully understand this dependence it is necessary to deepen the process for generating the Voronoi tessellation and its dual, the Delauanay triangulation. The Voronoi pattern consists of a spatial region discretized by convex polygons that fill the domain without overlapping. The construction process begins with the definition of a set of points (also called seeds, sites or generators) within the generic design domain, as illustrated in Figure 2A.

FIGURE 2

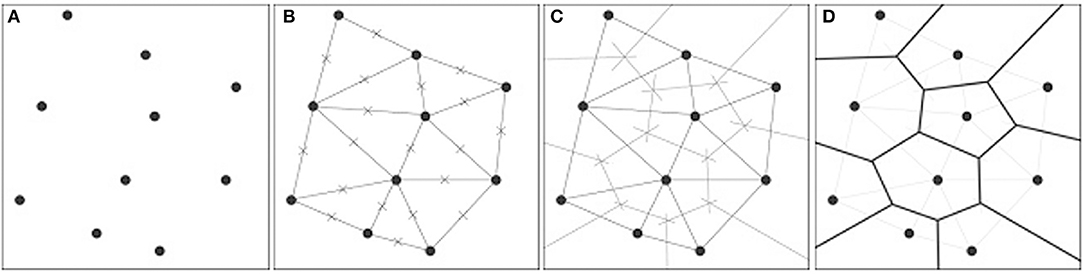
Figure 2. Generation process of the Voronoi diagram. (A) Distribution of the seeds within the design domain, (B) Delauney triangulation, (C) Identification of the bisector lines, (D) Voronoi tessellation.

As a consequence, each point is connected with the nearest adjacent points, without overlapping; the resulting geometry is called Delaunay triangulation (Figure 2B).

To identify the centers of Delaunay triangles, the midpoints on each segment are marked and the bisector lines are drawn (Figure 2C). The lines generated by the union of these orthogonal segments (highlighted in Figure 2D) represent the edges of the Voronoi regions. The final result is a set of polygonal cells that define the Voronoi diagram.

Geometrical Construction of Voronoi Pattern

To study the applicability of Voronoi systems for tall buildings, it is essential to investigate the scientific progress made in the context of the cellular solid field and thus transfer this theoretical knowledge into the structural engineering environment.

Because the regular or random distribution of the nucleation points leads to various configurations of the microstructures, Voronoi tessellation is a commonly used method for analyzing cellular solids and capturing the random features of the foam microstructures (Silva and Gibson, 1997; Zhu et al., 2001b; Gibson, 2005). A Voronoi tessellation based on a random set of points is, indeed, topologically very similar to an isotropic structure resulting from a growth process.

Two main approaches are generally adopted in the literature to generate the Voronoi geometry numerically, as described below: (i) the perturbation approach of the nodal locations, starting from a regular honeycomb, and (ii) the so-called random Voronoi approach.

Random Voronoi Approach

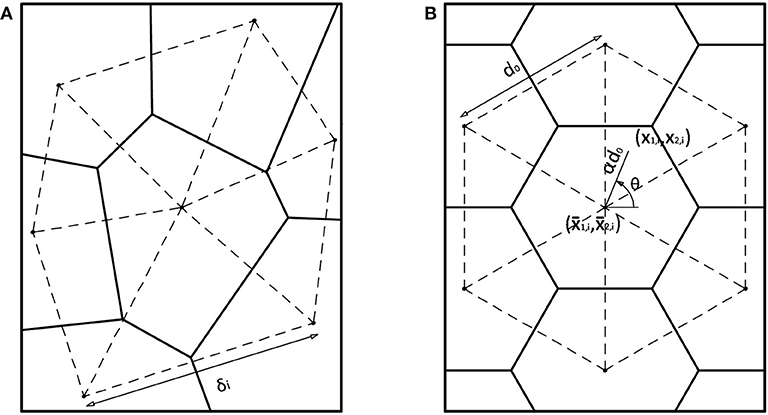
The random Voronoi method (Figure 3A), proposed by Silva and Gibson (1997) and Zhu et al. (2001b), consists in generating n random seeds in an arbitrary square area (A₀).

FIGURE 3

Figure 3. (A) Random Voronoi approach and (B) Perturbation of regular Voronoi approach.

For regular honeycombs, made up of identical cells with six sides and an angle of the vertex of 120°, the distance δ_i between two neighboring points is everywhere constant and equal to d₀, with:

$\begin{array}{ll}{d}_0=\sqrt{\frac{2A_0}{n\sqrt{3}}}& (1)\end{array}$

To obtain n cells in the area A₀, it is essential that the distance between any two adjacent nuclei in the random configuration (δ_i) is less than the distance between two seeds in the regular grid (d₀).

The periodic Voronoi pattern is generated simply by copying these points to adjacent regions and deleting the parts from the squared area. A measure of the degree of irregularity of a Voronoi tessellation can be obtained through:

$\begin{array}{ll}\alpha =1-\frac{\delta }{d_0}& (2)\end{array}$

which informs about the perturbated nature of the pattern.

Perturbation Approach

As discussed by Glaessgen et al. (2003), a Voronoi tessellation is completely determined by the initial location of the seeds. Therefore, an alternative approach (Van der Burg et al., 1997; Fazekas et al., 2002) consists in starting from a regular distribution of seeds to generate a regular Voronoi diagram, i.e., a hexagonal honeycomb system (Figure 3B). This latter approach is assumed in the following sections, since the adoption of a regular initial unit cells allows to simplify the derivation of the relationships of the structural properties and to dominate the original random problem.

Once the regular structure is generated, a small random translation of each nucleus is applied in a restricted area around the initial position. This process allows to assume the nodal coordinates of irregular cells as a perturbated function of the regular cells through a random angle (θ_i), a random scale factor (φ_i) and the irregularity factor (α). According to Li et al. (2005), this leads to:

$\begin{array}{l}{x}_{1,i}={\overline{x}}_{1,i}+\alpha (d_{0}cos{\theta }_i){\phi }_i\\ x_{2,i}={\overline{x}}_{2,i}+\alpha (d_{0}sin{\theta }_i){\phi }_i& (3)\end{array}$

Where,

${\overline{x}}_{1,i}$, ${\overline{x}}_{2,i}$ are the coordinates of the i-th seed of the regular honeycomb.

x_1,i,x_2,i are the perturbated coordinates of the Voronoi grid.

In practice, given a regular starting grid of seeds, the irregular configuration is obtained by arbitrarily disturbing the position of the initial nodes. By increasing or decreasing the range of the scale factor φ_i of a value between 0 and 1 and that of the angle θ_i of a value between 0 and 2π, a Voronoi configuration is generated. Therefore, the final disordered grid has the same number of seeds as the regular configuration and a certain degree of irregularity that strictly depends on the values assumed for the two variables. Examples of this procedure are illustrated in Figure 4.

FIGURE 4

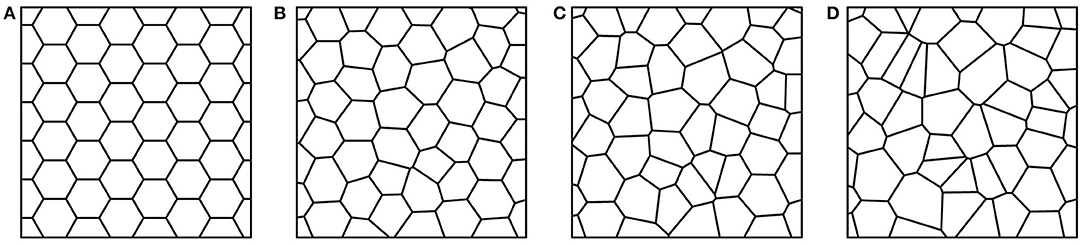
Figure 4. Voronoi tessellation with varying α: (A) regular α = 0, (B) α = 0.5, (C) α = 0.7, and (D) fully random α = 1.

For a regular honeycomb, the distance between two seeds is constant, so δ is equal to d₀, and the level of irregularity α is 0 (Figure 4A). On the other hand, for a fully random Voronoi tessellation, δ is equal to 0 and α = 1(Figure 4D). Any arrangement between these two extreme conditions is admissible as shown in Figure 4B for a Voronoi grid with α = 0.5 and in Figure 4C for a Voronoi grid with α = 0.7.

Effective Mechanical Properties of Voronoi Grid

Several works in the field of materials science have shown that a periodic microstructure, composed of an isotropic linear elastic material, behaves macroscopically as isotropic material.

According to this statement, it can be deduced that the macroscopic mechanical properties, also called “effective properties,” of the cellular structures are influenced by microstructural parameters, e.g., relative density, cell size and cell morphology (Fazekas et al., 2002).

Silva and Gibson (1997) studied the effects of non-periodic microstructure on the compressive failure behavior of Voronoi honeycombs. Their results have shown that cellular materials with random microstructural variations tend to reduce the strength of Voronoi honeycombs by 30–35%, resulting in higher strains.

We analyzed the effects of non-periodic microstructure and defects on the compressive failure behavior of Voronoi honeycombs using finite element analysis. Our results indicate that the non-periodic arrangement of cell walls in random Voronoi honeycombs (with cells approximately uniform in size) results in higher strains in a small number of cell walls compared to periodic, hexagonal honeycombs. Consequently, the Voronoi honeycombs were approximately 30% weaker than periodic, hexagonal honeycombs of the same density.

The difference between elastic behaviors and failures derives from the wider distribution of the local strain of the Voronoi honeycomb, due to the presence of imperfections in the cell geometry, leading to a failure at a lower effective stress (or strain) compared to the periodic case.

Fazekas et al. (2002) studied the effects of cell topology on stiffness and strength properties and found that a disorder in the regular structure leads to an increase of the Young's modulus. They confirmed that the introduction of microstructural perturbation is advantageous in terms of stiffness and detrimental in terms of strength, which drastically decreases as soon as the microstructure loses regularity. In fact, due to the distribution of local stress and strain for a non-regular honeycomb, the first plastic hinge appears at a lower global stress than regular structures.

Li et al. (2005) have generated models that incorporate the effects of two co-existing imperfections: cell shapes and non-uniform cell thickness on the elastic properties of 2D Voronoi grids. He found that the elastic response of the honeycombs is isotropic regardless of changes in the irregularity of the cell shape, the non-uniformity of the cell wall thickness and the relative density. For irregular honeycombs with cell walls of uniform thickness, as the shape of the cells becomes more irregular, on average, the elastic modulus increases considerably, while the Poisson's ratios are insignificantly affected. Also Zhu et al. (2001a) demonstrated that the Young's modulus and the shear modulus increase as the cell irregularity increases, while preserving their isotropic behavior and a Poisson's ratio close to 1. On the other hand, the Young's modulus and the Poisson's ratio of random Voronoi combs with different degrees of regularity α, gradually decrease with increasing relative density ρ.

The mechanical characterization of the regular honeycomb grid and the conversion to the Voronoi-like pattern using the homogenization approach proposed in the literature are presented in this section. The main assumption in the design of irregular grids for tall buildings, indeed, is to consider the Voronoi tessellation as the micro-structure of the perimeter tube, i.e., the macro-structure.

To capture the essential characteristics of the microstructure of a typical cell, extracted from the global Voronoi tessellation, many models have been developed based on idealized unit cells. This allows to reduce computational times and costs, otherwise prohibitive, of micro-to-macro simulations of all the structural members.

The unit cell can easily reproduce the overall geometry of a 2D regular structure through direct replication, however, it cannot predict its mechanical performances, unless manipulations are made on its definition. To this end, the model of a Representative Volume Element (RVE) was developed by the researchers (Hill, 1963), to take into account the geometric properties of the unit cell together with the prediction on deformation and internal forces.

It is clear that the accuracy and applicability of the method strictly depends on the choice of the RVE, which should be both realistic and computationally efficient (Smit et al., 1998; Kouznetsova et al., 2001). Since the RVE numerically simulates the mechanical behavior of the elastic deformations, to evaluate the information on the static behavior of the grid structure and to establish the deformation modes and the internal forces arising in the unit cell, uniaxial compression tests (along two orthogonal directions) and shear tests must be performed.

Although the unit cell-based models have been successfully adopted to simplify periodic honeycomb patterns, providing reliable results with closed-form relations, their applicability toward irregular non-periodic Voronoi geometries is significantly limited, given the disordered nature of the cells. Thus, in the case of irregular grid structures, it is necessary to introduce statistical models to take into account the stochastic nature of the problem. However, as already discussed in section The Voronoi tessellation: geometrical and mechanical properties, the Voronoi grid can be generated from a regular honeycomb grid by perturbing two random variables (θ_i and ϕ_i). This observation suggested Hohe and Beckmann (2012) to introduce a statistically representative Testing Volume Element (TVE) to replace the RVE, which is able to capture only the structural behavior of regular periodic grids.

To evaluate the structural performances of irregular grids, the three main study models are described in detail below, i.e., the unit cell, the Representative Volume Element (RVE) and the Testing Volume Element (TVE).

The Unit Cell

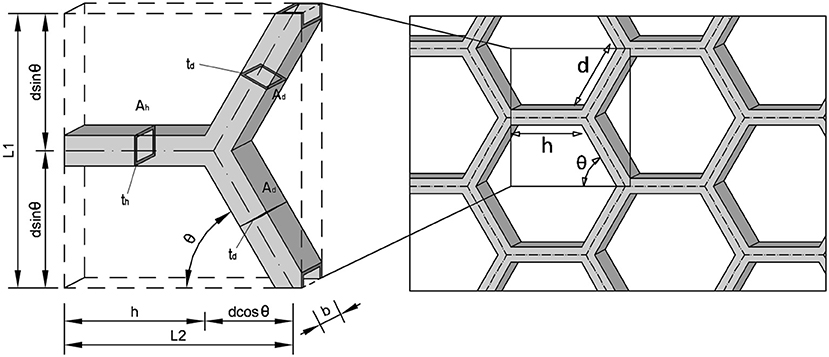
The unit cell, as shown in Figure 5, can be described as a region A₀ containing an elementary geometry capable of reproducing the overall structure through replication, without overlaps or gaps. This repetitive unit is usually a hexagonal cell for 2D systems and cubic, tetrahedral, dodecahedral or tetrakaidecahedral cells for 3D cases.

FIGURE 5

Figure 5. Regular Voronoi with horizontal grid and definition of the unit cell.

An essential geometrical parameter of the unit cell is the relative density ρ, defined as the ratio between the volume occupied by the solid material (ρ*) and the total volume of the unit cell (ρ_vol):

$\begin{array}{ll}\rho =\frac{{\rho }^{*}}{{\rho }_{vol}}=\frac{{\displaystyle {\sum }_{i=1}^N}{t}_i{A}_i}{L_1{L}_{2}b}& (4)\end{array}$

where N is the total number of cell walls, L₁, L₂, and b are, respectively, the vertical and horizontal dimensions and the thickness of the square unit cell, A_i and t_i are, respectively, the section area and the thickness of the i-th grid member, adopting a generic form. Referring to Figure 5, each unit cell is made up of three elements (i.e., an horizontal member and two diagonal members). Therefore, the section A_i assumes in (4) the values of A_h and A_d, respectively, while the thickness t_i assumes the values t_h and t_d, respectively, depending on whether the element under examination is diagonal or horizontal.

The relative density coefficient of the structure informs about the density of the solid material on a prescribed area of the domain. In the case of regular Voronoi honeycombs, the previous relation becomes:

$\begin{array}{ll}{\rho }_H=\frac{h{A}_h+2(d{A}_d)}{\left[(h+dcos\theta )(2dsen\theta )\right]b}& (5)\end{array}$

where

h and A_h are the length and the cross-sectional area of the horizontal element, respectively, d and A_d are the length and the cross-sectional area of the diagonal element, θ is the angle between the diagonal member and the horizon. For the sake of clarity, all the parameters are illustrated in Figure 5.

The Representative Volume Element (RVE)

The RVE model allows to obtain a homogenized macro-response of the mechanical behavior of the global structure, considering only a small portion of it (Nemat-Nasser and Hori, 2013). Because the RVE is representative of the mechanical behavior of the unit cell, uniaxial compression and shear tests must be numerically performed to establish the axial stiffness and shear stiffness modification factors of the honeycomb grid. A Voronoi grid, both regular and irregular is generally a bending dominated structure consisting of short members with high radius of gyration sections and low slenderness ratios. While in the case of slender elements there is only a vertical deflection of the diagonal elements due to bending, when the members become thicker also the axial deformation and the shear deformation must be taken into account.

Axial Stiffness Modification Factor

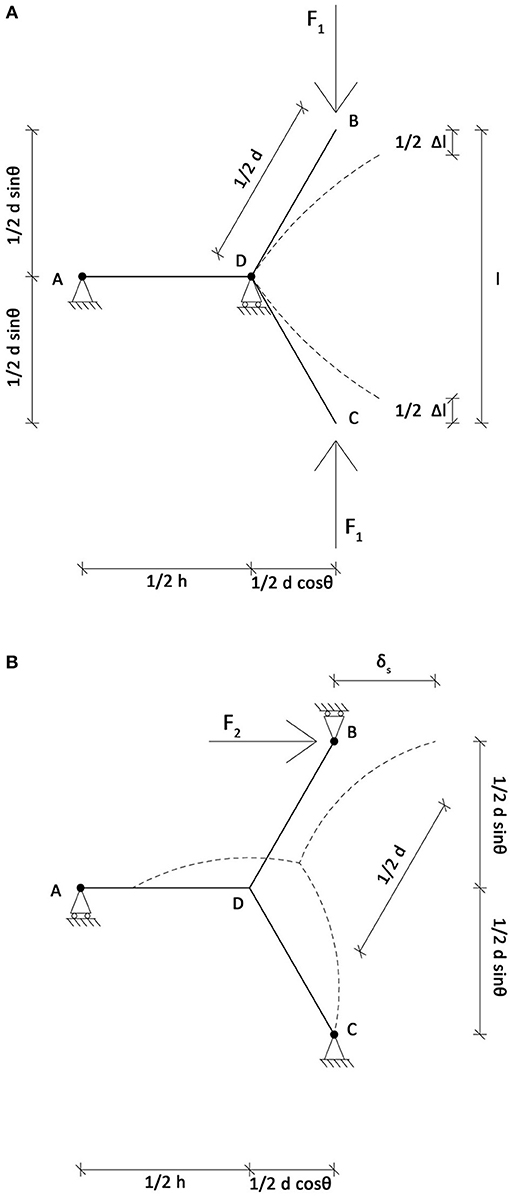
On the left of Figure 6, the diagrams of internal forces of a regular Voronoi grid subjected to uniaxial compression are illustrated. As can be observed, on the horizontal member no bending moments (Figure 6A), axial forces (Figure 6B) and shears (Figure 6C) arise. In the diagonal elements the bending moment in the middle is zero and the value at the ends is maximum.

FIGURE 6

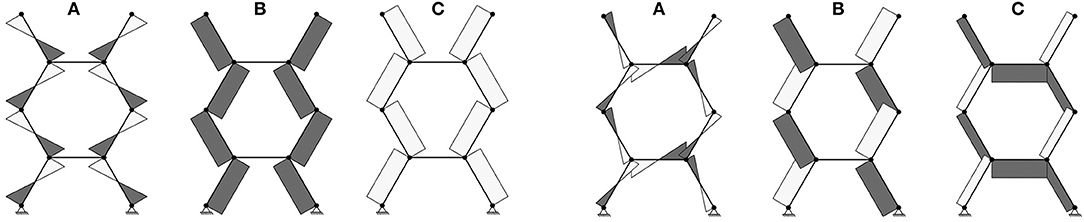
Figure 6. Distribution of (A) bending moment, (B) shear and (C) axial forces under uniaxial compression (left) and under shear load (right).

Basing on the distribution of bending moments, fictitious hinges are modeled at half the length of the diagonal and horizontal elements to reproduce the information obtained on the member deformation modes and the local resisting mechanisms. This schematization converts the unit cell model into a RVE (two half diagonals and one half horizontal), which allows to define the axial modification factors of a regular Voronoi grid through a uniaxial compression test.

According to the Hooke's law, the effective elastic modulus ($E_1^{*}$) is defined as the uniaxial normal stress (σ) divided by the axial strain (ε). The normal stress is the average normal force acting perpendicularly on a surface per unit cross-sectional area and the axial strain is the shortening, or lengthening of the RVE divided by the initial length, l, in the loaded direction:

$\begin{array}{ll}{E}_1^{*}=\frac{\sigma }{\epsilon }=\frac{F_1/A}{(\Delta l)/l}& (6)\end{array}$

To determine the effective axial stiffness, the distributed stress, σ, acting on the unit cell is converted into a concentrated load, F₁, acting at the border of the RVE model (Figure 7A).

FIGURE 7

Figure 7. Uniaxial compression test (A) and shear test (B) schemes on the RVE model.

The global strain (ε) of the RVE in x-direction can be thought as the sum of bending, axial and shear deformations of the structural elements through the superposition principle, divided by half the height of the unit cell, l (with l = d senθ):

$\begin{array}{ll}\epsilon =\frac{\Delta l_{axial}+\Delta l_{shear}{+\Delta l}_{bending}}{l}& (7)\end{array}$

The effective Young's modulus of the unit cell in x-direction, $E_1^{*}$, normalized to the Young's modulus of the solid material E_S, gives the axial stiffness modification factor. Expressing this ratio in terms of geometrical properties of the microstructure leads to de Meijer (2012):

$\begin{array}{ll}\frac{E_1^{\ast }}{E_s}\text{}=\text{}\frac{12A_d{I}_d\sin \theta }{b\left(h+d\cos \theta \right)({\cos }^2\theta (A_d{d}^2+24I_d{\chi }_d\left(1+\nu \right)+12I_d{\sin }^2\theta )}& (8)\end{array}$

where I_d is the moment of inertia of the diagonal member, ν is the Poisson's ratio of the solid material and χ_d is the shear correction factor of the diagonal element.

It is worth noticing here that the horizontal members do not contribute to the definition of the axial stiffness modification factor, since no bending moment, shear forces and axial forces arise from the application of a uniaxial compression load.

2. Shear Stiffness Modification Factors

The derivation of the effective shear stiffness modification factor is worked out analogously to the case of axial stiffness. Axial force, shear force and bending moment diagrams of a regular honeycomb grid under shear load are displayed on the right of Figure 6, showing that bending in the horizontal members is twice the moments in the diagonal elements.

According to the distribution of the bending moments, fictitious hinges are modeled where the bending moments are equal to zero. The effective shear modulus ($G_{12}^{*}$) is defined as the ratio of the shear stress (τ) divided by the shear strain (γ). The shear stress is computed as the applied force divided by the cross-sectional area, while the shear strain is the transverse displacement divided by the initial length, l.

$\begin{array}{ll}{G}_{12}^{*}=\frac{\tau }{\gamma }=\frac{F_2/A}{(\Delta l)/l}& (9)\end{array}$

To determine the shear stiffness, the shear stress τ acting on the unit cell is converted into a concentrated horizontal load, F₂, acting at the border of the RVE model (Figure 7B).

The resulting mechanical model produces a statically indeterminate system. Thus, to calculate the shear displacement at the location and in the direction of the force, the Castigliano' s second theorem is adopted:

$\begin{array}{ll}\delta =\frac{\partial U}{\partial F}& (10)\end{array}$

where the displacements (δ_axial, δ_shear, and δ_bending) are obtained through the partial derivative of the strain energies (U_axial, U_shear and U_bending) with respect to the correspondent forces (F).

The effective shear stiffness of the unit cell $G_{12}^{*}$, normalized to the shear modulus of the member solid material G_S, gives the shear stiffness modification factor. Expressing this ratio in terms of geometrical properties of the microstructure leads to de Meijer (2012):

$\begin{array}{ll}\frac{G_{12}^{*}}{G_s}=\frac{24A_d{A}_h{I}_d{I}_h\sin \theta \left(1+\nu \right)\left(h+d\cos \theta \right)}{\left[\begin{array}{c}12A_h{I}_d{I}_{h}b\cos \theta \left(2dh+\cos \theta \left(d^2+h^2\right)\right)\\ +b{\sin }^2\theta (\left(12A_h{I}_d{I}_h{\chi }_d\left(d^2+2h^2\left(1+\nu \right)\right)\right)\\ +(A_{d}dh(A_{h}h\left(2h{I}_d+d{I}_h\right)+48I_d{I}_h{\chi }_h\left(1+\nu \right))))\end{array}\right]}& (11)\end{array}$

where I_h is the moment of inertia of the horizontal member, χ_h is the shear correction factor of the horizontal element.

The axial stiffness modification factor $\frac{E_1^{*}}{E_S}$ and the shear stiffness modification factor $\frac{G_{12}^{*}}{G_S}$, defined in Equations (8, 11), respectively, depend exclusively on the geometry of the unit cell and the Poisson's ratio of the solid material. These parameters allow to calculate the macroscopic properties of the regular Voronoi grid using a micro-mechanical homogenization approach based on unit cells. Therefore, the effective Young's modulus (E_grid) and the effective shear modulus (G_grid) of the honeycomb depend on the mechanical properties of the microstructure and also on the mechanical properties of the solid structure. It is clear that, in the case of a solid perimeter tube, both the stiffness modification factors are equal to 1 and the effective Young's and shear moduli of the grid are equal to the effective properties of the solid, which leads to:

$\begin{array}{l}{E}_{grid}=\frac{E_1^{*}}{E_s}{E}_s\\ G_{grid}=\frac{G_{12}^{*}}{G_s}{G}_s& (12)\end{array}$

where E_S and G_S are, respectively the elastic and shear moduli of the solid material of which the grid members are made. As already discussed, $(E_1^{*})/E_S$ and $(G_{12}^{*})/G_S$ are the axial and shear stiffness modification factors, respectively and $E_1^{*}$ and $G_{12}^{*}$ are obtained by numerical tests.

In order to adopt the standard equations of the solid tube for the description of the mechanical behavior of the homogenized grid structure, it is necessary to define an effective bending stiffness (EI)_{grid, eff} and an effective shear stiffness (GA)_{grid, eff} of the regular Voronoi grid. This leads to:

$\begin{array}{l}{(EI)}_{grid, eff}=\left(\frac{E_1^{*}}{E_s}{E}_s\right)I_s\\ {(GA)}_{grid, eff}=\left(\frac{G_{12}^{*}}{G_s}{G}_s\right)A_s& (13)\end{array}$

where EI_{grid, eff} and GA_{grid, eff} are the effective bending stiffness and effective shear stiffness of the grid structure, respectively; $\left(E_1^{*}\right)/E_s$ and $\left(G_{12}^{*}\right)/G_s$ are the axial modification factor and the shear modification factor of the grid structure, respectively; E_s I_s and G_s A_s are the bending stiffness and shear stiffness of the corresponding solid, respectively.

Since the effective stiffness of the unit cell is used to determine the stiffness modification factor, this coefficient must take into account the geometrical arrangement of the grid and the connections between the members as well as the geometric and elastic properties of the structural parts.

Modified RVE

As outlined by Montuori et al. (2015), the application of the aforementioned procedure, proposed by de Meijer (de Meijer, 2012), for designing tall buildings with regular honeycomb tessellation, showed significant disagreements with the numerical results obtained through finite element analyses. In particular, this effect was mainly observed on the flange panels, orthogonal to the wind direction, rather than on the web façades, parallel to the wind direction.

To deeply understand this problem, it is convenient to recall here the main assumptions in the design of high-rise buildings. The tall building, indeed, can be conceived as a vertical cantilever beam fixed at the base and subject to wind loads, with two web faces resisting shear forces and two flange faces resisting bending through tension and compression stresses, depending on the direction of loading. It is usually assumed that the floor slabs have infinite in-plane stiffness, constraining perimeter system and core to have the same horizontal deflection. On this assumption, it is possible to employ diaphragm constraints, reflecting real behavior quite well. Since the diaphragm constraint at each slab causes a stiffening effect that reduces the vertical deformation of the overall building, it should be included in the RVE model, paying particular attention to the number of floors present along the unit cell. For this purpose Mele et al. (2016) introduced the so-called Modified RVE model that simply modifies the reference volume element of the regular honeycomb grid to account for the additional constraint of rigid diaphragm.

Since in the present work, all Voronoi models are generated from an initial regular grid, which takes into account unit cells as twice the interstorey height, the equation (8) of the axial stiffness modification factor is modified as follows:

$\begin{array}{ll}\frac{E_1^{*}}{E_s}=\frac{\frac{1}{\left(h+dcos\theta \right)b}}{\left[\frac{1}{A_{d}sin\theta }+\frac{cos\theta \left(\frac{d^2}{12I_d}+\frac{2\chi \left(1+\nu \right)}{A_d}-\frac{1}{A_d}\right)}{A_{d}sin\theta \left(\frac{d^2{sin}^2\theta }{12I_{d}cos\theta }+\frac{2\chi \left(1+\nu \right){sin}^2\theta }{A_{d}cos\theta }+\frac{cos\theta }{A_h}\right)}\right]}& (14)\end{array}$

On the other hand, the shear stiffness modification factor is not affected by the presence of the diaphragm constraint, therefore it is still provided by Equation (11).

It is worth specifying that, since the axial stiffness modification factor strictly depends on the number of floors along the unit cell, the relationship expressed in Equation (14) is closely related to the preliminary modeling assumptions made in this study. In other words, assuming different initial modeling parameters inevitably leads to a variation in the calculation of $\frac{E_1^{*}}{E_s}$.

The Testing Volume Element (TVE)

Since the effective mechanical parameters of the system are determined numerically using a homogenization of the regular honeycomb microstructure, as described up to here, in the case of irregular Voronoi grids a probabilistic strain energy homogenization scheme is required to account for the disordered nature of the unit cells. The approach, first proposed by Hohe and Beckmann (2012) consists in performing a large set of repeated numerical analyses, i.e., axial and shear tests, on small scale models, constructed for each couple of values of density ρ and irregularity α. The Voronoi-like grids are generated through a repositioning of the honeycomb cell walls, assuming a Gaussian distribution for the perturbation. The numerical simulations allow to access the effective mechanical properties of the testing models, in terms of effective axial stiffness of the k-th Voronoi TVE ($E_{1,V,k}^{*}$) and effective shear stiffness ($G_{12,V,k}^{*}$). The correlation of the mechanical properties of irregular Voronoi tessellations with those of regular honeycombs can be reached through appropriate correction factors (Montuori et al., 2016):

$\begin{array}{ll}{\eta }_{E_i}=\frac{E_{i,V}^{*}}{E_{i,H}^{*}},{\eta }_{G_{ij}}=\frac{G_{ij,V}^{*}}{G_{ij,H}^{*}}& (15)\end{array}$

where the subscripts H and V refer, respectively, to the regular and irregular Voronoi grid.

Because the effective mechanical properties of the Voronoi grid structure strictly depend on the level of irregularity α, the relative density ρ, the random angle θ_i and the random scale factor ϕ_i, it is straightforward to notice that the modification factors are functions of these parameters as well.

Voronoi Pattern for Tall Buildings

Preliminary Design Procedure

In order to make the mechanical property equations, described in section Effective mechanical properties of Voronoi grid, relevant to the purpose of the paper, it is necessary to include them inside standard relations for preliminary design of tall buildings.

This section deals with the analytical model assumptions, which we refer to in common practice, and illustrate a hand calculation method to determine preliminary section sizes for Voronoi-like grids under stiffness requirements. The following procedure has been already proposed by other authors (de Meijer, 2012; Mele et al., 2016; Montuori et al., 2016), however it is recalled here for the sake of clarity.

The method considers the building as a vertical cantilever. This simplification makes the problem statically determinate and allows calculating the global deformations as the sum of two contributes: bending deformation (δ_bending) and shear deformation (δ_shear):

$\begin{array}{l}{\delta }_{TOT}={\delta }_{bending}+{\delta }_{shear}\end{array}$

with

$\begin{array}{l}{\delta }_{bending}=\frac{q{H}^4}{8EI}\end{array}$

and

$\begin{array}{ll}{\delta }_{shear}=+\frac{q{H}^2}{2GA}\chi & (16)\end{array}$

where q is the wind lateral load, H is the height of the cantilever beam, i.e., of the building, A is the cross-sectional area, E is the Young's modulus, I is the moment of inertia, G is the shear modulus and χ is the shear factor.

This latter approach was introduced by Kwan (1994) for framed tubes and considers the overall structure as a box beam with web and flange panels, with uniform stiffness throughout the building height.

Kwan compared the structural analysis of grid structures with a corresponding solid of the same width, height, and depth, as the grid-like structure. The Young's modulus of the solid is the same as the modulus used for the individual members of the grid structure; the same material is used in both the grid and the solid. Shear and bending deformations contribute to total building deflection through:

$\begin{array}{ll}{\delta }_{TOT}={\delta }_{bending}+{\delta }_{shear}=\frac{q{H}^4}{8{(EI)}_{grid}}+\frac{q{H}^2}{2{(GA)}_{grid}}\chi & (17)\end{array}$

(EI)_grid and (GA)_grid represent, respectively the effective bending stiffness and the effective shear stiffness of the regular Voronoi grid that, according to Equations (13, 15), are evaluated through:

$\begin{array}{l}\begin{array}{l}E{I}_{grid}= (E_{1,H}^{*} {\eta }_{E_1}) I_s\hfill \end{array}\\ G{A}_{grid}=(G_{12,H}^{*}{\eta }_{G_{12}}) A_s& (18)\end{array}$

Because in tall buildings, drift problems related to lateral loads are a dominant issue, so controlling lateral displacement becomes fundamental. In order to estimate lateral displacements, the top drift (Δ) parameter is considered and compared to the limit state set by codes. Drift Δ corresponds to the maximum top displacement with respect to the base:

$\begin{array}{ll}\Delta =u_{top}-u_{base}\le H/500& (19)\end{array}$

where u_top and u_base are the displacements of the top and the base, respectively, and H is the total height of the building.

The resulting equation (18) can be used to determine preliminary section sizes while accompanying horizontal displacements. The relation takes into account the characteristics of the patterns through homogenization procedures and therefore is applicable to any structural pattern.

Case Study

The reference structure assumed for the case study is 351 meters high with a 36 × 36 m doubly symmetric plan, an 18 × 18 m steel gravity core and a typical story height of 3.9 m. The central core (inner tube) is a rigid steel braced frame structure and occupies almost 25% of the total floor (Figure 8F).

FIGURE 8

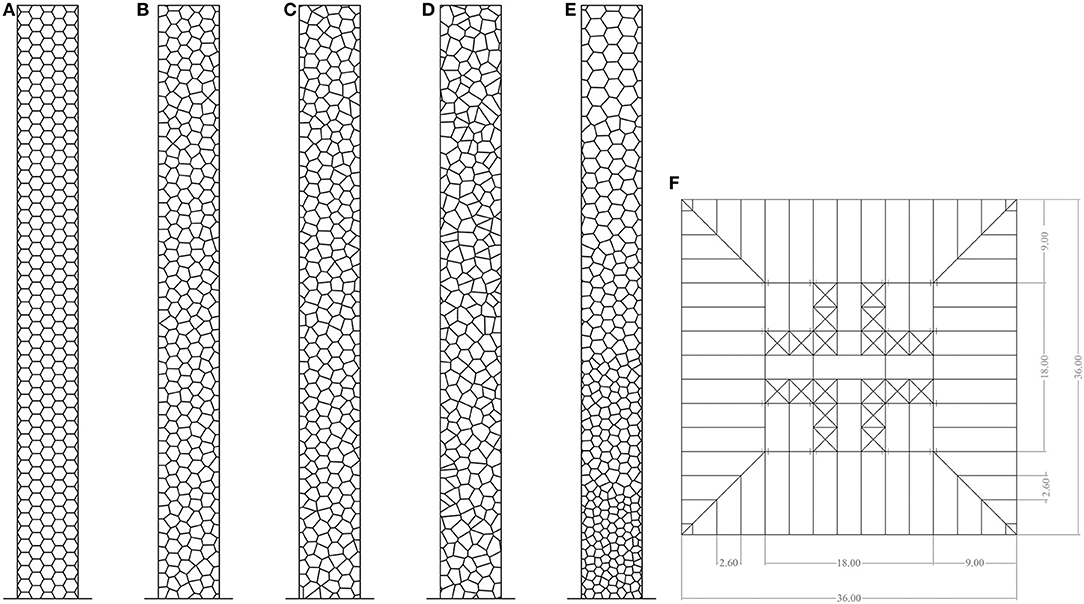
Figure 8. Building model: (A) Regular hexagrid (α = 0.0), (B) Voronoi grid with α = 0.3, (C) Voronoi grid with α = 0.7, (D) Voronoi grid with α = 1.0, (E) Voronoi grid with varying density ρ and (F) plan dimensions.

The outer and inner systems collaborate in resisting both lateral and gravity loads. Floor slabs are placed between the two tubes. It is usually assumed that the floor slabs have infinite in-plane stiffness, constraining outer tube and core to have the same horizontal deflection.

On this assumption, slabs are modeled as thin concrete shell elements between the floor beams and a diaphragm constraint is employed. The perimeter Voronoi pattern is assumed S275 steel material (with f_yk = 275 N/mm²), as also the framed core members and the framing floor structures.

Support conditions are assumed to be fixed. The connections between the exoskeleton and the inner core are provided with adequate plan-bracings to allow for the transmission of shear stresses (induced by horizontal loads) between the two systems.

The wind load is established according to ASCE 7–05 (Minimum Design Loads for Buildings and Other Structures) provisions. The building is assumed to be within category III, with a basic wind speed of 50 m/s. The lateral wind load is statically applied to the framework as horizontal point-loads on the diaphragms of each floor. Live loads of 2.0 kN/m² are applied as uniformly distributed on the floor slab.

Pattern Generation Through Parametric Modeling

The need to explore alternative Voronoi-grid designs requires the use of parametric modeling software, which allows speeding up the procedure and managing complex geometries simply modifying its governing parameters.

To this end, models are generated in Grasshopper environment (Rhinoceros 3D).

The pattern construction follows the theoretical procedure described in section The Voronoi tessellation: geometrical and mechanical properties gradually altering the coordinates of regular equidistant points to obtain an irregular tessellation.

This approach results particularly convenient in the present case, as it allows dealing with several irregular cell arrangements starting from a single regular reference model.

It is well-known that the Voronoi's diagram, based on a regular distribution of points, results in a honeycomb grid. Therefore, once the rectangular domain is set (351 × 36 m), which represents the building façade, the radius of each hexagon and the total number of hexagons in the x-direction and y-direction must be defined, this allows identifying the centers of the hexagons, i.e., the seeds of the Voronoi grid. Because in the present case each hexagon is two story height (7.8 m) and the total number of hexagons along the rectangular width is set to 5, radius is calculated accordingly.

Each of these generated points undergoes a random translation and rotation in the 2D space, according to a random angle (θ_i) and a random scale factor (φ_i). Although the alteration of the seed locations is completely random, the range of maximum and minimum variation is included in a user-defined domain, which allows controlling the grid variation. The random angle is defined on the domain [0; 2π] and the random scale factor on the domain [−h; h], where h represents the story height.

Increasing or reducing the range of the scale factor φ_i and that of the angle θ_i leads to different irregularity degrees (α_i), whereas the variation in the number of seed points along the building width causes changes in the relative density (ρ_i).

Consequently the Voronoi-grid is generated through the Grasshopper component “Voronoi,” which creates the final tessellation, providing the initial rectangle boundaries as an extreme limit for the pattern. Four Voronoi-grid alternatives are generated assuming 6 seeds in the x-direction (i.e., assuming a constant ρ): models with α = 0.0 (Figure 8A), α = 0.3 (Figure 8B), α = 0.7 (Figure 8C), and α = 1.0 (Figure 8D).

Numerical and Theoretical Results

The effectiveness of the hand calculation formula proposed by Montuori et al. (2016) for the design of tall buildings with structural systems constituted by irregular patterns are investigated and comparisons with the numerical results obtained through a finite element analysis are made.

Using standard deflection formulae for a cantilever beam and referring the bending and shear stiffness of the grid to an equivalent orthotropic membrane fixed at the base, Equation (18) can be rewritten as:

$\begin{array}{ll}{\delta }_{TOT}=\frac{q{H}^4}{8(E_{1,H}^{\ast }{\eta }_{E_1})I_s}+\frac{q{H}^2}{2(G_{12,H}^{\ast }{\eta }_{G_{12}})A_s}\chi \le \frac{H}{500}& (20)\end{array}$

where χ is the shear correction factor of the solid cantilever beam. According to Young (1989), an approximate shear factor for box beams can be set to 1.0 when considering only the area of web panels in the calculation of the building cross-sectional area.

For the hand calculations, a uniform distributed wind load q is applied, which is converted to concentrated loads acting at each floor when checking the model with the finite element program.

According to the ASCE design code and assuming as a reference the Chicago area, the wind load q is set equal to 394.06 kN.

The main advantage of Equation (20) is that the mechanical characteristics of the building with a Voronoi-like grid can be entirely assessed from the regular hexagrid, simplifying the procedure. In fact, once the irregular grid is generated by perturbating the initial honeycomb pattern, all parameters relating to building geometry (H, χ, I_s, A_s, E_s) and hexagonal grid $\left(E_{1,H}^{*},G_{12,H}^{*}\right)$ are known.

The influence of grid geometry on the global behavior of the homogenized structure is taken into account through correlation factors. It is quite evident that in the case of a regular honeycomb pattern, both η_E1 and η_G12 equal to one. As already discussed in section Effective mechanical properties of Voronoi grid, these correlation factors are evaluated on a statistical basis through axial and shear tests on a set of randomly generated specimens. Further information on the calculation of the correction factors and the related equations are provided in the reference (Mele et al., 2016).

The correction factors are strictly dependent on the regular grid geometry, i.e., its module height, the number of floors contained in it and the angle between the members and it is sufficient to calculate them only one time. Because each specimen is obtained by perturbating a regular honeycomb grid, the whole set accounts for different couples of α and ρ, thus, including copious variations of the grid arrangement.

The simulation strategy is performed according to the steps described below.

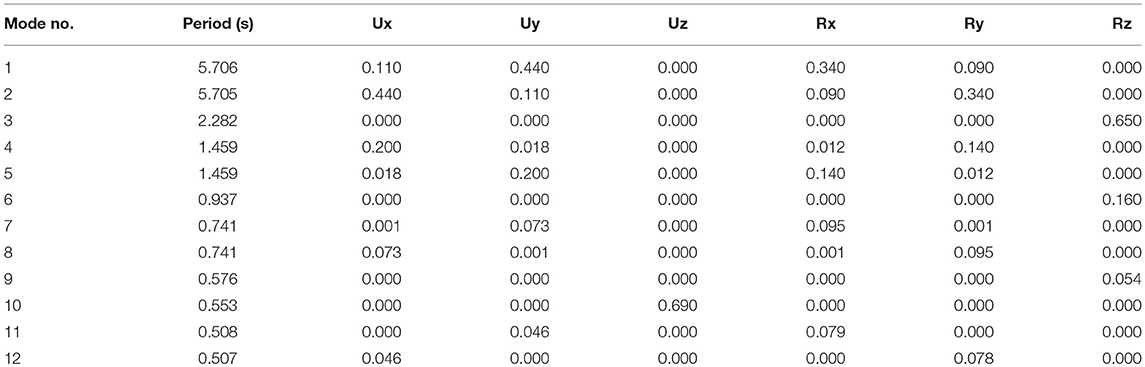
The regular honeycomb grid (α = 0.0) is assumed as a reference model and proper parameters are entered in Equation (20) to obtain preliminary cross-sections and perform the static analyses. Since the correction factors η_E1 and η_G12 are equal to 1 for hexagonal grids and $E_{1,H}^{*}$, and $G_{12,H}^{*}$ are computed as described in section Effective mechanical properties of Voronoi grid, a steel box section of 1,300 × 1,300 × 160 mm is obtained iteratively. Adopting a constant cross-section for all the grid members, a finite element analysis is performed for the honeycomb, which produces a displacement of 0.436 m.

In order to evaluate the influence of micro-structural parameters on the mechanical properties of the tall building, i.e., relative density ρ and irregular degree α, the same cross section adopted for the regular honeycomb case, is used here for models with varying irregular factor.

Starting from hexagonal grid, several TVE specimens are generated, which possess the same overall geometry and number of unit cells but variable relative density value and different degrees of irregularity. The specimens have been modeled as assemblies of Timoshenko beam elements, for each one two axial tests (along x-and y- directions) and a shear test are performed using the finite element program. The results obtained are acquired and elaborated using the relations in Mele et al. (2016).

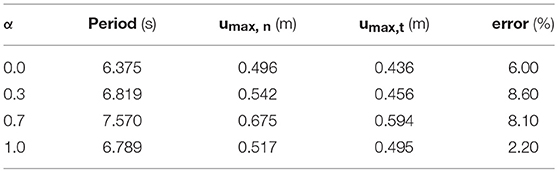
From hand calculations emerges that irregular grid models with α = 0.3, α = 0.7, and α = 1.0 exhibit lateral displacements of 0.456, 0.594, and 0.495 m, respectively.

The structures, designed using these preliminary sections, are analyzed through finite element analyses to assess the global behavior and validate the correctness of the theoretical method. A preliminary serviceability check is carried out considering the top drift. Codes set the limit state at H/500, corresponding to 0,702 m in the case-study. The inter-story drift parameter δ is also considered in this study and is defined as the difference between the maximum displacements of two subsequent floors:

$\begin{array}{ll}\delta ={\delta }_{\text{i}}-{\delta }_{\text{i}-1}<h_i/300& (21)\end{array}$

where h_i represents the relative floor height. Inter-story drift ratio along the building is assumed equal to h/300, corresponding to 0,013 m. Both targets are shown in the following figures with vertical lines.

Figure 9 provides the deflection curves of the regular and irregular grid structures with respect to building height.

FIGURE 9

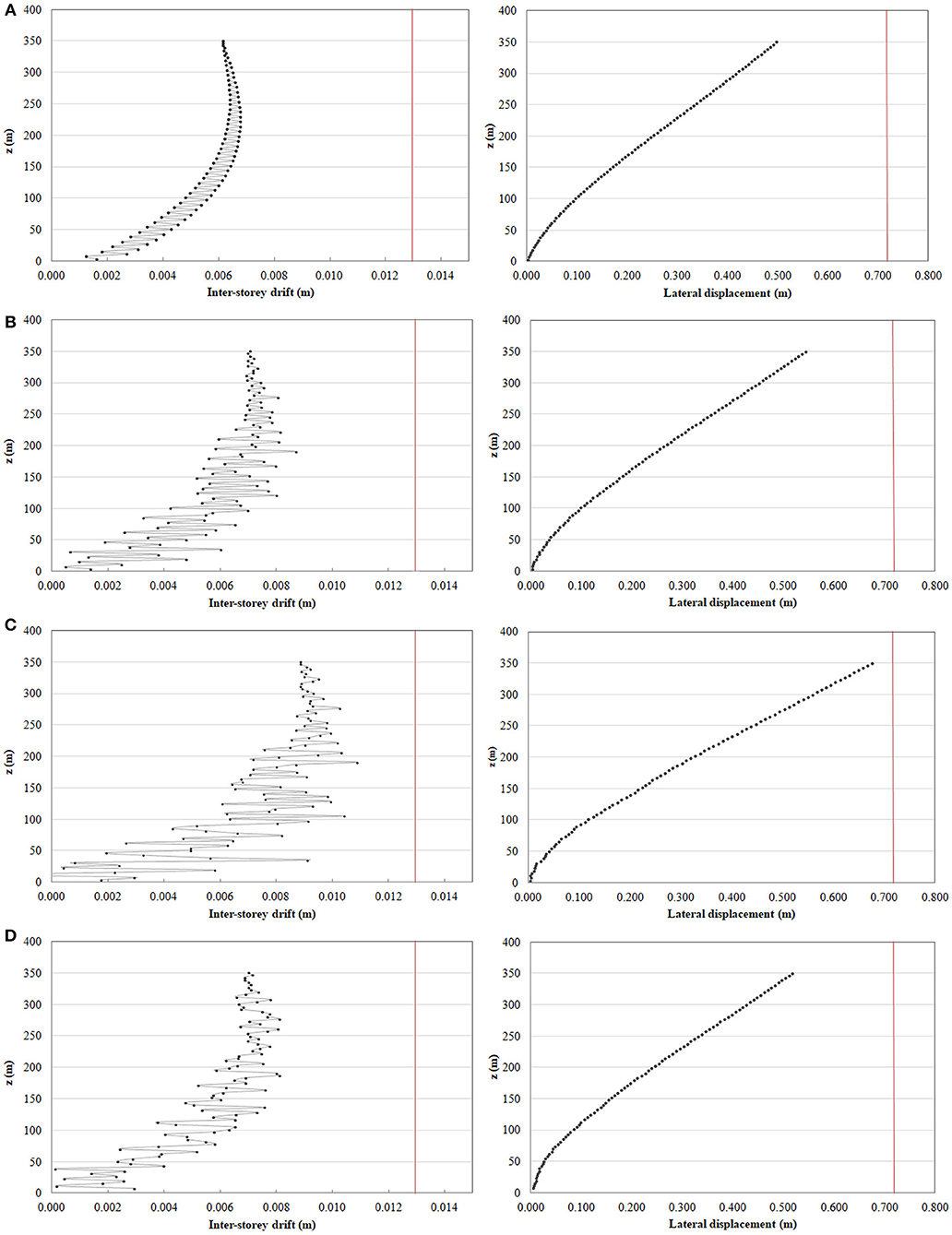
Figure 9. Inter-story drifts (on the left) and lateral displacements (on the right) under wind forces: (A) regular hexagrid model with α = 0.0, (B) model with α = 0.3, (C) model with α = 0.7 and (D) model with α = 1.0.

For all the cases investigated in this study, more than the 90% of the total lateral displacement is caused by bending deformation. Results obtained from numerical analyses and hand calculations (as shown in Table 1) differ from 2.2 to 8.6% with an overestimation of the top displacements for the analytical method, this demonstrates that the approximate preliminary design procedure is reliable and quite accurate. The differences between results, in fact, are reasonable if one considers that the methodology does not consider the contribution of the central core, which inevitably contributes to the overall lateral stiffness. However, the method allows assessing immediate evaluations of the effects of varying geometrical and mechanical parameters on the overall structural behavior. It can be also used for manual checking of the computer analysis results.

TABLE 1

Table 1. Comparison of numerical and analytical results.

Changing Density Voronoi Tessellation

As already observed by Angelucci and Mollaioli (2017) for diagrid structures, a changing density along the height of the building allows for gradual lateral stiffness change with uniform distribution along the building height, without developing sudden rigidity peaks. In fact, authors demonstrated that, despite considerable weight reduction, a local density increment is not an efficient strategy in restraining top displacement within the targets. More efficient solutions involve a varying pattern density, rarefying the diagonal members from the base toward the top of the building. A similar approach allows for gradual lateral stiffness change with uniform distribution along the building height, without developing sudden rigidity peaks.

The same strategy of allocating stiffness demand by form, rather than by section size, is adopted here for tube structural systems with Voronoi tessellation in order to investigate the influence of pattern gradation on the mechanical properties of the tall building. To this end, an additional Voronoi pattern with a rarefying grid along the height is provided (Figure 8E), basing on mechanical and modeling considerations. This solution accounts for a variable relative density ρ that increases toward the base and reduces toward the top (according to the bending distribution of a cantilever beam) while keeping a fixed irregularity factor α.

Among all the patterns analyzed, the one with an irregularity of 0.3 is evaluated as the best compromise, having an acceptable easy-to-modify geometry while exhibiting a satisfying lateral stiffness

The initial grid with constant irregularity is split into five modules along the height and a perturbation method is adopted, which assigns a varying relative density from the base to the top (Figure 8E). Density variation is assessed by progressively increasing the number of generation seed along the width of the building from 9 to 5.

The model is initially analyzed adopting, for all the members, a constant cross-section of 1,300 × 1,300 × 160 mm, in order to estimate potential performance improvements with respect to models with fixed density. Comparing maximum displacement results emerges that, for a given irregularity (α = 0.3), the solution with varying density pattern along the height (Figure 10A) develops higher stiffness than a constant density configuration (Figure 9B). The strength check, performed for the changing density model under gravity and imposed later loads, shows a section utilization lower than 50% for the grid members. The analyses, in fact, demonstrate that the adoption of a uniform cross-section for the varying density grid (total weight equal to 216,963.07 ton), equivalent to that of the regular density model (total weight equal to 190,160.02 ton), leads to overestimate strength and stiffness requirements.

FIGURE 10

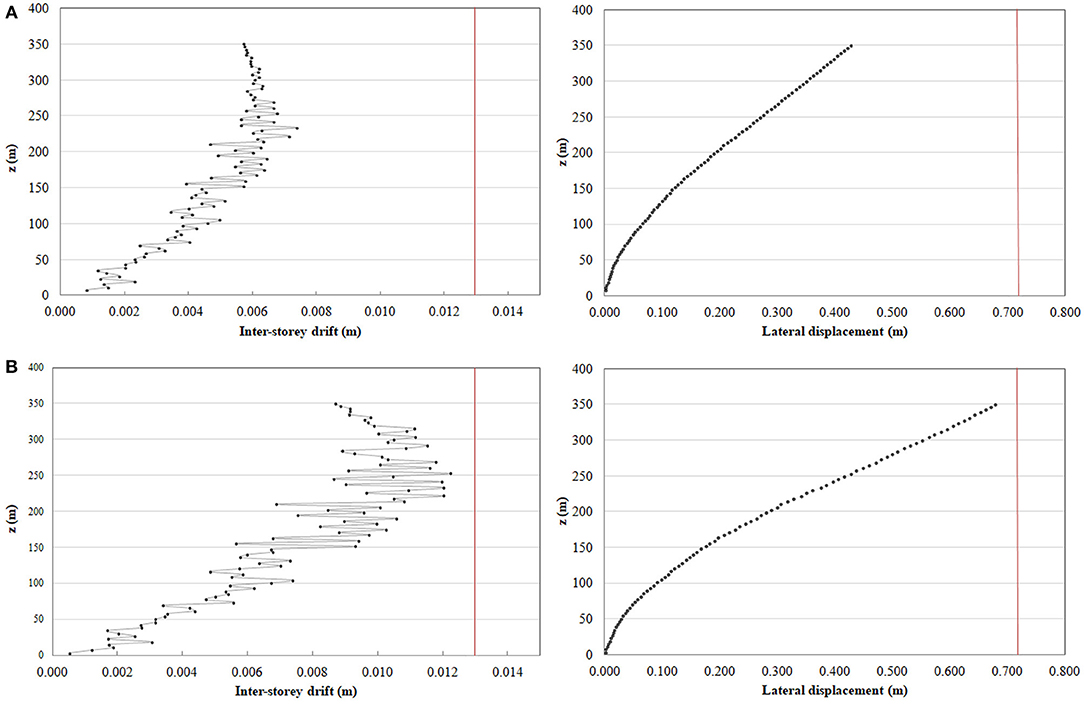
Figure 10. Inter-story drifts (on the left) and lateral displacements (on the right) under wind forces: varying density Voronoi pattern with constant cross-sections (A) and optimized cross-sections (B).

This consideration suggests the employment of an iterative member minimization technique to increase the cross-section utilization while satisfying a prescribed displacement.

Member Size Optimization

The iterative design process is carried out within SAP2000 program routine to check adequacy of member cross-sections for each design load combination (CSI, 2007). The program automatically design the optimal least weight section according to the envelope of the member demand to capacity ratios (DCR).

The program calculates the flexural, axial, and shear forces at several locations along the length of a member, and then compares those calculated values with acceptable limits prescribed by the design code. This comparison produces a demand/capacity ratio, i.e., a measure of the acceptability of the member section, which should not exceed a prescribed maximum value. In this case, the demand to capacity ratio is set equal to 80%, which represents the maximum allowable cross-section utilization.

The program also checks the other requirements on a pass or fail basis. If the capacity ratio remains less than or equal to the D/C ratio limit, the section is considered to be adequate; otherwise the section is considered to have failed. Thus, each structural member on the perimeter is designed to satisfy its most critical stress state under lateral loading conditions (strength-based member optimization).

In practice, model height is split into modules and a section list is assigned to every group. The program can automatically evaluate each section in the list and select the most economical and least weight section that passes checks. The only constraint imposed by the user is that all the members of a single module must match identical cross sections. This tremendously reduces the computational time of the optimization routine and allows simplifying the problem. Due to the high concentration of members on the perimeter, a full size optimization process cannot be carefully monitored by the user and, moreover, such a large number of steel sections is actually unfeasible and uneconomical to be built.

The cross-sections obtained by the iterative optimization, imposing a demand-to-capacity ratio (DCR) of 80% and a displacement limit of 0.7 m, are: 1,300 × 1,300 × 120 mm for the bottom module, 1,300 × 1,300 × 100 mm for the second module, 1,300 × 1,300 × 90 mm for the third module, 1,300 × 1,300 × 70 mm for the fourth module and 1,300 × 1,300 × 50 mm for the top module.

The adoption of optimized cross-sections provides a structural weight reduction from 216,963.07 ton when uniform member sections are assumed to 136,527.25 ton when optimized cross-sections are used. The steel utilization is drastically reduced of around 40%, which highlights the economic advantages of the size optimization routine.

Analyses and Checks

The structural system is designed to render its response elastic under most load conditions. The design of high-rise buildings must assess three criteria: serviceability (related to human comfort), strength and stability. The strength requirements are checked through the member demand to capacity ratio (DCR). Serviceability is satisfied by limiting drifts, and stability by a sufficient factor of safety against buckling and P-Delta effects.

In order to estimate lateral displacements, two drift parameters are considered: top drift (Δ) and inter-story drift (δ). Member forces are calculated by a second-order non-linear elastic analysis, which allows evaluating the effects of the loads acting on the equilibrium of the deformed geometry of the structure. A rigorous second order analysis or an amplification of first order analysis results are often required by standard design codes to estimate the effect of second order effects. In the first case, the required strengths are determined directly from the analysis results without any amplification factor. However, to properly capture the P-δ effect in a finite element analysis, each element, especially column elements, must be broken into multiple finite elements, which is not convenient for other analysis purposes.

To overcome the issue of discretizing each structural member, the P-Delta analysis is based on amplification of responses from first-order analysis for calculating the required flexural strengths. The second order behavior is accounted for in the static analysis, by creating a static non-linear load case for each load combination.

Relative inter-story drifts and maximum lateral displacements of the Voronoi pattern using optimized cross-sections are plotted in Figure 10B. The charts show an increase of relative and absolute drift values. Because the displacement growth provides indications on stiffness distribution along the height, it can be clearly observed that the reduction of grid cross-section sizes results in a decrease of the global lateral stiffness. However, if one considers the optimal solution as the one that meets stiffness demand with the highest material saving, it is easy to demonstrate that the model with varying pattern density and changing section sizes along the height represents the most efficient solution among all the analyzed cases.

Seismic BEHAVIOR of the Voronoi Grid

The seismic design of tall buildings has advanced significantly in the last years. This growing recognition is mainly due to the fact that current building codes generally refer only to conventional low- or medium-rise buildings. Such structures are designed for strength requirements and their seismic response is typically dominated by the first translational mode of vibration of the structure.

Otherwise, tall building response is strongly influenced by their complex dynamic behavior, since higher modes of vibration may be more important than the first. Higher modes, in fact, can result in higher flexural and shear demands. Neglecting these requirements during the design stage can lead to excessive damage, large residual deformations and possible collapses. The seismic lateral forces, indeed, can produce critical stresses in the structure and cause excessive lateral oscillations.

The efficiency of the perimeter tube system with Voronoi tessellation for tall buildings is studied under earthquake loading. Indeed, in addition to the wind loading scenario, the building model is subjected to earthquake ground motion as a further test to demonstrate the potential of the varying density Voronoi pattern (described in the previous section). The building is assumed to be in Istanbul, which is a region of the Anatolian fault. Due to its location, Istanbul is particularly vulnerable to damaging levels of seismic hazards, making it imperative to include seismic load in the design of the high-rise building. In the design process the Design Basis Earthquake (DBE) is taken into account, which is defined as the site dependent ground motion with 10% probability of exceedance in 50 years. For more detailed information about the design spectrum adopted to perform the response spectrum analysis, see the reference (Erdik et al., 2011).

A response spectrum analysis is performed. The design dead load is assumed to be 7.0 kN/m² and live loads of 2.0 kN/m² are applied as uniformly distributed on the floor slabs.

To evaluate the seismic performance of the Voronoi model, a seismic combination accounting for the gravity loads and the equivalent static loads due to the earthquake ground motion, obtained through the response spectrum analysis, is performed. The results obtained are expressed in terms of inter-story drift, story deflection, and modal parameters. The response spectrum method of seismic analysis informs how the building response characteristics vary with the structure frequency and allows to predict displacements and member forces in the structural system.

The high vulnerability to the lateral load of the selected area can be considered comparable to that of the previous case located in Chicago. In fact, although different actions are considered, i.e., earthquake on one side and wind on the other, in a preliminary phase it is legitimate to assume for the pattern Voronoi of the building located in Istanbul the identical sections of beams obtained from pre-sizing with wind loading. This assumption also makes it possible to compare the different behavior of the building according to the load and determine which is the worst condition.

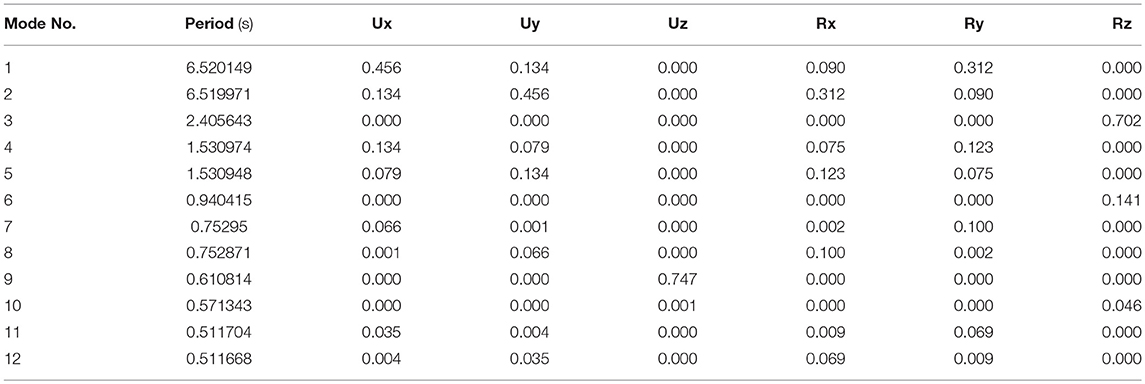
The building is analyzed assuming a square box cross-sections (1,300 × 1,300 × 160 mm) for all the grid members. The results of the modal analysis are plotted in Table 2.

TABLE 2

Table 2. Results of the modal analysis for the model with constant member cross-sections.

The outcomes of the lateral displacements and inter-story drifts, obtained from the response spectrum analysis, are shown in Figure 11A with consideration of second order effects, as explained in the previous paragraph. The charts illustrate that the model exhibits a maximum top displacement of 0.63 m and a maximum inter-story drift of 0.010 m.

FIGURE 11

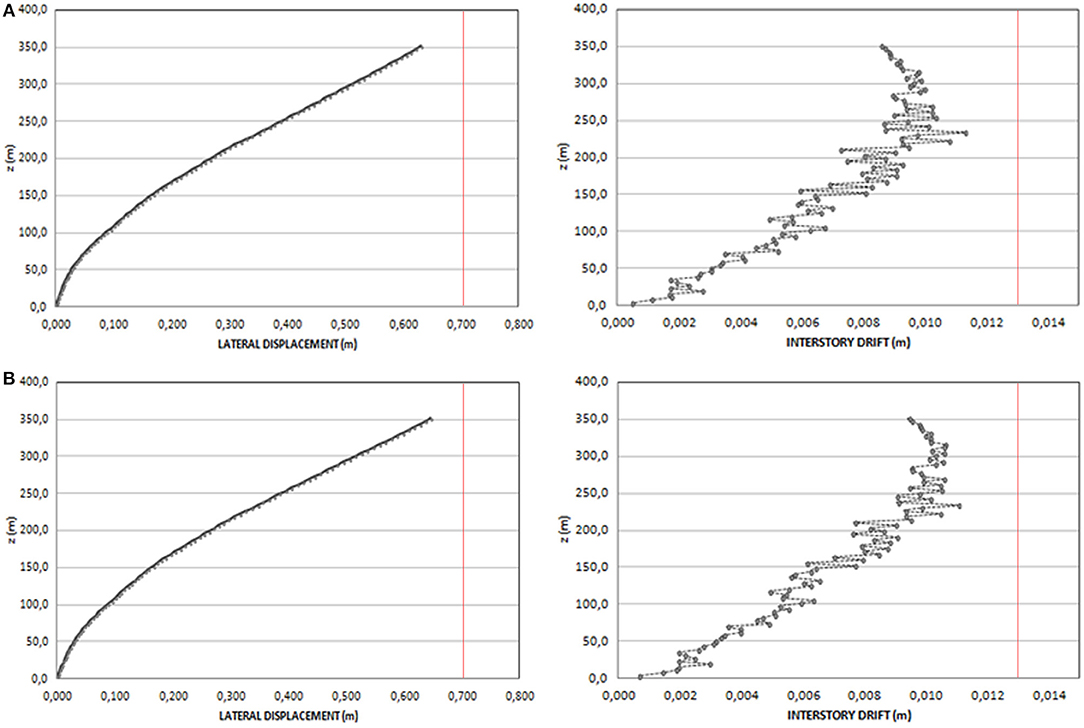
Figure 11. Lateral displacements (on the left) and inter-storey drifts (on the right) under seismic load: varying density Voronoi pattern with constant cross-sections (A) and optimized cross-sections (B).

This confirms that the preliminary design of the structural system, which takes into account the uniform distributed wind load, provides reliable cross-sections, even in the case of seismic areas.

A comparison between the effects of the earthquake ground motion and those of the wind load can be assessed in terms of base shear and base overturning moments to provide further information on the main differences during the preliminary design stage. The maximum shear and overturning moment computed at the base of the building are 2,527.13 MN and 56,927.24 MNm, respectively, when the model is subjected to wind action plus vertical loads. On the other hand, the maximum shear and overturning moment computed at the base of the building are 1,547.13 MN and 37,141.35 MNm, respectively, when the model is subjected to earthquake ground motion plus gravity loads.

Analogously to the wind scenario, a member size optimization is performed to assess the most economical and least weight sections that meet the prescribed strength and displacement requirements under the seismic load combination. The cross-sections obtained by the iterative optimization, imposing a demand-to-capacity ratio (DCR) of 80% and a displacement limit of 0.7 m, are: 1,300 × 1,300 × 140 mm for the bottom module, 1,300 × 1,300 × 120 mm for the second module, 1,300 × 1,300 × 100 mm for the third module, 1,300 × 1,300 × 90 mm for the fourth module and 1,300 × 1,300 × 70 mm for the top module. The adoption of optimized cross-sections provides a remarkable reduction of the structural weight of about 30%. The results of the modal analysis are plotted in Table 3.

TABLE 3

Table 3. Results of the modal analysis for the model with optimized member cross-sections.

Inter-story drifts and lateral displacements of the Voronoi pattern with changing density using optimized member sections are illustrated in Figure 11B. The charts show maximum values of 0.011 m and 0.65 m for the inter-story drifts and the lateral displacements, respectively. Despite a small reduction of the global stiffness with respect to the non-optimized configuration, the Voronoi model with optimized members still exhibit the best solution in terms of section utilization (i.e., strength requirements) and drift control (i.e., stiffness requirements).

Comparing the results obtained for the same building located in Istanbul (area of high seismicity) with those obtained in the Chicago area (high wind load), it emerges that the preliminary design according to seismic requirements is more stringent than that of the wind. This allows to observe that, despite the tall buildings are particularly vulnerable to the wind action given their high slenderness, in areas of high seismic hazard it is essential to take this aspect into consideration as well.

Conclusions

The paper investigates the potentialities of non-regular grids for structural systems of tall building on the global mechanical behavior, particularly; the study concentrates on periodic and non-periodic Voronoi tessellation.

The work deals with the generation procedure of Voronoi-like patterns through parametric modeling, gradually perturbating a regular honeycomb configuration. Since the mechanical response of the building strongly depends on the geometric parameters of the microstructure, the paper focuses on the influence of the grid arrangement on the global lateral stiffness of the perimeter tube, thus on the displacement constraint, which is an essential requirement in the design of tall buildings. To this end, five case studies, representing different levels of irregularity and relative densities, are generated and analyzed through static and modal analysis in the elastic field.

To appreciate the consistency of the preliminary design equations proposed in the literature, the numerical and analytical results are compared. An error lower than 10% occurs for hand calculations. However, if the contribution of the central core to the lateral stiffness is neglected, this margin is even lower. It can be concluded that the method proposed by the literature is rather accurate and represents a useful tool to simultaneously appreciate the variation of mechanical performance when modifying grid arrangements. The results show that, at the same density rate, cell irregularity does not significantly affect the building performance in terms of lateral stiffness, even though they provide higher displacements than the regular honeycomb configuration.

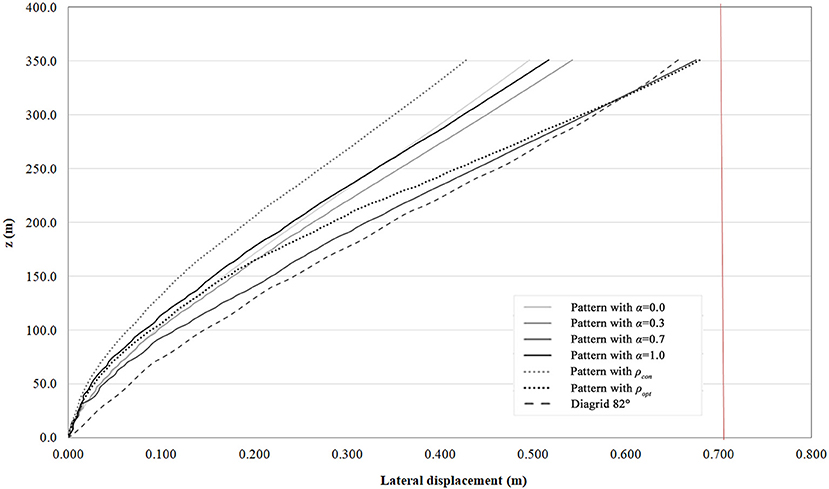
Outcomes of the maximum displacement for the Voronoi grid models are compared in Figure 12.

FIGURE 12

Figure 12. Comparison of lateral displacements under wind forces of the analyzed models.

It emerges that the model with a gradual increasing density toward the base and a constant cross-section (ρ_con) possesses the highest lateral stiffness. On the other hand, the case with changing density and optimized cross-section (ρ_opt), obtained through displacement-based size minimization, exhibits the maximum top drift. However, it represents the best compromise between strength and displacement requirements, while providing a significant weight reduction of the structural members at the same time.

It has been demonstrated that a gradual rarefying density pattern is a suitable strategy for tall buildings with a Voronoi-like grid, due to the higher efficiency in containing top displacements within specific targets. Moreover, the chart is integrated with the results obtained for a regular diagrid structure with optimized cross-sections and a diagonal inclination of 82°, in order to have a comparable number of five modules as the Voronoi model with varying density. Although a direct comparison on the material usage is meaningless, due to the non-comparable number of structural members, from a mechanical point of view it can be observed that the diagrid stiffness performance results of the same order as Voronoi-like grid models.

In addition to the wind loading scenario, the efficiency of the building model with varying density Voronoi pattern, is tested for seismic ground motion through a response spectrum analysis. The results obtained assuming constant cross-sections for all the grid members are compared with those achieved using optimized cross-sections, leading to a remarkable reduction of the structural weight of about 30%.

In conclusion, the paper confirms the potential applications of Voronoi tessellation for tall buildings, demonstrating that the innovative irregular patterns represent a valid alternative to conventional grid, for both regions with high wind load conditions and areas of high seismicity. For this reason their application to tall building designs should be further investigated and encouraged.

Author Contributions

FM contributed to the selection of the topic and the solution of various structural issues. GA contributed to the analyses and to the optimization issue.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

This work was partially supported by the Italian Ministry of Instruction, University and Research (MIUR). This support is gratefully acknowledged. Any opinions, findings, and conclusions or recommendations expressed in this paper are those of the authors and do not necessarily reflect those of the sponsor. Finally, the contribution of the reviewers is greatly acknowledged.

Footnotes

1. ^http://www.evolo.us/a-city-within-a-skyscraper-for-battery-park/

2. ^http://www.l-a-v-a.net/projects/bionic-tower/

References

Angelucci, G., and Mollaioli, F. (2017). Diagrid structural systems for tall buildings: changing pattern configuration through topological assessments. Struct. Design Tall Special Build. 26:e1396. doi: 10.1002/tal.1396

CrossRef Full Text | Google Scholar

Beghini, L. L., Beghini, A., Katz, N., Baker, W. F., and Paulino, G. H. (2014). Connecting architecture and engineering through structural topology optimization. Eng. Struct. 59, 716–726. doi: 10.1016/j.engstruct.2013.10.032

CrossRef Full Text | Google Scholar

CSI (2007). Steel Frame Design Manual. (C. and Structures, Ed.). (Berkeley, California Inc.).

de Meijer, J. (2012). Lateral Stiffness of Hexagrid Structures. Eindhoven University of Technology.

Google Scholar

Erdik, M., Sesetyan, K., Demircioglu, M. B., and Yenidogan, C. (2011). Assessment of Site-Specific Earthquake Hazard for The Kartal dr. Lütfi kirdar training and research state hospital in Istanbul.

Fazekas, A., Dendievel, R., Salvo, L., and Bréchet, Y. (2002). Effect of microstructural topology upon the stiffness and strength of 2D cellular structures. Int. J. Mech. Sci. 44, 2047–2066. doi: 10.1016/S0020-7403(02)00171-6

CrossRef Full Text | Google Scholar

Gibson, L. J. (2005). Biomechanics of cellular solids. J. Biomech. 38, 377–399. doi: 10.1016/j.jbiomech.2004.09.027

PubMed Abstract | CrossRef Full Text | Google Scholar

Glaessgen, E., Phillips, D., Iesulauro, E., Saether, E., and Piascik, R. (2003). “A multiscale approach to modeling fracture in metallic materials containing nonmetallic inclusions,” in 44th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference (Norfolk), 1616. doi: 10.2514/6.2003-1616

CrossRef Full Text | Google Scholar

Hill, R. (1963). Elastic properties of reinforced solids: some theoretical principles. J. Mech. Phys. Solids 11, 357–372. doi: 10.1016/0022-5096(63)90036-X

CrossRef Full Text | Google Scholar

Hohe, J., and Beckmann, C. (2012). Probabilistic homogenization of hexagonal honeycombs with perturbed microstructure. Mech. Mater. 49, 13–29. doi: 10.1016/j.mechmat.2012.01.010

CrossRef Full Text | Google Scholar

Khan, F. R. (1969). “Recent structural systems in steel for high-rise buildings,” in Proceedings of the British Constructional Steelwork Association Conference on Steel in Architecture (London), 67–78.

Kouznetsova, V. G., Brekelmans, W. A. M., and Baaijens, F. P. T. (2001). Approach to micro-macro modeling of heterogeneous materials an approach to micro-macro modeling of heterogeneous materials. Comput. Mech. 27, 37–48. doi: 10.1007/s004660000212

CrossRef Full Text | Google Scholar

Kwan, A. K. H. (1994). Simple method for approximate analysis of framed tube structures. J. Struct. Eng. 120, 1221–1239. doi: 10.1061/(ASCE)0733-9445(1994)120:4(1221)

CrossRef Full Text | Google Scholar

Li, K., Gao, X. L., and Subhash, G. (2005). Effects of cell shape and cell wall thickness variations on the elastic properties of two-dimensional cellular solids. Int. J. Solids Struct. 42, 1777–1795. doi: 10.1016/j.ijsolstr.2004.08.005

CrossRef Full Text | Google Scholar

Mele, E., Fraldi, M., Montuori, G. M., and Perrella, G. (2016). “Non-conventional structural patterns for tall buildings : from diagrid to hexagrid and beyond,” in Fifth International Workshop on Design in Civil and Environmental Engineering, October6-8, 2016 (Rome: Sapienza University of Rome Representative).

Google Scholar

Montuori, G., Perrella, G., Fraldi, M., and Mele, E. (2016). “Micro-mega - nature inspired structural patterns for tall buildings : modeling, analysis, design,” in Structures and Architecture: Beyond their Limits, ed P. J. da Sousa Cruz (CRC Press), 173–1180. doi: 10.1201/b20891-161

CrossRef Full Text

Montuori, G. M., Fadda, M., Perrella, G., and Mele, E. (2015). Hexagrid–hexagonal tube structures for tall buildings: patterns, modeling, and design. Struct. Design Tall Special Build. 24, 912–940. doi: 10.1002/tal.1218

CrossRef Full Text | Google Scholar

Moon, K. S. (2010). Stiffness-based design methodology for steel braced tube structures: a sustainable approach. Eng. Struct. 32, 3163–3170. doi: 10.1016/j.engstruct.2010.06.004

CrossRef Full Text | Google Scholar

Moon, K. S., Connor, J. J., and Fernandez, J. E. (2007). Diagrid structural systems for tall buildings: characteristics and methodology for preliminary design. Struct. Design Tall Special Build. 16, 205–230. doi: 10.1002/tal.311

CrossRef Full Text | Google Scholar

Nemat-Nasser, S., and Hori, M. (2013). Micromechanics: Overall Properties of Heterogeneous Materials. Amsterdam: Elsevier, Ed.

Google Scholar

Silva, M. J., and Gibson, L. J. (1997). The effects of non-periodic microstructure and defects on the compressive strength of two-dimensional cellular solids. Int. J. Mech. Sci. 39, 549–563. doi: 10.1016/S0020-7403(96)00065-3

CrossRef Full Text | Google Scholar

Smit, R. J. M., Brekelmans, W. A. M., and Meijer, H. E. H. (1998). Prediction of the mechanical behavior of nonlinear heterogeneous systems by multi-level finite element modeling. Comput. Methods Appl. Mech. Eng. 155, 181–192. doi: 10.1016/S0045-7825(97)00139-4

CrossRef Full Text | Google Scholar

Taranath, S. D., Mahantesh, N. B., and Patil, M. B. (2014). Comparative study of pentagrid and hexagrid structural system for tall building. J. Civil Eng. Environ. Technol. 1, 10–15.

Google Scholar

Vajjhala, S., Kraynik, A. M., and Gibson, L. J. (2000). A cellular solid model for modulus reduction due to resorption of trabeculae in bone. J. Biomech. Eng. 122, 511–515. doi: 10.1115/1.1289996

PubMed Abstract | CrossRef Full Text | Google Scholar

Van der Burg, M. W. D., Shulmeister, V., Van der Geissen, E., and Marissen, R. (1997). On the linear elastic properties of regular and random open-cell foam models. J. Cell. Plastics 33, 31–54. doi: 10.1177/0021955X9703300103

CrossRef Full Text | Google Scholar

Voronoi, G. (1908). ouvelles applications des paramètres continus à la théorie des formes quadratiques. Deuxième mémoire. Recherches sur les parallélloèdres primitifs. J. Für Die Reine Angew. Math. 134, 198–287.

Google Scholar

Wigner, E., and Seitz, F. (1933). On the constitution of metallic sodium. Phys. Rev. 43:804. doi: 10.1103/PhysRev.43.804

CrossRef Full Text | Google Scholar

Young, W. (1989). Roark's Formulas for Stress and Strain, 6th Edn. (New York, NY, McGraw-Hill, Ed.).

Zhu, H. X., Hobdell, J. R., and Windle, A. H. (2001a). Effects of cell irregularity on the elastic properties of 2D Voronoi honeycombs. J. Mech. Phys. Solids 49, 857–870. doi: 10.1016/S0022-5096(00)00046-6

CrossRef Full Text | Google Scholar

Zhu, H. X., Thorpe, S. M., and Windle, A. H. (2001b). The geometrical properties of irregular two-dimensional Voronoi tessellations. Phil. Mag. A Phys. 81, 2765–2783. doi: 10.1080/01418610010032364

CrossRef Full Text | Google Scholar