Cyclic Fractional Plastic Model for Granular Soils

Introduction

According to many experimental (Aursudkij et al., 2009; Nimbalkar et al., 2012; Nimbalkar and Indraratna, 2016; Sun et al., 2017a, 2018e) and numerical (de Bono and McDowell, 2014; McDowell and Li, 2016; Li et al., 2018) studies, it is widely recognized that granular soils, including sand, ballast and rockfill, usually exhibit complex strength and deformation behavior, such as contraction accompanied by strain hardening and dilation accompanied by strain softening, when subjected to static and dynamic loads. Correct representation of such complex behavior of granular soils is the key factor for the design and safe operation of engineering facilities, for example, railroad and retaining wall (Nimbalkar and Choudhury, 2008; Nimbalkar et al., 2018). Hence, a number of different approaches, e.g., elastoplasticity, viscoplasticity, damage-plasticity, and bounding surface plasticity has been proposed. The models can be divided into three categories: (i) models that did not consider state dependence; (ii) models that cannot reflect non-associated flow; (iii) models that were not suitable for cyclic loading. For category (i), a number of constitutive methods can be found, for example, the disturbed state concept by Desai and Toth (1996) which was adopted for constitutive modeling of rockfills (Varadarajan et al., 2006) under different confining pressures; the damage-plasticity concept (Einav et al., 2007; Sun et al., 2015a), the diffuse failure models by Daouadji et al. (2011), the micromechanical models by Yin et al. (2010, 2017), the fractional cumulative models (Sun et al., 2015b, 2016a,b), the bounding surace models (Dafalias, 1986; Sun et al., 2014, 2017b; Sun and Shen, 2017). Some other models captured the state dependence but fall within category (ii), for example, the elastoplastic models by Sun et al. (2013, 2018c,f). In addition, most monotonic models cannot appropriately simulate the cyclic behavior of soil without modification on material flow and hardening, and thus fall within category (iii), for example, the state-dependent plastic models (Gajo and Muir Wood, 1999b; Li and Dafalias, 2000; Einav et al., 2007; Sun and Xiao, 2017; Sun et al., 2018d, 2019a).

To capture the state-dependent non-associated plastic behavior of sand, Been and Jefferies (1985) firstly suggested the concept of state dependence for sands, which was then promptly developed in various constitutive models (Li and Dafalias, 2000; Yang and Li, 2004; Sun et al., 2018a,b,c, 2019a). However, most of these models usually assumed a plastic flow rule that was only suitable for monotonic loads. For more complex loading conditions, for example, the cyclic loading case, more work needs to be carried out. In addition, classical constitutive models (Gajo and Muir Wood, 1999b; Imam et al., 2005; Collins et al., 2010) were usually dependent on the assumption of an additional plastic potential function, in order to correctly capture the non-associated stress-strain behavior of granular soils under either monotonic or cyclic loads. Is there a possible way to capture the state-dependent non-associated behavior of granular soils without using additional plastic potential? Sumelka (2014a,b) suggested the incorporation of fractional-order derivatives into classical associated plasticity, from which a non-associated plastic flow rule can be achieved, without using additional plastic potential. However, the approach did not consider the physical practice in geomaterials, thus cannot reflect the underlying strength and deformation mechanisms of granular soil, unless proper modifications have been made. By connecting the state-dependent stress-dilatancy phenomenon with fractional plastic flow rule, a family of fractional plasticity models has been developed and applied in characterizing the non-associated stress-strain behavior of granular soil (Sun et al., 2017c, 2018b,c,d,f, 2019b,c). As demonstrated, the directions of plastic flow are no longer necessarily normal to the yielding or potential surfaces. However, these models did not consider the flow and hardening differences between loading, unloading and reloading, thus cannot properly capture the cyclic behavior of granular soils.

In fact, unlike the integer order derivative usually used in classical plasticity, the fractional order derivatives are non-local which induces a strong memory of the loading stress σ. Therefore, by using fractional derivative, the plastic flow of a material point was not only determined by the current stress state but also by its loading history. The size of the history and collection of yielding information are dependent on the employed definition of the derivative, for example, the Riesz-Caputo definition used by Sumelka and Nowak (2016) and the Riemann-Liouville definition used by Sun et al. (2016b). The choice of whatever fractional operator should rely on the specific physical issues is to be taken into consideration.

However, the present fractional plasticity models were mainly based on monotonic fractional flow rule, and cannot be used for capturing the cyclic behavior of granular soils, without possible modifications. Unlike monotonic models (Gajo and Muir Wood, 1999a; Li, 2002; Yang and Li, 2004), the plastic flow behavior and hardening/softening behavior loading, unloading and reloading should be different. Thus, the previous fractional plasticity model cannot properly capture the cyclic behavior of granular soils. To extend the fractional plasticity approach, a possible extension of the previous fractional plastic flow rule and hardening modulus for monotonic loading should be carried out. In contrast to previous works (Sun et al., 2018d, 2019c), this paper presents a simplified fractional-order elastoplastic model for granular soils subjected to cyclic loads, based on a general fractional plastic flow rule suitable for both monotonic and cyclic loads, which is the main innovation of this study. The study is structured as follows: section Definition of Fractional Derivative presents the basic definition of the fractional derivatives, while section Constitutive Model presents the basic constitutive relations; section Calibration of Model Parameters discusses how to identify each model parameters, while section Model Performance validates the proposed model; section Conclusions concludes the study by summarizing several main findings.

Definition of Fractional Derivative

To begin, it is necessary to present a clear definition of the fractional derivative being used. According to the theory of fractional calculus, the fractional derivatives of the loading and unloading dynamic processes are different. In previous studies (Sun and Shen, 2017; Sun and Xiao, 2017), only the triaxial behavior of granular soils subjected to monotonic loading was considered. Therefore, only the left-sided Caputo fractional derivative with moving upper terminal (loading stress, σ′) and fixed lower terminal (initial stress state, ${{\sigma }^{\prime }}_0$) was introduced in constitutive modeling. However, in this study, both the loading and unloading behaviors in triaxial tests will be addressed. The left-sided fractional derivative is suitable for describing the loading and unloading states of a material under triaxial compression where the deviator stress q > 0, while the right-sided fractional derivative is an operator performed on the loading and unloading states of a material subjected to triaxial extension where the deviator stress q < 0. Therefore, in this study, both the left-sided and right-sided Caputo's fractional derivatives (Agrawal, 2007) of a function f are used, such that:

$\begin{array}{cc}{}_a{D}_x^{\alpha }f(x)=\frac{1}{\text{Γ}(n-\alpha )}{\displaystyle \underset{a}{\overset{x}{\int }}\frac{f^{(n)}(\tau )d\tau }{{(x-\tau )}^{\alpha +1-n}}},x>a& (1)\end{array}$

$\begin{array}{cc}{}_x{D}_b^{\alpha }f(x)=\frac{{(-1)}^n}{\text{Γ}(n-\alpha )}{\displaystyle \underset{x}{\overset{b}{\int }}\frac{f^{(n)}(\tau )d\tau }{{(\tau -x)}^{\alpha +1-n}}},b>x& (2)\end{array}$

where D means derivation; Γ denotes the gamma function, defined as $\text{Γ}(x)={\int }_0^{\infty }{e}^{-\tau }{\tau }^{x-1}d\tau$. a and b are the lower and upper terminals used for integration. x is an independent variable and is designated as loading stress, σ, in this study. The fractional order, α, ranges from n−1 to n, where n = 1 or 2. Clearly, the fractional derivative is defined on an interval that is contrary to the integer order differential operators defined at a single point. Therefore, due to this non-locality, fractional approach in this study would intrinsically memorize the cyclic loading history.

Constitutive Model

In this study, only homogeneous and isotropic materials loaded under triaxial stress conditions are under consideration, where compressive stress and strain are regarded as positive. All the stresses used for derivation are effective stresses unless otherwise specified. Therefore, the following triaxial stress notations can be given:

$\begin{array}{cc}\begin{array}{lll}{\text{ε}}^e& =& {\left[{\epsilon }_v^e,{\epsilon }_s^e\right]}^T\end{array}& (3)\end{array}$

$\begin{array}{cc}\begin{array}{lll}{\text{ε}}^p& =& {\left[{\epsilon }_v^p,{\epsilon }_s^p\right]}^T\end{array}& (4)\end{array}$

where ε indicates strain tensor for triaxial loading while the superscripts, e and p, indicate elastic and plastic components, respectively. The total volumetric (ε_v) and shear (ε_s) strains can be, respectively, defined as:

$\begin{array}{cc}\begin{array}{lll}{\epsilon }_v^{}& =& {\epsilon }_1^{}+2{\epsilon }_3^{}\end{array}& (5)\end{array}$

$\begin{array}{cc}\begin{array}{lll}{\epsilon }_s^{}& =& 2({\epsilon }_1^{}-{\epsilon }_3^{})/3\end{array}& (6)\end{array}$

where ${\epsilon }_1^{}$ and ${\epsilon }_3^{}$ are the first and third principal strains, respectively. The total strain tensor ε = ε^e+ε^p, while the effective stress tensor, σ′, can be expressed as:

$\begin{array}{cc}\begin{array}{l}\text{σ}={\left[p^{\prime },q\right]}^T\end{array}& (7)\end{array}$

where the mean effective principal and deviator stresses can be, respectively, defined as:

$\begin{array}{cc}\begin{array}{lll}{p}^{\prime }& =& ({{\sigma }^{\prime }}_1+2{{\sigma }^{\prime }}_3)/3\end{array}& (8)\end{array}$

$\begin{array}{cc}\begin{array}{lll}q& =& {{\sigma }^{\prime }}_1-{{\sigma }^{\prime }}_3\end{array}& (9)\end{array}$

in which ${{\sigma }^{\prime }}_1$ and ${{\sigma }^{\prime }}_3$ are the first and third effective principal stresses, respectively. In this study, calculation of the elastic stress and strain response is based on the traditional theory of elasticity. However, the plastic strain is determined by using fractional plasticity (Sun and Xiao, 2017). A fundamental difference between classical and fractional plasticity is the calculation of the incremental plastic strain. In classical plasticity, the incremental plastic strain tensor, ${\stackrel{\bullet }{\text{ε}}}^p$, is obtained by:

$\begin{array}{cc}\begin{array}{l}{\stackrel{\bullet }{\text{ε}}}^p=\text{Λ}{D}^{1}f(\text{σ})\end{array}& (10)\end{array}$

where a superimposed dot indicates increment. Λ is the plastic multiplier and f often denotes the plastic potential or yielding function, depending on the flow rule that is chosen. Due to the equivalence between the first-order derivative and the classical differentiation of a point, the derivative interval in Equation (10) is omitted for clarity. As can be expected from Equation (10), the direction of plastic flow is fixed at each stress point once the function f is given. However, the plastic flow of granular soil varies with soil types. A plastic flow rule without considering the varied plastic flow was usually not able to unified modelling of the constitutive behavior of granular soils. Therefore, a flow rule for granular soils modified by using fractional-order differential operator was proposed (Sun and Shen, 2017; Sun and Xiao, 2017) where the incremental plastic strain tensor, ${\stackrel{\bullet }{\text{ε}}}^p$, can be determined by:

$\begin{array}{cc}\begin{array}{l}{\stackrel{\bullet }{\text{ε}}}^p=\text{Λ}{D}_{}^{\alpha }f(\text{σ})\end{array}& (11)\end{array}$

where the modified Cambridge (Schofield and Wroth, 1968) relation (f) is used in this study for simplification:

$\begin{array}{cc}f={(2p^{\prime }-{p^{\prime }}_0)}^2+{\left(\frac{2q}{M}\right)}^2-{{\displaystyle p^{\prime }}}_0^2=0& (12)\end{array}$

where ${p^{\prime }}_0$ is the intercept of f with the abscissa. M = 6sin φ_c/(3t−sinφ_c), is the critical-state stress ratio under triaxial compression. t = +1 for compressive loading whereas t = −1 for extensive loading. According to Sun and Xiao (2017), the plastic strain can be expressed as:

$\begin{array}{cc}\begin{array}{l}{\stackrel{\bullet }{\text{ε}}}^p=\frac{1}{\text{Π}}{\text{m}}^T\text{n}\stackrel{\bullet }{\text{σ}}\end{array}& (13)\end{array}$

where the generalized flow direction (n) can be expressed as:

$\begin{array}{cc}\begin{array}{l}\text{n}={\left[n_v^{},n_s^{}\right]}^T\end{array}& (14)\end{array}$

in which n_v and n_s are the flow directions induced by compression and shearing, respectively. Due to the distinct formulae of the fractional derivatives in describing loading and unloading, a generalized plastic flow rule suitable for both cases can be derived by substituting Equation (12) into Equations (1) and (2) (Sun et al., 2018a), such that:

$\begin{array}{cc}{n}_v=t\frac{8\left[p^{\prime }-(2-\alpha ){p^{\prime }}_0/2\right]{p^{\prime }}^{1-\alpha }}{\text{Γ}(3-\alpha )\Vert D^{\alpha }f({\sigma }^{\prime })\Vert }& (15)\end{array}$

$\begin{array}{cc}{n}_s=t\frac{8M^{-2}{\left|q\right|}^{1-\alpha }}{\text{Γ}(3-\alpha )\Vert D^{\alpha }f({\sigma }^{\prime })\Vert }& (16)\end{array}$

where the gradient, ||D^αf(σ′)||, is defined as:

$\begin{array}{cc}\Vert D^{\alpha }f({\sigma }^{\prime })\Vert =\frac{8}{\text{Γ}(3-\alpha )}\sqrt{{\left(\frac{q^{1-\alpha }}{M^2}\right)}^2+{\left[p^{\prime }-\left(1-\frac{\alpha }{2}\right){p^{\prime }}_0\right]}^2{p^{\prime }}^{2-2\alpha }}& (17)\end{array}$

The stress-dilatancy relationship for loading and unloading can be therefore obtained by using Equations (16) and (17), where the classical modified Cam-clay stress-dilatancy relationship can be also achieved by using α = 1. Detailed derivations of Equations (15) and (16) can be found in Sun et al. (2018a) and thus not repeated here for simplicity. In addition, the loading tensor m is assumed to be the same as the flowing tensor, such that:

$\begin{array}{cc}\begin{array}{lll}{m}_v& =& t\frac{d}{\sqrt{1+d_{}^2}}\end{array}& (18)\end{array}$

$\begin{array}{cc}\begin{array}{lll}{m}_s& =& t\frac{1}{\sqrt{1+d_{}^2}}\end{array}& (19)\end{array}$

where the dilatancy ratio d can be defined as:

$\begin{array}{cc}\begin{array}{l}d=\frac{M_{}^2-(1-\alpha /2)\left[{\eta }^2+M_{}^2\right]}{t{\left|\eta \right|}^{2-\alpha }}\end{array}& (20)\end{array}$

The hardening modulus Π should satisfy the following conditions according to Li (2002): (i) Π = +∞ when the stress ratio η = q/p′ = 0, (ii) Π = 0 when specimens are at the critical and drained peak stress states. Therefore, the loading plastic modulus Π can be expressed as:

$\begin{array}{cc}\begin{array}{l}\text{Π}=h_{L}G\frac{t{\eta }_p-\eta }{\eta }{e}^{m\psi }\end{array}& (21)\end{array}$

where m is a model constant; the shear modulus (G) is defined as:

$\begin{array}{cc}\begin{array}{l}G=G_0\frac{{(2.97-e)}^2}{1+e}{p}_a\sqrt{\frac{p^{\prime }}{p_a}}\end{array}& (22)\end{array}$

in which G₀ is the elastic modulus of the material and

$\begin{array}{cc}\begin{array}{l}{h}_L=(h_1-h_2\psi )\end{array}& (23)\end{array}$

where h₁ and h₂ are hardening parameters. The state parameter ψ is defined as

$\begin{array}{cc}\begin{array}{l}\psi =e-e_c\end{array}& (24)\end{array}$

where e is the current void ratio; e_c is the critical-state void ratio that can be expressed as (Li and Wang, 1998):

$\begin{array}{cc}\begin{array}{l}{e}_c=e_{\text{Γ}}-\lambda {(p^{\prime }/p_a)}^{\xi }\end{array}& (25)\end{array}$

where λ, e_Γ, and ξ are critical state parameters, describing the critical state line in the e−p′^ξ plane. It should be noted that the current model does not explicitly consider the particle breakage behavior of granular soil. But, as evidenced by laboratory tests (Bandini and Coop, 2011; Ghafghazi et al., 2014; Yu, 2017a,b), the influence of particle breakage on the mechanical behavior of granular soil was reflected by shifting the critical state line in the e−ln p′ plane. To capture this behavior, numerous critical state lines incorporating particle breakage in the e−ln p′ plane were proposed. However, as suggested in Li and Wang (1998), a linear representation of the critical state line in the e−p′^ξ plane can be simply used to implicitly consider the particle breakage, which had been used by a number of researchers, including Gajo and Muir Wood (1999a,b) and Dafalias and Taiebat (2016), etc.

Moreover, a slight difference of the hardening parameter is found between the current and previous study (Sun and Xiao, 2017) where h_L was correlated to the initial ψ₀ and e₀ rather than the evolution of the current ψ and e. However, one may not be able to know the initial ψ₀ and e₀ of soils that have been already sheared. In such cases, the modification shown in Equation (23) works. η_p is the virtual peak stress ratio, which can be correlated to the state parameter as:

$\begin{array}{cc}\begin{array}{l}{\eta }_p=M{e}^{-m\psi }\end{array}& (26)\end{array}$

For reloading, the plastic modulus can be further expressed as:

$\begin{array}{cc}\begin{array}{l}\text{Π}=h_L{h}_{C}G\frac{t{\eta }_p-\eta }{\eta }{e}^{m\psi }{\left(1+\frac{tM}{\eta }\right)}^n\end{array}& (27)\end{array}$

where $h_C=e^{-r{\epsilon }_v}$, is the densification factor, considering accumulation of strain caused by loading and reloading; and n and r are material constants, which are only used for capturing cyclic loading. For undrained loading condition, ε_v = 0, the plastic modulus is not affected by h_C, as suggested by Ling and Yang (2006). Hence, the dependence of material hardening on the material density occurs via its dependence on ψ.

To characterize the unloading behavior of granular soils, the unloading plastic modulus by Ling and Yang (2006) is used:

$\begin{array}{cc}\begin{array}{l}\text{Π}=h_U{h}_{C}G{\left(\frac{M}{{\eta }_U}\right)}^{\vartheta }\end{array}& (28)\end{array}$

where h_U and ϑ are model parameters. η_U is the stress ratio at which the unloading occurs. For tests with |M/η_U| ≤ 1, ϑ = 0

To consider the elastic deformation during loading and unloading, the hyperelasticity is used to determine the elastic incremental strain, such that:

$\begin{array}{cc}\begin{array}{l}{\stackrel{\bullet }{\text{ε}}}^e={\text{C}}^e:\stackrel{\bullet }{\text{σ}}\end{array}& (29)\end{array}$

where C^e is the elastic compliance tensor:

$\begin{array}{cc}{C}^e=\left[\begin{array}{cc}1/K& \\ & 1/(3G)\end{array}\right]& (30)\end{array}$

where the bulk modulus (K) can be defined as:

$\begin{array}{cc}\begin{array}{l}K=\frac{(2+2\nu )}{3(1-2\nu )}G\end{array}& (31)\end{array}$

where ν is the Poisson's ratio, describing the lateral deformation capability of the material. Thus, a complete description of the elastoplastic stress-strain behavior of granular soils under cyclic loads can be achieved, by using Equations (13) and (29).

Calibration of Model Parameters

There are in total 14 model parameters, i.e., four critical state parameters (φ_c, λ, e_Γ, ξ), one fractional order (α), seven hardening parameters (h₁, h₂, m, h_U, r, n, ϑ) and two elastic constants (G₀, ν). Details of how to determine the model parameters are described as follows.

The critical state parameters (φ_c, λ, e_Γ, ξ) define the critical state of the material, which can be determined by fitting the critical state points in the p′−q and e−p′ planes. For most granular soils, the critical state friction parameters are independent of the loading state.

The fractional order, α, determines the plastic flow directions of the material. Therefore, it can be determined by using the least-squares method to fit the stress-dilation relationship as shown in Figures 1, 2. To be compatible with the critical state soil mechanics, α is equal to unit when the critical state void ratio is reached.

FIGURE 1

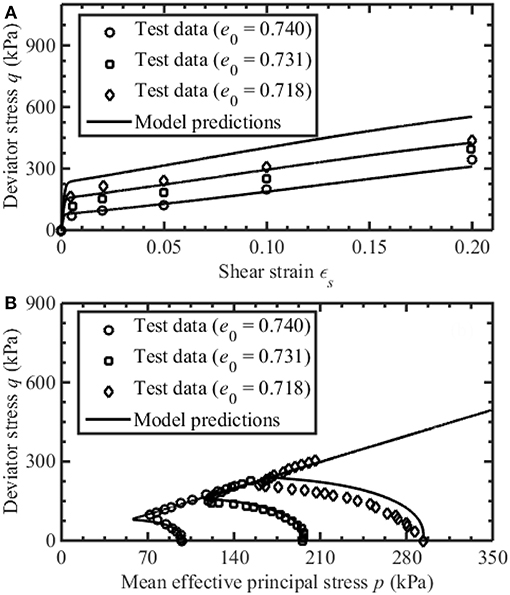
Figure 1. Model prediction of the undrained monotonic behavior of Fuji River sand (Ishihara et al., 1975): (A) deviator stress vs. shear strain, (B) deviator stress vs. mean effective principal stress.

FIGURE 2

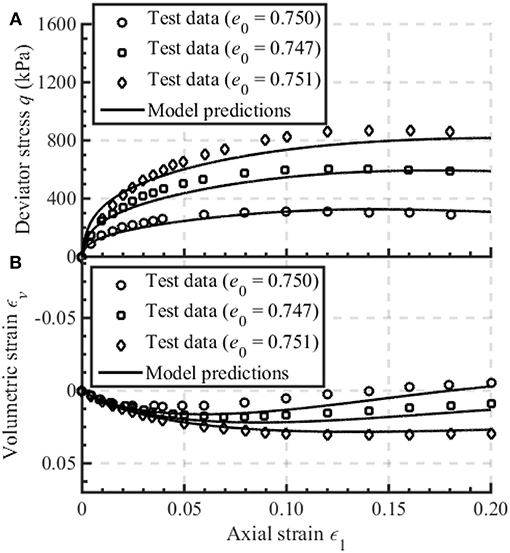
Figure 2. Model prediction of the drained monotonic behavior of Fuji River sand (Ishihara et al., 1975): (A) deviator stress vs. axial strain, (B) volumetric strain vs. axial strain.

The hardening parameters, h₁ and h₂, determine the hardening and softening behavior of the material, which can be determined by fitting the ε_s−η relationship of specimens under different initial monotonic test conditions, as discussed in Sun and Shen (2017). The peak failure constant, m, can be calibrated from the stress points at peak failure state by using:

$\begin{array}{cc}\begin{array}{l}m=\frac{1}{{\psi }_p}ln\frac{M}{{\eta }_p}\end{array}& (32)\end{array}$

where ψ_p and η_p are two values of ψ and η at the peak stress state. The peak stress decreases as k increases. There are four hardening parameters (h_U, θ, r, n) for describing the unloading/reloading behavior of the material. h_Usb can be determined by fitting the slope of the first unloading stress-strain curve while ϑ can be determined from the rate of change of the slope of the first unloading curve. r is determined by fitting the hysteretic loops in the stress-strain curve. n can be obtained by fitting the first reloading stress-strain curve of the material. Detailed discussions on determining the hardening parameters for cyclic loads can be found in Ling and Yang (2006) and thus not repeated here.

The elastic constant, G₀, mainly determines the elastic characteristics of the material, which can be obtained by rearranging Equation (19):

$\begin{array}{cc}\begin{array}{l}{G}_0=\frac{(1+e)G}{{(2.97-e)}^2\sqrt{p^{\prime }{p}_a}}\end{array}& (33)\end{array}$

The Poisson ratio, ν, usually ranges between 0.05 and 0.35 for most granular soils. It defines the lateral deformation ability that can be determined by:

$\begin{array}{cc}\begin{array}{l}\nu \approx \frac{9{\epsilon }_s-2{\epsilon }_v}{18{\epsilon }_s+2{\epsilon }_v}\end{array}& (34)\end{array}$

Detailed values of the model parameters of each material simulated in this study can be found in Table 1.

TABLE 1

Table 1. Model parameters related to monotonic loading.

Model Performance

In this section, the proposed fractional order elastoplastic model is validated by simulating the drained and undrained triaxial behaviors of different granular soils, including sand and rockfill. Specifically, Figures 1–3 present the model simulations of the monotonic and cyclic behavior of Fuji River sand (Ishihara et al., 1975). The model simulations of the drained triaxial behavior of rockfill (Li, 1988; Fu et al., 2014) are shown in Figures 4–6.

FIGURE 3

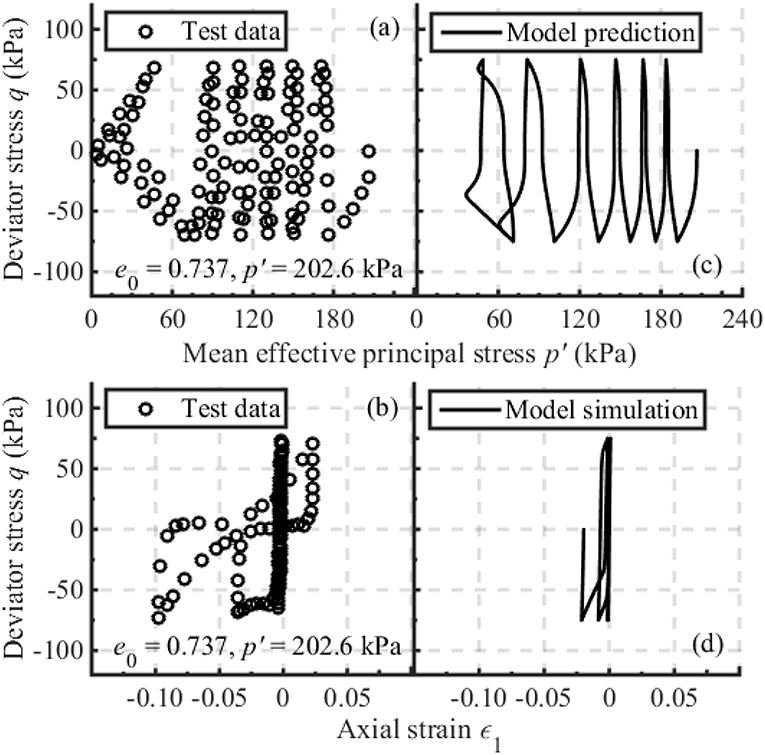
Figure 3. Model prediction of the undrained cyclic behavior of Fuji River sand (Ishihara et al., 1975) (a) measured deviator stress vs. measured mean effective principal stress, (b) measured deviator stress vs. measured axial strain, (c) predicted deviator stress vs. predicted mean effective principal stress, (d) predicted deviator stress vs. predicted axial strain.

FIGURE 4

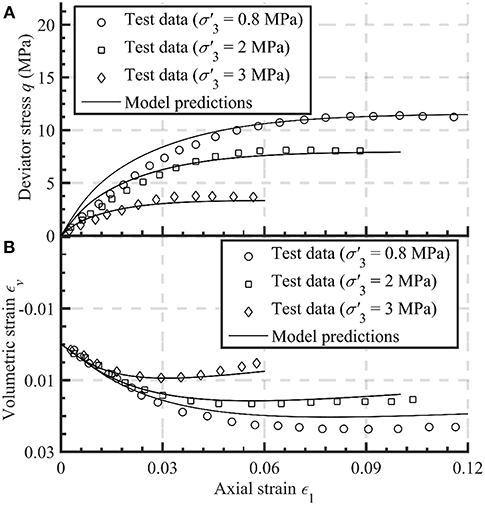
Figure 4. Model prediction of the drained monotonic behavior of Xiaolangdi rockfill (Fu et al., 2014): (A) deviator stress vs. axial strain, (B) volumetric strain vs. axial strain.

Figures 1–3 present the model predictions of the drained and undrained triaxial behavior of Fuji River sand (Ishihara et al., 1975). The material primarily consisted of sub-angular aggregates with d₅₀ of 0.22 mm and C_u of 2.21. Samples of 50 mm in diameter and 100 mm in height were prepared by pluviating fresh sand into the molds which were filled with deaired water. The e₀ used for simulating undrained tests are 0.740, 0.731, and 0.718, with the corresponding ${{\sigma }^{\prime }}_3$ equal to 98, 196, and 294 kPa, respectively. The e₀ for simulating drained monotonic tests are 0.750, 0.747, and 0.751, with the corresponding ${{\sigma }^{\prime }}_3$ equal to 98, 196, and 294 kPa, respectively. It can be observed in Figures 1, 2 that the undrained and drained monotonic stress-strain relationship of Fuji River sand with various initial conditions can be well-captured by using α = 0.95. The initial contraction and the subsequent dilation of the samples (Figure 2) are well-simulated, highlighting the rationality of the adopted fractional flow rule. Moreover, the simulated deviator stress increases rapidly until reaching a critical state, which agrees well with the experimental results shown in Figure 2. The undrained cyclic performance of Fuji River sand with e₀ = 0.737 and ${{\sigma }^{\prime }}_3$ = 206.5 kPa is simulated in Figure 3, by using the additional model parameters: h_L = 0.5, h_U = 0.1, r = 130, n = 1, ϑ = 4. It is found that the model simulation of the stress path is in reasonable agreement with the corresponding test results prior to liquefaction. However, the simulation result of the variation of deviator stress vs. axial strain is less favorable as strain increases.

Monotonic and cyclic test results of Xiaolangdi rockfill reported by Fu et al. (2014) and Li (1988) are simulated in Figures 4–6. The material primarily consisted of slightly weathered sandstones. The e₀ equal to 0.199 was used for all the tests. Figure 4 shows the model prediction of the monotonic stress-strain behavior of Xiaolangdi rockfill (Fu et al., 2014). Concordance between the model simulations and corresponding test results can be observed by using α = 0.93. More specifically, the material hardening and softening accompanied by volumetric contraction at high confining pressure and dilation at relatively low confining pressure are well-characterized. Figures 5, 6 show the model simulations of the cyclic behavior of rockfill. The initial ${{\sigma }^{\prime }}_3$ = 0.5 and 1 MPa while the additional model parameters used for model simulation are: h_L = 0.2, h_U = 8, r = 10, n = 2, ϑ = 3.3. It can be observed that the loading and unloading stress-strain responses can be reasonably simulated by the proposed fractional-order model.

FIGURE 5

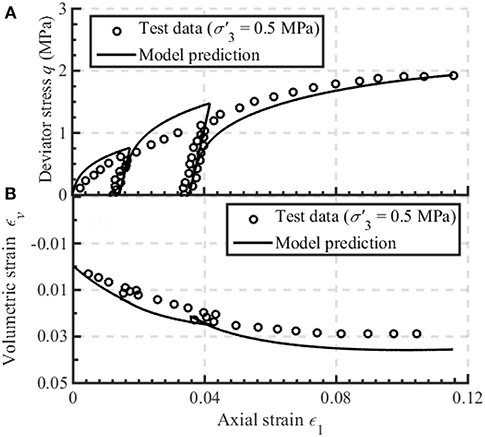
Figure 5. Model prediction of the drained cyclic behavior of Xiaolangdi rockfill (Li, 1988) at low confining pressure: (A) deviator stress vs. axial strain, (B) volumetric strain vs. axial strain.

FIGURE 6

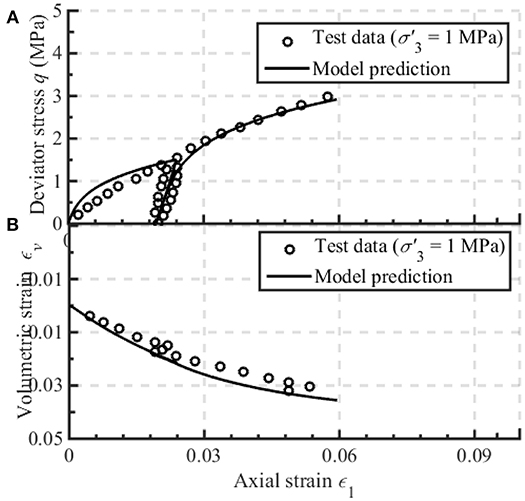
Figure 6. Model prediction of the drained cyclic behavior of Xiaolangdi rockfill (Li, 1988) at high confining pressure: (A) deviator stress vs. axial strain, (B) volumetric strain vs. axial strain.

Conclusions

A fractional-order plastic flow rule was suggested in previous studies. However, due to the limitations induced by the mathematical definitions of the (left-sided) fractional derivative, the suggested fractional-order flow rule can only be applied to model the monotonic stress-strain response of granular soils. To solve this problem, a new cyclic fractional plasticity model was developed in this study. The main conclusions can be drawn as:

(1) A generalized fractional flow rule for both monotonic and cyclic loading conditions was proposed in this study by using the left-sided and right-sided Caputo fractional derivatives.

(2) Then, a fractional plasticity model for granular soils under cyclic loads was proposed in this study. The proposed model contained fourteen parameters that can be all obtained from triaxial tests.

(3) The proposed model was further validated by simulating a variety of test results for different granular soils, e.g., sand, ballast, and rockfill subjected to monotonic and cyclic loads. It was found that the simulation results were in good agreement with corresponding experimental data. The model was able to characterize the key features, for example, loading/unloading stress-dilatancy behavior, strain hardening and softening as well as monotonic and cyclic liquefactions, of granular soils.

(4) However, it should be noted that only limited cyclic test conditions, e.g., undrained test with constant stress amplitudes and drained test without extension, were examined by the proposed model in this study. A more comprehensive application of the proposed model to simulate the cyclic performance of granular soils under a number of different test conditions needs to be conducted in future.

Author Contributions

All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We would like to express our sincere gratitude to Prof. Wen Chen in Hohai University, for his lifelong inspiration on fractional mechanics.

References

Agrawal, O. P. (2007). Fractional variational calculus in terms of Riesz fractional derivatives. J. Phys. A Math. Theor. 40, 6287–6303. doi: 10.1088/1751-8113/40/24/003

CrossRef Full Text | Google Scholar

Aursudkij, B., McDowell, G. R., and Collop, A. C. (2009). Cyclic loading of railway ballast under triaxial conditions and in a railway test facility. Granular Matter 11, 391–401. doi: 10.1007/s10035-009-0144-4

CrossRef Full Text | Google Scholar

Bandini, V., and Coop, M. R. (2011). The influence of particle breakage on the location of the critical state line of sands. Soils Found. 51, 591–600. doi: 10.3208/sandf.51.591

CrossRef Full Text | Google Scholar

Been, K., and Jefferies, M. G. (1985). A state parameter for sands. Géotechnique 35, 99–112. doi: 10.1016/0148-9062(85)90263-3

CrossRef Full Text | Google Scholar

Collins, I. F., Muhunthan, B., and Qu, B. (2010). Thermomechanical state parameter models for sands. Géotechnique 60, 611–622. doi: 10.1680/geot.8.P.127

CrossRef Full Text | Google Scholar

Dafalias, Y. F. (1986). Bounding surface plasticity. I. Mathematical foundation and hypoplasticity. J. Eng. Mech. 112, 966–987. doi: 10.1061/(ASCE)0733-9399(1986)112:9(966)

CrossRef Full Text | Google Scholar

Dafalias, Y. F., and Taiebat, M. (2016). SANISAND-Z: zero elastic range sand plasticity model. Géotechnique 66, 999–1013. doi: 10.1680/jgeot.15.P.271

CrossRef Full Text | Google Scholar

Daouadji, A., Darve, F., Al Gali, H., Hicher, P. Y., Laouafa, F., Lignon, S., et al. (2011). Diffuse failure in geomaterials: experiments, theory and modelling. Int. J. Numer. Anal. Meth. Geomech. 35, 1731–1773. doi: 10.1002/nag.975

CrossRef Full Text | Google Scholar

de Bono, J. P., and McDowell, G. R. (2014). DEM of triaxial tests on crushable sand. Granular Matter 16, 551–562. doi: 10.1007/s10035-014-0500-x

CrossRef Full Text | Google Scholar

Desai, C. S., and Toth, J. (1996). Disturbed state constitutive modeling based on stress-strain and nondestructive behavior. Int. J. Solids Struct. 33, 1619–1650. doi: 10.1016/0020-7683(95)00115-8

CrossRef Full Text | Google Scholar

Einav, I., Houlsby, G. T., and Nguyen, G. D. (2007). Coupled damage and plasticity models derived from energy and dissipation potentials. Int. J. Solids Struct. 44, 2487–2508. doi: 10.1016/j.ijsolstr.2006.07.019

CrossRef Full Text | Google Scholar

Fu, Z., Chen, S., and Peng, C. (2014). Modeling cyclic behavior of rockfill materials in a framework of generalized plasticity. Int. J. Geomech. 14, 191–204. doi: 10.1061/(ASCE)GM.1943-5622.0000302

CrossRef Full Text | Google Scholar

Gajo, A., and Muir Wood, D. (1999a). A kinematic hardening constitutive model for sands: the multiaxial formulation. Int. J. Numer. Anal. Meth. Geomech. 23, 925–965. doi: 10.1002/(SICI)1096-9853(19990810)23:9<925::AID-NAG19>3.0.CO;2-M

CrossRef Full Text | Google Scholar

Gajo, A., and Muir Wood, D. (1999b). SevernTrent sand: a kinematic-hardening constitutive model: the q-p formulation. Géotechnique 49, 595–614. doi: 10.1680/geot.1999.49.5.595

CrossRef Full Text | Google Scholar

Ghafghazi, M., Shuttle, D. A., and DeJong, J. T. (2014). Particle breakage and the critical state of sand. Soils Found. 54, 451–461. doi: 10.1016/j.sandf.2014.04.016

CrossRef Full Text | Google Scholar

Imam, S. M. R., Morgenstern, N. R., Robertson, P. K., and Chan, D. H. (2005). A critical-state constitutive model for liquefiable sand. Can. Geotech. J. 42, 830–855. doi: 10.1139/t05-014

CrossRef Full Text | Google Scholar

Ishihara, K., Tatsuoka, F., and Yasuda, S. (1975). Undrained deformation and liquefaction of sand under cyclic stresses. Soils Found. 15, 29–44. doi: 10.3208/sandf1972.15.29

CrossRef Full Text | Google Scholar

Li, G. X. (1988). Triaxial Experiments on Dry and Saturated Rockfill Materials Used in Xiaolangdi Earth Dam. Research Report 17-1-2-88031. Beijing: Tsinghua University.

Google Scholar

Li, L., Nimbalkar, S., and Zhong, R. (2018). Finite element model of ballasted railway with infinite boundaries considering effects of moving train loads and Rayleigh waves. Soil Dyn. Earthq. Eng. 114, 147–153. doi: 10.1016/j.soildyn.2018.06.033

CrossRef Full Text | Google Scholar

Li, X. (2002). A sand model with state-dapendent dilatancy. Géotechnique 52, 173–186. doi: 10.1680/geot.2002.52.3.173

CrossRef Full Text | Google Scholar

Li, X., and Dafalias, Y. (2000). Dilatancy for cohesionless soils. Géotechnique 50, 449–460. doi: 10.1680/geot.2000.50.4.449

CrossRef Full Text | Google Scholar

Li, X., and Wang, Y. (1998). Linear representation of steady-state line for sand. J. Geotech. Geoenviron. Eng. 124, 1215–1217. doi: 10.1061/(ASCE)1090-0241(1998)124:12(1215)

CrossRef Full Text | Google Scholar

Ling, H. I., and Yang, S. (2006). Unified sand model based on the critical state and generalized plasticity. J. Eng. Mech. 132, 1380–1391. doi: 10.1061/(ASCE)0733-9399(2006)132:12(1380)

CrossRef Full Text | Google Scholar

McDowell, G. R., and Li, H. (2016). Discrete element modelling of scaled railway ballast under triaxial conditions. Granular Matter 18, 1–10. doi: 10.1007/s10035-016-0663-8

CrossRef Full Text | Google Scholar

Nimbalkar, S., Annapareddy, V. S. R., and Pain, A. (2018). A simplified approach to assess seismic stability of tailings dams. J. Rock Mech. Geotech. Eng. 10, 1082–1090. doi: 10.1016/j.jrmge.2018.06.003

CrossRef Full Text | Google Scholar

Nimbalkar, S., and Choudhury, D. (2008). Seismic design of retaining wall by considering wall-soil inertia for active case. Int. J. Geotech. Eng. 2, 319–328. doi: 10.3328/IJGE.2008.02.04.319-328

CrossRef Full Text | Google Scholar

Nimbalkar, S., and Indraratna, B. (2016). Improved performance of ballasted rail track using geosynthetics and rubber shockmat. J. Geotech. Geoenviron. Eng. 142:04016031. doi: 10.1061/(ASCE)GT.1943-5606.0001491

CrossRef Full Text | Google Scholar

Nimbalkar, S., Indraratna, B., Dash, S. K., and Christie, D. (2012). Improved performance of railway ballast under impact loads using shock mats. J. Geotech. Geoenviron. Eng. 138, 281–294. doi: 10.1061/(Asce)Gt.1943-5606.0000598

CrossRef Full Text | Google Scholar

Schofield, A., and Wroth, P. (1968). Critical State Soil Mechanics. New York, NY: McGraw-Hill London.

Google Scholar

Sumelka, W. (2014a). Fractional viscoplasticity. Mech. Res. Commun. 56, 31–36. doi: 10.1016/j.mechrescom.2013.11.005

CrossRef Full Text | Google Scholar

Sumelka, W. (2014b). A note on non-associated Drucker-Prager plastic flow in terms of fractional calculus. J. Theoret. Appl. Mech. 52, 571–574. doi: 10.15632/jtam-pl.53.4.959

CrossRef Full Text | Google Scholar

Sumelka, W., and Nowak, M. (2016). Non-normality and induced plastic anisotropy under fractional plastic flow rule: a numerical study. Int. J. Numer. Anal. Meth. Geomech. 40, 651–675. doi: 10.1002/nag.2421

CrossRef Full Text | Google Scholar

Sun, Y., Chen, C., and Nimbalkar, S. (2017a). Identification of ballast grading for rail track. J. Rock Mech. Geotech. Eng. 9, 945–954. doi: 10.1016/j.jrmge.2017.04.006

CrossRef Full Text | Google Scholar

Sun, Y., Chen, C., and Song, S. (2018a). “Generalized fractional flow rule and its modelling of the monotonic and cyclic behavior of granular soils,” in Proceedings GeoShanghai 2018 International Conference: Fundamentals of Soil Behaviours, eds. A. Zhou, J. Tao, X. Gu and L. Hu (Singapore: Springer), 299–307.

Google Scholar

Sun, Y., Gao, Y., and Chen, C. (2019a). Critical-state fractional model and its numerical scheme for isotropic granular soil considering state-dependence. Int. J. Geomech. 13:04018202. doi: 10.1061/(ASCE)GM.1943-5622.0001353

CrossRef Full Text | Google Scholar

Sun, Y., Gao, Y., and Ju, W. (2018b). Fractional plasticity and its application in constitutive model for sands. Chinese J. Geotech. Eng. 40, 1535–1541. doi: 10.11779/CJGE201808021

CrossRef Full Text | Google Scholar

Sun, Y., Gao, Y., and Shen, Y. (2019b). Mathematical aspect of the state-dependent stress-dilatancy of granular soil under triaxial loading. Géotechnique 69, 158–165. doi: 10.1680/jgeot.17.t.029

CrossRef Full Text | Google Scholar

Sun, Y., Gao, Y., and Shen, Y. (2019c). Non-associative fractional-order bounding-surface model for granular aoils considering state dependence. Int. J. Civil Eng. 17, 171–179. doi: 10.1007/s40999-017-0255-y

CrossRef Full Text | Google Scholar

Sun, Y., Gao, Y., and Song, S. (2018c). Effect of integrating memory on the performance of the fractional plasticity model for geomaterials. Acta Mech. Sin. 34, 896–901. doi: 10.1007/s10409-018-0777-9

CrossRef Full Text | Google Scholar

Sun, Y., Gao, Y., and Zhu, Q. (2018d). Fractional order plasticity modelling of state-dependent behaviour of granular soils without using plastic potential. Int. J. Plasticity 102, 53–69. doi: 10.1016/j.ijplas.2017.12.001

CrossRef Full Text | Google Scholar

Sun, Y., Indraratna, B., Carter, J. P., Marchant, T., and Nimbalkar, S. (2017b). Application of fractional calculus in modelling ballast deformation under cyclic loading. Comput. Geotech. 82, 16–30. doi: 10.1016/j.compgeo.2016.09.010

CrossRef Full Text | Google Scholar

Sun, Y., Liu, H., Yang, G., and Xiao, Y. (2013). Formulation of cross-anisotropic failure criterion for soils. Water Sci. Eng. 6, 456–468. doi: 10.3882/j.issn.1674-2370.2013.04.009

CrossRef Full Text | Google Scholar

Sun, Y., Nimbalkar, S., and Chen, C. (2018e). Grading and frequency dependence of the resilient modulus of ballast. Géotechnique Lett. 8, 305–309. doi: 10.1680/jgele.18.00084

CrossRef Full Text | Google Scholar

Sun, Y., and Shen, Y. (2017). Constitutive model of granular soils using fractional order plastic flow rule. Int. J. Geomech. 17:04017025. doi: 10.1061/(ASCE)GM.1943-5622.0000904

CrossRef Full Text | Google Scholar

Sun, Y., Shen, Y., and Liu, H. (2018f). Fractional strain rate and its relation with fractal dimension of granular soils. Rock Soil Mech. 39, 297–302. doi: 10.16285/j.rsm.2017.1320

CrossRef Full Text | Google Scholar

Sun, Y., Song, S., Xiao, Y., and Zhang, J. (2017c). Development and application of state-dependent fractional plasticity in modeling the non-associated behavior of granular aggregates. Acta Mech. Solida Sin. 30, 507–519. doi: 10.1016/j.camss.2017.09.002

CrossRef Full Text | Google Scholar

Sun, Y., and Xiao, Y. (2017). Fractional order plasticity model for granular soils subjected to monotonic triaxial compression. Int. J. Solids Struct. 118–119, 224–234. doi: 10.1016/j.ijsolstr.2017.03.005

CrossRef Full Text | Google Scholar

Sun, Y., Xiao, Y., and Hanif, K. F. (2015a). Compressibility dependence on grain size distribution and relative density in sands. Sci. China Technol. Sci. 58, 443–448. doi: 10.1007/s11431-015-5768-5

CrossRef Full Text | Google Scholar

Sun, Y., Xiao, Y., and Hanif, K. F. (2015b). Fractional order modelling of the cumulative deformation of granular soils under cyclic loading. Acta Mech. Solida Sin. 28, 647–658. doi: 10.1016/S0894-9166(16)30006-4

CrossRef Full Text | Google Scholar

Sun, Y., Xiao, Y., and Ji, H. (2016a). Dilation and breakage dissipation of granular soils subjected to monotonic loading. Acta Mech. Sin. 32, 1065–1074. doi: 10.1007/s10409-016-0569-z

CrossRef Full Text | Google Scholar

Sun, Y., Xiao, Y., and Ju, W. (2014). Bounding surface model for ballast with additional attention on the evolution of particle size distribution. Sci. China Technol. Sci. 57, 1352–1360. doi: 10.1007/s11431-014-5575-4

CrossRef Full Text | Google Scholar

Sun, Y., Xiao, Y., Zheng, C., and Hanif, K. F. (2016b). Modelling long-term deformation of granular soils incorporating the concept of fractional calculus. Acta Mech. Sin. 32, 112–124. doi: 10.1007/s10409-015-0490-x

CrossRef Full Text | Google Scholar

Varadarajan, A., Sharma, K., Abbas, S., and Dhawan, A. (2006). Constitutive model for rockfill materials and determination of material constants. Int. J. Geomech. 6, 226–237. doi: 10.1061/(ASCE)1532-3641(2006)6:4(226)

CrossRef Full Text | Google Scholar

Yang, J., and Li, X. (2004). State-dependent strength of sands from the perspective of unified modeling. J. Geotech. Geoenviron. Eng. 130, 186–198. doi: 10.1061/(ASCE)1090-0241(2004)130:2(186)

CrossRef Full Text | Google Scholar

Yin, Z., Chang, C. S., Karstunen, M., and Hicher, P. (2010). An anisotropic elastic–viscoplastic model for soft clays. Int. J. Solids Struct. 47, 665–677. doi: 10.1016/j.ijsolstr.2009.11.004

CrossRef Full Text | Google Scholar

Yin, Z., Jin, Y., Shen, S., and Huang, H. (2017). An efficient optimization method for identifying parameters of soft structured clay by an enhanced genetic algorithm and elastic–viscoplastic model. Acta Geotech. 12, 849–867. doi: 10.1007/s11440-016-0486-0

CrossRef Full Text | Google Scholar

Yu, F. (2017a). Characteristics of particle breakage of sand in triaxial shear. Powder Technol. 320, 656–667. doi: 10.1016/j.powtec.2017.08.001

CrossRef Full Text | Google Scholar

Yu, F. (2017b). Particle breakage and the critical state of sands. Géotechnique 67, 713–719. doi: 10.1680/jgeot.15.P.250

CrossRef Full Text | Google Scholar