- 1Department of European and Mediterranean Cultures (Architecture, Environment and Cultural Heritage), University of Basilicata, Matera, Italy
- 2DiSG – Department of Structural Engineering, Sapienza University of Rome, Rome, Italy
The seismic risk assessment of the historical and architectural heritage is, nowadays, a very relevant topic due the potential human and economic losses involved in case of global or partial collapse. In order to preserve the inestimable value of such heritage, the prevention and mitigation of the seismic risk is needed and it cannot be postponed. Among the several methods available in the literature to perform vulnerability assessment on cultural heritage, this study focuses on two simplified methods proposed by the current Italian Directive, containing the guide lines for assessment and reduction of cultural heritage seismic risk. Furthermore, a new simplified method is applied, capable at a territorial scale of quickly ranking the seismic behavior of ancient churches. In the paper, the considered evaluation methods are applied to the case study of the Matera Cathedral, named SS. Maria della Bruna. The obtained results are then compared with others of similar ancient churches, all belonging to the historical centre “Sassi of Matera,” a site protected by UNESCO having a moderate seismic hazard.
Introduction
Natural disasters, such as volcanoes, floods, landslides, hurricanes, earthquakes, and climatic changes, represent a real danger for the conservation of the existing cultural heritage. Nevertheless, insufficient programs have been applied, aimed at reducing the vulnerability, and the related risk of cultural heritages. An idea of the problem dimensions is given by analyzing the costs required in the last natural disasters in order to manage the emergencies, repairs, and reconstruction. According to an estimation provided by World Bank (World Bank Indipendent Evaluation Group, 2006), natural disaster damage costs are increasing, and they have achieved about 652 billion US dollars in the 1990s. These costs result 15 times higher than the ones registered in the 1950s, even for natural disasters. Another piece of important information is obtained: if one considers that one-third of the cost to the global economy (about 50 billion US dollars) is spent on predicting, preventing, and mitigating disasters and the other two thirds represent the direct costs of the damage (Alexander, 2017).
The ability to react to these disasters is directly related to the public awareness about the future destructive events that may occur. In this context, it is necessary to design and to apply prevention measures addressed for protecting the cultural heritage, where experts of different fields (engineering, statistics, chemistry, seismology, etc.) are involved. Thanks to this cooperation, different documents have been proposed such as, among the others, the Mexican risk identification atlas (CENAPRED, 2014), and the territorial information systems proposed in ISCR (2017).
In line with these premises, this paper presents a comparative study of the seismic performance of ancient masonry churches. To this scope, the simplified methods reported within the Italian Directive (GU. n. 47, 09/02/2011) are considered, with particular attention to Level of Valuation 1 (LV1, for an evaluation at a territorial dimension) and Level of Valuation 2 (LV2, considering the macro-elements approach). Furthermore, a new simplified method proposed in (CENAPRED, 2006) and validated in D'Amato et al. (2018), useful at a territorial scale for preliminary scoring and classifying the seismic behavior of churches, is applied. This methodology has also been recently validated for ancient adobe Chilean Churches (Fuentes et al., 2019).
The seismic performance evaluation in this study is conducted by considering in detail the case study of the Cathedral of Matera (Italy), an ancient masonry church dedicated to SS Maria Della Bruna. The obtained results are then compared with other churches, similar to the Cathedral with respect to materials, geometrical characteristics, and constructions details. All the churches considered fall within the historic centre of Matera, named “Sassi of Matera,” recognized since 1993 as a World Heritage Site by UNESCO.
The main feature of the considered methods is that they can be used within a multilevel seismic vulnerability approach. In fact, they are based only on simple surveys characterized by visual and geometric detections, implying limited costs. Thus, these methods can also be applied as decision making tools in order to rank priorities and to proceed to further material and structural investigations for performing advanced structural analyses. Within this multi-level approach, the new simplified method recently proposed can be intended as a “Level of Valuation 0” (“LV0 method”), by allowing a very rapid seismic assessment, even at a larger territorial scale. Moreover, the comparisons among the obtained results show that the simplified methods may also overestimate the seismic actual response. Therefore, they remain useful for comparing and ranking the case studies, but they cannot substitute more refined methods for realistically simulating the seismic behavior of churches.
Seismic Assessment Methods Indicated in the Italian Directive
The Italian directive, specific for Cultural Heritage (G. U. n. 47, 26/02/2011), defines three levels of valuation, namely the LV1, LV2, and LV3 method for assessing the seismic performance of different historical constructions. These methods have an increasing complexity, requiring in parallel an increasing amount of information regarding structural details and materials properties.
As regards to the LV1 method, it is suitable when a comparative seismic performance at a territorial level is conducted. Basically, the idea of this method is to relate the seismic performance to a global vulnerability index of a structure. No intervention may be designed with this method. Recent applications and similar approaches to this method may be found, for instance, in Lourenço and Roque (2006); Lourenço et al. (2013); Caprili et al. (2017); Formisano et al. (2017, 2018); Marotta et al. (2018); Sarhosis et al. (2018);Valente and Milani (2018a).
A more refined seismic performance evaluation may be obtained with the LV2 method. It consists of evaluating the local mechanisms of architectural parts of a structure, named “macro-elements,” and the global vulnerability corresponds to the activation of the most vulnerable mechanism considered. The macro-elements approach has been proposed after the damage surveys suffered by ancient churches during some recent Italian earthquakes. The conducted surveys have highlighted a systematic repetition of the detected damages, suggesting that the church structural system should be considered as a group of architectural parts, showing independent response mechanisms under seismic lateral loading. The macro-elements are identified as architectural parts (such as the main façade, lateral walls, longitudinal and transverse colonnade of main nave, triumphal arch, bell tower, dome, etc.), evaluating possible interactions with adjacent elements. Applications of this approach may be found, among the others, in Betti et al. (2018), Brandonisio et al. (2013), D'Ayala and Paganoni (2011), Doglioni et al. (1994), Formisano and Marzo (2017), Lagomarsino and Podestà (2004a,b), while a recent investigation on the estimation of main frequency of ancient masonry churches may be found in Lopez et al. (2019).
Non-linear finite element analyses are considered in the LV3 method (G. U. n. 47, 26/02/2011), and they may regard limited parts or a whole structure. The adopted models must reproduce the real distribution of stiffness and mass, as well as the material non-linear behavior. Of course, the results obtained may realistically simulate the structural behavior only if the numerical assumptions made are true. This is strictly dependent on the knowledge of structural details (such as, for instance, wall connections, connections with the roof parts, and clear knowledge of the structure evolution during the past). The amount of these available data, and consequently, the reliability of the obtained results may increase if an in-depth and critical investigation campaign, through in situ tests and inspections, is performed. However, it should be carefully considered that in-situ tests should be focused at first on structural details more than on material mechanical properties, since the former dominate the response influencing the elements interaction more than the latter. Discussion about this issue may be found in Clementi et al. (2016), Castori et al. (2017), and Valente et al. (2017). In addition, the use of non-linear methods, such as the conventional pushover approach, implies the decisive choice of the control point on which the non-linear global response and the evaluation of the seismic performance depend. A discussion of this aspect may be found, among others, in Betti et al. (2018). While a general discussion on the application of non-linear analyses and the comparisons with the macro-element approach may be found in Castellazzi et al. (2013) and Valente and Milani (2018b).
Although it is the most simplified one, the LV1 method is useful for evaluations at a territorial scale capable of providing, through a vulnerability index, an estimation of the ground acceleration related to the collapse. It requires only visual inspections and a qualitative judgment of some structural details. On the other hand, a local analysis may be performed with the LV2 method (macro-element approach) also designing local interventions, where the potential interaction among the structural part may also be taken into account. The most refined approach is represented, without any doubt, by the LV3 method, where non-linear FE models are required. However, as discussed previously, this approach required a high amount of data and it may be extremely high time consuming from a computational point of view.
In the following, only the LV1 and LV2 methods are described in detail and, later on, are applied to some case studies. In addition, in this study a new simplified method for seismic assessment of the considered cases is also considered, proposed as LV0 in continuity with the Italian Directive approach. The obtained results will be compared, in order to establish if a general correspondence in terms of the predicted seismic performance among the examined methods exists.
LV1 Method
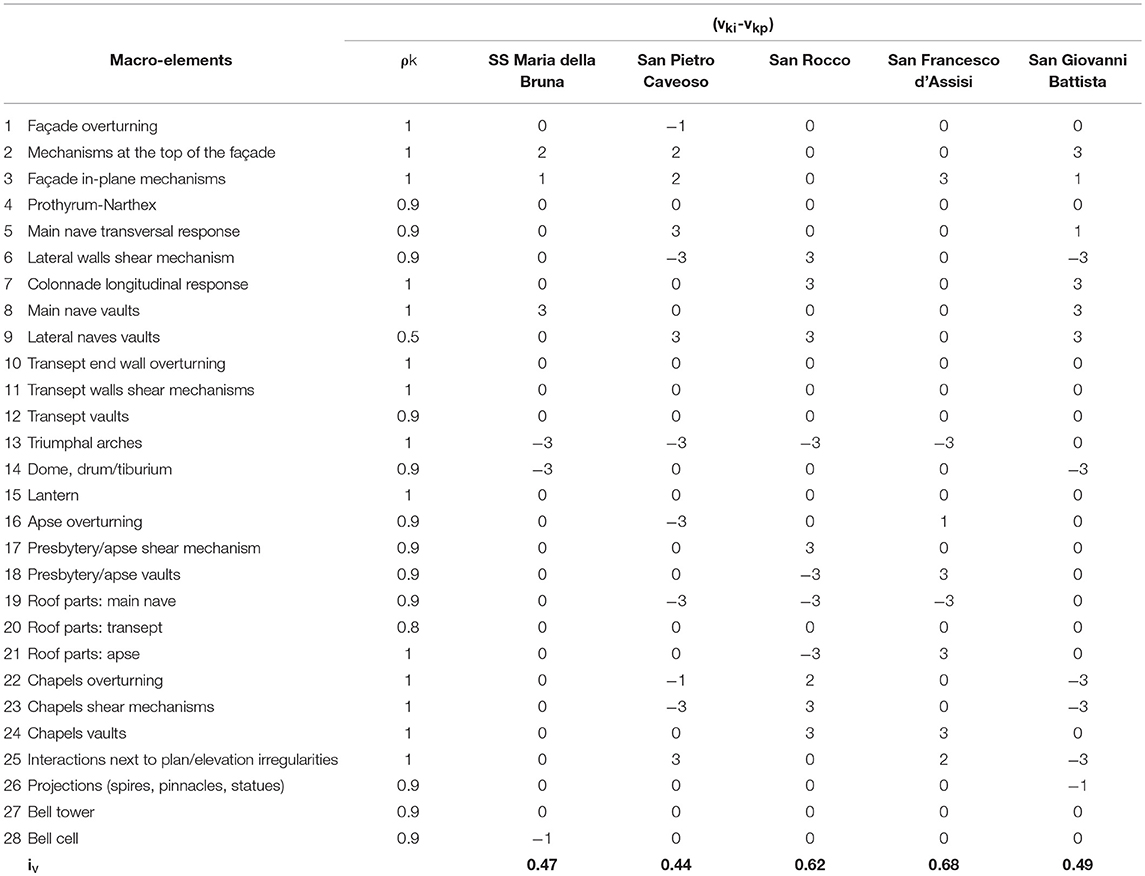
The LV1 method is the simplest method for assessing the seismic performance of a structure, revealing particularly adaptation for territorial scale evaluation (G. U. n. 47, 26/02/2011). The method requires defining, only through a visual survey, the global vulnerability index iv calculated as weighted combination of 28 possible damage mechanisms with the following relationship:
where iv may vary between 0 and 1, and the other parameters may assume the following values:
ρk is the response mechanism weight, varying from 0.5 to 1. If the considered mechanism is absent or not involved, it must be set equal to zero;
vki and vkp measure, from the k-th response mechanism, the vulnerability and the efficiency of any possible seismic-resistant device. It is indicated to assume the value 1 for the most important response mechanisms, such as main façade overturning, triumphal arch response, longitudinal nave response, etc.; while, as for secondary mechanisms, such as mechanisms of transept and chapels, or prothyrum—narthex response, the value may range from 0.5 to 1.
Then, the ground acceleration corresponding to the attainment of Damage Limit State (DLS) and Life-Safety Limit State (LSLS) may be estimated by applying the following expressions:
where S is the stratigraphic amplification depending on the foundation soil. The previous equations have been established on a statistical basis starting from the surveys carried out in some recent Italian earthquakes.
By knowing aLS, one may calculate the safety index ILS:
where TLS is related to the seismic action aLS for LSLS or DLS (that is the seismic capacity), and TR, LS is the expected reference return period for LSLS or DLS (that is the seismic demand). TLS may be calculated with the following expression (GU. n. 47, 09/02/2011):
where a1S1 and a2S2 define the interval of the seismic hazard in which aLS is included; S is the stratigraphic amplification; TR1 and TR2 correspond to the return periods associated with a1 and a2, and Fc represents the confidence factor depending on the knowledge level of the structure.
Whereas, as for the return period TR, LS associated to the expected seismic action, it is obtained through the Equation 6 depending on the reference period (VR), and the probability of exceedance (PVR) is associated with the considered limit state, having a PVR equal to 61 and 10%, respectively, for the DLS and LSLS.
Another ratio that may be particularly useful for seismic assessment is the acceleration factor fa, LS, expressing the structure strength with respect to the seismic demand:
where aLS corresponds to the achievement of the considered limit state and ag, LS is the expected one at the site, both referred to a rigid soil. It should be remarked that if a certain seismic protection level is satisfied, both ILS and fa, LS are major than unity.
LV2 Method
This method is based on the analysis of rigid bodies by the means of the kinematic model (kinematic analysis). The failure mechanism considered may be schematized as a group of rigid blocks forming a kinematic chain, unstable with respect to the lateral actions, where all bodies are connected to each other with flexural hinges placed where the cracking likely occurs. The method is applied under the hypotheses (Heyman, 1966) that the masonry strength in compression is infinite and in tension is neglectable, and that any sliding between two adjacent blocks is restrained. It is suitable also for designing local interventions, if they do not modify the entire response of a structure.
The method involves an incremental approach, consisting of increasing a distribution of lateral forces, applied to the rigid blocks, proportional to the bodies mass. The lateral forces are increased until the failure arising when an inadmissible thrust line verifies. The beginning of the failure mechanism, according to Eurocode 8 (CEN, 2004) and Italian Design Code (Ministerial Decree, 14/01/2008), corresponds to the Damage Limit State (DLS) and it is associated with a lateral forces multiplier usually indicated as α0.
Certainly in this method, a primary importance is represented by the definition of the macro-elements that, as known, are strictly dependent on manufacturing techniques and structural details such as, for instance, elements connections or existing cracks. Investigations in this regard may be found in Lagomarsino and Resemini (2009) as for the compressive strength influence, or in Lagomarsino (2012) for the no-tensile strength assumption. Whereas, as far as the influence of orthogonal walls connection in the overturning mechanism is concerned, it is worth noting the study carried out by de Felice and Giannini (2001), D'Ayala and Speranza (2003), and Lagomarsino (2012). To this regard, recently in Instructions for the application of the Ministerial Decree MD (17/01/2018), it is also recommended to take into account in the calculation of the wall overturning mechanism and the stabilizing friction contribution of the orthogonal walls due to an effective connection. As it will be shown later, this contribution is neglected in this paper, and, therefore, the so-found activation multipliers underestimate the real ones.
The failure mode activation multiplier α0 of a rigid block chain is defined according to the following expression, representing an application of the Theorem of Virtual Works (Instructions for the application of the Ministerial Decree MD, 14/01/2008):
where:
- n is the rigid blocks number involved;
- m is the forces number that do not directly act on the rigid blocks. Their masses are considered in the calculation of horizontal inertial forces under the seismic action;
- o is the external force number applied to the different blocks and not associated to masses;
- Pi is the dead weight of the generic rigid block;
- Pj is the force that does not directly act on the rigid block. Its mass is considered producing a horizontal inertial force;
- δx, i and δx, j are the virtual displacements in the horizontal direction of the application points of Pi and Pj, respectively. It is assumed as positive vs. associated to direction of the considered seismic action;
- δy, i is the virtual displacement in the vertical direction (positive is upward) of the application point Pi,;
- Fh is an external generic force (in absolute value) applied to a rigid block;
- δh is the application point virtual displacement of the Fh force (positive if having discordant vs. from Fh);
- Lfi corresponds to the internal forces virtual work, assumed equal to zero.
Subsequently, it is possible to determine the equivalent non-linear response of a single degree of freedom (SDOF) system, deriving the seismic spectral acceleration from the calculated activation multiplier α0. , which may be calculated with the Equation (9), descending from the standard modal analysis principles:
In the previous equation:
- g is the gravity acceleration;
- represents the dead weights sum. Their masses produce horizontal inertial force under seismic action to consider in the kinematic chain schematization;
- FC indicates the Factor of Confidence;
- From M* representing the effective participating mass:
it is possible to calculate e*, that is the participating mass fraction related to M*:
As for the DLS, has to be compared with the acceleration spectrum demand ag(PVR)·S, that is the expected Peak Ground Acceleration:
where PVR is the exceedance probability for considered limit state (in this case DLS) in the reference life (VR), and S is the soil stratigraphic amplification. The Equation (12) refers to the macro-elements that are directly connected at ground level, and it neglects the dynamic motion amplification due to structural deformability (Doherty et al., 2002).
Whereas, when they are considered macro-element responses that are not directly connected to the ground floor (as the gable overturning), the dynamic amplification of the response has to be considered, according to the Equation (13).
where z is the constraints barycenter height of rigid blocks considered; Se(T1) is the spectral ordinate evaluated for T1, that is the entire structure vibration period along the considered direction; ψ(z) is the shape of the first vibration mode, normalized at the structure top. It may be assumed equal to ψ(z) = z/H, where H is the structure height with respect to the foundation floor; γ is the modal participating coefficient assumed in a simplified way equal to γ = 3N/(2N+1) with N the number of structure stories. The simplified relationship for estimating the churches fundamental period of oscillation T1, proposed by Lagomarsino and Podestà (2005), should also be mentioned:
where H represents the structure height, measured up to the lowest point of the roof.
As regards to the LSLS, the behavior factor q (Ministerial Decree, 14/01/2008) has to be considered in the previous formulations. Therefore, in the case of ground-connected mechanisms, we have:
where it is applied, in the case of not directly ground-connected mechanisms, the Equation (16).
In the previous equations, the behavior factor q may be assumed equal to 2. The symbols used in Equations (15, 16) are the same as Equations (12, 13), respectively. It should be pointed out that, in the Instructions for the application of the Ministerial Decree MD (17/01/2018), a more refined approach for calculating the floor design spectra of the horizontal seismic action is indicated and, consequently, the seismic demand of the response mechanism is not directly ground connected (such as, for instance, the gable overturning). However, although more precise, this approach requires knowledge of the dynamic characteristics of the considered mechanism that, for the detail level of this work, are unknown. Therefore, the formulations reported in the Equations (13, 16) will be applied, indicated in the previous Instructions for the application of the Ministerial Decree MD (14/01/2008), where a first evaluation of the seismic demand may be done independently on the fundamental period of the response mechanism considered.
A New Simplified Approach for Assessing the Seismic Risk
In Dìaz (2016), a new simplified methodology capable of assessing the seismic risk of ancient masonry churches has been proposed. Subsequently, this methodology has been preliminarily validated in D'Amato et al. (2018), and recently also extended to the case of Chilean Churches in Fuentes et al. (2019).
The simplified methodology provides a seismic risk score R, applying the known symbol equation (UNDRO, 1979; FEMA, 2004):
where E, H, and V represent the exposure of elements or assets at risk, the seismic hazard, and the vulnerability, respectively.
The seismic risk score R is obtained by multiplying the scores E, H, and V, separately evaluated by applying three different tools, that are:
• Tool 1: it provides a score associated to the exposition factor E, and accounting for the cultural value;
• Tool 2: with this tool a score it is calculated associated to the seismic hazard H. Different threats may be considered consulting, for example, published maps such as, for instance, the Italian Risk Map (CENAPRED, 2006; ISCR, 2017) and (Degg and Chester, 2005);
• Tool 3: the seismic vulnerability index V is calculated considering additional information provided in some seismic vulnerability forms such as the DGPTA (2003) and Chilean Norm N. 3332 (2013).
As proposed in Dìaz (2016), the simplified method may also be applied as the scoring method by neglecting the exposition value, that is the E score within the Equation (17). Hence, the seismic score R is given by:
obtained by considering only the scores separately obtained with the Tool 2 and the Tool 3. In the previous equation, H is increased as a unity for obtaining a seismic score R more major than 1. One may note that as R increases, the seismic risk also increases. The proposed method is particularly suitable for conducting, at a territorial scale, a seismic comparative analysis, with the simplicity of requiring few information to be applied. Instructions on how to calculate the vulnerability (V) and seismic hazard (H) scores may be found in Dìaz (2016) and in D'Amato et al. (2018).
Case Studies
The city of Matera is located at the south of Italy, in the region of Basilicata. Specifically, the SS Maria della Bruna church is located in the city center, called “Sassi of Matera,” consisting of two areas protected, since 1993, by UNESCO and reported within the World Heritage List. As shown in Figure 1, the church is characterized by a main body composed of three naves, having a latin cross configuration in plan. As in the Cristian tradition, the church main façade is oriented toward the west while the altar is oriented toward the east. The Cathedral construction started between 1226 and 1231 (Morelli, 1970). An inscription on the bell tower door reports that in 1270 the construction finished. Between the 15 and 16th centuries some chapels were annexed to the main body on the north side. As for the bell tower, two distinct parts may be clearly identified, since the upper zone was built later than the rest of the tower but not after 1709, given that this part appears in a fresco. The choir was originally completed in 1729 and, later, completely reconstructed in 1738. Additionally, it is supposed that due to a partial collapse, the dome was reconstructed. Regarding the bell tower, it is possible that the upper section was built later than the rest of the tower but not after 1709, given that this part appears in a fresco after this year (Ragone et al., 2017). The façade of the Cathedral presents several ornamental elements with religious meanings. Above the main entrance, a statue of SS Maria della Bruna, the Saint Patron of the City, is situated. At the top of the main façade, a finely decorated oculus is situated. A plan of the church is reported in Figure 1.
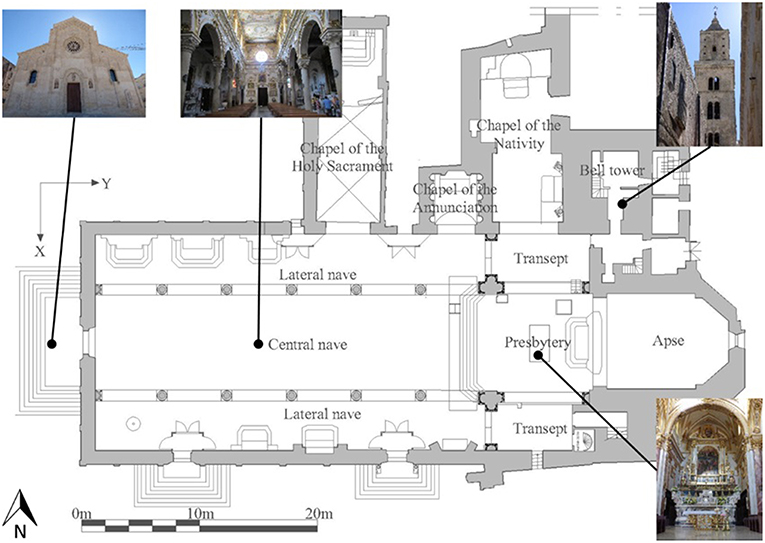
Figure 1. Plan of the SS Maria della Bruna church (Ramirez et al., 2019).
The results obtained from the considered case study are also compared in this work with four similar ancient masonry churches, all located within the “Sassi of Matera” area. The four additional churches, examined in a previous work (D'Amato et al., 2018) are: San Pietro Caveoso, San Rocco, San Francesco d'Assisi, and San Giovanni Battista. The considered churches are illustrated in Table 1, where for each of them, the main facade, an interior view and the floor plan is reported. For each considered church, original drawings reporting the geometrical dimensions were retrieved. In addition, specific detailed surveys were conducted in order to control any possible existing cracking pattern, material deterioration or structural instability. No in-situ tests were carried out since the calculation methods applied in this study do not depend on the mechanical properties of the involved materials. In the following, a summary of the description of the considered churches is reported.
San Pietro Caveoso Church
The church is placed in front of a large square, and along the canyon rocky ridge of Gravina river. The main façade is in baroque style, with three different portals, suggesting the subdivision of the internal structure into three naves. Above the portals, three semicircular niches contain the statues of Saints Peter and Paul, respectively to the left and to the right, with the Madonna della Misericordia in a central position. The façade is advanced with respect to its original position and connected to the internal longitudinal space through vaults in the Lecce style. Inside there are three naves and four of the eight original chapels overlooking the left nave. The original ceiling of the central nave is hidden today by a wooden false ceiling decorated with paintings. The main nave ends with a deep choir containing the presbytery with the eighteenth-century altar. On the left of the façade rises the bell tower with three orders, culminating with a pyramidal spire.
San Rocco Church
The main entrance of the church is served by an imposing staircase. The internal layout has a division into two aisles: the largest exhibits a barrel-vaulted roof, supported by round arches crossing, and along the right side, niches with altars. The lateral aisle is made up of four quadrangular spans, covered by cross vaults with a slightly raised profile and accompanied by exquisite workmanship altars, embellished with paintings and sculptures from various eras. Through a triumphal arch it is possible to reach the presbytery area, covered by a pseudo-sail vault and concluded by a semicircular apse where the choir with the organ is placed.
San Francesco d'Assisi Church
This church was built on top of the rupestrian church of Saints Peter and Paul. It presents an imponent façade and is divided into three distinct naves internally. On the lateral aisles are present nine chapels: four chapels on the right side and five chapels on the left side, with the characteristic that each of these is covered by a different vaulted system. Behind the presbytery there are additional spaces, among which sits the choir area hosting also a huge organ. On the right side, there is an environment linking the church with the bell cell.
San Giovanni Battista Church
This church presents a basilica layout with three naves, with a Greek cross plan. The pillars delimiting the central nave have a cruciform plan, composed of four half-columns, of which only one supports the vault of the central nave. The church has a conspicuous development in height, with different vaulted systems, such as a star-shaped, Lecce-type, and cross-shaped, respectively. The aisles, delimited by cruciform pillars and columns projecting from the internal walls, intersect the transept and are divided into two equal parts, composed of two spans each with a cross-shaped roof.
After collecting all the main information, the principal characteristics of the considered churches may be summarized as follows:
Configuration in plan: SS Maria della Bruna, San Giovanni Battista, and San Pietro Caveoso are characterized by plan configuration with three naves, where San Rocco and San Francesco d'Assisi churches have a one-nave plan-configuration;
Roof structures: SS Maria della Bruna, San Rocco, and San Giovanni Battista have a vaulted system, while roof structures of San Pietro Caveoso and San Francesco d'Assisi are made also by truss wooden structures in the central main nave;
Configuration in elevation: in all cases the roof structures are covering the main nave and the lateral ones. No additional floor was detected.
The construction material for all the churches was represented by tufo, a local calcarenite rock. The state of conservation of masonry elements was good with a regular texture, and no cracking patter was encountered in each church. Similar approaches may be found in Laterza et al. (2016), D'Amato et al. (2017), and Fabbrocino et al. (2018). Whereas, a discussion of some critical aspects in investigating structural details may be found, among the others, in Krstevska et al. (2010); Luchin et al. (2018), and Marghella et al. (2016).
Definition of Performance Levels and Seismic Hazard
With the aim of requalifying the highest number of manufacts of the Italian cultural heritage, the Italian directive (G.U. n. 47, 26/02/2011) allows for improving the seismic performance without imposing a complete retrofitting. This consequently allows us to design small and cheap interventions, instead of heavy, widespread and invasive ones. In this way each manufact can be considered as seismically protected for a lower action level (i.e., for a lower Return Period, TR). In other words, it is permitted to reduce the observation time in which the seismic action is evaluated. This interval, defined as reduced nominal life VN, Red, has to be assumed equal to or higher than 20 years (G.U. n. 47, 26/02/2011).
In line with this criterion, the seismic analyses presented herein are performed considering a reduced nominal life VN, Red assumed corresponding to 20 years, and a standard nominal life VN = 50 years, as requested for newly designed buildings. The coefficient of use adopted in both the cases is CU = 1.5, and, therefore, the observation time is adopted to define the seismic action results VR = 30 years for VN, Red = 20 years and VR = 75 years for VN = 50 years.
The city of Matera falls in a moderate seismicity zone, and many moderate seismic events hit it in the past years. Specifically, in the Italian historic catalog (CPTI, 2015), some events with macro-seismic intensity equal to 7 and many events with intensity equal to 6 are found. The seismic action is defined in accordance with the Italian seismic code (Ministerial Decree, 14/01/2008) by considering the Damage Limit State (DLS) and the Life Safety Limit state (LSLS). By assuming the observation periods discussed above, we obtain a return period TR equal to 30 and 75 years for the DLS, and TR equal to 285 and 712 years for the LSLS.
In Figure 2 the considered elastic and design spectra for the horizontal component of seismic action are shown. It should be noted that, according to what observed in Paulay and Priestley (1992) for masonry structures, the elastic spectra is calculated by considering a damping ratio equal to 10%. Furthermore, a behavior factor q = 2 is considered for the design spectra, according to the Italian code suggestions.
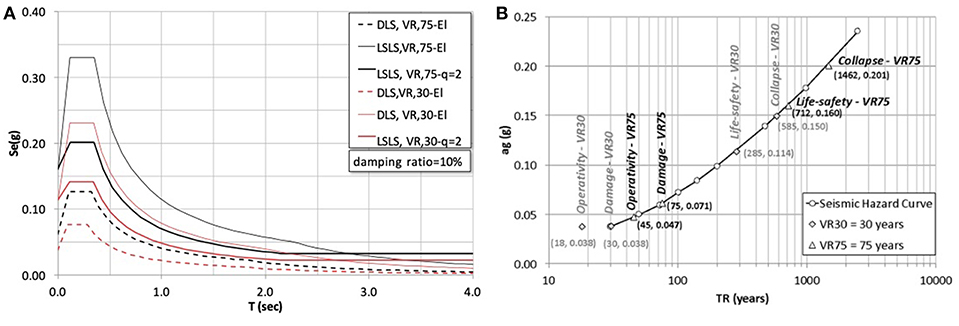
Figure 2. (A)Spectra of the horizontal seismic action corresponding to DLS and LSLS (B) Seismic Hazard of the site (in semi-logarithmic scale).
Application of LV1 Method
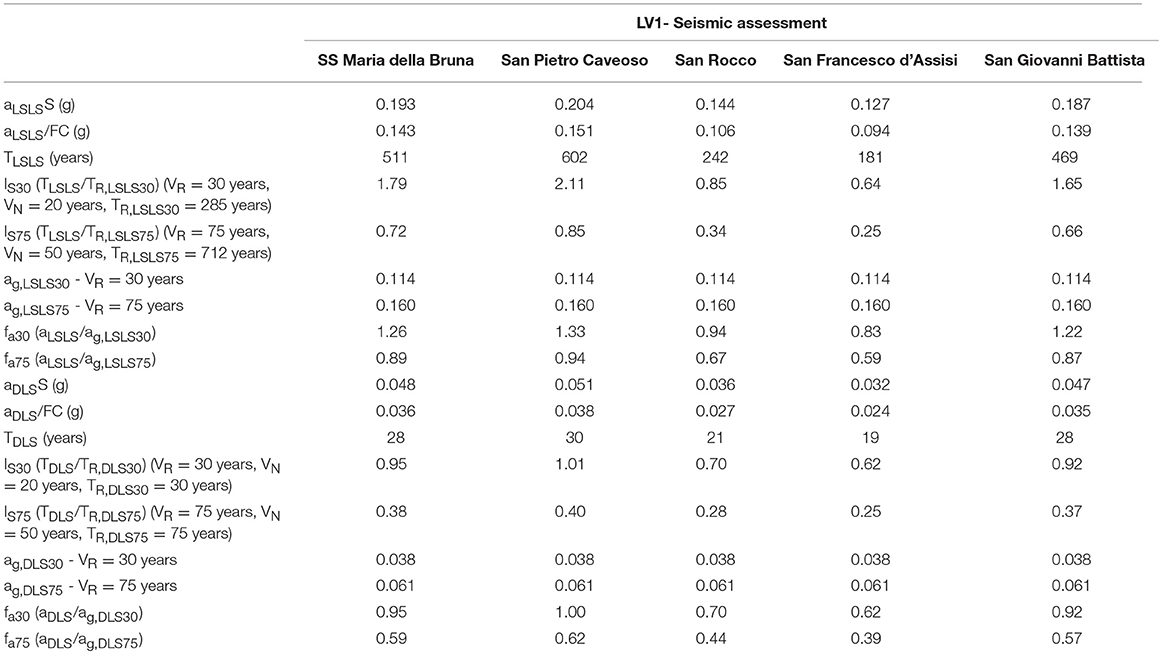
In order to apply the LV1 method, Table 2 numerically reports, for each macro-element considered, the score assigned to the actual vulnerability (vki) and seismic-resistant device (vKp). With these scores, it has been possible to calculate for each church the vulnerability index iv (Equation 1), and then the seismic capacity measured through aLSLS and aDLS (Equations 2, 3). The obtained results are summarized in Table 3, where they are reported as the acceleration factor fa (Equation 7) and the seismic safety index IS (Equation 4). These parameters are calculated by considering two observation periods, that are VR = 30 years (obtaining Is, 30 and fa, 30) and VR = 75 years (obtaining IS, 75 and fa, 75). The seismic verifications are conducted by referring to both the LSLS (having a PVR = 10 %) and to the DLS (having instead a PVR = 63 %). Moreover, in comparing the results, the following additional assumptions have been made: FC = 1.35 (factor of confidence), S = 1 (soil stratigraphic factor).
Firstly, the results are presented in terms of return periods (TLSLS and TDLS, for LSLS and DLS, respectively) obtained on the predicted accelerations (aLSLS/FC and aDLS/FC) of each case study. It must be noted that the expected return period TDLS results are always, except for San Pietro Caveoso church, lower than 30 years, corresponding to the first point available of the site seismic hazard (Figure 2B). Therefore, in these cases, by following the Italian Design Code, ag, DLS30 has been considered equal to the one provided for a return period of 30 years (in this case it results ag, DLS30 = 0.038g). For sake of completeness, Figure 3 illustrates the numerical results summarized in Table 3 for the two considered limit states.
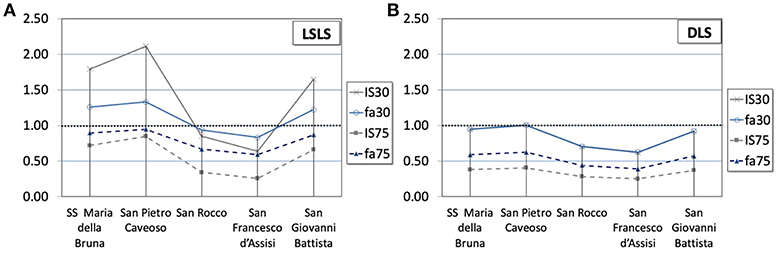
Figure 3A shows the considered indexes obtained for LSLS (i.e., Is and fa), evaluated for all the analyzed churches and for the two considered observation periods. For VR = 30 years, the SS Maria della Bruna church shows a low vulnerability, having both indexes exceeding the unity: Is30 = 1.65 and fa30 = 1.26. On the contrary, these indexes are significantly lower than unity if the observation period is equal to 75 years: in this case it results as Is75 = 0.66, and fa75 = 0.89. It is worth noting that SS Maria della Bruna church shows a low vulnerability if compared with others, except for San Pietro Caveoso church, where it is found Is30 = 2.11 (Is75 = 0.85) and fa30 = 1.33 (fa75 = 0.94). In Figure 3B, the resulting indexes for DLS are shown. In this case, the SS Maria della Bruna church provides, in all cases, numerical values that are always lower than unity: Is30 = 0.92 (Is75 = 0.37) and fa30 = 0.95 (fa75 = 0.59), even though higher than the other ones, except again for San Pietro Caveoso church where it is found that Is30 = 1.01 (Is75 = 0.40) and fa30 = 1.00 (fa75 = 0.62).
One may note that, as for the LSLS, the seismic safety index Is constantly reduces by about 2.5 times in all the churches (about 1.4 times in the case of fa), passing from VR = 30 years to VR = 75 years. This constant value may be justified by the fact that the ratio Is30/Is75 (or fa30/fa75) is dependent only on the return periods of the seismic actions expected on the site (accelerations expected on the site). The same conclusion may be done for the DLS, where Is30/Is75 results at about 2.5 (fa30/fa75 ≅ 1.6).
The results of Figure 3 clearly show that all the plotted curves for LSLS and DLS have qualitatively the same shape. In other words, the ranking of the seismic performances is always the same independently from the Limit State and from the index considered.
Application of LV2 Method
Seven failure mechanisms have been considered in this study: four directly connected to the ground, and the other three are not directly ground-connected. The considered mechanisms are the following:
- Façade simple overturning, where the stabilizing friction contribution of the orthogonal walls is neglected due to an effective connection;
- Colonnade longitudinal response, that is the macro-element separating the main nave from the lateral ones. It is composed of columns and arches placed in the longitudinal direction;
- Transversal response of triumphal arch, considering also (if present) the adjacent arches belonging to the lateral naves;
- Transversal response of lateral nave, that is an overturning mechanism considered separated from the main aula;
- Top façade simple overturning, façade portion overturning, starting from the highest point of lateral naves roof up to the façade peak;
- Gable simple overturning, simple overturning of the triangular portion placed at the façade top;
- Gable out-of-plane breakout, out-of-plane mechanism involving the triangular portion at the façade top activated by the means of three symmetrical cylindrical hinges.
For all the macro-elements, since the local masonry disintegration may be excluded, a monolithic behavior has been assumed. The macro-elements considered, as previously described, have been schematized starting from only visual investigations and geometric reliefs, since no clear cracking patterns have been encountered. In addition, no stabilizing contribution for each mechanism has been considered (such as interaction of transversal walls, or additional restrains). Therefore, the calculated activation multipliers underestimate the real ones. Furthermore, for simplicity, only the most vulnerable mechanisms have been considered in this study, not considering the in-plane response ones since they typically show higher activation multipliers.
Figure 4 illustrates the failure mechanisms in the case of SS Maria della Bruna church. It must be clarified that, for the comparison with the other churches, in the case of San Rocco and San Giovanni Battista churches, the triumphal arch mechanism has not been considered due to the absence of this architectonic element.
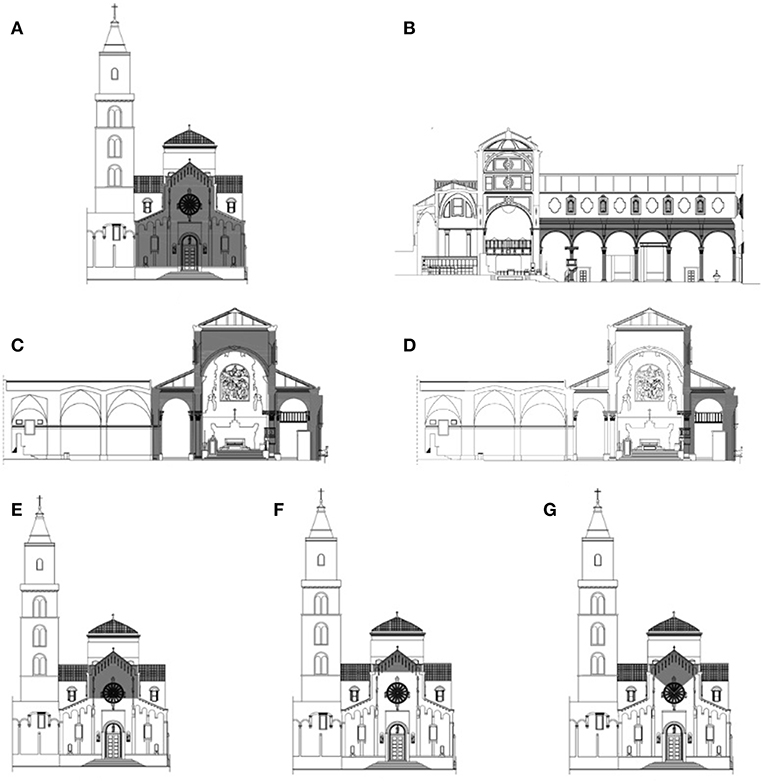
Figure 4. SS Maria della Bruna church. Response mechanisms considered: (A) Façade simple overturning, (B) longitudinal response of the colonnade, (C) triumphal arch transversal response, (D) lateral nave transversal response, (E) top façade overturning, (F) gable simple overturning, (G) gable out-of-plane breakout.
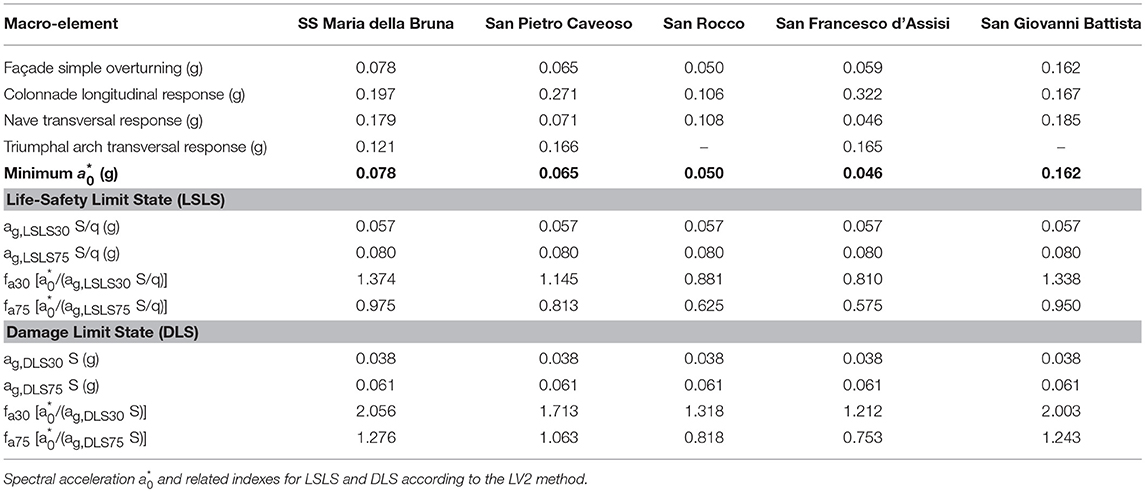
The spectral accelerations (derived from α0 according to the Equation 9), related to the activation of the considered macro-elements mechanism connected to the ground are shown in Table 4 and graphed in Figure 5A. Moreover, Table 4 reported the acceleration factors fa for a VR = 30 years and a VR = 75 years, calculated as follows:
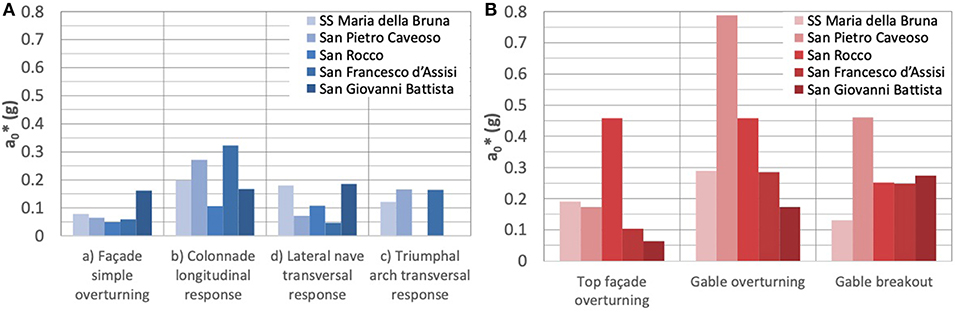
Figure 5. Spectral accelerations corresponding to the activation of a response mechanism (A) directly and (B) not directly ground-connected according to the LV2 method.
In Equation (19) for each church, it is considered the minimum values of for a given limit state (i.e., the most vulnerable failure mode). Whereas, ademand corresponds to the related expected seismic demand equal to: ag, LSLS30 S/q (or ag, LSLS75 S/q), or to ag, DLS30 S (ag, DLS75 S). Again, S has been assumed equal to 1 and q equal to 2.
The façade overturning results in the most vulnerable mechanism, with an activation acceleration of = 0.078 g, while the others have acceleration significantly higher (i.e., transversal response of triumphal arch = 0.121 g, about 55% higher than the value obtained for the façade overturning). It results that the most vulnerable mechanism for all churches is the simple overturning of the main façade, except for San Francesco d'Assisi church. In this case, the lowest spectral acceleration corresponds to the nave transversal response ( = 0.046 g). Furthermore, it should be remarked that in the case of San Giovanni Battista church, the accelerations obtained for all the mechanisms are significantly higher than the others, with a minimum value of 0.162 g that is more than twice of the one obtained for the SS Maria della Bruna Church. Moreover, Table 5 and Figure 6A satisfy the seismic performance requirements in the case of VR = 30 years for both LSLS and DLS, and in the case of VR = 75 years for DLS only while for LSLS fa75it is slightly < 1 (I.e. fa75 = 0.975). Again, as observed for the LV1 method, the Cathedral is close to satisfying all the required seismic safety obtaining indexes, and this satisfaction level is similar or higher than the other considered churches, except for San Giovanni Battista.
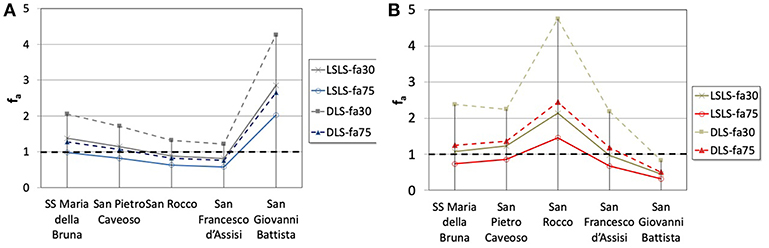
Figure 6. LV2 method. (A) Acceleration factors fa of macro-elements mechanisms directly ground-connected and (B) not directly connected to the ground for LSLSL and DLS.
In Table 5 and Figure 5B the accelerations relative to the macro-elements that are not directly ground-connected are shown. For SS Maria della Bruna church, the most vulnerable mechanism is the gable breakout with an activation acceleration of 0.131 g. By comparing the results with the others, it should be noted that only San Francesco d'Assisi and San Giovanni Battista churches have low , and therefore, the Cathedral is the third most vulnerable regarding these mechanisms. The seismic demand ademand is calculated in these cases as Se(T1)30ψ(Z)γ/q for VR = 30 years [or Se(T1)75ψ(Z)γ/q for VR = 75 years] for the LSLS, and as Se(T1)30ψ(Z)γVR = 30 years [or Se(T1)75ψ(Z)γ for VR = 75 years] for the DLS. Given this seismic demand, the acceleration factors can be calculated as the ratio of and such demands (i.e., fa30 = /Se(T1)30ψ(Z)γ/q and fa75 = /Se(T1)75ψ(Z)γ/q). By analyzing these acceleration factors (Figure 6B), it is worthy of noting that the SS Maria della Bruna church has values that are close or beyond the unity (i.e., for LSLS fa30 = 1.074, fa75 = 0.736; while for DLS fa30 = 2.382, fa75 = 1.284), confirming the need for only light interventions in order to obtain the required seismic performances. Furthermore, it should be remarked that the most vulnerable church regarding these mechanisms is San Giovanni Battista (i.e., = 0.064 g top façade overturning), which is less vulnerable regarding the mechanisms directly connected to the ground.
Comparative Seismic Assessment
The comparisons of the results calculated with the LV1 and LV2 methods of the Italian directive (G.U. n. 47, 26/02/2011) are illustrated in Figure 7. It should be specified that, in the case of the LV2 method, only the ground connected mechanisms are considered in these comparisons. Precisely, Figures 7A,B show the results for LSLS by referring to VR = 30 years and VR = 75 years, respectively. It is worth to note that for the Matera Cathedral the LV1 method, which is simpler and less accurate, overestimates the results if compared with the LV2 one. This trend is also found for San Pietro Caveoso church. However, for SS Maria della Bruna the scatter is low and, at least for VR = 30 years, the ratios are always beyond the unity. Whereas, in Figures 7C,D, the comparisons between the two adopted methods for the considered DLS are shown. Contrarily to the LSLS, in this case the LV1 method is, for the considered churches, always conservative with respect to the LV2 one. With the LV1 method only, the San Pietro Caveoso church exhibits, for VR = 30 years, a seismic capacity closer to the demand. As for the LV2 method, the capacity of all churches is always higher than demand except for San Rocco and San Francesco d'Assisi for VR = 75 years. Anyway, it should be remarked that the vulnerability classification provided by considering the two methods separately would be very similar since, as illustrated in the Figure 7, the trends found are quite the same. Nevertheless, by increasing the detail level of the analysis (from LV1 to LV2), it is found that in the analyzed cases, the LV1 overestimates the seismic performance, as for SS Maria della Bruna and San Pietro Caveoso church. However, it should be kept in mind that in this study, for simplicity, the LV2 results have been obtained by neglecting, as previously described, all the stabilizing contributions. Therefore, the actual results will be higher than those discussed here, and higher than the ones provided by the LV1 method. This confirms that after a first and fast numerical evaluation, useful for classifying the case studies, there is always the need to implement more realistic numerical models that cannot be generalized since they are related to the boundary conditions of the analyzed problem.
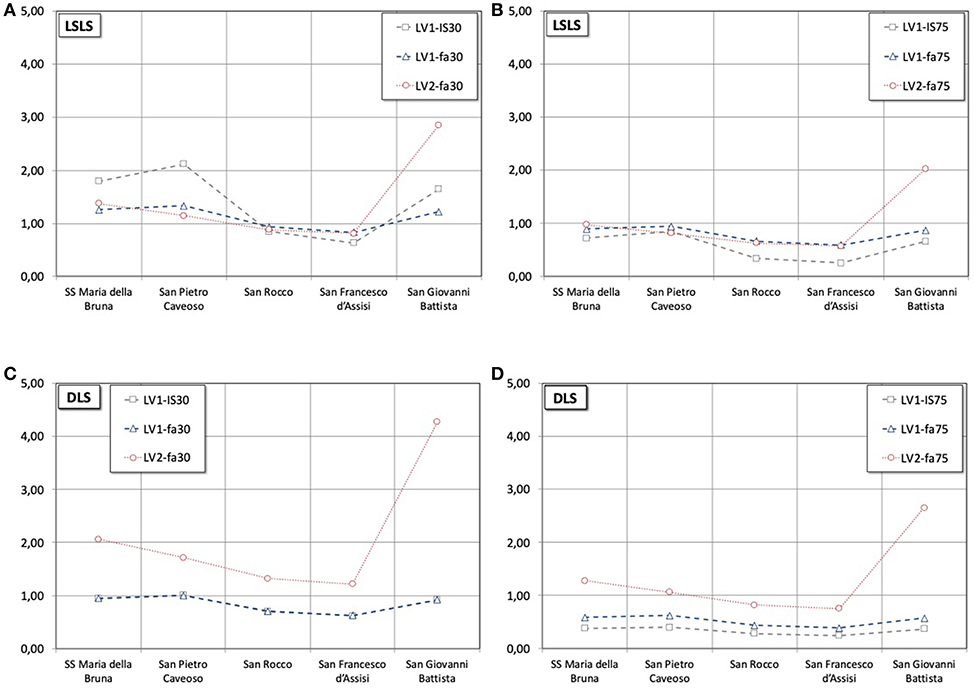
Figure 7. LV1 and LV2 methods. LSLS: (A) VR = 30 years and (B) VR = 75 years. DLS: (C) VR = 30 years and (D) VR = 75 years.
Finally, in this study a comparison with the method proposed in (Dìaz, 2016) is illustrated and then validated in D'Amato et al. (2018). Its application is numerically reported in Table 6. With this method, the SS Maria della Bruna church obtains a score of R = 22.15, resulting as the lowest value. All the obtained results are compared in relative terms in Figure 8: at first, each seismic score (Ri) is divided by the minimum value found (Rmin); then, all resulting ratios (Ri/Rmin) are represented in ascending order. For comparison, in Figure 8 the values calculated with the LV1 method are also reported. In detail, the dimensionless return period Ti, LSLS/TLSLSmin, where Ti, LSLS is the returning period corresponding to the LSLS achievement and TLSLSmin is the minimum value found among the churches (corresponding to 181 years for the San Francesco d'Assisi church), are plotted. In addition, in Figure 8 the dimensionless ground acceleration capacity ai, LSLS/aLSLSmin is also reported, where ai, LSLS is the ground acceleration related to the LSLS achievement and aLSLSmin is the lowest value found (that is 0.127 g corresponding, again, to the San Francesco d'Assisi church). One may consider these ratios as relative seismic vulnerability indexes: the ratio Ti, LSLS/TLSLSmin (or ai, LSLS/aLSLSmin) increases as the relative seismic vulnerability (Ri/Rmin) decreases, where both indexes are calculated with respect to the most vulnerable church (in this case San Francesco d'Assisi church). The results found confirm the applicability of the new simplified method proposed in Dìaz (2016) and validated in D'Amato et al. (2018). This method may be intended, in a multi-level frame-work approach, as a “Level of Evaluation 0” (LV0) since it permits rapidly ranking the seismic performance at a territorial level. In this way, useful information for individuating the priorities may be found, to be investigated in more detail with more refined approaches (such as LV1, LV2, or LV3).
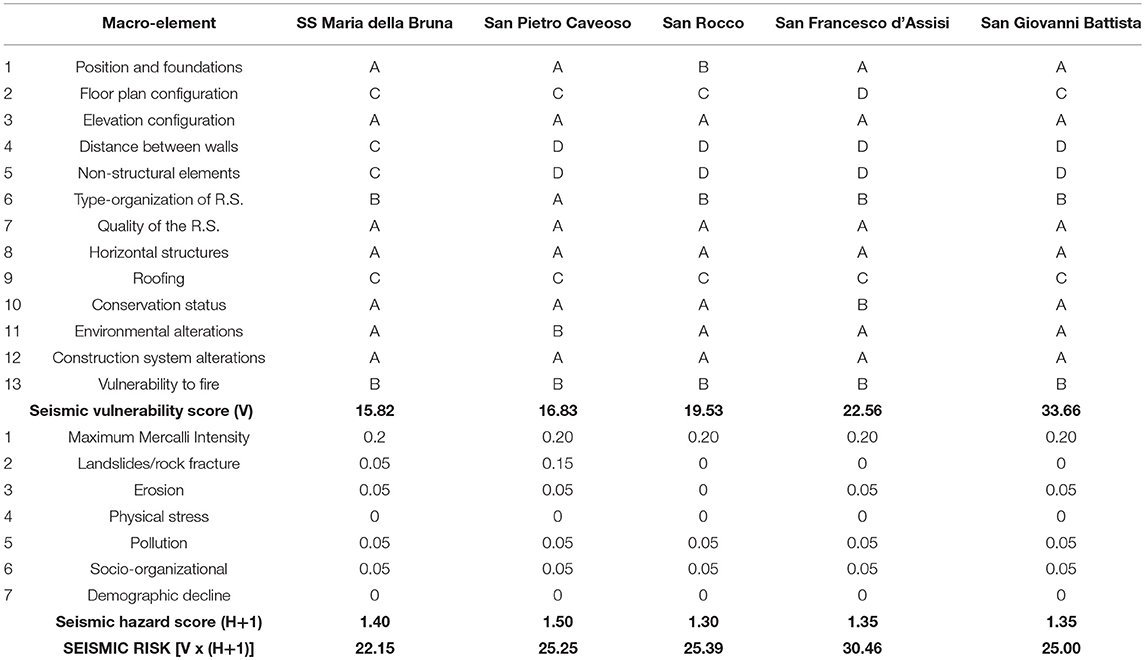
Table 6. New simplified seismic risk assessment scoring (Dìaz, 2016).
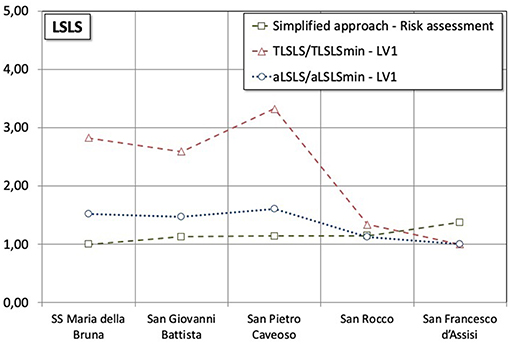
Figure 8. Comparisons among the results obtained with the LV1 and LV2 methods, and with the seismic risk assessment method (LSLS).
Conclusions
In this work, it has been conducted as a comparative analysis among the seismic performances of ancient masonry churches, by the means of different simplified methods. At first, the seismic vulnerability of the Matera Cathedral, called SS Maria della Bruna of Matera, has been investigated, and then the obtained results have been compared with the ones of four churches located in the Matera city center. The great advantage of these methods is that they don't imply advanced structural analyses and investigations. Thus, they can be used as decision making tools for identifying the priorities, and consequently, for performing further analyses and designing the potential interventions.
The analyses performed with the methods, indicated as LV1 and LV2 within the Italian directive (G.U. n. 47, 26/02/2011), have highlighted that, among the churches analyzed, the Matera Cathedral is one of the less vulnerable. Specifically, according to the LV2 method, it satisfies the seismic protection level required in the case of VR = 30 years, both for LSLS and for DLS. On the contrary, for VR = 75 years, few and light interventions are requested in order to achieve the required seismic demand for LSLS.
Finally, the comparisons with the new simplified method for seismic risk assessment confirm that it may be considered as a preliminary appraisal method for comparing the seismic performances of ancient churches at a territorial level. It may be proposed as a LV0 approach, since it requires limited and qualitative information for ranking the seismic performance at a territorial scale. However, by analyzing the obtained results, it has emerged that, in general, simpler methods may overestimate the actual seismic performance of a church. Therefore, the simplified methods, although useful for comparing and ranking the churches seismic performances at a territorial level, cannot substitute the refined ones for realistically assessing the seismic behavior of a structure.
Data Availability
All data generated or analyzed during this study are included in this published article.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Betti, M., Boschi, S., Borghini, A., Ciavattone, A., and Vignoli, A. (2018). Comparative seismic risk assessment of basilica-type churches. J. Earthquake Eng. 22, 62–95. doi: 10.1080/13632469.2017.1309602
Brandonisio, G., Lucibello, G., Mele, E., and De Luca, A. (2013). Damage and performance evaluation of masonry churches in the 2009 L'Aquila earthquake. Eng. Failure Anal. 34, 693–714. doi: 10.1016/j.engfailanal.2013.01.021
Caprili, S., Mangini, F., Salvatore, W., Bevilacqua, M. G., Karwacka Codini, E., Squeglia, N., et al. (2017). A knowledge-based approach for the structural assessment of cultural heritage, a case study: La Sapienza Palace in Pisa. Bull. Earthquake Eng. 15, 4851–4886. doi: 10.1007/s10518-017-0158-y
Castellazzi, G., Gentilini, C., and Nobile, L. (2013). Seismic vulnerability assessment of a historical church: limit analysis and nonlinear finite element analysis. Adv. Civil Eng. 2013:517454. doi: 10.1155/2013/517454
Castori, G., Borri, A., Corradi, M., De Maria, A., and Sisti, R. (2017). Seismic vulnerability assessment of a monumental masonry building. Eng. Struct. 136, 454–465. doi: 10.1016/j.engstruct.2017.01.035
CEN, CE. (2004). Design of Strctures for Earthquake Resistance. Part 3: Assessment and Retrofitting of Buildings. Brussels: CEN, Comité Européen de Normalisation.
CENAPRED (2006). Guía Básica Para la Elaboración de Atlas Estatales y Municipales de Peligros y Riesgos. Conceptos básicos sobre peligros, riesgos y su representación geográfica. Mexico City.
CENAPRED (2014). Diagnóstico de Peligros e Identificación de Riesgo de Desastres en México. Centro Nacional de Prevención de Desaster, Coyoacán.
Chilean Norm N. 3332 (2013). Estructuras - Intervención de Construcciones Patrimoniales de Tierra Cruda - Requisitos del Proyecto Estructural. Santiago: INN, Instituto Nacional de Normalización Chile (in Spanish).
Clementi, F., Gazzani, V., Poiani, M., and Lenci, S. (2016). Assessment of seismic behaviour of heritage masonry buildings using numerical modelling. J. Build. Eng. 8, 29–47. doi: 10.1016/j.jobe.2016.09.005
CPTI (2015). Parametric Catalogue of Italian Earthquakes. Retrieved from: https://emidius.mi.ingv.it/CPTI15-DBMI15/index_en.htm
D'Amato, M., Laterza, M., and Casamassima, V. M. (2017). Seismic performance evaluation of a multi-span existing masonry arch bridge. Open Civil Eng. J. 11(Suppl. 5), 1191–1207. doi: 10.2174/1874149501711011191
D'Amato, M., Laterza, M., and Dìaz Fuentes, D. (2018). Simplified seismic analyses of ancient churches in matera's landscape. Int. J. Architect. Heritage. doi: 10.1080/15583058.2018.1511000. [Epub ahead of print].
D'Ayala, D., and Speranza, E. (2003). Definition of collapse mechanisms and seismic vulnerability of historic masonry buildings. Earthquake Spectra 18, 479–509. doi: 10.1193/1.1599896
D'Ayala, D. F., and Paganoni, S. (2011). Assessment and analysis of damage in L'Aquila historic city centre after 6th April 2009. Bull. Earthquake Eng. 9, 81–104. doi: 10.1007/s10518-010-9224-4
de Felice, G., and Giannini, R. (2001). Out of plane seismic resistance of masonry walls. J. Earthquake Eng. 5, 253–271. doi: 10.1080/13632460109350394
Degg, M., and Chester, D. (2005). Seismic and volcanic hazards in Peru: changing attitudes to disaster mitigation. Geogr. J. 171, 125–145. doi: 10.1111/j.1475-4959.2005.00155.x
DGPTA (2003). Rilevamento Della Vulnerabilità Sismica Degli Edifici in Muratura. Manuale Per la Compilazione Della Scheda GNDT/CNR di II Livello. Roma: Direzione Generale delle Politiche Territoriali e Ambientali.
Dìaz, D. (2016). Diseño de Herramientas de Evaluación del Riesgo Para la Conservación del Patrimonio Cultural Inmueble. Aplicación en dos Casos de Estudio del Norte Andino Chileno. México: Publicaciones ENCRyM-INAH.
Doglioni, F., Moretti, A., and Petrini, V. (1994). Churches and the Earthquake. Trieste: Ed. LINT (in Italian).
Doherty, K., Griffith, M., Lam, N., and Wilson, J. (2002). Displacement-based seismic analysis for out-of-plane bending of unreinforced masonry walls. Earthquake Eng. Struct. Dyn. 31, 833–850. doi: 10.1002/eqe.126
Fabbrocino, F., Vaiano, G., and Formisano, A. (2018). “Parametric analysis on local collapse mechanisms of masonry churches,”in 16th International Conference of Numerical Analysis and Applied Mathematics - ICNAAM 2018. Rhodes 13-18 September 2018: Proceedings of AIP Conference.
FEMA (2004). Primer for Design Professionals (FEMA389). Washington, DC: Department of Homeland Security Emergency Preparedness and Response Directorate.
Formisano, A., Ciccone, G., and Mele, A. (2017). “Large scale seismic vulnerability and risk evaluation of a masonry churches sample in the historical centre of Naples,” 13th International Conference of Computational Methods in Sciences and Engineering (ICCMSE 2017) - AIP Conference Proceedings 1906, 1906. Thessaloniki, 21-25 April 2017.
Formisano, A., and Marzo, A. (2017). Simplified and refined methods for seismic vulnerability assessment and retrofitting of an Italian cultural heritage masonry building. Comput. Struct. 180, 13–26. doi: 10.1016/j.compstruc.2016.07.005
Formisano, A., Vaiano, G., Fabbrocino, F., and Milani, G. (2018). Seismic vulnerability of Italian masonry churches: the case of the Nativity of Blessed Virgin Mary in Stellata of Bondeno. J. Build. Eng. 20, 179–200. doi: 10.1016/j.jobe.2018
Fuentes, D. D., D'Amato, M., and Laterza, M. (2019). “Seismic vulnerability and risk assessment of historic constructions: the case of masonry and adobe churches in Italy and Chile. SAHC 2018,” 11th International Conference on Structural Analysis of Historical Constructions. Cusco, 11-13 September 2018: RILEM Bookseries, 1127–1137.
GU. n. 47 (09/02/2011). Directive of the Prime Minister dated on 09/02/2011. Assessment and mitigation of seismic risk of cultural heritage with refeence to the technical code for the design of construction issued by D.M. 14/01/2008 (in Italian).
Heyman, J. (1966). The stone skeleton. Int. J. Solids Struct. 2, 249–279. doi: 10.1016/0020-7683(66)90018-7
Instructions for the application of the Ministerial Decree MD (14/01/2008). “Circolare 2 Febbraio 2009 n. 617 – Istruzioni per l'applicazione delle Nuove Norme Tecniche per le Costruzioni di cui al D.M. 14 Gennaio 2008”. S.O. n. 27 of the Official Gazette of the Italian Republic published on 26/02/2009, n. 47 (in Italian).
Instructions for the application of the Ministerial Decree MD (17/01/2018). “Circolare 21 Febbraio 2019 n. 7 – Istruzioni per l'applicazione dell'Aggiornamento delle Nuove Norme Tecniche per le Costruzioni di cui al D.M. 17 Gennaio 2018.” S.O. n. 8 of the Official Gazette of the Italian Republic published on 20/02/2018, n. 42 (in Italian).
ISCR, I. S. (2017). Carta del Rischio. Retrieved from: http://www.cartadelrischio.it/
Krstevska, L., Tashkov, L., Naumovski, N., Florio, G., Formisano, A., Fornaro, A., et al. (2010). “In-situ experimental testing of four historical buildings damaged during the 2009 L'Aquila earthquake,”in COST ACTION C26: Urban Habitat Constructions under Catastrophic Events - Proceedings of the Final Conference (Naples), 427–432.
Lagomarsino, S. (2012). Damage assessment of churches after l'Aquila earthquake (2009). Bull. Earthquake Eng. 10, 73–92. doi: 10.1007/s10518-011-9307-x
Lagomarsino, S., and Podestà, A. (2004a). Seismic vulnerability of ancient churches. Part 1: damage assessment and emergency planning. Earthquake Spectra 20, 377–394. doi: 10.1193/1.1737735
Lagomarsino, S., and Podestà, S. (2004b). Seismic vulnerability of ancient churches. Part 2: statistical analysis of surveyed data and methods for risk analysis. Earthquake Spectra 20, 395–412. doi: 10.1193/1.1737736
Lagomarsino, S., and Podestà, S. (2005). Inventario e Vulnerabilità del Patrimonio Monumentale dei Parchi dell'Italia Centro-Meridionale, Vol. III - Analisi di Vulnerabilità e Rischio Degli Edifici Monumentali. L'Aquila: INGV/GNDT - Istituto Nazionale di Geofisica e Vulcanologia/Gruppo Nazionale per la Difesa dai Terremoti.
Lagomarsino, S., and Resemini, S. (2009). The assessment of damage limitation state in the seismic analysis of monumental buildings. Earthquake Spectra 25, 323–346. doi: 10.1193/1.3110242
Laterza, M., D'Amato, M., and Casamassima, V. M. (2016). “Seismic performance evaluation of multi-span existing masonry arch bridge,” in Proceedings of the 14th International Conference of Numerical Analysis and Applied Mathematics - ICNAAM 2016. 1863, p. Article n. 450010. Rodos Palace Hotel, Rhodes, September 19th-25th 2016: AIP Conference Proceedings.
Lopez, S., D'Amato, M., Ramos, L., Laterza, M., and Lourenço, P. B. (2019). Simplified formulation for estimating the main frequencies of ancient masonry churches. Front. Built Environ. 5:18. doi: 10.3389/fbuil.2019.00018
Lourenço, P. B., Oliveira, D. V., Leite, J. C., Ingham, J. M., Modena, C., and da Porto, F. (2013). Simplified indexes for the seismic assessment of masonry buildings: international database and validation. Eng. Failure Anal. 34, 585–605. doi: 10.1016/j.engfailanal.2013.02.014
Lourenço, P. B., and Roque, J. A. (2006). Simplified indexes for the seismic vulnerability of ancient masonry buildings. Construct. Build. Mater. 20, 200–208. doi: 10.1016/j.conbuildmat.2005.08.027
Luchin, G., Luis, L. F., and D'Amato, M. (2018). Sonic tomography for masonry walls characterization. Int. J. Architect. Heritage. doi: 10.1080/15583058.2018.1554723. [Epub ahead of print].
Marghella, G., Marzo, A., Carpani, B., Indirli, M., and Formisano, A. (2016). “Comparison between in situ experimental data and Italian code standard values,”in 16th International Brick and Block Masonry Conference, IBMAC 2016, Padova, 1707–1714.
Marotta, A., Sorrentino, L., Liberatore, D., and Ingham, J. M. (2018). Seismic risk assessment of New Zealand unreinforced masonry churches using statistical procedures. Int. J. Architect. Heritage 12, 448–464. doi: 10.1080/15583058.2017.1323242
Ministerial Decree (14/01/2008). Norme Tecniche per le Costruzioni. S.O. n. 30 of the Official Gazette of the Italian Republic 2008 n. 29.
Paulay, T., and Priestley, M. (1992). Seismic Design of Reinforced Concrete and Masonry Buildings. New York, NY: John Wiley and Sons, Inc.
Ragone, A., Ippolito, A., Liberatore, D., and Sorrentino, L. (2017). “Emerging technologies for the seismic assessment of historical churches: the case of the bell tower of the Cathedral of Matera,”in Handbook of Research on Emerging Technologies for Architectural and Archaeological Heritage Hershey, PA: IGI Global, 159–196.
Ramirez, E., Lourenco, P. B., and D'Amato, M. (2019). “Seismic assessment of the matera cathedral,”in SAHC 2018, 11th International Conference on Structural Analysis of Historical Constructions, Cusco, 11-13 September 2018: RILEM Bookseries, 1346–1354.
Sarhosis, V., Milani, G., Formisano, A., and Fabbrocino, F. (2018). Evaluation of different approaches for the estimation of the seismic vulnerability of masonry towers. Bull. Earthquake Eng. 16, 1511–1545. doi: 10.1007/s10518-017-0258-8
UNDRO (1979). Natural Disasters Vulnerability Analysis. United Nations Disaster Relief Organisation.
Valente, M., Barbieri, G., and Biolzi, L. (2017). Seismic assessment of two masonry Baroque churches damaged by the 2012 Emilia earthquake. Eng. Failure Anal. 79, 773–802. doi: 10.1016/j.engfailanal.2017.05.026
Valente, M., and Milani, G. (2018a). Damage assessment and partial failure mechanisms activation of historical masonry churches under seismic actions: three case studies in Mantua. Eng. Failure Anal. 92, 495–519. doi: 10.1016/j.engfailanal.2018.06.017
Keywords: ancient churches, cultural heritage protection, masonry, seismic vulnerability, seismic risk
Citation: D'Amato M, Gigliotti R and Laguardia R (2019) Comparative Seismic Assessment of Ancient Masonry Churches. Front. Built Environ. 5:56. doi: 10.3389/fbuil.2019.00056
Received: 13 February 2019; Accepted: 12 April 2019;
Published: 03 May 2019.
Edited by:
Solomon Tesfamariam, University of British Columbia, CanadaReviewed by:
Michele Betti, University of Florence, ItalyAntonio Formisano, University of Naples Federico II, Italy
Marco Valente, Politecnico di Milano, Italy
Copyright © 2019 D'Amato, Gigliotti and Laguardia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Michele D'Amato, bWljaGVsZS5kYW1hdG9AdW5pYmFzLml0
 Michele D'Amato
Michele D'Amato Rosario Gigliotti
Rosario Gigliotti Raffaele Laguardia
Raffaele Laguardia