- 1Dipartimento di Ingegneria Civile, Ambientale, Aerospaziale, dei Materiali, Università degli Studi di Palermo, Palermo, Italy
- 2Department of Mathematical Sciences, University of Liverpool, Liverpool, United Kingdom
In this paper, the use of hybrid passive control strategies to mitigate the seismic response of a base-isolated structure is examined. The control performance of three different types of devices used for reducing base displacements of isolated buildings is investigated. Specifically, the Tuned Mass Damper (TMD), the New Tuned Mass Damper (New TMD) and the Tuned Liquid Column Damper (TLCD), each one associated to a Base Isolated structure (BI), have been considered. The seismic induced vibration control of base-isolated structures equipped with the TMD, New TMD or the TLCD is examined and compared with that of the base-isolated system without devices, using real recorded seismic signals as external input. Data show that the New TMD is the most effective in controlling the response of base-isolated structures so that it can be considered as a practical and appealing means to mitigate the dynamic response of base-isolated structures.
Introduction
In the context of passive vibration control, the base isolation (BI) is recognized as a valid strategy in preserving buildings from damage and collapse due to earthquakes, especially for those structures located in high hazard seismic areas and with strategic importance.
Undoubtedly, one of the advantages deriving from the installation of seismic isolators is the considerable reduction of the inter-story drift which leads to a quasi-rigid motion of the superstructure.
The effectiveness of the base isolation technique motivated many researchers to focus on its optimization limiting its detrimental features. Specifically, particular attention should be paid in a design phase to the displacements which elastomeric bearings can be subjected to. In this regard, these devices can undergo considerable deformations because of their low lateral stiffness; accordingly, some issues could arise: large displacements could cause adjacent buildings to collide; further, the need to adapt utilities and connection systems at the interface between the super-structure and the sub-structure should be considered; and finally, irreversible damage could occur in the isolators that lose their functionality.
Among several alternatives analyzed in literature for improving BI system performance, one is related to the addition of some linear viscous dampers to the BI system, or to the increase of its damping (Kelly, 1990, 1999). However, although it has been demonstrated that higher values of damping in the BI system lead to smaller deformations at the base, other drawbacks, such as the increase of both inter-story drifts and floor accelerations of the main structure, may arise (Kelly, 1999).
The idea to combine the BI system with other types of passive control systems, generally used individually in a unique control system, was proposed in Yang et al. (1991), where a structure isolated by rubber bearings and equipped with a Tuned Mass Damper placed on the base has been considered. Further, the effectiveness of such hybrid strategy has been demonstrated on the basis of numerical analysis carried out on a 20-DOFs building.
Notably, this idea arose by observing essentially two phenomena:
- through the installation of the isolation system, the frequency of total structure drops and the structure is dominated mainly by only one mode shape.
- the Tuned Mass Dampers (TMDs) reliability on suppressing structural vibrations and preventing resonance behavior in structures characterized by a prevalent vibration mode (Den Hartog, 1956).
In this regard, the coupling between the base isolation and the Tuned Mass Damper (BI+TMD) was also analyzed in Palazzo and Petti (1994, 1999), where the validity of this system in limiting the deformations at the base has been proved.
The factors influencing the performance of the TMD on the structural response of base isolated structures, such as the input frequency, the choice of the optimum tuning frequency and the damping ratio of the TMD, have been investigated in Tsai (1995). Specifically, it has been demonstrated that TMDs increase the damping of the total structure and consequently the response after the first seconds of the seismic input. In order to attenuate the structural response during the first phase of excitation, the concept of a possible efficient accelerated TMD has been proposed, but it remained only a mathematical suggestion, hardly to be realized.
As far as the position of the TMD is concerned, the effect of varying the placement of the TMD on different floor levels has been studied in Stanikzai et al. (2019) and it has been found that for low-rise buildings, the placement of TMD mass has no significant role in reducing the response of the buildings.
The need to consider larger masses to improve the efficiency of the TMD has led to consider the possibility to place multiple TMDs (MTMDs) or distributed MTMDs (d-MTMDs) along the height of buildings (Stanikzai et al., 2018). The use of multiple TMDs can represent a more robust solution also when variation of soil parameters is taken into account in the soil-structure interaction. Indeed, as demonstrated in Elias and Matsagar (2017) for the case of the combination of the TMDs with base isolated bridges, the soil type can affects the performance of the TMD, and the installation of multiple TMDs compared to a single TMD, are more effective in controlling the structural response.
Furthermore, as demonstrated in Stanikzai et al. (2018), the use of MTMDs or d-MTMDs represents an effective solution to tune the devices to higher modal frequencies too, and in order to avoid detuning effects of a single TMD with the main frequency of the structure.
However, in real cases, it could result more convenient to attach the TMD in correspondence of the level of the isolation system as detailed in Melkumyan (2012).
A practical implementation of the seismic base isolation in conjunction with a TMD, placed at the basement, to a real case study, has been examined in De Domenico and Ricciardi (2018a,b). Aiming at improving the seismic performance of a reinforced concrete building, it has been proposed to insert a TMD at the center of the basement of the building, built as a box filled with aggregate concrete, attached below the isolation floor. In this case, the role of the TMD damper and spring is supposed to be played by additional isolators which connect the TMD to the base, while the TMD is disconnected from the ground by means of sliding elements.
On this base, it can be clearly argued that the base displacement demand of isolated structure can be reduced through the use of a traditional TMD, depending on the TMD mass itself. Specifically, bigger TMD masses could lead to a greater reduction of the response of the seismic bearings.
On the other hand, the presence of a TMD on the basement may also yield some drawbacks which need to be considered: firstly, the big mass that should be added to the system; secondly, the TMD's stroke that should be taken into account in the design of the spaces for its location.
To deal with these limitations, some variants of the classic TMD have been studied; for instance, a TMD with non-linear characteristics has been proposed in Nissen et al. (1985), Natsiavas (1992), and Vakakis et al. (2003) and it has been demonstrated to be effective in minimizing deformations of the isolators despite the instability phenomena related to the non-linearities.
Another type of TMD, referred to as New TMD or non-traditional TMD, has been introduced by in Ren (2001), and in Cheung and Wong (2011) and Xiang and Nishitani (2014) the optimization of the New TMD combined with the base isolation (BI + New TMD) has been discussed.
Compared to the traditional TMD, the New TMD alters the position of the dampers. Specifically, in the New TMD, a dashpot is located between the TMD mass and the ground, rather than the TMD mass and the base of the BI system, as in a traditional TMD.
Notably, from a theoretical point of view, the installation of the New TMD involves higher dissipative forces and could attenuate the TMD stroke, consequently, it needs less space for its placing.
Among the strategies which couple passive control devices with base isolation systems, the BI + TMD and its variants are certainly the most investigated in the literature. In this context, an enhanced version of the TMD has been explored in De Domenico and Ricciardi (2018a,b) and references therein), and in De Angelis et al. (2019), by endowing the TMD with a mechanical device, called inerter, providing additional rotational inertia to the device. However, recently other solutions have been considered.
In this regard, Tuned Liquid Column Dampers (TLCDs) have been proposed as possible alternative to the TMD also in the field of hybrid control systems. Specifically, the TLCD, which consists of a U-shaped vessel filled with a certain amount of liquid, generally water, is placed on the base of the structure and, unlike TMDs, does not need mechanical components. Recently, some contributions regarding the TLCD optimization and experimentation have been presented in Di Matteo et al. (2017a,b), where it has been shown that the effectiveness of the TLCD, if carefully designed, could be comparable or slightly lower than the TMD one. Moreover, compared to the TMD, the use of TLCDs is often preferable because of its easier installation. Further, it is cheaper and it could be employed as a water reserve in case of fire, so it represents an appealing and convenient solution.
Nevertheless, equations of motion of the TLCD may involve computationally expensive calculations due to the presence of non-linear terms and the identification of dynamic parameters that characterize this device is not so immediate.
In order to overcome these drawbacks, a simpler equivalent linear system has been introduced (Gao and Kwok, 1997; Chang, 1999; Yalla and Kareem, 2000; Wu et al., 2009), and the determination of the optimal design parameters has been studied by employing statistical linearization techniques (SLT) (Sakai et al., 1989; Di Matteo et al., 2017a,b).
Recently in Di Matteo et al. (2017a), a direct method has been developed to optimize the dynamic parameters of a TLCD attached to an isolated building, supposing a Gaussian white noise process as external input. Results derived from this approach show a good agreement with those obtained by applying the classical statistical linearization technique (SLT) which involves longer computational time (Roberts and Spanos, 1990).
On the base of this conspectus, this paper aims at comparing and investigating on the most promising strategy, among the main passive control devices coupled with the BI system, to minimize the base displacements of isolated buildings, preserving the benefits of the BI system (small inter-story drifts and accelerations).
Specifically, the analyzed hybrid systems (Figure 1A), are:
- BI + TMD (shown in Figure 1B);
- BI + New TMD (shown in Figure 1C);
- BI + TLCD (shown in Figure 1D).
In this study, the mass of each considered device is intended to be placed on the basement of isolated structure. To the best of the authors' knowledge, although several studies exist in the literature about the different types of the aforementioned absorbers, few of them consider the TLCD at the base of isolated structure and the comparison of such a device with the New TMD has not been analyzed.
In passing, it is noted that the term “New TMD” mentioned throughout the paper refers to the device proposed in Xiang and Nishitani (2014). Thus, no new device has been introduced in this paper, and readers interested on some specific insights on this control systems are referred to Xiang and Nishitani (2014) and references therein.
Problem Formulation
In this section the equations of motion of all the exanimated systems (BI, BI + TMD, BI + New TMD, and BI + TLCD systems) in the time domain are presented, and relations in the frequency domain are also introduced. In particular, the displacement transfer functions, relating the base displacement of each system to the input force, have been determined for a full understanding of the dynamic behavior of all the systems.
BI System
Consider a BI plane frame structure, with n+1 degrees of freedom, excited by a horizontal earthquake ground acceleration ẍg(t) (Figure 1A). Let mb, Kb, Cb denote mass, the stiffness and damping coefficient of the base isolation story in the BI model, assumed as a linear system. The displacement of mass mb relative to the ground is denoted as xb(t). The superstructure has n degrees of freedom. The ith superstructural degree of freedom has lumped mass Mi.
The corresponding displacement component xi(t) represents the superstructural displacement relative to the base. The total mass is:
In the time domain, the response of the isolated structure is governed by the following n+1 equations of motion:
(i = 1, …, n)
In which Ci, j and Ki, j are the entries of the damping and stiffness matrices of the superstructure.
When dealing with a main structure having a Single Degree Of Freedom (SDOF), i.e., n = 1, the equations of motion are given by:
Where μb = M1/Mtot represents the mass ratio; and ζb = Cb/(2ωbMtot) are the natural frequency and damping ratio of the base isolation system respectively; and ζ1 = C1/(2ω1M1) are the natural frequency and damping ratio of the SDOF main structure.
In the frequency domain, the Fourier transform of system (3) leads to:
The transfer function of the base displacement (Hb(ω) = Xb(ω)/Ẍg(ω)) can be written as:
The transfer function of the displacement at the top of the superstructure(HX1(ω) = X1(ω)/Ẍg(ω)) is:
where:
Aiming at reducing the displacement occurring within the BI system, consider now the case of the above described base isolated structure in which the BI system is connected to an additional passive dissipation mechanism (such as the TMD, the TLCD or the New TMD).
Hybrid Strategy 1—BI +TMD
The hybrid control strategy combining classical TMD device with base isolation system (BI + TMD) is shown in Figure 1B. The TMD is modeled as a SDOF linear system with mass md, stiffness kd and damping cd. The displacement of the TMD relative to the base is denoted as xd(t). The n+2 equations of motion of a base isolated building equipped with a TMD can be written as:
For a SDOF main structure (n = 1), equations of motion are particularized as:
where and ζd = cd/(2ωdmd) are the natural frequency and damping ratio of the TMD and the other symbols have the same meaning of those defined in section BI System.
In the frequency domain, the Fourier transform of system (9) leads to:
Therefore, the base-isolation displacement transfer function (Hb(ω) = Xb(ω)/Ẍg(ω)) can be written as
while the main structure displacement transfer function (HX1(ω) = X1(ω)/Ẍg(ω)) and the TMD displacement transfer function (Hd(ω) = Xd(ω)/Ẍg(ω)) respectively are:
in which
Hybrid Strategy 2—BI + New TMD
The hybrid control strategy coupling the so called New TMD or non-traditional TMD with the base isolation system (BI + New TMD) is shown in Figure 1C.
The New Tuned Mass Damper is modeled similarly to the TMD but, unlike the TMD, the New TMD is directly connected to the ground by a dashpot. From a theoretical point of view, this condition leads to higher damping forces compared to the traditional TMD.
The n+2 equations of motion of a base isolated building equipped with a New TMD can be written as:
As it can be seen in the second line of Equation (14), the particular configuration of the New TMD, endowed with a dashpot directly connected to the ground, leads to a dissipative force Fd = cdẋd + cdẋb, which is larger than that related to the traditional TMD (Fd = cdẋd, see Equation (8)] since it is proportional to both the velocities of the device and the BI system.
For a SDOF main structure (n = 1), equations of motion are particularized as:
Where the symbols have the known meaning of those defined in the section Hybrid strategy 1—BI +TMD for the traditional TMD.
Considering the system in the frequency domain, the Fourier transform of system (15) leads to:
Therefore, the base-isolation displacement transfer function (Hb(ω) = Xb(ω)/Ẍg(ω)) can be written as
while the main structure displacement transfer function (HX1(ω) = X1(ω)/Ẍg(ω)) and the New TMD displacement transfer function (Hd(ω) = Xd(ω)/Ẍg(ω)), respectively are:
in which
Hybrid Strategy 3—BI+TLCD
Another means to control the seismic response of base isolated structure consists of the use of TLCD located on the basement of the main structure (BI+TLCD) (Figure 1D). Denoting with g the gravitational acceleration, Lv and Lh the vertical and horizontal liquid length, respectively, L = Lh + 2Lv the total length of the liquid column inside the TLCD, the n+2 dimensional system of equations can be expressed by:
Here α = Lh/L is the so called length ratio and describes the fraction of effectively moving liquid in horizontal direction mh = αm, to the total liquid mass m inside the tube, y(t) is the vertical liquid displacement and ξ is a head loss factor dependent on the type of flow and its interaction with container wall or on the presence of orifice inside the TLCD. When n = 1 (SDOF main structure), equations of motion can be written as:
Where, μ2 = m/Mtot is the liquid mass ratio and is the frequency associated with the liquid inside the TLCD (Hochrainer and Ziegler, 2006).
It is worth noting that, unlike traditional TMDs, the TLCD response is non-linear due to the presence of term in the second equation of the system (21) (Di Matteo et al., 2012, 2014a,b).
However, in order to avoid onerous calculus and complex optimization procedure due to the presence of the non-linear damping term, the original non-linear system (21) usually is replaced by a linear equivalent one. Using the “Statistical Linearization Technique” (SLT), the equations of the BI + TLCD system can be written in the following form:
where ζ2 is the equivalent damping ratio, which can be calculated through a direct optimization procedure of the TLCD design parameters performed in Di Matteo et al. (2014a,b, 2015, 2017a,b) and explained in the Appendix. Specifically, following the analysis in Roberts and Spanos (1990), Di Matteo et al. (2014a), the relationship between ζ2 and ξ is:
where σẎ is the standard deviation of the velocity of the liquid inside in the TLCD (see Appendix A for further details).
In the frequency domain, the Fourier transform of system Equation (22) leads to:
Therefore, the base-isolation displacement transfer function (Hb(ω) = Xb(ω)/Ẍg(ω)) can be written as
while the main structure displacement transfer function (HX1(ω) = X1(ω)/Ẍg(ω)) and the fluid displacement transfer function, respectively, are
In which
The aforementioned closed form solutions to evaluate the frequency response functions (FRFs) of the systems have been directly considered to carry out the frequency analysis in the following.
Analysis of the Control Performance
In order to investigate on the efficacy of the proposed hybrid strategies to reduce the base displacement and acceleration without increasing other structural quantities (such as roof displacements and accelerations), here a numerical example, involving two different main systems, has been developed.
The first structural system is a SDOF base isolated structure model, while the second one is a MDOF base isolated structure model. Both structures have been analyzed equipped each time with the aforementioned passive vibration control devices (TMD, TLCD, and New TMD) and subjected to selected recorded accelerograms, to take into account the influence of the non-stationary nature of real earthquakes.
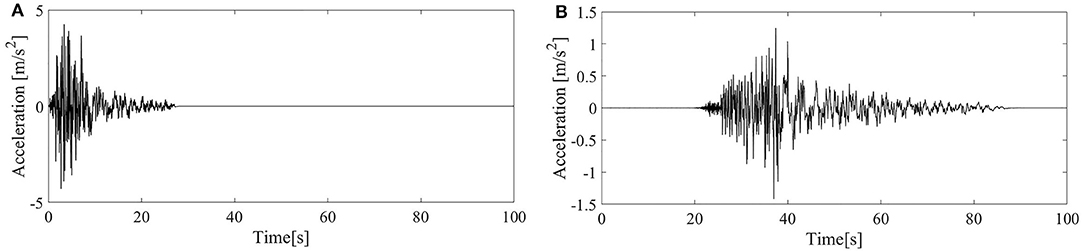
Specifically, the San Fernando and the Chi-Chi recorded earthquakes have been used as input forces (Figures 2A,B), taken by the FEMA P-695-FF (FEMA P-695, 2009), a collection of ground motions with a magnitude between 6.5 and 7.6 recorded on NEHRP site classes C (soft rock) and D (stiff soil).
Note that these two earthquakes records present quite different characteristics since the first has high impulsive content in the first instants of motion, which is known to be an unfavorable condition for the efficiency of control devices.
The analysis has been carried out both in the time and in the frequency domain.
In the following numerical simulations carried out on the SDOF base isolated structure, controlled by a passive control device, the FRFs have been found using the closed form solutions reported in section Problem Formulation. For the multi-degree of freedom (MDOF) superstructure, the FRFs have been computed by means of the fft function in MatLab, which computes the discrete Fourier transform of a signal using a Fast Fourier Transform (FFT) algorithm (Frigo and Johnson, 1998).
Analysis of the Control Performance of a SDOF Base-Isolated Structure
In this section the control performance of the BI system equipped with the TMD, the New TMD and the TLCD is investigated in terms of base displacement, acceleration, and roof displacement time-histories. The analysis has been firstly carried out in the time domain and then in the frequency domain.
The benchmark structure used for the numerical analysis is a base-isolated SDOF building (n = 1) as reported in Xiang and Nishitani (2014). The superstructure has a mass story kg, an elastic story stiffness kN/m, and a damping coefficient kNs/m (corresponding to a damping ratio of ζ1 = 0.01).
As far as the base-isolation system is concerned, its mass is kg, while stiffness and damping coefficient are assumed to be kN/m (corresponding to a natural frequency ωb = 1.57rad/s) and (corresponding to a damping ratio ζb = 0.05), respectively.
As far as the passive control devices are concerned, the mass ratio is supposed to be the same for all the considered systems. Hence, the TLCD incorporated to the BI system has a mass ratio μ2 = 5% equal to the TMD mass ratio μd = 5% and to the New TMD mass ratio μd = 5%.
The specific dynamic parameters of the considered devices coupled with the BI system have been chosen on the basis of some optimization procedures reported in Appendix A.
The TLCD placed on the BI system has a length ratio α = 0.6, and the frequency ratio νopt = 0.943 and the head loss coefficient ξopt = 10.427 have been determined from the optimization procedure proposed in Di Matteo et al. (2017a) and described in Appendix A.
The TMD frequency ratio and damping coefficient are νopt = 0.94 and ζd, opt = 0.11 respectively, found using the TMD optimization technique proposed in Di Matteo et al. (2019).
Finally, the New TMD parameters are: the frequency ratio νopt = 4.47 and damping coefficient ζd, opt = 0.393, found using the optimal New TMD parameters computed as described in Xiang and Nishitani (2014).
For sake of simplicity, the main structure and the base-isolation subsystem have been supposed to be linear systems. Clearly, many real base-isolation systems may show characteristic non-linear features. In De Domenico et al. (2018), for instance, an improved response spectrum analysis taking into account a more realistic non-linear behavior of the BI system, has been developed.
The corresponding response time histories of the base-isolated reference structure with and without control devices are shown in Figures 3–5, respectively.
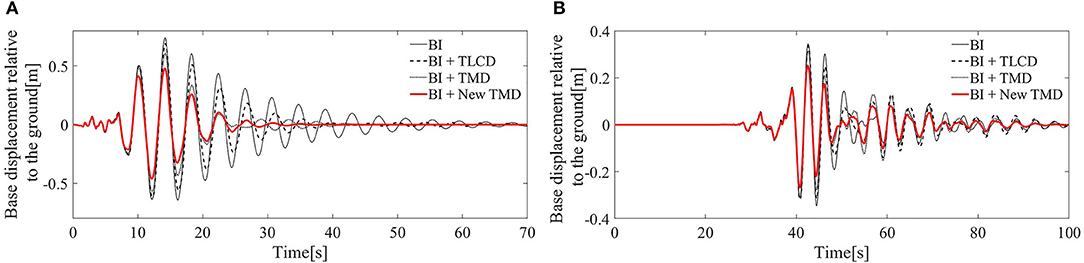
Figure 3. Base isolation displacements relative to the ground: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake. BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
Figures 3A,B show that for both the seismic ground motions, the New TMD device incorporated to a BI system (red thick line), is the most efficient strategy in terms of reducing of peak base deformation (with a decrease of almost 37% for the San Fernando record and 26% for the Chi-Chi record). From Figures 4, 5 it emerges the New TMD can reduce base acceleration (49% for the San Fernando record and 36% for the Chi-Chi record) (Figures 4A,B) and top floor displacements too (Figures 5A,B).
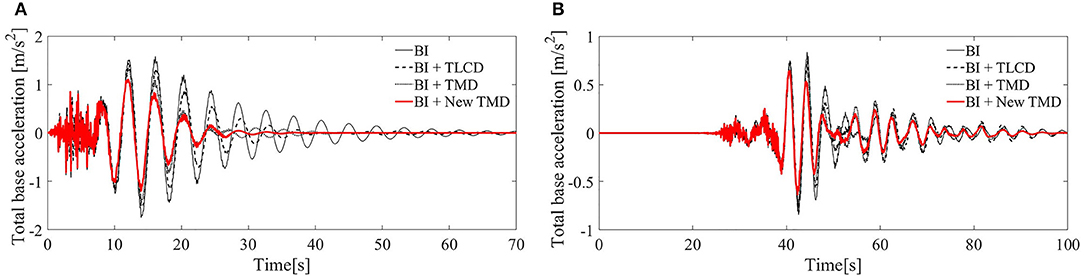
Figure 4. Total base accelerations: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
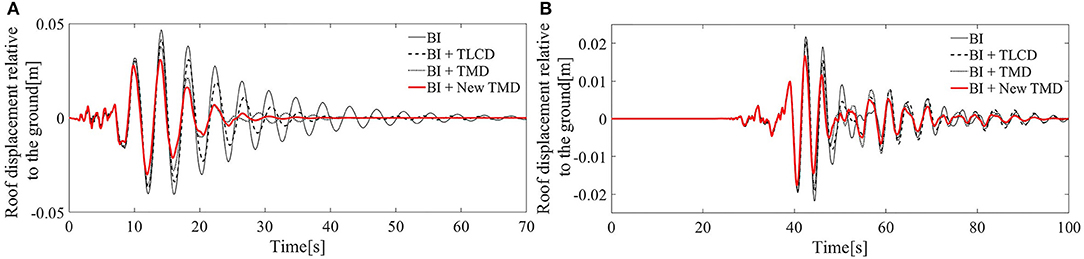
Figure 5. Roof displacements relative to the ground: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
Finally, the stroke of the New TMD and TMD, defined as xb(t)−xd(t), is plotted in Figure 6. Note that, the displacement of the TLCD device is not shown since, being represented by the vertical displacement of the liquid inside the device, as depicted in Figure 1D, it is not directly comparable to the horizontal displacement of the TMD and New TMD (Figures 1B,C).
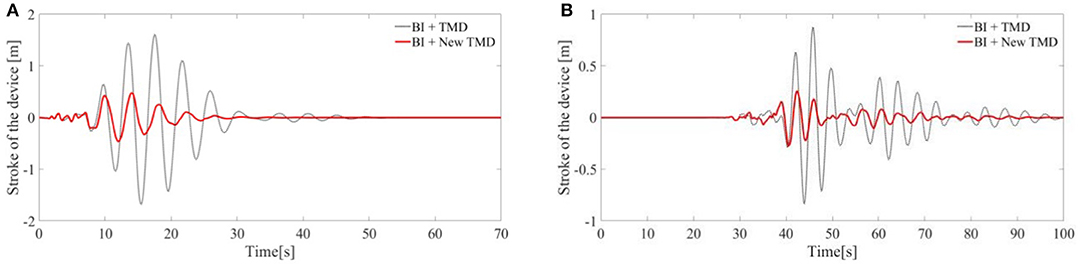
Figure 6. Stroke of the device: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
As it can be seen, the New TMD design yields smaller displacements compared to the traditional TMD for the two considered inputs. This is due to the particular configuration of the dashpot in the device New TMD which leads to larger dissipative forces compared to the TMD. This result is in agreement with results described in Xiang and Nishitani (2014).
Notably, this aspect can be particularly advantageous in practical cases where the space designed to host the device is limited.
Once introduced the FRFs of each hybrid strategy, a frequency analysis is developed in order to understand the dynamic behavior of each system in the frequency domain.
The base-isolation displacement transfer function of the simple BI system is compared to that of the base isolated one equipped with the TMD, the New TMD and the TLCD, respectively, as shown in Figure 7.
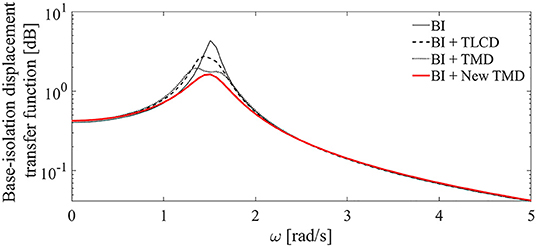
Figure 7. Magnitudes of the base-isolation displacement transfer function of the BI system (black line), BI system with the TLCD (black dashed line), BI system with the TMD (black dotted line), and BI system with the New TMD (red thick line).
As it can be seen, the presence of a passive control device reduces the amplitude of the frequency response of the BI system (black line). Again, according to the frequency analysis, the New TMD (red thick line), achieves the best control of the structural response.
Analysis of the Control Performance of a MDOF-Story Base-Isolated Structure
In this section the analysis of the control performance of the BI system equipped with the TMD, New TMD or the TLCD is extended to the case of a MDOF superstructure, both in the time and in the frequency domain, to take into account also the case of tall structures.
In order to investigate the influence of the non-stationary nature of real ground motions, the control performances of the base-isolated structure equipped with each device has been examined in the time domain by using 44 different selected recorded accelerograms extracted by data of the recorded far-field ground motions of the FEMA P-695-FF set described in FEMA P-695 (2009).
The superstructure used for the numerical analysis is a base-isolated 20-story building (n = 20) (Yang et al., 1991).
The structural properties of each story unit are as follows: story mass kg, elastic story stiffness kN/m, damping coefficient Ci = 2261kN s/m (corresponding to a damping ratio of the first mode ζ1 = 0.005), and height of each story hi = 3.0 m. As far as the base-isolation system is concerned, its mass is kg, while stiffness and damping coefficient are assumed to be kN/m (corresponding to a natural frequency ωb = 2.5rad/s) and Cb = 320kNs/m (corresponding to a damping ratio ζb = 0.01), respectively.
The TLCD incorporated to the BI system has a mass ratio μ2 = 5% and length ratio α = 0.6, the frequency ratio is νopt = 0.96 and the head loss coefficient is ξopt = 6.71, obtained on the basis of Di Matteo et al. (2017a) and as described in Appendix A.
The TMD parameters are: mass ratio μd = 5%, the frequency ratio νopt = 0.94 and damping coefficient ζd, opt = 0.11, found using the TMD optimization procedure proposed in Di Matteo et al. (2019).
Finally, the New TMD parameters are: mass ratio μd = 5%, the frequency ratio νopt = 4.47 and damping coefficient ζd, opt = 0.397, found using the New TMD optimization procedure proposed in Xiang and Nishitani (2014). Also in this case, the basic hypotheses suppose the linearity of the main structure and of the base-isolation subsystem.
For each of the FEMA P-695-FF 44 records, the displacement relative to the ground (Figure 8A) and interstorey drift ratio (Figure 8B) of the base-isolation subsystem and of the main structure are determined for the base-isolated structure and the base-isolated structure controlled by the TMD, TLCD and the New TMD.
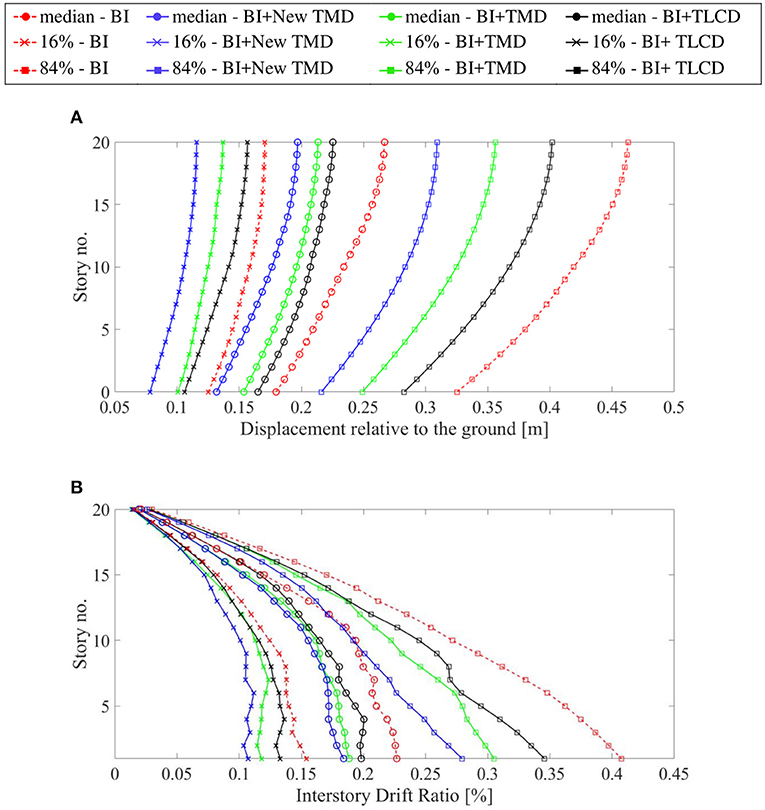
Figure 8. Response profiles for hybrid controlled structure with TLCD (black solid line), with TMD (green solid line), with New TMD (blue solid line) and base-isolated structure (red dashed line) subjected to the 44 FEMA P-695-FF records: circles, median; crosses, 16th percentile; squares, 84th percentiles. (A) In terms of peak floor displacement relative to the ground. (B) In terms of peak floor displacement interstorey drift ratio.
In this regard, Figure 8 show the profiles (median, 16 and 84th percentiles) of the peak response quantities of the base-isolated structure without devices (red dashed line), with TLCD (black solid line), TMD (green solid line), and New TMD (blue solid line).
As can be seen in Figure 8, the New TMD device in combination with the base-isolation subsystem outperforms the other devices in reducing the structural responses.
Specifically, results for the same recorded accelerograms (the San Fernando and Chi-Chi earthquakes) of the section Analysis of the control performance of a SDOF base-isolated structure as the external inputs.
The corresponding response time histories of the base-isolated reference structure with and without control devices are shown in Figures 9–11, respectively.
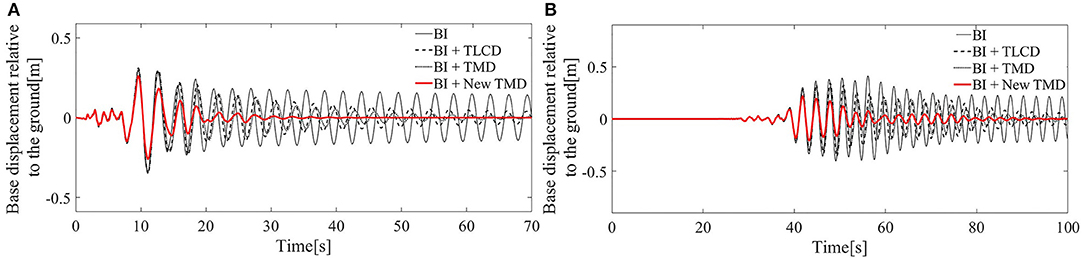
Figure 9. Base isolation displacements relative to the ground: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD—black dotted line; BI system with the New TMD, red thick line.
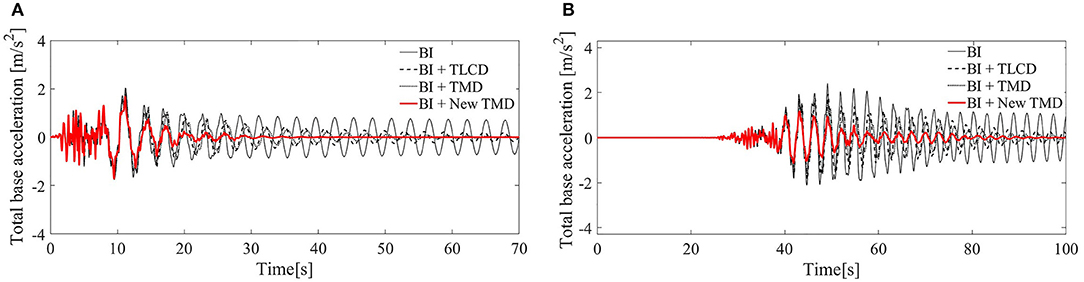
Figure 10. Total base accelerations: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
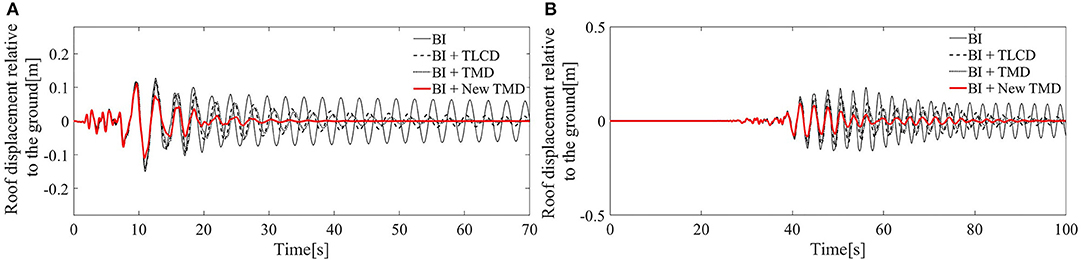
Figure 11. Roof displacements relative to the ground: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system, black line; BI system with the TLCD, black dashed line; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
It emerges that, for the San Fernando seismic action, the New TMD device incorporated to a BI system (red thick line), can reduce the base deformation (with a decrease of the peak base deformation of almost 16 %) (Figure 9A), base acceleration (20%) (Figure 11A) and top floor displacements (58%) (Figure 11A).
Moreover, the New TMD can achieve greater reductions for the Chi-Chi earthquake: the maximum peak of the base displacement can be reduced of almost 80%, while of almost 60% with the BI + TMD system and 41% with the BI + TLCD system (Figure 9B).
Furthermore, although TMDs, as well as the New TMDs and TLCDs cannot mitigate the structural responses in the first seconds of the excitation, since in this cases, the use of an active system device or a sort of accelerated TMD could be necessary (Tsai and Lin, 1993; Tsai, 1995; Yalla and Kareem, 2003; Hochrainer and Ziegler, 2006), the overall effect of such a passive control device on the BI system is a significant decrease of all the response quantities, as shown in Figures 9–11.
Moreover, as it can be seen from Figure 12, the stroke length of the New TMD is greatly reduced compared with the traditional TMD for both the considered earthquakes. In this regard, the New TMD may represent an advantageous solution in real cases when the space designed to host the device is limited.
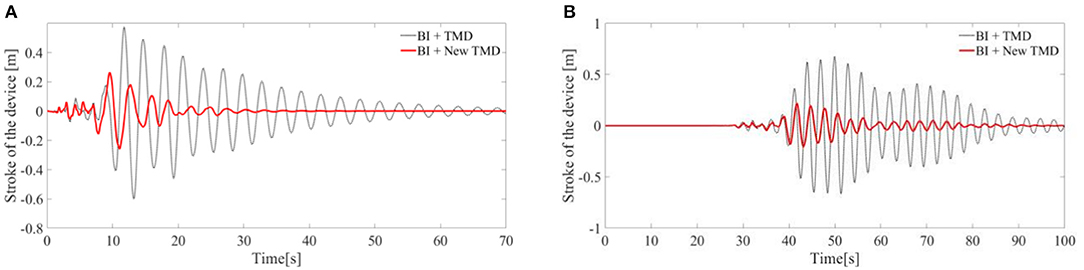
Figure 12. Stroke of the device: (A) Response to the San Fernando earthquake. (B) Response to the Chi-Chi earthquake; BI system with the TMD, black dotted line; BI system with the New TMD, red thick line.
It emerges that the New TMD device, compared to the traditional TMD and to the TLCD, yields a higher dissipation of the structural vibrations.
As far as the analysis in the frequency domain is concerned, the results of a frequency analysis on the 20-DOFs base isolated structure equipped with an energy dissipation mechanism are shown in the following considering the mean of the FRFs obtained for each of the FEMA P-695-FF 44 records. Here the FRFs have been obtained numerically by using MatLab built-in function FFT—Fast Fourier Transform (Frigo and Johnson, 1998). Specifically, in Figure 13 it can be observed the New TMD (red thick line), similarly to the TMD (black dotted line), is more effective in reducing the peak of the frequency transfer function of the base displacement of the BI system (black line).
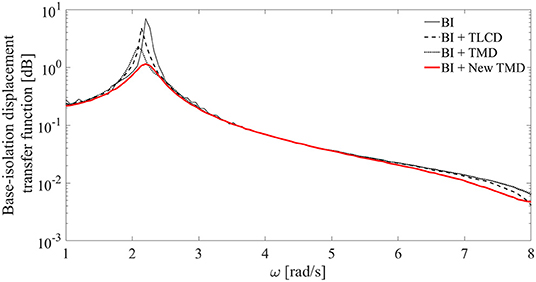
Figure 13. Magnitudes of the base displacement transfer function of the BI system (black line), BI system with the TLCD (black dashed line), BI system with the TMD (black dotted line), and BI system with the NEW TMD (red thick line).
Conclusion
In this study the dynamic behavior of base-isolated buildings equipped with several types of passive control systems is investigated. In particular, strategies which combine the Base Isolation with the Tuned Mass Damper, the New Tuned Mass Damper and the Tuned Liquid Column Damper have been examined. The effectiveness of each device in reducing the dynamic response of base isolated structure is stressed by comparison with the response of the simple base isolated structure.
Mathematical formulations of the all above described hybrid strategies have been given in the time and in the frequency domain. Moreover, the control performance of each device connected to the base-isolated structure has been examined considering firstly a SDOF base-isolated shear-type frame structure subjected to two specific recorded accelerograms with different features. Numerical simulations show that the New TMD is particularly effective in controlling the base isolated displacement demand (with a significantly reduction of the maximum base displacement value of almost 80% in the case of a MDOF isolated building under the Chi-Chi earthquake), compared to the base-isolated structure without any passive control device. Finally, results suggest that the New TMD can further reduce relative base-isolation displacements and the other response quantities, such as the base acceleration, the top floor displacement, the stroke of the device, and the amplitude of the base displacement frequency transfer function, even compared to the most common devices such as the TMD and the TLCD.
Although results may be influenced by several parameters such as the typology of the structure, the considered accelerograms and soil type, the analyses, carried out on a 20-story base-isolated shear-type frame structure by using a set of 44 different ground motions with different magnitudes and taking into account several soil site classes (between soft and stiff soil), confirm that the design of the New TMD parameters is quite reliable for different types of earthquakes and that the New TMD can represent an effective means to reduce the response of base-isolated structures.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Author Contributions
All authors listed have made a substantial, direct and intellectual contribution to the work, and approved it for publication.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors gratefully acknowledge financial support from the Italian Ministry of Education, University and Research (MIUR) under the Prin 2017 grant Multiscale Innovative Materials and Structures.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2019.00132/full#supplementary-material
References
Bakre, S. V., and Jangid, R. S. (2007). Optimum parameters of tuned mass damper for damped main system. Struc. Control Health Monit. 14, 448–470. doi: 10.1002/stc.166
Chang, C. C. (1999). Mass dampers and their optimal designs for building vibration control. Eng. Struct. 21, 454–463. doi: 10.1016/S0141-0296(97)00213-7
Cheung, Y. L., and Wong, W. O. (2011). Optimization of a non-traditional dynamic vibration absorber for vibration control of structures under random force excitation. J. Sound Vibration 330, 1039–1044. doi: 10.1016/j.jsv.2010.10.031
De Angelis, M., Giaralis, A., Petrini, F., and Pietrosanti, D. (2019). Optimal tuning and assessment of inertial dampers with grounded inerter for vibration control of seismically excited base-isolated systems. Eng. Struct. 196:109250. doi: 10.1016/j.engstruct.2019.05.091
De Domenico, D., Falsone, G., and Ricciardi, G. (2018). Improved response-spectrum analysis of base-isolated buildings: a substructure-based response spectrum method. Eng. Struct. 162, 198–212. doi: 10.1016/j.engstruct.2018.02.037
De Domenico, D., and Ricciardi, G. (2018a). Earthquake-resilient design of base isolated buildings with TMD at basement: application to a case study. Soil Dyn. Earthquake Eng. 113, 503–521. doi: 10.1016/j.soildyn.2018.06.022
De Domenico, D., and Ricciardi, G. (2018b). An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthquake Eng. Struct. Dyn. 47, 1169–1192. doi: 10.1002/eqe.3011
Di Matteo, A., Furtmuller, T., Adam, C., and Pirrotta, A. (2017a). Optimal design of tuned liquid column dampers for seismic response control of base-isolated structures. Acta Mechanica 229:437–454. doi: 10.1007/s00707-017-1980-7
Di Matteo, A., Furtmuller, T., Adam, C., and Pirrotta, A. (2017b). Earthquake excited base-isolated structures protected by tuned liquid column dampers: design approach and experimental verification. Proc. Eng. 199, 1574–1579. doi: 10.1016/j.proeng.2017.09.060
Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2012). “The TLCD passive control: numerical investigations vs experimental results,” in ASME 2012 InternationalMechanical Engineering Congress and Exposition Dynamics, Control and Uncertainty, Vol. 4 (New York, NY: ASME), 1283–1290. doi: 10.1115/IMECE2012-86568
Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2014a). Direct evaluation of the equivalent linear damping for TLCD systems in random vibration for pre-design purposes. Int. J. Nonlinear Mech. 63, 19–30. doi: 10.1016/j.ijnonlinmec.2014.03.009
Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2014b). Experimental validation of a direct pre-design formula for TLCD. Eng. Struct. 75, 528–538. doi: 10.1016/j.engstruct.2014.05.045
Di Matteo, A., Lo Iacono, F., Navarra, G., and Pirrotta, A. (2015). Optimal tuning of tuned liquid column damper systems in random vibration by means of an approximate formulation. Meccanica 50, 795–808. doi: 10.1007/s11012-014-0051-6
Di Matteo, A., Masnata, C., and Pirrotta, A. (2019). Simplified analytical solution for the optimal design of tuned mass damper inerter for base isolated structures. Mech. Syst. Signal. Proc. 134C:106337. doi: 10.1016/j.ymssp.2019.106337
Elias, S., and Matsagar, V. A. (2017). Effectiveness of tuned mass dampers in seismic response control of isolated bridges including soil-structure interaction. Latin Am. J. Solids Struct. 14, 2324–2341. doi: 10.1590/1679-78253893
FEMA P-695 (2009). Quantification of Building Seismic Performance Factors Technical Representative Federal Emergency Agency. Washington, DC.
Frigo, M., and Johnson, S. G. (1998). “FFTW: an Adaptive Software Architecture for the FFT,” in Proceedings of the International Conference on Acoustics, Speech, and Signal Processing (Seattle, WA), 1381–1384. doi: 10.1109/ICASSP.1998.681704
Gao, H., and Kwok, K. C. S. (1997). Optimization of tuned liquid column dampers. Eng. Struct. 19, 476–486. doi: 10.1016/S0141-0296(96)00099-5
Hochrainer, M. J., and Ziegler, F. (2006). Control of tall building vibrations by sealed tuned liquid column dampers. Struct. Control. Health Monit. 13, 980–1002. doi: 10.1002/stc.90
Kelly, J. M. (1990). Base isolation: linear theory and design. J. Earthquake Spectra 6, 223–244. doi: 10.1193/1.1585566
Kelly, J. M. (1999). The role of damping in seismic isolation. Earthquake Eng. Struct. Dyn. 28, 3–20.
Melkumyan, M. G. (2012). “New concept of a dynamic damper to restrict the displacements of seismically isolated buildings,” Conference: International Conference on Advances in Materials Science and Engineering, Seoul, Korea.
Natsiavas, S. (1992). Steady state oscillations and stability of non-linear dynamic vibration absorbers. J. Sound Vibration 156, 227–245. doi: 10.1016/0022-460X(92)90695-T
Nissen, J. C., Popp, K., and Schmalhorst, B. (1985). Optimization of a non-linear dynamic vibration absorber. J. Sound Vibration 99, 149–154. doi: 10.1016/0022-460X(85)90454-7
Palazzo, B., and Petti, L. (1994). “Seismic Response Control in Base Isolated Systems Using Tuned Mass Dampers,” in Proceedings of First World Conference on Structural Control, Los Angeles, California.
Palazzo, B., and Petti, L. (1999). Combined control strategy: based isolation and tuned mass damping. ISET J. Earthquake Technol. 36, 121–137.
Perez, R., and Behdinan, K. (2007). Particle swarm approach for structural design optimization. Comput. Struct. 85, 1579–88. doi: 10.1016/j.compstruc.2006.10.013
Ren, M. Z. (2001). A variant design of the dynamic vibration absorber. J. Sound Vibration 245, 762–770. doi: 10.1006/jsvi.2001.3564
Roberts, J. B., and Spanos, P. D. (1990). Random Vibration and Statistical Linearization. New York, NY: Wiley.
Sakai, F., Takeda, S., and Tamaki, T. (1989). “Tuned Liquid Column Damper- New Type Device for Suppression of Building Vibration,” in Proceedings of the International Conference on Highrise Buildings (Nanjing), 926–931.
Stanikzai, M. H., Elias, S., Matsagar, V. A., and Jain, A. K. (2018). Seismic response control of base-isolated buildings using multiple tuned mass dampers. Struct. Design Tall Special Build. 28:e1576. doi: 10.1002/tal.1576
Stanikzai, M. H., Elias, S., Matsagar, V. A., and Jain, A. K. (2019). Seismic response control of base-isolated buildings using tuned mass damper. Aust. J. Struct. Eng. doi: 10.1080/13287982.2019.1635307. [Epub ahead of print].
Tsai, H.-C., and Lin, G. C. (1993). Optimum tuned-mass dampers for minimizing steady-state response of supportexcited and damped structures. Earthquake Eng. Struct. Dyn. 22, 957–913. doi: 10.1002/eqe.4290221104
Tsai, H. C. (1995). The effect of tuned-mass damper on the seismic response of base-isolated structures. Int. J. Solids Struct. 32, 1195–1210. doi: 10.1016/0020-7683(94)00150-U
Vakakis, A. F., Manevitch, L. I., Gendelman, O., and Bergman, L. A. (2003). Dynamics of linear discrete systems connected to local, essentially non-linear attachments. J. Sound Vibration 264, 559–577. doi: 10.1016/S0022-460X(02)01207-5
Wu, J. C., Chang, C. H., and Lin, Y. Y. (2009). Optimal design of non-uniform tuned liquid column dampers in horizontal motion. J. Sound Vibration 326, 104–122. doi: 10.1016/j.jsv.2009.04.027
Xiang, P., and Nishitani, A. (2014). Optimum design for more effective tuned mass damper system and its application to base-isolated buildings. Struct. Control Health Monit. 21, 98–114. doi: 10.1002/stc.1556
Yalla, S., and Kareem, A. (2000). Optimum absorber parameters for tuned liquid column dampers. J. Struct. Eng. 126, 906–915. doi: 10.1061/(ASCE)0733-9445(2000)126:8(906)
Yalla, S. K., and Kareem, A. (2003). Semiactive tuned liquid column dampers: experimental study. J. Struct. Eng. 129, 960–971. doi: 10.1061/(ASCE)0733-9445(2003)129:7(960)
Keywords: hybrid structural control, base isolation, optimal design, tuned mass damper, inerter
Citation: Di Matteo A, Masnata C and Pirrotta A (2019) Hybrid Passive Control Strategies for Reducing the Displacements at the Base of Seismic Isolated Structures. Front. Built Environ. 5:132. doi: 10.3389/fbuil.2019.00132
Received: 31 July 2019; Accepted: 24 October 2019;
Published: 13 November 2019.
Edited by:
Dario De Domenico, University of Messina, ItalyReviewed by:
Said Elias Rahimi, University of Iceland, IcelandQinhua Wang, Shantou University, China
Copyright © 2019 Di Matteo, Masnata and Pirrotta. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alberto Di Matteo, YWxiZXJ0by5kaW1hdHRlb0B1bmlwYS5pdA==
 Alberto Di Matteo
Alberto Di Matteo Chiara Masnata1
Chiara Masnata1 Antonina Pirrotta
Antonina Pirrotta