Effectiveness of Seismic Isolation for Long-Period Structures Subject to Far-Field and Near-Field Excitations

Introduction

Base isolation (BI) systems were originally applied to short-period structures (e.g., low-rise buildings) subjected to short-period ground excitations such as far-field (FF) earthquakes recorded on firm-soil profiles. In the past decade, BI has been used even for rather tall (long-period) buildings and long-period ground motions such as those present in most near-field (NF) excitations. Examples of isolated tall buildings are the 41-story residential Thousand Tower and the Sendai MTI 18-story building in Japan, and the 33-story Nunoa Capital building in Chile (Komuro et al., 2005; Lagos et al., 2017). Despite these specific examples, consensus does not exist on the effectiveness of the BI technique for long-period (flexible) structures and for long-period ground motions.

The concerns regarding the application of BI systems in flexible structures (e.g., high-rise buildings) subject to FF excitations arise primarily from the relatively long fundamental period of the fixed-base superstructure. For most typical FF earthquake ground motions, spectral acceleration responses are relatively high in short period regions (e.g., periods less than 0.5 s), and as the period increases to intermediate values (e.g., 2.0–3.0 s), the spectral acceleration ordinates significantly decrease. Therefore, increasing the fundamental period of common bridges and short-rise buildings to 2.0–3.0 s, which is feasible by the BI technique, can reduce the seismic force demands under FF ground motions significantly. Conversely, in most typical FF ground motions, for periods greater than 2.0–3.0 s, the absolute values of spectral acceleration responses are already relatively small. Therefore, one might question the use of seismic isolation to further increase the periods of relatively long-period structures to reduce seismic force demands. However, as the results of the present research and a few previous studies illustrate, seismic isolation can considerably reduce the mean acceleration and base shear responses of relatively long-period structures (e.g., up to 50% for the cases studied in this paper). Although these reductions might not be as pronounced as those for short-period structures, they are significant as compared to the improvements achieved in the responses of long-period structures using other well-adopted seismic protection systems. For example, tuned mass dampers with practical mass ratios (e.g., 1–5%) can provide reductions in the base shear and floor acceleration responses of high-rise buildings not greater than 20–30% (e.g., see Soto-Brito and Ruiz, 1999; Bekdas̨ and Nigdeli, 2013; Anajafi and Medina, 2018; Naderpour et al., 2019). Furthermore, as shown in the present study, for FF excitations, the lateral-strength reduction caused by isolation systems can potentially even reduce the global displacement responses of the structures with relatively long non-isolated periods.

Significant concerns also exist in the application of seismic isolation for NF ground motions. Many (not all) ground motions recorded in NF regions (typically within 15 km of causative faults) are characterized by one or several long-period pulse motions caused by forward-directivity (FD) effects. The long period of these pulse-type motions can coincide with the fundamental periods of flexible structures, such as isolated structures, imposing large spectral acceleration responses on these structures. This may reduce the efficacy of the seismic isolation technique in terms of base-shear response reduction and also cause significant superstructure displacement responses. Numerous studies in the past have illustrated that for the same PGA and duration of shaking, NF ground motions could impose higher seismic demands (e.g., base shear, and global displacement) on flexible structures, as compared to ordinary FF excitations (e.g., see Hall et al., 1995; Malhotra, 1999; Liao et al., 2000, 2004; Shen et al., 2004; Li et al., 2007; Jäger and Adam, 2013; Beiraghi et al., 2016; Günes̨ and Ulucan, 2019). Specific examples of isolated structures damaged due to NF effects are presented in Li et al. (2008), Wang and Lee (2009), and Jónsson et al. (2010). The abovementioned studies provide significant insight into understanding the behavior of isolated structures subjected to NF excitations. However, when interpreting the results of these studies, several important points should be considered. First, in many cases, the damaged base-isolated structures in NF events presented in these studies were designed without NF considerations (e.g., the examples studied in Li et al., 2008; Wang and Lee, 2009; Jónsson et al., 2010). Therefore, the poor seismic performance of these structures cannot be considered evidence of the inefficacy of the BI technique for structures constructed in NF regions. Second, some of these studies show that the BI technique is, on average, more effective for FF excitations than for NF excitations (e.g., Liao et al., 2004). The present study, while corroborating the validity of this statement for structures with short non-isolated periods, illustrates that this is not always the case for structures with relatively long non-isolated periods. Additionally, a more rational approach to evaluate the effectiveness of seismic isolation for NF excitations should also consider comparing the responses of a base-isolated structure and its non-isolated counterpart rather than a sole comparison with the responses under FF excitations. Last but not least, many of these studies investigated the behavior of isolated structures with relatively short non-isolated periods (e.g., Liao et al., 2004), and as a result, the increase in the displacement responses due to seismic isolation was significant under NF excitations. However, structures with relatively long periods are already influenced by directivity pulses of NF excitations, and it is not trivial that seismic isolation would further increase their displacement responses significantly.

An evaluation of the results of a few previous studies that investigated responses of relatively long-period structures under NF excitations illustrates that the values of the initial periods of the non-isolated and isolated counterparts are key parameters to predict the level of decrease/increase caused by seismic isolation in force and displacement demands (e.g., see examples presented in Takewaki, 2008; Ma et al., 2014; Fujita et al., 2017; Lagos et al., 2017; Anajafi and Medina, 2018; Naderpour et al., 2019). This evaluation shows that seismic isolation for NF excitations can, in many cases, reduce the mean force demands significantly (up to 70–80%). The extent of this reduction depends on the values of the non-isolated and isolated periods. However, the trends observed for displacement responses in these studies suggest establishing limitations for the initial periods and lateral strength of isolated structures. The evaluation of the results of these studies leads to the hypothesis that seismic isolation is effective for long-period structures subject to NF excitations when the initial periods of the non-isolated and isolated counterparts are both in the range of 2.0–2.5 s. In this case, while mean force demands on the substructure reduce significantly, the mean displacement responses of the isolated superstructure remain within ranges used in practice. In these examples, it is observed that when seismic isolation results in initial periods greater than 3.0–4.0 s, mean displacement demands imposed on the superstructure might significantly increase under NF excitations, although the mean force demands still reduce to some extent.

The present study investigates the effects of seismic isolation on the performance of structures with relatively long non-isolated periods under NF and FF excitations. The primary objective is to evaluate the accuracy of the hypotheses made in the previous expositions based on the results of studies available in the literature.

Following the seminal works of Veletsos in collaboration with Newmark (Veletsos et al., 1965), the inelastic response spectrum concept has been widely used as a promising tool to study the inelastic responses of structures and equipment to dynamic excitations. This study employs this simple yet profound concept to systematically evaluate the effects of the two fundamental aspects of seismic isolation, i.e., period elongation and lateral-strength reduction. The results of inelastic ground response spectra are used to roughly estimate a near-optimum range for the characteristics of seismic isolators for relatively long-period structures. To illustrate the accuracy of the predictions of the implemented approach, isolated and non-isolated bridges with relatively stiff and flexible substructures are studied. The case-study structures are developed based on the real-world isolated Rudshur bridge. This bridge has a relatively flexible substructure and is located in an NF region. Despite being constructed in an NF region, the Rudshur bridge was designed based on a typical ground spectrum that did not consider NF effects. Therefore, an additional objective of this study is to evaluate the performance of the Rudshur bridge for NF ground motions and propose possible required rehabilitations.

The rest of this paper is organized as follows. First, the adopted method of approach is elaborated. This is followed by a section discussing the NF and FF record pair selection for inelastic response history analyses. A next section presents a preliminary evaluation of the effectiveness of seismic isolation for long-period structures using the inelastic spectrum concept. Subsequently, case-study structural models are used to further validate the results of inelastic response spectra. The paper ends with a section proposing a rehabilitation scheme for improving the seismic performance of the isolated Rudshur bridge under NF excitations.

Method of Approach

The adopted method of approach consists of using: (1) ground response spectrum concept; and (2) non-linear response history analysis of case-study structures; to evaluate the effectiveness of seismic isolation for long-period structures subjected to FF and NF excitations. The following two subsections discuss these two approaches in more detail.

Ground Response Spectrum Concept

Inelastic response spectra are widely used to understand the effect of the inelastic behavior of structures subject to ground excitations. Ground response spectra illustrate maximum seismic demands (e.g., displacement, force, ductility, etc.) on single-degree-of-freedom (SDOF) systems with predefined viscous damping ratios, initial periods, and force-deformation relationships subject to a given ground excitation. Many studies in the past have developed inelastic spectra for NF and FF ground motions (e.g., see Rahnama and Krawinkler, 1993; Chopra and Chintanapakdee, 2004; Chenouda and Ayoub, 2008; Iervolino et al., 2012). The results of these studies have provided significant insight into understanding the effect of inelastic behavior on the seismic responses of structures. This study re-produces these results to establish a basis for the evaluation of the effectiveness of seismic isolation for long-period structures.

In the literature, different types of inelastic spectra have been developed, including constant ductility, constant damage, constant strength, and constant strength reduction factor (constant-R) spectra. For example, in the constant ductility and constant-R approaches, the inelastic spectra are developed based on a predefined “displacement ductility demand” and “lateral-strength reduction factor,” respectively. In principle, the seismic isolation technique causes an increase in the period and a reduction in the lateral-strength of a structure. The constant-R spectrum approach can be used to “systematically” evaluate the influence of the lateral-strength reduction and period shift caused by the seismic isolation technique.

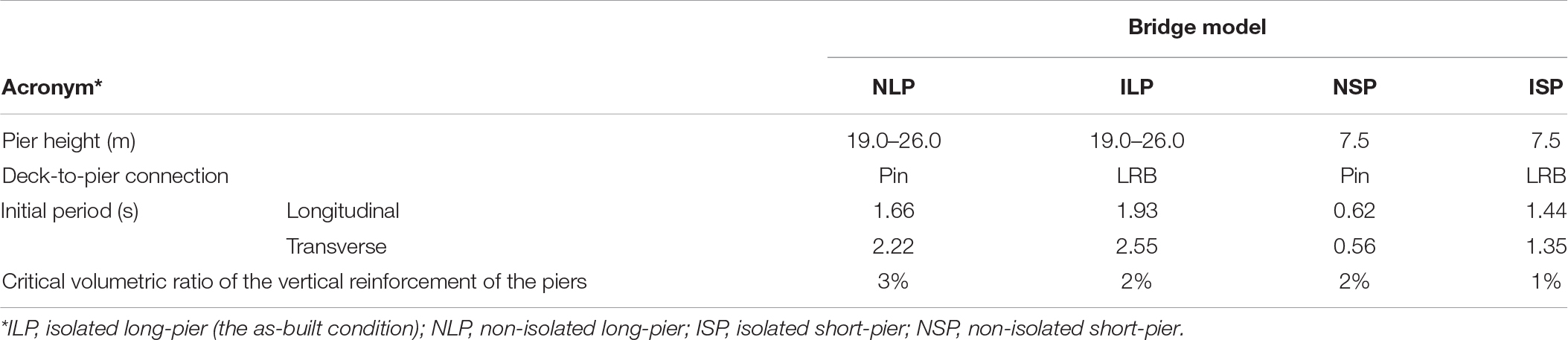
Figure 1A illustrates the bilinear force-deformation relationship of an inelastic SDOF system and the corresponding elastic system used in this study to develop ground response spectra. In this figure, the elastic stiffness is k_s and the post-elastic stiffness is αk_s, where α is the post-yield stiffness ratio. The yield strength is f_y and the yield deformation is u_y. Within the elastic range, the SDOF system has a natural period $T_{\text{n}}=2\mathrm{\pi }\sqrt{m_{\text{s}}/k_{\text{s}}}$, where m_s is the mass of the system. The yield-strength reduction factor, R, is defined by Equation (1) (Chopra and Chintanapakdee, 2004).

$$R=\frac{f_{\text{o}}}{f_{\text{y}}}=\frac{u_{\text{o}}}{u_{\text{y}}}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.5em}\hspace{1em}}(1)$$

FIGURE 1

Figure 1. (A) Bilinear force-deformation relationship of inelastic SDOF system and corresponding elastic system (adopted from Chopra and Chintanapakdee, 2004); (B) elastic and inelastic normalized force demand spectra for a representative ground motion.

where f_o and u_o are the minimum yield strength and yield deformation required for the system to remain elastic during the ground motion, or the peak response values for the corresponding linear system (Chopra and Chintanapakdee, 2004). f_m and u_m are the peak force and displacement demands on the inelastic system, respectively. In this study, u_m is denoted as the spectral displacement response, S _d.

The inelastic ground response spectra are computed as explained next (Obando and Lopez-Garcia, 2018). SDOF systems are defined by the natural period T_n, the damping ratio ξ, and the response modification (reduction) factor R. For a given SDOF system, first, peak displacement (u_o) and peak force (f_o) demands are computed through linear response history analysis under a sample ground acceleration. The parameters yield displacement and yield force are then calculated as u_y = u_o/R and f_y = f_o/R, and the sample values S_d and f_m of the same inelastic SDOF system (i.e., same natural period, T_n, and same damping ratio, ξ) are then obtained through non-linear time history analysis under the same sample ground acceleration.

The peak elastic force demand is usually normalized to the SDOF weight (W_s) and is denoted as the elastic pseudo-spectral acceleration response, S_a:

$$S_{\text{a}}=\frac{f_{\text{o}}}{W_{\text{s}}}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}(2)$$

The S_a parameter is usually used to evaluate the elastic responses of structures to earthquake ground motions. The seismic force demand reduction due to the inelastic behavior of the SDOF system can be quantified using the R^∗ parameter given by Equation (3):

$$R^{{}^{*}}=\frac{f_{\text{o}}}{f_{\text{m}}}\mathit{\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}}(3)$$

Figure 1B illustrates the elastic and constant-R inelastic normalized force spectra, f_m/W_s, for a representative ground motion.

Non-linear Time History Analysis

Non-linear response history analyses are performed on several case-study structural models to further validate the preliminary results obtained from inelastic response spectra. The case-study models are developed based on a real-world isolated bridge. Response history analyses are conducted using two different sets of ground motion records. Full three-dimensional (3D) finite element models of the bridges are developed. The two horizontal components of each record pair are applied to the two principal directions of the bridge deck plane. This analysis approach is referred to as 3D analysis. It is worthwhile noting that an evaluation of the results illustrates that for isolated structures (in general, for long-period structures) subjected to NF excitations, the responses of the two components do not need to be added vectorially to obtain the maximum resultant responses (the term resultant refers to the square root of sum of squares). It is shown that in this case, the maximum resultant responses can be reasonably approximated from a 2D analysis with the forward-directivity component only (see Supplementary Material Appendix IV and also Jangid and Kelly, 2001). This approach could eliminate the complexity of a 3D analysis and reduce the computational efforts significantly.

Figure 2 illustrates a summary of the method of approach used in this paper.

FIGURE 2

Figure 2. Summary of the adopted method of approach to evaluate the effectiveness of seismic isolation.

Near-Field and Far-Field Record Pair Selection

Twenty NF record pairs containing forward directivity (FD) pulses are selected from the NGA-West2 database. The detailed characteristics of the NF record pairs can be seen in Supplementary Tables S1, S3. These ground motions were classified as pulse-like using the approach proposed by Baker (2007) and Shahi and Baker (2014) that is based on signal processing through wavelet analysis. In this approach, a ground motion is classified as pulse-like if its velocity time-history contains a pulse that is a large portion of the ground motion itself. It is worthwhile noting that a more recent criterion, denoted as pulse-index, was proposed by Quaglini et al. (2017) for the classification of the pulse-like characteristic of earthquake ground motions. The pulse-index was defined based on the ratio between the duration of the ground motion and the time interval during which most of the seismic energy is imparted to a structure. Quaglini et al. (2017) illustrated that the predictions of this approach are in good agreement with those of Baker (2007). The most salient characteristic of many (not all) NF excitations is the occurrence of a large velocity pulse at the beginning of the time history of the record in the FD orientation. This large pulse of motion causes the component in the directivity orientation (denoted as the FD component herein) to be significantly stronger than the component perpendicular to the directivity orientation (denoted as PD herein) at periods usually longer than 0.5 s (Somerville, 2005). This difference is not observed in the two components of ordinary far-field ground motions. Studies of ground motion directionality have shown that the azimuth of the FD component (i.e., the strongest observed pulse) is arbitrary for fault distances greater than approximately 3–5 km (Campbell and Bozorgnia, 2008). At closer fault distances, however, the azimuth of this component tends to align with the strike-normal orientation (Huang et al., 2008). Ground motions are usually recorded at two arbitrary orientations that are not necessarily the orientations of the strongest (FD) and weakest (PD) pulses. In this study, each NF pair is rotated to derive its FD and PD components, as illustrated in Supplementary Material Appendix II.

Twenty ordinary record pairs without velocity pulses, denoted as far-field (FF), are also selected for this study (see Supplementary Material Appendix II for the details of the selection of the FF record pairs and their characteristics). The PGA of each FF and NF record pair is scaled to a design PGA (i.e., 0.45 g). This scaling eliminates the effect of PGA on the conducted evaluations.

Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation

This section presents a preliminary evaluation of the effectiveness of the seismic isolation using the ground response spectrum concept. The characteristics of the SDOF systems to generate ground response spectra are defined in such a way that they represent typical seismic isolators. To this end, the viscous damping ratio of the SDOF oscillators is assumed to be 2.5%; a bilinear model with a 9% post-yielding stiffness ratio represents the inelastic behavior of the SDOF oscillators; it is assumed that the unloading and re-loading of the hysteretic system occur without any deterioration of stiffness or strength. These characteristics are consistent with those of the isolators used in the case-studies of this paper. The initial period of the SDOF systems ranges from 0 to 10.0 s with increments of 0.01 s, and the R factor is varied from 1.0 to 15.0.

Figures 3A,B illustrate, respectively, the 2.5%-damped pseudo-spectral acceleration responses for the FD and PD components of the scaled rotated NF excitations. Figures 3C,D present similar graphs for the north-south (NS) and east-west (EW) components of the FF excitations. The terms “scaled” and “rotated” are omitted hereinafter for brevity.

FIGURE 3

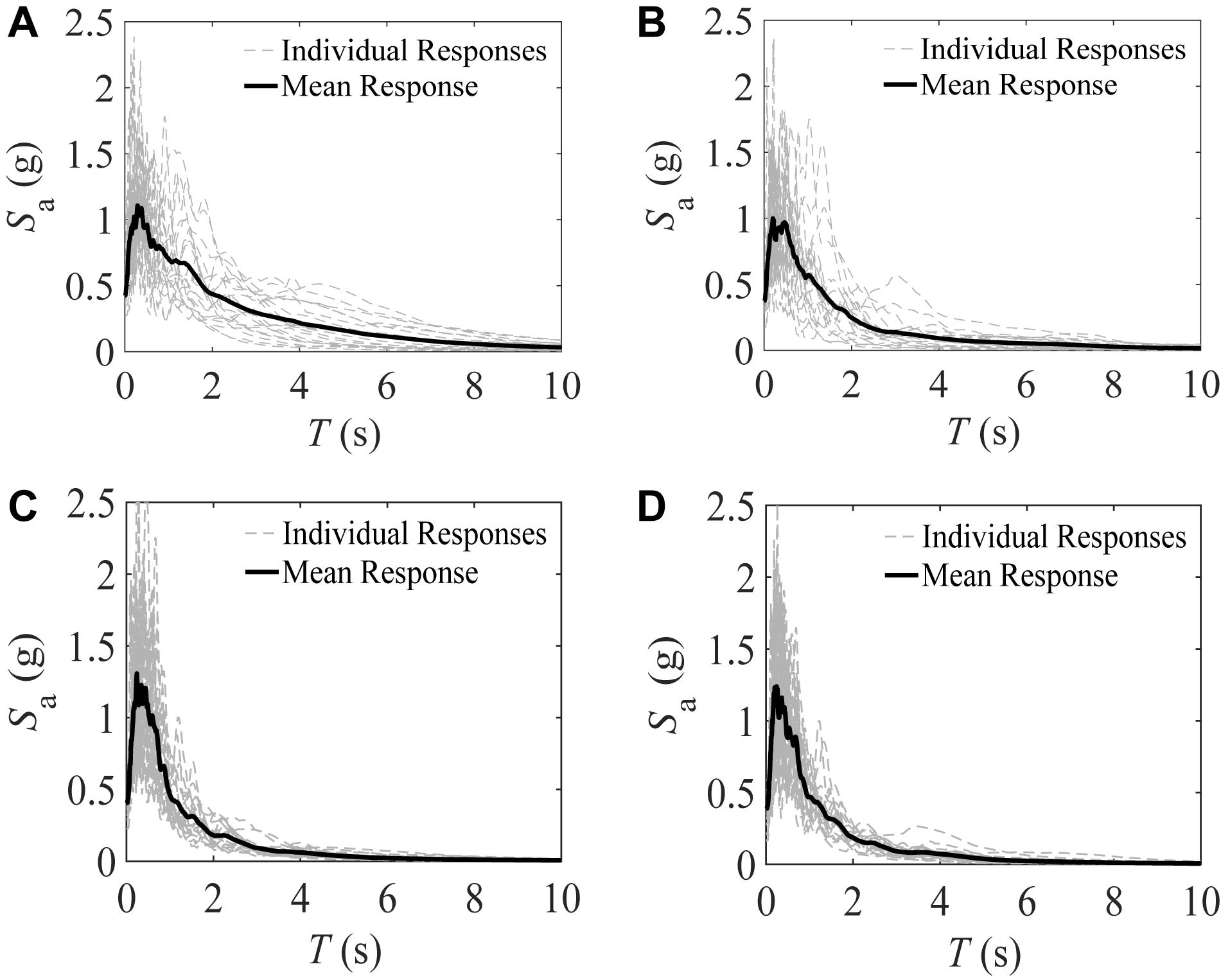
Figure 3. 2.5%-damped pseudo-acceleration response spectra for the: (A,B) FD and PD components of the NF excitations; (C,D) NS and EW components of the FF excitations.

As seen in Figure 3:

• In the relatively long-period region (e.g., T > 2.0 s), the FD-NF components are, on average, much stronger than the PD-NF components. This difference is not highlighted for the two components of the FF record pairs. These conclusions were reported in many previous studies (e.g., see Archila et al., 2017). For both record suites, the maximum value of the mean acceleration spectra occurs in the short-period region (e.g., T < 0.5 s), and with increasing the period, the mean spectral acceleration responses consistently reduce. The reduction rates for the NS-FF and EW-FF components are comparable and larger than those for the NF components.

• Period-elongation is most effective in reducing the mean elastic force demands in the case of relatively short-period structures subject to the FF records. However, it could still significantly reduce mean elastic force demands for all other scenarios, i.e., (i) short-period structures subject to the NF excitations; (ii) relatively long-period structures subject to the FF excitations; and (iii) relatively long-period structures subject to the NF excitations. For example, let SDOF systems with initial periods of 0.3 and 2.0 s represent a relatively short- and long-period non-isolated structure, respectively. Assume that the target initial isolated period is 4.0 s. In this case, increasing the period from 0.3 to 4.0 s reduces the mean S_a under the NS-FF records by 95% (i.e., from 1.17 to 0.06 g). This reduction for the case of the same period-shift under the FD-NF records is 80%; and for the period-shift from 2.0 to 4.0 s under the NS-FF and FD-NF excitations is 67 and 50%, respectively.

• The relatively large S_a values for the FD-NF records at relatively long periods imply that, in this case, the period-elongation due to seismic isolation might result in significant elastic spectral displacement responses.

Figure 4A illustrates the mean inelastic displacement spectra, yield displacement spectra and force-reduction factor spectra for the FF excitations assuming different R-values. Given that the NS-FF and EW-FF components are not significantly different, the mean values of all 40 FF components are computed and shown without differentiating based on the NS and EW directions. Figures 4B,C depict similar results for the FD-NF and PD-NF components that are considered separately due to their significance difference.

FIGURE 4

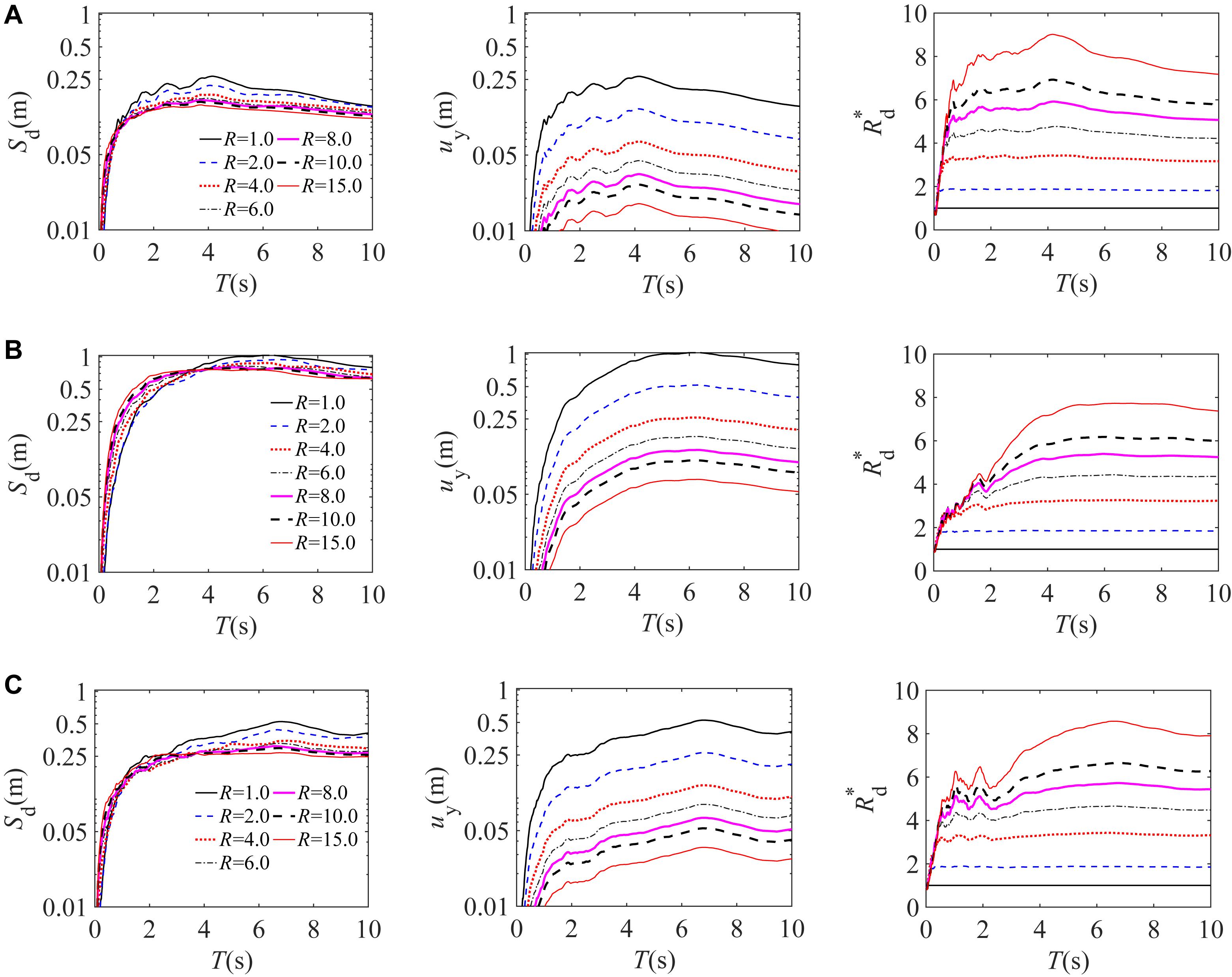
Figure 4. Mean inelastic displacement spectra, yield displacement spectra and force-reduction factor spectra for the (A) 40 FF components; (B) 20 FD-NF components; (C) 20 PD-NF components.

The most important conclusions of Figures 4A–C regarding the effectiveness of seismic isolation for structures with relatively long fixed-base periods are summarized next.

For the FF excitations, it is observed that:

• Consistent with numerous previous studies (e.g., Chopra and Chintanapakdee, 2004; Chenouda and Ayoub, 2008), for intermediate- and relatively long-period SDOF systems (e.g., T > 1.0 s), reducing the yield strength can decrease the mean displacement demands. The largest reduction occurs in the period range 3.0 < T < 5.0 s, suggesting that for structures with initial periods in this range, reducing the lateral strength can significantly reduce the mean displacement demands. The desired low lateral strength in conventional seismic design approaches can be achieved by using low yield-strength material in the lateral-force-resisting systems. However, in many cases, the high strength required for gravity loads may cause difficulties in achieving this characteristic. Seismic isolation systems by incorporating a relatively low yield-strength seismic fuse (i.e., isolators) at a specific level (e.g., at the base) can effectively provide this characteristic. It is observed that in the relatively large-period region (e.g., T > 4.0 s), as the period increases, the inelastic spectral displacement responses consistently reduce.

• For an R-value greater than 4.0, the yield displacement responses are consistently smaller than 0.05 m that is within the practical range of yield displacement for common types of seismic isolators, such as Lead Rubber Bearings.

• For periods greater than the constant acceleration region (e.g., T > 0.5 s), the reduction in the force demand (i.e., the value of R^∗) due to the inelastic behavior is significant. In this region, the magnitude of R^∗ for lower R factors is approximately constant and close to the value of R (e.g., assuming R = 2.0, this parameter varies between 0.90 and 0.94 R for different periods). For greater R factors, the amplitude of R^∗ is significantly smaller than the value of R (e.g., for R = 15.0, this parameter varies from 0.48 to 0.60 R).

• These results imply that for a structure with a relatively long non-isolated period, seismic isolation (i.e., a simultaneous period-lengthening and lateral-strength reduction), not only reduces force demands significantly but also can reduce the mean global displacement demands with respect to the non-isolated counterpart responses. For example, let an SDOF system with an initial period of 4.0 s and R factor of 1.0 represent a flexible non-isolated structure. Assume that the seismic isolation technique increases the R factor of this system to 8.0 while the initial period remains constant. In this case, the mean spectral displacement response reduces from 0.26 to 0.15 m (i.e., 42% reduction) and the mean force demand reduces by 83% (i.e., an R^∗ factor of 5.9 is achieved). The validity of these results is investigated in Section “Case-Study Bridges.”

For the NF excitations:

• Inelasticity can reduce seismic force demands on relatively long-period structures under the NF excitations; this reduction is as pronounced as that for the FF excitations. For example, for an SDOF system with an initial period of 4.0 s, adopting an R factor of 8.0 reduces the mean force demand under the FD-NF excitations by 81% (i.e., R^∗ = 5.15), whereas, this reduction for the FF excitations is 83% (i.e., R^∗ = 5.9).

• For relatively long periods (e.g., approximately T > 3.0 s), the mean elastic displacement responses are significant (i.e., as great as 1.0 m). Although the inelastic behavior can reduce these responses to some extent, they are still relatively large (i.e., up to 0.7 m). The accommodation of these relatively large displacement responses might be challenging in practice. For this period region, yield displacement values associated with smaller R factors are unrealistically large (i.e., much higher than ranges used in practice). In other words, the target R factors cannot be achieved by adopting yield displacements that lie in ranges used in practice (i.e., u_y < 0.05 m). Therefore, designing isolation systems with initial periods in this range may prove to be challenging. For the intermediate periods of 1.5–2.5 s, the displacement responses are in ranges used in practice (i.e., S_d < 0.5 m). For these periods, assuming R > 4.0, the yield displacement values are also within a practical range. For example, adopting an initial period of 2.0 s and Rfactor of 6.0 results in a u_y value of 0.05 m. However, for these intermediate periods, reducing the lateral strength could considerably increase the displacement demands implying that a relatively low R-value might be preferred in design to limit displacement responses.

• These results suggest that seismic isolation is an effective approach under NF excitations when (i) the initial period of the isolated structure is smaller than approximately 2.5 s (ii) the R factor of the isolation system is roughly between 4.0 and 6.0. The validity of these statements is investigated in Section “Case-Study Bridges.”

Bridges with tall and slender piers and high-rise buildings are of common long-period structures to be considered for seismic isolation. For high-rise buildings, additional challenges arise from the P-delta effects, heavy overturning moments, and gravity loads exerted on isolator bearings. In bridges, isolators are installed between the deck and piers as opposed to at the base in buildings. Therefore, the latter concerns are much less pronounced in long-period bridges. In the next section, bridge models with different isolated and non-isolated periods and lateral-strength levels are studied to validate further the preliminary results obtained from studying the ground response spectra. Most importantly, the results of the next section illustrate that with the proper selection of the lateral-strength and stiffness of bearings, the seismic isolation technique can be effectively applied to relatively long-period structures not only for FF excitations but also for NF excitations. It is also shown that the characteristics of isolator bearings can be reasonably approximated based on the results of inelastic ground response spectra.

Case-Study Bridges

This section uses the responses of case-study bridges to the selected NF and FF excitations to validate the results of the preliminary investigations conducted in Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation.” The case-study models are developed based on the real-world isolated Rudshur bridge. The initial periods of the Rudshur bridge in the longitudinal and transverse directions are 1.93 and 2.55 s, respectively. The superstructure of the bridge is decoupled from the substructure through Lead Rubber Bearings (LRBs) having an overall lateral yield strength, Q_y, equal to 0.06 of the seismically effective weight of the bridge deck. Assuming that the FD-NF and PD-NF are applied to the longitudinal and transverse directions, respectively, the mean resultant (SRSS) elastic S_a for the NF excitations is 0.50 g. For the FF excitations, assuming that the NS-FF and EW-FF are applied to the longitudinal and transverse directions, respectively, the mean resultant (SRSS) elastic S_a is 0.24 g. Using Equations (1) and (2), the R factor for the NF and FF excitations is 8.3 and 4.0, respectively. The bridge piers are relatively tall and slender resulting in a relatively large initial period of 2.22 s for the non-isolated counterpart. Based on the results of the preliminary investigations of Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation,” seismic isolation of this bridge can be an effective design scheme for the FF excitations. As of the NF excitations, the initial isolated and non-isolated periods of the bridge are in the desired range of 1.5–2.5 s obtained in Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation.” However, the existence of the relatively large R factor of 8.3 might result in relatively large displacement responses. The accuracy of these predictions is investigated in this section. To evaluate the effect of the substructure flexibility on the performance of the isolation system, a variant of the bridge with a relatively stiff substructure is also developed.

Rudshur Bridge

Rudshur bridge (Figure 5A) spans the Parand valley in the Tehran–Hamadan railway in Iran and was opened to traffic in 2013. According to the American Association of State Highway and Transportation Officials [AASHTO] (2017), this bridge is categorized as an essential structure as it provides an emergency link in an interstate transportation network connecting the historical province of Hamedan to Tehran, the capital city of Iran. The 600-m-long superstructure of the bridge is a composite steel box-girder (Figure 5B) that is continuous over the 12 spans of equal length. The width of the seismic gaps provided at the deck two ends is 0.40 m. The bridge substructure is composed of 11 intermediate single-column piers and two abutments. The bridge piers are of different heights ranging from 19.0 to 26.0 m. Considering their slenderness, the piers are relatively flexible. All pier types have a reinforced concrete square hollow cross-section with external dimensions 2.8m×2.8m (Figure 5C). The thickness of both the flange and the web is 0.6 m. The longitudinal reinforcement at the bottom 6.0 m of the piers is 128Φ32 (i.e., a total of 128 rebars with a diameter of 32 mm), resulting in a volumetric ratio of 2.1%. The longitudinal reinforcement for the next 9.0 m decreases to 1.6% (i.e., 64Φ32 + 64Φ25) and for the rest of the pier length to 1.2% (i.e., 128Φ25). The typical confining reinforcement is 7Φ14@0.1 m and 2Φ14@0.1 m in the long and short directions of the pier walls, respectively. The expected compressive strength and the ultimate strength of the unconfined concrete are 39 and 25 MPa, respectively. These values for the confined concrete are 50 and 35 MPa, respectively. The compressive strain corresponding to the maximum compressive strength and the ultimate compressive strength for the unconfined concrete is 0.002 and 0.005, respectively. These quantities for the confined concrete are 0.007 and 0.030, respectively. The expected yield strength and the ultimate strength of the reinforcing rebars are 460 and 600 MPa, respectively. The ultimate strain capacity of the rebar material is assumed to be 0.05.

FIGURE 5

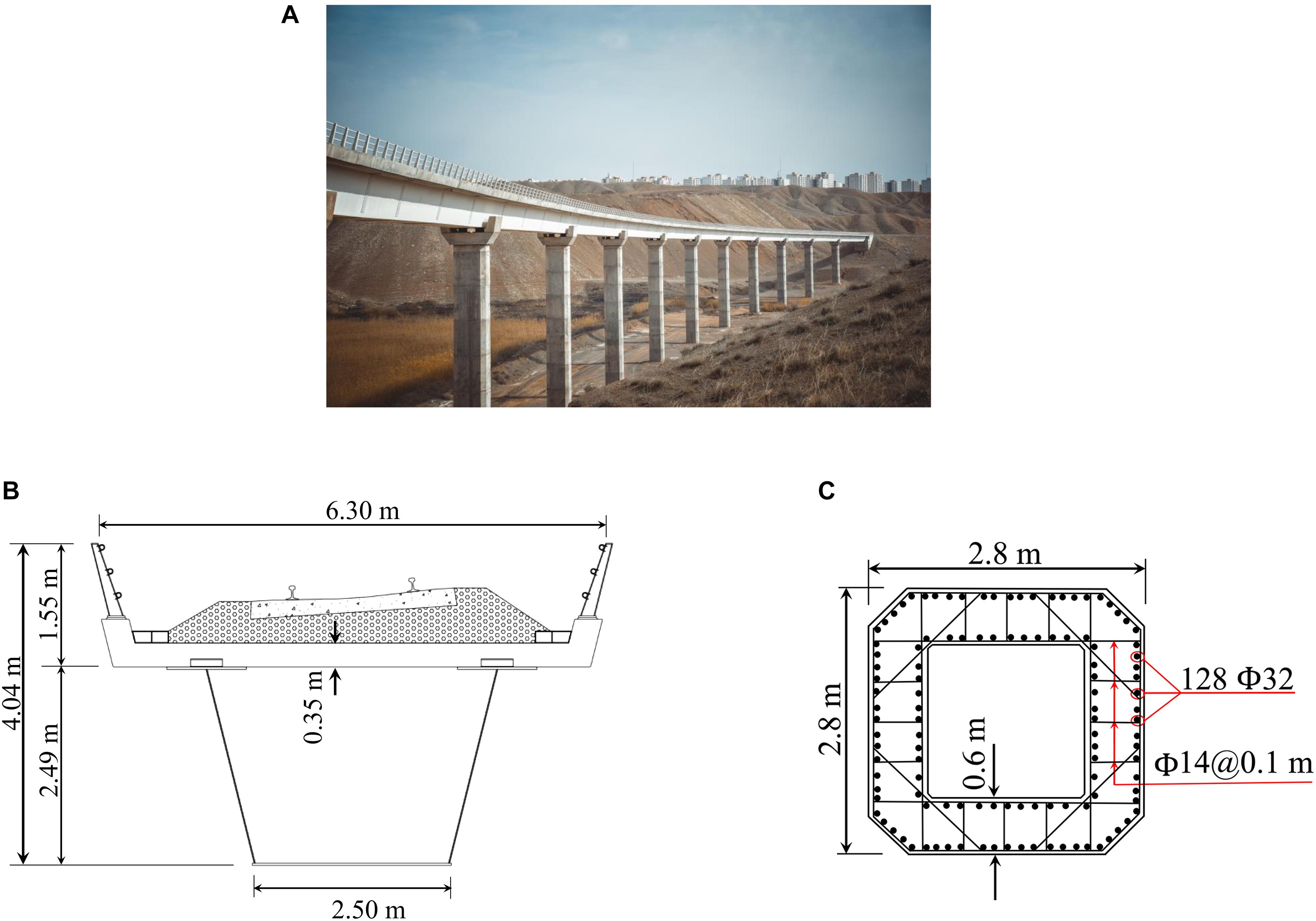
Figure 5. (A) The isolated Rudshur bridge; (B) typical cross-section of the deck; (C) typical reinforcement of the piers at the critical section.

At the top of each pier, a rectangular concrete cap-beam with a plan dimension of 4.5m×3.2m and a thickness of 1.0 m was constructed. Above the cap-beam of each pier and above each abutment, two LRBs with a plan dimension of 0.67m×0.67m, a height of 0.37 m, and a lead core of 0.17 m diameter were installed. The seismically effective weight of the deck (i.e., dead load plus 0.50 live load), W_eff, is approximately 100 MN. The lateral yielding force, yielding displacement, and post-elastic hardening ratio of a single LRB is 225 kN, 23 mm, and 9%, respectively. The lateral elastic stiffness of the rubber and the lead material is 0.88 and 8.91 kN/m, respectively. The lateral displacement capacity of the LRBs is 0.40 m, which is the minimum value obtained from different damage states, including the break of the rubber compound due to shear strain, and the buckling and overturning thresholds (Skinner et al., 2011). The elastic compressive stiffness of each LRB is 934.5 kN/mm. The behavior of the rubber material in tension is assumed to be bilinear with an initial stiffness of 24.4 kN/mm and a stiffness hardening ratio of 4%.

The site-specific seismic hazard studies illustrate that the closest fault to the Rudshur bridge is an inferred fault with a length of 30 km at a distance of 4.5 km (according to the Joyner–Boore criterion). Two faults are also located within 50–70 km of the site. Although the bridge was constructed in an NF region, it was designed assuming a typical response spectrum per the third edition of the Iranian seismic design code (Building and Housing Research Center, 2005) with no considerations for the NF effects. The design PGA of the spectrum was selected as 0.45 g. Note that the designPGA is equivalent to 0.4S_DSI_P, where I_P is the bridge importance factor, and S_DS is the short-period pseudo-spectral acceleration for the site. The elastic 0.05-damped design spectral acceleration for periods smaller and greater than 0.70 s was considered to be 2.50 PGA and 2.75 PGA(0.70/T)^2/3, respectively, where T is the structural period in the direction of interest. For designing the bridge substructure, the elastic force demands were reduced by a factor of R_iso(ξ_equiv./0.05)^0.3, where ξ_equiv. is the equivalent viscous damping ratio provided by the LRBs, and R_iso is the response modification factor that is 1.5 for an isolated bridge with single-column piers (American Association of State Highway and Transportation Officials [AASHTO], 2010).

Additional Bridge Models

To evaluate the efficacy of the seismic isolation technique for the Rudshur bridge, a baseline non-isolated (NI) variant of the bridge with the same geometry and gravity loading but a different bearing condition and pier reinforcement is developed. In this model, it is assumed that the bridge deck is supported by ordinary elastomeric bearings (i.e., low-damping bearings with a relatively small height) that allow for the rotation of the deck with respect to the piers. It is assumed that shear keys are installed between the deck and piers to prevent the relative translational movements between the deck and piers. This bearing condition is equivalent to a pinned connection meaning that only shear forces and gravity loads can be transmitted from the deck to the piers. In this model, to provide a consistent lateral-yielding mechanism in the substructure, each abutment is replaced by a pier with the same characteristics as the side piers. Spectral analysis is conducted, and the bridge piers are redesigned for the updated forces per the AASHTO LRFD provisions. The seismic force-resisting system of this NI scheme in the transverse and longitudinal directions consists of single-column piers. Hence, in this case, an R factor of 3.0 is used for the flexural design of piers. The longitudinal reinforcement at the bottom 6.0 m of the piers (i.e., the critical section for flexural design) is obtained as 160Φ36 with a volumetric ratio of 3%. The longitudinal reinforcement for the next 9.0 m decreases to 2.3% (80Φ36 and 80Φ25) and for the rest of the pier’s length to 1.5% (160Φ25). The confining reinforcement is 14Φ14@0.1 m and 2Φ14@0.1 m in the long and short directions of the pier walls, respectively. The maximum and ultimate compressive strength of the concrete and corresponding strain values are updated for the concrete material based on the new confinement details. The shear reinforcing is performed following the capacity design philosophy meaning that the design shear force is determined based on the pier overstrength moment resistance.

A second substructure scenario is also adopted in which the heights of all piers are reduced to 7.5 m. For this scenario, which represents a relatively short-period substructure, an isolated model with the same LRBs as those used in the as-built bridge and an NI counterpart are developed. In both bridge models, the piers are designed using the response spectrum method. For this substructure scheme, all piers have a reinforced concrete square hollow cross-section with dimensions of 2.2 m × 2.2 m × 0.5 m. The longitudinal reinforcing rebars of the piers for these NI and isolated models are obtained to be 2 and 1%, respectively. The confining rebar is 5Φ14@0.1 m and 2Φ14@0.1 m in the long and short directions of the pier walls and remains the same for both models.

In summary, this section considers four different bridge models: (i) the isolated long-pier (ILP) model that corresponds to the as-built condition of the Rudshur bridge, (ii) the non-isolated long-pier (NLP) model, (iii) the isolated short-pier model (ISP), and (iv) the non-isolated short-pier (NSP) model. The most salient characteristics of the four considered models are summarized in Table 1. To determine the initial fundamental periods, the cracked moment of inertia of the piers is considered to be 0.35I_g, where I_g is the gross moment of inertia of the cross-section; for the isolated models, the initial stiffness of the LRBs is used.

TABLE 1

Table 1. The most salient characteristics of different structural models studied in this section.

Finite Element Modeling and Analysis

The primary finite element modeling and analysis are conducted using OpenSees (McKenna et al., 2000). Independent modeling is carried out in SAP2000 (Computers and Structures Inc., 2019) for verification purposes. The detail of finite element modeling is provided in Supplementary Material Appendix III.

Each record pair, including perpendicular components A and B, is used twice for the 3D non-linear response history analyses performed on a given bridge model. First, component A of a record pair is applied in the longitudinal direction of the bridge, and component B is applied in the transverse direction. Then, the components are swapped. Therefore, for each model, 40 non-linear response history analyses are performed using the NF record pairs and 40 analyses using the FF record pairs. For the FF set, the loading condition in which the SN and EW components of a record pair are applied to the longitudinal and transverse directions of the bridge, respectively, is referred to as Loading Condition 1 (LC 1). The loading condition in which the components are swapped is denoted as LC 2. For the NF excitations, the LC 1 implies the loading condition in which the FD and PD components are applied to the longitudinal and transverse directions, respectively. In the next sections, unless otherwise mentioned, the results are presented for LC 1.

Seismic Performance of Different Bridge Models Subject to Near-Field and Far-Field Excitations

Figure 6A illustrates the time history of the resultant displacement of the deck at the location of pier P₇ for the long-pier models under an FF record pair from the 1995 Kobe earthquake [record pair No. 20 in Supplementary Table S2 (Supplementary Material Appendix I)]. Note that in this context, the resultant response is the square root of the sum of squares of the longitudinal and transverse responses. Figure 6B presents similar graphs for the short-pier models. As it can be observed from Figure 6A, for the long-pier models, the maximum displacement responses of the isolated and non-isolated deck are 0.28 and 0.32 m, respectively, implying that in this case, seismic isolation has reduced the maximum displacement response by 13%. This observation can be interpreted based on the trend observed in non-linear displacement response spectra of the FF ground motions in Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation.” For relatively long-period structures, such as the NLP model studied herein, reducing the lateral yield strength can lead to a reduction in global displacement responses subject to the FF excitations. Given that the yield strength of the isolator bearings in the ILP model is much smaller than that of the concrete piers in the NLP model, in this case, seismic isolation can reduce the deck displacement responses. On the contrary, for the short-pier models, as shown in Figure 6B, the maximum displacement response of the isolated deck with a relatively long period is significantly higher than that of the non-isolated deck with a relatively short period (i.e., 0.28 m versus 0.11 m). This latter observation has been reported in numerous studies available in the literature (e.g., see Liao et al., 2004). It is important to note that in this case, the displacement responses of the isolated deck, although greater than those of the non-isolated deck, are within practical ranges and can be accommodated using typical LRBs and seismic gaps.

FIGURE 6

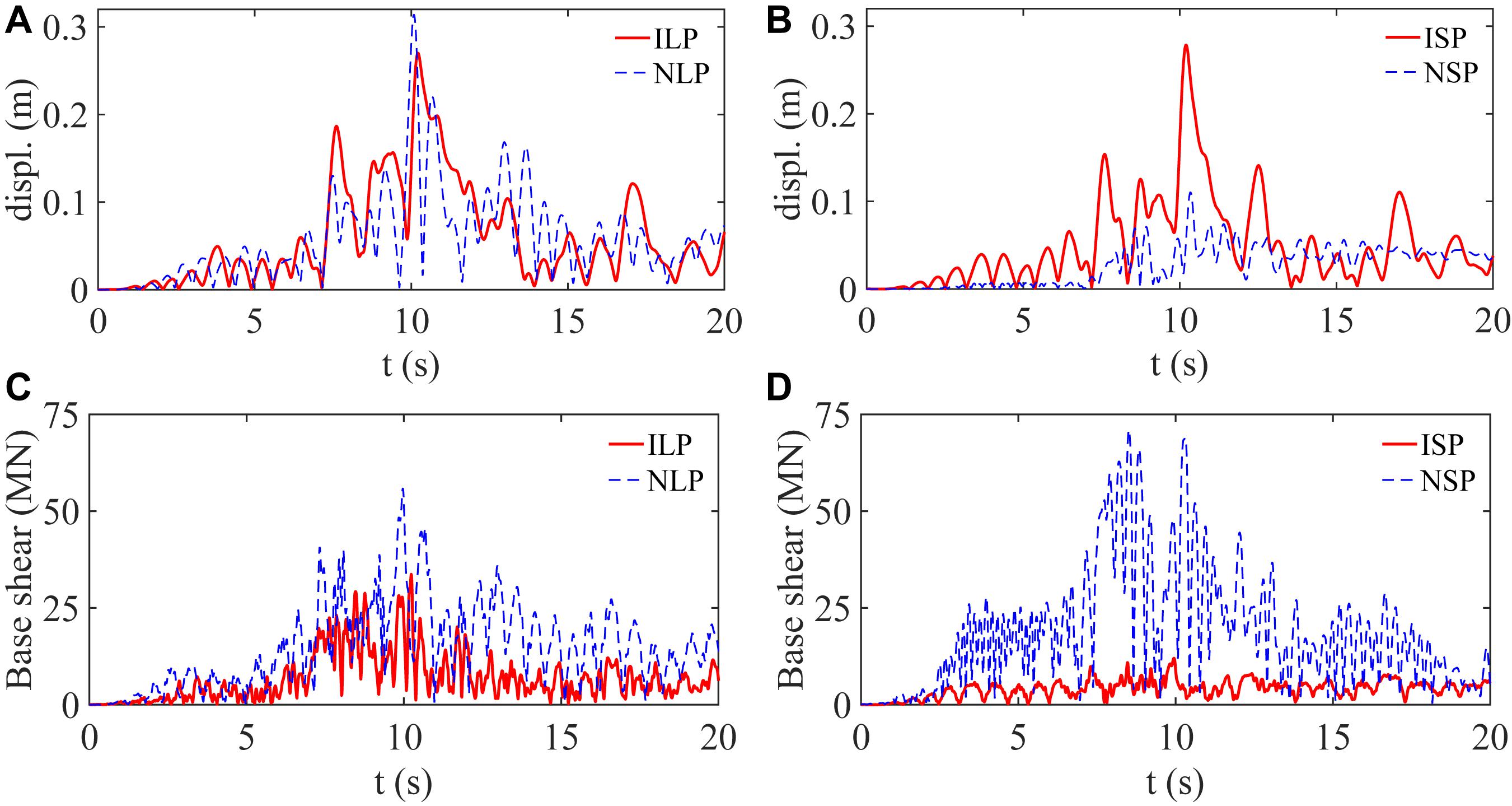
Figure 6. Time history of the resultant responses of different bridge models under an FF record pair from the 1995 Kobe earthquake: (A,B) the deck resultant displacement at the location of pier P₇; (C,D) the bridge resultant base-shear.

Figures 6C,D show, respectively, the time history of the resultant base-shear for the long-pier and short-pier models under the FF record pair referred above. As seen, seismic isolation in the long-pier model reduces the maximum resultant base shear from 52 MN to 30 MN (i.e., 42% reduction) and in the short-pier model from 70 MN to 10 MN (i.e., 86% reduction). As seen, the number of strong cycles in the base-shear responses of the isolated models is less than that of the corresponding non-isolated ones.

Figures 7A,B illustrate the mean values of the maximum resultant displacement responses at the locations of piers P₁ to P₁₃ for different components (i.e., deck, piers, and LRBs) of the four models under the 20 FF record pairs. As seen in Figure 7A, for the long-pier model (i.e., the case with a flexible substructure), seismic isolation under the FF excitations does not cause a significant increase in the mean deck displacement responses. For the case with a stiff substructure shown in Figure 7B, seismic isolation leads to a significant increase in the mean deck displacement responses, although these responses are still within practical range.

FIGURE 7

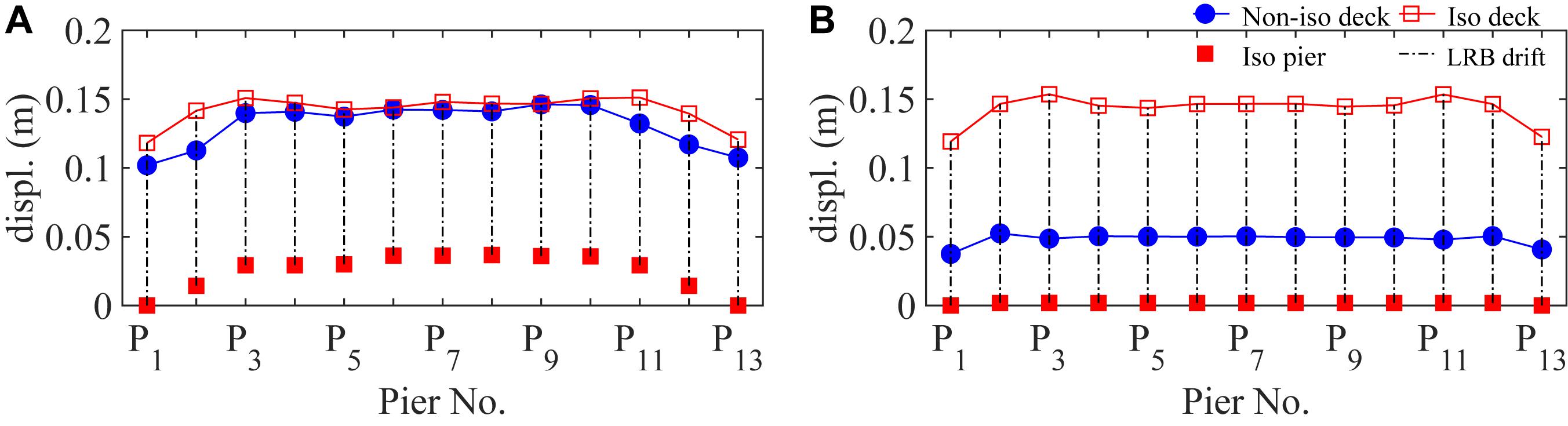
Figure 7. The mean value of the maximum resultant displacement responses under the FF record pairs at piers P₁ to P₁₃: (A) long-pier models; (B) short-pier models.

Figures 8A,B illustrate the time history of the resultant displacement response of the deck at the location of pier P₇ under a representative NF record pair [record pair No. 3 in Supplementary Table S1 (Supplementary Material Appendix I)] for the long-pier and short-pier structural models, respectively. As seen, the deck displacement response in both isolated models and also the non-isolated model with a relatively long period is characterized by a relatively large pulse that appears at the beginning of the response. This displacement pulse is analogous to the velocity pulse observed in the time history of the FD component of the NF record pair shown in Figure 9. This observation, which is consistent with the results of many previous studies (e.g., see Jónsson et al., 2010), reiterates the significant effect of forward directivity pulses on flexible structures.

FIGURE 8

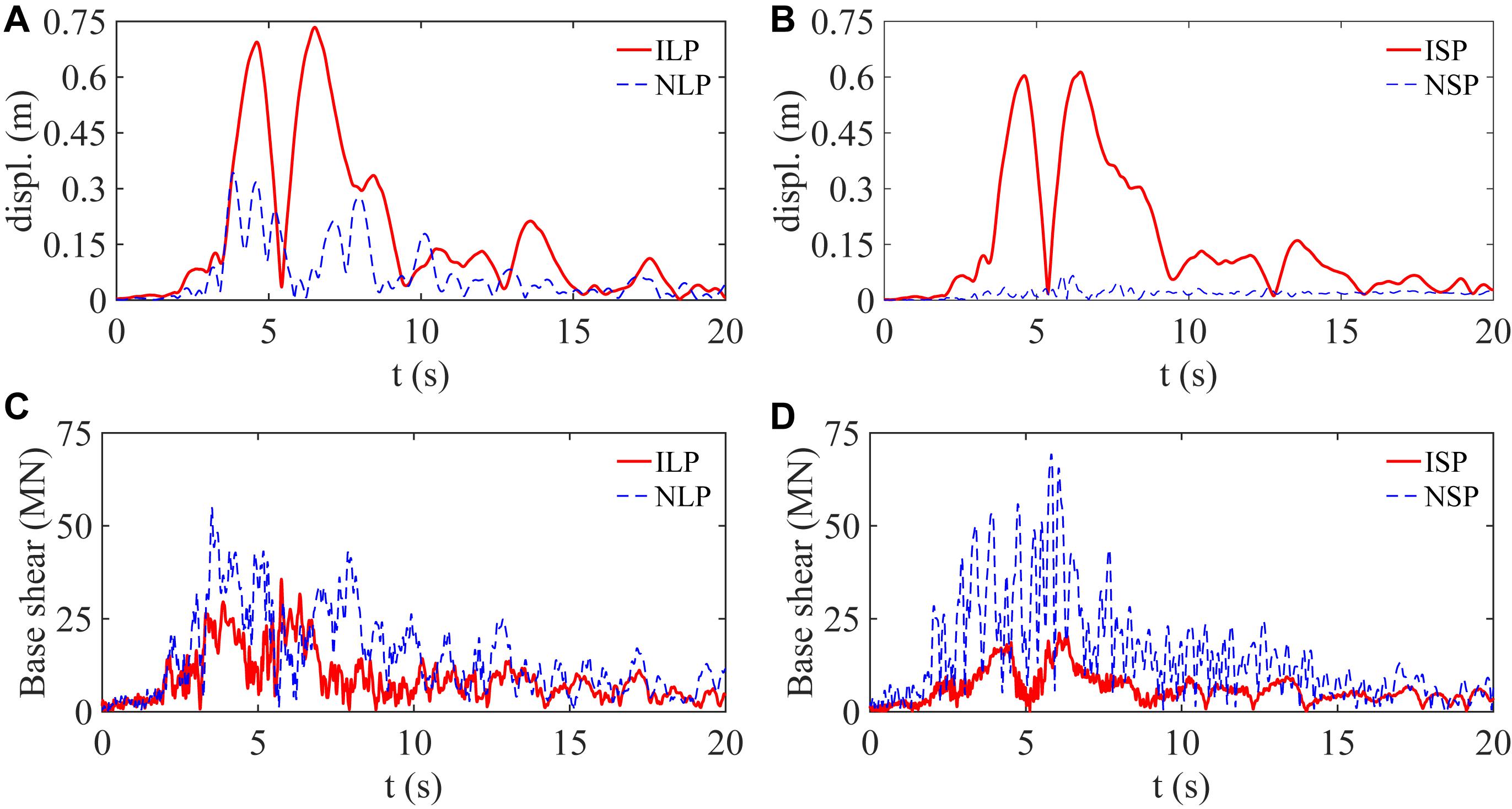
Figure 8. Time history of the resultant responses of different bridge models under an NF record pair from the 1979 Imperial Valley earthquake: (A,B) the deck resultant displacement at the location of pier P₇; (C,D) the bridge resultant base-shear.

FIGURE 9

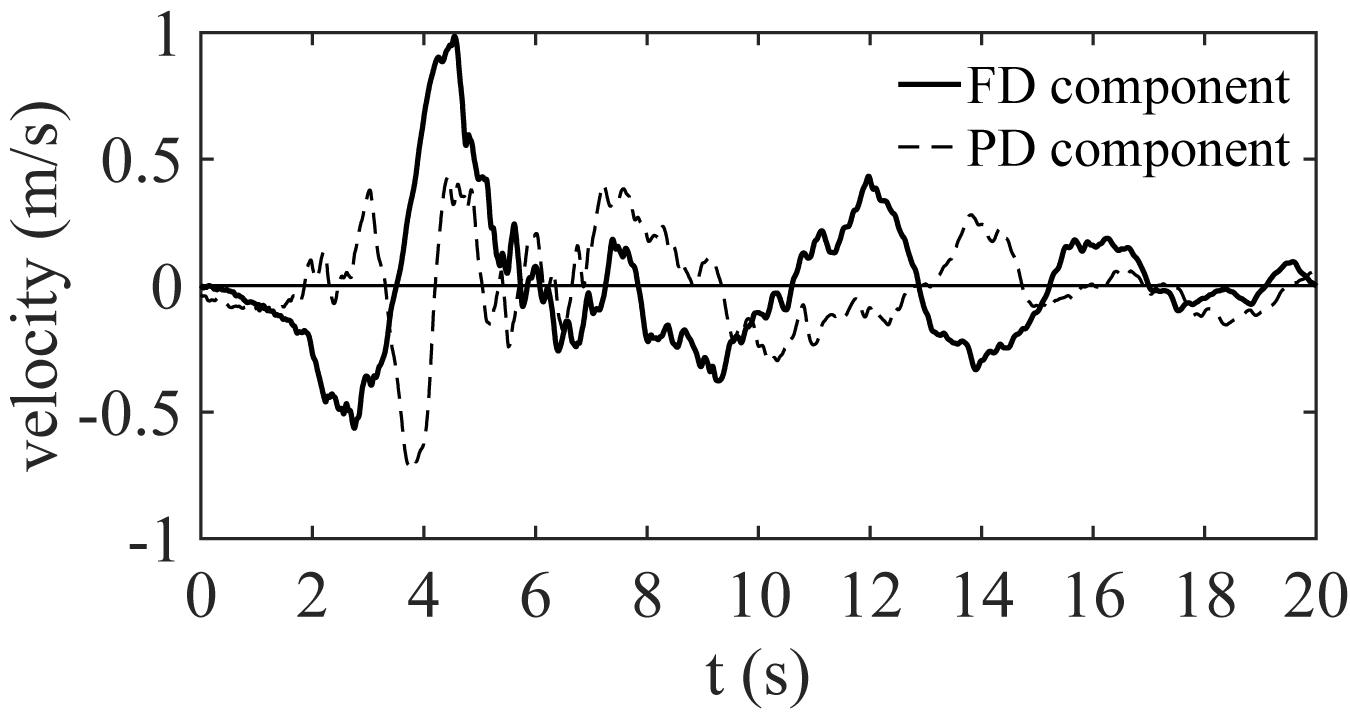
Figure 9. The velocity time history of the FD and PD components of an NF record pair from the 1979 Imperial Valley event.

Figures 8C,D illustrate, respectively, the time history of the resultant base-shear for the long-pier and short-pier models subjected to the NF record pair No. 3. As seen, under this NF excitation, seismic isolation reduces the maximum resultant base-shear response of the long-pier model from 52 MN to 33 MN (i.e., 34% reduction) and of the short-pier model from 65 MN to 20 MN (i.e., 69% reduction). As an important observation, the number of strong cycles in the base-shear response of the isolated models is less than that of the corresponding non-isolated ones.

Figures 10A,B illustrate the mean values of the maximum resultant displacement responses at the locations of piers P₁ to P₁₃ for different components of the four models under the 20 NF record pairs. As seen, for the NF excitations, seismic isolation leads to a significant increase in the deck displacement responses. This increase is less pronounced in the case of the flexible substructure scenario. This is relevant because the non-isolated counterpart of the flexible substructure scenario, unlike that of the stiff substructure scenario, is itself long-period and hence, experiences relatively large displacement responses under the NF excitations. As a result, in this case, the difference between the displacement responses of the isolated and non-isolated models is smaller. For example, the increase in the mean deck displacement at pier P₇ for the long-pier model (flexible substructure scenario) is 0.28 m, whereas for the short-pier model (stiff substructure scenario) is 0.45 m. As seen, the LRBs’ drift responses in the isolated short-pier model are more significant.

FIGURE 10

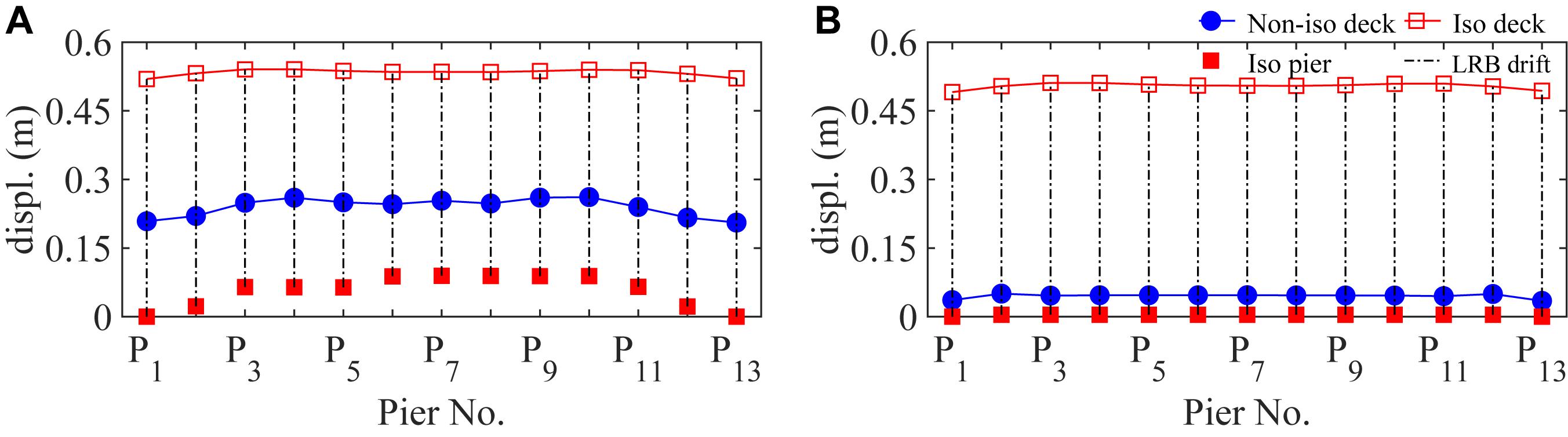
Figure 10. The mean value of the maximum resultant displacement responses under the NF record pairs at piers P₁ to P₁₃ (A) long-pier models; (B) short-pier models.

The adverse effect of seismic isolation under the NF excitations is the relatively large mean displacement responses of the isolated deck that can be as great as 0.55 m. Further evaluation of the results illustrates that for the as-built Rudshur bridge model, almost under half of the NF excitations, the LRBs’ drift responses exceed their failure threshold. These observations show that for the isolated Rudshur bridge, which was designed only for ordinary FF excitations, the main problem under the NF excitations is the relatively large displacement responses of the isolated deck.

Further Evaluation of the Effectiveness of Seismic Isolation for the Long-Period Model

This section aims to further (1) clarify the extent to which seismic isolation is effective in improving the performance of the long-period bridge model (i.e., the as-built model of the Rudshur bridge) with respect to the short-period one; (2) evaluate the effectiveness of the seismic isolation for the long-period model under the NF excitations with respect to that under the FF excitations. To this end, for a given earthquake excitation, the maximum resultant response of an isolated model is normalized to that of its non-isolated counterpart. As mentioned earlier in this section, a total of 40 NF and 40 FF excitations are used in the response history analyses. Therefore, for a given structural response of an isolated model, the adopted approach results in 40 normalized values under each ground motion set. These values (i.e., response ratios) are used to determine the probability of exceedance of the maximum resultant response of an isolated model from its non-isolated counterpart. Figure 11 illustrates such analysis results for the four analysis cases considered herein: the ILP model subject to the NF records; the ILP model subject to the FF records; the ISP model subject to the NF records; the ISP model subject to the FF records. In this figure, “the probability of exceedance equal to 0.5” is the median value of a response ratio.

FIGURE 11

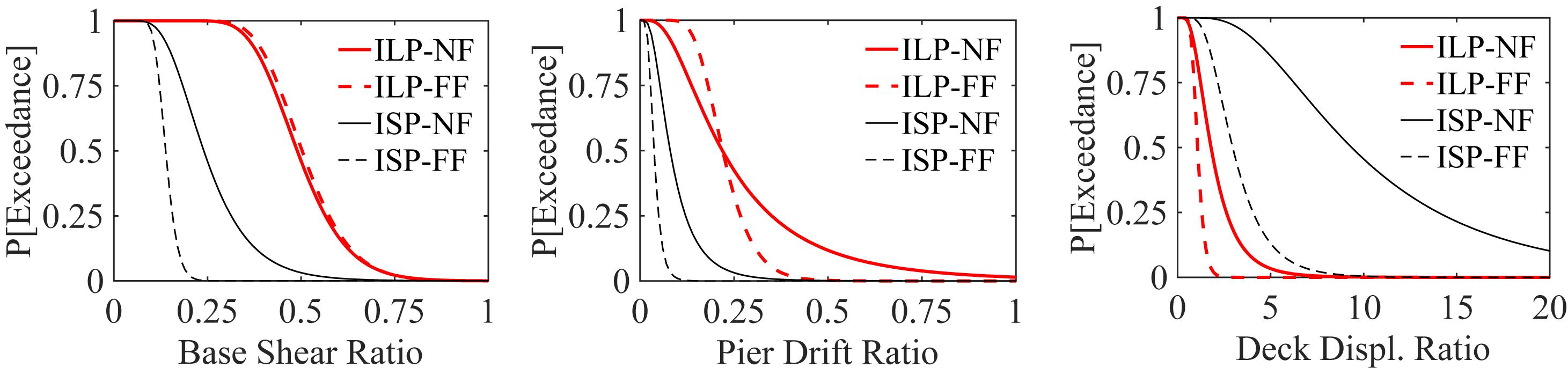
Figure 11. Probability of exceeding the ratio of the maximum resultant responses of the isolated models from a given value.

An evaluation of the results shown in Figure 11 illustrates that, in terms of the substructure response reduction, seismic isolation is most effective for the bridge model with the short-period substructure under the FF excitations (i.e., the ISP-FF analysis case) as the smallest base-shear and pier-drift ratios are obtained for this case. As seen, the median base-shear response for this case is decreased by 86% (a response ratio of 0.14). However, seismic isolation is still an effective method to reduce the seismic demands on the substructure in the three other cases. As seen, the median base-shear reduction for the ISP-NF, ILP-FF, and ILP-NF cases is 76, 49, and 51%, respectively (i.e., still significant). The base-shear and pier-drift ratios for these analysis cases are always smaller than unity (with different extents), implying a consistent performance improvement due to seismic isolation. In summary, seismic isolation is effective in reducing mean force demands for all four cases considered. However, it is observed that this approach:

(i) subject to the FF excitations, is to some extent more effective for stiff structures than for flexible structures;

(ii) for stiff structures, is more effective under the FF excitations than under the NF excitations; this latter conclusion is consistent with the results presented in Liao et al. (2004);

(iii) for flexible structures, is approximately equally effective under the NF and FF excitations;

These observations are consistent with the effects of the period-shift caused by isolation system on the spectral acceleration demands for the NF and FF excitations.

In terms of the superstructure displacement response, for the cases ILP-NF, ISP-FF, and ISP-FF, the deck displacement ratios are always greater than 1.0 (with different extent) meaning that seismic isolation consistently increases the deck displacement response. However, for the ILP-FF case, the probability of the displacement ratio being smaller than 1.0 is 55% meaning that under 22 out of the 40 FF excitations, the maximum resultant displacement response of the isolated deck is smaller than that of the non-isolated deck. It is observed that the effect of the NF records on the maximum displacement responses of the isolated superstructure is more highlighted for the short-pier bridge model than for the long-pier one. Indeed, in the first case, the median displacement ratio can be as great as 9.34, while in the latter case, this quaintly is only 1.80. This observation is related to the frequency content of the NF ground motions (i.e., pulse period). As previously discussed, the non-isolated long-pier model is already long-period and more affected by the pulse motions of the NF records. Therefore, in this case, the difference between the displacement responses of the isolated and non-isolated superstructure is smaller.

The results of the previous sections illustrate that for the isolated Rudshur bridge (the ILP model with a relatively flexible substructure) subject to the FF excitations, seismic isolation is not only effective in reducing the substructure seismic demands but also can reduce the median (and mean) deck displacement responses; although, in this case, the substructure demand reduction might not be as pronounced as that in the stiff-substructure model. As of the NF excitations, seismic isolation provides significant reduction in the substructure responses of this bridge, however, due to the relatively small lateral strength of the LRBs, the deck displacement responses become relatively large. These results verify the accuracy of the predictions made in the outset of Section “Case-Study Bridges” based on the results of the inelastic ground response spectra. The next section proposes a retrofit scheme to reduce the deck displacement responses of the Rudshur bridge without much altering (deteriorating) the substructure seismic demands.

Improving the Performance of the Isolated Rudshur Bridge for Near-Field Excitations

The normalized yield strength of the LRBs, Q_y/W_eff, used is the Rudshur bridge is relatively low (i.e., 6%) as the bridge was designed for ordinary FF (non-pulse) ground motions. This normalized yield strength for the NF excitations is equivalent to an R factor of 8.3. As illustrated in Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation” and verified in Section “Further Evaluation of the Effectiveness of Seismic Isolation for the Long-Period Model,” for NF excitations, this low yield strength (i.e., relatively large R-value) causes relatively large superstructure displacement responses under the NF excitations. Assume that a target superstructure displacement response of 0.30 m is desired. The results of Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation” suggest that for the range of the initial period of the isolated Rudshur bridge, the use of an R-value between 4.0 and 6.0 (i.e., a Q_y/W_eff ratio of 12–15%) can limit the maximum displacement response of the superstructure to this target value. This prediction is consistent with the results of Jangid (2007). Jangid performed parametric studies on a few numerical models subject to six NF excitations and illustrated that a Q_y/W_eff value in the range 10–15% can result in an optimum design meaning that acceleration and force demands are significantly reduced and bearing displacement responses are within ranges used in practice. In this section, the normalized yield strength of the LRBs is increased from the existing value of 6% to 12% to examine the accuracy of these predictions. The other characteristics of the LRBs, including their elastic and post-elastic stiffness values, remain unchanged. 3D non-linear response history analyses are conducted on the isolated Rudshur bridge (ILP model) with the new LRBs subject to the 20 NF and 20 FF record pairs (for LC1).

The maximum resultant responses of the ILP models with Q_y/W_eff values of 6 and 12% are normalized to those of the baseline non-isolated counterpart (NLP model). These normalized values are used to evaluate the probability of exceedance of the responses of the ILP models from those of the NLP model. This evaluation can illustrate whether the seismic isolation technique with the new LRBs can improve the seismic behavior of the Rudshur bridge subject to the NF and FF excitations. Figure 12A shows the probability of exceedance of the normalized responses of the ILP models from a given value for the FF excitations. Figure 12B presents a similar evaluation for the NF excitations. As seen, increasing the yield strength of the LRBs to 12% can significantly improve the performance of the isolated model under the NF excitations in terms of the deck displacement responses. For example, for the case with Q_y/W_eff = 6%, the probability that the displacement ratio of the isolated deck exceeds 2.0 is 51%, whereas for the case with Q_y/W_eff = 12%, this quantity reduces to 24%. The performance of the ILP model under the FF excitations has remained almost unaffected in terms of the deck displacement response. Increasing the yield strength of the LRBs degrades the performance of the ILP model in terms of the base-shear and acceleration response reduction. The most highlighted adverse effect of increasing the LRBs’ yield strength is the increase of the deck acceleration responses under the FF excitations. For example, the probability that the acceleration ratio of the isolated deck under the FF and NF excitations exceeds 0.50, for the case with Q_y/W_eff = 6% is 35 and 20%, respectively, whereas these quantities for the case with Q_y/W_eff = 12% are 98 and 77%, respectively. However, these increased acceleration responses (and base shear responses) are still quite below those of the non-isolated counterpart. This is further investigated next.

FIGURE 12

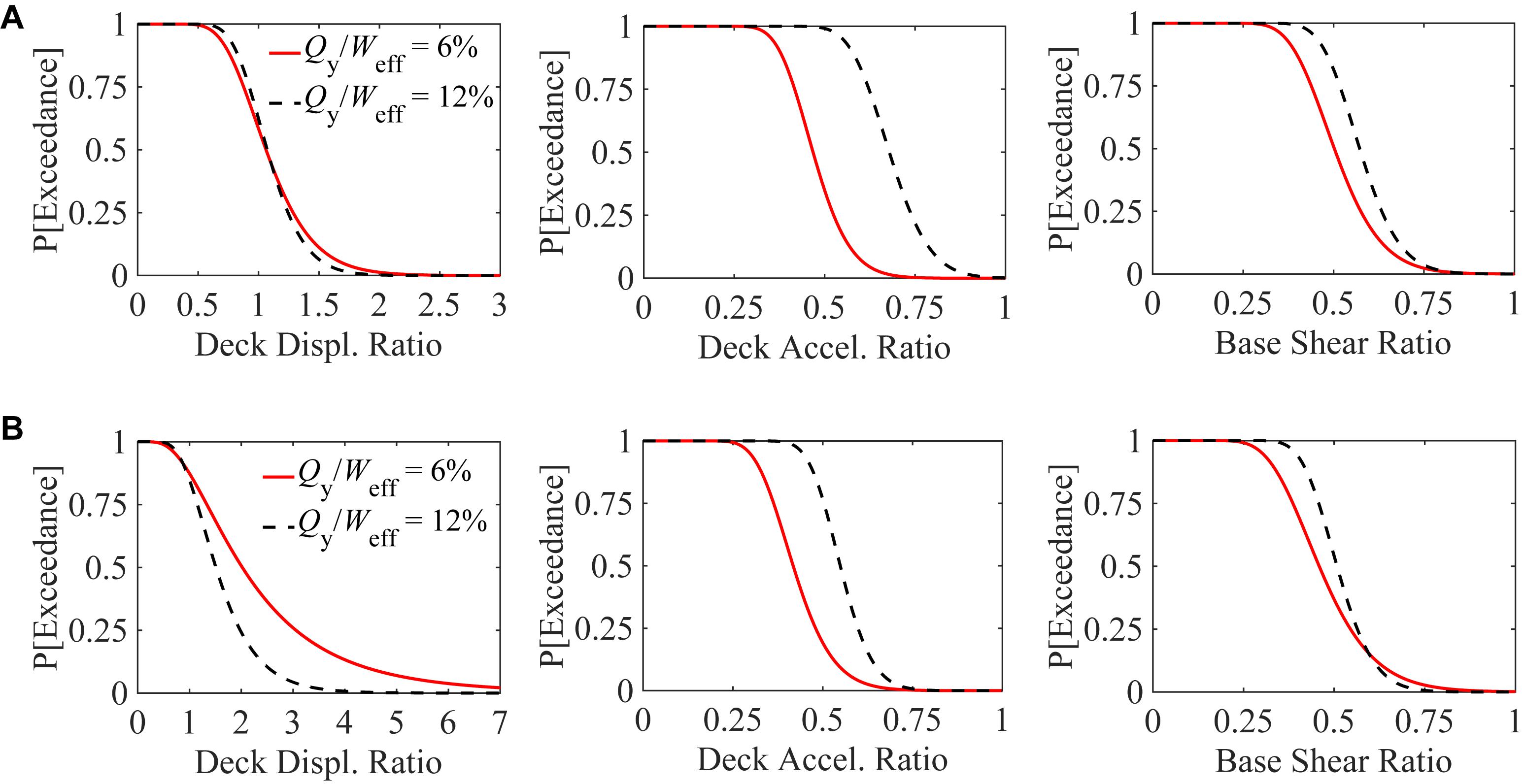
Figure 12. Probability of exceeding the ratio of the maximum resultant responses of the isolated long-pier models from a given value for the (A) FF; (B) NF excitations.

Table 2 presents the values of the maximum resultant seismic responses of the ILP model with Q_y/W_eff = 6% and 12% and also of the NLP model. As seen, using the higher-strength LRBs reduces the mean deck displacement responses under the NF excitations from 0.53 to 0.33 m (i.e., 38% reduction) that is smaller than the LRBs’ drift capacity and also than the width of seismic gaps at the two ends of the deck. This conclusion verifies the prediction made at the outset of this section regarding the use of an R factor of 4.0 to limit the superstructure displacement response to 0.30 m. As an adverse effect, the mean deck acceleration response under the FF excitations increases from 0.23 to 0.28 g and under the NF excitations from 0.22 to 0.33 g. However, these increased acceleration responses are still 42 and 38% below the responses of the non-isolated counterpart, respectively. Furthermore, while in building structures, a primary objective of seismic isolation is to minimize the superstructure acceleration responses to protect acceleration-sensitive equipment and non-structural components, most bridges do not contain such components. Therefore, the slight deterioration in the performance of the isolated bridge in terms of the superstructure acceleration response cannot be considered a significant drawback of increasing LRBs’ yield strength, especially when these responses are still quite below the responses of the non-isolated counterpart. These results, consistent with those of studying inelastic ground response spectra in Section “Ground Spectra to Preliminary Evaluate the Effectiveness of Seismic Isolation,” illustrate that when designed properly (i.e., initial period and lateral strength of the isolation system are within certain ranges), seismic isolation can be an effective approach for intermediate- and relatively long-period structures subjected to both FF and NF excitations.

TABLE 2

Table 2. The mean value of the maximum resultant seismic responses under the NF and FF record pairs for the LC 1.

It is worthwhile noting that a few other studies have also proposed solutions for the relatively large responses of isolated superstructures, including an adaptive semi-active control system (Rabiee and Chae, 2019), gap hysteretic dampers operating in parallel to the isolation system (De Domenico et al., 2020), and tuned-mass-damper inerters (De Domenico and Ricciardi, 2018; De Domenico et al., 2019), among others. In future studies, the use of these control systems for reducing the displacement responses of the superstructure of isolated structures with long non-isolated periods subjected to NF excitations can be investigated.

Conclusion

It is well established that seismic isolation is effective for short-period (stiff) structures exposed to short-period ground excitations such as ordinary far-field (FF) motions. However, the use of this technique for structures with relatively long non-isolated periods and also for pulse-like motions, such as many near-field (NF) excitations, has remained controversial. This study addresses this controversy. Constant-R inelastic ground response spectra are used to systematically evaluate the effects of the two fundamental aspects of seismic isolation, i.e., period lengthening and lateral-strength reduction, on the responses of relatively long-period structures. To verify the results, non-linear response history analyses are conducted on isolated and non-isolated case-study bridges with different periods and lateral strength. These bridge models are developed based on the real-world isolated Rudshur bridge. In the as-built condition, the piers are relatively tall and flexible, resulting in a relatively long non-isolated period of 2.22 s. This bridge, which is located in the Tehran–Hamadan railway in Iran, is categorized as an essential infrastructure according to the AASHTO LRFD provisions. With the length of 600 m, the continuous deck of the bridge is decoupled from the substructure by Lead Rubber Bearing (LRBs) installed between the deck and substructure. In spite of the existence of a major fault within 10 km of the site, this structure was designed for ordinary FF ground motions without NF considerations. This design resulted in LRBs with relatively low yield strength (i.e., equal to 6% of the seismic weight of the deck). An additional objective of this study is to assess the seismic performance of the Rudshur bridge and propose a rehabilitation scheme, if necessary.

A set of 20 NF record pairs containing forward directivity (FD) pulses and a set of 20 ordinary FF (non-pulse) record pairs are used in the response history analyses. To investigate the FD effects, each NF record pair is rotated to the FD/PD directions, where the FD is the orientation that dominates the seismic hazard at the recording site, and the PD is the orientation perpendicular to the FD. Peak ground acceleration (PGA) of all FF and NF record pairs is scaled to the design value of 0.45 g. Elastic/inelastic acceleration and displacement response spectra are developed for the selected ground motions. Non-linear response history analyses are also conducted on the case-study bridges.

The effectiveness of seismic isolation is investigated for four different scenarios: short-period structures subject to FF excitations, short-period structures subject to NF excitations, long-period structures subject to FF excitations, and long-period structures subject to NF excitations. The structural responses used to evaluate this effectiveness are superstructure displacement and acceleration responses, and substructure drift and shear force demands. The most salient results of the present study are summarized next:

(1) Inelastic constant-R ground spectra, including the spectral displacement, yield displacement, and force-reduction spectra together, can be used for the preliminary design of seismic isolation systems. It is shown that they can reasonably predict the global displacement responses of isolated structures.

(2) In terms of the superstructure acceleration response reduction and substructure force demand reduction, it is observed that:

• Seismic isolation is most effective for short-period structures subject to FF excitations but still significantly effective for the other three cases. In general, subject to FF excitations, seismic isolation is to some extent more effective for stiff structures than for flexible structures; for stiff structures, this approach is more effective under FF excitations than under NF excitations; for flexible structures, is approximately equally effective under NF and FF excitations. For example, for the case-study bridge models, the reduction in the median value of the maximum base-shear responses due to seismic isolation for the stiff-FF, stiff-NF, flexible-FF and flexible-NF cases is 86, 76, 49, and 51%, respectively. These results are consistent with the frequency contents of the NF and FF excitations and their significant different effects on structures with short and long periods.

• Reducing the yield strength of isolator bearings can consistently reduce mean seismic force and acceleration demands under both NF and FF excitations.

• For structures with relatively long non-isolated periods, the mean force demand reduction under NF excitations can be even more highlighted than that under FF excitations. This observation is opposite to that for structures with short non-isolated periods.

(3) In terms of superstructure displacement response, it is observed that:

• Seismic isolation does not result in a significant increase of the mean responses of the superstructure in long-period structures under FF excitations, and in some cases, can even reduce these responses. However, for NF excitations, when the initial period of the isolated structure is relatively large (approximately greater than 2.5 s), seismic isolation can impose relatively large superstructure displacement demands (e.g., as great as 1.0 m for the studied cases). In this case, if the initial isolated period lies in the intermediate region (e.g., 1.5–2.5 s), and the lateral strength of the isolators is relatively high (e.g., the R factor is 4.0–6.0), the displacement responses remain within ranges used in practice.

(4) The isolated Rudshur bridge was designed for ordinary ground motions resulting in isolator bearings with a relatively low yield strength that is equal to 6% of the deck seismic weight (i.e., the design resulted in the relatively large equivalent R factor of 8.3). This design causes relatively large deck displacement responses under NF excitations. The results illustrate that for many individual NF excitations, the drift demands on LRBs exceed their failure capacity. Increasing the LRBs’ lateral yield strength from 6 to 12% of the deck seismic weight while reducing the superstructure displacements under the NF excitations to acceptable values, only slightly increases base shear and acceleration responses. It is shown that these increased values are still quite smaller than those of the non-isolated counterpart.

Tall buildings and bridges with tall/slender piers are of common long-period structures. The important challenges of applying base isolation to tall buildings are the P-delta effects, and heavy overturning moments and gravity loads exerted on bearings that may cause difficulties in the operation and design of isolator bearings. In bridges, isolators are installed between the deck and piers as opposed to at the base in buildings. Therefore, the concerns arising from the heavy overturning moments and gravity loads of tall buildings are much less pronounced in bridges. This statement, combined with the results of the conducted numerical studies, suggests that seismic isolation is an effective approach for bridges with relatively flexible piers (i.e., relatively long non-isolated periods).

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

HA developed the research idea, performed the literature review, designed the bridge models, performed finite element modeling and analysis, processed the results, drafted the article, and addressed the review comments. KP contributed to the finite element modeling, record selection, and design of the bridge models. MR contributed to the finite element modeling, analysis and writing the first two sections of the article. ES-B supervised and proofread the article.

Conflict of Interest

KP was employed by the company Pars Seismic Co.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2020.00024/full#supplementary-material

References

American Association of State Highway and Transportation Officials [AASHTO] (2010). Guide Specifications for Seismic Isolation Design. Washington, DC: AASHTO.

Google Scholar

American Association of State Highway and Transportation Officials [AASHTO] (2017). AASHTO LRFD Bridge Design Specifications. Washington, DC: AASHTO.

Google Scholar

Anajafi, H., and Medina, R. A. (2018). Partial mass isolation system for seismic vibration control of buildings. Struct. Control Health Monit. 25:e2088. doi: 10.1002/stc.2088

CrossRef Full Text | Google Scholar

Archila, M., Ventura, C. E., and Liam Finn, W. (2017). New insights on effects of directionality and duration of near-field ground motions on seismic response of tall buildings. Struct. Des. Tall Spec. Build. 26:e1363. doi: 10.1002/tal.1363

CrossRef Full Text | Google Scholar

Baker, J. W. (2007). Quantitative classification of near-fault ground motions using wavelet analysis. Bull. Seismol. Soc. Am. 97, 1486–1501. doi: 10.1785/0120060255

CrossRef Full Text | Google Scholar

Beiraghi, H., Kheyroddin, A., and Kafi, M. A. (2016). Forward directivity near-fault and far-fault ground motion effects on the behavior of reinforced concrete wall tall buildings with one and more plastic hinges. Struct. Des. Tall Spec. Build. 25, 519–539. doi: 10.1002/tal.1270

CrossRef Full Text | Google Scholar

Bekdas̨, G., and Nigdeli, S. M. (2013). Mass ratio factor for optimum tuned mass damper strategies. Int. J. Mech. Sci. 71, 68–84. doi: 10.1016/j.ijmecsci.2013.03.014

CrossRef Full Text | Google Scholar

Building and Housing Research Center (2005). Iranian Code of Practice for Seismic Resistant Design of Buildings (Standard No. 2800), 3rd Edn. Tehran: BHRC Publication.

Google Scholar

Campbell, K. W., and Bozorgnia, Y. (2008). NGA ground motion model for the geometric mean horizontal component of PGA, PGV, PGD and 5% damped linear elastic response spectra for periods ranging from 0.01 to 10 s. Earthq. Spectra 24, 139–171. doi: 10.1193/1.2857546

CrossRef Full Text | Google Scholar

Chenouda, M., and Ayoub, A. (2008). Inelastic displacement ratios of degrading systems. J. Struct. Eng. 134, 1030–1045. doi: 10.1061/(asce)0733-9445(2008)134:6(1030)

CrossRef Full Text | Google Scholar

Chopra, A. K., and Chintanapakdee, C. (2004). Inelastic deformation ratios for design and evaluation of structures: single-degree-of-freedom bilinear systems. J. Struct. Eng. 130, 1309–1319. doi: 10.1061/(asce)0733-9445(2004)130:9(1309)

CrossRef Full Text | Google Scholar

De Domenico, D., Deastra, P., Ricciardi, G., Sims, N. D., and Wagg, D. J. (2019). Novel fluid inerter based tuned mass dampers for optimised structural control of base-isolated buildings. J. Franklin Inst. 356, 7626–7649. doi: 10.1016/j.jfranklin.2018.11.012

CrossRef Full Text | Google Scholar

De Domenico, D., Gandelli, E., and Quaglini, V. (2020). Effective base isolation combining low-friction curved surface sliders and hysteretic gap dampers. Soil Dyn. Earthq. Eng. 130:105989. doi: 10.1016/j.soildyn.2019.105989

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018). An enhanced base isolation system equipped with optimal tuned mass damper inerter (TMDI). Earthq. Eng. Struct. Dyn. 47, 1169–1192. doi: 10.1002/eqe.3011

CrossRef Full Text | Google Scholar

Fujita, K., Yasuda, K., Kanno, Y., and Takewaki, I. (2017). Robustness evaluation of elastoplastic base-isolated high-rise buildings subjected to critical double impulse. Front. Built Environ. 3:31. doi: 10.3389/fbuil.2017.00031

CrossRef Full Text | Google Scholar

Günes̨, N., and Ulucan, Z. Ç (2019). Nonlinear dynamic response of a tall building to near-fault pulse-like ground motions. Bull. Earthq. Eng. 17, 2989–3013. doi: 10.1007/s10518-019-00570-y

CrossRef Full Text | Google Scholar

Hall, J. F., Heaton, T. H., Halling, M. W., and Wald, D. J. (1995). Near-source ground motion and its effects on flexible buildings. Earthq. Spectra 11, 569–605. doi: 10.1193/1.1585828

CrossRef Full Text | Google Scholar

Huang, Y. N., Whittaker, A. S., and Luco, N. (2008). Maximum spectral demands in the near-fault region. Earthq. Spectra 24, 319–341. doi: 10.1193/1.2830435

CrossRef Full Text | Google Scholar

Iervolino, I., Chioccarelli, E., and Baltzopoulos, G. (2012). Inelastic displacement ratio of near-source pulse-like ground motions. Earthq. Eng. Struct. Dyn. 41, 2351–2357.

Google Scholar

Jäger, C., and Adam, C. (2013). Influence of collapse definition and near-field effects on collapse capacity spectra. J. Earthq. Eng. 17, 859–878. doi: 10.1080/13632469.2013.795842

CrossRef Full Text | Google Scholar

Jangid, R., and Kelly, J. (2001). Base isolation for near-fault motions. Earthq. Eng. Struct. Dyn. 30, 691–707. doi: 10.1016/j.heliyon.2016.e00069

PubMed Abstract | CrossRef Full Text | Google Scholar

Jangid, R. S. (2007). Optimum lead-rubber isolation bearings for near-fault motions. Eng. Struct. 29, 2503–2513. doi: 10.1016/j.engstruct.2006.12.010

CrossRef Full Text | Google Scholar

Jónsson, M. H., Bessason, B., and Haflidason, E. (2010). Earthquake response of a base-isolated bridge subjected to strong near-fault ground motion. Soil Dyn. Earthq. Eng. 30, 447–455. doi: 10.1016/j.soildyn.2010.01.001

CrossRef Full Text | Google Scholar

Komuro, T., Nishikawa, Y., Kimura, Y., and Isshiki, Y. (2005). Development and realization of base isolation system for high-rise buildings. J. Adv. Concr. Technol. 3, 233–239. doi: 10.3151/jact.3.233

CrossRef Full Text | Google Scholar

Lagos, R., Boroschek, R., Retamales, R., Lafontaine, M., Friskel, K., and Kasalanati, A. (2017). “Seismic Isolation of the Nunoa Capital Building, the Tallest Base Isolated Building in the Americas,” in Proceedings of the 16th World Conference on Earthquake Engineering, Santiago.

Google Scholar

Li, J., Peng, T., and Xu, Y. (2008). Damage investigation of girder bridges under the Wenchuan earthquake and corresponding seismic design recommendations. Earthq. Eng. Eng. Vib. 7, 337–344. doi: 10.1007/s11803-008-1005-6

CrossRef Full Text | Google Scholar

Li, X., Dou, H., and Zhu, X. (2007). Engineering characteristics of near-fault vertical ground motions and their effect on the seismic response of bridges. Earthq. Eng. Eng. Vib. 6, 345–350. doi: 10.1007/s11803-007-0723-5

CrossRef Full Text | Google Scholar

Liao, W. I., Loh, C. H., and Lee, B. H. (2004). Comparison of dynamic response of isolated and non-isolated continuous girder bridges subjected to near-fault ground motions. Eng. Struct. 26, 2173–2183. doi: 10.1016/j.engstruct.2004.07.016

CrossRef Full Text | Google Scholar

Liao, W. I., Loh, C. H., Wan, S., Jean, W. Y., and Chai, J. F. (2000). Dynamic responses of bridges subjected to near-fault ground motions. J. Chin. Inst. Eng. 23, 455–464. doi: 10.1080/02533839.2000.9670566

CrossRef Full Text | Google Scholar

Ma, C., Zhang, Y., Tan, P., and Zhou, F. (2014). Seismic response of base-isolated high-rise buildings under fully nonstationary excitation. Shock Vib. 2014:401469.

Google Scholar

Malhotra, P. K. (1999). Response of buildings to near-field pulse-like ground motions. Earthq. Eng. Struct. Dyn. 28, 1309–1326. doi: 10.1002/(sici)1096-9845(199911)28:11<1309::aid-eqe868>3.0.co;2-u

CrossRef Full Text | Google Scholar

McKenna, F., Fenves, G., and Scott, M. (2000). Open System for Earthquake Engineering Simulation. Berkeley, CA: University of California.

Google Scholar

Naderpour, H., Naji, N., Burkacki, D., and Jankowski, R. (2019). Seismic response of high-rise buildings equipped with base isolation and non-traditional tuned mass dampers. Appl. Sci. 9:1201. doi: 10.3390/app9061201

CrossRef Full Text | Google Scholar

Obando, J., and Lopez-Garcia, D. (2018). Inelastic displacement ratios for nonstructural components subjected to floor accelerations. J. Earthq. Eng. 22, 569–594. doi: 10.1080/13632469.2016.1244131

CrossRef Full Text | Google Scholar

Quaglini, V., Gandelli, E., Dubini, P., and Limongelli, M. P. (2017). Total displacement of curved surface sliders under nonseismic and seismic actions: a parametric study. Struct. Control Health Monit. 24:e2031.

Google Scholar

Rabiee, R., and Chae, Y. (2019). Adaptive base isolation system to achieve structural resiliency under both short-and long-period earthquake ground motions. J. Intell. Mater. Syst. Struct. 30, 16–31. doi: 10.1177/1045389x18806403

CrossRef Full Text | Google Scholar

Rahnama, M., and Krawinkler, H. (1993). Effects of soft soil and hysteresis model on seismic demands, John A. Blume Earthquake Engineering Center Standford. Stanford, CA: Stanford University.

Google Scholar

Shahi, S. K., and Baker, J. W. (2014). An efficient algorithm to identify strong-velocity pulses in multicomponent ground motions. Bull. Seismol. Soc. Am. 104, 2456–2466. doi: 10.1785/0120130191

CrossRef Full Text | Google Scholar

Shen, J., Tsai, M. H., Chang, K. C., and Lee, G. C. (2004). Performance of a seismically isolated bridge under near-fault earthquake ground motions. J. Struct. Eng. 130, 861–868. doi: 10.1061/(asce)0733-9445(2004)130:6(861)

CrossRef Full Text | Google Scholar

Skinner, R. I., Kelly, T. E., Robinson, W. H., Robinson Seismic, L., and Holmes Consulting, G. (2011). Seismic Isolation for Designers and Structural Engineers. Wellington: Robinson Seismic Ltd.

Google Scholar

Somerville, P. G. (2005). “Engineering characterization of near fault ground motions,” in Proceedings of the 2005 NZSEE Conference, (Pasadena, CA: URS Corporation), 1–8.

Google Scholar

Soto-Brito, R., and Ruiz, S. E. (1999). Influence of ground motion intensity on the effectiveness of tuned mass dampers. Earthq. Eng. Struct. Dyn. 28, 1255–1271. doi: 10.1002/(sici)1096-9845(199911)28:11<1255::aid-eqe865>3.0.co;2-c

CrossRef Full Text | Google Scholar

Takewaki, I. (2008). Robustness of base-isolated high-rise buildings under code-specified ground motions. Struct. Des. Tall Spec. Build. 17, 257–271. doi: 10.1002/tal.350

CrossRef Full Text | Google Scholar

Veletsos, A., Newmark, N., and Chelapati, C. (1965). “Deformation spectra for elastic and elastoplastic systems subjected to ground shock and earthquake motions,” in Proceedings of the 3rd World Conference on Earthquake Engineering, Wellington, 663–682.

Google Scholar

Wang, Z., and Lee, G. C. (2009). A comparative study of bridge damage due to the Wenchuan, Northridge, Loma Prieta and San Fernando earthquakes. Earthq. Eng. Eng. Vib. 8, 251–261. doi: 10.1007/s11803-009-9063-y

CrossRef Full Text | Google Scholar