A Design Method for Viscous Dampers Connecting Adjacent Structures

Introduction

Many experimental and analytical studies have proven that the introduction of damping devices between adjacent buildings provides an efficient mean for improving the seismic performance of the two systems. The behavior of adjacent structures linked by rigid, active, or passive control devices (Soong and Spencer, 2002; Christopoulos and Filiatrault, 2006; Takewaki, 2009) has been object of study of many papers in the last decades (Xu et al., 1999; Ni et al., 2001; Kim et al., 2006; Cimellaro and Lopez-Garcia, 2007; Roh et al., 2011; Richardson and Walsh, 2012; Tubaldi et al., 2014; Tubaldi, 2015). These studies have shown that the interaction between two systems with different dynamic properties through the connecting devices allows to reduce the structural seismic responses in terms of displacements and accelerations with respect to the unconnected case. The dissipative coupling constitutes also an effective tool to mitigate the seismic pounding (Sorace and Terenzi, 2013; Abdeddaim et al., 2016; Karabork and Aydin, 2019) between adjacent buildings without sufficient seismic joint, by avoiding invasive retrofit interventions finalized to joint enlargement.

The dissipative coupling of adjacent structures also includes the case of existing structures connected to new external systems. This retrofit measure has been recently investigated in different studies (Gioiella et al., 2018a; Reggio et al., 2019), because it presents several advantages compared to other methods (e.g., dissipative braces inserted within the frames), thanks to the reduced interferences with the existing frame and the low downtime associated with the installation of the retrofit measure. There can be different arrangements for the external protection system, which can be for example a new external reaction tower or an exoskeleton structure wrapping the building to be protected. The study reported in (Gioiella et al., 2018a), investigated the modal properties and the seismic response of an r.c. frame building coupled with an external pinned-rocking truss equipped with linear fluid viscous at its base and connected at the floor level with the building to protect. Also in (Impollonia and Palmeri, 2018) a similar system is investigated, but in this case, the external reaction towers have been equipped with non-linear devices. In (Gioiella et al., 2018b), a comparison was made in terms of efficiency between alternative external retrofitting systems, one consisting in a pinned-rocking truss with dampers at its base, and the other in a fixed base external structure with the dampers located at floor level. In (Reggio et al., 2019), the behavior of a primary structure protected by an external self-supporting exoskeleton system, rigidly connected to the inner frame is assessed.

A significant number of the studies reported above has focused on the definition of procedures or closed-form expressions for the design of the optimal damper properties of the connecting dampers. Many works have considered the simplified case of adjacent buildings modeled as single degree of freedom (SDOF) systems. In this context, Zhu and Iemura (2000) and Zhu and Xu (2005) derived analytical expressions for the optimal properties of respectively a Kelvin-type damper and a Maxwell-type connecting damper, under a white-noise ground excitation. The optimal properties have been evaluated by minimizing the averaged vibration energy of either the primary structure or the two adjacent structures. Bhaskararao and Jangid (2007) also derived closed-form expressions for the optimal linear viscous damper properties that minimize the systems' relative displacements and absolute accelerations under harmonic excitation, and the mean square responses under stationary white-noise random excitation. Hwang et al. (2007), based on complex modal analysis, proposed a closed-form expressions of the relation between the viscous constant of the linear viscous dampers and the damping factors of the adjacent connected SDOF systems. The optimal properties of hysteretic dampers were evaluated by Basili and De Angelis (2007a) by minimizing an energy performance index, i.e., the ratio of the maximum value of the energy dissipated in the device, to the corresponding maximum value of the input energy.

In general, different approaches can be followed to evaluate the optimal properties of the connecting system. Some authors (Zhang and Xu, 1999; Kim et al., 2006; Tubaldi et al., 2014), perform extensive parametric analyses, other (Basili and De Angelis, 2007a; Ok et al., 2008; Bigdeli et al., 2012) suggest optimization procedures, which are generally able to provide the optimal damper location as well. An alternative strategy could be that of looking only at the damping in correspondence of one or more vibration modes (Luco and De Barros, 1998), or reducing the model order, i.e., by transforming the multiple degree of freedom (MDOF) models into two simplified equivalent SDOF systems (Aida et al., 2001; Basili and De Angelis, 2007b; Zhu et al., 2010), and then defining the damper properties based on already available closed-form expressions or methodologies.

In this paper, the seismic response of adjacent buildings connected by energy dissipation devices is further investigated, with specific focus on the use of fluid viscous dampers (FVDs). The effectiveness for seismic protection purposes of such class of devices has been extensively analyzed in the past decades (Symans and Constantiou, 1998; Pekcan et al., 1999; Lin and Chopra, 2002; Christopoulos and Filiatrault, 2006; Takewaki, 2009), and specific issues have been also studied. These include the effect of the ground motion variability on the response of systems equipped with linear or non-linear viscous dampers (Tubaldi et al., 2015; Dall'Asta et al., 2016) and the influence of the variability of the damper properties, due to the device manufacturing process, on the seismic performance of the system (Lavan and Avishur, 2013; Dall'Asta et al., 2017; Scozzese et al., 2019).

Moreover, this study aims at developing a design strategy for fluid viscous dampers connecting adjacent buildings based on a linearized reduced order model. Starting from the knowledge of the dynamical properties of the unconnected buildings, the design method requires an assumption on the distribution of the dampers at the various floors. Once the amount of added damping necessary to protect one of the two frames is decided, the dimensions of FVDs are determined. A simplified expression for the design of the dampers, applicable in many situations, is also provided. Finally, a stochastic linearization technique is used to extend the design procedure to the case of non-linear dampers, which are diffused in design practice. In the last part of the paper, extensive analyses of various case studies are reported, in order to compare the results achieved by the MDOF systems and by the reduced order model, considering linear, and non-linear dampers, as well as different damper configurations.

Problem Formulation

In this section, the formulation of the problem involving two adjacent MDOF structures coupled by fluid viscous dampers is presented in general terms, in section “Equation of Motion for MDOF Systems Connected by Non-Linear Viscous Dampers” with reference to non-linear devices and in section “MDOF Systems Connected by Linear FVDs and Reduced Order Model” for the case of linear ones. In this latter section, a reduced order model of the coupled systems is developed. Moreover, a simplified formula for estimating the added damping ratio is derived, which can be used for design purposes. Afterwards, in section “Non-Linear System and Linear Equivalence Based on Stochastic Response”, an equivalence criterion is used to relate the properties of non-linear FVDs to linear ones, to be used along with the design approach proposed.

Equation of Motion for MDOF Systems Connected by Non-Linear Viscous Dampers

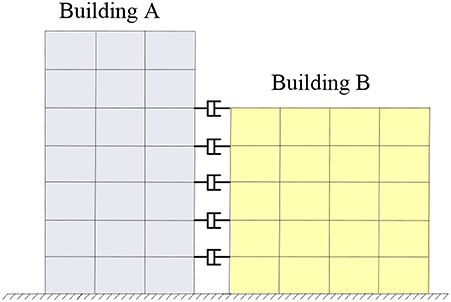
The equation of motion of two adjacent MDOF systems, A and B, coupled by viscous dampers (Figure 1), is:

$\begin{array}{ll}\text{M}\ddot{\text{u}}(t)+\text{C}\stackrel{\bullet }{\text{u}}(t)+K\text{u}(t)+\text{f}[\stackrel{\bullet }{\text{u}}(t)]=-\text{M}\text{r}{\ddot{u}}_g(t)& (1)\end{array}$

where M, C, and K are linear operators (i.e., matrices) describing the mass, damping and stiffness distribution in the two systems; r is the load distribution vector; $\ddot{u}$_g(t) is a function describing the seismic input; $\text{f}[\stackrel{\bullet }{\text{u}}(t)]$ is the vector of forces due to coupling damper devices; a superposed dot denotes differentiation with respect to time. The vector u(t), describing the floor motion, can be split into two vectors collecting the displacements at floor level of structural system A and structural system B, i.e., $u=\left[\begin{array}{l}{u}_{\text{A}\left(m\right)}\\ u_{\text{B}\left(n\right)}\end{array}\right]$. Accordingly, the linear operators can be split into: $M=\left[\begin{array}{cc}{M}_{\text{A}\left(mxm\right)}& 0_{\left(mxn\right)}\\ 0_{\left(nxm\right)}& M_{\text{B}\left(nxn\right)}\end{array}\right];K=\left[\begin{array}{cc}{K}_{\text{A}\left(mxm\right)}& 0_{\left(mxn\right)}\\ 0_{\left(nxm\right)}& K_{\text{B}\left(nxn\right)}\end{array}\right]; C=\left[\begin{array}{cc}{C}_{\text{A}\left(mxm\right)}& 0_{\left(mxn\right)}\\ 0_{\left(nxm\right)}& C_{\text{B}\left(nxn\right)}\end{array}\right]$.

FIGURE 1

Figure 1. Frame structures connected by means of fluid viscous dampers.

The vector $\text{f}[\stackrel{\bullet }{\text{u}}(t)]$ has the following expression:

$\begin{array}{ll}\text{f}\left[\stackrel{\bullet }{\text{u}}(t)\right]=\left[\begin{array}{c}{\text{f}}_d{\left[\stackrel{\bullet }{\text{u}}(t)\right]}_{(n)}\\ 0_{{}_{(m-n)}}\\ -{\text{f}}_d{\left[\stackrel{\bullet }{\text{u}}(t)\right]}_{{}_{(n)}}\end{array}\right]& (2)\end{array}$

where ${\text{f}}_d[\stackrel{\bullet }{\text{u}}(t)]={\text{f}}_d(t)$ is a n-dimension vector, whose j-th component is given by:

$\begin{array}{l}{\text{f}}_{dj}\left[\stackrel{\bullet }{\text{u}}(t)\right]=c_{d,j}{|{\stackrel{\bullet }{\text{u}}}_j(t)-{\stackrel{\bullet }{\text{u}}}_{j+m}(t)|}^{\alpha }\text{sgn}\left[{\stackrel{\bullet }{\text{u}}}_j(t)-{\stackrel{\bullet }{\text{u}}}_{j+m}(t)\right]\\ j=1:n& (3)\end{array}$

where c_{d, j} represents the viscous constant of the j-th damper with behavior described by the value of the constant α. When α = 1 the behavior of the dampers is linear, instead when α <1 the behavior is non-linear.

MDOF Systems Connected by Linear FVDs and Reduced Order Model

In the case of linear dampers, Equation (1) can be rewritten as:

$\begin{array}{ll}\text{M}\ddot{\text{u}}(t)+(\text{C}+{\text{C}}_d)\stackrel{\bullet }{\text{u}}(t)+K\text{u}(t)=-\text{M}\text{r}{\ddot{u}}_g(t)& (4)\end{array}$

in which matrix C_d describes the properties and the location of the linear viscous dampers connecting the adjacent buildings. According to the previous general expression of $\text{f}[\stackrel{\bullet }{\text{u}}(t)]$, matrix C_d has the following expression:

$\begin{array}{ll}{\text{C}}_d=\left[\begin{array}{ccc}{{\text{C}}_{d0}}_{(n\text{x}n)}& 0_{(n\text{x}(m-n))}& -{{\text{C}}_{d0}}_{(n\text{x}n)}\\ 0_{((m-n)\text{x}n)}& 0_{((m-n)\text{x}n)}& 0_{((m-n)\text{x}n)}\\ -{{\text{C}}_{d0}}_{(n\text{x}n)}& 0_{(n\text{x}(m-n))}& {{\text{C}}_{d0}}_{(n\text{x}n)}\end{array}\right]& (5)\end{array}$

where C_d0 is the diagonal matrix, containing the values c_{d0, j} of the viscous constants of the dampers at each connected story.

In order to simplify the problem and develop a reduced order model, suitable for the design of the dissipative system, the following decomposition of the motion is considered for the system:

$\begin{array}{ll}\text{u}(t)=\Phi \text{q}(t)& (6)\end{array}$

where Φ is the matrix containing the undamped eigenvectors (modal shapes) of the combined system and q(t) is a vector of order n+m, containing the generalized displacements. In this case, the set of all the modal shapes consists of the two separated sets containing the modal shapes of A and the modal shapes of B.

After substituting Equation (6) into Equation (4) and premultiplying by Φ^T, one obtains:

$\begin{array}{l}{\Phi }^{T}M\Phi \ddot{q}\left(t\right)+{\Phi }^T\text{}\left(C+C_d\right)\Phi \dot{q}\left(t\right)+{\Phi }^{T}K\Phi q\left(t\right)\\ =-{\Phi }^{T}Mr{\ddot{u}}_g\left(t\right)& (7)\end{array}$

This corresponds to a system of n+m coupled equations.

To develop a reduced order model capable to describe the coupled system dynamic behavior with good accuracy, at least the first undamped modes of each building alone have to be considered. Let φ_Au and φ_Bu denote the vectors containing the first modal shapes of building A and B, respectively. Matrix Φ reduces to:

$\begin{array}{ll}\Phi =\left[\begin{array}{cc}{\phi }_{\text{A}}& {\phi }_{\text{B}}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{c}{{\phi }_{\text{A}u}}_{{}_{(m)}}\\ 0_{(n)}\end{array}& \begin{array}{c}{0}_{(m)}\\ {\phi }_{\text{B}{u}_{(n)}}\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{c}{{\phi }_{\text{A}ud}}_{{}_{(m)}}\\ {\phi }_{\text{A}u{u}_{(m-n)}}\\ 0_{(n)}\end{array}& \begin{array}{c}{0}_{(n)}\\ 0_{(m-n)}\\ {\phi }_{\text{B}u{d}_{(n)}}\end{array}\end{array}\right]& (8)\end{array}$

where φ_Bud = φ_Bu and φ_Au is further split into φ_Aud, containing the modal displacements of building A for the first n degree of freedom, and φ_Auu containing the modal displacements of building A for the upper stories, from n+1 to m, not connected to building B.

Under this approximation, the vector q contains two components only, denoted as q_A and q_B, and Equation (7) reads as follows:

$\begin{array}{l}{{\phi }_{\text{A}u}}^T{\text{M}}_{\text{A}}{\phi }_{\text{A}u}{\ddot{q}}_{\text{A}}(t)+{{\phi }_{\text{A}u}}^T{\text{C}}_{\text{A}}{\phi }_{\text{A}u}{\stackrel{\bullet }{q}}_{\text{A}}(t)+{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}{\stackrel{\bullet }{q}}_{\text{A}}(t)\\ -{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}{\stackrel{\bullet }{q}}_{\text{B}}(t)+\\ +{{\phi }_{\text{A}u}}^T{\text{K}}_{\text{A}}{\phi }_{\text{A}u}{q}_{\text{A}}(t)=-{{\phi }_{\text{A}u}}^T{\text{M}}_{\text{A}}\text{r}{\ddot{u}}_g(t)\\ {{\phi }_{\text{B}u}}^T{\text{M}}_{\text{B}}{\phi }_{\text{B}u}{\ddot{q}}_{\text{B}}(t)+{{\phi }_{\text{B}u}}^T{\text{C}}_{\text{B}}{\phi }_{\text{B}u}{\stackrel{\bullet }{q}}_{\text{B}}(t)+{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}{\stackrel{\bullet }{q}}_{\text{B}}(t)\\ -{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}{\stackrel{\bullet }{q}}_{\text{A}}(t)+\\ +{{\phi }_{\text{B}u}}^T{\text{K}}_{\text{B}}{\phi }_{\text{B}u}{q}_{\text{B}}(t)=-{{\phi }_{\text{B}u}}^T{\text{M}}_{\text{B}}\text{r}{\ddot{u}}_g(t)& (9)\end{array}$

After posing:

$\begin{array}{l}{m}_i={{\phi }_{iu}}^T{\text{M}}_i{\phi }_{iu}\\ c_i={{\phi }_{iu}}^T{\text{C}}_i{\phi }_{iu}\\ k_i={{\phi }_{iu}}^T{\text{K}}_i{\phi }_{iu}\text{ for}i=\text{A},\text{ B}\\ {l_{eff,}}_i={{\phi }_{iu}}^T{\text{M}}_i\text{r}\\ {\gamma }_i=\frac{{l_{eff,}}_i}{m_i}& (10)\end{array}$

and dividing by the modal participation factor γ_i, Equation (9) can be rewritten as:

$\begin{array}{l}{\ddot{\overline{q}}}_{\text{A}}(t)+2{\xi }_{\text{A}}{\omega }_{\text{A}}{\stackrel{\bullet }{\overline{q}}}_{\text{A}}(t)+\frac{{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}}{m_{\text{A}}}{\stackrel{\bullet }{\overline{q}}}_{\text{A}}(t)\\ -\frac{{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}}{m_{\text{A}}}{\stackrel{\bullet }{\overline{q}}}_{\text{B}}(t)+{\omega }_{\text{A}}^2{\overline{q}}_{\text{A}}(t)=-{\ddot{u}}_g(t)\\ {\ddot{\overline{q}}}_{\text{B}}(t)+2{\xi }_{\text{B}}{\omega }_{\text{B}}{\stackrel{\bullet }{\overline{q}}}_{\text{B}}(t)+\frac{{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}}{m_{\text{B}}}{\stackrel{\bullet }{\overline{q}}}_{\text{B}}(t)\\ -\frac{{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}}{m_{\text{B}}}{\stackrel{\bullet }{\overline{q}}}_{\text{A}}(t)+{\omega }_{\text{B}}^2{\overline{q}}_{\text{B}}(t)=-{\ddot{u}}_g(t)& (11)\end{array}$

where ${\overline{q}}_i(t)=\frac{q_i(t)}{{\gamma }_i}$, $\frac{c_i}{m_i}=2{\xi }_i{\omega }_i$ and $\frac{k_i}{m_i}={\omega }_i^2$ for i = A, B. This way, there is a clear correspondence between the MDOF systems and the reduced order model.

The total amount of damping due to the frame and to the dissipative connection of the equivalent 2-SDOF system can be expressed as follows:

$\begin{array}{l}{\overline{\xi }}_{\text{A}}={\xi }_{\text{A}}+\frac{{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}}{2m_{\text{A}}{\omega }_{\text{A}}}-\frac{{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}}{2m_{\text{A}}{\omega }_{\text{A}}}\\ {\overline{\xi }}_{\text{B}}={\xi }_B+\frac{{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}}{2m_B{\omega }_B}-\frac{{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}}{2m_B{\omega }_B}& (12)\end{array}$

In the case of a single damper with viscous constant c_{d0, r} connecting story r of buildings A and B, these expressions coincide with those reported in (Aida et al., 2001):

$\begin{array}{l}{\overline{\xi }}_{\text{A}}={\xi }_{\text{A}}+\frac{c_{d0,r}}{2m_{\text{A}}{\omega }_{\text{A}}}{\phi }_{\text{A}ud,r}^2-\frac{c_{d0,r}{\phi }_{\text{A}ud,r}{\phi }_{Bud,r}}{2m_{\text{A}}{\omega }_{\text{A}}}\\ {\overline{\xi }}_B={\xi }_B+\frac{c_{d0,r}}{2m_B{\omega }_B}{\phi }_{Bud,r}^2-\frac{c_{d0,r}{\phi }_{\text{A}ud,r}{\phi }_{Bud,r}}{2m_B{\omega }_B}& (13)\end{array}$

In general, the system is non-classically damped (Sivandi-Pour et al., 2014, 2015) because of the non-zero term ${{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}$. By neglecting the off-diagonal terms in Equation (12), the following approximate expressions of the damping ratio for the first two fundamental vibration modes of the coupled system can be obtained:

$\begin{array}{l}{\overline{\xi }}_{\text{A},app}={\xi }_{\text{A}}+\frac{{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}}{2m_{\text{A}}{\omega }_{\text{A}}}\\ {\overline{\xi }}_{\text{B},app}={\xi }_B+\frac{{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}}{2m_B{\omega }_B}& (14)\end{array}$

The study of Hwang et al. (Hwang et al., 2007), based on complex modal analysis of two adjacent SDOF systems connected by a viscous damper, has shown that the decoupling approximation yields very accurate results in the case of well-separated vibration frequencies of the two systems and low added damping. Usually, for ratios ω_B/ω_A > 1.5 ÷ 2, Equation (14) can be assumed to provide accurate estimates of the buildings damping ratios (Hwang et al., 2007). It is noteworthy that the dampers connecting adjacent buildings are efficient in dissipating energy only for buildings with different dynamic properties and that in the case of two identical adjacent buildings, the dampers would not be activated.

It is worth to note that, under the approximation of Equation (14) and recalling the expression of C_d0, the addition of dampers between two adjacent buildings induces a mass-proportional damping in each system (Trombetti and Silvestri, 2004). Thus, the dissipation capacity of the added dampers depends on the absolute displacements of each system, rather than on the interstorey drifts (stiffness-proportional damping), and obviously is different from building to building.

Non-Linear System and Linear Equivalence Based on Stochastic Response

Non-linear devices are widely diffused, due to their ability to reduce dampers forces in case of high velocity (Tubaldi et al., 2015), and thus it is useful to establish a link between the linear formulation of section “Equation of motion for MDOF systems connected by nonlinear viscous dampers” and the non-linear one of section “MDOF systems connected by linear FVDs and reduced order model”. This can be achieved by choosing an equivalence condition between the two systems and by defining the relationship between the parameters of the non-linear FVDs and the parameters of the equivalent linear FVDs. On this regard, in literature there are different linearization approaches, one of the most diffused being based on energy considerations under harmonic inputs [see Christopoulos and Filiatrault (2006)]. In this work. a stochastic linearization technique, already employed in Rüdinger and Krenk (2003), Rüdinger (2006), Rudinger (2007), Di Paola et al. (2007), Di Paola and Navarra (2009), and De Domenico and Ricciardi (2018, 2019), is chosen to identify the equivalent linear expression for non-linear devices.

For this purpose, it is assumed here that the input $\ddot{u}$_g(t) to the non-linear system of Equation (1) is a Gaussian stochastic stationary process. Equation (1) becomes a stochastic equation and the displacement response and relevant derivatives are also stochastic quantities. The equation of the equivalent linear system is:

$\begin{array}{ll}\text{M}\ddot{\text{U}}(t)+\left(\text{C}+{\text{C}}_d^{eq}\right)\stackrel{\bullet }{\text{U}}(t)+K\text{U}(t)=-\text{M}\text{R}{\ddot{u}}_g(t)& (15)\end{array}$

where the effect of the non-linear dampers is expressed by the equivalent linear matrix ${\text{C}}_d^{eq}$, whose terms are evaluated using a force-based equivalent criterion (De Domenico and Ricciardi, 2018, 2019). In particular, the matrix ${\text{C}}_d^{eq}$ has the same structure of the matrix C_d, shown in Equation (5), where ${\text{C}}_{d0}^{eq}$ is a nxn diagonal submatrix containing the values of the equivalent viscous constant, determined as follows:

$\begin{array}{ll}{c}_{d0,j}^{eq}=c_{d,j}^{NL}\frac{2^{1+\frac{\alpha }{2}}\Gamma \left(1+\frac{\alpha }{2}\right)}{\sqrt{2\pi }}{\sigma }_{\Delta {\stackrel{\bullet }{\text{u}}}_j}^{\alpha -1}j=1:n& (16)\end{array}$

where ${\sigma }_{\Delta {\stackrel{\bullet }{\text{u}}}_j}$ is the standard deviation of the relative velocity between the ends of the damper at the j-th floor.

It is evident that the equivalence holds only for the assigned stationary process $\ddot{u}$_g(t), that can be described by its power spectral density S_Üg(ω), so equivalent parameters vary by varying the input intensity and the input frequency content. In the considered case, oriented to study the seismic response, the equivalence is found by considering a Kanai-Tajimi process (Kanai, 1957; Tajimi, 1960).

Passing from the MDOF systems to the reduced order model, Equation (16) becomes:

$\begin{array}{ll}{c}_{d0,j}^{eq}=c_{d,j}^{NL}E\left[{\left|\Delta {\dot{u}}_j\right|}^{\alpha -1}\right]=\frac{2^{\alpha /2}\Gamma \left(\frac{\alpha }{2}\right)}{\sqrt{2\pi }}{\sigma }_{\Delta {\dot{u}}_j}^{\alpha -1}j=1:n& (17)\end{array}$

where:

$\begin{array}{l}{\sigma }_{\Delta {\stackrel{\bullet }{\text{U}}}_j}=\sqrt{E\left[\Delta {{\stackrel{\bullet }{\text{u}}}_j}^2\right]}\\ =\sqrt{{\phi }_{\text{A}u,j}^{2}E\left[{{\stackrel{\bullet }{q}}_{\text{A}}}^2\right]+{\phi }_{\text{B}u,j+m}^{2}E\left[{{\stackrel{\bullet }{q}}_{\text{B}}}^2\right]-2{\phi }_{\text{A}u,j}{\phi }_{\text{B}u,j+m}E\left[{\stackrel{\bullet }{q}}_{\text{A}}{\stackrel{\bullet }{q}}_{\text{B}}\right]}\\ j=1:n& (18)\end{array}$

and where φ_{i, r} denotes the value of modal shape i at degree of freedom r.

Fluid Viscous Dampers Design

The dissipative system is designed by exploiting the classically damped reduced order model.

The distribution of dampers is described by ${\text{C}}_{d0}=\lambda {\tilde{\text{C}}}_{d0}$, where ${\tilde{\text{C}}}_{d0}$ is an arbitrary diagonal matrix fixed in advance and controlling the dampers' distribution story by story and λ is a scale factor controlling the global dimension of the dissipative system. The components of the matrix ${\tilde{\text{C}}}_{d0}$ are ${\tilde{c}}_{d0,j}$.

The scale factor λ is determined by requiring that the damping added to one of the two frames, denoted as primary structure in the following and conventionally coinciding with system B, is equal to a target value ξ_add. The value of λ can be obtained from Equation (14), and its expression is the following:

$\begin{array}{ll}\lambda =\frac{2m_{\text{B}}{\omega }_{\text{B}}{\xi }_{add}}{{{\phi }_{\text{B}ud}}^T{\tilde{\text{C}}}_{d0}{\phi }_{\text{B}ud}}& (19)\end{array}$

Once λ is known, the constant of the damper connecting the j-th level is $c_{d0,j}=\lambda {\tilde{c}}_{d0,j}$. There can be a large number of dampers arrangements equivalent in terms of ξ_add; in the following examples two different arrangements of dampers, widely diffused in applications, are analyzed.

In the case of non-linear dissipative system with damping exponent α, it is possible to exploit the equivalence condition described above, but it is necessary to fix the properties of the stochastic process Ü_g(t) at which the equivalent condition must hold. Many times, the frequency contents are fixed and it is only necessary to assign a scale factor related to the intensity level, as in the following application where a Kanai-Taijmi process is assumed and the scale factor of the power spectral density (PSD) describing the process is calibrated according to the intensity of the design action.

In order to assign the properties of the non-linear dampers, the MDOF linear system obtained for the previous design procedure is assumed as the equivalent linear system and the variance of the relative velocity at each story ${\sigma }_{\Delta {\stackrel{\bullet }{\text{u}}}_j}^{}$ is evaluated by using the numerical procedure described in Appendix A, starting from the PSD of the input.

At this point, the constants of the non-linear dampers ensuring an equivalent response for the assumed input intensity can be obtained from Equation (20).

$\begin{array}{ll}{c}_{d,j}^{NL}=\lambda {\tilde{c}}_{d0,j}\frac{\sqrt{2\pi }}{2^{1+\frac{\alpha }{2}}\Gamma \left(1+\frac{\alpha }{2}\right){\sigma }_{\Delta {\stackrel{\bullet }{\text{u}}}_j}^{\alpha -1}}j=1:n& (20)\end{array}$

Application Examples

In this section, the proposed design method for the dampers is applied with reference to a case study, involving two planar structures of different story number. Parametric analysis is conducted, both in the case of linear and non-linear dampers, by varying the values of the viscous damping constants and of the parameter α. Two different configurations of dissipative connection are analyzed, the first one, defined as uniform distribution, considers the installation of devices with equal properties at all the stories of the lower building. The second configuration involves the installation of a single damper at the last floor of the lower structure. The response parameters monitored, both in the MDOF system and in the reduced order model, are the floor displacements, the absolute accelerations and the dampers' forces. Finally, the behavior of linear and non-linear devices is analyzed for different levels of the seismic intensity, far from the design condition.

Case Study and Seismic Input

Two coupled steel moment-resisting frame buildings with shear-type behavior are considered as case study in this application example (Figure 1). The properties of these buildings, assumed as deterministic, are taken from (Tubaldi et al., 2014). Building A is an 8-story frame with constant floor mass, m_A = 454,540 kg, and stiffness, k_A = 628,801 kN/m. Building B is a four-story building with constant story mass, m_B = 454,540 kg, and stiffness, k_B = 470,840 kN/m. The story heights are equal to 3.2 m. Matrices C_A (with dimensions 8 × 8) and C_B (with dimensions 4 × 4) describe the inherent buildings' damping. They are based on the Rayleigh model and are obtained by assuming a damping factor ζ_A = ζ_B = 2% for the first and last fundamental vibration modes of each system. The fundamental vibration periods of building A and B are T_A = 0.915 and T_B = 0.562 s, respectively.

The two degrees of freedom reduced order model corresponding to the adjacent buildings has the following properties: m_A = l_eff,_A = 3113.9 kNs²/m, m_B = l_eff,_B = 1624.4 kNs²/m, k_A = 1.4669·10⁵ kN/m, k_B = 2.0295·10⁵ kN/m, c_A = 854.91 kNs/m, c_B = 726.28 kNs/m.

The stochastic seismic input considered in all the examples is modeled as a stationary Gaussian process whose PSD function is described by the widely-used Kanai-Tajimi model (Kanai, 1957; Tajimi, 1960) i.e.,

$\begin{array}{ll}{S}_{KT}(\omega )=S_0·\frac{{\omega }_g^4+4·{\xi }_g^2·{\omega }^2·{\omega }_g^2}{{\left[{\omega }_g^2-{\omega }^2\right]}^2+4·{\xi }_g^2·{\omega }^2·{\omega }_g^2}& (21)\end{array}$

in which: S₀ is the amplitude of the bedrock excitation spectrum, modeled as a white noise process; ω_g and ζ_g are the fundamental circular frequency and the damping factor of the soil, respectively. The following values of the parameters are used hereinafter: ω_g = 12.5 rad/s, ζ_g = 0.6.

Figure 2A shows the PSD function for S₀ = 1 m²/s³ whereas Figure 2B shows the relationship between the parameter S₀ of the Kanai-Tajimi spectrum and the average peak ground acceleration (PGA) at the site. This relation has been assessed empirically based on the procedure reported in Tubaldi et al. (2012).

FIGURE 2

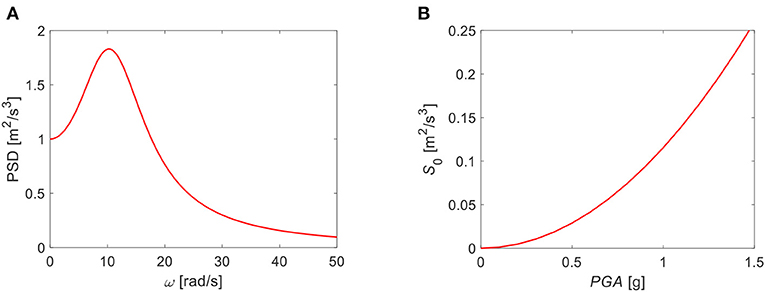
Figure 2. Input ground motion: (A) PSD function of the seismic input process, and (B) relation between S₀ and PGA.

Fluid Viscous Dampers Design

The dissipative system is designed by using the procedure described above. Two different arrangements of dampers widely diffused in applications are considered. The first refers to a uniform distribution of dampers with equal properties placed, connecting the first four floors of building A and B. In this case the shape of the damper distribution is described by ${\tilde{c}}_{d0,j}=1$ and the viscous constants are:

$\begin{array}{ll}{c}_{d0,j}=\frac{2m_{\text{B}}{\omega }_{\text{B}}{\xi }_{add}}{{\displaystyle \sum _{j=1}^{ndofB}}{\phi }_{B,j}^2}& (22)\end{array}$

The second configuration, instead, corresponds to a single damper placed between the fourth floors of building A and B, where the velocities are expected to be the highest. In this case the shape of the damper distribution is described by ${\tilde{c}}_{d0,j}=0$ for j = 1:3, ${\tilde{c}}_{d0,4}=1$ and the viscous constant at the forth level is:

$\begin{array}{ll}{c}_{d0,4}=\frac{2m_B{\omega }_B{\xi }_{add}}{{\phi }_{B,4}^2}& (23)\end{array}$

The amount of added damping used for the dampers' design is ξ_add = 0.10, applied to the shorter building B (the expected value of the total damping is $\overline{\xi }=0.12$, being ξ = 0.02 the amount of inherent damping).

According to the MDOFs, for the case with four dampers, the design damping constant of each device from Equation (22) is c_{d0, j} = 1016.0 kNs/m; for the case of the single damper at the fourth floor the viscous damping constant from Equation (23) is c_{d0, 4} = 2357.50 kNs/m.

In the case of non-linear dissipative system with characteristic parameter α, the equivalence condition is applied with reference to the stationary input describing the design seismic input (PGA_ref = 0.3 g).

The values of the coefficient $c_{d,j}^{NL}$ of the equivalent linear viscous dampers depend on the value assumed for the velocity exponent α. Figure 3 shows the variation with α of the $c_{d,j}^{NL}$ values evaluated via Equation (16), for both the cases of dampers at each floor with homogeneous properties (Figure 3A) and of single damper (Figure 3B).

FIGURE 3

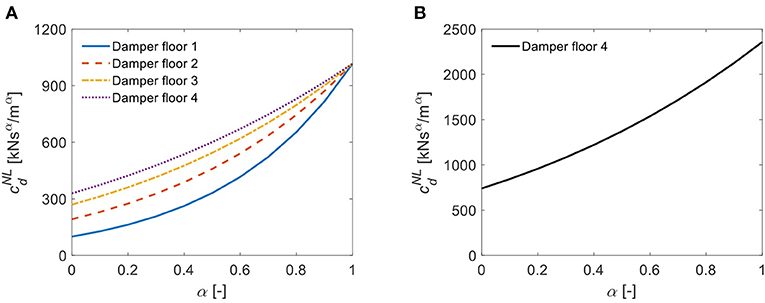
Figure 3. Design equivalent viscous coefficients for non-linear dampers vs. damper exponent α : (A) Dampers at each floor with homogeneous properties, (B) Single damper.

Modal Properties of the Systems With Linear Dampers Before and After the Coupling

Complex modal analysis of the two uncoupled and coupled MDOF adjacent buildings is carried out and the relevant results are summarized in Table 1, in terms of modal vibration periods and damping factors. As expected, the coupled buildings are non-classically damped and tend to vibrate together, as a single system. However, because of the low added damping, the vibration shapes for each of the composite vibration modes are such that the displacements of a building prevail over the displacement of the other building, and thus pertinent modal shapes can be identified for each building (labeled as A if the modal displacement of A prevails, as B otherwise).

TABLE 1

Table 1. Modal analysis results for uncoupled buildings (subscript “0”) and coupled buildings (subscript “d”).

It is observed (Table 1) that the addition of viscous dampers does not significantly affect the vibration periods of the systems, whereas it increases significantly the modal damping factor. The increase of damping, more relevant for building B (the shorter structure), is significant only at the lower vibration modes. Moreover, the effects on the system dynamic properties are comparable between the two considered dampers configurations (single and uniform).

Response Statistics Assessment at the Dampers Design Conditions

In the following, the performance of the MDOF coupled system, assumed as reference solution, is compared with the one of the non-classically damped reduced order model. The reduced order model equipped with linear dampers is characterized by the following damping matrix components. For what concerns the buildings coupled with dampers uniformly distributed along the first four floors one has $2{\xi }_{\text{A}}{m}_{{}_{\text{A}}}{\omega }_{\text{A}}+{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}=2321.2kNs/m$, $2{\xi }_{\text{B}}{m}_{{}_{\text{B}}}{\omega }_{\text{B}}+{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}=4357.5kNs/m$, and ${{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}={{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}=2299.6kNs/m$. For the case of a single damper at the fourth floor, instead, the damping parameters are $2{\xi }_{\text{A}}{m}_{{}_{\text{A}}}{\omega }_{\text{A}}+{{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}=2579.6kNs/m$, $2{\xi }_{\text{B}}{m}_{{}_{\text{B}}}{\omega }_{\text{B}}+{{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}=4357.7kNs/m$ and ${{\phi }_{\text{A}ud}}^T{\text{C}}_{d0}{\phi }_{\text{B}ud}={{\phi }_{\text{B}ud}}^T{\text{C}}_{d0}{\phi }_{\text{A}ud}=2502.6kNs/m$.

In the case of dampers at each floor, the damping factors for the first two modes of the coupled buildings are, respectively, ${\overline{\xi }}_{\text{A}}=0.0535$ and ${\overline{\xi }}_{\text{B}}=0.121$, in very good agreement with the corresponding values evaluated by considering the refined MDOF model (Table 1). In the case of a single damper connecting the two buildings, the corresponding damping factors for the first two modes of the coupled buildings are, respectively, ${\overline{\xi }}_{\text{A}}=0.0595$ and ${\overline{\xi }}_{\text{B}}=0.121$, again in very good agreement with the corresponding values evaluated by considering the refined model (Table 1).

Figure 4 compares the root mean square (RMS) stationary response (i.e., the standard deviation of the response) of both the uncoupled and coupled buildings with uniform dampers subjected to the seismic input described in the previous section. Figure 5 compares the response for the buildings coupled by a single damper. The comparison is made in terms of RMS of floor displacements (Figures 4A, 5A), floor absolute accelerations (Figures 4B, 5B) and relative displacements between the first four floors (Figures 4C, 5C), which are demand parameters particularly useful to describe the effectiveness of the dissipative coupling strategy in improving the performance of the buildings. Moreover, Figures 4C, 5C show the relative displacement demands between the first four floors of the adjacent buildings, which is the parameter controlling the pounding probability.

FIGURE 4

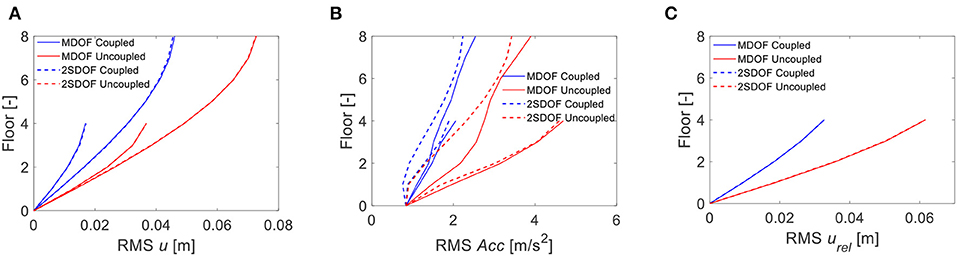
Figure 4. RMS displacement (A), acceleration response (B), and relative displacement (C) of the uncoupled and coupled buildings with uniform dampers, according to the refined model (MDOF) and the reduced order model (2SDOF).

FIGURE 5

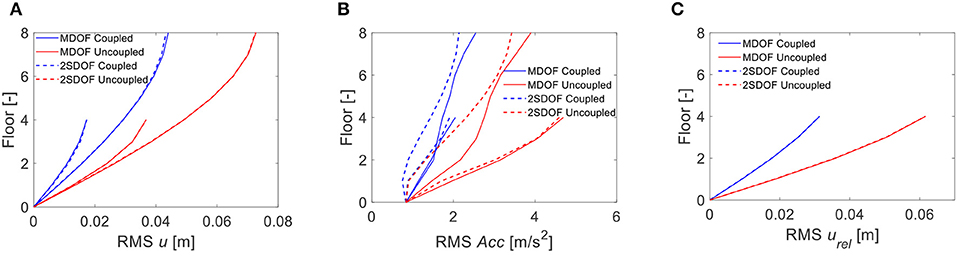
Figure 5. RMS displacement (A), acceleration response (B), and relative displacement (C) of the uncoupled and coupled buildings with single damper, according to the refined model (MDOF), and the reduced order model (2SDOF).

In general, it is observed that the dampers are effective in reducing the displacement and acceleration response of both the buildings, as well as the relative displacements. The displacement response of building B is more damped than that of building A, as expected from the results of modal analysis of the coupled buildings. Similar trends are observed for the acceleration responses. Finally, it is noted that the reduced order model provides accurate estimates of the response in terms of displacements, being the responses of the 2SDOF model very close to those corresponding to the refined MDOF model. Higher deviations are observed between the responses in terms of RMS acceleration.

Figure 6 compares the RMS forces of the dampers. For the uniform dampers configuration (Figure 6A) these forces increase with increasing building height, because the absolute and relative velocities of the two buildings increase along the height. Again, a very good agreement is observed between the estimates of the reduced order and the refined model. For the case with single damper (Figure 6B), the agreement between the results from the reduced order and the refined model is very good, too.

FIGURE 6

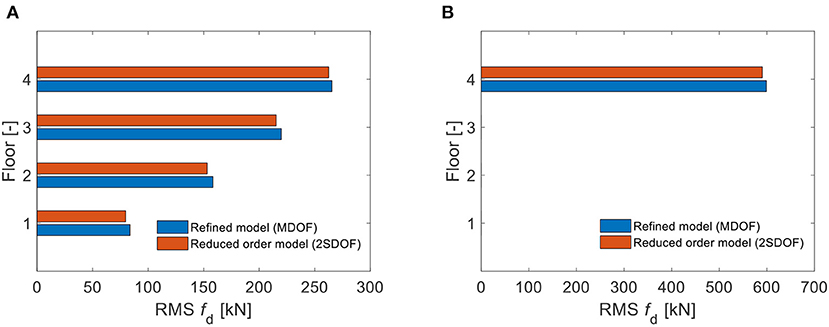
Figure 6. Comparison of RMS damper forces according to the refined model (MDOF) and the reduced order model (2SDOF): (A) Case with uniform dampers; (B) Case with single damper.

Furthermore, it is observed that, for a given level of added damping ratio, the sum of the forces experienced by the dampers placed according to the uniform distribution is much lower than the force of the single damper placed at the top floor of building B. This result has important effects on the costs of the retrofit strategy, being the damper cost strictly related to the damper force (Altieri et al., 2018).

Parametric Study and Response Statistics Assessment

The following subsections analyses the stochastic response sensitivity to the following parameters: the viscous coefficients c_{d0, j} and c_{d0, 4}, the velocity exponent α, and the seismic input intensity.

Influence of the Viscous Coefficient

In this section, a parametric study is carried out to evaluate the effectiveness of the dampers in mitigating the building stationary responses to the previously described seismic input. This study also permits to assess the accuracy of the reduced order model for different damper properties. For this purpose, the value of the viscous coefficients c_{d0, j} and c_{d0, 4} is varied in a range between 0.0 and 5,000 kNs/m.

Figure 7 plots and compares the damping ratios of the first two modes of the coupled system (corresponding to the modes of building A and B, respectively) for the following three different models: (1) the refined model (MDOF), (2) the reduced order model (2SDOF) with CMA, and (3) the 2SDOF model with the approximation introduced by Equation (15) (i.e., neglecting the off-diagonal terms). Curves related to building A are shown in red, those of building B in blue; solid, dashed and dotted styles are used to distinguish the results concerning the MDOF, the 2SDOF and the approximated approach, respectively. It is worth noting that the estimates obtained by using the refined model are exact, thus they are assumed as reference solution.

FIGURE 7

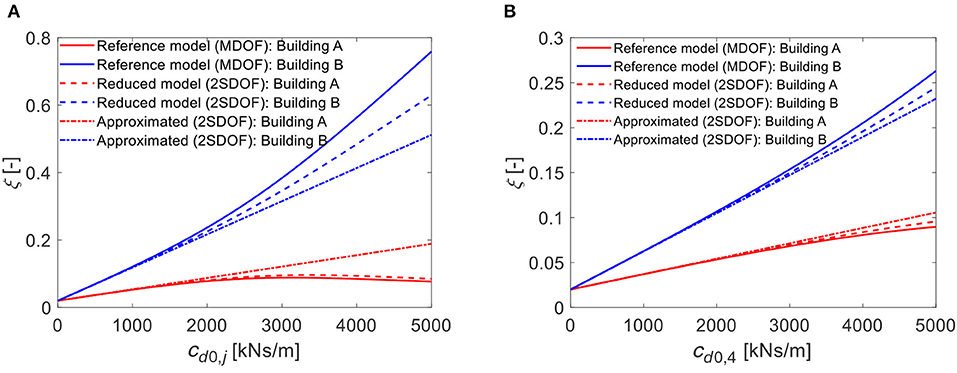
Figure 7. Comparison between first two modes damping ratios evaluated by using different models: (A) case with uniform dampers; (B) case with single damper.

In general, it is noted that the addition of viscous dampers between the two adjacent buildings increases the damping factor of the second vibration mode, related to building B, rather than that of the first mode, related to the vibration of the building A. It is also observed that the three models provide equivalent results for low values of the added damping. For high values of c_{d0, j} and c_{d0, 4}, the two modal damping factors evaluated by applying complex modal analysis on the 2DOF model are still quite accurate (in particular for Building A vibration mode), whereas the damping factors evaluated by applying Equation (14) become very inaccurate for increasing values of c_{d0, j} and c_{d0, 4}. Similar results were observed in the works (Tubaldi et al., 2014) and (Tubaldi et al., 2012). A better agreement among the estimates of the different models is observed when a single damper configuration is used (Figure 7B).

The parametric study is also extended to evaluate the stochastic response in terms of buildings' displacements (Figures 8A,C) and damper forces (Figures 8B,D).

FIGURE 8

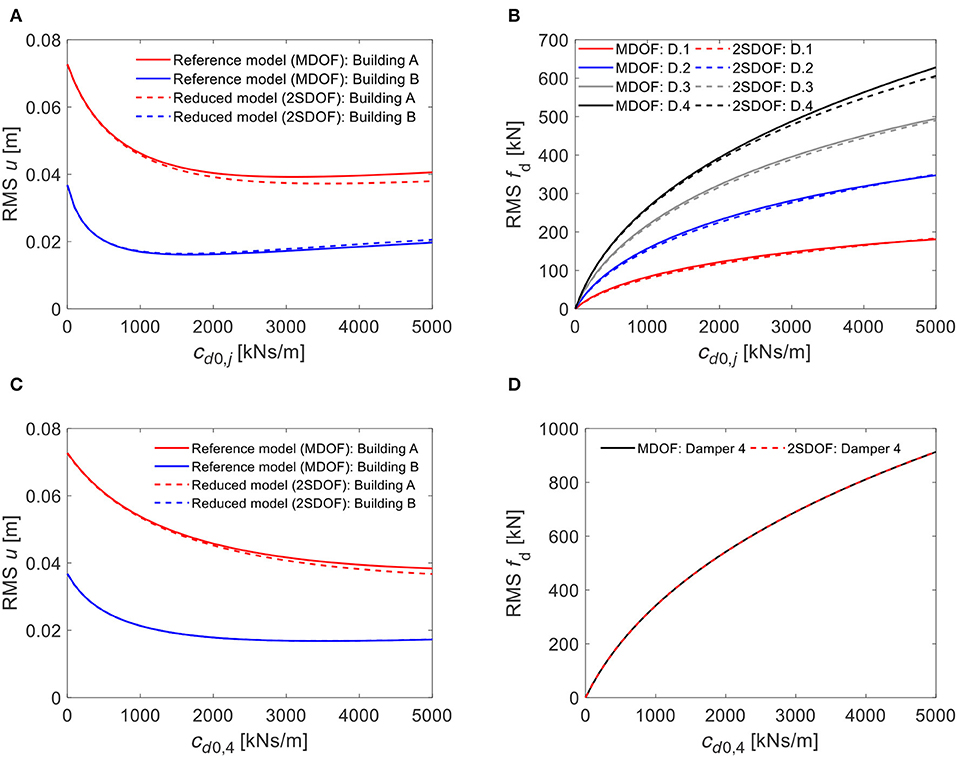
Figure 8. Stationary response vs. damping viscous constant: (A) Top-floor displacement of building A and B (uniform dampers case), (B) Damper forces (uniform dampers case), (C) Top-floor displacement of building A and B (single damper case), (D) damper forces (single damper case).

With reference to the arrangement with uniform dampers, it is observed that:

• For both the buildings, there exists an optimal value of the damping constant c_{d0, j} that minimizes the displacement response. For values of c_{d0, j} higher than 1,500 kNs/m the displacement response of building B does not change significantly, while for the building A this happens for values of c_{d0, j} higher than 3,000 kNs/m.

• The dampers force always increases for increasing values of c_{d0, j}, although the relative velocities between the two buildings reduce.

• The reduced order model provides very accurate estimates of the building displacement response and of the damper forces for a wide range of damper properties. Its accuracy slightly decreases for increasing c_{d0, j} values.

Influence of the Damper Non-Linearity

A second parametric study is performed by considering the case of non-linear viscous dampers connecting the two buildings in the same configurations already analyzed before, i.e., uniform distribution with equal properties at the first four floors and a single device at the last elevation of building B. The values of the dampers viscous constants, c_{d0, j} and c_{d0, 4} are varied in the range between 0 and 5,000 kNs/m. The discrete values of the damper exponent considered are α = 0.3, 0.5, 0.7, and 1, this latter for comparison purpose only. The optimal damping constant for building A and B are summarized in Table 2. Figure 9 reports the stationary response in terms of building top displacements and forces of the damper at the fourth floor for different values of c_d0 and of α.

TABLE 2

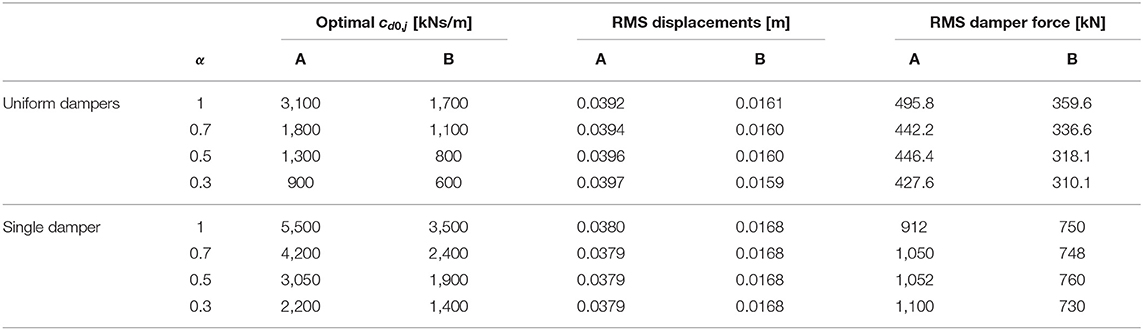
Table 2. Optimal damping constants for different α values and corresponding RMS building top displacements and 4th story damper force.

FIGURE 9

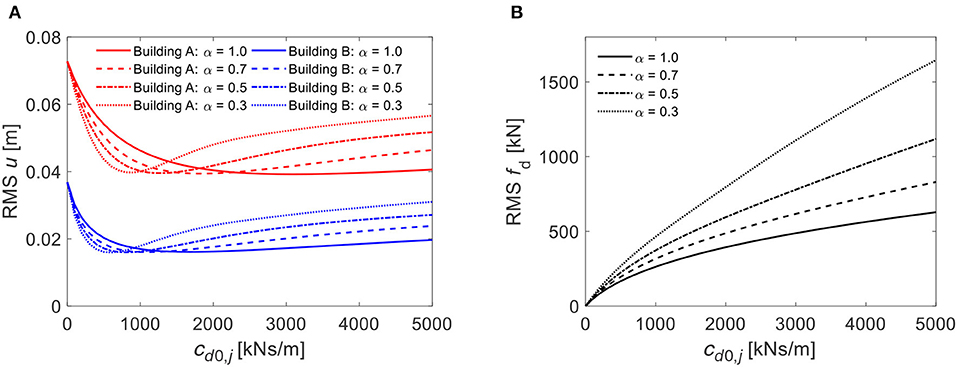
Figure 9. Stationary response vs. damping viscous constant c_{d0, j} for different α values: (A) Top-floor displacement of building A and B, (B) 4th floor damper force. Case with uniform dampers.

The optimal damping constant for building A and B are summarized in Table 2.

In Figures 9A, 10A it is observed that the optimal damper viscous constant reduces significantly for decreasing α values and that the RMS displacements at the optimal damping constant value are practically insensitive to the exponent α (Table 2). Thus, if the properties of the non-linear viscous dampers are appropriately calibrated, the same performance in terms of response reduction of the linear viscous dampers can be achieved.

FIGURE 10

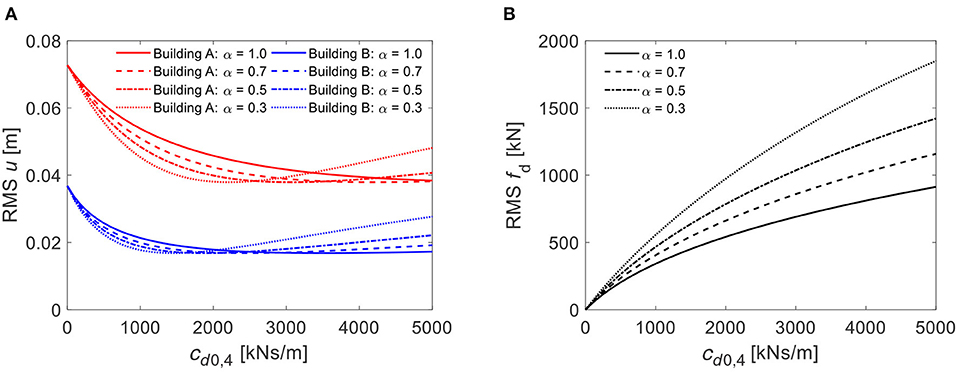
Figure 10. Stationary response vs. damping viscous constant c_{d0, 4} for different α values: (A) top-floor displacement of building A and B, (B) 4th floor damper force. Case with single damper.

The results reported in Figures 9B, 10B show that, for a given c_{d0, j} value, the damper force increases for decreasing α values. However, the damper forces at the optimal c_{d0, j} values evaluated for the different exponents α are comparable (Table 2) and reduce only slightly for increasing α values. Thus, the non-linear viscous dampers with optimal properties exhibit a performance similar to the linear viscous dampers with optimal properties also in terms of damper forces.

Influence of the Seismic Intensity

In order to compare the efficiency of the dampers, the seismic response corresponding to the optimal damper properties obtained for building B for the different α values and for PGA_ref = 0.3 g, is evaluated by considering different seismic intensities, as described by the PGA (Figure 11).

FIGURE 11

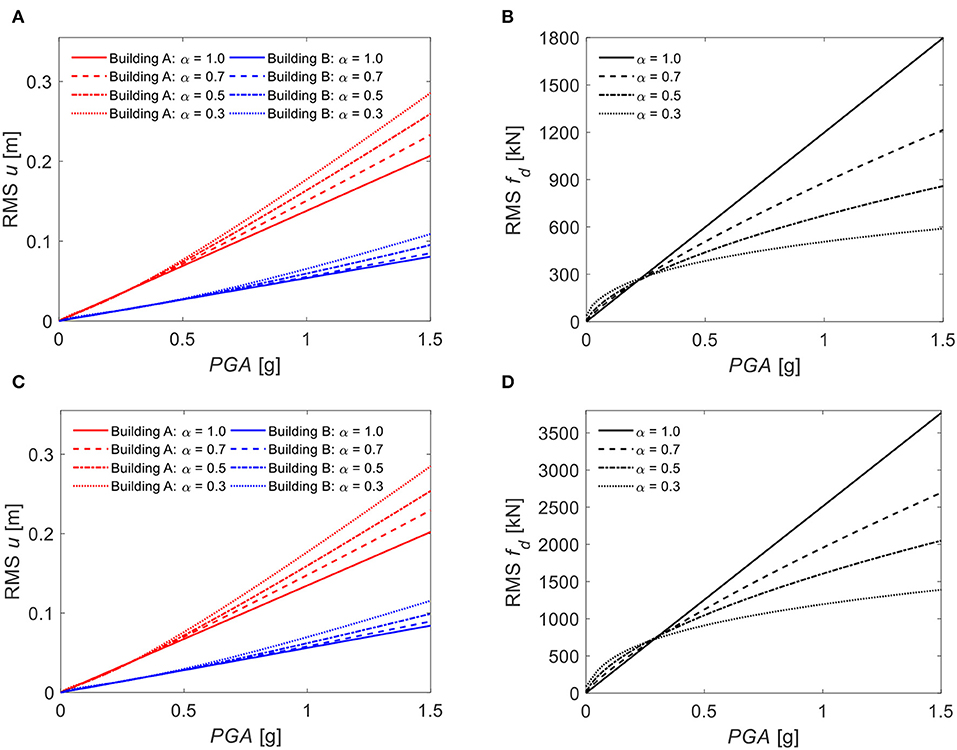
Figure 11. RMS response for increasing seismic intensities: (A) top-floor displacement of building A and B (uniform dampers case), (B) 4th floor damper force (uniform dampers case), (C) top-floor displacement of building A and B (single damper case), (D) 4th floor damper force (single damper case).

The buildings coupled by the dampers with different exponents exhibit comparable displacement responses for the various seismic intensities considered. In fact, the top displacement responses of building A and B tend to increase only slightly for increasing damper non-linearity (i.e., for decreasing α values). On the other hand, the damper forces reduce significantly for decreasing α values and for PGA values higher than the reference design value PGA_ref = 0.3 g. This result is extremely important because the viscous damper costs depend on the design force rather than on the viscous constant (Tubaldi and Kougioumtzoglou, 2015; Altieri et al., 2018).

Conclusions

In this paper, the seismic response of adjacent buildings connected by fluid viscous dampers is analyzed. A simplified dampers design strategy is proposed, which relies on a linearized reduced order model of the coupled system. A stochastic linearization technique is adopted with the aim of extending the design method to non-linear viscous dampers. The effectiveness of the design method and of the coupling strategy is assessed via numerical analysis of two adjacent buildings with shear-type behavior connected by linear or non-linear viscous dampers and subjected to Gaussian stochastic base acceleration. Among the possible damper arrangements consistent to the target amount of added damping, two limit configurations are analyzed, consisting of: a uniform distribution along the height; a single damper at the last elevation of the shorter building. The performance of the coupled system is investigated by considering different response parameters including buildings' displacements and accelerations as well as dampers' forces.

The outcomes of this study show that the reduced order model provides accurate estimates of the building displacement response and of the damper forces for a wide range of damper properties. Its accuracy slightly decreases for increasing values of the viscous constants.

For what concerns the use of linear dampers, the following conclusions can be drawn:

- The use of dampers to connect the adjacent buildings can improve significantly the performance of both the buildings.

- An optimal value of the damping constant exists for both the buildings and minimizes the displacement response.

- The dampers force always increases for increasing values of the viscous constant, although the relative velocities between the two buildings reduce. The increase of the root mean square force is less than linear for both the cases of uniform dampers and single damper.

- Linear viscous dampers are more effective in damping the displacement response for seismic intensities higher than the reference seismic intensity, at the expense of significantly increased damper forces.

For what concerns the use of non-linear devices, it is concluded that:

- The configuration with a single damper placed at the fourth floor provides forces that are notably lower than the sum of the forces of the fourth viscous damper employed in the alternative arrangement. This result has important effects on the optimization of the costs associated to the retrofit of adjacent buildings with viscous dampers.

- The optimal damper viscous constant reduces significantly for decreasing α values and the displacement response in correspondence of the optimal damper constant value are insensitive to the exponent α. Thus, an appropriate calibration of the non-linear dampers provides the same performance in terms of seismic response reduction as for the case with linear devices.

To conclude, it is worth noting that the proposed damper design method is valid for a wide range of ω_B/ω_A ratios, however the results presented in this study may quantitatively change by varying the features of the buildings. More precisely, the efficiency of the coupling strategy diminishes for systems with similar fundamental vibration periods, because of the in-phase dynamic motion experienced by the buildings.

Future developments of this work should also aim to assess the effectiveness of the dynamic coupling for mitigating seismic pounding hazard.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

ET, LG, FS, LR, and AD wrote the formulation of the problem, performed the numerical analyses and processed the analytical results. All authors have contributed to the manuscript revision, read and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2020.00025/full#supplementary-material

References

Abdeddaim, M., Ounis, A., Djedoui, N., and Shrimali, M. K. (2016). Pounding hazard mitigation between adjacent planar buildings using coupling strategy. J. Civil Struct. Health Monit. 6, 603–617. doi: 10.1007/s13349-016-0177-4

CrossRef Full Text | Google Scholar

Aida, T., Aso, T., Takeshita, K., Takiuchi, T., and Fuji, T. (2001). Improvement of the structure damping performance by interconnection. J Sound Vibration 242, 333–53. doi: 10.1006/jsvi.2000.3349

CrossRef Full Text | Google Scholar

Altieri, D., Tubaldi, E., De Angelis, M., Patelli, E., and Dall'Asta, A. (2018). Reliability-based optimal design of nonlinear viscous dampers for the seismic protection of structural systems. Bull. Earthquake Eng. 16, 963–982. doi: 10.1007/s10518-017-0233-4

CrossRef Full Text | Google Scholar

Basili, M., and De Angelis, M. (2007a). Optimal passive control of adjacent structures interconnected with nonlinear hysteretic devices. J. Sound Vibration 301, 106–125. doi: 10.1016/j.jsv.2006.09.027

CrossRef Full Text | Google Scholar

Basili, M., and De Angelis, M. (2007b). A reduced order model for optimal design of 2-mdof adjacent structures connected by hysteretic dampers. J Sound Vibration 306, 297–317. doi: 10.1016/j.jsv.2007.05.012

CrossRef Full Text | Google Scholar

Bhaskararao, A. V., and Jangid, R. S. (2007). Optimum viscous damper for connecting adjacent SDOF structures for harmonic and stationary white-noise random excitations. Earthquake Eng. Struct. Dyn. 36, 563–571. doi: 10.1002/eqe.636

CrossRef Full Text | Google Scholar

Bigdeli, K., Hare, W., and Tesfamariam, S. (2012). Configuration optimization of dampers for adjacent buildings under seismic excitations. Eng Optimization 12, 1491–1509. doi: 10.1080/0305215X.2012.654788

CrossRef Full Text | Google Scholar

Christopoulos, C., and Filiatrault, A. (2006). Principles of Passive Supplemental Damping and Seismic Isolation. IUSS Press, Pavia, Italy.

Cimellaro, G. P., and Lopez-Garcia, D. (2007). “Seismic response of adjacent buildings connected by nonlinear viscous dampers,” in Forensic Engineering Conference at Structures Congress (Long Beach, CA).

Google Scholar

Dall'Asta, A., Scozzese, F., Ragni, L., and Tubaldi, E. (2017). Effect of the damper property variability on the seismic reliability of linear systems equipped with viscous dampers. Bull Earthquake Eng. 15, 5025–5053. doi: 10.1007/s10518-017-0169-8

CrossRef Full Text | Google Scholar

Dall'Asta, A., Tubaldi, E., and Ragni, L. (2016). Influence of the nonlinear behaviour of viscous dampers on the seismic demand hazard of building frames. Earthquake 45, 149–169. doi: 10.1002/eqe.2623

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2018). Improved stochastic linearization technique for structures with nonlinear viscous dampers. Soil Dyn. Earthquake Eng. 113, 1–818. doi: 10.1016/j.soildyn.2018.06.015

CrossRef Full Text | Google Scholar

De Domenico, D., and Ricciardi, G. (2019). Earthquake protection of structures with nonlinear viscous dampers optimized through an energy-based stochastic approach. Eng. Struct. 179, 523–539. doi: 10.1016/j.engstruct.2018.09.076

CrossRef Full Text | Google Scholar

Di Paola, M., La Mendola, L., and Navarra, G. (2007). Stochastic seismic analysis of structures with nonlinear viscous dampers. J. Struct. Eng. 133, 1475–1478. doi: 10.1061/(ASCE)0733-9445(2007)133:10(1475)

CrossRef Full Text | Google Scholar

Di Paola, M., and Navarra, G. (2009). Stochastic seismic analysis of MDOF structures with nonlinear viscous dampers. Struct. Control Health Monit. 16, 303–318. doi: 10.1002/stc.254

CrossRef Full Text | Google Scholar

Gioiella, L., Tubaldi, E., Gara, F., Dezi, L., and Dall'Asta, A. (2018a). Modal properties and seismic behaviour of buildings equipped with external dissipative pinned rocking braced frames. Eng. Struct. 172, 432–439. doi: 10.1016/j.engstruct.2018.06.043

CrossRef Full Text | Google Scholar

Gioiella, L., Tubaldi, E., Gara, F., Dezi, L., and Dall'Asta, A. (2018b). Stochastic seismic analysis and comparison of alternative external dissipative systems. Shock Vibrations 47:5403737. doi: 10.1155/2018/5403737

CrossRef Full Text | Google Scholar

Hwang, J. S., Wang, S. J., Huang, Y. N., and Chen, J. F. (2007). A seismic retrofit method by connecting viscous dampers for microelectronics factories. Earth Eng. Struct. Dyn. 36, 1461–1480. doi: 10.1002/eqe.689

CrossRef Full Text | Google Scholar

Impollonia, N., and Palmeri, A. (2018). Seismic performance of buildings retrofitted with nonlinear viscous dampers and adjacent reaction towers. Earthquake Eng. Struct. Dyn. 47, 1329–1351. doi: 10.1002/eqe.3020

CrossRef Full Text | Google Scholar

Kanai, K. (1957). Semi-empirical formula for the seismic characteristics of the ground motion. Bull. Earthq. Res. Inst. Univ. 35, 309–325.

Google Scholar

Karabork, T., and Aydin, E. (2019). Optimum design of viscous dampers to prevent pounding of adjacent structures. Earthquakes Struct. 16, 437–453. doi: 10.12989/eas.2019.16.4.437

CrossRef Full Text | Google Scholar

Kim, K., Rye, J., and Chung, L. (2006). Seismic performance of structures connected by viscoelastic dampers. Eng. Struct. 28, 83–195. doi: 10.1016/j.engstruct.2005.05.014

CrossRef Full Text | Google Scholar

Lavan, O., and Avishur, M. (2013). Seismic behavior of viscously damped yielding frames under structural and damping uncertainties. Bull. Earthquake Eng. 11, 2309–2332. doi: 10.1007/s10518-013-9479-7

CrossRef Full Text | Google Scholar

Lin, W.-H., and Chopra, A. K. (2002). Earthquake response of elastic SDF systems with non-linear fluid viscous dampers. Earthquake Eng. Struct. Dyn. 31, 1623–1642. doi: 10.1002/eqe.179

CrossRef Full Text | Google Scholar

Luco, J. E., and De Barros, F. C. P. (1998). Optimal damping between two adjacent elastic structures. Earthquake Eng. Struct. Dyn. 27, 649–659. doi: 10.1002/(SICI)1096-9845(199807)27:7<649::AID-EQE748>3.0.CO;2-5

CrossRef Full Text | Google Scholar

Ni, Y. Q., Ko, J. M., and Ying, Z. G. (2001). Random seismic response analysis of adjacent buildings coupled with non-linear hysteretic dampers. J. Sound Vib. 26, 403–417. doi: 10.1006/jsvi.2001.3679

CrossRef Full Text | Google Scholar

Ok, S., Song, J., and Park, K. (2008). Optimal design of hysteretic dampers connecting adjacent structures using multiobjective genetic algorithm and stochastic linearization method. Eng. Struct. 30, 1240–1249. doi: 10.1016/j.engstruct.2007.07.019

CrossRef Full Text | Google Scholar

Pekcan, G., Mander, J. B., and Chen, S. S. (1999). "Fundamental considerations for the design of nonlinear viscous dampers. Earthquake Eng. Struct. Dyn. 28, 1405–1425. doi: 10.1002/(SICI)1096-9845(199911)28:11&lt;1405::AID-EQE875&gt;3.0.CO;2-A

CrossRef Full Text | Google Scholar

Reggio, A., Restuccia, L., Martelli, L., and Ferro, G. A. (2019). Seismic performance of exoskeleton structures. Eng. Struct. 198. doi: 10.1016/j.engstruct.2019.109459

CrossRef Full Text | Google Scholar

Richardson, A., Walsh, K. K., and Abdullah, M. M. (2012). Closed-form equations for coupling linear structures using stiffness and damping elements. Struct. Control Health Monit. 20, 259–281. doi: 10.1002/stc.490

CrossRef Full Text | Google Scholar

Roh, H., Cimellaro, G. P., and Lopez-Garcia, D. (2011). Seismic response of adjacent steel structures connected by passive device. Adv. Struct. Eng. 14, 499–517. doi: 10.1260/1369-4332.14.3.499

CrossRef Full Text | Google Scholar

Rüdinger, F. (2006). Optimal vibration absorber with nonlinear viscous power law damping and white noise excitation. J. Eng. Mech. 132, 46–53. doi: 10.1061/(ASCE)0733-9399(2006)132:1(46)

CrossRef Full Text | Google Scholar

Rudinger, F. (2007). Tuned mass damper with nonlinear viscous damping. J. Sound Vibrat. 300, 932–948. doi: 10.1016/j.jsv.2006.09.009

CrossRef Full Text | Google Scholar

Rüdinger, F., and Krenk, S. (2003). Spectral density of an oscillator with power law damping excited by white noise. J. Sound Vib. 261, 365–371. doi: 10.1016/S0022-460X(02)01183-5

CrossRef Full Text | Google Scholar

Scozzese, F., Dall'Asta, A., and Tubaldi, E. (2019). Seismic risk sensitivity of structures equipped with anti-seismic devices with uncertain properties. Struct. Safety 77, 30–47. doi: 10.1016/j.strusafe.2018.10.003

CrossRef Full Text | Google Scholar

Sivandi-Pour, A., Gerami, M., and Kheyroddin, A. (2015). Determination of modal damping ratios for non-classically damped rehabilitated steel structures. Iranian J. Sci. Tech. 39:81. doi: 10.1007/s40999-016-0003-8

CrossRef Full Text | Google Scholar

Sivandi-Pour, A., Gerami, M., and Khodayarnezhad, D. (2014). Equivalent modal damping ratios for non-classically damped hybrid steel concrete buildings with transitional storey. Struct. Eng. Mech. 50, 383–401. doi: 10.12989/sem.2014.50.3.383

CrossRef Full Text | Google Scholar

Soong, T. T., and Spencer, B. F. (2002). Supplemental energy dissipation: state-of-the-art and state-of-the-practice. Eng. Struct. 24, 243–259. doi: 10.1016/S0141-0296(01)00092-X

CrossRef Full Text | Google Scholar

Sorace, S., and Terenzi, G. (2013). Damped interconnection-based mitigation of seismic pounding between adjacent R/C buildings. Int. J. Eng. Tech. 5, 406–412. doi: 10.7763/IJET.2013.V5.585

CrossRef Full Text | Google Scholar

Symans, M. D., and Constantiou, M. C. (1998). Passive fluid viscous damping systems for seismic energy dissipation. ISET J. Earthquake Tech. 35, 185–206.

Google Scholar

Tajimi, H. (1960). “A statistical method of determining the maximum response of a building structure during an earthquake,” in Proceedings of the 2nd WCEE, II (Tokyo: Science Council of Japan), 781–798.

Google Scholar

Takewaki, I. (2009). Building Control With Passive Dampers: Optimal Performance-Based Design for Earthquakes. Singapore: John Wiley & Sons.

Google Scholar

Trombetti, T., and Silvestri, S. (2004). Added viscous dampers in shear-type structures: the effectiveness of mass proportional damping. J. Earthquake Eng. 8, 275–313. doi: 10.1080/13632460409350490

CrossRef Full Text | Google Scholar

Tubaldi, E. (2015). Dynamic behavior of adjacent buildings connected by linear viscous/viscoelastic dampers. Struct. Control Health Monit. 22, 1086–1102. doi: 10.1002/stc.1734

CrossRef Full Text | Google Scholar

Tubaldi, E., Barbato, M., and Dall'Asta, A. (2014). Performance-based seismic risk assessment for buildings equipped with linear and nonlinear viscous dampers. Eng. Structures 78, 90–99. doi: 10.1016/j.engstruct.2014.04.052

CrossRef Full Text | Google Scholar

Tubaldi, E., Barbato, M., and Ghazizadeh, S. A. (2012). Probabilistic performance-based risk assessment approach for seismic pounding with efficient application to linear systems. Structural Safety 36–37:14–22. doi: 10.1016/j.strusafe.2012.01.002

CrossRef Full Text | Google Scholar

Tubaldi, E., and Kougioumtzoglou, I. A. (2015). Nonstationary stochastic response of structural systems equipped with nonlinear viscous dampers under seismic excitation. Earthquake Eng. Struct. Dyn. 44, 121–138. doi: 10.1002/eqe.2462

CrossRef Full Text | Google Scholar

Tubaldi, E., Ragni, L., and Dall'Asta, A. (2015). Probabilistic seismic response assessment of linear systems equipped with nonlinear viscous dampers. Earthquake Eng. Struct. Dyn. 44, 101–120. doi: 10.1002/eqe.2461

CrossRef Full Text | Google Scholar

Xu, Y. L., He, Q., and Ko, J. M. (1999). Dynamic response of damper-connected adjacent buildings under earthquake excitation. Eng. Struct. 21, 135–48. doi: 10.1016/S0141-0296(97)00154-5

CrossRef Full Text | Google Scholar

Zhang, W. S., and Xu, Y. L. (1999). Dynamic characteristics and seismic response of adjacent buildings linked by discrete dampers. Earth Eng. Struct. Dyn. 28, 1163–1185. doi: 10.1002/(SICI)1096-9845(199910)28:10&lt;1163::AID-EQE860&gt;3.0.CO;2-0

CrossRef Full Text | Google Scholar

Zhu, H., Ge, D., and Huang, X. (2010). Optimum connecting dampers to reduce the seismic responses of parallel structures. J. Sound Vibration 330, 1931–1949. doi: 10.1016/j.jsv.2010.11.016

CrossRef Full Text | Google Scholar

Zhu, H. P., and Iemura, H. (2000). A study of response control on the passive coupling element between parallel structures. Struct. Eng. Mech. 9, 383–396. doi: 10.12989/sem.2000.9.4.383

CrossRef Full Text | Google Scholar

Zhu, H. P., and Xu, Y. L. (2005). Optimum parameters of Maxwell model-defined dampers used to link adjacent structures. J. Sound Vibration 279, 253–274. doi: 10.1016/j.jsv.2003.10.035

CrossRef Full Text | Google Scholar