Discrete and Continuous Approaches for the Failure Analysis of Masonry Structures Subjected to Settlements

Numerical modeling of masonry structures is nowadays still an active research field, and this is partly due to a number of open issues related to preservation and restoration of historical constructions and the availability of computational tools that have become more and more refined. This work focuses on the analysis of settlement-induced failure patterns characterizing the in-plane response of two-dimensional dry-joints masonry panels, which differ in terms of texture, geometry, and settlement configuration. Brick-block masonry, interpreted as a jointed assembly of prismatic particles in dry contact, can be modeled as a discrete system of rigid blocks interacting through contact surfaces with no tensile strength and finite friction, modeled as zero thickness elasto-plastic Mohr-Coulomb interfaces. Different approaches and numerical models have been adopted herein: Limit Analysis (LA), a discrete model DEM, and a continuous Finite Element Model (FEM). Limit Analysis is able to provide fast and reliable results in terms of collapse multiplier and relative kinematics. In this work, a standard LA procedure was coded through Linearized Mathematical Programming to take into account sliding mechanisms through dilatant joints. Discrete models are particularly suitable to study historical masonry materials, where rigid bodies interact between contact and friction. Here, a combined Finite/Discrete Element approach (FEM/DEM) is adopted. Finally, analyses are conducted through the Finite Element approach, resorting to a continuum anisotropic elastic perfectly plastic constitutive model. Some selected case studies have been investigated and found to have adopted the above mentioned models, and numerical results have been interpreted to highlight the capability of the approaches to predict failure patterns for various geometrical features of the structure and settlement configurations.

1. Introduction

Masonry is one of the most ancient structural materials and constitutes a vast majority of the World's architectural heritage. It is a composite and heterogeneous medium, resulting from the assemblage of natural or artificial blocks by means of mortar layers or dry joints. Being characterized by an internal structure, which is reflected in a complex mechanical response, masonry and its constitutive behavior still represent a challenging research field. Thanks to the availability of more and more powerful computational resources, over the last decades, a large number of numerical applications have been developed, many of which have resorted to using different constitutive assumptions and solution algorithms. Nonetheless, it is not possible to argue that each of these models suit just any structural problem their applicability needs to be evaluated case by case on the basis of geometrical features, the extent of the structure, and the boundary conditions. Among the available numerical modeling techniques for masonry structures, a broad distinction can be made between micromechanical, micromechanical, and multiscale models defined as follows. A significant classification can be found in D'Altri et al. (2019).

According to micromodeling strategy, the constituents, namely, the units, mortar (if present), and unit/mortar interfaces, are separately modeled, and each part is assigned a properly calibrated constitutive law. This approach is particularly suitable if the response of the assemblage needs to be accurately described (Lotfi and Shing, 1994; Lourenço and Rots, 1997; Oliveira and Lourenço, 2004; Alfano and Sacco, 2006; Serpieri et al., 2017), but a major hindrance is still represented by its high computational cost, a consequence of the large number of degrees of freedom needed to describe the structural configuration (Clementi et al., 2019, 2020). In addition, the adopted constitutive assumptions often imply the calibration of a large set of parameters, which are not always easily determined.

Following a macromechanical approach, the heterogeneous medium is modeled as a continuum, and the constitutive behavior is usually described through phenomenologically based mathematical relations in which degrading phenomena are the product of damage or friction variables. In this case, macroscopic mechanical properties are more easily derived from standard experimental tests on small masonry specimens. These models are, if compared to micromechanical ones, more efficient from a computational point of view (Del Piero, 1989; Gambarotta and Lagomarsino, 1997; Roca et al., 2005; Sangirardi et al., 2019a) and are widely used for real-scale applications in which, depending on the complexity of the geometry of the structure, different discretization strategies might result in the adoption of monodimensional, bidimensional, or three-dimensional finite elements.

Multiscale, i.e., micro-macro, continuum models represent a very promising approach for the analysis of masonry structures since they can accurately keep track of the mechanical and geometrical properties of the material at the microstructure with a reduced computational cost if compared to a fully micromechanical model (Masiani and Trovalusci, 1996; De Buhan and de Felice, 1997; de Felice et al., 2010; Trovalusci et al., 2010; Leonetti et al., 2018; Reccia et al., 2018). These models are often derived by considering two material scales: a microscale where, having deduced the mechanical properties of the components through experimental tests, a material representative volume element (RVE) is defined and a macroscale structural level, where a homogeneous continuum is obtained by performing a homogenization procedure based on the solution of boundary conditions problems for the RVE (Addessi et al., 2016, 2018; Greco et al., 2016, 2017). Other multiscale strategies make use of different homogenization techniques based on the so-called Cauchy rule and its generalizations (Capecchi et al., 2011), allowing the derivation of generalized continua, such as micropolar continua able to properly represent scale effects, that, in masonry materials, are significant (Masiani and Trovalusci, 1996; Trovalusci and Masiani, 2003; Pau and Trovalusci, 2012; Fantuzzi et al., 2019; Leonetti et al., 2019).

Due to their characteristics, masonry constructions have proven to be particularly vulnerable not only to earthquakes but also to structural settlements. Cracking and damage, in fact, often occur as a consequence of ground movements. In urban areas, this phenomenon is related to the realization of underground infrastructures or, more generally, to anthropic triggering factors, while natural hazards (e.g., slow-moving landslides, liquefaction, or consolidation processes) are more likely to interfere with masonry constructions in rural areas. In both cases, the understanding of the phenomenon and its description are fundamental to identifying the causes as well as preventing the effects with appropriate protection measures, both for modern and historical constructions. Several approaches to the prediction of settlement-induced damage that consider masonry either as an assembly of discrete blocks (DeJong, 2016; Portioli and Cascini, 2016) or as a continuum medium (Burd et al., 2000; Amorosi et al., 2014) may be found in the literature. The comparison between discrete and continuous models is also a widespread topic (Casalegno et al., 2013; de Felice and Malena, 2019; Malena et al., 2019; Zampieri et al., 2019; Landolfo et al., 2020).

In this work, three modeling techniques have been adopted to describe settlement induced crack patterns in masonry panels characterized by different geometrical configurations and boundary conditions, reproducing the ground movement as a downward moving rigid block. Equations governing systems of rigid blocks interacting though no tension and frictional interfaces formally correspond to those of perfect plastic systems with non-associative flow rule (Fichera, 1964). Limit Analysis, largely recognized as a very effective tool to estimate collapse load and collapse mechanisms for masonry structures (Baggio and Trovalusci, 2000; Milani, 2011; Portioli et al., 2014; Milani and Taliercio, 2016; Pavlovic et al., 2016; Cascini et al., 2018; Pepe et al., 2019b), is used to determine the failure configuration of dry joints masonry panels subjected to settlements, modeling the walls (according to the microscale approach) as an assemblage of rigid blocks in contact through frictional interfaces. It is important to underline that the Limit Analysis model presented here is based on the perfect plasticity hypothesis, and information about the ultimate displacement entities is thus not available. Moreover, results have only been compared in terms of crack patterns because the upper bound approach provides the collapse mechanism of the structure without giving information about the contact actions between the blocks and, in particular, about the base reaction.

The results of the analyses, performed on panels, walls with openings, and facades, are compared with the ones obtained through an FEM/DEM approach (Baraldi et al., 2018) and with those obtained by means of a continuum (macroscale) Finite Element approach, adopting an elasto-plastic anisotropic constitutive model (Lasciarrea et al., 2019; Sangirardi et al., 2019b). The main features of the models are recalled in section 2, the selected case-studies and the results of the analyses are then presented in section 3 and critically compared in order to highlight the influence of walls aspect ratio, width of the settling area, and presence of openings. Finally in section 4, some remarks and future developments are reported.

2. Adopted Micromodels

2.1. Rigid Block Model for Limit Analysis

The first adopted model is framed within the Limit Analysis (LA) theory, taking into account the presence of friction. The model considers as a system of n rigid blocks directly interacting through m contact surfaces that are unable to carry tension and are resistant to sliding by friction. The blocks can translate and rotate about the edges of the contact surfaces (hinging) as well as sliding along the joints.

In order to provide the mechanical details of the model, consider two simple blocks represented in Figure 1A, introducing ${\underset{\_}{e}}_i={\left\{e_1,e_2,e_3\right\}}^T$, the orthonormal basis in the three-dimensional space. Loads are applied to the centroid of each rigid block i−th: static “dead” loads are collected in vector $f_0^i={\left\{f_{01}^i,f_{02}^i,m_{03}^i\right\}}^T$, and live loads are collected in the vector $f_L^i={\left\{f_{L1}^i,f_{L2}^i,m_{L3}^i\right\}}^T$. For the whole structure, $f_0=\left\{f_0^i\right\}$ and $f_L=\left\{f_L^i\right\}$, with i = 1, …, n. The vector of the load over the whole system is f = f₀ + αf_L, where live loads are proportional to the dead loads through a non-negative coefficient, α, called the collapse multiplier. Let $u^i=\left\{u_1^i,u_2^i,{\theta }_3^i\right\}$ denote the vector of generalized displacement of the centroid of each i−th block. The vector u = {uⁱ}, with i = 1, …, n, collects the displacement for the whole structure, which correspond in a virtual work sense to loads f.

FIGURE 1

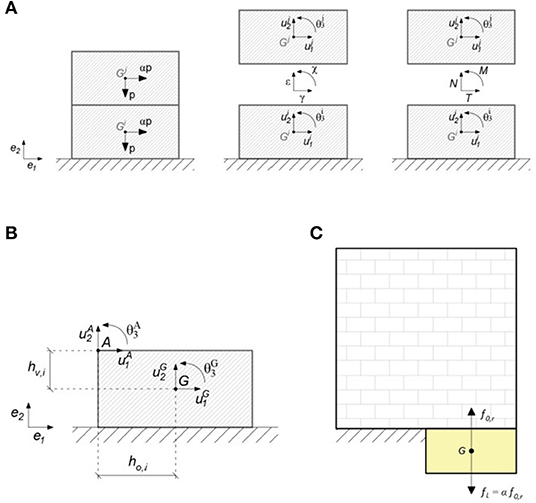
Figure 1. (A) Simple two-blocks structure (B) Displacement components for a rigid block (C) Model for settlement: panel with fictitious block.

The static variables are the internal forces acting at each j−th contact surface between blocks, that is, the normal force N^j, the shear force T^j, and the moment M^j. For each joint, they are collected in vector σ^j = {N^j, T^j, M^j}T. The vector σ = {σ^j}, with j = 1, …, m, refers to the whole structure.

The kinematic variables, or generalized strain, are the relative displacement rates at joints: normal displacement ξ^j, tangential displacement γ^j, and rotation χ^j. For each joint j = 1, …, m, they are collected in the vector ε^j = {ξ^j, γ^j, χ^j}T. The vector ε = {ε^j} refers to the whole structure and corresponds in a virtual work sense to the vector of static variables σ.

The kinematic compatibility for the whole system is expressed by equation

$\begin{array}{ll}\epsilon =Bu,& (1)\end{array}$

where B represents the compatibility matrix defined in Baggio and Trovalusci (2000).

The equilibrium of the whole structure is defined by the equation

$\begin{array}{ll}{B}^T\sigma +f=0.& (2)\end{array}$

The generalized yield domain of the system can be written as

$\begin{array}{ll}y=N^T\sigma \le 0,& (3)\end{array}$

where N is the block-diagonal gradient matrix referred to the adopted failure surface.

The flow rule expresses the vector ε as a linear combination of non-negative coefficients λ, called inelastic multiplier, and it can be written as

$\begin{array}{ll}\epsilon =M\lambda .& (4)\end{array}$

The plastic behavior of contact surfaces is defined through the complementarity condition

$\begin{array}{ll}{\lambda }^{T}y=0.& (5)\end{array}$

Furthermore, the non-negative work of the live loads which cause the collapse mechanism is defined by the following equation

$\begin{array}{ll}{f}_L^{T}u=1.& (6)\end{array}$

In Baggio and Trovalusci (2000) the authors presented a homemade code, ALMA (Analisi Limite Murature Attritive) based on a two-step procedure, to deal with the non-linear and non-convex programming problem (NLNCP) related to the presence of frictional interfaces (non-standard LA) of bidimensional and three-dimensional block masonry structures.

As reported in Pepe et al. (2019a,b), following the approach in Baggio and Trovalusci (2000), a new version of the code, ALMA 2.0, was implemented using MATLAB^® for linear optimization and a Python^TM interface for pre and post processing operations. In particular, this new version is based on the kinematic approach of Limit Analysis and considers for sliding a linearized behavior of joints. This aspect is significant because the computational effort due to the solution of the NLNCP is avoided. Indeed, the advantage of a linear mathematical programming technique, deriving by the presence of the dilatant behavior of the contact surfaces, can provide a unique and quite fast solution of the problem.

Here, the optimization problem presented in Pepe et al. (2019b) has been modified to include the presence of settlements into the model (Pepe, 2020). A preliminary modification of the model has been the introduction of the possibility to add kinematic constraints to the block of the structure. The displacement components of every points of a generic ith block have been expressed as function of the displacement components of its center of gravity. Let consider a generic point A of the ith block shown in Figure 1B. Equation of rigid motion, describing its horizontal, vertical, and rotation movement are reported as follows

$\begin{array}{ll}\begin{array}{c}{\widehat{u}}_1^A=u_1^G-{\theta }_3^G{h}_{v,i},\hfill \\ {\widehat{u}}_2^A=u_2^G+{\theta }_3^G{h}_{o,i},\hfill \\ {\widehat{\theta }}_3^A={\theta }_3^G,\hfill \end{array}\hfill & (7)\end{array}$

assumed in a compact form as

$\begin{array}{ll}\widehat{u}=Vu,& (8)\end{array}$

where, for the whole structure, the matrix V contains the geometrical information of the points where the kinematical constraints are inserted. In particular, the components of displacement $\widehat{u}$ became identically null depending on the typology of the external constraint considered. The modified programming problem, considering the expression of u, written as a function of the inelastic multiplier λ, is represented by,

$\begin{array}{ll}\begin{array}{c}\text{min }\alpha =-{\lambda }^T{(A_0{N}_1)}^T{f}_0\text{subjected to}\hfill \\ (A{N}_1-N_2)\lambda =0,\hfill \\ {\lambda }^T{(A_0{N}_1)}^T{f}_L-1=0,\hfill \\ V{A}_0{N}_1\lambda =0,\hfill \\ \lambda \ge 0,\hfill \end{array}\hfill & (9)\end{array}$

where introducing B₁, i.e., the kinematical submatrix of maximum rank, and B₂, the rest of the kinematical matrix, the matrix A₀ is the inverse of B₁. The matrix is defined as $A=B_2{B}_1^{-1}$, and N is the transpose of block-diagonal gradient matrix (N = [N₁, N₂]).

The equation (AN₁ − N₂)λ = 0 represents the kinematic compatibility conditions, ${\lambda }^T{(A_0{N}_1)}^T{f}_L-1=0$ is the positive work of live loads and VA₀N₁λ = 0 represents the equations used to introduce the kinematical constraints on rigid blocks.

Following the idea of Portioli and Cascini (2016), in order to introduce a local foundation settlement into the model, the mathematical and geometrical formulation of the model has been modified with the addition of a fictitious rigid block, with degrees of freedom associated to the imposed movement. In Figure 1C, an example of the modified geometric model for a simple masonry panel is shown, indicating in yellow the fictitious rigid block.

Another difference introduced into the model concerns the definition of the loads applied to the blocks. Indeed, in that case, every block of the structure is subjected only to its dead load, while live load is applied only on the block that simulates the settlement. In detail, for that block, dead load is an upward force assumed to be proportional to an admissible base reaction without foundation settlement, considering a uniform distribution of vertical loads in the structure, and it is denoted as f_{(0, r)}, while live load f_L is a downward force equal to dead load f_{(0, r)} and proportional to the collapse multiplier α. In the case of LA based on a lower bound approach, the collapse multiplier gives information about the base reaction at failure. Otherwise, since the code here presented is based on upper bound approach, it represents a mathematical expedient to define analytically the settlement of the fictitious block.

Figure 1C shows the loading condition for the support block. The optimization problem has been changed, taking advantage of the previous modification developed to include kinematic constraints. Indeed the displacement components of any point of the fictitious block ${\widehat{u}}_s$ are related to displacement components of the centroid u_s by means a matrix S that plays the same role of matrix V introduced for kinematic constraints

$\begin{array}{ll}{\widehat{u}}_s=S{u}_s.& (10)\end{array}$

It is consequently possible to particularize the movement of the support block u_s using the components described by the vector ${\widehat{u}}_s$. Indeed, purely translational or rotational displacements are allowed, provided the ${\widehat{u}}_s$ vector coherently defined. The modified programming problem, considering the expression u_s written as a function of the inelastic multiplier λ, is represented by,

$\begin{array}{ll}\begin{array}{c}\text{min }\alpha =-{\lambda }^T{(A_0{N}_1)}^T{f}_0\text{subjected to}\hfill \\ (A{N}_1-N_2)\lambda =0,\hfill \\ {\lambda }^T{(A_0{N}_1)}^T{f}_L-1=0,\hfill \\ S{A}_0{N}_1\lambda =0,\hfill \\ \lambda \ge 0,\hfill \end{array}\hfill & (11)\end{array}$

The equation SA₀N₁λ = 0 is the additional equality constraint to take into account the kinematic of the rigid fictitious block.

2.2. Combined Finite/Discrete Element Model

A discrete model, made by means of a combined Finite-Discrete Element Model (FEM/DEM) approach, has been adopted here.

Discrete Element Models (DEM) (Cundall, 1988) are a specific class of discrete models in which distinct elements can move independently, can come in or loose contact with other elements (the contact detection is governed by a molecular algorithm), and large displacements are considered (Cundall and Hart, 1992). DEM are suitable to study non-linear problems characterized by the mutual movement of rigid bodies interacting by means of both contact and friction, such as jointed rock and granular assemblies (Cundall and Strack, 1979), and they have recently been adopted for masonry modeling (Cecchi and Sab, 2004, 2009; Lemos, 2007; Baraldi et al., 2015a).

In order to describe the deformability of the elements, simple FE discretizations have been proposed since the beginning of the development of DE Method (Cundall et al., 1985). Here, the combined FEM/DEM approach proposed by Munjiza (2004) and developed by the Toronto Geo Group (Mahabadi et al., 2010) has been adopted. The approach relies on a combination of FEM and DEM: DEs are meshed into FEs with embedded crack elements that activate whenever the peak strength is reached. In this way, elastic deformation in the continuum is accounted by FEs, while interaction, fracture, and fragmentation processes are modeled by DEs.

The FEM/DEM approach adopted here has been successfully adopted for masonry structures by some of the authors (Reccia et al., 2012, 2016, 2018; Baraldi et al., 2013, 2015b, 2018, 2019; Pepe et al., 2019a,b) and by other research groups (Smoljanović et al., 2013, 2015, 2017).

Numerical analyses are performed through the open source computer codes Y2D/Y-GUI (Mahabadi et al., 2010) and Y-Geo (Mahabadi et al., 2012), while input and results have been processed by means of CAD, ad-hoc MATLAB^® scripts and spreadsheets.

The specimens were discretized through a triangular CST FEs mesh under plane stress hypotheses. As rigid and cracking can only occur in the joints, masonry units were modeled as zero-thickness interfaces based on a Mohr-Coulomb strength criterion with no cohesion holds. Since the aim of the work was to compare the results of different models with those obtained with LA, which implicitly considers the blocks non-deformable, in order to avoid cracks inside the bricks, the FEM/DEM model units were characterized by a very high value of Young's Modulus.

2.3. FEM

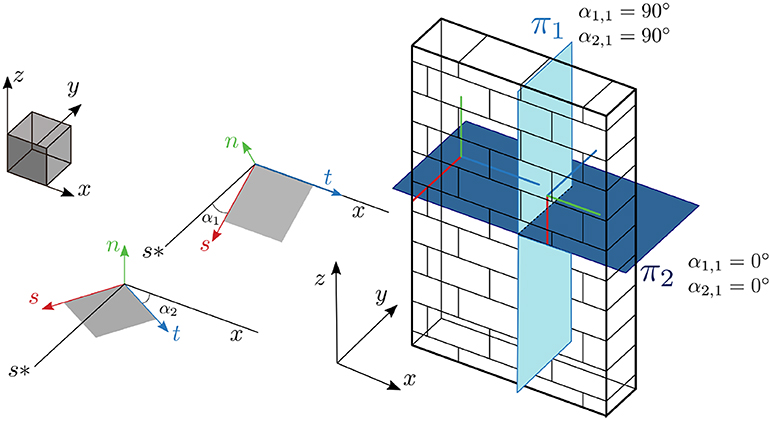
The third approach adopted to analyze failure mechanisms characterizing the response to settlements of masonry constructions is a continuum finite element (FE) one. The constitutive model, implemented in the FE code PLAXIS 3D^®, is a three-dimensional anisotropic elastic-perfectly plastic one. It stems from the Jointed Rock Model, and it has been enriched with consideration for the block aspect ratio and staggering joints effects. The Jointed Masonry Model (Lasciarrea et al., 2019) is characterized by isotropic elasticity and anisotropic yielding and can be included in the class of multi-laminates models (Pietruszczak and Niu, 1992). Macroscopic elastic properties of the continuum are derived from the joints and blocks ones through a homogenization procedure (De Buhan and de Felice, 1997; de Felice et al., 2010), and an equivalent isotropic behavior can also be assumed assigning the material an average elastic modulus E as in the presented case-studies. A set of three sliding directions (maximum), on which failure is meant to occur, is defined in the xyz space and described by means of dip (α₁) and strike (α₂). These parameters represent, for each plane, the positive rotation along the x-axis and the negative rotation along the z-axis, respectively. In the case of masonry panels with regular texture, these angles can be easily defined according to Figure 2.

FIGURE 2

Figure 2. JMM bed and head joint plane orientation.

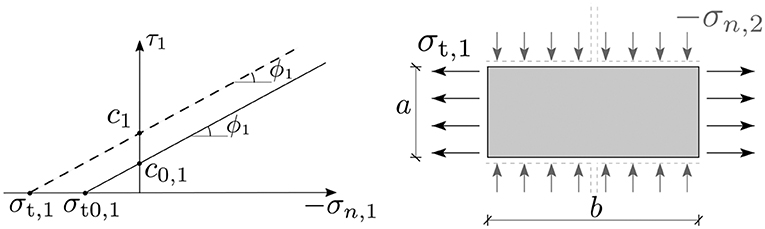
In the proposed examples, only two planes (head and bed joints) are activated, while a third plane might be considered in the case of walls with double facing. Yield functions are defined, for each orientation, in terms of local stress components according to Coulomb's and tensile criterion:

$\begin{array}{l}\hfill f_{\text{i}}^c=\left|{\tau }_{\text{i}}\right|+{\sigma }_{n,\text{i}}tan{\varphi }_{\text{i}}-c_{\text{i}}\\ \hfill f_{\text{i}}^t={\sigma }_{n,\text{i}}-{\sigma }_{\text{t},\text{i}}& (12)\end{array}$

where i = 1,2, and 3 is the plane id, σ_{n, i}, and τ_i are the normal and the shear stress along each orientation, ϕ_i is the friction angle, c_i is the cohesion, and σ_{t, i} is the tensile strength along the joints. The interlocking effect is accounted by modifying the strength parameters on the head-joints plane, stemming from equilibrium conditions and considering the aspect ratio of the blocks through the parameter β, which also depends on the friction angle of the bed joints:

$\begin{array}{ll}\beta =tan{\varphi }_2\frac{b}{2a}& (13)\end{array}$

The tensile strength and cohesion on the head joints are thus

$\begin{array}{l}\hfill {\sigma }_{t,1}={\sigma }_{\text{t}0,1}-\beta {\sigma }_{n,2}+c_{0,2}\frac{\beta }{tan{\varphi }_2}\\ \hfill c_1=c_{0,1}-(\beta {\sigma }_{n,2}-c_{0,2}\frac{\beta }{tan{\varphi }_2})tan{\varphi }_1& (14)\end{array}$

and the modified strength criterion is reported in Figure 3.

FIGURE 3

Figure 3. Modified Mohr-Coulomb criterion.

In the analyses performed the following model parameters have been assumed: all the tests are characterized by a unit weight γ = 12 kN/m³, σ_{t, i} = c_{0, i} = 0 MPa and ϕ_i = 21.8°. An associated flow rule for plasticity has been assumed, but different values of dilatancy ψ_i can, in principle, be defined. For Tests 8C and 12C the homogenized shear modulus is equal to 477 MPa, while G = 511 MPa in all the other cases. According to the different values of block dimensions ratio assumed in the examples, those reproduced from Portioli and Cascini (2016) are characterized by β = 0.8; for all the other walls β is equal to 0.4.

3. Numerical Analyses

The models have been validated using, as a benchmark, the experimental and numerical results obtained by Portioli and Cascini (2016) who studied the collapse of different wall masonry panels made of dry jointed tuff blocks subjected to settlements. The test set-up has been designed ad-hoc, allowing a downward displacement of a portion of the structure (600 × 200 mm³) with the rest of the wall being simply supported. Block dimensions are equal to 100 × 200 × 50 mm³; the two walls are 1,100 mm wide and 100 mm thick, and differ in terms of height since Test 8C is made of eight courses, resulting in a height of 400 mm, while Test 12C is made of 12 courses, resulting in a height of 600 mm.

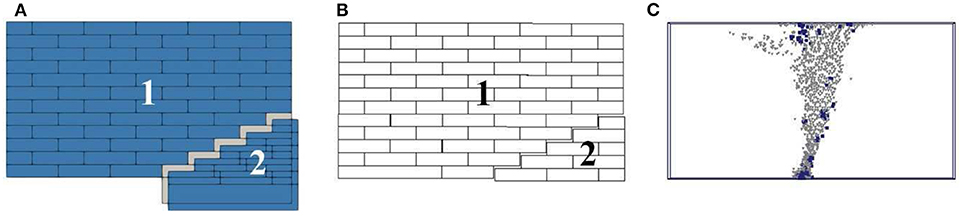
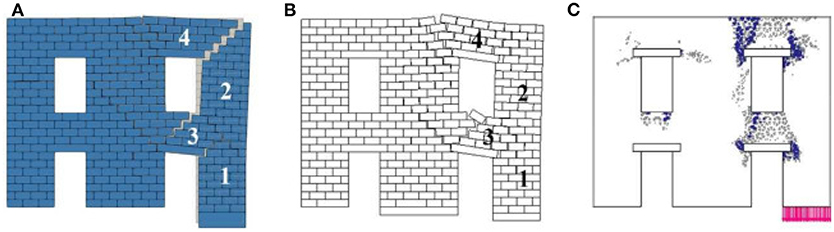
Figure 4 shows the experimental and numerical benchmark results producing a mechanism characterized by three macro-blocks: a first one, which behaves as a rigid block, at the left bottom side of the panel; a central one that rotates around the outer right vertex of the first macro-block in which the blocks are subjected to sliding and rocking; and a third macro-block that is separated by the others through a “stair-stepped” path and lies on the moving support. Figure 5 shows the collapse mechanism obtained with the different models for Test 8C. Figures 5A,B present the mechanism of collapse obtained with LA and FEM/DEM. Both mechanisms agree with experimental and numerical results obtained by Portioli, producing a collapse where the three macro-blocks previously described can be easily identified. Figure 5C reports the distribution of the plastic points (blue points indicate tensile failure while gray points localize shear failure points). According to the typically observed crack patterns in case of long settlement (Mastrodicasa, 1958), tensile failure points are concentrated on the top part of the wall, while shear failure point are located along an approximately 45° oriented direction going through the panel.

FIGURE 4

Figure 4. (A) Experimental and (B) Numerical results for Test 8C. [Courtesy of Prof. F. Portioli].

FIGURE 5

Figure 5. (A) LA, (B) FEM/DEM, and (C) FEM results for Test 8C.

Figure 6 shows the experimental and numerical benchmark results producing a mechanism characterized by two macro-blocks separated by a “stair-stepped” crack: the first macro-block, which is supported by the fixed base, and the second one, translating downwards on the movable support. Figure 7 presents the failure mechanisms obtained with the different models for Test 12C. Figures 7A,B present the mechanism obtained with LA and FEM/DEM, which are in good agreement with the experimental as well as with the numerical results obtained by the author. Indeed, also in this case, the two macro-blocks previously described were easily distinguishable. Figure 7C refers to continuum FEM modeling results. The plastic point distribution is the one at failure, i.e., once the vertical reaction at the base of the moving support is constant and, if compared to Test 8C case, fewer tensile plastic points can be observed. The FEM approach allows us to keep track of the entire settlement process and its evolution. In this paper, however, FEM results were reported only at the final stage of the analysis, thus information on the plastic points evolution has not been provided in the figures. In case of shorter settlements, shear failure first appears at the lower right corner of the wall, and the upper part of the panel is involved only in the last stages of the analysis. Conversely, in case of Panel 8C, for which the geometry of the problem more clearly outlines a long settlement condition, the first plastic points to appear are the tensile ones in the upper portion of the specimen. Another aspect might clarify the apparent lack of accuracy that the FEM model seems to show in these tests compared to LA and FEM/DEM approaches. The clear distinction between the failure modes (tensile and shear failure) that the model is able to catch would be far more evident in case of more marked differences in boundary conditions. In fact, in the two cases analyzed, both geometries (albeit with some differences) would be defined as long according to Mastrodicasa (1958) since the settling portion is 600 mm long, and the specimen 8C and 12C are 400 and 600 mm high, respectively.

FIGURE 6

Figure 6. (A) Experimental and (B) Numerical results for Test 12C. [Courtesy of Prof. F. Portioli].

FIGURE 7

Figure 7. (A) LA, (B) FEM/DEM, and (C) FEM results for Test 12C.

3.1. Square Panels With Opening

After this first validation, some geometries of masonry walls with openings or façades were analyzed under settlement conditions involving a portion of the structure.

Two identical dry joints masonry walls, named Panel 1 and Panel 2, both characterized by the presence of an opening, have been considered. The panels are constituted by 55 blocks of the dimensions 50 × 100 × 50 mm³, and they are 600 mm wide, 50 mm thick, and 550 mm high; the opening dimensions are 300 × 250 mm². They differ in terms of length of the settling area, namely, 200 × 50 mm² for Panel 1 and 300 × 50 mm² for Panel 2; the effect of this feature is here investigated with the three approaches.

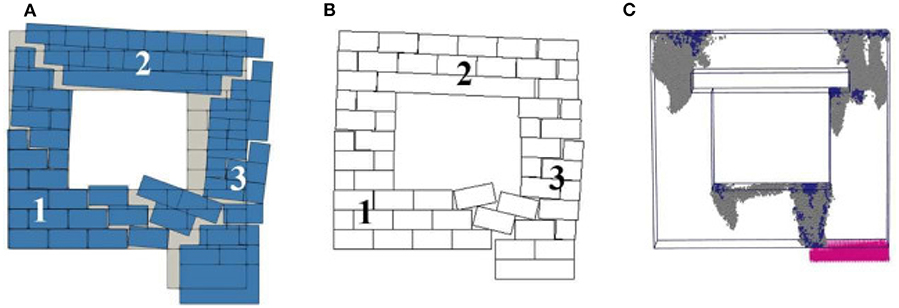
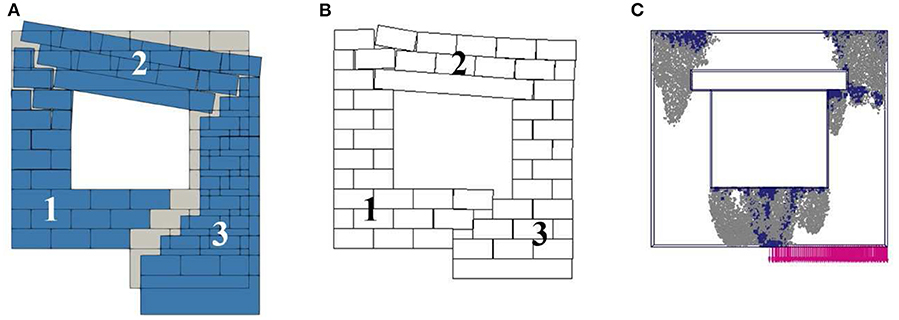
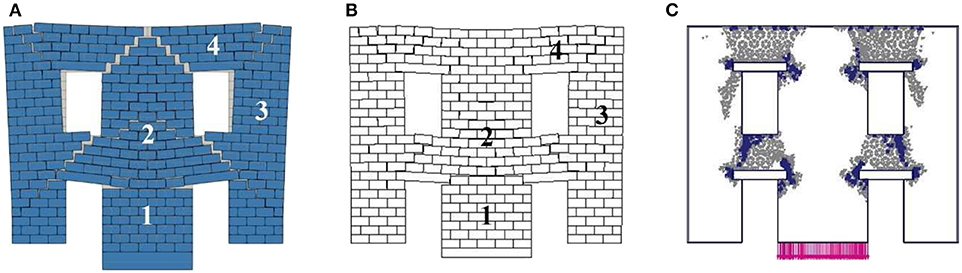
Figure 8 presents the collapse mechanism obtained with the different models, referring to Panel 1. LA, Figure 8A, and FEM/DEM, Figure 8B, show fragile behavior, with the macro-block (1) cracking into several parts, some rotating and others sliding; the portion upon the architrave (2) slides while the macro-block upon the fictitious block (3) follows its downward movement cracking into several portions, which rotate and slide. Figure 8C reports the plastic points distribution at collapse obtained with the FEM approach. Tensile failure points are located at the top of the panel and at the lower right corner of the architrave, which is modeled here as an elastic element. The configuration described by this plastic point distribution is in good agreement with the results of the LA and FEM/DEM analysis.

FIGURE 8

Figure 8. (A) LA, (B) FEM/DEM, and (C) FEM results for Panel 1 case.

Figure 9 presents the collapse mechanism of Panel 2. LA and FEM/DEM, Figures 9A,B, exhibit the formation of three distinct macro-blocks divided by “stair-stepped” cracks: a first one remains stable (1), a second one is represented by the portion upon the architrave rotates around the upper right corner of the first block, and a third portion of the wall (3) follows, without crashing, the downward movement of the fictitious block. FEM results show that the overall collapse mechanism is affected by the length of the settlement only in the supported part of the wall, while, in the top part, as in the other two approaches, cracking is located at the corners.

FIGURE 9

Figure 9. (A) LA, (B) FEM/DEM, and (C) FEM results for Panel 2 case.

3.2. Slender Panels With Opening

In the following analyses, the effect of settlement configuration is investigated together with the influence of wall height and presence of openings. Three slender panels, characterized by different height and number of openings, named Panel 3, Panel 4, and Panel 5, have been studied. The dimensions of the blocks are 50 × 100 × 50 mm³ for all the specimens, and the openings are 100 × 250 mm² wide. Panel 3 and Panel 4 are both made of 73 blocks and have the same dimensions: 400 mm width, 50 mm thickness, and 900 mm height, but they differ because of the extension of the portion involved in the settlement. The fictitious downward moving block has dimension of 100 × 150 × 50 mm³ for Panel 3 and dimension 100 × 250 × 50 mm³ for Panel 4. Panel 5 is taller and characterized by the presence of three openings. It is 400 mm wide, 100 mm thick, and 1,300 mm high and is made of 105 blocks. The dimensions of the fictitious block are the same adopted in the Panel 4 case.

For Panel 3 and Panel 4, as expected, results show that the collapse mechanism is affected by the extent of the settling portion of the structure.

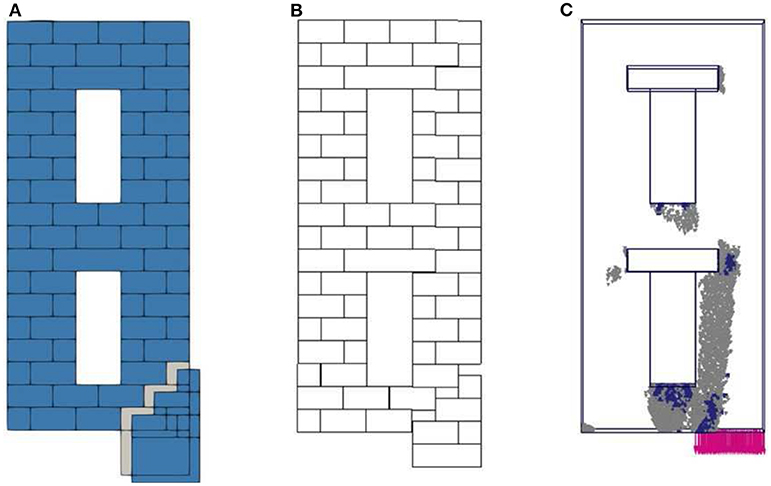
Figure 10 presents the mechanism obtained using the different models, referring to Panel 3. Results of LA and FEM, Figures 10A,B, indicate that the masonry wall is almost stable with the separation of only one little macro-block, which follows the downward movement of the settlement. The FEM simulation (Figure 10C) is in partial agreement with the results of the two previous methods since the portion affected by the settlement is larger. Nonetheless, apart from a slight localization of the shear failure point on the first floor spandrel, it can be observed that the continuum model is able to reproduce the collapse configuration in which the settlement only involves the supported portion of the wall.

FIGURE 10

Figure 10. (A) LA, (B) FEM/DEM, and (C) FEM results for Panel 3 case.

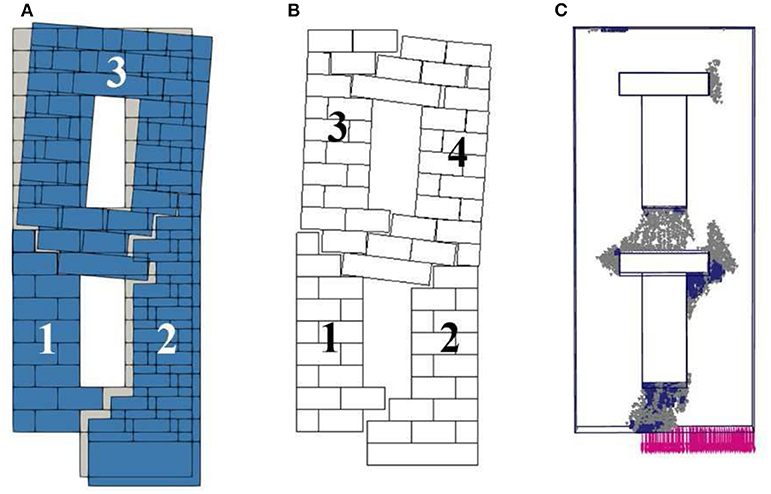
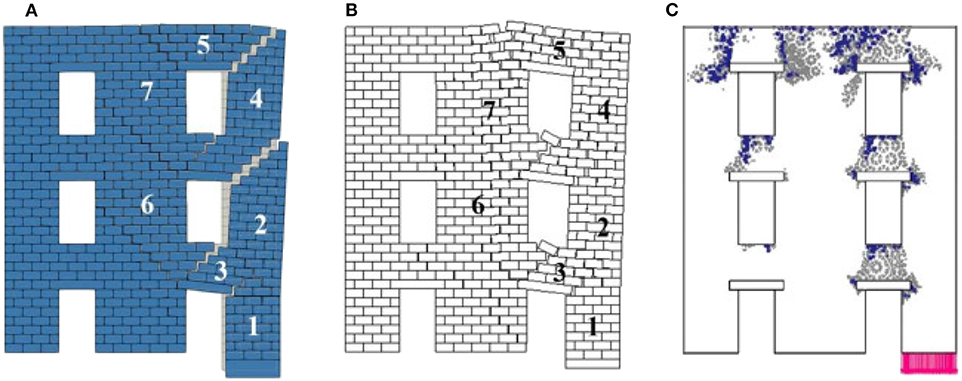
Figure 11 refers to Panel 4. The collapse mechanism obtained with LA, Figure 11A, involves three distinct macro-blocks separated by “stair-stepped” cracks: the first one (1), at ground level, remains stable, the second portion of the panel (2) follows, without crashing, the downward movement of the fictitious block, and the third one (3), which corresponds to the portion of the panel upon the architrave of the first opening, rotates without cracking around the upper left corner of the first macro-block. The FEM/DEM model, Figure 11B, produces a similar collapse, but the portion of the panel at the first floor, differently from LA results, splits in two macro-block (3) and (4) with an almost symmetric mechanism if compared with that occurring at ground level. FEM simulation results (Figure 11C) show a localization of the plastic points that reflects the kinematics described above. In fact, failure involves the bottom spandrel at the end of the supported part as well as the first floor spandrel with prevalence of shear failure mechanisms, and it is possible to see the formation of tensile failure points at the top left part of the wall according to the mechanism obtained through a FEM/DEM approach.

FIGURE 11

Figure 11. (A) LA, (B) FEM/DEM, and (C) FEM results for Panel 4 case.

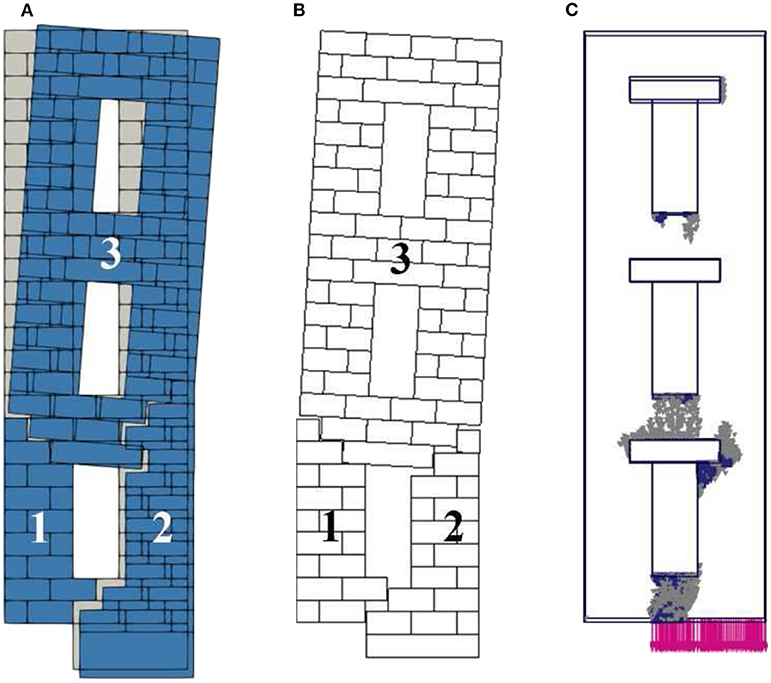
Figure 12 refers to Panel 5. The different height of the panel does not influence the collapse mechanism obtained with LA and FEM, Figures 12A,B, which results are similar to those obtained for Panel 4. In particular, we can observed the formation of three macro-blocks: portion (1) is stable, portion (2) follows the downward movement of the fictitious block, and the portion (3) acts as a unique rigid body that rotates around the lower right corner of the macro-block (2). Furthermore, the presence of two openings does not affect the collapse mechanism of this portion of the wall. Apart from the slight cracking occurring in the top spandrel, FEM results (Figure 12C) are in fair agreement with the observations reported above, and the failure mechanism described by the plastic points is very similar to Panel 4 one.

FIGURE 12

Figure 12. (A) LA, (B) FEM/DEM, and (C) FEM results for Panel 5 case.

3.3. Façades With Opening

The collapse mechanism of two-story and three-story masonry façades characterized by different geometries has been investigated. Façade 1 and Façade 2 have the same geometry and are characterized by the presence of four openings, two doors at the ground level, and two windows at the first floor which have the same dimensions (200 × 350 mm²). Each façade is 1,500 mm wide, 50 mm thick, and 1,200 mm high, and they are made up of 320 blocks with dimensions 50 × 100 × 50 mm³. The dimension of the fictitious block is 100 × 300 × 50 mm³ for both the analyzed cases. Façade 1 is affected by a lateral settlement, while Façade 2 is affected by a central settlement.

Figure 13 presents the collapse mechanism referring to Façade 1. LA, Figure 13A, and FEM/DEM, Figure 13B, present a similar mechanism with the façade being split into two distinct portions. The right side, which is involved into settlement, presents part (1), which is stable and follows the downward settlement movement, and part (2), which slightly rotates around the upper right corner of macro-block (1) without cracking, and the rigid parts (3) and (4), which are in correspondence with the architraves of the ground and first floor that both exhibit a hinging behavior. The left side of the façade, not involved in the settlement, remains stable, as expected. Interesting to notice is the presence of two diagonal cracks, starting from the upper left corner of the right door and the right window, which pass through all of the central portion of the masonry façade. The continuum FEM approach (Figure 13C) is able to reproduce the failure pattern occurring in this case, and the results show that the most affected parts of the structure are the top right and the first floor spandrel in which both tensile and shear failure occurs. Differently to what described by the two previous approaches, in the continuum FEM model, a slight damage occurs also in the supported left part, but the kinematic described in Figures 13A,B reflects in the accumulation of tensile plastic points at the top of the façades, indicating a rotation of the top spandrel.

FIGURE 13

Figure 13. (A) LA, (B) FEM/DEM and (C) FEM results for Façade 1 case.

Figure 14 shows the collapse mechanism of Façade 2. Also in this case, LA and FEM, Figures 14A,B, produce a similar collapse exhibiting an anti-symmetric mechanism with respect to the central portion of the structure. Macro-block (1), located upon the fictitious block, follows rigidly the settlement movement and consequently the part (2) moves downward, hinging and sliding, with the formation of several diagonal cracks that reach the two lateral sides of the façade. Here, a macro-block (3), including portions of the two stories, rotates without cracking around the lower right corner of the lateral stable portion of the structure and the macro-block (4), corresponding to the portion upon the architrave of the first floor windows, and hinges around the upper left corner of part (3). The symmetry of this failure mechanism is reflected in the plastic points pattern reported in Figure 14C. The downward movement of the central pier causes the shear failure of the spandrels while tensile failure is mainly concentrated at the lintel ends.

FIGURE 14

Figure 14. (A) LA, (B) FEM/DEM, and (C) FEM results for Façade 2 case.

In conclusion, a three-story structure, named Façade 3, shown in Figure 15 and subjected to a foundation settlement at the right pier, was analyzed. The structure is characterized by the presence of six openings, two doors at ground level and four windows, two for each story, all being 200 mm wide and 350 mm high. The façade is 1,500 mm wide, 50 mm thick, and 1,800 mm high. It is made of 480 blocks with dimensions 50 × 100 × 50 mm³. The dimension of the fictitious block is 100 × 300 × 50 mm³. Figure 15 presents the collapse obtained with the different models. As for previously analyzed cases, the mechanisms obtained with LA, Figure 15A, and FEM, Figure 15B, are in good agreement, being possible to identify the formation of similar macro-blocks: part (1), positioned upon the fictitious block, follows the downward movement of the settlement without cracking. The part (2) similarly follows the movement of the portion below with a slight sliding behavior and a more evident rotation around its lower right corner; part (3), corresponding to the portion of masonry upon the architrave of the right door at ground level, rotates rigidly, as does part (4), which includes a portion of masonry upon the architrave of the window at first floor and a portion of the lateral side of the façade at the second story. Macro-block (5), corresponding to the final portion of masonry upon the architrave of the window at second floor, rotates around the lower left corner of the architrave. As for other façades, the presence of diagonal cracks passing through the central portion of the façade originate from the upper right corner of door and windows. From the analysis of the collapse mechanism it is possible to notice also a little rigid rotation of the macro-block (6) and (7) identified by those diagonal cracks. The left side of structure as well as the central wall at ground level remain stable. FEM analysis results (Figure 15C) show a concentration of tensile failure points in the top part of the wall, which is compatible with the formation of block 5 reported in the LA and FEM/DEM results and its clock-wise rotation. As in the two previous cases, at collapse, only slight damage occurs in the supported part of the structure, while tensile and shear cracking affects the right portion above the downward moving pier.

FIGURE 15

Figure 15. (A) LA, (B) FEM/DEM, and (C) FEM results for Façade 3 case.

4. Concluding Remarks

This work presents the comparison of failure patterns characterizing the response of dry joints masonry walls subjected to settlements. Three numerical formulations have been adopted: a Limit Analysis as well as an FEM/DEM and FEM approach. The models have been briefly described and gone through preliminary validation, referring to experimental and numerical literature results. A comparative study has then been performed, varying the main factors affecting the response of masonry structures in the case of settlements, namely, wall dimensions, the presence of openings, and the extension of the settling area. All the models have proven to be very efficient from a computational point of view and able to reproduce the collapse mechanisms, and they can thus be considered a useful tool with which to back-analyze real-scale problems in order to identify the causes of observed crack patterns or to predict the damage distribution when a settlement is expected to occur, as in the case of underground excavation or in case of natural triggering factors. The adoption of micro-models, i.e., Limit Analysis and FEM/DEM, implies that the structure is described with its real texture, taking into account block dimensions and the internal structure of the wall. While in most continuum approaches this aspect is only marginally considered, the FEM model adopted in this study is founded on a constitutive model in which both joint orientations and block proportions are taken into account. A specific advantage of the Limit Analysis approach is the low number of parameters required to perform analysis, as friction and self-weight per unit volume are the only pieces of mechanical information needed. The same holds true for the FEM model, but the elastic parameters adopted need to be determined through a homogenization procedure in order to be assigned to the continuum. The comparisons have been made on a total set of eight walls (if the benchmark cases are excluded), and results have been compared in terms of crack pattern at collapse (LA and FEM/DEM) and failure (plastic) points (FEM) in which either tensile or shear criterion is reached. In all the analyzed cases the models are in good agreement, showing the strong influence of the extension of the settling area and of the opening distribution. The cases of Panel 4 and Panel 5 have shown an almost negligible effect of the panel height (over a certain slenderness of the structure) in the case of localized settlement.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation, to any qualified researcher.

Author Contributions

MPe and MPi developed a novel feature of ALMA 2.0 that takes into account the effect of foundation settlement and performed the analysis with the LA approach. ER and MS carried out the analysis with the FEM/DEM and FEM approach, respectively. All authors equally contributed to the common sections and took care of the description of the adopted models. PT and GF supervised the whole work during the entire process.

Funding

PT, MPi, and MPe acknowledge the support of the Italian Ministry of University and Research PRIN 2017, project No. 2017HFPKZY (B88D19001130001) and Sapienza Research Grants Progetti Medi 2017 (B83C17001440005), Progetti Grandi 2018 (B81G19000060005). ER fully acknowledges the research project funded by P.O.R. SARDEGNA F.S.E. 2014-2020 - Axis III Education and Training, Thematic Objective: 10, Specific Objective: 10.5, Action of the Partnership Agreement: 10.5.12, Call for Funding of Research Projects Year 2017 MS and GF acknowledge the financial support of the Regione Lazio SiCura 2018-2020 Research Grant.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Addessi, D., De Bellis, M., and Sacco, E. (2016). A micromechanical approach for the cosserat modeling of composites. Meccanica 51, 569–592. doi: 10.1007/s11012-015-0224-y

CrossRef Full Text | Google Scholar

Addessi, D., Sacco, E., and Di Re, P. (2018). “Multi-scale analysis of masonry structures,” in Proceedings of the International Masonry Society Conferences, 307–323.

Google Scholar

Alfano, G., and Sacco, E. (2006). Combining interface damage and friction in a cohesive-zone model. Int. J. Numer. Methods Eng. 68, 542–582. doi: 10.1002/nme.1728

CrossRef Full Text | Google Scholar

Amorosi, A., Boldini, D. D., De Felice, G., Malena, M., and Sebastianelli, M. (2014). Tunnelling-induced deformation and damage on historical masonry structures. Géotechnique 64, 118–130. doi: 10.1680/geot.13.P.032

CrossRef Full Text | Google Scholar

Baggio, C., and Trovalusci, P. (2000). Collapse behaviour of three-dimensional brick-block systems using non-linear programming. Struct. Eng. Mech. 10, 181–195. doi: 10.12989/sem.2000.10.2.181

CrossRef Full Text | Google Scholar

Baraldi, D., Cecchi, A., and Tralli, A. (2015a). Continuous and discrete models for masonry like material: a critical comparative study. Eur. J. Mech. A Solids 50, 39–58. doi: 10.1016/j.euromechsol.2014.10.007

CrossRef Full Text | Google Scholar

Baraldi, D., De Carvalho Bello, C. B., Cecchi, A., Meroi, E., and Reccia, E. (2019). Nonlinear behavior of masonry walls: FE, DE, and FE/DE models. Composites 10, 253–272. doi: 10.1615/CompMechComputApplIntJ.2019026998

CrossRef Full Text | Google Scholar

Baraldi, D., Reccia, E., Cazzani, A., and Cecchi, A. (2013). Comparative analysis of numerical discrete and finite element models: the case of in-plane loaded periodic brickwork. Composites 4, 319–344. doi: 10.1615/CompMechComputApplIntJ.v4.i4.40

CrossRef Full Text | Google Scholar

Baraldi, D., Reccia, E., and Cecchi, A. (2015b). “DEM & FEM/DEM models for laterally loaded masonry walls,” in Eccomas Proceedia ID: 3528, Conference Proceeding ID: 715 (Crete), 2144–2157.

PubMed Abstract | Google Scholar

Baraldi, D., Reccia, E., and Cecchi, A. (2018). In plane loaded masonry walls: DEM and FEM/DEM models. A critical review. Meccanica 53, 1613–1628. doi: 10.1007/s11012-017-0704-3

CrossRef Full Text | Google Scholar

Burd, H., Houlsby, G., Augarde, C., and Liu, G. (2000). Modelling tunnelling-induced settlement of masonry buildings. Proc. Inst. Civil Eng. Geotech. Eng. 143, 17–29. doi: 10.1680/geng.2000.143.1.17

CrossRef Full Text | Google Scholar

Capecchi, D., Ruta, G., and Trovalusci, P. (2011). Voigt and Poincare's mechanistic-energetic approaches to linear elasticity and suggestions for multiscale modelling. Arch. Appl. Mech. 81, 1573–1584. doi: 10.1007/s00419-010-0502-z

CrossRef Full Text | Google Scholar

Casalegno, C., Cecchi, A., Reccia, E., and Russo, S. (2013). Heterogeneous and continuous models: comparative analysis of masonry wall subjected to differential settlements. Composites 4, 187–207. doi: 10.1615/CompMechComputApplIntJ.v4.i3.10

CrossRef Full Text | Google Scholar

Cascini, L., Gagliardo, R., and Portioli, F. (2018). Liablock_3d: a software tool for collapse mechanism analysis of historic masonry structures. Int. J. Arch. Heritage 14, 1–20. doi: 10.1080/15583058.2018.1509155

CrossRef Full Text | Google Scholar

Cecchi, A., and Sab, K. (2004). A comparison between a 3D discrete model and two homogenised plate models for periodic elastic brickwork. Int. J. Solids Struct. 41, 2259–2276. doi: 10.1016/j.ijsolstr.2003.12.020

CrossRef Full Text | Google Scholar

Cecchi, A., and Sab, K. (2009). Discrete and continuous models for in plane loaded random elastic brickwork. Eur. J. Mech. A Solids 28, 610–625. doi: 10.1016/j.euromechsol.2008.10.007

CrossRef Full Text | Google Scholar

Clementi, F., Ferrante, A., Giordano, E., Dubois, F., and Lenci, S. (2019). Damage assessment of ancient masonry churches stroked by the Central Italy earthquakes of 2016 by the non-smooth contact dynamics method. Bull. Earthquake Eng. 18, 455–486. doi: 10.1007/s10518-019-00613-4

CrossRef Full Text | Google Scholar

Clementi, F., Milani, G., Ferrante, A., Valente, M., and Lenci, S. (2020). Crumbling of Amatrice clock tower during 2016 Central Italy seismic sequence: advanced numerical insights. Frattura Integr. Strut. 51, 313–335. doi: 10.3221/IGF-ESIS.51.24

CrossRef Full Text | Google Scholar

Cundall, P. (1988). Formulation of a three-dimensional distinct element model-part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. 25, 107–116.

Google Scholar

Cundall, P., Hart, R., and Itasca Consulting Group (1985). Development of Generalized 2-D and 3-D Distinct Element Programs for Modeling Jointed Rock. Tech. Rep. Sl-85-1. Washington, DC: US Army Corps of Engineers.

Google Scholar

Cundall, P., and Strack, O. (1979). Discrete numerical model for granular assemblies. Geotechnique 29, 47–65.

Google Scholar

Cundall, P. A., and Hart, R. D. (1992). Numerical modelling of discontinua. Eng. Comput. 9, 101–113.

Google Scholar

D'Altri, A., Sarhosis, V., Milani, G., Rots, J., Cattari, S., Lagomarsino, S., et al. (2019). Modeling strategies for the computational analysis of unreinforced masonry structures: review and classification. Arch. Comput. Methods Eng. doi: 10.1007/s11831-019-09351-x. [Epub ahead of print].

CrossRef Full Text | Google Scholar

De Buhan, P., and de Felice, G. (1997). A homogenization approach to the ultimate strength of brick masonry. J. Mech. Phys. Solids 45, 1085–1104.

Google Scholar

de Felice, G., Amorosi, A., and Malena, M. (2010). Elasto-plastic analysis of block structures through a homogenization method. Int. J. Numer. Anal. Methods Geomechan. 34, 221–247. doi: 10.1002/nag.799

CrossRef Full Text | Google Scholar

de Felice, G., and Malena, M. (2019). Failure pattern prediction in masonry. J. Mech. Mater. Struct. 14, 663–682. doi: 10.2140/jomms.2019.14.663

CrossRef Full Text | Google Scholar

DeJong, M. J. (2016). “Settlement effects on masonry structures,” in Structural Analysis of Historical Constructions: Anamnesis, Diagnosis, Therapy, Controls - Proceedings of the 10th International Conference on Structural Analysis of Historical Constructions, SAHC 2016 (Leuven), 449–456.

Google Scholar

Del Piero, G. (1989). Constitutive equation and compatibility of the external loads for linear elastic masonry-like materials. Meccanica 24, 150–162. doi: 10.1007/BF01559418

CrossRef Full Text | Google Scholar

Fantuzzi, N., Trovalusci, P., and Dharasura, S. (2019). Mechanical behavior of anisotropic composite materials as micropolar continua. Front. Mater. 6:59. doi: 10.3389/fmats.2019.00059

CrossRef Full Text | Google Scholar

Fichera, G. (1964). Problemi Elastici con Vincoli Unilaterali: il Problema di Signorini con Ambigue Condizioni al Contorno. Atti dell'Accademia Nazionale dei Lincei, VIII(VII).

Google Scholar

Gambarotta, L., and Lagomarsino, S. (1997). Damage models for the seismic response of brick masonry shear walls. Part II: the continuum model and its applications. Earthq. Eng. Struct. Dyn. 26, 441–462. doi: 10.1002/(SICI)1096-9845(199704)26:4<441::AID-EQE651>3.0.CO;2-0

CrossRef Full Text | Google Scholar

Greco, F., Leonetti, L., Luciano, R., and Nevone Blasi, P. (2016). An adaptive multiscale strategy for the damage analysis of masonry modeled as a composite material. Composite Struct. 153, 972–988. doi: 10.1016/j.compstruct.2016.06.066

CrossRef Full Text | Google Scholar

Greco, F., Leonetti, L., Luciano, R., and Trovalusci, P. (2017). Multiscale failure analysis of periodic masonry structures with traditional and fiber-reinforced mortar joints. Composites Part B Eng. 118, 75–95. doi: 10.1016/j.compositesb.2017.03.004

CrossRef Full Text | Google Scholar

Landolfo, R., Gagliardo, R., Cascini, L., Portioli, F., Malena, M., Tomaselli, G., and de Felice, G. (2020). Rigid block and finite element analysis of settlement-induced failure mechanisms in historic masonry walls. Frattura Integr Strut. 51, 517–533. doi: 10.3221/IGF-ESIS.51.39

CrossRef Full Text | Google Scholar

Lasciarrea, W. G., Amorosi, A., Boldini, D., de Felice, G., and Malena, M. (2019). Jointed masonry M: a constitutive law for 3D soil-structure interaction analysis. Eng. Struct. 201:109803. doi: 10.1016/j.engstruct.2019.109803

CrossRef Full Text | Google Scholar

Lemos, J. (2007). Discrete element modeling of masonry structures. Int. J. Architect. Heritage 1, 190–213. doi: 10.1080/15583050601176868

CrossRef Full Text | Google Scholar

Leonetti, L., Fantuzzi, N., Trovalusci, P., and Tornabene, F. (2019). Scale effects in orthotropic composite assemblies as micropolar continua: a comparison between weakand strong-form finite element solutions. Materials 12:758. doi: 10.3390/ma12050758

PubMed Abstract | CrossRef Full Text | Google Scholar

Leonetti, L., Greco, F., Trovalusci, P., Luciano, R., and Masiani, R. (2018). A multiscale damage analysis of periodic composites using a couple-stress/Cauchy multidomain model: application to masonry structures. Composites Part B Eng. 141, 50–59. doi: 10.1016/j.compositesb.2017.12.025

CrossRef Full Text | Google Scholar

Lotfi, H., and Shing, P. (1994). Interface model applied to fracture of masonry structures. J. Struct. Eng. 120, 63–80. doi: 10.1061/(ASCE)0733-9445(1994)120:1(63)

CrossRef Full Text | Google Scholar

Lourenço, P., and Rots, J. (1997). Multisurface interface model for analysis of masonry structures. J. Eng. Mech. 123, 660–668. doi: 10.1061/(ASCE)0733-9399(1997)123:7(660)

CrossRef Full Text | Google Scholar

Mahabadi, O., Lisjak, A., Munjiza, A., and Grasselli, G. (2012). Y-Geo: new combined finite-discrete element numerical code for geomechanical applications. Int. J. Geomech. 12, 676–688. doi: 10.1061/(ASCE)GM.1943-5622.0000216

CrossRef Full Text | Google Scholar

Mahabadi, O. K., Lisjak, A., Grasselli, G., Lukas, T., and Munjiza, A. (2010). “Numerical modelling of a triaxial test of homogeneous rocks using the combined finite-discrete element method,” in Rock Mechanics in Civil and Environmental Engineering - Proceedings of the European Rock Mechanics Symposium, EUROCK 2010 (Lausanne), 173–176.

Google Scholar

Malena, M., Portioli, F., Gagliardo, R., Tomaselli, G., Cascini, L., and de Felice, G. (2019). Collapse mechanism analysis of historic masonry structures subjected to lateral loads: a comparison between continuous and discrete models. Comput. Struct. 220, 14–31. doi: 10.1016/j.compstruc.2019.04.005

CrossRef Full Text | Google Scholar

Masiani, R., and Trovalusci, P. (1996). Cosserat and Cauchy materials as continuum models of brick masonry. Meccanica 31, 421–432. doi: 10.1007/BF00429930

CrossRef Full Text | Google Scholar

Mastrodicasa, S. (1958). Dissesti Statici Delle Strutture Edilizie. Diagnosi e Consolidamento. Milano: HOEPLI, 876.

Google Scholar

Milani, G. (2011). Simple lower bound limit analysis homogenization model for in- and out-of-plane loaded masonry walls. Constr. Build. Mater. 25, 4426–4443. doi: 10.1016/j.conbuildmat.2011.01.012

CrossRef Full Text | Google Scholar

Milani, G., and Taliercio, A. (2016). Limit analysis of transversally loaded masonry walls using an innovative macroscopic strength criterion. Int. J. Solids Struct. 81, 274–293. doi: 10.1016/j.ijsolstr.2015.12.004

CrossRef Full Text | Google Scholar

Munjiza, A. (2004). The Combined Finite-Discrete Element Method. Chichester: John Wiley & Sons. 333. doi: 10.1002/0470020180

CrossRef Full Text | Google Scholar

Oliveira, D., and Lourenço, P. (2004). Implementation and validation of a constitutive model for the cyclic behaviour of interface elements. Comput. Struct. 82, 1451–1461. doi: 10.1016/j.compstruc.2004.03.041

CrossRef Full Text | Google Scholar

Pau, A., and Trovalusci, P. (2012). Block masonry as equivalent micropolar continua: the role of relative rotations. Acta Mech. 223, 1455–1471. doi: 10.1007/s00707-012-0662-8

CrossRef Full Text | Google Scholar

Pavlovic, M., Reccia, E., and Cecchi, A. (2016). A procedure to investigate the collapse behavior of masonry domes: some meaningful cases. Int. J. Architect. Heritage 10, 67–83. doi: 10.1080/15583058.2014.951797

CrossRef Full Text | Google Scholar

Pepe, M. (2020). Numerical modeling for masonry: ALMA 2.0, A computational code for the limit analysis of historical masonry structures (Ph.D. thesis). Sapienza University of Rome, Rome, Italy.

Google Scholar

Pepe, M., Pingaro, M., Reccia, E., and Trovalusci, P. (2019a). “Micromodels for the in-plane failure analysis of masonry walls with friction: limit analysis and dem-fem/dem approaches,” in AIMETA 2019 XXIV conference. The Italian Association of Theoretical and Applied Mechanics (Rome).

Google Scholar

Pepe, M., Pingaro, M., Trovalusci, P., Reccia, E., and Leonetti, L. (2019b). Micromodels for the in-plane failure analysis of masonry walls: limit analysis, FEM and FEM/DEM approaches. Frattura Integr. Strut. 14, 504–516. doi: 10.3221/IGF-ESIS.51.38

CrossRef Full Text | Google Scholar

Pietruszczak, S., and Niu, X. (1992). A mathematical description of macroscopic behaviour of brick masonry. Int. J. Solids Struct. 29, 531–546. doi: 10.1016/0020-7683(92)90052-U

CrossRef Full Text | Google Scholar

Portioli, F., Casapulla, C., Gilbert, M., and Cascini, L. (2014). Limit analysis of 3D masonry block structures with non-associative frictional joints using cone programming. Comput. Struct. 143, 108–121. doi: 10.1016/j.compstruc.2014.07.010

CrossRef Full Text | Google Scholar

Portioli, F., and Cascini, L. (2016). Assessment of masonry structures subjected to foundation settlements using rigid block limit analysis. Eng. Struct. 113, 347–361. doi: 10.1016/j.engstruct.2016.02.002

CrossRef Full Text | Google Scholar

Reccia, E., Cazzani, A., and Cecchi, A. (2012). FEM-DEM modeling for out-of-plane loaded masonry panels: a limit analysis approach. Open Civil Eng. J. 6, 231–238. doi: 10.2174/1874149501206010231

CrossRef Full Text | Google Scholar

Reccia, E., Cecchi, A., and Milani, G. (2016). “A finite element-discrete element approach for the analysis of the venice trans-lagoon railway bridge,” Civil-Comp Proceedings (Stirlingshire), 110.

Google Scholar

Reccia, E., Leonetti, L., Trovalusci, P., and Cecchi, A. (2018). A multiscale/multidomain model for the failure analysis of masonry walls: a validation with a combined FEM/DEM approach. Int. J. Multiscale Comput. Eng. 16, 325–343. doi: 10.1615/IntJMultCompEng.2018026988

CrossRef Full Text | Google Scholar

Roca, P., Molins, C., and Marí, A. R. (2005). Strength capacity of masonry wall structures by the equivalent frame method. J. Struct. Eng. 131, 1601–1610. doi: 10.1061/(ASCE)0733-9445(2005)131:10(1601)

CrossRef Full Text | Google Scholar

Sangirardi, M., Liberatore, D., and Addessi, D. (2019a). Equivalent frame modelling of masonry walls based on plasticity and damage. Int. J. Architect. Heritage 13, 1098–1109. doi: 10.1080/15583058.2019.1645240

CrossRef Full Text | Google Scholar

Sangirardi, M., Malena, M., and deFelice, G. (2019b). “Settlement-induced crack pattern prediction through the jointed masonry model,” in AIMETA 2019 XXIV conference. The Italian Association of Theoretical and Applied Mechanics (Rome).

Google Scholar

Serpieri, R., Albarella, M., Alfano, G., and Sacco, E. (2017). Analysis of failure in quasi-brittle materials by 3D multiplane cohesive zone models combining damage, friction and interlocking. Proc. Struct. Integr. 3, 441–449. doi: 10.1016/j.prostr.2017.04.066

CrossRef Full Text | Google Scholar

Smoljanović, H., and Željana Nikolić, Živaljić, N. (2015). A combined finite-discrete numerical model for analysis of masonry structures. Eng. Fract. Mech. 136, 1–14. doi: 10.1016/j.engfracmech.2015.02.006

CrossRef Full Text | Google Scholar

Smoljanović, H., Živaljić, N., and Željana Nikolić (2013). A combined finite-discrete element analysis of dry stone masonry structures. Eng. Struct. 52, 89–100. doi: 10.1016/j.engstruct.2013.02.010

CrossRef Full Text | Google Scholar

Smoljanović, H., Živaljić, N., and Željana Nikolić Munjiza, A. (2017). Numerical analysis of 3d dry-stone masonry structures by combined finite-discrete element method. Int. J. Solids Struct. 136–137, 150–157. doi: 10.1016/j.ijsolstr.2017.12.012

CrossRef Full Text | Google Scholar

Trovalusci, P., and Masiani, R. (2003). Non-linear micropolar and classical continua for anisotropic discontinous materials. Int. J. Solids Struct. 40, 1281–1297. doi: 10.1016/S0020-7683(02)00584-X

CrossRef Full Text | Google Scholar

Trovalusci, P., Varano, V., and Rega, G. (2010). A generalized continuum formulation for composite microcracked materials and wave propagation in a bar. J. Appl. Mech. Trans. ASME 77:061002. doi: 10.1115/1.4001639

CrossRef Full Text | Google Scholar

Zampieri, P., Amoroso, M., and Pellegrino, C. (2019). The masonry buttressed arch on spreading support. Structures 20, 226–236. doi: 10.1016/j.istruc.2019.03.008

CrossRef Full Text | Google Scholar