Seismic Performance Evaluation of Shape Memory Alloy (SMA) Reinforced Concrete Bridge Bents Under Long-Duration Motion

Introduction

Recent devastating earthquakes around the world were of high magnitude as well as lasted for a longer period of time. For instance, the approximate duration of the magnitude (Mw) 9.0 Tohoku earthquake in Japan (2011), the Mw 8.8 Chile earthquake (2010), and the Mw 7.9 Wenchuan Earthquake in China (2008) was 300, 200, and 180 s, respectively. An increasing number of experimental and numerical studies conducted on structural response under long-duration motions reflects the increasing attention to this topic. These include experimental investigation of bridge piers (Ou et al., 2014; Mohammed, 2016; Lopez et al., 2020), numerical investigation on concrete frames (Ruiz-Garcia, 2010; Raghunandan and Liel, 2013; Belejo et al., 2017), steel frames (Chandramohan et al., 2016; Barbosa et al., 2017), concrete dams (Zhang et al., 2013; Wang et al., 2015), timber frames (Pan et al., 2018), seismically isolated bridges (Hassan and Billah, 2020), and masonry structures (Bommer et al., 2004). Kempton and Stewart (2006) identified ground motion duration to be a significant parameter for structures susceptible to strength degradation under cyclic loading. While most of the researchers reported ground motion duration to have a detrimental effect on structural performance, few studies reported no meaningful impact arising from the duration of ground motion. The mixed conclusions drawn from past studies can be attributed to the consideration of different types of structures, strategies for ground motion selection, adopted modeling techniques, and lack of adequate historical long-duration motions.

Following the 2008 China (Wenchuan) Earthquake, Han et al. (2009) surveyed 320 damaged bridges and reported that 39% of surveyed bridges experienced moderate damage while 14% bridges suffered severe damage. Van de Lindt and Goh (2004) concluded that long-duration motions have a significant effect on structural reliability and should be considered in performance-based design. Ruiz-Garcia (2010) found that long-duration motion imparts higher residual drift demand in the upper stories of flexible frames. Chandramohan et al. (2016) reported the detrimental effect of long-duration motions on the collapse performance of a bridge pier and steel moment frame. Ou et al. (2014) tested several concrete bridge piers under long-duration motions and reported its effect on column strength degradation as a result of longitudinal bar buckling resulting from the repeated cyclic loading. Barbosa et al. (2017) found that with increasing spectral intensities, long-duration motions increase the drift demand in steel frames which was very minimal for low values of spectral acceleration.

Under any seismic excitation, the bridge piers are expected to experience more inelastic deformation than any other component. Increased number of load reversals during a long-duration motion can step up the damage significantly through degradation of strength and stiffness. Shake table tests conducted on substandard bridge columns by Lopez et al. (2020) showed that long-duration motions cause significant damage to bridge piers compared to the short duration motions. Observations from the past earthquakes showed the susceptibility of conventional bridge piers experiencing large residual drift. Under long-duration motions, conventional bridges might experience higher residual deformation as they are subjected to a large number of loading cycles. Lopez et al. (2020) also observed larger residual crack widths in bridge piers when subjected to long-duration motions. In this context, self-centering bridge piers have gained popularity due to their ability to return to their original position even after a strong earthquake excitation (Kwan and Billington, 2003; Saiidi et al., 2009; Billah and Alam, 2015; Sideris et al., 2015). Researchers have used advanced materials in the critical regions (i.e., plastic hinge) of bridge piers to limit the residual drift and to control the damage. These include Ni-Ti SMA and Engineered Cementitious Composite (ECC) (Saiidi et al., 2009), Cu-based SMA and ECC (Hosseini et al., 2015), Iron-based SMA and conventional concrete (Billah and Alam, 2018), Ni-Ti SMA, ECC, and elastomeric pad (Cruz Noguez and Saiidi, 2012), and coupled SMA-Steel reinforcement (Xiang et al., 2020). Alternatively, unbonded post-tensioned RC piers have been used by different researchers (Kwan and Billington, 2003; Sideris et al., 2015) as an effective strategy to control the residual deformation and improve the post-earthquake functionality of bridges. All past applications of SMA as longitudinal reinforcement in bridge piers have shown its ability in reducing the residual deformation and improving the overall seismic performance of the bridge pier.

Bridge bents represent a significant element in a bridge which are designed to have sufficient deformation capacity and behave in a ductile manner. Multi-column bridge bents are very common for highway bridges that support the superstructure. All past studies on structural applications of SMA rebar in bridges have been dedicated to improving the seismic response and performance of bridge piers only. However, the response of a multi-column bridge bent can be significantly different from a single, cantilever pier under seismic excitations. No study has been dedicated to understanding the effect of using SMA rebar on the dynamic response of bridge bents under long-duration motions. The objective of this study is to numerically examine the influence of SMA rebar on the seismic behavior of a multi-column bent under long-duration ground motions and compare the results with the conventional steel-reinforced bridge bent. To investigate the duration effect, the SMA-RC and Steel-RC bents are also analyzed under spectrally equivalent non-pulse type short duration motions. Bridge bents with three different longitudinal reinforcement arrangements are considered in this study, such as (a) SMA-B: SMA only in the bottom plastic hinge region of the pier and regular Steel bar in the remaining portion, (b) SMA-B-T: SMA in the bottom and top plastic hinge region of the pier and regular Steel bar in the remaining portion, and (c) Steel-RC: bridge bent reinforced with steel rebar. Using a pair of forty long-duration and spectrally equivalent short duration motions, the performance of the SMA reinforced bridge bents are evaluated and compared with the regular Steel-RC bent. The performance of the bridge bents is compared in terms of maximum drift, residual drift, and performance criteria, such as yielding of reinforcement, spalling of cover concrete, and crushing of core concrete. The outcome of this study is expected to aid in identifying the relative effectiveness of SMA reinforced bridge bents from a performance-based perspective under long-duration ground motions.

Duration of Ground Motion

To study the ground motion duration effect on structures, it is important to define the duration of strong motion. Since different definitions hold different assumptions, significant variations can be expected in the computed strong-motion duration (Lin et al., 2010). Thirty definitions of strong-motion duration were studied by Bommer and Martinez-Pereira (1999). Among different duration definitions, significant duration (t_D5–95) (Trifunac and Brady, 1975), bracketed duration (D_B) (Page et al., 1972), Cumulative Absolute Velocity (CAV) (Reed and Kassawara, 1990), arias intensity (AI) (Arias, 1970), and dimensionless duration metric (I_D) (Cosenza and Manfredi, 1997) are repeatedly used by researchers for seismic performance evaluation of structures. The use of different definitions of strong motion is structure-specific and depends on the purpose of the study. Among different definitions, many researchers (Iervolino et al., 2006; Raghunandan and Liel, 2013; Chandramohan et al., 2016) recommended and used 5–95% significant duration (t_D5–95) as the defining parameter. Moreover, Bommer and Martinez-Pereira (1999) reported that significant duration is independent of ground motion scaling and comparatively stable in terms of start and end threshold definitions. Chandramohan et al. (2016) reported that 5–95% significant duration (t_D5–95) is better suited for hazard characterization and selection of ground motion. As recommended by past studies and its effectiveness in capturing the duration effect, significant duration (t_D5–95) is considered in this study for defining the ground motion duration. Figure 1A compares the acceleration time histories of two ground motions with similar intensities (PGA) having different significant durations. The significant duration of the two ground motions is also shown in the figure. In Figure 1B the % of arias intensity (AI) of the two ground motions is shown which illustrates that the energy accumulation in long-duration motion occurs over a long period of time.

FIGURE 1

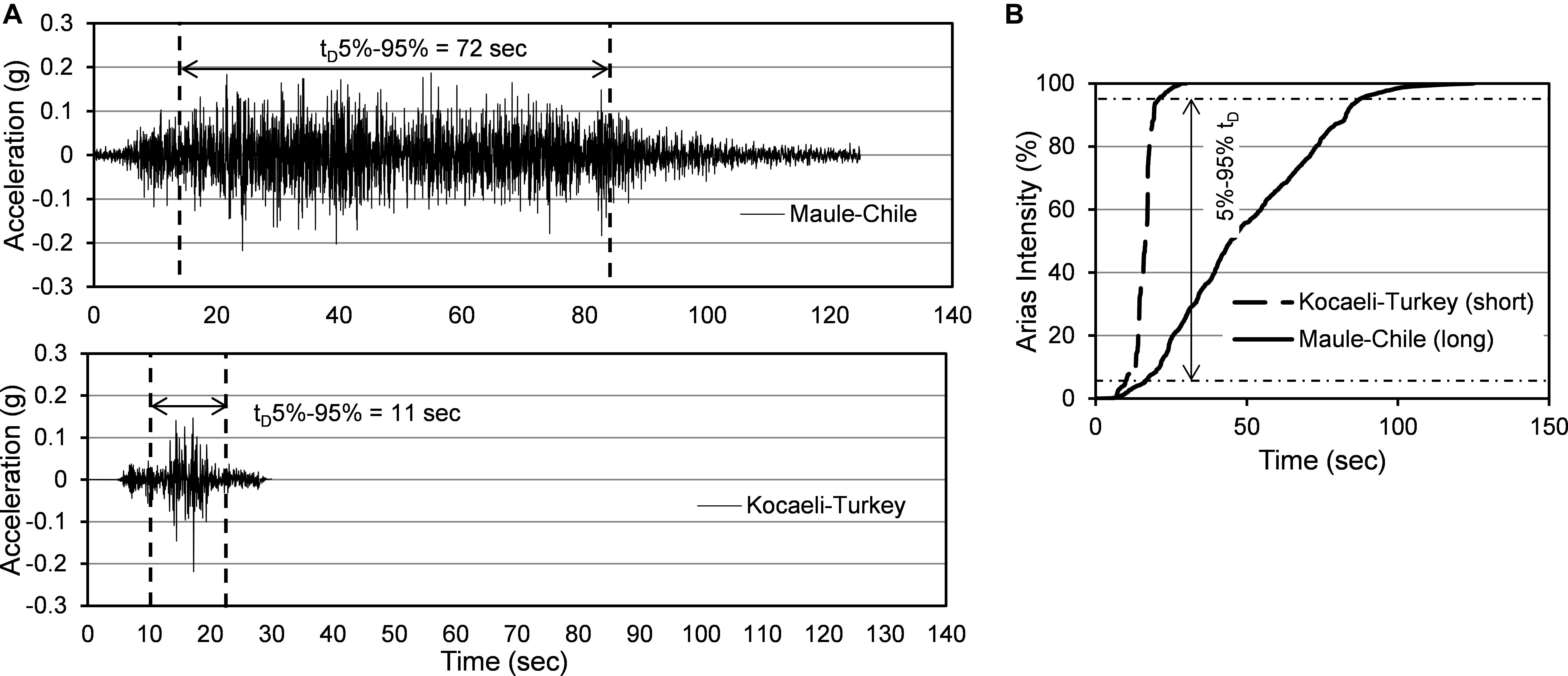
Figure 1. (A) Acceleration time history and (B) Arias Intensity of a long duration and short duration motion having similar PGA.

Ground Motion Selection

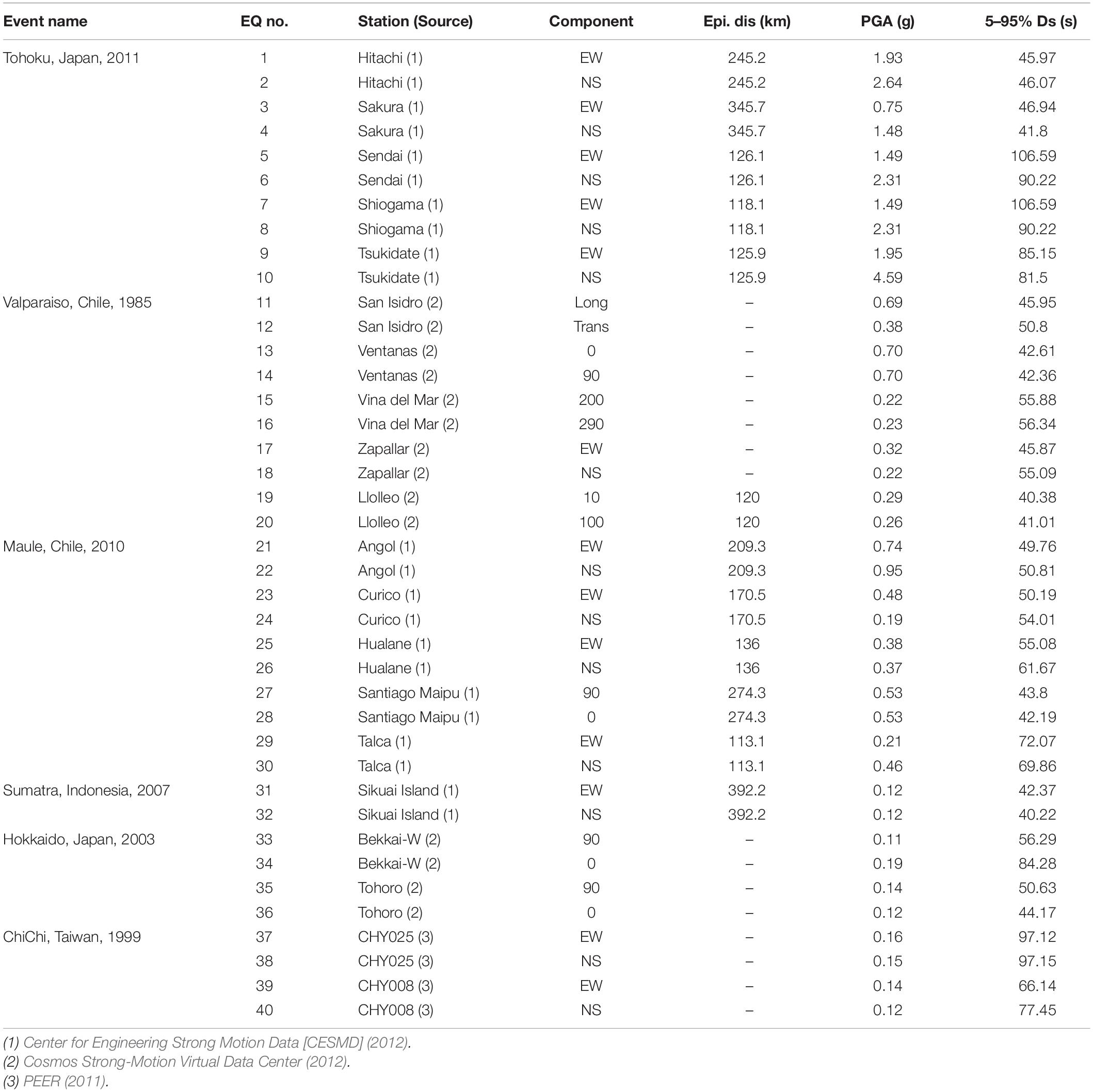
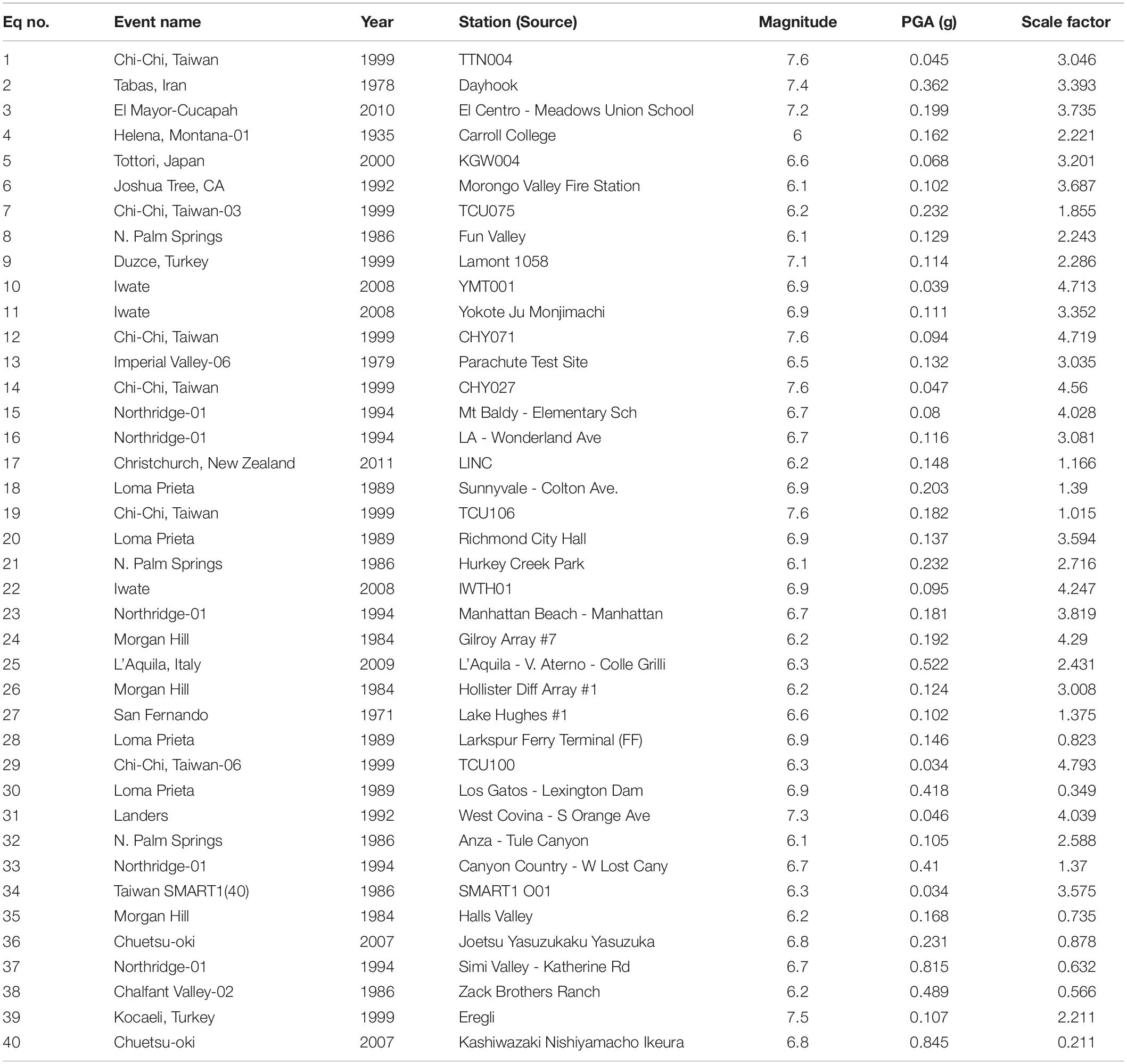
To quantify the effect of the duration of ground motions, 40 pairs of spectrally equivalent long and short duration record sets are assembled according to the procedure proposed by Chandramohan et al. (2016). First, a set of 100 long-duration motions are obtained from the world wide database of past earthquakes (PEER, COSMOC, CESMD). Records with significant duration (t_D5–95) >40 s are considered as long-duration motions. Out of those 100 records, 62 records matched these criteria resulting a geometric mean t_D5–95 of 64 s. This subset of 62 long-duration records has a PGA >0.1 g and PGV >10 cm/s. All these ground motions represent different historical events, such as the mega quakes of Chile (1985, 2010), Taiwan (1999), Japan (2003, 2010), and Indonesia (2007). Next, 100 short duration motions (non-pulse type) are obtained from the PEER NGA ground motion database (2011). Records with significant duration (t_D5–95) <40 s and epicentral distance >15 km are considered as short duration motions. To achieve spectral equivalency of the short and long-duration motions, matching is performed within the period range of 0.05–4.0 s. The records of the short set are scaled in such a way that each short record matches the 5% acceleration response spectrum of one long-duration record within the period range of interest. To avoid bias in scaling, a scale factor of 5 is considered as the maximum. This also allowed to minimize the sum of squared error differences of the 5% acceleration response spectrum between the short and long record sets. To avoid event bias, a maximum of 10 records (5 pairs) were selected from each event. This record selection process provided 40 pairs of spectrally equivalent long and short duration record sets. This matching process allowed eliminating dissimilarities in spectral shape between a record pair thus allowing to consider duration as the single factor responsible for differences in seismic response. The information pertaining to the selected long and short duration record sets are summarized in Tables 1, 2, respectively. The distribution of significant durations in the selected 40 pairs of ground motions are shown in Figure 2. A comparison of the acceleration time histories and 5% acceleration response spectrum of two spectrally equivalent long and short duration motions are depicted in Figure 3.

TABLE 1

Table 1. List of long duration motions.

TABLE 2

Table 2. List of spectrally equivalent short duration motions.

FIGURE 2

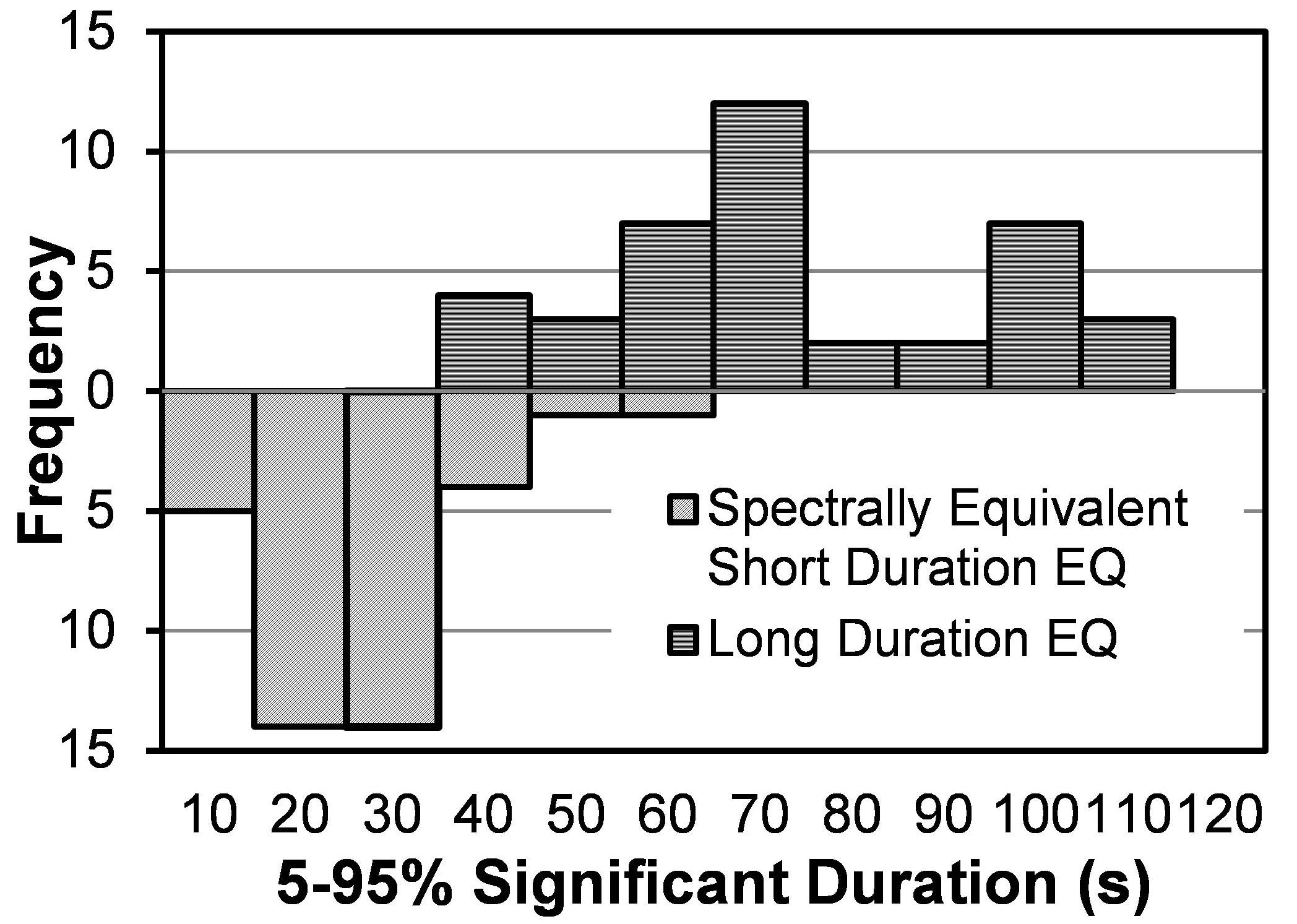
Figure 2. Distribution of ground motion duration in the selected long and spectrally equivalent short duration set.

FIGURE 3

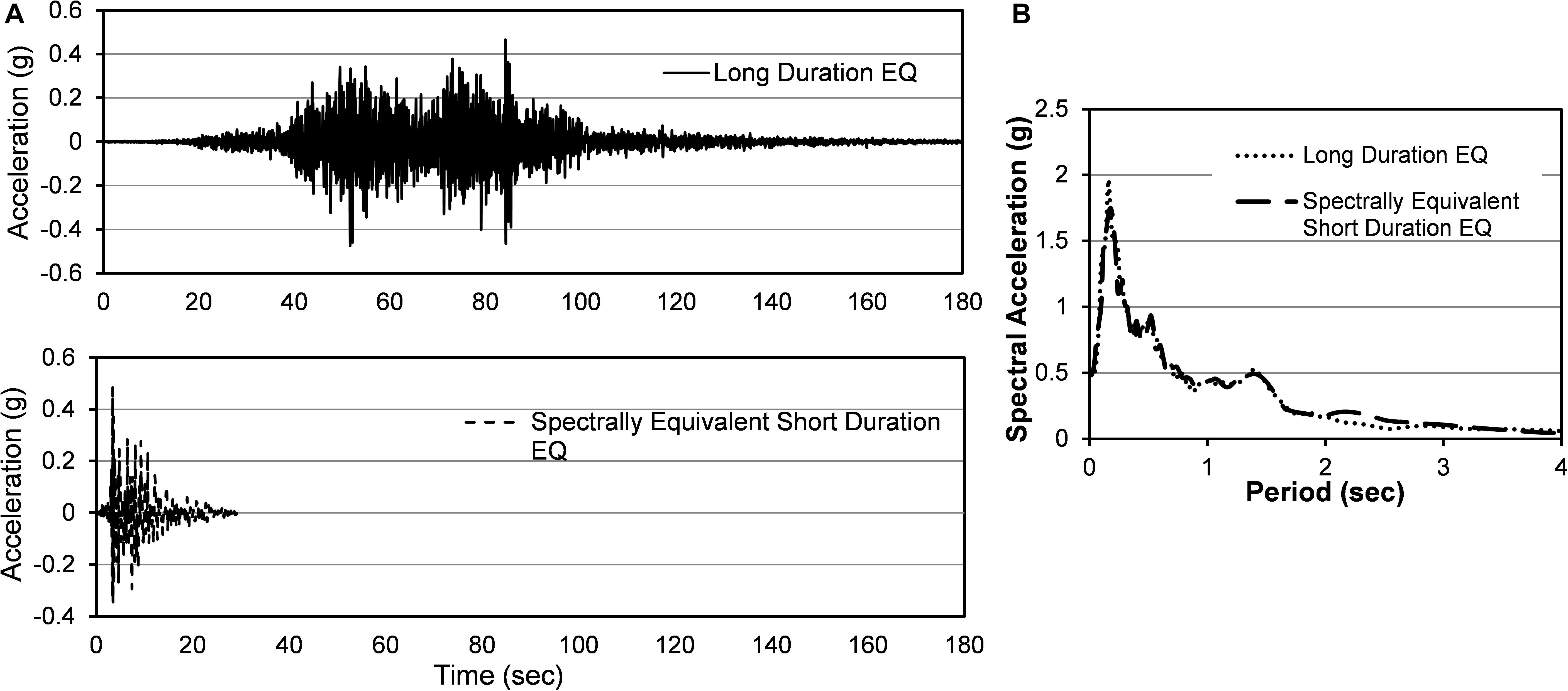
Figure 3. (A) Acceleration time history and (B) response spectra of a long duration and spectrally equivalent short duration motion.

Design and Geometry of Bridge Bent

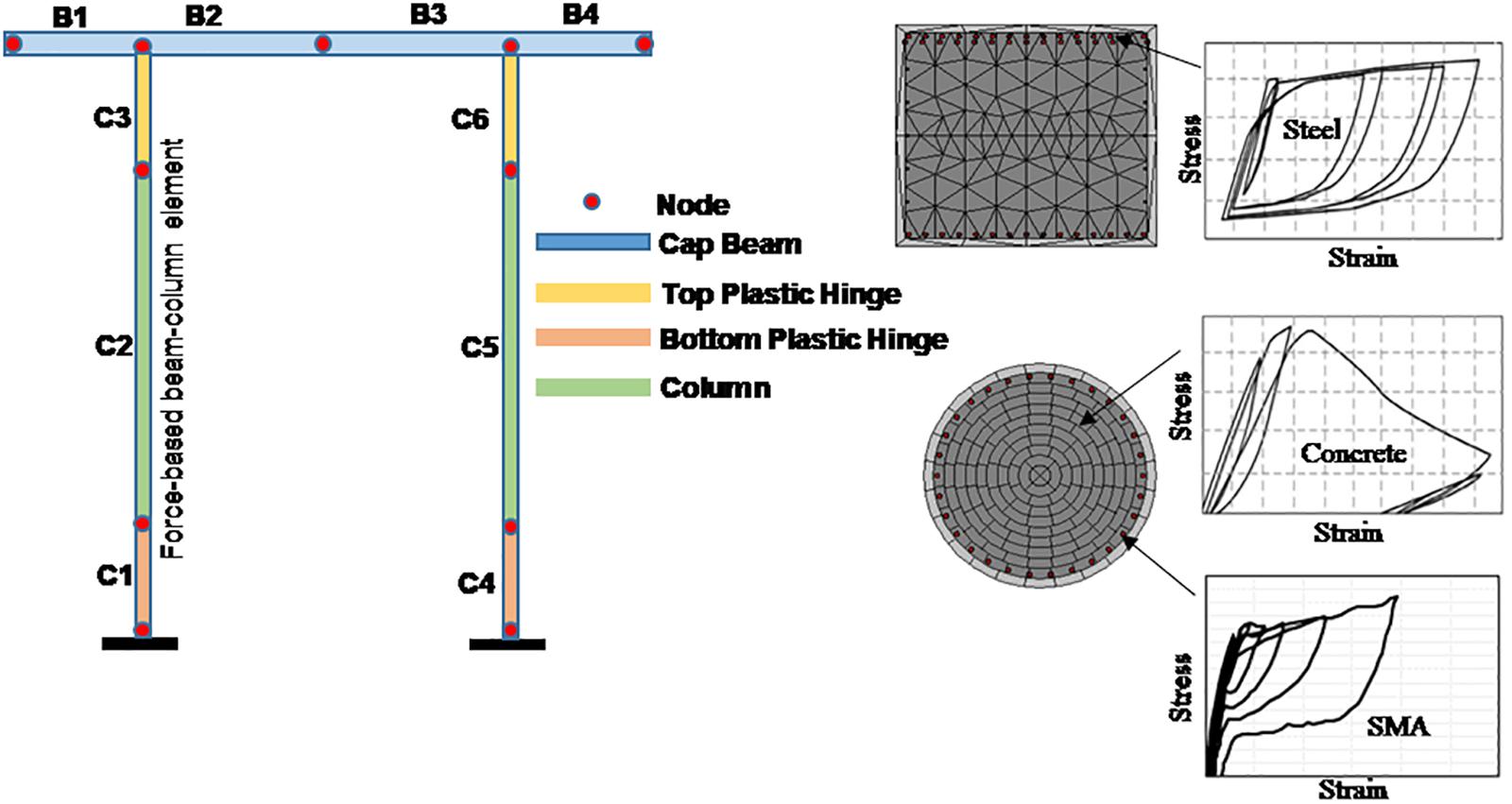
The bridge bent considered in this study consists of two circular columns connected by a rectangular bent cap. A simple geometric configuration is considered here so that the dynamic behavior is mainly governed by the fundamental mode. The two-column bent considered here constitutes the substructure of a multi-span steel girder bridge located in Vancouver, BC, Canada. The bent is designed following the seismic design guideline outlined in the Canadian Highway Bridge Design Code (Canadian Standard Association [CSA], 2019). Figure 4 shows the details of the bridge bent. The bent cap is a rectangular one (1,600 mm × 1,800 mm) reinforced with 28–30 M bars at the top, 14–30 M bars at the bottom, and 5–20 M bars equally spaced on each of the two sides (Figure 4B). Three different configurations of pier longitudinal reinforcement are considered here. The 1.5 m circular bridge columns have 28 longitudinal rebars which consisted of 30 M steel (diameter 29.9 mm) rebar or SMA30 (diameter 31 mm) bars in the plastic hinge region (Figure 4C). Here, the top and bottom plastic hinge zones of the columns are reinforced with Ni-Ti SMA and regular steel rebar is used elsewhere. The transverse reinforcement consists of 15 M spiral at 65 and 150 mm pitch within and outside the plastic hinge, respectively. The potential plastic hinge length of the SMA reinforced columns is estimated using the analytical formula proposed by Billah and Alam (2016c) (Eq. 1):

$$\frac{L_p}{d}=1.05+\left(0.25\frac{P}{f_c^{{}^{\prime }}{A}_g}\right)+\left(0.08\frac{L}{d}\right)+\left(0.0002f_{y-\mathit{SMA}}\right)-\left(0.16{\mathrm{\rho }}_l\right)-\left(0.019f_c^{{}^{\prime }}\right)-\left(0.24{\mathrm{\rho }}_s\right)(1)$$

FIGURE 4

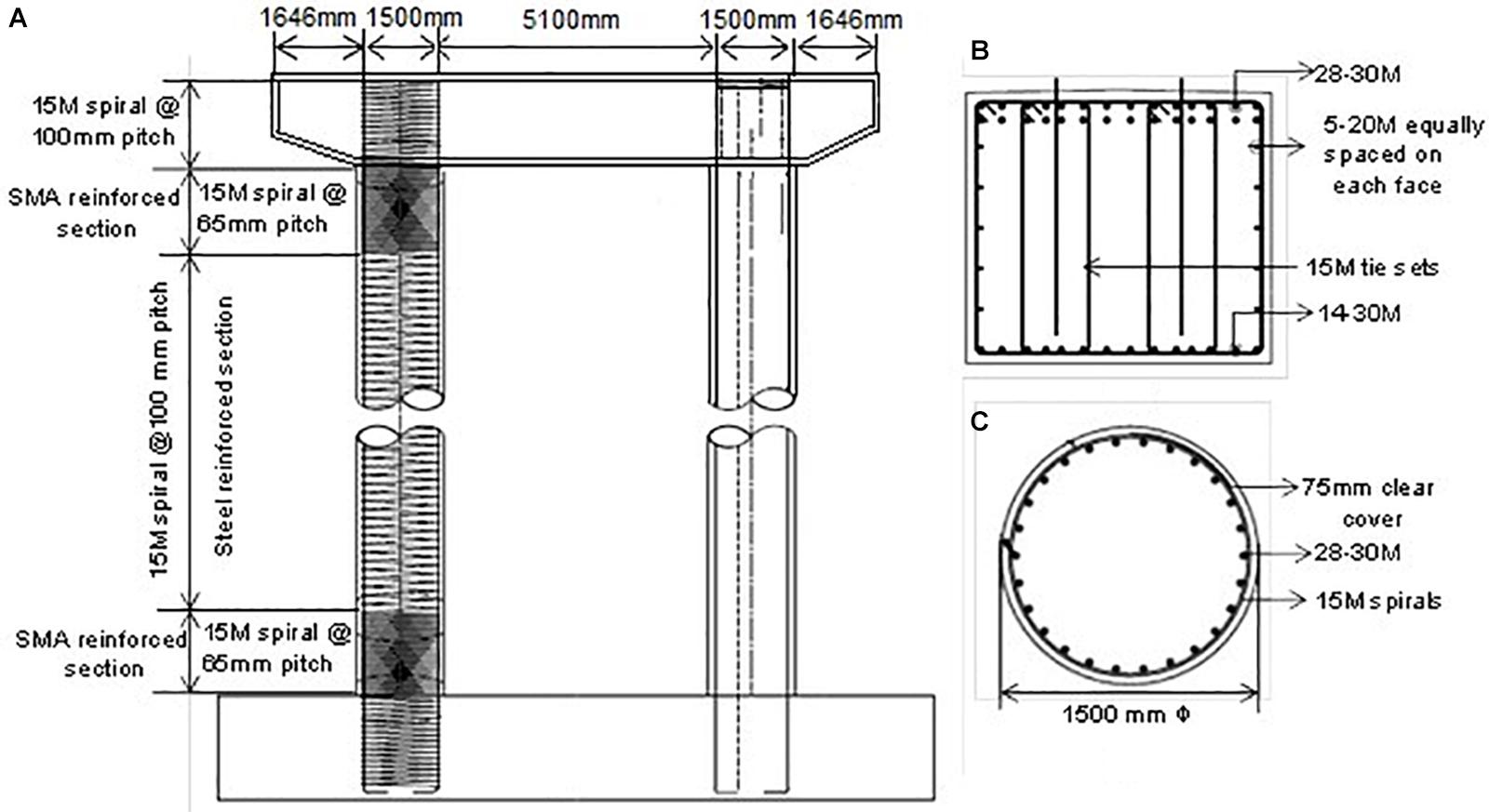
Figure 4. (A) Bent elevation and reinforcement arrangement, (B) bent cap section, (C) pier cross section.

where, L_p is the plastic hinge length, d is the diameter of the pier, L/d is the aspect ratio, P/f_c’A_g is the axial load ratio, ρ_l = longitudinal reinforcement ratio, ρ_s = transverse reinforcement ratio, f_y–SMA = yield strength of SMA rebar and f_c’ = concrete compressive strength.

The calculated plastic hinge length of the 15 m long piers are found to be 1,940 mm. On the other hand, the plastic hinge length in the steel-RC bent is calculated as 1,500 mm according to the Paulay and Priestley (1992) equation:

$$L{}_p=0.08L+0.022d{}_{b}f{}_y(2)$$

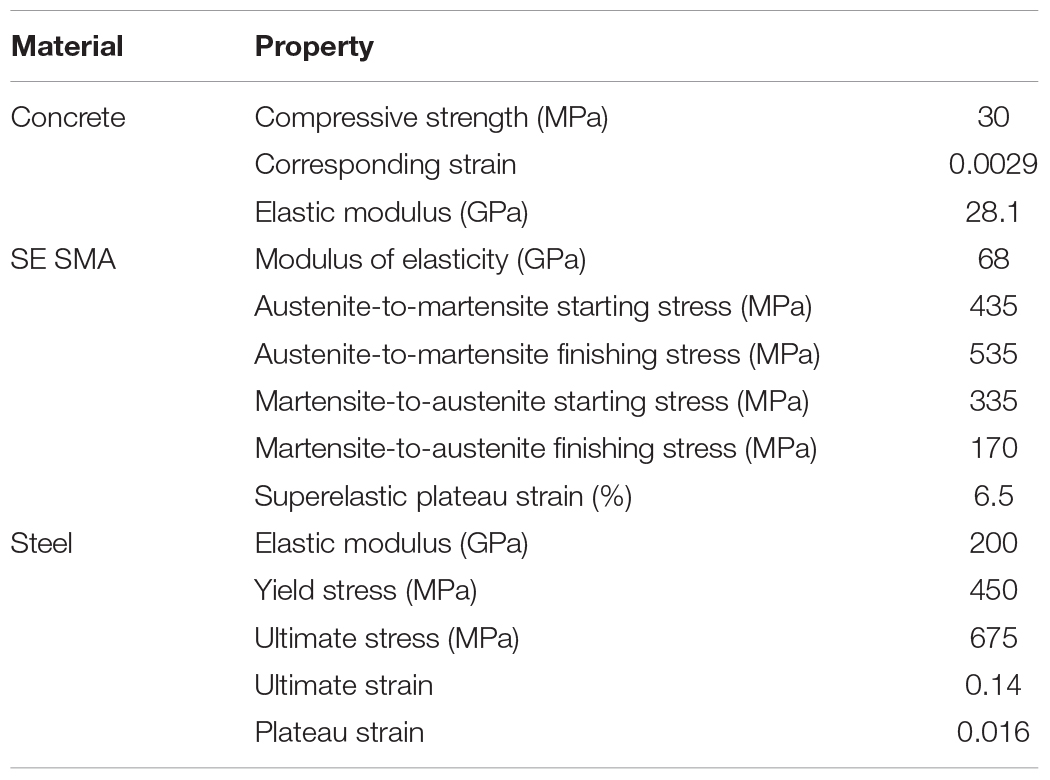
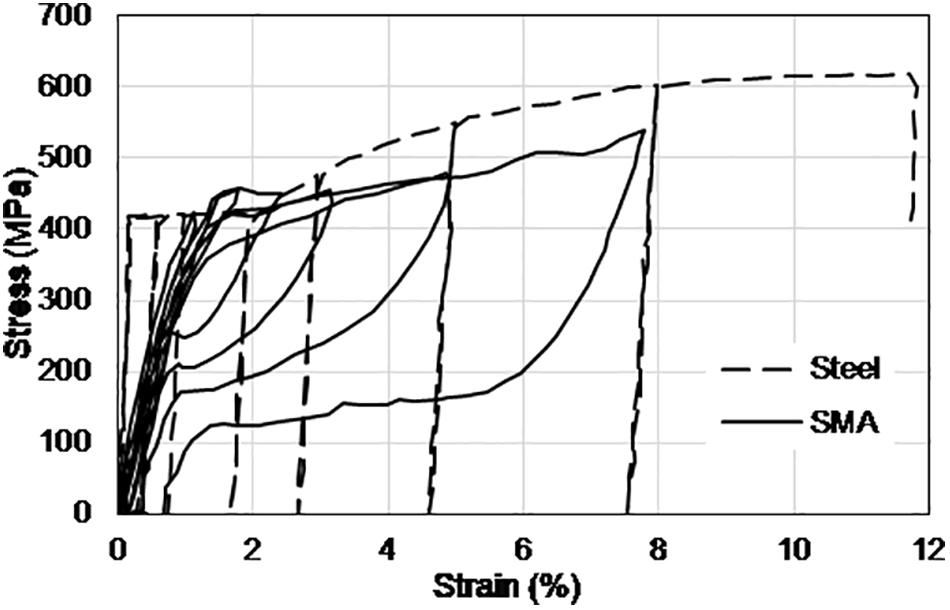
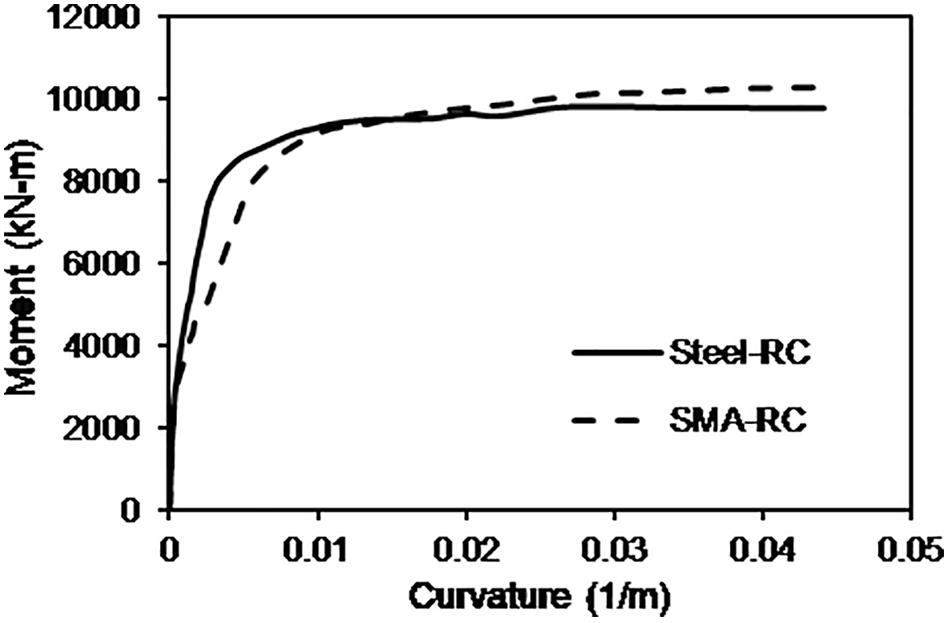
The material properties of Ni-Ti SMA, steel rebar, and concrete considered for the bridge bents are summarized in Table 3. Figure 5 compares the stress-strain behavior of the superelastic Ni-Ti SMA and the mild steel rebar under cyclic loading. The presence of SMA rebar in the plastic hinge region did not alter the moment capacities of the bridge piers significantly as observed from the comparable moment capacities as illustrated in Figure 6. The moment-curvature response of the SMA and Steel-reinforced sections are shown in Figure 6 which show lower stiffness of the SMA reinforced section resulting from the lower elastic modulus of Ni-Ti SMA.

TABLE 3

Table 3. Material properties for SMA-RC and Steel-RC bridge pier.

FIGURE 5

Figure 5. Cyclic stress-strain response of steel and SMA rebar.

FIGURE 6

Figure 6. Moment curvature relationship of steel-RC and SMA-RC section.

Analytical Modeling of Bridge Bents

Employing an accurate analytical model that incorporates the cyclic deterioration of strength and stiffness is a prerequisite to get a realistic approximation of seismic response under long-duration motion. The analytical model should be capable of predicting the anticipated strength and stiffness degradation of different components (Ibarra et al., 2005; Lignos and Krawinkler, 2011). Figure 7 shows the details of the non-linear 3D model of the bridge bent developed in this study using SeismoStruct (SeismoSoft, 2020). The FE model includes some idealizations and realistic assumptions for representing different components. Force-based fiber elements in SeismoStruct are employed for modeling the steel and SMA reinforced concrete columns and the steel-reinforced bent cap. Confined and unconfined fiber sections are defined using the Mander et al. (1988) concrete model. The stress-strain behavior for steel reinforcement is defined using the Menegotto and Pinto (1973) constitutive relationship that includes the isotropic strain hardening property. The SMA uniaxial model proposed by Auricchio and Sacco (1997) is used to simulate the Ni-Ti SMA fiber sections. This study employed a zero-length inelastic spring to simulate the bond-slip behavior of SMA rebar in concrete. The bond slip spring is modeled based on the experimental bond stress-slip relation developed by Billah and Alam (2016a). More details about the modeling of the bond-slip behavior can be found in Billah and Alam (2018).

FIGURE 7

Figure 7. Idealized numerical bridge bent model and fiber discretized cross section.

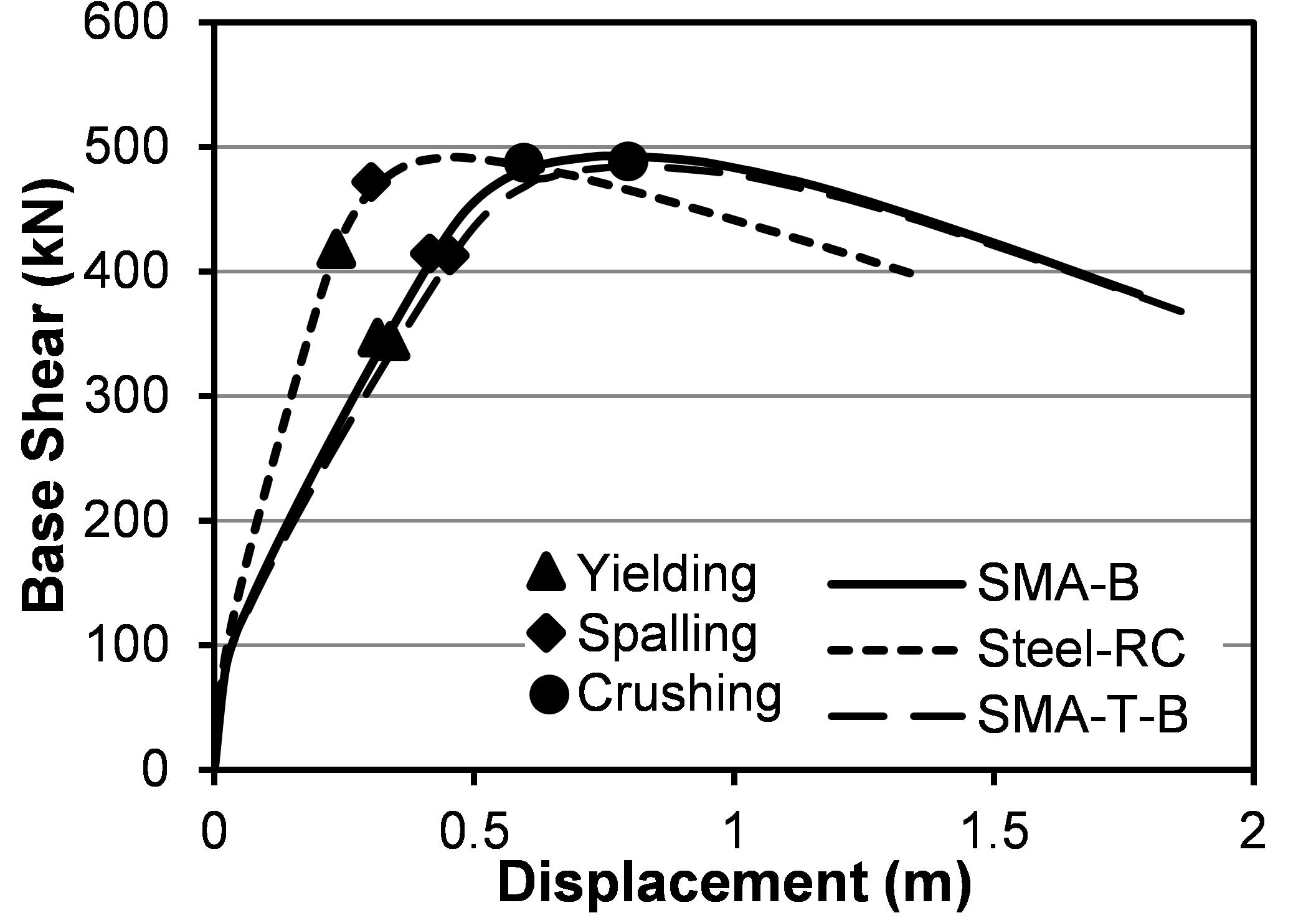
To evaluate the effectiveness of the adopted modeling approach, a comparison is performed against experimental results from the literature. Mohammed (2016) performed shake table investigations on large-scale bridge piers to evaluate the seismic performance under long-duration motions. In this study, the bridge pier tested by Mohammed (2016) (specimen-LD-J2) is modeled using the distributed plasticity approach as described above. Figure 8A compares the experimental force-displacement relationship from Mohammed (2016) (specimen-LD-J2) and the results obtained using the adopted modeling technique. From Figure 8A it is evident that the adopted modeling technique predicted the experimental response with a certain level of accuracy. The numerical model overestimated the maximum drift by 3.5%, whereas it underestimated the residual drift by 5%. In terms of cumulative energy dissipation, the model overestimated by 7%. Comparison of the results presented in Figure 8A highlights that the adopted modeling approach demonstrated reasonable accuracy in reproducing the experimental response and captured reasonably well the in-cycle and cyclic deterioration as well as the stiffness and strength degradation of the specimen tested.

FIGURE 8

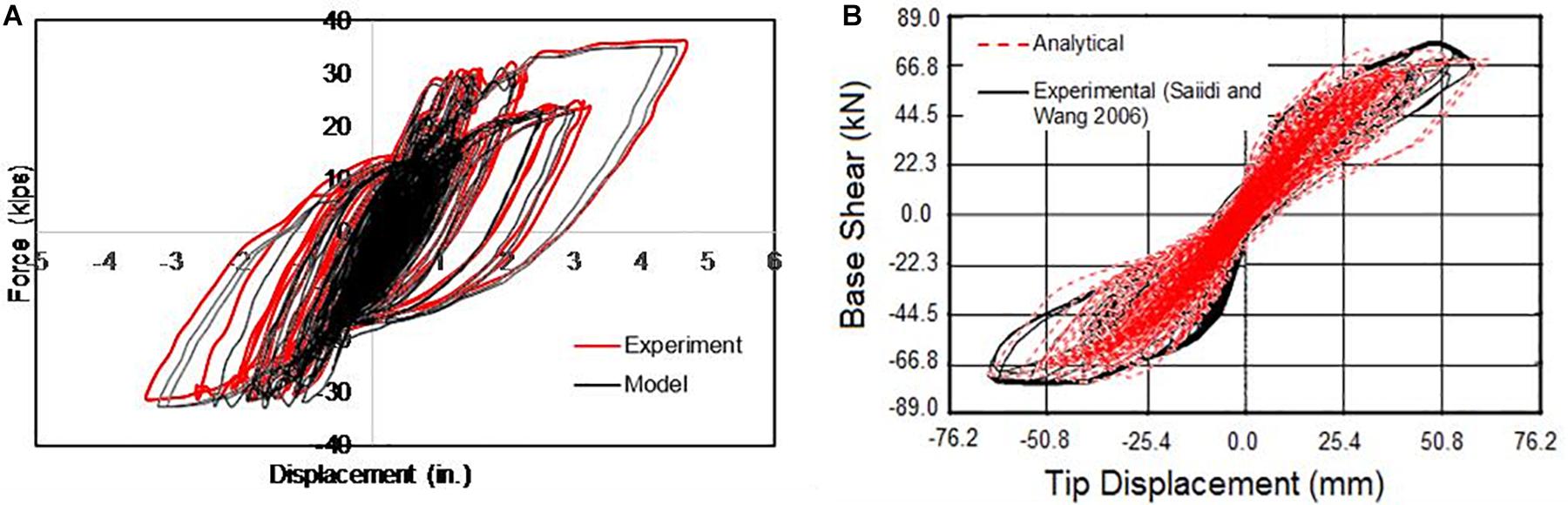
Figure 8. Comparison with experimental result (A) simulating cyclic degradation of Steel-RC pier and (B) SMA-RC bridge pier.

In addition, Figure 8B shows the validation of the experimental result from the shake table test of a SMA-RC bridge pier (Saiidi and Wang, 2006). Since no tests have been performed on SMA-RC bridge piers under long-duration motion, the ability of the numerical model in predicting the dynamic response of SMA-RC bridge pier is demonstrated in Figure 8B. The numerical results obtained from SeismoStruct could predict the experimental result of Saiidi and Wang (2006) accurately where the variations are only 5.6, 6.1, and 9.4% for base shear, tip displacement, and amount of energy dissipation, respectively.

After developing the detailed numerical models of the steel and SMA reinforced bridge bents, eigenvalue analysis is performed on all three bents. The natural period of the steel-RC, SMA-B, and SMA-B-T bridge bents were found to be 0.46, 0.48, and 0.49 s, respectively. The Steel-RC has a slightly lower fundamental period than the SMA bents. This can be attributed to the lower stiffness of the SMA rebar which resulted in higher flexibility of the SMA-RC bents.

Effect of Ground Motion Duration of Seismic Response

After validating the finite element model, the three bridge bents are analyzed using incremental dynamic analysis (IDA) (Vamvatsikos and Cornell, 2002) under the suite of 40 long-duration and 40 spectrally equivalent short duration motions. Each ground motions are scaled to multiple intensity levels to obtain dynamic instability or collapse of the bridge bent. This allowed for the effect of ground motion duration to be isolated. For each ground motion pair, IDA is performed for a least 20 intensity levels. Each IDA curve represents the relationship between the selected intensity measure (IM) with an engineering demand parameter (EDP) of the structural system (e.g., drift, acceleration). Wide varieties of IMs have been used by different researchers for the collapse assessment of structures using IDA. Spectral acceleration at the fundamental period of the structure (S_a, T1) is one of the most commonly used IM in practice and considered as the preferred IM in this study. Many past studies (Iervolino et al., 2006; Foschaar et al., 2012; Chandramohan et al., 2016) have used S_a (T1, 5%) as the IM to investigate the ground motion duration effect on the seismic response of buildings and bridges.

Characterization of Performance Limits

A critical step in performance-based design and assessment is to predict different damage states or performance levels under different levels of ground motions. To compare the performance of the three bents, a set of performance-based limit states, in terms of engineering performance criteria, are first established. In addition to maximum and residual drift, various quantitative performance limits (cracking, yielding, strength degradation) corresponding to different drift levels are developed for the steel and SMA reinforced bents.

Three quantitative performance limit states are defined for the three bents in terms of drift (%). These limit states for the three bents are developed following the different drift-based functional and performance levels proposed by Billah and Alam (2016b). Tables 4, 5 summarize the three performance and functional levels, the damage description, and the corresponding limiting drifts for the Steel and SMA reinforced bents, respectively. In this study three performance levels are considered where first yielding of the longitudinal rebar represents the yielding performance level, the onset of cover spalling denotes the local mechanism initiation and crushing of core concrete characterizes the strength degradation of the bent. The drift corresponding to each stage is obtained by tracking the corresponding material (concrete and steel/SMA) strain. The yield strain of steel and SMA rebar is obtained by dividing the yield stress by the corresponding elastic modulus which is found to be 0.0025 and 0.00704, respectively. Since there is no definite yield stress for SMA, the austenite-to-martensite starting stress is referred to as the yield stress for SMA rebar. As suggested by Priestley et al. (1996), concrete spalling is expected to start at a strain of 0.004. Crushing of core concrete represents significant strength degradation which typically occurs when confined concrete strain is between 0.015 and 0.05 (Paulay and Priestley, 1992). In this study, the concrete crushing strain is calculated using Eq. 3 proposed by Paulay and Priestly (1992):

$${\mathrm{\epsilon }}_{\mathit{cu}}=0.004+1.4{\mathrm{\rho }}_s{f}_{\mathit{yh}}{\mathrm{\epsilon }}_{\mathit{sm}}/f^{\prime }{}_c(3)$$

TABLE 4

Table 4. Damage states of steel-RC bridge bents in terms of performance criteria.

TABLE 5

Table 5. Damage states of SMA-RC bridge bents in terms of performance criteria.

Where, ε_cu is the ultimate compression strain, ε_sm is the steel strain at maximum tensile stress, f_c’ is the concrete compressive strength in MPa, f_yh is the yield strength of transverse steel in MPa, and ρ_s is the volumetric ratio of confining steel. Based on the transverse reinforcement, the crushing strain is calculated to be 0.016.

After obtaining the material strains corresponding to different performance criteria, non-linear static pushover analysis is performed on the three bents. Non-linear static pushover analysis is employed to estimate and compare the lateral load and deformation capacities of the three bents. A displacement-controlled pushover analysis was carried out by applying displacement as incremental load. The first occurrence of each material strain (yield, spalling, and crushing) is recorded from the response of the concrete and reinforcing material fiber which is translated to drift limits by obtaining the corresponding displacement. The pushover curves and the three performance limits associated with each bent are shown in Figure 9. The calculated drift limits of each performance level are summarized in Tables 4, 5. The SMA reinforced bents have slightly higher yield drift limit due to the higher yield strain of Ni-Ti SMA rebar. In addition, the lower stiffness of SMA rebar reduced the overall stiffness of the bent and resulted in higher drift before yielding. Similarly, higher limiting drift values are found for the SMA reinforced bents at the spalling and crushing performance limits. Due to the smooth surface of the SMA rebar, it caused more slippage and resulted in less cracking that subsequently delayed the concrete spalling. Past experiments on SMA reinforced concrete members (Youssef et al., 2008; Saiidi et al., 2009) reported similar delayed concrete spalling.

FIGURE 9

Figure 9. Pushover response curves for steel and SMA reinforced bridge bents.

Under lateral load, the core concrete crushing took place at a higher drift level for the SMA reinforced bents compare to the steel-reinforced counterpart. The crushing drift is determined when the strain in core concrete reaches or exceeds 0.016. The first occurrence of core crushing is observed at a drift of 4.78 and 3.90% for the SMA and Steel-reinforced bent, respectively. Saiidi et al. (2009) also reported higher crushing drift for SMA reinforced columns compared to steel-reinforced ones. Experimental studies on concrete beam-column joints by Alam et al. (2009) also reported higher drift sustained by SMA reinforced joints compared to steel-reinforced ones at similar damage levels.

Maximum Drift

The comparative seismic response of three bridge bents under the long-duration and equivalent short duration ground motions are evaluated in terms of maximum drift. Using IDA results obtained from each set of 40 ground motions, IDA curves are developed leveraging the EDP-IM relationship. The developed IDA curves, depicted in Figures 10–12, compare the response of the three bents under the two sets of ground motions. To facilitate comparisons between the three bents, percentile IDA curves are calculated using the EDP given IM (i.e., EDP| IM) percentiles (Vamvatsikos and Cornell, 2002). Along with the individual IDA curves, the median (50% percentile), 16 and 84% percentile IDA curves are also presented here. Assuming a lognormal distribution of the maximum drift as a function of S_a(T1), the median IDA curves represent the central value while the two percentiles (84 and 16%) denote the median times e^±dispersion, where “dispersion” is the standard deviation of the logarithms of the values (Jalayer and Cornell, 2003).

FIGURE 10

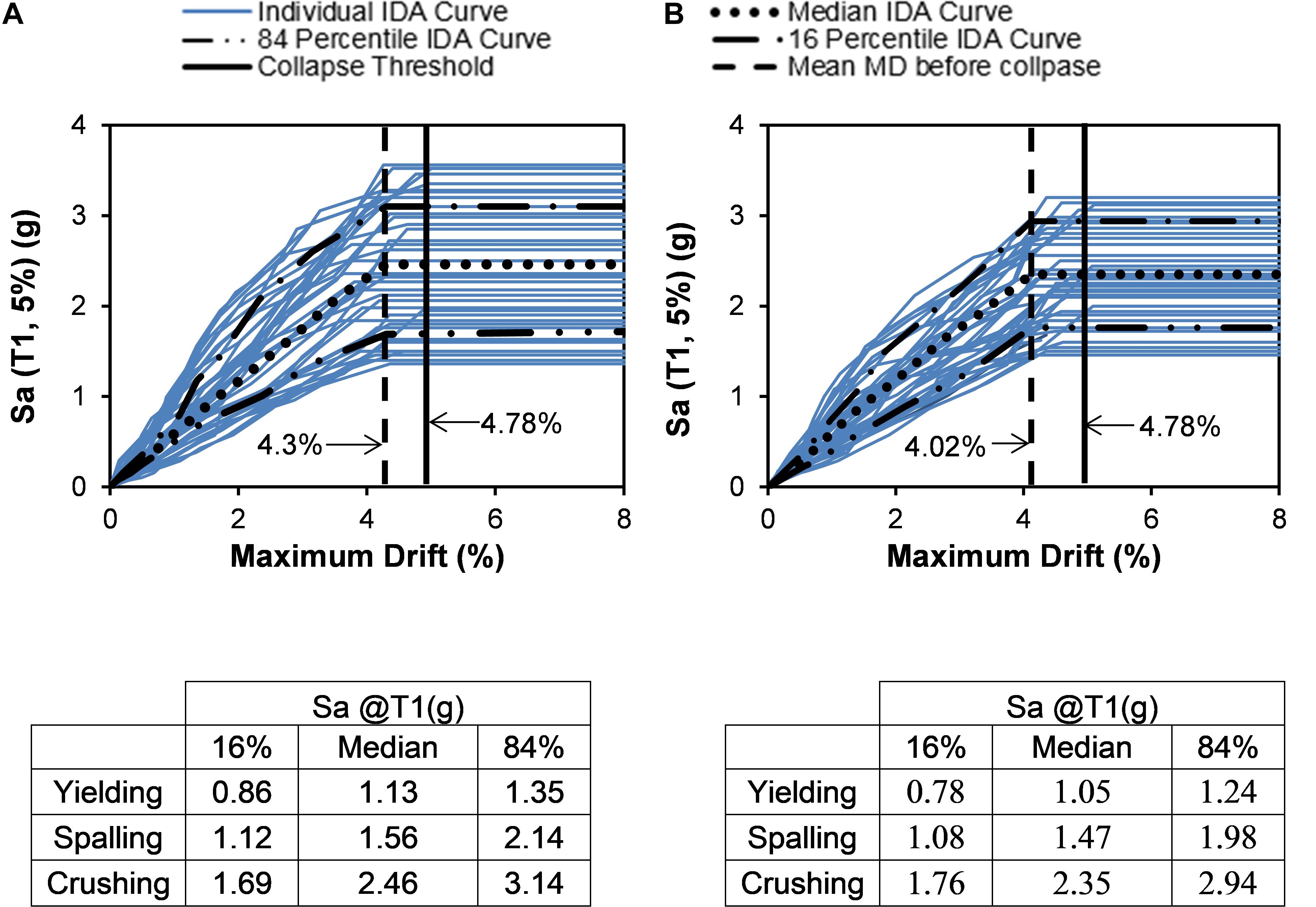
Figure 10. IDA curves for maximum drift for reinforced concrete bridge bent with SMA at the bottom plastic hinge (SMA-B) (A) short duration motion (B) long duration motion.

Using the limit states described in the previous section, the performance of the three bents is assessed using IDA curves. Using the EDP based rule (Vamvatsikos and Cornell, 2002), the limit states for each performance level are identified from the IDA curves. The corresponding IM at which the limit state is exceeded is also tabulated under each figure. Figures 10A,B show the IDA curves for the SMA-B bent and the results for different limit states under short and long-duration motions, respectively. The median S_a at yielding for the SMA-B bent is found to be 1.13 and 1.05 g for the short duration and long-duration motion sets, respectively. A similar observation can be made for concrete crushing where the median S_a for long and short duration motions are 2.36 and 2.46 g, respectively. These figures also show the maximum drift threshold of 4.78% (solid vertical line) which is used to indicate the collapse of the SMA-B bent. From Figure 10 it can be seen that under short duration motions, the SMA-B bent experienced an average maximum drift of 4.30% just before collapse (dashed vertical line), compared to 4.02% experienced under the long-duration motions. This can be attributed to the large inelastic deformation caused by cyclic deterioration resulting from a large number of displacement cycles of the long-duration motions.

The IDA curves for the SMA-B-T bent are shown in Figures 11A,B. Similar trend is also observed in the case of the SMA-B-T bent. These figures show the maximum drift collapse threshold and the mean maximum drift before the collapse. Under short duration ground motions, SMA-B-T bent sustained an average maximum drift of 4.65% just before collapse (vertical line), compared to 4.35% experienced under the long-duration ground motions. Similarly, for yielding and spalling, the median S_a required for short duration motions is 6.3 and 16.7% higher as compared to the long-duration motions, respectively.

FIGURE 11

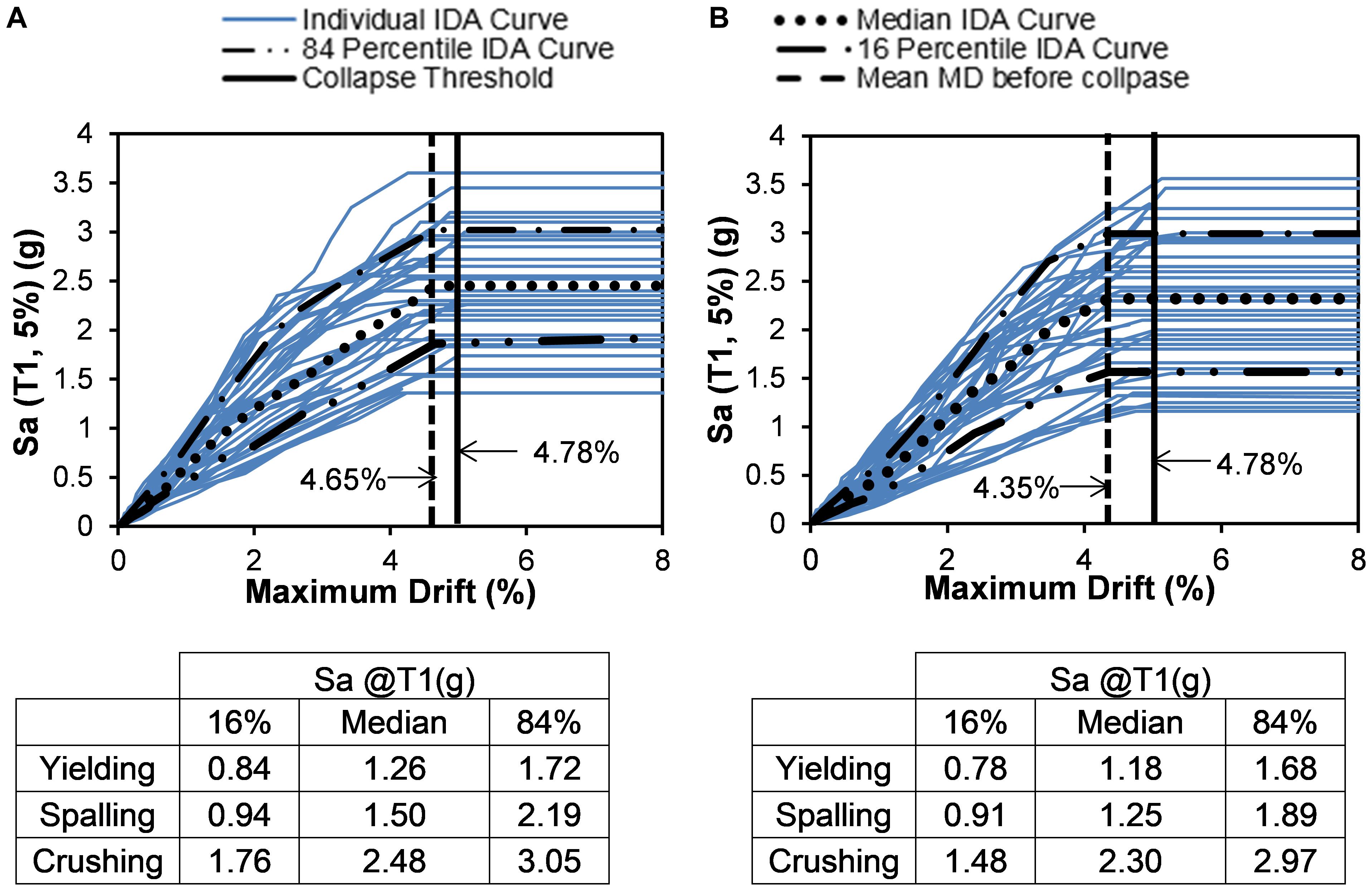
Figure 11. IDA curves for maximum drift for reinforced concrete bridge bent with SMA at the bottom and top plastic hinge (SMA-B-T) (A) short duration motion (B) long duration motion.

Figures 12A,B compare the IDA curves for the Steel-reinforced bent under the two sets of ground motions. Similar to the SMA reinforced bents, the long-duration motions yielded collapse at a smaller drift of 3.46% compared to 3.68% required under the short duration motions for the steel-reinforced one. However, the maximum drift collapse threshold of steel-RC bridge bent (3.90%) is significantly lower than the maximum drift collapse threshold of SMA-RC bridge bent (4.78%). The median collapse S_a for short duration motion is 2.40 g which is 5% higher than the median collapse S_a for long-duration motion set. The median S_a for yielding and spalling limit states are found to increase by 8.9 and 9.8%, respectively, for the short duration motions as compared to the long-duration counterparts.

FIGURE 12

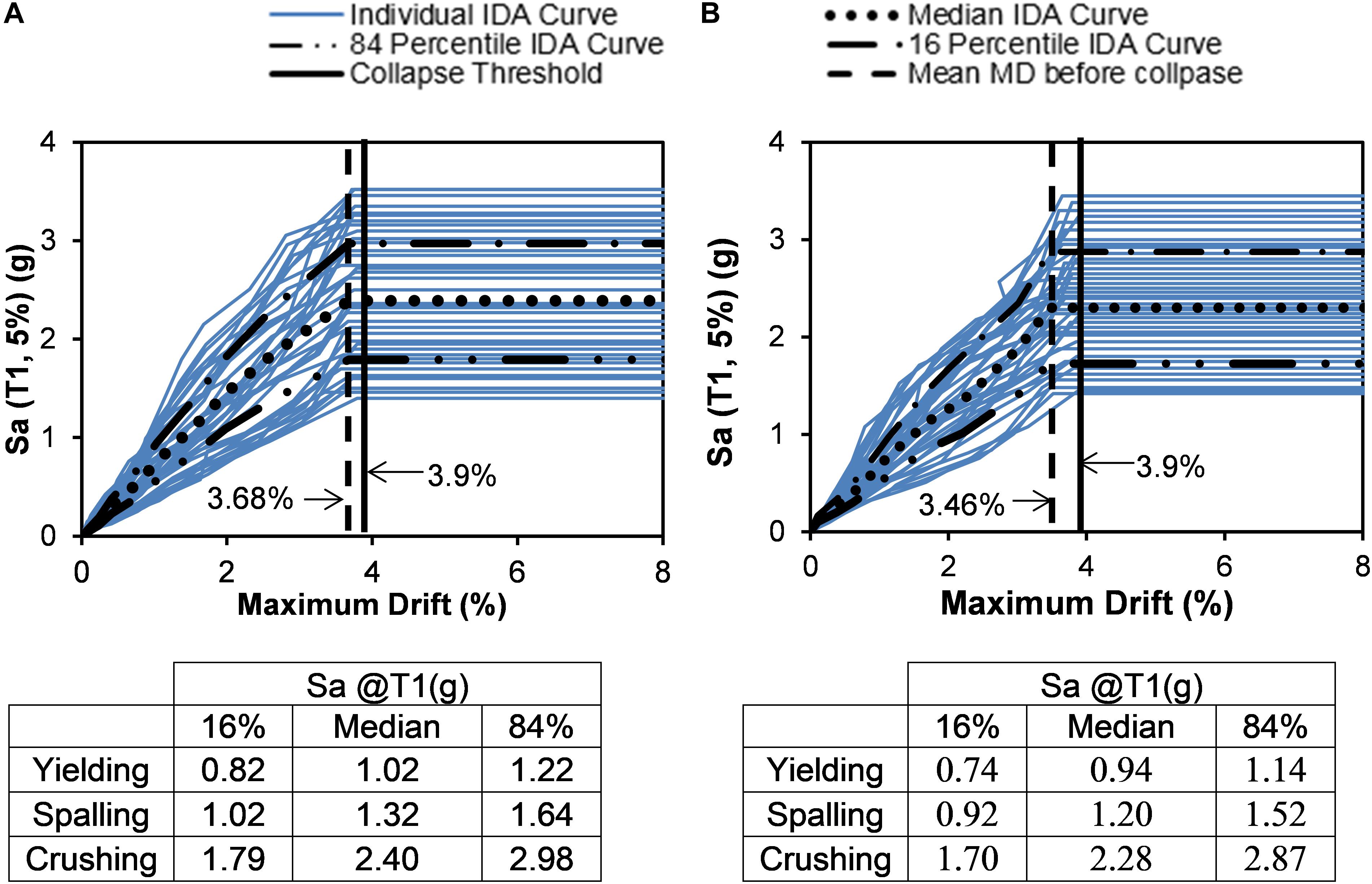
Figure 12. IDA curves for maximum drift for Steel reinforced concrete bridge bent (Steel-RC) (A) short duration motion (B) long duration motion.

Performance comparison of the three different bents aid in comprehending the efficacy of including SMA rebar in the bridge bents under the long-duration motions. It is evident from the above discussion that all three bridge bents experienced collapse before reaching the collapse threshold obtained using non-linear pushover analyses. Irrespective of the ground motion duration, the SMA-B-T bent could sustain a higher drift before the collapse. Under long-duration motions, SMA-B-T bent experienced collapse at a maximum drift of 4.35% which is 9% lower than the collapse threshold. However, the SMA-B and Steel-RC bent reached collapse at a maximum drift which is 15.9 and 11.3% less than the specified collapse threshold, respectively. Since SMA was used in both top and bottom plastic hinge regions of the SMA-B-T bent, it had lower stiffness which allowed it to deform more before the collapse.

Residual Drift

Ensuring adequate post-earthquake functionality is one of the major objectives of performance-based seismic design. Residual drift encountered during an earthquake controls the post-earthquake functionality of any structure (Ramirez and Miranda, 2012; Yazgan and Dazio, 2012). Although a significant performance indicator, bridge design codes and guidelines do not prescribe any limits or measures for controlling residual drift with the exception being the Japanese code for highway bridge design (Japan Road Association, 2006). After the 1995 Kobe earthquake, an increasing number of solutions have been proposed by various researchers for controlling the residual drift and proposed different residual drift limit states for bridges and buildings. If a bridge pier exceeds 1% residual drift, Lee and Billington (2011) recommended the bridge to be replaced. In an attempt to develop a residual drift based design guidelines for SMA-RC bridge pier, Billah and Alam (2016b) proposed residual drift based damage states for bridge piers. In this study, the residual drift limit states are considered based on the recommendations of Billah and Alam (2016b). When the pier sustains residual drift below 0.25% it is considered to be a fully functional bent while exceeding 1% residual drift is considered as the collapse limit state.

Figure 13 shows the comparative performance of the three bents under long-duration motions. Here, the collapse threshold of residual drift is considered as 1% which is shown by the solid vertical lines in the figures. These figures also show the mean collapse residual drift of each bridge bent (dashed vertical line) when subjected to long-duration motions. Figure 13 reveals that the SMA-B-T bent, reinforced with SMA in the top and bottom plastic hinge, could undergo large residual drift (0.58%) before collapse which is 10.3 and 58.6% higher than the SMA-B and steel-RC bent, respectively. The median collapse S_a for SMA-B-T bent is found to be 2.45 g which is 24.5 and 49% higher than the collapse S_a of SMA-B and steel-RC bent, respectively.

FIGURE 13

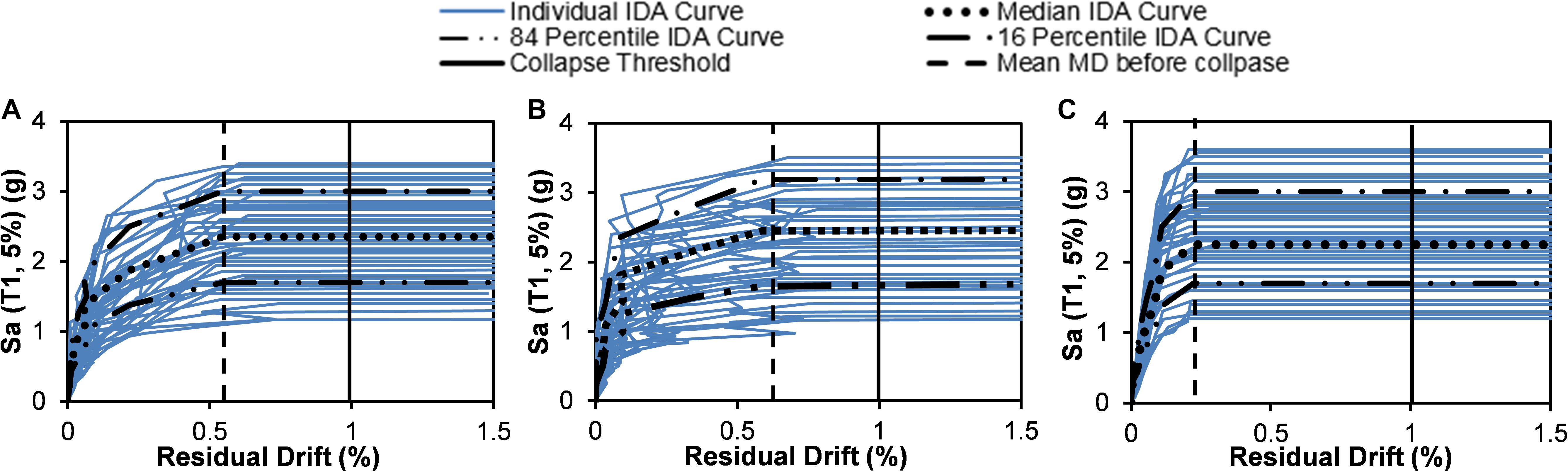
Figure 13. IDA curves for residual drift for (A) SMA-B, (B) SMA-B-T, and (C) Steel-RC bent under long duration motion.

Figure 14 shows the comparative performance of three bridge bents under spectrally matched short duration motions. Observation from the figures reveals that the SMA-B-T bridge bent experienced a residual drift of 0.68% before collapse which is 10.3 and 27.9% higher than the SMA-B and steel-RC bent, respectively. It shows that bridge bent reinforced with SMA at the top and bottom plastic hinge (SMA-B-T) is more effective than bridge bent reinforced with SMA in the bottom plastic hinge under both short and long-duration motions. The median collapse S_a for the SMA-B-T bent is 2.64 g which is 2.3 and 6% higher than the median collapse S_a of SMA-B and steel-RC bridge bent, respectively.

FIGURE 14

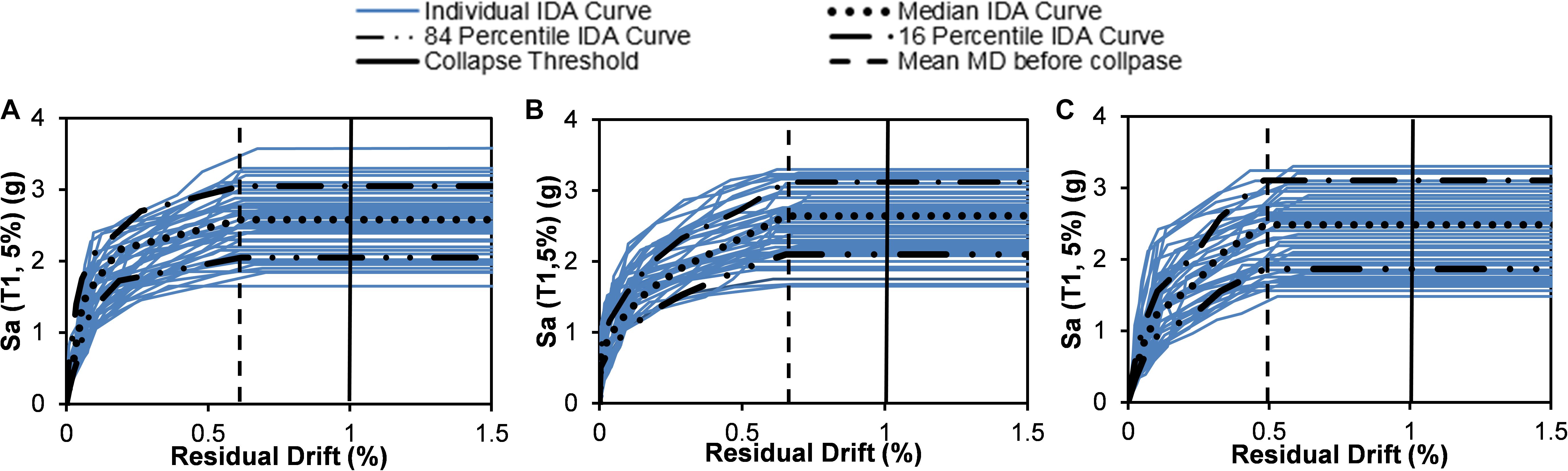
Figure 14. IDA curves for residual drift for (A) SMA-B, (B) SMA-B-T, and (C) Steel-RC bent under short duration motion.

Performance comparison of the three bents under spectrally equivalent short and long-duration motions revealed that the ground motion duration considerably affects the collapse capacity in terms of residual drift. The analysis result showed that the effect of SMA is more pronounced under long-duration motions. The median collapse S_a for the SMA-B-T bent is 27.9% higher for the long-duration motions and only 6% higher for the short duration motions as compared to the steel-RC bent. Similar performance is observed in the case of SMA-B bent where the median collapse S_a is 7.8 and 4% higher (compared to steel-RC bent) for the long and short duration motion, respectively. These results show the effectiveness of SMA in reducing the residual drift even under long-duration motions.

Cumulative Energy Dissipation

Reinforced concrete structures are subjected to a number of load reversals during an earthquake thus expected to dissipate a large amount of seismic energy through inelastic deformation or damage. During a long duration motion, structures undergo an increased number of load reversals which significantly affect the overall seismic response (Hassan and Billah, 2020). Previous researchers (Iervolino et al., 2006; Raghunandan and Liel, 2013; Ou et al., 2014) have concluded that long duration motions considerably increase the energy demand by imposing greater inelastic deformation. On the other hand, Champion and Liel (2012) concluded that short duration motion can be more damaging because of the pulse effect. The damage in structures depends on various factors, such as the load-deformation characteristics of the structure, the yield strength, and the intensity and duration of the ground motion. In this study comparative non-linear response of three different bridge bents are also quantified in terms of cumulative energy dissipation.

The hysteretic energy dissipated by a bridge bent over the duration of ground shaking was calculated as the area enclosed by the hysteresis loop formed by the earthquake-induced shear forces and the relative displacement between the column base and bent cap. The cumulative energy dissipated by the bridge bents during each seismic excitation was calculated by summing up the dissipated energy in successive load-displacement loops throughout the analysis. Figures 15A,B show the average cumulative energy dissipation of the three bridge bents under long duration and spectrally matched short duration record sets, respectively. From the figure it is evident that all three bridge bents dissipated significant amount of higher energy under long duration motions as compared to the spectrally matched short duration motions. Figure 15A depicts that the steel-RC bridge bent is unable to withstand for the whole duration of the long duration ground motions and dissipated 29.6 and 16.5% less energy as compared to the SMA-B-T and SMA-B bent, respectively. Under the long duration motions, the SMA-B-T bent dissipated 11% higher amount of energy as compared to the SMA-B bent. As expected, an opposite trend is observed under short duration motions where the steel-RC bent dissipated 17.6 and 7.5% higher energy as compared to the SMA-B-T and SMA-B bent, respectively. A comparison of Figures 15A,B reveal that the steel-RC bridge bent dissipated 15% higher energy under long duration motion as compared to short duration motion. Under long duration motions the SMA-B-T bent dissipated 76% higher energy on average as compared to the spectrally matched short duration motion. These results indicate that when SMA reinforced element undergoes large number of cycles they can sustain these load reversals and dissipate significant amount of energy. These results highlight the benefit of using SMA in regions susceptible to long duration motions, such as in the subduction zones.

FIGURE 15

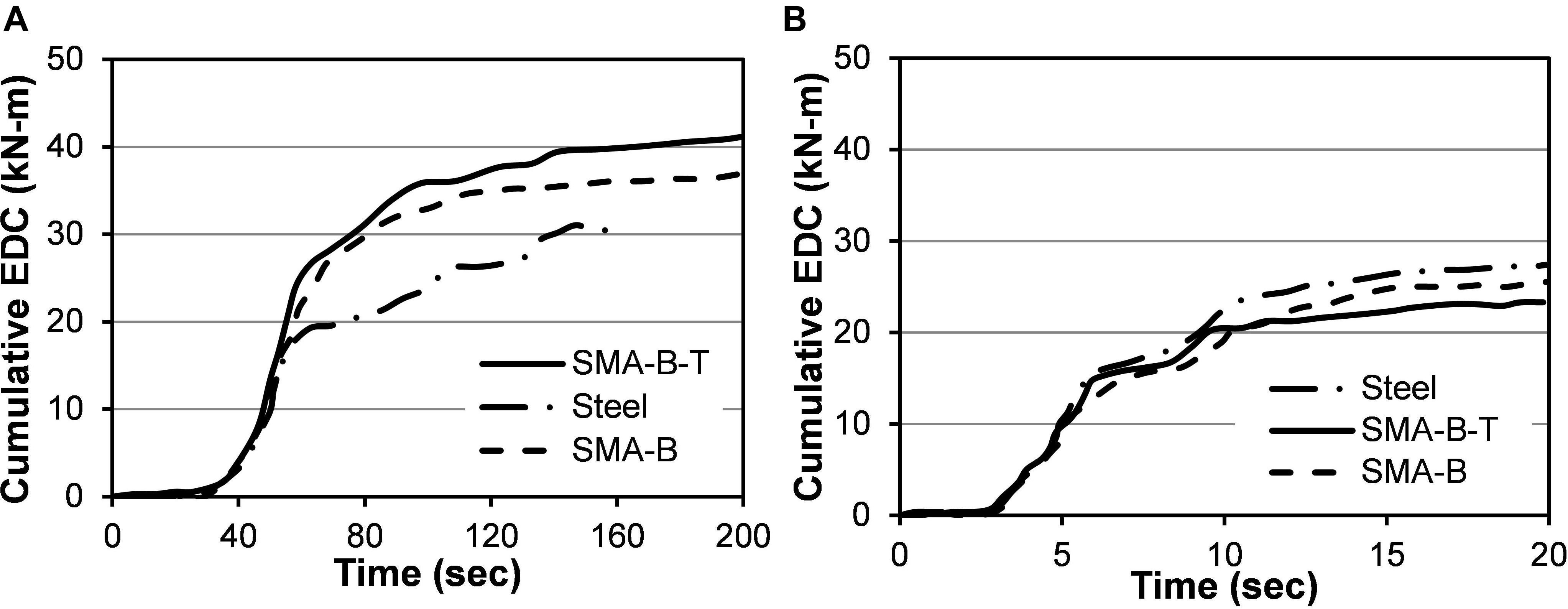
Figure 15. Average cumulative energy dissipation of three bridge bents under (A) long duration and (B) spectrally equivalent short duration motions.

Conclusion

Comparative seismic response of SMA reinforced and Steel-reinforced bridge bents under long-duration motions considering different reinforcement arrangements are presented in this paper. Using validated numerical models, the effect of ground motion duration and the incorporation of SMA rebar in the bridge bents are investigated. Additionally, spectrally equivalent short duration motions are considered for seismic response comparison of the SMA and Steel-reinforced bridge bents. Based on the observed results, the following conclusions are drawn:

1. The effect of ground motion duration is significantly affected by reinforcing materials and detailing. The numerical analysis performed in this study indicated that typical steel-reinforced bridge bents are more vulnerable under long-duration motions since they are unable to withstand a large number of load reversals. As a result, they fail to dissipate considerable energy thus accumulate significant damage. In contrast, SMA reinforced bridge bent dissipated a significant amount of energy with an increased number of inelastic displacement cycles thereby reduced the damage potential.

2. Bridge bent collapse capacity is considerably affected by the duration of ground motions. Structures under long-duration motions experienced collapse much earlier before reaching their collapse limit state. Under long-duration motions, SMA-B-T bent experienced collapse at a maximum drift that is 9% lower than the collapse threshold, whereas under short duration motions the difference is only 2.7%. Similar behavior can also be observed for the SMA- B and steel-RC bent.

3. Ground motion duration significantly affects the residual drift demand in bridge bents. The SMA-B-T bent sustained a mean residual drift of 0.58% just before collapse under long-duration motions compared to 0.68% of residual drift under the short duration ground motions.

4. The inclusion of SMA rebar in the plastic hinge region resulted in a significant transformation in recentering performance as well as improving the collapse behavior considering different performance criteria under the long-duration motions. The SMA reinforced bents sustained greater drift before exceeding a particular performance level. The median S_a at yielding is 1.05 and 1.18 g for the SMA-B and SMA-B-T bent, respectively, whereas the same for steel-RC bent is 0.94 g.

The present investigation is limited to a single bridge bent type without explicit considerations of uncertainties in bent geometry and constituent materials. Further studies need to be performed considering diverse bent configurations with epistemic uncertainties and accounting for the effects of different types of SMAs for improved understanding of the positive influences of SMA reinforced bridge bents under long-duration ground motions.

Data Availability Statement

All datasets generated for this study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

JR: investigation, methodology, formal analysis, and validation, writing—original draft, and visualization. AB: conceptualization, writing—review and editing, supervision, funding acquisition, resources, and software. All authors contributed to the article and approved the submitted version.

Funding

The research was supported by the NSERC Canada through the Discovery Grant. The financial support was greatly appreciated.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Alam, M. S., Nehdi, M., and Youssef, M. A. (2009). Seismic performance of concrete frame structures reinforced with superelastic shape memory alloys. Smart Struct. Syst. 5, 565–585. doi: 10.12989/sss.2009.5.5.565

CrossRef Full Text | Google Scholar

Arias, A. (1970). “A measure of earthquake intensity,” in Seismic Design for Nuclear Power Plants, ed. Robert J Hansen (Cambridge, Mass: Massachusetts Inst. of Tech. Press), 438–483.

Google Scholar

Auricchio, F., and Sacco, E. (1997). A superelastic shape-memory-alloy beam model. J.Intell. Mater. Syst. Struct. 8, 489–501. doi: 10.1177/1045389x9700800602

CrossRef Full Text | Google Scholar

Barbosa, A. R., Ribeiro, F. L., and Neves, L. A. (2017). Influence of earthquake ground−motion duration on damage estimation: application to steel moment resisting frames. Earthq. Eng. Struct. Dyn. 46, 27–49. doi: 10.1002/eqe.2769

CrossRef Full Text | Google Scholar

Belejo, A., Barbosa, A. R., and Bento, R. (2017). Influence of ground motion duration on damage index-based fragility assessment of a plan-asymmetric non-ductile reinforced concrete building. Eng. Struct. 151, 682–703. doi: 10.1016/j.engstruct.2017.08.042

CrossRef Full Text | Google Scholar

Billah, A. H. M. M., and Alam, M. S. (2015). Seismic fragility assessment of concrete bridge pier reinforced with superelastic shape memory alloy. Earthq. Spect. 31, 1515–1541. doi: 10.1193/112512eqs337m

CrossRef Full Text | Google Scholar

Billah, A. H. M. M., and Alam, M. S. (2016a). Bond behavior of smooth and sand-coated shape memory alloy (SMA) rebar in concrete. Structures 5, 186–195. doi: 10.1016/j.istruc.2015.11.005

CrossRef Full Text | Google Scholar

Billah, A. H. M. M., and Alam, M. S. (2016b). Performance based seismic design of concrete bridge pier reinforced with Shape Memory Alloy-Part 1: Development of Performance-Based Damage States. ASCE J. Struct. Eng. 142, 1–11.

Google Scholar

Billah, A. H. M. M., and Alam, M. S. (2016c). Plastic hinge length of shape memory alloy (SMA) reinforced concrete bridge pier. Eng. Struct. 117, 321–331. doi: 10.1016/j.engstruct.2016.02.050

CrossRef Full Text | Google Scholar

Billah, A. H. M. M., and Alam, M. S. (2018). Probabilistic seismic risk assessment of concrete bridge piers reinforced with different types of shape memory alloys. Eng. Struct. 162, 97–108. doi: 10.1016/j.engstruct.2018.02.034

CrossRef Full Text | Google Scholar

Bommer, J. J., and Martinez-Pereira, A. (1999). The effective duration of earthquake strong motion. J. Earthq. Eng. 3, 127–172. doi: 10.1080/13632469909350343

CrossRef Full Text | Google Scholar

Bommer, J. J., Magenes, G., Hancock, J., and Penazzo, P. (2004). The influence of strong-motion duration on the seismic response of masonry structures. Bull. Earthq. Eng. 2, 1–26. doi: 10.1023/b:beee.0000038948.95616.bf

CrossRef Full Text | Google Scholar

Canadian Standard Association [CSA] (2019). CAN/CSA-S6-19. Canadian Highway Bridge Design Code. Toronto, ON: Canadian Standard Association.

Google Scholar

Center for Engineering Strong Motion Data [CESMD] (2012). Center for Engineering Strong Motion Data. Available online at: http://www.strongmotioncenter.org/ (accessed on June 1, 2019).

Google Scholar

Champion, C., and Liel, A. B. (2012). The effect of near-fault directivity on building seismic collapse risk. Earthq. Eng. Struct. Dyn. 41, 1391–1409. doi: 10.1002/eqe.1188

CrossRef Full Text | Google Scholar

Chandramohan, R., Baker, J. W., and Deierlein, G. G. (2016). Quantifying the influence of ground motion duration on structural collapse capacity using spectrally equivalent records. Earthq. Spect. 32, 927–950. doi: 10.1193/122813eqs298mr2

CrossRef Full Text | Google Scholar

Cosenza, E., and Manfredi, G. (1997). “The improvement of the seismic resistant design for existing and new structures using damage concept,” in Seismic Design Methodologies for the Next Generation of Codes, ed. P. Fajfar (London: Routledge), 207–215.

Google Scholar

Cosmos Strong-Motion Virtual Data Center (2012). COSMOS strong-motion virtual data center. Consortium of Organizations for Strong Motion Observation Systems. Available online at: http://www.cosmos-eq.org/VDC/index.html (accessed on June 3, 2013).

Google Scholar

Cruz Noguez, C. A., and Saiidi, M. S. (2012). Shake-table studies of a four-span bridge model with advanced materials. J. Struct. Eng. 138, 183–192. doi: 10.1061/(asce)st.1943-541x.0000457

PubMed Abstract | CrossRef Full Text | Google Scholar

Foschaar, J., Baker, J., and Deierlein, G. (2012). “Preliminary assessment of ground motion duration effects on structural collapse,” in 15th World Conference on Earthquake Engineering. Lisbon, Portugal, (Portugal: WCEE).

Google Scholar

Han, Q., Du, X., Liu, J., Li, Z., Li, L., and Zhao, J. (2009). Seismic damage of highway bridges during the 2008 Wenchuan earthquake. Earthq. Eng. Eng. Vib. 8, 263–273. doi: 10.1007/s11803-009-8162-0

CrossRef Full Text | Google Scholar

Hassan, A. L., and Billah, A. M. (2020). Influence of ground motion duration and isolation bearings on the seismic response of base-isolated bridges. Eng. Struct. 222:111129. doi: 10.1016/j.engstruct.2020.111129

CrossRef Full Text | Google Scholar

Hosseini, F., Gencturk, B., Lahpour, S., and Gil, D. I. (2015). An experimental investigation of innovative bridge columns with engineered cementitious composites and Cu–Al–Mn super-elastic alloys. Smart Mater. Struct. 24:085029. doi: 10.1088/0964-1726/24/8/085029

CrossRef Full Text | Google Scholar

Ibarra, L. F., Medina, R. A., and Krawinkler, H. (2005). Hysteretic models that incorporate strength and stiffness deterioration. Earthq. Eng. Struct. Dyn. 34, 1489–1511. doi: 10.1002/eqe.495

CrossRef Full Text | Google Scholar

Iervolino, I., Manfredi, G., and Cosenza, E. (2006). Ground motion duration effects on nonlinear seismic response. Earthq. Eng. Struct. Dyn. 35, 21–38. doi: 10.1002/eqe.529

CrossRef Full Text | Google Scholar

Jalayer, F., and Cornell, C. A. (2003). A technical framework for probability-based demand and capacity factor (DCFD) seismic formats. RMS. Princeton, NJ: CiteSeerX.

Google Scholar

Japan Road Association (2006). Specifications for Highway Bridges. Japan: Japan Road Association.

Google Scholar

Kempton, J. J., and Stewart, J. P. (2006). Prediction equations for significant duration of earthquake ground motions considering site and near-source effects. Earthq. Spect. 22, 985–1013. doi: 10.1193/1.2358175

CrossRef Full Text | Google Scholar

Kwan, W.-P., and Billington, S. L. (2003). Unbonded posttensioned concrete bridge piers. I: Monotonic and cyclic analyses. J. Bridge Eng. 8, 92–101. doi: 10.1061/(asce)1084-0702(2003)8:2(92)

CrossRef Full Text | Google Scholar

Lee, W. K., and Billington, S. L. (2011). Performance−based earthquake engineering assessment of a self−centering, post−tensioned concrete bridge system. Earthq. Eng. Struct. Dyn. 40, 887–902. doi: 10.1002/eqe.1065

CrossRef Full Text | Google Scholar

Lignos, D. G., and Krawinkler, H. (2011). Deterioration modeling of steel components in support of collapse prediction of steel moment frames under earthquake loading. J. Struct. Eng. 137, 1291–1302. doi: 10.1061/(asce)st.1943-541x.0000376

PubMed Abstract | CrossRef Full Text | Google Scholar

Lin, L., Naumoski, N., Saatcioglu, M., and Foo, S. (2010). “Effects of strong-motion duration on the response of reinforced concrete frame buildings,” in Ninth US National and 10th Canadian Conference on Earthquake Engineering, (Toronto: 10CCEE).

Google Scholar

Lopez, A., Dusicka, P., and Bazaez, R. (2020). Performance of seismically substandard bridge reinforced concrete columns subjected to subduction and crustal earthquakes. Eng. Struct. 207:110216. doi: 10.1016/j.engstruct.2020.110216

CrossRef Full Text | Google Scholar

Mander, J. B., Priestley, M. J., and Park, R. (1988). Theoretical stress-strain model for confined concrete. J. Struct. Eng. 114, 1804–1826. doi: 10.1061/(asce)0733-9445(1988)114:8(1804)

CrossRef Full Text | Google Scholar

Menegotto, M., and Pinto, P. E. (1973). “Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending,” in Proceeding. of the IABSE symposium on resistance and ultimate deformability of structures acted on by well defined repeated loads, (Switzerland: IABSE), 15–22.

Google Scholar

Mohammed, M. S. (2016). Effect of Earthquake Duration on Reinforced Concrete Bridge Columns. [Ph.D thesis]. Department of Civil Engineering. Nevada: University of Nevada, Reno.

Google Scholar

Ou, Y. C., Song, J., Wang, P.-H., Adidharma, L., Chang, K.-C., and Lee, G. C. (2014). Ground motion duration effects on hysteretic behavior of reinforced concrete bridge columns. J. Struct. Eng. 140:04013065. doi: 10.1061/(asce)st.1943-541x.0000856

PubMed Abstract | CrossRef Full Text | Google Scholar

Page, R. A., Boore, D. M., Joyner, W. B., and Coulter, H. W. (1972). Ground motion values for use in seismic design of the Trans-Alaska pipeline system. US Geologic. Survey Circul. 672:15.

Google Scholar

Pan, Y., Ventura, C. E., and Liam Finn, W. (2018). Effects of ground motion duration on the seismic performance and collapse rate of light-frame wood houses. J. Struct. Eng. 144:04018112. doi: 10.1061/(asce)st.1943-541x.0002104

PubMed Abstract | CrossRef Full Text | Google Scholar

Paulay, T., and Priestley, M. N. (1992). Seismic Design of Reinforced Concrete and Masonry Buildings. New York, NY: John Wiley & Sons, Inc.

Google Scholar

PEER (2011). New Ground Motion Selection Procedures and Selected Motions for the PEER Transportation Research Program (PEER Report 2011/03), Pacific Earthquake Engineering Research Center. California: University of California.

Google Scholar

Priestley, M. N., Seible, F., and Calvi, G. M. (1996). Seismic Design and Retrofit of Bridges. New York, NY: John Wiley & Sons.

Google Scholar

Raghunandan, M., and Liel, A. B. (2013). Effect of ground motion duration on earthquake-induced structural collapse. Struct. Safe. 41, 119–133. doi: 10.1016/j.strusafe.2012.12.002

CrossRef Full Text | Google Scholar

Ramirez, C. M., and Miranda, E. (2012). Significance of residual drifts in building earthquake loss estimation. Earthq. Eng. Struct. Dyn. 41, 1477–1493. doi: 10.1002/eqe.2217

CrossRef Full Text | Google Scholar

Reed, J. W., and Kassawara, R. P. (1990). A criterion for determining exceedance of the operating basis earthquake. Nucl. Eng. Design 123, 387–396. doi: 10.1016/0029-5493(90)90259-z

CrossRef Full Text | Google Scholar

Ruiz-Garcia, J. (2010). On the influence of strong-ground motion duration on residual displacement demands. Earthq. Struct. 1, 327–344. doi: 10.12989/eas.2010.1.4.327

CrossRef Full Text | Google Scholar

Saiidi, M. S., and Wang, H. (2006). Exploratory study of seismic response of concrete columns with shape memory alloys reinforcement. ACI Mat. J. 103, 436–443. doi: 10.14359/15322

CrossRef Full Text | Google Scholar

Saiidi, M. S., O’Brien, M., and Sadrossadat-Zadeh, M. (2009). Cyclic Response of Concrete Bridge Columns Using Superelastic Nitinol and Bendable Concrete. ACI Struct. J. 106, 69–77.

Google Scholar

SeismoSoft (2020). A Computer Program for Static and Dynamic Nonlinear Analysis of Framed Structures. Available online at: http://www.seismosoft.com (accessed March, 2020).

Google Scholar

Sideris, P., Aref, A. J., and Filiatrault, A. (2015). Experimental seismic performance of a hybrid sliding–rocking bridge for various specimen configurations and seismic loading conditions. J. Bridge Eng. 20:04015009. doi: 10.1061/(asce)be.1943-5592.0000742

PubMed Abstract | CrossRef Full Text | Google Scholar

Trifunac, M. D., and Brady, A. G. (1975). A study on the duration of strong earthquake ground motion. Bull. Seismol. Soc. Am. 65, 581–626.

Google Scholar

Vamvatsikos, D., and Cornell, C. A. (2002). Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 31, 491–514.

Google Scholar

Van de Lindt, J., and Goh, G.-H. (2004). Effect of earthquake duration on structural reliability. Eng. struct. 26, 1585–1597. doi: 10.1016/j.engstruct.2004.05.017

CrossRef Full Text | Google Scholar

Wang, G., Zhang, S., and Zhou, C. (2015). Correlation between strong motion durations and damage measures of concrete gravity dams. Soil Dyn. Earthq. Eng. 69, 148–162. doi: 10.1016/j.soildyn.2014.11.001

CrossRef Full Text | Google Scholar

Xiang, N., Chen, X., and Alam, M. S. (2020). Probabilistic seismic fragility and loss analysis of concrete bridge piers with superelastic shape memory alloy-steel coupled reinforcing bars. Eng. Struct. 207:110229. doi: 10.1016/j.engstruct.2020.110229

CrossRef Full Text | Google Scholar

Yazgan, U., and Dazio, A. (2012). Post−earthquake damage assessment using residual displacements. Earthq. Eng. Struct. Dyn. 41, 1257–1276. doi: 10.1002/eqe.1184

CrossRef Full Text | Google Scholar

Youssef, M., Alam, M., and Nehdi, M. (2008). Experimental investigation on the seismic behavior of beam-column joints reinforced with superelastic shape memory alloys. J. Earthq. Eng. 12, 1205–1222. doi: 10.1080/13632460802003082

CrossRef Full Text | Google Scholar

Zhang, S., Wang, G., Pang, B., and Du, C. (2013). The effects of strong motion duration on the dynamic response and accumulated damage of concrete gravity dams. Soil Dyn. Earthq. Eng. 45, 112–124. doi: 10.1016/j.soildyn.2012.11.011

CrossRef Full Text | Google Scholar