Tension Estimation Method for Cable With Damper Using Natural Frequencies

Introduction

In the maintenance of cable structures such as cable-stayed bridges and extra-dosed bridges, the estimation of tension acting on the cables plays an important role. The tension of cables is measured either using a direct measuring method with devices such as a load cell or hydraulic jack, or using an indirect estimation method that considers the cable’s vibration characteristics. The former method is difficult to apply in practical situations owing to the high cost and required installation of complicated devices. Therefore, the latter method is used in practice because it is easy to implement and achieves high estimation accuracy.

In current practices in Japan, the tension of cables is mainly estimated using the vibration method proposed by Shinke et al. (1980) or the higher-order vibration method proposed by Yamagiwa et al. (2000), which considers the cable’s natural frequencies.

The vibration method proposed by Shinke et al. (1980) is based on theory of strings, whereby the tension of the cable is proportional to the square of the frequency. However, the actual cable is not a pure thread, and the effect of the bending stiffness is not negligible. Therefore, the effect of the bending stiffness is considered in the form of a correlation factor. In this method, it is necessary to determine the bending stiffness of the cable in advance. However, the correct bending stiffness is difficult to determine because bridge cables are typically PC (prestressed concrete) steel strands rather than single steel wires.

To address this problem, Yamagiwa et al. (2000) proposed a higher-order vibration method based on the tensioned Bernoulli-Euler beam theory. In this method, the natural frequency of the ith mode is expressed by a polynomial of mode order i with the bending stiffness and the tension as coefficients. The tension and the bending stiffness of the cable are simultaneously estimated using the natural frequencies of multiple modes, and the bending stiffness does not need to be determined in advance. Currently, this method is more frequently used for estimating tension.

In addition to the abovementioned studies, various studies based on modal data have investigated cable estimation techniques. For example, studies have employed methods using mode shapes, methods dealing with complicated boundary conditions (Chen et al., 2016; Chen et al., 2018; Yan et al., 2019), methods dealing with inclined cables (Kim and Park, 2007; Ma, 2017), methods using genetic algorithm and particle swarm optimization (Zarbaf et al., 2017) and methods using neural networks (Zarbaf et al., 2018). Studies are also conducted to relate tension to the natural frequencies of tensegrity structures using a finite element formulation (Ashwear and Eriksson, 2014; Ashwear and Eriksson, 2017).

In recent years, the length of bridges and the length of the installed cables has also been increasing. Because the damping performance of the cable itself is small, the vibration caused by the wind is notable. To suppress the aerodynamic vibration of cables, dampers are installed onto the cables. In the maintenance of cables with dampers, the direct use of the vibration method or higher-order vibration method is inappropriate because the damper changes the natural frequencies. Typically, the damper increases the cable’s natural frequencies. Because a cable with a larger tension force has higher natural frequencies, the tension will be overestimated if the vibration-based method is directly applied to the cable with a damper. Therefore, in practice, the damper is detached from the cable; then, the natural frequencies of the cable without a damper are measured, and the damper is attached to the cable again. Because the process of detaching and attaching the damper is time consuming and labor intensive, it is useful to develop a tension estimation method for a cable with a damper to estimate the cable tension without detaching the damper from the cable.

Previous studies on cables with dampers have mostly focused on optimal design methods for dampers to suppress the cable amplitude (Pacheco et al., 1993; Lazar et al., 2016; Shi and Zhu, 2018; Javanbakht et al., 2019), and have not dealt with the tension estimation method. Krenk (2000) derived a theoretical equation to obtain the complex eigenfrequencies, from which the natural frequencies and the damping ratios were obtained. However, the cable was modeled as a string and the effect of the cable’s bending stiffness was ignored. Therefore, these equations cannot be used to estimate the tension of a cable with bending stiffness.

With this background, the objective of this study was to develop a new tension estimation method for a cable with a damper. Using the higher-order vibration method, which is based on the tensioned Bernoulli-Euler beam theory, this study derived a theoretical equation for estimating the natural frequencies of a cable with a damper. The natural frequencies estimated by the theoretical equation depends on the tension and bending stiffness of cable and damper parameters. Therefore, by inversely solving the theoretical equation, the tension and bending stiffness of cable and damper parameters can be estimated from natural frequencies. The bending stiffness of cable and the damper parameters do not need to be determined in advance and can be estimated simultaneously with cable tension.

In Tension Estimation Method, the higher-order vibration method for estimating the tension of a cable without a damper is first described. Next, a new estimation method is proposed to estimate the tension of a cable with a damper. Numerical Verification presents the numerical verification of 80 numerical models. The natural frequencies of the cable with a damper were calculated by the eigenvalue analysis of the finite element method, and input to the proposed method. The estimated tension is compared with the assumed value, which was input to the eigenvalue analysis, and the accuracy and validity of the proposed method are discussed. Experimental Verification presents the experimental verification of the proposed method. The estimated tension is compared with the tension measured by the load cell, and the accuracy and validity of the proposed method are discussed.

Tension Estimation Method

Vibration Equation of Tensioned Bernoulli-Euler Beam

This section explains the cable vibration equation. If the cable is considered as a tensioned Bernoulli-Euler beam, the following partial differential equation can be established.

$\rho A\frac{{\partial }^{2}y\left(x,t\right)}{\partial t^2}+EI\frac{{\partial }^{4}y\left(x,t\right)}{\partial x^4}-T\frac{{\partial }^{2}y\left(x,t\right)}{\partial x^2}=0(1)$

where y(x,t) is the deflection, which is a function in terms of position x and time t; ρ is the density, A is the cross-sectional area, EI is the bending stiffness, and T is the tension.

The partial differential equation can be solved using the variable separation method. The deflection y(x,t) is transformed as follows.

$y\left(x,t\right)=Y\left(x\right)\text{exp}\left(j\omega t\right)(2)$

where Y(x) is the modal function for position x ; j is the imaginary unit; ω is the circular frequency.

By substituting Eq. (2) into Eq. (1), the following ordinary differential equation for function Y(x) can be derived.

$-\rho A{\omega }^{2}Y\left(x\right)+EI\frac{d^{4}Y\left(x\right)}{d{x}^4}-T\frac{d^{2}Y\left(x\right)}{d{x}^2}=0(3)$

The general solution of Eq. (3) is obtained as follows.

$Y\left(x\right)=C_1\text{cos}\alpha x+C_2\text{sin}\alpha x+C_3\text{cosh}\beta x+C_4\text{sinh}\beta x(4)$

where C₁, C₂, C₃, and C₄ are the integration constants; α and β are expressed, respectively, as follows.

$\alpha =\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\omega }^2}{EI}}-\frac{T}{2EI}}(5)$

$\beta =\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\omega }^2}{EI}}+\frac{T}{2EI}}(6)$

Higher-Order Vibration Method for Estimating Cable Tension Proposed by Yamagiwa et al. (2000)

Theoretical Equation for Obtaining Natural Frequencies

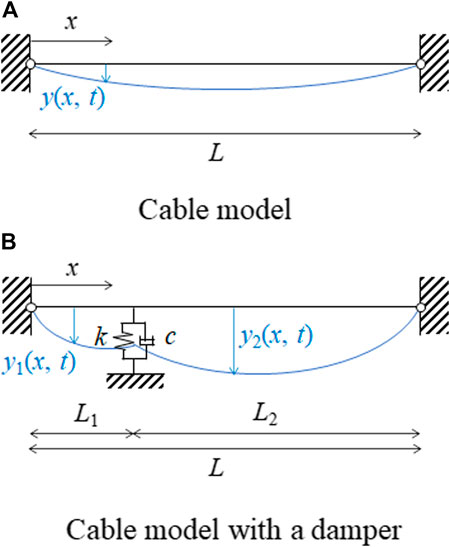
This section explains the higher-order vibration method proposed by Yamagiwa et al. (2000). Let us consider a cable with length L and pinned supports at the two ends, as shown in Figure 1A. Since the displacement is 0 and the second derivative of displacement is also 0 at the two ends with pinned supports, four boundary conditions are established.

FIGURE 1

FIGURE 1. Analytical model: (A) cable model; (B) cable model with damper.

By substituting Eq. (4) into the four boundary conditions, four simultaneous equations are obtained for the integral constants C₁, C₂, C₃, and C₄. Let us introduce the matrix notation for the simultaneous equations, as follows:

$\left[{\mathbf{X}}_{\mathbf{C}}\right]{\left\{\begin{array}{ccc}{C}_1& C_2& \begin{array}{cc}{C}_3& C_4\end{array}\end{array}\right\}}^T=0(7)$

where [X_c] is the 4 × 4 coefficient matrix of the simultaneous equations.

If the solutions of Eq. (7) are zero ( C₁ = C₂ = C₃ = C₄ = 0), the modal function Y(x) also becomes zero. To obtain any non-zero solution, the determinant of the coefficient matrix must be zero.

From this, the following equation is obtained.

$\text{sin}\alpha L=0(8)$

In Eq. (8), there are infinite solutions for α. These solutions can be expressed with a positive integer i, as follows.

${\alpha }_{i}L=i\pi i=\mathrm{1,2},\dots (9)$

By substituting Eq. (5) into Eq. (9), the natural circular frequency ω_i of the i^th mode can be obtained as follows.

${\omega }_i^2=\frac{{\pi }^{4}EI}{\rho A{L}^4}{i}^4+\frac{{\pi }^{2}T}{\rho A{L}^2}{i}^{2}i=1, 2,\dots (10)$

Finally, the theoretical equation for estimating the natural frequencies f^t_i of the i^th mode can be obtained as follows.

$f_i^t=\sqrt{\frac{{\pi }^{2}EI}{4\rho A{L}^4}{i}^4+\frac{T}{4\rho A{L}^2}{i}^2} i=\mathrm{1,2},\dots (11)$

From the cable parameters, such as ρ, A, L, EI, and T, the i^th mode natural frequencies f^t_i can be calculated using Eq. (11).

Optimization Problem

In the higher-order vibration method, T and EI are inversely estimated from ρ, A, L, and i, and the measured natural frequency f^m_i of the i^th mode. The objective function becomes as follows.

$minimizeF(T,EI)={\displaystyle \sum }_{i=1}^n{\left\{\left(\frac{{\pi }^{2}EI}{4\rho A{L}^4}{i}^4+\frac{T}{4\rho A{L}^2}{i}^2\right)-{\left(f_i^m\right)}^2\right\}}^2(12)$

where n is the number of natural frequencies and must be at least equal to two because there are two unknowns, T and EI. The least squares error between the square of the theoretical natural frequencies and the square of the measured natural frequencies for several modes is minimized. Because this is a linear optimization problem, it is easy to estimate the two unknowns T and EI.

Generally, the natural frequencies of the cable are measured from the Fourier spectrum or Power spectrum of the acceleration history after hitting the cable with a hammer. To accurately measure natural frequencies of several modes under traffic and wind loads, the power spectrum method is used in practice (Kim and Park, 2007; Yang et al., 2015) and the advanced method has been proposed (Feng et al., 2010).

The advantage of the higher-order vibration method is that the bending stiffness EI is estimated simultaneously with tension T, and the pre-evaluation of the bending stiffness is not needed.

Proposed Method for Estimating Tension of Cable With Damper

Theoretical Equation for Obtaining Natural Frequencies

This section explains the new tension estimation method proposed in this paper. Figure 1B shows the analytical model for a cable with a damper and pinned supports at the two ends. The damper shown in Figure 1B is the viscous shear damper with a spring constant k and damping constant c. The distance from the damper position to the left and right ends is L₁ and L₂(=L−L₁), respectively. The deflection of the cable on the left and right sides with regard to the damper position x is denoted as y₁(x,t) and y₂(x,t) , respectively. The deflection is expressed similarly to Eq. (2), as follows.

$y_1\left(x,t\right)=Y_1\left(x\right)\text{exp}\left(j\omega t\right)(13)$

$y_2\left(x,t\right)=Y_2\left(x\right)\text{exp}\left(j\omega t\right)(14)$

where Y₁(x) and Y₂(x) are the modal functions on the left and right sides of the cable with regard to the damper position.

The general solutions of Y₁(x) and Y₂(x) are as follows.

$Y_1\left(x\right)=D_1\text{cos}\alpha x+D_2\text{sin}\alpha x+D_3\text{cosh}\beta x+D_4\text{sinh}\beta x\left(0\le x\le L_1\right)(15)$

$Y_2\left(x\right)=D_5\text{cos}\alpha \left(x-L_1\right)+D_6\text{sin}\alpha \left(x-L_1\right)+D_7\text{cosh}\beta \left(x-L_1\right)+D_8\text{sinh}\beta \left(x-L_1\right)\left(L_1\le x\le L\right)(16)$

where D₁, D₂, D₃, D₄, D₅, D₆, D₇, and D₈ are the integration constants, and α and β are expressed by Eqs. 5, 6, respectively.

Next, the following boundary conditions are established.

$Y_1\left(0\right)=0(17)$

$\frac{d^2{Y}_1\left(0\right)}{d{x}^2}=0(18)$

$Y_2\left(L\right)=0(19)$

$\frac{d^2{Y}_2\left(L\right)}{d{x}^2}=0(20)$

$Y_1\left(L_1\right)=Y_2\left(L_1\right)(21)$

$\frac{d{Y}_1\left(L_1\right)}{dx}=\frac{d{Y}_2\left(L_1\right)}{dx}(22)$

$\frac{d^2{Y}_1\left(L_1\right)}{d{x}^2}=\frac{d^2{Y}_2\left(L_1\right)}{d{x}^2}(23)$

$EI\frac{d^3{Y}_1\left(L_1\right)}{d{x}^3}-EI\frac{d^3{Y}_2\left(L_1\right)}{d{x}^3}=k{Y}_1\left(L_1\right)+j\omega c{Y}_1\left(L_1\right)(24)$

where Eqs. (17–20) express the pinned supports at the two ends, and Eqs. (21–24) express the continuity conditions at the damper position.

By substituting Eqs. 15, 16 into the eight boundary conditions expressed by Eqs. (17–24), eight simultaneous equations can be obtained for the integral constants D₁, D₂, D₃, D₄, D₅, D₆, D₇, and D₈. The following matrix notation is used for the simultaneous equations.

$\left[{\mathbf{X}}_{\mathbf{D}}\right]{\left\{\begin{array}{ccc}{D}_1& \cdots & D_8\end{array}\right\}}^T=0(25)$

where [X_D] is the 8 × 8 coefficient matrix of the simultaneous equations.

To obtain any non-zero solution, the determinant of the coefficient matrix must be zero.

$det\left[{\mathbf{X}}_{\mathbf{D}}\right]=0(26)$

From Eq. (26), the following equation is obtained.

$\text{sin}\alpha L\left\{\left({\alpha }^2+{\beta }^2\right)+\frac{k^{\ast }}{EI}\left(\frac{\text{sin}\alpha L_1\text{cos}\alpha L_1}{\alpha }-\frac{\text{sinh}\beta L_1\text{sinh}\beta L_2}{\beta \text{sinh}\beta L}\right)\right\}-\text{cos}\alpha L\left(\frac{k^{\ast }}{EI}\frac{{\text{sin}}^2\alpha L_1}{\alpha }\right)=0(27)$

where k^∗ is the complex stiffness of the damper. A unified notation k^∗ is used to model various types of dampers. In the case of the viscous shear damper, the complex stiffness k^∗ is written with a spring constant k and damping coefficient c, as follows.

$k^{\ast }=k+j\omega c(28)$

In the case of the high-damping rubber damper, the complex stiffness k^∗ is written with k_u and k_v, which are the real and imaginary parts of the complex stiffness, as follows.

$k^{\ast }=k_u+j{k}_v(29)$

The viscous shear damper is a damper that utilizes the shear resistance of a viscos material. The high-damping rubber damper uses high-damping rubber as a damper, which is made by adding rubber or filler showing high damping to natural rubber. The imaginary part of the complex stiffness is proportional to the frequency in the case of the viscous shear damper and constant in the case of the high-damping rubber damper.

Then, Eq. (27) is transformed into the following equation.

$\text{sin}\left(\alpha L-\theta \right)=0(30)$

where

$\text{tan}\theta =\frac{\frac{k^{\ast }}{EI}\frac{{\text{sin}}^2\alpha L_1}{\alpha }}{\left({\alpha }^2+{\beta }^2\right)+\frac{k^{\ast }}{EI}\left(\frac{\text{sin}\alpha L_1\text{cos}\alpha L_1}{\alpha }-\frac{\text{sinh}\beta L_1\text{sinh}\beta L_2}{\beta \text{sinh}\beta L}\right)}(31)$

In Eq. (30), there are infinite solutions for α. These solutions are expressed with a positive integer i.

${\alpha }_{i}L-{\theta }_i=i\pi i=\mathrm{1,2},\dots (32)$

By substituting Eq. (5) into Eq. (32), the natural circular frequency ω_i of the i^th mode can be obtained as follows.

${\omega }_i^2=\frac{{\pi }^{4}EI}{\rho A{L}^4}{\left(i+\frac{{\theta }_i}{\pi }\right)}^4+\frac{{\pi }^{2}T}{\rho A{L}^2}{\left(i+\frac{{\theta }_i}{\pi }\right)}^{2}i=\mathrm{1,2},\dots (33)$

Finally, the theoretical equation for estimating the natural frequencies f^t_i of the i^th mode, and the relevant equations are expressed as follows.

$f_i^t=\sqrt{\frac{{\pi }^{2}EI}{4\rho A{L}^4}{\left(i+\frac{{\theta }_i}{\pi }\right)}^4+\frac{T}{4\rho A{L}^2}{\left(i+\frac{{\theta }_i}{\pi }\right)}^2}i=\mathrm{1,2},\dots (34)$

$\text{tan}{\theta }_i=\frac{\frac{k_i^{\ast }}{EI}\frac{{\text{sin}}^2{\alpha }_i{L}_1}{{\alpha }_i}}{\left({\alpha }_i^2+{\beta }_i^2\right)+\frac{k_i^{\ast }}{EI}\left(\frac{\text{sin}{\alpha }_i{L}_1\text{cos}{\alpha }_i{L}_1}{{\alpha }_i}-\frac{\text{sinh}{\beta }_i{L}_1\text{sinh}{\beta }_i{L}_2}{{\beta }_i\text{sinh}{\beta }_{i}L}\right)}(35)$

${\alpha }_i=\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\left(2\pi f_i^t\right)}^2}{EI}}-\frac{T}{2EI}}(36)$

${\beta }_i=\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\left(2\pi f_i^t\right)}^2}{EI}}+\frac{T}{2EI}}(37)$

$k_i^{\ast }=\{\begin{array}{cc}k+j\left(2\pi f_i^t\right)c& \left(\text{viscous}\text{shear}\text{damper}\right)\\ k_u+j{k}_v& (\text{high}-\text{damping}\text{rubber}\text{damper})\end{array}$(38a), (38b)

From the cable parameters, such as ρ, A, L, EI, and T, and the damper parameters k and c or k_u and k_v, the i^th mode natural frequencies f^t_i can be calculated using Eqs. (34–38). Interestingly, Eq. (34) of the proposed method becomes identical to Eq. (11) of the higher-order vibration method when the damper parameters are zero (k^∗_i = 0).

Notably, the natural frequency f^t_i of the i^th mode is included on the right-hand side of Eqs. (36,37,38a). Therefore, Eqs. (34–38) must be simultaneously satisfied and iteratively calculated.

Because the complex stiffness of the viscous shear damper k^∗_i depends on the frequency, the value is different for each mode number i, whereas the complex stiffness of the high-damping rubber damper is the same regardless of the mode number.

Furthermore, f^t_i in Eq. (34) has a complex value if k^∗ is complex. Therefore, this study considers f^t_i as a complex natural frequency to distinguish it from the general natural frequencies of the real values. The time term of Eq. (2) can be divided into the vibration part and amplitude decaying part as follows.

$\exp \left(j{\omega }_{i}t\right)=\exp \left[\frac{j\left\{\text{Re}\left(f_i^t\right)+j\text{Im}\left(f_i^t\right)\right\}t}{2\pi }\right]=\exp \left\{\frac{j\text{Re}\left(f_i^t\right)t}{2\pi }\right\}\exp \left\{-\frac{\text{Im}\left(f_i^t\right)t}{2\pi }\right\}(39)$

where the real part of the frequency Re(f^t_i) corresponds to the vibration frequencies, and the imaginary part of the frequency Im(f^t_i) corresponds to the amplitude decaying part.

Hence, it is determined that the real part Re(f^t_i) comprises the natural frequencies of the cable with a damper, and can be obtained by measurement. Therefore, Re(f^t_i) is equivalent to the measured natural frequencies (f^m_i).

The imaginary part Im(f^t_i) is difficult to measure. In theory, it is possible to measure the imaginary part from the waveform of each mode’s free vibration. However, it is difficult to clearly obtain the free vibration waveform by decomposing each mode. Therefore, the estimated accuracy of the imaginary part is presumably low. Hence, this study measured only the natural frequencies of each mode, that is, the real part of the theoretical complex natural frequency Re(f^t_i).

Optimization Problem

The proposed method inversely estimates T, EI, k, and c for the viscous shear damper, or T, EI, k_u, and k_v for the high-damping rubber damper from ρ, A, L, i, and the measured natural frequency f^m_i of the i^th mode.

Here, an optimization problem arises and must be solved using Eqs. (34–38). However, as mentioned previously, the natural frequency f^t_i on the left-hand side of Eq. (35) is included on the right-hand side of Eqs. (36,37,38a). Therefore, iterative calculation is needed to determine the natural frequency f^t_i. This means that the objective function, which must be iteratively calculated, includes a function that also requires iterative calculation. Therefore, the computation time becomes enormous and convergence is often difficult to obtain. Hence, this study proposes a simple approximation method. Because the damping factor of each mode caused by the damper is not very large, this study proposes the substitution of the measured natural frequencies f^m_i to f^t_i in Eqs. (36,37,38a). This means that the imaginary part of the natural frequency f^t_i is partially ignored, and the natural frequency f^t_i can be calculated non-iteratively. The effect of partially ignoring the imaginary part of the natural frequency is discussed in the next section.

The approximated parameters, such as $\overline{f_i^t}$, are denoted with an overline. To summarize the procedure, the approximated natural frequency $\overline{f_i^t}$ is estimated by performing one-way calculation using Eqs. (40–44).

$\overline{{\alpha }_i}=\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\left(2\pi f_i^m\right)}^2}{EI}}-\frac{T}{2EI}}(40)$

$\overline{{\beta }_i}=\sqrt{\sqrt{{\left(\frac{T}{2EI}\right)}^2+\frac{\rho A{\left(2\pi f_i^m\right)}^2}{EI}}+\frac{T}{2EI}}(41)$

$\overline{k_i^{\ast }}=\{\begin{array}{cc}k+j\left(2\pi f_i^m\right)c& \left(\text{viscous}\text{shear}\text{damper}\right)\\ k_u+j{k}_v& \left(\text{high}-\text{damping}\text{rubber}\text{damper}\right)\end{array}$(42a),(42b)

$\text{tan}\overline{{\theta }_i}=\frac{\frac{\overline{k_i^{\ast }}}{EI}\frac{{\text{sin}}^2\overline{{\alpha }_i}{L}_1}{\overline{{\alpha }_i}}}{\left({\overline{{\alpha }_i}}^2+{\overline{{\beta }_i}}^2\right)+\frac{k_i^{\ast }}{EI}\left(\frac{\text{sin}\overline{{\alpha }_i}{L}_1\text{cos}\overline{{\alpha }_i}{L}_1}{\overline{{\alpha }_i}}-\frac{\text{sinh}\overline{{\beta }_i}{L}_1\text{sinh}\overline{{\beta }_i}{L}_2}{\overline{{\beta }_i}\text{sinh}\overline{{\beta }_i}L}\right)}(43)$

$\overline{f_i^t}=\sqrt{\frac{{\pi }^{2}EI}{4\rho A{L}^4}{\left(i+\frac{\overline{{\theta }_i}}{\pi }\right)}^4+\frac{T}{4\rho A{L}^2}{\left(i+\frac{\overline{{\theta }_i}}{\pi }\right)}^2}i=\mathrm{1,2},\dots (44)$

Additionally, the objective function is expressed as follows.

$minimize G\left(T,EI,k,c\right)={\displaystyle \sum }_{i=1}^n{\left\{\text{Re}\left(\overline{f_i^t}\right)-f_i^m\right\}}^2 \left(\text{high}-\text{damping}\text{rubber}\text{damper}\right)(\mathrm{45a})$

$minimizeG\left(T,EI,k_u,k_v\right)={\displaystyle \sum }_{i=1}^n{\left\{\text{Re}\left(\overline{f_i^t}\right)-f_i^m\right\}}^2\left(\text{high}-\text{damping}\text{rubber}\text{damper}\right)(\mathrm{45b})$

where n is the number of natural frequencies and must be at least four because there are four unknowns, namely,T, EI, k, and c, or T, EI, k_u, and k_v. The least squares error between the theoretical natural frequencies and the measured natural frequencies for several modes is minimized.

Because this is a nonlinear least squares problem, there may be multiple local minimum solutions, although the global minimum solution is preferable. The solution depends on the initial points (initial parameters for the unknowns). Therefore, this study used the MultiStart algorithm (MathWorks, 2020), wherein the solver attempts to find multiple local minima solutions to a problem by starting from various initial points. The final solution is the one with the best objective function value amongst the local minimum solutions. Although there is no guarantee that this algorithm will always find the global minimum solution, it can still find a better solution than the general nonlinear least squares method using only one starting point.

The advantage of the proposed method is that the bending stiffness EI and damper parameters k and c, or k_u and k_v are estimated simultaneously with tension T, and the pre-evaluation of the bending stiffness and damper parameters is not required.

In Japan, the higher-order vibration method is used to estimate tension of cables without damper. The proposed method follows the same experimental procedure as the higher-order vibration method. Therefore, the application of the proposed method to actual structures is feasible.

Numerical Verification

Overview

The validity of the proposed method was verified by numerical simulation, as described in this section. First, the values for the cable parameters (ρ, A, L, L₁, T, and EI) and damper parameters (k and c, or k_u and k_v) were assumed. Next, the natural frequencies of the cable with a damper were calculated through the eigenvalue analysis of the finite element method. Then, the calculated natural frequencies were input into the proposed method to estimate T, EI, k, and c, or T, EI, k_u, and k_v. The estimation accuracy was investigated by comparing the estimated values to the assumed values.

Analytical Conditions

Analytical Cases

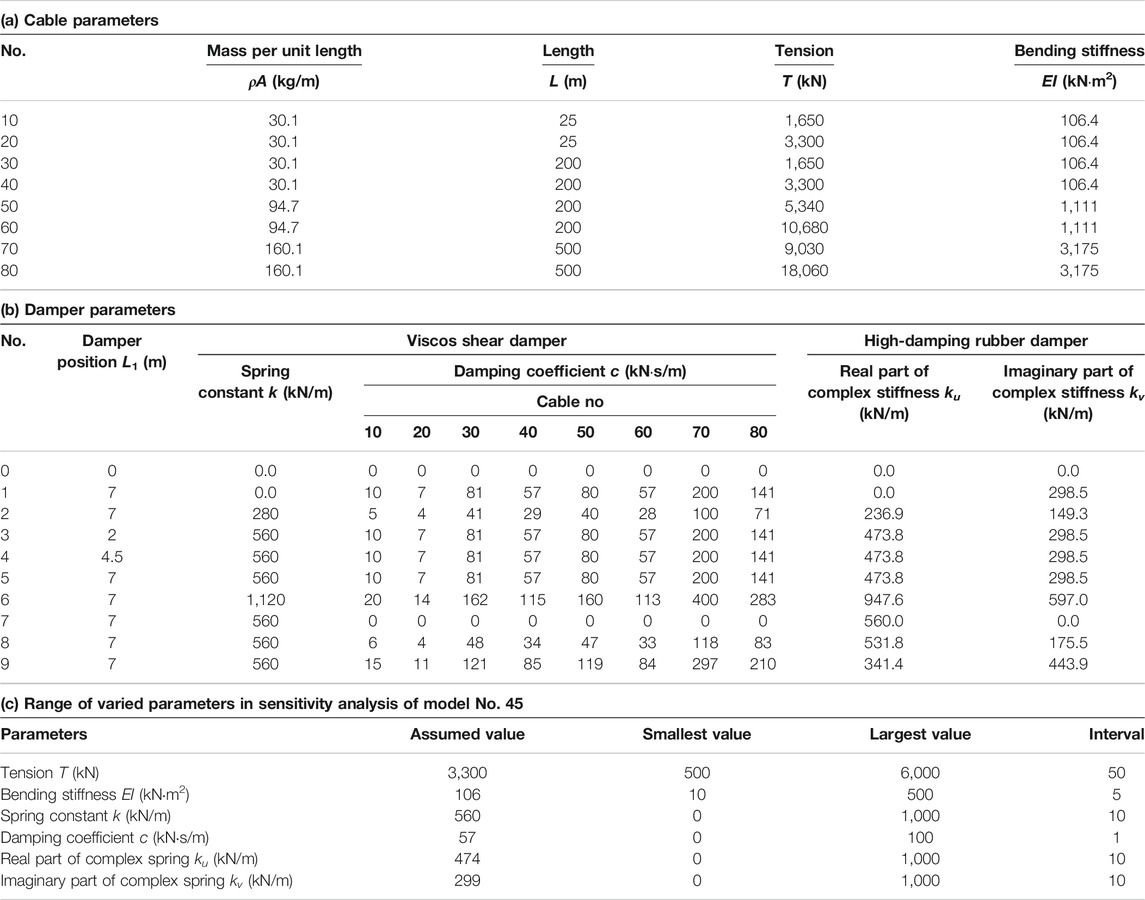
The cable parameters are listed in Table 1a, and the damper parameters are listed in Table 1b. These values were set to cover a wide variety of cables and dampers. Since the damper is installed near the girder in practice, the damper location, L₁, was set to be a small value compared to the cable length, L.

TABLE 1

TABLE 1. Analytical parameters.

Two damper types were compared, namely, a viscous shear damper and a high-damping rubber damper.

For the high-damping rubber damper, the values of the real part k_u and imaginary part k_v of the complex stiffness k^∗_i are listed in Table 1b.

For the viscous shear damper, the spring constant k was set to the same value as |k^∗_i| of the high-damping rubber damper. The damping coefficient c was determined such that the imaginary part of the first mode complex stiffness k^∗₁ was approximately the same for the two damper models. The values of k and c are listed in Table 1b.

By combining eight cable models and 10 damper models, 80 numerical models were created in total. The model number is defined as the sum of the cable number and damper number. For example, the analytical model No. 15 consists of the cable model No. 10 and damper model No. 5.

Finite Element model

The natural frequencies calculated through the eigenvalue analysis of the two-dimensional finite element method were input to the proposed method.

For the viscous shear damper model, the real mass, damping, and stiffness matrices were constructed, and regular complex eigenvalue analysis was conducted to obtain the eigenvalues. For the high-damping rubber damper, the real mass and complex stiffness matrices were constructed, and the complex eigenvalues were calculated. Then, the natural frequencies were calculated from the complex eigenvalues.

In the development of the finite element model, the cables were divided into 500 elements, such that the approximation accuracy of the finite element method was sufficiently high. The boundary conditions at the two ends are pinned supports, and the degree of freedom in the cable’s axial direction was ignored.

Number of Natural Frequencies Used in Estimation

As has been mentioned, there are four unknowns in the proposed method, T, EI, k, and c for the viscous shear damper, and T, EI, k_u, and k_v for the high-damping rubber damper. Therefore, at least four natural frequencies are required to estimate the four unknowns.

From the authors’ previous experience in measuring the natural frequencies of a cable with a damper, it is known that there are cases wherein the natural frequencies can be measured only up to the 7^th mode. The natural frequencies of the higher modes are occasionally difficult to measure because the higher mode vibration rapidly dissipates owing to the existence of dampers. Therefore, the natural frequencies of the first seven modes can be used to estimate the unknowns.

Nonlinear Optimization

As mentioned in the previous section, the combination of the MultiStart algorithm with the nonlinear least squares method was used to estimate the unknowns. The estimation accuracy depends on the number of initial points and the lower and upper bounds of each unknown.

This study randomly generated 10,000 sets of initial points for the four unknowns to avoid a local minimum solution. For the lower and upper bounds of the unknowns in the search for solutions, only the lower bounds were considered. For tension T, the lower value was set to 1. For the bending stiffness EI, the lower value was set to 0.0001. For the damper parameters (k, c, k_u, and k_v), all lower values were set to zero. The lower value of EI was not zero because Eqs. (35–37) include division by EI. Additionally, the lower value T was not equal to zero because, in some cases, the solution did not converge if the lower value was set to zero.

The linear least squares method is used in the higher-order vibration method. Because the method is linear, a unique solution is obtained. Additionally, the lower and upper bounds are not considered in the higher-order vibration method.

Comparison Between Estimation Accuracy of Proposed Method and Higher-Order Vibration Method

Results of Tension Estimation

The first to seventh mode natural frequencies calculated by the eigenvalue analysis were input into the proposed method and higher-order vibration method.

The comparison of the estimation accuracy for tension T between the proposed method and the higher-order vibration method is presented in Figures 2A and 3A. Figure 2 presents the results for the viscous shear damper model and Figure 3 presents the results for the high-damping rubber damper. The horizontal axis is the model number. The vertical axis is the ratio of the estimated tension value to the assumed tension value in Table 1a. A vertical axis value closer to 1.0 means that the estimation accuracy is higher. Previous studies have reported that, for a cable without a damper, the tension estimation accuracy of the higher-order vibration method is 5% (Shinko Wire Company Ltd, 2020). Therefore, in this study, the target accuracy of the proposed method for a cable with a damper was set to 5%.

FIGURE 2

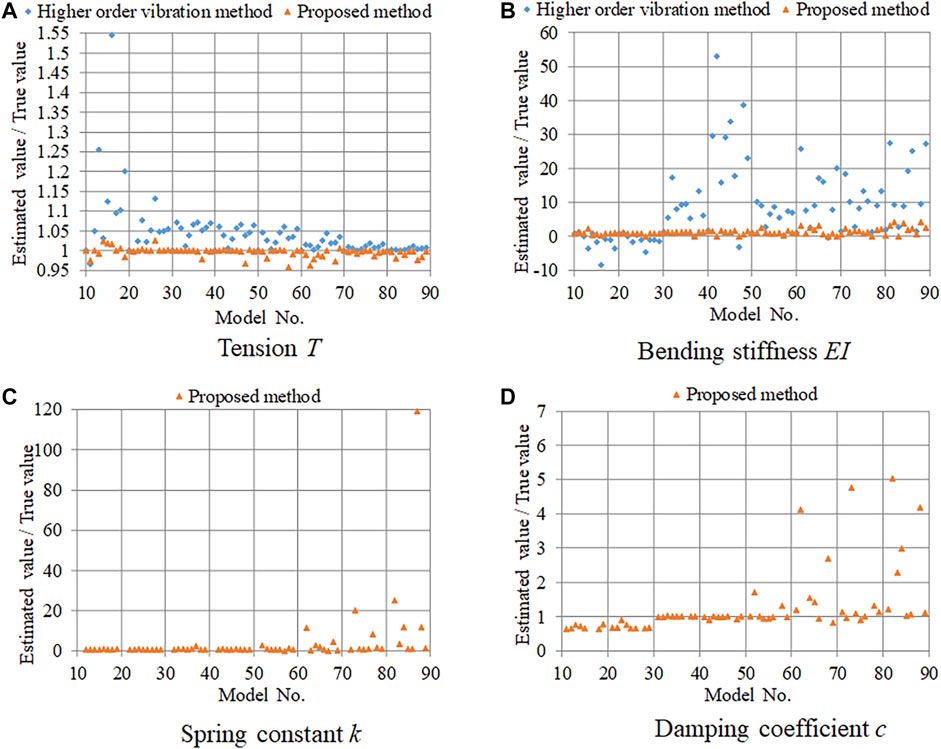
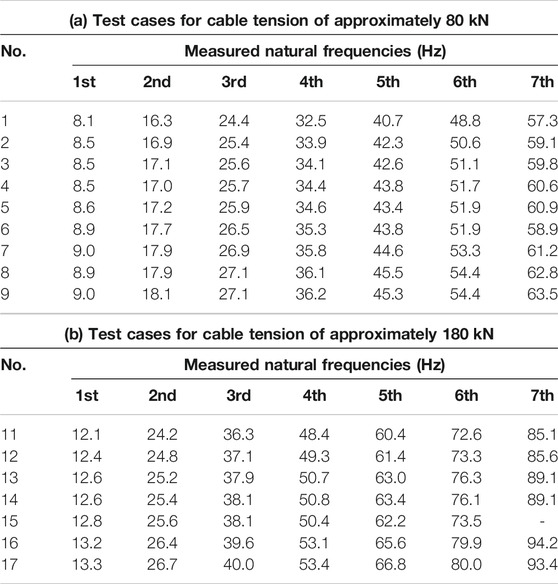
FIGURE 2. Estimation accuracy of viscous shear damper model: (A) tension; (B) bending stiffness; (C) spring constant; (D) damping coefficient.

FIGURE 3

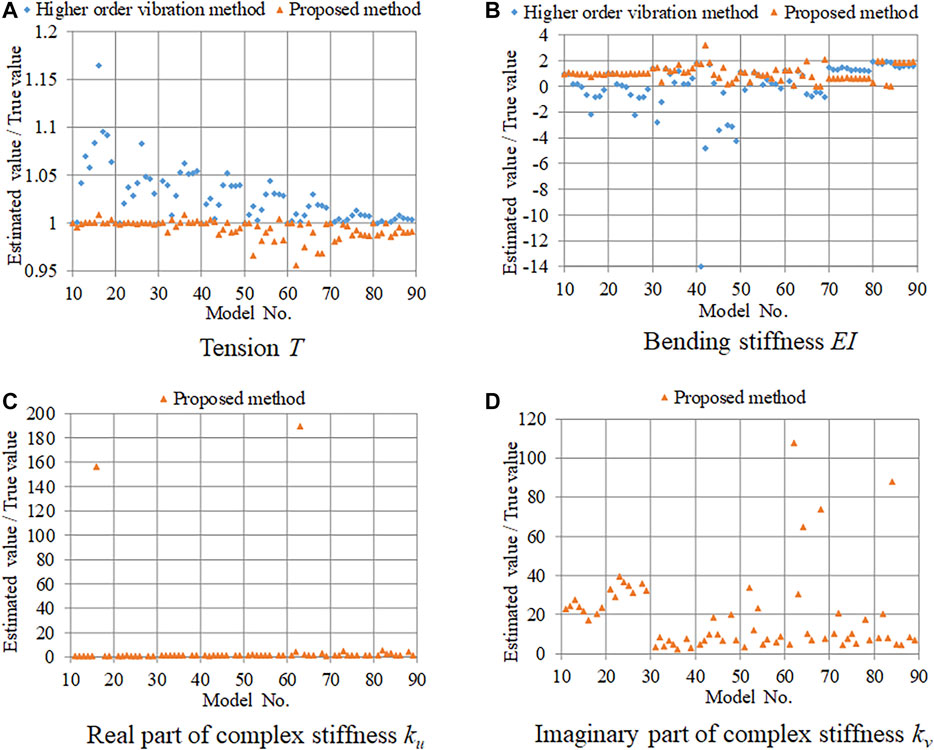
FIGURE 3. Estimation accuracy of high-damping rubber damper model: (A) tension; (B) bending stiffness; (C) real part of complex stiffness; (D) imaginary part of complex stiffness.

Models No. 10, 20, 30, 40, 50, 60, 70, and 80 are the cases without a damper. In these cases, both methods produced approximately the same results with high accuracy. However, the estimation accuracy of the higher-order vibration method was lower when a damper existed. Particularly, in cases wherein the cable length was short or the damper stiffness was large, the accuracy of the higher-order vibration method was low because the damper exerted strong influence. The estimation accuracy of the proposed method was quite high regardless of the model number and damper type. In all cases of both damper models, the estimation error of the proposed method was smaller than 5%, and the comparison revealed that the proposed method has a notable advantage.

Results of Bending Stiffness Estimation

The comparison between the bending stiffness, EI, estimation accuracy of the proposed method and higher-order vibration method is presented in Figures 2B and 3B. The advantage of the proposed method over the higher-order vibration method is clear. Moreover, the accuracy of the higher-order vibration method is notably low. In the case of the higher-order vibration method, the estimated bending stiffness was negative for some models because a lower bound value was not set for the unknowns when the linear least squares method was applied according to current practices.

Notably, the proposed method has higher accuracy compared with the higher-order vibration method for the bending stiffness. However, the bending stiffness estimation accuracy was low compared with the tension estimation accuracy, because only the low frequencies from the first to the seventh modes were used in the estimation. As can be seen from Eq. (34), the sensitivity of the bending stiffness EI over the natural frequencies f^t_i was low, because the EI coefficient was much smaller than the T coefficient in the lower mode. Therefore, to estimate the bending stiffness with high accuracy, it is necessary to use higher-order natural frequencies. However, considering that the higher-mode vibration rapidly dissipates owing to the existence of the damper, it is difficult to measure the higher-mode natural frequencies in practical situations. Therefore, it is concluded that estimating the bending stiffness with high accuracy is difficult in actual situations.

Results of Damper Parameter Estimation

The damper parameter estimation accuracy of the proposed method is presented in Figures 2C and D and Figures 3C and D. Because the true value of k and ku is zero for damper Nos. 0 and 1, these results were omitted. Identically, because the true value of c and kv is zero for damper Nos. 0 and 7, these results were also omitted. However, the tendencies in the results are the same as those in the other cases.

An accuracy as good as that of tension estimation is difficult to achieve for the damper parameter estimation because the value k^∗_i is not independent from the bending stiffness EI, as follows from Eq. (35). The k^∗_i/EI ratio is an independent parameter; therefore, the accuracy of the damper parameter estimation depends on the accuracy of the bending stiffness estimation. Because the accuracy of the bending stiffness estimation is not high, the accuracy of the damper parameters is also not high.

Effect of Partially Ignoring the Imaginary Part of the Complex Frequency

As mentioned in the previous section, this paper proposes the substitution of the measured natural frequencies f^m_i to f^t_i in Eqs. (36,37,38a). This means that the imaginary part of the natural frequency f^t_i is partially ignored. This section discusses the influence of partially ignoring the imaginary part of the natural frequency f^t_i by comparing the estimation accuracy of the case wherein the imaginary part was partially ignored to that of the case wherein the imaginary part was considered.

Figures 4 and 5 present the comparison of the estimation accuracy between the case wherein the imaginary part was partially ignored and the case wherein the imaginary part was considered. Considering the imaginary part means that the complex natural frequency f^t_i was obtained by the eigenvalue analysis and input into Eqs. (40,41,42a), instead of f^m_i.

FIGURE 4

FIGURE 4. Effect of partially ignoring imaginary part of complex natural frequency in viscous shear damper model: (A) tension; (B) bending stiffness; (C) spring constant; (D) damping coefficient.

FIGURE 5

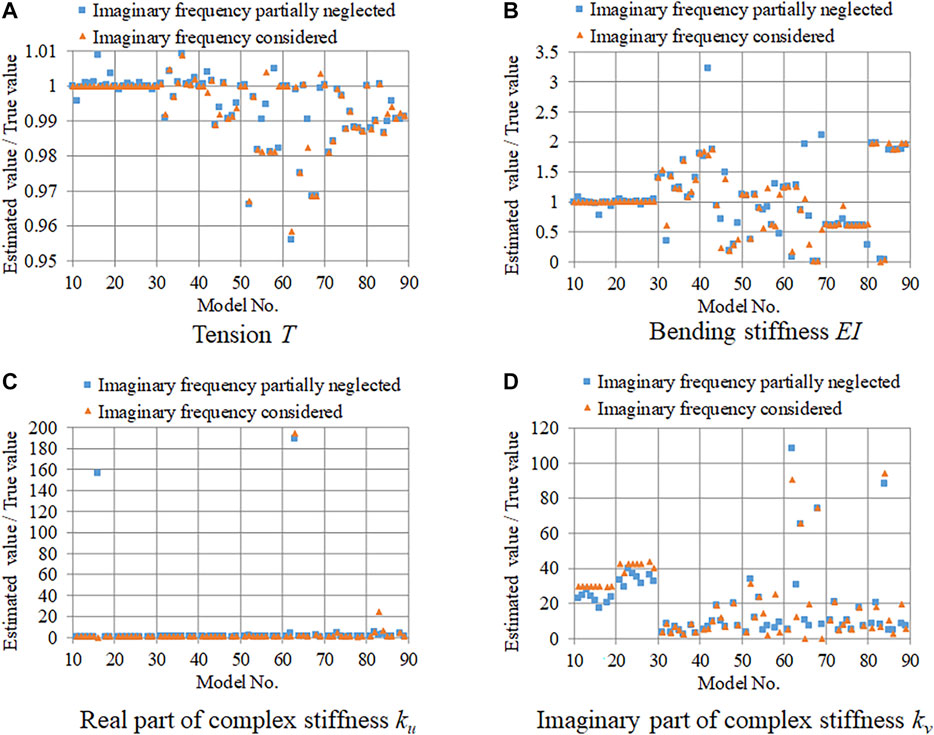
FIGURE 5. Effect of partially ignoring imaginary part of complex natural frequency in high-damping rubber damper model: (A) tension; (B) bending stiffness; (C) real part of complex stiffness; (D) imaginary part of complex stiffness.

The effect of partially ignoring the imaginary part of the complex frequency was very small. Additionally, it was found that the low accuracy of the bending stiffness and damper parameter estimation did not result from partially ignoring the imaginary part of the complex stiffness.

Sensitivity Analysis

Analytical Condition

The two previous sections discussed that the high accuracy achieved in the tension estimation. However, the estimation accuracy of the other three parameters was not as high as the tension estimation accuracy.

This section presents the sensitivity analysis results for the four unknowns. The first to seventh natural frequencies were calculated by only changing one parameter while keeping the other three parameters fixed. Model No. 45 is considered as an example. Table 1c lists the assumed values, the range of the varied parameters (the smallest and largest values), and the interval for each parameter.

Results of Sensitivity Analysis

The relationships between the varied parameter and the first to seventh natural frequencies are shown in Figures 6 and 7. Only the parameters in the horizontal axis varied while the other parameters were fixed to the assumed value.

FIGURE 6

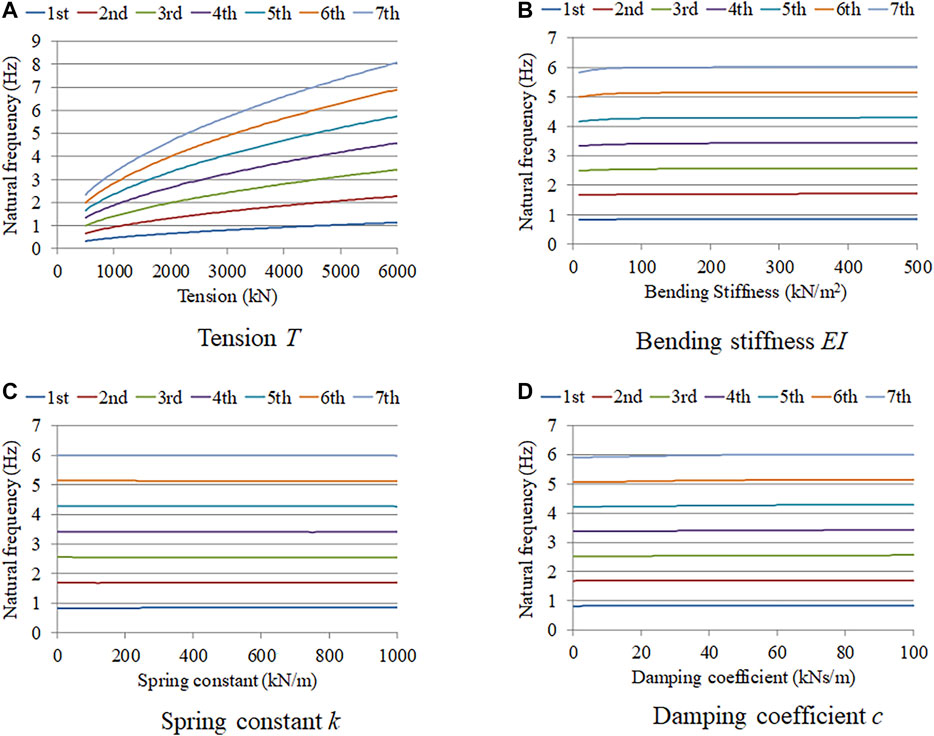
FIGURE 6. Sensitivity analysis results for viscous shear damper: (A) tension; (B) bending stiffness; (C) spring constant; (D) damping coefficient.

FIGURE 7

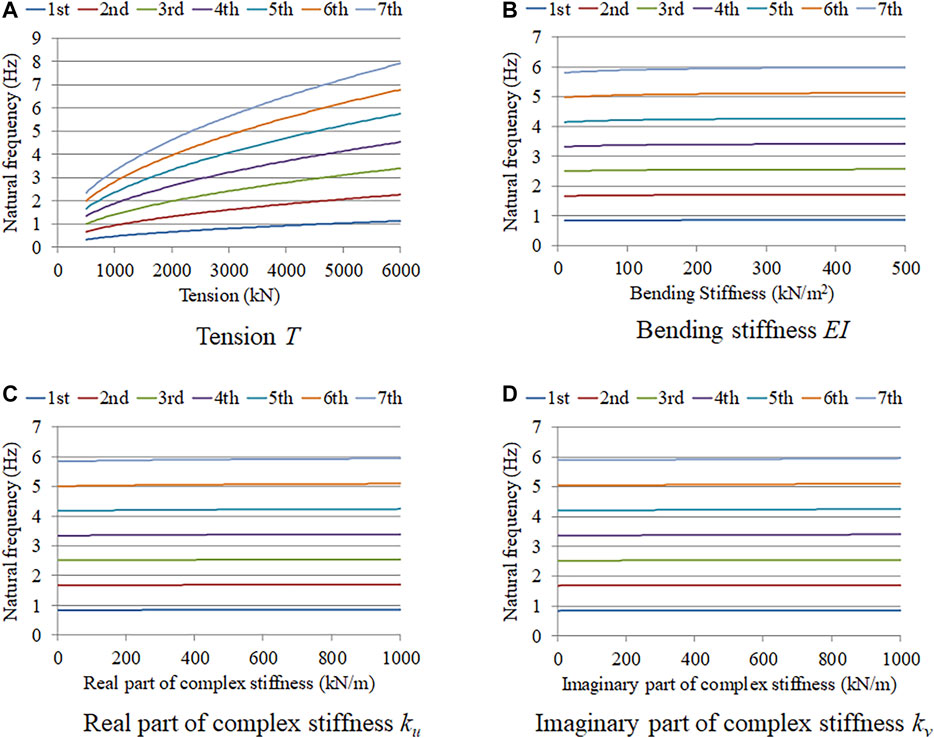
FIGURE 7. Sensitivity analysis results for high-damping rubber damper: (A) tension; (B) bending stiffness; (C) real part of complex stiffness; (D) imaginary part of complex stiffness.

For both damper models, the natural frequencies increased with the tension. However, the natural frequencies were approximately constant regardless of the bending stiffness value and all damper parameters. Thus, the tension sensitivity was high, whereas the sensitivity of the other three parameters was very small.

Because tension is the only parameter with sensitivity to the natural frequencies, it is considered that the proposed method is capable of estimating the tension with high accuracy. Even though the accuracy of estimating the other parameters was low, this did not affect the tension estimation accuracy.

Effect of Measurement Noise on Tension Estimation Accuracy

Analysis Condition

When measuring the vibration of an actual bridge cable, the natural frequencies always contain measurement noise. Therefore, this section discusses the effect of measurement noise on the tension estimation accuracy. Artificial measurement noise was added to the natural frequencies calculated by eigenvalue analysis, and the tension, bending stiffness, and damper parameters were estimated. Because the bending stiffness and damper parameter estimation accuracy was not satisfactory in the case without measurement error, only the estimation accuracy of the tension was considered.

First, the natural frequencies f^t_i were calculated by eigenvalue analysis for 80 models and for two damper types. Then, a uniform random number, rand, between −1 and 1 was generated. When the noise ratio was η, the natural frequencies with artificial measurement error were calculated as follows according to the approach used by Thyagarajan et al. (1998).

$f_i^{noise}=\left(1+\eta rand\right)\text{Re}\left(f_i^t\right)i=\mathrm{1,2},\dots (46)$

The effect of measurement noise with a noise ratio η, from 0 to 0.1 was investigated.

Then, the tension was estimated using the higher-order vibration method and proposed method by inputting the natural frequencies with measurement noise. The accuracy can be expressed in the form of the root mean squares error ratio (RMSER), as follows:

$\text{RMSER}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(T_i^{estimated}/T_i^{true}-1\right)}^2}(47)$

where i is the model number, n is the total number of models equal to 80, T_i^estimated is the estimated tension of model number i, and T_i^true is the assumed true tension of model number i.

Moreover, the natural frequencies with measurement noise of the cable without a damper (model Nos. 10, 20, 30, 40, 50, 60, 70, and 80) were also input to the higher-order vibration method, and the estimated tension was input to Eq. (47), where n = 8.

Results

Figure 8 shows the relationship between the noise ratio η and the RMSER. In both damper types, the estimation error in the form of the RMSER increased with the noise ratio. The estimation error of the proposed method was smaller than that of the higher-order vibration method when a damper existed. For the proposed method, the effect of measurement noise on the tension estimation accuracy was not large. When the measurement noise was less than 0.03, the estimation error was smaller than 0.05. Even in the case wherein the noise ratio was 0.1, the tension estimation error was 0.12 or 0.15. Therefore, if the noise ratio was kept within 3%, the target error of 5% was obtained. Because the RMSER of tension was slightly larger than the error ratio, the proposed method is considered to be robust against measurement error.

FIGURE 8

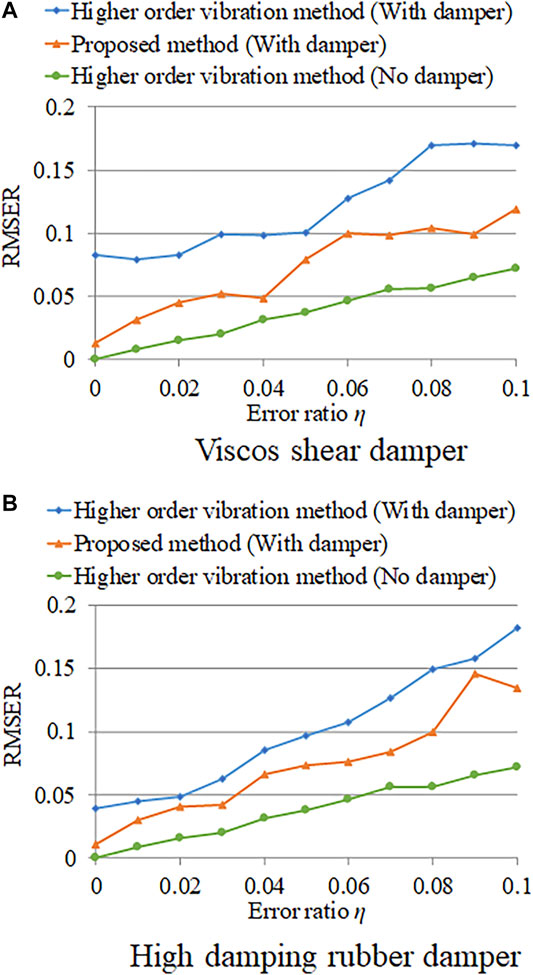
FIGURE 8. Effect of measurement noise on estimation accuracy: (A) viscous shear damper; (B) high damping rubber damper.

Next, the RMSER obtained by the proposed method in the case with a damper is compared with the RMSER obtained by the higher-order vibration method in the case without a damper. The estimation accuracy of the proposed method was approximately twice as large as that of the higher-order vibration method. Therefore, the robustness of the proposed method in tension estimation is considered to be inferior to that of the higher-order vibration method without a damper. The reason for this may be that the proposed method has two additional unknowns.

Experimental Verification

Experimental Condition

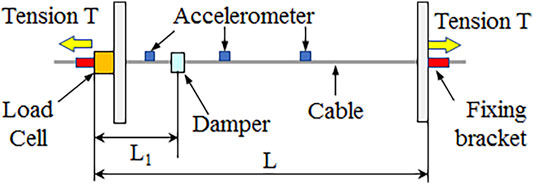
This section describes the experimental validation of the proposed method. The experimental setting is shown in Figure 9. The experiment was conducted using a horizontal cable with a length of 16.78 m. The distance between the two ends was considered as the cable length. A load cell was installed at the left end. The tension value measured by the load cell was considered as the true tension of the cable. The cable was hit by a hammer between the damper position and the right end. Additionally, the acceleration histories were measured by accelerometers. The natural frequencies were measured by reading the peak frequencies of the acceleration Fourier spectra.

FIGURE 9

FIGURE 9. Experimental setting.

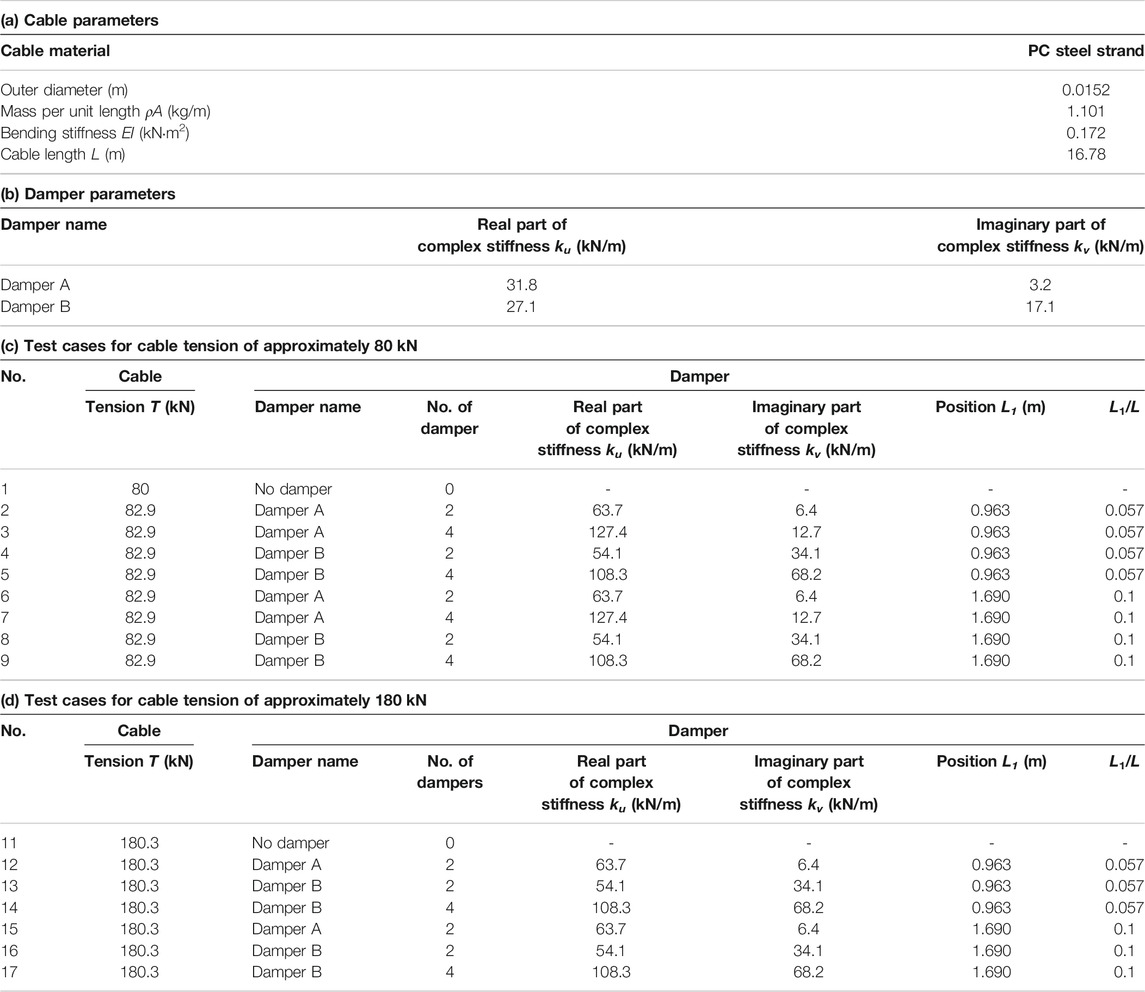
The cable parameters are presented in Table 2a. The PC (prestressed concrete) steel strand was used for the cable, because it is used in actual bridge cables.

TABLE 2

TABLE 2. Parameters of test specimen and test cases in experimental verification.

The damper parameters are listed in Table 2b. Two damper types were used, and both types were modelled with a high-damping rubber damper.

The test cases are listed in Table 2c and d. Table 2c lists nine cases, from No. 1 to No. 9, with a tension of approximately 80 kN. Table 2d lists seven cases, from No. 11 to No. 17, with a tension of approximately 180 kN. Cases No. 1 and No. 11 are the cases without a damper. The stiffness of the damper was changed by combining two or four sets of dampers. Moreover, two cases were considered with regard to the damper position. Because the damper is typically placed close to the cable end, in the experiment, the damper positions were set close to the left end.

Table 3 lists the first to seventh measured natural frequencies. The seventh mode natural frequency of No. 15 is blank because it was difficult to read.

TABLE 3

TABLE 3. Measured natural frequencies.

Results

The measured natural frequencies were input into the proposed method, and the cable’s tension, bending stiffness, and damper parameters were estimated. Figure 10 shows the results obtained for the cases with a tension of approximately 80 kN. Figure 11 shows the results obtained for the cases with a tension of approximately 180 kN. The estimation accuracy of the tension is expressed as the ratio of the estimated values to the true values, which are measured directly by the load cell. Moreover, the bending stiffness and damper parameter estimation accuracy is expressed as the ratio of the estimated value to the design value. The design values were calculated using the design equation. The tension and bending stiffness results obtained by the higher-order vibration method were also considered for comparison.

FIGURE 10

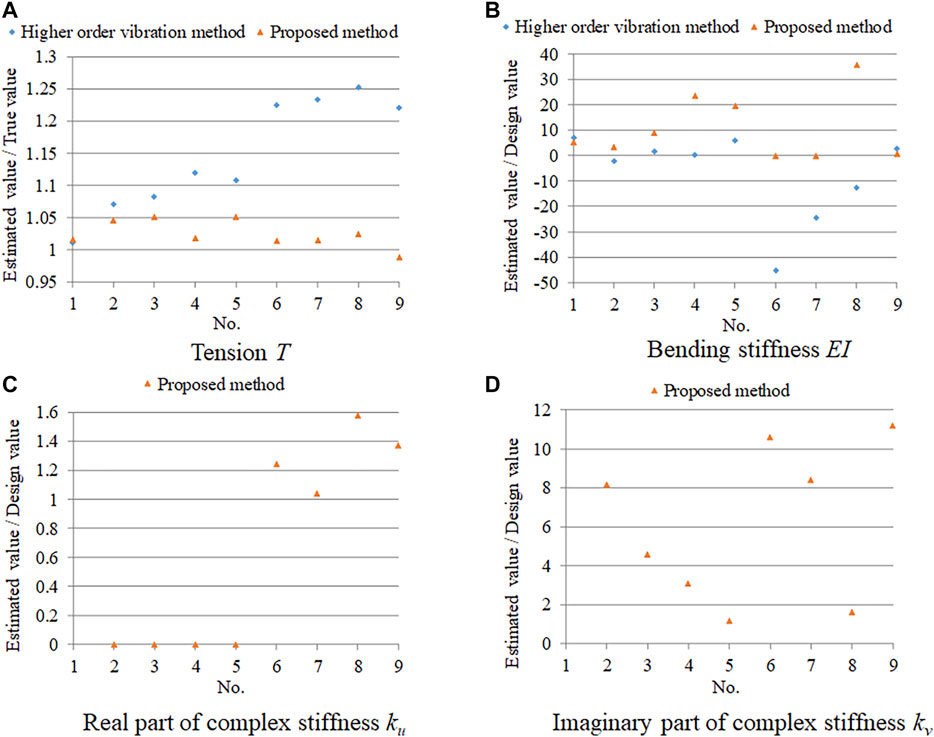
FIGURE 10. Estimation accuracy for Nos. 1–9 (80 kN): (A) tension; (B) bending stiffness; (C) real part of complex stiffness; (D) imaginary part of complex stiffness.

FIGURE 11

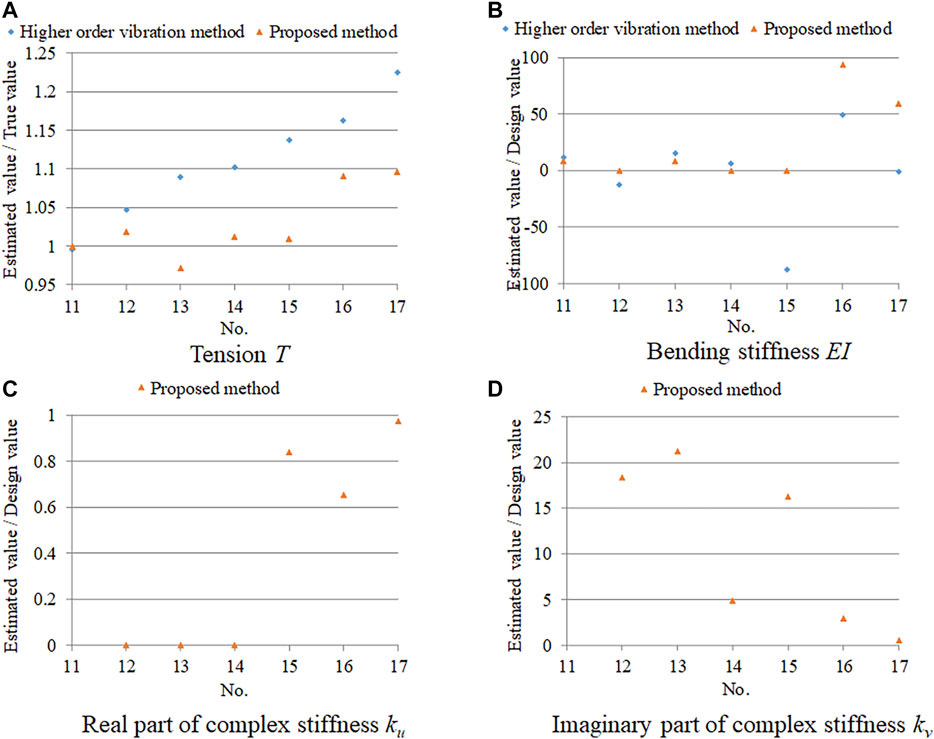
FIGURE 11. Estimation accuracy for Nos. 11–17 (180 kN): (A) tension; (B) bending stiffness; (C) real part of complex stiffness; (D) imaginary part of complex stiffness.

First, the tension estimation accuracy is discussed. In the case without a damper (Nos. 1 and 11), the accuracy achieved by the higher-order vibration method was approximately the same as that achieved by the proposed method, and also quite high. In both cases with a tension of 80 and 180 kN, respectively, the accuracy of the higher-order vibration method decreased as the stiffness of the damper increased and the damper position increased, because the higher-order vibration method is the method without a damper. In contrast, the accuracy of the proposed method was much higher in the case with dampers, and the estimation error was within 10%. If the two cases of Nos. 16 and 17 are excluded, the estimation error is within 5%.

Next, the estimation accuracy of the other three parameters is discussed. Similarly to the results obtained by numerical verification, the estimation accuracy of the bending stiffness and damper parameters was low. Therefore, it is concluded that the proposed method can only be used for tension estimation.

If the damper is detached from the cable and the tension is estimated using the higher-order vibration method, the tension can be estimated more accurately compared with the proposed method. However, with the proposed method, it is possible to estimate the cable tension without detaching the damper. The fact that the cable does not have to be detached is a great advantage in terms of work efficiency.

In this paper, the experimental verification was conducted rather than the verification using measurement data of the real bridges in order to test many cases with different damper location, damper parameter and tension force. In the future study, the verification by the field measurement of real bridge would be conducted.

Conclusion

This paper proposes a method for estimating the tension of a cable with a damper using the natural frequencies. In the proposed method, the damper does not have to be removed from the cable, and the cable tension is estimated simultaneously with the cable bending stiffness and damper parameters.

In Tension Estimation Method, the equations for calculating the natural frequency of a cable with a damper were derived from the vibration equation of a beam in tension. Owing to the existence of the damper, the theoretical natural frequency was determined as a complex value, that is, as a complex natural frequency. The real part of the complex natural frequency was an actual natural frequency, as measured in the experiment. The imaginary part of the complex natural frequency was determined as a term related to the envelope function of free vibration. Therefore, the equation for estimating the cable tension from the measured natural frequencies was developed such that the real parts of the complex natural frequencies matched the measured natural frequencies. This paper presents the procedure for estimating the tension from the natural frequencies. The proposed method adopts the method whereby the imaginary part of the complex stiffness is partially ignored, which makes the optimization problem simpler.

In Numerical Verification, the validity of the proposed method was investigated using numerical simulations. The natural frequencies of a cable with a damper were calculated by the eigenvalue analysis of the finite element method, and input to the proposed method. The estimation accuracy was investigated by taking the ratio of the estimated value to the true value, which was then input to the eigenvalue analysis. In total, 80 numerical models were established with eight cable models and 10 damper models.

The cable tension was estimated with high accuracy, but the other three parameters, namely, the bending stiffness of the cable and the two damper parameters, were difficult to estimate with high accuracy. The effect of partially ignoring the imaginary part of the complex natural frequency was investigated, and it was found that the estimation accuracy did not degrade by partially ignoring the imaginary part.

Then, sensitivity analysis was conducted. The estimation accuracy of the bending stiffness and damper parameters was low because these parameters had low sensitivity to the natural frequencies. Moreover, the tension estimation accuracy of the proposed method was high because the sensitivity of tension to the natural frequencies was also high, whereas the sensitivity of the other parameters was low.

The influence of the measurement error on the tension estimation accuracy was investigated. The proposed method achieved excellent tension estimation accuracy, even with the existence of measurement noise. Even when the measured natural frequencies contained 3% error, the tension estimation error was approximately 5%.

Finally, as described in Experimental Verification, the validity of the proposed method was confirmed by an experiment using a cable with a length of 16.78 m. There were 16 cases: two cases without a damper and 14 cases with a damper. Among the 14 cases with a damper, the tension estimation error of 12 cases was within 5% and that of the two remaining cases was within 10%.

The proposed method’s tension estimation for a cable with a damper is not as good as that of the higher-order vibration method for a cable without a damper. However, with the proposed method, it is possible to estimate the cable tension without detaching the damper. The fact that the cable does not have to be detached is a great advantage in terms of work efficiency.

In this study, the proposed method was verified for 80 numerical models and 17 experimental cases. However, the proposed method has not been verified for cases other than these 97 cases. In the future, the applicability of the proposed method to more cases would be verified. Furthermore, the verification using measurement data of real bridge would be also conducted.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

AF and HK developed the proposed method and the source code for estimating the cable tension, and carried out the numerical analysis. AF developed the source code for the finite element method and eigenvalue analysis. RK conducted the verification experiment.

Conflict of Interest

RK was employed by Shinko Wire Company, Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Ashwear, N., and Eriksson, A. (2014). Natural frequencies describe the pre-stress in tensegrity structures. Comput. Structures 138, 162–171. doi:10.1016/j.compstruc.2014.01.020

CrossRef Full Text | Google Scholar

Ashwear, N., and Eriksson, A. (2017). Vibration health monitoring for tensegrity structures. Mech. Syst. Signal Process. 85 (15), 625–637. doi:10.1016/j.ymssp.2016.08.039

CrossRef Full Text | Google Scholar

Chen, C.-C., Wu, W.-H., Chen, S.-Y., and Lai, G. (2018). A novel tension estimation approach for elastic cables by elimination of complex boundary condition effects employing mode shape functions. Eng. Structures 166, 152–166. doi:10.1016/j.engstruct.2018.03.070

CrossRef Full Text | Google Scholar

Chen, C.-C., Wu, W.-H., Leu, M.-R., and Lai, G. (2016). Tension determination of stay cable or external tendon with complicated constraints using multiple vibration measurements. Measurement 86, 182–195. doi:10.1016/j.measurement.2016.02.053

CrossRef Full Text | Google Scholar

Feng, Z., Wang, X., and Chen, Z. (2010). “A method of fundamental frequency hybrid recognition for cable tension measurement of cable-stayed bridges,” in 8th IEEE international conference on control and automation, Xiamen,China, June 9–June 11, 2010 (IEEE). doi:10.1109/ICCA.2010.5524186

CrossRef Full Text | Google Scholar

Javanbakht, M., Cheng, S., and Ghrib, F. (2019). Control-oriented model for the dynamic response of a damped cable. J. Sound Vibration 442, 249–267. doi:10.1016/j.jsv.2018.10.036

CrossRef Full Text | Google Scholar

Kim, B. H., and Park, T. (2007). Estimation of cable tension force using the frequency-based system identification method. J. Sound Vibration 304, 660–676. doi:10.1016/j.jsv.2007.03.012

CrossRef Full Text | Google Scholar

Krenk, S. (2000). Vibrations of a taut cable with an external damper. J. Appl. Mech. ASME 67, 772–776. doi:10.1115/1.1322037

CrossRef Full Text | Google Scholar

Lazar, I. F., Neild, S. A., and Wagg, D. J. (2016). Vibration suppression of cables using tuned inerter dampers. Eng. Structures 122, 62–71. doi:10.1016/j.engstruct.2016.04.017

CrossRef Full Text | Google Scholar

Ma, L. (2017). A highly precise frequency-based method for estimating the tension of an inclined cable with unknown boundary conditions. J. Sound Vibration 409, 65–80. doi:10.1016/j.jsv.2017.07.043

CrossRef Full Text | Google Scholar

MathWorks (2020). MATLAB documentation, multiStart. Available at: https://jp.mathworks.com/help/gads/multistart.html (Accessed March 23, 2020).

Google Scholar

Pacheco, B. M., Fujino, Y., and Sulekh, A. (1993). Estimation curve for modal damping in stay cables with viscous damper. J. Struct. Eng. 119 (6), 1961–1979. doi:10.1061/(asce)0733-9445(1993)119:6(1961)

CrossRef Full Text | Google Scholar

Shi, X., and Zhu, S. (2018). Dynamic characteristics of stay cables with inerter dampers. J. Sound Vibration 423, 287–305. doi:10.1016/j.jsv.2018.02.042

CrossRef Full Text | Google Scholar

Shinke, T., Hironaka, K., Zui, H., and Nishimura, H. (1980). Practical formulas for estimation of cable tension by vibration method. Proc. Jpn. Soc. Civil Eng. 1980, 25–32. doi:10.2208/jscej1969.1980.294_25

CrossRef Full Text | Google Scholar

Shinko Wire Company, Ltd (2020). Tension measuring technique for outer cables. Available at: http://www.shinko-wire.co.jp/products/vibration.html (Accessed March 23, 2020).

Google Scholar

Thyagarajan, S. K., Schulz, M. J., Pai, P. F., and Chung, J. (1998). Detecting structural damage using frequency response functions. J. Sound Vibration 210, 162–170. doi:10.1006/jsvi.1997.1308

CrossRef Full Text | Google Scholar

Yamagiwa, I., Utsuno, H., Endo, K., and Sugii, K. (2000). Identification of flexural rigidity and tension of the one-dimensional structure by measuring eigenvalues in higher order. Jsmet 66 (649), 2905–2911. doi:10.1299/kikaic.66.2905

CrossRef Full Text | Google Scholar

Yan, B., Chen, W., Yu, J., and Jiang, X. (2019). Mode shape-aided tension force estimation of cable with arbitrary boundary conditions. J. Sound Vibration 440, 315–331. doi:10.1016/j.jsv.2018.10.018

CrossRef Full Text | Google Scholar

Yang, Y., Wang, X., and Wu, Z. (2015). Experimental study of vibration characteristics of FRP cables for long-span cable-stayed bridges. J. Bridge Eng. ASCE 20 (4). doi:10.1061/(asce)be.1943-5592.0000656

CrossRef Full Text | Google Scholar

Zarbaf, E, Norouzi, M., Allemang, R., Hunt, V., and Helmicki, A. (2017). Stay cable tension estimation of cable-stayed bridges using genetic algorithm and particle swarm optimization. J. Bridge Eng. 22 (10).

Google Scholar

Zarbaf, E, Norouzi, M., Allemang, R., Hunt, V., Helmicki, A., and Venkatesh, C. (2018). Vibration-based cable condition assessment: a novel application of neural networks. Eng. Structures 177, 291–305. doi:10.1016/j.engstruct.2018.09.060

CrossRef Full Text | Google Scholar