Modeling the Dynamic Behavior of Track Transitions Along Shared Track Corridors

This paper presents findings from an analytical modeling effort undertaken to study the dynamic response of track transitions along shared-track corridors. A recently developed train-track-bridge model was used for this purpose. First, the model predictions are verified using field instrumentation data as well as data from other published literatures. Subsequently, the model is used to analyze the dynamic response of a typical bridge approach under the passage of a high-speed passenger train as well as six different freight trains comprising different freight car types. A speed sensitivity analysis of a freight train comprising one specific freight car type is also carried out. Geometric configuration of different freight trains is assessed as well as weight and speed of operation. Different track response parameters, including vertical displacement and rail-tie reaction force, are considered to highlight the differences in the track dynamic behavior under freight and passenger train loading. Analyses in both time and frequency domains illustrate the difference in track behavior under freight and passenger train loading. The significance of gap development at the tie-ballast interface near track transitions has been emphasized by illustrating the effect of tie gap on the dynamic track behavior. The paper concludes by emphasizing the importance of special consideration to track dynamic behavior for shared-track corridors.

Introduction

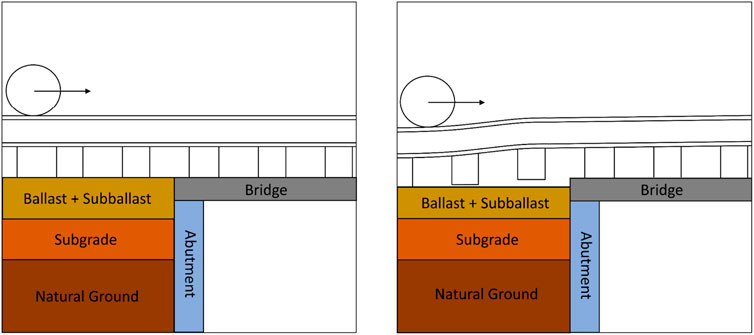
A track transition zone is defined as a section of track which marks a location of discontinuity in certain track characteristics. One common example is a bridge approach, where the track “transitions” from being supported by the embankment, to being supported by the bridge abutment. This sudden change in the track support conditions, and hence stiffness/modulus, leads to significant difference in the track behavior as a train traverses across the transition zone. Other examples include: tunnels, culverts, turnouts, frogs, etc. Due to the sudden change in track characteristics and track behavior under loading, track transition zones often experience expedited geometry deterioration as well as degradation in the structural health of the system. To overcome this challenge railroad companies often must dedicate significant resources for regular maintenance and resurfacing of track transitions.

Railroad bridge approaches can be subjected to millions of wheel load applications during their service lives; discontinuities in certain track characteristics such as track stiffness can lead to amplified wheel loads under train passage. The “stiff” side of a track transition, i.e., the bridge deck, undergoes lower deformations under train loading when compared to the “softer” approach where track substructure rests directly on an embankment fill, or in-place subgrade. This differential transient deflection can lead to differences in the rail profile, thus causing impact loading as the train goes across the interface. Figure 1 presents that at track transitions where hanging ties are, tracks sometimes experience impact loading conditions and nonlinear track components. The problem of differential transient movement and the resulting increased dynamic loading can present a negative feedback loop scenario, which results in cumulative deterioration of the track quality. The differential transient movement ultimately leads to the development of the “Bump at the End of the Bridge” problem (Woodward et al., 2007; Luangboriboon et al., 2008; Banimahd et al., 2012; Hou et al., 2021). According to the ASCE Infrastructure Report Card (2017), in the United States railroad network alone, there are over 100,000 bridges, where track transition related problems can be encountered. Accordingly, adequate monitoring and maintenance of railroad bridge approaches is critical to efficient performance of the United States railroad network.

FIGURE 1

FIGURE 1. Degradation of track transition zone.

Although detailed discussion of different factors governing poor performance of track transitions is not the primary focus of this manuscript, this aspect has been discussed in great details by the following researchers: Li and Davis (2005), Tutumluer et al. (2012), Mishra et al. (2014), Mishra et al. (2017), and Boler et al. (2018). According to Nicks (2009), remedial measures aimed at mitigating the bump problem at railway bridges can be divided into different interrelated categories, such as: 1) reducing approach settlement, 2) decreasing the track modulus on the bridge deck, 3) increasing the modulus of the approach section, 4) reducing ballast wear and movement, and 5) increasing track damping on the bridge deck. Researchers have also suggested converting open-deck bridges to ballast-deck ones (Hyslip et al., 2009), constructing approach slabs (Sharpe et al., 2002), as well as applying chemical grouts (Woodward et al., 2007; Hyslip et al., 2009) and stone blowing (Chrismer 1990; McMichael and McNaughton 2003) as alternatives to mitigate track transition problems.

The problem at railroad track transitions can become even more critical when the track is used by trains with different speeds, load magnitudes, and axle configurations. Shared passenger and freight corridors, known as joint corridors or mixed traffic lines, are becoming more common nowadays and require more attention for maintaining rail network safety and reliability. Lin and Saat. (2017) classified these corridors into three categories: 1) shared track; 2) shared right of way, and 3) shared corridor. Shared corridor refers to a track system with the distance between adjacent track centers in the range of 7.62–60.96 m (25–200 ft). Shared track refers to a track system where both track as well as infrastructure get shared between the passenger and freight trains. Finally, shared right of way refers to a system marked by sharing of the infrastructure only. Lin and Saat (2017) recommended that shared track rail corridors must provide an efficient use of existing infrastructure and smooth transfer of freight and passengers. Joint corridors can face several different types of operational challenges. For example, Caughron et al. (2012) found that there is a higher frequency on trespasser-train accidents at shared track rail corridors. Harrod (2009) reported that conflicts between freight trains traveling at different speeds are as common as conflicts between freight and passenger train schedules.

In many countries, the demand for shared track rail corridor is clearly on the increase. In Mexico, majority of the existing railroad infrastructure is dedicated to freight transportation, while passenger transit is mainly achieved on abandoned tracks or corridors with additional capacity. Many Mexican cities are facing land use and financial problems; Camacho and Martin (2015) specified that there is a demand for integrated transportation systems, and one of the solutions is to apply mixed rail operation on the existing infrastructure. Borndörfer et al. (2016) reported that track infrastructure is shared substantially by freight and passenger trains in Germany. In Turkey, sharing High Speed Train (HST) infrastructure with both freight and passenger trains is advised; it is believed to be practical and economically efficient, especially for transporting small cargo and postal mail using HSTs (Ertem and Özcan, 2016). Warg (2012) indicated that there are requirements for increasing the maximum speed of HST and adding more new regional stops for flexibility in Sweden. Ramaraju (2013) stated that train speed and capacity are critical problems in India because of challenges associated with track sharing between passenger and freight trains. With gradually increasing demand for a reliable passenger rail network in the United States, several freight-only rail lines are being upgraded for joint freight and passenger train operation. As speed of operation for freight trains is significantly lower than that for passenger trains, the track infrastructure requires significant upgrades along joint corridors.

In the United States, there is approximately 140,000 mileage of track shared by passenger and freight trains (ASCE Infrastructure Report Card 2017). The most important challenge of operating shared track rail corridor trains at track transition zones is that passenger trains traveling at relatively high speeds and heavy freight trains running relatively at low speeds apply dynamic loads with different characteristics on the same track structure. According to Coelho et al. (2011) the extent of track structure impacted by dynamic loads becomes larger as the train speed increases at transition zones. Tutumluer et al. (2012) reported that at bridge approaches along shared track rail corridors, differential settlement is still the most common and important problem, which could result in extreme dynamic loading magnitudes and lead to tie deterioration, rail seat pad deterioration and rail surface fatigue. Li (2013) pointed out that the accident risk would be higher when freight trains travel at a higher speed through locations like turnouts and rail joints which would produce severe dynamic impacts on trains and freight. Eliminating differential settlement would result in less maintenance required and this would reduce the associated maintenance costs and accident risks. This elimination could further help plan passenger and freight train operation schedules with no delays. Although many research efforts have focused on issues related to track transition zones or shared track rail corridor, studies of track transition zones on shared track rail corridors are limited.

Numerous models have been developed by researchers over the years to study dynamic track response under loading. For example, Bian et al. (2018) developed a 2.5-D finite element model to simulate the ground vibrations induced by High-Speed Rail (HSR). Huang et al. (2014) developed a fully coupled 3-D train track soil model including three-dimensional continuum representation of the subgrade. Zhai et al. (2013) developed a model to analyze train-track-bridge dynamic interactions, accounting for the problem of continuity of the track system. Varandas et al. (2011) proved that the existence of a group of consecutive hanging crossties was the main cause for higher displacements registered at transition zones. Wang and Markine (2018) developed an iterative procedure combining finite element model and an empirical settlement model of ballast to analyze the effect of differential settlement on track dynamic response at transition zones. Recently, Hou et al. (2021) developed an analytical train-track-bridge model, which considers the coupled effect of open track and bridge deck together as well as the nature of track substructure being discretely supported by ties. Although there have been numerous studies on addressing the sudden stiffness change at bridge approaches, there is an increasing need to address problems such as unsupported hanging ties and differential settlement. The validated model by Hou et al. (2021) can take these aspects into consideration. The current study uses a newly developed analytical train-track-bridge model to study the dynamic behavior of railroad tracks along shared-track corridors.

Train-Track-Bridge Analytical Model

Development of Discretely Supported Train-Track-Bridge Model

A new train-track-bridge model was recently developed (Hou et al., 2021) comprising the following key components: train, track and open-deck bridge (see Figure 2). The train is assumed to travel from the embankment side to the bridge (therefore, entering the bridge from the embankment). For this study, any track location that is not affected by the presence of the bridge, is termed as “Open-Track Location (OTL)”. On the other hand, any location on the track that is affected by the presence of the bridge (any point that constitutes the transition zone) is termed as “Near-Bridge Location (NBL)”. The working hypothesis during the development of this model was that there will be a difference in the track dynamic behavior between the OTL and the NBL. Note that validation of this model was carried out using field instrumentation data collected as part of a research project undertaken at the University of Illinois that focused on investigating different factors contributing to the problem of differential movement at track transitions. Findings from the above-mentioned research project have been presented in multiple manuscript over the past decade (Mishra et al., 2012; Tutumluer et al., 2012; Mishra et al., 2014; Mishra et al., 2016; Tutumluer et al., 2016; Boler et al., 2018; Hou et al., 2021). In-line with the field instrumentation effort, a point lying 18.3-m (60-ft.) away from the bridge abutment was taken to present OTL, whereas a point lying at a distance of 4.6 m (15 ft) from the bridge abutment was taken as being representative of NBL.

FIGURE 2

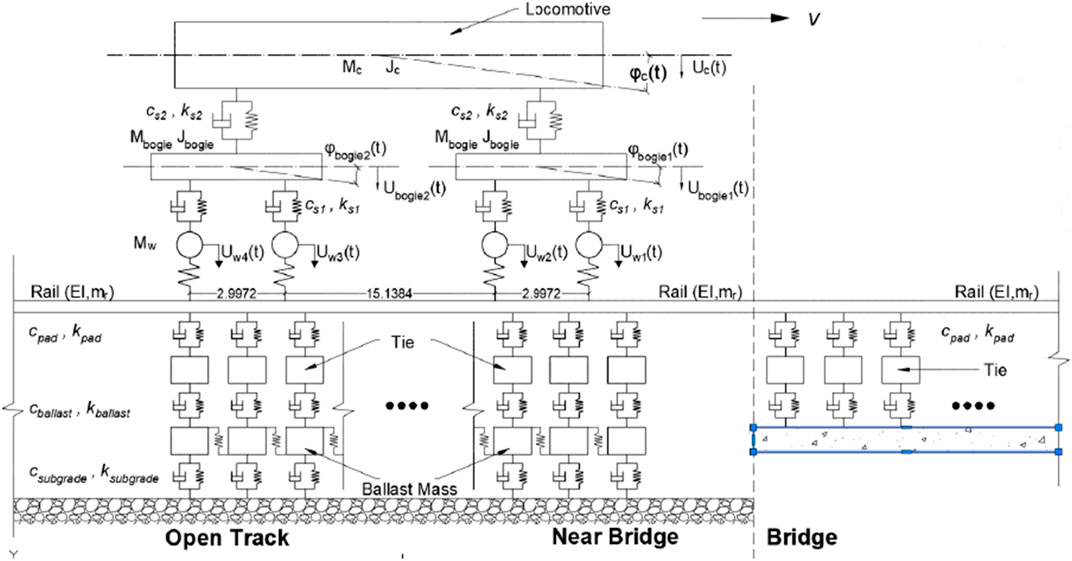
FIGURE 2. Schematic of discretely supported train-track-bridge model (from Hou et al., 2021).

The train moves from the OTL through the NBL to the bridge deck at a constant speed of $v$. Track response is monitored at the two above-mentioned representative locations (18.3 and 4.6 m from the bridge abutment, respectively) to investigate how different train operational parameters affect the dynamic track response. Amtrak’s Acela Express passenger train operating along the Northeast Corridor was chosen as the representative passenger train in this study. An Acela Express train set includes two locomotives at each end of the train and six passenger-cars in the middle. Beside modeling of the Acela Express passenger trains, six different configurations of freight trains were also considered in this study, each comprising a different type of freight car. To save time and computational effort, the length of a typical freight train was reduced significantly in the model; each freight train was assumed to comprise two locomotives (one at each end) and six freight cars in between.

In the analytical model, the car body, bogies and wheel sets are assumed to be non-deformable rigid bodies that only experience vertical and pitch movements (Figure 2). Each passenger car, freight car as well as locomotive with two-axle bogies (for passenger trains) was modeled as a 10 degree-of-freedom system; locomotives with three-axle bogies (for freight trains) were modeled as 12 degree-of-freedom systems. The rail was modeled as an infinite Euler beam. At the OTL, the rail is discretely supported by three layers of visco-elastic springs and dampers, representing rail pads, ballast, and soil, and two layers of masses, representing the crossties and ballast. The crossties and ballast have been represented in the model as non-deformable rigid bodies; shear interaction between the ballast particles is considered. Comparing to the open track embankment side, ballast layer is not considered on bridge since the field instrumented bridge is an open deck bridge, the crossties directly sit on top of the rigid bridge deck. Therefore, on the bridge deck, the rail is discretely supported by two layers of visco-elastic springs and dampers, corresponding to the rail pad and the crossties.

Detailed discussion of different model components has not been presented in the current manuscript for the sake of brevity. Interested readers are recommended to refer to Hou et al. (2021) for such information.

One of the unique capabilities of the newly developed model concerns its ability to model the presence of gaps at the tie-ballast interface. As has been reported by researches in the past (Coelho et al., 2011; Varandas et al., 2011), presence of a gap at the tie-ballast interface creates a condition known as the “hanging tie condition” and can significantly affect the dynamic response of the track under train loading. The newly developed train-track-bridge model is capable of simulating this behavior where certain ties may not be in full contact with the ballast in an unloaded situation. When a load is applied, the rail bends, thereby, gradually bringing the tie into contact (depending on the magnitude of the wheel load as well as the tie gap) with the underlying ballast layer. This phenomenon is schematically represented in Figure 3. Figure 3A shows a case where the tie is in complete contact with the underlying ballast layer, and no gap exists at the tie-ballast interface. Accordingly, the force vs. displacement curve starts from the origin, and has a constant slope. Figure 3B, on the other hand, represents a scenario where the tie is not in complete contact with the ballast layer in the absence of a load. When a load is applied to the rail, no reaction force is immediately generated at the tie-ballast interface; part of the load goes into closing of the gap. As a result, the reaction force at the tie-ballast interface remains zero until the gap is completely closed. Once the gap is closed, the reaction force develops at a constant slope, just like it would in the case where no gap existed at the tie-ballast interface. Figure 3C schematically illustrates the entire scenario, as reproduced from Sussmann et al. (2001). The new train-track-bridge model developed by Hou et al. (2021) can successfully capture this behavior. In-line with findings from the field instrumentation effort, the current study considers a case where a gap of 1.5 mm exists under the tie at the NBL. The first sixteen (16) ties at the end of the approach (lying at the embankment-bridge interface) have been modeled in this study with a gap of 1.5 mm at the tie-ballast interface. Complete mathematical representation of the model has not been provided in this manuscript for the sake of brevity, and can be found elsewhere (Hou et al., 2021).

FIGURE 3

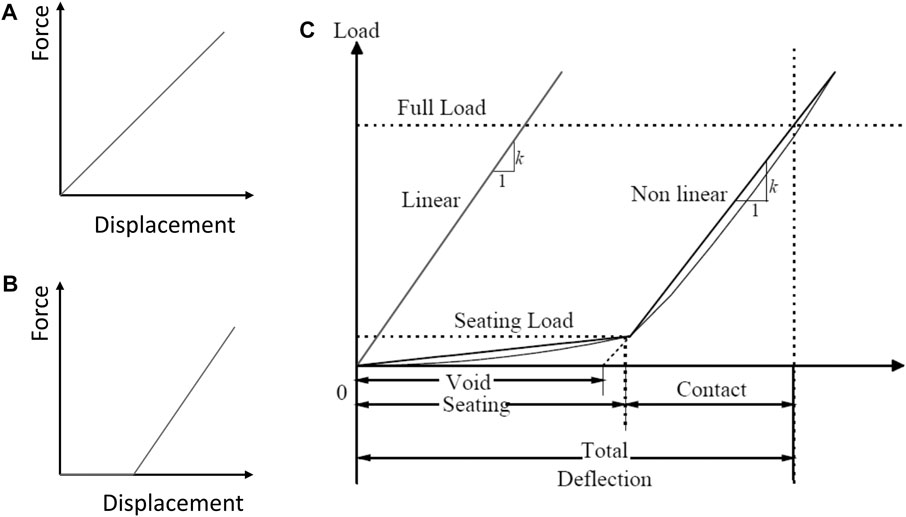
FIGURE 3. Schematic of force displacement behavior at the tie-ballast interfae: (A) No gap; (B) In the pressence of a gap; (C) Theoretical representation of the behavior (reproduced from Sussmann et al., 2001).

Model Validation

Once the model development was complete, the first task involved validating the model against field instrumentation data, and/or other validated models. Results from the validation effort have been presented in the current section.

Model Results of Passenger Train Passage

Model validation was carried out using field instrumentation data from a recently completed research study at recent research effort carried out at the University of Illinois in the United States. This research study involved instrumentation of several bridge approaches using Multi-Depth Deflectometers (MDDs) and strain gauges to identify different factors contributing to the problem of differential movement at bridge approaches. Three of the instrumented bridge approaches were in Chester, Pennsylvania, along Amtrak’s Northeast Corridor. At these instrumentation locations, Amtrak’s Acela Express train has an operating speed of approximately 177 km/h (110 mph). Field instrumentation data collected from the Upland Street bridge approach were used for the purpose of model verification and calibration. Details regarding the instrumentation effort and relevant findings have been presented elsewhere (Mishra et al., 2012; Tutumluer et al., 2012; Mishra et al., 2014; Mishra et al., 2016; Tutumluer et al., 2016; Boler et al., 2018; Hou et al., 2021).

Figure 4 presents schematics of an Acela Express passenger train, showing the notations for car axle spacing and distance between cars. As seen from the figure, the locomotives for passenger trains were taken to comprise a total of four axles (two bogies; two axles per bogie). However, the number of axles on the locomotive was changed to six (two bogies: three axles per bogie) while simulating the passage of freight trains. It should be noted that in the United States, locomotives with 2-axle as well as 3-axle bogies are commonly used in freight train sets. Both passenger as well as freight cars were modeled with four axles each. The length of freight trains was significantly shortened for the sake of computational efficiency (the train sets were taken to comprise only six cars between the two locomotives).

FIGURE 4

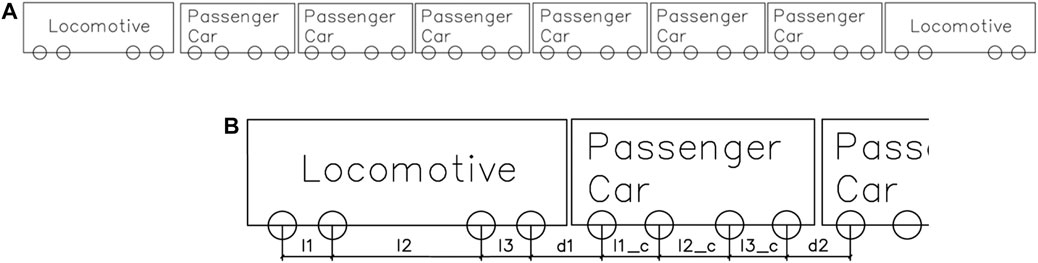
FIGURE 4. Schematic representation of the acela express train highlighting the axle spacings considered in this model: (A) Layout of the entire train; (B) Zoomed-In view showing the axle spacings.

The section of track modeled included a total of one thousand (500 on the embankment; 500 on the bridge deck) crossites, placed at a center-to-center spacing of 0.61 m (24 in.). The model-calculated track responses include transient deflection of different components, reaction forces, velocities, and corresponding accelerations. To obtain realistic dynamic responses from the model, vehicle and track parameters need to be chosen with physical relevance. Model results were validated comparing the transient deflections predicted from the model with those recorded in the field.

The track and passenger train parameters used as model inputs are listed in supplement data. Some track properties, such as crosstie spacing and rail properties, were selected to match the values from the instrumentation site (Upland Street bridge approach near Chester, Pennsylvania, United States). The other track properties, such as spring stiffness and ballast mass, etc., were selected based on previously published studies (Cantero et al., 2016; Cai et al., 2019). Parameters for the Amtrak Acela Express were selected from a previously published research report (Judge et al., 2018).

Figure 5A shows a comparison between the model-predicted simulation results for the rail transient vertical displacement with those measured in the field (location = OTL; field data collected in January, 2015). Just like the field data, the model-predicted displacement time history contains thirty-two (32) peaks, corresponding to the thirty-two axles on an Acela Express train. The higher peaks in the displacement time history correspond to the two locomotives with significantly higher axle loads compared to the passenger cars. Figure 5B shows a similar comparison for the NBL. It should be noted that sixteen (16) ties corresponding to the NBL were modeled with a gap of 1.5 mm at the tie-ballast interface. As seen from Figure 5B, the peak transient rail displacements at the NBL are significantly higher than those at the OTL. While the model results closely match the peak magnitudes recorded in the field, there is a difference between the field and model results when one considers the points lying between two adjacent peaks. In other words, the model does not adequately capture the “rebound” behavior of the track between the passage of two consecutive wheels. Nevertheless, since the current study primarily focuses on the peak displacement magnitudes, predictions from the newly developed train-track-bridge model are deemed to be adequate.

FIGURE 5

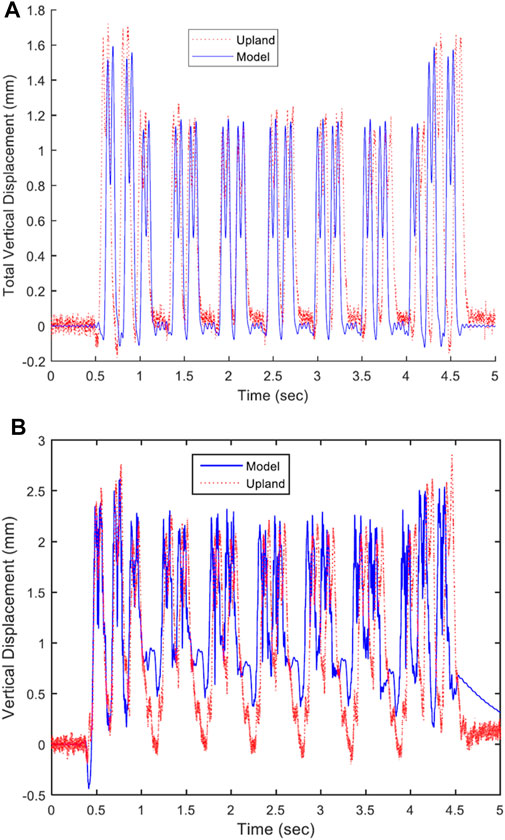
FIGURE 5. Comparisons between field-measured and model-predicted transient displacements under the passage of an Acela Express passenger train at two different locations: (A) OTL (B) NBL (from Hou et al., 2021).

Model Results of Freight Train Passage

As already mentioned, the primary objective of this study was to investigate the effect of combined freight and passenger train loading on track dynamic behavior at bridge approaches. Accordingly, it was also important to verify the accuracy of the model-predicted results by comparison with field data or other validated numerical models. Unfortunately, no reliable field data was available for model verification under freight train loading. Accordingly, the researchers opted to verify the model predictions against data reported in the literature.

Six different categories of freight cars, namely: box cars, tank cars, flat cars, hopper cars, covered hopper cars, and gondola cars, were selected for model simulation. All freight cars simulated in this study were assumed to be fully loaded. The train sets were assumed to comprise two locomotives (each with two bogies; three axles per bogies) at either end. The total weight of one locomotive was taken to be 2,134 kN (480 kips). As already mentioned, the freight trains simulated in this study were assumed to have a similar configuration to that of the Acela express trains (shown in Figure 4A). The primary difference was that the freight locomotives comprised three axles per bogie. For modeling purposes, the car geometry (in terms of axle spacing, wheel load, etc.) was varied to match the freight car type being simulated. To eliminate boundary effects associated with the of train entering and leaving the track section, the model was defined to span over a total of one thousand (1,000) ties. Five hundred (500) of the ties were on the embankment, whereas the remaining 500 were on the bridge deck.

Axle configurations and other relevant parameters for the locomotives as well as different freight car types were obtained through one of the major freight railroad companies in the United States (BNSF Equipment, 2020 Webpage, accessed; BNSF Locomotives, 2020 Webpage, accessed). A list of all the car parameters used in the model has not been included in the main body of the paper for the sake of brevity (the list is provided as supplement data). Suspension system parameters for the vehicles were selected from previously published literature (Martino, 2011; Lou et al., 2012; Zeng et al., 2016; Bosso et al., 2018; Chen and Fang, 2019).

Table 1 lists the parameters used in the model for each freight train passage, including speed of operation, and total weight of an individual freight car. All the freight cars were assumed to be fully loaded. As seen from Table 1, both 263-kip (1,169.9-kN) and 286-kip (1,272.2-kN) car types were considered during the modeling effort. Also, operational speeds for the different train sets were taken based on common freight train speed in the United States. According to the FRA (2013), the average freight train speed up to 60 mph can realize the revenue potential identified. Figure 6 shows the model-predicted displacement time histories under the passage of a freight train comprising gondola cars only (speed of operation = 80.5 km/h). As seen from the figure, the transient rail displacements at the NBL are significantly higher than those at the OTL. Part of this can be attributed to the presence of the gap (gap magnitude = 1.5 mm) at the NBL tie-ballast interface. Interestingly, no significant difference between the peak transient displacements under locomotive or freight car loading was observed (the vertical displacement time histories are of almost equal height within a subplot). This can be attributed to similar loads per axle. For example, the static load of a freight locomotive is 2,134 kN (480 kips). With a 6-axle configuration, this results in 355.7 kN (80 kips) per axle, or 177.8 kN (40 kips) for wheel. On the other hand, a fully loaded freight car weighing 1,272.2 kN (286 kips) has a 4-axle configuration, thus resulting in 318.1 kN (71.5 kips) per axle (159 kN or 35.75 kips per wheel). Accordingly, there is only about 19 kN difference between the wheel loads for a freight locomotive and a fully loaded hopper car. This, combined with the dynamics of car body movement, may have resulted in the difference between the peak transient rail deflections being not significant.

TABLE 1

TABLE 1. Parameters of freight trains passage.

FIGURE 6

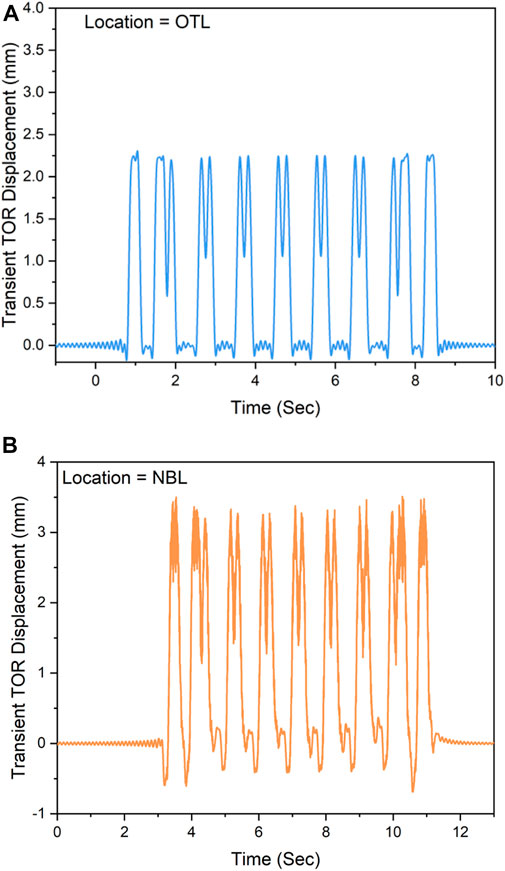
FIGURE 6. Model-predicted transient rail displacement time histories under the passage of a freight train comprising Gondola cars only (speed of operation = 80.5 km/h): (A) OTL; (B) NBL.

Before the any further analysis can be conducted on the effects of different car configurations on the track dynamic behavior, it is important to first study the effect of train speed on the model-predicted dynamic response. This was carried out by comparing the model-predicted track response parameters under the passage of a freight train (gondola cars only) with the speed varying between 64.4 km/h (40 mph) and 96.6 km/h (60 mph). Results from these comparisons have been plotted in Figure 7. As seen from the figure, there is a significant difference in the transient rail displacements between the NBL and OTL. However, as the speed is increased from 64.4 km/h (40 mph) to 96.6 km/h (60 mph), no significant difference in the transient rail displacements is observed. This clearly establishes that in this study train speed does not affect transient rail displacement significantly. This observation is likely to change as the train speed approaches the track critical speed.

FIGURE 7

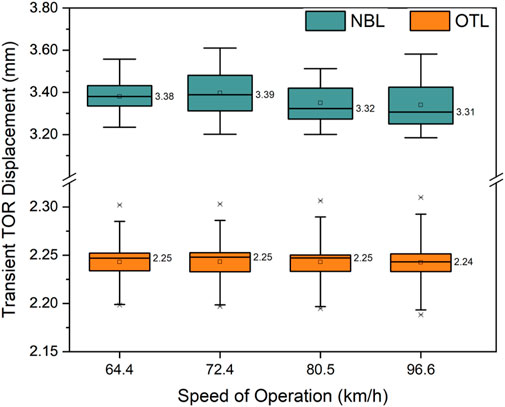
FIGURE 7. Box plots showing the effect of train speed on transient rail displacement for a freight train set comprising gondola cars.

Table 2 lists the peak displacements corresponding to the passage of each freight train, and shows that a freight train comprising Hopper cars corresponded to the maximum peak transient rail displacement. Table 2 also shows the normalized peak transient displacement values per kN of wheel load. This normalization has been performed to account for the fact that different freight car types were assigned different weights during the model simulations. Several different trends can be observed from Table 2. For example, comparing the cases of a train with Hopper Cars vs. Covered, Hopper cars, it can be seen that the only difference in the input parameters concerns the operating speed (64.4 kmph for the Hopper Car; 96.6 kmph for the Covered Hopper Car). Even though the speed of operation varies significantly, the peak transient displacement hardly changes between the two cases (1.67 x 10⁻² mm/kN vs. 1.66 x 10⁻² mm/kN). This is in agreement with the data shown in Figure 7. Additionally, for freight cars with the same total weight as well as speed of operation (Box Car, and Gondola Car in Table 2), the normalized peak deflection still shows some variation (1.52 x 10⁻² mm/kN vs. 1.45 x 10⁻² mm/kN). The only model parameters that are different between these runs concern the geometric configuration of the train axles (axle spacings, etc.). Accordingly, this data clearly establishes that the peak transient rail displacement values depend not only on the wheel load magnitudes, but also on the geometric configuration of the car.

TABLE 2

TABLE 2. Peak rail displacement comparison between freight trains at OTL.

As already mentioned, no reliable first-hand field data was available to verify the model predictions for freight trains. Accordingly, the researchers relied on peak transient rail displacement values published in the literature to check the accuracy of the model-predicted values. Figure 8 presents a comparison between the transient rail displacement values under freight trains from the current study and those published in the literature. Table 3 lists the train operational characteristics reported by different studies in the literature along with the corresponding peak transient rail displacements. Some of the studies considered tie support conditions by incorporating gaps at the tie-ballast interface. For example, Shi et al. (2013) studied considered at 4-mm gap at the tie-ballast interface during their analysis. Zakeri et al. (2020) also considered fully supported as well as unsupported (gap = 0.8 mm) ties in their analysis. Several of the other studies reported findings from field instrumentation data. Comparing the peak transient rail displacements predicted by the current train-track-bridge model to those in the literature, the values are similar. This clearly establishes the current train-track-bridge model developed by Hou et al. (2021) as a viable analysis tool for studying track dynamic response under different types of train loading.

FIGURE 8

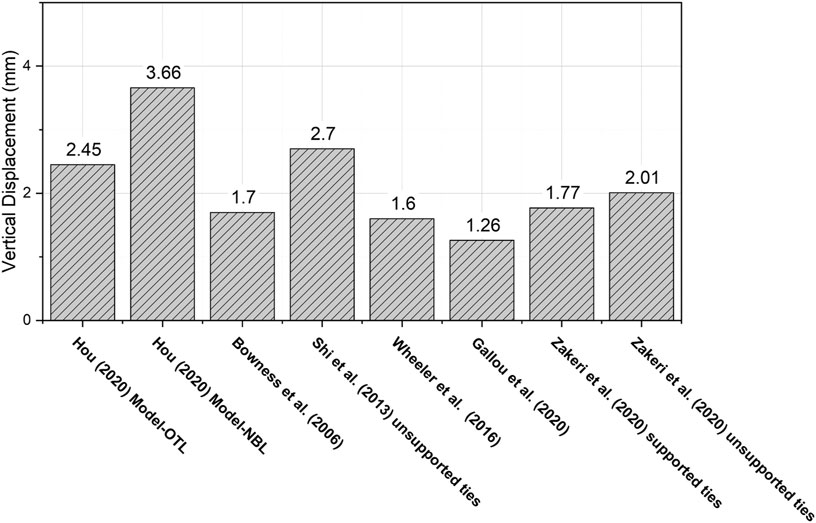
FIGURE 8. Comparison of rail vertical displacements with freight trains passage predicted by model and obtained from other studies.

TABLE 3

TABLE 3. Freight trains speed and axle load in different studies.

Simulation of Freight and Passenger Train Passage on Shared Track Rail Corridors

Once the model predictions were verified for both passenger as well as freight train sets, the next step involved comparing the track dynamic response parameters under the passage of passenger and freight trains. The primary objective here was to study how the passage of different train types will affect track behavior along a shared track corridor. As bridge approaches continue to present significant challenges with respect to track quality and maintenance scheduling for passenger as well as fright tracks, it is critical to study how the behavior of track transitions such as bridge approaches would be affected due to joint application of passenger and freight train loading. Data from different model runs have been analyzed in this section, and relevant inferences have been drawn. Note: positive and negative responses shown in the following figures represent downward and upward movements, respectively.

Rail Vertical Displacement Analysis

Figure 9 shows box plots of the peak transient rail displacements predicted by the model under the passage of different freight train sets as listed in Table 2. The box plots clearly illustrate that freight trains with heavier loads result in larger peak transient rail displacements at both the OTL as well as the NBL. It should be noted that all freight train sets were modeled with the same locomotive type. The only differences were in the car weights (box cars, tank cars, and gondolas were modeled in the 263-kip variant) and the speed of operation. It was already established through Figure 7 that train speed does not have a significant effect on the peak transient rail displacement. Accordingly, any difference observed in the box plots in Figure 9 can be attributed to differences in the car weights and/or in the geometric configuration of the axles. The peak rail displacements recorded for the Acela Express were significantly lower than those under the freight train, both at the NBL and the OTL. Therefore, from the perspective of transient track displacement, shared track corridors are likely to experience significantly higher displacements under the heavier freight train loading.

FIGURE 9

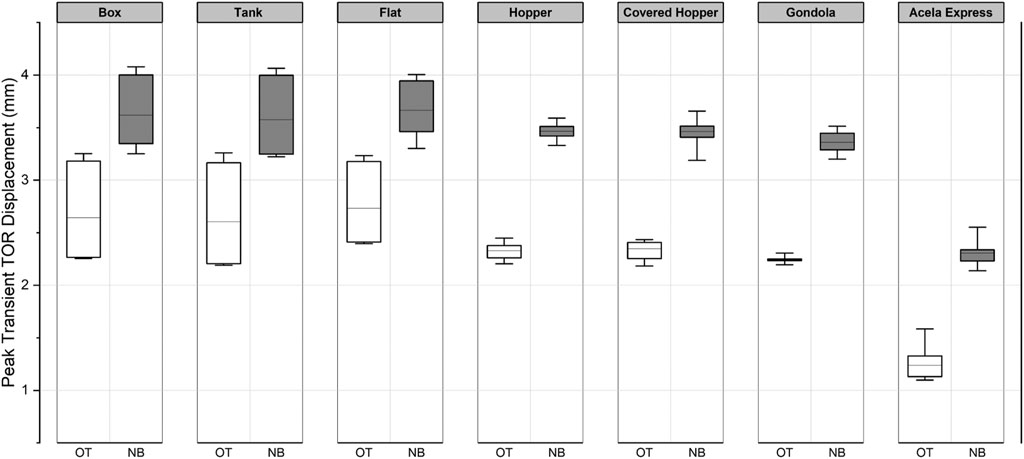
FIGURE 9. Comparison of peak rail vertical displacement with passenger train passage and freight trains passage on shared track rail corridor.

Analysis of Reaction Forces at the Rail-Tie Interface

The problem of track geometry at transition zones such as bridge approaches can gradually get worse due to compounding effects. Gaps that form undeneath at the tie-ballast interface, not only results in greater transient displacements, but also can lead to amplified dynamic loads. Reasearchers in the past have established that unsupported ties can result in significantly amplified rail-tie reaction forces (Zhu, 2011). In the current study, the sixteen ties at the NBL were modled with a gap of 1.5 mm at the tie-ballast interface. Accordingly, the next step was to compare the peak forces at the rail-tie interface under the passage of different train sets. The results have been plotted in Figure 10. It is important to note that the time step selected during analysis can have a significant effect on the model results. Selecting a time step that is too big can lead to unrealistic results. On the other hand, selecting a time step that is too small, can lead to a significant increase in the required computational effort. For the current manuscript, the authors have attempted to run the model at time steps of 0.001 and 0.0001 s. When using a time step of 0.001 s, the model run time on a standard desktop computer (3.6 GHz processor and 32 GB RAM) equals 4–5 h. However, when the time step of reduced to 0.0001 s, the model time increases significantly. For the sake of comparison, the authors used a Supercomputer available at Oklahoma State University (https://hpcc.okstate.edu/pete-supercomputer.html). Even with the use of the supercomputer, the model run time was 30 + hours. Obviously, it was not possible to perform each run of the model at such a small timestep. Therefore, results from the run at 0.001 s have been retained for this publication. Comparing with results obtained at a timestep of 0.0001 s, the authors concluded that the time step of 0.001 s is adequate for the sake of the current comparisons.

FIGURE 10

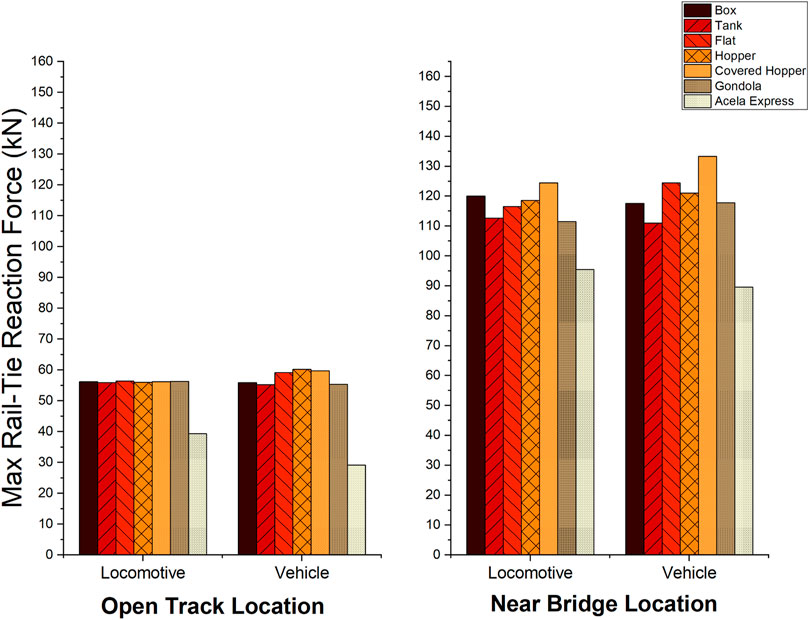
FIGURE 10. Comparison of maximum rail-tie reaction forces with freight trains and passenger trains passage on shared track rail corridor.

As seen from the figure, the maximum rail-tie reaction forces corresponding to the Open-Track Location (OTL) were significantly lower than those at the Near-Bridge Location (NBL). Moreover, no significant difference in the reaction forces were observed between different freight train types. A closer look at the individual bars would indicate that the flat car, hopper and covered hopper train sets, which are loaded with heavier cargo, induce slightly larger reaction forces at the rail-tie interface. The load magnitudes were significantly higher at the NBL for all train types. Finally, the reaction forces corresonding to the passage of an Acela Express train were significatnly lower than those corresponding to freigth trains. Once again, this clearly demonstrates that the heaver wheel loads corresponding to the freight trains play a more significant role in governing the reaction forces at the rail-tie interface, compared to the higher speed of operation for an Acela Express train.

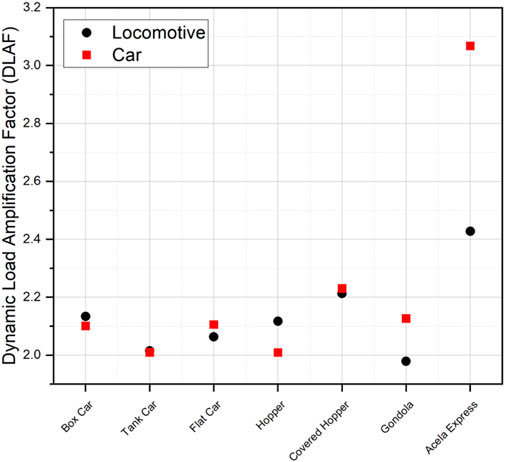
To get a better picture about the wheel load amplifications resulting from the tie gap at the NBL, a Dynamic Load Amplification Factor (DLAF) was calculated from the loads at the rail-tie interface. The DLAF is defined as below:

$\begin{array}{l}DLAF=\frac{Rail-TieInterfaceLoadattheNBL}{Rail-TieInterfaceLoadattheOTL}\\ where\\ DLAF:DynamicLoadAmplificationFactor\end{array}$

The DLAF values corresponding to different train sets have been plotted in Figure 11. It can be seen that the Acela Express train, with its significantly higher operating speed (177 km/h or 110 mph) experiences the higher DLAF values. A train set with covered hopper cars, operating at 96.6 km/h (second highest speed considered in this simulation effort) as the second highest DLAF values. Another interesting observation can be made by looking at the DLAF values for the Acela Express train. The wheel loads corresponding to the locomotive are significantly greater than those for the passenger cars. However, the DLAF values for the Acela Express locomotive are significantly lower than those for the passenger cars. Therefore, in this case, the DLAF is larger for lighter wheel loads. As the train sets considered in this modeling effort often had different weight-speed-axle spacing configurations, it is difficult to isolate the effects of individual factors without a detailed sensitivity study. Such as sensitivity study is beyond the scope of the current manuscript, and results from such comparisons will be included in future manuscripts.

FIGURE 11

FIGURE 11. Maximum rail-tie reaction forces amplification.

Analysis of Tie Accelerations in Frequency Domain

To get a thorough understanding of the dynamic behavior of different track components, it is common practice to perform frequency-domain analysis. As already discussed in this manuscript, the primary difference between the peak transient rail displacements under freight and passenger train loading was due to wheel load magnitude. However, frequency-domain analysis of the track response parameters can give a better picture of the frequency magnitudes that contribute towards vibration of the track components. Figure 12 presents the tie acceleration values in frequency domain, under the passage of an Acela Express (Figure 12A) and a freight train comprising gondola cars (Figure 12B). Note: tie acceleration numbers have been taken for the frequency domain analysis as it is the vibration of ties at railroad bridge approaches that leads to excessive movement of the ballast layer, and results in the development of gaps at the tie-ballast interface. The frequency values have been plotted along the x axis, whereas the y axis shows the power as Mean Square Amplitude (MSA). The height of the curve at a particular frequency value indicates the contribution of that frequency towards the overall vibration spectrum. Note that only values lower than 20 Hz have been presented here based on justification provided by Boler et al. (2018).

FIGURE 12

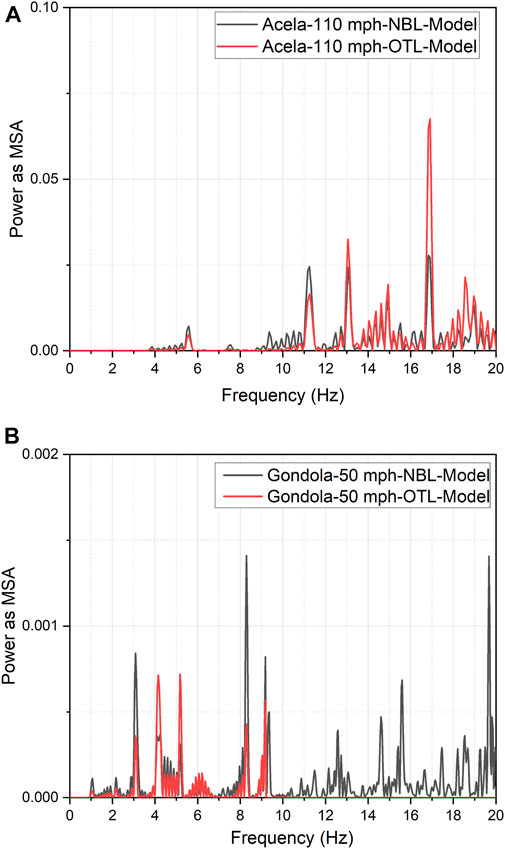
FIGURE 12. Frequency aomain analysis of tie acceleration under the passage of (A) Amtrak’s Acela Express train moving at 177 km/h; (B) A train set comprising gondola cars moving at 80.5 km/h.

From Figure 12A, it can clearly be seen that the dominant vibration frequencies under the Acela Express train were approximately: 11, 13, 15, and 17 Hz. These values remain unchanged irrespective of whether the response is recorded at the NBL or the OTL. Interestingly these value show excellent match with the field-measured data reported by Boler et al. (2018). From analysis of the field instrumentation data under the passage of an Acela Express train, Boler et al. (2018) reported the following dominant frequencies for tie acceleration: 5.5, 9, 11, 13, 15.5, and 16.5 Hz. The slight differences between the model and field data (and absence of two of the frequency numbers from the model-predicted results) can be attributed to field conditions that could not be exactly measured and replicated in the model. Once again, this establishes the newly developed train-track-bridge model as a viable tool to analyze the dynamic response of track transitions.

Close inspection of Figure 12B, on the other hand, shows a completely different picture for the track response under a freight train set comprising gondola cars. First, there is a significant difference in the dominant frequencies between the NBL and OTL. The NBL registered significant vibrations at frequencies between 14 and 20 Hz; these frequencies are absent from the OTL response. It is hypothesized that these additional vibrations are due to the presence of the gap at the tie-ballast interface. The slower operation speed for a freight train also leads to stronger contributions at lower frequencies compared to the fast-moving Acela express train. It should also be noted that the vibration responses for NBL and OTL are very similar under the Acela express loading, whereas they are significantly different under the freight train loading. Figure 13 shows the frequency domain response of tie acceleration for all six freight train types considered in this study for both the OTL as well as the NBL. As seen from the figure, the relative contributions of different vibration frequencies can be significantly different between the two locations. Although some of the differences in the peaks between different freight train types can be attributed to different speeds of operation, the axle configuration also plays a major role. Nevertheless, it is important to note that the dominant vibration frequencies between passenger trains and freight trains can be significantly different, thus making it critical to understand the detailed dynamic behavior of the bridge approaches along shared track corridors.

FIGURE 13

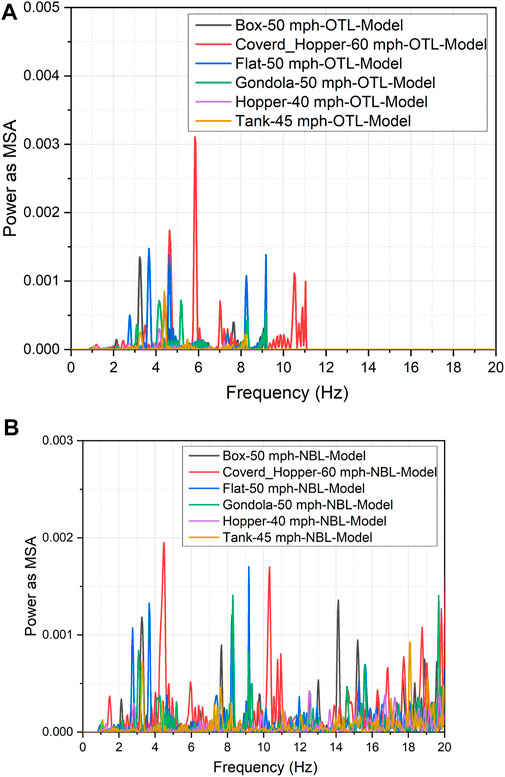
FIGURE 13. Frequency domain analysis of tie acceleration under the passage of different freight train sets: (A) OTL; (B) NBL.

Significance of Gap at the Tie-Ballast Interface

One of the primary challenges observed at track transitions on ballasted tracks involves the development of gaps at the tie-ballast interface. Lack of contact between the tie and the ballast results in “hanging tie” conditions, which in turn leads to amplified wheel loads and greater transient displacements under loading. Presence of the tie gap also leads to increased vibrations of the tie under loading, causing increased settlement of the ballast layer, and worsening of the hanging tie condition. This negative feedback loop forces railroad agencies to resurface the track frequently to mitigate the problem. Due to the heavier weight of freight trains, the transient rail vertical displacements with freight train passage are higher compared to those under passenger trains. The larger rail displacements as well as the different tie vibration frequencies under freight trains can lead to worsening of the gap problem at the tie-ballast interface.

To illustrate the effect of tie gap on track dynamic behavior, Figure 14 shows the forces at the wheel-rail interface at the OTL as well as the NBL under the passage of an Acela Express train. At the OTL, wheel-rail reaction forces fluctuate around the mean wheel load of 128 kN. Based on the field instrumentation data, the field-measured wheel loads ranged between 70 and 140 kN at the Upland Street OTL. Moreover, Zhu. (2011) and Wang and Markine (2019) also report that it is reasonable for the wheel-rail reaction forces to fluctuate around wheel load with fully supported ties. At the NBL, on the other hand, the wheel-rail reaction forces increase drastically. This effect is even more magnified in the presence of larger tie gaps. The model predicted numbers show reasonable match with those reported in the literature (Wang and Markine, 2018; Wang and Markine 2019). Wang and Markine (2019) also reported that the maximum wheel-rail reaction forces correspond to the maximum tie vertical velocity. This can further compound the detrimental effects of a gap at the tie-ballast interface. Varying load magnitudes and vibration frequencies experienced by shared track corridors make the problem even more critical. Note that the time step selected during analysis can have a significant effect on the model results. For the current manuscript, the authors have attempted to run the model at time steps of 0.001 and 0.0001 s. Comparing with results obtained at a timestep of 0.0001 s, the authors concluded that the time step of 0.001 s is adequate for the sake of the current comparisons. Therefore, results from the run at 0.001 s have been retained for this publication.

FIGURE 14

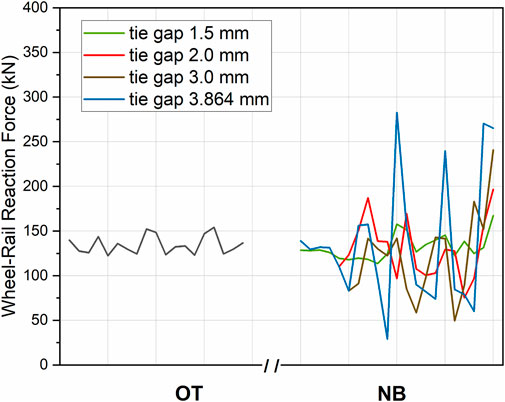
FIGURE 14. Reaction force between wheel and rail of wheel 1 with passenger train passage at the NBL when tie gap was varied between 1.5, 2, 3, and 3.864 mm.

Summary and Conclusion

This manuscript presented results from an analytical modeling effort undertaken to study the effects of combined freight and passenger train loading on track transitions along shared track corridors. A recently developed train-track-bridge model was used for this purpose, and critical track response parameters were compared under passenger as well as freight train loading. The model predictions were first verified using field instrumentation data collected under passenger train loading. Model predictions for the freight trains were verified against similar data found in the literature. Once the model was verified, dynamic track responses at a typical railroad bridge approach were studied under loading by passenger trains as well as freight trains comprising different car types.

The model-predictions clearly established that the dynamic track response can be significantly different under passenger and freight train loading. These differences can be attributed to differences in: 1) train speeds; 2) wheel load magnitudes; and 3) axle configurations. The problem becomes even more aggravated in the presence of gaps at the tie-ballast interface. Existence of gaps at the tie-ballast interface at a track transition can lead to significant amplification of the wheel load magnitudes. The magnitude of this amplification is affected by train speeds as well as axle loads. Larger wheel loads as well as different vibration frequencies under freight train loading can lead to rapid deterioration of the track geometry at track transitions.

The difference in dynamic track response under the passage of passenger vs. freight trains can be different based on whether the data for Open-Track Locations (OTLs) or Near-Bridge Locations (NBLs) are being analyzed. Frequency-domain analysis of the tie accelerations illustrated that passenger and freight trains induce different vibration frequencies in the track components. Also, the vibration frequencies for the NBL were significantly different than those for the OTL under freight train passage.

Increased magnitude of track dynamic responses under freight train passage, and the cumulative effects are likely to rapidly aggravate the tie gap magnitude, which will further compound the problem. Note that the current version of the model described in this manuscript simulates the transient behavior of the track only, and therefore, cumulative effects on the track due to repeated train loading cannot accommodated. Nevertheless, past researchers have consistently established the detrimental effects of increased axle loading on dynamic track response (Wang and Wang, 2018; Zakeri et al., 2020; Zhou et al., 2021). Therefore, passage of the freight train across a track transition with existing tie gaps can further aggravate the gap magnitude. Subsequent operation of faster passenger trains on the same track can pose increased risk of damage to the train as well as the track components, along with causing passenger discomfort.

Increased demand for a reliable passenger rail transportation network in the United States has brought the concept of shared track corridors into discussion. Although there are significant economic benefits to be realized through the deployment of shared-track corridors, careful consideration of the track dynamic response is imperative for safe operation of trains along such shared-track corridors. Track transitions, traditionally established as “problematic spots” irrespective of the track class, need even greater consideration in this regard. Implementation of high-quality track construction and maintenance strategies, that would improve the overall dynamic response of the track, is necessary to address these challenges.

Limitations of Current Study, and Future Research Plans

Although the newly developed train-track-bridge model shows significant promise in understanding dynamic track behavior under train loading, the following limitations of the model must be noted before the results are generalized.

1) In its current version, the model considers only vertical response of the train as well as the track; lateral responses are not considered.

2) The model currently does not take cumulative effects of train passage into account. In other words, the model-predicted track response under train loading is independent of the loading history.

3) Irregularities in track geometry (vertical or horizontal) have not been incorporated into the model at this stage. Accordingly, using the current version of the model, there is no way to account for the existence of “bumps” in the track profile near transition zones;

Future research plans by the authors include the development of a 3-dimensional model that will incorporate lateral response of the car-body as well as the track components. Future research plans by the authors include the development of a 3-dimensional model that will incorporate lateral response of the car-body as well as the track components. Track irregularities and the cumulative effects of train passage will also be taken into consideration in this new 3-dimensional model. Multiple parametric analyses, including parameters such as: 1) the number of consecutive hanging ties; 2) magnitude of gap at the tie-ballast interface; and 3) level of track irregularity will be carried out in future study.

Track critical speed is another major aspect that significantly influences rail vibration and track subgrade (Gao et al., 2017). According to Bian et al. (2016), track dynamic responses do not always increase with train speed. Peak track vibration intensity can be reached within a train speed range, including the critical speed, while track vibration remains small if train speed is out of the range. The research reported in the current manuscript does not consider the track critical speed. Accordingly, for all the analyses presented in the current manuscript, the train speeds have not been compared against the track critical speed. This topic will be addressed by the authors in the near future through the development of an enhanced model.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

The authors confirm contribution to the paper as follows: study conception and design: WL, DM, WH, and ET; data collection and model development: WL, WH, ET, and DM; analysis and interpretation of results: DM, WL, WH, and ET; draft manuscript preparation: WL, DM, ET, and WH. All authors reviewed the results and approved the final version of the manuscript.

Funding

Some of the computing for this project was performed at the High Performance Computing Center at Oklahoma State University (OSU) supported in part through the National Science Foundation grant OAC-1531128.

Conflict of Interest

Author WH is currently employed as a data scientist by Boston Consulting Group.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to acknowledge support by Christopher Barkan (University of Illinois), J. Riley Edwards (University of Illinois) and C. Tyler Dick (University of Illinois) for helping with freight train parameters and standards acquisition.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2021.693744/full#supplementary-material

References

Banimahd, M., Woodward, P. K., Kennedy, J., and Medero, G. M. (2012). Behavior of Train-Track Interaction in Stiffness Transitions. Proceed. Institution of Civil Engineers-Transport 165 (3), 205–214. doi:10.1680/tran.10.00030

Bian, X., Chen, Y., and Hu, T. (2008). Numerical Simulation of High-Speed Train Induced Ground Vibrations Using 2.5D Finite Element Approach. Sci. China Ser. G-phys. Mech. Astron. 51 (6), 632–650. doi:10.1007/s11433-008-0060-3

CrossRef Full Text | Google Scholar

Bian, X., Cheng, C., Jiang, J., Chen, R., and Chen, Y. (2016). Numerical Analysis of Soil Vibrations Due to Trains Moving at Critical Speed. Acta Geotech. 11, 281–294. doi:10.1007/s11440-014-0323-2

CrossRef Full Text | Google Scholar

BNSF Equipment (2020). Available at: https://www.bnsf.com/ship-with-bnsf/ways-of-shipping/equipment/ (Accessed July 15, 2020).

BNSF Locomotives (2020). Available at: https://www.bnsf.com/about-bnsf/virtual-train-tour/locomotive.html (Accessed July 15, 2020).

Boler, H., Mishra, D., Hou, W., and Tutumluer, E. (2018). Understanding Track Substructure Behavior: Field Instrumentation Data Analysis and Development of Numerical Models. Transportation Geotechnics 17, 109–121. doi:10.1016/j.trgeo.2018.10.001

CrossRef Full Text | Google Scholar

Borndörfer, R., Klug, T., Schlechte, T., Fügenschuh, A., Schang, T., and Schülldorf, H. (2016). The Freight Train Routing Problem for Congested Railway Networks with Mixed Traffic. Transportation Sci. 50 (2), 408–423. doi:10.1287/trsc.2015.0656

CrossRef Full Text | Google Scholar

Bosso, N., Gugliotta, A., and Zampieri, N. (2018). Evaluation of the Impact on Track of Different Locomotive Running Gear Architectures. Aust. J. Mech. Eng. 16 (2), 84–97. doi:10.1080/14484846.2018.1457257

CrossRef Full Text | Google Scholar

Bowness, D., Lock, A. C., Powrie, W., Priest, J. A., and Richards, D. J. (2007). Monitoring the Dynamic Displacements of Railway Track. Proc. Inst. Mech. Eng. F: J. Rail Rapid Transit 221 (1), 13–22. doi:10.1243/0954409JRRT51

CrossRef Full Text | Google Scholar

Cai, X., Zhong, Y., Hao, X., Zhang, Y., and Cui, R. (2019). Dynamic Behavior of a Polyurethane Foam Solidified Ballasted Track in a Heavy Haul Railway Tunnel. Adv. Struct. Eng. 22 (3), 751–764. doi:10.1177/1369433218799154

CrossRef Full Text | Google Scholar

Camacho, D., and Martin, U. (2015). “An Approach for the Evaluation and Implementation of Mixed Rail Operations in Harmony with Non-motorized Trails and Urban Structure: The Case of Xalapa, Mexico,” in 10th International Conference on Urban Regeneration and Sustainability. Medellin, Colombia. Medellin, 335–347. doi:10.2495/SC150301

CrossRef Full Text | Google Scholar

Cantero, D., Arvidsson, T., OBrien, E., and Karoumi, R. (2016). Train-track-bridge Modelling and Review of Parameters. Struct. Infrastructure Eng. 12 (9), 1051–1064. doi:10.1080/15732479.2015.1076854

CrossRef Full Text | Google Scholar

Caughron, B., Saat, M., and Barkan, C. (2012). “Identifying and Prioritizing Shared Rail Corridor Technical Challenges,” in Proceedings of the American Railway Engineering and Maintenance-of-Way Association Annual Conference. Chicago, IL.

Google Scholar

Chen, Z., and Fang, H. (2019). An Alternative Solution of Train-Track Dynamic Interaction. Shock and Vibration 2019, 1–14. doi:10.1155/2019/1859261

CrossRef Full Text | Google Scholar

Chrismer, S. (1990). Track Surfacing with Conventional Tamping and Stone Injection. Chicago: Association of American Railroads Research ReportAAR Technical Center. No. R-719.

Coelho, B., Hölscher, P., Priest, J., Powrie, W., and Barends, F. (2011). An Assessment of Transition Zone Performance. Proc. Inst. Mech. Eng. Part F: J. Rail Rapid Transit 225 (2), 129–139. doi:10.1177/09544097JRRT389

CrossRef Full Text | Google Scholar

Ertem, M. A., and Keskin Özcan, M. (2016). Freight Transportation Using High-Speed Train Systems. Transportation Lett. 8 (5), 250–258. doi:10.1080/19427867.2015.1122395

CrossRef Full Text | Google Scholar

FRA (2013). Higher Speed Freight Truck Market Analysis. Available at: https://railroads.dot.gov/elibrary/higher-speed-freight-truck-market-analysis (Accessed July 15, 2020).

Google Scholar

Gallou, M., Frost, M., El-Hamalawi, A., and Hardwick, C. (2020). The Application of Track Deflection Measurements Made by Video Gauge. Proc. Inst. Civil Eng. - Transport 173 (4), 245–257. doi:10.1680/jtran.18.00003

CrossRef Full Text | Google Scholar

Gao, Y., Huang, H., Ho, C. L., and Hyslip, J. P. (2017). High Speed Railway Track Dynamic Behavior Near Critical Speed. Soil Dyn. Earthquake Eng. 101, 285–294. doi:10.1016/j.soildyn.2017.08.001

CrossRef Full Text | Google Scholar

Harrod, S. (2009). Capacity Factors of a Mixed Speed Railway Network. Transportation Res. E: Logistics Transportation Rev. 45, 830–841. doi:10.1016/j.tre.2009.03.004

CrossRef Full Text | Google Scholar

Hou, W., Tutumluer, E., and Li, W. (2021) A Validated Train-Track-Bridge Model with Nonlinear Support Conditions at Bridge Approaches. Infrastructures, 6(4). 59. doi:10.3390/infrastructures6040059

CrossRef Full Text | Google Scholar

Huang, H., Gao, Y., and Stoffels, S. (2014). Fully Coupled Three-Dimensional Train-Track-Soil Model for High-Speed Rail. Transportation Res. Rec. 2448 (2448), 87–93. doi:10.3141/2448-11

CrossRef Full Text | Google Scholar

Hyslip, J. P., Li, D., and McDaniel, C. R. (2009). “Railway Bridge Transition Case Study,” in Proceedings of the 8th International Conference on the Bearing Capacity of Roads, Railways and Airfields, 2, 1341–1348. Champaign, Illinois,USA.doi:10.1201/9780203865286.ch140

CrossRef Full Text | Google Scholar

Judge, A., Ho, C., Huang, H., Hyslip, J., and Gao, Y. (2018). Field Investigation and Modeling of Track Substructure Performance under Trains Moving at Critical Speed. No. DOT/FRA/ORD-18/21.

Li, D., and Davis, D. (2005). Transition of railroad Bridge Approaches. J. Geotech. Geoenviron. Eng. 131 (11), 1392–1398. doi:10.1061/(asce)1090-0241(2005)131:11(1392)

CrossRef Full Text | Google Scholar

Li, M. (2013). Association Analysis in Loading Reinforcement Safety of Railway General Freight and Speed. Chengdu: Southwest Jiaotong University. Master’s thesis

Lin, C.-Y., and Saat, M. (2017). “Semi-Quantitative Risk Assessment of Adjacent Track Accidents on Shared-Use Rail Corridors,” in Proceedings of the 11th International Heavy Haul Association Conference. Colorado Springs.

Google Scholar

Lou, P., Yu, Z.-W., and Au, F. T. K. (2012). Rail-bridge Coupling Element of Unequal Lengths for Analysing Train-Track-Bridge Interaction Systems. Appl. Math. Model. 36 (4), 1395–1414. doi:10.1016/j.apm.2011.08.041

CrossRef Full Text | Google Scholar

Luangboriboon, N., Kaewunruen, S., and Sussman, J. (2018). “Lifecycle Cost Analysis for Operations,” in 5th International Conference on Business and Industrial Research. Bangkok, Thailand. IC BIR. doi:10.1109/ICBIR.2018.8391231

Google Scholar

Martino, D. (2011). Train-Bridge Interaction on Freight Railway Lines. Stockholm: KTH. Master's thesis.

McMichael, P., and McNaughton, A. (2003). “The Stoneblower–Delivering the Promise. Development, Testing and Operation of Anew Track Maintenance System,” in Proceedings of the 82nd annual meeting of the Transportation Research Board, Washington, DC,USA.

Google Scholar

Mishra, D., Boler, H., Tutumluer, E., Hou, W., and Hyslip, J. P. (2017). Deformation and Dynamic Load Amplification Trends at Railroad Bridge Approaches. Transportation Res. Rec. 2607 (1), 43–53. doi:10.3141/2607-07

CrossRef Full Text | Google Scholar

Mishra, D., Boler, H., Tutumluer, E., and Hyslip, J. P. (2016). “Effectiveness of Chemical Grouting and Stone Blowing as Remedial Measures to Mitigate Differential Movement at Railroad Track Transitions,” in 2016 Joint Rail Conference. American Society of Mechanical Engineers (ASME). doi:10.1115/JRC2016-5805

CrossRef Full Text | Google Scholar

Mishra, D., Tutumluer, E., Boler, H., Hyslip, J. P., and Sussmann, T. R. (2014). Railroad Track Transitions with Multidepth Deflectometers and Strain Gauges. Transportation Res. Rec. 2448 (2448), 105–114. doi:10.3141/2448-13

CrossRef Full Text | Google Scholar

Mishra, D., Tutumluer, E., Stark, T. D., Hyslip, J. P., Chrismer, S. M., and Tomas, M. (2012). Investigation of Differential Movement at railroad Bridge Approaches through Geotechnical Instrumentation. J. Zhejiang Univ. Sci. A. 13 (11), 814–824. doi:10.1631/jzus.A12ISGT7

CrossRef Full Text | Google Scholar

Nicks, J. (2009). The Bump at the End of the Railway Bridge. College Station, Texas A&M. PhD Thesis College Station.

Ramaraju, A. (2013). Operational Efficiency of Indian Railways. Int. J. Manage. 4 (3), 209–216. Available at: https://www.academia.edu/19909337/OPERATIONAL_EFFICIENCY_OF_INDIAN_RAILWAYS (Accessed June 25, 2020).

Google Scholar

Sharpe, P., Armitage, R. J., Heggie, W. G., and Rogers, A. (2002). “Innovative Design of Transition Zones. Railway Engineering 2002,” in 5th International Conference and Exhibition. London, UK.

Google Scholar

Shi, J., Chan, A. H., and Burrow, M. P. (2013). Influence of Unsupported Sleepers on the Dynamic Response of a Heavy Haul Railway Embankment. Proc. Inst. Mech. Eng. Part F: J. Rail Rapid Transit 227 (6), 657–667. doi:10.1177/0954409713495016

CrossRef Full Text | Google Scholar

Sussman, T. R., Ebersöhn, W., and Selig, E. T. (2001). Fundamental Nonlinear Track Load-Deflection Behavior for Condition Evaluation. Transportation Res. Rec. 1742 (1742), 61–67. doi:10.3141/1742-08

CrossRef Full Text | Google Scholar

Tutumluer, E., Mishra, D., Boler, H., Hyslip, J. P., and Thomas, M. (2016). “Dynamic Responses of Bridge Approach Concrete Ties after the Applications of Polyurethane Injection, Stone Blowing and Under-tie Pad Remedial Measures,” In International Crosstie and Fastening System Symposium, June 2016

Google Scholar

Tutumluer, E., Stark, T. D., Mishra, D., and Hyslip, J. P. (2012). Investigation and Mitigation of Differential Movement at Railway Transitions for US High Speed Passenger Rail and Joint Passenger/freight Corridors,” in 2012 Joint Rail Conference. JRC, 75–84. doi:10.1115/JRC2012-74074

CrossRef Full Text | Google Scholar

Varandas, J. N., Hölscher, P., and Silva, M. A. G. (2011). Dynamic Behaviour of Railway Tracks on Transitions Zones. Comput. Structures 89 (13-14), 1468–1479. doi:10.1016/j.compstruc.2011.02.013

CrossRef Full Text | Google Scholar

Wang, H., and Markine, V. (2019). Dynamic Behaviour of the Track in Transitions Zones Considering the Differential Settlement. J. Sound Vibration, 459. 114863. doi:10.1016/j.jsv.2019.114863

CrossRef Full Text | Google Scholar

Wang, H., and Markine, V. L. (2018). Methodology for the Comprehensive Analysis of Railway Transition Zones. Comput. Geotechnics 99, 64–79. doi:10.1016/j.compgeo.2018.03.001

CrossRef Full Text | Google Scholar

Wang, P., and Wang, S. (2018). A Study on the Calculation Model and Influence Factors of Rail Wear Distribution for Heavy Haul Railway. Zhendong yu Chongji/Journal of Vibration and Shock 37 (24), 72–79. doi:10.13465/j.cnki.jvs.2018.24.012

CrossRef Full Text | Google Scholar

Warg, J. (2012). Effects of Increased Traffic Volume and Speed Heterogeneity on the Capacity of a Railway with Dense Mixed Traffic. WIT Trans. Built Environ. 127, 485–497. doi:10.2495/CR120411

CrossRef Full Text | Google Scholar

Wheeler, L. N., Take, W. A., and Hoult, N. A. (2016). Measurement of Rail Deflection on Soft Subgrades Using DIC. Proc. Inst. Civil Eng. - Geotechnical Eng. 169 (5), 383–398. doi:10.1680/jgeen.15.00171

CrossRef Full Text | Google Scholar

Woodward, P. K., Thompson, D., and Banimahd, M. (2007). Geocomposite Technology: Reducing Railway Maintenance. Proc. Inst. Civil Eng. - Transport 160 (3), 109–115. doi:10.1680/tran.2007.160.3.109

CrossRef Full Text | Google Scholar

Zakeri, J. A., Fattahi, M., Nouri, M., and Janatabadi, F. (2020). Influence of Rail Pad Stiffness and Axle Loads on Dynamic Responses of Train-Track Interaction with Unsupported Sleepers. Period. Polytech. Civil Eng. 64 (2), 524–534. doi:10.3311/PPci.14826

CrossRef Full Text | Google Scholar

Zeng, Z.-P., Liu, F.-S., Lou, P., Zhao, Y.-G., and Peng, L.-M. (2016). Formulation of Three-Dimensional Equations of Motion for Train-Slab Track-Bridge Interaction System and its Application to Random Vibration Analysis. Appl. Math. Model. 40 (11-12), 5891–5929. doi:10.1016/j.apm.2016.01.020

CrossRef Full Text | Google Scholar

Zhai, W., Xia, H., Cai, C., Gao, M., Li, X., Guo, X., et al. (2013). High-speed Train-Track-Bridge Dynamic Interactions - Part I: Theoretical Model and Numerical Simulation. Int. J. Rail Transportation 1 (1-2), 3–24. doi:10.1080/23248378.2013.791498

CrossRef Full Text | Google Scholar

Zhou, X., Jing, L., and Ma, X. (2021). Dynamic Finite Element Simulation of Wheel-Rail Contact Response for the Straight Track Case. Adv. Struct. Eng. 24 (5), 856–869. doi:10.1177/1369433220971733

CrossRef Full Text | Google Scholar

Zhu, J. Y., Thompson, D. J., and Jones, C. J. C. (2011). On the Effect of Unsupported Sleepers on the Dynamic Behaviour of a Railway Track. Vehicle Syst. Dyn. 49 (9), 1389–1408. doi:10.1080/00423114.2010.524303

CrossRef Full Text | Google Scholar