Toward four-dimensional materials: The true nature of undamageable materials and bimodal self-regenerating materials

1 Introduction

The basic principles of damage mechanics were laid out in the fifities with the pioneering work of Kachanov (1958). More recent work on this topic was made by Lee et al. (1985), Voyiadjis and Kattan (1992, 2005, 2006, 2009), Sidoroff (1981), and Kattan and Voyiadjis (1993, 2001a, 2001b).

Kachanov (1958) developed the fundamental basis of continuum damage mechanics using the concept of effective stress. More recent advancements in this topic were made by Rabotnov (1969) and by others later (Ladeveze and Lemaitre, 1984; Kattan and Voyiadjis, 2001a; 2001b; Voyiadjis and Kattan, 2005; 2006; 2009; 2012a; 2012c). The value of the damage variable ranges between 0 and 1 but usually cannot exceed 0.3. In the two extreme cases of 0 and 1, the material is in the virgin state and totally damaged, respectively.

Many advancements were made in damage mechaics recently (Rice, 1971; Sidoroff, 1981; Ladeveze et al., 1982; Lee et al., 1985; Voyiadjis, 1988; Kattan and Voyiadjis, 1990; 1993; Voyiadjis and Kattan, 1990; 1992; Hansen and Schreyer, 1994; Doghri, 2000; Luccioni and Oller, 2003; Celentano et al., 2004; Lubineau and Ladeveze, 2008; Lubineau, 2010).

Basaran and coworkers develop the theory further to apply it to novel materials (Basaran and Yan, 1998; Basaran and Tang, 2002; Basaran et al., 2003; Basaran and Nie, 2004; 2007). Other theoretical developments appeared later by Sosnovkiy and Sherbakov (2016). A relation has also been made thus far linking damage mechaics to biological systems. For details about the concept of the fourth dimension, check the Appendix.

This work consists of three major sections. In Section 2 the principles of the mechanics of undamageable materials are reviewed. The section starts with a review of higher-order strain energy form. This is followed by a study of the damage variable and the proof that the undamageable material maintains a zero value for the damage variable throughout the process of deformation and damage. Finally, the elastic stiffness equations for undamageable materials are presented.

In Section 3 the principles of the mechanics of self-regenerating materials are presented. First the theoretical formulation is reviewed. This is followed by the elastic stiffness equations and how the elastic stiffness recovers in self-regenerating materials. Finally, the road to bimodal materials is explored by studying self-regenerating materials when the exponent $n$ goes to infinity. In this extreme case it is seen that the elastic stiffness disappears and appears suddenly again. Thus these materials at the extreme case are called bimodal materrials.

Finally in the Conclusion it is postulated that both undamageable materials and bimodal materials are types of four-dimensional materials. It is seen that when infinity is reached, a dimension is crossed and we enter into the world of four-dimensional materials.

The original issue in this work is the term “fourth-dimensional material” and its associated conepts. This term has never appeared before in the literature or anywhere else. However, the theories of undamageable materials and bimodal materials have been presented before by the authors and they review them here along with their associated concepts and equations (Voyiadjis and Kattan, 2013a; 2017d). The presentation here is brief and updates the previous work of the authors.

As it was stated in the conclusion this work addresses both the theory of undamageable materials and the theory of self-regenerating materials. In particular both the undamageable material and the proposed bimodal material are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into the four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodular materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.

2 Mechanics of undamageable materials

In this section the mechanics of undamageable materials are reviewed. One starts with the higher-order strain energy forms, then proceeds to a study of the damage variable in these materials, then the elastic stiffness equations are presented.

2.1 Higher-order strain energy forms

Higher order strain energy forms are studied and introduced in this section. These new forms are usually linked to non-linear stress-strain relations and are studied in detail in this work These new proposed types of materials are called here Voyiadjis-Kattan materials (Voyiadjis and Kattan, 2013a, 2013b).

One first starts with the linear relation. The linear stress-strain relation $\sigma =E\epsilon$ corresponds to the classsical strain energy form $U=\frac{1}{2}\sigma \epsilon$. Now, suppose higher powers of the stain are suggested in the expressions like the following $\frac{1}{2}\sigma {\epsilon }^2$, $\frac{1}{2}\sigma {\epsilon }^3$, What happens to the stress-strain relations in these cases? This issue is studies in the sequel.

Use will be made of the terminology by Voyiadjis-Kattan material of order $n$ to designate any non-linear elastic material that has a higher-order strain energy of the form $\frac{1}{2}\sigma {\epsilon }^n$.

One first starts with the most general from of the stress-strain equation: $\sigma =Ef\left(\epsilon \right)$, where $f\left(\epsilon \right)$ is an unknown function of the strain that is to be determined. Ther strain energy $U$ in this case is obtained using the following equation:

$U={\displaystyle \int \sigma d\epsilon }(1)$

One now illustrates the general case using the higher-order strain energy form $U=\frac{1}{2}\sigma {\epsilon }^n$. Substituting this expression for $U$ into Eq. 1, one obtains:

$\frac{1}{2}\sigma {\epsilon }^n={\displaystyle \int \sigma d\epsilon }(2)$

Next, one substitutes the general stress-strain relation $\sigma =Ef\left(\epsilon \right)$ into Eq. 2 to obtain:

$\frac{1}{2}Ef\left(\epsilon \right){\epsilon }^n=E{\displaystyle \int f\left(\epsilon \right)d\epsilon }(3)$

Simplifying the above relation, one obtains:

$f\left(\epsilon \right){\epsilon }^n=2{\displaystyle \int f\left(\epsilon \right)d\epsilon }(4)$

Differentiating both sides of the above equations lead to the following:

$f^{/}\left(\epsilon \right){\epsilon }^n+nf\left(\epsilon \right){\epsilon }^{n-1}=2f\left(\epsilon \right)(5)$

The above is the governing differential equation of the system and is solved using the MATLAB Symbolic Math Toolbox. The solution is obtained as follows:

$f\left(\epsilon \right)=\frac{1}{{\epsilon }^n}{e}^{-2/\left[\left(n-1\right){\epsilon }^{\left(n-1\right)}\right]}(6)$

Substituting the above expression into the general constitutive relation $\sigma =Ef\left(\epsilon \right)$, one obtains:

$\sigma =E\frac{1}{{\epsilon }^n}{e}^{-2/\left[\left(n-1\right){\epsilon }^{\left(n-1\right)}\right]}(7)$

The above solution is obtained after applying the initial condition that the stress is zero when the strain is zero. The above equation is a non-linear stress-strain relationship that governs the behavior of the Voyiadjis-Kattan material of order $n$.

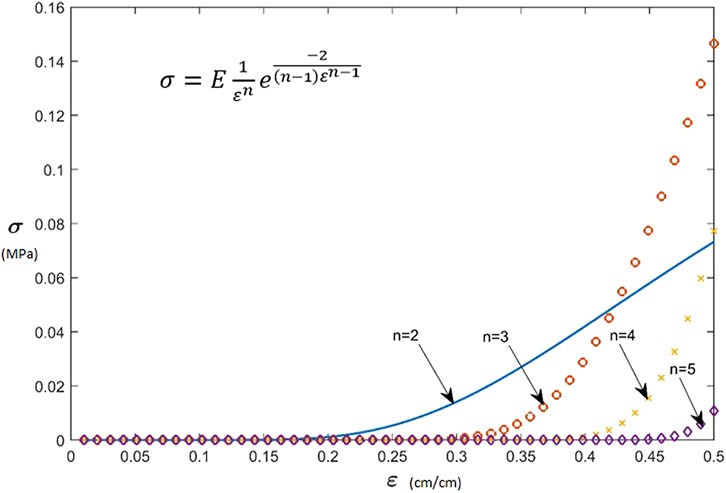
For certain selected values of n, the results are shown in Table 1. Other existing materials similar to the Voyiajdis-Kattan material are shown in Table 2. Figure 1 showns a graph of the various stress-strain relations of Table 1. Figure 1 is generated based on Eq. 7 and proper units appear on the figure.

TABLE 1

TABLE 1. The proposed higher-order strain energy forms and their corresponding stress-strain relations (constitutive equations for Voyiadjis-Kattan material of order $n$).

TABLE 2

TABLE 2. Comparison between the Voyiadjis-Kattan material of order $n$ and other non-linear elastic materials from the literature.

FIGURE 1

FIGURE 1. Valid stress-strain curves for various values of n.

2.2 The damage variable

One considers a linear elastic material with modulus of elasticity $E$. Another confiuguration of the material is considered that is fictitious with no damage with the modulus $\overline{{\rm E}}$. In order to compute the effective elastic modulus $\overline{{\rm E}}$ in this case, one may use the hypothesis of elastic energy equivalence where the elastic strain energy is assumed to be equal in both configurations (Sidoroff, 1981). Figure 2 is obtained based on Eq. 9 and Eq. 11 below. Proper units and a proper legend now appear on the figure.

FIGURE 2

FIGURE 2. Damaged and effective moduli of elasticity.

The scalar damage variable $\ell$ is defined in terms of the reduction in the elastic modulus as follows:

$\ell =\frac{\overline{E}-E}{E}(8)$

where $E$ is the elastic modulus in the damaged state while $\overline{E}$ is the effective elastic modulus (in the fictitious state) with $\overline{E}>E$ (see Figure 2). Other researchers used the new damage variable in their wrok—Celentano et al. (2004) and Voyiadjis (1988) and Voyiadjis and Kattan (2009). The expression in Eq. 8 can be re-written as follows:

$\overline{E}=E(1+\ell )(9)$

Using the hypothesis of elastic energy equivalence one assumes the complementary elastic strain energy ($\frac{{\sigma }^2}{2E}$ ) to be equal in both configurations, i.e.,

$\frac{{\sigma }^2}{2E}=\frac{{\overline{\sigma }}^2}{2\overline{E}}(10)$

Using the hypothesis of elastic energy equivalence and using Eq. 10, one obtains $\overline{\sigma }=\sqrt{\frac{\overline{E}}{E}}\sigma$. In this case, it can be easily shown that the damage variable $\ell =\frac{\overline{E}-E}{E}$ will yield the relation $\overline{\sigma }=\sigma \sqrt{1+\ell }$.

Postulating a new hypothesis of higher-order energy equivalence in the form

$\frac{1}{2}{\sigma }^2\epsilon =\frac{1}{2}{\overline{\sigma }}^2\overline{\epsilon }(\mathrm{11a})$

one consequently obtains:

$\frac{{\sigma }^3}{2E}=\frac{{\overline{\sigma }}^3}{2\overline{E}}(\mathrm{11b})$

Finally, one obtains the relation

$\overline{\sigma }=\sqrt[3]{\frac{\overline{E}}{E}}(\mathrm{11c})$

In this case, it is easily shown that using $\ell =\frac{\overline{E}-E}{E}$ will yield the relation

$\overline{\sigma }=\sigma \sqrt[3]{1+\ell }(\mathrm{11d})$

For the general case and for a general value of n, one obtains:

$\overline{\sigma }=\sqrt[n]{\frac{\overline{E}}{E}}(\mathrm{12a})$

In this case, it is easily shown that using $\ell =\frac{\overline{E}-E}{E}$ will yield the general relation

$\overline{\sigma }=\sigma \sqrt[n]{1+\ell }(\mathrm{12b})$

Several curves are plotted on the same graph paper to show the relations between the ratio of the stresses $\frac{\overline{\sigma }}{\sigma }$ and $\ell$ using Eqs 11b, 12b (see Figure 3). It is clear that for the limiting case when $n\to \infty$, the curve has a constant value at 1. Figure 3 is generated based on Eq. 12b and proper units appear on the figure.

FIGURE 3

FIGURE 3. Relation between ${\ell }_1$ and the ratio of the stresses.

One now explains the above results using the formulas derived for $\ell$. Starting with the formula $\overline{\sigma }=\sigma \sqrt[n]{1+\ell }$ of Eq. 12b which was derived in the previous paragraphs one now studies the case when $n\to \infty$. In this case, the following is obtained:

$\overline{\sigma }=\sigma \sqrt[n]{1+\ell }=\sigma {\left(1+\ell \right)}^{\frac{1}{n}}=\sigma {\left(1+\ell \right)}^{\frac{1}{\infty }}=\sigma {\left(1+\ell \right)}^0=\sigma \cdot 1=\sigma (13)$

Therefore one obtains $\overline{\sigma }=\sigma$ irrespective of the value of the damage variable $\ell$. The following is a summary of the main concepts and results in this section:

1. The Voyiadjis-Kattan material of order $n$ is a non-linear elastic material which has strain energy of the form $\frac{1}{2}\sigma {\epsilon }^n$, where $n$ is greater than 1.

2. The undamageable material is the limit of the Voyiadjis-Kattan material of order $n$ as $n$ goes to infinity.

3. The linear elastic material is a type of Voyiadjis-Kattan material of order 1.

4. In an undamageable material, the value of the stress will remain equal to zero throughout the deformation process. Also, the damage variable will be equal to zero throughout.

5. The undamageable material has zero strain energy.

6. The undamageable material has non-zero strain values. Thus, the undamageable material is a type of deformable body, not a rigid body.

7. The Voyiadjis-Kattan material of order $n$ has non-zero stress values. The range of the non-zero stress values changes depending on the value of $n$. The higher the value of $n$, the narrower the range of non-zero stress values.

2.3 Elastic stiffness equations

In this section, the precise equations governing the elastic stiffness transformation for Voyiadjis-Kattan materials are derived (Voyiadjis and Kattan, 2013a; 2012b; 2012c; 2013b; 2014). For this derivation, use is made of the classical damage variable that is defined in terms of area reduction. In this regard, the effective stress is given by:

$\overline{\sigma }=\frac{\sigma }{1-\phi }(14)$

where $\sigma$ is the Cauchy stress and $\varphi$ is the classical damage variable.

Utilizing a hypothesis of higher-order energy equivalence in the following form:

$\frac{1}{2}\overline{\sigma }{\overline{\epsilon }}^n=\frac{1}{2}\sigma {\epsilon }^n(15)$

and substituting Eq. 14 into Eq. 15, and simplifying, one obtains the following expression for the effective strain:

${\overline{\epsilon }}^n=\left(1-\phi \right){\epsilon }^n(16)$

It should be noted that the stress-strain relationship for the Voyiadjis-Kattan material of order $n$ is given by Eq. 7. Rewriting Eq. 7 in the effective fictitious configuration, one obtains:

$\overline{\sigma }=\overline{E}\frac{1}{{\overline{\epsilon }}^n}{e}^{-2/\left[\left(n-1\right){\overline{\epsilon }}^{\left(n-1\right)}\right]}(17)$

Substituting for the effective stress from Eq. 14 into Eq. 17, one obtains:

$\sigma =\left(1-\phi \right)\overline{E}\frac{1}{{\overline{\epsilon }}^n}{e}^{-2/\left[\left(n-1\right){\overline{\epsilon }}^{\left(n-1\right)}\right]}(18)$

Next, substituting for the stress from Eq. 7 into Eq. 18 and simplifying the resulting equation, one obtains:

$\frac{E}{\overline{E}}\frac{{\overline{\epsilon }}^n}{{\epsilon }^n}=\left(1-\phi \right)\frac{e^{-2/((n-1){\epsilon }^{n-1})}}{e^{-2/\left((n-1){\overline{\epsilon }}^{n-1}\right)}}(19)$

and furthermore substituting Eq. 16 into Eq. 19 and simplifying one obtains:

$\frac{E}{\overline{E}}=e^{\frac{2{\overline{\epsilon }}^{n-1}-2{\epsilon }^{n-1}}{\left(n-1\right){\overline{\epsilon }}^{n-1}{\epsilon }^{n-1}}}(20)$

The above relation can be re-written in the following form:

$\ln \frac{E}{\overline{E}}=\frac{2{\overline{\epsilon }}^{n-1}-2{\epsilon }^{n-1}}{\left(n-1\right){\overline{\epsilon }}^{n-1}{\epsilon }^{n-1}}(21)$

Again, substituting Eq. 16 into Eq. 21 and simplifying, one obtains:

$\ln \frac{E}{\overline{E}}=\frac{2\left[{\left(1-\phi \right)}^{1-1/n}-1\right]}{\left(n-1\right){\left(1-\phi \right)}^{1-1/n}{\epsilon }^{n-1}}(22)$

It should be noted that as one approaches infinity, a dimension is crossed and evolves into of four dimensions. Thus undamageable materials are a type of four-dimensional material. Their realization in the manufacturing technology will require work in the fourth dimension. Another type of four-dimensional materials will be the bimodal material of Section 3.3 below where infinity is approached and a dimension is crossed again.

3 Mechanics of self-regenerating materials

In this section the mechanics of self-regenerating materials are presented. One starts with the scalar formulation then this is followed by the recovery of elastic stiffness in these materials. Finally the extreme case when the exponent $n$ goes to infinity is studied and the science of bimodal materials evolves.

3.1 Scalar formulation

Based on the recent work of the authors (Voyiadjis and Kattan, 2017a; 2017b), one utilizes a new scalar bur non-linear damage variable ${\phi }^{\ast }$ defined as follows:

${\phi }^{\ast }=\sqrt{2\phi -{\phi }^2}(23)$

It is noted from Figure 4 that both damage variables satisfy the same boundary condition but while $\phi$ is linear, the new damage variable ${\phi }^{\ast }$ is non-linear. Figure 4 is generated based on Eq. 23 and it now appears with units and a proper legend.

FIGURE 4

FIGURE 4. Comparison between the linear and non-linear damage variables.

Based on the above equations, one can then write the following relation:

$\overline{\sigma }=\frac{\sigma }{1-{\phi }^{\ast }}=\frac{\sigma }{1-\sqrt{2\phi -{\phi }^2}}(24)$

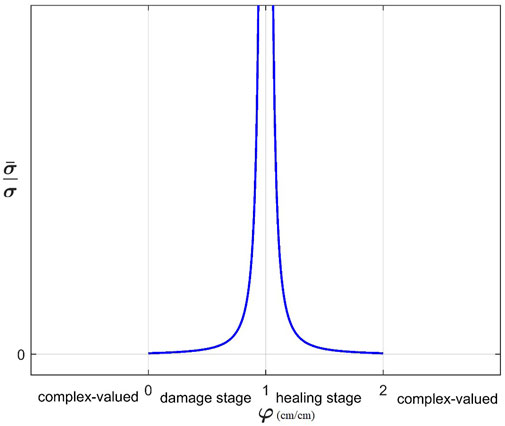
The values of the effective stress are real when the damage variable $\phi$ has values in the range $0<\phi <2$. A plot of the expression of the effective stress of Eq. 24 is shown in Figure 5 for the range of values $0<\phi <2$. The value of two for the damage variable is twice the rupture value of 1 for the damage variable in classical damage mechanics. However, the authors have no physical interpretation for the value of two for the damage variable.

FIGURE 5

FIGURE 5. Effective stress behavior for self-regenerating materials.

The following observations are made regarding Figure 5 and the associated Eq. 7: Note that Figure 5 is generated based on Eq. 24 and appears with proper units.

1. The simple expression shown in Eq. 24, along with Figure 5, clearly describes a damage stage that is followed by a healing stage.

2. The behavior observed in Figure 5 is a characteristic of soft materials, especially for biological tissue.

3. The expression given in Eq. 24 is the basis for a new hypothetical type of material to be called Self-Regenerating Material (SRGM). This material may be developed in the future when the manufacturing technology may address such challenges.

4. The constitutive equations of Self-Regenerating Materials in terms of elastic stiffness are developed in Section 4.

5. Upon loading, the virgin (undamaged) material undergoes damage in the range $0<\phi <1$. This observed behavior continues until the material ruptures and the effective stress explodes at $\phi =1$. The behavior in this primary stage is in accordance with the classical formulation of continuum damage mechanics and applies to currently existing materials.

6. Upon further loading, beyond $\phi =1$, something unexpected happens. In the range $1<\phi <2$, some form of re-integration or re-assembly of the material occurs during a stage of healing and strengthening of the elastic modulus. This secondary stage continues until all the damage is recovered and the virgin (undamaged) material restored to its original configuration at $\phi =2$.

7. The two boundary cases at $\phi =0$ and $\phi =2$ are exactly identical, and the virgin material is restored completely. In fact it is clear that the graph in Figure 5 is symmetrical around $\phi =1$. That is why it is termed bimodular as it reverts back to its initial configuaration.

3.2 Recovery of elastic stiffness

Using the hypothesis of elastic strain equivalence, substituting the elastic constitutive relations $\epsilon =\sigma /E$ and $\overline{\epsilon }=\overline{\sigma }/\overline{E}$, along with using Eq. 24, and simplifying, one obtains the following expression for the elastic stiffness transformation:

$E=\overline{E}\left(1-\sqrt{2\phi -{\phi }^2}\right)(25)$

Alternatively, using the hypothesis of elastic energy equivalence, substituting Eq. 24 into Eq. 10, and simplifying (while assuming $n=1$), one obtains the following expression for the elastic strain transformation:

$\overline{\epsilon }=\epsilon \left(1-\sqrt{2\phi -{\phi }^2}\right)(26)$

Finally one obtains the following expression for the elastic stiffness in this case:

$E=\overline{E}{\left(1-\sqrt{2\phi -{\phi }^2}\right)}^2(27)$

The relations of Eqs 27, 25 are plotted in Figure 6. The results of this section are summarized in Table 3.

FIGURE 6

FIGURE 6. Elastic stiffness degradation and recovery for the.

TABLE 3

TABLE 3. Elastic stiffness degradation and recovery equations in the scalar case.

3.3 Toward a science of bimodal materials

Further developments of the theory derived in Section 4 for self-regenerating materials are shown in this section especially with the loss of stiffness and its further recovery. These results can be extended to the hypothetical case when $n\to \infty$. In this case interesting results are obtained, and a new type of material emerges that can be constructed mathematically. This new limit material is termed a bimodal material.

3.4 Two hypotheses of damage mechanics

Both Eqs 25, 27 for the elastic stiffness transformation due to damage can be generalized using the following expression:

$E=\overline{E}{\left(1-\sqrt{2\phi -{\phi }^2}\right)}^n(28)$

where $n$ is an integer exponent with $n=1,2,3,4,\mathrm{.....}$. It is noted that Eq. 25 of the hypothesis of elastic strain equivalence is recovered using $n=1$, while Eq. 27 of the hypothesis of elastic energy equivalence is recovered using $n=2$. The material behavior described by the generalized Eq. 11 is called a self-regenerating material of order $n$ (see Figure 6). Note that Figure 6 is generated based on Eq. 28 and appears with proper units.

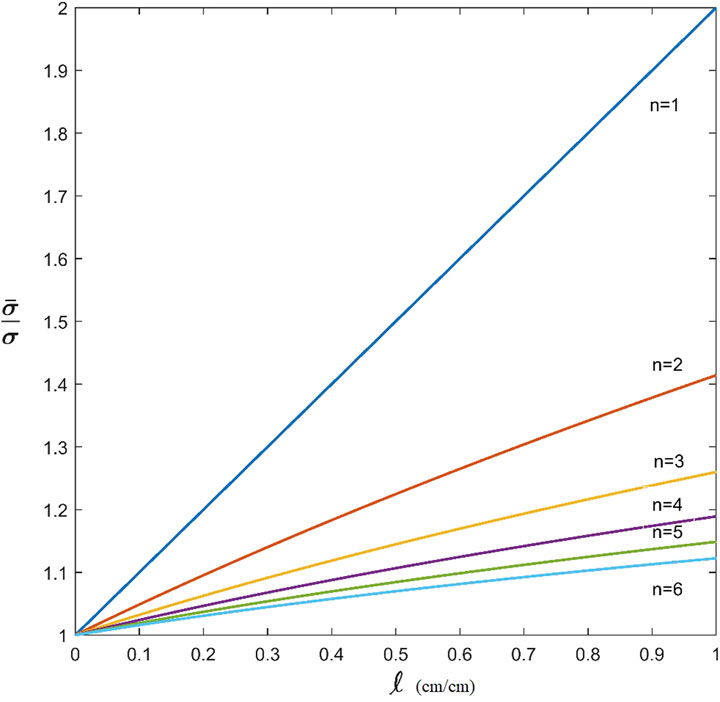
The expression of Eq. 28 is plotted in Figure 7 for several values of the integer exponent $n$. The special case when $n\to \infty$ is illustrated separately in Figure 6. The curve obtained in Figure 8 represents the limit of the sequence of curves appearing in Figure 7 as $n\to \infty$. This limiting case is very interesting as it gives rise to a new type of material that has some curious and strange characteristics. It should be noted that both the self-regenerating materials of order $n$ of Figure 7, as well as the hypothetical limit material of Figure 8 do not currently exist except as biological tissue which is explained in Section 4. Figures 7, 8 are generated based on Eq. 28 and appear with proper units.

FIGURE 7

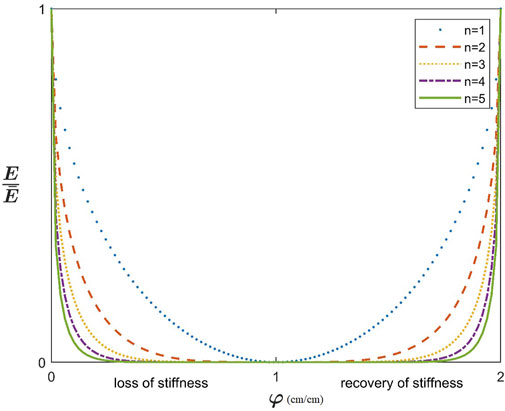
FIGURE 7. Elastic stiffness degradation and recovery for different values of the integer exponent n.

FIGURE 8

FIGURE 8. Elastic stiffness behavior as n approaches infinity.

It is very interesting and paramount to observe in this section the strange behavior of the limit material of Figure 8 which naturally exists as biological tissue with its capability to fully heal itself (see Section 4) As shown in Figure 8, the elastic stiffness of this material is zero everywhere except at the two end points, i.e., at $\phi =0$ and $\phi =2$. This means that the stiffness of the material vanishes as soon as the loading starts and remains vanished until the final load is applied at the end of the deformation and damage process. At the final point of loading, it seems that the elastic stiffness appears suddenly, behaving in a bimodal way, to its full extent. Thus, this material exhibits vital behavior in the sense that the elastic stiffness disappears due to excessive damage at the start of loading, and biologically mends itself through tissue regeneration at the end of loading. The elastic stiffness vanishes throughout the loading process between the start point and the end point. Therefore, the material exhibiting the characteristics shown in Figure 8 is termed a bimodal material. It is emphasized that the bimodal material is the limit of the self-regenerating material of order $n$ as $n\to \infty$. The bimodal material does not exist currently but the basic equations governing its behavior are formulated in this work.

The main characteristics of the postulated bimodal material are summarized below based on Eq. 28 and Figure 8:

1. The bimodal material suffers a sudden drop of its elastic stiffness from $\overline{E}$ to zero at the starting point of loading.

2. The bimodal material breaks down (or its elastic stiffness vanishes completely) upon the start of loading and remains in this vanished state until the end point of loading.

3. The bimodal material undergoes a sudden gain in elastic stiffness from zero to its maximum value of $\overline{E}$ at the ending point of loading.

4. It seems that the elastic stiffness of the bimodal material suddenly disappears upon the start of loading and suddenly re-appears upon the end of loading. This strange behavior gives this material its name.

5. The bimodal material is the limit of the self-regenerating material of order $n$ as $n\to \infty$.

It should be noted that as one reaches infinity, a dimension is crossed and enters the mathematics of four dimensions. Thus this bimodal material is another type of four-dimensional materials. The first type of four-dimensional material was the undamageable material of Section 2.

4 Conclusion

This work has been divided into two major parts, existing mainly in Sections 2, 3. In Section 2 the theory of undamageable materials is presented while in Section 3 the theory of self-regenerating materials is presented. In particular both the undamageable material of Section 2 and the bimodal material of Section 3.3 are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodal materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.

As it was stated here this work addresses both the theory of undamageable materials and the theory of self-regenerating materials. In particular both the undamageable material and the proposed bimodal material are of vital interest to the manufacturing world. Both these materials are achieved mathematically as one approaches infinity. It is noted that as infinity is approached a dimension is crossed and one evolves into the four-dimensional materials. This fact was proved mathematically in the authors’ own work on the subject (Voyiadjis and Kattan, 2017c). Thus it is seen that both undamageable materials and bimodular materials are types of four-dimensional materials. This is the true nature of these hypothetical materials.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Basaran, C., Lin, M., and Ye, H. (2003). A thermodynamic model for electrical current induced damage. Int. J. Solids Struct. 40 (26), 7315–7327. doi:10.1016/j.ijsolstr.2003.08.018

CrossRef Full Text | Google Scholar

Basaran, C., and Nie, S. (2007). A thermodynamics based damage mechanics model for particulate composites. Int. J. Solids Struct. 44, 1099–1114. doi:10.1016/j.ijsolstr.2006.06.001

CrossRef Full Text | Google Scholar

Basaran, C., and Nie, S. (2004). An irreversible thermodynamics theory for damage mechanics of solids. Int. J. Damage Mech. 13 (3), 205–223. doi:10.1177/1056789504041058

CrossRef Full Text | Google Scholar

Basaran, C., and Tang, H. (2002). Implementation of a thermodynamic framework for damage mechanics of solder interconnects in microelectronics packaging. Int. J. Damage Mech. 11 (1), 87–108. doi:10.1106/105678902022259

CrossRef Full Text | Google Scholar

Basaran, C., and Yan, C. Y. (1998). A thermodynamic framework for damage mechanics of solder joints. Trans. ASME, J. Electron. Packag. 120, 379–384. doi:10.1115/1.2792650

CrossRef Full Text | Google Scholar

Bower, A. F. (2009). Applied mechanics of solids. Boca Raton, FL, USA: CRC Press.

Google Scholar

Celentano, D. J., Tapia, P. E., and Chaboche, J-L. (2004). “Experimental and numerical characterization of damage evolution in steels,”. Editors G. Buscaglia, E. Dari, and O. Zamonsky (Argentina: Bariloche), XXIII.Mec. Comput.

Google Scholar

Doghri, I. (2000). Mechanics of deformable solids: Linear and nonlinear, analytical and computational aspects. Münster, Germany: Springer-Verlag.

Google Scholar

Hansen, N. R., and Schreyer, H. L. (1994). A thermodynamically consistent framework for theories of elastoplasticity coupled with damage. Int. J. Solids Struct. 31 (3), 359–389. doi:10.1016/0020-7683(94)90112-0

CrossRef Full Text | Google Scholar

Kachanov, L. (1958). On the creep fracture time. Izv. Akad. Nauk. USSR Otd. Tech. 8, 26–31. (in Russian).

Google Scholar

Kattan, P. I., and Voyiadjis, G. Z. (1990). A coupled theory of damage mechanics and finite strain elasto-plasticity – Part I: Damage and elastic deformations. Int. J. Eng. Sci. 28 (5), 421–435. doi:10.1016/0020-7225(90)90007-6

CrossRef Full Text | Google Scholar

Kattan, P. I., and Voyiadjis, G. Z. (1993). A plasticity-damage theory for large deformation of solids – Part II: Applications to finite simple shear. Int. J. Eng. Sci. 31 (1), 183–199. doi:10.1016/0020-7225(93)90075-6

CrossRef Full Text | Google Scholar

Kattan, P. I., and Voyiadjis, G. Z. (2001b). Damage mechanics with finite elements: Practical applications with computer tools. Munster, Germany: Springer-Verlag.

Google Scholar

Kattan, P. I., and Voyiadjis, G. Z. (2001a). Decomposition of damage tensor in continuum damage mechanics. J. Eng. Mech. ASCE 127 (9), 940–944. doi:10.1061/(asce)0733-9399(2001)127:9(940)

CrossRef Full Text | Google Scholar

Ladeveze, P., and Lemaitre, J. (1984). “Damage effective stress in quasi-unilateral conditions,” in Proceedings of the The 16th International Cogress of Theoretical and Applied Mechanics, Pennsylvania, USA, December 1984 (Denmark: Lyngby).

Google Scholar

Ladeveze, P., Poss, M., and Proslier, L. (1982). Damage and fracture of tridirectional composites. Jpn. Soc. Compos. Mater. 1, 649–658.

Google Scholar

Lee, H., Peng, K., and Wang, J. (1985). An anisotropic damage criterion for deformation instability and its application to forming limit analysis of metal plates. Eng. Fract. Mech. 21, 1031–1054. doi:10.1016/0013-7944(85)90008-6

CrossRef Full Text | Google Scholar

Lubineau, G., and Ladeveze, P. (2008). Construction of a micromechanics-based intralaminar mesomodel, and illustrations in ABAQUS/standard. Comput. Mater. Sci. 43 (1), 137–145. doi:10.1016/j.commatsci.2007.07.050

CrossRef Full Text | Google Scholar

Lubineau, G. (2010). A pyramidal modeling scheme for laminates – identification of transverse cracking. Int. J. Damage Mech. 19 (4), 499–518. doi:10.1177/1056789509102725

CrossRef Full Text | Google Scholar

Luccioni, B., and Oller, S. (2003). A directional damage model. Comput. Methods Appl. Mech. Eng. 192, 1119–1145. doi:10.1016/s0045-7825(02)00577-7

CrossRef Full Text | Google Scholar

Rabotnov, Y. (1969). “Creep rupture,” in Proceedings, Twelfth International Congress of Applied Mechanics, Berlin, Germany, October 1969. Editors M. Hetenyi, W. G. Vincenti, and Stanford (Springer-Verlag), 342–349.

CrossRef Full Text | Google Scholar

Rice, J. R. (1971). Inelastic constitutive relations for solids: An internal variable theory and its application to metal plasticity. J. Mech. Phys. Solids 19, 433–455. doi:10.1016/0022-5096(71)90010-x

CrossRef Full Text | Google Scholar

Roizen, M. (2014). The healing of injured soft tissues. https://chiro-trust.org/whiplash/healing-injured-soft-tissues-including-neck-back/.

Google Scholar

Sidoroff, F. (1981). “Description of anisotropic damage application in elasticity,” in IUTAM colloqium on physical nonlinearities in structural analysis (Berlin, Germany: Springer-Verlag), 237–244.

CrossRef Full Text | Google Scholar

Sosnovskiy, L. A., and Sherbakov, S. (2016). Mechanothermodynamic entropy and analysis of damage state of complex systems. Entropy 18, 268. doi:10.3390/e18070268

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z. (1988). Degradation of elastic modulus in elastoplastic coupling with finite strains. Int. J. Plasticity 4, 335–353. doi:10.1016/0749-6419(88)90023-x

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2009). A comparative study of damage variables in continuum damage mechanics. Int. J. Damage Mech. 18 (4), 315–340. doi:10.1177/1056789508097546

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (1990). A coupled theory of damage mechanics and finite strain elasto-plasticity – Part II: Damage and finite strain plasticity. Int. J. Eng. Sci. 28 (6), 505–524. doi:10.1016/0020-7225(90)90053-l

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2017c). A generalized hypothesis of elastic energy equivalence in continuum damage mechanics. Eng. Trans. 65 (2), 351–369.

Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2012b). A new class of damage variables in continuum damage mechanics. ASME J. Eng. Mater. Technol. 134 (2). doi:10.1115/1.4004422

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (1992). A plasticity-damage theory for large deformation of solids – Part I: Theoretical formulation. Int. J. Eng. Sci. 30 (9), 1089–1108. doi:10.1016/0020-7225(92)90059-p

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2017d). A theory of damage and self-regenerating materials. Acta Mech. 228, 4249–4268. doi:10.1007/s00707-017-1928-y

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2006). Advances in damage mechanics: Metals and metal matrix composites with an introduction to fabric tensors. Second. Amsterdam, Netherlands: Elsevier.

Google Scholar

Voyiadjis, G. Z., and Kattan, P. I., 2005, Damage mechanics, Taylor and Francis (CRC Press).Boca Raton, FL, USA.

Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2017b). Decomposition of elastic stiffness degradation in continuum damage mechanics. ASME, J. Eng. Mater. Technol. 139 (2). doi:10.1115/1.4035292

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2014). Healing and super healing in continuum damage mechanics. Int. J. Damage Mech. 23 (2), 245–260. doi:10.1177/1056789513491773

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2013a). Introduction to the mechanics and design of undamageable materials. Int. J. Damage Mech. 22 (3), 323–335. doi:10.1177/1056789512446518

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2012a). Mechanics of damage processes in series and in parallel: A conceptual framework. Acta Mech. 223 (9), 1863–1878. doi:10.1007/s00707-012-0678-0

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2017a). Mechanics of damage, healing, damageability, and integrity of materials: A conceptual framework. Int. J. Damage Mech. 26 (1), 50–103. doi:10.1177/1056789516635730

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., and Kattan, P. I. (2013b). On the theory of elastic undamageable materials. ASME J. Eng. Mater. Technol. 135 (2), 021002–021016. doi:10.1115/1.4023770

CrossRef Full Text | Google Scholar

Voyiadjis, G. Z., Yousef, M. A., and Kattan, P. I. (2012c). New tensors for anisotropic damage in continuum damage mechanics. ASME J. Eng. Mater. Technol. 134 (2). doi:10.1115/1.4006067

CrossRef Full Text | Google Scholar

Watson, T. (2003). Soft tissue healing. Touch 104, 2–9.

Google Scholar

Watson, T. (2006). Tissue repair: The current state of the art. Touch 28, 8–12.

Google Scholar