Pseudo-input signal generation for smart structural control and fast seismic response analysis

A pseudo-input signal generation method that realizes the pre-specified structural responses is proposed for fast and accurate analysis. The proposed generation method is based on the singular value decomposition and unit impulse responses in a discrete time system. When the given conditions cannot be fully satisfied, the proposed method provides approximate signals. One of the most effective uses of the proposed method is the replacement of the leading part of the original input ground motion by the generated input ground motion with the smaller time steps. This leads to an efficient and accurate analysis of the structural responses because the responses under the leading part of the original motion are accurately simulated by the generated motion. Furthermore, the proposed method is applicable not only to a single-point input ground motion but also to multiple-point input ground motions. The effectiveness of the proposed method is demonstrated through numerical examples. Moreover, it is explained that the proposed method can be applied to the characterization of pulse-like ground motions, the generation of finite impulse ground motions, and the down-sampling of input signals.

1 Introduction

With recent improvements in computer performance, optimization methods have been actively incorporated into the structural design process. From the viewpoint of seismic resistant design, time-history response analysis is essential for the accurate evaluation of the nonlinear structural responses. However, the iterative analysis of large-scale structural models for optimization requires much computational load and time. To address this, some researchers proposed reduction methods of the total number of time-steps of input ground motion data (Reyes et al., 2021; He et al., 2023; Majidi et al., 2023; Akehashi and Fujita, 2025). These studies primarily focus on the trimming and down-sampling techniques. Most of these methods do not compensate the effect of the trimmed acceleration data. In addition, these methods require advanced technique such as FFT or wavelet transform for down-sampling. In contrast, Akehashi and Fujita (2025) proposed a method that adds single impulse input as a correction process after trimming of the leading part of the ground motion and the effectiveness is demonstrated through numerical examples for a full-scale elastic-plastic high-rise building model. Although this is a simple and effective approach, it may overestimate the maximum floor acceleration of short-period structures. In addition, Akehashi and Fujita (2025) proposed an in-time domain down-sampling method, which needs just weighting sum of acceleration data. Note that all these studies deal with single-point input ground motion, and none address multiple-point input ground motions or horizontal load.

In relation to the above, methods for estimating input signals from system responses have been previously proposed (Verhaegen, 1994; Reynders, 2012; Suzuki, 2019). Verhaegen (1994) developed two identification methods for a multiple-input, multiple-output state space model perturbed input-output data. Reynders (2012) reviewed operational modal analysis approaches and related system identification methods. Suzuki (2019) proposed an iterative in time-domain inversion method based on numerical sensitivity. In general, a low-pass filter is often applied when the obserbed input signals contain noisy high-frequency components, however the selection of filter is empirical. While the time-history response analysis is a deductive procedure, the process of back-calculating input signals from system responses can be considered a type of inverse problem (Porter, 1970; Gladwell, 1986; Enokida et al., 2014; Suzuki, 2019; Akehashi and Takewaki, 2022a; Akehashi et al., 2025). In civil engineering, while this approach is often applied to structural health monitoring (Chang et al., 2003; Sohn et al., 2003; Farrar and Worden, 2007), it is rarely linked to response analysis and structural design. If input signal generation as a back-calculation procedure can be successfully incorporated into deductive processes such as time-history response analysis and structural design, this integration will lead to more efficient and accurate implementation of these processes.

In this paper, a pseudo-input signal generation method that realizes the pre-specified structural responses is proposed for fast and accurate analysis. In Section 2, the overview of the proposed method is presented. It is also explained that the proposed method enables an efficient and accurate analysis of the structural responses because the responses under the trimmed part of the original motion are accurately simulated by the generated motion. In Section 3, the input signal generation methods for single-point input ground motions and multiple-point input ground motions are derived. In addition, the relation between the phase angle of the target response, the duration and amplitude of the generated input ground motion is discussed. In Section 4, the effectiveness of the proposed method is investigated through numerical examples. In the Appendix section, the applicability of the proposed method to the characterization of pulse-like ground motions, the generation of finite impulse ground motions, and the down-sampling of input signals is explained.

2 Overview of proposed method

The proposed method is a pseudo-input signal generation method that realizes the pre-specified structural responses and is based on the singular value decomposition and unit impulse responses in a discrete time system. The proposed method can be considered a type of inverse problem (Porter, 1970; Gladwell, 1986; Enokida et al., 2014; Suzuki, 2019; Akehashi and Takewaki, 2022a; Akehashi et al., 2025) while the time-history response analysis is deductive. Although the proposed method has multiple possible uses, one of the most effective uses of the proposed method is the replacement of the leading part of the original input ground motion by the generated input ground motion with the smaller time steps (Figures 1a,b). The procedure is described below:

Step 1: Trim the weak leading part of the original input ground motion (Akehashi and Fujita, 2025).

Step 2: Select several lower eigenmodes and create corresponding SDOF models.

Step 3: Perform the time-history response analysis for the SDOF models under the trimmed leading part of the ground motion. Then record the responses at the final time step of the trimming range.

Step 4: Generate an input ground motion with shorter duration that achieves the same responses as the recorded ones.

Step 5: Connect the generated input ground motion to the remaining ground motion.

Figure 1

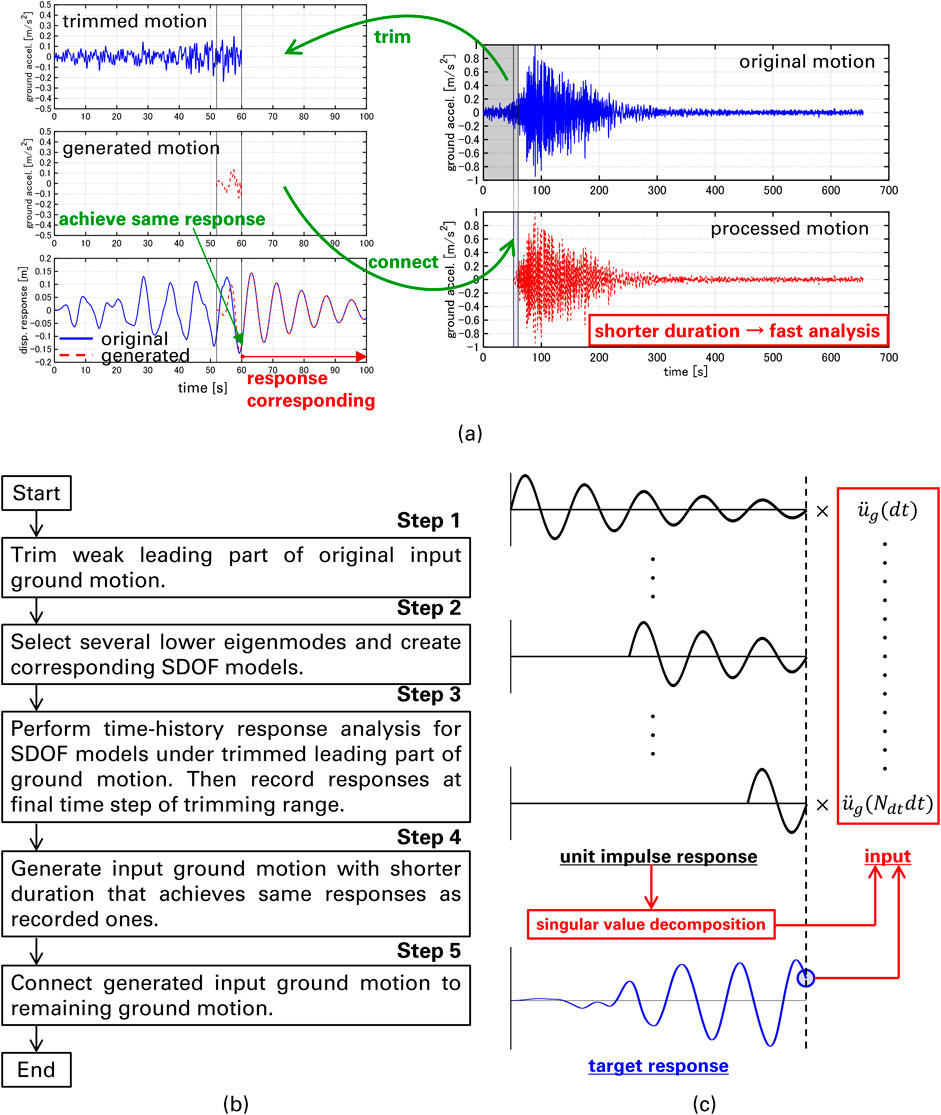
Figure 1. Overview of proposed method, (a) schematic diagram, (b) procedure, (c) input signal generation.

The proposed generation method is based on the singular value decomposition and unit impulse responses in a discrete time system. The matrix consisting of the unit impulse response at each time step is decomposed and the substitute ground motion with shorter duration is generated. The details of the generation method are explained in Section 3. The response under the original ground motion and that under the finally obtained ground motion almost correspond after the end time of the trimming range. This is because linear elastic models are treated, and the superposition principle holds for the responses under the trimmed and remaining parts of ground motion. When the maximum responses occur after the trimming end time, the maximum responses can be evaluated accurately and efficiently. Furthermore, when the trimming range is short enough, the responses of elastic-plastic models under those ground motions almost correspond since the models will remain elastic under the leading part of the ground motion. The trimming range is rationally determined through ground acceleration and velocity power, which measure intensity of a ground motion (Takewaki, 2004; Akehashi and Fujita, 2025). Note that the selection of SDOF models should be changed depending on the targeted structural model. How many eigenmodes should be chosen for generating ground motion can be determined based on the effective modal mass.

It should be noted that the proposed method can be applied to the characterization and simplification of pulse-like ground motions (Baker, 2007; He and Agrawal, 2008; Zhai et al., 2013; Yang and Zhou, 2015; Li et al., 2017), the generation of finite impulse ground motions (Kojima and Takewaki, 2015), the active response control (Symans and Constantinou, 1999; Spencer and Nagarajaiah, 2003; Symans et al., 2008), and the down-sampling of input signals (Rabiner and Gold, 1975). The applicability to these uses is explained in the Appendix section.

3 Pseudo-input signal generation method

In this section, the input signal generation methods for single-point input ground motions and multiple-point input ground motions are derived. In addition, the relation between the phase angle of the target response, the duration and amplitude of the generated input ground motion is discussed.

3.1 Single-point input ground motion

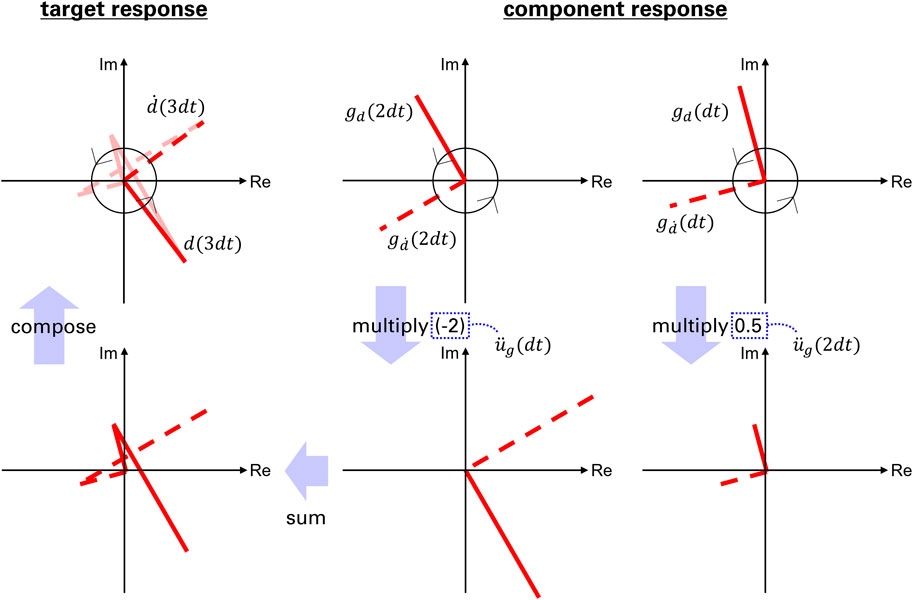
Consider $N$ sets of SDOF building models for covering a broad frequency range. Let ${\omega }_1,\dots ,{\omega }_N,h_1,\dots ,h_N$ denote the natural circular frequencies and the damping ratios, respectively. The ground acceleration ${\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right),,{\ddot{u}}_g\left(\left(N_{dt}+1\right)dt\right),\dots ,{\ddot{u}}_g\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)$ is defined in a discrete time system with time step $dt$. Note that $N_{dt}dt$ is the effective duration of the generated ground motion and ${\ddot{u}}_g\left(\left(N_{dt}+1\right)dt\right),\dots ,{\ddot{u}}_g\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)$ are set to 0. The displacement and velocity responses $d\left({\omega }_i,h_i,\left(N_{dt}+\Delta N_{dt}\right)dt\right),\dot{d}\left({\omega }_i,h_i,\left(N_{dt}+\Delta N_{dt}\right)dt\right)$ at $t=\left(N_{dt}+\Delta N_{dt}\right)dt$ are expressed as

$\left[\begin{array}{c}\mathbf{d}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\\ \dot{\mathbf{d}}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\end{array}\right]=\mathbf{G}\left[\begin{array}{c}{\ddot{u}}_g\left(dt\right)\\ ⋮\\ {\ddot{u}}_g\left(N_{dt}dt\right)\end{array}\right](1)$

where

$\mathbf{d}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)={\left[d\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}\right)dt\right),\dots ,d\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}\right)dt\right)\right]}^T(2)$

$\dot{\mathbf{d}}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)={\left[\dot{d}\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}\right)dt\right),\dots ,\dot{d}\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}\right)dt\right)\right]}^T(3)$

$\mathbf{G}=\left[\begin{array}{ccc}{g}_d\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_d\left({\omega }_1,h_1,\Delta N_{dt}dt\right)\\ ⋮& & ⋮\\ g_d\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_d\left({\omega }_N,h_N,\Delta N_{dt}dt\right)\\ g_{\dot{d}}\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{\dot{d}}\left({\omega }_1,h_1,\Delta N_{dt}dt\right)\\ ⋮& & ⋮\\ g_{\dot{d}}\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{\dot{d}}\left({\omega }_N,h_N,\Delta N_{dt}dt\right)\end{array}\right](4)$

$g_d\left(\omega ,h,\Delta t\right),g_{\dot{d}}\left(\omega ,h,\Delta t\right)$ are the displacement and velocity responses after $\Delta t$ seconds for the SDOF model with natural circular frequency $\omega$ and damping ratio $h$ under the triangular wave, which has a unit acceleration only at $t=0$ and zero acceleration at all other time (Akehashi and Takewaki, 2022b). When $\left(1/dt\right)$ is multiplied by the acceleration amplitude and the operation $dt\to 0$ is taken, the triangular wave becomes equivalent to the impulsive ground motion ${\ddot{u}}_g=\delta \left(t\right)$. $g_d\left(\omega ,h,\Delta t\right),g_{\dot{d}}\left(\omega ,h,\Delta t\right)$ can be also regarded as the unit impulse response in the discrete time system. Note that $\mathbf{G}$ is $2N\times N_{dt}$ dimensional matrix. The singular value decomposition of $\mathbf{G}$ is expressed as

$\mathbf{G}=\mathbf{U}\mathbf{\sigma }{\mathbf{V}}^T=\left[{\mathbf{u}}_1,\dots ,{\mathbf{u}}_n\right]\left[\begin{array}{ccc}{\sigma }_1& & \mathbf{O}\\ & \ddots & \\ \mathbf{O}& & {\sigma }_n\end{array}\right]{\left[{\mathbf{v}}_1,\dots ,{\mathbf{v}}_n\right]}^T(5)$

where $\mathbf{U},\mathbf{V}$ are matrices composed of the left-singular vectors and right-singular vectors, and $\mathbf{\sigma }$ is a $n\times n$ diagonal matrix composed of the singular values, and $n=\min \left\{2N,N_{dt}\right\}$. ${\mathbf{u}}_1,\dots ,{\mathbf{u}}_n$ are orthogonal to each other, and ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_n$ are also orthogonal to each other. The substitution of Equation 5 into Equation 1 and the pre-multiplication of $\mathbf{V}{\mathbf{\sigma }}^{-1}{\mathbf{U}}^T$ leads to

$\mathbf{V}{\mathbf{\sigma }}^{-1}{\mathbf{U}}^T\left[\begin{array}{c}\mathbf{d}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\\ \dot{\mathbf{d}}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\end{array}\right]=\mathbf{V}{\mathbf{V}}^T\left[\begin{array}{c}{\ddot{u}}_g\left(dt\right)\\ ⋮\\ {\ddot{u}}_g\left(N_{dt}dt\right)\end{array}\right](6)$

It should be pointed out that $\mathbf{V}{\mathbf{V}}^T={\mathbf{v}}_1{\mathbf{v}}_1^T+\dots +{\mathbf{v}}_n{\mathbf{v}}_n^T$ is the projection matrix into the subspace composed by ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_n$. Then, ${\left[{\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right)\right]}^T$ can be obtained as

$\left[\begin{array}{c}{\ddot{u}}_g\left(dt\right)\\ ⋮\\ {\ddot{u}}_g\left(N_{dt}dt\right)\end{array}\right]={\displaystyle \sum _{i=1}^n}\left[\left(1/{\sigma }_i\right)\left\{{\mathbf{u}}_i^T\left[\begin{array}{c}\mathbf{d}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\\ \dot{\mathbf{d}}\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\end{array}\right]\right\}{\mathbf{v}}_i\right]+{\ddot{\mathbf{u}}}_{g,r}(7)$

where ${\ddot{\mathbf{u}}}_{g,r}$ is a residual vector and it is composed of the orthogonal vectors to ${\mathbf{v}}_1,\dots ,{\mathbf{v}}_n$. ${\ddot{\mathbf{u}}}_{g,r}$ is usually set to $\mathbf{0}$. When $2N\le N_{dt}$, the responses under ${\left[{\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right)\right]}^T$ correspond to $\mathbf{d},\dot{\mathbf{d}}$. When $2N>N_{dt}$, ${\left[{\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right)\right]}^T$ provides an approximation.

Note that the acceleration responses $\ddot{\mathbf{d}}$ do not have to be taken into the formulation because $\ddot{\mathbf{d}}$ are derived by solving the equation of motion.

It is also noted that the proposed method works as a response-based filter, and the response and the obtained signals satisfy the equation of motion for every time step. In relation to this, the application to down-sampling of input signals is explained in Supplementary Appendix SC.

Let us consider a simple example for obtaining ${\ddot{u}}_g\left(dt\right),{\ddot{u}}_g\left(2dt\right)$ from the target responses $d\left(3dt\right),\dot{d}\left(3dt\right)$ of an undamped SDOF model. In this example, $N=1,N_{dt}=2,\Delta N_{dt}=0$. Figure 2 illustrates the target responses $d\left(3dt\right),\dot{d}\left(3dt\right)$ and $g_d\left(dt\right),g_{\dot{d}}\left(dt\right),g_d\left(2dt\right),g_{\dot{d}}\left(2dt\right)$ in complex plane. Another part of the complex conjugate solutions is not illustrated here. The red lines correspond to $d\left(3dt\right),\dot{d}\left(3dt\right),g_d\left(dt\right),g_{\dot{d}}\left(dt\right),g_d\left(2dt\right),g_{\dot{d}}\left(2dt\right)$, and the lines rotate counterclockwise with the model’s natural circular frequency. $g_d\left(dt\right),g_{\dot{d}}\left(dt\right),g_d\left(2dt\right),g_{\dot{d}}\left(2dt\right)$ and ${\ddot{u}}_g\left(dt\right),{\ddot{u}}_g\left(2dt\right)$ can be interpreted as the component responses and the weighting coefficients because the target responses satisfy $d\left(3dt\right)={\ddot{u}}_g\left(dt\right)g_d\left(2dt\right)+{\ddot{u}}_g\left(2dt\right)g_d\left(dt\right)$ and $\dot{d}\left(3dt\right)={\ddot{u}}_g\left(dt\right)g_{\dot{d}}\left(2dt\right)+{\ddot{u}}_g\left(2dt\right)g_{\dot{d}}\left(dt\right)$. In other words, when the target responses $d\left(3dt\right),\dot{d}\left(3dt\right)$ are geometrically expressed in the two-dimensional complex plane, $g_d\left(dt\right),g_{\dot{d}}\left(dt\right),g_d\left(2dt\right),g_{\dot{d}}\left(2dt\right)$ correspond to the component vectors.

Figure 2

Figure 2. In-complex plane display of target and component responses.

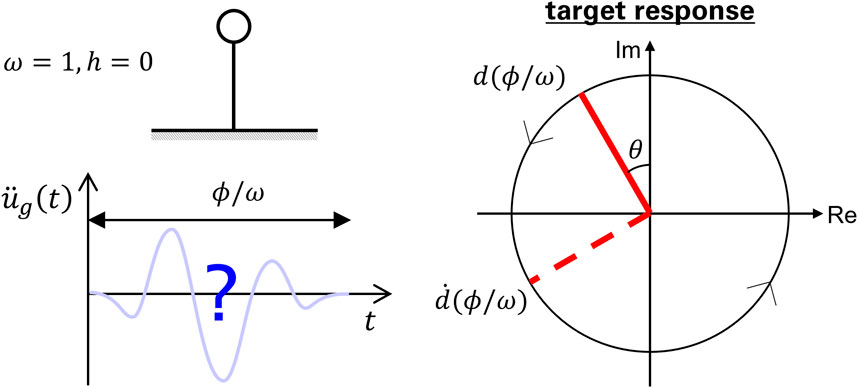
Next, the relation between the phase angle of the target response, the duration and amplitude of the generated input ground motion is investigated.

Consider an SDOF building model with mass $m$, natural circular frequency $\omega =1$ and damping ratio $h=0$. Let $\varphi /\omega ,d\left(\varphi /\omega \right)=-\sin \theta ,\dot{d}\left(\varphi /\omega \right)=-\cos \theta$ denote the duration of the generated ground motions, the target displacement and velocity responses, where $\theta$ is the phase angle of $d\left(\varphi /\omega \right)$ (Figure 3). When $\varphi =2\pi$, the duration is equal to the natural period of the SDOF model. It should be noted that the difference between the phase angles of $d\left(\varphi /\omega \right)$ and $\dot{d}\left(\varphi /\omega \right)$ is $\pi /2$ since $h=0$. It should also be pointed out that the mechanical energy at $t=\left(\varphi /\omega \right)$ is $\left(1/2\right)m$, regardless of $\theta$.

Figure 3

Figure 3. Explanation of $\varphi$ and $\theta$.

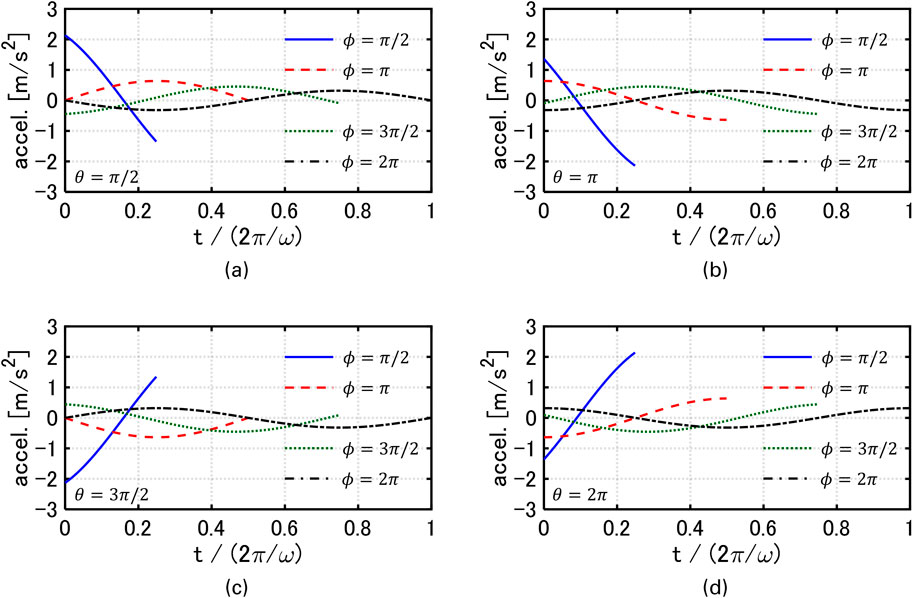
Figures 4, 5 show the relationship between $\varphi ,\theta$ and the peak ground acceleration (PGA). It can be observed that when $\theta$ is constant, PGA decreases almost monotonically as $\varphi$ increases, namely, as the duration becomes longer. On the other hand, when $\varphi$ is constant, PGA varies almost periodically with respect to $\theta$. However, in the range where $\varphi \ge \pi$, $\theta$ hardly influences PGA. From these results, to reduce PGA of the generated ground motion, it is recommended to set the duration longer than half the natural period of the building model.

Figure 4

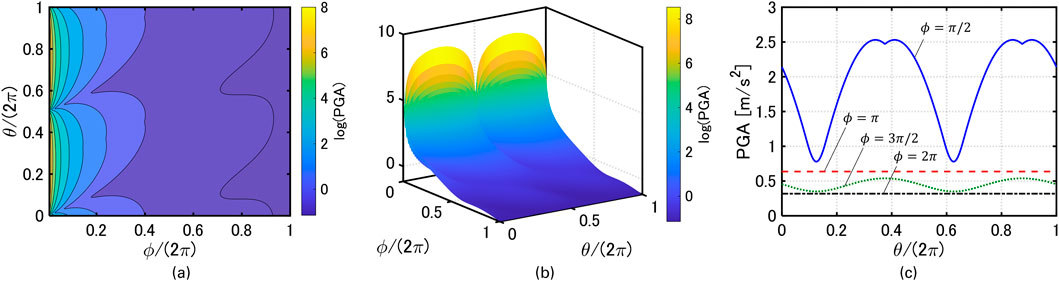
Figure 4. Relationship between $\varphi ,\theta$ and PGA (a) filled contour plot, (b) a three-dimensional surface plot, (c) Relationship between $\theta$ and PGA for $\varphi =\pi /2,\pi ,3\pi /2,2\pi$.

Figure 5

Figure 5. Generated input ground motion, (a) $\theta =\pi /2$, (b) $\theta =\pi$, (c) $\theta =3\pi /2$, (d) $\theta =2\pi$

Note that the setting $\omega =1,h=0$ is just for explanation. This discussion is extended to any combination of $\omega ,h$ to arrange $\dot{d}\left(\varphi /\omega \right)=-\omega \cos \left(\theta +{\theta }^{\prime }\right)$, where ${\theta }^{\prime }=\arctan \left(h/\sqrt{1-h^2}\right)$ and the difference between the phase angles of $d\left(\varphi /\omega \right)$ and $\dot{d}\left(\varphi /\omega \right)$ is $\pi /2+{\theta }^{\prime }$.

3.2 Multiple-point input ground motion

The formulations presented in Section 3.1 are extended to multiple-point input ground motions. Specifically, the input ground motion is expressed in terms of the ground velocity and displacement rather than the ground acceleration.

The equation of motion for an SDOF model with natural circular frequency $\omega$ and damping ratio $h$ excited by a ground motion is expressed by

${\ddot{d}}_a+2h\omega {\dot{d}}_a+{\omega }^2{d}_a=2h\omega {\dot{u}}_g+{\omega }^2{u}_g(8)$

$d_a=d+u_g(9)$

where $d_a,d,{\dot{u}}_g,u_g$ denote the absolute and relative displacement responses, and the ground velocity and displacement. Following the manner of Equation 9, Equation 1 can be rewritten as

$\left[\begin{array}{c}{\mathbf{d}}_a\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\\ {\dot{\mathbf{d}}}_a\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)\end{array}\right]={\mathbf{G}}_a\left[\begin{array}{c}{\dot{u}}_g\left(dt\right)\\ ⋮\\ {\dot{u}}_g\left(N_{dt}dt\right)\\ u_g\left(dt\right)\\ ⋮\\ u_g\left(N_{dt}dt\right)\end{array}\right]={\mathbf{G}}_a\left[\begin{array}{c}\mathbf{P}\\ \mathbf{PP}\end{array}\right]\left[\begin{array}{c}{\ddot{u}}_g\left(dt\right)\\ ⋮\\ {\ddot{u}}_g\left(N_{dt}dt\right)\end{array}\right](10)$

where

${\mathbf{d}}_a\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)={\left[d_a\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}\right)dt\right),\dots ,d_a\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}\right)dt\right)\right]}^T(11)$

${\dot{\mathbf{d}}}_a\left(\left(N_{dt}+\Delta N_{dt}\right)dt\right)={\left[{\dot{d}}_a\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}\right)dt\right),\dots ,{\dot{d}}_a\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}\right)dt\right)\right]}^T(12)$

${\mathbf{G}}_a=\left[\begin{array}{cc}\left[\begin{array}{ccc}2h_1{\omega }_1& & \mathbf{O}\\ & \ddots & \\ \mathbf{O}& & 2h_N{\omega }_N\end{array}\right]{\mathbf{G}}_{d_a}& \left[\begin{array}{ccc}{\omega }_1^2& & \mathbf{O}\\ & \ddots & \\ \mathbf{O}& & {\omega }_N^2\end{array}\right]{\mathbf{G}}_{d_a}\\ \left[\begin{array}{ccc}2h_1{\omega }_1& & \mathbf{O}\\ & \ddots & \\ \mathbf{O}& & 2h_N{\omega }_N\end{array}\right]{\mathbf{G}}_{{\dot{d}}_a}& \left[\begin{array}{ccc}{\omega }_1^2& & \mathbf{O}\\ & \ddots & \\ \mathbf{O}& & {\omega }_N^2\end{array}\right]{\mathbf{G}}_{{\dot{d}}_a}\end{array}\right](13)$

${\mathbf{G}}_{d_a}=\left[\begin{array}{ccc}{g}_{d_a}\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{d_a}\left({\omega }_1,h_1,\Delta N_{dt}dt\right)\\ ⋮& & ⋮\\ g_{d_a}\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{d_a}\left({\omega }_N,h_N,\Delta N_{dt}dt\right)\end{array}\right](14)$

${\mathbf{G}}_{{\dot{d}}_a}=\left[\begin{array}{ccc}{g}_{{\dot{d}}_a}\left({\omega }_1,h_1,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{{\dot{d}}_a}\left({\omega }_1,h_1,\Delta N_{dt}dt\right)\\ ⋮& & ⋮\\ g_{{\dot{d}}_a}\left({\omega }_N,h_N,\left(N_{dt}+\Delta N_{dt}-1\right)dt\right)& \cdots & g_{{\dot{d}}_a}\left({\omega }_N,h_N,\Delta N_{dt}dt\right)\end{array}\right](15)$

$g_{d_a}\left(\omega ,h,\Delta t\right),g_{{\dot{d}}_a}\left(\omega ,h,\Delta t\right)$ are the absolute displacement and velocity responses after $\Delta t$ seconds for the SDOF model with natural circular frequency $\omega$ and damping ratio $h$ excited by the triangular lateral load, which has a unit amplitude only at $t=0$ and zero amplitude at all other time. Note that ${\mathbf{G}}_a$ and ${\left(\mathbf{P},\mathbf{PP}\right)}^T$ are $2N\times 2N_{dt}$ and $2N_{dt}\times N_{dt}$ dimensional matrices. $\mathbf{P}$ is a $N_{dt}\times N_{dt}$ dimensional matrix which operates time integration. When the trapezoidal rule is adopted, $\mathbf{P}$ is expressed as

$\mathbf{P}=dt\left[\begin{array}{cccc}1/2& & & \mathbf{O}\\ 1& \ddots & & \\ ⋮& \ddots & \ddots & \\ 1& \cdots & 1& 1/2\end{array}\right](16)$

${\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right)$ is obtained through the singular value decomposition of ${\mathbf{G}}_a{\left(\mathbf{P},\mathbf{PP}\right)}^T$, and then ${\dot{u}}_g\left(dt\right),\dots ,{\dot{u}}_g\left(N_{dt}dt\right),$$u_g\left(dt\right),\dots ,u_g\left(N_{dt}dt\right)$ are obtained through multiplying ${\left(\mathbf{P},\mathbf{PP}\right)}^T$ to ${\ddot{u}}_g\left(dt\right),\dots ,{\ddot{u}}_g\left(N_{dt}dt\right)$.

When dealing with multiple-point input ground motions, the above procedure is repeated for each input point. Moreover, the proposed method can be extended to lateral wind loads in a similar manner.

4 Numerical examples

In this section, the effectiveness of the proposed method is investigated through numerical examples for single and multiple-point input ground motions. In addition, the applicability to a full-scale elastic-plastic high-rise building model is also investigated.

4.1 Single-point input ground motion

An artificial ground motion OS1 is treated. OS1 is often used in Japan as a representative of long-duration, long-period ground motions. The duration is about 650 s, and the trimming range is set to $0\le t\le 60$ s. Four SDOF models with natural periods $T_1,\dots ,T_4=1,2,4,8$ s, and damping ratios $h_1,\dots ,h_4=0.05$ are adopted for generating an input ground motion with a duration of 8s. Consequently, the total reduced time is 52s and it corresponds to about 10% of the duration of the original motion. The ground acceleration of the original and generated motions is shown in Figure 1.

Figures 6a,b show the displacement responses of the four SDOF models under the original and generated motions. Figure 6c shows the generated ground motion. It can be observed that the displacement responses under the generated motions closely match those under the original motion in the range of $t\ge 60$ s.

Figure 6

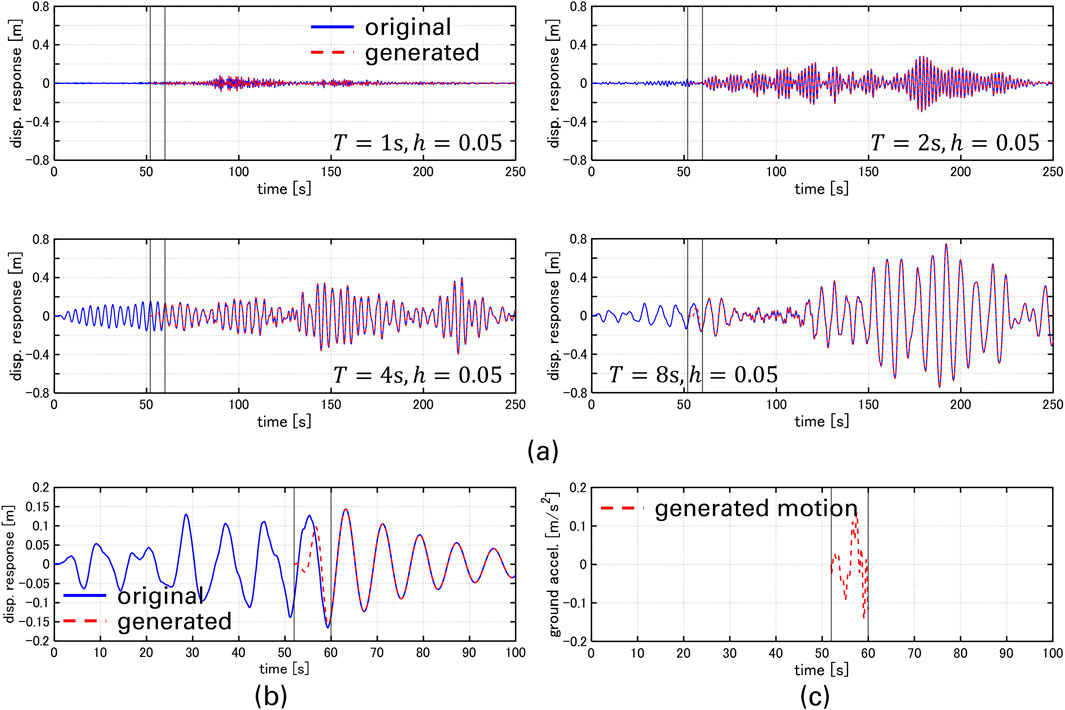
Figure 6. Time-history displacement responses under original and generated motions, (a) displacement responses, (b) enlarged view of displacement responses for SDOF with $T=8s,h=0.05$, (c) generated ground motion.

4.2 Multiple-point input ground motion

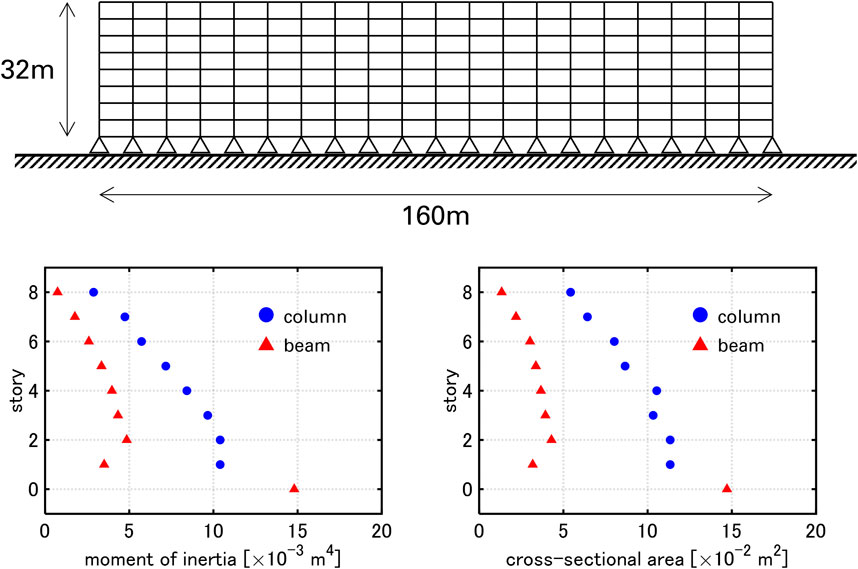
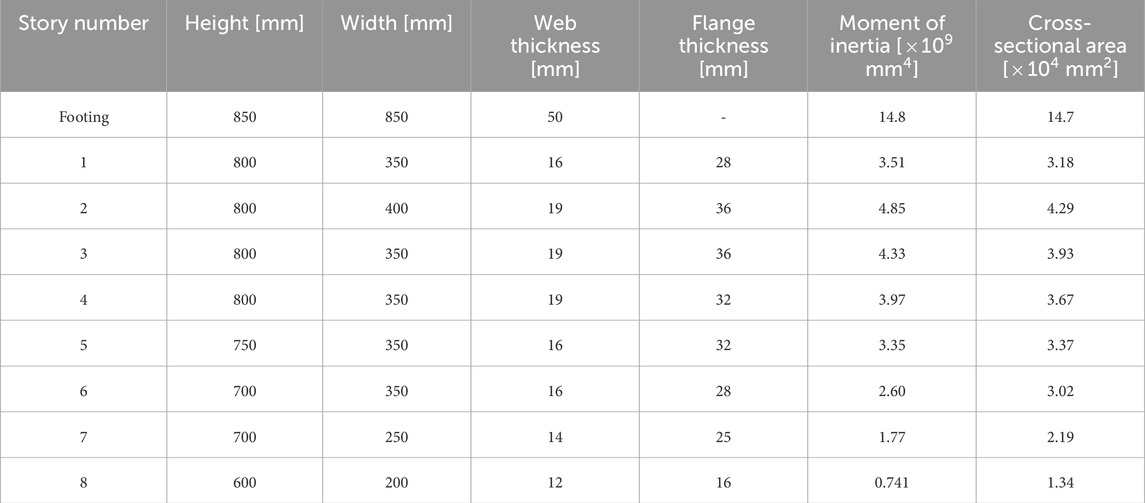
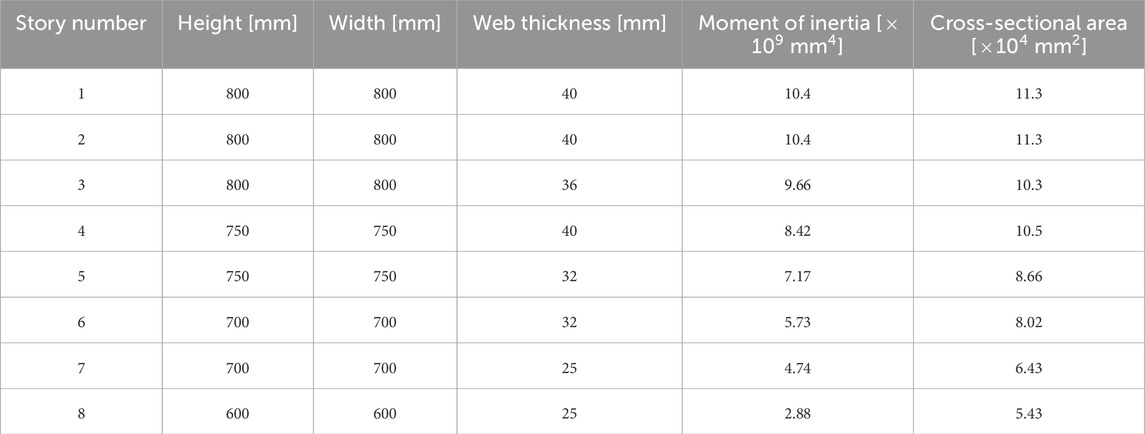
An 8-story, 20-bay planar steel moment frame is treated (Figure 7). The common story height is 4 m, and the common span length is 8 m. The total mass of each floor is 1280 t. A mass of 32 t is allocated to the top nodes of the corner columns, and a mass of 64 t is allocated to the top nodes of the interior columns. The cross-sections dimensions, moment of inertia and cross-sectional area of the frame are listed in Tables 1, 2. H-shape sections are applied to beam sections except for the footing beams, and square box sections are applied to column sections and the footing beams. The cross-sections of columns and beams are common within each story. The moment of inertia and cross-sectional area of the columns and beams are also shown in Figure 7. Young’s modulus is set to $2.05\times {10}^5$ N/mm². The damping ratio of the fundamental eigenmode is 0.02 (stiffness-proportional type). The dynamic parameters of the frame are listed in Table 3.

Figure 7

Figure 7. Planar moment-resisting frame and parameters of cross-sections.

Table 1

Table 1. Cross-sections dimensions, moment of inertia and cross-sectional area of beams.

Table 2

Table 2. Cross-sections dimensions, moment of inertia and cross-sectional area of columns.

Table 3

Table 3. Dynamic parameters of 8-story, 20-bay planar steel moment frame under assumption where horizontal displacements of nodes in same floor are identical.

The input ground motion is explained. The ground motion is specified at the engineering bedrock with S-wave velocity $V_s=400\mathrm{m}/\mathrm{s}$ based on the design response spectrum (Ministry of Construction, 2000). The signal phase of Hachinohe EW component during the 1968 Tokachi-oki Earthquake is employed. Note that Hachinohe EW component contains low-frequency components. The ground consists of a single sandy soil layer with S-wave velocity $V_s=200\mathrm{m}/\mathrm{s}$, density of 1.73 g/cm³, and thickness of 30 m. The nonlinear characteristics of the soil layer is considered by the equivalent linearization technique (Schnabel et al., 1972; Koyamada et al., 2005). The time phase difference of ground motion inputs at both ends of the frame is set to 0.5s.

The duration of the ground motion at each input point is 120 s, and the time-history response analysis is performed in the range of $0\le t\le 120.5\mathrm{s}$. The trimming range is set to $0\le t\le 17\mathrm{s}$ and the duration of the generated motion is 2 s. Consequently, the total reduced time is 15s, corresponding to about 12.5% of the duration of the original motion. Note that the time range of trimming is common for all the input points. Figure 8 shows the ground displacement and the displacement, velocity, and acceleration response spectrums $S_D,S_V,S_A$.

Figure 8

Figure 8. Input ground motion and response spectrums.

When the horizontal displacements of nodes in the same floor are assumed to be identical, the 1-6 th natural circular frequencies and damping ratios are $\left[{\omega }_1,\dots ,{\omega }_6\right]=\left[6.01,16.0,28.6,44.6,64.5,87.1\right]$ and $\left[h_1,\dots ,h_6\right]=\left(0.02/{\omega }_1\right)\times \left[{\omega }_1,\dots ,{\omega }_6\right]$. These parameters are adopted to create SDOF models, which are then used to generate ground motions. It should be pointed out that this assumption is not considered in the time-history response analysis. Note that the sum of 1-6th effective modal mass is larger than 99% of the total mass of the frame.

Figure 9 shows the generated ground displacement, the 5th floor and top acceleration responses of the moment frame under the original and generated motions. The reference nodes are also illustrated. It can be observed that the displacement responses under the generated motions closely match those under the original motion in the range of $t\ge 17$ s.

Figure 9

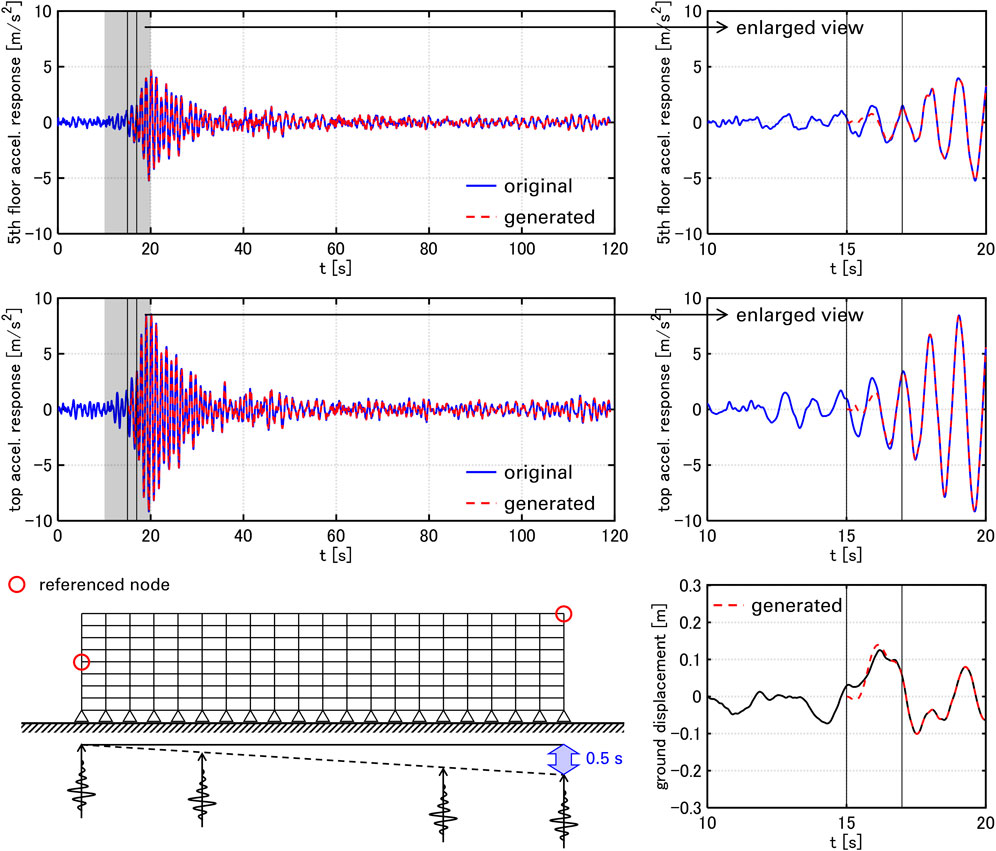
Figure 9. Top and 5th floor acceleration responses under original and generated ground motions and generated ground displacement.

4.3 Full-scale elastic-plastic high-rise building

A full-scale 35-story elastic-plastic building model with a strong back core frame is treated to compare the proposed method with the previous paper (Akehashi and Fujita, 2025). The building model and the ground motion OS1 treated in the previous paper are also used in this paper. The main frame is a reinforced-concrete moment-resisting frame and the subframe is a reinforced-concrete shear-wall structure (Figure 10a). The details of the model are explained in the previous papers (Kawai et al., 2021; Akehashi and Fujita, 2025). PGA of OS1 is set to 2 m/s². The ranges where the ground acceleration power is below 1% or exceeds 96% of the total are trimmed. Although the previous paper adds single impulse input as a correction process after trimming of the leading part of the ground motion, a generated ground motion whose duration is equal to the fundamental natural period is connected in this paper. The natural eigenmodes are selected in descending order of the effective modal mass until the cumulative mass is larger than 90% of the total mass of the frame. Table 4 shows the natural circular frequencies, the damping ratios and the effective modal mass ratios for x-directional ground motion.

Figure 10

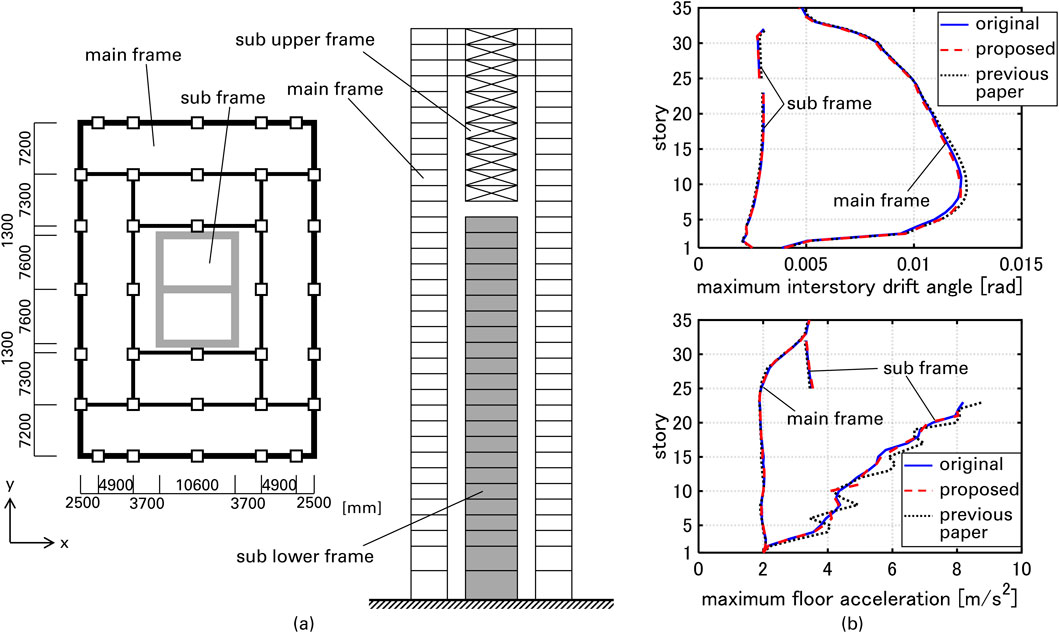
Figure 10. Overview of building model and maximum interstory drift angle and maximum floor accelerations under OS1, (a) plan and section, (b) maximum interstory drift angle and maximum floor accelerations.

Table 4

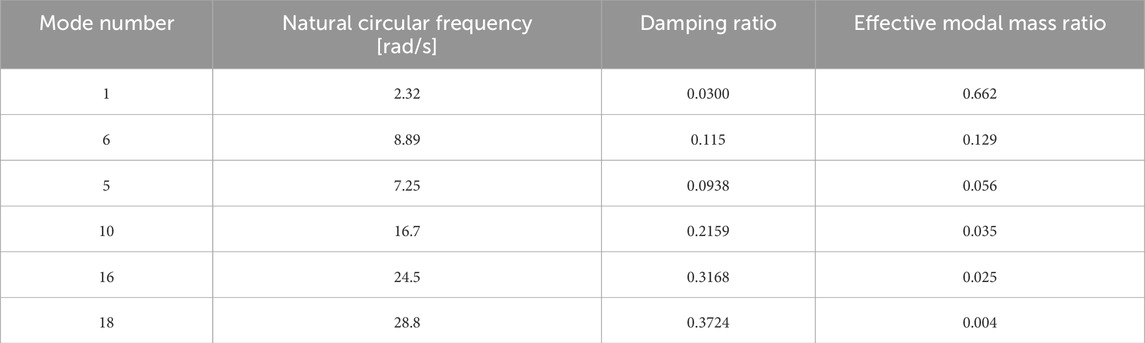
Table 4. Dynamic parameters of full-scale 35-story building model (in descending order of the effective modal mass).

Figure 10b presents the maximum interstory drift angle and the maximum floor accelerations. It can be observed that the maximum interstory drift angle and the maximum floor accelerations evaluated by the proposed method show better correspondence with the results for the original motion compared to those evaluated by the previous method. It should be pointed out that the generated ground motion accurately evaluates the higher-mode responses, although the impulse input at the initial time step strongly excites the higher-mode response. Note that it took 75484 s for the analysis under the original motion, and it took 23623, 24084 s for the evaluation by the previous and proposed method.

5 Conclusion

In this paper, a pseudo-input signal generation method that realizes the pre-specified structural responses was proposed. The main conclusions can be summarized as follows.

(1) The proposed input signal generation method is based on the singular value decomposition and unit impulse responses in a discrete time system. The proposed method is applicable not only to a single-point input ground motion but also to multiple-point input ground motions.

(2) One of the most effective uses of the proposed method is the replacement of the leading part of the original input ground motion by the generated input ground motion with the smaller time steps. This leads to an efficient and accurate analysis of the structural responses under not only to a single-point input ground motion but also to multiple-point input ground motions.

(3) The amplitude of the generated signal depends on both the duration of the generated signal and the phase angle of the target response. The amplitude decreases almost monotonically as the duration becomes longer. Additionally, the amplitude varies almost periodically with respect to the phase angle of the target response. However, the phase angle hardly influences the amplitudes when the duration is sufficiently long.

(4) It was demonstrated through the numerical examples for SDOF models, a planar moment-resisting frame, and a full-sacle elastic-plastic high-rise building model under multiple input ground motions that the proposed method accurately and efficiently evaluates the structural responses.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

HA: Conceptualization, Writing – original draft, Supervision, Methodology, Visualization, Writing – review and editing, Validation. BW: Methodology, Supervision, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that no financial support was received for the research and/or publication of this article.

Conflict of interest

Authors HA and BW were employed by Takenaka Corporation.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fbuil.2025.1598751/full#supplementary-material

References

Akehashi, H., and Fujita, N. (2025). A new processing method of ground acceleration data for fast and accurate evaluation of maximum seismic structural response. Jpn. Archit. Rev. 8 (1), e70008. doi:10.1002/2475-8876.70008

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022a). Inverse optimal damper placement via shear model for elastic–plastic moment-resisting frames under large-amplitude ground motions. Eng. Struct. 250, 113457. doi:10.1016/j.engstruct.2021.113457

CrossRef Full Text | Google Scholar

Akehashi, H., and Takewaki, I. (2022b). Bounding of earthquake response via critical double impulse for efficient optimal design of viscous dampers for elastic-plastic moment frames. Jpn. Archit. Rev. 5 (2), 131–149. doi:10.1002/2475-8876.12262

CrossRef Full Text | Google Scholar

Akehashi, H., Watai, K., and Kamoshita, N. (2025). Inverse eigenmode modeling and multi-scale seismic analysis of irregular frame structure by shear spring-multi floor mass system. Struct. Des. Tall. Spec. Build. 34 (2), e2215. doi:10.1002/tal.2215

CrossRef Full Text | Google Scholar

Baker, J. W. (2007). Quantitative classification of near-fault ground motions using wavelet analysis. Bullet. Seism. Soc. Am. 97 (5), 1486–1501. doi:10.1785/0120060255

CrossRef Full Text | Google Scholar

Chang, P. C., Flatau, A., and Liu, S. C. (2003). Review paper: health monitoring of civil infrastructure. Struct. Health Monit. 2 (3), 257–267. doi:10.1177/1475921703036169

CrossRef Full Text | Google Scholar

Chioccarelli, E., and Iervolino, I. (2010). Near-source seismic demand and pulse-like records: a discussion for L’Aquila earthquake. Earthq. Eng. Struct. Dyn. 39 (9), 1039–1062. doi:10.1002/eqe.987

CrossRef Full Text | Google Scholar

Enokida, R., Takewaki, I., and Stoten, D. (2014). A nonlinear signal-based control method and its applications to input identification for nonlinear SIMO problems. J. Sound. Vibr. 333 (24), 6607–6622. doi:10.1016/j.jsv.2014.07.014

CrossRef Full Text | Google Scholar

Farrar, C. R., and Worden, K. (2007). An introduction to structural health monitoring. Philosophical Trans. R. Soc. A Math. Phys. Eng. Sci. 365 (1851), 303–315. doi:10.1098/rsta.2006.1928

PubMed Abstract | CrossRef Full Text | Google Scholar

Gladwell, G. M. (1986). Inverse problems in vibration. Appl. Mech. Rev. 39, 1013–1018. doi:10.1115/1.3149517

CrossRef Full Text | Google Scholar

He, W. L., and Agrawal, A. K. (2008). Analytical model of ground motion pulses for the design and assessment of seismic protective systems. J. Struct. Eng. 134 (7), 1177–1188. doi:10.1061/(asce)0733-9445(2008)134:7(1177)

CrossRef Full Text | Google Scholar

He, Y., Li, S., Wei, Y., and Xie, L. (2023). A novel strong ground motion duration to reduce computation time of structural time history analysis. Soil Dyn. Earthq. Eng. 164, 107641. doi:10.1016/j.soildyn.2022.107641

CrossRef Full Text | Google Scholar

Kawai, A., Maeda, T., and Takewaki, I. (2021). Critical response of high-rise buildings with deformation-concentration seismic control system under double and multi impulses representing pulse-type and long-duration ground motions. Front. Built Environ. 7, 649224. doi:10.3389/fbuil.2021.649224

CrossRef Full Text | Google Scholar

Kojima, K., and Takewaki, I. (2015). Critical earthquake response of elastic–plastic structures under near-fault ground motions (Part 1: fling-step input). Front. Built Environ. 1, 12. doi:10.3389/fbuil.2015.00012

CrossRef Full Text | Google Scholar

Koyamada, K., Miyamoto, Y., and Miura, K. (2005). “Nonlinear property for surface strata from natural soil samples,” in Proc. Japan national conf. Geotech. Eng., volume JGS38, session ID 1039, 2077–2078.

Google Scholar

Li, S., Zhang, F., Wang, J. Q., Alam, M. S., and Zhang, J. (2017). Effects of near-fault motions and artificial pulse-type ground motions on super-span cable-stayed bridge systems. J. Bridge Eng. 22 (3), 04016128. doi:10.1061/(asce)be.1943-5592.0001008

CrossRef Full Text | Google Scholar

Majidi, N., Riahi, H. T., and Zandi, S. M. (2023). Evaluating the performance of different mother wavelet functions for down-sampling of earthquake records. Structures 51, 846–879. doi:10.1016/j.istruc.2023.03.032

CrossRef Full Text | Google Scholar

Mazza, F., and Labernarda, R. (2021). “Concave surface base-isolation system against seismic pounding of irregular adjacent buildings,” in 14th world congress in computational mechanics (WCCM), ECCOMAS congress 2020.

Google Scholar

Mazza, F., and Labernarda, R. (2022a). Internal pounding between structural parts of seismically isolated buildings. J. Earthq. Eng. 26 (10), 5175–5203. doi:10.1080/13632469.2020.1866122

CrossRef Full Text | Google Scholar

Mazza, F., and Labernarda, R. (2022b). Effects of near-fault acceleration and non-acceleration pulses on pounding between in-plan irregular fixed-base and base-isolated buildings. Struct. Contr. Health Monit. 29 (9), e2992. doi:10.1002/stc.2992

CrossRef Full Text | Google Scholar

Ministry of Construction (2000). Notification No. 1461, Gazette (Extra No. 106).

Google Scholar

Pant, D. R., and Wijeyewickrema, A. C. (2013). Influence of near-fault ground motions on the response of base-isolated reinforced concrete buildings considering seismic pounding. Adv. Struct. Eng. 16 (12), 1973–1988. doi:10.1260/1369-4332.16.12.1973

CrossRef Full Text | Google Scholar

Porter, B. (1970). Synthesis of linear lumped-parameter vibrating systems by an inverse Holzer technique. J. Mech. Eng. Sci. 12 (1), 17–19. doi:10.1243/jmes_jour_1970_012_005_02

CrossRef Full Text | Google Scholar

Rabiner, L. R., and Gold, B. (1975). Theory and application of digital signal processing. Englewood Cliffs: Prentice-Hall.

Google Scholar

Reyes, J. C., Avila, W. A., Kalkan, E., and Sierra, A. (2021). Reducing processing time of nonlinear analysis of symmetric-plan buildings. J. Struct. Eng. 147 (6), 04021073. doi:10.1061/(asce)st.1943-541x.0003000

CrossRef Full Text | Google Scholar

Reynders, E. (2012). System identification methods for (operational) modal analysis: review and comparison. Arch. Comput. Meth. Eng. 19, 51–124. doi:10.1007/s11831-012-9069-x

CrossRef Full Text | Google Scholar

Schnabel, P. B., Lysmer, J., and Seed, H. B. (1972). “SHAKE: a computer program for earthquake response analysis of horizontally layered sites,” in A computer program distributed by NISEE/Computer Applications. Berkeley.

Google Scholar

Sohn, H., Farrar, C. R., Hemez, F. M., Shunk, D. D., Stinemates, D. W., Nadler, B. R., et al. (2003). A review of structural health monitoring literature: 1996–2001, 1. USA: Los Alamos National Laboratory, 16.

Google Scholar

Spencer, Jr. B. F., and Nagarajaiah, S. (2003). State of the art of structural control. J. Struct. Eng. 129 (7), 845–856. doi:10.1061/(asce)0733-9445(2003)129:7(845)

CrossRef Full Text | Google Scholar

Suzuki, T. (2019). Input motion inversion in elastoplastic soil model using modal iterative error correction method. Jpn. Archit. Rev. 2, 340–348. doi:10.1002/2475-8876.12092

CrossRef Full Text | Google Scholar

Symans, M. D., Charney, F. A., Whittaker, A. S., Constantinou, M. C., Kircher, C. A., Johnson, M. W., et al. (2008). Energy dissipation systems for seismic applications: current practice and recent developments. J. Struct. Eng. 134 (1), 3–21. doi:10.1061/(asce)0733-9445(2008)134:1(3)

CrossRef Full Text | Google Scholar

Symans, M. D., and Constantinou, M. C. (1999). Semi-active control systems for seismic protection of structures: a state-of-the-art review. Eng. Struct. 21 (6), 469–487. doi:10.1016/s0141-0296(97)00225-3

CrossRef Full Text | Google Scholar

Takewaki, I. (2004). Bound of earthquake input energy. J. Struct. Eng. 130 (9), 1289–1297. doi:10.1061/(asce)0733-9445(2004)130:9(1289)

CrossRef Full Text | Google Scholar

Verhaegen, M. (1994). Identification of the deterministic part of MIMO state space models given in innovations form from input-output data. Automatica 30 (1), 61–74. doi:10.1016/0005-1098(94)90229-1

CrossRef Full Text | Google Scholar

Yang, D., and Zhou, J. (2015). A stochastic model and synthesis for near-fault impulsive ground motions. Earthq. Eng. Struct. Dyn. 44 (2), 243–264. doi:10.1002/eqe.2468

CrossRef Full Text | Google Scholar

Zhai, C., Chang, Z., Li, S., Chen, Z., and Xie, L. (2013). Quantitative identification of near-fault pulse-like ground motions based on energy. Bullet. Seism. Soc. Am. 103 (5), 2591–2603. doi:10.1785/0120120320

CrossRef Full Text | Google Scholar